线性代数样卷
线性代数试题及详细答案

线性代数试题及详细答案线性代数试题及详细答案————————————————————————————————作者:————————————————————————————————日期:线性代数(试卷一)一、填空题(本题总计20分,每小题2分) 1. 排列7623451的逆序数是_______。
2. 若122211211=a a a a ,则=16030322211211a a a a 3. 已知n 阶矩阵A 、B 和C 满足E ABC =,其中E 为n 阶单位矩阵,则CAB =-1。
4. 若A 为n m ?矩阵,则非齐次线性方程组AX b =有唯一解的充分要条件是_________5. 设A 为86?的矩阵,已知它的秩为4,则以A 为系数矩阵的齐次线性方程组的解空间维数为__2___________。
6. 设A 为三阶可逆阵,=-1230120011A,则=*A 7.若A 为n m ?矩阵,则齐次线性方程组0Ax =有非零解的充分必要条件是8.已知五阶行列式1234532011111112140354321=D ,则=++++4544434241A A A A A 9. 向量α=(2,1,0,2)T-的模(范数)______________。
10.若()Tk 11=α与()T121-=β正交,则=k二、选择题(本题总计10分,每小题2分)1. 向量组r ααα,,,21Λ线性相关且秩为s ,则(D) A.s r = B.s r ≤C.r s ≤ D.r s <2. 若A 为三阶方阵,且043,02,02=-=+=+E A E A E A ,则=A(A)A.8 B.8-C.34 D.34-3.设向量组A 能由向量组B 线性表示,则( d )A.)()(A R B R ≤ B.)()(A R B R <C.)()(A R B R =D.)()(A R B R ≥4. 设n 阶矩阵A 的行列式等于D ,则()*kA 等于_____。
线性代数单元测试卷(含答案)

线性代数单元测试卷(含答案)一、选择题(每题2分,共20分)1. 在线性代数中,什么是矩阵的秩?A. 矩阵的行数B. 矩阵的列数C. 矩阵的非零行数D. 矩阵的最大线性无关行数正确答案:D2. 下列哪个不是矩阵的运算?A. 矩阵的加法B. 矩阵的减法C. 矩阵的除法D. 矩阵的乘法正确答案:C3. 矩阵的转置满足下列哪个性质?A. (A^T)^T = AB. (AB)^T = B^T * A^TC. (A + B)^T = A^T + B^TD. (AB)^T = A^T + B^T正确答案:B4. 什么是向量的线性组合?A. 向量相加B. 向量相减C. 向量乘以常数后相加D. 向量与常数相乘正确答案:C5. 下列哪组向量线性无关?A. (1, 0)B. (0, 1)C. (1, 1)D. (1, -1)正确答案:C二、填空题(每题3分,共30分)1. 给定矩阵A = [[1, 2], [3, 4]],求A的逆矩阵。
正确答案:[[-2, 1], [1.5, -0.5]]2. 给定矩阵B = [[2, 4], [1, 3]],求B的特征值。
正确答案:[5, 0]3. 给定向量v = (1, 2, 3),求v的范数。
正确答案:sqrt(14)4. 给定矩阵C = [[1, 2, 3], [4, 5, 6]],求C的秩。
正确答案:25. 给定矩阵D = [[1, 2], [3, 4], [5, 6]],求D的转置矩阵。
正确答案:[[1, 3, 5], [2, 4, 6]]三、解答题(每题10分,共40分)1. 什么是线性相关和线性无关?线性相关表示向量之间存在线性组合的系数不全为零的情况,即存在非零向量组合得到零向量。
线性无关表示向量之间不存在这样的关系,即只有全为零的线性组合才能得到零向量。
2. 什么是矩阵的行列式?矩阵的行列式是一个标量,它是一个方阵中各个元素按照一定规律相乘再求和的结果。
行列式可以用来判断方阵的逆是否存在,以及计算方阵的特征值等。
(完整word版)线性代数经典试题4套及答案

线性代数经典试题4套及答案试卷1一、单项选择题(本大题共14小题,每小题2分,共28分)在每小题列出的四个选项中只有一个是符合题目要求的,请将其代码填在题后的括号内。
错选或未选均无分。
1.设行列式a aa a11122122=m,a aa a13112321=n,则行列式a a aa a a111213212223++等于()A. m+nB. -(m+n)C. n-mD. m-n2.设矩阵A=100020003⎛⎝⎫⎭⎪⎪⎪,则A-1等于()A.130012001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪B.100120013⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪C.13000100012⎛⎝⎫⎭⎪⎪⎪⎪⎪D.120013001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪3.设矩阵A=312101214---⎛⎝⎫⎭⎪⎪⎪,A*是A的伴随矩阵,则A *中位于(1,2)的元素是()A. –6B. 6C. 2D. –24.设A是方阵,如有矩阵关系式AB=AC,则必有()A. A =0B. B≠C时A=0C. A≠0时B=CD. |A|≠0时B=C5.已知3×4矩阵A的行向量组线性无关,则秩(A T)等于()A. 1B. 2C. 3D. 46.设两个向量组α1,α2,…,αs和β1,β2,…,βs均线性相关,则()A.有不全为0的数λ1,λ2,…,λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λs βs=0B.有不全为0的数λ1,λ2,…,λs使λ1(α1+β1)+λ2(α2+β2)+…+λs(αs+βs)=0C.有不全为0的数λ1,λ2,…,λs使λ1(α1-β1)+λ2(α2-β2)+…+λs(αs-βs)=0D.有不全为0的数λ1,λ2,…,λs和不全为0的数μ1,μ2,…,μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=07.设矩阵A的秩为r,则A中()A.所有r-1阶子式都不为0B.所有r-1阶子式全为0C.至少有一个r阶子式不等于0D.所有r阶子式都不为08.设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是()A.η1+η2是Ax=0的一个解B.12η1+12η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解9.设n阶方阵A不可逆,则必有()A.秩(A)<nB.秩(A)=n-1C.A=0D.方程组Ax=0只有零解10.设A是一个n(≥3)阶方阵,下列陈述中正确的是()A.如存在数λ和向量α使Aα=λα,则α是A的属于特征值λ的特征向量B.如存在数λ和非零向量α,使(λE-A)α=0,则λ是A的特征值C.A的2个不同的特征值可以有同一个特征向量D.如λ1,λ2,λ3是A的3个互不相同的特征值,α1,α2,α3依次是A的属于λ1,λ2,λ3的特征向量,则α1,α2,α3有可能线性相关11.设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,则必有()A. k≤3B. k<3C. k=3D. k>312.设A是正交矩阵,则下列结论错误的是()A.|A|2必为1B.|A|必为1C.A-1=A TD.A的行(列)向量组是正交单位向量组13.设A是实对称矩阵,C是实可逆矩阵,B=C T AC.则()A.A与B相似B. A与B不等价C. A与B有相同的特征值D. A与B合同14.下列矩阵中是正定矩阵的为()A.2334⎛⎝⎫⎭⎪ B.3426⎛⎝⎫⎭⎪C.100023035--⎛⎝⎫⎭⎪⎪⎪D.111120102⎛⎝⎫⎭⎪⎪⎪第二部分非选择题(共72分)二、填空题(本大题共10小题,每小题2分,共20分)不写解答过程,将正确的答案写在每小题的空格内。
线性代数-多套复习试题简洁版(含答案)
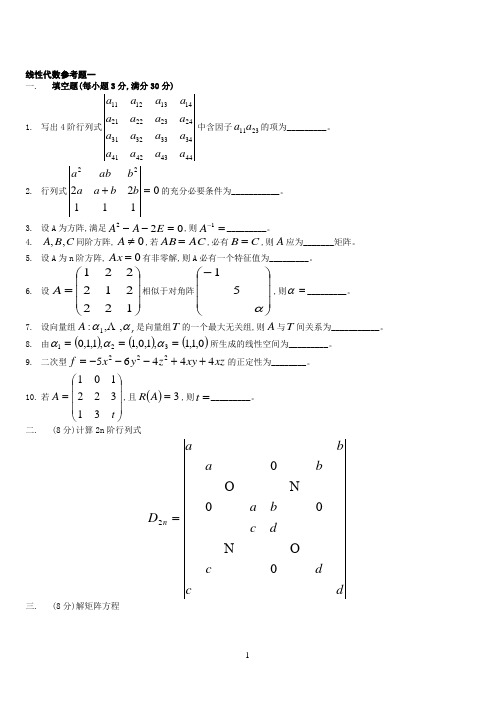
线性代数参考题一一. 填空题(每小题3分,满分30分)1. 写出4阶行列式44434241343332312423222114131211a a a a a a a a a a a a a a a a 中含因子2311a a 的项为_________。
2. 行列式01112222=+b b a a b ab a 的充分必要条件为___________。
3. 设A 为方阵,满足022=--E A A ,则=-1A _________。
4. C B A ,,同阶方阵,0≠A ,若AC AB =,必有C B =,则A 应为_______矩阵。
5.设A 为n 阶方阵,0=Ax 有非零解,则A 必有一个特征值为_________。
6.设⎪⎪⎪⎭⎫ ⎝⎛=122212221A 相似于对角阵⎪⎪⎪⎭⎫ ⎝⎛-α51,则=α_________。
7. 设向量组r A αα,,:1 是向量组T 的一个最大无关组,则A 与T 间关系为___________。
8.由()()()0,1,1,1,0,1,1,1,0321===ααα所生成的线性空间为_________。
9. 二次型xz xy z y x f 44465222++---=的正定性为________。
10. 若⎪⎪⎪⎭⎫ ⎝⎛=t A 31322101,且()3=A R ,则=t _________。
二. (8分)计算2n 阶行列式d cdc dc b a ba ba D n 0002=三. (8分)解矩阵方程⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛1302313512343122321X求?=X四. (10分)设向量组A:()()()()3,6,2,0,1,3,0,1,3,1,1,2,0,1,4,14321-=--=--==αααα求向量组A 的秩及一个最大无关组. 五. 12分)讨论方程组的解的情况⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x六. (16分)求正交变换PY X =,将二次型323121232221222222x x x x x x x x x f ---++=化为标准形,并写出其标准形. 七. (8分)设n n ααβααβαβ++=+== 121211,,,且n αα,,1 线性无关,证明:n ββ,,1 线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iE A i均不可逆.则A 可否对角化? 线性代数参考题二填空题(每小题3分,满分30分) 1. 设B A ,都是5阶矩阵,且2,31=-=-B A ,则=A B2. 已知0222=++I A A ,则=+-1)(I A (其中I 是n 阶单位阵)3.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=12241031xA 设,已知矩阵A 的秩r(A)=2,则=x4.()814370122222632144-==⨯ij a A 设,又ij A 是ij a 的代数余子式,则=+++44434241A A A A5.若一向量组只有唯一的极大无关组,则该向量组6.设3221232221321222),,(x tx x x x x x x x x f ++++=是正定二次型,则t 的取值区间为7.设A 是n阶正交矩阵,1-=A ,则()=*TA8.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=20002121x A 相似于对角阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--211,则=x9.设非齐次线性方程组b AX =的两个解为)(,,2121ξξξξ≠A 的秩为1-n ,则 b AX =的一般解=ξ .10.已知向量组[][][]1,4,2,1,0,,0,2,1,1,2,1321--==-=αααt 的 秩为2,则=t二.(8分)计算n 阶行列式ba a a ab a a a a b a D n nn n ---=212121三.(8分)求矩阵X 满足⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡1041120112201117241X四.(10分)设[][][][]10,2,1,2,4,1,5,1,3,6,3,11,5,5,10,2,3,2,1,24321-==-=-=αααα求向量组的秩及其一个极大无关组. 五. (12分)问常数b a ,各取何值时, 方程组()()⎪⎪⎩⎪⎪⎨⎧=+++++=++++=+-=+++,5853,34232,12,1432143214324321x a x x x b x x a x x x x x x x x x 无解,有唯一解,或有无穷多解,并在有无穷多解时写出其一般解. 六. (16分)求正交变换PY X =,将二次型()323121232221321222222,,x x x x x x x x x x x x f ---++=化为标准形,并写出其标准形.七. (8分)设向量432,,,1αααα线性无关,且43214432134321243211,,,ββββαββββαββββαββββα+---=-+--=--+-=---=证明向量组4321,,,ββββ线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iI A i均不可逆。
线性代数考试试题

线性代数考试试题一、选择题(每题3分,共30分)1. 下列矩阵中,哪个是可逆矩阵?A. [1, 2; 3, 4]B. [2, 0; 0, 1]C. [1, 1; 1, 1]D. [0, 1; 1, 0]2. 向量空间V的一组基具有n个向量,那么V的维数是:A. 0B. nC. 1D. 不确定3. 如果A和B是两个n阶方阵,那么AB和BA的行列式的值:A. 总是相等B. 只有在A和B可交换时相等C. 只有在A和B都是对角矩阵时相等D. 无法确定是否相等4. 对于任意的n维向量x,下列哪个选项是正确的?A. x^T * x是一个标量B. x^T * x是一个矩阵C. x * x^T是一个矩阵D. x + x^T是一个向量5. 特征值和特征向量的定义是什么?A. 对于矩阵A,如果存在标量λ和非零向量v,使得Av=λv,则λ是A的特征值,v是A的特征向量B. 对于矩阵A,如果存在标量λ和非零向量v,使得vA=λv,则λ是A的特征值,v是A的特征向量C. 对于矩阵A,如果存在标量λ和非零向量v,使得A^2v=λv,则λ是A的特征值,v是A的特征向量D. 以上都不是6. 下列哪个矩阵是对称矩阵?A. [1, 0; 0, -1]B. [0, 1; 1, 0]C. [1, 2; 2, 1]D. [2, 3; 3, 2]7. 对于矩阵A,其迹(trace)是:A. A的对角线元素之和B. A的行列式C. A的逆矩阵的对角线元素之和D. A的秩8. 如果矩阵A是正交矩阵,那么下列哪个陈述是正确的?A. A的行列式为1B. A的行列式为-1C. A的逆矩阵等于A的转置D. A的逆矩阵等于A本身9. 对于任意矩阵A,下列哪个选项是正确的?A. |A| 是 A 的行列式B. A^T 是 A 的转置C. A^-1 是 A 的逆矩阵D. A^* 是 A 的共轭转置10. 在线性代数中,线性无关的向量集合可以:A. 构成一个向量空间B. 构成一个基C. 确定一个唯一的解D. 以上都是二、填空题(每题4分,共20分)11. 矩阵的秩是指__________________________。
线性代数试题(附参考答案)

《 线性代数 》课程试题(附答案)一、 填空。
(3×8=24分)1.设A 为四阶方阵,且3=A ,则=-A 22.设⎪⎪⎪⎭⎫⎝⎛=003020100A ,则=-1A3.设⎪⎪⎭⎫⎝⎛=4321A ,则A 的伴随矩阵=*A 4.设CB A ,,为n 阶方阵,若0≠A ,且C AB =,则=B 5.矩阵A 可逆的充要条件为6.齐次线性方程组01=⨯⨯n n m X A 有非零解的充要条件为7.设n 维向量组321,,∂∂∂线性无关,则向量组32,∂∂ (填“线性相关”或“线性无关”)8.设n 元齐次线性方程组0=Ax ,且n r A r <=)(,则基础解系中含有 个解向量。
二、 计算行列式的值。
(10分)321103221033210=D三、 已知矩阵⎪⎪⎪⎭⎫ ⎝⎛---=145243121A ,求1-A 。
(10分)四、 设矩阵⎪⎪⎭⎫ ⎝⎛=1112A ,求矩阵X ,使E A AX 2+=。
(10分)五、 问K 取什么值时下列向量组线性相关(10分) T k )1,2,(1=α,T k )0,,2(2=α,T )1,1,1(3-=α。
六、 设A ,B 为n 阶矩阵且2B B =,E B A +=,证明A 可逆并求其逆(6分)七、 设矩阵⎪⎪⎪⎭⎫⎝⎛----=979634121121112A ,求矩阵A 的列向量组的秩及一个极大线性无关组,并把其余向量用极大线性无关组表示。
(15分)八、 求非齐次线性方程组⎪⎩⎪⎨⎧=--+=+--=--+0895443313432143214321x x x x x x x x x x x x 的通解。
(15分)《线性代数》课程试题参考答案一、 填空。
(3×8=24分)1.设A 为四阶方阵,且3=A ,则=-A 2482.设⎪⎪⎪⎭⎫ ⎝⎛=003020100A ,则=-1A ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛001021031003.设⎪⎪⎭⎫⎝⎛=4321A ,则A 的伴随矩阵=*A ⎪⎪⎭⎫ ⎝⎛--1324 4.设C B A ,,为n 阶方阵,若0≠A ,且C AB =,则=B C A 1- 5.矩阵A 可逆的充要条件为0≠A6.齐次线性方程组01=⨯⨯n n m X A 有非零解的充要条件为n A r <)(7.设n 维向量组321,,∂∂∂线性无关,则向量组32,∂∂线性无关(填“线性相关”或“线性无关”)8.设n 元齐次线性方程组0=Ax ,且n r A r <=)(,则基础解系中含有r n -个解向量。
线性代数练习题及答案10套

1 0 1 14.设矩阵 A= 0 2 0 ,矩阵 B A E ,则矩阵 B 的秩 r(B)= __2__. 0 0 1 0 0 1 B A E = 0 1 0 ,r(B)=2. 0 0 0
15.向量空间 V={x=(x1,x2,0)|x1,x2 为实数}的维数为__2__. 16.设向量 (1,2,3) , (3,2,1) ,则向量 , 的内积 ( , ) =__10__. 17.设 A 是 4×3 矩阵,若齐次线性方程组 Ax=0 只有零解,则矩阵 A 的秩 r(A)= __3__. 18 . 已 知 某 个 3 元 非 齐 次 线 性 方 程 组 Ax=b 的 增 广 矩 阵 A 经 初 等 行 变 换 化 为 :
三、计算题(本大题共 6 小题,每小题 9 分,共 54 分)
Ibugua
交大打造不挂女神的领跑者
123 23 3 21.计算 3 阶行列式 249 49 9 . 367 67 7 123 23 3 100 20 3 解: 249 49 9 200 40 9 0 . 367 67 7 300 60 7
线代练习题及答案(一)
一、单项选择题(本大题共 10 小题,每小题 2 分,共 20 分)
1.设 A 为 3 阶方阵,且 | A | 2 ,则 | 2 A 1 | ( D A.-4 B.-1 C. 1 ) D.4
| 2 A 1 | 2 3 | A | 1 8
1 4. 2
)
1 2 3 1 2 2. 设矩阵 A= (1, 2) , B= C= 则下列矩阵运算中有意义的是 ( B 4 5 6 , 3 4 ,
行成比例值为零.
a1b2 a 2 b2 a 3 b2
线性代数试题及答案

线性代数试题及答案一、选择题(每题2分,共20分)1. 以下哪个矩阵是可逆的?A. [1 0; 0 0]B. [1 2; 3 4]C. [1 0; 0 1]D. [0 1; 1 0]2. 矩阵的秩是指什么?A. 矩阵的行数B. 矩阵的列数C. 矩阵中线性无关的行或列的最大数目D. 矩阵的对角线元素的个数3. 线性方程组有唯一解的条件是什么?A. 方程个数等于未知数个数B. 方程组是齐次的C. 方程组的系数矩阵是可逆的D. 方程组的系数矩阵的秩等于增广矩阵的秩4. 向量空间的基具有什么性质?A. 基向量的数量必须为1B. 基向量必须是正交的C. 基向量必须是线性无关的D. 基向量必须是单位向量5. 特征值和特征向量的定义是什么?A. 对于矩阵A,如果存在非零向量v,使得Av=λv,则λ是A的特征值,v是A的特征向量B. 对于矩阵A,如果存在非零向量v,使得A^Tv=λv,则λ是A 的特征值,v是A的特征向量C. 对于矩阵A,如果存在非零向量v,使得A^-1v=λv,则λ是A 的特征值,v是A的特征向量D. 对于矩阵A,如果存在非零向量v,使得Av=v,则λ是A的特征值,v是A的特征向量6. 线性变换的矩阵表示是什么?A. 线性变换的逆矩阵B. 线性变换的转置矩阵C. 线性变换的雅可比矩阵D. 线性变换的对角矩阵7. 以下哪个不是线性代数中的基本概念?A. 向量B. 矩阵C. 行列式D. 微积分8. 什么是线性方程组的齐次解?A. 方程组的所有解B. 方程组的特解C. 方程组的零解D. 方程组的非平凡解9. 矩阵的迹是什么?A. 矩阵的对角线元素的和B. 矩阵的行列式C. 矩阵的秩D. 矩阵的逆10. 什么是正交矩阵?A. 矩阵的转置等于其逆矩阵B. 矩阵的所有行向量都是单位向量C. 矩阵的所有列向量都是单位向量D. 矩阵的所有行向量都是正交的答案:1-5 C C C C A;6-10 D D C A A二、简答题(每题10分,共20分)11. 请简述线性代数中的向量空间(Vector Space)的定义。
线性代数试题(完整试题与详细答案)

线性代数试题(完整试题与详细答案)一、单项选择题(本大题共10小题,每小题2分,共20分)1.行列式111101111011110------第二行第一列元素的代数余子式21A =( )A .-2B .-1C .1D .22.设A 为2阶矩阵,若A 3=3,则=A 2( ) A .21 B .1 C .34 D .23.设n 阶矩阵A 、B 、C 满足E ABC =,则=-1C ( ) A .AB B .BA C .11--B AD .11--A B4.已知2阶矩阵⎪⎪⎭⎫ ⎝⎛=d c b a A 的行列式1-=A ,则=-1*)(A ( ) A .⎪⎪⎭⎫⎝⎛----d c b aB .⎪⎪⎭⎫⎝⎛--a c b dC .⎪⎪⎭⎫ ⎝⎛--a cb d D .⎪⎪⎭⎫ ⎝⎛d c b a5.向量组)2(,,,21≥s s ααα 的秩不为零的充分必要条件是( ) A .s ααα,,,21 中没有线性相关的部分组 B .s ααα,,,21 中至少有一个非零向量 C .s ααα,,,21 全是非零向量D .s ααα,,,21 全是零向量6.设A 为n m ⨯矩阵,则n 元齐次线性方程组0=Ax 有非零解的充分必要条件是( )A .n r =)(AB .m r =)(AC .n r <)(AD .m r <)(A 7.已知3阶矩阵A 的特征值为-1,0,1,则下列矩阵中可逆的是( ) A .A B .AE - C .A E -- D .A E -2 8.下列矩阵中不是..初等矩阵的为( )A .⎪⎪⎪⎭⎫ ⎝⎛101010001B .⎪⎪⎪⎭⎫⎝⎛-101010001C .⎪⎪⎪⎭⎫⎝⎛100020001D .⎪⎪⎪⎭⎫⎝⎛1010110019.4元二次型4332412143212222),,,(x x x x x x x x x x x x f +++=的秩为( ) A .1B .2C .3D .410.设矩阵⎪⎪⎪⎭⎫ ⎝⎛=001010100A ,则二次型Ax x T 的规范形为( )A .232221z z z ++ B .232221z z z ---C .232221z z z --D .232221z z z -+二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
《线性代数》行列式测试试卷

《线性代数》行列式测试试卷姓名 学号 得分一、选择题(每小题3分,共36分)1.行列式cos sin sin cos αααα-=- ( ) A.1 B.sin α C.cos α D.cos2α 2.若行列式1202310101λλ=,则12,λλ必须满足 ( )A.122,0λλ==B.122λλ==C.12λ=,2λ可为任意数D.12,λλ可为任意数3.若行列式210120312x --=-,则x = ( )A.-2B.2C.-1D.14.如果1231231231a a a b b b c c c =,则123123123222333a a a b b b c c c --=- ( ) A.-6 B.6 C.5 D.-55.关于n 阶行列式,下面哪条命题是不正确的 ( )A.行列式可以按任一行(列) 展开,其值相等B.交换行列式的两行元素,行列式的值不变C.若行列式某两行对应元素全相等,则行列式为零D.D 与其转置 T D 相等6.方程组211112014x x =的全部解为( )A.0B.1C.2D.1和27. 0010010000011000=( )A.0B.-1C. 1D.28.在函数211112()3230001x xx f x x ---=-中3x 项的系数是( )A.0B.-1C.2D.19.若3阶行列式1112223331a b c a b c a b c =,则行列式111112222233333a b x a x b c a b x a x b c a b x a x b c ++++=++( ) A.21x + B.()21x -+ C.21x - D.()21x --10.四阶行列式αββββαββββαββββα的值为 ( ) A. ()33()αβαβ+- B. ()33()αβαβ+-C. ()33()αβαβ-+D. ()33()αβαβ-+ 11.四阶行列式11121314212223243132333441424344a a a a a a a a D a a a a a a a a =中含1122a a 的项有( )A.11223344a a a a -和11223443a a a aB.11223344a a a a -和11223443a a a a -C.11223344a a a a 和11223443a a a a -D.11223344a a a a 和11223443a a a a12.行列式00000000a bc dDe fg h== ( )A.acfh adeh bcfg bdeg-++ B.acfh adeh bcfg bdeg+-+C.acfh adeh bcfg bdeg--- D.acfh adeh bcfg bdeg--+二、填空题(每小题4分,共24分)1.排列614523的逆序数为2.四阶行列式130451 8620 3300 3000=3.行列式111234345中元素2的代数余子式为.4.行列式a b c dd c b bDb b b bc d a d=,则11121314A A A A+++=.5.行列式1234234134124123=.6.1101004aa a->的充分必要条件是.三、简答题(共40分)1.计算下列行列式的值.(每个7分,共14分)(1)3121123221400213- (2)2240413531232051-----2.设四阶行列式2151130632131476D ---=--,求 32333422M M M ---之值.(8分)3.计算行列式0123100010001x x D x a a a a --=-.(10分)4.解下列矩阵方程12121212311011x a a a x a D a a x a a a ==.(8分)。
线性代数试卷

线性代数试卷一、选择题1.在线性代数中,一组向量能够生成整个向量空间的充要条件是: A. 线性相关 B. 线性无关 C. 最大线性无关组D. 最小线性无关组2.设 A 为一阶方阵,若 A 的行列式为 0,则 A 的逆矩阵: A. 存在且不唯一 B. 不存在 C. 存在且唯一 D. 无法确定3.若 A 为 m×n 矩阵,B 为 n×p 矩阵,则矩阵积 AB 的维数是: A. m×p B. n×(m-p) C. (n-m)×p D. p×n4.若 A 是 n 阶方阵,且 A 的特征值全相等,则 A 必定是: A. 零矩阵 B. 对角矩阵 C. 存在逆矩阵 D. 非奇异矩阵5.对于 n 维向量空间中的向量组,如果向量的极大线性无关组的个数与向量组中向量的个数相等,那么向量组的维数为: A. 无法确定 B. n C. 0 D. n-1二、填空题1.若 A 为 n 阶方阵,且 A 的秩为 r,则 A 的零空间维数为n-r。
2.设 A 为 m×n 矩阵,若 AX = 0 的解集是 n 维零向量 0,则 A 的列空间维数为n。
3.设 A 为 m×n 矩阵,若 AX = 0 的解集非零解存在,则 A 的秩为r。
4.设 A、B 为 n 阶方阵,且 AB = BA,则 A 和 B 可同时对角化的充要条件是 A 和 B 对应的特征向量线性无关。
5.设 A 为 n 阶方阵,若 A 的所有特征值都为正数,则A 是正定矩阵。
三、解答题1.给定矩阵 A = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5& 6 \end{bmatrix}\),求矩阵 A 的伴随矩阵。
2.给定方程组 AX = B,其中 A = \(\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\),B =\(\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\),求方程组的解集。
线性代数期末考试考核试卷

4.以下哪个向量组构成一个基?
A. (1, 0, 0), (0, 1, 0), (0, 0, 0)
B. (1, 2, 3), (4, 5, 6), (7, 8, 9)
C. (1, 2, 3), (2, 4, 6), (1, 1, 1)
D. (1, 1, 0), (0, 1, 1), (1, 0, 1)
...
20.(根据实际题目内容填写答案)
二、多选题
1. BCD
2. ABCD
3. ABC
4. AB
5. ABC
...
20.(根据实际题目内容填写答案)
三、填题
1. 1
2.线性无关
3.主
...
10.(根据实际题目内容填写答案)
四、判断题
1. √
2. √
3. √
...
10. ×
五、主观题(参考)
1.向量组线性无关,可以通过计算行列式不为零来证明。一个可以由给定向量组线性表示的向量可以是它们的线性组合,例如\(a\vec{v}_1 + b\vec{v}_2 + c\vec{v}_3\),其中\(a, b, c\)是适当的系数。
D. (1, 1), (1, -1)
(答题括号:________)
5.在求解线性方程组时,以下哪些情况下可以使用高斯消元法?
A.系数矩阵是方阵
B.系数矩阵是非奇异的
C.方程组中方程的个数等于未知数的个数
D.方程组可能有无穷多解
(答题括号:________)
(以下题目类似,省略以节约空间)
6. ...
A.若A为m×n矩阵,则A的转置为n×m矩阵
B.若A为m×n矩阵,则A的转置为m×n矩阵
线性代数试卷及答案3套

线性代数试卷及答案3套线性代数A卷一、填空题(共6小题,满分18分)1.设α=(1,0,-1,2),β=(0,1,0,1),令A=αTβ,则A4 = .2.设矩阵且BA=B+E,则B-1= .3.设α1,α2是2维的列向量,令A=(2α1+α2,α1-α2),B=(α1,α2),若|A|=-6, 则|B|= .4.设A为n阶方阵,且A2=A,则R(A)+ R(A- E) = .5.设α1=(1,1,1),α2=(a,0,b),α3=(1,2,3)线性相关,则a与b应满足的关系式为.6. 设α+2β=(2,1,t,-1),2α-β=(-1,2,0,1),且α与β正交,则t= .二、单项选择题(共6小题,满分18分)1. 设A为n阶方阵,且AA T= E,|A|<0,则A+ E为[ ].(A) 非奇异矩阵,(B) 奇异矩阵,(C)正交矩阵,(D)正定矩阵.2.设A是4×3矩阵,且R(A)=2,若则R(AB)为[ ].(A) 2,(B) 3,(C)4,(D) 0.3. 设A为n阶可逆矩阵,k≠0为常数,则(k A)*为[ ].(A) k A*,(B) k n-1 A*,(C) k n A*,(D) k n A.4. 设向量组α1,α2,α3线性无关,则下面向量组线性相关的是[ ].(A) α1-α2,α2-α3,α3-α1,(B) α1+α2,α2+α3,α3+α1,(C)α1-2α2,α2-2α3,α3-2α1,(D) α1+2α2,α2+2α3,α3+2α1.5.设矩阵A n×m,B m×n,且n<m,若AB=E,则下面结论正确的是[ ].(A) A的行向量组线性相关,(B) A的列向量组线性无关,(C) 线性方程组Bx=0仅有零解,(D) 线性方程组Bx=0必有非零解.6.设3阶方阵A与B相似,且A的特征值为,则tr(B-1- E)为[ ].(A) 2,(B) 3,(C)4,(D) 6.三、解答题(共6小题,满分42分)1.设A为4阶方阵,A*是A的伴随矩阵,且|A|=0,而A*≠O.α1,α2,α3是线性方程组Ax=b的三个解向量,其中,求线性方程组Ax=b的通解.2.设向量组,问a为何值时,向量组α1,α2,α3,α4线性相关,并求此时的极大无关组.3.求一组非零向量α1,α2与已知向量α3=(1,1,1)T正交,并把它们化成R3的一个标准正交基.4.设矩阵,且A*相似于B,其中A*是A的伴随矩阵,求x,y.5.设二次型,其中二次型的矩阵A的特征值之和为1,特征值之积为-12,求a,b.6.设V是二阶实对称矩阵全体的集合,对于通常矩阵的加法与数乘运算所构成的实数域R上的线性空间.且是V的一个基,试证也是V的一个基.并求V中的向量在该组基下的坐标.四、(本题满分11分)已知齐次线性方程组(Ⅰ)(Ⅱ)同解,求a,b,c的值.五、(本题满分11分)设矩阵3阶实对称矩阵A的各行元素之和为3,且R(A)=1.①求A的特征值与特征向量;②求正交矩阵P和对角矩阵Λ,使P-1AP=Λ;③求A及.线性代数B卷一、填空题(共6小题,每小题3分,满分18分)1.设4阶矩阵A的行列式|A| =3,则行列式.2.设A为3阶正交矩阵,且A T= -A*,其中A*是A的伴随矩阵,则|A| = .3.设α1,α2是n(n3)元齐次线性方程组Ax=0的基础解系,则R(A)= .4.设线性空间R2的两个基A:α1=(1,0)T,α2=(1,1)T;B:β1=(1,1)T,β2=(-1,1)T,则A组基到B组基的过渡矩阵为.5.设3阶矩阵A的特征值为1、3、5,则A的迹tr A= .6.若二次型f(x1,x2,x3)=x12+4x22+2x32+2tx1x2+2x1x3正定,则t满足.二、单项选择题(共6小题,每小题3分,满分18分)1.设A为m×n矩阵.B为n×m矩阵,则[ ].(A)当时,必有|AB|≠0;(B)当时,必有|AB|=0;(C)当时,必有|AB|≠0;(D)当时,必有|AB|=0.2.设α1,α2,α3是齐次线性方程组Ax=0的基础解系,则该方程组的基础解系还可为[ ].(A)α1-α2,α2-α3,α3-α1;(B)与α1,α2,α3等秩的一个向量组;(C)α1,α1+α2,α1+α2+α3;(D)与α1,α2,α3等价的一个向量组.3.设A为n阶非奇异阵(n2),A*是A的伴随阵,则[ ].(A) (A*)*= |A|n -2A;(B) (A*)*=|A|n+2A;(C) (A*)*= |A|n -1A; (D) (A*)*=|A|n+1A.4.设A为m×n矩阵,C为n阶可逆矩阵,R(A)=r,矩阵B=AC 的秩为r1,则[ ].(A) r >r1; (B) r<r1;< p="">(C) r与r1关系依赖与矩阵C; (D) r=r1.5.设A,B为n阶矩阵,若[ ],则A与B合同.(A) 存在n阶可逆矩阵P、Q,且PAQ=B;(B) 存在n阶可逆矩阵P,且P-1AP= B;(C) 存在n阶正交矩阵Q,且Q-1AQ= B;(D) 存在n阶方阵C、U,且CAU= B.6.n阶方阵A具有n个不同的特征值是A与对角阵相似的[ ].(A) 充分必要条件;(B) 充分而非必要条件;(C) 必要而非充分条件;(D) 既非充分也非必要条件.三、解答题(共5小题,每小题9分,满分45分)1. 计算4阶行列式.2.设向量组α1=(1,0,2,1)T,α2=(1,2,0,1)T,α3=(2,1,3,0)T,α4=(2,5,-1,4)T.(1) 判断向量组的线性相关性;(2) 求它的秩和一个极大无关组;(3) 把不在极大无关组中的向量用这个极大无关组线性表示.3. 设向量α1=(1,2,1)T和α2=(1,1,2)T都是方阵A的属于特征值λ=2的特征向量,又向量β=α1+2α2,求A2β.4.设3阶方阵A、B满足AB= 2A+B,其中求A.5. 已知线性空间R[x]3={a0+a1x+a2x2| a0,a1,a2 R},(1) 证明1,1+x,(1+x)2是R[x]3的一个基;(2) 求由基1,x,x2到基1,1+x,(1+x)2的过渡矩阵.四、(本题满分9分)设线性方程组(Ⅰ)与(Ⅱ)x1+3x2+3x3=a-3有公共解,求a的值和所有的公共解.五、(本题满分10分)设实二次型f(x1,x2,x3)=x T Ax的秩为2,且α1=(1,0,0)T 是(A-2E)x=0的解,α2=(0,-1,1)T是(A-6E)x=0的解.(1)求矩阵A的特征值与特征向量;(2)用正交变换将该二次型化成标准形,并写出所用的正交变换和所化的标准形;(3)写出该二次型.线性代数C卷一、填空题(共6小题,每小题3分,满分18分)1.设A为3阶方阵,|A|=1,则| -2A|=__________.2.设A是n阶方阵,x1,x2均为线性方程组Ax=b的解,且x1≠x2,则|A|=____ ____ .3.设A为n阶可逆阵,且A2=|A|E,则A*= . 4.若n阶方阵A 与单位阵E相似,则A= .5.设4阶方阵A,R(A)=2,则R(A*)= .6. 若二次型是正定的,则t应满足.二、单项选择题(共6小题,每小题3分,满分18分)1. 设A为实对称矩阵,Ax1=λ1x1,Ax2=λ2x2,且λ1≠λ2,则(x1,x2) =[ ].(A) 1;(B) -1;(C) 0;(D) 2. 2.设A、B均为n阶可逆阵,则[ ].(A) ((AB)2)-1=(B2)-1(A2)-1;(B) 存在可逆阵P、Q,使PAQ=B;(C) 存在可逆阵P, 使A=P-1BP;(D) 存在可逆阵P,使P T AP=B.,则3.设A为m×n矩阵,C为n阶可逆矩阵,R(A)=r,矩阵B=AC的秩为r1 [ ].(A)r>r1;(B)r< p="">4.设α1,α2,α3是齐次线性方程组Ax=0的基础解系,则该方程组的基础解系还可为 [ ].(A)α1,α1+α2,α1+α2+α3;(B) 与α1,α2,α3等价的一个向量组;(C) α1-α2,α2-α3,α3-α1;(D) 与α1,α2,α3等秩的一个向组.5.向量组α1,α2,…,αs线性无关的充要条件是[ ].(A) α1,α2,…,αs都不是零向量;(B) α1,α2,…,αs中任意两个向量都线性无关;(C) α1,α2,…,αs中任一向量都不能用其余向量线性表出;(D) α1,α2,…,αs中任意s-1个向量都线性无关.6. 如果[ ],则A与B相似.(A) |A|=|B|; (B) R(A)=R(B);(C) A与B有相同的特征多项式;(D) n阶矩阵A与B有相同的特征值且n个特征值各不相同.三、解答题(共5小题,每小题9分,满分45分)1.计算行列式.2.设3阶方阵A、B满足AB= 2A+B,其中求A.3. 设向量组α1=(1,0,2,1)T,α2=(1,2,0,1)T,α3=(2,1,3,0)T,α4=(2,5,-1,4)T.(1) 判断向量组的线性相关性;(2) 求它的秩和一个极大无关组;(3) 把不在极大无关组中的向量用极大无关组线性表示.4.设矩阵,求(1)A2;(2)A n.5. 已知是矩阵的一个特征向量.(1) 试确定参数a,b及特征向量ξ所对应的特征值;(2) 问A能否相似于对角阵?说明理由.四、(本题满分9分)设3维向量组试问:(1) 当λ取何值时,β可由α1,α2,α3线性表示,且表示法唯一;(2) 当λ取何值时,β可由α1,α2,α3线性表示,但表示法不唯一;(3) 当λ取何值时,β不能由α1,α2,α3线性表示.五、(本题满分10分)设实二次型f(x1,x2,x3)=x T Ax的秩为2,且α1=(1,0,0)T 是(A-2E)x=0的解,α2=(0,-1,1)T是(A-6E)x=0的解.(1)求矩阵A的特征值与特征向量;(2)用正交变换将该二次型化成标准形,并写出所用的正交变换和所化的标准形;(3)写出该二次型.<></r1;<>。
线性代数模拟试卷及答案4套

线性代数模拟试卷(一)一、 填空题(每小题3分,共6小题,总分18分)1、四阶行列式44434241343332312423222114131211a a a a a a a a a a a a a a a a 展开式中,含有因子3214a a 且带正号的项为___________2、设A 为n 阶可逆方阵,将A 的第i 行和第j 行对换后得到的矩阵记为B ,则AB -1=_________3、已知向量组)2- 5, 4,- ,0( , )0 t,0, ,2( , )1 1,- 2, ,1(321'='='=ααα线性相关,则t =_________4、设三阶方阵) , ,(B ), , ,(2121γγβγγα==A ,其中 , ,,21γγβα都是三维列向量且2B 1, ==A ,则=- 2B A _________5、A 为n 阶正交矩阵, , ,,21n ααα 为A 的列向量组,当i ≠j 时,)21 ,31(j i αα=_________ 6、三阶方阵A 的特征值为1,-2,-3,则 A =_______; E+A -1的特征值为______ 二、 单项选择题(每小题2分,共6小题,总分12分) 1、 设齐次线性方程组AX=0有非零解,其中A=()nn ija ⨯,A ij 为a ij (i,j=1,2,…n) 的代数余子式,则( ) (A)0111=∑=ni i i A a(B)0111≠∑=ni i i A a(C)n A ani i i =∑=111(D)n A ani i i ≠∑=1112、若A -1+ E, E+A, A 均为可逆矩阵,E 为单位矩阵,则(A -1+ E)-1=( ) (A) A+E (B) (A+E)-1 (C) A -1+ E (D) A(A+E)-13、设A, B 为n 阶方阵 ,A*,B*分别为A, B 对应的伴随矩阵,分块矩阵⎪⎪⎭⎫ ⎝⎛=B 00 A C ,则C 的伴随矩阵C* =( )(A) ⎪⎪⎭⎫⎝⎛*A B 0 0 *B A (B) ⎪⎪⎭⎫⎝⎛*B A 0 0 *A B(C) ⎪⎪⎭⎫⎝⎛*B B 0 0 *A A (D) ⎪⎪⎭⎫⎝⎛*A A 0 0 *B B 4、若向量组 , ,,21m ααα 的秩为r ,则( )(A) 必有 r<m (B)向量组中任意小于 r 个向量的部分组线性无关 (C) 向量组中任意 r 个向量线性无关(D) 向量组中任意 r+1个向量必线性相关5、已知 ,,321ααα是四元非齐次线性方程组AX=B 的三个解,且r(A)=3, 已知)3 2, 1, ,0( , )4 3, 2, ,1(321'=+'=ααα,C 为任意常数,则AX=B 通解X=( )(A) ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛11114321C (B)⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛32104321C(C) ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛54324321C (D) ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛65434321C6、设A 为三阶方阵,有特征值λ1=1,λ2= -1, λ3=2,其对应的特征向量分别为 ,,321ααα,记P=(132 ,ααα),则P -1AP=( )(A) ⎪⎪⎪⎭⎫⎝⎛1 2 1- (B)⎪⎪⎪⎭⎫⎝⎛1- 1 2(C) ⎪⎪⎪⎭⎫⎝⎛2 1- 1 (D) ⎪⎪⎪⎭⎫⎝⎛2 1 1-三、计算下列行列式 (12分)1、 D=1- 3 3- 131 1 41- 3 0 5-21- 1 3 2、D n = n1 1 1 1.....................1 1 3 1 111 12 111 1 1 1四、已知A 、B 同为3阶方阵,且满足AB=4A+2B (12分) (1)证明:矩阵A-2E 可逆(2)若B=⎪⎪⎪⎭⎫⎝⎛2 0 00 2 10 2- 1 ,求A五、求向量组 )1 1, 1,- ,1( , )3 2, 1, ,1(21'='=αα, , )6 5, 2,- ,4( , )1 3, 3, ,1( 43'='=αα)7- 4,- 1,- ,3(5'-=α的一个极大无关组,并将其余向量用该极大无关组线性表示(10分)六、已知线性方程组⎪⎪⎩⎪⎪⎨⎧=---=+++-=+-=+-+bx x x x x ax x x x x x x x x x 432143214314321 6 - 17231 4 032 ,讨论参数a 、b 为何值方程组有解,在有解时,求出通解 (12分)七、用正交变换化二次型323121232221321222333),,(x x x x x x x x x x x x f ---++=为标准形,并写出相应的正交变换 (16分)八、已知 ,,,4321αααα是AX = 0的一个基础解系,若322211,ααβααβt t +=+=,144433,ααβααβt t +=+=,讨论t 为何值, ,,,4321ββββ是AX = 0的一个基础解系 (8分)线性代数模拟试卷(二)三、 填空题(每小题3分,共5小题,总分15分)1、j i a a a a a 53544231是五阶行列式展开式中带正号的一项,则i=_____, j=_____2、设n 阶方阵A 满足A 2 =A ,则A+E 可逆且(A+E )-1=_______________(E 为n 阶单位阵)3、已知向量组)0 6, 1,- ,1( , )2k - k,- ,3 ,1( , )2- 2, 1, ,1(321'='='=ααα 若该向量组的秩为2,则k =_________4、已知四阶方阵A 相似于B ,A 的特征值为2,3,4,5,E 是单位阵,则=- E B _________5、 向量α=(4,0,5)′在基)1 ,1- ,1(,)0 ,1 ,1( ,)1 ,2 ,1(321'='='=ηηη下的坐标为_________四、 单项选择题(每小题2分,共5小题,总分10分)1、 设 A 是三阶方阵A 的行列式,A 的三个列向量以γβα ,,表示,则 A =( ) (A)αβγ (B) γβα---(C)αγγββα+++ (D) γβαβαα+++2、设A, B ,C 为n 阶方阵, 若 AB = BA, AC = CA, 则ABC=( ) (A) BCA (B) ACB (C) CBA (D) CAB3、 A, B 均为n 阶方阵, A*为A 的伴随矩阵, 3B 2, -==A ,则21-*B A = ( )(A) 32 12--n (B) 32 1--n (C) 23 12--n (D) 23 1--n4、已知向量组 , ,,4321αααα线性无关,则向量组( ) (A)14433221 , , ,αααααααα++++线性无关(B)14433221 , , ,αααααααα----线性无关(C)14433221 , , ,αααααααα-+++线性无关 (D)14433221 , , ,αααααααα--++线性无关5、若A ~ B ,则 有 ( )(A) A 、B 有相同的特征矩阵 (B) B =A(C) 对于相同的特征值λ,矩阵A 与B 有相同的特征向量 (D) A 、B 均与同一个对角矩阵相似三、计算下列行列式 (13分)2、 D=2- 3 0 112 1 - 121 0 331- 2 1 4、D n = 11 1 111 x 1 1 (1)1 1 1 x 1 1 1 1 x x ++++a)设B= ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1 0 0 01- 1 0 00 1- 1 00 0 1- 1 ,C=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2 0 0 01 2 0 03 12 043 12 ,且矩阵A 满足 E C B C E A =''--)(1, 试将关系式化简并求A (12分)b)求向量组, )4 1,- 2, ,1(1'=α )2 3, 1, ,0( 2'=α, , )14 0, 7, 3,(3'=α , )10 1, 5, 2,( 4'=α)0 2,- 2, ,1(5'=α的一个极大无关组,并将其余向量用该极大无关组线性表示 (13分)六、k 为何值时,线性方程组⎪⎪⎩⎪⎪⎨⎧=+-=++---=+++=+++kx x x x x k x x x x x x x x x x x 9 10 5 - 3)5(2 31 6 3 13 2 4321432143214321 有无穷多个解并求出通解 (14分)七、用正交变换化二次型31232221321422),,(x x x x x x x x f +-+=为标准形,并写出相应的正交变换 (16分)八、若矩阵A=⎪⎪⎪⎭⎫ ⎝⎛0y 10 1- 01 x0 有三个线性无关的特征向量,证明:x – y = 0线性代数模拟试卷(三)一、填空题(每小题3分,共18分)1、A 是三阶方阵,且|A|=6,则 |(3A)-1|= 。
2022年线性代数试卷及答案6套

线性代数试卷及答案6套.试卷(一): 一. 填空题(每小题4分,共20分)1.已知正交矩阵P 使得⎪⎪⎪⎭⎫ ⎝⎛--=200010001AP P T ,则.________)(2006=+P A E A P T2.设A 为n 阶方阵,n λλ,,1 为A 的n 个特征值,则 ._________)det(2=A 3.设A 是n m ⨯矩阵,B 是m 维列向量,则方程组B AX =有无数多个解的充分必要条件是:._________4.若向量组T T T t )3,2,(,)1,3,2(,)2,4,0(===γβα的秩为2,则._____=t5.,27859453251151)(32--=x x x x D 则0)(=x D 的全部根为:_________.二. 选择题 (每小题4分,共20分)1.行列式001010100 ---的值为( ).A. 1B. -1C. 2)1()1(--n n D. 2)1()1(+-n n2. 对矩阵n m A ⨯施行一次行变换相当于( ).A. 左乘一个m 阶初等矩阵B. 右乘一个m 阶初等矩阵C. 左乘一个n 阶初等矩阵D. 右乘一个n 阶初等矩阵 3. 若A 为n m ⨯矩阵,{},,0|,)(n R X AX X M n r A r ∈==<= 则( ). A. M 是m 维向量空间 B. M 是n 维向量空间 C. M 是r m -维向量空间 D. M 是r n -维向量空间 4. 若n 阶方阵A 满足,,02=A 则下列命题哪一个成立 ( ).A. 0)(=A rB. 2)(n A r =C. 2)(n A r ≥D. 2)(nA r ≤5. 若A 是n 阶正交矩阵,则下列命题哪一个不成立( ). A. 矩阵T A 为正交矩阵 B. 矩阵1-A 为正交矩阵 C. 矩阵A 的行列式是1± D. 矩阵A 的特征值是1±三. 解下列各题(每小题6分,共30分)1. 若A 为3阶正交矩阵, *A 为A 的伴随矩阵, 求).det(*A2. 计算行列式.111111111111aa a a 3. 设,,100002020B A AB A -=⎪⎪⎪⎭⎫ ⎝⎛=求矩阵.B4. 求向量组,)2,1,2,1(1T =α,)2,1,0,1(2T =α,)0,0,1,1(3T =αT )4,2,1,1(4=α的一个 最大无关组.5. 求向量T )1,2,1(=ω在基,)1,1,1(T =α,)1,1,0(T =βT )1,1,1(-=γ下的坐标. 四. (12分) 求方程组⎪⎩⎪⎨⎧=+--+=+++-=++-+631052372322543215432154321x x x x x x x x x x x x x x x的通解(用基础解系与特解表示).五.(12分) 用正交变换化下列二次型为标准型, 并写出正交变换矩阵3123222132122),,(x x x x x x x x x f -++= 六. 证明题(6分)设r ξξξβ ,,,021≠是线性方程组β=AX 对应的齐次线性方程组的一个 基础解系,η是线性方程组β=AX 的一个解, 求证ηηξηξηξ,,,,21+++r 线性无关.试卷(二):一.计算下列各题:(每小题6分,共30分)(1),180380162176380162225379162(2)求,3222E A A ++其中⎪⎪⎭⎫⎝⎛-=3112A(3)已知向量组T T T t ),2,1(,)3,3,2(,)3,2,0(321-===ααα线性相关,求.t (4) 求向量T )4,2,1(-=α在基T T T )1,2,1(,)1,1,0(,)1,0,1(321-===ααα下的坐标.(5) 设⎪⎪⎭⎫⎝⎛=5321A , 求A 的特征值.二.(8分) 设⎪⎪⎪⎭⎫ ⎝⎛=200002130A ,且,B A AB T +=求矩阵B.三. (8分) 计算行列式: 100200300321x c b a四. (8分) 设有向量组,)6,0,2,3,3(,)7,2,0,1,1(,)5,2,1,0,1(,)3,2,1,1,0(4321T T T T -=--===αααα 求该向量组的秩以及它的一个最大线性无关组.五. (8分) 求下列方程组的通解以及对应的齐次方程组的一个基础解系.⎪⎩⎪⎨⎧=--+=+-+-=-+-+.18257,432,1042354315432154321x x x x x x x x x x x x x x六. (8分) 求出把二次型323121232221222)(x x x x x x x x x a f -++++=化为标准形的正交变换,并求出使f 为正定时参数a 的取值范围.七. (10分) 设三阶实对称矩阵A 的特征值为3(二重根)、4(一重根),T )2,2,1(1=α是A 的属于特征值4的一个特征向量,求.A 八. (10分) 当b a ,为何值时,方程组⎪⎩⎪⎨⎧=++=++=++,233,1032,4321321321x bx x x bx x x x ax 有惟一解、无穷多解、无解?九.(10分) (每小题5分,共10分) 证明下列各题(1) 设A 是可逆矩阵, ,~B A 证明B 也可逆, 且.~11--B A (2) 设βα,是非零1⨯n 向量,证明α是n n ⨯矩阵T αβ的特征向量.试卷(三):一. 填空题(共20分)1. 设A 是n m ⨯矩阵,B 是m 维列向量,则方程组B AX =有唯一解的充分必要条件是:2. 已知E 为单位矩阵, 若可逆矩阵P 使得11223,P AP P A P E --+= 则当E A -可逆时, 3A =3. 若t 为实数, 则向量组α=(0,4,t ),β=(2,3,1),γ=(t ,2,3+t )的秩为:4. 若A 为2009阶正交矩阵,*A 为A 的伴随矩阵, 则*A =5. 设A 为n 阶方阵,12,,,n λλλ⋅⋅⋅⋅⋅⋅是A 的n 个特征根,则1ni i i i E A λ=-∑ =二. 选择题(共20分)1. 如果将单位矩阵E 的第i 行乘k 加到第j 行得到的矩阵为)),(,(k i j P 将矩阵n m A ⨯的第i 列乘k 加到第j 列相当于把A :A, 左乘一个));(,(k j i P B ,右乘一个));(,(k j i PC . 左乘一个));(,(k i j PD ,右乘一个)).(,(k i j P2. 若A 为m ×n 矩阵,B 是m 维非零列向量,()min{,}r A r m n =<。
北京大学《线性代数》六套试卷与答案
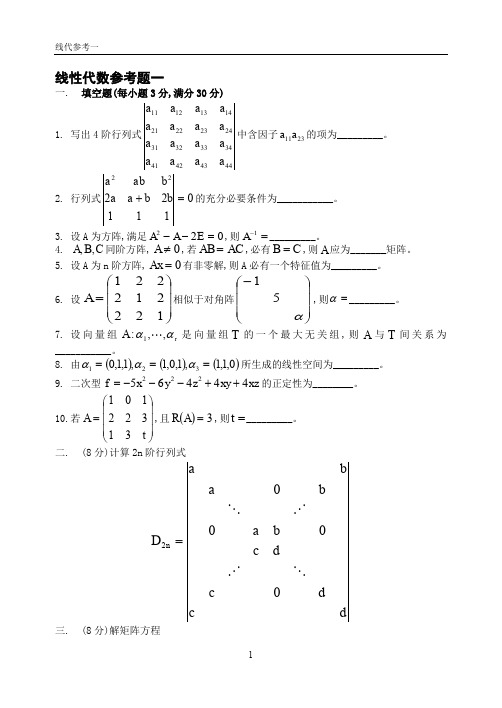
线性代数参考题一一. 填空题(每小题3分,满分30分)1. 写出4阶行列式44434241343332312423222114131211a a a a a a a a a a a a a a a a 中含因子2311a a 的项为_________。
2. 行列式01112222=+b b a a b ab a 的充分必要条件为___________。
3. 设A 为方阵,满足022=--E A A ,则=-1A _________。
4. C B A ,,同阶方阵,0≠A ,若AC AB =,必有C B =,则A 应为_______矩阵。
5. 设A 为n 阶方阵,0=Ax 有非零解,则A 必有一个特征值为_________。
6. 设⎪⎪⎪⎭⎫⎝⎛=122212221A 相似于对角阵⎪⎪⎪⎭⎫⎝⎛-α51,则=α_________。
7. 设向量组r A αα,,:1 是向量组T 的一个最大无关组,则A 与T 间关系为___________。
8. 由()()()0,1,1,1,0,1,1,1,0321===ααα所生成的线性空间为_________。
9. 二次型xz xy z y x f 44465222++---=的正定性为________。
10.若⎪⎪⎪⎭⎫⎝⎛=t A 31322101,且()3=A R ,则=t _________。
二. (8分)计算2n 阶行列式d cdc dc b a ba ba D n 0002=三. (8分)解矩阵方程⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛1302313512343122321X求?=X四. (10分)设向量组A:()()()()3,6,2,0,1,3,0,1,3,1,1,2,0,1,4,14321-=--=--==αααα求向量组A 的秩及一个最大无关组. 五. 12分)讨论方程组的解的情况⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x六. (16分)求正交变换PY X =,将二次型323121232221222222x x x x x x x x x f ---++=化为标准形,并写出其标准形.七. (8分)设n n ααβααβαβ++=+== 121211,,,且n αα,,1 线性无关, 证明:n ββ,,1 线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iE A i均不可逆.则A 可否对角化?线性代数参考题二一、 填空题(每小题3分,满分30分) 1. 设B A ,都是5阶矩阵,且2,31=-=-B A ,则=A B2. 已知0222=++I A A ,则=+-1)(I A (其中I 是n 阶单位阵)3. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=12241031x A 设,已知矩阵A 的秩r(A)=2,则=x4.()814370122222632144-==⨯ija A 设,又ij A 是ij a 的代数余子式,则=+++44434241A A A A5.若一向量组只有唯一的极大无关组,则该向量组6.设3221232221321222),,(x tx x x x x x x x x f ++++=是正定二次型, 则t 的取值区间为7.设A 是n 阶正交矩阵,1-=A ,则()=*TA8.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=20002121x A 相似于对角阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--211,则=x9.设非齐次线性方程组b AX =的两个解为)(,,2121ξξξξ≠A 的秩为1-n ,则 b AX =的一般解=ξ .10.已知向量组[][][]1,4,2,1,0,,0,2,1,1,2,1321--==-=αααt 的秩为2,则=t 二.(8分)计算n 阶行列式ba a a ab a a a a b a D n n n n ---=212121三.(8分)求矩阵X 满足⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡1041120112201117241X 四.(10分)设[][][][]10,2,1,2,4,1,5,1,3,6,3,11,5,5,10,2,3,2,1,24321-==-=-=αααα求向量组的秩及其一个极大无关组. 五. (12分)问常数b a ,各取何值时, 方程组()()⎪⎪⎩⎪⎪⎨⎧=+++++=++++=+-=+++,5853,34232,12,1432143214324321x a x x x b x x a x x x x x x x x x 无解,有唯一解,或有无穷多解,并在有无穷多解时写出其一般解. 六. (16分)求正交变换PY X =,将二次型()323121232221321222222,,x x x x x x x x x x x x f ---++=化为标准形,并写出其标准形.七. (8分)设向量432,,,1αααα线性无关,且43214432134321243211,,,ββββαββββαββββαββββα+---=-+--=--+-=---=证明向量组4321,,,ββββ线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iI A i均不可逆。
线性代数试题及答案.

线性代数(试卷一)一、填空题(本题总计20分,每小题2分)1. 排列7623451的逆序数是_______。
2. 2. 若若122211211=a a aa ,则=16030322211211a a a a 3. 已知n 阶矩阵A 、B 和C 满足E ABC =,其中E 为n 阶单位矩阵,则CAB =-1。
4. 若A 为n m ´矩阵,则非齐次线性方程组AX b =有唯一解的充分要条件是_________ 5.设A 为86´的矩阵,已知它的秩为4,则以A 为系数矩阵的齐次线性方程组的解空间维数为__2___________。
6. 6. 设设A 为三阶可逆阵,÷÷÷øöçççèæ=-1230120011A ,则=*A 7.7.若若A 为n m ´矩阵,则齐次线性方程组0Ax =有非零解的充分必要条件是8.8.已知五阶行列式已知五阶行列式1234532011111112140354321=D ,则=++++4544434241A A A A A 9. 向量a =(2,1,0,2)T-的模(范数)______________。
10.10.若若()Tk 11=a 与()T121-=b 正交,则=k 二、选择题(本题总计10分,每小题2分)1. 1. 向量组向量组r a a a ,,,21 线性相关且秩为s ,则,则(D) (D) A.s r = B.s r £ C.r s £ D.r s <2. 2. 若若A 为三阶方阵,且043,02,02=-=+=+E A E A E A ,则=A (A)A.8 B.8-C.34D.34-3.设向量组A 能由向量组B 线性表示,则线性表示,则( d ) ( d )A.)()(A R B R £ B.)()(A R B R <C.)()(A R B R =D.)()(A R B R ³4. 设n 阶矩阵A 的行列式等于D ,则()*kA 等于_____。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重 庆 第 二 师 范 学 院 试 题
年秋季学期 期末考试
课程名称: 线性代数
适用专业: 2013移动互联网、2013软件工程、2013物联网工程、2013应用化学
试卷类别: A 卷
命题教师:
考核方式: 考试 考试方式: 闭卷
题 号:
一
二 三
四 五 总分 分 数:
试卷说明:
1. 本试卷共计 6 页,共 5 大部分,请勿漏答;
2. 考试时间为 120分钟,请掌握好答题时间;
3. 答题之前,请将试卷和答题纸上的系(部、院)、专业、学号、姓名填写
清楚;
4. 答题完毕,请将试卷整理好交回,不得带出考场。
得分 评卷人
一、选择题(本大题共5小题,每小题3分,共15分)请在每小题的空格中选择正确答案。
错选、不选均无分。
1.设A ,B 为两个n 阶矩阵,|A|=2, |B|=3, 则乘积|AB|=( )
A. 2
B. 3
C. 5
D. 6 2.设2阶方阵A 、B 满足AB=I ,且A ⎪
⎪⎭
⎫
⎝⎛--=2173,则B=( ) A. ⎪⎪⎭
⎫
⎝⎛--3172 B.
⎪⎪⎭⎫ ⎝⎛3172 C. ⎪
⎪⎭
⎫
⎝⎛--3172 D. ⎪⎪⎭
⎫ ⎝⎛2173 3.向量组()0,0,11=α,()1,0,02=α,下列向量可以由1α,2α线性表出的是( )
系(部、院) 专业 学号 姓名 ………………………密………… 封…………线…………内…………不…………要…………答…………题…………………………
审 卷 人 印制份数
A. ()0,0,2
B. ()4,2,3-
C. ()0,1,1
D. ()0,1,0- 4. 设A 为n 阶矩阵,且2=A ,则2A =( )
A. n 2
B. 12-n
C. 12+n
D. 1
5.如果向量组t 1β,,β 可由向量组s 1α,,α 线性表示,且t 1β,,β 线性无关,那么( )
A. s t ≤
B. s t <
C. s t ≥
D. s t >
得分 评卷人
二、填空题(本大题共5小题,每小题3分,共15分)请在每小题的空格中填上正确答案。
错填、不填均无分。
1.行列式某行元素全为0,则行列式的值为_________. 2.设A 为2015阶方阵,且
4=A ,则=-A _____________.
3.设矩阵⎪⎪⎪⎪⎪
⎭
⎫ ⎝⎛=400000030000002000000
100A ,则=-1
A _____________.
4. 设行列式
111221
22a a m a a =,13112321a a n a a =, 则行列式
111213
212223
a a a a a a ++为
_____________.
5.设A ,B 均为4阶矩阵,若A 可逆,秩(B )=4,那么秩(AB )=_______.
得分 评卷人
三、判断题(本大题共5小题,每小题3分,共15分)正确的打“√”,错误的打“×”。
1.包含零向量的向量组是线性无关的. ( )
2.设A ,B 同为n 阶方阵,则2222-)(B AB A B A +=-. ( )
3.向量组部分线性相关,则整体也线性相关. ( )
4. 任意的n 阶矩阵A 可以表示为对称矩阵与反对称矩阵的和. ( )
5. 矩阵A 可逆的充要条件是
0≠A . ( )
得分 评卷人
四、计算题(共35分),需要详细的计算过程。
1.(10分) 计算n 阶行列式
x a a a a x a a D a a x a a a a x
= .
0 21 1 1 2111A -⎛⎫
⎪= ⎪
⎪---⎝⎭
的逆矩阵.
3. (15分) 求方程组0=Ax 的基础解系和一般解, 其中
12111243111213300
242A ⎛⎫ ⎪
⎪= ⎪
---
⎪
-⎝⎭
.
得分 评卷人
五、证明题(共20分),需要详细的证明过程。
1. (10分) 设n 维向量i
(0, , 0, 1, 0, , 0) ,ε= 即第i 个分量为1,其余分量
为0, 则12, , , n εεε 是线性无关的.
2.(10分) 对于任意的n 阶矩阵A , 证明: T A A +是对称矩阵, T A A -是反对称矩
阵.。
