扭转(1)
扭转习题1
mB
mA
mC
n
(b)
B
A
C
3
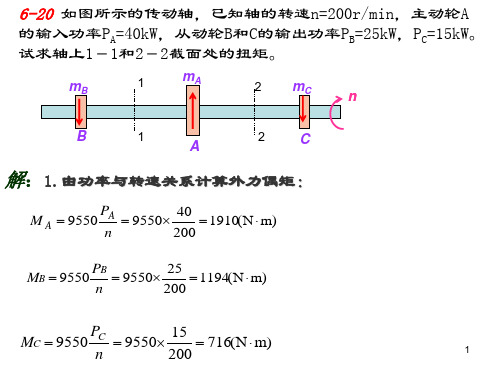
解:1.由功率与转速关系计算外力偶矩:
MA
9550 PA n
9550 36 200
1719(N m)
MB 9550 PB 9550 22 1050(N m)
n
200
MC 9550 PC 9550 14 669(N m)
(2)1-1截面的最大剪应力
(3)轴AB的最大剪应力
1 mC=0.2kNm
mB=0.1kNm
φ50 φ40
A
1D
mA=0.3kNm
解:画扭矩图
T
0.3kNm
+
C
B
0.1kNm
+
x
8
(1)在AD段上,D1=50mm,T1=300N.m
Ip1=0.1D14=0.1 ×504 =6.25×105
当ρ=20mm 时 ,
=
T1 I1
300 6.25105
20=0.9610-2(Mpa)
(2)在AD段上,R1=25mm
m ax1
T1 Ip1
R1
300 6.25105
25 1.2102 (Mpa)
(3)在DC段上, T1=300N.m, D2=40mm ,R2=20mm
Ip2=0.1D24=0.1 ×404 =2.56×105
14
6--28实心圆轴如图所示,已知输出扭矩MB=MC=1.64kN.m; MD=2.18kN.m,材料G=80Mpa,【τ】=40Mpa,【θ】=1。/m。 (1)求输入扭矩MA;
(2)试设计轴的直径;
材料力学-扭转1ppt课件

横截面上 —
max
T IP
max
IP
T
max
T WP
Ip—截面的极惯性矩,单位:m4 , mm 4
WP
Ip
max
WP —抗扭截面模量,单位:m3, mm3.
整个圆轴上——等直杆:
max
Tm a x WP
三、公式的使用条件: 1、等直的圆轴, 2、弹性范围内工作。
30
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
d
dx
d / dx-扭转角变化率
二)物理关系:
弹性范围内 max P
G → G
G
d
dx
方向垂直于半径。
28
三)静力关系:
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dxp
29
二、圆轴中τmax的确定
结论:
横截面上 0, 0 0 0
根据对称性可知剪应力沿圆周均匀分布;
t D, 可认为剪应力沿壁厚均匀分布,
且方向垂直于其半径方向。
t
D
20
3、剪应力的计算公式:
T
AdA.r0
2 0
r0
2td
r02t2
d
T
2r0 2t
薄壁圆筒横截面上的剪应力计算式
21
二、关于剪应力的若干重要性质
例题: 1、一传动轴作200r/min的匀速转动,轴上装有五个轮子。 主动轮2输入的功率为60kW,从动轮1、3、4、5依次输出的 功率为18kW、12kW、22kW和8kW。试作出该轴的扭矩图。
扭转1

GI p
d
dx
d
dx
T GI p
代入物理关系式
扭转变形计算式
G
d
dx
得:
T
Ip
圆轴扭转时横截面上任一点的剪应力计算式。
二、圆轴中τmax的确定
横截面上 —
max
T IP
max
IP
T
max
T WP
Ip—截面的极惯性矩,单位:m4 , mm 4
WP
Ip
max
第四章 扭 转
§4-1 扭转概念和工程实例 §4-2 自由扭转杆件的内力计算 §4-3 关于切应力的若干重要性质 §4-4 圆轴扭转时横截面上的应力 §4-5 扭转变形 扭转强度和刚度计算 §4-6 圆轴扭转破坏分析 §4-7 矩形截面杆的自由扭转
§4-1 扭转概念和工程实例
一、扭转的工程实例 1、螺丝刀杆工作时受扭。
0
2π( 4
)
d/2
πd
4
4 0 32
Wp
Ip d /2
πd 3 16
空心圆截面:
D
Ip
2 d
2π
3
d
2
d
π D4 d 4
D
32
πD4 1 4
32
D d
O
d A 2π d
Wp
Ip D/2
π
D4 d 16D
4
πD3 1 4
2、扭矩的符号规定:按右手螺旋法则判断。
右手的四指代表扭矩的旋转方向,大拇指代表其矢量方向,若 其矢量方向与截面的外法线方向相同,则扭矩规定为正值,反之为 负值。
材料力学 扭转(1)

注意:对于空心圆截面
π D 4 d 4 Ip 32
π D 3 d 3 Wp 16
四、扭转强度计算 1、强度条件:
max [ ]
变截面圆轴: max
M W p max
M n max 等截面圆轴: max Wp
2、强度条件应用:
4
D 32
AC 外
d 4 6.38 cm 4
(3)计算应力
AC max
T D T I P1 2 WP1
37.5 106 Pa 37.5 MPa
0 0
Mn
t布;
t D, 可认为切应力沿壁厚均
匀分布, 且方向垂直于其半径方向。
3、切应力的计算公式:
Mn
dA.r
A 2
0 2
2
0
r0 td r0 t 2
d
Mn 2 2r0 t
薄壁圆筒横截面上的切应力计算式
m
x
0, M n T 0
Mn T
取右段为研究对象:
T
Mn Mn
x
T
m
x
0, T M n 0
Mn T
内力偶矩——扭矩 M n。
x
3、扭矩的符号规定:按右手螺旋法则判断。
右手的四指代表扭矩的旋转方向,大拇指代表其矢量方向,若其矢 量方向与截面的外法线方向相同,则扭矩规定为正值,反之为负值。
即该轴满足强度条件。
n 360 r/ min 例 AB轴传递的功率为 N 7.5 kW ,转速 。 如图所示,轴AC段为实心圆截面,CB段为空心圆截面。 , 已知D 3 cm d 2 cm 。试计算AC以及CB段的最大切应力。
扭转角公式(一)

扭转角公式(一)扭转角公式什么是扭转角公式?扭转角公式是用来计算两条直线之间的扭转角的数学公式。
它在几何学和物理学中非常常见,被广泛应用于各种领域。
扭转角公式的公式表达式扭转角公式的一般表达式如下:θ = arccos((a·b) / (|a|·|b|))其中,θ代表两条直线之间的扭转角,a和b分别是两条直线的方向向量。
·表示向量的点积,|a|表示向量a的模。
扭转角公式的解释扭转角公式用于计算两条直线之间的夹角,其基本思想是计算两条直线方向向量的夹角。
当两条直线的方向相同时,夹角为0度;当两条直线的方向完全相反时,夹角为180度。
以三维空间为例,假设有两条直线a和b,它们的方向向量分别为a = (1, 0, 0)和b = (0, 1, 0)。
根据扭转角公式,我们可以计算出它们之间的夹角θ。
θ = arccos((1·0 + 0·1 + 0·0) / (sqrt(1^2+0^2+0^2)·s qrt(0^2+1^2+0^2)))= arccos(0 / (1·1))= arccos(0)= 90°所以,直线a和直线b之间的夹角θ为90度。
扭转角公式的应用举例1. 机械工程中的轴扭转角计算在机械工程中,轴的扭转角是一个非常重要的参数。
通过扭转角公式,可以计算出轴在旋转过程中的扭转程度,从而为该设计提供参考依据。
2. 电子游戏中的摄像机跟踪角度计算在电子游戏中,摄像机通常会跟踪某个对象或角色。
通过计算摄像机与目标之间的扭转角,可以确定摄像机应该以何种角度跟踪目标,从而提供更好的游戏体验。
3. 导航系统中的车辆与目标之间的角度计算在导航系统中,需要计算车辆与目标之间的夹角,从而确定车辆应该如何转向以达到目标。
扭转角公式可以用于计算这种夹角,提供导航系统更准确的指引。
总结扭转角公式是一种用于计算两条直线之间夹角的数学公式。
材料力学(扭转) PPT课件

y
3、斜截面上的 应力分析
x
n
x
z
t
Fn 0 dA zdAcos sin dAsin cos 0
Ft 0 dA dAcos cos dAsin sin 0
sin 2
讨论:
外力偶矩的计算、扭矩和扭矩图
功率、转速和外力偶矩之间的关系
ω = 2π n /60 ,1 kW = 1000 N•m/s
功率:P 角速度: 转速:n 外力偶矩:T 功率、转速和外力偶矩之间的关系:
T P P 2n
若功率P的单位为千瓦,转速n的单位为转/分:
T 9549 P ( N m) n
T
第三章 扭转
§3-2 外力偶矩、扭矩和扭矩图
例4-1 NA=19kW,NB=44kW,
TA
NC=25kW, n=150rpm
求:作图示传动轴的扭矩图
解:1. 求外力偶
TA
TA= 9549 19 =1210Nm
150
同样 TB=2800Nm, TC=1590Nm
TA
Mn
2.截面法求内力( 设正法)
Mn IPFra bibliotek变形
Mnl GI p
强度条件 max
Mn Wp
刚度条件 d Mn 180
dx G I p
第三章的基本要求
1.掌握根据轴的传递功率和转速计算外力偶矩;
2.掌握扭转时内力(即扭矩)的计算以及扭矩图的画 法;
3.掌握扭转切应力的计算方法;
45
第三章 扭转
材料力学 03章1-3扭转

TB
1210
Tn 2
x
Tn
-1590
A
B
C
19 TA 9549 1210 Nm 150 同样 TB =2800Nm, TC =1590Nm
Tn
-2800
x
-1590
接下来该讨论圆轴扭转时的应力问题了!
关于应力的三个问题:
存在什么应力 应力如何分布 应力如何计算 TK 先研究一个比较简单的问题 TK A
MA A
MD D x
PA 60kW , PB 10kW P C 20kW , P D 30kW
试画轴的扭矩图。
1面 MB
3面
T3
MD D x
解:求外力偶矩
B MB B
P 由M 9549 解得: n M A 1910 N m M B 318 N m M C 637 N m M D 955 N m
Me
Pk t Pk Pk M t
Me
e
Me
n r / min(转 / 分);
rad /(弧度 9549 Pk 2 n n M e 9549 60 n
2. 扭矩
横截面上的内力偶矩
确定方法:截面法 符号:T 由静平衡确定其大小 正负规定:右手法则
TK
y
dy o dx
a
,
b
c x
TK
( dy)
与
( dx)
,
z
d
组成一力偶,由力偶平衡得:
( dy)dx ( dx)dy 0
,
,
剪应力互等定理 :在相互垂直的两个面上,剪应力必然成 对出现,且大小相等,方向或指向、或背离两面的交线。
材料力学 第 三 章 扭转

以及间距不变,半径仍为直线。
定性分析横截面上的应力
(1)∵ε = 0∴σ = 0
(2)∵ γ ≠ 0∴τ ≠ 0
因为同一圆周上切应变相同,所以同 一圆周上切应力大小相等,并且方向 垂直于其半径方向。
切应变的变化规律:
D’
取楔形体
O1O2ABCD 为 研究对象
γ ≈ tgγ = DD' = Rdϕ
dx dx
微段扭转
变形 dϕ
γ ρ ≈ tgγ ρ = dd′ = ρ ⋅ dϕ
dx dx
γ
ρ
=
ρ
dϕ
dx
dϕ / dx-扭转角变化率
圆轴横截面上任一点的切应变γρ
与该点到圆心的距离ρ成正比。
(二)物理关系:由应变的变化规律→应力的分布规律
弹性范围内 τ max ≤ τ P
τ max
=
T
2π r 2t
=
180 ×103
2π × 0.132× 0.03
= 56.5MPa
(2) 利用精确的扭转理论可求得
τ max
=
π D3
T
(1−α 4 )
16
=
180 ×103
π×
0.293
⎡ ⎢1 −
⎜⎛
230
⎟⎞
4
⎤ ⎥
16 ⎢⎣ ⎝ 290 ⎠ ⎥⎦
= 62.2MPa
思考题
由两种不同材料组成的圆轴,里层和外层材料的 切变模量分别为G1和G2,且G1=2G2。圆轴尺寸如 图所示。圆轴受扭时,里、外层之间无相对滑动。 关于横截面上的切应力分布,有图中(A)、(B)、 (C)、(D)所示的四种结论,请判断哪一种是正 确的。
材料力学扭转

材料力学扭转材料力学是研究材料在外力作用下的变形和破坏规律的一门学科,而扭转则是材料力学中非常重要的一种变形形式。
在工程实践中,我们经常会遇到各种扭转现象,比如轴承、螺纹、螺栓等零部件的扭转变形。
因此,了解材料力学中的扭转现象对于工程设计和实际应用具有重要意义。
首先,我们来看一下什么是扭转。
扭转是指材料在外力作用下沿着一定轴线发生的旋转变形。
在扭转过程中,材料内部会受到剪切应力的作用,从而导致材料发生扭转变形。
扭转变形不仅会影响材料的外观和尺寸,还会对材料的力学性能产生影响。
在材料力学中,我们通常用剪切模量来描述材料的扭转性能。
剪切模量是指材料在扭转过程中所表现出的抗扭转能力。
剪切模量越大,材料的抗扭转能力就越强,反之则越弱。
因此,在工程设计中,我们需要根据材料的剪切模量来选择合适的材料,以满足工程的扭转性能要求。
除了剪切模量,材料的断裂韧性也是影响材料扭转性能的重要因素。
断裂韧性是指材料在扭转过程中抵抗断裂的能力。
材料的断裂韧性越大,其扭转性能就越好,能够更好地抵抗扭转变形和破坏。
因此,在工程设计中,我们还需要考虑材料的断裂韧性,以确保材料在扭转过程中不会发生过早的断裂。
此外,材料的微观结构也会对其扭转性能产生影响。
晶粒的大小、形状以及晶界的性质都会影响材料的扭转性能。
一般来说,晶粒越细小,晶界越强化,材料的扭转性能就会越好。
因此,在材料的制备过程中,我们需要通过控制材料的微观结构来提高其扭转性能。
总的来说,材料力学中的扭转现象是工程设计中不可忽视的重要问题。
了解材料的扭转性能,选择合适的材料,并通过控制材料的微观结构来提高其扭转性能,对于保证工程零部件的稳定性和可靠性具有重要意义。
希望本文能够对大家对材料力学中的扭转问题有所帮助。
第8章扭转[1]
![第8章扭转[1]](https://img.taocdn.com/s3/m/8f682ce019e8b8f67c1cb9ff.png)
• 强度条件- 破坏形式
塑性材料
脆性材料
• 强度条件: 最大切应力不得超过材料的许用切
应力[τ],即 τmax ≤ [τ]
强度校核、设计轴的截面和确定最大扭力。
• 横截面的合理设计 :
τ max
=
TR Ip
=
T Wp
如果实心圆轴和空心圆轴承担相同的扭矩,则
空心轴消耗的材料少,更轻,更经济。
• 例5 有一传动轴,已知轴的转速 n=100rpm,传递功率N=10kw,许用剪应
• 静力学方面
∫ ρτ ρ dA = T
A
τρ
= Gρ
dφ
dx
dφ = T
dx GI p
τρ
=
Tρ
Ip
∫ I p = ρ 2dA 称为极惯性矩 A
• 公式分析
1. 式中:T—扭矩,IP— 横截面极惯性矩, GIP —轴截 面的抗扭刚度 。
2. 圆轴受扭的剪应力公式,式中ρ为计算之点到圆心的 距离。τρ沿半径线性分布,其沿扭矩方向垂直于半
单元体
• 切应力互等定律 在单元体的两个互相垂直的截面
上,切应力必然成对出现,其大小相等,方向相反, 同时指向(或背离)两截面的交线。
τ= τ´
剪切虎克定律
• 在线弹性范围内,切应力和切应变成线性关系。
τ =G γ
• G- 剪切弹性模量,其值与材料有关。
8.5 实心圆轴横截面上的应力及强度条件
A
B
解
• 例9 图示阶梯圆轴,已知D=20mm,L=0.5m,
M=10Nm,剪切弹性模量G=80GPa,许用扭转角
[θ]=0.5°/m,试画扭矩图,并校核轴的刚度。
解 绘出扭矩图,校核刚
扭转时间的公式(一)

扭转时间的公式(一)扭转时间的公式1. 时间加速公式•公式:T’ = T / (1 + v/c)–T’为运动时钟的时间–T为静止时钟的时间–v为物体的相对速度–c为光速•示例解释:假设有两个人,一个处于静止状态,一个以接近光速的速度运动。
他们各自携带一个时钟,并同时开始运行。
根据时间加速公式,运动的人的时钟会比静止的人慢,这是因为运动的人相对于静止的人经历了更多的时间扭曲。
2. 时间膨胀公式•公式:T’ = T * sqrt(1 - v2/c2)–T’为运动时钟的时间–T为静止时钟的时间–v为物体的相对速度–c为光速•示例解释:假设有两个人,一个处于静止状态,一个以接近光速的速度运动。
他们各自携带一个时钟,并同时开始运行。
根据时间膨胀公式,运动的人的时钟会比静止的人快,这是因为运动的人相对于静止的人经历了更多的时间扭曲。
3. 时间收缩公式•公式:L’ = L * sqrt(1 - v2/c2)–L’为物体在运动方向上的长度–L为物体在静止状态下的长度–v为物体的相对速度–c为光速•示例解释:假设有一根棍子,在静止状态下测量出长度为L。
当这根棍子以接近光速的速度运动时,测量时发现其长度收缩为L’。
这是因为随着物体运动速度的增加,物体在运动方向上的长度会发生收缩。
4. 双生子佯谬•公式:Δt = Δt’ / sqrt(1 - v2/c2)–Δt为地面上的人测量的时间–Δt’为以接近光速运动的人测量的时间–v为物体的相对速度–c为光速•示例解释:假设有一对双胞胎,其中一个留在地球上,另一个乘坐航天飞船以接近光速的速度飞行。
当飞船返回地球时,地面上的双胞胎会发现在他离开地球的时间段内自己的年龄比飞船上的双胞胎年龄更多。
这是因为以接近光速运动的人在时间上经历了更少的扭曲。
5. 相对论能量-动量关系•公式:E^2 = (mc2)2 + (pc)^2–E为物体的总能量–m为物体的静止质量–c为光速–p为物体的动量•示例解释:相对论能量-动量关系用于描述物体在运动过程中的能量与动量之间的关系。
9扭转-1

扭矩计算
已知:Me1= 6M
Me2= M ,Me3= 2M
M = 3M Me1 1 Me2
2
Me3 3 Me4
e4
1
2
3
求:计算各段扭矩
Me1
Me2 T2 T2 Me3 Me4 解:∑Mx=0,T2-Me1 +Me2 = 0
T2=Me1-Me2= 5M
∑Mx=0 , -T2+Me3+Me4= 0 , T2= Me3+Me4 = 5M
4.1 概述
一、工程实例
Me
Me
11
传动轴 12
13
Me
Me φAB
A
B
l
二、扭转的特点
受力特点:扭转外力偶; 变形特点:横截面绕轴线转过不同角度。 相对扭转角 φAB : B 截面相对A 截面
绕轴线转过的角度。 轴 :以扭转变形为主的杆件,如圆轴。
14
三、传动轴上的外力偶矩计算
N Me = 9549 n ( N·m)
NA n
= 9549 × 150 300
= 4774.5 N ⋅ m
MB
=
9549
NB n
=
9549 ×
75 300
= 2387.3 N ⋅ m
MC
= 9549 NC n
= 9549 × 45 300
= 1432.4 N ⋅ m
MD
= 9549 N D n
=
9549 × 30 300
= 954.9 N ⋅ m
25
Me
T
τ
2. 横截面上的剪应力
各点剪应变相同,所以 各点剪应力τ相同, 分布规律: ⅰ 沿壁厚均匀分布; ⅱ 垂直于所在半径; ⅲ 方向:对轴线的矩与
材料力学-第四章 扭转_1

该轴满足强度条件的要求。
§5-5圆轴的扭转变形与刚度条件
d T d x GI p
T d dx GI p
T dx GI p l
d
Tl 若T const,则 GIp
比较拉压变形:
Nl l EA
公式适用条件:
1)当p(剪切比例极限)公式才成立
2)仅适用于圆杆(平面假设对圆杆才成立)
扭矩T的符号规定:
n
n
T Me
㈩
T Me
㈩
[例5-1]图示传动轴,主动轮A输入功率NA=50 马力,从 动轮B、C、D输出功率分别为 NB=NC=15马力 ,ND=20马 力,轴的转速为n=300转/分。作轴的扭矩图。
解:
NA 50 M A 7024 7024 1170 N m n 300 NB 15 M B M C 7024 7024 351 Nm n 300 NC 20 M D 7024 7024 468N m n 300
外表面dx rd d r dx
横截面上距形心为 的任一点处应变
d
dx d d
dx
(a)
2. 物理关系
剪应力方向垂直于半径。根据剪切胡克定律, 当剪 应力不超过材料的剪切比例极限时 d G G (b) dx
(5-6) (5-7)
max
Wt
T max T Wt Ip
Ip
max
(抗扭截面模量 )
max
max
4.圆与圆环的极惯性矩 I p和抗扭截面模量 Wt
Ip
d /2
0
Байду номын сангаас
扭转变形的生活例子

扭转变形的生活例子
扭转变形的例子:拧毛巾、拧衣物。
凡物体受到外力而发生形状变化谓之“形变”。
物体由于外因或内在缺陷,物质微粒的相对位置发生改变,也可引起形态的变化。
形变的种类有:
1、纵向形变:杆的两端受到压力或拉力时,长度发生改变;
例如:拉橡皮筋。
2、体积形变:物体体积大小的改变;
例如:吹气球。
3、切变:物体两相对的表面受到在表面内的(切向)力偶作用时,两表面发生相对位移,称为切变;
例如:放在桌子上切过的苹果。
4、扭转:一个圆柱状物体,两端各受方向相反的力矩作用而扭转,称扭转形变;
例如:拧毛巾
5、弯曲:两端固定的钢筋,因负荷而弯曲,称弯曲形变。
无论产生什么形变,都可归结为长变与切变。
材料力学-扭转1
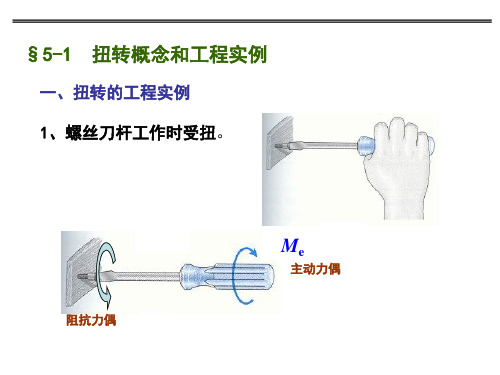
max
T Wt
1930 29 106
66.7106 Pa
66.7MPa [ ] 70MPa 满足强度要求
例 如把上例中的传动轴改为实心 轴,要求它与原来的空心轴强度相 同,试确定其直径。并比较实心轴 和空心轴的重量。
解:当实心轴和空心轴的最大应力同 为[]时,两轴的许可扭矩分别为
解:1)作扭矩图
Tmax 4.5KN m
2)设计轴的直径
由强度条件:
max
Tm a x WP
≤
由刚度条件:
max
Tmax GI p
180
[ ]
取 d = 102 mm
d 3 16Tmax 66mm
[ ]
d 4
32Tmax 180
G 2[ ]
102mm
3)计算全轴的相对扭转角D-A
(2)求所需键数n。
P
§5-6 扭转静不定问题
扭转静不定问题
已知:AB 阶梯轴两端固定,C 处作用 A 外力偶矩Me, AC抗扭刚度为G1Ip1, CB抗扭刚度为G2Ip2 。求:轴的扭矩。
Me
CB Me
解:1)静力学关系
mx 0, Me M A M B 0
2)变形几何关系
BA CA BC 0
G → G
G
d
dx
方向垂直于半径。
三)静力关系:
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dx
G
d
dx
T Ip
二、圆轴中τmax的确定
横截面上 —
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
取右段为研究对象:
x
m
x
0, T M n 0
T
x
Mn T
内力偶矩——扭矩 M n。
3、扭矩的符号规定:按右手螺旋法则判断。
右手的四指代表扭矩的旋转方向,大拇指代表其矢量方向,若其矢 量方向与截面的外法线方向相同,则扭矩规定为正值,反之为负值。
T
Mn
Mn
T
+
Mn
-
4、内力图(扭矩图)
M
n 2
τ
2 r0 t
τ
p
τ
s
τ
b
r0 l
γ
剪切虎克定律:
在弹性范围内切应力与 切应变成正比关系。
p,
G 剪切虎克定律
G —— 剪切弹性模量 2、三个材料常数E,G, 之间关系
弹性模量E,剪切弹性模量G,泊松比 是表征材料性质的三个常 数,其数值均由实验确定。对于各向同性材料,可以证明这三个常数之
y
'
dy
d x d z
O
'
假设单元体四个侧面上的 剪应力分别为 , , , 。 x x y y 根据静力平衡条件 d yd z F y 0 自动满足
x
z
dx
Fx 0
存在τ'
y
'
dy
d x d z
d yd z
O
M
z
0
'
3、切应力的计算公式:
M
n
A
dA . r0
2 2
2
0
r0 td r0 t 2
M
d
n 2
2 r0 t
薄壁圆筒横截面上的切应力计算式
二、关于切应力的若干重要性质
l
1、剪切虎克定律
为扭转角
r0 l
即
r0 l
做薄壁圆筒的扭转试验可得 m——
d / dx-扭转角变化率
2、物理关系
由应变的变化规律→应力的分布规律
弹性范围内
max P
→
G
G
G
d dx
方向垂直于半径。
3、静力关系: 由横截面上的扭矩与应力的关系→应力的计算公式
M
n
A d A G
2
d dx
B
T1 (9.55 10
3
C
A
D
500 300
3
) N m 15.9kN m
150 ) N m 4.78kN m
T2 T3 (9.55 10
300 200 3 T4 (9.55 10 ) N m 6.37kN m 300
二、分别计算各段的扭矩
表示构件各横截面扭矩沿轴线变化的图形。 扭矩图作法:同轴力图。
例1 一传动轴如图,转速 n = 300r/min; 主动轮输入的功率 P1=500kW,三个从动轮输出的功率分别为:P2= 150kW, P3= 150kW, P4= 200kW。试作轴的扭矩图。 解:一、计算作用
在各轮上的外力偶矩
T2 T3 T1 T4
M n ( x) M A mx
M n ( x) m(l x)
3、绘扭矩图
表示扭矩沿杆件轴线变化的图线(Mn- x曲线)-扭矩图。
§3-3 薄壁圆管的扭转 切应力的重要性质
一、薄壁圆管横截面上的应力 (壁厚
t 1 r 10 0
, r0为平均半径)
1、实验观察: 2、变形规律:
圆周线——形状、大小、间距不 变,各圆周线只是绕轴线转动了 一个角度。 纵向线——倾斜了同一个角度, 小方格变成了平行四边形。
m
60 N k 2n
9.55
Nk n
(kN m)
二、扭转杆件的内力——扭矩及扭矩图
1、扭转杆件的内力 圆轴受扭时其横截面上的内力偶矩称为扭矩,用符号 T 表示。扭矩大小可利用截面法来确定。 2、截面法求内力 T T 取左段为研究对象:
m
x
0,
Mn T 0
Mn T
T
Mn Mn
A dA
2
Mn
τρ
dA
令 I p A dA
d dx T GI p
M
n
GI
d
p
ρ
dx
扭转变形计算式
d G 代入物理关系式 dx
得:
Mn Ip
圆轴扭转时横截面上任一点的剪应力计算式。
二、圆轴中τmax的确定
横截面上 — max
M IP
n
M
nmax
[ ]
3)确定外荷载: M nmax≤ W P [ ] m
例 已知 Mn=1.5 kN . m,[ ] = 50 MPa,试根据强度条件设 t 计实心圆轴与 a = 0.9 的空心圆轴。 解:1. 确定实心圆轴直径
max [ ]
max
Mn πd
3
Mn π 16
Me
主动力偶
阻抗力偶
2、汽车方向盘的转动轴工作时受扭。
3、机器中的传动轴工作时受扭。
4 、汽车传动轴
传动轴
5、拧螺母的不同方式
二、扭转的概念
受力特点:杆两端作用着大小相等、方向相反的力偶, 且力偶作用面垂直于杆的轴线。
变形特点:杆任意两截面绕轴线发生相对转动。
Me
mA
阻抗力偶
主动力偶
me
发生扭转变形的杆——轴。
圆周线——形状、大小、间距不 变,各圆周线只是绕轴线转动了 一个角度。
纵向线——倾斜了同一个角度 ,小方格变成了平行四边形。
'
结论:
横截面上
0, 0
0 0
Mn
t
D
根据对称性可知切应力沿圆周均匀分布;
t D , 可认为切应力沿壁厚均
匀分布, 且方向垂直于其半径方向。
D’
取楔形体O1O2ABCD 为研究对象
tg
DD ' dx Rd dx
楔形体扭转变形
tg
dd dx
d
dx
tg
DD ' dx
Rd dx
tg
dd dx
d
dx
d dx
第三章
§3-1 扭转的概念
§3-2 扭矩和扭矩图
扭 转
外力偶矩的计算
§3-3 薄壁圆管的扭转 切应力的重要性质
§3-4 圆轴扭转时的应力和强度条件
§3-5 圆轴扭转时的变形和刚度计算
§3-6 圆轴扭转破坏现象分析 §3-7 矩形截面杆的扭转
§3-1
扭转的概念
一、扭转的工程实例
1、螺丝刀杆工作时受扭。
M n max Wp
变截面圆轴: max
M W p
max
2、强度条件应用: 1)校核强度: max 2)设计截面尺寸:
M
n max
WP
≤
WP D 3 实心 , 16 3 D 4 (1 ) 空心 . 16
WP≥
1、实心圆截面:
Ip
d
dA
2 A
2 0
(2 π d )
2
4
d
O
2 π(
4
4
d /2
)
0
πd 32
Wp
Ip d /2
πd 16
3
d A 2π d
2、空心圆截面:
D
Ip
2 d 2
2 π
π
3
d
d
4
d D
32
D
4
4
D d
O
πD 32
x
d y d z d x d x d z d y
得
z
dx
切应力互等定理:
在相互垂直的两个面上,切应力总是成对出现,并 且大小相等,方向同时指向或同时背离两个面的交线。
§3-4 圆轴扭转时的应力和强度条件
一、圆轴扭转时横截面上的应力
1、几何关系:
由实验找出变形规律 →应变的变化规律 1)、实验观察变形规律: 圆周线——形状、大小、间 距不变,各圆周线只是绕轴 线转动了一个不同的角度。 纵向线——倾斜了同一个角 度,小方格变成了平行四边 形。
2)、扭转平面假设: 变形前的横截面,变形后仍为平面,且形状 、大小 以及间距不变,半径仍为直线。 3)定性分析横截面上的应力
(1) 0 0
(2) 0 0 因为同一圆周上剪应变相同,所以同一圆周上切应力 大小相等,并且方向垂直于其半径方向。
4)剪应变的变化规律:
TA A
Ⅰ
TB
Ⅱ
TC
B
22
C
解: 1、求内力,作出轴的扭矩图
Mn图(kN· m)
14
2、计算轴横截面上的最大切应力并校核强度
22
Mn图(kN· m)
AB段
1 , max
M
n1
22 10 N mm
6
14
