离散数学第2章关系
离散数学第二章关系

例9 .设A={1,2,3,4} ,B={2,4,6,8,10} 。 R={(1,2),(2,4),(3,6)}。
则 (R) = {1,2,3}A , (R) = {2,4,6}B 。
二.关系的一些关联性质 17
离散数学
定理1. 设R1,R2 A×B是两个关系。若 R1 R2 ,则
(1)保序性: (R1) (R2) ; (2)保序性: (R1) (R2) ;
注:笛卡尔(1596-1650 ),法国数学家, 1637年发表《方法论》之 一《几何学》,首次提出坐标及变量概念。这里是其概念的推广。
定义2. • 二个集合A,B的(二维或二重)叉积定义为 A×B ={(a, b): a A bB} ; •其元素——二元组(a, b)通常称为序偶或偶对(ordered
故 (R1)∩ (R2) = {1,2 }
21
离散数学
所以 (R1)∩ (R2) (R1 ∩ R2) 。
元素aA和集合A1A在关系R A×B下的关联集 (1)a的R-关联集(R-relative set of a):
R(a)={b : bBaRb }B ;
(2) A1的R-关联集(R-relative set of A1): R(A1)={b : bB (aA1)(aRb) }B 。
•当A=B时,即RA×A,则称R是A上的一个二元关 系。
例1 . 设A是西安交通大学全体同学组成的集合。 11
离散数学
R={(a,b) : aAbAa与b是同乡}A×A 于是,R是西安交通大学同学之间的同乡关系。
例2 . 设A是某一大家庭。
R1 = {(a,b) : aAbAa是b的父亲或母亲}A×A R2 = {(a,b) : aAbAa是b的哥哥或姐姐}A×A R3 = {(a,b) : aAbAa是b的丈夫或妻子}A×A 于是,
《离散数学》课件-第二章 谓词逻辑(A)

• 谓词是用来说明个体的性质或个体间的关系。
• 例如,小王是个大学生
•
谓词
•
个体词
3大于2
个体词
个体词
谓词
2
谓词
• 形如“b是A”类型的命题可表达为A(b);
• 表示多个个体间关系的命题,可表达为B(a,b),或P(a,b, c)
• 定义2.1.2 和一个个体相联系的谓词称为一元谓词,和二个 个体相联系的谓词称为二元谓词,和n个个体相联系的谓词 称为n元谓词。
• yxP(x,y)表示命题:“存在实数y,对每一个实数x,都 有x+y>10成立”,这是个假命题,真值为0。
• 注意:除非所有量词都是全称量词或存在量词,否则,多个 量词同时出现时,不能随意颠倒量词的顺序,颠倒后会改变 原命题的含义。
18
2.2 谓词演算公式
• 一个谓词P和n个个体变元,如x1,x2,x3, xn,表示成P(x1,x2,x3,
都是谓词公式。 • 如果A是谓词公式,x是其中的任一变元,则xA和xA都是谓
词公式。 • 当且仅当有限次地应用上面的步骤得到的符号串才是谓词公式。
20
量词的辖域及变元的约束
• 定义2.2.2 • 谓词公式xA和xA中出现在量词和后面的变元x称为量词的指导变元。 • 每个量词后面的最小的谓词子公式,称为该量词的辖域。 • 在量词的辖域中,x的所有出现都称为约束出现。约束出现的变元称为约束
• 一个谓词常项P和几个个体变元如x,y,z,表示成P(x,y,z, )的形式,称为命题函数,其中的个体变元可以代表任意一个个体。
• 注意:命题的谓词表达式是有真值的,命题函数的真值是不确定的。
4
例题 • 写出下列命题的谓词表达式。
离散数学知识点总结

总结离散数学知识点第二章命题逻辑1.→,前键为真,后键为假才为假;<—>,相同为真,不同为假;2.主析取范式:极小项(m)之和;主合取范式:极大项(M)之积;3.求极小项时,命题变元的肯定为1,否定为0,求极大项时相反;4.求极大极小项时,每个变元或变元的否定只能出现一次,求极小项时变元不够合取真,求极大项时变元不够析取假;5.求范式时,为保证编码不错,命题变元最好按P,Q,R的顺序依次写;6.真值表中值为1的项为极小项,值为0的项为极大项;7.n个变元共有n2个极小项或极大项,这n2为(0~n2-1)刚好为化简完后的主析取加主合取;8.永真式没有主合取范式,永假式没有主析取范式;9.推证蕴含式的方法(=>):真值表法;分析法(假定前键为真推出后键为真,假定前键为假推出后键也为假)10.命题逻辑的推理演算方法:P规则,T规则①真值表法;②直接证法;③归谬法;④附加前提法;第三章谓词逻辑1.一元谓词:谓词只有一个个体,一元谓词描述命题的性质;多元谓词:谓词有n个个体,多元谓词描述个体之间的关系;2.全称量词用蕴含→,存在量词用合取^;3.既有存在又有全称量词时,先消存在量词,再消全称量词;第四章集合1.N,表示自然数集,1,2,3……,不包括0;2.基:集合A中不同元素的个数,|A|;3.幂集:给定集合A,以集合A的所有子集为元素组成的集合,P(A);4.若集合A有n个元素,幂集P(A)有n2个元素,|P(A)|=||2A=n2;5.集合的分划:(等价关系)①每一个分划都是由集合A的几个子集构成的集合;②这几个子集相交为空,相并为全(A);6.集合的分划与覆盖的比较:分划:每个元素均应出现且仅出现一次在子集中;覆盖:只要求每个元素都出现,没有要求只出现一次;第五章关系1.若集合A有m个元素,集合B有n个元素,则笛卡尔A×B的基数为2种不同的关系;mn,A到B上可以定义mn2.若集合A有n个元素,则|A×A|=2n,A上有22n个不同的关系;3.全关系的性质:自反性,对称性,传递性;空关系的性质:反自反性,反对称性,传递性;全封闭环的性质:自反性,对称性,反对称性,传递性;4.前域(domR):所有元素x组成的集合;后域(ranR):所有元素y组成的集合;5.自反闭包:r(R)=RUI;x对称闭包:s(R)=RU1-R;传递闭包:t(R)=RU2R U3R U……6.等价关系:集合A上的二元关系R满足自反性,对称性和传递性,则R称为等价关系;7.偏序关系:集合A上的关系R满足自反性,反对称性和传递性,则称R是A上的一个偏序关系;8.covA={<x,y>|x,y属于A,y盖住x};9.极小元:集合A中没有比它更小的元素(若存在可能不唯一);极大元:集合A中没有比它更大的元素(若存在可能不唯一);最小元:比集合A中任何其他元素都小(若存在就一定唯一);最大元:比集合A中任何其他元素都大(若存在就一定唯一);10.前提:B是A的子集上界:A中的某个元素比B中任意元素都大,称这个元素是B的上界(若存在,可能不唯一);下界:A中的某个元素比B中任意元素都小,称这个元素是B的下界(若存在,可能不唯一);上确界:最小的上界(若存在就一定唯一);下确界:最大的下界(若存在就一定唯一);第六章函数2种不同的关系,有m n种不同的函1.若|X|=m,|Y|=n,则从X到Y有mn数;2.在一个有n个元素的集合上,可以有22n种不同的关系,有n n种不同的函数,有n!种不同的双射;3.若|X|=m,|Y|=n,且m<=n,则从X到Y有A m n种不同的单射;4.单射:f:X-Y,对任意x,2x属于X,且1x≠2x,若f(1x)≠f(2x);1满射:f:X-Y,对值域中任意一个元素y在前域中都有一个或多个元素对应;双射:f:X-Y,若f既是单射又是满射,则f是双射;5.复合函数:fºg=g(f(x));6.设函数f:A-B,g:B-C,那么①如果f,g都是单射,则fºg也是单射;②如果f,g都是满射,则fºg也是满射;③如果f,g都是双射,则fºg也是双射;④如果fºg是双射,则f是单射,g是满射;第七章代数系统1.二元运算:集合A上的二元运算就是2A到A的映射;2.集合A上可定义的二元运算个数就是从A×A到A上的映射的个数,即从从A×A到A上函数的个数,若|A|=2,则集合A上的二元运算的个数为2*22=42=16种;3.判断二元运算的性质方法:①封闭性:运算表内只有所给元素;②交换律:主对角线两边元素对称相等;③幂等律:主对角线上每个元素与所在行列表头元素相同;④有幺元:元素所对应的行和列的元素依次与运算表的行和列相同;⑤有零元:元素所对应的行和列的元素都与该元素相同;4.同态映射:<A,*>,<B,^>,满足f(a*b)=f(a)^f(b),则f为由<A,*>到<B,^>的同态映射;若f是双射,则称为同构;第八章群1.广群的性质:封闭性;半群的性质:封闭性,结合律;含幺半群(独异点):封闭性,结合律,有幺元;群的性质:封闭性,结合律,有幺元,有逆元;2.群没有零元;3.阿贝尔群(交换群):封闭性,结合律,有幺元,有逆元,交换律;4.循环群中幺元不能是生成元;5.任何一个循环群必定是阿贝尔群;第十章格与布尔代数1.格:偏序集合A中任意两个元素都有上、下确界;2.格的基本性质:1) 自反性a≤a 对偶: a≥a2) 反对称性a≤b ^ b≥a => a=b对偶:a≥b ^ b≤a => a=b3) 传递性a≤b ^ b≤c => a≤c对偶:a≥b ^ b≥c => a≥c4) 最大下界描述之一a^b≤a 对偶 avb≥aA^b≤b 对偶 avb≥b5)最大下界描述之二c≤a,c≤b => c≤a^b对偶c≥a,c≥b =>c≥avb6) 结合律a^(b^c)=(a^b)^c对偶 av(bvc)=(avb)vc7)等幂律a^a=a 对偶 ava=a8) 吸收律a^(avb)=a 对偶 av(a^b)=a9) a≤b <=> a^b=a avb=b10) a≤c,b≤d => a^b≤c^d avb≤cvd11) 保序性b≤c => a^b≤a^c avb≤avc12)分配不等式av(b^c)≤(avb)^(avc)对偶 a^(bvc)≥(a^b)v(a^c)13)模不等式a≤c <=> av(b^c)≤(avb)^c3.分配格:满足a^(bvc)=(a^b)v(a^c)和av(b^c)=(avb)^(avc);4.分配格的充要条件:该格没有任何子格与钻石格或五环格同构;5.链格一定是分配格,分配格必定是模格;6.全上界:集合A中的某个元素a大于等于该集合中的任何元素,则称a为格<A,<=>的全上界,记为1;(若存在则唯一)全下界:集合A中的某个元素b小于等于该集合中的任何元素,则称b为格<A,<=>的全下界,记为0;(若存在则唯一)7.有界格:有全上界和全下界的格称为有界格,即有0和1的格;8.补元:在有界格内,如果a^b=0,avb=1,则a和b互为补元;9.有补格:在有界格内,每个元素都至少有一个补元;10.有补分配格(布尔格):既是有补格,又是分配格;11.布尔代数:一个有补分配格称为布尔代数;第十一章图论1.邻接:两点之间有边连接,则点与点邻接;2.关联:两点之间有边连接,则这两点与边关联;3.平凡图:只有一个孤立点构成的图;4.简单图:不含平行边和环的图;5.无向完全图:n个节点任意两个节点之间都有边相连的简单无向图;有向完全图:n个节点任意两个节点之间都有边相连的简单有向图;6.无向完全图有n(n-1)/2条边,有向完全图有n(n-1)条边;7.r-正则图:每个节点度数均为r的图;8.握手定理:节点度数的总和等于边的两倍;9.任何图中,度数为奇数的节点个数必定是偶数个;10.任何有向图中,所有节点入度之和等于所有节点的出度之和;11.每个节点的度数至少为2的图必定包含一条回路;12.可达:对于图中的两个节点v,j v,若存在连接i v到j v的路,则称i vi与v相互可达,也称i v与j v是连通的;在有向图中,若存在i v到j v的j路,则称v到j v可达;i13.强连通:有向图章任意两节点相互可达;单向连通:图中两节点至少有一个方向可达;弱连通:无向图的连通;(弱连通必定是单向连通)14.点割集:删去图中的某些点后所得的子图不连通了,如果删去其他几个点后子图之间仍是连通的,则这些点组成的集合称为点割集;割点:如果一个点构成点割集,即删去图中的一个点后所得子图是不连通的,则该点称为割点;15.关联矩阵:M(G),m是i v与j e关联的次数,节点为行,边为列;ij无向图:点与边无关系关联数为0,有关系为1,有环为2;有向图:点与边无关系关联数为0,有关系起点为1终点为-1,关联矩阵的特点:无向图:①行:每个节点关联的边,即节点的度;②列:每条边关联的节点;有向图:③所有的入度(1)=所有的出度(0);16.邻接矩阵:A(G),a是i v邻接到j v的边的数目,点为行,点为列;ij17.可达矩阵:P(G),至少存在一条回路的矩阵,点为行,点为列; P(G)=A(G)+2A(G)+3A(G)+4A(G)可达矩阵的特点:表明图中任意两节点之间是否至少存在一条路,以及在任何节点上是否存在回路;A(G)中所有数的和:表示图中路径长度为1的通路条数;2A(G)中所有数的和:表示图中路径长度为2的通路条数;3A(G)中所有数的和:表示图中路径长度为3的通路条数;4A(G)中所有数的和:表示图中路径长度为4的通路条数;P(G)中主对角线所有数的和:表示图中的回路条数;18.布尔矩阵:B(G),v到j v有路为1,无路则为0,点为行,点为列;i19.代价矩阵:邻接矩阵元素为1的用权值表示,为0的用无穷大表示,节点自身到自身的权值为0;20.生成树:只访问每个节点一次,经过的节点和边构成的子图;21.构造生成树的两种方法:深度优先;广度优先;深度优先:①选定起始点v;②选择一个与v邻接且未被访问过的节点1v;③从v出发按邻接方向继续访问,当遇到一个节点所1有邻接点均已被访问时,回到该节点的前一个点,再寻求未被访问过的邻接点,直到所有节点都被访问过一次;广度优先:①选定起始点v;②访问与v邻接的所有节点1v,2v,……,k v,这些作为第一层节点;③在第一层节点中选定一个节点v为起点;1④重复②③,直到所有节点都被访问过一次;22.最小生成树:具有最小权值(T)的生成树;23.构造最小生成树的三种方法:克鲁斯卡尔方法;管梅谷算法;普利姆算法;(1)克鲁斯卡尔方法①将所有权值按从小到大排列;②先画权值最小的边,然后去掉其边值;重新按小到大排序;③再画权值最小的边,若最小的边有几条相同的,选择时要满足不能出现回路,然后去掉其边值;重新按小到大排序;④重复③,直到所有节点都被访问过一次;(2)管梅谷算法(破圈法)①在图中取一回路,去掉回路中最大权值的边得一子图;②在子图中再取一回路,去掉回路中最大权值的边再得一子图;③重复②,直到所有节点都被访问过一次;(3)普利姆算法①在图中任取一点为起点v,连接边值最小的邻接点2v;1②以邻接点v为起点,找到2v邻接的最小边值,如果最小边值2比v邻接的所有边值都小(除已连接的边值),直接连接,否则退回1v,1连接v现在的最小边值(除已连接的边值);1③重复操作,直到所有节点都被访问过一次;24.关键路径例2 求PERT图中各顶点的最早完成时间, 最晚完成时间, 缓冲时间及关键路径.解:最早完成时间TE(v1)=0TE(v2)=max{0+1}=1TE(v3)=max{0+2,1+0}=2TE(v4)=max{0+3,2+2}=4TE(v5)=max{1+3,4+4}=8TE(v6)=max{2+4,8+1}=9TE(v7)=max{1+4,2+4}=6TE(v8)=max{9+1,6+6}=12 最晚完成时间TL(v8)=12TL(v7)=min{12-6}=6TL(v6)=min{12-1}=11TL(v5)=min{11-1}=10TL(v4)=min{10-4}=6TL(v3)=min{6-2,11-4,6-4}=2 TL(v2)=min{2-0,10-3,6-4}=2 TL(v1)=min{2-1,2-2,6-3}=0 缓冲时间TS(v1)=0-0=0TS(v2)=2-1=1TS(v3)=2-2=0TS(v4)=6-4=2TS(v5=10-8=2TS(v6)=11-9=2TS(v7)=6-6=0TS(v8)=12-12=0关键路径: v1-v3-v7-v825.欧拉路:经过图中每条边一次且仅一次的通路;欧拉回路:经过图中每条边一次且仅一次的回路;欧拉图:具有欧拉回路的图;单向欧拉路:经过有向图中每条边一次且仅一次的单向路;欧拉单向回路:经过有向图中每条边一次且仅一次的单向回路;26.(1)无向图中存在欧拉路的充要条件:①连通图;②有0个或2个奇数度节点;(2)无向图中存在欧拉回路的充要条件:①连通图;②所有节点度数均为偶数;(3)连通有向图含有单向欧拉路的充要条件:①除两个节点外,每个节点入度=出度;②这两个节点中,一个节点的入度比出度多1,另一个节点的入;度比出度少1;(4)连通有向图含有单向欧拉回路的充要条件:图中每个节点的出度=入度;27.哈密顿路:经过图中每个节点一次且仅一次的通路;哈密顿回路:经过图中每个节点一次且仅一次的回路;哈密顿图:具有哈密顿回路的图;28.判定哈密顿图(没有充要条件)必要条件:任意去掉图中n个节点及关联的边后,得到的分图数目小于等于n;充分条件:图中每一对节点的度数之和都大于等于图中的总节点数;29.哈密顿图的应用:安排圆桌会议;方法:将每一个人看做一个节点,将每个人与和他能交流的人连接,找到一条经过每个节点一次且仅一次的回路(哈密顿图),即可;30.平面图:将图形的交叉边进行改造后,不会出现边的交叉,则是平面图;31.面次:面的边界回路长度称为该面的次;32.一个有限平面图,面的次数之和等于其边数的两倍;33.欧拉定理:假设一个连通平面图有v个节点,e条边,r个面,则 v-e+r=2;34.判断是平面图的必要条件:(若不满足,就一定不是平面图)设图G是v个节点,e条边的简单连通平面图,若v>=3,则e<=3v-6;35.同胚:对于两个图G1,G2,如果它们是同构的,或者通过反复插入和除去2度节点可以变成同构的图,则称G1,G2是同胚的;36.判断G是平面图的充要条件:图G不含同胚于K3.3或K5的子图;37.二部图:①无向图的节点集合可以划分为两个子集V1,V2;②图中每条边的一个端点在V1,另一个则在V2中;完全二部图:二部图中V1的每个节点都与V2的每个节点邻接;判定无向图G为二部图的充要条件:图中每条回路经过边的条数均为偶数;38.树:具有n个顶点n-1条边的无回路连通无向图;39.节点的层数:从树根到该节点经过的边的条数;40.树高:层数最大的顶点的层数;41.二叉树:①二叉树额基本结构状态有5种;②二叉树内节点的度数只考虑出度,不考虑入度;③二叉树内树叶的节点度数为0,而树内树叶节点度数为1;④二叉树内节点的度数=边的总数(只算出度);握手定理“节点数=边的两倍”是在同时计算入度和出度的时成立;⑤二叉树内节点的总数=边的总数+1;⑥位于二叉树第k层上的节点,最多有12 k个(k>=1);⑦深度为k的二叉树的节点总数最多为k2-1个,最少k个(k>=1);⑧如果有n个叶子,2n个2度节点,则0n=2n+1;42.二叉树的节点遍历方法:先根顺序(DLR);中根顺序(LDR);后根顺序(LRD);43.哈夫曼树:用哈夫曼算法构造的最优二叉树;44.最优二叉树的构造方法:①将给定的权值按从小到大排序;②取两个最小值分支点的左右子树(左小右大),去掉已选的这两个权值,并将这两个最小值加起来作为下一轮排序的权值;③重复②,直达所有权值构造完毕;45.哈夫曼编码:在最优二叉树上,按照左0右1的规则,用0和1代替所有边的权值;每个节点的编码:从根到该节点经过的0和1组成的一排编码;欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求。
离散数学第二章

P (t1 , t2 , , tn ) 是原子公式。
32
§2.1.3 谓词逻辑公式(公式 )
定义 谓词公式由下述各条规定组成: (1)原子公式是谓词公式。 (2)若A是谓词公式,则﹁ A也是谓词公式。 (3)若A和B是谓词公式,则A ∨ B,A ∧ B,A → B, 也是谓词公式。
22
2.存在量词
注意:1.在存在量词 的作用下,x不再起变量的作用, 存在量词也“约束”了x的变量作用。 注意:2.在存在量词作用下,命题中的特性谓词与命题 变元之间必须采用联结词合取,而不能用条件。 注意:3.命题的表示形式与个体域密切相关。 例:有些狗是聪明的。 若个体域为所有狗的集合,则该命题表示为:
这种“描述主语性质的谓语结构的抽象形式或描述主语所 涉及对象之间的关系的抽象形式”就是谓词。语句中的主 语称为个体。 在原子命题中引进谓词和个体的概念,这种以命题中的谓 词为基础的分析研究,称为谓词逻辑(或称谓词演算)。
7
§2.1.1 谓词与个体
在谓词逻辑中,将原子命题分解为谓词与个体两部分。
F (a1 , a2 , , an )
例如, T(a):a是教师。 D(3,2):3大于2。 C(武汉,北京,广州):武汉位于北 京和 广州之间。 注意顺序
9
§2.1.1 谓词与个体
在一个谓词中,个体是可以变化的,如 “是大学生” 中个体是可以变化的,可以是“张华是大学生” 也可
以是“何勇是大学生” ,等等。
31
§2.1.3 谓词逻辑公式(公式 )
定义( 项 ) (1)个体常量符是项;
(2)个体变量符是项;
(3)设f是n元函数符,
t1 , t2 , , tn 为项,则
离散数学ch2.二元关系(5、6、7节)

VS
详细描述
关系的对称差运算可以用符号表示为 R△S,其中 R 和 S 是两个关系。它包括 属于 R 但不属于 S,以及属于 S 但不属 于 R 的所有有序对。如果 (a, b) 在 R△S 中,那么 (a, b) 或者只属于 R,或者只属 于 S。
04
CATALOGUE
关系的闭包
闭包的定义
1 2
关系的交运算可以用符号表示为 R ∩ S,其中 R 和 S 是两个关系 。它包括同时属于 R 和 S 的所有 有序对。如果 (a, b) 在 R ∩ S 中 ,那么 (a, b) 同时是 R 和 S 的差是一种集合差集操作,它从第一个 关系中去除与第二个关系共有的元素。
中可以推导出的新事实。
数据完整性
03
在数据库设计中,闭包的概念用于确保数据的完整性和准确性
,防止出现冗余和不一致的情况。
05
CATALOGUE
关系的类型
函数关系
总结词
函数关系是一种特殊的二元关系,它满足每 个自变量都有唯一的因变量与之对应。
详细描述
在函数关系中,对于定义域中的每一个元素 ,在值域中都有唯一一个元素与之对应。这 种关系具有明确性、确定性和无重复性。常 见的函数关系有数学函数、映射函数等。
离散数学ch2.二元 关系(5、6、7节)
contents
目录
• 引言 • 二元关系的性质 • 关系的运算 • 关系的闭包 • 关系的类型 • 关系在数据库中的应用 • 关系在人工智能中的应用
01
CATALOGUE
引言
定义与概念
定义
二元关系是集合论中的一个基本概念 ,它描述了两个元素之间的联系。
在设计关系型数据库时,需要考虑数据结构、数据完整性、数据冗余和数 据安全性等方面。
第2章 关系

f ( x) y ( x, y) f .
f {( a,2), (b,3), (c,3)}.
A到B的关系是不是A到B的函数? R {( a,2), (a,3), (c,3)} ?
结论:不是任何一个集合A到B的关系都可构成 集合A到B的函数。
函数的关系定义
A到B的关系f 满足什么条件成为A到B的函数? ⑴domf=A:A中任意元素都有B中元素与之对应. ⑵对于任意x∈A,若(x, y1)∈f且(x,y2)∈f,则y1=y2 : 一个x∈A只能有唯一的y与之对应。
计算: R S , R S , R, R S , R S .
先求出R和S,再计算。 解: R = {(2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6)} S = {(2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}
例 A = {a, b}, B = {1, 2, 3},判断下式是否成立。
R {( a,3), (a,2), (b,1), (b,3)} A B ? A B {( a,1), (a,2), (a,3), (b,1), (b,2), (b,3)}.
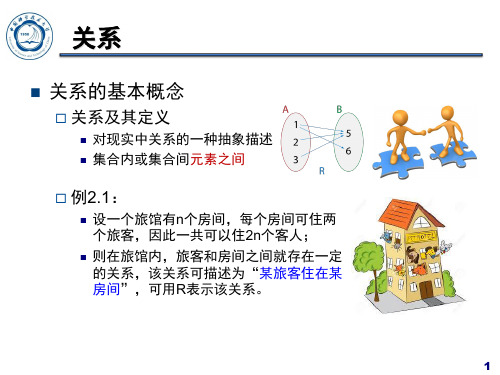
2.1 关系的概念
空关系
设A,B是集合,R是A到B的二元关系,若R= , 则称R为空关系。
Chapter 2 关系
贾 敏
母 女
母女
母子
父 子 表兄妹
Chapter 2 关系
Chapter 2 关系
三个学生选修了5门课程中部分课程,并且根据 学习情况由任课教师给出了他们的成绩。如何表 达学生、课程和成绩之间的关系?
离散数学第二章
注意:
有些关系既不是对称的也不是反对称的;
0 1 0 1 0 1 0 0 0
可以是既是对称的,也是反对称的
如相等关系
24
定义2.10:在集合X上的关系R,如果有:
x, y R且 y, z R ,则必有 x, z R ,
即非对角线上的1, 对称位置必须是0; 而非对角线上的0 不做要求
判断方法:
1. 如果如果存在a到b的有向边,就不存在b到a的有向边。 (逆命题不成立,即可以两条有向边都不存在); 2. 关系矩阵中,如果 a j ,i 1则ai , j 0,这里i j
(注意:a j ,i 0不一定ai , j 1)
n个
容易证明: n m nm m n i: R R R , R R mn ,m,n均为正整数 0 ii: R 是相等关系,即: R0 ={(x,x)|x∈A} 1 iii: R R
13
逆关系
由于关系中的元素是有序偶,则如果将该有序偶的顺
序颠倒,会得到一个新的关系,称之为逆关系。
~ ~ ~
~
补集的逆关系
~ ~ ~
(5) R S R S , R S R S
注意,这个跟德· 摩根律不一样
(6) R S R S
~
~
~
18
关系的重要性质
定义2.6:在集合X上的关系R,如果对任意 x X , 有 x, x R ,则称R是自反的。
如:整数集合上的相等关系、" " 关系等;
如果 miq mqj 1 即mij 0 ,则 miq mqj 1 即 ai , aq R且 aq , a j R 由传递性的定义可知,如果R为传递的, 必有 ai , a j R ,即应有 mij 1 2 即:当R是A上的传递关系时,如果 M R 中的元素 bij 0 , 则必须有 mij 1 ,反之亦然
离散数学第2章 谓词逻辑

在命题函数前加上量词(x)和(x)分别叫做个体变元x 被全称量化和存在量化。一般地说,命题函数不是命题, 如果对命题函数中所有命题变元进行全称量化或存在量化, 该函数就变成了命题。这一结论在例2.3中得到验证。
为假。 ⑵ 如果5大于3,则2大于6。 解:设G(x,y): x大于y a:5,b:3,c:2,d:6 该命题符号化为:G(a,b)→G(c,d) G(a,b)表示5大于3,它是真命题。G(c,d)表示2大于6,
ห้องสมุดไป่ตู้这是个假命题。所以G(a,b)→G(c,d)为假。
(3) 2 是无理数, 而 3 是有理数 解 :设F(x): x是无理数, G(x): x是有理数 符号化为 F( 2) G( 3) 真值为 0 (4) 如果2>3,则3<4 解:设 F(x,y): x>y, G(x,y): x<y, 符号化为 F(2,3)G(3,4) 真值为1
谓词:刻划个体性质或个体之间相互关系的模式叫做谓词。谓 词常用大写英文字母表示,叫做谓词标识符。
例如可以用F,G,H表示上面三个命题中谓词: F:„是优秀共产党员。 G:„比„高。 H:„坐在„和„的中间。
第2章 谓词逻辑
一元谓词:与一个个体相关联的谓词。如上例中的F。 二元谓词:与两个个体相关联的谓词。如上例中的G。 三元谓词:与三个个体相关联的谓词。如上例中的H。
返回章目录
第2章 谓词逻辑
课外作业
• 教材P59-60页: 练习题(需要做在练习本上) (1) (2) a)、c) 、d)、e)、 f)、i)、k)、l)
返回章目录
离散数学第二章

5
3 量词的有关概念
1. 全称量词: “所有的”,“任何一个”,“每 全称量词: 所有的” 任何一个” 一个” 凡是” 一切” 一个”,“凡是”,“一切”表示个体域中每一 表示,称为全称量词。 用符号“ 个,用符号“∀”表示,称为全称量词。
如,所有的人都要呼吸。 所有的人都要呼吸。
16
常用一阶逻辑中的基本等值式
1. 有限个体域 有限个体域D={a1, a2, … ,an }中消去量词 中消去量词 等值式: 等值式
1) ∀xA( x) ⇔ A(a1 ) ∧ A(a2 ) ∧⋯∧ A(an );
2) ∃xA( x ) ⇔ A(a1 ) ∨ A(a2 ) ∨ ⋯ ∨ A(an ).
10
指导变项( 指导变项(元)等概念
在合式公式∀ 和 在合式公式∀xA和∃xA中,称x是指导变元,称A为相应量词 中 是指导变元, 为相应量词 作用域或辖域。 的作用域或辖域。 在辖域中x的出现称为 在公式 中的约束出现 在辖域中 的出现称为x在公式 中的约束出现; 的出现称为 在公式A中的约束出现; 公式A中不是约束出现的其它变元称为该变元的自由出现. 中不是约束出现的其它变元称为该变元的自由出现 公式 中不是约束出现的其它变元称为该变元的自由出现 例1 指出下列公式中的指导变项、量词的辖域、个体变项的 指出下列公式中的指导变项、量词的辖域、 自由出现和约束出现. 自由出现和约束出现 1) 2) ∀xF(x,y)→∃x(G(x) ∧¬ ∀zP(x,z)) → ∀x ∃ y(A(x,y)→∃z(B(x) ∧P(x,z))) →
永假式 如果 在任何解释下均为假 称A为矛盾 如果A在任何解释下均为假 解释下均为假,称 为 或称永假式 式(或称永假式 ; 或称永假式); 如果存在一个解释使A为真 则称A为 为真,则称 可满足式 如果存在一个解释使 为真 则称 为 可满足式; 可满足式;
离散数学导论(第5版)-第二篇 集合论

18
• • 四个次序关系间的关系: • • • R是拟序则r (R) = R • • • R是偏序则R-Q是拟序 • • • 字典次序关系必为线性次序关系 • • • R是拟序则必反对称 • 八个概念: • • 最大元素(最小元素) • • 极大元素(极小元素) • • 上界(下界) • • 上确界(下确界)
• • |A∪B|=|A|+|B|-|A∩B|
• •|A∪B∪C| = |A|+|B|+|C| - |A∩B| - |A∩C| -|B∩C|+|A∩B∩C| n
i=1 1≤i<j≤n
1≤i<j<k≤n
• •|S1∪S2∪…∪Sn|n-=1∑|Si|-∑ |Si∩Sj|+ ∑
• |Si∩Sj∩Sk|(-1)∑ |S1∩S2∩…∩S n|
§3.1 函数的基本概念
• (1)一个基本概念——函数的基本概念。
•
函数建立了从一个集合到另一个集合的特殊对应关系。
设有集合X与Y,如果我们有一种对应关系f,使X的任一元素x能
与y中的一个唯一的元素y相对应,则这个对应关系f叫从X到Y的
函数或叫从X到Y的映射。x所对应的y内的元素y叫x的像,而x则
叫y的像源。上述函数我们可以表示成f:XY;或写成XY;
以及y=f(x)。
•
(2)三种不同性质函数:
•
• 满射与内射
离散数学第2章 谓词逻辑

33
§3 谓词公式与翻译
例5:凡是实数不是大于0,就是等于0或者小于0。 设R(x):x是实数。 P(x,0):x大于0。 Q(x,0):x等于0。 S(x,0):x小于0。 (x) (R(x) → ( P(x,0) Q(x,0) S(x,0) ) )
例:所有的人都是会死的。
设M(x):x是人。S(x):x是会死的。
个体域约定为{人类}:(x) (S(x))
全总个体域:
(x) ( M(x) → S(x) )
例:有一些人是不怕死的。
设M(x):x是人。F(x):x是不怕死的。
个体域约定为{人类}:(x) (F(x))
全总个体域:
(x) ( M(x) ∧ F(x) )
定义:在反映判断的句子中,用以刻划客体的性质或 关系的即是谓词。
5
§1 谓词的概念与表示法
客体,是指可以独立存在的事物,它可以是具体 的,也可以是抽象的,如张明,计算机,精神等。
表示特定的个体,称为客体常元,以a,b,c… 或带下标的ai,bi,ci…表示;
表示不确定的个体,称为客体变元,以x,y, z…或xi,yi,zi…表示。
4. 谓词中通常只写客体变元,因此不是命题,仅当 所有客体变元做出具体指定时,谓词才成为命题, 才有真值。
12
第二章 谓词逻辑
§1 谓词的概念与表示法 §2 命题函数与量词 §3 谓词公式与翻译 §4 变元的约束 §5 谓词演算的等价式与蕴含式 §6 前束范式 §7 谓词演算的推理理论
13
§2 命题函数与量词
离散数学 第二章:一阶逻辑

(2) xF(x) G(x, y);
(3) xyR(x, y) L(y, z) xH(x, y).
2.闭式
定义6. 设A为任一公式,若A中无自由出现的个体变项,则称A是 封闭的合式公式,简记闭式.
例: xF(x) G(x),xyF(x) G(x, y) 闭式, 但 xF(x) G(x, y),zyL(x, y, z) 不是闭式.
(1)所有的人都要死的. (2)有的人活百岁以上.
全称量词:一切,所有,任意. 用 表示.
1.量词
x:表示对个体域中的所有个
xF(x)体:表. 示个体域中的所有个体都具有性质F.
存在量词:存在着,有一个,至少有一个. 用 表示.
x:表示存在个体域里的个体.
xF ( x):表示存在着个体域中的个体具有性质F.
(2)xR(x) G(x), 其中 G(x): x是整数.
3) 同2).
例3. 将下面命题符号化. (1)对所有的x ,均有 x2-1=(x+1)(x-1). (2)存在x,使得 x+5=2.
要求: 1)个体域为自然数集合. 2)个体域为实数集合.
解:1) 不用引入特性谓词.
(1)xF(x), 其中 F(x): x2-1=(x+1)(x-1). 真命题
(3) xF(x) yF(y) L(x, y),
其中 F(x): x是自然数, L(x,y): y是 x的先驱数.
§2.2 一阶逻辑合式公式及解释
一、合式公式
1.字母表 定义1.字母表如下: (1)个体常项: a,b,c,… (2)个体变项: x,y,z,… (3)函数符号: f,g,h,… (4)谓词符号: F,G,H,…
离散数学第二章一阶逻辑知识点总结

数理逻辑部分第2章一阶逻辑2。
1 一阶逻辑基本概念个体词(个体): 所研究对象中可以独立存在的具体或抽象的客体个体常项:具体的事物,用a, b,c表示个体变项:抽象的事物,用x,y,z表示个体域: 个体变项的取值范围有限个体域,如{a,b, c}, {1, 2}无限个体域,如N, Z, R,…全总个体域:宇宙间一切事物组成谓词:表示个体词性质或相互之间关系的词谓词常项:F(a):a是人谓词变项:F(x):x具有性质F一元谓词:表示事物的性质多元谓词(n元谓词, n≥2): 表示事物之间的关系如L(x,y):x与y有关系L,L(x,y):x≥y,…0元谓词: 不含个体变项的谓词, 即命题常项或命题变项量词:表示数量的词全称量词∀:表示任意的, 所有的,一切的等如∀x 表示对个体域中所有的x存在量词∃:表示存在,有的,至少有一个等如$x表示在个体域中存在x一阶逻辑中命题符号化例1 用0元谓词将命题符号化要求:先将它们在命题逻辑中符号化,再在一阶逻辑中符号化(1) 墨西哥位于南美洲在命题逻辑中,设p:墨西哥位于南美洲符号化为 p, 这是真命题在一阶逻辑中, 设a:墨西哥,F(x):x位于南美洲符号化为F(a)例2 在一阶逻辑中将下面命题符号化(1)人都爱美; (2) 有人用左手写字分别取(a) D为人类集合, (b)D为全总个体域。
解:(a) (1) 设G(x):x爱美, 符号化为∀x G(x)(2) 设G(x):x用左手写字, 符号化为$x G(x)(b) 设F(x):x为人,G(x):同(a)中(1) ∀x (F(x)→G(x))(2) $x (F(x)∧G(x))这是两个基本公式, 注意这两个基本公式的使用。
例3 在一阶逻辑中将下面命题符号化(1) 正数都大于负数(2)有的无理数大于有的有理数解注意: 题目中没给个体域, 一律用全总个体域(1)令F(x):x为正数,G(y):y为负数, L(x,y): x>y x(F(x)→y(G(y)→L(x,y))) 或∀x y(F(x)∧G(y)→L(x,y)) 两者等值(2) 令F(x):x是无理数,G(y): y是有理数,L(x,y):x>y∃x(F(x)∧∃y(G(y)∧L(x,y)))或$x$y(F(x)∧G(y)∧L(x,y)) 两者等值几点注意:1元谓词与多元谓词的区分无特别要求,用全总个体域量词顺序一般不能随便颠倒否定式的使用思考:①没有不呼吸的人②不是所有的人都喜欢吃糖③不是所有的火车都比所有的汽车快以上命题应如何符号化?2。
离散数学 第2章 谓词逻辑

对于一个谓词,如其中的每一个变量都在一个量词的作用之下, 对于一个谓词,如其中的每一个变量都在一个量词的作用之下,则它就 不再是一个命题函数,而是一个命题了 不再是一个命题函数, 如论域D={a1,a2,…,an} 如论域 则 ∀ xG(x)为G(a1) ∧G(a2) ∧… ∧G(an) 为
∃ xG(x)为G(a1) ∨G(a2) ∨… ∨G(an)
数学分析中极限定义为: 数学分析中极限定义为:任给小正数 ε ,则存在一个正数 δ,使得当 0<|x-a|< δ 时有 时有|f(x)-b|< ε,此时即 limf f ( x) = b
x→a
解设P(x,y)表示“x大于y” Q(x,y)表示”x小于y” 则
limf f ( x) = b
x→a
表示
例如:函数f(x)表示“x的父亲”,谓词P(x)表示“x是教授”,c表示 个体李四。则P(f(c))表示“李四的父亲是教授”。这里c是项, f(c)也是项。 函数f(x, y)表示x+y,谓词N(x)表示“x是自然数”,f(2, 3)表示5,则 N(f(2, 3))表示5是自然数。这里x, y是项, f(x, y)也是项。
2.1 谓词逻辑的基本概念
2.1.1 个体、谓词 2.1.2 命题函数 2.1.3 量词
2.1.2 命题函数
定义2.1.2 由一个谓词(如P)和n个个体变元(x1, x2, …, xn)组成的P(x1, 定义 x2, … , xn),称为n元原子谓词或n元命题函数,简称n元谓词。 当n=1时,P称为一元谓词;当n=2时,P称为二元谓词;当n=0时,P称为 零元谓词。零元谓词即是命题。一元谓词刻划了个体的性质,多元谓词刻划 了个体之间的关系。 个体变元的取值范围D称为个体域或论域。如果不事先指明,认为论域 是一切可以作为对象的东西的集合,这样的论域称为全总个体域。 例2.1.1 设S(x)表示“x是田径运动员”,B(x)表示“x是篮球运动员”,则 ¬S(x)表示“x不是田径运动员”,S(x)∨B(x)表示“x是田径运动员或篮球运动 员”。 命题函数不是命题,只有当其中的个体变元用特定个体或个体常量替换 时,才能成为一个命题。但个体变元在哪些范围内取特定值,对是否成为命 题及命题的真值极有影响。 例2.1.3 设S(x)表示“x是大学生”。若x的取值范围为某大学的计算机系 的全体学生,则S(x)是永真式。若x的取值范围为某中学的全体学生,则S(x) 是永假式。若x的取值范围为某电影院的观众,则S(x)的真值不能确定。
离散数学基础(洪帆)第二章_关系

二、 两关系矩阵的乘积
定义
设M1是一个(i,j)通路(即第i行、第j列的元素)为
r 的l×m关系矩阵,
(2) r M2是一个(i,j)通路为 ij 的m×n关系矩阵,
(1) ij
则M1与M2乘积记为M1﹒M2是一个l×n的矩阵,
其(i,j)通路为: rij
(r r )
(1) ik (2) kj k=1
1 1 2
2
3
4
3
4
图(1)
图(2)
4. 关系矩阵 定义 设集合A={a1,a2,…,an},B={b1,b2,…,bm} 是由A到B的关系, 则 的关系矩阵 定义为一个n行、m列的矩阵, 记为 M , 且关系矩阵的第i行、第j列的元素 rij
定义如下:
1 若 a i b j rij 0 若 a i 'b j
1 0 1 0
1 1 0 0
1 1 1 1
2.3 关系的复合
一、关系的一般运算:交、并、补、差 例1 设A={4,6,9,10}, 1 和 2 是A上的两个关系:
1 ={(a,b)|(a-b)/2是正整数}, 2 ={(a,b)|(a-b)/3是正整数}
试求:1 2 , 1 2 , 1 , 1 2 , 1 2 ,
例3 设A={a,b,c,d},A上的关系: ={(a,a),(a,b),(b,d),(c,a),(d,c)} 4 试求复合关系 。
2.4 复合关系的关系矩阵和关系图
一、布尔运算 布尔运算只涉及数字0和1, 数字的加法和乘法按照以下方式进行: 0+0=0 0+1=1+0=1+1=1 1· 1=1 1· 0=0· 1=0· 0=0 如:(1· 1)+(0· 1· 1)+(1· 0· 0)+1+0=1
离散数学2二元关系

(4)笛卡儿积运算对并和交运算满足分配律,即
A×(B∪C)=(A×B)∪(A×C) (B∪C)×A=(B×A)∪(C×A) A×(B∩C)=(A×B)∩(A×C) (B∩C)×A=(B×A)∩(C×A)
(5)AC ∧ BD A×B C×D
A×(B∪C)=(A×B)∪(A×C)的证明
任取 <x,y> <x,y>∈A×(B∪C) x∈A ∧ y∈B∪C x∈A ∧ (y∈B∨y∈C) (x∈A∧y∈B) ∨ (x∈A∧y∈C) <x,y>∈A×B ∨ <x,y>∈A×C <x,y>∈(A×B)∪(A×C) 所以 A×(B∪C)=(A×B)∪(A×C)
关于AC∧BD A×BC×D的讨论
该性质的逆命题不成立,可分以下情况讨论。 (1)当A=B=时,显然有AC 和 BD 成立。 (2)当A≠且B≠时,也有AC和BD成立,证明如下:
任取x∈A,由于B≠,必存在y∈B,因此有 x∈A∧y∈B
<x,y>∈A×B <x,y>∈C×D x∈C∧y∈D x∈C 从而证明了 AC。 同理可证 BD。
关于AC∧BD A×BC×D的讨论
该性质的逆命题不成立,可分以下情况讨论。 (3)当A=而B≠时,有AC成立,但不一定有BD成立。
反例:令A=,B={1},C={3},D={4}。 (4)当A≠而B=时,有BD成立,但不一定有AC成立。
反例略。
例7.2
例7.2 设A={1,2},求P(A)×A。
解答 P(A)×A = {,{1},{2},{1,2}}×{1,2} = {<,1>,<,2>, <{1},1>,<{1},2>, <{2},1>,<{2},2>, <{1,2},1>,<{1,2},2>}
离散数学第二章谓词逻辑

则xP和xP都是谓词公式
(5)当且仅当能够有限次地应用(1)-(4)所得到的
式子是谓词公式
二、谓词公式的概念
谓词公式是命题公式的扩展,约定最外层圆括号可 以省略,但量词后面若有括号则不省略。
例如 (P(x,y)→(Q(x)→R(y,z)))
P(x,y,z)∧(P(x,y,z)→Q)
y((A(x)∧A(y))→F(x,y,0))
2.2 命题函数与量词
例2.2.6 翻译命题
甲村人与乙村人都同姓。
解 设A(x):x是甲村人。 B(y):y是乙村人。 P(x,y):x与y同姓。 (1)全总个体域 xy((A(x)∧B(y))→P(x,y)) (2)x的论域:甲村人 xy(P(x,y)) y的论域:乙村人
1.令F(x):x是金属。G(y):y是液体。H(x,y):x可以溶解在y 中。则命题“任何金属可以溶解在某种液体中。”可翻译 为( )。 A.x(F(x)∧y(G(y)∧H(x,y))) B.xy(F(x)→(G(y)→H(x,y))) C.x(F(x)→y(G(y)∧H(x,y))) D.x(F(x)→y(G(y)→H(x,y))) 2.令F(x):x是火车。G(y):y是汽车。H(x,y):x比y快。则命 题“某些汽车比所有火车慢。”可翻译为( )。 A.y(G(y)→x(F(x) ∧H(x,y))) B.y(G(y)∧x(F(x)→H(x,y))) C.xy(G(y)→(F(x)∧H(x,y))) D.y(G(y)→x(F(x)→H(x,y)))
由一个谓词常量或谓词变量A,n(n≥0)个个体变量 x1,x2,…,xn组成的表达式A(x1,x2,…,xn) 注意:0元谓词是命题,谓词逻辑是命题逻辑的扩 展。
