人教A版选修1-1教案:3.2立体几何中的向量方法第2课时(含答案)
高中数学选修2-1精品教案1:3.2 立体几何中的向量方法(二)教学设计

3.2立体几何中的向量方法(二)教学目标:掌握利用向量法解决空间中的垂直关系教学重点:证明空间中垂直关系的方法教学难点:空间中的垂直关系如何转化为向量的运算问题教学过程:一.复习引入直线的方向向量和平面的法向量二.思考分析直线的方向向量和平面的法向量可以确定直线和平面的位置.因此,可用向量方法解决线面垂直关系的判断及证明.问题1:直线的方向向量与一平面的法向量平行,则该直线与平面有什么关系?提示:垂直.问题2:若两平面的法向量垂直,则两平面垂直吗?提示:垂直.三.抽象概括证明垂直关系的向量方法用向量法证明线线、线面、面面之间的垂直关系,主要是找出直线的方向向量、平面的法向量之间的关系,因此求直线的方向向量及平面的法向量是解题关键.四.例题分析及练习[例1]在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是AB,BC上的动点,且AE=BF,求证:A1F⊥C1E.[思路点拨]分析题意→建立空间直角坐标系→表示出A1,F,C1,E的坐标→A1F⊥C1E[精解详析]以O为坐标原点建立如图所示的空间直角坐标系,则A1(a,0,a),C1(0,a,a).设AE =BF =x ,则E (a ,x,0),F (a -x ,a,0).∴1A F u u u r=(-x ,a ,-a ), 1C E u u u r=(a ,x -a ,-a ). ∵1A F u u u r ·1C E u u u r =(-x ,a ,-a )·(a ,x -a ,-a )=-ax +ax -a 2+a 2=0, ∴1A F u u u r ⊥1C E u u u r,即A 1F ⊥C 1E .[感悟体会] 利用向量法证明线线垂直往往转化为证明直线的方向向量垂直,即证明它们的方向向量的数量积为0.证明的关键是建立恰当的空间直角坐标系,正确地表示出点的坐标进而求直线的方向向量. 训练题组11.设直线l 1的方向向量为a =(2,1,-2),直线l 2的方向向量为b =(2,2,m ),若l 1⊥l 2,则m =( )A .1B .-2C .-3D .3解析:l 1⊥l 2⇔a ⊥b ,∴2×2+1×2+(-2)×m =0,∴m =3. 答案:D2.正方体ABCD -A 1B 1C 1D 1中,E 为AC 的中点.证明:(1)BD 1⊥AC ;(2)BD 1⊥EB 1.证明:以D 为原点,DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴建立如图所示 的空间直角坐标系Dxyz .设正方体的棱长为1,则B (1,1,0),D 1(0,0,1),A (1,0,0),C (0,1,0), E (12,12,0),B 1(1,1,1).(1) 1BD u u u r=(-1,-1,1),AC uuu r =(-1,1,0),∴1BD u u u r ·AC uuu r =(-1)×(-1)+(-1)×1+1×0=0,∴1BD u u u r ⊥AC uuur ,∴BD 1⊥AC .(2) 1BD u u u r =(-1,-1,1),1EB u u u r =(12,12,1),∴1BD u u u r ·1EB u u u r =(-1)×12+(-1)×12+1×1=0,∴1BD u u u r ⊥1EB u u u r,∴BD 1⊥EB 1.[例2] 如图所示,在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,D 1B 1的中点. 求证:EF ⊥平面B 1AC .[思路点拨] 思路一:EF ⊥AB 1→EF ⊥B 1C →EF ⊥平面B 1AC思路二:求平面B 1AC 的法向量n EF ⊥平面B 1AC[精解详析] 法一:设AB uu u r =a ,AD uuu r=c ,1AA u u u r =b ,则EF uuu r =1EB u u u r +1B F u u u r =12(1BB u u u r +11B D u u u u r )=12(1AA u u u r +BD uuu r )=12(1AA u u u r +AD uuu r -AB uu u r)=12(-a +b +c ). ∵1AB u u u r =AB uu u r +1AA u u ur =a +b ,∴EF uuu r ·1AB u u u r =12(-a +b +c )·(a +b )=12(b 2-a 2+c ·a +c ·b )=12(|b |2-|a |2+0+0)=0.∴EF uuu r ⊥1AB u u ur ,即EF ⊥AB 1.同理,EF ⊥B 1C .又AB 1∩B 1C =B 1,∴EF ⊥平面B 1AC .法二:设正方体的棱长为2,以D 为原点,以DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,则A (2,0,0),C (0,2,0),B 1(2,2,2),E (2,2,1),F (1,1,2).∴EF uuu r=(1,1,2)-(2,2,1)=(-1,-1,1),1AB u u u r=(2,2,2)-(2,0,0)=(0,2,2), AC uuu r=(0,2,0)-(2,0,0)=(-2,2,0).∴EF uuu r ·1AB u u ur =(-1,-1,1)·(0,2,2)=(-1)×0+(-1)×2+1×2=0,EF uuu r ·AC uuur =(-1,-1,1)·(-2,2,0)=2-2+0=0,∴EF uuu r ⊥1AB u u u r ,EF uuu r ⊥AC uuur ,∴EF ⊥AB 1,EF ⊥AC .又AB 1∩AC =A ,∴EF ⊥平面B 1AC .法三:同法二得1AB u u u r =(0,2,2),AC uuu r =(-2,2,0),EF uuu r=(-1,-1,1).设平面B 1AC 的法向量n =(x ,y ,z ),则1AB u u u r·n =0,AC uuu r ·n =0,即⎩⎪⎨⎪⎧2y +2z =0,-2x +2y =0.取x =1,则y =1,z =-1,∴n =(1,1,-1), ∴EF uuu r =-n ,∴EF uuu r∥n ,∴EF ⊥平面B 1AC .[感悟体会] 法一选基底,将相关向量用基底表示出来,然后利用向量的计算来证明.法二、法三建立空间直角坐标系,利用坐标将向量的运算转化为实数(坐标)的运算,以达到证明的目的. 训练题组23.已知直线l 与平面α垂直,直线的一个方向向量为u =(1,3,z ),向量v =(3,-2,1)与平面α平行,则z =________.解析:∵l ⊥α,v ∥α,∴u ⊥v .∴(1,3,z )·(3,-2,1)=0,即3-6+z =0,z =3. 答案:34.如图所示,在正方体ABCD -A 1B 1C 1D 1中,O 为AC 与BD 的交点,G 为CC 1的中点,求证:A 1O ⊥平面GBD .证明:法一:设11A B u u u u r =a ,11AD u u u u r =b ,1A A u u u r =c ,则a ·b =0,b ·c =0,a ·c =0. 而1AO u u u r =1A A u u u r +AO uuu r =1A A u u u r +12(AB uu u r +AD uuu r )=c +12(a +b ), BD uuu r =AD uuu r -AB uu u r=b -a , OG uuu r =OC uuu r +OG uuu r =12(AB uu u r +AD uuu r )+121CC u u u r =12(a +b )-12c ,∴1AO u u u r ·BD uuu r =(c +12a +12b )·(b -a )=c ·(b -a )+12(a +b )·(b -a )=c ·b -c ·a +12(b 2-a 2) =12(|b |2-|a |2)=0. ∴1AO u u u r ⊥BD uuu r ,∴A 1O ⊥BD .同理可证,A 1O ⊥OG .又∵OG ∩BD =O ,∴A 1O ⊥平面GBD .法二:如图,取D 为坐标原点,DA ,DC ,DD 1所在的直线分别为x 轴,y 轴,z 轴建立空间直角坐标系.设正方体棱长为2,则O (1,1,0),A 1(2,0,2),G (0,2,1),B (2,2,0),D (0,0,0),∴1OA u u u r =(1,-1,2),OB uuu r =(1,1,0),BG uuu r =(-2,0,1).而1OA u u u r ·OB uuur =1-1+0=0, 1OA u u u r ·BG uuu r =-2+0+2=0,∴1OA u u u r ⊥OB uuu r ,1OA u u u r ⊥BG uuur ,即OA 1⊥OB ,OA 1⊥BG .而OB ∩BG =B ,∴OA 1⊥平面GBD .[例3] 三棱锥被平行于底面ABC 的平面所截得的几何体如右图所示,截面为A 1B 1C 1,∠BAC =90°,A 1A ⊥平面ABC ,A 1A =3,AB =AC =2A 1C 1=2,D 为BC 的中点.证明:平面A 1AD ⊥平面BCC 1B 1.[思路点拨] 思路一:证明BC ⊥AD →证明BC ⊥AA 1→BC ⊥平面A 1AD →平面A 1AD ⊥平面BCC 1B 1思路二:求平面A 1AD 的法向量n 1→求平面BCC 1B 1的法向量n 2→证明n 1·n 2=0→ 平面A 1AD ⊥平面BCC 1B 1[精解详析] 法一:如下图,建立空间直角坐标系,则A (0,0,0),B (2,0,0),C (0,2,0),A 1(0,0,3),C 1(0,1,3).∵D 为BC 的中点,∴D 点坐标为(1,1,0).∴AD uuu r=(1,1,0),1AA u u u r =(0,0,3),BC uuu r =(-2,2,0).∴AD uuu r ·BC uuur =1×(-2)+1×2+0×0=0,1AA u u u r ·BC uuu r =0×(-2)+0×2+3×0=0. ∴AD uuu r ⊥BC uuur ,1AA u u u r ⊥BC uuu r .∴BC ⊥AD ,BC ⊥AA 1.又A 1A ∩AD =A ,∴BC ⊥平面A 1AD .又BC ⊂平面BCC 1B 1,∴平面A 1AD ⊥平面BCC 1B 1.法二:同证法一建系后,得1AA u u u r =(0,0,3),AD uuu r=(1,1,0),BC uuu r =(-2,2,0),1CC u u u r =(0,-1,3).设平面A 1AD 的法向量为n 1=(x 1,y 1,z 1),平面BCC 1B 1的法向量为n 2=(x 2,y 2,z 2).由⎩⎪⎨⎪⎧n 1·1AA u u u r =0,n 1·AD uuu r=0,得⎩⎨⎧3z 1=0,x 1+y 1=0.令y 1=-1,则x 1=1,z 1=0,∴n 1=(1,-1,0). 由⎩⎪⎨⎪⎧n 2·BC uuu r =0,n 2·1CC u u u r =0,得⎩⎨⎧-2x 2+2y 2=0,-y 2+3z 2=0.令y 2=1,则x 2=1,z 2=33,∴n 2=(1,1,33).∵n 1·n 2=1-1+0=0,∴n 1⊥n 2.∴平面A 1AD ⊥平面BCC 1B 1.[感悟体会] 证明面面垂直通常有两种方法,一是利用面面垂直的判定定理转化为线面垂直、线线垂直去证明;二是证明两个平面的法向量互相垂直. 训练题组35.在正棱锥P -ABC 中,三条侧棱两两互相垂直,G 是△P AB 的重心,E ,F 分别为BC ,PB 上的点,且BE ∶EC =PF ∶FB =1∶2.求证:平面GEF ⊥平面PBC .证明:法一:如图,以三棱锥的顶点P 为原点,以P A ,PB ,PC 所在直线分别作为x 轴,y 轴,z 轴建立空间直角坐标系.令P A =PB =PC =3,则A (3,0,0),B (0,3,0),C (0,0,3),E (0,2,1),F (0,1,0),G (1,1,0),P (0,0,0),于是PA u u r =(3,0,0),FG uuu r =(1,0,0),故PA u u r=3FG uuu r ,∴P A ∥FG .而P A ⊥平面PBC ,∴FG ⊥平面PBC .又FG ⊂平面EFG ,∴平面EFG ⊥平面PBC . 法二:同证法一,建立空间直角坐标系,则E (0,2,1),F (0,1,0),G (1,1,0).∴EF uuu r=(0,-1,-1),EG uuu r =(1,-1,-1).设平面EFG 的法向量是n =(x ,y ,z ),则有n ⊥EF uuu r,n ⊥EG uuu r .∴⎩⎪⎨⎪⎧y +z =0,x -y -z =0.令y =1,得z =-1,x =0,即n =(0,1,-1). 显然PA u u r=(3,0,0)是平面PBC 的一个法向量.又n ·PA u u r =0,∴n ⊥PA u u r ,即平面PBC 的法向量与平面EFG 的法向量互相垂直,∴平面EFG ⊥平面PBC .6.正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点,求证:平面AED ⊥平面A 1FD 1. 证明:如图,建立空间直角坐标系Dxyz .设正方体棱长为1,则E (1,1,12),D 1(0,0,1),F (0,12,0),A (1,0,0).∴DA uuu r =(1,0,0)=11D A u u u u r ,DE uuu r =(1,1,12), 1D F u u u u r =(0,12,-1).设m =(x 1,y 1,z 1),n =(x 2,y 2,z 2)分别是平面AED 和A 1FD 1的一个法向量.由⎩⎨⎧m ·DA uuu r =0,m ·DE uuu r =0⇒⎩⎪⎨⎪⎧ x 1=0,x 1+y 1+12z 1=0.令y 1=1,得m =(0,1,-2). 又由⎩⎪⎨⎪⎧n ·11D A u u u u r=0,n ·1D F u u u u r=0⇒⎩⎪⎨⎪⎧x 2=0,12y 2-z 2=0.令z 2=1,得n =(0,2,1). ∵m ·n =(0,1,-2)·(0,2,1)=0,∴m ⊥n ,故平面AED ⊥平面A 1FD 1. 五.课堂小结与归纳1.用向量法证明线面垂直的方法与步骤(1)基向量法⎩⎪⎨⎪⎧①设出基向量,用基向量表示直线的方向向量②找出平面内两条不共线向量并分别用基向量表示③分别证明直线的方向向量与平面内两不共线向量垂直(2)坐标法⎩⎪⎪⎨⎪⎪⎧方法一⎩⎪⎨⎪⎧①建立空间直角坐标系②将直线的方向向量用坐标表示③将平面内任意两条相交直线的方向向量用坐标表示④分别证明直线的方向向量与平面内两向量垂直方法二⎩⎪⎨⎪⎧①建立空间坐标系②将直线的方向向量、平面的法向量分别用坐标表示④证明平面的法向量与直线的方向向量平行2.利用空间向量证明面面垂直,通常可以有两个途径,一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直,进而转化为线线垂直;二是直接求解两个平面的法向量,证明两个法向量垂直,从而得到两个平面垂直. 六.当堂训练1.若两个不同平面α,β的法向量分别为u =(1,2,-1),v =(2,3,8),则( ) A .α∥β B .α⊥βC .α,β相交但不垂直 D .以上均不正确 解析:u ·v =(1,2,-1)·(2,3,8)=1×2+2×3-1×8=0,∴u ⊥v .∴α⊥β.答案:B2.若直线l ∥α,且l 的方向向量为(2,m,1),平面α的法向量为(1,12,2),则m 为( )A .-4B .-6C .-8D .8解析:∵l ∥α,平面α的法向量为(1,12,2),∴(2,m,1)·(1,12,2)=0.∴2+12m +2=0.∴m =-8.答案:C3.已知AB uu u r =(1,5,-2),BC uuu r =(3,1,z ),若AB uu u r ⊥BC uuu r ,BP u u u r =(x -1,y ,-3),且BPu u u r⊥平面ABC ,则BP u u u r等于( )A .(337,-157,4)B .(337,-157,-3)C .(407,-157,4)D .(407,157,-3)解析:由AB uu u r ·BC uuu r =0得3+5-2z =0,∴z =4.又BP u u u r⊥平面ABC , ∴⎩⎨⎧BP u u u r ·AB uu u r =0, BP u u u r ·BC uuur =0,即⎩⎪⎨⎪⎧x -1+5y +6=0,3x -3+y -12=0,解得⎩⎨⎧x =407,y =-157.答案:B4.在正方体ABCD -A 1B 1C 1D 1中,若E 为A 1C 1的中点,则直线CE 垂直于( ) A .AC B .BD C .A 1DD .AA 1解析:建立如图所示的坐标系.设正方体棱长为1,则A (1,0,0),B (1,1,0), C (0,1,0),D (0,0,0),A 1(1,0,1),E (12,12,1).∴CE ―→=(12,12,1)-(0,1,0)=(12,-12,1),AC uuu r =(-1,1,0),BD uuu r=(-1,-1,0),1A D u u u r =(-1,0,-1),1A A u u u r =(0,0,-1).∵CE u u u r ·BD uuu r =(12,-12,1)·(-1,-1,0)=-12+12+0=0, ∴CE u u u r ⊥BD uuu r,∴CE ⊥BD .答案:B5.在直角坐标系Oxyz 中,已知点P (2cos x +1,2cos 2x +2,0)和点Q (cos x ,-1,3),其中x ∈[0,π].若直线OP 与直线OQ 垂直,则x 的值为________.解析:由题意得OP uuu r ⊥OQ uuu r.∴cos x ·(2cos x +1)-(2cos 2x +2)=0.∴2cos 2x -cos x =0.∴cos x =0或cos x =12.又x ∈[0,π],∴x =π2或x =π3.答案:π2或π36.已知点P 是平行四边形ABCD 所在的平面外一点,且有AB uu u r =(2,-1,-4),ADuuu r=(4,2,0),AP uu u r =(-1,2,-1).给出结论:①AP ⊥AB ;②AP ⊥AD ;③AP uu u r是平面ABCD的法向量;④AP uu u r ∥BD uuu r.其中正确的是________.解析:由AP uu u r ·AB uu u r=-2-2+4=0知AP ⊥AB ,故①正确; 由AP uu u r ·AD uuu r=-4+4+0=0,知AP ⊥AD ,故②正确;由①②知AP uu u r是平面ABCD 的法向量,故③正确,④不正确.答案:①②③7.如图,在四棱锥P -ABCD 中,底面ABCD 是矩形,P A ⊥平面ABCD ,AP =AB =2,BC =22,E ,F 分别是AD ,PC 的中点.求证:PC ⊥平面BEF .解:如图,以A 为坐标原点,AB ,AD ,AP 所在直线分别为x ,y ,z 轴建立空间直角坐标系.∵AP =AB =2,BC =AD =22,四边形ABCD 是矩形,∴A ,B ,C ,D ,P 的坐标为A (0,0,0),B (2,0,0),C (2,22,0),D (0,22,0),P (0,0,2). 又E ,F 分别是AD ,PC 的中点,∴E (0,2,0),F (1,2,1).∴PC uuu r (2,22,-2),BF uuu r =(-1,2,1),EF uuu r=(1,0,1), ∴PC uuu r ·BF uuu r =-2+4-2=0,PC uuu r ·EF uuu r =2+0-2=0,∴PC uuu r ⊥BF uuu r ,PC uuu r ⊥EF uuu r ,∴PC ⊥BF ,PC ⊥EF .又BF ∩EF =F ,∴PC ⊥平面BEF . 8.已知正方体ABCD -A 1B 1C 1D 1中,E 为棱CC 1上的动点.(1)求证:A 1E ⊥BD ;(2)若平面A 1BD ⊥平面EBD ,试确定E 点的位置.解:以D 为坐标原点,以DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系.设正方体棱长为a ,则A (a,0,0),B (a ,a,0),C (0,a,0),A 1(a,0,a ),C 1(0,a ,a ).设E (0,a ,e )(0≤e ≤a ).(1) 1A E u u u r =(-a ,a ,e -a ),BD uuu r =(-a ,-a,0),1A E u u u r ·BD uuu r =a 2-a 2+(e -a )·0=0, ∴1A E u u u r ⊥BD uuu r,即A 1E ⊥BD .(2)设平面A 1BD ,平面EBD 的法向量分别为n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2).∵DB uuu r =(a ,a,0),1DA u u u r =(a,0,a ),DE uuu r =(0,a ,e ),∴⎩⎪⎨⎪⎧ax 1+ay 1=0,ax 1+az 1=0.⎩⎪⎨⎪⎧ax 2+ay 2=0,ay 2+ez 2=0. 取x 1=x 2=1,得n 1=(1,-1,-1),n 2=(1,-1,ae ).由平面A 1BD ⊥平面EBD 得n 1⊥n 2.∴2-a e =0,即e =a 2.∴当E 为CC 1的中点时,平面A 1BD ⊥平面EBD .。
高中数学人教A版选修1-1第3章3-2立体几何中的向量方法教案

即 a2 = 3x2 + 2(3x2 cos )
x=
1a
3 + 6 cos
∴ 这个四棱柱的对角线的长可以确定棱长。
(3)本题的晶体中相对的两个平面之间的距离是多少?(提示:求
两个平行平面的距离,通常归结为求两点间的距离)
分析:面面距离 点面距离 向量的模 回归图形
解: 过 A1点作 A1H ⊥ 平面 AC 于点 H.
解:
设平面 AEF 的法向量为
则有
6,如图所示建立坐标系,有
为平面 AEF 的单位法向量。
分别求平面 SAB 与平面 SDC 的法向量,并求出它们夹角的余弦。 解:因为 y 轴 平面 SAB,所以平面 SAB 的法向量为 设平面 SDC 的法向量为, 由
§3.2.2 空间角与距离的计算举例
【学情分析】:
空间中的几何元素
如图,在空间中,我们取一点 O 作为基点,那么空间中任意一点 P 点、直线、平面的
的位置就可以用向量 OP 来表示.称向量 OP 为点的位置向量。
位置的向量表示方 法。
●P
基点 O●
2. 思考:在空间中给定一个定点 A 和一个定方向(向量),能确定一条直
线在空间的位置吗? l
a
P
A
AP = a( R)
∴ sin BAD = 1− 9 = 32 , 105 35
五、小结 六、作业
∴ S ABCD =| AB | | AD | sin BAD = 8 6 .
1. 点、直线、平面的位置的向量表示。 2. 线线、线面、面面间的平行与垂直关系的向量表示。 A,预习课本 105~110 的例题。 B,书面作业:
(1)求证: AP 是平面 ABCD 的法向量; (2)求平行四边形 ABCD 的面积.
新人教A版(选修2-1)3.2《立体几何中的向量方法》word教案

3.2立体几何中的向量方法教学目标:1. 掌握好向量的相关知识:概念、基本运算、建系方法、坐标求法(不定点的坐标)、平行与垂直、法向量求法2. 掌握向量作为工具解决立几问题的方法3. 向量解题后建议多思考传统的方法,不仅可以锻炼思维能力,还可以深刻认识空间几何的本质重点难点:向量作为工具解决立几问题的方法教学过程:相关知识与能力: 一.空间距离的计算1. 空间两点间的距离:设A 、B 是空间两点,则A 、B 两点间的距离d=||2.两条异面直线间的距离:设a 、b 是两条异面直线,是a 、b 的公共法向量(即b n a n ⊥⊥且),点A ∈a,B ∈b则异面直线a 、b 间的距离d =即在方向上的射影长为异面直线a 、b 间的距离。
3.点(或线)到平面的距离:1)设,.,外一点是平面点的法向量ααo P P是平面α内任一点,则P Od =2)直线与平面(或平面与平面)的距离转化为点到平面的距离。
二.空间角度的计算1. 两条异面直线所成的角:设l 1与l 2两条异面直线,∥l 1 , ∥l 2,则l 1与l 2所成的角α=<n ,m >或α=л -<n ,m > (0<α≤2π) 所示图)见第一3.cos sin ==βθcos<n ,(0<α≤2π) 2. 斜线P 0P 与平面α所成的角θ)20(πθ<<3.二面角:设相交平面α与β的法向量分别为m n ,,则α与β所成的角的大小为<m n ,> 或><-m n ,π(如何确定?)典例分析:例1.在棱长为1的正方体1111D C B A ABCD -中,E 、F 分别是BD D D ,1的中点,G 在棱CD 上,且CD CG 41=,H 为C 1G 的中点,应用空间向量方法求解下列问题。
(1)求证:EF ⊥B 1C ;(2)求EF 与C 1G 所成的角的余弦; (3)求FH 的长。
人教A版高中数学选修2-1《3.2立体几何中的向量方法(二)》课件

知识点二 向量法判断线面垂直
思考
若直线 l 的方向向量为 μ1=2,43,1,平面 α 的法向量为 μ2= 3,2,32,则直线 l 与平面 α 的位置关系是怎样的?如何用向量 法判断直线与平面的位置关系? 答案
梳理
设直线l的方向向量a=(a1,b1,c1),平面α的法向量μ=(a2,b2,c2),则 l⊥α⇔a∥μ⇔ a=kμ(k∈R) .
思考
若直线l1的方向向量为μ1=(1,3,2),直线l2的方向向量为μ2= (1,-1,1),那么两直线是否垂直?用向量法判断两条直线垂 直的一般方法是什么? 答案
梳理
设直线l的方向向量为a=(a1,a2,a3),直线m的方向向量为b=(b1,b2,b3), 则l⊥m⇔ a·b=0 ⇔ a1b1+a2b2+a3b3=0 .
跟踪训练3 在四面体ABCD中,AB⊥平面BCD,BC=CD,∠BCD= 90°,∠ADB=30°,E、F分别是AC、AD的中点,求证:平面BEF⊥ 平面ABC. 证明
当堂训练
1.下列命题中,正确命题的个数为 答案 解析
①若n1,n2分别是平面α,β的法向量,则n1∥n2⇔α∥β; ②若n1,n2分别是平面α,β的法向量,则α⊥β ⇔ n1·n2=0; ③若n是平面α的法向量,a与平面α平行,则n·a=0;
C.a=(0,1,-1),b=(0,-1,1)
D.a=(1,0,0),b=(-1,0,0)
因为a=(0,1,0),b=(1,0,1),所以a·b=0×1+1×0+0×1=0,所 以a⊥b,故选B.
12345
3.若直线l的方向向量为a=(1,0,2),平面α的法向量为μ=(-2,0,-4),则
A.l∥α
规律与方法
几何法
人教A版选修1-1教案:3.1空间向量及其运算第2课时(含答案)

§3.1.2空间向量的数乘运算【学情分析】:本节,空间向量的数乘运算共有4个知识点:空间向量的数乘、共线向量或平行向量、方向向量与共面向量、空间向量的分解定理这一节是全章的重点,有了第一节空间向量加减法的基础,我们就很容易把平面向量及其运算推广到空间向量由于本教材学习空间向量的主要目的是,解决一些立体几何问题,所以例习题的编排也主要是立体几何问题当我们把平面向量推广到空间向量后,很自然地要认识空间向量的两个最基本的子空间:共线向量和共面向量把平行向量基本定理和平面向量基本定理推广到空间然后由这两个定理推出空间直线和平面的向量表达式有了这两个表达式,我们就可以很方便地使用向量工具解决空间的共线和共面问题【教学目标】:(1)知识与技能:掌握空间向量的数乘运算(2)过程与方法:进行类比学习,会用空间向量的运算意义和运算律解决立几问题(3)情感态度与价值观:会用平面的向量表达式解决共面问题【教学重点】:空间向量的数乘运算及运算律【教学难点】:用向量解决立几问题OP OA x AB y AC=++推论:已知空间任意一点O和不共线的三点分别是空间四边形ABCD的边AB、的中点,用向量方法证明(1)E、F、G、练习与测试:(基础题)1. 已知空间四边形ABCD ,连结,AC BD ,设,M G 分别是,BC CD 的中点,化简下列各表达式,并标出化简结果向量:(1)AB BC CD ++; AD(2)1()2AB BD BC ++; AG (3)1()2AG AB AC -+.MG(中等题)2、在平行六面体ABCD -A 1B 1C 1D 1中,向量1D A 、1D C 、是( ) A .有相同起点的向量 B .等长向量 C .共面向量 D .不共面向量 3.直三棱柱ABC —A 1B 1C 1中,若====A CC 11,,,则( ) A .-+ B .+- C .++- D . -+-BCDMGA。
高二数学人教A版选修2-1(第3.2 立体几何中的向量方法) Word版含解析

绝密★启用前人教版选修2-1 课时3.2立体几何中的向量方法一、选择题1.【题文】已知三条直线l 1,l 2,l 3的一个方向向量分别为a =(4,-1,0),b =(1,4,5),c =(-3,12,-9),则 ( )A .l 1⊥l 2,但l 1与l 3不垂直B .l 1⊥l 3,但l 1与l 2不垂直C .l 2⊥l 3,但l 2与l 1不垂直D .l 1,l 2,l 3两两互相垂直2.【题文】已知直线l 1的方向向量为a =(2,4,x ),直线l 2的方向向量为b =(2,y,2),若|a |=6,且a ⊥b ,则x +y 的值是( ) A .-3或1 B .3或-1 C .-3 D .13.【题文】已知(2,2,5)u =-,(6,4,4)v =-,u ,分别是平面α,β的法向量,则平面α,β的位置关系式( )A .平行B .垂直C .所成的二面角为锐角D .所成的二面角为钝角4.【题文】在空间直角坐标系中,点B 是()1,2,3A 在yOz 坐标平面内的射影,O 为坐标原点,则OB 等于( )A .14B .13C .23D .115.【题文】长方体1111ABCD A BC D -中,AB =AA 1=2,AD =1,E 为CC 1的中点,则异面直线BC 1与AE 所成角的余弦值为 ( ) A. 1010B.3010 C. 21510D.310106.【题文】在棱长为的正方体1111ABCD A B C D -中,平面1AB C 与平面11A C D 间的 距离为( )A .63B .33 C .332 D .237.【题文】如图,在四面体OABC 中,G 是底面△ABC 的重心,则OG 等于()GCABOA.OC OB OA ++B.111222OA OB OC ++C.111236OA OB OC ++ D.111333OA OB OC ++8.【题文】在直三棱柱111C B A ABC -中,底面是等腰直角三角形, 90=∠ACB ,侧棱21=AA ,D ,E 分别是1CC 与B A 1的中点,点E 在平面ABD 上的射影是ABD ∆的重心G .则B A 1与平面AB D 所成角的余弦值 ()A .32 B .37C .23D .73二、填空题9.【题文】如图,在直三棱柱111ABC A B C -中,∠ACB =90°,AA 1=2,AC =BC =1,则异面直线A 1B 与AC 所成角的余弦值是________.10.【题文】已知正四棱锥P ABCD -的侧棱与底面所成角为60°,M 为PA 的中点,连接DM ,则DM 与平面PAC 所成角的大小是________.11.【题文】如图所示,正方体1111ABCD A BC D -的棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =23a ,则MN 与平面BB 1C 1C 的位置关系是______.三、解答题12.【题文】如图,AB 是圆的直径,PA 垂直于圆所在的平面,C 是圆上异于A 、B 的点.(1)求证:平面PAC ⊥平面PBC ;(2)若AB =2,AC =1,PA =1,求二面角C PB A --的余弦值.13.【题文】如图,直三棱柱111ABC A B C -中,△ABC 是等边三角形,D 是BC 的中点.(1)求证:A 1B ∥平面ADC 1;(2)若AB =BB 1=2,求A 1D 与平面AC 1D 所成角的正弦值.14.【题文】直四棱柱1111ABCD A BC D -中,底面A B C D为菱形,且160,,BAD A A AB E ∠==为1BB 延长线上的一点,1D E ⊥面1D AC .设2AB =. (1)求二面角1E AC D --的大小;(2)在1D E 上是否存在一点P ,使1//A P 面EAC ?若存在,求1:D P PE 的值;若不存在,说明理由.人教版选修2-1 课时3.2立体几何中的向量方法参考答案与解析一、选择题 1. 【答案】A【解析】∵a ·b =(4,-1,0)·(1,4,5)=4-4+0=0,a ·c =(4,-1,0)·( -3,12,-9)=-12-12+0=-24≠0.b ·c =(1,4,5)·(-3,12,-9)=-3+48-45=0,∴a ⊥b ,a 与c 不垂直,b ⊥c . ∴l 1⊥l 2,l 2⊥l 3,但l 1不垂直于l 3. 考点:直线的方向向量. 【题型】选择题 【难度】较易 2. 【答案】A【解析】|a |=2222+4+6x =,∴x =±4,又∵a ⊥b ,∴a ·b =2×2+4y +2x =0, ∴y =-1-12x ,∴当x =4时,y =-3,当x =-4时,y =1,∴x +y =1或-3. 考点:直线的方向向量. 【题型】选择题 【难度】较易 3. 【答案】B【解析】由(2,2,5)u =-,(6,4,4)v =-,可得262(4)540u v ⋅=-⨯+⨯-+⨯=,所以u v ⊥,又u ,分别是平面α,β的法向量,所以αβ⊥,故选B. 考点:空间向量在解决空间垂直中的应用. 【题型】选择题【难度】较易 4. 【答案】B【解析】因为点B 是()1,2,3A 在yOz 坐标平面内的射影,所以(0,2,3)B ,22202313∴=++=OB .故选B . 考点:空间中两点间的距离. 【题型】选择题 【难度】较易 5. 【答案】B【解析】建立坐标系如图所示,则A (1, 0, 0),E (0, 2, 1),B (1, 2, 0),C 1(0, 2, 2),则1BC =(-1, 0, 2),AE =(-1,2, 1).cos 〈1BC ,AE 〉=11AE BC AE BC ⋅⋅=3010. 所以异面直线BC 1与AE所成角的余弦值为3010.故选B.考点:异面直线所成角的向量求法. 【题型】选择题 【难度】较易 6.【答案】B【解析】建立如图所示的直角坐标系,设平面11A C D 的法向量(,,1)n x y =,则1100n DA n DC ⎧⋅=⎪⎨⋅=⎪⎩,即()()()(),,11,0,10,,,10,1,10x y x y ⋅-=⎧⎪⎨⋅-=⎪⎩()1,1,1,1,1,x n y =⎧⇒∴=⎨=⎩又(1,0,0)AD =-,∴平面1AB C 与平面11A C D 间的距离()()2221,0,01,1,133111AD n d n⋅-⋅===++,故选B.考点:面与面间的距离的向量求法. 【题型】选择题 【难度】一般 7. 【答案】D【解析】由题意知,()()11=+=+=33OG OA AG OA AC AB OA OC OA OB OA ++-+- =111333OA OB OC ++,故选D. 考点:空间向量的运算. 【题型】选择题 【难度】一般 8. 【答案】B【解析】以C 为坐标原点,CA 所在直线为轴,CB 所在直线为y 轴,1CC 所在直线为轴,建立直角坐标系,设a CB CA ==,则(),0,0A a ,()0,,0B a ,)(2,0,1a A ,)(1,0,0D ,则)(1,2,2a a E ,)(31,3,3a a G ,则)(32,6,6a a GE =,)(1,,0a BD -=, ∵点E 在平面ABD 上的射影是ABD ∆的重心G , ∴⊥GE 平面ABD ,∴0=⋅BD GE ,解得2=a .∴)(32,31,31=GE ,)(2,2,21-=BA , ∵⊥GE 平面ABD ,∴GE 为平面ABD 的一个法向量.32323634||||,cos 111=⋅=⋅⋅>=<BA GE BA GE BA GE , ∴B A 1与平面ABD 所成的角的余弦值为37,故选B.考点:线面角的空间向量求法. 【题型】选择题 【难度】较难二、填空题 9. 【答案】66【解析】以C 为坐标原点,CA ,CB ,CC 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,则A 1(1, 0, 2),B (0, 1, 0),A (1, 0, 0),C (0, 0, 0),则1A B =(-1, 1,-2),AC =(-1, 0, 0),cos 〈1A B ,AC 〉=11A B AC A B AC⋅⋅=1114++=66. 考点:异面直线夹角的向量求法. 【题型】填空题 【难度】较易 10. 【答案】45°【解析】设底面正方形的边长为a ,由已知可得正四棱锥的高为62a ,建立如图所示的空间直角坐标系,则平面PAC 的一个法向量为n =(1,0,0),D 2,0,02a ⎛⎫- ⎪ ⎪⎝⎭,P 60,0,2a ⎛⎫ ⎪ ⎪⎝⎭,M 260,,44a a ⎛⎫- ⎪ ⎪⎝⎭,则DM =226,,244a a a ⎛⎫- ⎪ ⎪⎝⎭,所以cos 〈DM ,n 〉=n DM n DM⋅⋅=22,所以DM 与平面PAC 所成的角为45°.考点:线面角的空间向量求法. 【题型】填空题 【难度】一般 11. 【答案】平行【解析】分别以C 1B 1、C 1D 1、C 1C 所在直线为x ,y ,z 轴,建立空间直角坐标系, 如图所示.∵A 1M =AN =23a ,∴M 2(,,)33a a a ,N 22(,,)33a a a ,∴MN =2(,0,)33a a .又C 1(0,0,0),D 1(0,a,0),∴11C D =(0,a,0),∴MN ·11C D =0,∴MN ⊥11C D .∵11C D 是平面BB 1C 1C 的一个法向量,且MN ⊄平面BB 1C 1C ,∴MN ∥平面BB 1C 1C .考点:向量法求线面关系. 【题型】填空题 【难度】一般三、解答题 12.【答案】(1)见解析(2)64【解析】(1)证明:由AB 是圆的直径,得AC ⊥BC ,由PA ⊥平面ABC ,BC ⊂平面ABC ,得PA ⊥BC .又PA ∩AC =A ,PA ⊂平面PAC ,AC ⊂平面PAC , 所以BC ⊥平面PAC .又BC ⊂平面PBC ,所以平面PBC ⊥平面PAC . (2)过C 作CM ∥AP ,则CM ⊥平面ABC .如图,以点C 为坐标原点,分别以直线CB ,CA ,CM 为x 轴、y 轴、z 轴建立空间直角坐标系.在Rt △ABC 中,因为AB =2,AC =1,所以BC =3.又因为PA =1,所以A (0,1,0),B (3,0,0),P (0,1,1),故CB =(3,0,0),CP =(0,1,1),设平面BCP 的法向量为1n =(x 1,y 1,z 1),则110,0,n CB n CP ⎧⋅=⎪⎨⋅=⎪⎩所以111300x y z ⎧⎪⎨⎪⎩=,+=,令y 1=1,则1n =(0,1,-1).AP =(0,0,1),AB =(3,-1,0),设平面ABP 的法向量为2n =(x 2,y 2,z 2),则220,0,n AP n AB ⎧⋅=⎪⎨⋅=⎪⎩所以222300x y z ⎧⎪⎨⎪⎩-=,=,令x 2=1,则2n =(1,3,0).于是cos 〈1n ,2n 〉=322=64.由题意可知二面角C PB A --的余弦值为64. 考点:空间二面角的向量求法. 【题型】解答题 【难度】一般 13.【答案】(1)见解析(2)23535【解析】(1)证明:因为三棱柱111ABC A B C -是直三棱柱,所以四边形A 1ACC 1是矩形.连接A 1C 交AC 1于O ,连接OD ,则O 是A 1C 的中点,又D 是BC 的中点,所以在△A 1BC 中,OD ∥A 1B ,因为A 1B ⊄平面ADC 1,OD ⊂平面ADC 1,所以A 1B ∥平面ADC 1. (2)因为△ABC 是等边三角形,D 是BC 的中点,所以AD ⊥BC .以D 为原点,建立如图所示空间坐标系D xyz -.由已知AB =BB 1=2,得D (0,0,0),A (3,0, 0),A 1(3,0, 2),C 1(0,-1, 2),则DA =(3,0, 0),1DC =(0,-1,2),设平面AC 1D 的法向量为=(x ,y ,z ),则10,0,n DA n DC ⎧⋅=⎪⎨⋅=⎪⎩即30,20,x y z ⎧=⎪⎨-+=⎪⎩取z =1,则x =0,y =2,∴=(0,2,1), 又1DA =(3,0,2),∴cos 〈1DA ,〉=257⋅=23535,设A 1D 与平面ADC 1所成角为θ,则sin θ=|cos 〈1DA ,〉|=23535, 故A 1D 与平面ADC 1所成角的正弦值为23535.考点:线面角的向量求法. 【题型】解答题 【难度】一般 14.【答案】(1)45︒(2)存在点P 使1//A P 面,EAC 此时1:3:2D P PE = 【解析】(1)设AC 与BD 交于O ,设1B E h =,如图所示建立空间直角坐标系O xyz -,则1(3,0,0),(0,1,0),(3,0,0),(0,1,0),(0,1,2),A B C D D --- (0,1,2),E h +则11(0,2,),(23,0,0),(3,1,2),D E h CA D A ===-1D E ⊥平面1D AC ,111,D E AC D E D A ∴⊥⊥,220,1,h h ∴-=∴=即(0,1,3)E .1(0,2,1),(3,1,3)D E AE ∴==-,设平面EAC 的法向量为(,,)m x y z =, 则,,m CA m AE ⎧⊥⎪⎨⊥⎪⎩即230,330,x x y z ⎧=⎪⎨-++=⎪⎩令1z =-,则0,3x y ==,()0,3,1m ∴=-. 又平面1D AC 的一个法向量为()10,2,1D E =,1112cos ,==2m D E m D E m D E⋅∴⋅, ∴二面角1E AC D --大小为45.(2)设111(),D P PE D E D P λλ==-得112(0,,),111D P D E λλλλλλ==+++ 111121(3,1,0)(0,,)(3,,)1111A P A D D P λλλλλλλλ-∴=+==--+=-++++,1//A P 面113,,303(1)0,,112EAC A P m λλλλλ-∴⊥∴-⨯+⨯+-⨯=∴=++ ∴存在点P 使1//A P 面,EAC 此时1:3:2D P PE =考点:空间向量法求二面角. 【题型】解答题 【难度】一般。
高中数学选修2-1教案第三章空间向量与立体几何3.2立体几何中的向量方法

23.2立体几何中的向量方法第一课时 立体几何中的向量方法(1)教学要求:向量运算在几何证明与计算中的应用. 掌握利用向量运算解几何题的方法,并能解简单的立体几何问题.教学重点:向量运算在几何证明与计算中的应用. 教学难点:向量运算在几何证明与计算中的应用. 教学过程: 一、复习引入1.用向量解决立体几何中的一些典型问题的基本思考方法是:⑴如何把已知的几何条件 (如线段、角度等)转化为向量表示;⑵考虑一些未知的向量能否用基向量或其他已知向量表式; ⑶如何对已经表示出来的向量进行运算,才能获得需要的结论?2. 通法分析:利用两个向量的数量积的定义及其性质可以解决哪些问题呢?⑴利用定义 a • b = |a ||b |cos v a ,b >或cos v a ,b >=卫b ,可求两个向量的数量积或夹角 问题;⑵利用性质a 丄a • b = 0可以解决线段或直线的垂直问题; ⑶利用性质aa =| a 丨2,可以解决线段的长或两点间的距离问题. 二、例题讲解1. 出示例1:已知空间四边形 OABC 中,:.OAf_BC ” OB _ AC •求证: 证明:OC AB = OC (OB -OA) = OC OB — OC OA .TT••• OA _ BC , OB _ AC , • OA BC 0, OB AC 0 ,)「0 , OB (OC -OA) =0 .• OA OC =OA OB , OB OC =OB OA .4•小结:利用向量解几何题的一般方法:把线段或角度转化为向量表示式,并用已知向量 表示未知向量,然后通过OC _ AB .二 OC OB = OC OA , OCAB = 0. ••• OC _ AB2.出示例2:如图,已知线段.DBD ' =30;,如果 AB = a , 解:由AC ,可知AC 由.DBD' =30;可知,v •汙『=(CA AB BD) AB BD )2 2 2 2 - 2 2=b a b 2b cos120 = a b .AB 在平面a 内,线段AC _,线段BD 丄AB ,线段DD ' _ :-,AC = BD = b ,求C 、D 间的距离.CA,BD >= 120 ,2= |CA |2 + | AB |2 + | BD |2 + 2( CA AB + CA BD +• CD a 2 b 2 .3.出示例3:如图,M 、N 分别是棱长为1的正方体 ABCD -A'B'C'D'的 棱BB'、B'C'的中点.求异面直线 MN 与CD'所成的角.1解:••• MN = - (CC ' BC ),2 1• MN CD' = (CC' BC)2 CD' = CC' CD ,(C? CD) = 1(|C^|2 + CC -L CD2+ BC CC' +BC CD ).•/ CC'_CD , CC'_BC , 1 2 1• MN CD' = |CC' |2 =2 2BC =0, BC CD =0 ,…求得 cos v MN ,CD' >BC CC 0 ,1 ,•••< MN ,CD' >= 60 ._CD ,向量的运算去计算或证明.2第二课时 立体几何中的向量方法(2)教学要求:向量运算在几何证明与计算中的应用. 掌握利用向量运算解几何题的方法,并能解简单的立体几何问题.教学重点:向量运算在几何证明与计算中的应用. 教学难点:向量运算在几何证明与计算中的应用. 教学过程: 一、复习引入讨论:将立体几何问题转化为向量问题的途径?(1 )通过一组基向量研究的向量法,它利用向量的概念及其运算解决问题;(2)通过空间直角坐标系研究的坐标法,它通过坐标把向量转化为数及其运算来解决问二、例题讲解1.出示例1:如图,在正方体 ABCD-ABGD I 中,E 、F 分别是BB l 、 CD 的中点,求证:UF _平面ADE .证明:不妨设已知正方体的棱长为1个单位长度, 且设DA = i , "DC =j , DD 1 = k .以i 、j 、k 为坐标向量建立空间直角坐标系D — xyz ,贝U1 1••• AD = (-1,0,0), D 1F = (0,,-1), ••• AD • D 1F = (-1,0,0) .(0,,-1)= 0, ••• D 1F _AD .的一些数据,以使问题的解决简单化.如在立体几何中求角的大小、判定直线与直线或直线 与平面的位置关系时,可以约定一些基本的长度.⑵空间直角坐标些建立,可以选取任意一 点和一个单位正交基底, 但具体设置时仍应注意几何体中的点、线、面的特征,把它们放在 恰当的位置,才能方便计算和证明.2.例:证:如果两条直线同垂直于一个平面,则这两条直线平行.改写为:已知:直线 OA 丄平面a,直线BD 丄平面a, O 、B 为垂足.求证: 证明:以点O 为原点,以射线OA 为非负z 轴,建立空间直角坐标系 O-xyz , i ,j ,k 为沿x 轴,y 轴,z 轴的坐标向量,且设 BD = (x, y,z).•/ BD 丄 a, • BD 丄 i , BD 丄 j ,• BD • i = (x,y,z) •(1,0,0) = x = 0, , BD • j = (x, y, z) • (0,1,0) = y = 0, • BD = (0,0,z). • BD = z k .即BD //k .由已知 O 、B 为两个不同的点,•3. 法向量定义:如果表示向量a 的有向线段所在直线垂直于平面a,则称这个向量垂直于平面a,记作a 丄a.如果a 丄a,那么向量a 叫做平面a 的法向量.4. 小结:向量法解题“三步曲” :(1)化为向量问题 7( 2)进行向量运算 7( 3)回到图形问题.A E = (0,1,-),2AD^AE =A ,• AED 1F = (0,1,1)21(0, ,-1)= 0,2说明:⑴“不妨设”是我们在解题中常用的小技巧,通常可用于设定某些与题目要求无关OA//BD .OA//BD .第三课时立体几何中的向量方法(3)教学要求:向量运算在几何证明与计算中的应用. 掌握利用向量运算解几何题的方法,并能解简单的立体几何问题.教学重点:向量运算在几何证明与计算中的应用. 教学难点:向量运算在几何证明与计算中的应用. 教学过程: 一、复习引入呻 呻1.法向量定义:如果直线I _平面:•,取直线I 的方向向量为a ,则向量a 叫作平面a 的法 向量(normal vectors ).利用法向量,可以巧妙的解决空间角度和距离2.讨论:如何利用法向量求线面角?T 面面角?直线AB 与平面a 所成的角日,可看成是向量 AB 所在直线与平面a 的法向量n 所在直 线夹角的余角,从而求线面角转化为求直线所在的向量与平面的法向量的所成的线线角,根a b据两个向量所成角的余弦公式 cosf a, b),我们可以得到如下向量法的2.变式:用向量法求:二面角A -DE -O 余弦;OF 与DE 的距离;O 点到平面DEF 的距公式:3. 讨论:如何利用向量求空间距离?两异面直线的距离,转化为与两异面直线都相交的线段在公垂向量上的投影长 点到平面的距离,转化为过这点的平面的斜线在平面的法向量上的投影长 二、例题讲解:1.出示例 1:长方体 ABCD - ARGD ,中,AD= AA ,=2, AB=4, E 、 点,0是BC 1与EC 的交点.求直线OF 与平面DEF 所成角的正弦•解:以点D 为空间直角坐标系的原点, DA 、DC 、DD 1为坐标轴,建立如图所示的空间直角坐标系.则D(2,2,0), E(1,0,2), F(2,2,0), 0(1,4,1), C(0,4,0).4设平面DEF 的法向量为 n =(x,y,z), 而 DE =(1,0,2) , DF =(2,2,0). 片 —* n _DE 则n _ DFnLDE =0 • ^=0■/ n *OF =| n ||OF J cos :, n *OF. • cos 2 2 22-|n"OF 丨(-2)2 - 22 - t.J 2 - (一2)2 • (-1)所以,直线OF 与平面DEF 所成角的正弦为 乙6 .18,即 •OF 丄x 2z = 0仏+2^0‘ 解得心:—2:2:1,而 OF =(1,-2,-1). -2 1 2 (-2) 1 (-1) 2•• n =(-2,2,1).7 618sin 日=cos (AB‘, n。
高二数学 3.2《立体几何中的向量方法(一)》课件(新人教A版选修2-1)

线线垂直 线面垂直
r r rr
l⊥m a⊥b ab 0;
rr r r
l ⊥ a ∥u a ku;
面面垂直 ⊥ u ⊥ v u v 0.
画出图形意会
rr
设直线 l, m 的方向向量分别为 a, b ,平面 ,
rr
的法向量分别为 u, v ,则
rr
B A 以及一个定
A
方向确定.
⑵直线
空间中任意一条直线 l 的位置可以由 l 上一
个定点 A 以及一个定方向确定.
r a
P
对于直线 l 存在实数 t 使得
上的任一点
uuur uuur AP t AB
P
,
此方程称为直线的向量参数方程
B uuur uuur r uuur uuur uuur
OP OA ta 或 OP xOA yOB (x y 1)
1答案
2答案
3答案
练习
1.已知两点 A(1, 2,3),B(2,1, 3),,
求直线 AB 与坐标平面 yOz 的交点.
解:设直线 AB 与 yOz 平面的交点为 C(0, y1, y2 )
uuur
uuur uuur
由OC (1 t)OA tOB得
(0,y1,z1 )(1 t)(1, 2, 3) t(2,1, 3) (u0uu,ry1,z1) (1 t, 2 3t,3 6t) OC (0, 5,9)
立体几何中的向量方法(一)
引入
知识要点
方向向量、 法向量的运 用思考
练习
本课小结
作业:课本 P113练习 1,2
立体几何中的向量方法(一)
前面,我们把 平面向量
高中数学 3.2.2立体几何中的向量方法(二)课件 新人教A

设点F的坐标为(x, y, z),则PF (x, y, z 1)
因为PF k PB 所以( x, y, z 1) k(1,1, 1)
Z
P
(k,k,k)
即x k, y k, z 1 k
F
E
因为PB • DF 0
所以(1,1,1) • (k, k,1 k)
k k 1 k 3k 1 0A 所以k 1 F (1,1,2) X
平面 , 的法向量分别为 u, v ,则
rr
(3) , 的夹角为, 则cosθ = cos < u,v >
u
v
例2 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB
P
(2)求证:PB 平面EFD
6 1
3
1 2
所以EFD 60o,即二面角 C PB D的大小为 60o.
例3、在底面是直角梯形的四棱锥S ABCD中,
ABC 90, SA 平面ABCD, SA AB BC 1,
AD 1 .求平面SCD与平面SBA所成的二面角的
2
z
正切值.
y
S
B
A
D
C x
A B C D 练1.在长方体ABCD
(3)求二面角C-PB-D的大小。
F
E
D A
C B
例2 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB
P
(2)求证:PB 平面EFD
人教版高中数学选修(2-1)-3.2《立体几何中的向量方法(第2课时)》教学课件2

AC 1,CB 2,侧棱AA1 1,侧面AA1B1B的
D
两条对角线交点为D, B1C1的中点为M . 求证CD 平面BDM
C
B
B1
A1
C1
M
∴ A1O ⊥ 平面GBD
变式:
B' C'
在三棱柱ABC A' B 'C '中,
A'
底面是正三角形,AA' 底面ABC,
A'C AB ',求证:BC ' AB '
C
B
A
小结
1.用空间向量方法证明立体几何中的平行与 垂直问题,主要运用了直线的方向向量和平面的法 向量,同时也要借助空间中已有的一些关于平行、 垂直的定理.
平行;三是证明 MN可以用平面 A1BD中的两不共线向量线性 表示.
D! A!
D A
C! N B! M
C B
例1 如图,在正方形ABCD-A1B1C1D1中,M,N分别是C1C、
B1C1的中点,求证:MN∥平面A1BD
法1:建立如图所示的空间直角坐标系. z
设正方体的棱长为1,则可求得
D!
C!
N
M(0,1,1/2),N(1/2,1,1),D(0,0 A!
3.2 立体几何中的向量方法(二)
--利用向量解决平行与垂直问题
用向量运算处理平行关系
设直线 l, m 的方向向量分别为 a, b ,平面 ,
的法向量分别为 u, v ,则
线线平行 l ∥ m a ∥ b a kb ; 线面平行 l ∥ a u a u 0 ;
O A
OG
OC
人教a版选修1-1教案:3.2立体几何中的向量方法第1课时(含答案)

§3.2.1直线的方向向量与平面的法向量【学情分析】:教学对象是高二的学生,学生已经具备空间向量与立方体几何的相关知识,所以本节课是通过这些知识理解空间的几个元素点、直线、平面的位置的向量表示,并且用向量及其运算表示线线、线面、面面间的平行与垂直的位置关系,可以比较顺利地进行教学.【教学目标】:(1)知识与技能:理解直线的方向向量和平面的法向量;会用向量及其运算表示线线、线面、面面间的位置关系.(2)过程与方法:在解决问题中,通过数形结合的思想方法,加深对相关知识的理解。
(3)情感态度与价值观:开始体会把立方体几何几何转化为向量问题优势.【教学重点】:平面的法向量.【教学难点】:用向量及其运算表示线线、线面、面面间的平行与垂直关系.(1)求证:AP 是平面的法向量;1,2,1)(4,2,0)-⋅AP AB ⊥AD A =2)||(2)AB =,2||4AD =AD ⋅=,cos(,)AB AD =1BAD ∠=-ABCD=点、直线、平面的位置的向量表示练习与测试:(基础题)1,与两点和所成向量同方向的单位向量是。
解:向量,它的模则所求单位向量为。
2,从点沿向量的方向取长为6的线段,求点坐标。
解:设点坐标为,由题设有;由可得。
则,于是所求坐标为。
3,设直线l,m的方向向量分别为)1,0,3(),3,2,1(-==,判断l,m的位置关系。
解:因为(1,2,3)(-3,0,1)=0,所以两直线垂直。
4,设平面βα,的法向量分别为)12,6,2(),6,3,1(-=--=vu,判断平面βα,的位置关系。
解:易知所给二法向量平行,故平面βα,平行。
(中等题)5,已知空间四点坐标分别为A(1,0,0)、B(1,1,0)、E(1,1/2,1)、F(0,1/2,0),求平面AEF的单位法向量。
解:设平面AEF的法向量为则有为平面AEF的单位法向量。
6,如图所示建立坐标系,有分别求平面SAB与平面SDC的法向量,并求出它们夹角的余弦。
人教A版选修1-1教案:3.2立体几何中的向量方法第3课时(含答案)
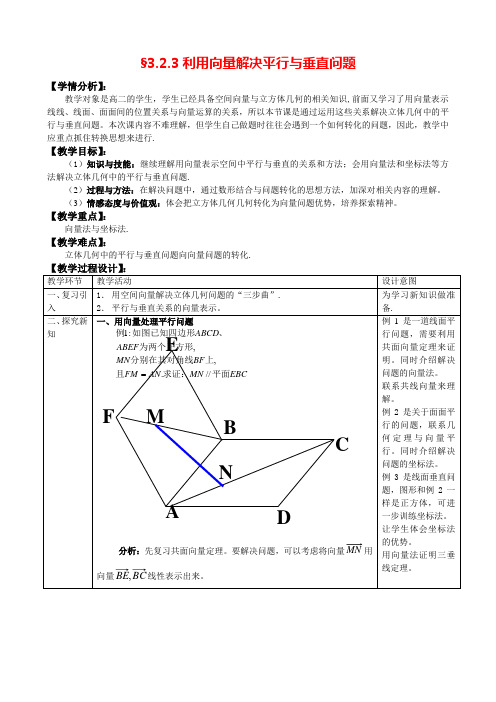
§3.2.3利用向量解决平行与垂直问题【学情分析】:教学对象是高二的学生,学生已经具备空间向量与立方体几何的相关知识,前面又学习了用向量表示线线、线面、面面间的位置关系与向量运算的关系,所以本节课是通过运用这些关系解决立体几何中的平行与垂直问题。
本次课内容不难理解,但学生自己做题时往往会遇到一个如何转化的问题,因此,教学中应重点抓住转换思想来进行.【教学目标】:(1)知识与技能:继续理解用向量表示空间中平行与垂直的关系和方法;会用向量法和坐标法等方法解决立体几何中的平行与垂直问题.(2)过程与方法:在解决问题中,通过数形结合与问题转化的思想方法,加深对相关内容的理解。
(3)情感态度与价值观:体会把立方体几何几何转化为向量问题优势,培养探索精神。
【教学重点】:向量法与坐标法.【教学难点】:立体几何中的平行与垂直问题向向量问题的转化.评注: 向量p 与两个不共线的向量a 、b 共面的充要条件是存在实数对p=x a+利用共面向量定理可以证明线面平行问题。
本题用的就是向量法。
(1).MN MF FA BE BA BE BE BC λλ=+++=-+11//.BD CB D 平面.,//MN BE BC M EBC MN EBC ∴∉∴、、共面平面平面所以,结论成立。
坐标法: 证明:(图略)2222(2)()(2)221c a a b b a a b a a b b a b -+-•+=-+•-=-=),,1,0('),,0,3h B h 2c b =•=四、小结利用向量解决平行与垂直问题1. 向量法:利用向量的概念技巧运算解决问题。
2. 坐标法:利用数及其运算解决问题。
两种方法经常结合起来使用。
反思归纳五、作业1,直三棱柱111C B A ABC 中,角ACB 是直角,AC =1,CB =2,侧棱1AA =1,侧面B B AA 11的两条对角线交点为D ,11C B 的中点为M ,求证CD 平面BDM 。
人教A版高中数学选修立体几何中的向量方法教案新

教学要求:向量运算在几何证明与计算中的应用.掌握利用向量运算解几何题的方法,并能解简单的立体几何问题.教学重点:向量运算在几何证明与计算中的应用.教学难点:向量运算在几何证明与计算中的应用.教学过程:一、复习引入1. 用向量解决立体几何中的一些典型问题的基本思考方法是:⑴如何把已知的几何条件(如线段、角度等)转化为向量表示; ⑵考虑一些未知的向量能否用基向量或其他已知向量表式; ⑶如何对已经表示出来的向量进行运算,才能获得需要的结论?2. 通法分析:利用两个向量的数量积的定义及其性质可以解决哪些问题呢?⑴利用定义a ·b =|a ||b |cos <a ,b >或cos <a ,b >=a b a b⋅⋅,可求两个向量的数量积或夹角问题;⑵利用性质a ⊥b ⇔a ·b =0可以解决线段或直线的垂直问题;⑶利用性质a ·a =|a |2,可以解决线段的长或两点间的距离问题.二、例题讲解1. 出示例1:已知空间四边形OABC 中,OA BC ⊥,OB AC ⊥.求证:OC AB ⊥.证明:·OC AB =·()OC OB OA - =·OC OB -·OC OA .∵OA BC ⊥,OB AC ⊥, ∴·0OA BC =,·0OB AC =, ·()0OA OC OB -=,·()0OB OC OA -=. ∴··OA OC OA OB =,··OB OC OB OA =. ∴·OC OB =·OC OA ,·OC AB =0. ∴OC AB ⊥ 2. 出示例2:如图,已知线段AB 在平面α内,线段AC α⊥,线段BD ⊥AB ,线段'DD α⊥,'30DBD ∠=,如果AB =a ,AC =BD =b ,求C 、D 间的距离.解:由AC α⊥,可知AC AB ⊥.由'30DBD ∠=可知,<,CA BD >=120,∴2||CD =2()CA AB BD ++=2||CA +2||AB +2||BD +2(·CA AB +·CA BD +·AB BD )=22222cos120b a b b +++=22a b +.∴CD =3. 出示例3:如图,M 、N 分别是棱长为1的正方体''''ABCD A B C D -的棱'BB 、''B C 的中点.求异面直线MN 与'CD 所成的角.解:∵MN =1(')2CC BC +,'CD ='CC CD +, ∴·'MN CD =1(')2CC BC +·(')CC CD +=12(2|'|CC +'CC CD +·'BC CC +·BC CD ). ∵'CC CD ⊥,'CC BC ⊥,BC CD ⊥,∴'0CC CD =,·'0BC CC =,·0BC CD =, ∴·'MN CD =122|'|CC =12. …求得 cos <,'MN CD >12=,∴<,'MN CD >=60. 4. 小结:利用向量解几何题的一般方法:把线段或角度转化为向量表示式,并用已知向量表示未知向量,然后通过向量的运算去计算或证明.三、巩固练习 作业:课本P 116 练习 1、2题.教学要求:向量运算在几何证明与计算中的应用.掌握利用向量运算解几何题的方法,并能解简单的立体几何问题.教学重点:向量运算在几何证明与计算中的应用.教学难点:向量运算在几何证明与计算中的应用.教学过程:一、复习引入讨论:将立体几何问题转化为向量问题的途径?(1)通过一组基向量研究的向量法,它利用向量的概念及其运算解决问题;(2)通过空间直角坐标系研究的坐标法,它通过坐标把向量转化为数及其运算来解决问题.二、例题讲解1. 出示例1: 如图,在正方体1111ABCD A B C D -中,E 、F 分别是1BB 、CD 的中点,求证:1D F ⊥平面ADE .证明:不妨设已知正方体的棱长为1个单位长度,且设DA =i ,DC =j ,1DD =k .以i 、j 、k 为坐标向量建立空间直角坐标系D -xyz ,则∵AD =(-1,0,0),1D F =(0,12,-1),∴AD ·1D F =(-1,0,0)·(0,12,-1)=0,∴1D F ⊥AD . 又 AE =(0,1,12),∴AE ·1D F =(0,1,12)·(0,12,-1)=0, ∴1D F ⊥ AE . 又 AD AE A =, ∴1D F ⊥平面ADE .说明:⑴“不妨设”是我们在解题中常用的小技巧,通常可用于设定某些与题目要求无关的一些数据,以使问题的解决简单化.如在立体几何中求角的大小、判定直线与直线或直线与平面的位置关系时,可以约定一些基本的长度.⑵空间直角坐标些建立,可以选取任意一点和一个单位正交基底,但具体设置时仍应注意几何体中的点、线、面的特征,把它们放在恰当的位置,才能方便计算和证明.2. 出示例2:课本P 116 例3分析:如何转化为向量问题?进行怎样的向量运算?3. 出示例3:课本P 118 例4分析:如何转化为向量问题?进行怎样的向量运算?4. 出示例4:证:如果两条直线同垂直于一个平面,则这两条直线平行.改写为:已知:直线OA ⊥平面α,直线BD ⊥平面α,O 、B 为垂足.求证:OA //BD . 证明:以点O 为原点,以射线OA 为非负z 轴,建立空间直角坐标系O -xyz ,i ,j ,k 为沿x 轴,y 轴,z 轴的坐标向量,且设BD =(,,)x y z . ∵BD ⊥α, ∴BD ⊥i ,BD ⊥j ,∴BD ·i =(,,)x y z ·(1,0,0)=x =0,BD ·j =(,,)x y z ·(0,1,0)=y =0,∴BD =(0,0,z ).∴BD =z k .即BD //k .由已知O 、B 为两个不同的点,∴OA //BD .5. 法向量定义:如果表示向量a 的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作a ⊥α.如果a ⊥α,那么向量a 叫做平面α的法向量.6. 小结:向量法解题“三步曲”:(1)化为向量问题 →(2)进行向量运算 →(3)回到图形问题.三、巩固练习 作业:课本P 120、 习题A 组 1、2题.第三课时: §3.2立体几何中的向量方法(三)教学要求:向量运算在几何证明与计算中的应用.掌握利用向量运算解几何题的方法,并能解简单的立体几何问题.教学重点:向量运算在几何证明与计算中的应用.教学难点:向量运算在几何证明与计算中的应用.教学过程:一、复习引入1. 法向量定义:如果直线l α⊥平面, 取直线l 的方向向量为a ,则向量a 叫作平面α的法向量(normal vectors ). 利用法向量,可以巧妙的解决空间角度和距离.2. 讨论:如何利用法向量求线面角? → 面面角?直线AB 与平面α所成的角θ,可看成是向量AB 所在直线与平面α的法向量所在直线夹角的余角,从而求线面角转化为求直线所在的向量与平面的法向量的所成的线线角,根据两个向量所成角的余弦公式cos ,a b a b a b =,我们可以得到如下向量法的公式: sin cos ,AB n AB n AB n θ==.3. 讨论:如何利用向量求空间距离?两异面直线的距离,转化为与两异面直线都相交的线段在公垂向量上的投影长.点到平面的距离,转化为过这点的平面的斜线在平面的法向量上的投影长.二、例题讲解:1. 出示例1:长方体1111ABCD A B C D -中,AD =1AA =2,AB =4,E 、F 分别是11A D 、AB 的中点,O 是11BC B C 与的交点. 求直线OF 与平面DEF 所成角的正弦.解:以点D 为空间直角坐标系的原点,DA 、DC 、1DD 为坐标轴,建立如图所示的空间直角坐标系. 则(2,2,0),(1,0,2),(2,2,0),(1,4,1),(0,4,0)D E F O C .设平面DEF 的法向量为 (,,)n x y z =, 则n DE n DF⎧⊥⎪⎨⊥⎪⎩ , 而(1,0,2)DE =, (2,2,0)DF =. ∴ 00n DE n DF ⎧=⎪⎨=⎪⎩ ,即20220x z x y +=⎧⎨+=⎩, 解得::2:2:1x y z =-, ∴ (2,2,1)n =-. ∵ ||||cos n OF n OF α∙= , 而(1,2,1)OF =--. ∴ cos α=2||||(11(2)n OF n OF ∙==∙-+- 所以,直线OF 与平面DEF 所成角的正弦为7618. 2. 变式: 用向量法求:二面角1A DE O --余弦;OF 与DE 的距离;O 点到平面DEF 的距离.三、巩固练习作业:课本P 121、 习题A 组 5、6题.。
人教A版选修1-1教案:立体几何中的向量方法第1课时(含答案)

§3.2.1直線的方向向量與平面的法向量【學情分析】:教學對象是高二的學生,學生已經具備空間向量與立方體幾何的相關知識,所以本節課是通過這些知識理解空間的幾個元素點、直線、平面的位置的向量表示,並且用向量及其運算表示線線、線面、面面間的平行與垂直的位置關係,可以比較順利地進行教學.【教學目標】:(1)知識與技能:理解直線的方向向量和平面的法向量;會用向量及其運算表示線線、線面、面面間的位置關係.(2)過程與方法:在解決問題中,通過數形結合的思想方法,加深對相關知識的理解。
(3)情感態度與價值觀:開始體會把立方體幾何幾何轉化為向量問題優勢.【教學重點】:平面的法向量.【教學難點】:用向量及其運算表示線線、線面、面面間的平行與垂直關係.(2,AB =-(4,2,0)AD =(1,AP =-(1)求證:AP 是平面的法向量;(2)求平行四邊形ABCD 的面積. (1)證明:∵(1,2,1)(2,AP AB ⋅=--⋅-(1,2,1)(4,2,0)AP AD ⋅=--⋅∴AP AB ⊥,AP AD ⊥,又AD A =∴AP 是平面ABCD 的法向量.(2)||(2)AB =,2||4AD =∴(2,6AB AD ⋅==,∴105cos(,)10521AB AD =, sin 1105BAD ∠=-||||sin ABCDAB AD =⋅∠點、直線、平面的位置的向量表示線線、線面、面面間的平行與垂直關係的向量表示六、作業A ,預習課本105~110的例題。
B ,書面作業:1,2,練習與測試:(基礎題)1,與兩點和所成向量同方向的單位向量是 。
解:向量,它的模則所求單位向量為 。
2,從點沿向量 的方向取長為6的線段 ,求點座標。
解:設點座標為,由題設有 ;由 可得。
則,於是所求座標為。
3,設直線l ,m 的方向向量分別為)1,0,3(),3,2,1(-==b a ,判斷l ,m 的位置關係。
解:因為(1,2,3)(-3,0,1)=0,所以兩直線垂直。
人教课标版高中数学选修2-1《立体几何中的向量方法(第2课时)》教案-新版

3.2.2 向量法在空间平行关系中的运用一、教学目标 (一)核心素养通过这节课学习,掌握利用空间向量证明空间平行关系. (二)学习目标1.利用直线方向向量证明空间中的线线平行2.利用直线方向向量和平面的法向量证明空间中的线面平行 3.利用平面的法向量证明空间中的面面平行 4.学会应用向量解决与平行相关的探究性问题 (三)学习重点1.利用直线方向向量证明空间中的线线平行.2.利用直线方向向量和平面的法向量证明空间中的线面平行集合的表示法:列举法、描述法. 3.利用平面的法向量证明空间中的面面平行常用数集的表示符号. (四)学习难点1.对向量法证明空间平行关系的理解. 2.对各种证明方法的熟练掌握. 3.怎样设空间中未知点的坐标. 二、教学设计 (一)课前设计 1.预习任务填一填:空间中平行关系的向量表示 (1)线线平行设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2),且2220a b c ≠,则//l m ⇔//a b ⇔a b λ= ⇔111222222(0)a b c a b c a b c ==≠ (2)线面平行设直线l 的方向向量为a =(a 1,b 1,c 1),平面α的法向量为n =(a 2,b 2,c 2),则//l α ⇔a n ⊥ ⇔0a n = ⇔a 1a 2+b 1b 2+c 1c 2=0(3)面面平行设平面α,β的法向量分别为1n =(a 1,b 1,c 1),2n =(a 2,b 2,c 2),则//αβ ⇔12//n n⇔12n n λ= ⇔ 111222222(0)a b c a b c a b c ==≠ 2.预习自测1.已知直线l 的方向向量为(1,m,1),平面α的法向量为1(1,,2)2,且l ∥α,则m =答案:-6解析:【知识点】用向量法判断直线和平面的位置关系的应用【解题过程】()11//,1,,11,,20,11120,622l m m m ⎛⎫=⨯+⨯+⨯==- ⎪⎝⎭∵∴∴∴α点拨:线面平行即是直线方向向量和平面的法向量垂直2.已知线段AB 的两端点的坐标为A (9,-3,4),B (9,2,1),则与线段AB 平行的坐标平面是( ) A .xOy B .xOz C .yOz D .xOy 或yOz 答案:C .解析:【知识点】用向量法判断直线和平面的位置关系 【解题过程】()()0,5,3,1,0,00AB AB =-∴=点拨:线面平行即是直线方向向量和平面的法向量垂直3.已知a =(2,4,5),b =(3,x ,y )分别是直线l 1、l 2的方向向量.若l 1∥l 2,则( ) A .x =6,y =15 B .x =3,y =152 C .x =3,y =15 D .x =6,y =152 答案:D .解析:【知识点】利用方向向量证明线线平行 【解题过程】()()15//,2,4,53,,,6,2a b x y x y λ∴=∴==点拨:用向量法证明线线平行即是证明两直线的方向向量平行. (二)课堂设计 1.知识回顾(1)直线方向向量和平面法向量的求法(2)利用直线方向向量判断直线和直线的位置关系 (3)利用平面的法向量判断平面和平面的位置关系 2.问题探究探究一 结合例子,认识向量证明空间平行关系的方法★ ●活动 归纳提炼概念上节课我们学习了直线的方向向量和平面的法向量,回忆一下,直线的方向向量和平面的法向量是否能够确定直线和平面的位置呢?(抢答)如果我们确定了直线和平面的位置后,直线和直线之间,直线和平面之间,平面与平面之间相对位置关系是不是也能确定了呢?(抢答) 想一想:那么空间直线的方向向量能够用来做什么呢? 可以证明两直线垂直,两直线平行,两直线间夹角等. 我们首先来研究用向量解决空间中的平行关系.思考:如何利用直线的方向向量证两直线平行?(可以抢答)设直线1l 和2l 的方向向量分别为1v 和2v ,则由向量共线的条件1212////v v l l ⇒.这样在证明12//l l 时,结合空间图形,分别在两直线上适当地选取方向向量1v 和2v ,证明12//l l 可转化为证明12//v v ,即证明12v kv = (k 是某个实数)想一想:我们怎样用向量法来判断直线与平面的平行呢? (可以抢答)设直线l 的方向向量为v 和平面α的法向量分别为n ,结合空间图形,显然当//v n l α⊥⇒.这样在证明//l α时,分别在直线l 上适当地选取方向向量v ,在平面α上适当地选取法向量n ,证明//l α可转化为证明v n ⊥,即证明0v n =想一想:我们怎样用法向量来判断两不同平面的位置关系呢? (可以抢答)设平面α和β的法向量分别为1n 和2n ,结合空间图形,显然有12////n n αβ⇒.这样在证明//αβ时,分别在两平面上适当地选取法向量1n 和2n ,证明//αβ可转化为证明12//n n ,即证明12n kn = (k 是某个实数)【设计意图】通过图象和实例,得出证明空间平行关系的方法 探究二 利用向量证明空间平行●活动① 利用直线的方向向量证明线线平行例1 如图所示,在长方体1111OAEB O A E B -中,3OA =,4OB =,12OO =,点P 在棱1AA 上,且12AP PA =,点S 在棱1BB 上,且12SB BS =,点,Q R 分别是11,O B AE 的中点,求证://PQ RS .答案:见解析解析:【知识点】利用方向向量证明线线平行 【解题过程】证明:如图所示,以O 为原点,建立空间直角坐标系,A (3,0,0)、B (0,4,0)、1O (0,0,2),1A (3,0,2)、B 1(0,4,2)、E (3,4,0),∵AP=2PA 1, ∴11223AP PA AA == 即()240,0,20,0,33AP ⎛⎫== ⎪⎝⎭∴P 点坐标为43,0,3⎛⎫ ⎪⎝⎭,同理可得Q (0,2,2),R (3,2,0),S (0,4,23),∴23,2,3PQ RS ⎛⎫=-= ⎪⎝⎭,∴//PQ RS又∵R ∉直线PQ ,∴PQ //RS.点拨:用直线的方向向量证明线线平行的一般步骤 (1)证明两直线的方向向量共线;(2)证明其中一个向量所在直线上一点不在另一个向量所在的直线上; (3)得出结论.变式训练1-1:在正方体1111ABCD A BC D -中,,O M 分别为111,DB DC 的中点.求证:1//OM BC .答案:见解析解析:【知识点】利用方向向量证明线线平行 【解题过程】证明:如图以D 为原点,分别以1,,AD DC DD 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系. 设正方体的棱长为2,则O (1,1,1)、M (0,1,2)、B (2,2,0)、1C (0,2,2),()()11,0,1,2,0,2OM BC =-=-, ∴112OM BC =∴1//OM BC . 又O ∉直线1BC , ∴1//OM BC .点拨:利用直线的方向向量证明线线平行的一般步骤(1)证明两直线的方向向量共线;(2)证明其中一个向量所在直线上一点不在另一个向量所在的直线上; (3)得出结论.【设计意图】通过例子熟练掌握空间中线线平行的证明 ●活动② 利用直线的方向向量和平面的法向量证明线面平行例2如图,在几何体ABCDE 中,四边形ABCD 是矩形,AB ⊥平面BEC ,BE CE ⊥,AB=BE=EC=2,G ,F 分别是线段BE ,DC 的中点.求证://GF 平面ADE ;【知识点】利用方向向量证明线面平行 【解题过程】证明:如图,在平面BEC 内,过点B 作//BQ EC ,因为BE CE ⊥,所以BQ BE ⊥. 又因为AB ⊥平面BEC ,所以,AB BE AB BQ ⊥⊥以B 为原点,分别以,,BE BQ BA 的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则A (0,0,2),B (0,0,0),E(2,0,0),D (2,2,2).()()1,0,0,2,2,1G F 设(,,)n x y z =为平面ADE 的法向量.又()()2,0,2,2,2,0AE AD =-=由00n AE n AD ⎧=⎪⎨=⎪⎩得220,220,x z x y -=⎧⎨+=⎩取1z =得=(1,-1,1)n . 又因为()1,2,1GF =,1210GF n =-+= 又G ∉平面ADE 上,所以//GF 平面ADE 点拨:利用向量证明线面平行的一般步骤 (1)证明直线的方向向量与平面的法向量垂直; (2)证明向量所在直线上一点不在平面上; (3)得出结论.同类训练:如图,已知直三棱柱ABC -A 1B 1C 1中,AC ⊥BC ,D 为AB 的中点,AC =BC =BB 1.求证:BC 1∥平面CA 1D .【知识点】利用方向向量证明线面平行 【解题过程】证明:如图,以C 1点为原点,C 1A 1,C 1B 1,C 1C 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系.设AC =BC =BB 1=2,则A (2,0,2),B (0,2,2),C (0,0,2),A 1(2,0,0),B 1(0,2,0),C 1(0,0,0),D (1,1,2).设(,,)n x y z =为平面CA 1D 的法向量.又()()12,0,2,C 1,1,0CA D =-=由100n CA n CD ⎧=⎪⎨=⎪⎩得220,0,x z x y -=⎧⎨+=⎩取1z =得=(1,-1,1)n . 又因为()10,2,2C B =,10220C B n =-+= 又1C ∉平面1CA D 上,所以1//BC 平面1CA D 点拨:利用向量证明线面平行的一般步骤 (1)证明直线的方向向量与平面的法向量垂直; (2)证明向量所在直线上一点不在平面上; (3)得出结论.【设计意图】通过例子熟练掌握空间中线面平行的证明 ●活动③ 利用直线的方向向量证明面面平行例3 已知正方体1111ABCD A BC D -的棱长为2,E 、F 、G 分别是BB 1、DD 1、DC 的中点,求证:平面ADE ∥平面B 1C 1F ; 【知识点】利用方向向量证明面面平行 【解题过程】证明:如图,以D 点为原点,DA ,DC ,1DD 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系.则A (2,0,0),E (2,2,1),F (0,0,1),B 1(2,2,2),C 1(0,2,2),D (0,0,0). 设1(,,)n x y z =为平面ADE 的法向量,2(,,)n x y z =为平面11B FC 的法向量. 又()()2,0,0,2,2,1DA DE ==由1100n DA n DE ⎧=⎪⎨=⎪⎩得20,220,x x y z ì=ïí++=ïî取2z =得1=(0,-1,2)n .又()()110,2,1,2,2,1FC FB ==由212100n FC n FB ⎧=⎪⎨=⎪⎩得20,220,y z x y z ì+=ïí++=ïî取2z =得2=(0,-1,2)n又因为12n n =,所以1n ∥2n .又1C ∉平面ADE 上,所以平面ADE ∥平面B 1C 1F 点拨:利用向量证明面面平行的一般步骤 (1)证明两平面的法向量平行; (2)证明一平面上一点不在另一平面上; (3)得出结论.同类训练:如图所示:正方体1111ABCD A BC D -中,,,,M N E F 分别是棱11111111,,,A B A D B C C D 的中点.求证:平面AMN ∥平面EFDB【知识点】利用方向向量证明面面平行 【解题过程】证明:如图,以D 点为原点,DA ,DC ,1DD 所在直线分别为x 轴、y 轴、z轴建立空间直角zy坐标系.设正方体棱长为2,则A (2,0,0),E (1,2,2),F (0,1,2),B (2,2,0),D (0,0,0),M (2,1,2),N (1,0,2) 设1(,,)n x y z =为平面AMN 的法向量,2(,,)n x y z =为平面DBEF 的法向量. 又()()0,1,2,1,0,2AM AN ==-由1100n AM n AN ⎧=⎪⎨=⎪⎩得20,20,y z x z +=⎧⎨-+=⎩取1z =得1=(2,-2,1)n . 又()()0,1,2,2,2,0DF DB ==由2200n DF n DB ⎧=⎪⎨=⎪⎩得20,220,y z x y +=⎧⎨+=⎩取1z =得2=(2,-2,1)n 又因为12n n =,所以1n ∥2n .又D ∉平面AMN 上,所以平面AMN ∥平面EFDB 小结:利用向量证明面面平行的一般步骤 (1)证明两平面的法向量平行; (2)证明一平面上一点不在另一平面上; (3)得出结论.【设计意图】通过例子熟练掌握空间中面面平行的证明 ●活动④ 探究性题型例4.如图,在棱长为2 的正方体1111ABCD A BC D -中,M 是11A B 的中点,点P 是侧面11CDD C 上的动点,且MP ∥截面1ABC ,则线段MP 长度的取值范围是( )A .B .C.D.⎤⎦答案:B解析:【知识点】利用方向向量求线段长度【解题过程】解:如图,以D 点为原点,DA ,DC ,1DD 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系.则A (2,0,0),M (2,1,2),B 1(2,2,2),C (0,2,0),D (0,0,0).设(,,)n x y z =为平面1ABC 的法向量.又()()12,2,0,0,2,2AC AB =-= 由100n AC n AB ⎧=⎪⎨=⎪⎩得220,220,x y y z -+=⎧⎨+=⎩取1z =得=(-1,-1,1)n .又因为点P 是侧面11CDD C 上一点,所以设(0,,)P y z ,[][]0,2,0,2y z ∈∈,则()2,1,2MP y z =---MP ∥截面1ABC ,2120MP n y z ∴=-++-=即1y z =+.4MP=+点拨:对于平面上的动点,用坐标表示位置比较好确定位置同类训练:如图,四棱锥S-ABCD P为侧棱SD 上的点,若SD⊥平面P AC ,侧棱SC 上是否存在一点E ,使得BE ∥平面PAC.若存在,求SE :EC 的值;若不存在,试说明理由.z答案:存在,SE:EC =2:1解析:【知识点】利用方向向量探究点的位置【解题过程】证明:连接BD ,设AC 交于BD 于O ,由题意知SO ABCD ⊥平面.以O 为坐标原点,,,OB OC OS 分别为x 轴、y 轴、z 轴正方向,建立坐标系O xyz -如图.设底面边长为a ,则高SO a =.于是),(,0,0)2S D a - ,0)2C 设在棱SC 上存在一点E 使//BE PAC 平面.由SD ⊥平面P AC 知DS 是平面PAC 的一个法向量,且26(,0),(0,,)2222DS a a CS a ==-设CE tCS =,则(,(1)22BE BC CE BC tCS a t =+=+=-- 由103BE DS t ⋅=⇒=即当:2:1SE EC =时,BE DS ⊥而BE 不在平面PAC 内,故//BE PAC 平面点拨:对于直线上的动点,同样用坐标表示位置比较好确定位置【设计意图】通过例子掌握探究性问题的解法3.课堂总结知识梳理(1)利用直线的方向向量证明线线平行的一般步骤①证明两直线的方向向量共线;②证明其中一个向量所在直线上一点不在另一个向量所在的直线上;③得出结论.(2)利用向量证明线面平行的一般步骤①证明直线的方向向量与平面的法向量垂直;②证明向量所在直线上一点不在平面上;③得出结论.(3)利用向量证明面面平行的一般步骤①证明两平面的法向量平行;②证明一平面上一点不在另一平面上;③得出结论.重难点归纳(1)利用直线的方向向量和平面的法向量解决线线平行、线面平行,面面平行等问题(2)在解决上述问题时,能建系的题目先建系,正确求出直线的方向向量和平面的法向量.(3)注意要排除直线与直线重合,直线在平面上,直线和平面重合的情况.(三)课后作业基础型 自主突破1.已知直线l 的方向向量是a =(3,2,1),平面α的法向量是μ=(-1,2,-1),则l 与α的位置关系是( )A .l ⊥αB .l ∥αC .l 与α相交但不垂直D .l ∥α或l ⊂α答案:D .解析:【知识点】向量法判断线面关系.【解题过程】因为a μ⋅=-3+4-1=0,所以a ⊥μ.所以l ∥α或l ⊂α..点拨:判断a 与u 的位置关系.2.已知直线l 的方向向量为(2,m,1),平面α的法向量为1(1,,2)2,且l ∥α,则m =________. 答案:-8解析:【知识点】向量法判断线面关系.【解题过程】∵//l α,∴l 的方向向量与α的法向量垂直,∴(2,m ,1)·1(1,,2)2=2+12m +2=0,∴m =-8. 点拨:线面平行即是直线方向向量和平面的法向量垂直.3.设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k ),若α∥β,则k =______.答案:4解析:【知识点】向量法判断面面关系.【解题过程】∵//αβ,∴β的法向量与α的法向量平行,∴()(1,2,2)2,4,4k k λ-=--∴=点拨:面面平行即是两平面的法向量平行.4.已知直线a ,b 的方向向量分别为m =(4,k ,k -1)和n =(k ,k +3,32),若a ∥b ,则k =______.答案:-2解析:【知识点】向量法判断空间直线间的关系.【解题过程】∵//a b ,∴a 的方向向量与b 的方向向量平行,①当k =0时,a 与b 不平行.②当k ≠0时,由4k =k k +3=k -132解得k =-2. 点拨:线线平行即是两直线的方向向量平行.5.在正方体ABCD —A 1B 1C 1D 1中,棱长为a ,M 、N 分别为1A B 、AC 的中点,则MN 与平面11BB C C 的位置关系是( )A .相交B .平行C .垂直D .不能确定答案:B.解析:【知识点】向量法判断线面关系.【解题过程】解:以1C 为原点,以11111,,C B C D C C 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系如图,(,,),(,,)2222a a a a N a M a ∴(,0,)22a a MN ∴=- 而平面11BB C C 的一个法向量为(0,,0)n a =,∴0MN n =又MN ⊄平面B 1BCC 1,∴MN 与平面B 1BCC 1平行.点拨:线面平行则直线的方向向量和平面的法向量垂直.6.在正方体1111ABCD A BC D -中,点N 在BD 上,点M 在1B C 上,且CM=DN ,求证:MN ∥平面11ABB A .答案:见解析解析:【知识点】向量法判断线面关系.【解题过程】证明:如图所示,以D 为坐标原点,DA ,DC ,DD 1所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,过N 作NF ⊥AB 于F ,过M 作1ME BB ⊥于E ,连接EF ,设正方体的棱长为a,DN=CM=b,则(,,0),(,,0),(,,),(,,),222222N F a b M a E a a∴(,,0)(,,)(0,,),2222EF a a a a =-=--2(,0)(,,)(0,,),222222MN a a =-=-- ∴MN ∥EF .又∵MN 与EF 无公共点,∴MN ∥EF .∵EF ⊂平面11ABB A ,∴MN ∥平面11ABB A .点拨:线面平行即是直线方向向量和平面的法向量垂直.能力型 师生共研7.如图,在四棱锥P -ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD =DC ,E 为PC 的中点,求证:PA ∥平面EDB ;A D C P BE答案:见解析解析:【知识点】向量法判断线面关系.【解题过程】证明:以D 为坐标原点,DA ,DC ,DP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系Dxyz ,如图,设DC =PD =1,则P (0,0,1),A (1,0,0),D (0,0,0),B (1,1,0),E 11(0,,)22.设(,,)n x y z =为平面BDE 的法向量.又()110,,,1,1,022DE DB ⎛⎫== ⎪⎝⎭由00n DE n DB ⎧=⎪⎨=⎪⎩得110,220,y z x y ⎧+=⎪⎨⎪+=⎩取1z =得=(1,-1,1)n . 又因为()1,0,1PA =-,0PA n =又∵PA ⊄平面EDB ,∴PA ∥平面EDB .点拨:线面平行即是直线方向向量和平面的法向量垂直.8.如图所示,在空间图形P —ABCD 中,PC ⊥平面ABCD ,PC =2,在四边形ABCD 中,CD ∥AB ,∠ABC =∠BCD =90°,AB =4,CD =1,点M 在PB 上,且PB =4PM ,∠PBC =30°,求证:CM ∥平面PAD .答案:见解析z y解析:【知识点】向量法判断线面关系.【解题过程】证明:建立如图所示的空间直角坐标系C-xyz .∵∠PBC =30°,PC =2,∴BC =23,PB =4.于是D (1,0,0),C (0,0,0),A (4,23,0),P (0,0,2).∵PB =4PM ,∴PM =1,M 3)2.可得,DP =(-1,0,2),DA =(3,23,0).设(,,)n x y z =为平面PAD 的法向量. 又()(3,23,0),1,0,2DA DP ==-由00n DP n DA ⎧=⎪⎨=⎪⎩得20,30,x z x -+=⎧⎪⎨+=⎪⎩取1x =得31=(1,-,)2n .又因为3)2CM =,0CM n =又∵CM ⊄平面PAD ,∴CM ∥平面PAD .点拨:线面平行证明即证明直线方向向量和平面的法向量垂直.探究型 多维突破9.如图,O 是正方体ABCD -A 1B 1C 1D 1的底面中心,P 是DD 1的中点,Q 点在CC 1上,问:当点Q 在CC 1的什么位置时,平面BD 1Q ∥平面APO?答案:见解析解析:【知识点】利用方向向量证明面面平行【解题过程】解:以D 为原点,分别以DA 、DC 、DD 1所在直线为x 、y 、z 轴,建立空间直角坐标系,设正方体的棱长为2,则O (1,1,0),P (0,0,1),A (2,0,0),B (2,2,0),D 1(0,0,2), 设Q (0,2,z )(0≤z ≤2),那么OP→=(-1,-1,1), 1BD =(-2,-2,2),∴OP →∥BD 1→,又B ∉OP ,∴OP ∥BD 1. 又AP→=(-2,0,1),BQ →=(-2,0,z ), 显然当z =1时,AP→∥BQ →,由于B ∉AP , ∴AP ∥BQ ,此时平面AOP ∥平面D 1BQ .∴当Q 为CC 1的中点时,平面AOP ∥平面D 1BQ .点拨:对于直线上的动点,同样用坐标表示位置比较好确定位置10.如图所示,直棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是直角梯形,∠BAD =∠ADC =90°,AB =2AD =2CD =2.在A 1B 1上是否存在一点P ,使得DP 与平面BCB 1和平面ACB 1都平行?证明你的结论.答案:见解析解析:【知识点】利用方向向量探究点的位置【解题过程】解:证明:以A 为坐标原点,AD ,AB ,AA 1所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,∵AD =CD =1,AB =2,∴D (1,0,0),B (0,2,0).设AA 1=a ,则A 1(0,0,a ),B 1(0,2,a ),C 1(1,1,a ),C (1,1,0). AC =(1,1,0),BC =(1,-1,0),1BB =(0,0,a ), ∵AC ·BC =1-1+0=0,AC ·1BB =0+0+0=0, ∴AC ⊥BC ,AC ⊥BB 1,又BC ∩BB 1=B ,∴AC ⊥平面BB 1C 1C . 假设存在一点P (0,y ,a ),则DP =(-1,y ,a ).又 平面BCB 1的法向量为AC . ∵DP ·AC =(-1,y ,a )·(1,1,0)=-1+y , 又∵DP ∥平面BCB 1,∴DP ·AC =0,∴y =1. 设n =(x ,y ,z )为平面ACB 1的一个法向量, ∴n ·AC =0,n ·1CB =0.又∵1CB =(-1,1,a ),∴⎩⎨⎧ x +y =0,y -x +az =0, ∴n 为2(,,)y y y a --.∵DP ∥平面ACB 1,∴DP ⊥n ,∴DP ·n =(-1)×(-y )+y ·y +a ·2()y a-=y 2-y =0, ∴y =0(舍去)或y =1,这与DP ·AC =0时相一致,故假设成立. ∴存在一点P ,且P 为A 1B 1中点,使DP 与平面BCB 1和平面ACB 1都平行. 点拨:对于平面上的动点,用坐标表示位置比较好确定位置 自助餐1.已知a =(2,2,5),b =(4,x ,y )分别是直线12,l l 的方向向量,若12//l l ,则( ) A .x =6,y =10B .x =3,y =15C .x =4,y =15D .x =4,y =10答案:D .解析:【知识点】向量法判断线线关系.【解题过程】∵12//l l ,∴//a b ,则有2254x y==,解方程得x =4,y =10 点拨:判断a 与b 的位置关系.2.设a,b 分别是不重合的直线12,l l 的方向向量,则根据下列条件能判断1l ∥2l 的是( )①a =(12,1,0),b =(-2,-4,0);②a =(4,6,-2),b =(-2,-3,1);③a =(5,0,2),b =(0,1,0); ④a =(-2,-1,1),b =(4,-2,-8).A .①②B.②③C.③④D .①④答案:A .解析:【知识点】向量法判断线线关系. 【解题过程】①14a b =-,∴12//l l ,排除B 、C,②2a b =-,∴12//l l . 点拨:本题为求解适合平行的充分条件,可逐一验证,因此适用排除法.3.已知直线l 的方向向量是n =(2,-1,3),平面β的法向量v =(12-,14,512),则直线l 与平面β的位置关系是( )A . 平行B.垂直C.相交D .平行或l ⊂β答案:D .解析:【知识点】向量法判断线面关系.【解题过程】∵0n v n v =∴⊥∴//l β或l β⊂点拨:判断n 与v 的位置关系. 4.如图,在平行六面体ABCD -A 1B 1C 1D 1中,点M ,P ,Q 分别为棱AB ,CD ,BC 的中点,平行六面体的各棱长均相等.给出下列结论:①A 1M ∥D 1P ;②A 1M ∥B 1Q ;③A 1M ∥平面DCC 1D 1;④A 1M ∥平面D 1PQB 1.这四个结论中正确的个数为( )A .1B .2C .3D .4答案C .解析:【知识点】向量法判断平行关系.【解题过程】∵A 1M →=AM →-AA 1→=D P →-DD 1→=D 1P →,∴A 1M ∥D 1P .∵D 1P ⊂面D 1PQB 1,∴A 1M ∥面D 1PQB 1.又D 1P ⊂面DCC 1D 1,∴A 1M ∥面DCC 1D 1.∵B 1Q 为平面B 1C 1C B 的斜线,∴B 1Q 与D 1P 不平行,∴A 1M 与B 1Q 不平行.答案:①③④点拨:用平行六面体在向量中的作用证明即可5.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M 、N 分别是C 1C 、B 1C 1的中点.求证:MN ∥平面A 1BD .【知识点】向量法判断平行关系.【解题过程】证明:如图所示,以D 为原点,DA 、DC 、DD 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,设正方体的棱长为1,则可求得M (0,1,12),N (12,1,1),D (0,0,0),A 1(1,0,1),B (1,1,0),于是MN →=(12,0,12),DA 1→=(1,0,1),DB →=(1,1,0), 设平面A 1BD 的法向量是n =(x ,y ,z ),则n ·DA 1→=0,且n ·DB →=0,得⎩⎨⎧x +z =0,x +y =0. 取x =1,得y =-1,z =-1,∴n =(1,-1,-1).又MN →·n =(12,0,12)·(1,-1,-1)=0,∴MN →⊥n .又MN ⊄平面A 1BD , ∴MN ∥平面A 1BD .点拨:证明直线的方向向量垂直于平面的法向量6.已知M 为长方体AC 1的棱BC 的中点,点P 在长方体的面CC 1D 1D 内,且PM ∥平面BB 1D 1D ,试探讨点P 的确切位置.答案:见解析解析:【知识点】向量法判断线面关系.【解题过程】以DA 、DC 、DD 1为x 、y 、z 轴,如图,建立空间直角坐标系,设DA =a ,DC =b ,DD 1=c .根据题意可设A (a,0,0),B (a ,b ,0),D 1(0,0,c ),P (0,y ,z ),则M 1(,,0)2a b . 设(,,)n x y z =为平面BB 1D 1D 的法向量.又()1(0,0,),,0DD c DB a b ==,由100n DD n DB ⎧=⎪⎨=⎪⎩得0,0,cz ax by =⎧⎨+=⎩取x b =得(),,0n b a =-.又PM ∥平面BB 1D 1D ,有()1(,,),,002PM n a b y z b a =---=解得2b y = ∴点P 在面DCC 1D 1的DC 的中垂线EF 上.点拨:对于平面上的动点,用坐标表示位置比较好确定位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【学情分析】:
教学对象是高二的学生,学生已经具备空间向量与立方体几何的相关知识,上次课已经学习了直线的
方向向量和平面的法向量,所以本节课是通过举例来求空间的距离和角。我们可以将空间中的有关距离
和角的问题,转化为空间向量的数量积来解决。
【教学目标】:
(1)知识与技能:能用向量方法进行有关距离的计算;能用向量方法解决线线、线面与面面的夹角
A.90° B. 60°
C,45° D. 30°
答:C。
4,已知 AB 是两条异面直线 AC, BD 的公垂线段, AB 1, AC BD 10,CD 301 ,则 AC, BD 所
成的角为
.
答: 600 或1200 。
(中等题)
5,一条线段夹在一个直二面角的两个面内,它和两个面所成的角都是
| A1E || CF |
a2 sin 2
a2 cos a2 cos cos( ) a2 cos cos( ) a2 cos2 a2 sin 2
cos 1 cos
∴可以确定这个四棱柱相邻两个夹角的余弦值。 练习:
(1)如图 4,60°的二面角的棱上有 A、B 两点,直线 AC、BD 分别 在这个二面角的两个半平面内,且都垂直 AB,已知 AB=4,AC=6,BD=8,求 CD 的长。
化为向量问题
依据向量的加法法则, AC1 AB AD AA1
进行向量运算
2
AC1
( AB
AD
AA1 ) 2
2
2
2
AB AD AA1 2(AB AD AB AA1 AD AA1)
111 2(cos 60 cos 60 cos 60) 6
| AC1 | 6
D1
C1
A1
B1
心,E、F 分别是 CC1 、AD 的中点。那么异面直线 OE 和 FD1 所成的角的余弦
值等于( )
10
A.
5
15
B.
5
4
C.
5
2
D.
3
D1 A1
C1 B1 E
D
C
F
O
A
B
答:B。
3,把正方形 ABCD 沿对角线 AC 折起,当以 A、B、C、D 四点为顶点的棱锥体积最大时,直线 BD 和平
面 ABC 所成的角的大小为 )
出用空间向量解决立体几何问题的“三步曲”:
转化为向量问题的
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的 步骤。
点、直线、平面,把立体几何问题转化为向量问题;(化为向量问题)
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之
间距离和夹角等问题;(进行向量运算)
(3)把向量的运算结果“翻译”成相应的几何意义。(回到图形问题)
二、例题 例 1:如图 1:一个结晶体的形状为四棱柱,其中,以顶点 A 为端点
的三条棱长都相等,且它们彼此的夹角都是 60°,那么以这个顶点为端 点的晶体的对角线的长与棱长有什么关系?
解:如图 1,设
AB AA1 AD 1,BAD BAA1 DAA1 60
例 1 的图形比较规 范,容易把握,可 以让学生很好地体 会向量解题的优势。
∴ 可算出 AB 的长。 (2)如果已知一个四棱柱的各棱长和一条对角线的长,并且以同一 顶点为端点的各棱间的夹角都相等,那么可以确定各棱之间夹角的余弦 值吗? 分析:如图,设以顶点 A 为端点的对角线长为 d,三条棱长分别为
a,b,c,各棱间夹角为 .
D1
C1
A1 B1
D
C
A
B
则
d
2
2
A1C
( AB
O
D C
E A
B
图2
例 2:如图 3,甲站在水库底面上的点 A 处,乙站在水坝斜面上的点 B 处。从 A,B 到直线 (库底与水坝的交线)的距离 AC 和 BD 分别为 a 和 b,CD 的长为 c, AB 的长为 d。求库底与水坝所成二面角的余弦值
例 2 是关于角的有 关问题,引导学生 找到相应的向量进 行转化。
教学环节
教学活动
设计意图
一、复习 1. 两个向量的数量积如何运算?
为探索新知识做准
引入
2. 向量的模与向量的数量积是什么关系?
备.
3. 向量的加法法则。
二、探究 一、用空间向量解决立体几何问题的“三步曲”
让学生通过回顾寻
与练习
学生回顾用平面向量解决平面几何问题的“三步曲”,与老师共同得 找将立体几何问题
D1 A1
C1 B1
D AE
C BF
解:如图,在平面 AB1 内过 A1 作 A1E⊥AB 于点 E,在平面 AC 内作 CF⊥AB 于 F。 则 A1E CF a sin ,AE BF a cos
cos cos EA1 ,FC cos A1E ,CF
A1E CF ( A1A AE) (CB BF )
则 A1H 为所求相对两个面之间的距离.
由A1AB A1AD BAD 且 AB AD AA1
让学生体会空间距 离的转化。
H 在 AC上.
2
AC
( AB
BC ) 2
11
2 cos 60
3
AC 3
AA1 AC AA1 ( AB BC) AA1 AB AA1 BC cos 60 cos 60 1.
分析:
设 AC1 a ,AB AD AA1 x ,BAD BAA1 DAA1
则由 AC1 AB AD AA1
提醒学生不能缺少 这一步。
转化为向量。
这是例题 1 的推广, 方法类似,学生进 一步体会.
2
2
2
2
AC1 AB AD AA1 2( AB AD AB AA1 AD AA1)
C
A B
D
图4
2)三棱柱 ABC-A1B1C1 中,底面是边长为 2 的正三角形, ∠A1AB=45°,∠A1AC=60°,求二面角 B-A A1-C 的平面角的余弦值。
A1 C1
B1
A
C
B
三、小结
图5 1. 用空间向量解决立体几何问题的“三步曲”。
2. 面面距离 点面距离 向量的模 回归图形
即 a2 3x2 2(3x2 cos )x31 6 cosa
∴ 这个四棱柱的对角线的长可以确定棱长。
(3)本题的晶体中相对的两个平面之间的距离是多少?(提示:求
两个平行平面的距离,通常归结为求两点间的距离)
分析:面面距离 点面距离 向量的模 回归图形
解: 过 A1点作 A1H 平面 AC 于点 H.
库底与水坝所成二面角的余弦值为
a2 b2 c2 d 2 .
2ab
思考:
(1)本题中如果夹角 可以测出,而 AB 未知,其他条件不变,可
以计算出 AB 的长吗?
分析:
由
2
AB
( AC
CD
DB)2
2
2
2
AB CD BD 2( AC CD AC DB CD DB)
a2 c2 b2 2ab cos
AC
CC1 ) 2
a2 c2 b2 2(ab bc ac) cos
cos d 2 a2 b2 c2
2(ab bc ac)
(3)如果已知一个四棱柱的各棱长都等 a,并且以某一顶点为端点
的各棱间的夹角都等于 ,那么可以确定这个四棱柱相邻两个夹角的余
弦值吗?
分析:二面角 平面角 向量的夹角 回归图形
30°,
这条线段与这个二面角的棱所成的角为
。
答: 450
6,棱长为 4 的正方体 ABCD A1B1C1D1 中, O 是正方形 A1B1C1D1 的中心,点 P 在棱 CC1 上,且
CC1 4CP . (Ⅰ)求直线 AP 与平面 BCC1B1 所成的角的三角函数值;
D1
·O A1
·H
C1 B1
四、作业
二面角 平面角 向量的夹角 回归图形
课本 P112 第 2、4 题。
反思归纳
练习与测试:
(基础题) 1. 正四棱锥的侧棱长与底面边长都是 1,则侧棱与底面所成的角为( )
A.75°
B.60°
C.45° D.30°
答:C。
2.如图,在棱长为 2 的正方体 ABCD A1B1C1D1 中,O 是底面 ABCD 的中
以下设计与例 1 类 似。
a2 c2 b2 2CA DB 2CA DB a2 b2 c2 d 2
设向量 CA 与 DB 的夹角为 , 就是库底与水坝所成的二面角。
因此
2ab cos a2 b2 c2 d 2.
cos a2 b2 c2 d 2 . 2ab
回到图形问题
B
C D
A
图3
解:如图 AC a ,BD b,CD c ,AB d.
化为向量问题
根据向量的加法法则 AB AC CD DB
进行向量运算
d
2
2
AB
( AC
CD
DB)2
2
2
2
AB CD BD 2( AC CD AC DB CD DB)
a2 c2 b2 2 AC DB
D C
A
B
图1
回到图形问题
这个晶体的对角线 AC1 的长是棱长的 6 倍。
思考: (1)本题中四棱柱的对角线 BD1 的长与棱长有什么关系?
分析: BD1 BA BC BB1 其中ABC ABB1 120,B1BC 60
(2)如果一个四棱柱的各条棱长都相等,并且以某一顶点为端点的 各棱间的夹角都等于 , 那么有这个四棱柱的对角线的长可以确定棱长 吗?
