上海初二下学期数学函数压轴题
2020-2021学年下学期沪教版八年级数学压轴题集第十一讲动点求函数解析式

第十一讲动点求函数解析式【要点导航】函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想.由于某--个点或某图形有条件地运动变化,引起未知量与已知量间的一种变化关系.这种变化关系就是动点问题中的函数关系.这部分压轴题主要是在图形运动变化的过程中探求两个变量之间的函数关系,并根据实际情况确定自变量的取值范围.【典型例题】【例1】在△ABC中,∠C=90°,AC=BC=4,在射线AC、CB上分别有两个动点M、N,且AM= BN,联结MN交AB于点P。
(1)如图1所示,当点M在边AC(与点A、C不重合)上,线段PM与线段PN之间有怎样的大小关系?试证明你得到的结论。
(2)当点M在射线AC上,若设AM=x,BP=y,求y与x的函数关系式及定义域。
(3)过点M作直线AB的垂线,垂足为Q,随着点M、N的移动,线段PQ的长能确定吗?若能确定.请求出PQ的长;若不能确定,请简要说明理由。
图1利用线段和差建立函数关系式.【例2】如图2所示, 在长方形ABCD中,AB= 8,AD= 6,点P、Q分别是AB边和CD 边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP= CQ,设AP= x,BE= y.(1)线段PQ的垂直平分线与BC边相交,设交点为点E,求y与x的函数关系式及x取值范围.(2)在(1)的条件下,是否存在x使△PQE为直角三角形? 若存在,请求出x的值;若不存在,请说明理由.图2方法点晴应用勾股定理建立函数解析式.1. (★★)如图3所示,在△ABC中,已知∠BAC=45°,AD⊥BC交BC边于点D,BD=2,DC=3,求AD的长。
小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。
请按照小萍的思路,探究并解答下列问题:(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,点D的对称点为E、F 两点,延长EB、FC相交于点G ,证明四边形AEGF是正方形。
2020上海市八年级数学第二学期期末压轴题三(教师版)

如图1,正方形ABCD 的边长为1,点E 、F 、G 分别在边AD 、AB 、CD 上(点E 、F 、G 与顶点不重合),FG ⊥BE ,垂足为H .(1)求证:FG =BE ;(2)联结FE 、EG 、GB ,设AE =x ,S 四边形BFEG =y ,求y 与x 之间的函数解析式,并写出定义域.图1动感体验打开几何画板文件名“20静安25”,拖动点E 在AD 上运动,观察函数图像,可以体验到,y 随x 的增大而增大.拖动点E 在AD 上运动,拖动点F 在AB 上运动,可以体验到,△ABE 与△MFG 始终保持全等.满分解答(1)如图2,作FM ⊥CD 于M ,得矩形AFMD .所以FM =AD =AB .因为FG ⊥BE ,所以∠1+∠BFH =90°.又因为∠2+∠BFH =90°,根据同角的余角相等,得∠1=∠2.所以△ABE ≌△MFG .所以FG =BE .(2)如图2,在Rt △ABE 中,AE =x ,AB =1,所以222=+BE AE AB =21+x .如图3,y =S 四边形BFEG =12⋅BE FG =212BE =212+x . 定义域是0<x <1.图2 图3如图1,在平面直角坐标系xOy 中,直线483y x =-+与x 、y 轴分别交于点A 、B ,此直线向下平移后与y 轴相交于点C 、与x 轴相交于点D ,四边形ABCD 的面积为18.(1)求直线CD 的表达式;(2)如果点E 在直线CD 上,四边形ABED 是等腰梯形,求点E 的坐标.图1动感体验打开几何画板文件名“20静安26”, 可以体验到,四边形ABED 有一组对边平行,当另一组对边EB 与DA 相等时,四边形ABED 是等腰梯形或平行四边形.满分解答(1)如图2,由483y x =-+,得A (6, 0),B (0, 8). 所以S △OAB =12⋅OA OB =1682⨯⨯=24. 设直线CD 的表达式为43=-+y x b ,则C (0, b ),D (34b , 0). 因为S 四边形ABCD =18,所以S △COD =24-18=6.所以13624⨯⨯=b b .解得b =±4(舍去负值). 所以直线CD 的表达式为443=-+y x . (2)【方法一】如图3,已知A (6, 0),B (0, 8),D (3, 0),设E (x ,443-+x ). 因为ED //AB ,所以四边形ABED 是梯形.若四边形ABED 是等腰梯形,那么EB =DA .根据EB 2=DA 2列方程,得2224(48)(63)3+-+-=-x x . 整理,得22596630++=x x .解得x1=2125-,x2=-3(此时四边形ABED是平行四边形,舍去).所以E(2125-,12825).【方法二】如图4,在x轴上取点M,使MA=MB,那么MB与CD的交点就是点E.设M(x, 0).根据MA2=MB2列方程,得x2+82=(6-x)2.解得x=73-.所以M(73-, 0).由B(0, 8)、M(73-, 0),得直线BM的解析式为y=2487+x.联立2487443⎧=+⎪⎪⎨⎪=-+⎪⎩y xy x,.解得212512825⎧=-⎪⎪⎨⎪=⎪⎩xy,.所以E(2125-,12825).【方法三】如图3,已知A(6, 0),B(0, 8),D(3, 0),设E(x,443-+x).因为等腰梯形的对角线相等,根据CA2=DB2列方程.【方法四】设AB的中点为M(3, 4),根据MD2=MC2列方程.图2 图3 图4 例2020年上海市闵行区初二下学期期末第25题如图1,在梯形ABCD中,AD∥BC,AD=12BC,点E为BC中点,联结ED,BD.(1)求证:四边形ABED是平行四边形;(2)如果∠ADB+∠DCB=90°,求证:四边形ABED是菱形.图1打开几何画板文件名“20闵行25”,拖动点D在平面上运动,可以体验到,四边形ABED 始终保持平行四边形的形状不变,当点D落在半圆上时,四边形ABED是菱形.满分解答(1)如图2,因为点E为BC中点,所以BE=EC=12 BC.已知AD=12BC,等量代换,得AD=BE.又因为AD∥BC,所以四边形ABED是平行四边形.(2)如图3,因为AD∥BC,所以∠ADB=∠DBC.已知∠ADB+∠DCB=90°,等量代换,得∠DBC+∠DCB=90°.所以∠BDC=90°,△BCD是直角三角形.又因为DE是斜边BC的中线,所以DE=BE.所以四边形ABED是菱形.图2 图3例2020年上海市闵行区初二下学期期末第26题如图1,在正方形ABCD中,AB=4.点M是边AB上的任意一点,点N在边BC的延长线上,且∠MDN=90°.联结MN,与正方形ABCD的对角线AC交于点E.设AM=x,AE=y.(1)求证:DM=DN;(2)求y关于x的函数解析式,并写出函数定义域;(3)联结BE,当△MBE是以BM为腰的等腰三角形时,求AM的长.图1打开几何画板文件名“20闵行26”,拖动点M在AB上运动,可以体验到,△MAD与△NCD 始终保持全等,△MEF与△NEC始终保持全等.观察函数图像可以体验到,y随x的增大而增大.点击屏幕左下方的按钮“第(2)题”,拖动点M在AB上运动,可以体验到,△MBE 始终保持等腰三角形的形状不变,当点M落在圆上时,△MBE是等边三角形.满分解答(1)如图2,由∠ADC=∠MDN=90°,得∠ADM=∠CDN.又因为∠DAM=∠DCN=90°,DA=DC,所以△DAM≌△DCN.所以DM=DN.(2)如图3,在Rt△ABC中,AB=BC=4,所以AC=42.作MF⊥AB,交AC于点F,得等腰直角三角形AMF.所以FM=AM=CN=x.所以AF=2x.由MF//BC,得∠FME=∠CNE.又因为∠MEF=∠NEC,所以△MEF≌△NEC.所以FE=CE=12CF=422-x.所以y=AE=AC-CE=422422--x=4222+x.定义域是0<x≤4.图2 图3(3)如图3,因为△MEF≌△NEC,所以ME=NE.所以BE是Rt△MBN斜边上的中线.所以BE=ME,△MBE是等腰三角形(如图4所示).如图5,若△MBE是以BM为腰的等腰三角形,那么BM=BE=ME.所以△MBE是等边三角形.在Rt△BMN中,BM=4-x,BN=4+x,∠BMN=60°,所以MN=2BM=8-2x.由勾股定理,得BM2+BN2=MN2.所以(4-x)2+(4+x)2=(8-2x)2.整理,得x2-16x+16=0.解得x1=843-,或x2=843+(舍).所以AM=843-.图4 图5例2020年上海市浦东区初二下学期期末第26题如图1,等腰三角形ABC中,AB=AC,点E、F分别是AB、AC的中点,CE⊥BF于点O.(1)求证:四边形EBCF是等腰梯形;(2)若EF=1,求四边形EBCF的面积.图1动感体验打开几何画板文件名“20浦东26”,可以体验到,△EFB与△CGF是等底等高的两个三角形,四边形EBCF的面积可以转化为△BFG的面积.满分解答(1)如图2,因为EF是△ABC的中位线,所以EF//BC,.所以四边形EBCF是梯形.又因为BE=12AB,CF=12AC,AB=AC,所以BE=CF.所以四边形EBCF是等腰梯形.(2)如图3,作FG//EC交BC的延长线于点G,得平行四边形CEFG.因为四边形EBCF是等腰梯形,所以BF=CE=GF.又因为CE⊥BF,所以GF⊥BF.所以△BFG是等腰直角三角形.因为EF是△ABC的中位线,所以BC=2EF=2.所以BG=BC+CG=BC+EF=2+1=3.所以BF=FG=2BG.所以S△BFG=12BF FG=214BG=94.如图4,因为△EFB与△CGF是等底等高的两个三角形,所以S△EFB=S△CGF.所以S四边形EBCF=S△EFB+S△CFB=S△CGF+S△CFB=S△BFG.所以S四边形EBCF=94.图2 图3 图4例2020年上海市浦东区初二下学期期末第27题在平面直角坐标系xOy中,若P,Q为某个矩形不相邻的两个顶点,且该矩形的边均与坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.如图1为P,Q的“相关矩形”的示意图.已知点A的坐标为(1, 2).(1)如图2,点B的坐标为(b, 0).①若b=-2,则点A,B的“相关矩形”的面积是______;②若点A,B的“相关矩形”的面积是8,则b的值为_______;(2)如图3,点C在直线y=-1上,若点A,C的“相关矩形”是正方形,求直线AC 的表达式;(3)如图4,等边三角形DEF的边DE在x轴,顶点F在y轴的正半轴上,点D的坐标为(1, 0),点M的坐标为(m, 2).若在△DEF的边上存在一点N,使得点M,N的“相关矩形”为正方形,请直接写出m的取值范围.图1 图2 图3 图4动感体验打开几何画板文件名“20浦东27”,拖动点M在直线y=2上运动,可以体验到,正方形MKNL是否存在,取决于点N是否在边FE、FD上.满分解答(1)①如图5,矩形AGBH为点A,B的“相关矩形”.由A(1, 2),B(-2, 0),得BG=3,AG=2.所以S矩形AGBH=3×2=6.②如图6,若S矩形AGBH=8,那么BG=4.当点B在点G左侧时,1-b=4.所以b=-3.当点B在点G右侧时,b-1=4.所以b=5.(2)如图7,矩形APCQ为点A,C的“相关矩形”.若矩形APCQ为正方形,那么CQ=AQ=3.当点C在点Q左侧时,C(-2,-1).由A(1, 2)、C(-2,-1),得直线AC的表达式为y=x+1.当点C在点Q右侧时,C(4,-1).由A(1, 2)、C(4,-1),得直线AC的表达式为y=-x+3.图5 图6 图7 (3)如图8,矩形MKNL为点M,N的“相关矩形”.若矩形MKNL为正方形,那么ML=NL,△MNL为等腰直角三角形.因为△DEF是等边三角形,FO⊥DE,所以OD=OE.在Rt△ODF中,因为OD=1,DF=DE=2,所以OF=3.图8 图9 图10 以点M的位置为分类标准,分两种情况讨论m的取值范围.①点M在y轴左侧.如图9,当点N与点E重合时,ML=NL=2,此时m=-3.如图10,当点N与点F重合时,ML=NL=23m32.②点M在y轴右侧.如图11,当点N与点F重合时,ML=NL=23m=23如图12,当点N 与点D 重合时,ML =NL =2,此时m =3.所以m 的取值范围为-3≤m ≤3-2或2-3≤m ≤3.图11 图12例 2020年上海市普陀区初二下学期期末第24题如图1,在平面直角坐标系中,已知一次函数的图像经过点A (0, 4)和B (2, 0).(1)求直线AB 的表达式;(2)把直线AB 向下平移,平移后的直线与x 轴、y 轴分别交于点C 、D ,点D 的坐标为(0,-6),点E 是直线CD 上的一点,如果四边形ABDE 是等腰梯形,求点E 的坐标.图1动感体验打开几何画板文件名“20普陀24”,可以体验到,四边形ABDE 有一组对边平行,当另一组对边EA 与DB 相等时,四边形ABDE 是等腰梯形或平行四边形.满分解答(1)设直线AB 的表达式为y =kx +4(k ≠0).代入点B (2, 0),得2k +4=0.解得k =-2.所以直线AB 的表达式为y =-2x +4.(2)如图2,因为AB //CD ,D (0,-6),所以直线CD 的表达式为y =-2x -6. 设E (x ,-2x -6).因为ED //AB ,所以四边形ABDE 是梯形.若四边形ABDE 是等腰梯形,那么EA =DB .根据EA 2=DB 2列方程,得2222(264)26+---=+x x .整理,得28120++=x x .解得x 1=-6,或x 2=-2.如图3,当x =-2时,四边形ABDE 是平行四边形,舍去.所以E(-6, 6).图2 图3例2020年上海市普陀区初二下学期期末第25题如图1,在正方形ABCD中,AB=4,P是射线AC上的一点,联结BP,过点P作BP 的垂线交射线DC于点F.(1)求证:PB=PF;(2)当点F在边DC上时,四边形PBCF的面积为y,设AP=x,求y关于x的函数解析式和定义域;(3)当以P、B、C、F为顶点的四边形的面积为12时,求AP的长.图1 备用图动感体验打开几何画板文件名“20普陀25”,拖动点P在AC上运动,观察函数图像,可以体验到,y随x的增大而减小.观察左图,可以体验到,△BPM和△FPN始终保持全等,四边形PBCF的面积可以转化为正方形PMCN的面积.观察右图,可以体验到,四边形PBFC的面积可以看成是两个同底三角形的面积和.满分解答(1)如图2,作PM⊥BC于M,PN⊥DC于N,得正方形PMCN.又因为BP⊥PF,根据同角的余角相等,得∠1=∠2.又因为PM=PN,所以△BPM≌△FPN(ASA).所以PB =PF .(2)由(1),得S 四边形PBCF =S △PBM +S 四边形PMCF =S △FPN +S 四边形PMCF =S 正方形PMCN =PN 2. 如图3,在等腰直角三角形ADC 中,AD =4,所以AC =42. 在等腰直角三角形PCN 中,PC =AC -AP =42-x ,所以PN =22PC =2(42)2-x . 所以y =22[(42)]2-x =2142162-+x x .定义域是0≤x <22.图2 图3(3)以点F 的位置为分类标准,分两种情况讨论.①如图2,当点F 在线段DC 上时,由(2),得S 四边形PBCF =PN 2=12. 所以PN =23.所以PC =2PN =26.所以AP =AC -PC =4226-.②如图4,当点F 在线段DC 的延长线上时,同理可得△BPM ≌△FPN .由S 四边形PBFC =12⋅BC NF =12,得14122⨯=NF .所以NF =6. 如图5,在等腰直角三角形AM ′P 中,M ′P =BM =NF =6,所以AP =2M ′P =62.图4 图5。
2020上海市八年级数学第二学期期末压轴题四(教师版)

2020上海市八年级数学第二学期期末压轴题四例2020年上海市青浦区初二下学期期末第24题如图1,在平面直角坐标系xOy中,已知直线y=x-4分别与x轴、y轴交于点A、B,直线BC与x轴交于点C(-1, 0).点D在第四象限,BD⊥BA.(1)求直线BC的解析式;(2)当S△ABD=4S△BOC时,求点D的坐标;(3)在(2)的条件下,已知点E在x轴上,点F在直线BC上.如果以C、D、F、E 为顶点的四边形是平行四边形,请直接写出线段OE的长.图1动感体验打开几何画板文件名“20青浦24”,可以体验到,以C、D、F、E为顶点的平行四边形存在三种情况.满分解答(1)由y=x-4,得A(4, 0),B(0,-4).设直线BC的解析式为y=kx-4(k≠0).代入点C(-1, 0),得-k-4=0.解得k=-4.所以直线BC的解析式为y=-4x-4.(2)如图2,在Rt△AOB中,AO=BO=4,所以AB=42ABO=45°.作DH⊥y轴于点H.因为BD⊥BA,所以△BDH为等腰直角三角形.又因为S△ABD=4S△BOC,所以11422⋅=⨯⋅AB BD OB OC.所以114244122⨯=⨯⨯⨯BD.解得BD=2在等腰直角三角形△BDH中,BH=DH 2=2.所以D(2,-6).图2(3)线段OE的长为12或52.思路如下:以CE为分类标准,分两种情况讨论.①如图3,当CE为平行四边形的边时,DF//CE//x轴.所以y F=y D=-6.将y=-6代入y=-4x-4,得x=12.所以F(12,-6).所以CE=DF=2-12=32.当点E在点C右侧时,OE=CE-OC=12.当点E在点C左侧时,OE=CE+OC=52.②如图4,当CE为平行四边形的对角线时,D、F两点在x轴的两侧,到x轴的距离相等.所以y F=-y D=6.将y=6代入y=-4x-4,得x=52-.所以F(52-,-6).作DM⊥x轴于M,作FN⊥x轴于N.由ME=CN,得2-x E=(-1)-5 ()2 -.解得x E=12.所以OE=12.图3 图4例2020年上海市青浦区初二下学期期末第25题如图1,在等腰梯形ABCD中,AD∥BC,AD=AB=23,BD⊥DC.M、N分别是AD、CD的中点,联结MN交BD于点Q,点P在线段BQ上.(1)求∠C的度数;(2)求线段DQ的长;(3)联结PM、PN.设PB=x,△PMN的面积为y,求y关于x的函数关系式.图1动感体验打开几何画板文件名“20青浦25”,可以体验到,图中的直角三角形都是含有30°角的直角三角形.拖动点P在BD上运动,可以体验到,△PMN的面积可以表示为两个同底三角形的面积之和,这两个同底三角形的高都是定值.满分解答(1)如图2,因为AD=AB,所以∠1=∠2.因为AD∥BC,所以∠2=∠3.所以∠1=∠2=∠3.设∠1=∠2=∠3=α.因为四边形ABCD是等腰梯形,所以∠C=∠ABC=2α.在Rt△DBC中,3α=90°.解得α=30°.所以∠C=2α=60°.(2)如图3,因为M、N分别是AD、CD的中点,AD=AB=DC=23,所以DM=DN=3.因为∠MDN=30°+90°=120°,所以∠DMN=∠DNM=30°.在Rt△QDN中,DN=3,设DQ=m,那么QN=2m.由勾股定理,得DN2+DQ2=QN2.所以3+m2=(2m)2.解得m=±1(舍去负值).所以DQ=1.(3)如图2,在Rt△BCD中,∠3=30°,DC=23,所以BC=43,BD=6.如图4,作MH⊥BD于H.在Rt△MHD中,∠MDH=30°,DM=3,所以MH=12DM=3.当点P在线段BQ上时,PQ=BD-PB-DQ=6-x-1=5-x.所以y=S△PMN=S△MPQ+S△NPQ=1()2PQ MH DN⋅+=13(5)(3)2x-⨯+=33(5)-x.图2 图3 图4例2020年上海市世外初二下学期期末第24题如图1,平行四边形ABCD的顶点A、B的坐标分别是A(-1, 0)、B(0,-2),顶点C、D 在反比例函数第一象限的图像上,边AD与y轴交于点E.(1)过点D作y轴的平行线交BC于点F,过点C作CH⊥DF,垂足为H,若点D的坐标为(a, b),求点C点坐标(用a、b表示).(2)若四边形BCDE的面积是△ABE的面积的5倍,求反比例函数的解析式.图1动感体验打开几何画板文件名“20世外24”,可以体验到,△AEB与△CDF全等,平行四边形BEDF 与△ABE有公共的底边BE,所以面积比可以转化为高之比.满分解答(1)如图2,因为DC//AB,DC=AB,所以点D按照由A到B的方向平移,就可以得到点C.因为点A(-1, 0)向右平移1个单位,向下平移2个单位得到点B(0,-2),所以点D(a, b)平移后得到点C的坐标为(a+1, b-2).(2)如图2,因为四边形ABCD是平行四边形,所以AB=DC,AD=BC,AD//BC.又因为DF//EB,所以四边形BEDF是平行四边形.所以EB=DF,ED=BF.所以AE=CF.所以△AEB≌△CFD(SSS).所以S△AEB=S△CFD.若S四边形BCDE=5S△ABE,那么S平行四边形BEDF=4S△ABE.所以1=42⋅⨯⋅DBE x BE OA.所以x D=2OA=2,即a=2.所以D(2, b),C(3, b-2).设反比例函数的解析式为=kyx(k≠0).将点D(2, b)、C(3, b-2)代入,得23(2)=⎧⎨-=⎩b kb k,.解得612=⎧⎨=⎩bk,.所以反比例函数的解析式为12=yx.图2例2020年上海市世外初二下学期期末第25题如图1,在矩形ABCD中,AB=2,BC=5.点P是边AD上一点,联结CP,将四边形ABCP沿CP所在直线翻折,落在四边形EFCP的位置,点A、B的对应点分别为点E、F,边CF与边AD的交点为点G.(1)当AP=2时,求PG的值;(2)如果AP=x,FG=y,求y关于x的函数解析式,并写出它的定义域;(3)联结BP并延长与线段CF交于点M,当△PGM是以MG为腰的等腰三角形,求AP的长.图1 备用图动感体验打开几何画板文件名“20世外25”,拖动点P在AD上运动,可以体验到,△GPC保持等腰三角形的形状不变,当△PGM是等腰三角形时,△BCM也是等腰三角形.观察函数图像,可以体验到,y随x的增大而增大.满分解答(1)如图2,因为AD//BC,所以∠1=∠3.又因为∠1=∠2,所以∠2=∠3.所以GP=GC.在Rt△DCG中,DC=2,设GC=GP=m,那么GD=AD-AP-PG=5-2-m=3-m.由勾股定理,得DC2+GD2=GC2.所以22+(3-m)2=m2.解得m=136.所以PG=136.(2)如图2,在Rt△DCG中,DC=2,PG=CG=5-y,所以GD=AD-AP-GP=5-x-(5-y)=y-x.由勾股定理,得DC2+GD2=GC2.所以22+(y-x)2=(5-y)2.整理,得y=221 210--xx.定义域是0<x≤3.当x=3时,G、D两点重合.(3)分两种情况讨论以MG为腰的等腰三角形PGM.①如图3,当MG=MP时,梯形PBCG是等腰梯形,此时AP=GD.所以x=y-x,即2x=y.所以2212210xxx-=-.解得11037+=x(舍),21037-=x.所以1037-=AP.②如图4,当GM=GP时,CM=CB=5,此时F、M两点重合.又因为CP平分∠BCF,根据等腰三角形的“三线合一”,可知CP⊥BF.于是可证PG是Rt△MPC斜边上的中线.所以GM=12MC=52.即y=221210--xx=52.解得x1=4(舍),x2=1.所以AP=1.图2 图3 图4例2020年上海市松江区初二下学期期末第25题如图1,已知在梯形ABCD中,AD∥BC,AD=AB,BC=2AD,点E是BC边的中点,AE、BD相交于点F.(1)求证:四边形AECD是平行四边形;(2)设边CD的中点为G,联结EG,求证:四边形FEGD是矩形.图1动感体验打开几何画板文件名“20松江25”,拖动点A运动,可以体验到,四边形AECD始终是平行四边形,四边形ABED始终是菱形,四边形FEGD始终是矩形.满分解答(1)如图2,因为点E是BC边中点,所以BC=2EC=2BE.因为BC=2AD,所以AD=EC=BE.又因为AD∥BC,所以四边形ABED和四边形AECD是都平行四边形.(2)如图2,因为AD=AB,所以平行四边形ABED是菱形.所以BD⊥AE,BD=2DF.如图3,因为EG是△BCD的中位线,所以EG//BD,BD=2EG.所以EG=DF,四边形FEGD是平行四边形.已知BD⊥AE,所以平行四边形FEGD是矩形.图2 图3例2020年上海市松江区初二下学期期末第26题如图1,已知在正方形ABCD中,AB=2,点E为线段AC上一点(点E不与A、C重合),联结DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG.(1)求证:DE=EF;(2)联结CG、EG,设AE=x,△ECG的面积为y,求y关于x的函数关系式,并写出定义域;(3)设EG、CD相交于点H,如果△EDH是等腰三角形,求线段AE的长.图1 备用图动感体验打开几何画板文件名“20松江26”,拖动点E在AC上运动,观察左图,可以体验到,四边形DEFG和四边形MNPQ都是正方形,图中的四个直角三角形全等.观察右图,可以体验到,△ECG是直角三角形.点击屏幕左下方的按钮“第(3)题”,拖动点E在AC上运动,可以体验到,△EDH的每个顶点各有一次机会落在对边的垂直平分线上.满分解答(1)如图2,构造矩形DEFG的外接矩形MNPQ,MN⊥AD.所以四边形MNCD和四边形PQDC是矩形.因为∠3和∠1都与∠2互余,根据同角的余角相等,得∠3=∠1.又因为MD=NC=NE,所以△DME≌△ENF(AAS).所以DE=EF.图2 图3(2)如图2,因为AD=MQ,所以AM=DQ=CP.又因为PG=ME,AM=ME,等量代换,得CP=PG.所以△CPG是等腰直角三角形,CG=AE.所以∠ECG=90°.在正方形ABCD中,AB=2,所以AC=22已知AE=x,所以EC=AC-AE=22x,CG=AE=x.如图3,y=S△ECG=12⋅EC CG=1(22)2⋅x x2122-x x.定义域是0<x<22(3)在正方形DEFG中,∠DEH=45°,分三种情况讨论等腰三角形EDH.①如图4,当DE=DH时,点A与点E重合,舍去.②如图5,当HD=HE时,△DEH是等腰直角三角形,点E是AC的中点.所以AE=12AC=2.③如图6,当ED=EH时,∠EDH=∠EHD=67.5°.在△CDE中,∠DCE=45°,∠EDC=67.5°,所以∠CED=67.5°.所以CE=CD=2.所以AE=AC-CE=222-.图4 图5 图6 例2020年上海市杨浦区初二下学期期末第25题如图1,已知在平面直角坐标系中,直线y=2x与反比例函数kyx=(k≠0)在第一象限内的图像交于点A(m, 2),将直线y=2x平移后与kyx=在第一象限内的图像交于点B,且△AOB的面积为2.(1)求k的值;(2)求平移后的直线表达式.图1动感体验打开几何画板文件名“20杨浦25”,拖动点B在反比例函数的图像上运动,观察左图,可以体验到,△AOP与△AOB是同底等高的两个三角形.观察右图,可以体验到,△AOB的面积与梯形AHGB的面积相等.满分解答(1)将A(m, 2)代入y=2x,得2m=2.解得m=1.所以A(1, 2).将A(1, 2)代入kyx=,得k=2.(2)如图2,设平移后的直线与y轴交于点P,联结AP.因为△AOP与△AOB是同底等高的两个三角形,所以S△AOP=S△AOB=2.所以122⋅=AOP x.已知A(1, 2),所以OP=4.①如图2,当点P在x轴上方时,P(0, 4).所以平移后的直线表达式为y=2x+4.②如图3,当点P在x轴下方时,P(0,-4).所以平移后的直线表达式为y=2x-4.图2 图3 考点延伸第(2)题△AOB的面积,还可以这样转化:如图4,如图5,作AG⊥x轴于点G,作BH⊥x轴于点H.因为A、B两点在反比例函数2yx上,所以S△BOH=S△AOG.所以S△AOB=S△BOH+S梯形AGHB-S△AOG=S梯形AGHB=2.图4 图5例2020年上海市杨浦区初二下学期期末第26题已知在平行四边形ABCD中,AB≠BC,将△ABC沿直线AC翻折,点B落在点E处,AD与CE相交于点O,联结DE.(1)如图1,求证:AC//DE;(2)如图2,如果∠B=90°,AB=3,BC=6,求△OAC的面积;(3)如果∠B=30°,AB=23,当△AED是直角三角形时,求BC的长.图1 图2 备用图动感体验打开几何画板文件名“20杨浦26”,拖动点E运动,观察左图,可以体验到,△ABC、△AEC与△CDA保持全等,ED与AC平行.观察右图,可以体验到,直角三角形AED存在两种情况.满分解答(1)如图3,因为△ABC≌△AEC,△ABC≌△CDA,所以△AEC≌△CDA.根据全等三角形对应边上的高相等,可知E、D两点到AC边的距离相等.所以AC//DE.(2)如图4,因为AD//BC,所以∠1=∠2.又因为∠2=∠3,所以∠1=∠3.所以OA=OC.在Rt△ODC中,DC=3,设OA=OC=x,那么OD=BC-OA=6-x.由勾股定理,得DC2+OD2=OC2.所以3+(6-x)2=x2.解得x=36.所以OA=OC=36.所以S△OAC=113692322⋅=⨯⨯=OA DC.图3 图4(3)分两种情况讨论直角三角形AED.①如图5,当∠EAD=90°时,延长EA交BC于点G.因为AD//BC,所以∠EGC=∠EAD=90°.在Rt△AGB中,∠B=30°,AB=3,所以AG3在Rt△EGC中,∠AEC=30°,EG=AE+AG=23333设GC=m,那么EC=2m.由勾股定理,得EG2+GC2=EC2.所以27+m2=(2m)2.解得m=±3(舍去负值).所以BC=EC=2m=6.②如图6,当∠AED=90°时,由ED//AC,得∠BAC=∠AED=90°.在Rt△BAC中,∠B=30°,AB=23AC=n,那么BC=2n.由勾股定理,得AB2+AC2=BC2.所以12+n2=(2n)2.解得m=±2(舍去负值).所以BC=2n=4.图5 图6第(3)题如果没有题干“AD与CE交于点O”的条件限制,还存在如图7、图8两种情况.如图7,四边形ACED是矩形,在Rt△ABC中,AB=23,AC=3,BC=3.如图8,在Rt△ADE中,AE=23,AD=2.所以BC=2.图7 图8例2020年上海市长宁区初二下学期期末第24题如图1,△ABC和△ADE都是等边三角形,点D在BC边上,EF//BC交AC于点F,联结BE.求证:四边形BEFC为平行四边形.图1动感体验打开几何画板文件名“20长宁24”,拖动点D在BC上运动,可以体验到,△AEB与△ADC始终保持全等,四边形BEFC为平行四边形.满分解答如图2,因为△ABC和△ADE都是等边三角形,所以AB=AC,AE=AD,∠EAD=∠BAC=∠C=∠ABC=60°.所以∠EAD-∠BAD=∠BAC-∠BAD,即∠1=∠2.所以△AEB≌△ADC(SAS).所以∠ABE=∠C=60°.所以∠EBC+∠C=120°+60°=180°.所以EB//FC.又因为EF//BC,所以四边形BEFC为平行四边形.图2例2020年上海市长宁区初二下学期期末第25题如图1,在正方形ABCD中,AB=1,E为边AB上的一点(点E不与端点A、B重合),F为BC延长线上的一点,且AE=CF,联结EF交对角线AC于点G.(1)求证:DE=DF;(2)联结DG,求证:DG⊥EF;(3)设AE=x,AG=y,求y关于x的函数解析式及定义域.图1动感体验打开几何画板文件名“20长宁25”,拖动点E在AB上运动,可以体验到,△EAD与△FCD 始终保持全等,△EGH与△FGC始终保持全等.观察函数图像可以体验到,y随x的增大而增大.满分解答(1)如图2,由DA=DC,∠DAE=∠DCF,AE=CF,得△EAD≌△FCD.所以DE=DF.图2 图3(2)如图3,作EH⊥AB交AC于点H,得等腰三角形AEH.所以EH=AE=CF.因为BC⊥AB,所以EH//BC.所以∠HEG=∠CFG.又因为∠EGH=∠FGC,所以△EGH≌△FGC.所以HG=CG,EG=FG.在△DEF中,DE=DF,EG=FG,由等腰三角形的“三线合一”,得DG⊥EF.(3)如图3,在Rt△ABC中,AB=BC=1,所以AC2在Rt△AEH中,AE=HE=x,所以AH2x.所以HG=CG=12CH22-x所以y=AG=AC-CG222-x22+x定义域是0<x<1.。
完整)上海八年级数学压轴题

完整)上海八年级数学压轴题1.在三角形ABC中,AD和BE是高,F是AB的中点,FG垂直于DE,G是垂足。
证明:G是DE的中点。
2.在三角形OBC中,点O为坐标原点,点C坐标为(4,0),点B坐标为(2,23),AB垂直于y轴,点A为垂足,OH垂直于BC,点H为垂足。
动点P、Q分别从点O、A同时出发,点P沿线段OH向点H运动,点Q沿线段AO向点O运动,速度都是每秒1个单位长度。
设点P的运动时间为t 秒。
1)证明:OB=CB;2)若△OPQ的面积为S,求S与t之间的函数关系式及定义域;3)当PQ垂直于OB(垂足为点M)时,求五边形ABHPQ的面积的值。
3.在三角形ABC中,AB=AC,点P是BC边上的一点,PD垂直于AB于点D,PE垂直于AC于点E,CM垂直于AB于点M。
探究线段PD、PE、CM的数量关系,并说明理由。
4.在直角三角形ABC中,AB=AC,∠A=90°,O为BC中点。
1)写出点O到△ABC三个顶点的距离之间的关系;2)如果点M、N分别在边AB、AC上移动,且保持AN=BM。
请判断△XXX的形状,并证明你的结论。
5.点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数y=k/x的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.1)求反比例函数y=k/x和直线OE的函数解析式;2)求四边形OAFC的面积。
6.已知:正比例函数的图象与反比例函数的图象交于点(1)。
试确定上述正比例函数和反比例函数的表达式;2)根据图象回答,在第一象限内,当取何值时,反比例函数的值大于正比例函数的值?3)在直线y=x上取一点P,它是反比例函数图象上的一动点,其中OP=3.过点P作直线与x轴交于点Q,与y轴交于点R。
过点Q作直线与y轴交于点S。
当四边形PQRS的面积为6时,请判断线段PS和线段QR的大小关系,并说明理由。
7.在直角三角形ABC中,∠C=90°,∠B=30°,AC=6,点D在边BC上,AD平分∠CAB,E为AC上的一个动点(不与A、C重合),EF垂直于AB,垂足为F。
根与系数的关系(压轴题)—2023-2024学年八年级数学下册(沪科版)(解析版)

z根与系数的关系分类讨论思想:当问题所给的对象不能进行统一研究时,我们就需要对研究对象进行分类,然后对每一类分别进行研究,得出每一类的结论,最后综合各类的结果,得到整个问题的解答。
分类讨论的分类并非是随心所欲的,而是要遵循以下基本原则:1. 不重(互斥性)不漏(完备性);2. 按同一标准划分(同一性);3. 逐级分类(逐级性)。
一、一元二次方程的根与系数的关系如果一元二次方程ax !+bx +c =0(a ≠0)的两个实数根是,那么,. 注意:它的使用条件为a ≠0, Δ≥0.也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.【典例1】已知:关于x 的一元二次方程kx !+2x +1−2k =0有两个实数根x ",x !.(1)若|x "|+|x !|=2√2,求k 的值; (2)当k 取哪些整数时,x ",x !均为整数; (3)当k 取哪些有理数时,x ",x !均为整数. 【思路点拨】(1)分两种情况:①若两根同号,②若两根异号;根据根与系数的关系结合根的判别式解答即可; (2)根据根与系数的关系可得若x "+x !=−!#为整数,可得整数k =±1,±2,然后结合两根之积、解方程分别验证即可;(3)显然,当k =−1时,符合题意;由两根之积可得k 应该是整数的倒数,不妨设k ="$,则方程可变形21x x ㄑa b x x -=+21ac x x =21◆思想方法◆典例分析◆知识点总结z为x !+2mx +m −2=0,即为(x +m )!=m !−m +2,再结合整数的意义即可解答. 解:(1)∵Δ=2!−4k (1−2k )=4−4k +8k !=88k !−"!k +"!9=88k −"%9!+&!>0, ∴不论k 为何值,关于x 的一元二次方程kx !+2x +1−2k =0都有两个实数根x ",x !, ∵关于x 的一元二次方程kx !+2x +1−2k =0有两个实数根x ",x !, ∴x "+x !=−!#,x "x !="'!##,分两种情况:①若两根同号,由|x "|+|x !|=2√2可得:x "+x !=2√2,或x "+x !=−2√2, 当x "+x !=2√2时,则−!#=2√2,解得k =−√!!; 当x "+x !=−2√2时,则−!#=−2√2,解得k =√!!; ②若两根异号,由|x "|+|x !|=2√2可得:(x "−x !)!=8, 即(x "+x !)!−4x "x !=8, ∴8−!#9!−4×"'!##=8,解得:k =1, 综上,k 的值为1或 ±√!!; (2)∵关于x 的一元二次方程kx !+2x +1−2k =0有两个实数根x ",x !, ∴x "+x !=−!#,x "x !="'!##,若x ",x !均为整数, 则x "+x !=−!#为整数, ∴整数k =±1,±2, 当k =±2时,x "x !="'!##不是整数,故应该舍去;当k =1时,此时方程为x !+2x −1=0,方程的两个根不是整数,故舍去;当k =−1时,此时方程为−x !+2x +3=0,方程的两个根为x "=−1,x !=3,都是整数,符合题意; 综上,当k 取−1时,x ",x !均为整数; (3)显然,当k =−1时,符合题意; 当k 为有理数时,由于x "x !="'!##="#−2为整数,zxx∴k 应该是整数的倒数,不妨设k ="$ (m ≠0),m 为整数, 则方程kx !+2x +1−2k =0即为x !+2mx +m −2=0, 配方得:(x +m )!=m !−m +2, 即x =−m ±√m !−m +2,当m =2即k ="!时,方程的两根为x "=0,x !=−4,都是整数,符合题意;当m ≠2时,m !−m +2=(m −"!)!+&%不是完全平方数,故不存在其它整数m 的值使上式成立; 综上,k =−1或"!.1.(22-23九年级上·湖北襄阳·自主招生)设方程ax !+bx +c =0(a ≠0)有两个根x "和x !,且1<x "<2<x !<4,那么方程cx !−bx +a =0的较小根x )的范围为( ) A ."!<x )<1 B .−4<x )<−2C .−"!<x )<−"%D .−1<x )<−"!【思路点拨】由根与系数的关系得出x "+x !=−*+,x "⋅x !=,+,再设方程cx !−bx +a =0的为m ,n ,根据根与系数的关系得出m +n =−("-!+"-"),mn ="-"⋅-!,从而得出方程cx !−bx +a =0的两根为−"-",−"-!,然后由1<x "<2<x !<4,求出−"-",−"-!的取值范围,从而得出结论.【解题过程】解:∵方程ax !+bx +c =0(a ≠0)有两个根x "和x !, ∴x "+x !=−*+,x "⋅x !=,+,设方程cx !−bx +a =0的两根为m ,n , 则m +n =*,,mn =+,,∵m +n =*,=−*+⋅(−+,),mn ="-"⋅-!,∴m +n =−(x "+x !)⋅"-"⋅-!=−-"/-!-"⋅-!=−("-!+"-"),∴方程cx !−bx +a =0的两根为−"-",−"-!,◆学霸必刷∵1<x"<2,2<x!<4,∴"!<"-"<1,"%<"-!<"!,∴−1<−"-"<−"!,−"!<−"-!<−"%,∵−"-"<−"-!,∴方程cx!−bx+a=0的较小根x)的范围为−1<x)<−"!.故选:D.2.(22-23九年级下·安徽安庆·阶段练习)若方程x!+2px−3p−2=0的两个不相等的实数根x"、x!满足x"!+x")=4−(x!!+x!)),则实数p的所有值之和为()A.0 B.−)%C.−1D.−0%【思路点拨】先根据一元二次方程解的定义和根与系数的关系得到x"!+2px"−3p−2=0,x"+x!=−2p,进而推出x")=3px"+2x"−2px"!,则x")+x"!=3px"+2x"−2px"!+x"!,x!)+x!!=3px!+2x!−2px!!+ x!!,即可推出(3p+2)(x"+x!)+(1−2p)(x"!+x!!)=4,然后代入x"+x!=−2p,x"!+x!!= (x"+x!)!−4p得到2p(4p+3)(p+1)=0,再根据判别式求出符号题意的值即可得到答案.【解题过程】解:∵x"、x!是方程x!+2px−3p−2=0的两个相等的实数根,∴x"!+2px"−3p−2=0,x"+x!=−2p,x"x!=−3p−2,∴x"!+2px"=3p+2,∴x")+2px"!=3px"+2x",∴x")=3px"+2x"−2px"!,∴x")+x"!=3px"+2x"−2px"!+x"!,同理得x!)+x!!=3px!+2x!−2px!!+x!!,∵x"!+x")=4−(x!!+x!)),∴x"!+x")+(x!!+x!))=4,∴3px"+2x"−2px"!+x"!+3px!+2x!−2px!!+x!!=4,∴(3p+2)(x"+x!)+(1−2p)(x"!+x!!)=4,∴(3p+2)(−2p)+(1−2p)[(−2p)!−2(−3p−2)]=4,∴−6p!−4p+(1−2p)(4p!+6p+4)=4,∴−6p!−4p+4p!+6p+4−2p(4p!+6p+4)=4,∴−2p!+2p−2p(4p!+6p+4)=0,∴−2p(4p!+6p+4+p−1)=0,∴2p(4p!+7p+3)=0,∴2p(4p+3)(p+1)=0,解得p"=0,p!=−1,p)=−)%,∵Δ=(2p)!+4(3p+2)>0,∴p!+3p+2>0,∴(p+1)(p+3)>0,∴p=−1不符合题意,∴p"+p)=−)%∴符合题意,故选B.3.(22-23八年级下·安徽合肥·期末)若关于x的一元二次方程x!−2x+a!+b!+ab=0的两个根为x"=m,x!=n,且a+b=1.下列说法正确的个数为( )①m·n>0;②m>0,n>0;③a!≥a;④关于x的一元二次方程(x+1)!+a!−a=0的两个根为x"= m−2,x!=n−2.A.1B.2C.3D.4【思路点拨】根据根与系数的关系得x"x!=mn=a!+b!+ab,利用a+b=1消去b得到mn=a!−a+1=8a−"!9! +)%>0,从而即可对①进行判断;由于x"+x!=m+n=2>0,x"x!=mn>0,利用有理数的性质可对②进行判断;根据根的判别式的意义得到Δ=4−4(a!+b!+ab)≥0,即4−4(a!−a+1)≥0,则可对③进行判断;利用a!+b!+ab=a!−a+1把方程x!−2x+a!+b!+ab=0化为(x−1)!+a!−a+1=0,由于方程(x−1)!+a!−a=0可变形为[(x+2)−1]!+a!−a=0,所以x+2=m或x+2=n,于是可对④进行判断.【解题过程】解:根据根与系数的关系得x"x!=mn=a!+b!+ab,∵a+b=1,∴b=1−a,∴mn=a!+(1−a)!+a(1−a)=a!−a+1=8a−"!9!+)%>0,所以①正确;∵x"+x!=m+n=2>0,x"x!=mn>0,∴m>0,n>0,所以②正确;∵Δ≥0,∴4−4(a!+b!+ab)≥0,即4−4(a!−a+1)≥0,∴a≥a!,所以③错误;∵a!+b!+ab=a!−a+1,∴方程x!−2x+a!+b!+ab=0化为(x−1)!+a!−a+1=0,即(x−1)!+a!−a=0,∵方程(x+1)!+a!−a=0可变形为[(x+2)−1]!+a!−a=0,∴x+2=m或x+2=n,解得x"=m−2,x!=n−2,所以④正确.故选:C.4.(22-23九年级上·浙江·自主招生)设a、b、c、d是4个两两不同的实数,若a、b是方程x!−8cx−9d=0的解,c、d是方程x!−8ax−9b=0的解,则a+b+c+d的值为.【思路点拨】由根与系数的关系得a+b,c+d的值,两式相加得的值,根据一元二次方程根的定义可得a!−8ac−9d= 0,代入可得a!−72a+9c−8ac=0,同理可得c!−72c+9a−8ac=0,两式相减即可得a+c的值,进而可得a+b+c+d的值.【解题过程】解:由根与系数的关系得a+b=8c,c+d=8a,两式相加得a+b+c+d=8(a+c).因为a是方程x!−8cx−9d=0的根,所以a!−8ac−9d=0,又d=8a−c,所以a!−72a+9c−8ac=0①同理可得c!−72c+9a−8ac=0②①-②得(a−c)(a+c−81)=0.因为a≠c,所以a+c=81,所以a+b+c+d=8(a+c)=648.故答案为648.5.(23-24九年级上·江苏南通·阶段练习)已知实数a,b,c满足:a+b+c=2,abc=4.求|a|+|b|+|c|的最小值【思路点拨】用分类讨论的思想,解决问题即可.【解题过程】解:不妨设a是a,b,c中的最大者,即a≥b,a≥c,由题设知a>0,,且b+c=2−a,bc=%+=0的两实根,于是b,c是一元二次方程x!−(2−a)x+%+≥0,即(a!+4)(a−4)≥0,∴Δ=(2−a)!−4×%+所以a≥4.又当a=4,b=c=−1时,满足题意.故a,b,c中最大者的最小值为4.因为abc=4>0,所以a,b,c为全大于0或一正二负.①若a,b,c均大于0,a,b,c中的最大者不小于4,这与a+b+c=2矛盾.②若a,b,c为或一正二负,不妨设a>0,b<0,c<0,则|a|+|b|+|c|=a−b−c=a−(2−a)=2a−2,∵a≥4,故2a−2≥6,当a=4,b=c=−1时,满足题设条件且使得不等式等号成立.故|a|+|b|+|c|的最小值为6.故答案为:6.6.(22-23九年级上·四川成都·期末)将两个关于x的一元二次方程整理成a(x+ℎ)!+k=0(a≠0,a、h、k均为常数)的形式,如果只有系数a不同,其余完全相同,我们就称这样的两个方程为“同源二次方程”.已知关于x的一元二次方程ax!+bx+c=0(a≠0)与方程(x+1)!−2=0是“同源二次方程”,且方程ax!+ bx+c=0(a≠0)有两个根为x"、x!,则b-2c=,ax"+x"x!+ax!的最大值是.【思路点拨】利用ax!+bx+c=0(a≠0)与方程(x+1)!−2=0是“同源二次方程”得出b=2a,c=a−2,即可求出b−2c;利用一元二次方程根与系数的关系可得x"+x!=−2,x"x!=+'!+,进而得出ax"+x"x!+ax!=−28a+"+9+1,设a+"+=t(t>0),得a!−t⋅a+1=0,根据方程a!−t⋅a+1=0有正数解可知Δ=t!−4≥0,求出t的取值范围即可求出ax"+x"x!+ax!的最大值.【解题过程】解:根据新的定义可知,方程ax!+bx+c=0(a≠0)可变形为a(x+1)!−2=0,∴a(x+1)!−2=ax!+bx+c,展开,ax!+2ax+a−2=ax!+bx+c,可得b=2a,c=a−2,∴b−2c=2a−2(a−2)=4;∵x"+x!=−2,x"x!=+'!+,∴ax"+x"x!+ax!=a(x"+x!)+x"x!=−2a++'!+=−28a+"+9+1,∵方程ax!+bx+c=0(a≠0)有两个根为x"、x!,∴Δ=b!−4ac=(2a)!−4a(a−2)=8a≥0,且a≠0,∴a>0,设a+"+=t(t>0),得a!−t⋅a+1=0,∵方程a!−t⋅a+1=0有正数解,∴Δ=t!−4≥0,解得t≥2,即a+"+≥2,∴ax"+x"x!+ax!=−28a+"+9+1≤−3.故答案为:4,-3.7.(23-24九年级上·山东济南·期末)已知xy+x+y=44,x!y+xy!=484,求x)+y).【思路点拨】本题主要考查了代数式求值、一元二次方程的根与系数的关系、因式分解的应用等知识点,综合应用所学知识成为解题的关键.设xy=m,x+y=n,等量代换后可得44=m+n、484=mn,则m、n为t!−44t+484=0的根,可解得m=n=22,然后再对x)+y)变形后将m=n=22代入计算即可.【解题过程】解:设xy=m,x+y=n,∴44=xy+x+y=m+n,484=x!y+xy!=xy(x+y)=mn,∴m、n为t!−44t+484=0的根,∴m=n=22,∴x)+y)=(x+y)(x!+y!−xy)=(x+y)[(x+y)!−3xy]=n[n!−3m]=n)−3mn=9196.8.(2024九年级·全国·竞赛)记一元二次方程x!+3x−5=0的两根分别为x"、x!.(1)求"-"'"+"-!'"的值;(2)求3x"!+6x"+x!!的值.【思路点拨】本题考查了一元二次方程根与系数的关系、一元二次方程的解.在利用根与系数的关系x"⋅x!=,+,x"+x!=−*+时,需要弄清楚a、b、c的意义.(1)利用根与系数的关系求得求"-"'"+"-!'"的值的值;(2)由一元二次方程的解可得x"!+3x"−5=0,再利用根与系数的关系求解即可.【解题过程】(1)∵x"+x!=−3,x"x!=−5,∴1x"−1+1x!−1=x!−1+x"−1 (x"−1)(x!−1)=x"+x!−2 x"x!−(x"+x!)+1=−3−2−5−(−3)+1=5;(2)∵x"是一元二次方程x!+3x−5=0的根,∴x"!+3x"−5=0,∴x"!+3x"=5,又∵x"+x!=−3,x"x!=−5,∴3x"!+6x"+x!!=2(x"!+3x")+(x"+x!)!−2x"x!=29.9.(23-24九年级下·北京·开学考试)已知关于x的方程x!−2mx+m!−n=0有两个不相等的实数根.(1)求n的取值范围;(2)若n为符合条件的最小整数,且该方程的较大根是较小根的3倍,求m的值.【思路点拨】本题考查一元二次方程根的判别式及根与系数的关系,对于一元二次方程ax!+bx+c=0(a≠0),当判别式Δ>0时方程有两个不相等的实数根,Δ=0时方程有两个相等的实数根,Δ<0时方程没有实数根,若方程的两个实数根为x"、x!,则x"+x!=−*+,x"⋅x!=,+.(1)根据方程x!−2mx+m!−n=0有两个不相等的实数根得出判别式Δ>0,列出不等式即可得答案;(2)根据(1)中结果得出n值,利用一元二次方程根与系数的关系列方程求出m的值即可.【解题过程】(1)解:∵关于x的方程x!−2mx+m!−n=0有两个不相等的实数根,∴Δ=(−2m)!−4(m!−n)>0,解得:n>0.(2)设方程的两个实数根为x"、x!,且x">x!,∴x"+x!=2m,x"⋅x!=m!−n,由(1)可知:n>0,∵n为符合条件的最小整数,∴n=1,∵该方程的较大根是较小根的3倍,∴x"=3x!,∴4x!=2m,3x!!=m!−1,∴3×$!%=m!−1,解得:m"=−2,m!=2.当m=2时,x!=1,则x"=3x!=3,符合题意,当m=−2时,x!=−1,则x"=3x!=−3<x!,与x">x!不符,舍去,∴m=2.10.(23-24九年级上·安徽淮南·阶段练习)若关于x的一元二次方程x!+2x−m!−m=0.(1)若α和β分别是该方程的两个根,且αβ=−2,求m的值;(2)当m=1,2,3,⋅⋅⋅,2024时,相应的一元二次方程的两个根分别记为α"、β",α!、β!,⋅⋅⋅,α!1!%、β!1!%,求"2"+"3"+"2!+"3!+⋯+"2!#!$+"3!#!$的值.【思路点拨】(1)根据一元二次方程的根与系数的关系进行求解即可;(2)根据一元二次方程的根与系数的关系x"+x!=−*+,x"⋅x!=,+可得:"-"+"-!=-"/-!-"⋅-!=!$!/$,进一步可寻找"2!#!$+"3!#!$的规律,即可求解.【解题过程】(1)解:∵关于x的一元二次方程x!+2x−m!−m=0,α和β分别是该方程的两个根,∴αβ=−m!−m∵αβ=−2,∴−2=−m!−m∴m=1或m=−2;(2)解:设方程x!+2x−m!−m=0的两个根为:x",x!则x"+x!=−*+=−2,x"⋅x!=,+=−m!−m,∴" -"+"-!=-"/-!-"·-!=!$!/$=!$($/")∴" 2"+"3"=!"×!,"2!+"3!=!!×),"2%+"3%=!)×%…..1α!1!%+1β!1!%=22024×2025∴" 2"+"3"+"2!+"3!+⋯+"2!#!$+"3!#!$=2×8""×!+"!×)+...+"!1!%×!1!09=2×X1−12+12−13+...+12024−12025Y=2×X1−1 2025Y=4048 202511.(22-23九年级上·湖北武汉·期中)已知α、β是关于x的一元二次方程x!+(2m+3)x+m!=0的两个不相等的实数根(1)直接写出m的取值范围(2)若满足"2+"3=−1,求m的值.(3)若α>2,求证:β>2;【思路点拨】(1)根据一元二次方程x!+(2m+3)x+m!=0的两个不相等的实数根,得Δ>0,即可列式作答;(2)结合一元二次方程根与系数的关系,得α+β=−(2m+3)和αβ=m!,因为"2+"3=−1,所以!$/)$!=1,解得m"=3,m2=−1,结合m>−)%,即可作答;(3)因为(α−2)(β−2)=αβ−2(α+β)+4,结合α+β=−(2m+3)和αβ=m!,得m!+2(2m+3)+ 4=(m+2)!+6,则(α−2)(β−2)≥6>0,又因为α>2,即可证明β>2.【解题过程】(1)解:∵一元二次方程x!+(2m+3)x+m!=0的两个不相等的实数根∴Δ=b!−4ac=(2m+3)!−4×1×m!=4m!+12m+9−4m!=12m+9>0,即m>−)%;(2)解:∵"2+"3=323+223=2/323=−1,且α+β=−*+=−(2m+3),αβ=,+=m!∴!$/)$!=1整理得m!−2m−3=0,解得:m"=3,m2=−1∵由(1)知m>−)%,∴m=3检验:当m=3时,m!≠0,即m=3;(3)证明:因为(α−2)(β−2)=αβ−2(α+β)+4,把α+β=−(2m+3)和αβ=m!代入上式,得m!+2(2m+3)+4=m!+4m+10=(m+2)!+6,∵(m +2)!≥0, ∴(m +2)!+6≥6 ∴(α−2)(β−2)≥6>0 ∵α>2, ∴α−2>0, ∴β−2>0, 即β>2.12.(22-23九年级·浙江·自主招生)已知方程x !+4x +1=0的两根是α、β. (1)求|α−β|的值; (2)求Z 23+Z 32的值;(3)求作一个新的一元二次方程,使其两根分别等于α、β的倒数的立方.(参考公式:x )+y )=(x +y)(x !+y !−xy ). 【思路点拨】(1)利用一元二次方程根与系数的关系可得α+β=−4,αβ=1,再求得(α−β)!的值,进而求得|α−β|的值.(2)先根据二次根式的性质将Z 23+Z 32化为√293+93√2,然后通分化简可得2/3923,最后将α+β=−4,αβ=1代入计算即可;(3)由题意可得新一元二次方程的两个根为8"29)和8"39),然后求得8"29)+8"39)和8"29)8"39)的值,然后根据一元二次方程根与系数的关系即可解答. 【解题过程】(1)解:∵方程x !+4x +1=0的两根是α、β ∴α+β=−4,αβ=1∴(α−β)!=(α+β)!−4αβ=12 ∴|α−β|=2√3;(2)解:由(1)可知:α<0,β<0,∵[\αβ+\βα]!=αβ+βα+2=α!+β!αβ+2=(α+β)!−2αβαβ+2=16,∴Z23+Z32=4(负值舍去);(3)解:由题意可得新一元二次方程的两个根为8"29)和8"39)则8"29)+8"39)=(1α+1β)^X1αY!+X1βY!−1αβ_=α+βαβ^α!+β!α!β!−1αβ_=α+βαβ^(α+β)!−2αβα!β!−1αβ_=−41`16−21!−1a=−52X 1αY)X1βY)=X1αβY)=1所以新的一元二次方程x!+52x+1=0.13.(22-23九年级上·福建泉州·期末)已知关于x的方程mx!−(m−1)x+2=0有实数根.(1)若方程的两根之和为整数,求m的值;(2)若方程的根为有理根,求整数m的值.【思路点拨】(1)根据关于x的方程mx!−(m−1)x+2=0有两个根,且为实数根,先利用一元二次方程的根的判别式确定m的取值范围,再根据一元二次方程的根与系数的关系,可知x"+x!=$'"$,若方程的两根之和为整数,即$'"$为整数,即可确定m的值;(2)分两种情况讨论:当m=0时,此时关于x的方程为x+2=0,求解可得x=−2,符合题意;当m≠0时,对于关于x的方程mx!−(m−1)x+2=0可有x=($'")±√$!'"1$/"!$,若方程的根为有理根,且m为整数,则Δ=m!−10m+1为某一有理数的平方,据此分析即可获得答案.【解题过程】(1)解:∵关于x的方程mx!−(m−1)x+2=0有两个根,且为实数根,∴m ≠0,且Δ=[−(m −1)]!−4m ×2=m !−10m +1≥0, 根据一元二次方程的根与系数的关系,可知x "+x !=−'($'")$=$'"$,若方程的两根之和为整数,即$'"$为整数,∵$'"$=1−"$,∴"$是整数, ∴m =±1,当m =1时,Δ=1−10+1=−8<0,不符合题意; 当m =−1时,Δ=1+10+1=12>0,$'"$='"'"'"=2,为整数,符合题意;∴m 的值为−1;(2)当m =0时,此时关于x 的方程为x +2=0,解得x =−2; 当m ≠0时,对于关于x 的方程mx !−(m −1)x +2=0的根为:x =($'")±√$!'"1$/"!$,若方程的根为有理根,且m 为整数, 则Δ=m !−10m +1为完全平方数, 设m !−10m +1=k !(k 为正整数), 则:m ="1±√"11'%/%#!!=5±√24+k !,∵m 为整数,设24+k !=n !(n 为正整数), ∴(k +n )(n −k )=24,∴b k +n =12n −k =2 或b k +n =6n −k =4 或b k +n =8n −k =3 或b k +n =24n −k =1 , 解得:bk =5n =7 或b k =1n =5 或d k =0!n =""!(不合题意,舍去)或d k =!)!n =!0!(不合题意,舍去) ∴m !−10m +1=1!=1或m !−10m +1=5!=25; 当m !−10m +1=1时,解得m =10或m =0(舍去); 当m !−10m +1=25时,解得m =−2或m =12,综上所述,若方程的根为有理根,则整数m 的值为0或10或−2或12.14.(22-23九年级下·浙江·自主招生)设m 为整数,关于x 的方程(m !+m −2)x !−(7m +2)x +12=0有两个整数实根. (1)求m 的值.(2)设△ABC 的三边长a,b,c 满足c =4√2,m !+a !m −12a =0,m !+b !m −12b =0.求△ABC 的面积. 【思路点拨】(1)设原方程的两个解分别为x ",x !,根据两个整数实根,则x "+x !=&$/!$!/$'!,x "x !="!$!/$'!都是整数,进而分类讨论,即可求解;(2)由(1)得出的m 的值,然后代入将m !+a !m −12a =0,m !+b !m −12b =0进行化简,得出a ,b 的值.然后再根据三角形三边的关系来确定符合条件的a ,b 的值,用三角形的面积公式得出三角形的面积. 【解题过程】(1)解:∵m !+m −2≠0, ∴m ≠−2或m =1, ∵方程有两个实数根,∴Δ=b !−4ac =[−(7m +2)]!−4×12×(m !+m −12) =m !−20m +580=(m −10)!+480>0 设原方程的两个解分别为x ",x !∴x "+x !=&$/!$!/$'!,x "x !=∴m !+m −2=1,2,3,4,6,12 m !+m −2=1,解得:m ='"±√")!(舍去) m !+m −2=2,解得:m ='"±√"&!(舍去) m !+m −2=3,解得:m ='"±√!"!(舍去)m !+m −2=4,解得:m =−3或m =2 m !+m −2=6,解得:m ='"±√))!(舍去)m !+m −2=12,解得:m ='"±√"!;!(舍去) 当m =−3时,&$/!$!/$'!='!"/!%=−";%不是整数,舍去当m =2时,&$/!$!/$'!="%/!%=4符合题意,综上所述,m=2;(2)把m=2代入两等式,化简得a!−6a+2=0,b!−6b+2=0,当a=b时,a=b=3±√7,当a≠b时,a、b是方程x!−6x+2=0的两根,而Δ>0,根据根与系数的关系可得,a+b=6>0,ab=2>0,则a>0、b>0,①a≠b,c=4√2时,由于a!+b!=(a+b)!−2ab=36−4=32=c!,故△ABC为直角三角形,且∠C=90°,S<=>?="!ab=1;②a=b=3−√7,c=4√2时,因2(3−√7)<4√2,故不能构成三角形,不合题意,舍去;;③a=b=3+√7,c=4√2时,因2(3+√7)>4√2,故能构成三角形,S<=>?="!×4√2×Z l3+√7m!−l2√2m!=4n4+3√7;综上,△ABC的面积为1或4n4+3√7.15.(22-23九年级上·湖南常德·期中)阅读材料:材料1:若关于x的一元二次方程ax!+bx+c=0(a≠0)的两个根为x1,x2,则x"+x!=−*+,x"x!=,+.材料2:已知一元二次方程x!−x−1=0的两个实数根分别为m,n,求m!n+mn!的值.解:∵一元二次方程x!−x−1=0的两个实数根分别为m,n,∴m+n=1,mn=−1,则m!n+mn!=mn(m+n)=−1×1=−1.根据上述材料,结合你所学的知识,完成下列问题:(1)材料理解:一元二次方程x!−3x−1=0的两个根为x1,x2,则x"+x!=___________,x"x!=___________.(2)类比应用:已知一元二次方程x!−3x−1=0的两根分别为m、n,求A$+$A的值.(3)思维拓展:已知实数s、t满足s!−3s−1=0,t!−3t−1=0,且s≠t,求"B −"C的值.【思路点拨】(1)直接利用一元二次方程根与系数的关系求解即可;(2)利用一元二次方程根与系数的关系可求出m+n=−*+=3,mn=,+=−1,再根据A$+$A=$!/A!$A=($/A)!'!$A$A,最后代入求值即可;(3)由题意可将s、t可以看作方程x!−3x−1=0的两个根,即得出s+t=−*+=3,s⋅t=,+=−1,从而可求出(t−s)!=(t+s)!−4st=13,即t−s=√13或t−s=−√13,最后分类讨论分别代入求值即可.【解题过程】(1)解:∵一元二次方程x!−3x−1=0的两个根为x1,x2,∴x"+x!=−*+=−')"=3,x"⋅x!=,+=−""=−1.故答案为:3,−1;(2)∵一元二次方程x!−3x−1=0的两根分别为m、n,∴m+n=−*+=3,mn=,+=−1,∴A $+$A=$!/A!$A=(m+n)!−2mnmn=3!−2×(−1)−1=−11;(3)∵实数s、t满足s!−3s−1=0,t!−3t−1=0,∴s、t可以看作方程x!−3x−1=0的两个根,∴s+t=−*+=3,st=,+=−1,∵(t−s)!=(t+s)!−4st=3!−4×(−1)=13∴t−s=√13或t−s=−√13,当t−s=√13时," B −"C=C'BBC=√")'"=−√13,当t−s=−√13时," B −"C=C'BBC='√")'"=√13,综上分析可知,"B −"C的值为√13或−√13.16.(23-24八年级上·北京海淀·期中)小聪学习多项式研究了多项式值为0的问题,发现当mx +n =0或px +q =0时,多项式A =(mx +n )(px +q )=mpx !+(mq +np )x +nq 的值为0,把此时x 的值称为多项式A 的零点.(1)已知多项式(3x +1)(x −2),则此多项式的零点为__________;(2)已知多项式B =(x −1)(bx +c )=ax !−(a −1)x −+!有一个零点为1,求多项式B 的另一个零点; (3)小聪继续研究(x −3)(x −1),x (x −4)及8x −0!98x −)!9等,发现在x 轴上表示这些多项式零点的两个点关于直线x =2对称,他把这些多项式称为“2系多项式”.若多项式M =(2ax +b )(cx −5c )=bx !−4cx −2a −4是“2系多项式”,求a 与c 的值. 【思路点拨】(1)根据多项式的零点的定义即可求解;(2)根据多项式的零点的定义将x =1代入ax !−(a −1)x −+!=0,求得a =2,再解一元二次方程即可求解;(3)令cx −5c =0,求得M 的一个零点为5,根据“2系多项式”的定义求得方程bx !−4cx −2a −4=0的两个根为x "=−1,x !=5,再利用根与系数的关系即可求解. 【解题过程】(1)解:令(3x +1)(x −2)=0, ∴3x +1=0或x −2=0, ∴x =−")或x =2,则此多项式的零点为−")或2; 故答案为:−")或2;(2)解:∵多项式B =(x −1)(bx +c )=ax !−(a −1)x −+!有一个零点为1,∴将x =1代入ax !−(a −1)x −+!=0,得a −(a −1)−+!=0,解得a =2,∴B =2x !−x −1=(x −1)(2x +1), 令2x +1=0,解得x =−"!, ∴多项式B 的另一个零点为−"!;(3)解:∵M=(2ax+b)(cx−5c)=bx!−4cx−2a−4是“2系多项式”,令cx−5c=0,解得x=5,即M的一个零点为5,∴设M的另一个零点为y,则D/0!=2,解得y=−1,即2ax+b=0时,x=−1,则−2a+b=0①,令M=bx!−4cx−2a−4=0,根据题意,方程bx!−4cx−2a−4=0的两个根为x"=−1,x!=5,∴x"+x!=−'%,*=5+(−1)=4,x"⋅x!='!+'%*=5×(−1)=−5,∴c=b②,5b−2a−4=0③,解①②③得c=b=1,a="!,∴a="!,c=1.17.(22-23九年级上·湖北黄石·期末)(1)x",x!是关于x的一元二次方程x!−2(k+1)x+k!+2=0的两实根,且(x"+1)⋅(x!+1)=8,求k的值.(2)已知:α,β(α>β)是一元二次方程x!−x−1=0的两个实数根,设s"=α+β,s!=α!+β!,…,s A=αA+βA.根据根的定义,有α!−α−1=0,β!−β−1=0,将两式相加,得(α!+β!)−(α+β)−2= 0,于是,得s!−s"−2=0.根据以上信息,解答下列问题:①直接写出s",s!的值.②经计算可得:s)=4,s%=7,s0=11,当n≥3时,请猜想s A,s A'",s A'!之间满足的数量关系,并给出证明.【思路点拨】(1)根据一元二次方程根与系数的关系可得出x"+x!=2(k+1),x"x!=k!+2.由(x"+1)(x!+1)=8,可得x"x!+(x"+x!)+1=8,即得出关于k的一元二次方程,解出k的值,再根据一元二次方程根的判别式验证,舍去不合题意的值即可;(2)①根据一元二次方程根与系数的关系可得出α+β=−*+=1,αβ=,+=−1,进而可求出s"=α+β=1,s!=α!+β!=(α+β)!−2αβ=3;②由一元二次方程的解的定义可得出α!−α−1=0,两边都乘以αA'!,得:αA−αA'"−αA'!=0①,同理可得:βA−βA'"−βA'!=0②,再由①+②,得:(αA+βA)−(αA'"+βA'")−(αA'!+βA'!)=0.最后结合题意即可得出s A−s A'"−s A'!=(αA+βA)−(αA'"+βA'")−(αA'!+βA'!)=0,即s A=s A'"+s A'!.【解题过程】解:(1)∵x",x!是关于x的一元二次方程x!−2(k+1)x+k!+2=0的两实根,∴x"+x!=−*+=−'!(#/")"=2(k+1),x"x!=,+=#!/!"=k!+2,∴(x"+1)(x!+1)=x"x!+(x"+x!)+1=k!+2+2(k+1)+1=8,整理,得:k!+2k−3=0,解得:k"=−3,k!=1.当k=−3时,Δ=b!−4ac=[−2(k+1)]!−4(k!+2)=[−2(−3+1)]!−4[(−3!)+2]=−28<0,∴此时原方程没有实数根,∴k=−3不符合题意;当k=1时,Δ=b!−4ac=[−2(k+1)]!−4(k!+2)=[−2×(1+1)]!−4(1!+2)=4>0,∴此时原方程有两个不相等的实数根,∴k=1符合题意,∴k的值为1;(2)①∵x!−x−1=0,∴a=1,b=−1,c=−1.∵α,β(α>β)是一元二次方程x!−x−1=0的两个实数根,∴α+β=−*+=1,αβ=,+=−1,∴s"=α+β=1,s!=α!+β!=(α+β)!−2αβ=1!−2×(−1)=3;②猜想:s A=s A'"+s A'!.证明:根据一元二次方程根的定义可得出α!−α−1=0,两边都乘以αA'!,得:αA−αA'"−αA'!=0①,同理可得:βA−βA'"−βA'!=0②,由①+②,得:(αA+βA)−(αA'"+βA'")−(αA'!+βA'!)=0,∵s A=αA+βA,s A'"=αA'"+βA'",s A'!=αA'!+βA'!,∴s A−s A'"−s A'!=(αA+βA)−(αA'"+βA'")−(αA'!+βA'!)=0,即s A=s A'"+s A'!.18.(23-24九年级上·福建宁德·期中)已知关于x的方程x!−(m+2)x+4m=0有两个实数根x",x!,其中x"<x!.(1)若m=−1,求x"!+x!!的值;(2)一次函数y=3x+1的图像上有两点A(x",y"),B(x!,y!),若AB=√10,求m的值;(3)边长为整数的直角三角形,其中两直角边的长度恰好为x"和x!,求该直角三角形的面积.【思路点拨】该题主要考查了一元二次方程的根判别式“Δ=b!−4ac”,根与系数关系“x"+x!=−*+,x"⋅x!=,+”,一次函数的性质,直角三角形的性质,勾股定理“直角三角形两直角边的平方之和等于斜边的平方”等知识点,解题的关键是分类谈论思想的运用;(1)将m=−1代入方程得出方程,再根据根与系数关系得到x"+x!=−*+=1,x"⋅x!=,+=−4,将x"!+x!!转化即可求解;(2)根据点A(x",y"),B(x!,y!)在函数图像上,得出Alx",3x"+1m,Blx!,3x!+1m,再根据根与系数关系得到x"+x!=m+2,x"⋅x!=4m,根据AB=√10即可求解;(3)根据直角三角形两直角边x",x!为整数,得出Δ=b!−4ac=m!−12m+4,令m!−12m+4=k!(k为正整数),得出(m+k−6)(m−k−6)=32,又m+k−6>m−k−6,然后分三种情况取值即可解答;【解题过程】(1)当m=−1时,方程为x!−x−4=0,Δ=b!−4ac=(−1)!−4×1×(−4)=17>0,∴x"+x!=−*+=1,x"⋅x!=,+=−4,即x"!+x!!=(x"+x!)!−2x"x!=1!−2×(−4)=9;(2)将A(x",y"),B(x!,y!)代入y=3x+1可得Alx",3x"+1m,Blx!,3x!+1m,又Δ=(m+2)!−4×4m>0,故x"+x!=m+2,x"⋅x!=4m,AB!=(x"−x!)!+(y"−y!)!=10(x"−x!)!,即10(x"−x!)!=10,(x"−x!)!=1,(x"−x!)!=(x"+x!)!−4x"x!=1,(m+2)!−4×4m=1,(m−6)!=33,m"=6+√33,m!=6−√33;(3)∵直角三角形两直角边x ",x !为整数,∴Δ=b !−4ac =(m +2)!−4×4m =m !−12m +4为平方数, 不妨令m !−12m +4=k !(k 为正整数), (m −6)!−32=k !,(m +k −6)(m −k −6)=32, m +k −6>m −k −6,当①∴m +k −6=32,m −k −6=1, 解得m =%0!(不合题意舍去);当②m +k −6=16,m −k −6=2, 解得m =15,∴方程x !−17x +60=0, x "=12,x !=5,则斜边为13, 即S =-"⋅-!!=30;当③m +k −6=8,m −k −6=4, 解得m =12,∴方程x !−14x +48=0,x "=6,x !=8,则斜边为10, 即S =-"⋅-!!=24,综上所述:该直角三角形的面积为30或24.19.(22-23九年级上·全国·单元测试)如果方程x !+px +q =0有两个实数根x ",x !,那么x "+x !=−p ,x "x !=q ,请根据以上结论,解决下列问题:(1)已知a ,b 是方程x !+15x +5=0的二根,则+*+*+=?(2)已知a 、b 、c 满足a +b +c =0,abc =16,求正数c 的最小值.(3)结合二元一次方程组的相关知识,解决问题:已知b x =x "y =y "和b x =x !y =y !是关于x ,y 的方程组t x !−y +k =0x −y =1 的两个不相等的实数解.问:是否存在实数k ,使得y "y !−-"-!−-!-"=2?若存在,求出的k 值,若不存在,请说明理由.【思路点拨】(1)根据a ,b 是方程x !+15x +5=0的二根,求出a +b ,ab 的值,即可求出+*+*+的值; (2)根据a +b +c =0,abc =16,得出a +b =−c ,ab ="E,,a 、b 是方程x !+cx +"E ,=0的解,再根据c !−4×"E ,≥0,即可求出c 的最小值;(3)运用根与系数的关系求出x "+x !=1,x "x !=k +1,再解y "y !−-"-!−-!-"=2,即可求出k 的值.【解题过程】(1)解:∵a ,b 是方程x !+15x +5=0的二根, ∴a +b =−15,ab =5, ∴+*+*+=(+/*)!'!+*+*=('"0)!'!×0=43,∴+*+*+=43;(2)∵a +b +c =0,abc =16, ∴a +b =−c ,ab ="E ,,∴a 、b 是方程x !+cx +"E ,=0的解,∴c !−4×"E ,≥0,∴c !−%%,≥0,∵c 是正数,∴c )−4)≥0, ∴c )≥4), ∴c ≥4,∴正数c 的最小值是4;(3)存在,当k =−2时,y "y !−-"-!−-!-"=2.理由如下: ∵u x !−y +k =0①x −y =1② ,由①得:y =x !+k , 由②得:y =x −1,∴x !+k =x −1,即x !−x +k +1=0,由题意思可知,x ",x !是方程x !−x +k +1=0的两个不相等的实数根, ∴d (−1)!−4(k +1)>0x "+x !=1x "x !=k +1 , 则k <−)%,∵b x =x "y =y " 和b x =x !y =y ! 是关于x ,y 的方程组t x !−y +k =0x −y =1 的两个不相等的实数解,∴y "y !=(x "−1)(x !−1), ∴y "y !−-"-!−-!-"=(x "−1)(x !−1)−(-"/-!)!'!-"-!-"-!=2,∴x "x !−(x "+x !)+1−(-"/-!)!'!-"-!-"-!=2,∴k +1−1+1−"'!(#/")#/"=2,整理得:k !+2k =0,解得:k "=−2,k !=0(舍去), ∴k 的值为−2.20.(22-23九年级上·四川资阳·期末)定义:已知x ",x !是关于x 的一元二次方程ax !+bx +c =0(a ≠0)的两个实数根,若x "<x !<0,且3<-"-!<4,则称这个方程为“限根方程”.如:一元二次方程x !+13x +30=0的两根为x "=−10,x !=−3,因−10<−3<0,3<'"1')<4,所以一元二次方程x !+13x +30=0为“限根方程”.请阅读以上材料,回答下列问题:(1)判断一元二次方程x !+9x +14=0是否为“限根方程”,并说明理由;(2)若关于x 的一元二次方程2x !+(k +7)x +k !+3=0是“限根方程”,且两根x "、x !满足x "+x !+x "x !=−1,求k 的值;(3)若关于x 的一元二次方程x !+(1−m )x −m =0是“限根方程”,求m 的取值范围. 【思路点拨】(1)解该一元二次方程,得出x "=−7,x !=−2,再根据“限根方程”的定义判断即可; (2)由一元二次方程根与系数的关系可得出x "+x !=−#/&!,x "x !=#!/)!,代入x "+x !+x "x !=−1,即可求出k "=2,k !=−1.再结合“限根方程”的定义分类讨论舍去不合题意的值即可;(3)解该一元二次方程,得出x"=−1,x!=m或x"=m,x!=−1.再根据此方程为“限根方程”,即得出此方程有两个不相等的实数根,结合一元二次方程根的判别式即可得出Δ>0,m<0且m≠−1,可求出m 的取值范围.最后分类讨论即可求解.【解题过程】(1)解:x!+9x+14=0,(x+2)(x+7)=0,∴x+2=0或x+7=0,∴x"=−7,x!=−2.∵−7<−2,3<'&'!=&!<4,∴此方程为“限根方程”;(2)∵方程2x!+(k+7)x+k!+3=0的两个根分比为x"、x!,∴x"+x!=−#/&!,x"x!=#!/)!.∵x"+x!+x"x!=−1,∴−#/&!+#!/)!=−1,解得:k"=2,k!=−1.分类讨论:①当k=2时,原方程为2x!+9x+7=0,∴x"=−&!,x!=−1,∴x"<x!<0,3<-"-!=&!<4,∴此时方程2x!+(k+7)x+k!+3=0是“限根方程”,∴k=2符合题意;②当k=−1时,原方程为2x!+6x+4=0,∴x"=−2,x!=−1,∴x"<x!<0,-"-!=2<3,∴此时方程2x!+(k+7)x+k!+3=0不是“限根方程”,∴k=−1不符合题意.综上可知k的值为2;(3)x!+(1−m)x−m=0,(x+1)(x−m)=0,∴x+1=0或x−m=0,∴x"=−1,x!=m或x"=m,x!=−1.∵此方程为“限根方程”,∴此方程有两个不相等的实数根,∴Δ>0,m<0且m≠−1,∴(1−m)!+4m>0,即(1+m)!>0,∴m<0且m≠−1.分类讨论:①当−1<m<0时,∴x"=−1,x!=m,∵3<-"-!<4,∴3<'"$<4,解得:−")<m<−"%;②当m<−1时,∴x"=m,x!=−1,∵3<-"-!<4,∴3<$'"<4,解得:−4<m<−3.综上所述,m的取值范围为−")<m<−"%或−4<m<−3.。
上海初二年级下学期数学函数压轴题

2013年上海初二数学函数压轴题 2013.2.111. 在梯形ABCD 中, AD ∥BC ,cm AD CD AB 5===,BC =11cm,点P 从点D 开始沿DA 边以每秒1cm 的速度移动,点Q 从点B 开始沿BC 边以每秒2cm 的速度移动当点P 到达点A 时,点P 与点Q 同时停止移动,假设点P 移动的时间为x 秒,四边形ABQP 的面积为y cm 2. 1求y 关于x 的函数解析式,并写出它的定义域;2在移动的过程中,求四边形ABQP 的面积与四边形QCDP 的面积相等时x 的值;3在移动的过程中,是否存在x 使得PQ=AB ,若存在求出所有x 的值,若不存在请说明理由.CB2. 如图,在正方形ABCD 中,点E 在边AB 上点E 与点A 、B 不重合,过点E 作FG ⊥DE ,FG 与边BC 相交于点F,与边DA 的延长线相交于点G.1由几个不同的位置,分别测量BF 、AG 、AE 的长,从中你能发现BF 、AG、AE 的数量之间具有怎样的关系 并证明你所得到的结论;2联结DF ,如果正方形的边长为2,设AE=x ,△DFG 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域;3如果正方形的边长为2,FG 的长为25,求点C 到直线DE 的距离.供操作实验用供证明计算用第2题图D ABGD AB3.如图,已知在矩形ABCD 中,对角线AC 、BD 交于点O ,CE =AE ,F 是AE 的中点,AB = 4,BC = 8.求线段OF的长.4已知一次函数421+-=x y 的图像与x 轴、y 轴分别相交于点A 、B .梯形AOBC 的边AC = 5. 1求点C 的坐标;2如果点A 、C 在一次函数y k x b =+k 、b 为常数,且k <0的图像上,求这个一次函数的解析式.5.如图,直角坐标平面xoy 中,点A 在x 轴上,点C 与点E 在y 轴上,且E 为OC 中点,BC //x 轴,且BE ⊥AE ,联结AB ,1求证:AE 平分∠BAO ;2当OE =6, BC=4时,求直线AB 的解析式.第4题图ABCDOEF 第3题图6.如图,△ABC 中,点D 、E 分别是边BC 、AC 的中点,过点A 作AF//BC 交线段DE 的延长线相交于F 点,取AF的中点G ,如果BC = 2 AB . 求证:1四边形ABDF 是菱形;2AC = 2DG .7.边长为4的正方形ABCD 中,点O 是对角线AC 的中点, P 是对角线AC 上一动点,过点P 作PF ⊥CD 于点F ,作PE ⊥PB 交直线CD 于点E ,设PA=x ,S ⊿PCE =y , ⑴ 求证:DF =EF ;5分⑵ 当点P 在线段AO 上时,求y 关于x 的函数关系式及自变量x 的取值范围;3分 ⑶ 在点P 的运动过程中,⊿PEC 能否为等腰三角形 如果能够,请直接写出PA 的长;如果不能,请简单说明理由;2分A BFDEG第6题图第26题图D CB AEFP;ODA8.已知一条直线b kx y +=在y 轴上的截距为2,它与x 轴、y 轴的交点分别为A 、B,且△ABO 的面积为4. 1求点A 的坐标;2若0<k ,在直角坐标平面内有一点D,使四边形ABOD 是一个梯形,且AD ∥BO,其面积又等于20平方单位,试求点D 的坐标.9.在边长为2的正方形ABCD 中,对角线AC 与BD 相交于点O,另一个正方形OHIG 绕点O 旋转如图,设OH 与边BC 交于点E 与点B 、C 不重合,OG 与边CD 交于点F. 1求证:BE=CF ;2在旋转过程中,四边形OECF 的面积是否会变化 若没有变化,求它的面积;若有变化,请简要说明理由; 3联结EF 交对角线AC 于点K,当△OEK 是等腰三角形时,求∠DOF 的度数.10 如图,已知矩形ABCD,过点C作∠A的角平分线AM的垂线,垂足为M,AM交BC于E,连接MB、MD.求证:MB = MD.11.如图,在菱形ABCD中,∠A = 60°,AB = 4,E是AB边上的一动点,过点E作EF⊥AB交AD的延长线于点F,交BD于点M、DC于点N.1请判断△DMF的形状,并说明理由;2设EB = x,△DMF的面积为y,求y与x之间的函数关系式,并写出x的取值范围;3当x取何值时,S△DMF = 错误!.12.如图1,在ABC中,AB = BC = 5,AC = 6,△ECD是△ABC沿BC方向平移得到的,连接AE、AC和BE相交于点O.1判断四边形ABCE是怎样的四边形,说明理由.2如图2,P是线段BC上的一动点图2,点P不与B、C重合,连PO并延长交线段AE于点Q,QR⊥BD,垂足为R.①四边形PQED的面积是否随点P的运动而发生变化若变化,请说明理由;若不变,求出四边形PQED的面积.②当P在线段BC上运动时,是否有△PQR与△BOC全等若全等,求BP的长;若不全等,请叙述理由.13,已知:如图,在菱形ABCD 中,AB =4,∠B =60°,点P 是射线BC 上的一个动点,∠PAQ =60°,交射线CD 于点Q ,设点P 到点B 的距离为x ,PQ =y . 1求证:△APQ 是等边三角形;2求y 关于x 的函数解析式,并写出它的定义域; 3如果PD ⊥AQ ,求BP 的值.14.如图,已知点E 是矩形ABCD 的边CB 延长线上一点,且CE CA =,联结AE ,过点C 作CF AE ⊥,垂足为点F ,联结BF 、FD .1求证:FBC ∆≌FAD ∆;2联结BD ,若35FB BD =,且10AC =,求FC 的值. FEDCBA图1备用图图2D15,A B ,两地盛产柑桔,A 地有柑桔200吨,B 地有柑桔300吨.现将这些柑桔运到C 、D 两个冷藏仓库,已知C 仓库可储存240吨,D 仓库可储存260吨;从A 地运往C 、D 两处的费用分别为每吨20元和25元,从B 地运往C 、D 两处的费用分别为每吨15元和18元.设从A 地运往C 仓库的柑桔重量为x 吨,A 、B 两地运往两仓库的柑桔运输费用分别为A y 元和B y 元.1请填写下表后分别求出A B y y ,与x 之间的函数关系式,并写出定义域; 解:2试讨论A B ,两地中,哪个运费较少; 解:16.,已知:正方形ABCD 的边长为28厘米,对角线AC 上的两个动点E F ,,点E 从点A 、点F 从点C 同时出发,沿对角线以1厘米/秒的相同速度运动,过E 作EH ⊥AC 交Rt ACD △的直角边于H ;过F 作FG ⊥AC 交Rt ACD △的直角边于G ,连接HG ,EB .设HE ,EF ,FG ,GH 围成的图形面积为1S ,AE ,EB ,BA 围成的图形面积为2S 这里规定:线段的面积为0.E 到达C F ,到达A 停止.若E 的运动时间为x 秒,解答下列问题:1如图①,判断四边形EFGH 是什么四边形,并证明; 2当08x <<时,求x 为何值时,12S S =;3若y 是1S 与2S 的和,试用x 的代数式表示y .图②为备用图 1解:图①图②17,如图,在平面直角坐标系中,直线l 经过点)3,2(-A ,与x 轴交于点B ,且与直线383-=x y 平行; 1求:直线l 的函数解析式及点B 的坐标;2如直线l 上有一点)6,(-a M ,过点M 作x 轴的垂线,交直线383-=x y 于点N ,在线段MN 上求一点P ,使PAB ∆是直角三角形,请求出点P 的坐标;18, 在梯形ABCD 中,AD ∥BC ,∠B = 90,∠C =45º,AB =8,BC =14,点E 、F 分别在边AB 、CD 上,EF //AD ,点P 与AD 在直线EF 的两侧,∠EPF =90º, PE =PF ,射线EP 、FP 与边BC 分别相交于点M 、N ,设AE =x ,MN =y .(1) 求边AD 的长;(2) 如图,当点P 在梯形ABCD 内部时,求y 关于x 的函数解析式,并写出定义域;(3) 如果MN 的长为2,求梯形AEFD 的面积.19, 如图,在△ABC 中,点D 是边BC 的中点,点E 在△ABC 内,AE 平分∠BAC ,CE ⊥AE ,点F 在边AB 上,EF //BC . 1求证:四边形BDEF 是平行四边形;2线段BF 、AB 、AC 的数量之间具有怎样的关系 证明你所得到的结论.20, 如图,一次函数42+=x y 的图像与x 、y 轴分别相交于点A 、B ,四边形ABCD 是正方形.1求点A 、B 、D 的坐标; 2求直线BD 的表达式.ABCDEF 第19题第18题BDA CEFN MP21, 有两个不透明的布袋,其中一个布袋中有一个红球和两个白球,另一个布袋中有一个红球和三个白球,它们除了颜色外其他都相同.在两个布袋中分别摸出一个球, (1) 用树形图或列表法展现可能出现的所有结果; (2) 求摸到一个红球和一个白球的概率.22,已知:梯形ABCD 中,AD ∥BC ,M 、N 分别是BD 、AC 的中点如图2. 求证:1MN ∥BC ;2)(21AD BC MN -=.ABCDM N图223,已知:正方形ABCD ,以A 为旋转中心,旋转AD 至AP ,联结BP 、DP . 1若将AD 顺时针旋转︒30至AP ,如图3所示,求BPD ∠的度数.2若将AD 顺时针旋转α度)900(︒<<︒α至AP ,求BPD ∠的度数.3若将AD 逆时针旋转α度)1800(︒<<︒α至AP ,请分别求出︒<<︒900α、︒=90α、︒<<︒18090α三种情况下的BPD ∠的度数图4、图5、图6.ABCDP图6ABCDPM图4ABC D P图3 ACDPB图524,25、某公路上一段道路的维修工程准备对外招标,现有甲、已两个工程队前来竟标,竟标资料显示:若由甲乙两队合作6天可以完成,共需工程费7800元,若单独完成此项工程甲队比乙队少用5天,但甲队每天的工程费比乙队多300元; 1甲、乙两队单独完成各需多少天 2从节约资金的角度上考虑,应选哪个队单独完成 并说明理由26.如图,在△ABC 中,E 是AB 的中点,CD 平分∠ACAB,AD ⊥CD 于带点D.求证:1DE=BC;2DE=21BC-AC.27.如图,在等腰梯形ABCD 中,AD ∥BC,AB=DC,点P 为BC 边上一点,PE ⊥AB,BG ⊥CD,垂足分别为E,F,G. 求证:PE+PF=BG28.如图,等腰梯形ABCD 中, AD ∥BC,M,N 分别是AD,BC 的中点,E,F 分别是BM,CM 的中点.1求证:四边形MENF 是菱形;2若四边形MENF 是正方形,请探索等腰梯形ABCD 的高和底边BC 的数量关系,并证明你的结论.29,.已知如图,在△ABC 中∠ACB=90°,AD 平分∠CAB 交BC 于D, CH ⊥AB 于H 交AD 于F,DE ⊥AB 于E.求证:B C DEAE FB NC AD M A BP E CFG D四边形CDEF 为菱形.30.如图.点P 是等腰直角三角形ABC 底边BC 上的一点,过P 作BA,AC 的垂线,垂足为E,F 设D 为BC 的中点.1求证:DE ⊥DF;2若点P 在BC 的延长线上是DE ⊥DF 吗 试证明你的结论.31,.如图,CD 为Rt △ABC 斜边AB 上的高,AE 平分∠BAC 交C,D 于E, EF ∥AB,交AB 于点F,求证:CE=BF.32.如图, Rt △ABC 中∠ACB=90°,CD ⊥AB 于D,AE 平分∠BAC 交CD 于F,过F 作FH ∥AB 交BC 于H.求证:CE=BH.33.如图,梯形ABCD 中AD ∥BC,AB=AD=DC,点E 为底边BC 的中点,且DE ∥AB,试判断△ABC 的形状,并 给出证明.CAB HEDFB D PC A E F C AD B FE CAD B H F EBECD A34.如图,已知□ABCD 中,E 为AD 的中点,CE 的延长线交BA 的延长线于点F.1求证:CD=FA;2若使∠F=∠BCF, □ABCD 边长之间还需要再添加一个什么条件 请补上这个条件,并进行证明.不再添辅助线.35.如图所示,已知矩形ABCD 的对角线AC,BD 相交于点O,E 为BC 上一动点点E 不与B,C 两点重合, EF ∥BD 交AC 于点F,EC ∥AC 交BD 于点G. 求证:四边形EFOG 的周长等于2OB.36,.已知一个六边形的六个内角都是120°,其连续四边的长依次是1cm,9cm,9cm,5cm,那么这个六边形的周长是多少厘米37,.矩形ABCD 中,O 是AC 与BD 的交点,过O 点的直线EF 与AB,CD 的延长线分别交于E,F;1求证:△BOE ≌△DOF;2当EF 与AC 满足什么条件时,四边形AECF 是棱形,并证明你的结论B B A F EC DBC M N AD O1cm 9cm9cm 5cm38,.等腰梯形ABCD 中,AD ∥BC,M,N 分别是AD,BC 的中点,E,F 分别是BM,CM 的中点. 求证: 1四边形MENF 是棱形;2若四边形MENF 是正方形,请探索等腰梯形ABCD 的高和底边BC 的数量关系,并证明你的结论39,.如图在△ABC 中,AB=AC,若将△ABC 绕点C 顺时针旋转180°得到△FEC.(1) 试猜想AE 与BF 有何关系 说明理由;(2) 若△ABC 的面积为23cm ,求四边形ABFE 的面积; (3) 当∠ACB 为多少度时,四边形ABFE 为矩形 说明理由40. 如图:棱形ABCD 中,AB=4,E 为BC 中点,AE ⊥BC,AF ⊥CD 于点F,CG ∥AE,CG 交AF 于点H,交AD 于点G.1求棱形ABCD 的度数.2求∠GHA 的度数.41,.已知:如图,正方形ABCD 中,M 是AB 的中点,E 是AB 延长线上一点,MN ⊥DM 且交∠CBE 的平分线于N. 1求证:MD=MN;2若将上述条件中“M 是AB 中点”改为“M 是AB 上任意一点”,其余条件不变如图乙,则结论“MD=MN ”还成立吗 如果成立,请证明;如果不成立,请说明理由.乙甲C F E BD A N MFE C B AC FDE B A GH42. 如图:∠MON=90°,在∠MON 的内部有一个正方形AOCD,点A,C 分别在射线OM,ON 上,点1B 是ON 上的任意一点,在∠MON 的内部作正方形D C AB 11. (1) 连接D D 1,求证:901=∠ADD ;(2) 连接C C 1,猜一猜, CN C 1∠的度数是多少 并证明你的结论;(3) 在ON 上再任取一点2B ,以2AB 为边,在∠MON 的内部作正方形D C AB 22,观察图形,并结合1,2的结论,请你再做出一个合理的判断.43. 已知:如图,在□ABCD 中,E,F 分别为边AB,CD 的中点,BD 是对角线,AG ∥DB 交CB 的延长线于G.1求证: △ADE≌△CBF;2若四边形BEDF 是棱形,则四边形AGBD 是什么特殊四边形 并证明你的结论.44.已知:如图, □ABCD 中,AB ⊥AC,AB=1,BC=5,对角线AC,BD 交于点0,将直线AC 绕0顺时针旋转,分别交BC,AD于点E,F.(1) 证明:当旋转角为90时,四边形ABEF 是平行四边形; (2) 试说明在旋转过程中,线段AF 与EC 总保持相等;3试说明在旋转过程中,四边形BEDF 可能是菱形吗 如果不能,请说明理由;如果能,说明理由.并求出此时AC 绕点O 顺时针旋转的度数.AC 交BD 于点O,四边形AODE 是平行四边形; 求证:四边形ABOE 、四边形DCOE 都是平行四边形; OADM AODCN1B1D 1C46.两个全等的含30°, 60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连结BD,取BD的中点M,连结ME,MC.试判断△EMC的形状,并说明理由.47.如图,在梯形纸片ABCD中,AD∥BC,AD > CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C’E1求证:四边形CDC’E是菱形;2若BC = CD + AD,试判断四边形ABED的形状,并加以证明.48.已知,点P是正方形ABCD内的一点,连PA、PB、PC.1将△PAB绕点B顺时针旋转90°到△P′CB的位置如图1.①设AB的长为a,PB的长为bb<a,求△PAB旋转到△P′CB的过程中边PA所扫过区域图1中阴影部分的面积;②若PA=2,PB=4,∠APB=135°,求PC的长.PA+PC=2PB,请说明点P必在对角线AC上.2如图2,若22249.如图:∠MON = 90°,在∠MON 的内部有一个正方形AOCD,点A 、C 分别在射线OM 、ON 上,点B1是ON 上的任意一点,在∠MON 的内部作正方形AB1C1D1; 1连续D1D,求证:∠ADD1 = 90°;2连结CC1,猜一猜,∠C1CN 的度数是多少 并证明你的结论;3在ON 上再任取一点B2,以AB2为边,在∠MON 的内部作正方形AB2C2D2,观察图形,并结合1、2的结论,请你再做出一个合理的判断;50.将两块全等的含30°角的三角尺如图1摆放在一起,设较短直角边为1.1四边形ABCD 是平行四边形吗 说出你的结论和理由:________________________.2如图2,将Rt △BCD 沿射线BD 方向平移到Rt △B 1C 1D 1的位置,四边形ABC 1D 1是平行四边形吗 说出你的结论和理由:_________________________________________.3在Rt △BCD 沿射线BD 方向平移的过程中,当点B 的移动距离为______时,四边形ABC 1D 1为矩形,其理由是ABCDP图2ABCDPP′图1图4 CADB 图3 CADB图2 D 1C 1B 1CADB 图130︒30︒B DAC_____________________________________;当点B的移动距离为______时,四边形ABC1D1为菱形,其理由是_______________________________.图3、图4用于探究51.如图,在△ABC中,D为BC上一个动点D点与B、C不重合,且DE∥AC交AB•于点E,DF∥AB交AC于点F.1试探究,当AD满足什么条件时,四边形AEDF是菱形并说明理由.2在1的条件下,△ABC满足什么条件时,四边形AEDF是正方形请说明理由.52.已知:如图,在△ABC中,D是AC的中点,E是线段BC•延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.1求证:AF=CE;2若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.53.如图,P是等边三角形ABC内的一点,连结PA、PB、PC,以BP•为边作∠PBQ=60°,且BQ=BP,连结CQ.1观察并猜想AP与CQ之间的大小关系,并证明你的结论.2若PA:PB:PC=3:4:5,连结PQ,试判断△PQC的形状,并说明理由.54.在正方形ABCD中,点P是CD上一动点,连结PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足分别为E、F,如图①. 1请探索BE、DF、EF这三条线段长度具有怎样的数量关系.若点P在DC•的延长线上如图②,那么这三条线段的长度之间又具有怎样的数量关系若点P在CD•的延长线上呢如图③请分别直接写出结论;2请在1中的三个结论中选择一个加以证明.55.如图,分别以Rt ABC ∆的直角边AC,BC 为边,在Rt ABC ∆外作两个等边三角形ACE ∆和BCF ∆,连结BE,AF.求证:BE=AF.56,填空或解答:点B 、C 、E 在同一直线上,点A 、D 在直线CE 的同侧,AB =AC ,EC =ED ,∠BAC =∠CED ,直线AE 、BD 交于点F ;1如图①,若∠BAC =60°,则∠AFB =_________;如图②,若∠BAC =90°,则∠AFB =_________;2如图③,若∠BAC =α,则∠AFB =_________用含α的式子表示;3将图③中的△ABC 绕点C 旋转点F 不与点A 、B 重合,得图④或图⑤;在图④中,∠AFB 与∠α的数量关系是________________;在图⑤中,∠AFB 与∠α的数量关系是________________;请你任选其中一个结论证明;57、如图,正方形ABCD 绕点A 逆时针旋转n 后得到正方形AEFG ,边EF 与CD 交于点O .1以图中已标有字母的点为端点连结两条线段正方形的对角线除外,要求所连结的两条线段相交且互相垂直.......,并说明这两条线段互相垂直的理由;B C EE F A A A B B B CC C DD DE E EF FF 图①图② 图③A AB B CCDD E EFF 图④ 图⑤2若正方形的边长为2cm,重叠部分四边形AEOD 的面积为243cm 3,求旋转的角度n .58、四边形ABCD 、DEFG 都是正方形,连接AE 、CG .1求证:AE =CG ;2观察图形,猜想AE 与CG 之间的位置关系,并证明你的猜想.59、已知:如图,在△ABC 中,AB =AC ,AD ⊥BC ,垂足为点D ,AN 是△ABC 外角∠CAM 的平分线,CE ⊥AN ,垂足为点E , 1求证:四边形ADCE 为矩形;2当△ABC 满足什么条件时,四边形ADCE 是一个正方形 并给出证明.60、将平行四边形纸片ABCD 按如图方式折叠,使点C 与A 重合,点D 落到D ′ 处,折痕为EF .1求证:△ABE ≌△AD ′F ;2连接CF,判断四边形AECF 是什么特殊四边形 证明你的结论.G D O FEA A MNE61、如图1,已知P 为正方形ABCD 的对角线AC 上一点不与A 、C 重合,PE ⊥BC 于点E ,PF ⊥CD 于点F . 1 求证:BP =DP ;2 如图2,若四边形PECF 绕点C 按逆时针方向旋转,在旋转过程中是否总有BP =DP 若是,请给予证明;若不是,请用反例加以说明;3 试选取正方形ABCD 的两个顶点,分别与四边形PECF 的两个顶点连结,使得到的两条线段在四边形PECF 绕点C 按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .A B C D E F D 12 3 4 5 6A B C D E F D ′2 1。
2020上海市八年级数学第二学期期末压轴题一(原卷版)
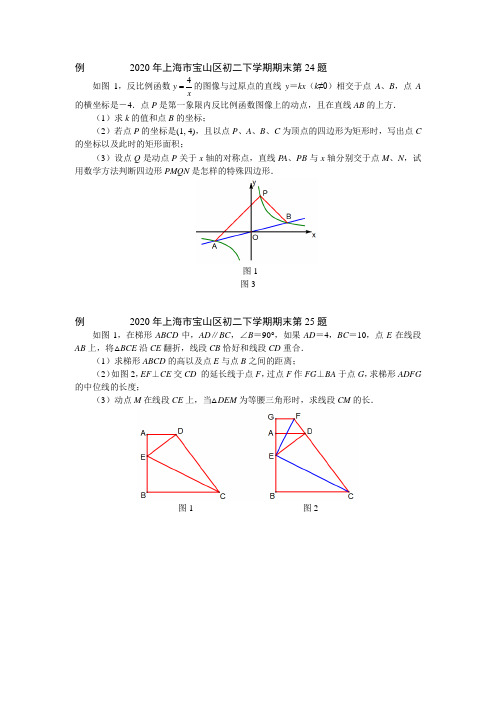
如图1,反比例函数4yx的图像与过原点的直线y=kx(k≠0)相交于点A、B,点A的横坐标是-4.点P是第一象限内反比例函数图像上的动点,且在直线AB的上方.(1)求k的值和点B的坐标;(2)若点P的坐标是(1, 4),且以点P、A、B、C为顶点的四边形为矩形时,写出点C 的坐标以及此时的矩形面积;(3)设点Q是动点P关于x轴的对称点,直线P A、PB与x轴分别交于点M、N,试用数学方法判断四边形PMQN是怎样的特殊四边形.图1图3例2020年上海市宝山区初二下学期期末第25题如图1,在梯形ABCD中,AD∥BC,∠B=90°,如果AD=4,BC=10,点E在线段AB上,将△BCE沿CE翻折,线段CB恰好和线段CD重合.(1)求梯形ABCD的高以及点E与点B之间的距离;(2)如图2,EF⊥CE交CD的延长线于点F,过点F作FG⊥BA于点G,求梯形ADFG 的中位线的长度;(3)动点M在线段CE上,当△DEM为等腰三角形时,求线段CM的长.图1 图2如图1,在平面直角坐标系中,已知点A(2, 0)、B(0, 4),点C为线段AB的中点,点D 为x轴上的动点.(1)求直线AB的函数表达式;(2)当直线CD与直线AB互相垂直时,求点D的坐标;(3)以A、C、D三点为顶点的三角形能否成为等腰三角形?若能,请直接写出D点的坐标;若不能,请说明理由.图1例2020年上海崇明区初二下学期期末第25题如图1,在矩形ABCD中,AB=6,BC=8,点P为边AD上一动点,把△ABP沿BP翻折后得到△EBP.(1)当点E恰好落在矩形对角线BD上时,求线段AP的长;(2)当直线PE与边BC相交于点F时,△FBP是否一定是等腰三角形?请给出你的结论,并证明你的结论;(3)当直线PE与边BC相交于点F,且点E在线段PF上时,设AP=x,BF=y,求y 关于x的函数解析式,并写出函数定义域.图1 备用图例2020年上海市奉贤区初二下学期期末第25题如图1,在平面直角坐标系xOy中,直线y=-3x+15交x轴于点A,交y轴于点B,点C在直线AB上,点D与点C关于原点对称,联结AD,过点C作CE∥AD交x轴于点E.(1)求点A、B坐标;(2)当点C的横坐标为2时,求点E坐标;(3)过点B作BF∥AD交直线DE于点F,如果四边形ABFD是矩形,求点C的坐标.例2020年上海市奉贤区初二下学期期末第26题如图1,四边形ABCD中,AD∥BC,∠A=90°,AD=4,DC=5,过点C作CE∥BD 交AD延长线于点E,联结BE交CD于点F.(1)当AB=AD时,求BC的长;(2)设BC=x,四边形BCED的面积为y,求y关于x的函数关系式,并写出定义域;(3)当△BDF为直角三角形时,求BC的长.图1例2020年上海市虹口区初二下学期期末第24题如图1,一次函数y=2x+4的图像与x、y轴分别相交于点A、B,以AB为边作正方形ABCD,点C、D在直线AB的下方.(1)求点A、B、C的坐标;(2)求直线CD的表达式;(3)设直线CD与x轴交于点E,点F为直角坐标平面xOy内一点,当四边形AECF 为等腰梯形时,请直接写出所有符合条件的点F的坐标.图1例2020年上海市虹口区初二下学期期末第25题如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=4,点D是射线CB上一点(点D与点C不重合),以AD为边作等边△ADE,且点E与点C在直线AD的异侧,过点E作EF⊥AB于点F.(1)求证:△ACD≌△AFE;(2)联结BE,设CD=x,BE=y,当点D在线段CB上时,求y关于x的函数关系式,并写出定义域;(3)当△ADB为等腰三角形时,求△ADB的面积.图1 备用图。
上海八年级数学第二学期压轴题集锦二(含答案)

(2015,黄埔)25.(本题满分8分)已知:直线1l 经过点()5,6A --且与直线2l :362y x =-+平行,直线2l 与x 轴、y 轴分别交于点B 、C .(1)求直线1l 的表达式及其与x 轴的交点D 的坐标;(2)判断四边形ABCD 是什么四边形?并证明你的结论;(3)若点E 是直线AB 上一点,平面内存在一点F ,使得四边形CBEF 是正方形,求点E 的坐标,请直接写出答案.O yx (第25题图)26.(本题满分10分)如图,已知梯形ABCD 中,AB ∥CD ,90C ∠=︒, AE ⊥CD ,点F 是射线BC 上一点,FG ⊥AD ,垂足为点G ,FG 交线段AE 于点H ,AB =12,CD =17,AD =13. (1)求梯形ABCD 的面积;(2)当点F 在线段BC 上时,设CF =x ,AH =y ,求y 关于x 的函数关系式及自变量x 的取值范围; (3)若BHF ∆是以BH 为腰的等腰三角形,请直接写出AH 的长.A B C E D F GH(第26题图)(2015静安)26.(本题满分8分,每小题4分)如图,在平面直角坐标系xOy 中,一次函数的图像与反比例函数的图像相交于点A 、B ,点A 的坐标为(2,3),点B 的横坐标为6.(1) 求反比例函数与一次函数的解析式;(2) 如果点C 、D 分别在x 轴、y 轴上,四边形ABCD 是平行四边形.求直线CD 的表达式. ABxy O(第26题图)27.(本题满分10分,每小题5分)如图,正方形ABCD 的边长为6,点E 、F 分别在边AD 、CD 上,∠FEB =∠EBC ,AB =6,EF 、BC 的延长线相交于点G ,设y BG x AE ==,.(1)求y 与x 之间函数解析式,并写定义域; (2)当点F 为CD 中点时,求AE 的长. (第27题图)ABCDEFG(2015嘉定)27.已知在△ABC 中,AB=AC=5,BC=8,射线AD 是∠BAC 的平分线交BC 于点D ,点E 是线段DC 上的一点,且EC ∶DE=1∶3.(1)如图4:求DE 的长;(2)如图4:点P 是线段AD 上一动点,联结PE ,设AP=x ,△PDE 的面积为y ,求y 与x 的函数关系式,并写出它的定义域; (3)若点P 是射线AD 上一动点,如果△ABC 面积等于△PDE 面积的3倍,求AP 的长. AB CDE备用图ABCD E图4P答案解析(2015黄埔)25.解:(1)设32y x b =-+,∵直线1l 经过点()5,6A --, ∴()3562b -⨯-+=-,∴272b =-,∴32722y x =--,…………………………………(1分) 当0y =时,327022x --=,9x =-,∴()9,0D -.………………………………………(1分) (2)方法一:四边形ABCD 是矩形. ………………………………………………………………………(1分)∵()5,6A --,()9,0D -,∴AD∵(4,0)B ,()0,6C ,∴BC =∴AD BC =,…………………………………………………………………………………(1分) 又∵AD ∥BC ,∴四边形ABCD 是平行四边形,……………………………………………(1分)∵4(9)13BD =--=,13AC =,∴BD =AC ,∴平行四边形ABCD 是矩形. ………………………………………………………………(1分) 方法二:四边形ABCD 是矩形. ………………………………………………………………………(1分) 过点A 作AH ⊥DB ,垂足为点H .∵∠BOC =∠DAH =90°,BO =DH =4,CO =AH =6,∴△COB ≌△AHD ,∴BC =AD ,…(1分) 又1l ∥2l ,∴四边形ABCD 是平行四边形,………………………………………………(1分)∵13AC =,()4913BD =--=,∴AC =BD ,∴平行四边形ABCD 是矩形. ………………………………………………………………(1分) (其他方法,参照上述评分标准酌情给分)(3)()12,4E --,()210,4E .………………………………………………………………(2分) 26.(1)解:∵AE ⊥CD ,∴∠AED =90°,又∠C =90°,∴∠AED =∠C =90°,∴AE ∥CB , 又AB ∥CD ,∴四边形AECB 是平行四边形,∴AB =EC ,∵AB =12,DC =17,∴EC =12,DE =5.…………………………………………(1分)∵AD =13,∠AED =90°,∴AE ,…………………………………………(1分) ∴()1=12+1712=1742ABCD S ⨯梯形.……………………………………………………………(1分) (2)过点C 作CM ∥FH ,交AE 于点M .…………………………………………………(1分) ∵AE ∥BC ,∴四边形HMCF 是平行四边形,∴FC =HM =x ,∵CM ∥FH ,∴∠FHE =∠CME , 又∠FHE =∠AHG ,∴∠CME =∠AHG ,∵FG ⊥AD ,∴∠AHG +∠GAH =90°,∵AE ⊥CD ,∴∠CME +∠ECM =90°,∴∠GAH =∠ECM .又∠AED =∠MEC =90°,EC =AE ,∴△AED ≌△MEC ,…………………………………(1分) ∴ME =DE =5,∴y +x =12-5,∴7(07)y x x =-≤≤.………………………………………(2分) (3)当BH =HF 时,AH =5,…………………………………………………………………(1分)(2015静安)26.解:(1)设反比例函数与一次函数的解析式分别为x ky =,b ax y +=.……………(1分) ∴23k=,6=k ,∴反比例函数解析式为x y 6=.……………………………(1分)∴B (6,1),∴⎩⎨⎧+=+=,23,61b a b a ……………………………………………………(1分)∴⎪⎩⎪⎨⎧=-=,4,21b a ∴一次函数的解析式为421+-=x y .…………………………(1分)(2)∵在□ABCD 中,CD //AB ,∴设直线CD 表达式为m x y +-=21,………………(1分)∴直线CD 与x 轴交点C (2m ,0),与y 轴交点D (0,m ).……………………(1分) ∵CD=AB ,∴22AB CD =,∴2222)31()26()0()20(-+-=-+-m m ,…………………………………………(1分) ∴2±=m (负值舍去).∴直线CD 的表达式221+-=x y .………………………(1分)27.解:(1)过点E 作EH ⊥BC ,垂足为H ,…………………………………………………(1分)∵四边形ABCD 是正方形,∴AH //BC ,BH //AB , ∴EH =AB =6,BH =AE =x ,GH = y –x ,∵∠FEB =∠EBC ,∴ EG=BG=y .………………………………………………(1分) ∵,222EH GH EG +=∴2226)(+-=x y y . …………………………………(1分)∴y 与x 之间函数解析式为xx y 2362+=,………………………………………(1分)定义域为60<<x .……………………………………………………………(1分) (2)∵AD //BC ,∴∠D =∠FCG ,又∵∠DFE =∠CFG ,DF =CF ,∴△DFE ≌CFG ,………………………………(1分)∴CG =DE =AD –AE = 6–x , ………………………………………………………(1分) ∴BG = BC +CG = 6+6–x = 12–x .∴xx x 236122+=-, ………………………………………………………………(1分)经检验,21=x ,62=x 都是方程的根,但6=x 不符合题意.∴AE 的长为2.……………………………………………………………………(1分)(2015嘉定) 27. 解:(1)∵AB=AC ,AD 平分∠BAC∴AD ⊥BC ,BD=DC=BC 21…………1分 ∵BC=8 ∴DC=4 ……………………1分 ∵EC ∶DE=1∶3 ∴DE=3……………1分(2)由(1)得△ADC 是直角三角形,得:222AC DC AD =+ 又DC=4,AC=5,∴AD=3,……1分 ∵AP=x ,∴PD=x -3∴)3(32121x PD DE y -⨯=⨯⨯= 即:2923+-=x y ……1分, 定义域为:30<≤x ……1分 (3)由(2)可得:AD=3,∴123821=⨯⨯=∆ABC S ,1分又△ABC 面积等于△PDE 面积的3倍当点P 在线段AD 上,得:12)3(3213=-⨯⨯x ,解得:31=x ……1分 当点P 在线段AD 延长线上,得:12)3(3213=-⨯⨯x ,解得:317=x ……1分所以AP 的长为31,317.……………………2分。
沪教版数学八年级的第二学期期末压轴题(答案)

1、已知:在矩形ABCD中, AB=10, BC=12,四边形 EFGH的三个极点E、F、H分别在矩形 ABCD边 AB、BC、DA上, AE=2.(1)如图①,当四边形EFGH为正方形时,求(2)如图②,当四边形EFGH为菱形,且BF 示);( 5 分)A H DEGB FC △GFC的面积;(5分)=a 时,求△GFC的面积(用含 a 的代数式表HA DEGB F C2、如图,直线y3x 4 3 与 x 轴订交于点 A ,与直线y3x 订交于点P.(1)求点 P的坐标.(2)请判断△ OPA 的形状并说明原因.(3)动点 E 从原点 O 出发,以每秒 1 个单位的速度沿着O P A 的路线向点 A 匀速运动( E 不与点O、 A 重合),过点 E 分别作EF x 轴于F,EB y 轴于 B .设运动t秒时,矩形 EBOF 与△ OPA 重叠部分的面积为S .求 S 与 t 之间的函数关系式.yyBPP EO F A xO A(备用图)x3、已知直角坐标平面上点A 2,0,P 是函数y x x 0 图像上一点,PQ⊥AP交y轴正半轴于点 Q(如图).(1)试证明:AP=PQ;(2)设点P的横坐标为a,点Q的纵坐标为b,那么b对于a的函数关系式是 _______;2S APQ 时,求点P的坐标.y(3)当 SAOQy=x 3PQO A x4、(此题满分10 分,第( 1)小题 6 分,第( 2)小题 4 分)已知点 E 是正方形 ABCD外的一点, EA=ED,线段 BE与对角线 AC订交于点 F,(1)如图 1,当BF=EF时,线段AF与 DE之间有如何的数目关系并证明;(2)如图 2,当△EAD为等边三角形时,写出线段AF、BF、 EF之间的一个数目关系,并证明.EEA DA DF FB C B C图 1 图 25、(此题满分 10 分,第( 1)小题 3 分,第( 2)小题 3 分 ,第(3)小题4分)如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA, OC=AB=4, BC=6,∠COA=45° , 动点P 从点O出发,在梯形OABC的边上运动,路径为O→ A→ B→ C,抵达点 C 时停止.作直线CP.(1)求梯形OABC的面积;(2)当直线CP把梯形OABC的面积分红相等的两部分时,求直线CP的分析式;(3)当 ?OCP是等腰三角形时,请写出点P 的坐标(不要求过程,只要写出结果)yC BO P A x6、如图已知一次函数y =- +7 与正比率函数y =4x 的图象交于点,且与 x 轴交于点 .x3AB(1)求点 A 和点 B 的坐标;(2)过点 A 作 AC ⊥ y 轴于点 C ,过点 B 作直线 l ∥ y 轴.动点 P 从点 O 出发,以每秒 1 个单位长的速度,沿 O ﹣ C ﹣A 的路线向点 A 运动;同时直线 l 从点 B 出发,以同样速度向左平移,在平移过程中,直线 l 交 x 轴于点 ,交线段 BA 或线段 于点 .当点 P 抵达点 A 时,点R AO QP 和直线 l 都停止运动.在运动过程中,设动点 P 运动的时间为 t 秒 (t0) .①当 t 为什么值时,以 A 、P 、 R 为极点的三角形的面积为 8②能否存在以 A 、P 、Q 为极点的三角形是 QA=QP 的等腰三角形若存在, 求 t 的值;若不存在,请说明原因.7、已知边长为 1 的正方形中,P 是对角线上的一个动点(与点 A 、 C 不重合),ABCDAC过点 P 作 PE ⊥ PB ,PE 交射线 DC 于点 E ,过点 E 作 EF ⊥AC ,垂足为点 F .(1)当点 E 落在线段 CD 上时(如图 10),① 求证: PB=PE ;② 在点 P 的运动过程中, PF 的长度能否发生变化若不变,试求出这个不变的值,若变化,试说明原因;(2)当点 E 落在线段 DC 的延伸线上时,在备用图上画出切合要求的大概图形,并判断上述( 1)中的结论能否仍旧成立(只要写出结论,不需要证明);( 3)在点 P 的运动过程中,⊿ PEC 可否为等腰三角形假如能,试求出AP 的长,假如不可以,试说明原因.ADA DP。
沪教版(五四制)八年级数学下册 压轴题复习

一、 因动点产生的相似三角形问题例1如图1,将抛物线2y x =-平移,平移后的抛物线与x 轴交于点A (1-,0)和B (3,0),与y 轴交于点C ,顶点为D 。
(1)求平移后的抛物线的表达式和点D 的坐标; (2)∠ACB 和∠ABD 是否相等?请证明你的结论;(3)点P 在平移后的抛物线的对称轴上,且△CDP 与△ABC 相似,求点P 的坐标。
图1第十五讲 压轴题复习如图1,在平面直角坐标系xOy 中,顶点为M 的抛物线2(0y ax bx a =+>)经过点A 和x 轴正半轴上的点B ,AO OB == 2,0120AOB ∠=.(1)求这条抛物线的表达式; (2)联结OM ,求AOM ∠的大小;(3)如果点C 在x 轴上,且△ABC 与△AOM 相似,求点C 的坐标.图1在平面直角坐标系中,一个二次函数的图象经过(1,0)(3,0)、两点。
A B(1)写出这个二次函数图象的对称轴;(2)设这个二次函数图象的顶点为D,与y轴交于点C,它的对称轴与x轴交于点E,连接AC、DE和DB,当AOC∆相似时,求这个二次函数的表达式。
∆与DEB例4如图1,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.图1例5如图1,已知点A (2,0),点B 在y 轴正半轴上,且OA OB 21=.将点B 绕点A 顺时针方向旋转 90至点C .旋转前后的点B 和点C 都在抛物线c bx x y ++-=265上.(1)求点B 、C 的坐标; (2)求该抛物线的表达式;(3)联结AC ,该抛物线上是否存在异于点B 的点D ,使点D 与AC 构成以AC 为直角边的等腰直角三角形?如果存在,求出所有符合条件的D 点坐标,如果不存在,请说明理由.图1例6如图1,在平面直角坐标系xOy 中,A 、B 为x 轴上两点,C 、D 为y 轴上的两点,经过 点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C 的坐标为(0,23-),点M 是抛物线C 2:m mx mx y 322--=(m <0)的顶点. (1)求A 、B 两点的坐标; (2)“蛋线”在第四象限上是否存在一点P ,使得△PBC 的面积最大?若存在,求出△PBC 面积的最大值;若不存在,请说明理由;(3)当△BDM 为直角三角形时,求m 的值.图1四、因动点产生的平行四边形问题例7如图1,抛物线254y x bx c =-++与y 轴交于点A (0,1),过点A 的直线与抛物线交于另一点B 5(3,)2,过点B 作BC x ⊥轴,垂足为C .(1)求抛物线的表达式;(2)点P 是x 轴正半轴上的一动点,过点P 作PN x ⊥轴,交直线AB 于点M ,交抛物线于点N ,设OP 的长度为m .①当点P 在线段OC 上(不与点O 、C 重合)时,试用含m 的代数式表示线段PM 的长度;②联结,CM BN ,当m 为何值时,四边形BCMN 为平行四边形?如图1,点A (2,6)和点B (点B 在点A 的右侧)在反比例函数的图像上,点C 在y 轴上,BC //x 轴,2tan =∠ACB ,二次函数的图像经过A 、B 、C 三点. (1)求反比例函数和二次函数的解析式;(2)如果点D 在x 轴的正半轴上,点E 在反比例函数的图像上,四边形ACDE 是平行四边形,求边CD 的长.图1如图1,已知抛物线y=-x2+bx+c经过A(0, 1)、B(4, 3)两点.(1)求抛物线的解析式;(2)求tan∠ABO的值;(3)过点B作BC⊥x轴,垂足为C,在对称轴的左侧且平行于y轴的直线交线段AB于点N,交抛物线于点M,若四边形MNCB为平行四边形,求点M的坐标.图1五、因动点产生的梯形问题例10如图1,已知二次函数mx x y 22+-=的图像经过点B (1,2),与x 轴的另一个交点为A ,点B 关于抛物线对称轴的对称点为C ,过点B 作直线BM ⊥x 轴垂足为点M . (1)求二次函数的解析式; (2)在直线BM 上有点P (1,23),联结CP 和CA ,判断直线CP 与直线CA 的位置关系, 并说明理由;(3)在(2)的条件下,在坐标轴上是否存在点E ,使得以A 、C 、P 、E 为顶点的四边形为直角梯形,若存在,求出所有满足条件的点E 的坐标;若不存在,请说明理由。
最新上海初二下学期数学函数压轴题(优选.)

上海初二数学函数压轴题1. 在梯形AB CD AD 5cmABCD 中, AD ∥BC , ,BC=11cm ,点 P 从点 D 开始沿 DA 边以每秒 1cm 的速度 移动,点 Q 从点 B 开始沿 BC 边以每秒 2cm 的速度移动(当点 P 到达点 A 时 ,点 P 与点 Q 同时停止移动),2 假设点 P 移动的时间为 x (秒),四边形 ABQP 的面积为 y (cm ).(1)求 y 关于 x 的函数解析式,并写出它的定义域;(2)在移动的过程中,求四边形 ABQP 的面积与四边形 QCDP 的面积相等时 x 的值;x x (3)在移动的过程中,是否存在 使得 PQ=AB ,若存在求出所有的值,若不存在请说明理由. PADBCQ2. 如图,在正方形ABCD 中,点E 在边 AB 上(点E 与点 A 、B 不重合),过点E 作 FG ⊥DE ,FG 与边 BC相交于点 F ,与边 DA 的延长线相交于点 G .(1)由几个不同的位置,分别测量 BF 、AG 、AE 的长,从中你能发现 BF 、AG 、AE 的数量之间具有怎 样的关系?并证明你所得到的结论;x y y x (2)联结 DF ,如果正方形的边长为 2,设 AE= ,△DFG 的面积为 ,求 与 之间的函数解析式, 并写出函数的定义域;5(3)如果正方形的边长为 2,FG 的长为 ,求点 C 到直线 DE 的距离.2CCDDFBAABEG(供证明计算用)(供操作实验用)(第 2 题图)3.如图,已知在矩形ABCD中,对角线AC、BD交于点O,CE=AE,F是AE的中点,AB = 4,BC = 8.求线段OF的长.F EA DOB C(第3题图)14已知一次函数y x4的图像与x轴、y轴分别相交于点A、B.梯形AOBC的边AC = 5.2(1)求点C的坐标;(2)如果点A、C在一次函数y k x b(k、b为常数,且k<0)的图像上,求这个一次函数的解析式.yBxO A(第4题图)5.如图,直角坐标平面xoy中,点A在x轴上,点C与点E在y轴上,且E为OC中点,BC//x轴,且BE⊥AE,联结AB,(1)求证:AE平分∠BAO;(2)当OE=6,BC=4时,求直线AB的解析式.yBCE。
2020上海市八年级数学第二学期期末压轴题四(原卷版)

2020上海市八年级数学第二学期期末压轴题四例2020年上海市青浦区初二下学期期末第24题如图1,在平面直角坐标系xOy中,已知直线y=x-4分别与x轴、y轴交于点A、B,直线BC与x轴交于点C(-1, 0).点D在第四象限,BD⊥BA.(1)求直线BC的解析式;(2)当S△ABD=4S△BOC时,求点D的坐标;(3)在(2)的条件下,已知点E在x轴上,点F在直线BC上.如果以C、D、F、E为顶点的四边形是平行四边形,请直接写出线段OE的长.图1例2020年上海市青浦区初二下学期期末第25题如图1,在等腰梯形ABCD中,AD∥BC,AD=AB=23,BD⊥DC.M、N分别是AD、CD的中点,联结MN交BD于点Q,点P在线段BQ上.(1)求∠C的度数;(2)求线段DQ的长;(3)联结PM、PN.设PB=x,△PMN的面积为y,求y关于x的函数关系式.图1如图1,平行四边形ABCD的顶点A、B的坐标分别是A(-1, 0)、B(0,-2),顶点C、D 在反比例函数第一象限的图像上,边AD与y轴交于点E.(1)过点D作y轴的平行线交BC于点F,过点C作CH⊥DF,垂足为H,若点D的坐标为(a, b),求点C点坐标(用a、b表示).(2)若四边形BCDE的面积是△ABE的面积的5倍,求反比例函数的解析式.图1例2020年上海市世外初二下学期期末第25题如图1,在矩形ABCD中,AB=2,BC=5.点P是边AD上一点,联结CP,将四边形ABCP沿CP所在直线翻折,落在四边形EFCP的位置,点A、B的对应点分别为点E、F,边CF与边AD的交点为点G.(1)当AP=2时,求PG的值;(2)如果AP=x,FG=y,求y关于x的函数解析式,并写出它的定义域;(3)联结BP并延长与线段CF交于点M,当△PGM是以MG为腰的等腰三角形,求AP的长.图1 备用图如图1,已知在梯形ABCD中,AD∥BC,AD=AB,BC=2AD,点E是BC边的中点,AE、BD相交于点F.(1)求证:四边形AECD是平行四边形;(2)设边CD的中点为G,联结EG,求证:四边形FEGD是矩形.图1例2020年上海市松江区初二下学期期末第26题如图1,已知在正方形ABCD中,AB=2,点E为线段AC上一点(点E不与A、C重合),联结DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG.(1)求证:DE=EF;(2)联结CG、EG,设AE=x,△ECG的面积为y,求y关于x的函数关系式,并写出定义域;(3)设EG、CD相交于点H,如果△EDH是等腰三角形,求线段AE的长.图1 备用图例2020年上海市杨浦区初二下学期期末第25题如图1,已知在平面直角坐标系中,直线y=2x与反比例函数kyx=(k≠0)在第一象限内的图像交于点A(m, 2),将直线y=2x平移后与kyx=在第一象限内的图像交于点B,且△AOB的面积为2.(1)求k的值;(2)求平移后的直线表达式.图1已知在平行四边形ABCD中,AB≠BC,将△ABC沿直线AC翻折,点B落在点E处,AD与CE相交于点O,联结DE.(1)如图1,求证:AC//DE;(2)如图2,如果∠B=90°,AB=3,BC=6,求△OAC的面积;(3)如果∠B=30°,AB=23,当△AED是直角三角形时,求BC的长.图1 图2 备用图例2020年上海市长宁区初二下学期期末第24题如图1,△ABC和△ADE都是等边三角形,点D在BC边上,EF//BC交AC于点F,联结BE.求证:四边形BEFC为平行四边形.图1如图1,在正方形ABCD中,AB=1,E为边AB上的一点(点E不与端点A、B重合),F为BC延长线上的一点,且AE=CF,联结EF交对角线AC于点G.(1)求证:DE=DF;(2)联结DG,求证:DG⊥EF;(3)设AE=x,AG=y,求y关于x的函数解析式及定义域.图1。
上海初二下压轴题

1.已知一次函数113y x =+的图像与x 轴、y 轴分别相交于点A 、B .点C 的坐标为(2,0). (1)求直线BC 的函数解析式;(2)点D 在y 轴上,若A 、B 、C 、D 四点恰好为梯形的四个顶点,求所有满足条件的D 点坐标.2. 已知一次函数333+-=x y 的图像与x 轴、y 轴分别相交于A 、B 两点,点C 、D 分别在线段OA 、AB 上,CD=CA . (1)求A 、B 两点的坐标; (2)求OCD ∠的度数;(3)如果△CDO 的面积是△ABO 面积的41,求点C 的坐标.3.如图,一次函数的图像与x 、y 轴分别相交于点A 、B ,以AB 为边作正方形ABCD . (1)求点A 、B 、D 的坐标;(2)设点M 在x 轴上,如果△ABM 为等腰三角形,求点M 的坐标.如图,O 为坐标原点,正方形OBAC 的边长为1,M 、N 分别在AC 、AB 上,若△MON 为正三角形,求M 、N 的坐标.4.如图,在正方形ABCD 中,点P 是射线BC 上的任意一点(点B 与点C 除外),联结DP ,分别过点C 、A 作直线DP 的垂线,垂足为点E 、F .(1)当点P 在BC 的延长线上时,那么线段AF 、CE 、EF 之间有怎样的数量关系?请证明你的结论;(2)当点P 在边BC 上时,正方形的边长为2.设CE = x ,AF = y . 求y 与x 的函数解析式,并写出函数的定义域; (3)在(2)的条件下,当x = 1时,求EF 的长.24y x =+ DCBA(第4题图)EF PGFNMECB DA如图,BD 、CE 分别是△ABC 的外角平分线,过A 作AF ⊥BD ,AG ⊥CE ,垂足分别是F 、G ,连结FG ,延长AF ,AG 与直线BC 相交于M 、N 。
(1)若FG =10cm ,求MN 的长;(2)若FG =X ,△ABC 的周长为Y ,求Y 关于X 的函数关系式(不要写定义域)在等腰梯形ABCD 中,AD ∥BC ,6064=∠==B BC AB ,,,点E 、F 是AB 和CD 边上的中点,点P 是线段EF 上的一个动点,过点P 作EF PM ⊥交BC 于点M ,过M 作MN ∥AB 交折线ADC 于点N ,联结PN ,设x EP = (1)填空:PM =____________;(2)如图1,当点N 在线段AD 上时,求PMN ∆的面积;(3)如图2,当点N 在线段CD 上时,设PMN ∆的面积为y ,求y 关于x 的函数关系式,并写出定义域;(4)当点N 在线段CD 上时,是否存在点P ,使P MN ∆为等腰三角形?若存在,直接写出所有满足要求的x 的值;若不满足,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1在梯形ABCD 中, AD ∥BC ,cm AD CD AB 5===,BC =11cm ,点P 从点D 开始沿DA 边以每秒1cm 的速度移动,点Q 从点B 开始沿BC 边以每秒2cm 的速度移动(当点P 到达点A 时,点P 与点Q 同时停止移动),假设点P 移动的时间为x (秒),四边形ABQP 的面积为y (cm 2). (1)求y 关于x 的函数解析式,并写出它的定义域;(2)在移动的过程中,求四边形ABQP 的面积与四边形QCDP 的面积相等时x 的值;(3)在移动的过程中,是否存在x 使得PQ=AB ,若存在求出所有x 的值,若不存在请说明理由.2. 如图,在正方形ABCD 中,点E 在边AB 上(点E 与点A 、B 不重合),过点E 作FG ⊥DE ,FG 与边BC 相交于点F ,与边DA 的延长线相交于点G .(1) 由几个不同的位置,分别测量BF 、AG 、AE 的长,从中你能发现BF 、AG 、AE 的数量之间具有怎样的关系?并证明你所得到的结论;(2) 联结DF ,如果正方形的边长为2,设AE=x ,△DFG 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域;(3) 如果正方形的边长为2,FG 的长为25,求点C 到直线DE 的距离.CBP(供操作实验用)(供证明计算用)(第2题图)D ABB3.如图,已知在矩形ABCD 中,对角线AC 、BD 交于点O ,CE =AE ,F 是AE 的中点,AB = 4,BC = 8.求线段OF 的长.4已知一次函数421+-=x y 的图像与x 轴、y 轴分别相交于点A 、B .梯形AOBC 的边AC = 5.(1)求点C 的坐标;为常数,且(2)如果点A 、C 在一次函数y k x b =+(k 、bk <0)的图像上,求这个一次函数的解析式.5.如图,直角坐标平面xoy 中,点A 在x 轴上,点C 与点E 在y且E 为OC 中点,BC //x 轴,且BE ⊥AE ,联结AB , (1)求证:AE 平分∠BAO ;(2)当OE =6, BC=4时,求直线AB 的解析式.6.如图,△ABC 中,点D 、E 分别是边BC 、AC 的中点,过点A 作AF//BC 交线段DE 的延长线相交于F 点,取AF 的中点G ,如果BC = 2 AB . 求证:(1)四边形ABDF 是菱形;(2)AC = 2DG .AB CDOEF(第3题图)(第4题图)A BFDEG第6题图7.边长为4的正方形ABCD 中,点O 是对角线AC 的中点, P 是对角线AC 上一动点,过点P 作PF ⊥CD 于点F ,作PE ⊥PB 交直线CD 于点E ,设PA=x ,S ⊿PCE =y , ⑴ 求证:DF =EF ;(5分)⑵ 当点P 在线段AO 上时,求y 关于x 的函数关系式及自变量x 的取值范围;(3分) ⑶ 在点P 的运动过程中,⊿PEC 能否为等腰三角形?如果能够,请直接写出PA 的长;如果不能,请简单说明理由。
(2分)8.已知一条直线b kx y +=在y 轴上的截距为2,它与x 轴、y 轴的交点分别为A 、B ,且△ABO 的面积为4.(1)求点A 的坐标;(2)若0<k ,在直角坐标平面内有一点D ,使四边形ABOD 是一个梯形,且AD ∥BO ,其面积又等于20(平方单位),试求点D 的坐标.第26题图D CB AEFP。
ODCBA 备用图O 。
9.在边长为2的正方形ABCD中,对角线AC与BD相交于点O,另一个正方形OHIG绕点O旋转(如图),设OH与边BC交于点E(与点B、C不重合),OG与边CD交于点F.(1)求证:BE=CF;(2)在旋转过程中,四边形OECF的面积是否会变化?若没有变化,求它的面积;若有变化,请简要说明理由;(3)联结EF交对角线AC于点K,当△OEK是等腰三角形时,求∠DOF的度数.10 如图,已知矩形ABCD,过点C作∠A的角平分线AM的垂线,垂足为M,AM交BC于E,连接MB、MD.求证:MB = MD.11.如图,在菱形ABCD中,∠A = 60°,AB = 4,E是AB边上的一动点,过点E作EF⊥AB交AD的延长线于点F,交BD于点M、DC于点N.(1)请判断△DMF的形状,并说明理由;(2)设EB = x,△DMF的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当x取何值时,S△DMF = 3 .12.如图1,在ABC 中,AB = BC = 5,AC = 6,△ECD 是△ABC 沿BC 方向平移得到的,连接AE 、AC 和BE相交于点O .(1)判断四边形ABCE 是怎样的四边形,说明理由.(2)如图2,P 是线段BC 上的一动点(图2),(点P 不与B 、C 重合),连PO 并延长交线段AE 于点Q ,QR⊥BD ,垂足为R .① 四边形PQED 的面积是否随点P 的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED 的面积.② 当P 在线段BC 上运动时,是否有△PQR 与△BOC 全等?若全等,求BP 的长;若不全等,请叙述理由.13,已知:如图,在菱形ABCD 中,AB =4,∠B =60°,点P 是射线BC 上的一个动点,∠PAQ =60°,交射线CD 于点Q ,设点P 到点B 的距离为x ,PQ =y . (1)求证:△APQ 是等边三角形;(2)求y 关于x 的函数解析式,并写出它的定义域; (3)如果PD ⊥AQ ,求BP 的值.14.如图,已知点E 是矩形ABCD 的边CB 延长线上一点,且CE CA =,联结AE ,过点C 作CF AE ⊥,垂足为点F ,联结BF 、FD .(1)求证:FBC ∆≌FAD ∆;(2)联结BD ,若35FB BD =,且10AC =,求FC 的值.图1 备用图 图2 D FEDCBA15,A B ,两地盛产柑桔,A 地有柑桔200吨,B 地有柑桔300吨.现将这些柑桔运到C 、D 两个冷藏仓库,已知C 仓库可储存240吨,D 仓库可储存260吨;从A 地运往C 、D 两处的费用分别为每吨20元和25元,从B 地运往C 、D 两处的费用分别为每吨15元和18元.设从A 地运往C 仓库的柑桔重量为x 吨,A 、B 两地运往两仓库的柑桔运输费用分别为A y 元和B y 元.(1)请填写下表后分别求出A B y y ,与x 之间的函数关系式,并写出定义域; 解:(2)试讨论A B ,两地中,哪个运费较少; 解:16.,已知:正方形ABCD 的边长为28厘米,对角线AC 上的两个动点E F ,,点E 从点A 、点F 从点C 同时出发,沿对角线以1厘米/秒的相同速度运动,过E 作EH ⊥AC 交Rt ACD △的直角边于H ;过F 作FG ⊥AC 交Rt ACD △的直角边于G ,连接HG ,EB .设HE ,EF ,FG ,GH 围成的图形面积为1S ,AE ,EB ,BA 围成的图形面积为2S (这里规定:线段的面积为0).E 到达C F ,到达A 停止.若E 的运动时间为x 秒,解答下列问题:(1)如图①,判断四边形EFGH 是什么四边形,并证明; (2)当08x <<时,求x 为何值时,12S S =;(3)若y 是1S 与2S 的和,试用x 的代数式表示y .(图②为备用图) (1)解:图①17,如图,在平面直角坐标系中,直线l 经过点)3,2(-A , 与x 轴交于点B ,且与直线383-=x y 平行。
(1) 求:直线l 的函数解析式及点B 的坐标;(2) 如直线l 上有一点)6,(-a M ,过点M 作x 轴的垂线,交直线383-=x y 于点N ,在线段MN 上求一点P ,使PAB ∆是直角三角形,请求出点P 的坐标。
:18, 在梯形ABCD 中,AD ∥BC ,∠B = 90,∠C =45º,AB =8,BC =14,点E 、F 分别在边AB 、CD 上,EF //AD ,点P 与AD 在直线EF 的两侧,∠EPF =90º,PE =PF ,射线EP 、FP 与边BC 分别相交于点M 、N ,设AE =x ,MN =y . (1) 求边AD 的长;(2) 如图,当点P 在梯形ABCD 内部时,求y 关于x 的函数解析式,并写出定义域;(3) 如果MN 的长为2,求梯形AEFD 的面积.19, 如图,在△ABC 中,点D 是边BC 的中点,点E 在△ABC(第18题)BDA CEFN MPA内,AE 平分∠BAC ,CE ⊥AE ,点F 在边AB 上,EF //BC . (1)求证:四边形BDEF 是平行四边形;(2)线段BF 、AB 、AC 的数量之间具有怎样的关系?证明你所得到的结论.20, 如图,一次函数42+=x y 的图像与x 、y 轴分别相交于点A 、B ,四边形ABCD 是正方形.(1)求点A 、B 、D 的坐标; (2)求直线BD 的表达式.21, 有两个不透明的布袋,其中一个布袋中有一个红球和两个白球,另一个布袋中有一个红球和三个白球,它们除了颜色外其他都相同.在两个布袋中分别摸出一个球, (1) 用树形图或列表法展现可能出现的所有结果; (2) 求摸到一个红球和一个白球的概率.22,已知:梯形ABCD 中,AD ∥BC ,M 、N 分别是BD 、AC 的中点(如图2).求证:(1)MN ∥BC ;(2))(21AD BC MN -=.ABCDM N图223,已知:正方形ABCD ,以A 为旋转中心,旋转AD 至AP ,联结BP 、DP . (1)若将AD 顺时针旋转︒30至AP ,如图3所示,求BPD ∠的度数.(2)若将AD 顺时针旋转α度)900(︒<<︒α至AP ,求BPD ∠的度数. (3)若将AD 逆时针旋转α度)1800(︒<<︒α至AP ,请分别求出︒<<︒900α、︒=90α、︒<<︒18090α三种情况下的BPD∠的度数(图4、图5、图6).解:24,25、某公路上一段道路的维修工程准备对外招标,现有甲、已两个工程队前来竟标,竟标资料显示:若由甲乙两队合作6天可以完成,共需工程费7800元,若单独完成此项工程甲队比乙队少用5天,但甲队每天的工程费比乙队多300元。
A B CDP图3ABCDPM图4ACDPB图5 ABCDP图6(1)甲、乙两队单独完成各需多少天?(2)从节约资金的角度上考虑,应选哪个队单独完成?并说明理由26.如图,在△ABC 中,E 是AB 的中点,CD 平分∠ACAB,AD ⊥CD 于带点D.求证:(1)DE=BC;(2)DE=21(BC-AC).27.如图,在等腰梯形ABCD 中,AD ∥BC,AB=DC,点P 为BC 边上一点,PE ⊥AB,BG ⊥CD,垂足分别为E,F,G. 求证:PE+PF=BG28.如图,等腰梯形ABCD 中, AD ∥BC,M,N 分别是AD,BC 的中点,E,F 分别是BM,CM 的中点.(1)求证:四边形MENF 是菱形;(2)若四边形MENF 是正方形,请探索等腰梯形ABCD 的高和底边BC 的数量关系,并证明你的结论.29,.已知如图,在△ABC 中∠ACB=90°,AD平分∠CAB 交BC 于D, CH ⊥AB 于H 交AD 于F,DE ⊥AB 于E.求证:四边形CDEF 为菱形.CBCD EAA B PECFG DE F B N C A D M30.如图.点P 是等腰直角三角形ABC 底边BC 上的一点,过P 作BA,AC 的垂线,垂足为E,F 设D 为BC 的中点.(1)求证:DE ⊥DF;(2)若点P 在BC 的延长线上是DE ⊥DF 吗?试证明你的结论.31,.如图,CD 为Rt △ABC 斜边AB 上的高,AE 平分∠BAC 交C,D 于E, EF ∥AB,交AB 于点F,求证:CE=BF.32.如图, Rt △ABC 中∠ACB=90°,CD ⊥AB 于D,AE 平分∠BAC 交CD 于F,过F 作FH ∥AB 交BC 于H.求证:CE=BH.33.如图,梯形ABCD 中AD ∥BC,AB=AD=DC,点E 为底边BC 的中点,且DE ∥AB,试判断△ABC 的形状,并 给出证明.34.如图,已知□ABCD 中,E 为AD 的中点,CE 的延长线交BA 的延长线于点F.(1)求证:CD=FA;(2)若使∠F=∠BCF, □ABCD 边长之间还需要再添加一个什么条件?请补上这个条件,并进行证明.(不再添辅助线).B D P CA E F C A DB F E CAD B H F EB E CD A C35.如图所示,已知矩形ABCD 的对角线AC,BD 相交于点O,E 为BC 上一动点(点E 不与B,C 两点重合), EF ∥BD 交AC 于点F,EC ∥AC 交BD 于点G. 求证:四边形EFOG 的周长等于2OB.36,.已知一个六边形的六个内角都是120°,其连续四边的长依次是1cm,9cm,9cm,5cm,那么这个六边形的周长是多少厘米?37,.矩形ABCD 中,O 是AC 与BD 的交点,过O 点的直线EF 与AB,CD 的延长线分别交于E,F; (1)求证:△BOE ≌△DOF;(2)当EF 与AC 满足什么条件时,四边形AECF 是棱形,并证明你的结论?BC M N AD O1cm 9cm9cm 5cm38,.等腰梯形ABCD 中,AD ∥BC,M,N 分别是AD,BC 的中点,E,F 分别是BM,CM 的中点. 求证: (1)四边形MENF 是棱形;(2)若四边形MENF 是正方形,请探索等腰梯形ABCD 的高和底边BC 的数量关系,并证明你的结论?39,.如图在△ABC 中,AB=AC,若将△ABC 绕点C 顺时针旋转180°得到△FEC.(1) 试猜想AE 与BF 有何关系?说明理由;(2) 若△ABC 的面积为23cm ,求四边形ABFE 的面积; (3) 当∠ACB 为多少度时,四边形ABFE 为矩形?说明理由?40. 如图:棱形ABCD 中,AB=4,E 为BC 中点,AE ⊥BC,AF ⊥CD 于点F,CG ∥AE,CG 交AF 于点H,交AD 于点G.(1)求棱形ABCD 的度数.(2)求∠GHA 的度数.41,.已知:如图,正方形ABCD 中,M 是AB 的中点,E 是AB 延长线上一点,MN ⊥DM 且交∠CBE 的平分线于N. (1)求证:MD=MN;(2)若将上述条件中“M 是AB 中点”改为“M 是AB 上任意一点”,其余条件不变(如图乙),则结论“MD=MN ”还成立吗?如果成立,请证明;如果不成立,请说明理由.C F E BD A N MFE C B AC FDE B A GH42. 如图:∠MON=90°,在∠MON 的内部有一个正方形AOCD,点A,C 分别在射线OM,ON 上,点1B 是ON 上的任意一点,在∠MON 的内部作正方形D C AB 11.(1) 连接D D 1,求证:901=∠ADD ;(2) 连接C C 1,猜一猜, CN C 1∠的度数是多少?并证明你的结论;(3) 在ON 上再任取一点2B ,以2AB 为边,在∠MON 的内部作正方形D C AB 22,观察图形,并结合(1),(2)的结论,请你再做出一个合理的判断.43. 已知:如图,在□ABCD 中,E,F 分别为边AB,CD 的中点,BD 是对角线,AG ∥DB 交CB 的延长线于G.(1)求证: △ADE ≌△CBF;(2)若四边形BEDF 是棱形,则四边形AGBD 是什么特殊四边形?并证明你的结论.44.已知:如图, □ABCD 中,AB ⊥AC,AB=1,BC=5,对角线AC,BD 交于点0,将直线AC 绕0顺时针旋转,分别交BC,AD 于点E,F.(1) 证明:当旋转角为90时,四边形ABEF 是平行四边形; (2) 试说明在旋转过程中,线段AF 与EC 总保持相等;(3)试说明在旋转过程中,四边形BEDF 可能是菱形吗?如果不能,请说明理由;如果能,说明理由.并求出此时AC 绕点O 顺时针旋转的度数.AC 交BD 于点O ,四边形AODE 是平行四边形。
