(完整版)三垂直模型与全等综合剖析

合集下载

初中几何模型：三垂直全等模型分析

三垂直全等模型“三垂直模型”是初中必会的一种几何模型，它是一个应用非常广泛的模型，它可以应用在三角形，矩形，平面直角坐标系，网格，一次函数，反比例函数，三角函数，二次函数以及圆等诸多的中考重要考点之中，所以这一知识点的掌握对于中考至关重要。

模型三垂直全等模型如图：∠D＝∠BCA＝∠E＝90°，BC＝AC.结论：Rt△BCD≌Rt△CAE.模型分析说到三垂直模型，不得不说一下弦图，弦图的运用在初中直角三角形中占有举足轻重的地位，很多利用垂直求角，勾股定理求边长，相似求边长都会用到从弦图支离出来的一部分几何图形去求解.图①和图②就是我们经常会见到的两种弦图。

图①图②三垂直图形变形如下图③、图④，这也是由弦图演变而来的。

图③图④DEABC例1如图，AB⊥BC，CD⊥BC，AE⊥DE，AE＝DE，求证：AB＋CD＝BC.D证明：∵AE⊥DE，AB⊥BC，DC⊥BC，A∴∠AED ＝∠B ＝∠C ＝90°.∴∠A ＋∠AEB ＝∠AEB ＋∠CED ＝90°.∴∠BAE ＝∠CED .在△ABE 和△ECD 中，B C A CED AE ED ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△ECD .∴AB ＝EC ，BE ＝CD .∴AB ＋CD ＝EC ＋BE ＝BC.例2 如图，∠ACB ＝90°，AC ＝BC ，BE ⊥CE ，AD ⊥CE 于D ，AD ＝2.5cm ，BE ＝0.8cm ，则DE 的长为多少？ EDA解答：∵BE ⊥CE ，AD ⊥CE ，∴∠E ＝∠ADC ＝90°.∴∠EBC ＋∠BCE ＝90°.∵∠BCE ＋∠ACD ＝90°，∴∠EBC ＝∠DCA .在△CEB 和△ADC 中，E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△CEB ≌△ADC .∴BE ＝DC ＝0.8cm ，CE ＝AD ＝2.5cm .∴DE ＝CE －CD ＝2.5－0.8＝1.7cm .例3 如图，在平面直角坐标系中，等腰Rt △ABC 有两个顶点在坐标轴上，求第三个顶点的坐标。

三角形全等中的三垂直模型

“三垂直”模型知识目标模块一三垂直基本模型知识导航一、三垂直模型的构成等腰直角△ABC过直角顶点A的直线l过两底角顶点B、C分别作直线l的垂线，垂足分别为M、N题型一三垂直模型基本应用例1过等腰Rt△ABC的直角顶点C作直线l，过A、B分别作AD⊥l于D，BE⊥l于E，已知AD＝5，BE＝3，求DE的长．CBACBACBA练习已知△ABC 中，∠BAC ＝90°，点E 在线段BC 上，点D 在线段AC 上，且△BDE 为等腰直角三角形，∠BDE ＝90°，BD ＝DE ，当∠ACB ＝30°时，试判断AD 与CE 的数量关系，并加以证明．模型二三垂直模型与“婆罗摩笈多”例2如图，△ABE 和△ACD 为等腰直角三角形，AM ⊥BC 于M ，MA 交ED 于N 求证：EN ＝DN ．练习如图，直线AB 分别与x 轴、y 轴相交于点A （2，0）和点B （0，4），以B 为顶点在第一象限作等腰Rt △ABC ．（1）在y 轴上存在一点M ，使得MA ＋MC 最小，请画出点M ；（保留画图痕迹）（2）求点C 的坐标；（3）若P 点为y 轴正半轴上一个动点，分别以AP 、OP 为腰在第一象限、第二象限作等腰Rt △APC 和等腰Rt △OPD ，连接CD 交y 轴于N 点，当点P 在y 轴正半轴上移动时，求PN 的长度．EDCBANMEDCBA模型三三垂直模型与“八字”全等综合例3（1）如图，已知等腰Rt △ABC ，∠C ＝90°，D 在AC 上，△BDE 为等腰直角三角形，∠DBE ＝90°，连AE 交BC 于F ，求证：BF ＋CF ＝CD ．（2）如图，D 点在AC 延长线上，其余条件不变，试探究BF 、CF 、CD 之间的关系．练习等腰Rt △ABC 中，∠B ＝90°，点P 在BC 上，以AP 为腰在△ABC 外侧作等腰Rt △APQ ，连PQ 交AB 于N ，连CQ 交AB 于M ．（1）如图，当P 在边BC 上，且CP ＝2BP 时，求CPBM的值．FEDCBA DABCEFN MQPCBA（2）P 点在CB 延长线上，且CP ＝nBP ，M 、N 分别在AB 边和AB 边的延长线上，求AMBM．真题演练（2016年江岸区八上期末第23题）如图，Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，E 点为射线CB 上一动点，连接AE ，作AF ⊥AE 且AF ＝AE （1）如图1，过F 点作FD ⊥AC 交AC 于点D ，求证：CE ＋CD ＝DF ；（2）如图2，连接BF 交AC 于点G ，若AGCG＝3，求证：E 为BC 中点；（3）当E 点在射线CB 上，连接BF 交直线AC 于点G ，若43BC BE，则AG CG＝．MNPQCB A图1FEDCBA图2GFECBA模块二三垂直模型与坐标系综合知识导航三垂直模型在坐标系中有着非常广泛的应用，尤其是与等腰直角三角形的综合，具体来说：已知等腰直角三角形三个顶点中任意两个点的坐标，便可以求出第三个点的坐标情况一如下图：直角顶点在坐标轴上情况二如下图：直角顶点不在坐标轴上例4（1）如图，△ABC 为等腰直角三角形，AC ＝BC ，AC ⊥BC ，A （0，3），C （1，0），求B 点坐标．B（2）如图，△ABC为等腰直角三角形，AC＝BC，AC⊥BC，A（－1，0），C（1，3），求B点坐标．（3）如图，△ABC为等腰直角三角形，AC＝BC，AC⊥BC，B（2，2），C（4，－2），求A点坐标．练习如图，在△ABC中，∠ACB＝90°，AC＝BC，BC与y轴交于D点，点C的坐标为（－2，0），点A的坐标为（－6，3），则D点的坐标是．真题演练如图，已知A（－2，0），（1）如图，以A为顶点，AB为腰在第三象限作等腰Rt△ABC，若B（0，－4），求C点坐标．（2）如图，P为y轴负半轴上一动点，以P为顶点，P A为腰做等Rt△APD，过D作DE⊥x轴于E点，当P点沿y轴负半轴向下运动时，试问OP－DE的值是否发生变化？若不变，求其值；若变化，请说明理由．（3）如图，已知F点坐标为（﹣4，﹣4），G是y轴负半轴上一点，以FG为直角边作等腰Rt△FGH，H 点在x轴上，∠GFH＝90°.设G（0，m），H（n，0），当G点在y轴负半轴上沿负方向运动时，m＋n的值是否变化？若不变，求其值；若变化，请说明理由．例5在平面直角坐标系中，A（2，﹣1），B（1，﹣4），C（5，﹣2），求∠ABC的度数．练习如图，在平面直角坐标系中，已知A（a，b），且a、b满足221b a a（1）求点A的坐标；（2）若点F（1，0），C（0，3），连AC、FC，试确定∠ACO＋∠FCO的值是否发生变化.若不变，说明理由.若变化，请求出变化范围．Array例6（2015年粮道街八上期中）在平面直角坐标系中，点A（4，0），B（0，8），以AB为斜边作等腰直角△ABC，则点C坐标为．练习在平面直角坐标系中，已知A（0，4），B（2，0），在第一象限内的点C，使△ABC为面积最小的等腰直角三角形，求点C的坐标以及面积的最小值．挑战压轴题如图1，已知A （a ，0），点B （0，b ）且a 、b 满足2(4)40ab（1）求A 、B 两点的坐标；（2）若点C 是第一象限内一点，且∠OCB ＝45°，过点A 作AD ⊥OC 于点F ，求证：F A ＝FC ；（3）如图2，若点D 的坐标为（0，1），过点A 作AE ⊥AD ，且AE ＝AD ，连接BE 交x 轴于点G ，求S △BOG ．本讲课后作业○A 基础巩固 1、如图，在△ABC 中，∠ACB ＝90°，AC ＝BC ，BC 与y 轴交于D 点，点C 的坐标为（﹣1，0），点A 的坐标为（﹣5，2），求点D 的坐标．2、在平面直角坐标系中，点A （2，0），B （0，4），以AB 为斜边作一个等腰直角三角形ABC ，则点C 的坐标为．图13、已知，△ABC是等腰直角三角形，BC＝AB，A点在x轴负半轴上，直角顶点B在y轴上，点C在x轴上方．（1）如图1所示，若A的坐标是（﹣3，0），点B的坐标是（0，1），求点C的坐标；（2）如图2，过点C作CD⊥y轴于D，请直接写出线段OA、OD、CD之间等量关系；（3）如图3，若x轴恰好平分∠BAC，BC与x轴交于点E，过点C作CF⊥x轴于F，问C F与AE有怎样的数量关系？并说明理由．综合练习4、如图1，OA ＝2，OB ＝4，以A 点为顶点、AB 为腰在第三象限作等腰Rt △ABC ．（1）求C 点坐标；（2）如图2，P 为y 轴负半轴上一个动点，当P 点向y 轴负半轴向下运动时，以P 为顶点，P A 为腰作等腰Rt △APD ，过D 作DE ⊥x 轴于E 点，求OP －DE 的值；（3）如图3，已知点F 坐标为（﹣2，﹣2），当点G 在y 轴负半轴上沿负方向运动时，作Rt △FGH ，始终保持∠GFH ＝90°，FG 与y 轴负半轴交于点G （0，m ），FH 与x 轴正半轴交于点H （n ，0），当G 点在y 轴的负半轴上沿负方向运动时，以下两个结论：①m －n 为定值；②m ＋n 为定值，其中只有一个结论是正确的，请找出正确的结论，并求出其值．x。

“一线三垂直”模型专题知识解读

“一线三垂直”模型专题知识解读【专题说明】一线三垂直问题，通常问题中有一线段绕某一点旋转90°，或者问题中有矩形或正方形的情况下考虑，作辅助线，构造全等三角形形或相似三角形，建立数量关系使问题得到解决。

【方法技巧】模型1 “全等型”一线三垂直模型如图一，∠D=∠BCA=∠E=90°，BC=AC 。

结论：Rt △BDC ≌Rt △CEA图1应用：（1）通过证明全等实现边角关系的转化，便于解决对应的几何问题；（2）平面直角坐标系中有直角求点的坐标，可以考虑作辅助线构造“三垂直”作辅助线的程序：过直角顶点再直角外部作水平线或竖直线，过另外两个顶点向上述直线作垂线段，即可得到“三垂直”模型。

如下图所示模型2 “相似型”一线三垂直模型如图2，ABD ADE C B ∆⇒∠=∠=∠∽DCE ∆（一线三直角）应用：（1）“相似型”三垂直基本应用C D E BA（2）平面直角坐标系中构造“相似型”三垂直。

作辅助线方法和模型1一样（3）平面直角坐标系中运动成直角【典例分析】【应用1 “全等型”三垂直基本应用】【典例1】在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE＝AD+BE；（2）当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由．【解答】（1）证明：①∵∠ACD+∠BCE＝90°∠DAC+∠ACD＝90°，∴∠DAC＝∠BCE．又AC＝BC，∠ADC＝∠BEC＝90°，∴△ADC≌△CEB．②∵△ADC≌△CEB，∴CD＝BE，AD＝CE．∴DE＝CE+CD＝AD+BE．（2）△ADC≌△CEB成立，DE＝AD+BE．不成立，此时应有DE＝AD﹣BE．证明：∵∠ACD+∠BCE＝90°∠DAC+∠ACD＝90°，∴∠DAC＝∠BCE．又AC＝BC，∠ADC＝∠BEC＝90°，∴△ADC≌△CEB．∴CD＝BE，AD＝CE．∴DE＝AD﹣BE．【变式1-1】如图，AC＝CE，∠ACE＝90°，AB⊥BD，ED⊥BD，AB＝6cm，DE＝2cm，则BD等于（）A．6cm B．8cm C．10cm D．4cm【答案】B【解答】解：∵AB⊥BD，ED⊥BD，∴∠B＝∠D＝∠ACE＝90°，∴∠BAC+∠ACB＝90°，∠ACB+∠ECD＝90°，∴∠BAC＝∠ECD，∵在Rt△ABC与Rt△CDE中，，∴Rt△ABC≌Rt△CDE（AAS），∴BC＝DE＝2cm，CD＝AB＝6cm，∴BD＝BC+CD＝2+6＝8cm，故选：B．【变式1-2】在△ABC中，∠BAC＝90°，AB＝AC，直线l经过点A，过点B、C分别作l 的垂线，垂足分别为点D、E．（1）特例体验：如图①，若直线l∥BC，AB＝AC＝，分别求出线段BD、CE和DE 的长；（2）规律探究：（Ⅰ）如图②，若直线l从图①状态开始绕点A旋转α（0＜α＜45°），请探究线段BD、CE和DE的数量关系并说明理由；（Ⅱ）如图③，若直线l从图①状态开始绕点A顺时针旋转α（45°＜α＜90°），与线段BC相交于点H，请再探线段BD、CE和DE的数量关系并说明理由；（3）尝试应用：在图③中，延长线段BD交线段AC于点F，若CE＝3，DE＝1，求S△BFC．【解答】解：（1）在△ABC中，∠BAC＝90°，AB＝AC，∴∠ABC＝∠ACB＝45°，∵l∥BC，∴∠DAB＝∠ABC＝45°，∠CAE＝∠ACB＝45°，∴∠DAB＝∠ABD＝45°，∠EAC＝∠ACE＝45°，∴AD＝BD，AE＝CE，∵AB＝AC＝，∴AD＝BD＝AE＝CE＝1，∴DE＝2；（2）（Ⅰ）DE＝BD+CE．理由如下：在Rt△ADB中，∠ABD+∠BAD＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∴∠ABD＝∠CAE，在△ABD和△CAE中，，∴△ABD≌△CAE（AAS）；∴CE＝AD，BD＝AE，∴DE＝AE+AD＝BD+CE．（Ⅱ）DE＝BD﹣CE．理由如下：在Rt△ADB中，∠ABD+∠BAD＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∴∠ABD＝∠CAE，在△ABD和△CAE中，，∴△ABD≌△CAE（AAS）；∴CE＝AD，BD＝AE，∴DE＝AE﹣AD＝BD﹣CE．（3）由（2）可知，∠ABD＝∠CAE，DE＝AE﹣AD＝BD﹣CE∵∠BAC＝∠ADB＝90°，∴△ABD∽△FBA，∴AB：FB＝BD：AB，∵CE＝3，DE＝1，∴AE＝BD＝4，∴AB＝5．∴BF＝．∴S△BFC＝S△ABC﹣S△ABF＝×52﹣×3×＝．【应用2 平面直角坐标系中构造“全等型”三垂直】【典例2】已知：在平面直角坐标系中，A为x轴负半轴上的点，B为y轴负半轴上的点．（1）如图1，以A点为顶点、AB为腰在第三象限作等腰Rt△ABC，若OA＝2，OB＝4，求C点的坐标；（2）如图2，若点A的坐标为（﹣2，0），点B的坐标为（0，﹣m），点D的纵坐标为n，以B为顶点，BA为腰作等腰Rt△ABD．当B点沿y轴负半轴向下运动且其他条件都不变时，整式4m+4n﹣9的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由；（3）如图3，若OA＝OB，OF⊥AB于点F，以OB为边作等边△OBM，连接AM交OF 于点N，若AN＝m，ON＝n，请直接写出线段AM的长．【解答】解：（1）如图1，过点C作CQ⊥OA于点Q，∴∠AQC＝90°∵△ABC等腰直角三角形，∴AC＝AB，∠CAB＝90°，∴∠ACQ＝∠BAO．∴△AQC≌△BOA（AAS），∴CQ＝AO，AQ＝BO．∵OA＝2，OB＝4，∴CQ＝2，AQ＝4，∴OQ＝6，∴C（﹣6，﹣2）．（2）整式4m+4n﹣9的值不会变化．理由如下：如图2，过点D作DP⊥OB于点P，∴∠BPD＝90°，∵△ABD等腰Rt△，∴AB＝BD，∠ABD＝∠ABO+∠OBD＝90°，∴∠ABO＝∠BDP，∴△AOB≌△BPD（AAS），∴AO＝BP，∵BP＝OB﹣PO＝m﹣（﹣n）＝m+n，∴A（﹣2，0），∴OA＝2，∴m+n＝2，∴当B点沿y轴负半轴向下运动时AO＝BP＝m+n＝2，∴4m+4n﹣9＝4×﹣9＝﹣，∴整式4m+4n﹣9的值不变，为﹣．（3）AM＝2m+n．证明：如图3，在MA上截取MG＝ON，连接BG，∵△OBM是等边三角形，∴BO＝BM＝MO，∠OBM＝∠OMB＝∠BOM＝60°，∴AO＝MO，∠ABM＝105°，∠HOM＝30°，∵OA＝OB，∴OA＝OM＝BM．∴∠OAN＝∠AMO＝15°，∴∠BAM＝30°，∠BMA＝45°，∵OF⊥AB，∴∠AOF＝45°，∴∠AOF＝∠BMA．∴△ANO≌△BGM（AAS），∴BG＝AN．∵ON＝MG，∴∠GBM＝∠OAN，∴∠GBM＝15°，∴∠ABG＝90°∴2BG＝AG，∴2AN＝AG，∵AG＝AM﹣GM，∴2AN+ON＝AM，即AM＝2m+n．【变式2-1】如图所示，在平面直角坐标系中，等腰Rt△ABC的直角顶点C在x轴上，点A 在y轴上，若点B坐标为（6，1），则点A坐标为（）A．（4，0）B．（5，0）C．（0，4）D．（0，5）【答案】D【解答】解：作BD⊥x轴于D，∵B（6，1），∴BD＝1，OD＝6，∵△ABC是等腰直角三角形，∴AC＝BC，∠ACB＝90°，∴∠ACO+∠BCD＝90°，∵∠ACO+∠OAC＝90°，∴∠BCD＝∠OAC，∵∠AOC＝∠BDO，∴△ACO≌△CBD（AAS），∴OC＝BD＝1，CD＝OA＝5，∴A（0，5），故选：D．【变式2-2】如图，在△PMN中，PM＝PN，PM⊥PN，P（0，2），N（2，﹣2），则M的坐标是（）A．（﹣2，0）B．（﹣2，0）C．（﹣2，0）D．（﹣4，0）【答案】D【解答】解：过点N作ND⊥y轴于点D，∵P（0，2），N（2，﹣2），∴OP＝2，OD＝2，DN＝2，∴PD＝4，∵PM⊥PN，∴∠MPN＝90°，∴∠MPO+∠DPN＝90°，又∵∠DPN+∠PND＝90°，∴∠MPO＝∠PND，又∵∠MOP＝∠PDN＝90°，∴△MOP≌△PDN（AAS），∴OM＝PD＝4，∴M（﹣4，0），故选：D．【应用3 “相似型”三垂直基本应用】【典例3】已知矩形ABCD的一条边AD＝8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．如图，已知折痕与边BC交于点O，连接AP、OP、OA．（1）求证：＝；（2）若OP与P A的比为1：2，求边AB的长．【解答】（1）证明：由折叠的性质可知，∠APO＝∠B＝90°，∴∠APD+∠OPC＝90°，∵四边形ABCD为矩形，∴∠D＝∠C＝90°，∴∠POC+∠OPC＝90°，∴∠APD＝∠POC，∴△OCP∽△PDA，∴＝；（2）解：∵△OCP∽△PDA，∴，∵OP与P A的比为1：2，AD＝8，∴，∴PC＝4，设AB＝x，则DC＝x，AP＝x，DP＝x﹣4，在Rt△APD中，AP2＝AD2+PD2，∴x2＝82+（x﹣4）2，解得：x＝10，∴AB＝10．【变式3】如图，在矩形ABCD中，E，F，G分别在AB，BC，CD上，DE⊥EF，EF⊥FG，BE＝3，BF＝2，FC＝6，则DG的长是（）A．4B．C．D．5【解答】解：∵EF⊥FG，∴∠EFB+∠GFC＝90°，∵四边形ABCD为矩形，∴∠A＝∠B＝∠C＝90°，AB＝CD，∴∠GFC+∠FGC＝90°，∴∠EFB＝∠FGC，∴△EFB∽△FGC，∴，∵BE＝3，BF＝2，FC＝6，∴，∴CG＝4，同理可得△DAE∽△EBF，∴，∴，∴AE＝，∴BA＝AE+BE＝+3＝，∴DG＝CD﹣CG＝﹣4＝．故选：B．【应用4 平面直角坐标系中构造“相似型”三垂直】【典例4】如图，在平面直角坐标系中，点O为坐标原点，直线y＝kx+2与y轴交于点A，与x轴交于点B，且OB＝2OA．（1）如图1，求直线的解析式；（2）如图2，点P在第三象限的直线AB上，点C在点A上方的y轴上，连接PC、BC，PC交x轴于点N，且tan∠APC＝，设点P的横坐标为t，△ABC的面积为S，求S与t的函数关系；（3）如图3，在（2）的条件下，点D在y轴的负半轴上，点E为AB的中点，连接DE、PD，AD＝ON，当∠PDE＝∠PCD时，求点D的坐标．【解答】解：（1）∵直线y＝kx+2与y轴交于点A，与x轴交于点B，令x＝0，则y＝2，∴点A的坐标为（0，2），∴OA＝2，∵OB＝2OA，∴OB＝4，∴B（﹣4，0），将（﹣4，0）代入y＝kx+2得：0＝﹣4k+2，解得：k＝，∴直线的解析式为：y＝；（2）过点A作EA⊥AB交PC于点E，过E点作EG⊥y轴，垂足为G，过点P作PF⊥y 轴，垂足为F，∵∠P AE＝90°，∴∠P AF+∠EAG＝90°，∵∠P AF+∠APF＝90°，∴∠APF＝∠EAG，∵∠EGA＝∠AFP＝90°，∴△AEG∽△P AF，∵tan∠APC＝，∴＝＝，设P（t，），则PF＝﹣t，AF＝﹣，∴AG＝＝﹣，EG＝＝﹣，∵点A的坐标为：（0，2），设PE的解析式为：y＝ax+b，由P（t，），E（）可得：，解得：，∴C（0，2﹣），∴AC＝2﹣﹣2＝﹣，∵BO＝4，∴S＝＝﹣t，（3）作EF⊥DE交PD于F，过点E作EG⊥y轴于点G，作FH⊥EG于H，由（2）得直线PC的解析式：y＝x+（2﹣），∴∠PCO＝45°，∴ON＝OC＝2﹣，∴AD＝ON＝2﹣，∴D（0，），∵∠PDE＝∠PCD＝45°，∴△DEG≌△EFH（AAS）．∴EG＝FH＝2，DG＝EH＝1﹣，设PD的解析式为：y＝mx+n，由P（t，）、D（0，）可得：，解得：，∴PD的解析式为：y＝，把点F（﹣3+）代入y＝得：t1＝﹣6，t2＝2（舍去），∴D（0，﹣3）．【变式4】（2022•禅城区二模）如图，抛物线经过原点O，对称轴为直线x＝2且与x轴交于点D，直线l：y＝﹣2x﹣1与y轴交于点A，与抛物线有且只有一个公共点B，并且点B在第四象限，直线l与直线x＝2交于点C．（1）连接AD，求证：AD⊥AC．（2）求抛物线的函数关系式．（3）在直线l上有一点动点P，抛物线上有一动点Q，当△PBQ是以PQ为斜边的等腰直角三角形时，直接写出此时点P的坐标．【解答】解：（1）如图1，过点C作CE⊥y轴于点E，则∠AEC＝∠DOA＝90°，∵直线y＝﹣2x﹣1与y轴交于点A，与直线x＝2交于点C，∴A（0，﹣1），C（2，﹣5），∴E（0，﹣5），∴OA＝1，OD＝2，CE＝2，AE＝4，∴＝，＝＝，∴＝，∵∠AEC＝∠DOA，∴△AEC∽△DOA，∴∠CAE＝∠ADO，∵∠ADO+∠DAO＝90°，∴∠CAE+∠DAO＝90°，∴∠DAC＝180°﹣（∠CAE+∠DAO）＝180°﹣90°＝90°，∴AD⊥AC．（2）设抛物线的函数关系式为y＝ax2+bx，∵对称轴为直线x＝2，∴＝2，∴b＝﹣4a，∴y＝ax2﹣4ax，由ax2﹣4ax＝﹣2x﹣1，整理得ax2+（2﹣4a）x+1＝0，∵直线y＝﹣2x﹣1与抛物线有且只有一个公共点B，∴Δ＝（2﹣4a）2﹣4a＝0，解得：a1＝，a2＝1，当a＝时，抛物线解析式为y＝x2﹣x，联立得x2﹣x＝﹣2x﹣1，解得：x1＝x2＝﹣2，∴B（﹣2，3）与点B在第四象限矛盾，故a＝不符合题意，舍去，当a＝1时，y＝x2﹣4x，联立得x2﹣4x＝﹣2x﹣1，解得：x1＝x2＝1，∴B（1，﹣3），点B在第四象限符合题意，∴a＝1，∴该抛物线的函数关系式为y＝x2﹣4x．（3）如图2，过点B作BQ⊥AB交抛物线于点Q，作GH∥x轴交y轴于点G，过点Q 作QH⊥GH，则∠AGB＝∠BHQ＝∠ABQ＝90°，∴∠ABG+∠QBH＝∠ABG+∠BAG＝90°，∴∠QBH＝∠BAG，∴△ABG∽△BQH，∴＝，设Q（t，t2﹣4t），∵A（0，﹣1），B（1，﹣3），∴AG＝2，BG＝1，BH＝t﹣1，QH＝t2﹣4t+3，∴＝，解得：t＝1（舍去）或t＝，∴BH＝﹣1＝，QH＝（）2﹣4×+3＝，过点B作EF∥y轴，过点P1作P1E⊥EF，过点P2作P2F⊥EF，∵△PBQ是以PQ为斜边的等腰直角三角形，∴P1B＝BQ＝P2B，∵∠P1BE+∠EBQ＝∠EBQ+∠QBH＝90°，∴∠P1BE＝∠QBH，∵∠BEP1＝∠BHQ＝90°，∴△BEP1≌△BHQ（AAS），∴EP1＝QH＝，BE＝BH＝，∴P1（﹣，﹣），同理可得：P2（，﹣），综上，点P的坐标为P1（﹣，﹣），P2（，﹣）．【应用5平面直角坐标系中运动成直角】【典例5】如图，已知抛物线y＝﹣x2+与x轴交于点A、B，与y轴交于点C．（1）则点A的坐标为，点B的坐标为，点C的坐标为；（2）设点P（x1，y1），Q（x2，y2）（其中x1＞x2）都在抛物线上，若x1+x2＝1，请证明：y1＞y2；（3）已知点M是线段BC上的动点，点N是线段BC上方抛物线上的动点，若∠CNM ＝90°，且△CMN与△OBC相似，试求此时点N的坐标．【解答】（1）证明：当x＝0时，y＝2，∴点C（0，2），当y＝0时，﹣x2+＝0，解得：x＝﹣1或x＝4，∴点A（﹣1，0），B（4，0）．（2）证明：由题意得：y1﹣y2＝﹣x12+x1+2﹣（﹣x22+x2+2）＝x22﹣x12+x1﹣x2＝（x2+x1）（x2﹣x1）+（x1﹣x2），∵x1+x2＝1，∴y1﹣y2＝x1﹣x2，又∵x1＞x2，∴y1＞y2．（3）解：设直线BC的解析式为y＝kx+b，则，解得：，∴直线BC的解析式为y＝﹣x+2，如图，过点N作NG⊥y轴于点G，过点M作MH⊥GN于点H，则∠CGN＝∠H＝90°，∴∠GNC+∠GCN＝90°，∵∠CNM＝90°，∴∠GNC+∠HNM＝90°，∴∠GCN＝∠HNM，∴△CNG∽△NMH，∴，设点N的坐标为（n，），则GN＝n，GC＝，①当△NCM∽△OCB时，，∵OB＝4，OC＝2，∴CN：MN＝OC：OB＝1：2，∴NH＝2CG＝2（）＝﹣n2+3n，HM＝2NG＝2n，∴GH＝GN+NH＝n+（﹣n2+3n）＝﹣n2+4n，y M＝GC+CO﹣MH＝+2﹣2n＝﹣n2﹣n+2，∴点M的坐标为（﹣n2+4n，﹣n2﹣n+2），∵点M在直线BC上，∴﹣（﹣n2+4n）+2＝﹣n2﹣n+2，解得：n＝0（舍去）或，∴点N坐标为（，）；②当△NCM∽△OBC时，，∵OB＝4，OC＝2，∴CN：MN＝OB：OC＝2：1，∴NH＝CG＝（）＝﹣n2+n，HM＝GN＝n，∴GH＝GN+NH＝n+（﹣n2+n）＝﹣n2+n，y M＝GC+CO﹣MH＝+2﹣n＝﹣n2+n+2，∴点M的坐标为（﹣n2+n，﹣n2+n+2），∴﹣（﹣n2+n）+2＝﹣n2+n+2，解得：n＝0（舍去）或n＝3，∴点N坐标为（3，2），综上所述，点N的坐标为（，）或（3，2）．【变式5】（2022•碑林区校级四模）如图，在平面直角坐标系中，抛物线C1：y＝ax2+bx+c 交x轴于点A（﹣5，0），B（﹣1，0），交y轴于点C（0，5）．（1）求抛物线C1的表达式和顶点D的坐标．（2）将抛物线C1关于y轴对称的抛物线记作C2，点E为抛物线C2上一点若△DOE是以DO为直角边的直角三角形，求点E的坐标．【解答】解：（1）将点A（﹣5，0），B（﹣1，0），C（0，5）代入y＝ax2+bx+c，∴，解得，∴y＝x2+6x+5，∵y＝x2+6x+5＝（x+3）2﹣4，∴顶点D（﹣3，﹣4）；（2）设抛物线C2上任意一点（x，y），则（x，y）关于y轴对称的点为（﹣x，y），∵点（﹣x，y）在抛物线C1上，∴抛物线记作C2的解析式为y＝x2﹣6x+5，设E（t，t2﹣6t+5），过点D作DG⊥x轴交于点G，过点E作EH⊥x轴交于点H，∵∠DOE＝90°，∴∠GOD+∠HOE＝90°，∵∠GOD+∠GDO＝90°，∴∠HOE＝∠GDO，∴△GDO∽△HOE，∴＝，∵DG＝4，GO＝3，HE＝﹣t2+6t﹣5，OH＝t，∴＝，∴t＝4或t＝，∴E（4，﹣3）或E（，﹣）．。

(完整版)三垂直模型与全等综合剖析

K模型图与全等知识点DE丄AB,垂足为E,本题8分)如图，在等腰Rt△ABC 中，/ ACB=90° D 为BC 的中点,过点B作BF // AC交DE的延长线于点F，连接CF.(1) 求证：AD丄CF;(2) 连接AF，求证：AF = CF .22.边长为1的正方形ABCD中，E是AB中点，连CE, 过B作BF丄CE交AC于F,求AF.【例8】基本图形【例9］等腰Rt△ ABC中Z ACB- 90°, AC=BC F 是BC上的中点，连AF,作CDL AF于E,交AB于D; 连FD.求证：AE> 2BD【例3］已知△ ABC中,Z C=90 ,AC=BC,D是AB的中点,E是BC上任一点,EP丄CB,PF丄AC,E、F为垂足,求证：△ DEF是等腰直角三角形E【例4】如图，D为线段AB的中点，在AB上取异于D的点C,分别以AC BC为斜边在AB 同侧作等腰直角三角形ACEA CD B与BCF连结DE DF EF,求证：△ DEF为等腰直角三角形。

【例5】如图，分别以厶ABC的边AB AC向外作等腰Rt △ ABD等腰Rt △ ACE连接DE= AF 是厶ABC的中线，EFA的延长线交DE于点H,求证：DE= 2AF【例6】如图，在正方形ABCD中，点N是BC边上的点。

连接AN MNL AN交/ DCB的外角平分线于点M求证：AN= MN9、如图，直线AB交x轴正半轴于点A (a, 0),交y轴正半轴于点B (0, b),且a、b 满足Ja 4 + |4 —b|=0(1)求A B两点的坐标；(2)D为OA的中点，连接BD过点O作OEL BD于F,交AB于E,求证/ BDO/ EDA(3)如图，P为x轴上A点右侧任意一点，以BP为边作等腰Rt△ PBM其中PB=PM直线MA交y轴于点Q当点P在x轴上运动时, 线段0Q的长是否发生变化？若不变，求其值；若变化，求线段0Q勺取值范围.(2012-2013 (2012.11)武汉二牛71出学、六中召上期自•團B192)在平面直角坐标系中7 A(a f b)在第一象限内，且念条件；b-a=^-(a-2)2,AB丄y軸于AC丄英抽于(1)求丄40C的盍积；卩(2)如霸，E为多殴坊上一点，逹HE, 丄肚交兀务于F,逹EF, ED平分zOEF交CM于D,过D作DG丄EF于求DG+；EF的值；*(3)如图Q为兀轴上一点= CD.E为察段0B±一动点，连DA、星线段CE閑宇, ^BF ± FK交卫D于K,请问啟BF的天小是否变化？芝不玫变，请戒其值；芝改芟，求出更化的范亂*24. （12分）如图，VCOD等腰直角三角形，CA丄x轴。

初中几何模型：三垂直全等模型分析

三垂直全等模型"三垂直模型"是初中必会的一种几何模型，它是一个应用非常广泛的模型，它可以应用在三角形，矩形，平面直角坐标系，网格，一次函数，反比例函数，三角函数，二次函数以及圆等诸多的中考重要考点之中，所以这一知识点的掌握对于中考至关重要。

模型三垂直全等模型如图：/ D =Z BCA =Z E = 90°, BC = AC. 结论：Rt △ BCD 也 Rt△ CAE.模型分析说到三垂直模型，不得不说一下弦图，弦图的运用在初中直角三角形中占有举足轻重的地位, 很多利用垂直求角，勾股定理求边长，相似求边长都会用到从弦图支离出来的一部分几何图形去求解•图①和图②就是我们经常会见到的两种弦图。

证明：••• AE 丄 DE , AB 丄BC , DC 丄 BC,三垂直图形变形如下图③、图④，这也是由弦图演变而来的。

如图,B 丄 BC ,D 丄BC AE 丄 DE AE = DE 求证：AB + CD = BC.B图① 图②BAID 图④C 图③A B C•••/AED =Z B = Z C = 90° .•••/ A +Z AEB = Z AEB +Z CED = 90° •••/ BAE = Z CED.在厶ABE 和厶ECD 中,A CEDAE ED• AB = EC , BE = CD.• AB + CD = EC + BE = BC.AC = BC , BE 丄 CE , AD 丄 CE 于 D , AD = 2.5cm , BE = 0.8cm ,解答：••• BE 丄CE , AD 丄CE ,E =Z ADC = 90° .EBC +Z BCE = 90 ° .BCE +Z ACD = 90EBC =Z DCA.CEB 和厶 ADC 中,E ADCEBC DCABC AC•••△ CEB ^A ADC.• DE = CE — CD = 2.5 — 0.8 =1.7cm.例3如图，在平面直角坐标系中，等腰的坐标。

三垂直模型奥数-概述说明以及解释

三垂直模型奥数-概述说明以及解释1.引言1.1 概述三垂直模型是奥数领域中一种重要的教学方法与思维模式。

它通过将奥数问题划分为三个垂直维度，即基础维度、拓展维度和深化维度，来帮助学生建立全面、深入的数学思维。

在三垂直模型中，基础维度聚焦于奥数的基本概念、基本技巧和基本思维能力的培养。

通过扎实的基础训练，学生能够熟练掌握奥数中的基本知识，为拓展维度的学习打下坚实的基础。

拓展维度则通过引入更加复杂和抽象的问题，帮助学生深入理解和应用所学的知识。

这一维度追求的是学生的创造性思维和问题解决能力的培养。

通过解决具有挑战性的问题，学生可以培养独立思考、灵活运用知识的能力。

深化维度是三垂直模型中最具挑战性的一部分，它要求学生深入挖掘数学问题背后的原理和内在联系。

通过深化对问题的理解，学生可以培养分析、推理和证明的能力，进一步提高数学思维的深度和广度。

三垂直模型的应用场景广泛，既适用于奥数教学，也可以应用于其他学科的教学。

它不仅能帮助学生建立扎实的数学基础，提高解决问题的能力，还能培养学生的创造性思维和批判性思维，使他们在面对各类问题时能够思维清晰、灵活应对。

然而，三垂直模型也存在一些局限性。

首先，由于其深入和抽象的特点，三垂直模型在初学者阶段可能会导致学生的学习困难。

此外，三垂直模型需要教师具备较高的教学能力和丰富的教学经验，才能够有效地引导学生进行学习。

总之，三垂直模型是一种具有深远影响的奥数教学模式。

它通过基础、拓展和深化三个垂直维度的训练，提供了一种全面、系统的学习方法。

相信在未来的奥数教育中，三垂直模型将会继续发挥重要作用，并为学生的数学学习带来更大的收益。

文章结构部分的内容如下：1.2 文章结构本文将首先通过引言部分介绍三垂直模型的背景和意义，然后在正文部分对三垂直模型的定义、应用场景以及优缺点进行详细探讨。

最后，在结论部分对三垂直模型的重要性进行总结，并展望其未来的发展前景。

整篇文章将按照以下结构展开：引言部分：- 1.1 概述：对奥数及其重要性进行简要介绍。

初中几何一线三垂直模型构造全等三角形

初中几何一线三垂直模型构造全等三角形一线三垂直模型构造全等三角形【模型说明】一线三垂直问题，通常问题中有一线段绕某一点旋转90º，或者问题中有矩形或正方形的情况下考虑，作辅助线，构造全等三角形形或相似三角形，建立数量关系使问题得到解决。

【知识总结】过等腰直角三角形的直角顶点或者正方形直角顶点的一条直线.过等腰直角三角形的另外两个顶点作该直线的垂线段，会有两个三角形全等（AAS）.常见的两种图形：【典型例题1】如图，在直角梯形ABCD中，AD∥BC，AB⊥BC,AD=2，BC=3，设∠BCD=α，以D为旋转中心，将腰DC绕点D逆时针旋转90°至DE.当α=45°时，求△EAD的面积.当α=30°时，求△EAD的面积当0°＜α＜90°，猜想△EAD的面积与α大小有无关系，若有关，写出△EAD 的面积S与α的关系式，若无关，请证明结论.【答案解析】∵AD∥BC,DG⊥BC∴∠GDF=90°又∵∠EDC=90°∴∠1=∠2在△CGD和△EFD中∠DGC=∠DFE∠1=∠2CD=DE∴△DCG≌△DEF更多内容见公众号：初中数学解题思路∴EF=CG∵AD∥BC,AB⊥BC,AD=2，BC=3∴BG=AD=2∴CG=1，EF=1，△EAD的面积与α无关【典型例题2】如图，向△ABC的外侧作正方形ABDE,正方形ACFG，过A作AH⊥BC于H，AH的反向延长线与EG交于点P，求证：BC=2AP【答案解析】过点G作GM⊥AP于点M,过点E作EN⊥AP交AP的延长线于点N∵四边形ACFG是正方形.更多内容见公众号：初中数学解题思路∴AC=AG,∠CAG=90°∴∠CAH+∠ACH=90°∴∠ACH=∠GAM在△ACH和△GAM中∠AHC=∠GMA∠ACH=∠GAMAC=GA∴△ACH≌△GAM∴CH=AM,AH=GM同理可证△ABH≌△EAN，△EPN≌△GPM∴NP=MP∴BC=BH+CH=AN+AM=AP+PN+AP-PM=2AP一线三垂直模型构造全等三角形【模型说明】一线三垂直问题，通常问题中有一线段绕某一点旋转90º，或者问题中有矩形或正方形的情况下考虑，作辅助线，构造全等三角形形或相似三角形，建立数量关系使问题得到解决。

三垂直模型与全等综合剖析.docx

K模型图与全等知识点基本图形本题 8 分）如图，在等腰Rt △ABC中，∠ACB=90 °，D为BC的中点，DE⊥AB，垂足为E，过点 B 作 BF∥AC 交 DE 的延长线于点 F，连接 CF．（1）求证：AD⊥CF；（2）连接AF，求证：AF＝CF．22 ．边长为 1 的正方形 ABCD 中， E 是 AB 中点，连CE，过 B 作 BF⊥ CE 交 AC 于 F，求AF.D CFHA EB 【例 8】CFEA D B【例 9 】等腰 Rt △ABC 中∠ACB ＝ 90 °，AC=BC ； F 是 BC 上的中点，连AF ，作 CD ⊥ AF 于 E，交 AB 于 D；连 FD. 求证： AD ＝2BD ；【例 3 】已知△ABC 中 ,∠C=90 ,AC=BC,D是AB的中点,E是BC上任一点,EP⊥ CB,PF⊥ AC,E、F为垂足 ,CFE求证 :△DEF 是等腰直角三角形.A D P B【例 4 】如图， D 为线段 AB 的中点，在AB 上取异于 D 的点 C，分别以 AC、BC 为斜边在AB 同侧作等腰直角三角形ACE 与 BCF，连结 DE、 DF、 EF，求证：△ DEF 为等腰直角三角形。

DFEHEAA C D BBFC【例 5 】如图，分别以△ ABC 的边 AB 、AC 向外作等腰Rt △ABD ，等腰 Rt △ACE；连接 DE。

AF 是△ABC 的中线，FA 的延长线交DE 于点 H ，求证： DE＝ 2AF【例 6 】如图，在正方形ABCD 中，点 N 是 BC 边上的点。

连接AN ，MN ⊥ AN 交∠DCB 的外角平分线于点M 。

求证： AN ＝ MN9、如图，直线AB 交 x 轴正半轴于点 A（a，0），交 y 轴正半轴于点B（0， b），且 a 、b 满足 a 4+ |4 －b|=0（1）求A、B两点的坐标；（2）D为OA的中点，连接BD，过点O作OE⊥BD于F，交AB 于 E，求证∠BDO=∠EDA；yBEFO D A x（3）如图，P为x轴上A点右侧任意一点，以BP 为边作等腰Rt△PBM ，其中 PB= PM，直线 MA 交 y 轴于点 Q，当点 P 在 x轴上运动时，线段 OQ 的长是否发生变化？若不变，求其值；若变化，求线段 OQ 的取值范围.yM BO A PxQ 1024 ．（ 12分）如图， VCOD 等腰直角三角形， CA ⊥ x 轴。

(完整版)关于“一线三垂直”模型及其在平面几何中的应用

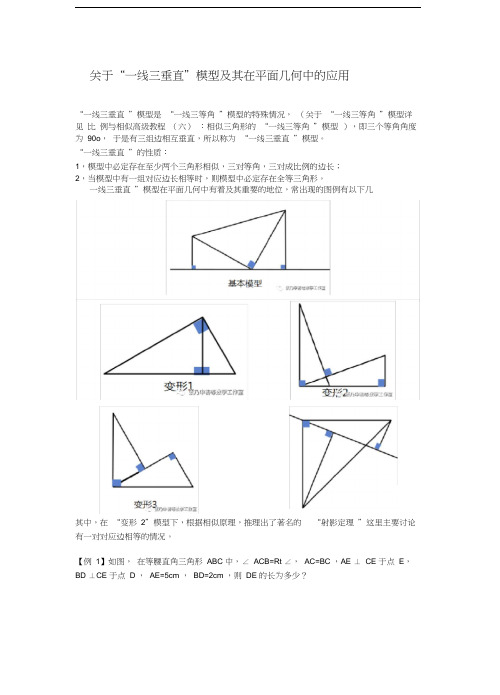
关于“一线三垂直”模型及其在平面几何中的应用“一线三垂直”模型是“一线三等角”模型的特殊情况，（关于“一线三等角”模型详见比例与相似高级教程（六）：相似三角形的“一线三等角”模型），即三个等角角度为90o，于是有三组边相互垂直，所以称为“一线三垂直”模型。

“一线三垂直”的性质：1，模型中必定存在至少两个三角形相似，三对等角，三对成比例的边长；2，当模型中有一组对应边长相等时，则模型中必定存在全等三角形。

其中，在“变形2”模型下，根据相似原理，推理出了著名的“射影定理”这里主要讨论有一对对应边相等的情况。

【例1】如图，在等腰直角三角形ABC 中，∠ ACB=Rt ∠，AC=BC ，AE ⊥ CE 于点E，BD ⊥CE 于点 D ，AE=5cm ，BD=2cm ，则DE 的长为多少？一线三垂直”模型在平面几何中有着及其重要的地位，常出现的图例有以下几种：【提示】根据“一线三垂直”模型的性质，△ACE≌△CBD ，于是CD=AE=5cm CE=BD=2cm ，DE=5-2=3 （cm ）【例2】如图，在△ ABC 中，CA=CB ，点 D 为BC 中点，CE⊥ AD 于点E，交AB 点F，连接DF 。

求证：AD=CF+DF.则易证△ ACD ≌△ CBG ，于是AD=CG=CF+FG ；BG=CD=BD ，BF=BF ，∠ DBF= ∠ GBF=45o ，故△ BDF ≌△ BGF ，于是FD=FG ，所以AD=CF+DF 。

【解析】此题乍一看起来和【例从要证明的结论来看，需要把BG ⊥ CB ，交CF 的延长线于1】相同，却不能照搬照抄。

AD 这条线段“转化”到直线CF 上。

如图，过点 BG。

关于“一线三垂直” 模型及其在平面几何中的应用（二）“一线三垂直”的性质：1，模型中必定存在至少两个三角形相似，三对等角，三对成比例的边长；2，当模型中有一组对应边长相等时，则模型中必定存在全等三角形。

【例3】如图，在△ ABC 中，AB=AC ，∠ BAC=90o ，分别过B，C 向过 A 点的直线作垂线，垂足分别为E，F。

专题07 一线三垂直与一线三等角(解析版)

专题07一线三垂直与一线三等角一、基础知识回顾1）三角形内角和定理：三角形三个内角和等于180°2）1平角=180度二、模型的概述：1）一线三垂直模型[模型概述]只要出现等腰直角三角形，可以过直角点作一条直线，然后过45°顶点作直线的垂线，构造三垂直，所得两个直角三角形全等。

根据全等三角形倒边，得到线段之间的数量关系。

基础构造1构造2一线三垂直模型一：如图AB⊥BC，AB=BC，CE⊥DE，AD⊥DE，则∆ABD≌∆BCE，DE=AD+EC证明：∵CE⊥DE，AD⊥DE，AB⊥BC∴∠CEB=∠ADB=∠ABC=90°∴∠1+∠2=90°，∠2+∠3=90°∴∠1=∠3在∆ABD和∆BCE中，∠1=∠3∠CEB=∠ADB=90°∴∆ABD≌∆BCE（AAS）∴AD=BE,EC=BDAB=BC则DE=BE+BD=AD+EC一线三垂直模型二：如图AB⊥BC，AB=BC，CE⊥DE，AD⊥DE，则∆ABD≌∆BCE，DE=AD-EC证明：∵CE⊥DE，AD⊥DE，AB⊥BC∴∠CEB=∠ADB=∠ABC=90°∴∠A+∠ABD=90°，∠ABD+∠CBE=90°∴∠A=∠CBE在∆ABD和∆BCE中，∠A=∠CBE∠CEB=∠ADB=90°∴∆ABD≌∆BCE（AAS）∴AD=BE,EC=BDAB=BC则DE=BE-BD=AD-EC一线三垂直其它模型1）图1，已知∠AOC=∠ADB=∠CED=90°，AB=DC，得∆ADB≌∆DEC2）图2，延长DE交AC于点F，已知∠DBE=∠ABC=∠EFC=90°，AC=DE，得∆ABC≌∆DBE图1图22）一线三等角模型[模型概述]三个等角的顶点在同一条直线，这个角可以是直角，也可以是锐角或钝角。

一线三等角类型：（同侧）已知∠A=∠CPD=∠B=∠α，CP=PD（异侧）已知∠EAC=∠ABD=∠DPC=∠α，CP=PD证明：以右图为例∵∠ACP+∠A+∠CPA=180°，∠DPB+∠CPD+∠CPA=180°而∠CAP=∠CPD=∠PBD=∠α∴∠ACP=∠DPB又∵CP=PD∴∆ACP≌∆BPD（AAS）【基础过关练】1．如下图所示，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．DE=6cm，AD=9cm，则BE的长是（）A．6cm B．1.5cm C．3cm D．4.5cm【答案】C【分析】本题可通过全等三角形来求BE的长．△BEC和△CDA中，已知了一组直角，∠CBE和∠ACD同为∠BCE的余角，AC=BC，可据此判定两三角形全等；那么可得出的条件为CE=AD，BE=CD，因此只需求出CD 的长即可．而CD的长可根据CE即AD的长和DE的长得出，由此可得解．【详解】解：∵∠ACB=90°，BE⊥CE，∴∠BCE+∠ACD=90°，∠BCE+∠CBE=90°；∴∠ACD=∠CBE，又AC=BC，∴△ACD≌△CBE；∴EC=AD，BE=DC；∵DE=6cm，AD=9cm，则BE的长是3cm．故选C．【点睛】三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．2．如图，在△ABC中，AB＝AC＝9，点E在边AC上，AE的中垂线交BC于点D，若∠ADE＝∠B，CD＝3BD，则CE等于（）A．3B．2C．94D．92【答案】A【分析】根据等腰三角形的性质得到∠B ＝∠C ，推出∠BAD ＝∠CDE ，根据线段垂直平分线的性质得到AD ＝ED ，根据全等三角形的性质得到CD ＝AB ＝9，BD ＝CE ，即可得到结论．【详解】解：∵AB ＝AC ＝9，∴∠B ＝∠C ，∵∠ADE ＝∠B ，∠BAD ＝180°﹣∠B ﹣∠ADB ，∠CDE ＝180°﹣∠ADE ﹣∠ADB ，∴∠BAD ＝∠CDE ，∵AE 的中垂线交BC 于点D ，∴AD ＝ED ，在△ABD 与△DCE 中，BAD CDE B C AD ED ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△DCE （AAS ），∴CD ＝AB ＝9，BD ＝CE ，∵CD ＝3BD ，∴CE ＝BD ＝3故选：A ．【点睛】本题考查了等腰三角形的性质，线段垂直平分线的性质，全等三角形的性质，属于基础题．3．如图，AC ＝CE ，∠ACE ＝90°，AB ⊥BD ，ED ⊥BD ，AB ＝6cm ，DE ＝2cm ，则BD 等于（）A ．6cmB ．8cmC ．10cmD ．4cm【答案】B 【分析】根据题意证明ABC CDE △≌△即可得出结论．【详解】解：∵AB ⊥BD ，ED ⊥BD ，∴90ABC CDE ∠=∠=︒，∵∠ACE ＝90°，∴90ACB DCE ∠+∠=︒，∵90ACB BAC ∠+∠=︒，∴BAC DCE ∠=∠，在ABC 和CDE 中，90ABC CDE BAC DCE AC CE ∠=∠=︒⎧⎪∠=∠⎪⎨⎪⎪⎩＝，∴()ABC CDE AAS ≌，∴6cm AB CD ==，2cm BC DE ==，∴268cm BD BC CD =+=+=，故选：B ．【点睛】本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定定理以及性质定理是解本题的关键．4．如图，ABC 中，,90,(0,3),(1,0)AC BC ACB A C =∠=︒，则点B 的坐标为________．【答案】（4，1）【分析】如图，过点B 作BD ⊥x 轴于D ，根据点A 、点C 坐标可得OA 、OC 的长，根据同角的余角相等可得∠OAC =∠DCB ，利用AAS 可证明△OAC ≌△DC B ，根据全等三角形的性质可得BD =OC ，CD =OA ，即可求出OD 的长，进而可得答案．【详解】如图，过点B 作BD ⊥x 轴于D ，∵A （0，3），C （1，0），∴OA =3，OC =1，∵∠ACB =90°，∴∠OCA +∠DCB =90°，∵∠OAC +∠OCA =90°，∴∠OAC =∠DCB ，在△OAC 和△DC B 中，AOC CDB OAC DCB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△OAC ≌△DC B ，∴BD =OC =1，CD =OA =3，∴OD =OC +CD =4，∴点B 坐标为（4，1）．故答案为：（4，1）【点睛】本题考查坐标与图形及全等三角形的判定与性质，熟练掌握全等三角形的判定定理是解题关键．5．如图，ABC 为等腰直角三角形AC BC =，若o −3，0)，o0，2)，则点B 的坐标为_________．【答案】(2，−1)【分析】过点B 作BT y ⊥轴于点T ．证明AOC CTB ≅ ，可得结论．【详解】解：如图中，过点B 作BT y ⊥轴于点T ．∵o −3，0)，o0，2)，∴3OA =，2OC =，∵90AOC ACB CTB ∠=∠=∠=︒，∴90ACO BCT ∠+∠=︒，90BCT CBT ∠+∠=︒，∴ACO CBT ∠=∠，在AOC 和CTB △中，===AOC CTB ACO CBT AC CB ∠∠⎧⎪∠∠⎨⎪⎩，∴AOC CTB ≅ （AAS ），∴3AO CT ==，2BT CO ==，∴-1OT CT CO ==，∴（2，−1），故答案为：(2，−1)．【点睛】本题考查了坐标与图形，等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．6．如图所示，ABC 中，,90AB AC BAC =∠=︒．直线l 经过点A ，过点B 作BE l ⊥于点E ，过点C 作CF l ⊥于点F ．若2,5==BE CF ，则EF =__________．【答案】7【分析】根据全等三角形来实现相等线段之间的关系，从而进行计算，即可得到答案；【详解】解：∵BE ⊥l ，CF ⊥l ，∴∠AEB =∠CFA =90°．∴∠EAB +∠EBA =90°．又∵∠BAC =90°，∴∠EAB +∠CAF =90°．∴∠EBA =∠CAF ．在△AEB 和△CFA 中∵∠AEB =∠CFA ，∠EBA =∠CAF ，AB =AC ，∴△AEB ≌△CFA ．∴AE =CF ，BE =AF ．∴AE +AF =BE +CF ．∴EF =BE +CF ．∵2,5==BE CF ，∴257EF =+=；故答案为：7．【点睛】本题考查了全等三角形的判定和性质，余角的性质，解题的关键是熟练掌握所学的知识，正确的证明三角形全等．7．如图，一个等腰直角三角形ABC 物件斜靠在墙角处（∠O ＝90°），若OA ＝50cm ，OB ＝28cm ，则点C 离地面的距离是____cm ．∴90CDB AOB ∠=∠=︒∵ABC ∆是等腰直角三角形∴AB =CB ，90ABC ∠=︒∴90ABO CBD ∠+∠=︒又90CBD BCD ∠+∠=︒∴ABO BCD∠=∠在ABO ∆和BCD ∆中，AOB BDC ABO BCD AB CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ABO BCD AAS ∆≅∆∴28cmCD BO ==故答案为：28．【点睛】本题主要考查了等腰直角三角形的性质、三角形全等的判定与性质，正确作出辅助线构造全等三角形是解答本题的关键．8．如图，AB ＝BC ，AB ⊥BC ，AE ⊥BD 于F ，BC ⊥CD ，求证：EC ＝AB －CD ．【答案】见解析【分析】利用ASA 证明出△ABE ≌△BCD ，在通过等量代换进行解答．【详解】证明：∵AB ⊥BC ，CD ⊥BC ，∴∠ABC ＝∠ACD ＝90°∴∠AEB ＋∠A ＝90°∵AE ⊥BD∴∠BFE ＝90°∴∠AEB ＋∠FBE ＝90°∴∠A ＝∠FBE ，又∵AB ＝BC ，∴△ABE ≌△BCD ，∴AB ＝BC ，BE ＝CD ，∴EC ＝BC －BE ＝AB －CD【点睛】本题考查了三角形全等的判定及性质，解题的关键是掌握三角形的判定定理，再利用等量代换的思想来间接证明．【提高测试】1．如图，在平面直角坐标系中，点A 、B 分别在x 轴的负半轴和正半轴上，以AB 为边向上作正方形ABCD ，四边形OEFG 是其内接正方形，若直线OF 的表达式是y ＝2x ，则ABCDOEFG S S 正方形正方形的值为（）A ．43B ．85C ．169D ．94【答案】B【分析】根据正方形性质易得GBO FCG ≅ ，从而可得CG BO =、FC GB =，设OB =a ，BG =b ，可得F 点坐标为(,)a b a b -+，根据F 点在直线OF 上，可求出3a b =，然后即可根据正方形面积和勾股定理求出面积比．【详解】解：在正方形ABCD ，正方形OEFG 中，90OBG OGF GCF ∠=∠=∠=︒，FG OG =，∴90OGB GOB OGB CGF ∠+∠=∠+∠=︒，∴GOB CGF ∠=∠，在GBO 和△FCG 中，OBG GCF GOB FGC OG FG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴GBO FCG ≅ （AAS ）∴CG BO =、FC GB =，设CG BO a ==、FC GB b ==，∴BC BG CG a b =+=+，HF OB FC a b =-=-，∴点F 坐标为(,)a b a b -+，∵直线OF 的表达式是y ＝2x ，∴2()a b a b -=+，2．如图，AE ⊥AB ，且AE =AB ，BC ⊥CD ，且BC =CD ，EF =6，BG =3，DH =4，计算图中实线所围成的图形的面积S 是______．3．已知直线l 经过正方形ABCD 的顶点A ，过点B 和点D 分别作直线的垂线BM 和DN ，垂足分别为点M 、点N ，如果5BM =，3DN =，那么点M 和点N 之间的距离为_______．（1）如图1，过A 的直线与斜边BC 不相交时，直接写出线段EF 、BE 、CF 的数量关系是______；（2）如图2，过A 的直线与斜边BC 相交时，探究线段EF 、BE 、CF 的数量关系并加以证明；（3）在（2）的条件下，如图3，直线FA 交BC 于点H ，延长BE 交AC 于点G ，连接BF 、FG 、HG ，若AHB GHC ∠=∠，6EF CF ==，2EH FH =，四边形ABFG 的面积是90，求GHC 的面积．【答案】（1）数量关系为：EF =BE +CF ；（2）数量关系为：EF =BE -CF ．证明见详解；（3）S △GHC =15．【分析】（1）数量关系为：EF =BE +CF ．利用一线三直角得到∠BEA =∠AFC =90°，∠EBA =∠FAC ，再证△GHC =S △ACF -S △HCF -S △AGH 5．如图1所示，已知ABC 中，90,ACB AC BC ∠=︒=，直线m 经过点C ，过A 、B 两点分别作直线m 的垂线，垂足分别为E 、F ．（1）如图1，当直线m 在A 、B 两点同侧时，求证：EF AE BF =+；（2）若直线m 绕点C 旋转到图2所示的位置时（BF AE <），其余条件不变，猜想EF 与AE ，BF 有什么数量关系？并证明你的猜想；（3）若直线m 绕点C 旋转到图3所示的位置时（BF AE >）其余条件不变，问EF 与AE ，BF 的关系如何？直接写出猜想结论，不需证明．【答案】（1）见解析；（2）EF AE BF =-，理由见解析；（3）EF BF AE =-，理由见解析【分析】（1）先证得90AEC BFC ∠=∠=︒，EAC FCB ∠=∠，根据AAS 证EAC FCB △≌△，推出CE BF =，AE CF =即可；（2）类比（1）证得对应的两个三角形全等，由此可推出CE BF =，AE CF =，再根据EF CF CE =-即可得到EF AE BF =-；（3）类比（1）证得对应的两个三角形全等，由此可推出CE BF =，AE CF =，再根据EF CE CF =-即可得到EF BF AE =-．【详解】（1）证明：AE EF ⊥Q ，BF EF ⊥，90ACB ∠=︒，90AEC BFC ACB ∴∠=∠=∠=︒，90EAC ECA ∴∠+∠=︒，90ECA FCB ∠+∠=︒，EAC FCB ∴∠=∠，在EAC 和FCB 中，AEC CFB EAC FCB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()EAC FCB AAS ∴△≌△，CE BF ∴=，AE CF =，∵EF CF CE =+，∴EF AE BF =+；（2）解：EF AE BF =-，理由如下：AE EF ⊥Q ，BF EF ⊥，90ACB ∠=︒，90AEC BFC ACB ∴∠=∠=∠=︒，90EAC ECA ∴∠+∠=︒，90ECA FCB ∠+∠=︒，EAC FCB ∴∠=∠，在EAC 和FCB 中，AEC CFB EAC FCB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()EAC FCB AAS ∴△≌△，CE BF ∴=，AE CF =，∵EF CF CE =-，∴EF AE BF =-；（3）解：EF BF AE =-，理由如下：AE EF ⊥Q ，BF EF ⊥，90ACB ∠=︒，90AEC BFC ACB ∴∠=∠=∠=︒，90EAC ECA ∴∠+∠=︒，90ECA FCB ∠+∠=︒，EAC FCB ∴∠=∠，在EAC 和FCB 中，AEC CFB EAC FCB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()EAC FCB AAS ∴△≌△，CE BF ∴=，AE CF =，∵EF CE CF =-，∴EF BF AE =-．【点睛】本题考查了全等三角形的判定与性质，主要涉及到了全等三角形的判定与性质，等量代换等知识点，难度不大，熟练掌握全等三角形的判定与性质是解决本题的关键．6．如图1，在平面直角坐标中，点()0,A m ，(),0B m ，()0,m C -，其中0m >，点P 为线段OA 上任意一点，连接BP ，CE BP ⊥于E ，AD BP ⊥于D ．（1）求证：AD BE =；（2）当3m =时，若点()3,0N -，请你在图1中连接CD ，EN 交于点Q ．求证：EN CD ⊥；（3）若将“点P 为线段OA 上任意一点”，改为“点P 为线段OA 延长线上任意一点”，其他条件不变，连接CD ，EN CD ⊥，垂足为F ，交y 轴于点H ，交x 轴于点N ，请在图2中补全图形，求点N 的坐标（用含m 的代数式表示）．【答案】（1）见解析；（2）见解析；（3）见解析，(),0m -【分析】（1）先根据点()0,A m ，(),0B m ，()0,C m -，得到OA OB OC m ===，则由三线合一定理得到，AB BC =，证明90ABC ∠= ，推出=CBE BAD ∠∠即可证明ABD BCE ≅ ，得到AD BE =；（2）先根据点()3,0N -，得到3OA OB OC ON ====，则6AC BN ==，再证明DAC EBN ∠=∠，即可利用SAS 证明DAC EBN ≅△△得到ACD BNE ∠=∠，再由NGF CGO ∠=∠，可以推出90NFG COG ∠=∠=o ，即CD EN ⊥；（3）同样先证明=CBE BAD ∠∠，推出ABD BCE ≅ ，得到AD BE =，即可得到CAD NBE ∠=∠，再由90NOH CFH ∠=∠=o ，OHN FHC ∠=∠，得到ACD BNE ∠=∠，则ACD BNE ≅△△，推出2AC BN m ==．【详解】证明：（1）如图1，∵点()0,A m ，(),0B m ，()0,C m -，∴OA OB OC m ===，∵OB AC ⊥，∴AB BC =，∵∠AOB =∠AOC =90°，∴45BAC BCA ABO CBO ∠=∠=∠=∠=o ，∴90ABC ∠= ，∵AD BP ⊥，CE BP ⊥，∴90ABC D CEB ∠=∠=∠=o∴90ABD CBE ABD BAD ∠+∠=∠+∠=o ，∴=CBE BAD ∠∠，∴()ABD BCE AAS ≅V V ，∴AD BE =；（2）如图2，由（1）得ABD BCE ≅ ，∴AD BE =，∵3m =，点()3,0N -，∴3OA OB OC ON ====，∴6AC BN ==，∵=CBE BAD ∠∠，45BAC CBO ∠=∠=o ，∴BAD BAC CBE CBO ∠-∠=∠-∠，∴DAC EBN ∠=∠，又∵BE =AD ，AC =BN ，∴()DAC EBN SAS ≅△△∴ACD BNE ∠=∠，∵NGF CGO ∠=∠，∴90NFG COG ∠=∠=o ，∴CD EN ⊥；（3）如图3，由（1）得OA OB OC m ===，AB BC =，45BAC CBO ∠=∠=o ，90ABC ∠= ，∵AD BP ⊥，CE BP ⊥，∴90ABC ADB CEB ∠=∠=∠=o ，∵90ABD CBE ABD BAD ∠+∠=∠+∠=o ，∴=CBE BAD ∠∠，∴()ABD BCE AAS ≅V V ，∴AD BE =，∵BAC BAD CBO CBE ∠+∠=∠+∠，∴CAD NBE ∠=∠，∵EN CD ⊥,x 轴y ⊥轴，∴90NOH CFH ∠=∠=o ，∵OHN FHC ∠=∠，∴ACD BNE ∠=∠，∴()ACD BNE AAS ≅△△∴2AC BN m ==，∴点N 的坐标为(),0m -．【点睛】本题主要考查了坐标与图形，全等三角形的性质与判定，等腰直角三角形的性质与判定等等，解题的关键在于能够熟练掌握全等三角形的性质与判定条件．7．在平面直角坐标系中，点A 的坐标为()4,0，点B 为y 轴正半轴上的一个动点，以B 为直角顶点，AB 为直角边在第一象限作等腰Rt ABC ．(1)如图1，若3OB =，则点C 的坐标为______；(2)如图2，若4OB =，点D 为OA 延长线上一点，以D 为直角顶点，BD 为直角边在第一象限作等腰Rt BDE △，连接AE ，求证：AE AB ⊥；(3)如图3，以B 为直角顶点，OB 为直角边在第三象限作等腰Rt OBF ．连接CF ，交y 轴于点P ，求线段BP 的长度．在△ABO 和△BCH 中，CHB AOB BCH ABO BC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABO ≌△BCH （AAS ），∴CH =OB =3，BH =AO =4，∴OH =7，∴点C （3，7），故答案为：（3，7）；（2）过点E 作EF ⊥x 轴于F ，∴∠EFD =∠BDE =∠BOD =90°，∴∠BDO +∠EDF =90°=∠BDO +∠DBO ，∴∠DBO =∠EDF ，在△BOD 和△DFE 中，BOD EFD DBO EDF BD ED ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BOD ≌△DFE （AAS ），∴BO =DF =4，OD =EF ，∵点A 的坐标为（4，0），∴OA =OB =4，∴∠BAO =45°，8．（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明∶DE=BD+CE．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．【答案】（1）见解析（2）成立，证明见解析（3）△DEF为等边三角形，证明见解析【分析】（1）因为DE=DA+AE，故由全等三角形的判定AAS证△ADB≌△CEA，得出DA=EC，AE=BD，从而证得DE=BD+CE；（2）成立，仍然通过证明△ADB≌△CEA，得出BD=AE，AD=CE，所以DE=DA+AE=EC+BD；（3）由△ADB≌△CEA得BD=AE，∠DBA=∠CAE，由△ABF和△ACF均等边三角形，得∠ABF=∠CAF=60°，FB=FA，所以∠DBA+∠ABF=∠CAE+∠CAF，即∠DBF=∠FAE，所以△DBF≌△EAF，所以FD=FE，∠BFD=∠AFE，再根据∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600得到△DEF是等边三角形．【详解】解：（1）证明：∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA=90°．∵∠BAC＝90°，∴∠BAD+∠CAE=90°．∵∠BAD+∠ABD=90°，∴∠CAE=∠ABD．又AB=AC，∴△ADB≌△CEA（AAS）．∴AE=BD，AD=CE．∴DE=AE+AD=BD+CE；（2）成立．证明如下：∵∠BDA=∠BAC=α，∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α．∴∠DBA=∠CAE．∵∠BDA=∠AEC=α，AB=AC，∴△ADB≌△CEA（AAS）．∴AE=BD，AD=CE．∴DE=AE+AD=BD+CE；（3）△DEF为等边三角形．理由如下：由（2）知，△ADB≌△CEA，BD=AE，∠DBA=∠CAE，∵△ABF和△ACF均为等边三角形，∴∠ABF=∠CAF=60°．∴∠DBA+∠ABF=∠CAE+∠CAF．∴∠DBF=∠FAE．∵BF=AF，∴△DBF≌△EAF（SAS）．∴DF=EF，∠BFD=∠AFE．∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°．∴△DEF为等边三角形．【点睛】此题考查了全等三角形的性质和判定、等边三角形的性质和判定，解题的关键是熟练掌握全等三角形的性质和判定，等边三角形的性质和判定．中，9．（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在ABC=+．∠=︒，AB ACBAC90=，直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点D，E．求证：DE BD CE（2）组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在ABC 中，AB AC =，D ，A ，E 三点都在直线l 上，并且有BDA AEC BAC α∠=∠=∠=，其中α为任意锐角或钝角．请问结论DE BD CE =+是否成立？若成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过ABC 的边AB ，AC 向外作正方形ABDE 和正方形ACFG ，AH 是BC 边上的高．延长HA 交EG 于点I ．若7AEG S =△，则AEI S =△______．【答案】（1）见解析；（2）结论成立，理由见解析；（3）3.5【分析】（1）由条件可证明△ABD ≌△CAE ，可得DA =CE ，AE =BD ，可得DE =BD +CE ；（2）由条件可知∠BAD +∠CAE =180°-α，且∠DBA +∠BAD =180°-α，可得∠DBA =∠CAE ，结合条件可证明△ABD ≌△CAE ，同（1）可得出结论；（3）由条件可知EM =AH =GN ，可得EM =GN ，结合条件可证明△EMI ≌△GNI ，可得出结论I 是EG 的中点．【详解】解：（1）证明：如图1中，∵BD ⊥直线l ，CE ⊥直线l ，∴∠BDA =∠CEA =90°，∵∠BAC =90°，∴∠BAD +∠CAE =90°，∵∠BAD +∠ABD =90°，∴∠CAE =∠ABD ，在△ADB 和△CEA 中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADB ≌△CEA （AAS ），∴AE =BD ，AD =CE ，∴DE =AE +AD =BD +CE ．（2）解：成立．理由：如图2中，∵∠BDA =∠BAC =α，∴∠DBA +∠BAD =∠BAD +∠CAE =180°-α，∴∠DBA =∠CAE ，10．如图，在ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（点D不与点B、C重合），连接AD，作∠ADE=40°，DE交线段AC于点E．（1）当∠BDA=115°时，∠EDC=______°，∠AED=______°；（2）线段DC的长度为何值时，△ABD≌△DCE，请说明理由；（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求∠BDA的度数；若不可以，请说明理由．【答案】（1）25°，65°；（2）2，理由见详解；（3）可以，110°或80°.【分析】（1）利用邻补角的性质和三角形内角和定理解题；（2）当DC=2时，利用∠DEC+∠EDC=140°，∠ADB+∠EDC=140°，求出∠ADB=∠DEC，再利用AB=DC=2，即可得出△ABD≌△DCE．（3）当∠BDA的度数为110°或80°时，△ADE的形状是等腰三角形．【详解】解：（1）∵∠B=40°，∠ADB=115°，∴∠BAD=180°-∠B-∠ADB=180°-115°-40°=25°，∵AB=AC，∴∠C=∠B=40°，∵∠EDC=180°-∠ADB-∠ADE=25°，∴∠DEC=180°-∠EDC-∠C=115°，∴∠AED=180°-∠DEC=180°-115°=65°；（2）当DC=2时，△ABD≌△DCE，理由：∵∠C=40°，∴∠DEC+∠EDC=140°，又∵∠ADE=40°，∴∠ADB+∠EDC=140°，∴∠ADB=∠DEC，又∵AB=DC=2，在△ABD和△DCE中，ADB DEC B C AB DC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝∴△ABD ≌△DCE （AAS ）；（3）当∠BDA 的度数为110°或80°时，△ADE 的形状是等腰三角形，∵∠BDA=110°时，∴∠ADC=70°，∵∠C=40°，∴∠DAC=70°，∴△ADE 的形状是等腰三角形；∵当∠BDA 的度数为80°时，∴∠ADC=100°，∵∠C=40°，∴∠DAC=40°，∴△ADE 的形状是等腰三角形．【点睛】本题主要考查学生对等腰三角形的判定与性质，全等三角形的判定与性质，三角形外角的性质等知识点的理解和掌握，此题涉及到的知识点较多，综合性较强，但难度不大，属于基础题．11．综合与探究：在平面直角坐标系中，已知A （0，a ），B （b ，0）且a ，b 满足（a ﹣3）2+|a ﹣2b ﹣1|＝0（1）求A ，B 两点的坐标（2）已知△ABC 中AB =CB ，∠ABC ＝90°，求C 点的坐标（3）已知AB ，试探究在x 轴上是否存在点P ，使△ABP 是以AB 为腰的等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．12．如图，在ABC 中，AB BC =．（1）如图①所示，直线NM 过点B ，AM MN ⊥于点M ，⊥CN MN 于点N ，且90ABC ∠=︒．求证：MN AM CN =+．（2）如图②所示，直线MN 过点B ，AM 交MN 于点M ，CN 交MN 于点N ，且AMB ABC BNC ∠=∠=∠，则MN AM CN =+是否成立？请说明理由．【答案】（1）见解析；（2）MN AM CN =+仍然成立，理由见解析【分析】（1）首先根据同角的余角相等得到BAM CBN ∠=∠，然后证明()AMB BNC AAS ≅△△，然后根据全等三角形对应边相等得到AM BN =，BM CN =，然后通过线段之间的转化即可证明MN AM CN =+；（2）首先根据三角形内角和定理得到MAB CBN ∠=∠，然后证明()AMB BNC AAS ≅△△，根据全等三角形对应边相等得到MN MB BN =+，最后通过线段之间的转化即可证明MN AM CN =+．【详解】证明：（1）∵AM MN ⊥，⊥CN MN ，∴90AMB BNC ∠=∠=︒，∴90ABM BAM ∠+∠=︒，∵90ABC ∠=︒，∴90ABM CBN Ð+Ð=°，∴BAM CBN ∠=∠，在AMB 和BNC 中，AMB BNC BAM CBN AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AMB BNC AAS ≅△△，∴AM BN =，BM CN =，∵BN MB MN +=，∴MN AM CN =+；（2）MN AM CN =+仍然成立，理由如下：∵180AMB MAB ABM ABM ABC CBN ∠+∠+∠=∠+∠+∠=︒，∵AMB ABC ∠=∠，∴MAB CBN ∠=∠，在AMB 和BNC 中，AMB BNC BAM CBN AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AMB BNC AAS ≅△△，∴AM BN =，NC MB =，∵MN MB BN =+，∴MN AM CN =+．【点睛】此题考查了全等三角形的性质和判定，同角的与相等，三角形内角和定理等知识，解题的关键是根据同角的余角相等或三角形内角和定理得到BAM CBN ∠=∠．13．通过对下面数学模型的研究学习，解决下列问题：（1）如图1，∠BAD ＝90°，AB ＝AD ，过点B 作BC ⊥AC 于点C ，过点D 作DE ⊥AC 于点E ．由∠1+∠2＝∠2+∠D ＝90°，得∠1＝∠D ．又∠ACB ＝∠AED ＝90°，可以推理得到△ABC ≌△DAE ．进而得到AC ＝，BC ＝AE ．我们把这个数学模型称为“K 字”模型或“一线三等角”模型；（2）如图2，∠BAD ＝∠CAE ＝90°，AB ＝AD ，AC ＝AE ，连接BC ，DE ，且BC ⊥AF 于点F ，DE 与直线AF 交于点G ．求证：点G 是DE 的中点；（深入探究）（3）如图，已知四边形ABCD 和DEGF 为正方形，△AFD 的面积为S 1，△DCE 的面积为S 2，则有S 1S 2（填“＞、＝、＜”）【答案】（1）DE ；（2）见解析；（3）=【分析】（1）根据全等三角形的性质可直接进行求解；（2）分别过点D 和点E 作DH ⊥FG 于点H ，EQ ⊥FG 于点Q ，进而可得∠BAF =∠ADH ，然后可证△ABF ≌△DAH ，则有AF =DH ，进而可得DH =EQ ，通过证明△DHG ≌△EQG 可求解问题；（3）过点D 作DO ⊥AF 交AF 于O ，过点E 作EN ⊥OD 交OD 延长线于N ，过点C 作CM ⊥OD 交OD 延长线于M ，由题意易得∠ADC =∠90°，AD =DC ，DF =DE ，然后可得∠ADO =∠DCM ，则有△AOD ≌△DMC ，△FOD ≌△DNE ，进而可得OD =NE ，通过证明△ENP ≌△CMP 及等积法可进行求解问题．【详解】解：（1）∵ABC DAE △≌△，∴AC DE =；（2）分别过点D 和点E 作DH ⊥FG 于点H ，EQ ⊥FG 于点Q ，如图所示：∴90DAH ADH ∠+∠=︒，∵90BAD ∠=︒，∴90BAF DAH ∠+∠=︒，∴BAF ADH ∠=∠，∵BC AF ⊥，∴90BFA AHD ∠=∠=︒，∵AB DA =，∴△ABF ≌△DAH ，∴AF =DH ，同理可知AF =EQ ，∴DH =EQ ，∵DH ⊥FG ，EQ ⊥FG ，∴90DHG EQG ∠=∠=︒，∵DGH EGQ∠=∠∴△DHG ≌△EQG ，∴DG =EG ，即点G 是DE 的中点；（3）12S S =，理由如下：如图所示，过点D 作DO ⊥AF 交AF 于O ，过点E 作EN ⊥OD 交OD 延长线于N ，过点C 作CM ⊥OD 交OD 延长线于M∵四边形ABCD 与四边形DEGF 都是正方形∴∠ADC =∠90°，AD =DC ，DF =DE∵DO ⊥AF ，CM ⊥OD ，∴∠AOD =∠CMD =90°，∠OAD +∠ODA =90°，∠CDM +∠DCM =90°，又∵∠ODA +∠CDM =90°，∴∠ADO =∠DCM ，∴△AOD ≌△DMC ，∴AOD DMC S S =△△，OD =MC ，同理可以证明△FOD ≌△DNE ，∴FOD DNE S S =△△，OD =NE ，∴MC =NE ，∵EN ⊥OD ，CM ⊥OD ，∠EPN =∠CMP ，∴△ENP ≌△CMP ，∴ENP CMP S S △△=，∵,ADF AOD FOD DCE DCM CMP DEN ENP S S S S S S S S =+=-++ ，∴DCE DCM DEN AOD FOD S S S S S =+=+ ,∴DCE ADF S S △△=即12S S =．【点睛】本题主要考查全等三角形的性质与判定、直角三角形的两个锐角互余及等积法，熟练掌握全等三角形的判定条件是解题的关键．14．已知：CD 是经过∠BCA 的顶点C 的一条直线，CA ＝CB ，E 、F 是直线CD 上两点，∠BEC ＝∠CFA ＝∠α．（1）若直线CD 经过∠BCA 的内部，∠BCD ＞∠ACD ．①如图1，∠BCA ＝90°，∠α＝90°，写出BE ，EF ，AF 间的等量关系：．②如图2，∠α与∠BCA 具有怎样的数量关系，能使①中的结论仍然成立？写出∠α与∠BCA 的数量关系．（2）如图3．若直线CD 经过∠BCA 的外部，∠α＝∠BCA ，①中的结论是否成立？若成立，进行证明；若不成立，写出新结论并进行证明．【答案】（1）①EF =BE -AF ；②∠α+∠BCA =180°，理由见解析；（2）不成立，EF =BE +AF ，证明见解析【分析】（1）①求出∠BEC =∠AFC =90°,∠CBE =∠ACF ，根据AAS 证△BCE ≌△CAF ，推出BE =CF ，CE =AF 即可得出结论；②求出∠BEC =∠AFC ,∠CBE =∠ACF ，根据AAS 证△BCE ≌△CAF ，推出BE =CF ，CE =AF 即可得出结论;（2）求出∠BEC =∠AFC ，∠CBE =∠ACF ，根据AAS 证△BCE ≌△CAF ，推出BE =CF ，CE =AF 即可得出结论．【详解】（1）①EF 、BE 、AF 的数量关系：EF =BE -AF ，证明：当α=90°时，∠BEC =∠CFA =90°，∵∠BCA =90°,∴∠BCE ＋∠ACF =90°,∵∠BCE ＋∠CBE =90°，∴∠ACF =∠CBE ，∵AC =BC ,∴△BCE ≌△CAF ,∴BE =CF ,CE =AF ,∵CF =CE ＋EF ,∴EF =CF -CE =BE -AF ；②∠α与∠BCA 关系：∠α+∠BCA =180°当∠α+∠BCA =180°时，①中结论仍然成立;理由是：如题图2，∵∠BEC =∠CFA =∠α,180CBE BCE BEC ∠+∠+∠=︒,∠α+∠ACB =180°,ACB CBE BCE∴∠=∠+∠又∵ACB ACF BCE∠=∠+∠∴∠CBE =∠ACF ,在△BCE 和△CAF 中BEC CFA CBE ACF BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BCE ≌△CAF (AAS),∴BE =CF ,CE =AF ，∴EF =CF -CE =BE -AF ;故答案为:∠α+∠BCA =180°；（2）EF 、BE 、AF 的数量关系:EF =BE +AF ，理由如下∵∠BEC =∠CFA =∠α,∠α=∠BCA ,又∵∠EBC +∠BCE ＋∠BEC =180°,∠BCE ＋∠ACF +∠ACB =180°,∴∠EBC ＋∠BCE =∠BCE ＋∠ACF∴∠EBC =∠ACF，在△BEC 和△CFA 中EBC FCA BEC CFA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CFA (AAS )∴AF =CE ，BE =CF∵EF =CE +CF ,∴EF =BE ＋AF ．【点睛】本题考查了全等三角形的性质和判定，证明△BCE ≌△CAF 是解题的关键．15．通过对数学模型“K 字”模型或“一线三等角”模型的研究学习，解决下列问题：[模型呈现]如图1，90BAD ∠=︒，AB AD =，过点B 作BC AC ⊥于点C ，过点D 作DE AC ⊥于点E ．求证：BC AE =．[模型应用]如图2，AE AB ⊥且AE AB =，BC CD ⊥且BC CD =，请按照图中所标注的数据，计算图中实线所围成的图形的面积为________________．[深入探究]如图3，90BAD CAE ∠=∠=︒，AB AD =，AC AE =，连接BC ，DE ，且BC AF ⊥于点F ，DE 与直线AF 交于点G ．若21BC =，12AF =，则ADG △的面积为_____________．【答案】[模型呈现]见解析；[模型应用]50；[深入探究]63【分析】[模型呈现]证明ABC DAE △≌△，根据全等三角形的对应边相等得到BC AE =；[模型应用]根据全等三角形的性质得到3AP BG ==，6,4AG EP CG DH ====，3CG BG ==，根据梯形的面积公式计算，得到答案；[深入探究]过点D 作DP AG ⊥于P ，过点E 作EQ AG ⊥交AG 的延长线于Q ，根据全等三角形的性质得到12,12,,DP AF EQ AF AP BF AQ CF ======，证明DPG EQG ≌，得到.PG GQ =，进而求出AG ，根2故答案为：50；[深入探究]过点D 作DP 由[模型呈现]可知，AFB ∴12,DP AF EQ ===。

三垂直模型与全等综合剖析

FEC F E DCB A K 模型图与全等知识点基本图形本题8分）如图，在等腰R t △ABC 中，∠ACB =90°，D 为BC 的中点，DE ⊥AB ，垂足为E ，过点B 作BF ∥AC 交DE 的延长线于点F ，连接CF ．（1）求证：AD ⊥CF ；（2）连接AF ，求证：AF ＝CF ．22．边长为1的正方形ABCD 中，E 是AB 中点，连CE ，过B 作BF ⊥CE 交AC 于F ，求AF.【例8】【例9】等腰Rt △ABC 中 ∠ACB ＝90°，AC=BC ；F 是BC 上的中点，连AF ，作CD ⊥AF 于E ，交AB 于D ；连FD. 求证：AD ＝2BD ；【例3】已知△ABC 中,∠C=90 ,AC=BC,D 是AB 的中点,E 是BC 上任一点,EP ⊥CB,PF ⊥AC,E 、F 为垂足, 求证:△DEF 是等腰直角三角形.H A B DCE FFED C BAH F ED C B A【例4】如图，D 为线段AB 的中点，在AB 上取异于D 的点C ，分别以AC 、BC 为斜边在AB同侧作等腰直角三角形ACE 与BCF ，连结DE 、DF 、EF ，求证：△DEF 为等腰直角三角形。

【例5】如图，分别以△ABC 的边AB 、AC 向外作等腰Rt △ABD ，等腰Rt △ACE ；连接DE 。

AF 是△ABC 的中线，FA 的延长线交DE 于点H ，求证：DE ＝2AF【例6】如图，在正方形ABCD 中，点N 是BC 边上的点。

连接AN ，MN ⊥AN 交∠DCB 的外角平分线于点M 。

求证：AN ＝MN9、如图，直线AB 交x 轴正半轴于点A （a ，0），交y 轴正半轴于点B （0， b ），且a 、b 满足4 a + |4－b |=0（1）求A 、B 两点的坐标；（2）D 为OA 的中点，连接BD ，过点O 作OE ⊥BD 于F ，交AB 于E ，求证∠BDO =∠EDA ；（3）如图，P 为x 轴上A 点右侧任意一点，以BP 为边作等腰Rt △PBM ，A BO D EFy x其中PB =PM ，直线MA 交y 轴于点Q ，当点P 在x 轴上运动时，线段OQ 的长是否发生变化？若不变，求其值；若变化，求线段OQ 的取值范围.10ABO MPQxyEDCB AOxyDCB AOxy P24．（12分）如图，COD 等腰直角三角形，CA ⊥x 轴。

(完整版)关于“一线三垂直”模型及其在平面几何中的应用

关于“一线三垂直”模型及其在平面几何中的应用“一线三垂直”模型是“一线三等角”模型的特殊情况，（关于“一线三等角”模型详见比例与相似高级教程（六）：相似三角形的“一线三等角”模型），即三个等角角度为90º，于是有三组边相互垂直，所以称为“一线三垂直”模型。

“一线三垂直”模型在平面几何中有着及其重要的地位，常出现的图例有以下几种：其中，在“变形2”模型下，根据相似原理，推理出了著名的“射影定理”这里主要讨论有一对对应边相等的情况。

【例1】如图，在等腰直角三角形ABC中，∠ACB=Rt∠，AC=BC，AE⊥CE于点E，BD⊥CE于点D，AE=5cm，BD=2cm，则DE的长为多少？【提示】根据“一线三垂直”模型的性质，△ACE≌△CBD，于是CD=AE=5cm，CE=BD=2cm，DE=5-2=3（cm）【例2】如图，在△ABC中，CA=CB，点D 为BC中点，CE⊥AD于点E，交AB于点F，连接DF。

求证：AD=CF+DF.【解析】此题乍一看起来和【例1】相同，却不能照搬照抄。

从要证明的结论来看，需要把AD这条线段“转化”到直线CF上。

如图，过点B作BG⊥CB，交CF的延长线于点G。

则易证△ACD≌△CBG，于是AD=CG=CF+FG；BG=CD=BD，BF=BF，∠DBF=∠GBF=45º，故△BDF≌△BGF，于是FD=FG，所以AD=CF+DF。

关于“一线三垂直”模型及其在平面几何中的应用（二）“一线三垂直”的性质：1，模型中必定存在至少两个三角形相似，三对等角，三对成比例的边长；2，当模型中有一组对应边长相等时，则模型中必定存在全等三角形。

【例3】如图，在△ABC中，AB=AC，∠BAC=90º，分别过B，C向过A点的直线作垂线，垂足分别为E，F。

专题11 全等三角形中的一线三等角模型(解析版)

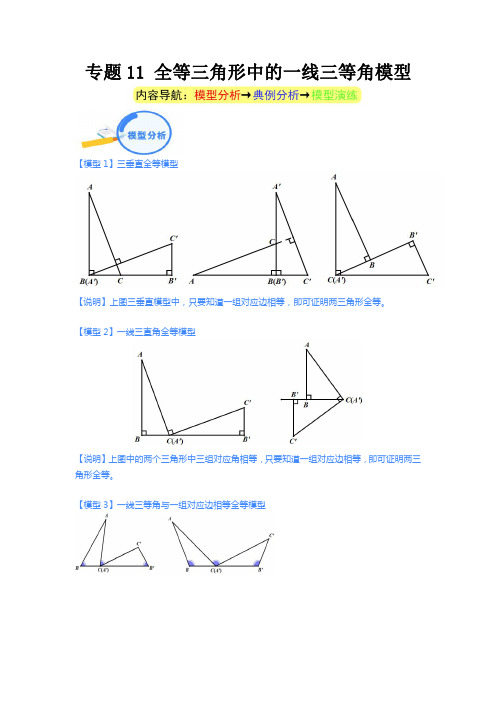
专题11全等三角形中的一线三等角模型【模型1】三垂直全等模型【说明】上图三垂直模型中，只要知道一组对应边相等，即可证明两三角形全等。

【模型2】一线三直角全等模型【说明】上图中的两个三角形中三组对应角相等，只要知道一组对应边相等，即可证明两三角形全等。

【模型3】一线三等角与一组对应边相等全等模型【说明】上图中可根据平角的概念和三角形内角和定理可求得的两个三角形中三组对应角相等，只要再知道一组对应边相等，即可证明两三角形全等。

【例1】如图，AC ＝CE ，∠ACE ＝90°，AB ⊥BD ，ED ⊥BD ，AB ＝6cm ，DE ＝2cm ，则BD 等于（）A ．6cmB ．8cmC ．10cmD ．4cm【答案】B 【分析】根据题意证明ABC CDE △≌△即可得出结论．【解析】解：∵AB ⊥BD ，ED ⊥BD ，∴90ABC CDE ∠=∠=︒，∵∠ACE ＝90°，∴90ACB DCE ∠+∠=︒，∵90ACB BAC ∠+∠=︒，∴BAC DCE ∠=∠，在ABC 和CDE △中，90ABC CDE BAC DCE AC CE ∠=∠=︒⎧⎪∠=∠⎪⎨⎪⎪⎩＝，∴()ABC CDE AAS ≌，∴6cm AB CD ==，2cm BC DE ==，∴268cm BD BC CD =+=+=，故选：B ．【例2】如图所示，ABC 中，,90AB AC BAC =∠=︒．直线l 经过点A ，过点B 作BE l ⊥于点E ，过点C 作CF l ⊥于点F ．若2,5==BE CF ，则EF =__________．【答案】7【分析】根据全等三角形来实现相等线段之间的关系，从而进行计算，即可得到答案；【解析】解：∵BE ⊥l ，CF ⊥l ，∴∠AEB =∠CFA =90°．∴∠EAB +∠EBA =90°．又∵∠BAC =90°，∴∠EAB +∠CAF =90°．∴∠EBA =∠CAF ．在△AEB 和△CFA 中∵∠AEB =∠CFA ，∠EBA =∠CAF ，AB =AC ，∴△AEB ≌△CFA ．∴AE =CF ，BE =AF ．∴AE +AF =BE +CF ．∴EF =BE +CF ．∵2,5==BE CF ，∴257EF =+=；故答案为：7．【例3】（1）观察理解：如图1，∠ACB ＝90°，AC ＝BC ，直线l 过点C ，点A ，B 在直线l 同侧，BD ⊥l ，AE ⊥l ，垂足分别为D ，E ，求证：△AEC ≌△CDB ．（2）理解应用：如图2，过△ABC边AB、AC分别向外作正方形ABDE和正方形ACFG，AH是BC边上的高，延长HA交EG于点I．利用（1）中的结论证明：I是EG的中点．（3）类比探究：①将图1中△AEC绕着点C旋转180°得到图3，则线段ED、EA和BD的关系_______；∥，AB⊥BC，AD＝2，BC＝3，将腰DC绕D点逆②如图4，直角梯形ABCD中，AD BC时针旋转90°至DE，△AED的面积为．【答案】（1）见解析；（2）见解析；（3）①ED=EA－BD；②1【分析】（1）根据同角的余角相等可得∠A＝∠BCD，再利用AAS证得△AEC≌△CDB，即可；（2）分别过点E、G向HI作垂线，垂足分别为M、N，由（1）可证得△EMA≌△AHB，△ANG ≌△CHA ，从而得到EM =GN ，可得到△EMI ≌△GNI ，从而得到EI =IG ，即可求证；（3）①由（1）得：△AEC ≌△CDB ，可得CE =BD ，AE =CD ，即可；②过点C 作CP ⊥AD 交AD 延长线于点P ，过点E 作EQ ⊥AD 交AD 延长线于点Q ，根据旋转的性质可得根据题意得：∠CDE =90°，CD =DE ，再由（1）可得△CDP ≌△DEQ ，从而得到DP =EQ ，然后根据两平行线间的距离，可得AP =BC ，进而得到PD =1，即可求解．【解析】（1）证明：∵BD ⊥l ，AE ⊥l ，∴∠AEC ＝∠BDC ＝90°，又∵∠ACB ＝90°∴∠A +∠ACE ＝∠ACE +∠BCD ＝90°，∴∠A ＝∠BCD ，在△AEC 和△CDB 中，AEC CDB A BCD AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AEC ≌△CDB （AAS ）；（2）证明：分别过点E 、G 向HI 作垂线，垂足分别为M 、N，由（1）得：△EMA ≌△AHB ，△ANG ≌△CHA ，∴EM ＝AH ，GN =AH ，∴EM =GN ，在△EMI 和△GNI 中，90EIM GIN EMI GNI EM GN ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△EMI ≌△GNI （AAS ）；∴EI =IG ，即I 是EG 的中点；（3）解：①由（1）得：△AEC ≌△CDB ，∴CE =BD ，AE =CD ，∵ED =CD -CE ，∴ED =EA －BD ；故答案为：ED =EA －BD②如图，过点C 作CP ⊥AD 交AD 延长线于点P ，过点E 作EQ ⊥AD 交AD 延长线于点Q ，根据题意得：∠CDE =90°，CD =DE ，由（1）得：△CDP ≌△DEQ ，∴DP =EQ ，直角梯形ABCD 中，AD BC ∥，AB ⊥BC ，∴AB ⊥AD ，∴AB ∥CP ，∴BC ⊥CP ，∵BC =3，∴AP =BC =3，∵AD =2，∴DP =AP -AD =1，∴EQ =1，∴△ADE 的面积为1121122AD EN 创=．故答案为：1一、单选题1．如图，点P ，D 分别是∠ABC 边BA ，BC 上的点，且4BD =，60ABC ∠=︒．连结PD ，以PD 为边，在PD 的右侧作等边△DPE ，连结BE ，则△BDE 的面积为（）A ．B ．2C ．4D ．【答案】A【分析】要求BDE ∆的面积，想到过点E 作EF BC ⊥，垂足为F ，因为题目已知60ABC ∠=︒，想到把ABC ∠放在直角三角形中，所以过点D 作DG BA ⊥，垂足为G ，利用勾股定理求出DG 的长，最后证明GPD FDE ∆≅∆即可解答．【解析】解：过点E 作EF BC ⊥，垂足为F ，过点D 作DG BA ⊥，垂足为G ，在Rt BGD 中，4BD =，60ABC ∠=︒，30BDG ∴∠=︒，122BG BD ∴==，GD ∴=PDE ∆是等边三角形，60PDE ∴∠=︒，PD DE =，180120PDB EDF PDE ∴∠+∠=︒-∠=︒，60ABC ∠=︒，180120PDB BPD ABC ∴∠+∠=︒-∠=︒，BPD EDF ∴∠=∠，90PGD DFE ∠=∠=︒，()GPD FDE AAS ∴∆≅∆，GD EF ∴==，BDE ∴∆的面积12BD EF =⋅，142=⨯⨯，=故选：A ．2．课间，小聪拿着老师的等腰直角三角板玩，不小心掉到两墙之间(如图)，∠ACB ＝90°，AC ＝BC ，从三角板的刻度可知AB ＝20cm ，小聪想知道砌墙砖块的厚度(每块砖的厚度相等)，下面为砌墙砖块厚度的平方的是（）．A ．20013cm 2B ．15013cm 2C ．10013cm 2D ．5013cm 2【答案】A【分析】设每块砖的厚度为x cm ，则AD =3x cm ，BE =2x cm ，然后证明△DAC ≌△ECB 得到CD =BE =2x cm ，再利用勾股定理求解即可．【解析】解：设每块砖的厚度为x cm ，则AD =3x cm ，BE =2x cm ，由题意得：∠ACB =∠ADC =∠BEC =90°，∴∠ACD +∠DAC =∠ACD +∠BCE =90°，∴∠DAC =∠ECB ，又∵AC =CB ，∴△DAC ≌△ECB （AAS ），∴CD =BE =2x cm ，∵222AC BC AB +=，222AD DC AC +=，∴()()222232220x x +=，∴220013x =，故选A ．3．一天课间，顽皮的小明同学拿着老师的等腰直角三角板玩，不小心将三角板掉到两根柱子之间，如图所示，这一幕恰巧被数学老师看见了，于是有了下面这道题：如果每块砖的厚度a ＝8cm ，则DE 的长为（）A ．40cmB ．48cmC ．56cmD ．64cm【答案】C 【分析】由等腰直角三角形的性质可得∠ACB ＝90°，AC ＝CB ，因此可以考虑证明△ACD 和△CBE 全等，可以证明DE 的长为7块砖的厚度的和．【解析】解：由题意得∠ADC ＝∠CEB ＝∠ACB ＝90°，AC ＝CB ，∴∠ACD ＝90°﹣∠BCE ＝∠CBE ，在△ACD 和△CBE 中，ADC CEB ACD CBE AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△CBE （AAS ），∴CD＝BE＝3a，AD＝CE＝4a，∴DE＝CD+CE＝3a+4a＝7a，∵a＝8cm，∴7a＝56cm，∴DE＝56cm，故选C．二、填空题4．如图，直线l1⊥l3，l2⊥l3，垂足分别为P、Q，一块含有45°的直角三角板的顶点A、B、C分别在直线l1、l2、线段PQ上，点O是斜边AB的中点，若PQ，则OQ的长等于_____．【答案】6【分析】由“AAS”可证△ACP≌△CBQ，可得AP＝CQ，PC＝BQ，由“AAS”可证△APO≌△BHO，可得AP＝BH，OP＝OH，由等腰直角三角形的性质和直角三角形的性质可求解．【解析】解：如图，连接PO，并延长交l2于点H，∵l1⊥l3，l2⊥l3，∴l1∥l3，∠APC＝∠BQC＝∠ACB＝90°，∴∠PAC+∠ACP＝90°＝∠ACP+∠BCQ，∴∠PAC＝∠BCQ，在△ACP和△CBQ中，∠=∠⎧⎪∠=∠⎨⎪=⎩PAC BCQ APC BQC AC BC ，∴△ACP ≌△CBQ （AAS ），∴AP ＝CQ ，PC ＝BQ ，∴PC +CQ ＝AP +BQ ＝PQ，∵AP ∥BQ ，∴∠OAP ＝∠OBH ，∵点O 是斜边AB 的中点，∴AO ＝BO ，在△APO 和△BHO 中，∠=∠⎧⎪∠=∠⎨⎪=⎩AOP BOH APO BHO AO BO ，∴△APO ≌△BHO （AAS ），∴AP ＝BH ，OP ＝OH ，∴BH +BQ ＝AP +BQ ＝PQ ，∴PQ ＝QH，∵∠PQH ＝90°，∴PHPQ ＝12，∵OP ＝OH ，∠PQH ＝90°，∴OQ ＝12PH ＝6．故答案为：65．如图，已知ABC 是等腰直角三角形，∠ACB ＝90°，AD ⊥DE 于点D ，BE ⊥DE 于点E ，且点C 在DE 上，若AD ＝5，BE ＝8，则DE 的长为_____．【答案】13【分析】先根据AD ⊥DE ，BE ⊥DE ，∠ADC =∠CEB =90°，则∠DAC +∠DCA =90°，△ABC 是等腰直角三角形，∠ACB =90°，可得AC =CB ，推出∠DAC =∠ECB ，即可证明△DAC ≌△ECB得到CE =AD =5，CD =BE =8，由此求解即可．【解析】解：∵AD ⊥DE ，BE ⊥DE ，∴∠ADC =∠CEB =90°，∴∠DAC +∠DCA =90°，∵△ABC 是等腰直角三角形，∠ACB =90°，∴∠DCA +∠BCE =90°，AC =CB∴∠DAC =∠ECB ，∴△DAC ≌△ECB （AAS ），∴CE =AD =5，CD =BE =8，∴DE =CD +CE =13，故答案为：13．三、解答题6．已知：如图，AB ⊥BD ，ED ⊥BD ，C 是BD 上的一点，AC ⊥CE ，AB ＝CD ，求证：BC ＝DE．【答案】见解析【分析】根据直角三角形全等的判定方法，ASA 即可判定三角形全等．【解析】证明：∵AB ⊥BD ，ED ⊥BD ，AC ⊥CE （已知）∴∠ACE ＝∠B ＝∠D ＝90°（垂直的意义）∵∠BCA +∠DCE +∠ACE ＝180°（平角的意义）∠ACE ＝90°（已证）∴∠BCA +∠DCE ＝90°（等式性质）∵∠BCA +∠A +∠B ＝180°（三角形内角和等于180°）∠B ＝90°（已证）∴∠BCA +∠A ＝90°（等式性质）∴∠DCE ＝∠A （同角的余角相等）在△ABC 和△CDE 中，A DCE AB CD B D ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABC ≌△CDE （ASA ）∴BC ＝DE （全等三角形对应边相等）7．如图，∠B =∠C =∠FDE =80°，DF =DE ，BF =1.5cm ，CE =2cm ，求BC的长．【答案】3.5【分析】由平角定义及三角形内角和定理解得EDC BFD ∠=∠，继而证明()BFD CDE AAS ≅V V ，得到=1.5,=2BF CD BD CE ==，最后根据线段的和差解题．【解析】解：∠B =∠C =∠FDE =80°，100,100BDF EDC BDF BFD ∴∠+∠=︒∠+∠=︒EDC BFD∴∠=∠在BFD △与CDE △中，B C EDC BFD DE DF ∠=∠⎧⎪∠=∠⎨⎪=⎩()BFD CDE AAS ∴≅=1.5,=2BF CD BD CE ∴==2 1.5 3.5BC BD DC ∴=+=+=．8．感知：（1）数学课上，老师给出了一个模型：如图1，90BAD ACB AED ∠=∠=∠=︒，由12180BAD ∠+∠+∠=︒，2180D AED ∠+∠+∠=︒，可得1D ∠=∠；又因为90ACB AED =∠=︒，可得ABC DAE △△∽，进而得到BC AC=______．我们把这个模型称为“一线三等角”模型．应用：（2）实战组受此模型的启发，将三等角变为非直角，如图2，在ABC 中，10AB AC ==，12BC =，点P 是BC 边上的一个动点（不与B 、C 重合），点D 是AC 边上的一个动点，且APD B ∠=∠．①求证：ABP PCD △△∽；②当点P 为BC 中点时，求CD 的长；拓展：（3）在（2）的条件下如图2，当APD △为等腰三角形时，请直接写出BP 的长．【答案】感知：（1）AEDE；应用：（2）①见解析；②3.6；拓展：（3）2或113【分析】（1）根据相似三角形的性质，即可求解；（2）①根据等腰三角形的性质得到∠B=∠C，根据三角形的外角性质得到∠BAP=∠CPD，即可求证；②根据相似三角形的性质计算，即可求解；（3）分PA=PD、AP=AD、DA=DP三种情况，根据等腰三角形的性质、相似三角形的性质，即可求解．【解析】感知：（1）∵△ABC∽△DAE，∴BC AC AE DE=，∴BC AE AC DE=，故答案为：AE DE；应用：（2）①∵∠APC=∠B+∠BAP，∠APC=∠APD+∠CPD，∠APD=∠B，∴∠BAP=∠CPD，∵AB=AC，∴∠B=∠C，∴△ABP∽△PCD；②BC=12，点P为BC中点，∴BP=PC=6，·∵△ABP∽△PCD，∴AB BPPC CD=，即1066CD=，解得：CD=3.6；拓展：（3）当PA=PD时，△ABP≌△PCD，∴PC=AB=10，∴BP=BC-PC=12-10=2；当AP=AD时，∠ADP=∠APD，∵∠APD =∠B =∠C ，∴∠ADP =∠C ，不合题意，∴AP ≠AD ；当DA =DP 时，∠DAP =∠APD =∠B ，∵∠C =∠C ，∴△BCA ∽△ACP ，∴BC AC AC CP =，即121010CP=，解得：253CP =，∴25111233BP BC CP =-=-=，综上所述，当APD △为等腰三角形时，BP 的长为2或113．9．问题背景：（1）如图①，已知ABC 中，90BAC ∠=︒，AB AC =，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D ，E ，易证：DE =______+______．（2）拓展延伸：如图②，将（1）中的条件改为：在ABC 中，AB AC =，D ，A ，E 三点都在直线m 上，并且有BDA AEC BAC ∠=∠=∠，请求出DE ，BD ，CE 三条线段的数量关系，并证明．（3）实际应用：如图③，在ACB △中，90ACB ∠=︒，AC BC =，点C 的坐标为()2,0-，点A 的坐标为()6,3-，请直接写出B 点的坐标．【答案】（1）BD ；CE ；证明见详解；（2）DE=BD+CE ；证明见详解；（3）点B 的坐标为()1,4B ．【分析】（1）根据全等三角形的判定和性质得到AE BD =，AD CE =，结合图形解答即可；（2）根据三角形内角和定理、平角的定义证明ABD CAE ∠=∠，证明ABD CAE ≌，根据全等三角形的性质得到AE BD =，AD CE =，结合图形解答即可；（3）根据AEC CFB ≌，得到3CF AE ==，4BF CE OE OC ==-=，根据坐标与图形性质解答即可．【解析】（1）证明：∵BD m ⊥，CE m ⊥，∴90ADB CEA ∠=∠=︒，∵90BAC ∠=︒，∴90BAD CAE ∠+∠=︒，∵90BAD ABD ∠+∠=︒，∴ CAE ABD ∠=∠，在ADB 和CEA 中ABD CAE ADB CEA AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ADB CEA ≌，∴AE BD =，AD CE =，∴DE AE AD BD CE =+=+，即：DE BD CE =+，故答案为：BD ；CE ；（2）解：数量关系：DE BD CE =+，证明：在ABD 中，180ABD ADB BAD ∠=︒-∠-∠，∵180CAE BAC BAD ∠=︒-∠-∠，BDA AEC ∠=∠，∴ABD CAE ∠=∠，在ABD 和CAE 中，ABD CAE BDA AEC AB CA ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝∴ABD CAE ≌，∴AE BD =，AD CE =，∴DE AD AE BD CE =+=+；（3）解：如图，作AE x ⊥轴于E ，BF x ⊥轴于F，由（1）可知，AEC CFB ≌，∴3CF AE ==，4BF CE OE OC ==-=，∴1OF CF OC =-=，∴点B 的坐标为()1,4B ．10．在直线m上依次取互不重合的三个点D，A，E，在直线m上方有AB＝AC，且满足∠BDA ＝∠AEC＝∠BAC＝α．(1)如图1，当α＝90°时，猜想线段DE，BD，CE之间的数量关系是；(2)如图2，当0＜α＜180时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由．【答案】(1)DE＝BD+CE．(2)DE＝BD+CE仍然成立，证明见解析【分析】（1）由∠BDA＝∠BAC＝∠AEC＝90°得到∠BAD+∠EAC＝∠BAD+∠DBA＝90°，进而得到∠DBA＝∠EAC，然后结合AB＝AC得证△DBA≌△EAC，最后得到DE＝BD+CE；（2）由∠BDA＝∠BAC＝∠AEC＝α得到∠BAD+∠EAC＝∠BAD+∠DBA＝180°﹣α，进而得到∠DBA＝∠EAC，然后结合AB＝AC得证△DBA≌△EAC，最后得到DE＝BD+CE．【解析】（1）解：DE＝BD+CE，理由如下，∵∠BDA＝∠BAC＝∠AEC＝90°，∴∠BAD+∠EAC＝∠BAD+∠DBA＝90°，∴∠DBA＝∠EAC，∵AB＝AC，∴△DBA≌△EAC（AAS），∴AD＝CE，BD＝AE，∴DE＝AD+AE＝BD+CE，故答案为：DE＝BD+CE．（2）DE＝BD+CE仍然成立，理由如下，∵∠BDA＝∠BAC＝∠AEC＝α，∴∠BAD+∠EAC＝∠BAD+∠DBA＝180°﹣α，∴∠DBA＝∠EAC，∵AB＝AC，∴△DBA≌△EAC（AAS），∴BD＝AE，AD＝CE，∴DE ＝AD +AE ＝BD +CE ；11．如图，90,ABC FA AB ∠=⊥于点A ，点D 在直线AB 上，,AD BC AF BD ==．(1)如图1，若点D 在线段AB 上，判断DF 与DC 的数量关系和位置关系，并说明理由；(2)如图2，若点D 在线段AB 的延长线上，其他条件不变，试判断（1）中结论是否成立，并说明理由．【答案】(1)DF =DC ，DF ⊥DC ；理由见解析(2)成立，理由见解析【分析】（1）先证△ADF ≌△BCD ，得DF =DC ，ADF BCD ∠=∠，再证∠FDC =90°即可得垂直；（2）先证△ADF ≌△BCD ，得DF =DC ，ADF BCD ∠=∠，再证∠FDC =90°即可得垂直．【解析】（1）解：∵90,ABC FA AB ∠=⊥，∴90ABC DAF ∠∠==，在△ADF 与△BCD 中AF BD DAF ABC AD BC =⎧⎪∠=∠⎨⎪=⎩，∴△ADF ≌△BCD ，∴DF =DC ，ADF BCD ∠=∠，∵∠BDC +∠BCD =90°，∴∠BDC +∠ADF =90°，∴∠FDC =90°，即DF ⊥DC ．（2）∵90,ABC FA AB ∠=⊥，∴90DBC DAF ∠∠==，在△ADF 与△BCD 中AF BD DAF DBC AD BC =⎧⎪∠=∠⎨⎪=⎩，∴△ADF ≌△BCD ，∴DF =DC ，ADF BCD ∠=∠，∵∠BDC +∠BCD =90°，∴∠BDC +∠ADF =90°，∴∠FDC =90°，即DF ⊥DC ．12．在直线m 上依次取互不重合的三个点,,D A E ，在直线m 上方有AB AC =，且满足BDA AEC BAC α∠=∠=∠=．(1)如图1，当90α=︒时，猜想线段,,DE BD CE 之间的数量关系是____________；(2)如图2，当0180α<<︒时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；(3)应用：如图3，在ABC 中，BAC ∠是钝角，AB AC =，,BAD CAE BDA AEC BAC ∠<∠∠=∠=∠，直线m 与CB 的延长线交于点F ，若3BC FB =，ABC 的面积是12，求FBD 与ACE 的面积之和．【答案】(1)DE ＝BD +CE(2)DE ＝BD +CE 仍然成立，理由见解析(3)△FBD 与△ACE 的面积之和为4【分析】（1）由∠BDA ＝∠BAC ＝∠AEC ＝90°得到∠BAD +∠EAC ＝∠BAD +∠DBA ＝90°，进而得到∠DBA ＝∠EAC ，然后结合AB ＝AC 得证△DBA ≌△EAC ，最后得到DE ＝BD +CE ；（2）由∠BDA ＝∠BAC ＝∠AEC ＝α得到∠BAD +∠EAC ＝∠BAD +∠DBA ＝180°﹣α，进而得到∠DBA ＝∠EAC ，然后结合AB ＝AC 得证△DBA ≌△EAC ，最后得到DE ＝BD +CE ；（3）由∠BAD ＞∠CAE ，∠BDA ＝∠AEC ＝∠BAC ，得出∠CAE ＝∠ABD ，由AAS 证得△ADB ≌△CAE ，得出S △ABD ＝S △CEA ，再由不同底等高的两个三角形的面积之比等于底的比，得出S △ABF 即可得出结果．【解析】（1）解：DE ＝BD +CE ，理由如下，∵∠BDA ＝∠BAC ＝∠AEC ＝90°，∴∠BAD +∠EAC ＝∠BAD +∠DBA ＝90°，∴∠DBA ＝∠EAC ，∵AB ＝AC ，∴△DBA ≌△EAC （AAS ），∴AD ＝CE ，BD ＝AE ，∴DE ＝AD +AE ＝BD +CE ，故答案为：DE ＝BD +CE ．（2）DE ＝BD +CE 仍然成立，理由如下，∵∠BDA ＝∠BAC ＝∠AEC ＝α，∴∠BAD +∠EAC ＝∠BAD +∠DBA ＝180°﹣α，∴∠DBA ＝∠EAC ，∵AB ＝AC ，∴△DBA ≌△EAC （AAS ），∴BD ＝AE ，AD ＝CE ，∴DE ＝AD +AE ＝BD +CE ；（3）解：∵∠BAD ＜∠CAE ，∠BDA ＝∠AEC ＝∠BAC ，∴∠CAE ＝∠ABD ，在△ABD 和△CAE 中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△CAE （AAS ），∴S △ABD ＝S △CAE ，设△ABC 的底边BC 上的高为h ，则△ABF 的底边BF 上的高为h ，∴S △ABC ＝12BC •h ＝12，S △ABF ＝12BF •h ，∵BC ＝3BF ，∴S △ABF ＝4，∵S △ABF ＝S △BDF +S △ABD ＝S △FBD +S △ACE ＝4，∴△FBD 与△ACE 的面积之和为4．13．通过对下面数学模型的研究学习，解决下列问题：（1）如图1，∠BAD ＝90°，AB ＝AD ，过点B 作BC ⊥AC 于点C ，过点D 作DE ⊥AC 于点E ．由∠1+∠2＝∠2+∠D ＝90°，得∠1＝∠D ．又∠ACB ＝∠AED ＝90°，可以推理得到△ABC ≌△DAE ．进而得到AC ＝，BC ＝AE ．我们把这个数学模型称为“K 字”模型或“一线三等角”模型；（2）如图2，∠BAD ＝∠CAE ＝90°，AB ＝AD ，AC ＝AE ，连接BC ，DE ，且BC ⊥AF 于点F ，DE 与直线AF 交于点G ．求证：点G 是DE 的中点；（深入探究）（3）如图，已知四边形ABCD 和DEGF 为正方形，△AFD 的面积为S 1，△DCE 的面积为S 2，则有S 1S 2（填“＞、＝、＜”）【答案】（1）DE ；（2）见解析；（3）=【分析】（1）根据全等三角形的性质可直接进行求解；（2）分别过点D 和点E 作DH ⊥FG 于点H ，EQ ⊥FG 于点Q ，进而可得∠BAF =∠ADH ，然后可证△ABF ≌△DAH ，则有AF =DH ，进而可得DH =EQ ，通过证明△DHG ≌△EQG 可求解问题；（3）过点D 作DO ⊥AF 交AF 于O ，过点E 作EN ⊥OD 交OD 延长线于N ，过点C 作CM ⊥OD 交OD 延长线于M ，由题意易得∠ADC =∠90°，AD =DC ，DF =DE ，然后可得∠ADO =∠DCM ，则有△AOD ≌△DMC ，△FOD ≌△DNE ，进而可得OD =NE ，通过证明△ENP ≌△CMP 及等积法可进行求解问题．【解析】解：（1）∵ABC DAE △≌△，∴AC DE =；（2）分别过点D 和点E 作DH ⊥FG 于点H ，EQ ⊥FG 于点Q ，如图所示：∴90DAH ADH ∠+∠=︒，∵90BAD ∠=︒，∴90BAF DAH ∠+∠=︒，∴BAF ADH ∠=∠，∵BC AF ⊥，∴90BFA AHD ∠=∠=︒，∵AB DA =，∴△ABF ≌△DAH ，∴AF =DH ，同理可知AF =EQ ，∴DH =EQ ，∵DH ⊥FG ，EQ ⊥FG ，∴90DHG EQG ∠=∠=︒，∵DGH EGQ∠=∠∴△DHG ≌△EQG ，∴DG =EG ，即点G 是DE 的中点；（3）12S S =，理由如下：如图所示，过点D 作DO ⊥AF 交AF 于O ，过点E 作EN ⊥OD 交OD 延长线于N ，过点C 作CM ⊥OD 交OD 延长线于M∵四边形ABCD 与四边形DEGF 都是正方形∴∠ADC =∠90°，AD =DC ，DF =DE∵DO ⊥AF ，CM ⊥OD ，∴∠AOD =∠CMD =90°，∠OAD +∠ODA =90°，∠CDM +∠DCM =90°，又∵∠ODA +∠CDM =90°，∴∠ADO =∠DCM ，∴△AOD ≌△DMC ，∴AOD DMC S S =△△，OD =MC ，同理可以证明△FOD ≌△DNE ，∴FOD DNE S S =△△，OD =NE ，∴MC =NE ，∵EN ⊥OD ，CM ⊥OD ，∠EPN =∠CMP ，∴△ENP ≌△CMP ，∴ENP CMP S S △△=，∵,ADF AOD FOD DCE DCM CMP DEN ENP SS S S S S S S =+=-++，∴DCE DCM DEN AOD FOD S S S S S =+=+,∴DCE ADF S S △△=即12S S =．14．（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在ABC 中，90BAC ∠=︒，AB AC =，直线l 经过点A ，BD ⊥直线l ，CE ⊥直线l ，垂足分别为点D ，E ．求证：DE BD CE =+．（2）组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在ABC 中，AB AC =，D ，A ，E 三点都在直线l 上，并且有BDA AEC BAC α∠=∠=∠=，其中α为任意锐角或钝角．请问结论DE BD CE =+是否成立？若成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过ABC 的边AB ，AC 向外作正方形ABDE 和正方形ACFG ，AH 是BC 边上的高．延长HA 交EG 于点I ．若7AEG S =△，则AEI S =△______．【答案】（1）见解析；（2）结论成立，理由见解析；（3）3.5【分析】（1）由条件可证明△ABD ≌△CAE ，可得DA =CE ，AE =BD ，可得DE =BD +CE ；（2）由条件可知∠BAD +∠CAE =180°-α，且∠DBA +∠BAD =180°-α，可得∠DBA =∠CAE ，结合条件可证明△ABD ≌△CAE ，同（1）可得出结论；（3）由条件可知EM =AH =GN ，可得EM =GN ，结合条件可证明△EMI ≌△GNI ，可得出结论I 是EG 的中点．【解析】解：（1）证明：如图1中，∵BD ⊥直线l ，CE ⊥直线l ，∴∠BDA =∠CEA =90°，∵∠BAC =90°，∴∠BAD +∠CAE =90°，∵∠BAD +∠ABD =90°，∴∠CAE =∠ABD ，在△ADB 和△CEA 中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADB ≌△CEA （AAS ），∴AE =BD ，AD =CE ，∴DE =AE +AD =BD +CE ．（2）解：成立．理由：如图2中，∵∠BDA =∠BAC =α，∴∠DBA +∠BAD =∠BAD +∠CAE =180°-α，∴∠DBA =∠CAE ，在△ADB 和△CEA 中，BDA AEC DBA CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADB ≌△CEA （AAS ），∴AE =BD ，AD =CE ，∴DE =AE +AD =BD +CE ．（3）如图3，过E 作EM ⊥HI 于M ，GN ⊥HI 的延长线于N．∴∠EMI =∠GNI =90°由（1）和（2）的结论可知EM =AH =GN∴EM =GN在△EMI 和△GNI 中，GIN EIM EM GN GNI EMI ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△EMI ≌△GNI （AAS ），∴EI =GI ，∴I 是EG 的中点．∴S △AEI =12S △AEG =3.5．故答案为：3.5．15．（1）模型建立，如图1，等腰直角三角形ABC 中，∠ACB ＝90°，CB ＝CA ，直线ED 经过点C ，过A 作AD ⊥ED 于D ，过B 作BE ⊥ED 于E ．求证：△BEC ≌△CDA ；（2）模型应用：①已知直线y ＝34x +3与y 轴交于A 点，与x 轴交于B 点，将线段AB 绕点B 逆时针旋转90度，得到线段BC ，过点A ，C 作直线，求直线AC 的解析式；②如图3，矩形ABCO ，O 为坐标原点，B 的坐标为(8，6)，A ，C 分别在坐标轴上，P 是线段BC 上动点，已知点D 在第一象限，且是直线y ＝2x ﹣5上的一点，若△APD 是不以A 为直角顶点的等腰直角三角形，请直接写出所有符合条件的点D的坐标．【答案】（1）见解析；（2）137y x =-+；（3）(3,1)或(913)，或1923(33，【分析】（1）由条件可求得EBC ACD ∠=∠，利用AAS 可证明BEC CDA ≌；（2）由直线解析式可求得A 、B 的坐标，利用模型结论可得CE BO =，BE AO =，从而可求得C 点坐标，利用待定系数法可求得直线AC 的解析式；（3）分两种情况考虑：如图2所示，当90ADP ∠=︒时，AD PD =，设D 点坐标为(,25)x x -，利用三角形全等得到1128x x -+=，易得D 点坐标；如图3所示，当90APD ∠=︒时，AP PD =，设点P 的坐标为(8,)m ，表示出D 点坐标为(14,8)m m -+，列出关于m 的方程，求出m 的值，即可确定出D 点坐标；如图4所示，当90ADP ∠=︒时，AD PD =时，同理求出D 的坐标．【解析】解：（1）由题意可得，90ACB ADC BEC ∠=∠=∠=︒，∴90EBC BCE BCE ACD ∠+∠=∠+∠=︒，∴EBC ACD ∠=∠，在BEC △和CDA 中EBC ACD E D BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()BEC CDA AAS ≌；（2）过点C 作CD x ⊥轴于点D ，如图2，在334y x =+中，令0y =可求得4x =-，令0x =可求得3y =，∴3OA =，4OB =同（1）可证得CDB BOA ≌，∴4CD BO ==，3BD AO ==，∴437OD =+=，∴()7,4C -且()0,3A ，设直线AC 解析式为3y kx =+，把C 点坐标代入可得734k -+=，解得17k =-，∴直线AC 解析式为137y x =-+；（3）如图2，当90ADP ∠=︒时，AD PD =，过点D 作DE OA ⊥于E ，过点D 作DF BC ⊥于F ，同理可得：AED DFP△≌△设D 点坐标为(,25)x x -，则6(25)112AE DF x x ==--=-，∵DE DF EF BC +==，即1128x x -+=，解得3x =，可得D 点坐标(3,1)；如图3，当90APD ∠=︒时，AP PD =，过点P 作PE OA ⊥于E ，过点D 作DF PE ⊥于F ，设点P 的坐标为()8,m ，同理可得：APE PDF ≌△△，∴6PF AE m ==-，8DF PE ==，∴D 点坐标为()14,8m m -+，∴()82145m m +=--，得5m =，∴D 点坐标(913)，；如图4，当90ADP ∠=︒时，AD PD =时，同理可得ADE DPF △△≌，设(,25)D n n -，则DE PF n ==，25OE n =-，AE DF =则256211DF AE n n ==--=-，∵8DE DF EF OC +===∴2118n n +-=，解得193n =，23253n -=∴D 点坐标1923()33，，综上可知满足条件的点D 的坐标分别为(3,1)或(913)，或1923(33，．。

【差中】全等三角形三垂直模型(解析版)

全等三角形之三垂直模型【模型讲解】模型1、三垂直模型如图：【巩固训练】1．如图，在△ABC和△CDE中，若∠ACB＝∠CED＝90°，AB＝CD，CE＝AC，则下列结论中正确的是（）A．E为BC中点B．2BE＝CD C．CB＝CD D．△ABC≌△CDE 【答案】D【分析】首先利用HL定理证明Rt△ABC≌Rt△CDE，然后根据全等三角形的性质，即可一一判断．【详解】∵∠ACB ＝∠CED ＝90°在Rt △ABC 与Rt △CDE 中，AB CD CE AC =⎧⎨=⎩，∴Rt △ABC ≌Rt △CDE （HL ），∴CB ＝DE ，CE ＝AC ，CD ＝AB ，△ABC ≌△CDE ，故D 符合题意，其他选项不符合题意故选：D ．【点睛】本题考查全等三角形的判定与性质，掌握HL 定理判定三角形全等是解题关键2．在ABC 中，AD BC ⊥于点D ，点E 为AD 上一点，连接CE ，CE ＝AB ，ED ＝BD ．（1）求证：ABD CED △≌△；（2）若22ACE ∠︒＝，则B Ð的度数为．【答案】（1）理由见解析；（2）67︒，理由见解析．【分析】（1）由SAS 证明ABD CED △≌△即可；（2）由全等三角形的性质，即可得出答案．【详解】解：（1）∵AD ⊥BC ，∴∠ADB ＝∠CDE ＝90°，在Rt ADB 与Rt CDE △中，CE AB ED BD =⎧⎨=⎩，∴Rt ADB Rt CDE HL ≌（）；（2）∵Rt ADB Rt CDE △≌△，∴AD ＝CD ，∴ADC 是等腰直角三角形，∴∠ACD ＝45°，∴∠ECD ＝∠ACD ﹣∠ACE ＝45°﹣22°＝23°，∴∠CED ＝90°﹣23°＝67°，∴∠B ＝∠CED ＝67°，【点睛】本题考查了三角形全等的判定、几何图形中角度的计算、等腰直角三角形的性质；关键在于熟练掌握证明三角形全的方式方法、运用等腰直角三角形的性质．3．如图，在等腰直角三角形ABC 中，,90AB BC ABC =∠=︒，点B 在直线l 上，过A 作AD l ⊥于D ，过C 作CE l ⊥于E ．下列给出四个结论：①BD CE =；②BAD ∠与BCE ∠互余；③AD CE DE +=．其中正确结论的序号是（）A ．①②B ．①③C ．②③D ．①②③【答案】D 【分析】证△ADB ≌△BEC 即可．【详解】证明：∵AD l ⊥，CE l ⊥，∴∠ADB=∠BEC=90°，∴∠BAD+∠ABD=90°，∠BCE+∠CBE=90°，∵90ABC ∠=︒，∴∠ABD+∠CBE=90°，∴∠BAD=∠CBE ，∴∠BCE+∠BAD=90°，故②正确；∵∠BAD=∠CBE ，∠ADB=∠BEC=90°，,AB BC =∴△ADB ≌△BEC ，∴BD CE =，AD=BE ，故①正确；DE=DB+BE=CE+AD ，故③正确；故选：D ．【点睛】本题考查了全等三角形的判定与性质，解题关键是找到并证明全等三角形．4．如图，两座建筑物AB ，CD 相距160km ，小月从点B 沿BC 走向点C ，行走ts 后她到达点E ，此时她仰望两座建筑物的顶点A 和D ，两条视线的夹角正好为90︒，且EA ED =．已知建筑物AB 的高为60m ，小月行走的速度为1/m s ，则小月行走的时间t 的值为（）A ．100B ．80C ．60D ．50【答案】A 【分析】首先证明∠A=∠DEC ，然后可利用AAS 判定△ABE ≌△ECD ，进而可得EC=AB=60m ，再求出BE 的长，然后利用路程除以速度可得时间．【详解】解：∵∠AED=90°，∴∠AEB+∠DEC=90°，∵∠ABE=90°，∴∠A+∠AEB=90°，∴∠A=∠DEC ，在△ABE 和△DCE 中B C A DEC AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ECD （AAS ），∴EC=AB=60m ，∵BC=160m ，∴BE=100m ，∴小华走的时间是100÷1=100（s ），故选：A ．【点睛】本题主要考查了全等三角形的应用，关键是正确判定△ABE ≌△ECD ．5．如图，90B C ∠=∠=︒，BAE CED ∠=∠，且AB CE =．（1）试说明：ADE 是等腰直角三角形；（2）若2CDE BAE ∠=∠，求CDE ∠的度数．【答案】（1）见解析；（2）60°．【分析】（1）利用ASA 证明△BAE ≌△CED ，可证AE=DE ，后利用∠BAE+∠BEA=90°，证明∠BEA+∠CED=90°，问题得证；（2）利用直角三角形的两个锐角互余，求解即可．【详解】（1）∵90B C ∠=∠=︒，BAE CED ∠=∠，且AB CE =，∴△BAE ≌△CED ，∴AE=DE ，∵∠BAE+∠BEA=90°，∴∠BEA+∠CED=90°，∴∠AED=90°，∴△AED 是等腰直角三角形；（2）∵2CDE BAE ∠=∠，BAE CED ∠=∠，∴2CDE CED ∠=∠，∵∠CDE+∠CED=90°，∴∠CDE=60°．【点睛】本题考查了三角形的全等，等腰直角三角形的定义，直角三角形的锐角互余的性质，根据图形，结合条件选择对应判定方法，根据性质构造基本的计算等式是解题的关键．6．将Rt ABC △的直角顶点C 置于直线l 上，AC BC =，分别过点A 、B 作直线l 的垂线，垂足分别为点D 、E ，连接AE ．若3BE =，5DE =．求ACE △的面积．【答案】32【分析】根据AAS 即可证明ACD CBE ≌，根据全等三角形的对应边相等，得出 3CD BE ==， AD CE =，所而 358CE CD DE =+=+=，从而求出AD 的长，则可得到ACE △的面积．【详解】解：∵ AD CE ⊥， BE CE ⊥，∴90ADC CEB ∠=∠=︒，∵90ACB ∠=︒，∴90ACD CBE ECB ∠=∠=︒-∠，在ACD △与CBE △中，ADC CEB ACD CBE AC BC ìïïïïÐ?=íïïïïî∴ACD CBE ≌ (AAS)∴ 3CD BE ==，AD CE =，∵ 358CE CD DE =+=+=，∴ 8AD =．ACE 11883222S CE AD ==创=g △．【点睛】本题考查全等三角形的判定与性质，余角的性质等知识，熟悉相关性质是解题的关键．7．如图，90ACB ∠=︒，AC BC =，AD CE ⊥，BE CE ⊥，垂足分别为D ，E ，2.5cm AD =，求1cm BE =，求DE的长．【答案】 1.5cm DE =．【分析】根据垂直定义求出∠BEC ＝∠ACB ＝∠ADC ，根据等式性质求出∠ACD ＝∠CBE ，根据AAS 证明△BCE ≌△CAD ；根据全等三角形的对应边相等得到AD ＝CE ，BE ＝CD ，利用DE ＝CE−CD ，即可解答．【详解】AD CE ⊥Q ,BE CE ⊥90ADC CEB ∴∠=∠=︒90BCE CBE ∴∠+∠=︒又90ACB ∠=︒ 90BCE ACD ∴∠+∠=︒CBE ACD∴=∠在ACD △和CBE △中ADC CEB ACD CBE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS ACD CBE ∴△≌△CD BE ∴=,AD CE=又2.5cm AD = ,1cm BE = 2.5cm CE ∴=,1cm=CD 2.51 1.5cm DE CE CD ∴=-=-=．【点睛】本题考查了全等三角形的性质和判定，垂线的定义等知识点的应用，解此题的关键是推出证明ACD CBE ∴ ≌的三个条件．模型2、一线三等角模型，如图：【巩固训练】1.如图，在△ABC 中，点D 是边BC 上一点，CD ＝AB ，点E 在边AC 上，且AD ＝DE ，∠BAD ＝∠CDE ．（1）如图1，求证：BD ＝CE ；（2）如图2，若DE 平分∠ADC ，在不添加辅助线的情况下，请直接写出图中所有与∠ADE 相等的角（∠ADE 除外）．【解题】（1）由“SAS ”可证△ABD ≌△DCE ，可得BD ＝CE ；（2）由全等三角形的性质可得∠B ＝∠C ，由三角形的外角性质和角平分线的性质可求解．【解答】解：（1）在△ABD 和△DCE 中，AB CD∠BAD ∠CDE AD DE，∴△ABD ≌△DCE （SAS ），∴BD ＝CE ；（2）∵△ABD ≌△DCE ，∴∠B ＝∠C ，∵DE 平分∠ADC ，∴∠ADE ＝∠CDE ＝∠BAD ，∵∠ADC ＝∠B +∠BAD ＝∠ADE +∠CDE ，∴∠B ＝∠ADE ＝∠BAD ＝∠EDC ＝∠C ，∴与∠ADE 相等的角有∠EDC ，∠BAD ，∠B ，∠C ．2．如图，在ABC 中，AB AC ＝，D 、A 、E 三点都在直线m 上，并且有BDA AEC BAC ∠∠∠＝＝，求证：DE BD CE =+．【答案】见解析【分析】首先根据等量代换得出CAE ABD ∠=∠，从而可证ADB CEA △≌△，最后利用全等三角形的性质即可得出结论．【详解】证明：设BDA BAC α∠=∠=，∴180-DBA BAD BAD CAE α∠+∠=∠+∠=︒，∴CAE ABD ∠=∠，∵在ADB △和CEA 中ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()ADB CEA AAS ≌△△，∴AE BD =，AD CE =，∴DE AE AD BD CE =+=+．【点睛】本题主要考查全等三角形的判定及性质，掌握全等三角形判定方法和性质是解题的关键．3．已知：D ，A ，E 三点都在直线m 上，在直线m 的同一侧作ABC ，使AB AC =，连接BD ，CE ．（1）如图①，若90BAC ∠=︒，BD m ⊥，CE m ⊥，求证ABD ACE ≅ ；（2）如图②，若BDA AEC BAC ∠=∠=∠，请判断BD ，CE ，DE 三条线段之间的数量关系，并说明理由．【答案】（1）见详解；（2）DE ＝BD ＋CE ．理由见详解【分析】（1）根据BD ⊥直线m ，CE ⊥直线m 得∠BDA ＝∠CEA ＝90°，而∠BAC ＝90°，根据等角的余角相等，得∠CAE ＝∠ABD ，然后根据“AAS”可判断△ABD ≌△CAE ；（2）由∠BDA ＝∠AEC ＝∠BAC ，就可以求出∠BAD ＝∠ACE ，进而由ASA 就可以得出△ABD ≌△CAE ，就可以得出BD ＝AE ，DA ＝CE ，即可得出结论．【详解】（1）证明：如图①，∵D ，A ，E 三点都在直线m 上，∠BAC ＝90°，∴∠BAD ＋∠CAE ＝90°，∵BD ⊥m ，CE ⊥m ，∴∠ADB ＝∠CEA ＝90°，∴∠BAD ＋∠ABD ＝90°，∴∠ABD ＝∠CAE ，在△ABD 和△CAE 中，ADB AEC ABD CAE AB AC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△CAE （AAS ）；（2）DE ＝BD ＋CE ．理由如下：如图②，∵∠BDA ＝∠AEC ＝∠BAC ，∴由三角形内角和及平角性质，得：∠BAD ＋∠ABD ＝∠BAD ＋∠CAE ＝∠CAE ＋∠ACE ，∴∠ABD ＝∠CAE ，∠BAD ＝∠ACE ，在△ABD 和△CAE 中，ABD CAE AB AC BAD ACE ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝，∴△ABD ≌△CAE （ASA ），∴BD ＝AE ，AD ＝CE ，∴DE ＝AD ＋AE ＝BD ＋CE ．【点睛】本题考查了全等三角形的判定与性质以及三角形内角和定理的综合应用，解题的关键是熟练掌握全等三角形的判定方法，灵活运用所学知识解决问题．4．（1）如图1，已知OAB 中，OA OB =，90AOB ∠=︒，直线l 经过点O ，BC ⊥直线l ，AD ⊥直线l ，垂足分别为点C ，D ．依题意补全图l ，并写出线段BC ，AD ，CD 之间的数量关系为______；（2）如图2，将（1）中的条件改为：在OAB 中，OA OB =，C ，O ，D 三点都在直线l 上，并且有BCO ODA BOA ∠=∠=∠，请问（1）中结论是否成立?若成立，请加以证明；若不成立，请说明理由；（3）如图3，在ABC 中，AB AC =，90CAB ∠=︒，点A 的坐标为(0,1)，点C 的坐标为()3,2，请直接写出点B 的坐标．【答案】（1）补全如图所示见解析；CD BC AD =+；（2）成立，证明见解析；（3）点B 的坐标为()1,2-．【分析】（1）依题意补全图，易证△AOD ≌△OBC ，则有AD =CO ，OD =BC ，从而可得CD BC AD =+；（2）利用三角形内角和易证23∠∠=，再证明BCO ODA ≌，同（1）即可证明结论；（3）过B 、C 两点作y 轴垂线，构造如（1）图形，即可得三角形全等，再将线段关系即可求出点B 坐标．【详解】（1）补全图1如图所示，CD BC AD =+；证明：∵90AOB ∠=︒，BC ⊥直线l ，AD ⊥直线l ，∴∠BCO =∠ODA =90°，∴∠BOC +∠OBC =90°，又∵90AOB ∠=︒，∴∠BOC +∠AOD =90°，∴∠OBC =∠AOD ，在△AOD 和△OBC 中BCO ODA OBC AOD BO AO ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AOD ≌△OBC （AAS ）∴AD =CO ，OD =BC ，∵CD OD CO =+，∴CD BC AD =+．（2）成立．证明：如图，∵12180BOA ∠+∠=︒-∠，13180BOA ∠+∠=︒-∠，BOA BCO ∠=∠∴23∠∠=在BCO 和ODA V 中32BCO ODA BO OA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴BCO ODA ≌（AAS ）∴BC OD =，CO AD =∴CD CO OD AD BC=+=+（3）点B 的坐标为()1,2-．过程如下：过B 、C 两点作y 轴垂线，垂足分别为M 、N，同理（1）可得，CN =AM ，AN =MB ，∵点A 的坐标为(0,1)，点C 的坐标为()3,2，∴CN =AM =3，ON =2，OA =1,∴MB =AN =ON -OA =1，OM =AM -OA =2，∵点B 在第四象限，∴点B 坐标为：()1,2-．【点睛】主要考查了等腰直角三角形的性质，全等三角形的判定和性质、图形与坐标变换，构造出全等三角形是解本题的关键．。

专题三三垂直模型

三垂直模型一,三垂直与勾股定理大正方形的面积=四个直角三角形+中心正方形面积=2ab+c2(a+b)2=2ab+c2c²= a²+b²，后人称其为“赵爽弦图”．如图是由弦图变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3．若S1＋S2＋S3＝10，则S2的值为( )A ．113B ．103C ．3D ．83【答案】B 2．如图，“赵爽弦图”由4个全等的直角三角形所围成，在Rt ABC △中，AC b =，BC a =，90ACB ∠=︒，若图中大正方形的面积为42，小正方形的面积为5，求2()a b +的值．【答案】2()=79a b + 3．（1）教材在探索平方差公式时利用了面积法，面积法可以帮助我们直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为a ，较小的直角边长都为b ，斜边长都为c ），大正方形的面积可以表示为c 2，也可以表示为4×12ab ＋(a －b )2，所以4×12ab ＋(a －b )2=c 2，即a 2＋b 2=c 2．由此推导出重要的勾股定理：如果直角三角形两条直角边长为a ，b ，斜边长为c ，则a 2＋b 2=c 2．图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理．(2)试用勾股定理解决以下问题：如果直角三角形ABC 的两直角边长为3和4，则斜边上的高为．(3)试构造一个图形，使它的面积能够解释(a －2b )2=a 2－4ab ＋4b 2，画在上面的网格中，并标出字母a ，b 所表示的线段．【答案】（1）见解析；（2）125；（3）见解析 4．（阅读理解）勾股定理是几何学中一颗光彩夺目的明珠．她反映了直角三角形的三边关系即直角三角形两直角边（即“勾”，“股”）边长的平方和等于斜边（即“弦”）边长的平方．也就是说，设直角三角形两直角边为a 和b ，斜边为c ，那么222+=a b c ．迄今为止，全世界发现勾股定理的证明方法约有400种．如：美国第二十任总统伽菲尔德的“总统证法”（如图1），利用三个直角三角形拼成一个直角梯形，于是直角梯形的面积可以表示为()212a b +或者是211222ab c ⨯+，因此得到()221112222a b ab c +=⨯+，运用乘法公式展开整理得到222+=a b c ．（尝试探究）（1）其实我国古人早就运用各种方法证明勾股定理，如图2用四个直角三角形拼成正方形，中间也是一个正方形，其中四个直角三角形直角边分别为a 、b ，斜边长为c ，请你根据古人的拼图完成证明．（2）如图3是2002年在中国北京召开的国际数学家大会会标，利用此图也能证明勾股定理，其中四个直角三角形直角边分别为a 、b ，斜边长为c ，请你帮助完成．（实践应用）（3）已知a 、b 、c 为Rt ABC △的三边()c b a >>，试比较代数式2222a ca b +与44c b -的大小关系．【答案】（1）见解析；（2）见解析；（3）代数式2222a c a b +与44c b -的大小关系是相等． 5．我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼制成一个大正方形（如下图），设勾a=3，弦c=5，则小正方形ABCD 的面积是_______【答案】1．6．把图1中长和宽分别为3和2的两个全等矩形沿对角线分成四个全等的直角三角形，将这四个全等的直角三角形拼成图2所示的正方形，则图2中小正方形ABCD 的面积为_____．【答案】1．规律总结:角边在斜边上的射影和斜边的比例中项.公式: 如图，Rt△ABC中，∠ABC=90°，BD是斜边AC上的高，则有射影定理如下：（1）(BD)²=AD•DC，（2）(AB)²=AD•AC ，（3）(BC)²=CD•CA.直角三角形射影定理的证明在△BAD与△BCD中，∵∠ABD+∠CBD=90°，且∠CBD+∠C=90°，∴∠ABD=∠C，又∵∠BDA=∠BDC=90°∴△BAD∽△CBD∴AD BDBD CD=即BD²=AD•DC.其余同理可得可证有射影定理如下：AB²=AD•AC，BC²=CD•CA两式相加得：AB²+BC²=（AD•AC）+（CD•AC）=（AD+CD)•AC=AC².CE a=，HG b=，则斜边BD的长是（）A ．+a bB ．⋅a bC ．D 【答案】C2．已知Rt △ABC 中，∠BAC =90°，AB =AC ，点E 为△ABC 内一点，连接AE ，CE ，CE ⊥AE ，过点B 作BD ⊥AE ，交AE 的延长线于D ．（1）如图1，求证BD=AE ；（2）如图2，点H 为BC 中点，分别连接EH ，DH ，求∠EDH 的度数；（3）如图3，在（2）的条件下，点M 为CH 上的一点，连接EM ，点F 为EM 的中点，连接FH ，过点D 作DG ⊥FH ，交FH 的延长线于点G ，若GH ：FH =6：5，△FHM 的面积为30，∠EHB =∠BHG ，求线段EH 的长．【答案】（1）见解析；（2）∠EDH ＝45°；（3）EH ＝．3．在△ABC 中，∠ACB ＝90°，AC ＝BC ，直线MN 经过点C ，且AD ⊥MN 于D ， BE ⊥MN 于E ．(1)当直线MN 绕点C 旋转到图1的位置时，求证：△ADC ≌△CEB ；(2)当直线MN 绕点C 旋转到图2的位置时，试问DE 、AD 、BE 的等量关系?并说明理由．【答案】（1）见解析；（2）DE=AD-BE ，理由见解析 4．在Rt AOB ∆中，AOB 90∠=．(1)如图①，以点A 为直角顶点，AB 为腰在AB 右侧作等腰Rt ABC ∆，过点C 作CD OA ⊥交OA 的延长线于点D ．求证：A AOB CD ∆∆≌．(2)如图②，以AB 为底边在AB 左侧作等腰Rt ABC ∆，连接OC ，求AOC ∠的度数．(3)如图③，Rt AOB ∆中，,OA OB OD AB =⊥,垂足为点D ，以OB 为边在OB 左侧作等边OBC ∆,连接AC 交OD 于E ，3AE =,2OE =,求AC 的长．【答案】（1）见解析；（2）135AOC ∴∠=；（3）85．如图1，在ABC ∆中，90ACB ∠=，AC BC =，直线MN 经过点C ，且AD MN ⊥于点D ，BE MN ⊥于点E ．易得DE AD BE =+（不需要证明）．（1）当直线MN 绕点C 旋转到图2的位置时，其余条件不变，你认为上述结论是否成立？若成立，写出证明过程；若不成立，请写出此时DE AD BE 、、之间的数量关系，并说明理由；（2）当直线MN 绕点C 旋转到图3的位置时，其余条件不变，请直接写出此时DE AD BE 、、之间的数量关系（不需要证明）．【答案】(1) 不成立，DE=AD-BE，理由见解析；(2) DE=BE-AD6．如图，Rt△ACB中，∠ACB＝90°，AC＝BC，E点为射线CB上一动点，连结AE，作AF⊥AE且AF＝AE．（1）如图1，过F点作FD⊥AC交AC于D点，求证：FD＝BC；（2）如图2，连结BF交AC于G点，若AG＝3，CG＝1，求证：E点为BC中点；（3）当E点在射线CB上，连结BF与直线AC交于G点，若BC＝4，BE＝3，则AGCG＝（直接写出结果）【答案】（1）见解析；（2）见解析；（3）113或53模型分析:规律总结:标为3-，求点B的坐标.【答案】B （0，-3）． 2．如图所示，()1,0A-，()0,3B ，以AB 为边作正方形ABCD ，求C ，D 的坐标.【答案】()3,4C -；()4,1D -3．如图，在平面直角坐标系中，等腰直角三角形ABC 的顶点A 在x 轴上，AB ＝AC ，∠BAC ＝90°，且A （2，0）、B （3，3），BC 交y 轴于M ，（1）求点C 的坐标；（2）连接AM ，求△AMB 的面积；（3）在x 轴上有一动点P ，当PB +PM 的值最小时，求此时P 的坐标．【答案】（1）C 的坐标是（﹣1，1）；（2）154；（3）点P 的坐标为（1，0）． 4．如图，在平面直角坐标系中，抛物线交x 轴正半轴于点A （1，0）和点B ，交y 轴于点C ．（1）如图1，直线3y x =-+经过点B 、点C ，求抛物线的解析式；（2）如图2，点E 为该抛物线223y x nx =-+的顶点，过点C 作x 轴的平行线交抛物线于另一点D ，该抛物线对称轴右侧的抛物线上有一点P ，当FP EP ⊥时，求P 点的纵坐标．（3）如图3，在（1）（2）的结论下，抛物线对称轴右侧的抛物线上有一点G ，作⊥GH x 轴于点H ，延长EP交GH 于K ，当GK =时，求G 点的坐标．【答案】（1）243y x x =-+；（2）点P 的纵坐标为2；（3）G 点的坐标为（2+，11）．5．如图，直线334y x =-+与x 轴、y 轴分别交于A B 、两点， O M AB ⊥于点M ，点P 为直线l 上不与点A B 、重合的一个动点. (1)求线段OM 的长；(2)当BOP △的面积是6时，求点P 的坐标；(3)在y 轴上是否存在点Q ，使得以O 、P 、Q 为顶点的三角形与OMP 全等，若存在，请直接写出所有符合条件的点P 的坐标，否则，说明理由.【答案】(1)12 5； (2) (-4，6)； (3) (125-，245)或(125，65)或(365，125-)或(45，125) 6．如图,直线AB 与坐标轴分别交于点A 、点B,且OA 、OB 的长分别为方程x 2－6x+8=0的两个根（OA ＜OB ）,点C在y 轴上,且OA ︰AC=2︰5,直线CD 垂直于直线AB 于点P,交x 轴于点D ．（1）求出点A 、点B 的坐标. （2）请求出直线CD 的解析式.（3）若点M 为坐标平面内任意一点,在坐标平面内是否存在这样的点M,使以点B 、P 、D 、M 为顶点的四边形是平行四边形?若存在,请直接写出点M 的坐标；若不存在,请说明理由.【答案】（1）A(0,2)，B(－4,0);（2）直线CD 的解析式:y CD =－2x+7;（3）存在，()15.53M -，，()29.53M ，，()3 2.53M --，．7．（模型建立）（1）如图1，等腰Rt △ABC 中，∠ACB ＝90°，CB ＝CA ，直线ED 经过点C ，过点A 作AD ⊥ED 于点D ，过点B 作BE ⊥ED 于点E ，求证：△BEC ≌△CDA ；（模型应用）（2）如图2，已知直线l 1：y ＝32x+3与x 轴交于点A ，与y 轴交于点B ，将直线l 1绕点A 逆时针旋转45°至直线l 2；求直线l 2的函数表达式；（3）如图3，平面直角坐标系内有一点B （3，﹣4），过点B 作BA ⊥x 轴于点A 、BC ⊥y 轴于点C ，点P 是线段AB 上的动点，点D 是直线y ＝﹣2x+1上的动点且在第四象限内．试探究△CPD 能否成为等腰直角三角形？若能，求出点D 的坐标，若不能，请说明理由．【答案】（1）见详解；（2）510y x =--；（3）点D 坐标得（113，193-）或（4，-7）或（83，133-）．8．如图，在平面直角坐标系中，直线AB 分别交x 、y 轴于点A 、B ，直线BC 分别交x 、y 轴于点C 、B ，点A 的坐标为（2，0），∠ABO=30，且AB ⊥BC ．（1）求直线BC 和AB 的解析式；（2）将点B 沿某条直线折叠到点O ，折痕分别交BC 、BA 于点E 、D ，在x 轴上是否存在点F ，使得点D 、E 、F 为顶点的三角形是以DE 为斜边的直角三角形？若存在，请求出F 点坐标；若不存在，请说明理由；【答案】（1）+；（2）（﹣2，0）或（0，0） 9．如图，在平面直角坐标系中，l 是经过A （2，0），B （0，b ）两点的直线，且b >0，点C 的坐标为（-2，0），当点B 移动时，过点C 作CD ⊥l 交于点D ．（1）求点D ，O 之间的距离；（2）当tan ∠CDO =12时，求直线l 的解析式；（3）在（2）的条件下，直接写出△ACD 与△AOB 重叠部分的面积．【答案】（1）2；（2）24y x =-+；（3）115ABCD 中，对角线AC BD 、相交于点O ，点E 为线段BO 上一点，连接CE ，将CE 绕C 点顺时针旋转90︒得到CF ，连接EF 交CD 于点G .（1）若4,ABBE ==，求CEF ∆的面积；（2）如图2，线段FE 的延长线交AB 于点H ，过点F 作FM CD ⊥于点M ，求证：2BH MG BE +=；（3）如图3，点E 为射线OD 上一点，线段FE 的延长线交直线CD 于点G ，交直线AB 于点H ，过点F作FM 垂直直线CD 于点M ，请直接写出线段BH MG BE 、、的数量关系.【答案】（1）5；（2）见解析；（3）2BHMG BE -=2．探究：如图1和2,四边形ABCD 中,已知AB AD =，90BAD ∠=︒，点E ，F 分别在BC 、CD 上，45EAF ∠=︒．（1）①如图 1,若B 、ADC ∠都是直角，把ABE △绕点A 逆时针旋转90︒至ADG ，使AB 与AD 重合，则能证得EF BE DF =+，请写出推理过程；②如图 2，若B 、D ∠都不是直角，则当B 与D ∠满足数量关系_______时，仍有EF BE DF =+;（2）拓展：如图3,在ABC 中，90BAC ∠=︒,AB AC ==D 、E 均在边BC 上,且45DAE ∠=︒．若1BD =，求DE 的长．【答案】（1）①见解析；②180B D ∠+∠=︒，理由见解析；（2）5=3DE 3．（操作发现）如图①，在正方形ABCD 中，点N 、M 分别在边BC 、CD 上，连结AM 、AN 、MN ．∠MAN ＝45°，将△AMD 绕点A 顺时针旋转90°，点D 与点B 重合，得到△ABE ．易证：△ANM ≌△ANE ，从而得DM +BN ＝MN ．（实践探究）（1）在图①条件下，若CN ＝3，CM ＝4，则正方形ABCD 的边长是．（2）如图②，点M 、N 分别在边CD 、AB 上，且BN ＝DM ．点E 、F 分别在BM 、DN 上，∠EAF ＝45°，连接EF ，猜想三条线段EF 、BE 、DF 之间满足的数量关系，并说明理由．（拓展）（3）如图③，在矩形ABCD 中，AB ＝3，AD ＝4，点M 、N 分别在边DC 、BC 上，连结AM ，AN ，已知∠MAN ＝45°，BN ＝1，求DM 的长．【答案】（1）6；（2）222EF BE FD =+，见解析；（3）24．如图，正方形ABCD 中，点E 、F 分别是BC 、AB 边上的点，且AE ⊥DF ，垂足为点O ，△AOD ，则图中阴影部分的面积为_____．【答案】5．如图所示，直线a 经过正方形ABCD 的顶点A ，分别过正方形的顶点B 、D 作BF ⊥a 于点F ，DE ⊥a 于点E ，若DE ＝8，BF ＝5，则EF 的长为__．【答案】136．如图，正方形ABCD 中，点E 、F 分别是边BC 、CD 上的点，且BE ＝CF ．求证：（1）AE ＝BF ；（2）AE ⊥BF ．【答案】（1）详见解析；（2）详见解析规律总结:E ，连接DE ．（1）判断DE 与O 的位置关系并说明理由；（2）求证：22DE CD OE =⋅．2．如图，以Rt △ABC 的AC 边为直径作⊙O 交斜边AB 于点E ，连接EO 并延长交BC 的延长线于点D ，点F 为BC 的中点，连接EF 和AD ．（1）求证：EF 是⊙O 的切线；（2）若⊙O 的半径为2，∠EAC ＝60°，求AD 的长．【答案】（1）见解析；（2）AD ＝3．如图，AD 是O 的直径，AB 为O 的弦，OE AD ⊥，OE 与AB 的延长线交于点E ，点C 在OE上，满足CBE ADB ∠=∠．（1）求证：BC 是O 的切线；（2）若30CBE ADB ∠=∠=，3OA =，求线段CE 的长．【答案】（1）见解析；（2）CE4．如图，AB 是△ABC 外接圆的直径，O 为圆心，CH ⏊AB ，垂足为H ，且∠PCA=∠ACH ， CD 平分∠ACB ，交⊙O 于点D ，连接BD ，AP=2．（1）判断直线PC 是否为⊙O 的切线，并说明理由；（2）若∠P=30°，求AC 、BC 、BD 的长．（3）若tan ∠ACP=12，求⊙O 半径．【答案】（1）PC 是⊙O 的切线，理由见解析；（2）AC=2；BC=BD=（3）⊙O 的半径为3．5．如图，AB 是O 的直径，点D 是弧AE 上一点，且BDE ∠=∠，BD 与AE 交与点F ．(1)求证：BC 是O 的切线；(2)若BD 平分ABE ∠，求证：2DE DF DB =⋅；(3)在(2)的条件下，延长ED ，BA 交于点P ，若PA AO =，2DE =，求PD 的长和O 的半径．【答案】（1）证明见解析；（2）证明见解析；（3）6．已知BC 是⊙O 的直径，点D 是BC 延长线上一点，AB=AD ，AE 是⊙O 的弦，∠AEC=30°．（1）求证：直线AD 是⊙O 的切线；（2）若AE ⊥BC ，垂足为M ，⊙O 的半径为4，求AE 的长．【答案】（1）证明见解析；（2）。

(完整版)三垂直模型与全等综合剖析

初中几何模型：三垂直全等模型分析

三角形全等中的三垂直模型

“一线三垂直”模型专题知识解读

(完整版)三垂直模型与全等综合剖析

初中几何模型：三垂直全等模型分析

三垂直模型 奥数-概述说明以及解释

初中几何一线三垂直模型构造全等三角形

三垂直模型与全等综合剖析.docx

(完整版)关于“一线三垂直”模型及其在平面几何中的应用

专题07 一线三垂直与一线三等角(解析版)

三垂直模型与全等综合剖析

(完整版)关于“一线三垂直”模型及其在平面几何中的应用

专题11 全等三角形中的一线三等角模型(解析版)

【差中】全等三角形三垂直模型(解析版)

专题三 三垂直模型

三垂直模型奥数-概述说明以及解释

专题三三垂直模型