理论力学第14章2

合集下载

理论力学第七版

equilibrium)
公理3 (Axiom 3) 加减平衡力系原理(The Principle of Addition or 公理
Subtraction Equilibrium Forces System)
推理1 推理 (Inference 1) 力的可传性(The Principle of Transmissibility) 推理2 推理 (Inference 2) 三力平衡汇交定理(Theorem of Three-force
被约束体
轴可在孔内任意转动，轴可在孔内任意转动，也可沿孔的中心线移动，也可沿孔的中心线移动，但轴承阻碍轴沿孔径向向外的约束位移。位移。
第一章静力学公理和物体的受力分析
1－2 约束和约束力－
1-2 Constraints and Reactions of Constraints 反力方向过接触点，沿接触面公法线指向轴心。过接触点，沿接触面公法线指向轴心。由于轴在孔内可任意转动，由于轴在孔内可任意转动，故而轴与孔的接触点位置是不定的。与孔的接触点位置是不定的。因此反力的方向一般预先不能确定。的方向一般预先不能确定。但这样的一个反力常用两个过轴心的，个反力常用两个过轴心的，大小未知的正交分力F 来表示。正交分力 AX、FAY来表示。此二力指向可任意假定。可任意假定。
1－2 约束和约束力－约束和约束力(Constraints and Reactions of Constraints)
约束特点阻碍物体沿接触面法线，并指向约束的运动。作用点接触点反力方向过接触点，沿接触面公法线，指向被约束物体
第一章静力学公理和物体的受力分析
1－2 约束和约束力－约束和约束力(Constraints and Reactions of Constraints)

《理论力学》课程教学大纲72

《理论⼒学》课程教学⼤纲72《理论⼒学》课程教学⼤纲⼀、课程的基本情况课程中⽂名称:理论⼒学课程英⽂名称：Theoretical Mechanics课程代码：0701017课程类别：专业基础课课程性质：必修课总学时：72 讲课学时：72 实验学时：0课程学分：4授课对象：机械类及相近专业本科学⽣前导课程：⾼等数学⼆、教学⽬的理论⼒学为⼯程类学科的基础课程之⼀。

理论⼒学教育不仅可以培养学⽣的⼒学素质，⽽且可以加强学⽣的⼯程概念。

这对于他们向其他学科或其他⼯程领域扩展是很有利的。

是相关专业后续课程的理论和设计以及⼯程设计规范的基础。

通过理论⼒学的学习可以使学⽣了解刚体的特性及其研究⽅法；了解理论⼒学基本理论以及在⼯程实际中的应⽤；了解理论⼒学与其他相关课程的联系。

三、教学基本要求绪论0.1理论⼒学的研究对象0.2理论⼒学的发展简史0.3理论⼒学的内容和研究⽅法0.4理论⼒学的应⽤及和其他学科的关系基本要求：1.了解理论⼒学的研究对象和内容。

2.了解理论⼒学与其他课程的关系。

3.了解理论⼒学在各个不同领域的应⽤。

重点与难点:1.理论⼒学的内容和研究⽅法。

第⼀部分静⼒学第1章静⼒学公理和物体的受⼒分析1.1静⼒学公理1.2约束和约束⼒1.3物体的受⼒分析和受⼒图基本要求：1.深⼊地理解⼒、刚体、平衡和约束等重要概念，深⼊理解⼒的基本性质。

2.明确基本约束的特征,正确地对物体系统进⾏受⼒分析。

重点与难点:1.约束和物体系的受⼒分析。

2.物体系统的受⼒分析和受⼒图。

第2章平⾯汇交⼒系与平⾯⼒偶系2.1平⾯汇交⼒系合成与平衡⼏何法2.2平⾯汇交⼒系合成与平衡的解析法2.2平⾯⼒对点之矩概念及计算2.3平⾯⼒偶基本要求：1.清晰的理解汇交⼒系和⼒偶系的合成。

2.熟练解汇交⼒系的平衡问题。

3.清晰的理解⼒对点的矩，并能熟练的计算。

4.深⼊理解⼒偶和⼒偶矩的概念。

明确⼒偶的性质和⼒偶的等效条件。

重点与难点:1.汇交⼒系的平衡⽅程。

昆明理工大学材料力知识学习题册14概念标准答案

^`第一章绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。

( × ) 1.2 内力只作用在杆件截面的形心处。

( × ) 1.3 杆件某截面上的内力是该截面上应力的代数和。

( × ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ∨ ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ∨ ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。

( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等，方向相同。

( × ) 1.9 同一截面上各点的切应力τ必相互平行。

( × ) 1.10 应变分为正应变ε和切应变γ。

( ∨ ) 1.11 应变为无量纲量。

( ∨ ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。

( ∨ ) 1.13 若物体内各点的应变均为零，则物体无位移。

( × ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。

( ∨ ) 1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。

( ∨ )1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。

( × )二、填空题1.1 材料力学主要研究受力后发生的以及由此产生1.2 拉伸或压缩的受力特征是，变形特征是。

B题1.15图题1.16图外力的合力作用线通过杆轴线杆件^`1.3 剪切的受力特征是，变形特征是。

1.4 扭转的受力特征是，变形特征是。

1.5 弯曲的受力特征是，变形特征是。

1.6 组合受力与变形是指。

1.7 构件的承载能力包括，和三个方面。

1.8 所谓，是指材料或构件抵抗破坏的能力。

理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章静力学公理和物体的受力分析一、是非判断题在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 两点受力的构件都是二力杆。

( × ) 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 力的平行四边形法则只适用于刚体。

( × ) 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 只要物体平衡，都能应用加减平衡力系公理。

( × ) 凡是平衡力系，它的作用效果都等于零。

( × ) 合力总是比分力大。

( × ) 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × )若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ )当软绳受两个等值反向的压力时，可以平衡。

( × )静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ )静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )凡是两端用铰链连接的直杆都是二力杆。

( × )如图所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )图3二、填空题力对物体的作用效应一般分为外效应和内效应。

对非自由体的运动所预加的限制条件称为约束；约束力的方向总是与约束所能阻止的物体的运动趋势的方向相反；约束力由主动力引起，且随主动力的改变而改变。

理论力学习题

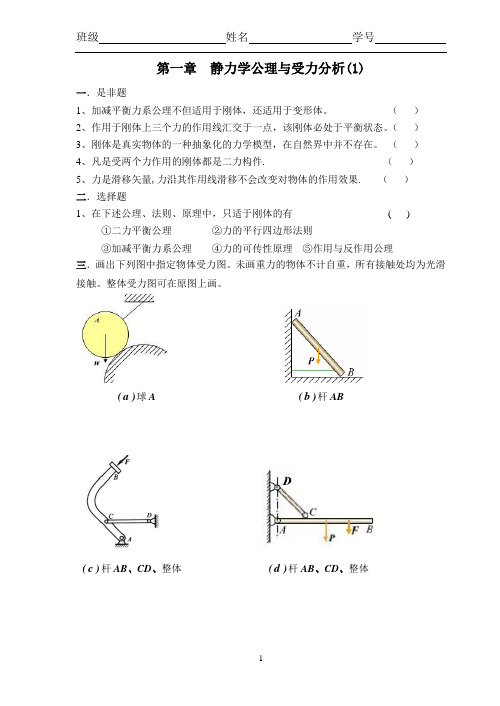
班级姓名学号第一章静力学公理与受力分析(1)一．是非题1、加减平衡力系公理不但适用于刚体，还适用于变形体。

（）2、作用于刚体上三个力的作用线汇交于一点，该刚体必处于平衡状态。

（）3、刚体是真实物体的一种抽象化的力学模型，在自然界中并不存在。

（）4、凡是受两个力作用的刚体都是二力构件.（）5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果. （）二．选择题1、在下述公理、法则、原理中，只适于刚体的有( )①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触。

整体受力图可在原图上画。

)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画.)a(球A、球B、整体)b(杆BC、杆AC、整体班级姓名学号第一章静力学公理与受力分析(2）一．画出下列图中指定物体受力图.未画重力的物体不计自重，所有接触处均为光滑接触.整体受力图可在原图上画.WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体)d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体班级姓名学号第二章平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F = — F ’，所以力偶的合力等于零。

( ）2、用解析法求平面汇交力系的合力时，若选用不同的直角坐标系，则所求得的合力不同。

（ )3、力偶矩就是力偶。

理论力学-静力学部分

静力学部分总结姓名：孟庆宇班级：15工9 学号：20150190218静力学是研究物体的受力分析与力系简化及平衡。

平面力系：1、平面汇交力系；2、平面力偶系；3、平面任意力系。

空间力系：1、空间汇交力系；2、空间力偶系；3、空间任意力系。

一、基本概念1、静力学；2、刚体；3、变形体；4、力；5、力系；6、等效力系；7平衡；8、平衡力系；9、平衡条件；10、平衡方程； 11、力系简化；12、合力；13分力；14、二力构件；15、自由体；16非自由体；17、约束；18、约束力；19主动力；20、被动力；21、施力体；22、受力体。

物体在受到力的作用后，产生的效应可以分为两种：(1)外效应也称为运动效应——使物体的运动状态发生改变；(2)内效应也称为变形效应——使物体的形状发生变化。

静力学研究物体的外效应。

材料力学主要研究力对物体的内效应。

23、平面力系；24、平面汇交力系；25、平面力对点的矩；26、平面力偶矩；27、平面任意力系；28、主矢；29、主矩；30、平面力系平衡条件；31、平面力系平衡方程；32、平面物体系统；33、平面物体系统的平衡；34、静定问题；35、超静定问题；36、平面桁架。

37、空间力系；38、空间汇交力系；39、空间力对点、对轴的矩；40、空间力偶矩；41、空间任意力系；42、主矢；43、主矩；43、空间力系平衡条件；44、空间力系平衡方程。

二、基本理论1、五大公理、两个推论及其应用。

2、工程中常见的八大约束类型及约束反力。

(1)光滑约束；(2)柔索约束；(3)圆柱销光滑铰链约束；(4)固定铰支座约束；(5)滚动支座约束；(6)球铰链约束；(7)止推轴承约束；(8)固定端约束。

3、力的投影定理及性质(平面、空间)；4、力矩、力偶矩的定义及性质(平面、空间)；5、合力投影定理及合力矩定理(平面、空间)；6、力的平移定理；7、任意力系的四种简化结果 (平面、空间)；(1) 0='RF 0≠O M ；(2) 0≠'R F 0=O M ；(3) 0≠'R F 0≠O M ； (4) 0='RF 0=O M 。

理论力学课后习题答案

理论力学(盛冬发)课后习题答案c h11(总18页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第11章动量矩定理一、是非题(正确的在括号内打“√”、错误的打“×”)1. 质点系对某固定点(或固定轴)的动量矩，等于质点系的动量对该点(或轴)的矩。

(×)2. 质点系所受外力对某点(或轴)之矩恒为零，则质点系对该点(或轴)的动量矩不变。

(√)3. 质点系动量矩的变化与外力有关，与内力无关。

(√)4. 质点系对某点动量矩守恒，则对过该点的任意轴也守恒。

(√)5. 定轴转动刚体对转轴的动量矩，等于刚体对该轴的转动惯量与角加速度之积。

(×)6. 在对所有平行于质心轴的转动惯量中，以对质心轴的转动惯量为最大。

(×)7. 质点系对某点的动量矩定理e 1d ()d nOO i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。

(√)18. 如图所示，固结在转盘上的均质杆AB ，对转轴的转动惯量为20A J J mr =+2213ml mr =+，式中m 为AB 杆的质量。

(×)9. 当选质点系速度瞬心P 为矩心时，动量矩定理一定有e 1d()d nP P i i t ==∑L M F 的形式，而不需附加任何条件。

(×)10. 平面运动刚体所受外力对质心的主矩等于零，则刚体只能做平动；若所受外力的主矢等于零，刚体只能作绕质心的转动。

(×)图二、填空题1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。

2. 质量为m ，绕z 轴转动的回旋半径为ρ，则刚体对z 轴的转动惯量为2ρm J z =。

3. 质点系的质量与质心速度的乘积称为质点系的动量。

24. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关，而与系统的内力无关。

5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零，质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数和等于零。

理论力学——第14章达朗贝尔原理

Fix(e) FIix 0 Fiy(e) FIiy 0 M O (Fi(e) ) M O (FIi ) 0
Fix(e) FIix 0 ,
M x (Fi(e) ) M x (FIi ) 0
Fiy(e) FIiy 0 ,
M y (Fi(e) ) M y (FIi ) 0
由于质点系的内力总是成对存在，且等值、反向、共线，有
F (i) i
0,
MO (Fi(i) ) 0
则上式可改写为
Fi(e) FIi 0 MO (Fi(e) ) MO (FIi ) 0
上式表明，作用于质点系上的所有外力与虚加在每个质点上惯性力在形式上组成平衡力系，这就是质点系达朗贝尔原理的又一表述。对整个质点系来说，动静法给出的平衡方程，只是质点系的惯性力系与其外力的平衡，而与内力无关。
MIO ri (miai ) ( miri )aC mrC aC
若选质心C为简化中心，则 rC=0，有： M IC 0
故平移刚体的惯性力系可以简化
为通过质心的合力，其力大小等
于刚体质量与加速度的乘积，合
力的方向与加速度方向相反。
2、定轴转动刚体如图示定轴转动刚体，考虑质点i，以O为简化中。有
l 2
2
0，aCt A
l
2
方向如图所示
角加速度的计算，以杆端点A为基点，B为动点
aB
aA
a
t BA
aB
aA
aBt A
aBt A aA
ll
aC aA aCt A
B
aBt A
aB
aA
aCt A C
aA
q
A aA
因此得此杆惯性力系得主矢为
FIR

《理论力学》第四版(赫桐生版)

第一章习题1-1.画出下列指定物体的受力图解:(1)因柱0 (2)杆AE ⑶ fFAE(4) frAB (5)刚架(15)起重杆AEB⑹ffAR(7)杆 AB 的杆AB 3)钱ABN BP(6)起重轩AB⑸別架习题1-2.(7)折梯整也M 环 BC 帮分解:BF山杆AE ・轮C ：⑵轮C- fFAE P⑶构件ACS 构件RC ：⑸曲柄2、滑块B ⑹起重弧梁AB 、整体(4)栗ACS 樂亡B 、整体(S)横梁AE 、立柱AE 、(1)杆AB.D (2)轮C，杆AB⑶构件AC、构件BC(4)梁AC、梁CB*整体(E ＞铮AB B 立柱AE 、整体RJ-刍BAD习题1-3 .画出下列各物系中指定物体的受力图⑶滑轻重物、杆DE、杆R6 ffAC t连同渦轮片W(4)杆AB (连同滑轮h杆AB(不连滑轮人整粹(1)轮&杆AB P)轮 6 BJ3R AB€)IB 解:a）轮良杆AE(2> 轮 6 BJJKAB⑶滑轮重ff DE.杆BC^ 杆AC（连同滑轮h整体T（4）杆AE （连廊轮人杆AB（不连滑轮人整体第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图，已知R=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。

解：属平面汇交力系；JJ=50x . +5O = 8Qjy22^=乙sintt + =50x 』+100 =140JV血+ 83合力大小和方向：R =+ 迟疔=加+ 佑=L612Vy y 1400 = arc tv——= arct& ---- = 603EX80习题2-2 .图示简支梁受集中荷载P=20kN 求图示两种情况下支座 A B 的约束反力。

解：（1）研究AB,受力分析:相似关系:\'ACDE CD CE ED几何关系:2 CD == 2,83wiED = -AD = 1^4T +27 = 2.24/M 2 2A jij j JL画力三角形:CE1N s= —xP =——x20 = 7.1R2V CD2.83ED 2 24凰卫=—xP = -—x20 =15.8KJV CD 2.83ED 2 口«= arc仗 ---- - -- ---- =26.6AB4⑵研究AB受力分析:画力三角形:相似关系:\'ACDECD CE EDED = 4CD2 +CE* =1,58/w约束反力:几何关系:BC=\A\m2CD1.41ED 1.58R,二一=——x 20 = 22.4KJVCD 1.^11CE值二4了一心吨—= 18.3"CD习题2-3 .电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定,撑杆BC支持。

理论力学-第2章(09)

x
y
范钦珊著：理论力学第章范钦珊著：理论力学/第2章 6
2.1 力对点之矩与力对轴之矩
(4)
力矩矢量的方向力对点之矩矢通过矩心O，力对点之矩矢通过矩心，矢量的长度表示力矩的大其指向符合右手螺旋法则右手螺旋法则，小，其指向符合右手螺旋法则，即当右手四个手指符合力矩转向时，大拇指所指的方向就是力矩矢的方向。力矩转向时，大拇指所指的方向就是力矩矢的方向。
M
O
F r
M=r×F
范钦珊著：理论力学第章范钦珊著：理论力学/第2章
7
2.1 力对点之矩与力对轴之矩
力对点之矩几点结论力对点之矩是一种矢量； n 力对点之矩是一种矢量； n 矢量的模 M (F) = F ； d O 矢量方向由右手定则确定； n 矢量方向由右手定则确定； n 矢量作用在点，垂直于和F 所在的平面。矢量作用在O点垂直于r 所在的平面。
范钦珊著第2章力系的等效与简化章
范钦珊著：理论力学第章范钦珊著：理论力学/第2章
1
第2章力系的等效与简化
作用在实际物体上的力系各式各样，作用在实际物体上的力系各式各样，但是都可归纳为两大类：为两大类：一类是力系中所有力的作用线都位于同一平面内，称为平面力系平面力系；面内，称为平面力系；另一类是力系中所有力的作用线空间力系。位于不同的平面内，称为空间力系位于不同的平面内，称为空间力系。这两类力系对物体所产生的运动效应是不同的。同一类力系，所产生的运动效应是不同的。同一类力系，虽然其中所包含的力不相同，包含的力不相同，却可能对同一物体产生相同的作用效这就是前一章中提到的力系等效的概念。力系等效的概念应。这就是前一章中提到的力系等效的概念。本章将在物理学的基础上，本章将在物理学的基础上，对力系的基本特征量加以扩展，引入力系主矢与主矩的概念；以此为基础，以扩展，引入力系主矢与主矩的概念；以此为基础，导出力系等效定理；出力系等效定理；进而应用力向一点平移定理以及力偶的概念对力系进行简化。的概念对力系进行简化。力系简化理论与方法将作为分析所有静力学和动力学问题的基础。析所有静力学和动力学问题的基础。

《理论力学》课后习题解答(赫桐生版)

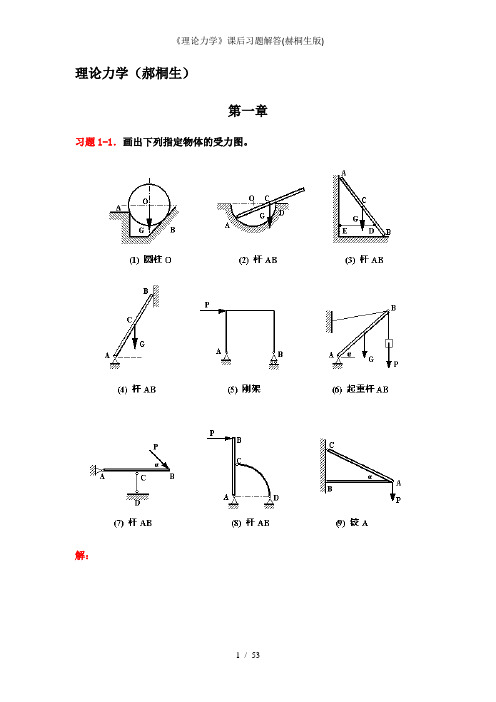
理论力学（郝桐生）第一章习题1-1．画出下列指定物体的受力图。

解：习题1-2．画出下列各物系中指定物体的受力图。

解：习题1-3．画出下列各物系中指定物体的受力图。

解：第二章习题2-1．铆接薄钢板在孔心A、B和C处受三力作用如图，已知P1=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。

解：属平面汇交力系；合力大小和方向：习题2-2．图示简支梁受集中荷载P=20kN，求图示两种情况下支座A、B的约束反力。

解：(1)研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：(2) 研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：习题2-3．电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定，B端以撑杆BC支持。

求撑杆BC所受的力。

解：(1)研究整体，受力分析：(2) 画力三角形：(3) 求BC受力习题2-4．简易起重机用钢丝绳吊起重量G=2kN的重物，不计杆件自重、磨擦及滑轮大小，A、B、C三处简化为铰链连接；求杆AB和AC所受的力。

解：(1) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆受拉，BC杆受压。

(2) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆实际受力方向与假设相反，为受压；BC杆受压。

习题2-5．三铰门式刚架受集中荷载P作用，不计架重；求图示两种情况下支座A、B的约束反力。

解：(1) 研究整体，受力分析（AC是二力杆）；画力三角形：求约束反力：(2) 研究整体，受力分析（BC是二力杆）；画力三角形：几何关系：求约束反力：习题2-6．四根绳索AC、CB、CE、ED连接如图，其中B、D两端固定在支架上，A端系在重物上，人在E点向下施力P，若P=400N，α=4o，求所能吊起的重量G。

解：(1) 研究铰E，受力分析，画力三角形：由图知：(2) 研究铰C，受力分析，画力三角形：由图知：习题2-7．夹具中所用的两种连杆增力机构如图所示，书籍推力P作用于A点，夹紧平衡时杆AB与水平线的夹角为；求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。

理论力学第一部分总结

第三章空间力系
小结
1.力在空间直角坐标轴上的投影 (1)直接投影法
Fx F cos F,i , Fy F cos F, j , Fz F cos F, k
(2)间接投影法(即二次投影法)
Fx F sin cos, Fy F sin sin , Fz F cos
2
第二章平面力系
小结
1.平面汇交力系的合力
(1)几何法:根据力多边形法则，合力矢为 FR Fi
合力作用线通过汇交点。
(2)解析法:合力的解析表达式为
FR Fxii Fyi j
FR
2
Fxi
2
Fyi
cos FR,i
Fxi , cos FR
物体滚动时，滚动摩阻力偶矩近似等于M max 。
21
5.空间任意力系平衡方程的基本形式
Fx 0 Fy 0 Fz 0
MxF0 My F0 Mz F0
6.几种特殊力系的平衡方程 (1)空间汇交力系
Fx 0 Fy 0 Fz 0
(2)空间力偶系
MxF0 My F0 Mz F0
10
12.桁架由二力杆铰接构成。求平面静定桁架各杆内力的两种方法:
(1)节点法: 逐个考虑桁架中所有节点的平衡，应用平面汇交力系的平衡方程求出各杆的内力。 (2)截面法: 截断待求内力的杆件，将桁架截割为两部分，取其中的一部分为研究对象，应用平面任意力系的平衡方程求出被截割各杆件的内力。
11
点O的主矩，即
n
n
MO MO Fi xi Fyi yi Fxi
i 1
i 1
7

四川大学理论力学答案

okey2012-11-30 00:37
求理论力学(武清玺陆晓敏殷德顺著)中国电力出版社课后答案
2701
6
a73588902010-10-19 15:40
理论力学(冯维明)课后答案国防工业出版社
179
1
q@q_3520982011-9-25 22:33
理论力学第2版(唐国兴王永廉)课后答案机械工业出版社
415
1
okey2012-11-7 10:57
理论力学(唐国兴王永廉)课后答案机械工业出版社
【篇三：理论力学3试卷a】
txt>（2005——2006学年第一学期）
课程号：30538240课序号：课程名称：理论力学Ⅲ任课教师：成绩：适用专业年级：04级学生人数：印题份数：学号：姓名：
2题间不留空，一般应题卷分开教务处试题编号：
b.分布力
c.外力
d.内力
10.力系平衡的充分必要条件是该力系的主矢及对于某一点的（）同时等于零：
( c )
a.力矩
b.力偶矩
c.主矩
d.合力
11.平面汇交力系有（）个独立的平衡方程：
( b )
a. 1
b. 2
c. 3
d. 4
12.利用平面任意力系平衡方程中的二力矩形式最多可以求解（）个未知力：
( c)
4
okey8小时前
理论力学第2版(李卓球)课后答案武汉理工大学出版社
理论力学第2版无课后答案根据高等学校理论力学课程教学的基本要求，《理论力学（第2版）》结合工科相关专业应用基础的特点，在保留理论力学经典内容的前提下，适当更新和精炼了教材内容。《理论力学（第2版）》主要内容为静力学、运动学、动力学三大部分。《理论力学（第2版）》适用于高等学校工科力学和工程类各专业的理论力学教材，各专业可以根据需要选用全部或部分内容，也可供有关工程技术人员参考。

理论力学简明教程(第二版)课后答案

第零章数学准备一泰勒展开式1 二项式的展开()()()()()m 23m m-1m m-1m-2f x 1x 1mx+x x 23=+=+++！！2 一般函数的展开()()()()()()()()230000000f x f x f xf x f x x-x x-x x-x 123!''''''=++++！！特别:00x =时,()()()()()23f 0f 0f 0f x f 0123!x x x ''''''=++++！！3 二元函数的展开(x=y=0处)()()00f f f x y f 0x+y x y ⎛⎫∂∂=++ ⎪∂∂⎝⎭，22222000221f f f x 2xy+y 2x x y y ⎛⎫∂∂∂++ ⎪ ⎪∂∂∂∂⎝⎭！评注：以上方法多用于近似处理与平衡态处的非线性问题向线性问题的转化。

在理论力问题的简单处理中，一般只需近似到三阶以内。

二常微分方程1 一阶非齐次常微分方程： ()()x x y+P y=Q通解：()()()P x dx P x dx y e c Q x e dx -⎛⎫⎰⎰=+ ⎪⎝⎭⎰注：()()(),P x dx P x dx Q x e dx ⎰±⎰⎰积分时不带任意常数，()x Q 可为常数。

2 一个特殊二阶微分方程2y A y B =-+ 通解：()02B y=K cos Ax+Aθ+注：0,K θ为由初始条件决定的常量 3 二阶非齐次常微分方程 ()x y ay by f ++=通解：*y y y =+；y 为对应齐次方程的特解，*y 为非齐次方程的一个特解。

非齐次方程的一个特解（1）对应齐次方程0y ay by ++=设x y e λ=得特征方程2a b 0λλ++=。

解出特解为1λ，2λ。

*若12R λλ≠∈则1x 1y e λ=，2x 2y e λ=；12x x 12y c e c e λλ=+*若12R λλ=∈则1x 1y e λ=，1x 2y xe λ=； 1x 12y e (c xc )λ=+*若12i λαβ=±则x 1y e cos x αβ=，x 2y e sin x αβ=；x 12y e (c cos x c sin x)αββ=+（2）若()2000x f a x b x c =++为二次多项式*b 0≠时，可设*2y Ax Bx C =++ *b 0≠时，可设*32y Ax Bx Cx D =+++注：以上1c ,2c ,A,B,C,D 均为常数，由初始条件决定。

理论力学(周衍柏第二版)第2章习题解答

之值。
2.8 一光滑球 A 与另一静止的光滑球 B 发生斜碰。如两者均为完全弹性体，且两球的质量相
等，则两球碰撞后的速度互相垂直，试证明之。 2.9 一光滑小球与另一相同的静止小球相碰撞。在碰撞前，第一小球运动的方向与碰撞时两
球的联心线成α 角。求碰撞后第一小球偏过的角度 β 以及在各种α 值下 β 角的最大值。设恢复系数 e 为已知。 2.10 质量为 m2 的光滑球用一不可伸长的绳系于固定点 A 。另一质量为 m1 的球以与绳成θ 角的速度 v1 与 m2 正碰。试求 m1 与 m2 碰后开始运动的速度 v1′ 及 v2′ 。设恢复系数 e 为已知。
离是一致的（因为两次运动水平方向上均以 v水平 = v0cosα 作匀速直线运动，运动的时间也相同）。所以我们只要比较人把物抛出后水平距离的变化即可。第一次
机枪后退的速度为
M ′ u − (M + M ′)2 − M 2 μg
Mபைடு நூலகம்
2mM
2.16 雨滴落下时，其质量的增加率与雨滴的表面积成正比例，求雨滴速度与时间的关系。
2.17 设用某种液体燃料发动的火箭，喷气速度为 2074 米/秒，单位时间内所消耗的燃料为
原始火箭总质量的 1 。如重力加速度 g 的值可以认为是常数，则利用此种火箭发射人造太 60
zc
=
∫ zdm ∫ dm
=
−
3 4
(a + b)2 (2a + b)
2.3 解建立如题 2.3.1 图所示的直角坐标，原来W人与共同作一个斜抛运动。 y v0
α
O
x
4
当达到最高点人把物体水皮抛出后，人的速度改变，设为 vx ，此人即以 vx 的速度作平抛运动。由此可知，两次运动过程中，在达到最高点时两次运动的水平距

理论力学第十四章拉格朗日方程 [同济大学]

动力学
韋林教授
第十四章拉格朗日方程(第二类方程) §14-1动力学普遍方程
达朗伯原理虚位移原理
例14-1 一套滑轮系统悬挂两个重物.设:绳,滑轮质量不计.求重为P1的物体上升的加速度a1。解:
(P 1F 1 g )δS1 ( P 2 F2 g )δS 2 0
(F F
i
r
r i δq j j 1 q j
广义力 r r r i i i q j, (1) vi r t j 1 q j
r
d T T )δq j 0, j q j dt q
Qj
δq j 0
V q j
广义速度
ri
d T T Qj, j q j dt q
T 1 1 1 2 m2v 2 (m1 m2 ) R 2 2 J 0 2 2 2
1 1 2 kR 2 2 L T V (m1 m2 )R 2 2 2

m1
V
1 l k k 2 2 mg θ (δ0 bθ )2 δ0 θ b 2 2 2 2 2
3
v0 v
x
L R 2 k1 k 2 ( y R )( R ),
d L L ( ) 0 dt y y L , m2 y y L ( y R )k 2 y
R 2 k1 ( y R)k 2 ( R) 0 m1 R 2
R 2 (k1 k 2 ) k 2 Ry m1 R 2
k 2 y k 2 R m2 y
r 1 3 3 xc x r sin 1 , c x r cos θ1θ x 1 v0 1 2 2 c 3 3 , v0 rθ x c r sin 1 yc r cos 1 , y 2 1 2 2 2 2 r 2 9 r 2θ 2 3θ θ 2 r 2 ( 3 r cos 2 3 2 3 r 2 cos θ vc2 2 1 2 1 cos θ1r 2 1 1 ) ( r sin 11 ) 2 2 1 1 4 2 2 2

理论力学知到章节答案智慧树2023年辽宁工程技术大学

理论力学知到章节测试答案智慧树2023年最新辽宁工程技术大学绪论单元测试1.理论力学研究的是宏观、低速的物体运动。

（）参考答案:对第一章测试1.画出各构件受力图。

参考答案:null2.画出轮O受力图。

参考答案:null3.如图所示结构，画出下列各构件受力图。

参考答案:null4.如图所示结构，画出下列各构件受力图。

参考答案:null5.一重物放在地面上，如图所示，P是重物的重力，F n是重物对地面的压力，F n′是地面对重物的约束力，作用力和反作用力及组成平衡的二力分别是：（）参考答案:F n和F n′，P和F n′6.约束给被约束物体的力叫参考答案:null7.作用于同一刚体上的两个力，使刚体保持平衡的必要与充分条件是：参考答案:null8.力作用三要素为：参考答案:null9.力是物体之间作用，这种作用使物体的或发生改变。

参考答案:null10.二力平衡原理适用于。

参考答案:null第二章测试1.平面桁架的支座和载荷如图所示。

ABC 为等边三角形，E，F 为两腰中点，又AD=DB。

求杆CD的内力F CD。

参考答案:null2.由AC 和CD 构成的组合梁通过铰链C 连接。

支承和受力如图所示。

已知均布载荷强度q＝10kN/m，力偶矩M=40kN•m，不计梁重。

求支座A、B、D 的约束力和铰链C 处所受的力。

参考答案:null3.图示简支梁中，求AB两端约束的约束反力。

参考答案:null4.沿边长为a=2m的正方形各边分别作用有F1，F2，F3，F4,且F1=F2=F3=F4=4KN，该力系向B点简化的结果为：主矢大小F`R= ，主矩大小M B= 。

参考答案:null5.平面系统受力偶矩为M=10KN·m的力偶作用。

当力偶M作用于AC杆时，A支座力的大小为；B支座力的大小为；当力偶M作用于BC杆时，A支座力的大小为；B支座力的大小为。

参考答案:null6.图示三铰钢架受力F作用，则A支座力的大小为，B支座力的大小为。

理论力学第十四章动荷载解析

三、动荷载的分类
1.惯性荷载 2.冲击荷载 3.振动荷载 4.交变荷载
实验表明：在静载荷下服从虎克定律的材料，只要应力不超过比例极限 ,在动载荷下虎克定律仍成立且 E静 = E动。
四、本章讨论的动载荷问题：
（1）构件作等加速直线运动和等速转动时的动应力计算；（2）构件在受冲击的动应力计算；
§14-2 等加速直线运动时构件的应力计算
P d
d2 2 st d 2h st 0
d 2 st d st ( 1
42st
2
8h st
st (1
1
2h
st
)
Kd st
1 2h )
st
其中 Kd 1
Fd d P st
1 Kd
2h
st
d Kd st
为冲击动荷系数
Fd Kd P
解决冲击问题,关键在于如何确定动荷系数Kd
图示装有飞轮的轴,飞轮的转速n=100r/min,转动惯
量I=0.5kN.m.s2.轴的直径d=100mm.刹车时使轴在
10秒内均匀减速至停止.求:轴内最大动应力
飞轮与轴的转动角速度:
0
n
30
10
3
角加速度: 1 0
角加速度与角速度方向相反, 按动静y法在飞轮上加惯性力:
Md
10
I
动静法：
达朗伯原理达朗伯原理认为处于不平衡状态的物体,存在惯性力,惯性力
的方向与加速度方向相反,惯性力的数值等于加速度与质量的乘积.只要在物体上加上惯性力,就可以把动力学问题在形式上作为
静力学问题来处理,这就是动静法.
惯性力大小等于质点的质量m与加速度a的乘积,方向与a 的

理论力学（第2版）习题答案

各章习题(计算题)部分答案第1章略第2章2-1 R 3284kN F .=，R cos()2063,.=︒F i ，R cos()1163,.=︒F j 2-2 3162kN T .=，30β=︒ 2-3 482.α=︒，R 496kN x F .= 2-4 11866N 50N x y F .F ==，2230N 40N x y F F ==-， 330N 60N x y F F ==， 44566N 566N x y F .F .==， 2-5 R 0F =2-6(a) 707kN 354kN 354kN Ax Ay B F .F .F .===，，(b) 05kN 5kN Ax Ay B F F F ===，，(c) 933kN 433kN 612kN Ax Ay B F .F .F .===，，(垂直于支撑面，指向简支梁) 2-7 min 15kN F =，N 25kN F =2-8 0866kN 05kN 1kN Ax Ay BD F .F .T ===，， 2-9 N N 1732kN 3464kN 15m A C F .F .AC .===，， 2-10 03436kN AB AC F F .==，2-11 BC F =，Ax F =，Ay F G = 2-12 N 65EF G F =+2-13 N N C D F F =2-14 231N 1155N 231N 845N AB AE BC BD F F .F F .====，，，2-15 (a) 33PF P F B Ay =-=，(b) P F F B A 32== (A F ，B F 方向相反，组成一力偶) (c) 0==B A F F2-16 1F，AB F，OA F =，7kN BC F =- 2-17 1905N 1905N 1905N 1905N Ax Ay Cx Cy F F F F =-===-，，， 2-18 3571N 3571N 3571N 3571N Ax Ay Cx Cy F F F F ==-=-=，，，·312··312·2-19 24kN m M =⋅，1155kN A B F F .== 第3章3-1 2400N Ax F =，1200N Ay F =，8485N BC F .= 3-2 R 0F'=，260N m O M =⋅ 3-3 (a) R F'qa =，221qa M O = (b) R12F'ql =，21ql q M O = 3-4(a) Ax F =，40kN Ay F =，120kN m A M =⋅，N C F = (b) 0=AxF ，25kN Ay F .=-，15kN By F =，D 25kN y F .=3-5 当60α=︒时，min 4AB PrF L= 3-6 0=Ax F ，qa F Ay2=，2qa M A =3-7 (a)2400N Ax F =，1000N Ay F =-，2400N Dx F =-，2000N Dy F = (b)2400N Ax F =-，1000N Ay F =-，2400N Dx F =，2000N Dy F =3-8 Ax F =，Ay F =，Bx F =，By F =3-9 rPLF Ax 2-=，P F Ay =，r PL F Bx 2=，P F By =，r PL F D 2=，P F C 2=3-10 R 32E F qa =-，qa F BD 22= 3-11 23kN Ax Cx F F .=-=-，1kN Ay Cy F F == 3-12 3PF AC -=，0=EF F ，32P F BD -= 3-13 2F F BC=，2F F DE = 第4章4-1 T 20kN F =，104kN OA F .=-，139kN OB F .=- 4-2 254kN m x M .=⋅，146kN m y M .=⋅，0=z M 4-3 0)(=P z M4-4 θαsin sin )(Pa M AB =P 4-5 3C A B WT T T ===4-6 1kN T =，0=Ax F ，750N Ay F =-，500N Az F =-，433N Bx F =，500N BZ F = 4-7 F F F -==61，F F =3，0542===F F F·313··313·4-8 321M a cM a b M +=，a M F Ay 3=，a M F Az 2=，0=Dx F ，a M F Dy 3-=，aM F Dz 2-= 4-9 4kN Ax F =，146kN Az F .=-，79kN Bx F .=，29kN Bz F .=-4-10 5kN Ox F =-，4kN Oy F =-，8kN Oz F =，32kN m Ox M =⋅，30kN m Oy M =-⋅，20kN m Oz M =⋅4-11 (a ) 10412kN N F .=，20213kN N F .=，30375kN N F .= 4-12 )(22221221r r r r x C --=，0=C y4-13 (a ) 589mm C x .=-，0=C y (b ) 797mm C x .=，349mm C y .= 4-14 )(22221221r r r r x C --=，0=C y4-15 0Ax F =，121(P )2Ay F P =-+，21P 2Az P F =+，0Cx F =，0Cy F =，22Cz P F =第5章5-1 min F =，s arctan f α= 5-2 )()m m sin +cos -P F αϕθϕ=，m θϕ=5-3 (1) A 先滑动，(2) A 、B 一起滑动 5-4 能保持平衡，S 201N F = 5-5 223.0=f5-6 3πarcsin 43πff α=+5-7 1s sin cos P F f αα=-，2s sin cos PF f αα=+，故21F F >5-8 min 845kN Q .= 5-9 435N P .=5-10 θ≤9926.︒5-11 120cm x >5-12 s 2(sin cos )Q R f L αα⋅+≤P ≤s 2(sin cos )Q Rf L αα⋅-5-13 min 1475N P .=5-14 4961N m .⋅≤C M ≤7039N m .⋅ 5-15 11cm b <5-16s s sin cos cos sin f Q f αααα-+≤P ≤s s sin cos cos sin f Q f αααα+- 5-17 arc ϕ=·314··314·5-18 500N P = 5-19 s f ≥15.0 5-20 75mm b .< 第6章6-1 (cos sin )x v lk kt kt =-，(cos sin )y v lk kt kt =-+； )sin (cos 2kt kt lk a x +-=，)sin (cos 2kt kt lk a y --= 6-2 (1) 0=s ；v R ω=；0a τ=，2n a R ω=(2) R s 23=；12v R ω=；2a ωτ=，2n 14a R ω= (3) R s =；0v =；2a R ωτ=-，n 0a =6-3 直角坐标法：t R x ω2cos =，t R y ω2sin =；2sin2x v R t ωω=-，2cos2y v R t ωω=； t R a x ωω2cos 42-=，t R a y ωω2sin 42-=自然坐标法：t R s ω2=；2v R ω=；0a τ=，2n 4a R ω= 6-4 ()sin M x l b t ω=+，()cos M y l b t ω=-；22221()()M M x y l b l b +=+-6.52222()1()x a y b l l-+=+6-6 22)sin (cos h t r l t r x B +-+=ωω，h y B -=6-7v =322xb u a -= 6-8 )cos sin arctan(00tr h tr ωωθ-=6-9 当0s t =时，157cm s M v ./=；0M a τ=，n2617cm s M a ./=当2s t =时，0M v =；2123cm s M a ./τ=-，n0M a =6-10 C x =C y =2C avv l=6-11 t e R t e y ωω222cos sin -+=；[cos v e t ωω=6-12 02cos4m x .t =；0566m s v ./=-；22263m s a ./=-6-13 0arctan rad v tbϕ=；02220rad s bv /b v t ω=+6-14 225t =ϕ；120m s v /=；236000m s n a /= 6-15 8rad s /ω=；2384rad s ./ε=-6-16 转轴O 的位置位于正方形的中心；1rad s /ω=，21rad s /ε=6-17 12C v r ω=；n 214C a r ω=，12C a r ετ=·315··315·6-18 12m s M v ./=；n 272m s M a ./=，206m s M a ./τ= 6-19 0377m s C v ./=6-20 2225000rad s /dεπ=；25922m s a ./= 6-21 32rad .ϕ=6-22 12mm h =6-23 02=ω，222r lb ωε-=6-24 02m s AB v ./=，2005m s AB a ./=；02m s C v ./=，n 20267m s C a ./=，2005m s C a ./τ=6-25 2012ωr a =，方向沿1AO ；2024ωr a =，指向轮心第7章7-1 x'vt =，cos()a kt y'ϕ=+，轨迹方程为cos()ky'a x'vϕ=+ 7-2 2cos M v R ωϕ=，方向水平向左 7-3 (a )2309rad s ./ω=； (b )2182rad s ./ω=7-4 (1)34OC v b ω=，34C lv v b=；(2)234K v a b = 7-5 当0ϕ︒=时，0v =；当30ϕ=︒时，100cm s v /=，向右；当90ϕ︒=时，200cm s v /=，向右7-6 126m s BC v ./=；2274m s BC a ./= 7-7 10cm s CD v /=；2346cm s CD a ./= 7-8 a a =7-9 3v ω=，方向向上7-10 1.732rad /s ω=，28.66rad /s ε=- 7-11 0.173m /s v =，20.05m /s a = 7-12 0.173m /s M v =，20.35m/s M a =7-13 πcos 15sin BC nr v αβ=7-14 23CD r v ω=；29310ωr a C D =7-15 a 3465mm s v ./=；21400mm s CD a /=第8章8-1 122v v r ω-=，122O v v v +=8-2 156cm s C v ./=,17cm s D v /=·316··316·8-3 877cm s C v ./=8-4 375rad s OB ./ω=，I 6rad s /ω=8-5 600mm s A v /=，200mm s B v /=，s C v /=；4rad s 3ABC /ω=，05rad s BD ./ω= 8-6 2rad s AB /ω=，2578rad s AB ./ε=-；667rad s BC ./ω=-，21926rad s BC ./ε=8-7 2()C A Rv a R r r=-，2Bx C a a τ=，2(2)()C By R r v a R r r -=- 8-8 2022ωr a B =，20211ωε=B O 8-9 032C v r ω=，20123ωr a C =8-10 01.15v l ω=8-11 16186rad s O C ./ω=，127817rad s O C ./ε=-8-12 s CD v /=，22m s 3CD a /= 8-13 n 2400cm s B a /=，21705cm s B a ./τ=-，21705cm s C a ./=-8-14 34e OC v v OB b ω==，OC ε=；12E v v =，E a = 8-15 21960mm s B a /=，298rad s AB ./ε=8-160C v ω，方向向左；rR B O 01ωω=，逆时针转向8-17 22()C Rv a R r =-，B a =8-18 n 202B a a ω=，2002)B a a ετ=-8-19 330ωω=B ；209)349(10ω+-=B a 8-20 2m s B v /=，2828m s C v ./=，28m s B a /=，21131m s C a ./= 第9章9-1 rgf=max ω 9-2 min 67r min n /=9-3 1v =9-4 0cos cos sin v x b kt kt k α=+，0sin sin vy kt kα=9-5 0cos x v t α=，201sin 2y v t gt α=+·317··317·9-6 0(1e )kt v s k-=- 9-7 202s t .=，707m s .= 9-8 172N F .=9-9 )(22g a amL F AC +=ω，)(22g a a mL F BC -=ω9-10 max 584kN F .=，min 536kN F .=9-11 g f f a ααααsin cos cos sin -+=，N cos sin W F f αα=- 9-12 )cos 1(200t m F t x ωωυ-+=第10章10-1 (a ) 12p mL ω=，方向水平向右；(b ) p mR ω=，方向水平向右；(c ) p me ω=，方向垂直于OC 的连线；(d ) C p mv =，方向水平向右10-2 30N x F =10-3 11221022a gP P P P F -++= 10-4 11r 12m v v v m m =++10-5 0(sin cos )v t g f'αα=-10-6 12(54)2l p m m ω=+，方向与曲柄垂直且向上 10-7 t m m l m x m m kx ωωsin 1211+=++10-8 2R s =10-9 (1) 3123123(22)cos ,2()C P L P P P L tx P P P ω+++=++ (2) 12123(2)sin ;2()C P P L t y P P P ω+=++2321max 222ωL gP P P F Ox ++=10-10 椭圆 2224l y x =+10-11 (1) 2sin G Wx l t P W Gω+=++ (2) 2m a x 2x G W F l g ω+=10-12 向右移377cm . 10-13 33(sin )cos ox R F m g m a r θθ=+，1233()(sin )sin oy RF m g m g a m g m a rθθ=+-++ 10-14 21212)(m m gm m f b m a ++-=·318··318·10-15 17cm A s =，向左移动；9cm B s =，向右移动 10-16 2max12(2)2ox r F F G G gω=++10-17 24(cos sin )3Ox mR F ωϕεϕπ=-+，24(sin cos )3Oy mR F mg ωϕεϕπ=+- 第11章11-1 (a ) ω2031ml L =，(b ) ω2021mR L =，(a ) ω2023mR L =11-2 208m s a ./=，2862kN T F .=，4626kN Oy F .=11-3 (1) ωωω22231ml mR Ml L O ---=，(2) ωω2231ml Ml L O --=11-4 θω22sin )312(l M m L O +=11-5 480r min n /=11-6 022ωωmr J ma J z z ++=11-7 0N 0Pr F fgt ω= 11-8 211212122()()R M R M'm m R R ε-=+11-9 )()(2212J i J gPR R PR Mi a ++-=11-10 t P P gkl)3(3cos210+=δϕ11-11 gR RW g J R W M a 2101sin +-=α，1T 1sin W F W a g α=+ 11-12 g J r m r m r m r m O++-=2222111122ε11-13 g R m r R m r R m a )()()(2222121ρ++++=，)()()(22221212ρρ+++-=R m r R m g m m Rr F11-14 v =T 13F mg =11-15 θsin 74g a =，θsin 71mg F -= 11-16 g a C 355.0=11-17 3)(2121m m gm m f F a ++-=·319··319·11-18 gr M R m r m R fm r m a 2222121ρ++-=，T 11A F m g m a =-，2T 2B m RF fm g a r=+11-19 2N 22sin 12D QL F a Lα=+，αcos g a Cx =，22212sin 12L a g a a Cy +=α 11-20 N 3633N B F .=11-21 P F F x O x O 516.021==，P F y O 434.11=，P F y O 164.12=第12章12-1 )cos 1(0ϕ+=mgr W AB ，)sin (cos 0θϕ-=mgr W AC 12-2 129904J F W .=，10500J f W =- 12-3 12206J W .=-，23206J W .=，031=W 12-4 (a) 2216T ml ω=，(b) 2234T mR ω=，(c) 2214T mR ω=，(d) 234C T mv =，12-5 10J W =重，503J W .=重12-6 θω222sin 61ml T = 12-7 21s s hf += 12-8 2122)cos (sin 2m m f gr m M r++-=ααϕϕω12-9 v=12-10 A v =12-11 A v =12-12 v =11/sin M R W a g W Wα-=+12-13 C v =45C a g =12-14 98N F .= 12-15 θωsin 3632121l g m m m m ++=，θεcos 23632121lgm m m m ++=12-16 C v =321321843)43(m m m gm m m F +++=12-17 (1) 2211)3()sin (2Rm m gR m M +-=αε， (2) R m m gR m M m F Ox )3(2)2sin cos 6(2121++=αα； ααsin )3()sin 3(21212⋅+++=Rm m gR m M m g m F Oy·320··320·12-18 v =m khmg a 34-=，41s 36F kh mg =+ 第13章13-1 αsin 32g a =13-2 g a 32=，T 3WF =13-3 Q P Pg a 322+=，QP PQF 32+=13-4 g P T a 3cos 2α=，N sin F P T α=-，s 1cos 3F T α= 13-5 22233cos sin 3()sin 2b a g b a ϕϕωϕ-=-13-6 445N ADF .=，54N BE F =13-7 2222(sin )cos sin J mr mr M ϕϕϕϕϕ++= 13-8 2222143)2(43ωr m gr m m M -+=，2143ωr m F Ox -=，4)2()(22121ωr m m g m m F Oy +-+= 13-9 0β=︒时，2329N Ax F =-，1382N Bx F =，1962N Ay By F F .==180β=︒时，12238N Ax F .=，592N Bx F =-，1962N Ay By F F .==13-10 2023ωmr F Ax -=，mgr F Ay =,20221ωmr F Bx =，mgr F By =13-11 g a a C x C 1712==，mg F 175= 13-12 l g 791=ε，lg 732-=ε，0=Ox F ，mg F Oy 72=第14章14-1 ctg 2P /Q /ϕ= 14-2 (3ctg 2)Ax F /P θ=14-3 A F P /=14-4 ctg Q P θ= 14-5 450N Q P /==14-6 12F F l =／2(cos )a ϕ14-7 05kN 21kN m Ax Ay A F F m ===⋅，，14-8 1866kN P .=14-9 2()F lx a k b=+14-10 2(kN)Ax F =， 3.804(kN)Ay F =，24(kN m)A M =-⋅，18.588(kN)B F =。