浙江高考历年真题之三角函数大题文科

合集下载

(精校版)《三角函数》高考真题文科总结及答案

28.（2015·山东卷 17）△ABC 中，角 A，B，C 所对的边分别为 a，b，c. 已知 cos B＝Error!，sin(A＋B)＝，ac＝2 ，
求 sin A 和 c 的值．
29。（2015·四川卷 19)已知 A,B，C 为△ABC 的内角,tan A，tan B 是关于 x 的方程 x2＋Error!px－p＋1＝0（p∈R)的两个实根．
24。（2015·湖南卷 17)设△ABC 的内角 A,B，C 的对边分别为 a，b，c，a＝btan A。
(1）证明：sin B＝cos A； 3
(2)若 sin C－sin Acos B＝，且 B 为钝角，求 A，B，C。 4
25。(2015·新课标 I 卷 17)已知 a，b，c 分别为△ABC 内角 A，B,C 的对边， sin2B＝2sin Asin C.
个单位长度后得到函数 g（x)的图象，且函数 g（x）的最大值为 2。 ①求函数 g(x)的解析式； ②证明:存在无穷多个互不相同的正整数 x0,使得 g（x0）〉0。
(直打版)《三角函数》高考真题文科总结及答案(word 版可编辑修改)
2015《三角函数》高考真题答案
1.【答案】B 2。【答案】B 3。【答案】B
4．(2015·安徽卷 4）下列函数中，既是偶函数又存在零点的是( )
A．y＝ln x
B．y＝x2＋1
C．y＝sin x
D．y＝cos x
5．（2015·广东卷 3)下列函数中，既不是奇函数，也不是偶函数的是( ）
A．y＝x＋sin 2x
B．y＝x2－cos x
C．y＝2x＋Error!
D．y＝x2＋sin x
22。（2015·江苏卷 15）在△ABC 中,已知 AB＝2，AC＝3，A＝60°。 (1)求 BC 的长; (2)求 sin 2C 的值．

2021 2021 高考全国卷三角函数解三角形真题汇编(文科)

2021 2021 高考全国卷三角函数解三角形真题汇编(文科)2021-2021高考全国卷三角函数、解三角形真题汇编(文科)2022-2022年全国高考卷三角函数与解三角形真题汇编（文科）学校：姓名：班级：考号：评分员得1分。

多项选择题1.[2021全国新课标卷i(文)]函数y=的部分图象大致为()-a、不列颠哥伦比亚省。

d.2.[2022年国家新课程标准第一卷（正文）]△ ABC的内角a、B和C分别是a、B和C。

已知SINB+Sina（sinc-COSC）=0，a=2，C=，然后C=（）a.b.c.d.3.函数f（x）=sin的最小正周期为（）a.4πB.2πC.πD4.[2021全国新课标卷iii(文)]已知sinα-cosα=,则sin2α=()a.-b.-c.d.5.[2022年国家新课程标准第三卷（文本）]函数f（x）=sin+cos-的最大值为（）a.b.1c d.6。

[2022年国家新课程标准第三卷（正文）]函数y=1+X+的部分图象大致为()第1页共4页a、 b。

c.D7.[2021高考全国新课标卷ⅰ(文),4]△abc的内角a,b,c的对边分别为a,b,c.已知A=，C=2，cosa=，然后B=（）a.b.c.2d.38.[2022年国家新课程标准高考第一卷（文本），6]将函数y=2Sin的图像向右移动一个周期，并生成图形象对应的函数为()a、 y=2sinb。

y=2sinc。

y=2sin-d。

y=2sin-9.[2022年国家新课程标准第一卷（正文），12]如果函数f（x）=x-sin2x+asinx单调增加（-∞, + ∞), 然后a的取值范围是()a、 [1,1]b-c-d--10.[2021高考全国新课标卷ⅱ(文),3]函数y=asin(ωx+φ)的部分图象如图所示,则()a、 y=2sin-b.y=2sin-c.y=2sind。

y=2英寸11.[2021高考全国新课标卷ⅱ(文),11]函数f(x)=cos2x+6cos-的最大值为()a.4b.5c.6d.712.[2022年国家新课程标准高考三（正文），6]若坦θ=-，则Cos2θ=（）第2页共4页a、 -b.-c.d。

(完整版)近五年浙江三角函数高考真题

近五年浙江三角函数高考真题一、（2013理）4．已知函数()cos()(0,0,R)f x A x A ωφωφ=+>>∈，则“()f x 是奇函数”是“2πφ=”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件6．已知R,sin 2cos ααα∈+=tan2α= A ．43B ．34 C ．34-D ．43-16．在△ABC 中，90C ∠=，M 是BC 的中点．若1sin 3BAM ∠=，则sin BAC ∠= ．（2013文）3．（与理4姐妹题）若R α∈，则“0α=”是“sin cos αα<”的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件6．函数()sin cos f x x x x =+的最小正周期和振幅分别是 A ．π，1 B ．π，2 C ．2π，1 D ．2π，218.在锐角△ABC 中，内角,,A B C 的对边分别为,,a b c ，且2sin a B =. （Ⅰ）求角A 的大小；（Ⅱ) 若6,8a b c =+=，求△ABC 的面积.二、（2012理）4.把函数cos21y x =+的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移 1个单位长度，得到的图像是18.（14分）在△ABC 中，内角,,A B C 的对边分别为,,a b c ．已知C B A cos 5sin ,32cos ==．（1）求tan C 的值；（2）若2a =ABC 的面积．（2012文） 6．（同理4）18．（ 14分）在△ABC 中，内角,,A B C 的对边分别为,,a b c ，且sin 3cos b A a B =．（Ⅰ）求角B 的大小；（Ⅱ）若3,sin 2sin b C A ==，求,a c 的值．三、（2011理） 6．若0,022ππαβ<<-<<，1cos()43πα+=，3cos()42πβ-=，则cos()2βα+= A 3B ．3C 53D ．618.（14分）在△ABC 中，角,,A B C 所对的边分别为,,a b c .已知sin sin sin (R)A C pB p +=∈，且214ac b =.（Ⅰ）当5,14p b ==时，求,a c 的值；(Ⅱ)若角B 为锐角，求p 的取值范围.（2011文）5．在ABC ∆中，角C B A ,,所对的边分别是c b a ,,，若B b A a sin cos =，则=+B A A 2cos cos sin（A ）21-（B ）21 （C ）1- （D ）118.（14分）已知函数()sin ()3f x A x πϕ=+，x R ∈，0A >，02πϕ<<.()y f x =的部分图像如图所示，P 、Q 分别为该图像的最高点和最低点，点P 的坐标为(1,)A .（Ⅰ）求()f x 的最小正周期及ϕ的值；（Ⅱ）若点R 的坐标为(1,0)，23PRQ π∠=，求A 的值.三、（2010理） 4．设02x π＜＜，则“2sin 1x x ＜”是“sin 1x x ＜”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件9．设函数()4sin(21)f x x x =+-，则在下列区间中函数()f x 不．存在零点的是（A ）[]4,2-- （B ）[]2,0- （C ）[]0,2 （D ）[]2,4 11.函数2()sin(2)224f x x x π=--的最小正周期是__________________ .18. (l4分)在△ABC 中,角,,A B C 所对的边分别为,,a b c ，已知1cos24C =-.(I)求sin C 的值；(Ⅱ)当2,2sin sin a A C ==时，求b 及c 的长．（2010文） 6．（同理4）12.（与理11姐妹题）函数2()sin (2)4f x x π=-的最小正周期是18.（本题满分）在△ABC ，角,,A B C 所对的边分别为,,a b c ,设S 为△ABC 的面积，满足2223()4S a b c =+-. （Ⅰ）求角C 的大小；（Ⅱ）求sin sin A B +的最大值.三、（2009理）8．已知a 是实数，则函数()1sin f x a ax =+的图象不可能．．．是D 【命题意图】此题是一个考查三角函数图象的问题，但考查的知识点因含有参数而丰富，结合图形考查使得所考查的问题形象而富有深度．18．（14分）在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，且满足25cos25A =，3=⋅AC AB ．（I ）求ABC ∆的面积；（II ）若6b c +=，求a 的值．（2009文） 10．（同理8） 18．（同理18）。

2021-2021 高考全国卷三角函数解三角形真题汇编(文科)

2021-2021 高考全国卷三角函数、解三角形真题汇编(文科)2021-2021 高考全国卷三角函数、解三角形真题汇编（文科）学校：姓名：班级：考号：评卷人得分一、选择题1. [2021・全国新课标卷I(文)]函数y=的部分图象大致为 ( ) -A. B. C.D.2. [2021・全国新课标卷I(文)]△ABC的内角A,B,C的对边分别为a,b,c.已知sinB+sin A(sin C-cos C)=0,a=2,c= ,则C= ( )A. B. C. D.3. [2021・全国新课标卷II(文)]函数f(x)=sin 的最小正周期为( ) A. 4πB. 2πC. πD.4. [2021・全国新课标卷III (文)]已知sin α-cos α=,则sin 2α= ( ) A. -B. -C.D.5. [2021・全国新课标卷III (文)]函数f(x)=sin +cos - 的最大值为 ( )A. B. 1 C. D. 6. [2021・全国新课标卷III (文)]函数y=1+x+的部分图象大致为( )第1页共4页A. B.C.D.7. [2021・高考全国新课标卷Ⅰ(文),4]△ABC的内角A,B,C的对边分别为a,b,c.已知a= ,c=2,cos A=,则b= ( )A. B. C. 2 D. 38. [2021・高考全国新课标卷Ⅰ(文),6]将函数y=2sin 的图象向右平移个周期后,所得图象对应的函数为 ( )A. y=2sinB. y=2sinC. y=2sin -D.y=2sin -9. [2021・高考全国新课标卷Ⅰ(文),12]若函数f(x)=x-sin 2x+asin x在(-∞,+∞)单调递增,则a的取值范围是 ( )A. [-1,1]B. -C. -D. - -10. [2021・高考全国新课标卷Ⅱ(文),3]函数y=Asin(ωx+φ)的部分图象如图所示,则 ( )A. y=2sin -B. y=2sin -C. y=2sinD. y=2sin11. [2021・高考全国新课标卷Ⅱ(文),11]函数f(x)=cos2x+6cos - 的最大值为( )A. 4B. 5C. 6D. 712. [2021・高考全国新课标卷Ⅲ(文),6]若tan θ=-,则cos 2θ= ( )第2页共4页A. -B. -C.D.13. [2021・高考全国新课标卷Ⅲ(文),9]在△ABC中,B=,BC边上的高等于BC,则sin A= ( ) A. B. C. D.14. [2021・高考全国新课标卷Ⅰ(文),8]函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )A. - ,k∈ZB. - ,k∈ZC. - ,k∈ZD. - ,k∈Z15. [2021�q高考全国新课标卷Ⅰ(文)，7]在函数①y＝cos|2x|,②y＝|cos x|,③y＝cos(2x＋),④y＝tan(2x－)中,最小正周期为π的所有函数为( )A. ②④B. ①③④C. ①②③D. ①③16. [2021・高考全国新课标卷I(文),9]函数f(x)=(1-cosx)sinx在[-π,π]的图象大致为( )A. B.C. D.17. [2021・高考全国新课标卷I(文),10]已知锐角△ABC的内角A,B,C的对边分别为2a,b,c,23cosA+cos2A=0,a=7,c=6,则b=( ) A. 10 B. 9 C.8 D. 5第3页共4页18. [2021・高考全国新课标卷II(文),4]△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为( )A. 2 +2B. +1C. 2 -2D. -119. [2021・高考全国新课标卷II(文),6]已知sin2α=,则cos(α+)=( ) A.B. C. D. 评卷人得分二、填空题220. [2021・全国新课标卷I(文)]已知α∈ ,tan α=2,则cos - = . 21. [2021・全国新课标卷II(文)]函数f(x)=2cos x+sin x的最大值为 . 22. [2021・全国新课标卷II(文)]△ABC的内角A,B,C的对边分别为a,b,c,若2bcos B=acos C+ccos A,则B= .23. [2021・全国新课标卷III (文)]△ABC的内角A,B,C的对边分别为a,b,c.已知C=60°,b= ,c=3,则A= .24. [2021・高考全国新课标卷Ⅰ(文),14]已知θ是第四象限角,且sin ,则tan - = .25. [2021・高考全国新课标卷Ⅱ(文),15]△ABC的内角A,B,C的对边分别为a,b,c,若cos A=,cos C=,a=1,则b= .26. [2021・高考全国新课标卷Ⅲ(文),14]函数y=sin x- cos x的图象可由函数y=2sin x的图象至少向右平移个单位长度得到.27. [2021�q高考全国新课标卷Ⅰ(文)，16]如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN＝60°,C点的仰角∠CAB＝45°以及∠MAC＝75°；从C点测得∠MCA＝60°.已知山高BC＝100 m,则山高MN＝________m.28. [2021�q高考全国新课标Ⅱ(文)，14]函数f(x)＝sin(x＋φ)－2sin φcos x的最大值为________. 29. [2021・高考全国新课标卷I(文),16]设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ= .30. [2021・高考全国新课标卷II(文),16]函数y=cos(2x+φ)(-π≤φ函数y=sin(2x+)的图象重合,则φ= .第4页共4页感谢您的阅读，祝您生活愉快。

专题09 三角函数——三年(2021-2021)高考真题文科数学分项汇编(原卷版)

专题 09 三角函数1.【2020年高考全国Ⅲ卷文数】已知sinθ+ sin（θ+π）=1 ，则sin（θ+π）=A.12B. 333C.236D. 222.【2020 年高考全国Ⅰ卷文数】设函数f (x) = cos(ωx +π) 在[−π，π]的图像大致如下图，则f（x）的最小正6周期为A.10π9C．4π3B．7π6D．3π23.【2020 年高考全国Ⅲ卷文数】已知函数f(x)=sin x+ 1，则sin xA．f(x)的最小值为2 B．f(x)的图像关于y 轴对称C．f(x)的图像关于直线x =π对称D．f(x)的图像关于直线x =π对称24.【2020 年高考天津】已知函数f (x) = sin(x +π) ．给出下列结论：3① f (x) 的最小正周期为2π；π② f ( )2是f (x) 的最大值；③把函数y = sin x 的图象上所有点向左平移π个单位长度，可得到函数y =3f (x) 的图象．其中所有正确结论的序号是A．①B．①③C．②③D．①②③5.【2020年高考北京】2020年3月14日是全球首个国际圆周率日（πDay）．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔·卡西的方法是：当正整数n 充分大时，计算单位圆的内接正6n 边形的周长和外切正6n 边形（各边均与圆相切的正6n 边形）的周长，将它们的算术平均数作为2π的近似值．按照阿尔·卡西的方法，π的近似值的表达式是33⎛ 30︒ 30︒ ⎫ ⎛ 30︒ 30︒ ⎫A. 3n sin n + tan ⎪n B. 6n sin n + tan ⎪n ⎝ ⎭⎝ ⎭⎛ 60︒ 60︒ ⎫⎛ 60︒ 60︒ ⎫ C. 3n sin n + tan ⎪n D. 6n sin n + tan ⎪n ⎝ ⎭⎝ ⎭6. 【2020 年新高考全国Ⅰ卷】下图是函数 y = sin(ωx +φ)的部分图像，则 sin(ωx +φ)=A. sin(x + π）B ． sin( π - 2x )C ． cos(2x + π）D ． cos( 5π- 2x )33 6 67. 【2019 年高考全国Ⅰ卷文数】函数 f (x ) =sin x + xcos x + x 2在[-π, π] 的图像大致为A.B ．C ．D ．8. 【2019 年高考全国Ⅰ卷文数】tan255°=A ．−2−B ．−2+C ．2−D ．2+ 9. 【2019 年高考全国Ⅱ卷文数】若 x 1= π ，x 2=3π是函数 f (x )= sin ωx (ω>0)两个相邻的极值点，则ω=443 A ．2 B ．21 C ．1D ．210. 【2019 年高考全国Ⅱ卷文数】已知 a ∈（0， π），2sin2α=cos2α+1，则 sin α=2A. 15 B.53 32 C.33D. 2 551. 【2019年高考全国Ⅲ卷文数】函数 f (x ) = 2sin x - sin2x 在[0，2π]的零点个数为A ．2B ．3C ．4D ．512. 【2019 年高考北京卷文数】设函数 f （x ）=cos x +b sin x （b 为常数），则“b =0”是“f （x ）为偶函数”的A. 充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件13. 【2019 年高考天津卷文数】已知函数 f (x ) = A sin(ωx +ϕ)( A > 0,ω> 0,|ϕ|< π) 是奇函数，且 f ( x ) 的最小正周期为π，将 y = f (x ) 的图象上所有点的横坐标伸长到原来的 2 倍（纵坐标不变），所得图象对应的函数为 g ( x ) .若 g ⎛ π ⎫=，则 f ⎛ 3π ⎫ =4 ⎪ 8 ⎪ ⎝ ⎭ ⎝ ⎭A ．−2B ． -C ．14. 【2018 年高考全国Ⅲ卷文数】函数 f (x )=πA ．4 D ．2 tan x1+ tan 2 xπB ．2的最小正周期为C ．π D ． 2π15. 【2018 年高考全国Ⅰ卷文数】已知函数 f ( x ) = 2 c os 2 x -sin 2 x + 2 ，则 A. f ( x ) 的最小正周期为π，最大值为 3 B. f (x ) 的最小正周期为π，最大值为 4 C. f (x ) 的最小正周期为2π，最大值为 3 D. f (x ) 的最小正周期为 2π，最大值为 4 16. 【2018 年高考天津卷文数】将函数 y = sin(2x + π) 的图象向右平移 π个单位长度，所得图象对应的函数[- π π510A. 在区间, ] 上单调递增B ．在区间上单调递减4 42 22 5 5π π πC ．在区间[ , ] 上单调递增D ．在区间[ , π] 上单调递减 4 2217. 【2018 年高考全国Ⅲ卷文数】若sin α= 1，则cos 2α= 387A.B ．9 9 C ． - 7 9D ． - 8 918. 【2018 年高考全国Ⅰ卷文数】已知角α的顶点为坐标原点，始边与 x 轴的非负半轴重合，终边上有两点A (1，a ) ，B (2 ，b ) ，且cos 2α= 2，则 a - b =3A. 1 B ． 55 5C ．D ．119. 【2018 年高考全国Ⅱ卷文数】若 f (x ) = cos x - sin x 在[0, a ] 是减函数，则 a 的最大值是 π πA.B ．4 2C ．3π D ．π 420. 【2018 年高考浙江卷】函数 y = 2 x sin2x 的图象可能是A.B ．C ．D ．21. 【2018 年高考北京卷文数】在平面直角坐标系中， AB , C D , E F , G H 是圆x 2 + y 2 = 1 上的四段弧（如图），点 P 在其中一段上，角α以 O x 为始边，OP 为终边，若tan α< cos α< sin α，则 P 所在的圆弧是A. AB B ． C D C ． E FD ． G H 2. 【2020年高考全国Ⅱ卷文数】若sin x = - 2，则cos 2x = ． 323. 【2020 年高考江苏】已知sin 2 ( π +α) = 2，则sin 2α的值是▲．4 324. 【2020 年高考北京】若函数 f (x ) = sin(x +ϕ) + cos x 的最大值为 2，则常数ϕ的一个取值为．25. 【2020 年高考浙江】已知tan θ= 2 ，则cos 2θ=， tan(θ- π) = ． 4 26. 【2020 年高考江苏】将函数 y = 3sin(2x π) 的图象向右平移 π个单位长度，则平移后的图象中与 y 轴最 ﹢ 4 6近的对称轴的方程是▲ ．27. 【2020 年新高考全国Ⅰ卷】某中学开展劳动实习，学生加工制作零件，零件的截面如图所示．O 为圆孔及轮廓圆弧 AB 所在圆的圆心，A 是圆弧 AB 与直线 AG 的切点，B 是圆弧 AB 与直线 BC 的切点，四边形 DEFG 为矩形，BC ⊥DG ，垂足为 C ，tan ∠ODC = 3， BH ∥DG ，EF =12 cm ，DE=2 cm ，A 到直线5 DE 和 EF 的距离均为 7 cm ，圆孔半径为 1 cm ，则图中阴影部分的面积为cm 2．28. 【2019 年高考全国Ⅰ卷文数】函数 f (x ) = sin(2x +3π) - 3cos x 的最小值为．2tan α = - 2 ⎛ π ⎫ 29. 【2019 年高考江苏卷】已知 tan ⎛α+ π ⎫ 3 ，则sin 2α+ 4 ⎪ 的值是 ▲.4 ⎪ ⎝ ⎭ ⎝ ⎭30.【2018 年高考全国Ⅱ卷文数】已知tan(α-5π) =1，则tanα=．4 531.【2018 年高考江苏卷】已知函数y = sin (2x +ϕ)(-π<ϕ<π) 的图象关于直线x =π对称，则ϕ的值2 2 3是．32.【2019 年高考浙江卷】设函数f (x) = sin x, x ∈R .（1）已知θ∈[0, 2π), 函数f (x +θ) 是偶函数，求θ的值；（2）求函数y = [ f (x +π)]2 +[ f (x +π)]2 的值域．12 43.【2018 年高考北京卷文数】已知函数f (x) = sin2x+3 sin x cos x .（1）求f (x) 的最小正周期；（2）若f (x) 在区间[-π, m] 上的最大值为3，求m 的最小值.3 234.【2018 年高考浙江卷】已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点P（-3，-4）．5 5（1）求sin（α+π）的值；5（2）若角β满足sin（α+β）=13，求cosβ的值．35．【2018年高考江苏卷】已知α,β为锐角，tanα=4，cos(α+β)=-5．3 5（1）求cos 2α的值；（2）求tan(α-β) 的值．。

三角函数历年高考题

三角函数历年高考题(总13页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除三角函数题型分类总结一．三角函数的求值、化简、证明问题常用的方法技巧有：a) 常数代换法：如：αα22cos sin 1+=b) 配角方法：ββαα-+=)(,()βαβαα-++=)(2,22βαβαα-++=,22βαβαβ--+=1、sin330︒= tan690° = o 585sin =2、（1）(10全国Ⅰ) α是第四象限角，12cos 13α=，则sin α=__________ （2）（11北京文）若4sin ,tan 05θθ=->，则cos θ= .(3) α是第三象限角，21)sin(=-πα，则αcos = )25cos(απ+=3、(1) (09陕西)已知sin ,5α=则44sin cos αα-= . (2)（12全国文）设(0,)2πα∈，若3sin 5α=)4πα+= .（3）（08福建）已知3(,),sin ,25παπα∈=则tan()4πα+=4. (1)(10福建) sin15cos75cos15sin105+= (2)（11陕西）cos 43cos77sin 43cos167o o o o += 。

（3）sin163sin 223sin 253sin313+= 。

5.(1) 若sin θ＋cos θ＝15，则sin 2θ=（2）已知3sin()45x π-=，则sin 2x 的值为(3) 若2tan =α ,则ααααcos sin cos sin -+=6. （10北京）若角α的终边经过点(12)P -，，则αcos = tan 2α= 7．（09浙江）已知cos()22πϕ+=，且||2πϕ<，则tan ϕ＝8.若cos 2π2sin 4αα=-⎛⎫- ⎪⎝⎭cos sin αα+= 9.（09重庆文）下列关系式中正确的是（）A ．000sin11cos10sin168<<B ．000sin168sin11cos10<<C ．000sin11sin168cos10<<D ．000sin168cos10sin11<<10．已知53)2cos(=-πα，则αα22cos sin -的值为（） A ．257 B ．2516- C ．259 D ．257-11．已知sin θ=－1312，θ∈（－2π，0），则cos （θ－4π）的值为（）A ．－2627 B ．2627 C ．－26217 D ．26217 12．已知f （cosx ）=cos3x ，则f （sin30°）的值是（）A ．1B ．23C ．0D ．－113．已知sin x －sin y = －32，cos x －cos y = 32，且x ，y 为锐角，则tan(x －y )的值是 ( ) A ．5142 B ．－5142 C ．±5142 D ．28145±14．已知tan160o ＝a ，则sin2000o 的值是 ( )A.a 1＋a 2B.－a 1＋a 2C.11＋a 2D.－11＋a 215.若02,sin 3cos απαα≤≤>，则α的取值范围是： ( )（Ａ）,32ππ⎛⎫ ⎪⎝⎭ （Ｂ）,3ππ⎛⎫⎪⎝⎭（Ｃ）4,33ππ⎛⎫ ⎪⎝⎭ （Ｄ）3,32ππ⎛⎫⎪⎝⎭16.已知cos （α-6π）+sin α=的值是则)67sin(,354πα+ ( ) （A ）-532 （B ）532 (C)-54 (D) 5417.若,5sin 2cos -=+a a 则a tan = （）（A ）21 （B ）2 （C ）21- （D ）2-二.最值1.（09福建）函数()sin cos f x x x =最小值是= 。

高考全国卷三角函数、解三角形真题汇编（文科）

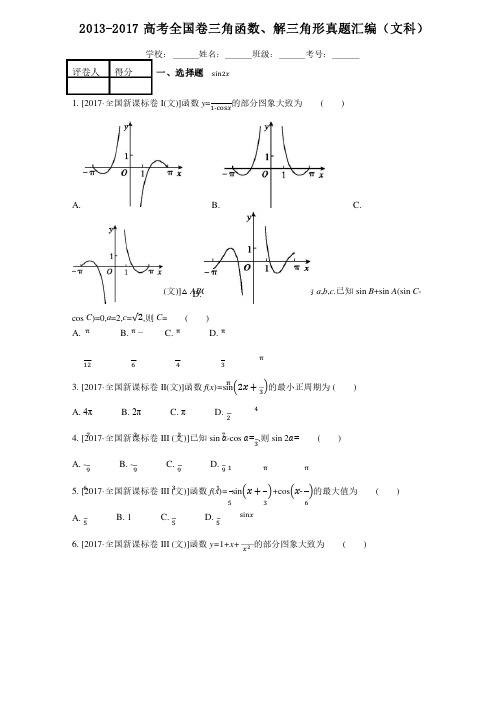
2013-2017 高考全国卷三角函数、解三角形真题汇编（文科）学校：姓名：班级：考号：评卷人评卷人得分得分一、选择题 1. [2017·全国新课标卷I(文)]函数y =sin2x 1-cosx 的部分图象大致为的部分图象大致为( ) A. B. C.D. 2. [2017·全国新课标卷I(文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.已知sin B +sin A (sin C -cos C )=0,a =2,c =√2,则C = ( )A. π12B. π6C. π4D. π3 3. [2017·全国新课标卷II(文)]函数f (x )=sin (2x +π3)的最小正周期为 ( ) A. 4π B. 2π C. π D. π24. [2017·全国新课标卷III (文)]已知sin α-cos α=43,则sin 2α= ( )A. -79B. -29C. 29D. 79 5. [2017·全国新课标卷III (文)]函数f (x )=15sin (x +π3)+cos (x (x--π6)的最大值为的最大值为 ( ) A. 65 B. 1 C. 35 D. 15 6. [2017·全国新课标卷III (文)]函数y=1+x+sinx x 2的部分图象大致为的部分图象大致为 ( )A. B.C. D.7. [2016·高考全国新课标卷Ⅰ(文),4]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知a =√5,c =2,cos A =23,则b = ( ) A. √2 B. √3C. 2D. 3 8. [2016·高考全国新课标卷Ⅰ(文),6]将函数y =2sin (2x +π6)的图象向右平移14个周期后,所得图象对应的函数为象对应的函数为 ( ) A. y =2sin (2x +π4) B. y =2sin (2x +π3) C. y =2sin (2x (2x--π4) D. y =2sin (2x (2x--π3) 9. [2016·高考全国新课标卷Ⅰ(文),12]若函数f (x )=x -13sin 2x +a sin x 在(-∞,+∞)单调递增,则a 的取值范围是的取值范围是 ( ) A. [-1,1] B. [-1,13] C. [-13,13] D. [-1,1,--13] 10. [2016·高考全国新课标卷Ⅱ(文),3]函数y =A sin(ωx +φ)的部分图象如图所示,则 ( ) A. y =2sin (2x (2x--π6) B. y =2sin (2x (2x--π3) C. y =2sin (x +π6) D. y =2sin (x +π3)11. [2016·高考全国新课标卷Ⅱ(文),11]函数f (x )=cos2x +6cos (π2-x)的最大值为( ) A. 4 B. 5 C. 6 D. 7 12. [2016·高考全国新课标卷Ⅲ(文),6]若tan θ=-13,则cos 2θ= ( )A. -45B. -15C. 15 D. 45 13. [2016·高考全国新课标卷Ⅲ(文),9]在△ABC 中,B =π4,BC 边上的高等于13BC ,则sin A = ( ) A. 310 B. √1010 C. √55 D. 3√101014. [2015·高考全国新课标卷Ⅰ(文),8]函数f (x )=cos(ωx+φ)的部分图象如图所示,则f (x )的单调递减区间为( )A. (kπ(kπ--14,kπ+34),k ∈Z B. (2kπ(2kπ--14,2kπ+34),k ∈Z C. (k (k--14,k +34),k ∈Z D. (2k (2k--14,2k +34),k ∈Z 15. [2014﹒高考全国新课标卷Ⅰ(文)，7]在函数①y ＝cos|2x |,②y ＝|cos x |,③y ＝cos(2x ＋π6),④y ＝tan(2x －π4)中,最小正周期为π的所有函数为( )A. ②④B. ①③④C. ①②③D. ①③16. [2013·高考全国新课标卷I(文),9]函数f (x )=(1-cos x )sin x 在[-π,π]的图象大致为( )A. B.C. D. 17. [2013·高考全国新课标卷I(文),10]已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2A+cos2A=0,a=7,c=6,则b=( )A. 10B. 9C. 8D. 518. [2013·高考全国新课标卷II(文),4]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知b=2,B=π6,C=π4,则△ABC 的面积为( )A. 2√3+2B. √3+1C. 2√3-2D. √3-1 19. [2013·高考全国新课标卷II(文),6]已知sin2α=23,则cos 2(α+π4)=( ) A. 16 B. 13 C. 12 D. 23 评卷人评卷人得分得分二、填空题20. [2017·全国新课标卷I(文)]已知α∈(0,π2),tan α=2,则cos (α(α--π4)= . 21. [2017·全国新课标卷II(文)]函数f (x )=2cos x+sin x 的最大值为 .22. [2017·全国新课标卷II(文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2b cos B=a cos C+c cos A ,则B= .23. [2017·全国新课标卷III (文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.已知C=60°60°,,b=√6,c=3,则A= .24.[2016·高考全国新课标卷Ⅰ(文),14]已知θ是第四象限角,且sin (θ+π4)=35,则tan (θ(θ--π4)= 25. [2016·高考全国新课标卷Ⅱ(文),15]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若cos A =45,cos C =513,a =1,则b = . 26. [2016·高考全国新课标卷Ⅲ(文),14]函数y =sin x -√3cos x 的图象可由函数y =2sin x 的图象至少向右平移个单位长度得到.27. [2014﹒高考全国新课标卷Ⅰ(文)，16]如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角∠MAN ＝60°60°,,C 点的仰角∠CAB ＝45°以及∠MAC ＝75°；从C 点测得∠MCA ＝60°60°..已知山高BC ＝100 m,则山高MN ＝________m.28. [2014﹒高考全国新课标Ⅱ(文)，14]函数f (x )＝sin(x ＋φ)－2sin φcos x 的最大值为________. 29. [2013·高考全国新课标卷I(文),16]设当x=θ时,函数f (x )=sin x-2cos x 取得最大值,则cos θ= .30. [2013·高考全国新课标卷II(文),16]函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移π2个单位后,与函数y=sin(2x+π3)的图象重合,则φ= .。

历年高考数学三角函数经典试题

历届高考中的“三角函数的图像与性质”试题精选（自我测试）(卷A)一、选择题：（每小题5分，计50分）题号12345678910答案１．（2009陕西理科）若3s i n c o s 0αα+=,则 21c o s s in2αα+的值为（A ）103（B ）（C ）23 (D) 2-２．（2007江苏）下列函数中，周期为2π的是（）A ．s in 2x y =B ．s in2y x =C ．co s 4xy = D ．c o s4y x =３．（2007江西文）若0＜x ＜2π，则下列命题中正确的是（） A ．sin x ＜x π2 B ．sin x ＞x π2 C ．sin x ＜x π3 D ．sin x ＞xπ3４．（2009山东）将函数y=sin2x 的图象向左平移4π个单位，再向上平移1个单位，所得图象的函数解析式是(A) y=2cos 2x（B ）y=2sin 2x (C) y=1+sin(2x+4π)(D)y=cos2xi5 .（2007福建理)已知函数f(x)＝sin()()的最小正周期为，则该函数的图象（）A 关于点（，0）对称B 关于直线x ＝对称C 关于点（，0）对称D 关于直线x ＝对称6（2007江苏）函数()s i n 3c o s ([,0])f x x x x π=-∈-的单调递增区间是（） A ．5[,]6ππ-- B ．5[,]66ππ-- C ．[,0]3π- D ．[,0]6π-7．（2005福建理）函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图，则（） A ．4,2πϕπω==B ．6,3πϕπω==C ．4,4πϕπω==D ．45,4πϕπω==８．(2009辽宁)已知函数()s i n ()(0)f x x ωϕω-+>的图象如图所示，则ω =９．（2009宁夏）有四个关于三角函数的命题：1p ：∃x ∈R, 2s i n+2c o s =122p : ∃x 、y ∈R, sin(x-y)=sinx-siny3p : ∀x ∈[]0,π,1cos 22x -=sinx 4p : sinx=cosy ⇒x+y=2π其中假命题的是（A ）1p ，4p （B ）2p ，4p （3）1p ，3p （4）2p ，4p10.(2009宁夏)已知函数y=sin （ωx+ϕ）（ω>0, -π≤ϕ<π）的图像如图所示，则ϕ=________________4．（2009江西）若函数()f x =（1+ 3tanx ）cos, 0≤x ＜2π,则()f x 的最大值为A ．1 B. 2 C. 3+1 D. 3+25.(2010天津)在△ABC 中，内角A,B,C 的对边分别是a,b,c ，若223a b b c -=，s i n 23s i n C B =，则A=6．（2003全国理，广东）函数)cos (sin sin 2x x x y +=的最大值为（） A ．21+B ．12-C ．2D ．27.( 2007广东文)已知简谐运动()2s i n ()(||)32f x x ππϕϕ=+<的图象经过点(0,1),则该简谐运动的最小正周期T 和初相ϕ分别为（）8.（2005浙江理）已知k ＜－4，则函数y ＝cos2x ＋k (cos x －1)的最小值是( )(A) 1 (B) －1 (C) 2k ＋1 (D) －2k ＋19．（2005全国Ⅰ卷文、理）当20π<<x 时，函数x xx x f 2sin sin 82cos 1)(2++=的最小值为( )（A ）2 （B ）32 （C ）4 （D ）3410. (2002年广东、江苏、河南，全国文、理，全国新课程文、理，天津文、理)在)2,0(π内，使xx cos sin >成立的x 的取值范围是（） (A))45,()2,4(ππππ (B)),4(ππ (C))45,4(ππ (D))23,45(),4(ππππ 二.填空题: （每小题5分，计20分）11.（2006湖南文）若)4sin(3)4sin()(ππ-++=x x a x f 是偶函数，则a = .12.（2004全国Ⅲ卷理）函数xx y cos 3sin +=在区间]2,0[π上的最小值为 .13.（2005上海文、理）函数()[]s i n2s i n 0,2f x x x x π=+∈的图像与直线y k =有且仅有两个不同的交点，则k 的取值范围是____________14.（2007四川理）下面有五个命题：①函数y =sin 4x -cos 4x 的最小正周期是π. ②终边在y 轴上的角的集合是{a |a =Z k k ∈π,2|. ③在同一坐标系中，函数y =sin x 的图象和函数y =x 的图象有三个公共点. ④把函数.2sin 36)32sin(3的图象得到的图象向右平移x y x y =ππ+= ⑤函数).2sin(π-=x y 在（0，π）上是减函数。

专题3 三角函数的图象与性质【高考文科数学】含答案

第一讲三角函数的图象与性质1．任意角的三角函数(1)设α是一个任意角，它的终边与单位圆交于点P (x ，y )，那么sin α＝y ，cos α＝x ，tan α＝yx.(2)各象限角的三角函数值的符号：一全正，二正弦，三正切，四余弦． 2 函数性质 y ＝sin xy ＝cos xy ＝tan x定义域RR{x |x ≠k π＋π2，k ∈Z}图象值域[－1,1] [－1,1]R对称性对称轴：x ＝k π＋π2(k ∈Z)；对称中心：(k π，0)(k ∈Z)对称轴：x ＝ k π(k ∈Z)；对称中心： (k π＋π2，0)(k ∈Z)对称中心：⎝⎛⎭⎪⎫k π2，0(k ∈Z)周期2π2ππ单调性单调增区间[2k π－π2，2k π＋π2](k ∈Z)；单调减区间[2k π＋π2，2k π＋3π2] (k ∈Z) 单调增区间 [2k π－π，2k π]( k ∈Z)；单调增区间 (k π－π2，k π＋π2)(k ∈Z)奇偶性奇偶奇3． y ＝A sin(ωx ＋φ)的图象及性质(1)五点作图法：五点的取法：设X ＝ωx ＋φ，X 取0，π2，π，3π2，2π时求相应的x值、y 值，再描点作图．(2)给出图象求函数表达式的题目，比较难求的是φ，一般是从“五点法”中的第一点(－φω，0)作为突破口． (3)图象变换y ＝sin x ―――――――――――――→向左φ>0或向右φ<0平移|φ|个单位y ＝sin(x ＋φ)――――――――――――→纵坐标变为原来的A 倍横坐标不变y ＝A sin(ωx ＋φ)．1． (2013·江西)函数y ＝sin 2x ＋23sin 2x 的最小正周期T 为________．答案 π解析 y ＝sin 2x ＋3(1－cos 2x )＝2sin ⎝ ⎛⎭⎪⎫2x －π3＋3， ∴T ＝π.2． (2013·山东)将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的一个可能取值为( ) A.3π4 B.π4C ．0D ．－π4答案 B解析把函数y ＝sin(2x ＋φ)沿x 轴向左平移π8个单位后得到函数y ＝sin 2⎝ ⎛⎭⎪⎫x ＋φ2＋π8＝sin ⎝⎛⎭⎪⎫2x ＋φ＋π4为偶函数，则φ＝π4.3． (2013·四川)函数f (x )＝2sin(ωx ＋φ)(ω>0，－π2<φ<π2)的部分图象如图所示，则ω，φ的值分别是( )A ．2，－π3B ．2，－π6C ．4，－π6D ．4，π3答案 A解析 34T ＝5π12－⎝ ⎛⎭⎪⎫－π3，T ＝π，∴ω＝2，∴2×5π12＋φ＝2k π＋π2，k ∈Z ，∴φ＝2k π－π3，k ∈Z .又φ∈⎝ ⎛⎭⎪⎫－π2，π2，∴φ＝－π3，选A. 4． (2012·课标全国)已知ω>0，函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π4在⎝ ⎛⎭⎪⎫π2，π上单调递减，则ω的取值范围是( )A.⎣⎢⎡⎦⎥⎤12，54B.⎣⎢⎡⎦⎥⎤12，34C.⎝ ⎛⎦⎥⎤0，12D ．(0,2]答案 A解析取ω＝54，f (x )＝sin ⎝ ⎛⎭⎪⎫54x ＋π4，其减区间为⎣⎢⎡⎦⎥⎤85k π＋π5，85k π＋π，k ∈Z ，显然⎝ ⎛⎭⎪⎫π2，π⊆⎣⎢⎡⎦⎥⎤85k π＋π5，85k π＋π，k ∈Z ，排除B ，C. 取ω＝2，f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π4，其减区间为⎣⎢⎡⎦⎥⎤k π＋π8，k π＋58π，k ∈Z ，显然⎝ ⎛⎭⎪⎫π2，π⃘⎣⎢⎡⎦⎥⎤k π＋π8，k π＋58π，k ∈Z ，排除D. 5． (2011·安徽)已知函数f (x )＝sin(2x ＋φ)，其中φ为实数．f (x )≤⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π6对x ∈R 恒成立，且f ⎝ ⎛⎭⎪⎫π2>f (π)，则f (x )的单调递增区间是( )A.⎣⎢⎡⎦⎥⎤k π－π3，k π＋π6(k ∈Z ) B.⎣⎢⎡⎦⎥⎤k π，k π＋π2(k ∈Z ) C.⎣⎢⎡⎦⎥⎤k π＋π6，k π＋2π3(k ∈Z ) D.⎣⎢⎡⎦⎥⎤k π－π2，k π(k ∈Z ) 答案 C解析由∀x ∈R ，有f (x )≤⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π6知，当x ＝π6时f (x )取最值，∴f ⎝ ⎛⎭⎪⎫π6＝sin ⎝ ⎛⎭⎪⎫π3＋φ＝±1，∴π3＋φ＝±π2＋2k π(k ∈Z )， ∴φ＝π6＋2k π或φ＝－5π6＋2k π(k ∈Z )，又∵f ⎝ ⎛⎭⎪⎫π2>f (π)，∴sin(π＋φ)>sin(2π＋φ)， ∴－sin φ>sin φ，∴sin φ<0.∴φ取－5π6＋2k π(k ∈Z )．不妨取φ＝－5π6，则f (x )＝sin ⎝⎛⎭⎪⎫2x －5π6. 令－π2＋2k π≤2x －5π6≤π2＋2k π(k ∈Z )，∴π3＋2k π≤2x ≤4π3＋2k π(k ∈Z )， ∴π6＋k π≤x ≤2π3＋k π(k ∈Z )． ∴f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤π6＋k π，2π3＋k π(k ∈Z )．题型一三角函数的概念问题例1 如图，以Ox 为始边作角α与β(0<β<α<π)，它们终边分别与单位圆相交于点P 、Q ，已知点P 的坐标为(－35，45)．(1)求sin 2α＋cos 2α＋11＋tan α的值；(2)若OP →·OQ →＝0，求sin(α＋β)．审题破题 (1)先根据三角函数的定义求sin α，cos α，代入求三角函数式子的值；(2)根据OP →⊥OQ →和β范围可求sin β，cos β.解 (1)由三角函数定义得cos α＝－35，sin α＝45，∴原式＝2sin αcos α＋2cos 2α1＋sin αcos α＝2cos αsin α＋cos αsin α＋cos αcos α＝2cos 2α＝2×(－35)2＝1825.(2)∵OP →·OQ →＝0，∴α－β＝π2，∴β＝α－π2，∴sin β＝sin(α－π2)＝－cos α＝35，cos β＝cos(α－π2)＝sin α＝45.∴sin(α＋β)＝sin αcos β＋cos αsin β＝45×45＋(－35)×35＝725. 反思归纳 (1)三角函数的定义是求三角函数值的基本依据，如果已知角终边上的点，则利用三角函数的定义，可求该角的正弦、余弦、正切值．(2)同角三角函数间的关系、诱导公式在三角函数式的化简中起着举足轻重的作用，应注意正确选择公式、注意公式应用的条件．变式训练1 (1)已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x上，则cos 2θ等于( )A ．－45B ．－35C.35D.45答案 B解析依题意得tan θ＝2，∴cos 2θ＝cos 2θ－sin 2θ＝cos 2θ－sin 2θcos 2θ＋sin 2θ＝1－tan 2θ1＋tan 2θ＝－35.(2)已知角α的顶点与原点重合，始边与x 轴的正半轴重合，终边上一点P (－4,3)，则cos ⎝ ⎛⎭⎪⎫π2＋αsin －π－αcos ⎝ ⎛⎭⎪⎫11π2－αsin ⎝ ⎛⎭⎪⎫9π2＋α的值为________．答案－34解析原式＝－sin α·sin α－sin α·cos α＝tan α.根据三角函数的定义，得tan α＝y x ＝－34，所以原式＝－34.题型二函数y ＝A sin(ωx ＋φ)的图象及应用例2 已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，|φ|<π2)在一个周期内的图象如图所示．(1)求函数的解析式；(2)设0<x <π，且方程f (x )＝m 有两个不同的实数根，求实数m 的取值范围以及这两个根的和．审题破题 (1)先由函数图象确定A ，ω，再代入点⎝ ⎛⎭⎪⎫π6，2求φ；(2)利用转化思想先把方程问题转化为函数问题，再利用数形结合法求解．解 (1)由图象知：A ＝2，34T ＝11π12－π6＝3π4，则T ＝π，所以ω＝2.又图象过点⎝ ⎛⎭⎪⎫π6，2，所以2×π6＋φ＝π2，即φ＝π6.所以所求的函数的解析式为f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6. (2)在同一坐标系中画出y ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6和y ＝m (m ∈R )的图象，如图所示，由图可知，－2<m <1或1<m <2时，直线y ＝m 与曲线有两个不同的交点，即原方程有两个不同的实数根，故m 的取值范围为－2<m <1或1<m <2.当－2<m <1时，两根之和为4π3；当1<m <2时，两根之和为π3.反思归纳 (1)已知图象求函数y ＝A sin(ωx ＋φ) (A >0，ω>0)的解析式时，常用的方法是待定系数法．由图中的最大、最小值求出A ，由周期确定ω，由适合解析式的点的坐标来确定φ(代点时尽量选最值点，或者搞清点的对应关系)；(2)利用数形结合思想从函数图象上可以清楚地看出当－2<m <1或1<m <2时，直线y ＝m 与曲线有两个不同的交点，即原方程有两个不同的实数根，利用图象的对称性便可求出两根之和．变式训练2 已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，－π<φ<π)的部分图象如图所示，则函数f (x )的解析式为( )A ．f (x )＝2sin ⎝ ⎛⎭⎪⎫12x ＋π4B ．f (x )＝2sin ⎝ ⎛⎭⎪⎫12x ＋3π4C ．f (x )＝2sin ⎝ ⎛⎭⎪⎫12x －π4D ．f (x )＝2sin ⎝ ⎛⎭⎪⎫12x －3π4答案 B解析由图象可知A ＝2，T 2＝3π2－⎝ ⎛⎭⎪⎫－π2＝2π，即T ＝4π.又T ＝2πω＝4π，所以ω＝12，所以函数f (x )＝2sin ⎝ ⎛⎭⎪⎫12x ＋φ.又f ⎝ ⎛⎭⎪⎫－π2＝2sin ⎣⎢⎡⎦⎥⎤12×⎝ ⎛⎭⎪⎫－π2＋φ＝2，即sin ⎝ ⎛⎭⎪⎫－π4＋φ＝1，即－π4＋φ＝π2＋2k π，k ∈Z ，即φ＝3π4＋2k π，k ∈Z ，因为－π<φ<π，所以φ＝3π4，所以函数为f (x )＝2sin ⎝ ⎛⎭⎪⎫12x ＋3π4，选B.题型三三角函数的性质例3 已知函数f (x )＝4sin ωx cos ⎝⎛⎭⎪⎫ωx ＋π3＋3(ω>0)的最小正周期为π.(1)求f (x )的解析式；(2)求f (x )在区间⎣⎢⎡⎦⎥⎤－π4，π6上的最大值和最小值及取得最值时x 的值．审题破题利用和差公式、倍角公式将f (x )化为A sin(ωx ＋φ)的形式，然后求三角函数的最值．解 (1)f (x )＝4sin ωx ⎝ ⎛⎭⎪⎫cos ωx cos π3－sin ωx sin π3＋ 3＝2sin ωx cos ωx －23sin 2ωx ＋ 3＝sin 2ωx ＋3cos 2ωx＝2sin ⎝⎛⎭⎪⎫2ωx ＋π3. ∵T ＝2π2ω＝π，∴ω＝1.∴f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π3. (2)∵－π4≤x ≤π6，∴－π6≤2x ＋π3≤2π3，∴－12≤sin ⎝⎛⎭⎪⎫2x ＋π3≤1，即－1≤f (x )≤2，当2x ＋π3＝－π6，即x ＝－π4时，f (x )min ＝－1，当2x ＋π3＝π2，即x ＝π12时，f (x )max ＝2.反思归纳 (1)求三角函数的周期、单调区间、最值及判断三角函数的奇偶性，往往是在定义域内，先化简三角函数式，尽量化为y ＝A sin(ωx ＋φ)＋B 的形式，然后再求解． (2)对于y ＝a sin ωx ＋b cos ωx 型的三角函数，要通过引入辅助角化为y ＝a 2＋b 2sin(ωx ＋φ)(cos φ＝a a 2＋b2，sin φ＝ba 2＋b 2)的形式来求．(3)讨论y ＝A sin(ωx ＋φ)＋B ，可以利用换元思想设t ＝ωx ＋φ，转化成函数y ＝A sint ＋B 结合函数的图象解决．变式训练3 (1)函数y ＝2sin ⎝⎛⎭⎪⎫π6－2x (x ∈[0，π])为增函数的区间是( ) A.⎣⎢⎡⎦⎥⎤0，π3B.⎣⎢⎡⎦⎥⎤π12，7π12C.⎣⎢⎡⎦⎥⎤π3，5π6D.⎣⎢⎡⎦⎥⎤5π6，π 答案 C解析因为y ＝2sin ⎝ ⎛⎭⎪⎫π6－2x ＝－2sin ⎝ ⎛⎭⎪⎫2x －π6，由π2＋2k π≤2x －π6≤3π2＋2k π，k∈Z ，解得π3＋k π≤x ≤5π6＋k π，k ∈Z ，即函数的增区间为⎣⎢⎡⎦⎥⎤π3＋k π，5π6＋k π(k ∈Z )，所以当k ＝0时，增区间为⎣⎢⎡⎦⎥⎤π3，5π6，选C.(2)设函数f (x )＝3cos(2x ＋φ)＋sin(2x ＋φ)⎝⎛⎭⎪⎫|φ|<π2，且其图象关于直线x ＝0对称，则( )A ．y ＝f (x )的最小正周期为π，且在⎝⎛⎭⎪⎫0，π2上为增函数B ．y ＝f (x )的最小正周期为π，且在⎝⎛⎭⎪⎫0，π2上为减函数C ．y ＝f (x )的最小正周期为π2，且在⎝⎛⎭⎪⎫0，π4上为增函数D ．y ＝f (x )的最小正周期为π2，且在⎝⎛⎭⎪⎫0，π4上为减函数答案 B解析 f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3＋φ，其图象关于直线x ＝0对称，∴f (0)＝±2，∴π3＋φ＝k π＋π2，k ∈Z .∴φ＝k π＋π6，又|φ|<π2，∴φ＝π6.∴f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π2＝2cos 2x . ∴y ＝f (x )的最小正周期为π，且在⎝ ⎛⎭⎪⎫0，π2上为减函数．题型四三角函数的应用例4 已知函数f (x )＝sin ωx ·cos ωx ＋3cos 2ωx －32(ω>0)，直线x ＝x 1，x ＝x 2是y ＝f (x )图象的任意两条对称轴，且|x 1－x 2|的最小值为π4.(1)求f (x )的表达式；(2)将函数f (x )的图象向右平移π8个单位后，再将得到的图象上各点的横坐标伸长为原来的2倍，纵坐标不变，得到函数y ＝g (x )的图象，若关于x 的方程g (x )＋k ＝0在区间⎣⎢⎡⎦⎥⎤0，π2上有且只有一个实数解，求实数k 的取值范围．审题破题 (1)首先化简f (x )再根据题意求出最小正周期，然后可求ω，即可得f (x )的表达式；(2)根据图象平移求出g (x )，然后利用换元法并结合图形求解．解 (1)f (x )＝12sin 2ωx ＋31＋cos 2ωx 2－32＝12sin 2ωx ＋32cos 2ωx ＝sin ⎝⎛⎭⎪⎫2ωx ＋π3，由题意知，最小正周期T ＝2×π4＝π2，T ＝2π2ω＝πω＝π2，所以ω＝2，所以f (x )＝sin ⎝ ⎛⎭⎪⎫4x ＋π3. (2)将f (x )的图象向右平移π8个单位后，得到y ＝sin ⎝⎛⎭⎪⎫4x －π6的图象，再将所得图象所有点的横坐标伸长到原来的2倍，纵坐标不变，得到y ＝sin ⎝⎛⎭⎪⎫2x －π6的图象．所以g (x )＝sin ⎝⎛⎭⎪⎫2x －π6. 令2x －π6＝t ，∵0≤x ≤π2，∴－π6≤t ≤5π6.g (x )＋k ＝0在区间⎣⎢⎡⎦⎥⎤0，π2上有且只有一个实数解，即函数g (x )＝sin t 与y ＝－k 在区间⎣⎢⎡⎦⎥⎤－π6，5π6上有且只有一个交点．如图，由正弦函数的图象可知－12≤－k <12或－k ＝1.所以－12<k ≤12或k ＝－1.反思归纳确定函数y ＝g (x )的解析式后，本题解法中利用两个数学思想：整体思想(设t ＝2x －π6，将2x －π6视为一个整体)．数形结合思想，将问题转化为g (x )＝sin t 与y＝－k 在⎣⎢⎡⎦⎥⎤－π6，5π6上只有一个交点的实数k 的取值范围．互动探究在例4(2)中条件不变的情况下，求函数y ＝g (x )在⎣⎢⎡⎦⎥⎤0，π2上的单调区间．解 g (x )＝sin ⎝⎛⎭⎪⎫2x －π6.令2k π－π2≤2x －π6≤2k π＋π2，k ∈Z ，得k π－π6≤x ≤k π＋π3，k ∈Z .又0≤x ≤π2，∴函数y ＝g (x )的单调递增区间是⎣⎢⎡⎦⎥⎤0，π3.令2k π＋π2≤2x －π6≤2k π＋32π，k ∈Z ，得k π＋π3≤x ≤k π＋56π，k ∈Z .又0≤x ≤π2，∴函数g (x )的单调递减区间是⎣⎢⎡⎦⎥⎤π3，π2. 变式训练4 (2013·天津一中高三月考)函数f (x )＝sin ⎝⎛⎭⎪⎫2x －π3(x ∈R )的图象为C ，以下结论正确的是________．(写出所有正确结论的编号)①图象C 关于直线x ＝11π12对称；②图象C 关于点⎝ ⎛⎭⎪⎫2π3，0对称；③函数f (x )在区间⎝ ⎛⎭⎪⎫－π12，5π12内是增函数； ④由y ＝sin 2x 的图象向右平移π3个单位长度可以得到图象C .答案 ①②③解析当x ＝11π12时，f ⎝ ⎛⎭⎪⎫11π12＝sin ⎝ ⎛⎭⎪⎫2×11π12－π3＝sin ⎝ ⎛⎭⎪⎫11π6－π3＝sin 3π2＝－1，为最小值，所以图象C 关于直线x ＝11π12对称，所以①正确；当x ＝2π3时，f ⎝ ⎛⎭⎪⎫2π3＝sin ⎝ ⎛⎭⎪⎫2×2π3－π3＝sin π＝0，图象C 关于点⎝ ⎛⎭⎪⎫2π3，0对称，所以②正确；当－π12≤x≤5π12时，－π2≤2x －π3≤π2，此时函数单调递增，所以③正确；y ＝sin 2x 的图象向右平移π3个单位长度，得到y ＝sin 2⎝ ⎛⎭⎪⎫x －π3＝sin ⎝ ⎛⎭⎪⎫2x －2π3，所以④错误，所以正确的是①②③.典例 (12分)已知函数f (x )＝12sin 2x sin φ＋cos 2x cos φ－12sin ⎝ ⎛⎭⎪⎫π2＋φ(0<φ<π)，其图象过点⎝ ⎛⎭⎪⎫π6，12.(1)求φ的值；(2)将函数y ＝f (x )的图象上各点的横坐标缩短到原来的12，纵坐标不变，得到函数y ＝g (x )的图象，求函数g (x )在⎣⎢⎡⎦⎥⎤0，π4上的最大值和最小值．规范解答解 (1)f (x )＝12sin 2x sin φ＋cos 2x ＋12cos φ－12cos φ＝12(sin 2x sin φ＋cos 2x cos φ) ＝12cos(2x －φ)． [3分]又∵f (x )过点⎝ ⎛⎭⎪⎫π6，12， ∴12＝12cos ⎝ ⎛⎭⎪⎫π3－φ，cos(π3－φ)＝1. 由0<φ<π知φ＝π3.[5分](2)由(1)知f (x )＝12cos ⎝⎛⎭⎪⎫2x －π3.[7分]将f (x )图象上所有点的横坐标缩短到原来的12，纵坐标不变，得到g (x )＝12cos(4x －π3)．[9分]∵0≤x ≤π4，∴－π3≤4x －π3≤2π3.当4x －π3＝0，即x ＝π12时，g (x )有最大值12；当4x －π3＝2π3，即x ＝π4时，g (x )有最小值－14.[12分]评分细则 (1)将点⎝ ⎛⎭⎪⎫π6，12代入解析式给1分；从cos ⎝ ⎛⎭⎪⎫π3－φ＝1，由0<φ<π，得φ＝π3得1分；(2)4x －π3范围计算正确，没有写出x 取何值时g (x )有最值不扣分．阅卷老师提醒 (1)解决此类问题时，一般先将函数解析式化为f (x )＝A sin(ωx ＋φ)或f (x )＝A cos(ωx ＋φ)的形式，然后在此基础上把ωx ＋φ看作一个整体，结合题目要求进行求解．(2)解决图象变换问题时，要分清变换的对象及平移(伸缩)的大小，避免出现错误．1． (2013·江苏)函数y ＝3sin ⎝⎛⎭⎪⎫2x ＋π4的最小正周期为 ________. 答案 π解析 ω＝2，T ＝2π|ω|＝π.2． (2013·湖北)将函数y ＝3cos x ＋sin x (x ∈R ) 的图象向左平移m (m ＞0)个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是( )A.π12B.π6C.π3D.5π6答案 B解析 y ＝3cos x ＋sin x ＝2sin(x ＋π3)向左平移m 个单位长度后得到y ＝2sin(x ＋π3＋m )，它关于y 轴对称可得sin(π3＋m )＝±1，∴π3＋m ＝k π＋π2，k ∈Z ， ∴m ＝k π＋π6，k ∈Z ，∵m >0，∴m 的最小值为π6.3．若点P (3，y )是角α终边上的一点，且满足y <0，cos α＝35，则tan α等于( )A ．－34B.34C.43D ．－43答案 D 解析 cos α＝39＋y 2＝35，∴y 2＝16. ∵y <0，∴y ＝－4，∴tan α＝－43.4．设函数y ＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫x ＋π3(x ∈R )，则f (x )( )A ．在区间⎣⎢⎡⎦⎥⎤－π，－π2上是减函数 B ．在区间⎣⎢⎡⎦⎥⎤2π3，7π6上是增函数C ．在区间⎣⎢⎡⎦⎥⎤π8，π4上是增函数D ．在区间⎣⎢⎡⎦⎥⎤π3，5π6上是减函数答案 B解析当2π3≤x ≤7π6时，2π3＋π3≤x ＋π3≤7π6＋π3，即π≤x ＋π3≤3π2，此时函数y＝sin ⎝ ⎛⎭⎪⎫x ＋π3单调递减，所以y ＝⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫x ＋π3在区间⎣⎢⎡⎦⎥⎤2π3，7π6上是增函数，选B.5．已知ω>0,0<φ<π，直线x ＝π4和x ＝5π4是函数f (x )＝sin(ωx ＋φ)图象的两条相邻的对称轴，则φ等于( )A.π4 B.π3C.π2D.3π4答案 A解析由题意得周期T ＝2⎝⎛⎭⎪⎫5π4－π4＝2π，∴2π＝2πω，即ω＝1，∴f (x )＝sin(x ＋φ)，∴f ⎝ ⎛⎭⎪⎫π4＝sin ⎝ ⎛⎭⎪⎫π4＋φ＝±1， ∵0<φ<π，∴π4<φ＋π4<5π4，∴φ＋π4＝π2，∴φ＝π4.6．函数f (x )＝A sin(ωx ＋φ)(其中A >0，|φ|<π2)的图象如图所示，为了得到g (x )＝sin3x 的图象，则只要将f (x )的图象( )A ．向右平移π4个单位长度B ．向右平移π12个单位长度C ．向左平移π4个单位长度D ．向左平移π12个单位长度答案 B解析由题意，得函数f (x )的周期T ＝4⎝⎛⎭⎪⎫5π12－π4＝2π3，ω＝3，所以sin ⎝ ⎛⎭⎪⎫3×5π12＋φ＝－1，又|φ|<π2，所以φ＝π4，所以f (x )＝sin ⎝ ⎛⎭⎪⎫3x ＋π4＝sin ⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫x ＋π12，所以将函数f (x )的图象向右平移π12个单位长度可以得到函数g (x )＝sin 3x 的图象．专题限时规范训练一、选择题1．已知sin θ＝k －1，cos θ＝4－3k ，且θ是第二象限角，则k 应满足的条件是( )A ．k >43B ．k ＝1C ．k ＝85D ．k >1答案 C解析根据已知(k －1)2＋(4－3k )2＝1，即5k 2－13k ＋8＝0，解得k ＝1或k ＝85，由于sin θ>0，cos θ<0，所以k >43，可得k ＝85.2．设tan α＝33，π<α<3π2，则sin α－cos α的值为( )A ．－12＋32B ．－12－32C.12＋32D.12－32答案 A解析由tan α＝33，π<α<3π2，不妨在角α的终边上取点P (－3，－3)，则|OP |＝23，于是由定义可得sin α＝－12，cos α＝－32，所以sin α－cos α＝－12＋32，故选A. 3．函数y ＝log 2sin x 在x ∈⎣⎢⎡⎦⎥⎤π6，π4时的值域为( ) A ．[－1,0]B.⎣⎢⎡⎦⎥⎤－1，－12 C ．[0,1)D ．[0,1]答案 B解析由x ∈⎣⎢⎡⎦⎥⎤π6，π4，得12≤sin x ≤22， ∴－1≤log 2sin x ≤－12.4．设函数y ＝3sin(2x ＋φ) (0<φ<π，x ∈R )的图象关于直线x ＝π3对称，则φ等于( ) A.π6B.π3C.2π3D.5π6答案 D解析由题意知，2×π3＋φ＝k π＋π2(k ∈Z )，所以φ＝k π－π6(k ∈Z )，又0<φ<π，故当k ＝1时，φ＝5π6，选D.5．将函数f (x )＝－4sin ⎝⎛⎭⎪⎫2x ＋π4的图象向右平移φ个单位，再将图象上每一点的横坐标缩短到原来的12倍，所得图象关于直线x ＝π4对称，则φ的最小正值为( )A.π8 B.38π C.34π D.π2答案 B解析依题意可得y ＝f (x )⇒y ＝－4sin[2(x －φ)＋π4]＝－4sin[2x －(2φ－π4)]⇒y ＝g (x )＝－4sin[4x －(2φ－π4)]，因为所得图象关于直线x ＝π4对称，所以g ⎝ ⎛⎭⎪⎫π4＝±4，得φ＝k 2π＋38π(k ∈Z )，故选B.6．已知函数f (x )＝A tan(ωx ＋φ)(ω>0，|φ|<π2)，y ＝f (x )的部分图象如图所示，则f (π24)等于( )A ．－ 3B ．－1 C. 3D ．1答案 C解析由图形知，T ＝πω＝2(3π8－π8)＝π2，ω＝2.由2×3π8＋φ＝k π，k ∈Z ，得φ＝k π－3π4，k ∈Z .又∵|φ|＜π2，∴φ＝π4.由A tan(2×0＋π4)＝1，知A ＝1，∴f (x )＝tan(2x ＋π4)，∴f (π24)＝tan(2×π24＋π4)＝tan π3＝ 3.7． (2012·课标全国)设函数f (x )＝cos ωx (ω>0)，将y ＝f (x )的图象向右平移π3个单位长度后，所得的图象与原图象重合，则ω的最小值等于( )A.13B ．3C ．6D ．9答案 C解析由题意可知，nT ＝π3(n ∈N *)，∴n ·2πω＝π3(n ∈N *)，∴ω＝6n (n ∈N *)，∴当n ＝1时，ω取得最小值6.8．已知函数f (x )＝3sin ωx ＋cos ωx (ω＞0)，y ＝f (x )的图象与直线y ＝2的两个相邻交点的距离等于π，则f (x )的单调递增区间是( )A ．[k π－π12，k π＋5π12]，k ∈ZB ．[k π＋5π12，k π＋11π12]，k ∈ZC ．[k π－π3，k π＋π6]，k ∈ZD ．[k π＋π6，k π＋2π3]，k ∈Z答案 C解析 f (x )＝3sin ωx ＋cos ωx ＝2sin (ωx ＋π6)(ω＞0)．∵f (x )的图象与直线y ＝2的两个相邻交点的距离等于π，恰好是f (x )的一个周期，∴2πω＝π，ω＝2.∴f (x )＝2sin (2x ＋π6)．故其单调增区间应满足2k π－π2≤2x ＋π6≤2k π＋π2(k ∈Z )．解得k π－π3≤x ≤k π＋π6(k ∈Z )．二、填空题9．函数f (x )＝3cos 25x ＋sin 25x 的图象相邻的两条对称轴之间的距离是________．答案 5π2解析 f (x )＝3cos 25x ＋sin 25x ＝2sin(25x ＋π3)，∴周期为T ＝2π25＝5π，则相邻的对称轴间的距离为T 2＝5π2.10．将函数y ＝sin(ωx ＋φ)(ω＞0，|φ|＜π2)的图象向左平移π3个单位，所得曲线的一部分如图所示，则ω、φ的值分别为________．答案 2、－π3解析由图可知T 4＝7π12－π3＝π4，∴T ＝π，∴ω＝2.把(7π12，－1)代入y ＝sin (2(x ＋π3)＋φ)得sin (7π6＋2π3＋φ)＝－1，∴11π6＋φ＝2k π＋3π2(k ∈Z )，φ＝2k π－π3(k ∈Z )，∵|φ|＜π2，∴φ＝－π3.11．已知函数f (x )＝3sin ⎝⎛⎭⎪⎫ωx －π6 (ω>0)和g (x )＝2cos(2x ＋φ)＋1的图象的对称轴完全相同．若x ∈⎣⎢⎡⎦⎥⎤0，π2，则f (x )的取值范围是__________．答案 ⎣⎢⎡⎦⎥⎤－32，3 解析 ∵f (x )和g (x )的对称轴完全相同，∴二者的周期相同，即ω＝2，f (x )＝3sin ⎝⎛⎭⎪⎫2x －π6. ∵x ∈⎣⎢⎡⎦⎥⎤0，π2，∴2x －π6∈⎣⎢⎡⎦⎥⎤－π6，5π6，sin ⎝⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤－12，1， ∴f (x )∈⎣⎢⎡⎦⎥⎤－32，3. 12．关于函数f (x )＝sin 2x －cos 2x 有下列命题：①y ＝f (x )的周期为π；②x ＝π4是y ＝f (x )的一条对称轴；③⎝ ⎛⎭⎪⎫π8，0是y ＝f (x )的一个对称中心；④将y ＝f (x )的图象向左平移π4个单位，可得到y ＝2sin 2x 的图象，其中正确命题的序号是______(把你认为正确命题的序号都写上)．答案 ①③解析由f (x )＝sin 2x －cos 2x ＝2sin ⎝⎛⎭⎪⎫2x －π4，得T ＝2π2＝π，故①对；f ⎝ ⎛⎭⎪⎫π4＝2sin π4≠±2，故②错； f ⎝ ⎛⎭⎪⎫π8＝2sin 0＝0，故③对； y ＝f (x )的图象向左平移π4个单位，得y ＝2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π4－π4＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4，故④错．故填①③. 三、解答题13．(2013·湖南)已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫x －π6＋cos ⎝⎛⎭⎪⎫x －π3，g (x )＝2sin 2x 2.(1)若α是第一象限角，且f (α)＝335，求g (α)的值；(2)求使f (x )≥g (x )成立的x 的取值集合．解 f (x )＝sin ⎝ ⎛⎭⎪⎫x －π6＋cos ⎝ ⎛⎭⎪⎫x －π3＝32sin x －12cos x ＋12cos x ＋32sin x ＝3sin x ，g (x )＝2sin 2x2＝1－cos x .(1)由f (α)＝335，得sin α＝35，又α是第一象限角，所以cos α>0.从而g (α)＝1－cos α＝1－1－sin 2α＝1－45＝15.(2)f (x )≥g (x )等价于3sin x ≥1－cos x ，即3sin x ＋cos x ≥1，于是sin ⎝⎛⎭⎪⎫x ＋π6≥12.从而2k π＋π6≤x ＋π6≤2k π＋5π6，k ∈Z ，即2k π≤x ≤2k π＋2π3，k ∈Z .故使f (x )≥g (x )成立的x 的取值集合为{x |2k π≤x ≤2k π＋2π3，k ∈Z }．14．已知函数f (x )＝3sin ωx cos ωx ＋cos 2ωx －12(ω>0)，其最小正周期为π2.(1)求f (x )的表达式；(2)将函数f (x )的图象向右平移π8个单位，再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y ＝g (x )的图象，若关于x 的方程g (x )＋k ＝0，在区间⎣⎢⎡⎦⎥⎤0，π2上有且只有一个实数解，求实数k 的取值范围．解 (1)f (x )＝3sin ωx cos ωx ＋cos 2ωx －12＝32sin 2ωx ＋cos 2ωx ＋12－12＝sin ⎝⎛⎭⎪⎫2ωx ＋π6. 由题意知f (x )的最小正周期T ＝π2，T ＝2π2ω＝πω＝π2，所以ω＝2，所以f (x )＝sin ⎝⎛⎭⎪⎫4x ＋π6. (2)将f (x )的图象向右平移π8个单位后，得到y ＝sin ⎝⎛⎭⎪⎫4x －π3的图象，再将所得图象所有点的横坐标伸长到原来的2倍，纵坐标不变，得到y ＝sin ⎝⎛⎭⎪⎫2x －π3的图象．所以g (x )＝sin ⎝⎛⎭⎪⎫2x －π3. 因为0≤x ≤π2，所以－π3≤2x －π3≤2π3.g (x )＋k ＝0在区间⎣⎢⎡⎦⎥⎤0，π2上有且只有一个实数解，即函数y ＝g (x )与y ＝－k 在区间⎣⎢⎡⎦⎥⎤0，π2上有且只有一个交点，由正弦函数的图象可知－32≤－k <32或－k ＝1. 所以－32<k ≤32或k ＝－1.。

三角函数—高考真题文科数学分项汇编(解析版)

y
f
(x)的图象．
其中所有正确结论的序号是
A．①
B．①③
【答案】B
C．②③
D．①②③
2
【解析】因为 f (x) sin(x )，所以周期T 2 2，故①正确；
3
f ( ) sin( ) sin5 1 1，故②不正确；
2
23
62
将函数 y sin x的图象上所有点向左平移个单位长度，得到 y sin(x )的图象，
2
D．2
【答案】C
sin x
【解析】 f (x)
tan x 1 tan2 x
cos 1(sin
x sin xcos x 1sin2x，
x) 2
2
cos x
故所求的最小正周期为T 2π π，故选 C. 2
【名师点睛】函数 y Asin(x ) B(A 0, 0)的性质：
(1) ymax=B+A，ymin B A.
对应的函数为
gx.若
g
π4
2
，则
f
3π 8
A．−2
B． 2
C． 2
D．2
【答案】C
【解析】∵ f (x)为奇函数，∴ f (0) Asin 0,=kπ,k Z,k 0, 0；
∵ f x的最小正周期为π，T
2π
π,∴
2，
∴ g(x) Asin 1x Asin x,
2
又 g(π) 2，∴ A 2，
f x max
3
2
5 2
4，故选
B.
【名师点睛】该题考查的是有关化简三角函数解析式，并且通过余弦型函数的相关性质得到函数的性质，在解题的过程中，要注意应用余弦倍角公式将式子降次升角，得到最简结果.

2012-2018年高考真题汇编：三角函数文科(带答案)

的值；
2
求
sin 2

sin 2 sin cos

cos
2
1
的值．
【答案】（1） 3 ；（2）1．
3、三角函数的图象和性质
10．（2014 大纲）设 a sin 33,b cos 55, c tan 35, 则（ C ） A． a b c B． b c a C． c b a D． c a b
2x－π 4
在区间
0，π 2
上的最小值为(
B
)
A．－1 B．－ 2 C. 2 D．0 22
21.(2014 浙江) 为了得到函数 y sin 3x cos 3x 的图象，可以将函数 y 2 sin 3x 的图象（ C ）

A.向右平移个单位
4

B.向左平移个单位 C.向右平移个单位
, 7 ] 上单调递减
B．在区间 [
, 7 ] 上单调递增
12 12
12 12
C．在区间[ , ] 上单调递减 D．在区间[ , ] 上单调递增
63
63
【简解】原函数平移后得到 y=3sin(2x- 2 ),单调减区间为[kπ+ 7 ,kπ+ 13 ],增区间为[kπ+ 1 ,kπ
满足
f (x
4)
f
(x)(x R)
，且在区间
(2, 2] 上，
f (x)

cos
x 2
,
0

x 2,
则
|
x

1 2
|, -2

x

0,

(浙江)高考三角函数解答题专项训练含答案(最新整理)

9、在△ABC 中，角 A、B、C 的对边分别为 a、b、c.已知 a+b=5，c= 7 ，
且 4sin 2 A B cos 2C 7 .
2
2
（1）求角 C 的大小；
（2）求△ABC 的面积.
解：（1）∵A+B+C=180°
由 4sin 2 A B cos 2C 7 得4 cos2 C cos 2C 7
4
f (x) 的最小正周期为 2
（2）依题意， x0
2k
3 4
（k
Z
），
由周期性， f (x0 ) f (2x0 ) f (3x0 )
(sin 3 cos 3 ) (sin 3 cos 3 ) (sin 9 cos 9 )
4
4
2
2
4
4
2 1
2、△ABC 的内角 A、B、C 的对边分别为 a、b、c，asinA＋csinC－ 2asinC＝bsinB.
(1)求 B；(2)若 A＝75°，b＝2，求 a，c.
解：(1) 由正弦定理得 a2＋c2－ 2ac＝b2.由余弦定理得 b2＝a2＋c2－2accosB.
2 故 cosB＝，因此 B＝45°.
2
2＋ 6
(2)sinA＝sin(30°＋45°)＝sin30°cos45°＋cos30°sin45°＝
ab 2
5
,
cos cos 2 sin sin 2 2 5
5
5
, ………………………………3 分
即 2 2 cos 4 , cos 3 . ……………………………6 分
5
5
（Ⅱ）0 , 0, 0 , ………………………7 分 22
cos

浙江高考历年真题之三角函数大题(文科)

浙江历年文科高考题之三角函数大题（教师版）1、（2005年）已知函数()2sin cos cos 2f x x x x =+(Ⅰ) 求()4f π的值； (Ⅱ) 设α∈(0，π)，()22f α=，求sin α的值．解析：(Ⅰ)∵()sin 2cos 2f x x x =+∴sin cos 1422f πππ⎛⎫=+= ⎪⎝⎭(Ⅱ) cos sin 2f ααα⎛⎫=+ ⎪⎝⎭ ∴1sin ,cos 424ππαα⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭13226sin sin 442ππαα⎛⎫=+-=⨯= ⎪⎝⎭∵()0απ∈，， ∴sin 0α>，故sin α=2、（2006年）如图，函数y=2sin(πx ＋φ),x ∈R,(其中0≤φ≤2π)的图象与y 轴交于点（0，1）. (Ⅰ)求φ的值； (Ⅱ)设P 是图象上的最高点，M 、N 是图象与x 轴的交点，求.与PM解析：（Ⅰ）因为函数图象过点（0，1），所以 2sin 1x =,，即 1sin 2x =因为02l π≤≤，所以6l π=. （Ⅱ）由函数2sin()6y x ππ=+及其图象，得115(,0),(,2),(,0),636M P N - 所以 11(,2,)(,2)22PM PN =--=-，从而cos ,PM PNPM PN PM PN ⋅<>=⋅1517= ，故15,arccos 17PM PN <>=.3、（2007年）已知ABC △1+，且sin sin A B C +=．（I ）求边AB 的长；（II ）若ABC △的面积为1sin 6C ，求角C 的度数．解析：（I ）由题意及正弦定理，得1AB BC AC ++=，BC AC +=，两式相减，得1AB =．（II ）由ABC △的面积11sin sin 26BC AC C C =，得13BC AC =，由余弦定理，得222cos 2AC BC AB C AC BC+-=22()2122AC BC AC BC AB AC BC +--==，所以60C =．4、（2009年）在ABC ∆中，角A,B,C 所对的边分别为a,b,c,且满足cos 25A =，3AB AC ⋅=. （Ⅰ）求ABC 的面积；（Ⅱ）若c=1，求a 的值.解析：（Ⅰ）531)552(212cos 2cos 22=-⨯=-=A A又),0(π∈A ，54cos 1sin 2=-=A A ，而353cos .===bc A ，所以5=bc ，所以ABC ∆的面积为：254521sin 21=⨯⨯=A bc （Ⅱ）由（Ⅰ）知5=bc ，而1=c ，所以5=b 所以5232125cos 222=⨯-+=-+=A bc c b a5、（2010年）在△ABC 中，角A ，B ，C 所对的边分别为a,b,c,设S 为△ABC 的面积，满足222()4S a b c =+-。

浙江高考数学三角大题十年合集

．
＝
所以
．
（2）由
，得
于是
由
，
．
．
及正弦定理
设△ ABC 的面积为 S，则
，得
．
．
【解析】略
5.【答案】解：（Ⅰ）∵△ABC 中，a≠b，c=√3，cos2A-cos2B=√3sinAcosA-√3sinBcosB，
1+2 1+2 √3
= sin2A-√3sin2B，
2
2
2
2
∴
第 7 页，共 13 页
5
又由 sin（α+β）=13，
得( + ) = ±√1 − 2 ( + )
=±√1 − ( 5 )2 = ± 12，
13
13
则 cosβ=cos[（α+β）-α]
=cos（α+β）cosα+sin（α+β）sinα
12
=
13
3
5
5
13
× (− ) +
4
56
× (− ) = − ，
∴sinB=sinAcosB-cosAsinB=sin（A-B），
∵A，B 是三角形中的内角，∴0< B<,-< A-B<,
∴-B=A-B 或 B=A-B,
∴A=(不合实际)或 A=2B，
即原题得证.
2 2
（Ⅱ）解：∵△ABC 的面积 S=
4 4
，
第 9 页，共 13 页
∴2bcsinA=a2，sinA≠0，
1
值，从而求得△ABC 的面积为2 ⋅ ⋅ 的值．
本题主要考查二倍角公式、两角和差的三角公式、正弦定理的应用，属于中档题．

三角函数部分高考题(带答案)

即 sin(B C) 0 ∴ B C
BC
6
A
(B
C)
2 3
由正弦定理
a sin A
b sin B
c sin C
得
1
b c a sin B 2 3 2 2
sin A
3
2
31.已知函数 f (t)
1 t 1 t ,
g ( x)
cos x
f
(sin
x)
sin
x
f
(cos x),
x ( ,
因此
0≤
sin
2πx 6
1 2
3≤
2
，即 f (x) 的取值范围为320，．
25.求函数 y 7 4sin x cos x 4cos 2 x 4cos 4 x 的最大值与最小值。
【解】： y 7 4sin x cos x 4cos 2 x 4cos 4 x
7 2sin 2x 4cos2 x 1 cos2 x
26.知函数
f (x) 2cos2x 2sinxcosx 1（ x R,
0 ）的最小值正周期是
2．
（Ⅰ）求的值；
（Ⅱ）求函数 f ( x) 的最大值，并且求使 f ( x) 取得最大值的 x 的集合．
（17）本小题主要考查特殊角三角函数值、两角和的正弦、二倍角的正弦与余弦、函数
y Asin(x ) 的性质等基础知识，考查基本运算能力．满分 12 分．
4 3
，所以
tan
2
tan tan 2 1 tan tan2
1
∵,
为锐角，∴ 0
2
3 2
，∴
2 =
3 4
30.在 ABC 中，角 A, B, C 所对应的边分别为 a, b, c ， a 2

高考真题汇编2010-2011 三角函数和平面向量大题文科

三角函数和平面向量（2011广东文）16．（本小题满分12分）已知函数1()2sin()36f x x π=-，x ∈R ．（1）求(0)f 的值；（2）设,0,2παβ⎡⎤∈⎢⎥⎣⎦，10(3)213f πα+=，6(32)5f βπ+=，求sin()αβ+的值．（2011北京文）15．（本小题共13分）已知函数()4cos sin()16f x x x π=+-.（Ⅰ）求()f x 的最小正周期：（Ⅱ）求()f x 在区间,64ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值. （2011四川文）18．（本小题共l2分）已知函数73()sin()cos()44f x x x ππ=++-，x ∈R ．（Ⅰ）求()f x 的最小正周期和最小值；（Ⅱ）已知4cos()5βα-=，4cos()5βα+=-，02παβ<<≤．求证：2[()]20f β-=．（2011福建文）21．（本小题满分12分）设函数f （θ）cos θθ+，其中，角θ的顶点与坐标原点重合，始边与x 轴非负半轴重合，终边经过点P （x,y ），且0θπ≤≤。

（1）若点P 的坐标为1(2，求f ()θ的值；（II ）若0.2πθ≤≤，求函数()f θ的最小值和最大值。

（2010上海文数19）.（本题满分12分）已知02x π<<，化简：2lg(cos tan 12sin))]lg(1sin 2)22x x x x x π⋅+-+--+.（2010浙江文数18） (本题满分l4分)在△ABC 中,角A 、B 、C 所对的边分别为a,b,c ，已知1cos 24C =- (I)求sinC 的值；(Ⅱ)当a=2， 2sinA=sinC 时，求b 及c 的长．（2010北京文数15）（本小题共13分）在△ABC 中，已知B=45°,D 是BC 边上的一点，AD=10,AC=14,DC=6，求AB 的长.（2010重庆文数18） (本小题满分13分), (Ⅰ)小问5分，(Ⅱ)小问8分.)设ABC ∆的内角A 、B 、C 的对边长分别为a 、b 、c,且32b +32c -32a(Ⅰ) 求sinA 的值； (Ⅱ)求2sin()sin()441cos 2A B C Aππ+++-的值.（2010浙江文数18）在△ABC 中，角A ，B ，C 所对的边分别为a,b,c,设S 为△ABC 的面积，满足222)4S a b c =+-。