Journal of Integer Sequences, Vol. 6 (2003), Article 03.1.5 OBJECTS COUNTED BY THE CENTRAL
一些特殊不定方程的整数解

第37卷第2期 (2021 年 3 月)福建师范大学学报(自然科学版)Journal of Fujian Normal University (Natural Science Edition)Vol. 37, No. 2Mar. 2021DOI:10. 12046/j. issn. 1000-5277. 2021. 02. 003 文章编号:1000-5277(2021)02-0018-08一些特殊不定方程的整数解高志贤,杨标桂(福建师范大学数学与信息学院,福建福州350117)摘要:通过引入平衡、余平衡、Lucas-balancing和Lucas-cobalancing数列,研冗其性质,再利用这些数列给出一些特殊不定方程的所有正整数解.关键词:不定方程;平衡数;余平衡数;Lucas-balancing数;Lucas-cobalancing数中图分类号:0156. 1文献标志码:AInteger Solutions of Some Special Diophantine EquationsGAO Zhixian, YANG Biaogui(College of Mathematics and Informatics ^Fujian formal University ^Fuzhou350117, China)Abstract:In this paper,balance,cobalancing,Lucas-balancing and Lucas-cobalancing sequence sequences are introduced to study their properties,and then all positive integer solutions of some special Diophantine equations are given by mean of these sequences.Key words :Diophantine;balancing numbers;cobalancing numbers;Lucas-balancing and Lucas-cobalancing numbers1999年,Behera等1引入了平衡数(balancingnumber),即平衡数m(m e Z+)是不定方程1 +2 + *-* + (m-l) = (m+l) + (m + 2) +••• +(m +r)(1)的解,称r(r e N)为平衡数m所对应的平衡因子(balancer).例如平衡数1、6、35、204分别对应 的平衡因子为0、2、14、84•由式(1)得m(m - 1)r(r + 1)----------------=mr + ---------------,225从而—(2m+ 1) + V8m2+ 1、r =-------------------2-----------------. 2对于n = 1,2,…,令' 表示第a i个平衡数.显然,由式(2)知圪是平衡数当且仅当+ 1是完全平方数.2005年,Panda等[2]通过修改式(1),从而引入了余平衡数(cobalanicng numbe),即余平衡数m(m e N)是不定方程12+••• +m =(m + 1) + (m + 2) + --- + (m+r)(3)的解,称e Z+)为余平衡数m所对应的余平衡因子(cobalancer).例如余平衡数0、2、14、84 分别对应的余平衡因子为1、6、35、204.由式(3)得m(m + 1)r(r+l)--------=mr + --------,22从而-(2/71 + 1) + \iSm2 + + 1..收稿日期:2020-09-15基金项目:国家自然科学基金资助项目(11761049)通信作者:杨标桂(1976-),男,副教授,研究方向为几何学、数论.bgyang@ 163. com第2期高志贤,等:一些特殊不定方程的整数解19对于n = 1,2,…,令表示第n个余平衡因子.由式(4)知是余平衡数当且仅当V叫+ 86… + 1是完全平方数.由于V8# + 1和^b2n + 86… + 1都是完全平方数,那么+ 1和+ 86… + 1都是正整数.诸多学者从多方面研究平衡数和余平衡数的性质及应用[3_6].Panda等;_7_分别令 C… = + 1,c…= -J^bl + 8fe… + 1,其中 C…为第 n个 Lucas-halancing数,cn为第 n个Lucas-cobalancing 数,并给出 了平衡、余平衡、Lucas-balancing和Lucas-cobalancing数列的二阶递推关 系:=6B…_ A-丨,A= i,b2=:6,(5)h=:66… -bn-l42,bx= 0,b2=2,(6)c n+l:~ Cn-\, C, = 3, C2=17,(7)C n+i = 6c…~ C n-1,ci = 1,c2=7.(8)同时也给出了平衡和余平衡数列的非线性递推关系:B…+1 = 3Bn + J%B2… + 1 ,(9)= 36… + 78^ + 86… + 1+ 1.(10) Panda等进一步还研究了平衡数与Lucas-丨)alancing数、余平衡数与Lucas-cobalancing数之间的关 系:C…tl =3C… + 8B…, (I Dcn+i = 3c…+ + 4_( 12)数列、IC…l和|c…l的比内公式分别为:a f-a f^(13)4V22(14)(15)(16)其中 a, = 1 + ,a: = 1 - •近年来,不定方程的研究有了新的进展,有学者对于不定方程的整数解提出了一些理论.K o-shy[8:研究不定方程-办2 = ±1和;c2 -办2 = &的整数解,具体见下面几个引理.引理1(1)设d是一个正整数且不是一个完全平方数,令(a,/8)为Pell方程V -办2 = 1的基础解,则它的全部解可由U…,y…)给出,(a + (3\[d)"+ (a -fi-Jd)"---------------------2---------------------,(a+/3^/d)n-(a-^J d)nJn 二-------------------------------------------’2-Jd其中(*i,) = (a,P )且灯彡2.(2)设cf是一个正整数且不是一个完全平方数,令(a,/3)为P ell方程;c2-办2 =- 1的基础解,则它的全部解可由(\,y…)给出,(a+p j d)2"-'+ (a-/3^/d)2"-'xn=------------------------------------," 2(a+P^Jd)2"-'-(a~/3-Jd)2n-'2-Jdyn=20福建师范大学学报(自然科学版)2021 年其中(U i) = (a,0 )且《 彡2.引理2 设r/是一个正整数且不是一个完全平方数,令(a ,y3 )为P e ll方程办2 = 1的基础 解,(u,为不定方程x2 -办2 = A的一个解,那么(au.+奶?;)2 - + m;)2 = A:,则是不定方程的一个解.这个递推公式可以用来生成不定方程的无限多个解,这些解与«;)是相关联的且它们属于同一类解.实际上,不定方程W -办2 = A的基础解不止一个.下面的引理为不定方程-办2 = &的基础解 U,t;)限定了范围.引理3设^/是一个非平方的正整数,令(a,0 )为不定方程;c2 -办2 = 1的基础解,(u,〃)为不定方程d -dy2 =A;的基础解,其中A:> 0,则《,j;满足0 < I u I0 ^ v ^ /3k2(a+ 1)事实上,如果r f>〇, A >0,且d不是平方数,那么不定方程办2 =々的解仅有有限类,且所 有类的基本解可以由引理3经过有限步求出,于是所有类所包含的全部解就是不定方程V -办2的全部解.若不定方程V-办2 =1没有解满足引理3,则不定方程x2-办2 = A无解.本文主要研究某些不定方程的正整数解是由一些特殊的整数序列给出的.首先引人平衡、余平衡、Lucas-halancing和Lucas-cobakndng数列并且研究其性质,再利用这些数列给出某些特殊不定方 程的所有正整数解.1定理及证明考虑尤2 + ;y2 - ± 8 = 0,x2 + y2 - 34xy ± 288 = 0 和a:' + 36).- - 36;cy ± 288 = 0 等不定方程的正整数解都是由特殊的整数数列给出的.1.1以Lucas-ba丨ancing数列| C J为整数解的不定方程由引理1,得到如下结果:定理1设n身1,则P ell方程;c2-8/= 1的所有正整数解为(*, y) = (C…, S J.证明P e ll方程a:2 -8/ = 1的基础解为(a,/S )= (3,1),由引理1(1)知P e ll方程x2 -8/ =1的全部正整数解可由(*,y)表出,其中(3 + 272 )" + (3 - 2V2 )"(1 + V2 )2" + (1 - V2 )2nX=-----------------------------------------------------------------------=---------------------------------------------------------------22(3 +2j2)n-(3- 2V2 )n(1 +72)2n - (1 - 72 )2ny-------------------------------=------------------------------•472 4V2又由数列1c…丨和丨fi…!的比内公式得(1+ V2 )2" + (1 -72)2n<+«2n^"=--------2--------=~T—=C"'(1 + 72 )2" - (1 - V2 )2"-a2ny=------------------------------=----------=B….4V2 4^2即定理得证.由定理1,可得到定理2、定理3.定理2设《 >丨,则不定方程-8/ + 16*y-9二0的所有正整数解为U,y) = (C…,B…+,).证明假设:t和y为不定方程P - 8/ + 16巧-9 = 0的正整数解.由于不定方程V - 8/ + 16y -9 = 0 等价于不定方程 9-t2 - 8(y - *)2 = 9,从而 9 丨(y -尤)2,即 3 丨(y - *).令 h = a:,u =第2期高志贤,等:一些特殊不定方程的整数解21^一,将;c = w和y = 3ti + u代人不定方程x2 - 8y2 + 16xy - 9 = 0中,可得it2 - 8(3ij + u)2 + 16«(3ii + u)- 9 = 0,整理得u由定理 1 知 u = C…,t; = B,,,即;《 = u = C…,y = 3d + u = + C… = 3B… + V賊 + 1=相反的,如果(*,y) = (C…,B…+1),由定理1和式(9)得C2n- 8B^, + \6Cn Bn+l -9= C] -S(3Bn+C n)2+ 16C…(3B… + C…) - 9 =Cl -8(9B2…+C2n+6BnCn) + 48BnC… + l6C2n-9 =9C2n-12B\ - 9 =9{C l -SB]-1) = 0,即定理得证.定理3设^1& 1,则不定方程*2 + / -6巧+ 8 = 0的所有正整数解为U,y) = (C…, C…+1).证明假设i和y为不定方程V+y2-6;c y+ 8 = 0的正整数解.由于不定方程W+/-6町+8 = 0 等价于(x-y)2-4xy + 8=0,从而41 (;c-y)2,即21 (x-y),从而*和y的奇偶性相同.接下来 按x和y的奇偶性分为以下两种情况:情形1x和y都为奇数.因为*为奇数,即8 I(V- 1),又由于不定方程%2+ /- 6xy + 8 = 0等价于(y- 3*)2-r一3尤8 (尤2 - 1) = 0,从而 64 1(y-3尤)2,即 81 (y-3x) •令 u=;c,i; = ^―-—,即 x u,y= 3u + 8f,O再将A: = a和;y = 3w + 8f代入不定方程尤2 + y2 - 6;cy + 8 = 0中得u2+ (3u+ 8t;)2-6u(3u+ Sv)+8=0,整理得u2-Sv2=1.由定理 1 知 “ =C...,I;二坟,即 X = u = ,y = 3u + % = 3C... + 8坎=C (1)相反的,如果h,y)= (Q,C…+1),那么C〗+0+1 -6C人+1 +8=0,下面用数学归纳法证明此 性质.当n = 1时显然成立.假设当n = m时此恒等式是成立的.当n=m+l时,由式(7)得Cm+1+ Cm+2~ 6C m+l Cm +2+ 8 =C>+ (6Cmtl - C J2 - 6Cm+1(6C m+1 - C J+ 8 =C, + ^ -6CmtlCm + 8-0.情形2 *和y都为偶数.令 * = 2;^,y = 2y,,将 x = 2;):,和 y= 2y,代人不定方程 a:2 + y2 - 6xy + 8 = 0 中,整理得 x丨+;^- 6*,;^ + 2 = 0,显然;t,和;y,的奇偶性相同.若;c,和y,都为偶数,令;《:, = 2*2,y,二2y2,再将*, = 2j c2和= 2y2代人不定方程4Z _ 6;^;^ + 2 = 0中,整理得知丨+ 4y〖-24»:2y2+ 2 = 0,显然4 1 (44+4H-24:«:2;k2),但4乜,产生矛盾.同理,若〜和:^同为奇数也会产生类似的矛盾,因此x和 y不可能都为偶数,即此定理得证.由定理3,可得到定理4和定理5.定理4设》為1,则不定方程8V- /- 8 = 0的所有正整数解为(X,y)= (C…,8S…).证明假设*和y为不定方程8x2-y2-8=0的正整数解•令u=;c,i;=;k + 3:v,即•* = “,y = r - 3u,再将x=u和y=t;-3u代入不定方程8a:2 - y2 - 8 = 0中得8u* ~ (v —3u)2 — 8 = 0,整理得u2+ v2-6uv+ 8=0.由定理 3 知 “ =C…,t; = C…+,,即 x = u = C…,y = t; - 3u = C…+1 - 3C… = 8B…•22福建师范大学学报(自然科学版)2021 年相反的,如果(*,y) = (C…,8B J,由式(11)和定理3得%C2…-(8B J2-8 = 8C^ -(C…+1-3C…)2-8 = -(C^ + C^+1-6C…C…+1+ 8) = 0,即定理得证.定理5设n >2,则不定方程;c2+y2 -34巧'+ 288 = 0的所有正整数解为(x,y)=证明假设x和y为不定方程V +/ - 34巧+ 288 = 0的正整数解.由于不定方程*2+/-+288 = 0 等价于(x + y)2 - 36xy + 288 = 0,即36 1(x+y)2,从而 61 (文+y) •令u = —,•" "6,即尤=6w —r,y=v,再将尤=6u —p和),=f代人不定方程a;2 + y2 _ 34xy + 288 = 0中得(6w - z;)2 + i;2 - 34(6w - v)i; + 288 二0,整理得u2+ v2-6uv + 8=0.由定理 3 知u = C...,i; = C...+1,即x = 6u - r= 6C... - (:...+| = (:..._,,y二i; = C (1)相反的,如果(*,y) = (C…_,,C…+I),由定理3和式(7)得C, +C, -34C…_,C…+, + 288 =C l, + (6C… - C…_,)2 - 34C….,(6C… - C…_,) + 288 =36C^_, + 36C^ - 216C…_,C… + 288 =36K -6C…_,C… + 8) = 0,即定理得证.由定理5和定理3,可得到如下结果.定理6设n & 1,则不定方程;c2 + 36y2 - 3知' + 288 = 0的所有正整数解为(*,y)= (6C…,C…+,).证明假设a:和;y是不定方程a:2 + 36y2 - 36xy + 288 = 0的正整数解.令u=;«-y,i;=y,即再将x=“+j;和y=t;代人不定方程x2 + 36y2 — 36巧+ 288 = 0中得(u+ v)2+36v2-36(u + v)v+ 288 = 0,整理得u2 + v~—3Auv + 288 = 0.由定理 5 知u = C..._,,r = C...+1,即x = w + t)= C..._, + C...+, = 6C...,y= i; = C (1)相反的,如果(;<:,y) = (6C…,C…+1),由定理3得(6C…)2 + 36C, -36(6C J C…+1 + 288 = 36(C X丨-6C…C…+1 +8) = 0,即定理得证.1.2以Lucas-cobalancing数列| C…|为整数解的不定方程结合式(14)、(16)和引理1,得到如下结果:定理7设《 & 2,则不定方程*2 - 8/ - 8y - 1 = 0的所有正整数解为(*,y) = (c…,6…).证明不定方程*2-872-8;^-1=0等价于*2-2(27+1)2=-1.令“=;»:,1;= 27+1,从而得 到Pel丨方程u2 - 2d2 二-1.P e ll方程的基础解为(《,0)= (1,1),由引理1(2)知P e ll方程的全部正整数解可由〇表出,其中(1+ V2 )2""' + (1 -V2 )2""*u =--------------------------,2 ,(1+V2 )2""' - (1 - V2 )2"-'v=---------------------------------------.i-fi同时,又由数列|c…丨和|6…|的比内公式得第2期高志贤,等:一些特殊不定方程的整数解23(1+72)2"-' + (1 -72)2n"(1+72)2n-' - (1 -72)2"-'--------------------------=262V2因此,A: = U = C…且y = ^ ,即定理得证.由定理7得到如下结果:定理8设y - a:三1(mod 3)且r a &1,则不定方程aT- 8广+ 16;cy + 8(;«- y) + 7= 0的所有正 整数解为 U,y) = (c n,/»…+|)•证明假设和y为不定方程的x2 - 8;y2+ 16a:y+ 8(x- y)+ 7 = 0正整数解.令u= :»:,u= -—---,即:《 = “,7 = “ + 31;+1,再将;》:= “和7 = « + 3|;+1代人不定方程;>:2-872 + 16町 + 8(X-y)+ 7 = 0 中得u'-8(u + 3i;+ I)2+ 16u(u + 3t)+ 1) +S[u-(u+3v+1)] + 7= 0,整理得u2- Sv2-8i>-1= 0.由定理 7 知 it = c…,i; = 6…,即 x = u = c… , y = “ + 3j;+ 1= cn+ 36n+ 1= 6n+1•相反的,如果U, y) = (c…,6…+,),由定理7和式(10)得cl ~ ^b2n+l +16c…6…tl + 8(c… -bn+l)+ 7 =4_ 8(c…+ + l)2+ 16c…(c… + 36… + 1) + 8[c… _ (c… + 36… + 1) ] + 7 =9c2n-72b2n-72bn-9 = 9(c2…-8b2n-8bn-1) = 0,即定理得证.由引理2和引理3得到如下结果.定理9 设n 3= 1,则不定方程a:2 + y2 - 6*y - 8 = 0的所有正整数解为(a:,y) = (cn,c n+1).证明不定方程;c2+y2- 6xy- 8 = 0 等价于不定方程(3y-x)2 - 2( 2y)2= 8,令 u= 3y-x,t; = 2y显然P e ll方程u2 -2t;2= l的基础解为(3, 2).令〇,,d,)为不定方程u2 -2«;2=8的基础解.由 引理3知,“丨和1)丨须满足不等式0<l u丨丨备4,0专&矣2,即-4矣U|矣4,0矣^^2,其中#0,从而基础解(U|,*;,)共有24种可能,其中只有这两种(±4, 2)是不定方程u2-2t;2=8的基 础解.由于(-4, 2)不是正整数解,则与它相关联的同一类解都不是正整数,那么不定方程u2-2i;2 =8满足条件的基础解只有一对,即(U|,V|)= (4, 2),从而此不定方程的所有正整数解是由基础解 (u,,%) = (4, 2)和与它相关联的同一类解构成的.由引理2知,与基础解(Ul,力)=(4, 2)相关联的同一类解(u,,可由下列表示:、2、'34、、丨、"34、h-'20、U2J、2 3,U丨)、2 3y w,14, "34、v厂3 4)〔20)016) U3^、2 \K v2 )、2 3八1七182 yp o-p4)卜、+ 4^.;U J b3J U…-i J+ 3l,…-ly乂+丨、,34)M ,3“… + VUn+1J、23J U J y2un + 2>v n,24福建师范大学学报(自然科学版)2021 年因此 u…+, = 3u… + 4n+l 二2u… + •下面利用数学归纳法证明!^+1 = 3c n+l~ C n和\+i =:2cn+1 *当n = 1时,有 u2 = 3c2 - c, = 20 和2c2 = 14,此时成立.假设当n = m- 1时,有=3c m-c和、=2c…x^ n = mU m+\=3um+ =3(3cm -'C m-1)■^4(2c J =\lcm-3c m_!=■I7cm-3(6cm -C m+1)=:3c m+1 - c m,V m+ l=2um+ 3vm=2(3cm -C m-\)-^3(2c J =12cm-2cm m-,=12cm~2(6c,n - C m+1)=2cm+l,从而不定方程^-2^=8的所有正整数解为(u,t;)= (3c…+1-c…,2c…+,)(n&l),因此= c…+,,3A: = y l;-u = 3c…+1 - (3c…+1 - c…) = c… .相反的,如果(*,;>〇= ((;…,^),那么£;〖+匕-6£:人+|-8= 0.下用数学归纳法证明此性质.当r a = 1时恒等式显然成立,假设当r a = m时恒等式成立,当n=m+l时,由式(8)得C m+1 + C m+2 ~ 6cm+lC m+2 ~ 8 ~C m+l + (6cm+l~ C m)2~6cm+l(6cm+l~ C m)" 8 =C l,+ C m+1_6cm C m+l -8=0,即定理得证.由定理9,可得到定理10和定理11.定理10 设n&1,则不定方程8*2 -y2 - 8y - 8 =0的所有正整数解为U,y)= (C…,86…).证明假设*和y为不定方程8*2- 8y- 8 = 0的正整数解.令u=A:,2;= 3^+y + 4,即* = u,y=t i-3u-4,再将;c=u和 — 4 代入不定方程 - y2 — 8y - 8 = 0 中得8u2—(v —3u — 4)" - 8(u — 3u — 4) —8=0,整理得u2+ v2-6uv -8=0.由定理9知“=(:…,1;二(;…+1,即;《= “=(;…,7=1;-37-4=«;…+1-3(;…-4= 86….相反的,如果 (*, y) = (C…,86J,由定理 9 和式(12)得84-(8/〇2-8(86…) -8 =8c^ _ (cn+i _ 3c… _ 4): _ 8(c…+i - 3cn - 4) - 8 =~ (cn+i+ cl ~+i-8) = 0,即定理得证.定理11 设n & 2,则不定方程*2+ /- 34外-288 = 0的所有正整数解为(*,y) = (c…_,,c…+1) •证明假设尤和y为不定方程W+ /-34*y -288 = 0的正整数解.由于不定方程V + /-34#-288 = 0 等价于方程U+ y)2- 36外-288 = 0,即36 I(* + y)2,从而 6 丨(a: + y) •令《=——1;=7,即》=:6(/_11,7 = 1;,再将:*:::611-1;和7=1)代人不定方程:*2+72_34;«:7_288 =0中6得(6u - v)1+ v2- 34(6u - v)v - 288 = 0,整理得u2+ v2- 6uv -8=0.由定理 9 知a = c...,t; = c...+1,B P尤=6a —i;= 6c... - c...+1 = y = r = c (1)相反的,如果U,c…+1),由定理9和式(8)得C l-\+ C l+\~ ^C n-\C n+\ ~288 =(6cn-c n+l)2 + c2n+l - 34(6cn - c…+1)c n+1 - 288 =第2期高志贤,等:一些特殊不定方程的整数解2536(4 + 4+1 - 丨- 8) = 〇,即定理得证.结合定理9和定理11,可得到如下结果.定理12假设n > 1,则不定方程;c2 + 36y2 - - 288 = 0的正整数解为(i,y)= (6c n,(:n+1).证明假设a:和y为不定方程;c2 + 36y2 - 36xy- 288 = 0的正整数解•令u=A:-y,i;=y,即尤= a +汐,y=汐,再将a;=w+i;和y=i;代人不定方程;c2 + 36y2 - 36xy - 288 = 0中得(u + v)2 + 36v2- 36(a + v)v- 288 = 0,整理得w, + iT - 34iu> - 288 = 0.由定理 11 知 u = c…_i,i; = c…+i,艮fU = u + i; = c…_i+ c…+i = 6c…,y = i; = c…+1 •相反的,如果(%,y) = (6c…, c…+1),由定理9得(6c J2 + 36c^+1 -36(6c j c n+1- 288 =36(4 + g+1 - 6c…c n+1 -8) = 0,即定理得证.参考文献:[1] BEHERA A, PANDA G K. On the square roots of triangular numbers [ J]. Fibonacci Quarterly, 1999, 37 (2) :98-105.[2] PANDA G K, RAY P K. Cobalancing numbers and cobalancers [ J]. International Journal of Mathematics and Mathematical Sciences, 2005, 2005 (8):1189-1200.[3] G〇ZRRI G K. On Pell, Pell-Lucas, and balancing numbers [J]. Journal of Inequalities and Applications, 2018, 2018(1): 1-16.[4] DASH K K, OTA R S, DASH S. Sequence t-balancing numbers [ J]. Int J Contemp Math Sciences, 2012, 7 (47):2305-2310.[5 ] KARAATLI 0, KESKIN R. On some Diophantine equations related to square triangular and balancing numbers [ J ]. J Algebra Number Theory, Adv Appl, 2010, 4 (2):71-89.[6] KESKIN R, KARAATLY 0. Some new properties of balancing numbers and square triangular numbers [ J]. Journal of Integer Sequences, 2012, 15 (1):1-13.[7] PANDA G K, RAY P K. Some links of balancing and cobalancing numbers with Pell and associated Pell numbers [ J].Bulletin of the Institute of Mathematics, Academia Sinica (New Series) , 2011, 6 ( 1) :41-72.[8] KOSHY T. Pell and Pell-Lucas numbers with applications [M].New York:Springer, 2014:31-55.(责任编辑:杨柳惠)。
MGARCH(BEKK和mGJR)过程模拟、估计和诊断手册说明书

Package‘mgarchBEKK’December6,2022Title Simulating,Estimating and Diagnosing MGARCH(BEKK and mGJR)ProcessesVersion0.0.5Description Procedures to simulate,estimate and diagnose MGARCHprocesses of BEKK and multivariate GJR(bivariate asymmetric GARCHmodel)specification.Depends R(>=3.2.3),tseries,mvtnormSuggests testthat,devtools,roxygen2License GPL-3Encoding UTF-8URL https:///vst/mgarchBEKK/RoxygenNote7.2.1NeedsCompilation yesAuthor Harald Schmidbauer[aut],Angi Roesch[aut],Vehbi Sinan Tunalioglu[cre,aut]Maintainer Vehbi Sinan Tunalioglu<***************>Repository CRANDate/Publication2022-12-0607:50:02UTCR topics documented:BEKK (2)diagnoseBEKK (4)mGJR (5)simulateBEKK (6)Index812BEKK BEKK Estimate MGARCH-BEKK processesDescriptionProvides the MGARCH-BEKK estimation procedure.UsageBEKK(eps,order=c(1,1),params=NULL,fixed=NULL,method="BFGS",verbose=F)Argumentseps Data frame holding time series.order BEKK(p,q)order.An integer vector of length2giving the orders of the model to befitted.order[2]refers to the ARCH order and order[1]to the GARCHorder.params Initial parameters for the optim function.fixed Vector of parameters to befixed.method The method that will be used by the optim function.verbose Indicates if we need verbose output during the estimation.DetailsBEKK estimates a BEKK(p,q)model,where p stands for the GARCH order,and q stands for the ARCH order.ValueEstimation results packaged as BEKK class instance.eps a data frame contaning all time serieslength length of the seriesorder order of the BEKK modelfittedestimation.time time to complete the estimation processtotal.time time to complete the whole routine within the mvBEKK.est processestimation estimation object returned from the optimization process,using optimBEKK3aic the AIC value of thefitted modelest.params list of estimated parameter matricesasy.se.coef list of asymptotic theory estimates of standard errors of estimated parameterscor list of estimated conditional correlation seriessd list of estimated conditional standard deviation seriesH.estimated list of estimated series of covariance matriceseigenvalues estimated eigenvalues for sum of Kronecker productsuncond.cov.matrix estimated unconditional covariance matrixresiduals list of estimated series of residualsReferencesBauwens L.,urent,J.V.K.Rombouts,Multivariate GARCH models:A survey,April,2003 Bollerslev T.,Modelling the coherence in short-run nominal exchange rate:A multivariate general-ized ARCH approach,Review of Economics and Statistics,498–505,72,1990Engle R.F.,K.F.Kroner,Multivariate simultaneous generalized ARCH,Econometric Theory,122-150,1995Engle R.F.,Dynamic conditional correlation:A new simple class of multivariate GARCH models, Journal of Business and Economic Statistics,339–350,20,2002Tse Y.K.,A.K.C.Tsui,A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations,Journal of Business and Economic Statistics,351-362,20, 2002Examples##Simulate series:simulated<-simulateBEKK(2,1000,c(1,1))##Prepare the matrix:simulated<-do.call(cbind,simulated$eps)##Estimate with default arguments:estimated<-BEKK(simulated)##Not run:##Show diagnostics:diagnoseBEKK(estimated)##End(Not run)4diagnoseBEKK diagnoseBEKK Diagnose BEKK process estimationDescriptionProvides diagnostics for a BEKK process estimation.UsagediagnoseBEKK(estimation)Argumentsestimation The return value of the mvBEKK.est functionDetailsThis procedure provides console output and browsable plots for a given BEKK process estimation.Therefore,it is meant to be interactive as the user needs to proceed by pressing c on the keyboard to see each plot one-by-one.ValueNothing specialExamples##Simulate series:simulated=simulateBEKK(2,1000,c(1,1))##Prepare the matrix:simulated=do.call(cbind,simulated$eps)##Estimate with default arguments:estimated=BEKK(simulated)##Not run:##Show diagnostics:diagnoseBEKK(estimated)##End(Not run)mGJR5 mGJR Bivariate GJR EstimationDescriptionProvides bivariate GJR(mGJR(p,q,g))estimation procedure.UsagemGJR(eps1,eps2,order=c(1,1,1),params=NULL,fixed=NULL,method="BFGS")Argumentseps1First time series.eps2Second time series.order mGJR(p,q,g)order a three element integer vector giving the order of the model to befitted.order[2]refers to the ARCH order and order[1]to the GARCHorder and order[3]to the GJR order.params Initial parameters for the optim function.fixed A two dimensional vector that contains the user specifiedfixed parameter values.method The method that will be used by the optim function.See?optim for available options.ValueEstimation results packaged as mGJR class instance.The values are defined as:eps1first time serieseps2second time serieslength length of each seriesorder order of the mGJR modelfittedestimation.time time to complete the estimation processtotal.time time to complete the whole routine within the mGJR.est processestimation estimation object returned from the optimization process,using optimaic the AIC value of thefitted modelest.params estimated parameter matricesasy.se.coef asymptotic theory estimates of standard errors of estimated parameterscor estimated conditional correlation seriessd1first estimated conditional standard deviation seriessd2second estimated conditional standard deviation seriesH.estimated estimated series of covariance matriceseigenvalues estimated eigenvalues for sum of Kronecker productsuncond.cov.matrix estimated unconditional covariance matrixresid1first estimated series of residualsresid2second estimated series of residualsReferencesBauwens L.,urent,J.V.K.Rombouts,Multivariate GARCH models:A survey,April,2003 Bollerslev T.,Modelling the coherence in short-run nominal exchange rate:A multivariate general-ized ARCH approach,Review of Economics and Statistics,498–505,72,1990Engle R.F.,K.F.Kroner,Multivariate simultaneous generalized ARCH,Econometric Theory,122-150,1995Engle R.F.,Dynamic conditional correlation:A new simple class of multivariate GARCH models, Journal of Business and Economic Statistics,339–350,20,2002Tse Y.K.,A.K.C.Tsui,A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations,Journal of Business and Economic Statistics,351-362,20, 2002Examples##Not run:sim=BEKK.sim(1000)est=mGJR(sim$eps1,sim$eps2)##End(Not run)simulateBEKK Simulate BEKK processesDescriptionProvides a procedure to simulate BEKK processes.UsagesimulateBEKK(series.count,T,order=c(1,1),params=NULL)Argumentsseries.count The number of series to be simulated.T The length of series to be simulated.order BEKK(p,q)order.An integer vector of length2giving the orders of the model tofit.order[2]refers to the ARCH order and order[1]to the GARCH order.params A vector containing a sequence of parameter matrices’values.DetailssimulateBEKK simulates an N dimensional BEKK(p,q)model for the given length,order list,and initial parameter list where N is also specified by the user.ValueSimulated series and auxiliary information packaged as a simulateBEKK class instance.Values are: length length of the series simulatedorder order of the BEKK modelparams a vector of the selected parameterstrue.params list of parameters in matrix formeigenvalues computed eigenvalues for sum of Kronecker productsuncond.cov.matrix unconditional covariance matrix of the processwhite.noise white noise series used for simulating the processeps a list of simulated seriescor list of series of conditional correlationssd list of series of conditional standard deviationsReferencesBauwens L.,urent,J.V.K.Rombouts,Multivariate GARCH models:A survey,April,2003 Bollerslev T.,Modelling the coherence in short-run nominal exchange rate:A multivariate general-ized ARCH approach,Review of Economics and Statistics,498–505,72,1990Engle R.F.,K.F.Kroner,Multivariate simultaneous generalized ARCH,Econometric Theory,122-150,1995Engle R.F.,Dynamic conditional correlation:A new simple class of multivariate GARCH models, Journal of Business and Economic Statistics,339–350,20,2002Tse Y.K.,A.K.C.Tsui,A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations,Journal of Business and Economic Statistics,351-362,20, 2002Examples##Simulate series:simulated=simulateBEKK(2,1000,c(1,1))IndexBEKK,2diagnoseBEKK,4mGJR,5simulateBEKK,68。
IEEEtran_HOWTO

How to Use the IEEEtran L A T E X ClassMichael Shell,Member,IEEE(Invited Paper)Abstract—This article describes how to use the IEEEtran class with L A T E X to produce high quality typeset papers that are suit-able for submission to the Institute of Electrical and Electronics Engineers(IEEE).IEEEtran can produce conference,journal and technical note(correspondence)papers with a suitable choice of class options.This document was produced using IEEEtran in journal mode.Index Terms—Class,IEEEtran,L A T E X,paper,style,template, typesetting.I.I NTRODUCTIONW ITH a recent IEEEtran classfile,a computer running L A T E X,and a basic understanding of the L A T E X language, an author can produce professional quality typeset research papers very quickly,inexpensively,and with minimal effort. The purpose of this article is to serve as a user guide of IEEEtran L A T E X class and to document its unique features and behavior.This document applies to version1.7and later of IEEEtran. Prior versions do not have all of the features described here. IEEEtran will display the version number on the user’s console when a document using it is being compiled.The latest version of IEEEtran and its supportfiles can be obtained from IEEE’s web site[1],or CTAN[2].This latter site may have some additional material,such as beta test versions andfiles related to non-IEEE uses of IEEEtran.See the IEEEtran homepage [3]for frequently asked questions and recent news about IEEEtran.Complimentary to this document are thefiles1bare_c onf.tex,bare_jrnl.tex and bare_jrnl_compsoc.te x which are“bare bones”example(template)files of a conference,journal and Computer Society journal paper2, respectively.Authors can quickly obtain a functional document by using thesefiles as starters for their own work.A more advanced example featuring the use of optional packages along with more complex usage techniques,can be found in bare_ adv.tex.Manuscript created February25,2002;revised January11,2007.This work was supported by the IEEE.This work is distributed under the L A T E X Project Public License(LPPL)(/)version1.3.A copy of the LPPL,version1.3,is included in the base L A T E X documentation of all distributions of L A T E X released2003/12/01or later.The opinions expressed here are entirely that of the author.No warranty is expressed or er assumes all risk.See /for current contact information.1Note that it is the convention of this document not to hyphenate command orfile names and to display them in typewriter font.Within such constructs,spaces are not implied at a line break and will be explicitly carried into the beginning of the next line.This behavior is not a feature of IEEEtran, but is used here to illustrate computer commands verbatim.2Computer Society conferences are not sufficiently different from traditional conferences to warrant a separate examplefile.It is assumed that the reader has at least a basic working knowledge of L A T E X.Those so lacking are strongly encouraged to read some of the excellent literature on the subject[4]–[6]. General support for L A T E X related questions can be obtained in the internet newsgroup comp.text.tex.There is also a searchable list of frequently asked questions about L A T E X[7]. Please note that the appendices sections contain information on installing the IEEEtran classfile as well as tips on how to avoid commonly made mistakes.II.C LASS O PTIONSThere are a number of class options that can be used to control the overall mode and behavior of IEEEtran.These are specified in the traditional L A T E X way.For example,\documentclass[9pt,technote]{IEEEtran}is used with correspondence(technote)papers.The various categories of options will now be discussed.For each category, the default option is shown in bold.The user must specify an option from each category in which the default is not the one desired.The various categories are totally orthogonal to each other—changes in one will not affect the defaults in the others.A.9pt,10pt,11pt,12ptThere are four possible values for the normal text size. 10pt is used by the vast majority of papers.Three notable exceptions are technote papers,which use9pt text,the initial submissions to some conferences that use11pt,and Computer Society papers which typically require12pt text.B.draft,draftcls,draftclsnofoot,finalIEEEtran provides for three draft modes as well as the normalfinal mode.The draft modes provide a larger(double) line spacing to allow for editing comments as well as one inch margins on all four sides of the paper.The standard draft option puts every package used in the document into draft mode.With most graphics packages,this has the effect of disabling the rendering offigures.If this is not desired,one can use the draftcls option instead to yield a draft mode that will be confined within the IEEEtran class so thatfigures will be included as normal.draftclsnofoot is like draftcls,but does not display the word“DRAFT”along with the date at the foot of each page.Both draft and draftclsnofoot modes imply draftcls(which is a subset of the other two).When using one of the draft modes,most users will also want to select the onecolumn option.0000–0000/00$00.00c 2007IEEEC.conference,journal,technote,peerreview,peerreviewca IEEEtran offersfive major modes to encompass conference, journal,correspondence(technote)and peer review papers. Journal and technote modes will produce papers very similar to those that appear in many IEEE T RANSACTIONS journals. When using technote,most users should also select the9pt option.The peerreview mode is much like the journal mode, but produces a single-column cover page(with the title,author names and abstract)to facilitate anonymous peer review.The title is repeated(without the author names or abstract)on the first page after the cover page.3Papers using the peer review options require an\IEEEpeerreviewmaketitle command (in addition to and after the traditional\maketitle)to be executed at the place the cover page is to end—usually just after the abstract.This command will be silently ignored with the non-peerreview modes.See the bare templatefiles for an example of the placement of this command.The peerreviewca mode is like peerreview,but allows the author name information to be entered and formatted as is done in conference mode(see Section IV-B2for details)so that author affiliation and contact information is more visible to the editors.1)Conference Mode Details:Conference mode makes a number of significant changes to the way IEEEtran behaves:•The margins are increased as the height of the text is reduced to about9.25in.In particular,the bottom margin will become larger than that of the top as IEEE wants extra clearance at the bottom.The text height will not be exactly9.25in,but will vary slightly with the normal font size to ensure an integer number of lines in a column.•Headings and page numbers are not displayed in the headers or footers.This,coupled with symmetric hori-zontal margins,means that there will not be a noticeable difference between the one and two sided options.•The\author text is placed within a tabular environment to allow for multicolumn formatting of author names and affiliations.Several commands are enabled to facilitate this formatting(see Section IV-B2for details).•The spacing after the authors’names is reduced.So is the spacing around the section names.•The special paper notice(if used)will appear between the author names and the title(not after as with journals).•Thefigure captions are centered.•The following commands are intentionally disabled:\t hanks,\IEEEPARstart,\IEEEbiography,\IEEEb iographynophoto,\IEEEpubid,\IEEEpubidadjco l,\IEEEmembership,and\IEEEaftertitletext.If needed,they can be reenabled by issuing the command: \IEEEoverridecommandlockouts.•Various reminder(related to camera ready work)and warning notices are enabled.When using conference mode,most users will also want to equalize the columns on the last page(see Section XIV).3A blank page may be inserted after the cover page when using the twoside (duplex printing)option so that the beginning of the paper does not appear on the back side of the cover psocThis option invokes a mode by which IEEEtran mimics the format of the publications of the IEEE Computer Society. Notable compsoc mode format features include:•the default text font is changed from Times Roman to Palatino/Palladio(non-conference compsoc modes only);•revised margins;•Arabic section numbering;•enabling of the\IEEEcompsocitemizethanks and\I EEEcompsocthanksitem commands to provide for the \thanks(first footnote)itemized list used for author affiliations;•enabling of the\IEEEcompsoctitleabstractindex text command to provide for a single column abstract and index terms sections;•various other styling changes such as the use of:a sans serif(Helvetica)font for titles,headings,etc.;a ruled line above thefirst footnote area;left aligned reference labels;etc.1)Compsoc Conference Mode:IEEEtran follows the pub-lished guidelines for IEEE Computer Society conference pa-pers[8].Perhaps surprisingly,this format nullifies many of the unique features of compsoc journals and is not so much different from traditional conference mode.However,Arabic section numbering is retained.It should be mentioned that Scott Pakin’s IEEEconf L A T E X class[9]also produces this format.E.letterpaper,a4paperIEEEtran supports both US letter(8.5in×11in)and A4 (210mm×297mm)paper sizes.Since IEEE primarily uses US letter,authors should usually select the letterpaper option before submitting their work to IEEE—unless told otherwise (typically by conferences held outside the United States). Changing the paper size will not alter the typesetting of the document—only the margins will be affected.In particular, documents using the a4paper option will have reduced side margins(A4is narrower than US letter)and a longer bottom margin(A4is longer than US letter).For both cases,the top margins will be the same and the text will be horizontally centered.Note that authors should ensure that all post-processing (ps,pdf,etc.)uses the same paper specification as the.tex document.Problems here are by far the number one reason for incorrect margins.See Appendix B for more details.F.oneside,twosideThese options control whether the layout follows that of single sided or two sided(duplex)printing.Because the side margins are normally centered,the main notable difference is in the format of the running headings.G.onecolumn,twocolumnThese options allow the user to select between one and two column text formatting.Since IEEE always uses two column text,the onecolumn option is of interest only with draft papers.SHELL:HOW TO USE THE IEEETRAN L A T E X CLASS3H.romanappendicesIEEEtran defaults to numbering appendices alphabetically(e.g.,A,B,etc.).Invoke this option to get Roman numbering.I.captionsoffInvoking this option will inhibit the display of captionswithinfigures and tables.This is done in a manner thatpreserves the operation of\label within\caption.Thisoption is intended for journals,such as IEEE T RANSACTIONS ON P OWER E LECTRONICS(TPE),that requirefigures and tables to placed,captionless,on pages of their own at the endof the document.Suchfigure placement can be achieved withthe help of James McCauley and Jeff Goldberg’s endfloat.stypackage[10]:\usepackage[nomarkers]{endfloat}Note that the TPE has other unusual formatting requirementsthat also require the draftclassnofoot and onecolumn optionsas well as the insertion of page breaks(\newpage)just priorto thefirst section as well as the bibliography.Such commandscan be enabled conditionally via the\ifCLASSOPTIONcapt ionsoff conditional(Section III-A).J.nofonttuneIEEEtran normally alters the default interword spacing to be like that used in IEEE publications.The result is text that requires less hyphenation and generally looks more pleasant, especially for two column text.The nofonttune option will disable the adjustment of these font parameters.This option should be of interest only to those who are using fonts specifically designed or modified for use with two column work.III.T HE CLASSINPUT,CLASSOPTION ANDCLASSINFO C ONTROLSIEEEtran offers three catagories of special commands that allow information to be passed between the classfile and the user’s document:•CLASSINPUTs are inputs that provide a way to cus-tomize the operation of IEEEtran by overriding some of the default settings(at the time IEEEtran is loaded);•CLASSOPTIONs which are outputs that allow for condi-tional compilation based on which IEEEtran class options have been selected;•CLASSINFOs which are outputs that allow the user a way to access additional information about the IEEEtran runtime environment.A.CLASSINPUTsThe available CLASSINPUTs include:\CLASSINPUTbase linestretch which sets the line spacing of the document; \CLASSINPUTinnersidemargin which sets the margin at the inner(binding)edge;\CLASSINPUToutersidemargin which sets the margin at the outer edge;\CLASSINPUTtopt extmargin which sets the top margin;\CLASSINPUTbotto mtextmargin which sets the bottom margin.Of course,such parameters can be set via the traditional L A T E X interface(\odd sidemargin,\topmargin,etc.).However,the advantage of of using the CLASSINPUT approach is that it allows IEEEtran to adjust other internal parameters and perform any additional calculations as needed.For example,setting the side margins in L A T E X requires a careful setting of\oddsidemargin,\e vensidemargin and\textwidth taking into consideration the paper size and whether or not duplex(two-sided)printing is being used.To invoke a CLASSINPUT,just define the relavant CLASS-INPUT as desired prior to the loading of IEEEtran.For example,\newcommand{\CLASSINPUTinnersidemargin}{17mm}\documentclass{IEEEtran}will yield a document that has17mm side margins—if only one of the innerside/outerside(or toptext/bottomtext)margin pair is specified,IEEEtran will assume the user wants sym-metric side(or top/bottom)margins and will set both values of the relavant pair to the(single)user specified value. IEEEtran uses thefixed values of12pt and0.25in for\h eadheight and\headsep,respectively.The position of the header can be altered after IEEEtran is loaded,without changing the margins as long as the sum of\topmargin, \headheight and\headsep is preserved.For example,the header can be shifted upwards0.2in using:\addtolength{\headsep}{0.2in}\addtolength{\topmargin}{-0.2in}Likewise,\footskip,which has a default value of0.4in,can easily be changed to alter the position of the footer within the bottom margin.When using\CLASSINPUTbaselinestretch,IEEEtran will automatically“digitize”\textheight so that an integer number of lines willfit on a page(as is done in the draft modes).Digitization is not done when the top or bottom margins are set via ers are cautioned that using CLASSINPUT controls can result in documents that are not compliant with the IEEE’s standards.The intended applications include:(1)conferences or societies that have unusual formatting requirements;(2)producing copies with nonstandard margins such as when binding for personal use; and(3)non-IEEE related work.B.CLASSOPTIONsCLASSOPTIONs are primarily T E X\if conditionals that are automatically set based on which IEEEtran options are being used.Thus,for example,a construct such as\ifCLASSOPTIONconference\typeout{in conference mode}\else\typeout{not in conference mode}\fican be used to provide for conditional code execution.Please note that,as mentioned in Section II-B,the draft and draft-clsnofoot options imply draftcls.So,most users will want to test\ifCLASSOPTIONdraftcls for detecting the draft modes.4JOURNAL OF L A T E X CLASS FILES,VOL.6,NO.1,JANUARY2007For the document’s point size options,\CLASSOPTIONp t is defined as a macro that expands to the numerical part of the selected point value(e.g.,9,10,11or12).For the paper size options,\CLASSOPTIONpaper will be a macro that contains the paper specification(e.g.,letter,a4).To use these as conditionals will require a string macro comparison: \newcommand{\myninestring}{9}\ifx\CLASSOPTIONpt\myninestring\typeout{document is9pt}\fiUsers should treat the CLASSOPTIONs as being“read-only”and not attempt to manually alter their values because IEEE-tran uses them internally asflags to determine which options have been selected—changing theseflags will likely result in improper formatting.C.CLASSINFOsThe available CLASSINFOs include the\ifCLASSINFOp df conditional which works much like Heiko Oberdiek’s if-pdf.sty package[11]to indicate if PDF output(from pdfL A T E X) is in effect:\ifCLASSINFOpdf\typeout{PDF mode}\fiIEEEtran.cls also provides the lengths\CLASSINFOnorma lsizebaselineskip,which is the\baselineskip of the normalsize font,and\CLASSINFOnormalsizeunitybaseli neskip,which is the\baselineskip of the normalsize font under unity\baselinestetch.Finally,there are the string macros(these are not condition-als or lengths)\CLASSINFOpaperwidth and\CLASSINF Opaperheight which contain the paper dimensions in their native specifications including units(e.g.,8.5in,22mm,etc.). As with CLASSOPTIONs,users should not attempt to alter the CLASSINFOs.IV.T HE T ITLE P AGEThe parts of the document unique to the title area are created using the standard L A T E X command\maketitle.Before this command is called,the author must declared all of the text objects which are to appear in the title area.A.Paper TitleThe paper title is declared like:\title{A Heuristic Coconut-based Algorithm}in the standard L A T E X manner.Line breaks(\\)may be used to equalize the length of the title lines.B.Author NamesThe name and associated information is declared with the \author command.\author behaves slightly differently depending on the document mode.1)Names in Journal/Technote Mode:A typical\author command for a journal or technote paper looks something like this:\author{Michael˜Shell,˜\IEEEmembership{Member,˜IEEE, }John˜Doe,˜\IEEEmembership{Fellow,˜OSA,}and˜Jane˜D oe,˜\IEEEmembership{Life˜Fellow,˜IEEE}%\thanks{Manuscript received January20,2002;revise d January30,2002.This work was supported by the I EEE.}%\thanks{M.Shell is with the Georgia Institute of Te chnology.}}The\IEEEmembership command is used to produce the italic font that indicates the authors’IEEE membership status. The\thanks command produces the“first footnotes.”Be-cause the L A T E X\thanks was not designed to contain multiple paragraphs4,authors will have to use a separate\thanks for each paragraph.However,if needed,regular line breaks (\\)can be used within\thanks.In order to get proper line breaks and spacing,it is important to correctly use and control the spaces within\e nonbreaking spaces(˜)to ensure that name/membership pairs remain together.A minor, but easy,mistake to make is to forget to prevent unwanted spaces from getting between commands which use delimited ({})arguments.Note the two%which serve to prevent the code line break on lines ending in a}from becoming an unwanted space.Such a space would not be ignored as an end-of-line space because,technically,the last\thanks is thefinal command on the line.“Phantom”spaces like these would append to the end of the last author’s name,causing the otherwise centered name line to shift very slightly to the left.2)Names in Conference Mode:The author name area is more complex when in conference mode because it also contains the authors’affiliations.For this reason,when in conference mode,the contents of\author{}are placed into a modified tabular environment.The commands\IE EEauthorblockN{}and\IEEEauthorblockA{}are also provided so that it is easy to correctly format the author names and affiliations,respectively.For papers with three or less affiliations,a multicolumn format is preferred:\author{\IEEEauthorblockN{Michael Shell}\IEEEauthorblockA{School of Electrical and\\Computer Engineering\\Georgia Institute of Technology\\Atlanta,Georgia30332--0250\\Email:mshell@}\and\IEEEauthorblockN{Homer Simpson}\IEEEauthorblockA{Twentieth Century Fox\\Springfield,USA\\Email:homer@}\and\IEEEauthorblockN{James Kirk\\and Montgomery Scott}\IEEEauthorblockA{Starfleet Academy\\San Francisco,California96678-2391\\Telephone:(800)555--1212\\Fax:(888)555--1212}}Use\and to separate the affiliation columns.The columns will automatically be centered with respect to each other and the side margins.4Although IEEEtran.cls does support it,the standard classes do not.SHELL:HOW TO USE THE IEEETRAN L A T E X CLASS5If there are more than three authors and/or the text is too wide tofit across the page,use an alternate format:\author{\IEEEauthorblockN{Michael Shell\IEEEauthorre fmark{1},Homer Simpson\IEEEauthorrefmark{2},James K irk\IEEEauthorrefmark{3},Montgomery Scott\IEEEautho rrefmark{3}and Eldon Tyrell\IEEEauthorrefmark{4}}\IEEEauthorblockA{\IEEEauthorrefmark{1}School of Ele ctrical and Computer Engineering\\Georgia Institute of Technology,Atlanta,Georgia30 332--0250\\Email:mshell@}\IEEEauthorblockA{\IEEEauthorrefmark{2}Twentieth Cen tury Fox,Springfield,USA\\Email:homer@}\IEEEauthorblockA{\IEEEauthorrefmark{3}Starfleet Aca demy,San Francisco,California96678-2391\\ Telephone:(800)555--1212,Fax:(888)555--1212}\IEEEauthorblockA{\IEEEauthorrefmark{4}Tyrell Inc., 123Replicant Street,Los Angeles,California90210 --4321}}The\IEEEauthorrefmark{}command will generate a foot-note symbol corresponding to the number in its e this to link the author names to their respective affiliations.It is not necessary prevent spaces from being between the\IEEEa uthorblock’s because each block starts a new group of lines and L A T E X will ignore spaces at the very end and beginning of lines.3)Names in Compsoc Journal Mode:One unique feature of Computer Society journals is that author affiliations are for-matted in an itemized list within thefirst(\thanks)footnote. In compsoc mode,IEEEtran provides a special form of\tha nks,\IEEEcompsocitemizethanks,to obtain this effect: \author{Michael˜Shell,˜\IEEEmembership{Member,˜IEEE, }John˜Doe,˜\IEEEmembership{Fellow,˜OSA,}and˜Jane˜D oe,˜\IEEEmembership{Life˜Fellow,˜IEEE}%\IEEEcompsocitemizethanks{\IEEEcompsocthanksitem M. Shell is with the Georgia Institute of Technology. \IEEEcompsocthanksitem J.Doe and J.Doe are with An onymous University.}%\thanks{Manuscript received January20,2002;revise d January30,2002.}}Within\IEEEcompsocitemizethanks,\IEEEcompsoctha nksitem works like\item to provide a bulleted affiliation group.To facilitate dual compilation,in non-compsoc mode, IEEEtran treats\IEEEcompsocitemizethanks as\thanks and sets\IEEEcompsocthanksitem to generate a line break with indentation.However,this is not entirely satisfactory as Computer Society journals place the author affiliations before the“manuscript received”line while traditional IEEE journals use the reverse order.If correct dual compilation is needed, the CLASSOPTION conditionals can be employed to swap the order as needed.4)Names in Compsoc Conference Mode:Names in comp-soc conference mode are done in the same way as traditional conference mode.However,because the compsoc conference mode uses much larger margins,there is typically room for only two(rather than three)affiliation columns before the alternate single column format is required.C.Running HeadingsThe running headings are declared with the\markboth{ }{}command.Thefirst argument contains the journal name information and the second contains the author name and paper title.For example:\markboth{Journal of Quantum Telecommunications,˜Vol .˜1,No.˜1,˜January˜2025}{Shell\MakeLowercase{\text it{et al.}}:A Novel Tin Can Link}Note that because the text in the running headings is automat-ically capitalized,the\MakeLowercase{}command must be used to obtain lower case text.The second argument is used as a page heading only for the odd number pages after the title page for two sided(duplex)journal papers.This page is such an example.Technote papers do not utilize the second argument.Conference papers do not have running headings, so\markboth{}{}has no effect when in conference mode. Authors should not put any name information in the headings (if used)of anonymous peer review papers.D.Publication ID MarksPublication ID marks can be placed on the title page of journal and technote papers via the\IEEEpubid{}command: \IEEEpubid{0000--0000/00\$00.00˜\copyright˜2007IEEE }Although authors do not yet have a valid publication ID at the time of paper submission,\IEEEpubid{}is useful because it provides a means to see how much of the title page text area will be unavailable in thefinal publication.This is especially important in technote papers because,in some journals,the publication ID space can consume more than one text line.If \IEEEpubid{}is used,a second command,\IEEEpubidad jcol must be issued somewhere in the second column of the title page.This is needed because L A T E X resets the text height at the beginning of each column.\IEEEpubidadjcol“pulls up”the text in the second column to prevent it from blindly running into the publication ID.Publication IDs are not to be placed by the author on camera ready conference papers so\IEEEpubid{}is disabled in conference mode.Instead the bottom margin is automatically increased by IEEEtran when in conference mode to give IEEE room for such marks at the time of publication.In draft mode, the publisher ID mark will not be printed at the bottom of the titlepage,but room will be cleared for it.Publication ID marks are perhaps less important with compsoc papers because Computer Society journals place the publisher ID marks within the bottom margin so as not to affect the amount of page space available for text.E.Special Paper NoticesSpecial paper notices,such as for invited papers,can be declared with:\IEEEspecialpapernotice{(Invited Paper)}Special paper notices in journal and technote papers appear between the author names and the main text.The title page of this document has an example.For conference papers,the special paper notice is placed between the title and the author names.Much more rarely,there is sometimes a need to gain access to the space across both columns just above the main text.6JOURNAL OF L A T E X CLASS FILES,VOL.6,NO.1,JANUARY2007For instance,a paper may have a dedication[12].IEEEtran provides the command\IEEEaftertitletext{}which can be used to insert text or to alter the spacing between the title area and the main text:\IEEEaftertitletext{\vspace{-1\baselineskip}} Authors should be aware that IEEEtran carefully calculates the spacing between the title area and main text to ensure that the main text height of thefirst page always is equal to an integer number of normal sized lines(unless the top or bottom margins have been overridden by CLASSINPUTs).Failure to do this can result in underfull vbox errors and paragraphs being“pulled apart”in the second column of thefirst page if there isn’t any rubber lengths(such as those around section headings)in that column.The contents of\IEEEaftertitle text{}are intentionally allowed to bypass this“dynamically determined title spacing”mechanism,so authors may have to manually tweak the height(by a few points)of the\IEEEa ftertitletext{}contents(if used)to avoid an underfull vbox warning.V.A BSTRACT AND I NDEX T ERMSThe abstract is generally thefirst part of a paper after\m aketitle.The abstract text is placed within the abstract environment:\begin{abstract}%\boldmath We propose...\end{abstract}To preserve the distinction between constructs such as vector and scalar forms,IEEEtran defaults to using non-bold math within the abstract.However,many IEEE journals do use bold math within the abstract to better match the bold text font.If this is desired,just issue a\boldmath command at the start of the abstract.Please note that the Computer Society typically does not allow math or citations to appear in the abstract. Journal and technote papers also have a list of key words (index terms)which can be declared with:\begin{IEEEkeywords}Broad band networks,quality of service,WDM.\end{IEEEkeywords}To obtain a list of valid keywords from the IEEE,just send a blank email to keywords@.A list of Computer Society approved keywords can be obtained at puter. org/mc/keywords/keywords.htm.The Computer Society format presents a difficulty in that compsoc journal(but not compsoc conferences)papers place the abstract and index terms sections in single column format just below the author names,but the other IEEE formats place them in thefirst column of the main text before thefirst section.To handle this,IEEEtran offers a command,\IEE Ecompsoctitleabstractindextext,that is to be declared before\maketitle,and whose single argument holds the text/sections that are to appear in single column format after the author names:\IEEEcompsoctitleabstractindextext{%\begin{abstract}%\boldmath We propose...\end{abstract}\begin{IEEEkeywords}Broad band networks,quality of service,WDM.\end{IEEEkeywords}}To facilitate dual compilation,IEEEtran provides another command,\IEEEdisplaynotcompsoctitleabstractin dextext,which will“become”whatever was declared in \IEEEcompsoctitleabstractindextext when in non-compsoc or conference mode(as compsoc conferences use the same placement for the abstract and index terms as traditional conferences do).That is to say,the abstract and index terms sections can be automatically“teleported’to the appropriate place they need to be depending on the document mode.\IE EEdisplaynotcompsoctitleabstractindextext should typically be placed just after\maketitle(and before\IEE Epeerreviewmaketitle if used).VI.S ECTIONSSections and their headings are declared in the usual L A T E X fashion via\section,\subsection,\subsubsection, and\paragraph.In the non-compsoc modes,the numbering for these sections is in upper case Roman numerals,upper case letters,Arabic numerals and lower case letters,respectively. In compsoc mode,Arabic numerals are used exclusively for (sub)section numbering.The\paragraph section is not allowed for technotes or compsoc conferences as these generally are not permitted to have such a deep section nesting depth.If needed,\paragra ph can be restored by issuing the command\setcounter{ secnumdepth}{4}in the document preamble.A.Initial Drop Cap LetterThefirst letter of a journal paper is a large,capital,oversized letter which descends one line below the baseline.Such a letter is called a“drop cap”letter.The other letters in thefirst word are rendered in upper case.This effect can be accurately produced using the IEEEtran command\IEEEPARstart{}{ }.Thefirst argument is thefirst letter of thefirst word,the second argument contains the remaining letters of thefirst word.The drop cap of this document was produced with:\IEEEPARstart{W}{ith}Note that some journals will also render the second word in upper case—especially if thefirst word is very short.For more usage examples,see the bare_jrnl.tex examplefile.VII.C ITATIONSCitations are made with the\cite command as usual. IEEEtran will produce citation numbers that are individually bracketed in IEEE style.(“[1],[5]”as opposed to the more common“[1,5]”form.)The base IEEEtran does not sort or produce compressed“ranges”when there are three or more adjacent citation numbers.However,IEEEtran pre-defines some format control macros to facilitate easy use with Donald Arseneau’s cite.sty package[13].So,all an author has to do is to call cite.sty:\usepackage{cite}。
java数据结构参考文献

java数据结构参考文献
以下是一些关于Java数据结构的参考文献:
1. 《数据结构与算法分析(Java语言描述)》, 机械工业出版社,作者: Mark Allen Weiss。
2. 《Java数据结构与算法》, 人民邮电出版社,作者: 王晓东。
3. 《Java核心技术卷II:高级特性(原书第10版)》,机械工业出版社,作者: Cay S. Horstmann、Gary Cornell。
4. 《算法图解(Python/Java版)》, 人民邮电出版社,作者: Aditya Bhargava。
5. 《大话数据结构与算法(Java版)》,清华大学出版社,作者: 宗哲。
6. 《数据结构与算法分析(Java版)》,清华大学出版社,作者: 孙秋华、赵凤芝。
7. 《Java编程思想(第4版)》,机械工业出版社,作者: Bruce Eckel。
8. 《Java数据结构和算法(第2版)》,清华大学出版社,作者: 罗卫、李晶、吴艳。
9. 《Java程序员面试宝典》,人民邮电出版社,作者: 陈小玉。
10. 《Java程序设计与数据结构(基础篇)》,人民邮电出版社,作者: 徐
宏英。
以上参考文献仅供参考,建议根据自身需求选择合适的书籍阅读。
Development_ofldeas_on_Computable_Intelligence

Journal of Human Cognition Vol.1No.1To find out the common features be-tween organisms爷野intelligence冶and ma-chines爷野intelligence冶,the concept of野uni-versal intelligence冶,which can be used in both living world and non-living world,was put forward6.It defines intelligence as野intel-ligence measures an agent爷s ability to achieve goals in a wide range of environments冶.We can find that most of definitions of Form1are very empirical and they lack ab-stractions of features,while Sterrett(S.Ster-rett,2002),Legg and Mutter(S.Legg and M. Hutter,2007)abstracted common features be-tween machine intelligence and universal in-telligence7.However,both Form1and Sr-errett have not fully accepted or put forward Gregory爷s definition that野intelligence is to select冶8.In definitions of different items, Legg and Hutter pointed out that agent was to put current input into memory for considera-tion to make next selection9.Therefore,Legg and Hutter accepted Gregory爷s viewpoint by and large.Therefore,we can accept the viewpoints of Gregory,Legg and Hutter,and abstract the definitions of AI in Form1as well as ma-chine intelligence actions put forward by Gre-gory so that we can have a concise(universal) definition of野intelligence冶that can be used both in the fields of human beings and ma-chines---野intelligence is to select冶(the base of the ability of selecting,of course,is a kind of野intentionality冶that having goals,which is the ability of achieving goals mentioned by Russell and Norving).That is essential ab-straction and concise expression of common features of the definitions of野intelligence冶(of both living objects and non-living ob-jects).In consideration of the common features of both human beings and machines,it is the dream of human beings to make machines in-telligent,and Turing machine is the mechani-cal implementation of that dream.There were some intelligent machines in history.For ex-ample,by finishing calculating,an abacus will have intelligence to some extent,so do mechanical computers(like the ones invented by Charles Babbage).However,those are all living examples of the implementation of in-telligence,not the universal models of me-chanical implementation of intelligence, which are the models that can depict all the theories(expressions)of mechanical imple-mentation of intelligence.In the papers of Intelligent Machinery10 and Computing Machinery and Intelligence11, A.M.Turing put forward an ideal that ma-chines could have the intelligence owned by80human beings.Although Turing admitted that Turing machine,as a model to implement in-telligence,designed by himself has some un-solvable problems(like paradoxes,Hilbert's tenth problem,etc.),those problems are also unsolvable for humans from the viewpoint of this paper(if people can solve those Turing爷s unsolvable problems by means of paradox solving,such as axiomatic set theory,com-puters,of course,can also solve those prob-lems by those means).Therefore,Turing ma-chine has provided mechanical methods of in-telligence implementation for dealing with discrete variable at least.A Turing machine(M)is a6-tuple:12M=<Q袁∑袁Г袁δ袁q0袁F>In which:Q:finite state set,like q1~q7in Form2.∑:inputted alphabet,like1,0in Form2 (exclude the symbol B that indicates blank space).Г:alphabet carried by the data,like B,1,0in Form2(include the symbol B that indi-cates blank space),∑(Г.δ:transfer function,like the function of the instruction set of(Q-F)×Г(Q×Г×{ L,R,S}in Form2;L,R,S respectively indi-cates left,right and stop.q0:original state,like q1,q0(Q in Form 2.F:stopped state,F(Q,Accept(F,Reject( F;(Q-F)indicates various states that won爷t appear in F before(so that F should be delet-ed.Accept:accepted state,one of the final states(as for the final character of the in-putted character string),which indicates the Turing machine accept the character string.Reject:rejected state,one of the final states(as for the final character of the in-putted character string),which indicates the Turing machine reject the character string.Accept≠Reject↓controllerWhy the operation of Turing machine isintelligent?Because its core mechanism fitsthe definition of intelligence---selecting.Themachine behavior of the read-write head ofTuring machine is completely determined byδ(transfer function),whileδ(transfer func-tion)is absolutely a selection.As shown inForm2(which takes Y=f(x)=2x as an ex-ample),all input for the data type is B(blankspace),0(character)and1(character).Thatmeans the environmental agent will make aselection under every circumstances,the re-sult of every selection(which indicates char-acter,left-right direction and the next state)will be shown in the Form,like(1,L,q7),and the selected terminal state is the comput-ed result of the function(the written result willbe arranged as character strings that droppedvertically).Therefore,the transfer function ofTuring machine abstracts the selection of en-vironment.The computed result of Turingmachine爷s transfer function fits the function爷s computing expectation,which is equal tothe realization of the goal(which amounts tohumans爷intentionality)mentioned by Gre-gory,Sterrett,Legg and Hutter.The Development of Ideas on Computable Intelligence81Journal of Human Cognition Vol.1No.1Why Turing machine is the model of ev-ery intelligent processing unit (IPU)of dis-crete variable and why we say Turing ma-chine is the model of all mechanical intelli-gence?There are 3reasons for those ques-tions:1.Turing machine 爷s behavior---move,stop,read(input)or write(output)---has highly general characteristics;it imitates all the cer-tain behavior (action)patterns of both organ-isms and machines;2.The essence of Turing machine is to reach the expected targets by selecting;and its sample space of selection and targets is large enough to cover the infor-mation abstraction of organisms and other physical worlds;3.Turing 爷s model (Turing machine)has mechanical realizability---effec-tiveness.Therefore,Turing machine becomes the universal intelligent model for the opera-tional mechanism of both organisms and ma-chines.Turing machine,so to speak,is the product of the ideological trend of mathemat-ical mechanization,and then is the expression of the reductive property ofintelligence.As a mechanical computing device,what is the mathematical model of Turing ma-chine 爷s transfer function.In essence,that is the question of the mathematical expression of models of intelligence,which is the ques-tion of the expression of the computability of intelligence.The computability of Turing machine,in fact,is the mechanical depiction of mathe-matics,which indicates whether it is possible to mechanically depict and find mathematical solutions.On the other hand,the pure mathe-matical question of what kind of mathemati-cal function computed by mathematical com-putations that have already been implemented is more abstracted than the depiction of me-chanical devices.Before the birth of Turing machine,the discussion about solving problems by using mathematical functions had been conducting in the fields of philosophy and mathematics,and it began to intervene in the cross field be-tween mechanical computing and mechanical depicting from the field of pure mathematics.That is the discussion about algorithms.The discussion of the essence and implementation of algorithms is an essentially discussion of mathematical mechanization.The essential meaning of 野algorithms 冶is effectiveness,and effectiveness is mechanical,which means it can be achieved through simple(intuitive and operational)steps.82In1900,David Hilbert put forth a most influential list of23unsolved problems at the International Congress of Mathematicians in Paris and predicted that those problems would be solved by the end of the20th centu-ry.Hilbert爷s10th problems is野to find an al-gorithm to determine whether a given polyno-mial Diophantine equation with integer coef-ficients has an integer solution冶,which means whether there is an algorithm that can find an integer solution13P66of the equation:a1x1b1 +a2x2b2+噎噎+an xnbn=c(1).That problem is the algorithmic problem that can decide whether there is an solution of the e-quation,and in order to solve that problem, Turing designed Turing machine.However,what is the mathematical ex-pression for the ubiquitous algorithms?Is there a function that can express all Turing爷s computability?In fact,recursive function is exactly equivalent to Turing's computability.Hilbert firstly used the concept of野re-currence冶in190414P51-102.In1923,Skolem brought forward the idea of recursive func-tion15,and he proved the relations(regardless of infinite computation),such as addition, subtraction,multiplication and division,all belong to recursive function.Since1931, when Godel extended the definition of recur-sive function1617,野universal recursive func-tion冶(short for野recursive function冶)have combined constant function,successor func-tion and projection function(those three func-tions are called primitive recursive function),as well as functions produced by the com-pound or recursion of those three functions, together with minimum function into the range of野universal recursive function冶.Ac-cording to Godel爷s definition of野universal recursive function冶,the later discovered Ack-ermann function,whose recursive speed is more faster,also belongs to universal recur-sive function.Those functions mentioned above should be all the numerable discrete variable functions known so far18.Alonzo Church had studied functions since1930s.In April,1934,Church used野re-cursive冶instead of野definable冶in the propo-sition of his thesis and submitted it to the American Mathematical Society in order to demonstrate that Church爷s Thesis is an effec-tively computable function,which is equal to recursive function19.In his proposition, Church interpreted野recursive function冶as the野universal recursive function冶20defined by Godel.Stephen C.Kleene explained Tur-ing's thesis(the Church-Turing thesis)as野ev-ery number-theoretic function(a1,a2,...,an) for which there is an algorithm---which is in-tuitively computable(one sometimes says耶ef-fectively calculable爷)---is Turing Computer-able;that is,there is a Turing machine which computes it...冶.21According to the concept of universal re-cursive function defined by Godel,recursive function(universal recursive function)should include these recursive functions and logical relations as listed bellow(in Form.3):Form.3The Classification of Recursive Function2223The Development of Ideas on Computable Intelligence83Journal of Human Cognition Vol.1No.1Therefore,Turing machine,in fact,be-comes the implementation model of recursive function.Because the selection mechanism of Turing machine is the intelligent depiction of essential features,Turning Machine and its recursive function of mathematical model be-come the expression of computable intelli-gence.What is the core nature of computable intelligence?Based on the understanding mentioned above,if intelligence can be re-stored as Turing computing,the essence of the question is:what is the core nature of Turing computing?Moreover,the question is equal to figure out the core nature of re cursive function.The recursive function formed by the re-cursion of the primitive recursive function f can be found in simultaneity equations(2)(3) 24:n)(2)f)(3)The features of the equations爷solvingprocess are listed below:The computing of the recursive functioncan be solved by the known functions g andh;The variable of h is also computed bythe unknown numbers---put the computedresult of(2)into the third variable of h(as isshown in the circuitous arrow);In the first step of the computing of theunknown number y,y is equal to0,as shownin equation(2);besides,as shown in the twoturn-round arrows of(3),y could increaseprogressively and the computing of function fafter every progressive increasing could beconducted through野substituting back f stepby step冶.Thus it can be seen that the core natureof recursive computing is that:recursion is aresolving computation in space and adivisional computation in time.The resolving computation is reflected inthat f is solved through g and h,and thevariable of h is solved through f;thedivisional computation is reflected in that thefunction of y is increasing progressively andeach progressive increasing result will beused in solving the last computing result.Thatis the implementation of the universalmathematical expression of Turing machine爷s transfer function.It is because of the resolvingcomputation in space and the divisionalcomputation in time that recursive computingcan conduct the computations on all kinds ofdiscrete variable functions.That means forcomplicated functions that contains unknownfunctions or unknown quantities,recursivecomputing can resolve them into thecomputations of known functions;forunknown numbers,recursive computing canconduct the computations through graduallyapproaching the result started with the initialvalue.It is a computing idea that makingcomplicated computations into simple ones,and just because of that idea,recursivecomputing can conduct computations onvarious functions as long as they can beresolved and divided in the process ofcomputing.84The discussion and evaluationmentioned above demonstrates that thehistory of ideas on computable intelligencecan be expressed by the formulas as below:Intelligence=Organism intelligence=Machine intelligence=Universal intelligence=Turing machine=The implementation ofrecursive function=The implementation ofuniversal recursive functionObviously,that is a historical prospect ofthe theory of computationalism and strongartificial intelligence.The refutation of thetheory mainly comes from the two aspectslisted asbelow.One of the representatives is JohnSearle.He said,野what kind of fact fits yourstatement耶I am painful now?爷...If we wantto conduct the reduction in the ontology,theessential features of pain will be omitted.冶25Searle proved that AI had non-reductibility byvirtue of that viewpoint.But he failed toexplain what is omitted between computation(or AI)and野pain冶.As a matter of fact,somepeople do view the features of consciousnessas intelligence or human beings爷advancedintelligence.However,Ludwig Wittgensteinrefuted that claim.26On the question that 野whether stones will feel painful or not冶,he had made some implicit answers,whichmeant that machines could have those kindsof feelings.In modern practices,people usephysical circuits to imitate the physical stateof sympathetic nerves.27This paper suggeststhat if the pain do not exceed the range ofphysical laws(which means to observephysical laws),it will be physical,whichindicates that the pain could be imitated orduplicated by physical quantities;in otherwords,the pain could be reproduced(althoughit may be have some discrepanciesindividually,it do not prevent researchersfrom reproducing that phenomenon and itsessence).Another tendency,which is unacceptable in this paper,is to propose that we should regard all low-level consciousnesses that do not belong to the rational,like emotion,feeling,potential consciousness and subconsciousness,as intelligence.The common sense in the fields of psychology and medical science is that not every consciousness is intelligence.We can divide consciousnesses into intelligence factors and non-intelligence factors.Emotion, feeling,potential consciousness, subconsciousness as well as emotional quotient(EQ),etc.should belong to non-intelligence factors.We can not deny machines爷having intelligence just because we believe machines do not own those features at present or in the future.In other words,even though machines are not able to completely conduct the reduction of some non-intelligence factors,such as experience and feelings,their intelligent features are stillundeniable.At themachine,incomputable functions and unsolvable problems had already been found. Turing made two examples of the problem of the test of the algorithm of Diophantine equation and the problem of the test of Godel's incompleteness theorems.Up to now, part of the content of Turing爷s incomputability has been discovered. Although Turing爷s incomputability has been proved,this paper believes that there is no certain answers for Turing爷s two examples of questions mentioned above.Therefore,the existence of those problems can not refute Turing爷scomputability.If we admit that intelligence is physical, The Development of Ideas on Computable Intelligence85Journal of Human Cognition Vol.1No.1not binary,we should admit that intelligence can be made artificially or be imitated physically.That idea,after a century爷s development,has become the idea of strong artificial intelligence.The key point of that idea is that the essence of intelligence is a selective action,which is mechanical,that tends to system objectives.Therefore, intelligence can be depicted and computed by discrete functions,and the superficial features of that computation are recursive functions, which are equal to universal recursive functions.Up to now,the idea of strong artificial intelligence has been proved by many experiments and there is no sufficient reasons and proofs to refute that idea. Although Turing爷s computability has its own limits,there is no evidence can show that human beings爷intelligent actions surpass Turing爷scomputation.1.8.Rechard Gregory.Seeing intelligence Jean Khalfa edited.What is Intelligence[M].The Press Syndicate of the University of Cambridge,1994.2.3.Susan G Sterrett.Too many instincts: contrasting philosophical views on intelligence in human and non-human[J].Journal of Experimental &Theoretical Artificial Intelligence,2002,14(1).4.5.Stuart Russell,Peter Norvig,人工智能要要要一种现代方法[M].第二版.北京:人民邮电出版社, 2009.6.7.9.Shane Legg,Marcus Hutter.Universal Intelligence:A Definition of Machine Intelligence [J].Mind&Machines,2007,(17).10. A.M.Turing Intelligent Machinery.Mechanical Intelligence[M].Collected Works of A.M.Turing. North-Holland,1992.11. A.M.Turing Computing Machinery and Intelligence[C].Mechanical Intelligence.Collected Works of A.M.Turing.North-Holland,1992.12.Alan Turing.On Computable Numbers,with an application to the Entscheidungsproblem,Proceedings of the London Mathematical Society,42(1936--1937):230,231,262.13.希尔伯特.数学问题[M].李文林,袁向东编译.大连:大连理工大学出版社袁2009.14.Robin Gandy.The Confluence of Ideas in1936. The Universal Turing Machine/A Half-Century Survey,Springer-verlag[M].Wien New York,1994, 1995.15.Thoralf Skolem.The foundation of elementary arithmetic established by means of the recursion mode of thought,without the use of apparent variables ranging over infinite domains./From Frege to Godel//A Source Book in Mathematical Logic, 1879~1931.Havard University Press,1977:302-333.16.Kurt Godel.On Formally Undecidable Propositions of Principia Mathematica and Related System I.From Frege to Godel,Harvard University Press,pp.592-617.17.22.24.哥德尔.论叶数学原理曳及其相关系统的形式不可判定命题(I)张寅生译.张寅生.证明方法与理论[M].北京:国防工业出版社,2015.18.23.张寅生.计算理论解析[M].北京:清华大学出版社袁国防工业出版社袁2016.19.Alonzo Church.An Unsolvable Problem of Elementary Number Theory[J].American Journal of Mathematics,1936,58,(2).20.Robert putability and Recursion, Bulletin of Symbolic Logic/Volume2/Issue03 /September,1996.21.Stephen C.Kleene.Turing爷s Analysis of Computability,and Major Applications of It,The Universal Turing Machine/A Half-Century Survey, Springer-verlag,Wien New York,1994,1995:15-49.25.塞尔.心灵的再发现[M].北京:中国人民大学出版社,2005.26.维特根斯坦.哲学研究[M].北京:商务印书馆,1994.27.Pentti O Haikonen.Consciousness and Robot Sentience.(One of Serials on Machine Consciousness),World Scientific Publishing Co.Pte. Ltd.2012.28.Edna E.Reiter,Clayton Matthew Johnson:Lim-its of Computation,An Introduction to the Undicid-able and Interctable.CRC Press,2012.86。
A low-noise, low-power VCO

A Low-Noise,Low-Power VCO with AutomaticAmplitude Control for Wireless ApplicationsMihai A.Margarit,Joo Leong(Julian)Tham,Member,IEEE,Robert G.Meyer,Fellow,IEEE,and M.Jamal Deen,Senior Member,IEEE Abstract—Voltage-controlled oscillators(VCO’s)used inportable wireless communications applications,such as cellulartelephony,are required to achieve low phase-noise levels whileconsuming minimal power.This paper presents the designchallenges of a monolithic VCO with automatic amplitudecontrol,which operates in the300MHz to1.2GHz frequencyrange using different external resonators.The VCO phase-noiselevel is0106dBc/Hz at100-KHz offset from an800-MHzcarrier,and it consumes1.6mA from a2.7-V power supply.An extensive phase-noise analysis is employed for this VCOdesign in order to identify the most important noise sourcesin the circuit and tofind the optimum tradeoff between noiseperformance and power consumption.Index Terms—Phase noise,voltage-controlled oscillator(VCO),wireless applications.I.I NTRODUCTIONT HE remarkable growth in telecommunication systems,such as cellular telephony,demands continuous efforts to-ward the improvement of radio-frequency(RF)circuit perfor-mance at ever increasing levels of plete trans-ceiver solutions that integrate low-noise amplifiers(LNA’s),mixers,voltage-controlled oscillators(VCO’s),and transmitmodulators already exist.Moreover,the stringent noise andspurious emissions requirements for cellular communicationssystems,such as GSM,DCS,and PCS,need to be achievedwith even lower power-consumption levels.This paper describes the analysis and implementation ofa monolithic VCO with automatic amplitude control(AAC),which is part of a one-chip transceiver dedicated for dual-bandcellular systems[1].The VCO is capable of operating from300MHz to1.2GHz using different resonators.The measuredphase-noise level is(a)(b)Fig.1.(a)Simplified diagram of a voltage-controlled oscillator.(b)V oltage-controlled oscillator with damping resistor R s:has negligible effect on the fundamental mode[2].However,care needs to be taken in the design,since too large a valueoffor the differential amplifier in order to maintain constantMARGARIT et al.:LOW-NOISE,LOW-POWER VCO763Fig.2.Schematic of the VCO with AAC.gain.for minimum phase-noise levels largely independent of considerations for proper oscillation startup. In steady-state operation,the AAC loop forces the dc signal provided by the rectifier and the low-passfilter at the sensing input to track the reference level applied at the reference input.This leads to the second advantage of using the AAC circuit of enabling the VCO to provide constant output power independent of theresonator(3)Since the system is timevariant,and observation timein(3)with theequivalent noise source of each individual node,the phase-noise contribution of each node can be calculated[5].To explore the oscillator excess phase response,each nodeof the circuit needs to be excited at evenly distributed timesteps of the oscillation period.Due to thehighis an integer chosen such that the oscillation waveform hassettled before the next pulse is applied.The ramp generator isreset by thefirst positive-going zero crossing of the oscillation.The ramp is then compared in COMP2with a staircase voltage,which is incremented ateachis the number of pulses to be injected.In this way,pulses areinjected with a period equalto764IEEE JOURNAL OF SOLID-STATE CIRCUITS,VOL.34,NO.6,JUNE1999(a)(b)(c)Fig.3.(a)Sequence of pulses used to excite the oscillator.(b)Block diagram of the behavioral test generator.(c)VCO test points for phase sensitivity to injectedcharge.Fig.4.Impulse shape.is almost constant from DC to 25GHz,which is sufficient for this design that uses a bipolar processwithCurrentsourcethe effect of thenoise voltage generatedbytheeffect of the resistive losses in theresonator(5)(6)The collector shot noise oftransistormA).Thecyclostationarityofis8.6MARGARIT et al.:LOW-NOISE,LOW-POWER VCO765Fig.5.Tail-current noise spectrum.(a)(b)Fig.6.(a)VCO output waveform.(b)Simulated function h8;I(t; )(vertical axis in degrees/pC).across the nodes“out”and“outb”(Fig.2),and it has thevaluefor current pulsesinjected at the tail of the emitter-coupled pair.This functionhas a periodicity that is half the oscillation period.To obtainmore meaningful information on the phase sensitivity forperturbations in the tail current of the VCO,the functionis plotted together with the oscillation outputwaveform.It can be seen that for perturbations injectedaround the zero crossings and the peaks of the oscillation,the phase sensitivity is close to zero and reaches its maxima766IEEE JOURNAL OF SOLID-STATE CIRCUITS,VOL.34,NO.6,JUNE1999Fig.7.Frequency spectrum of h 8;I (t; )(vertical axis in dBV).forwhereis shown in Fig.7.As expected,there areharmonics at multiples of double the oscillation frequency.The harmonics mix with the noise around these frequencies and contribute to the total phase noise.For calculation of the phase-noise contribution from the tail current,the Fourier coefficientsof[4]th harmonic of the oscillation fre-quency.In this analysis,the summation is performed over the first five harmonics.Higher order harmonics have insignificant contribution to the phase noise.Of particular interest is the dc component,coefficientregion of the phase noiseintersectstheis definedas(9)In the aboveequation,andhas a period equalto the oscillation period.Again,in order to see the effect of this noise source,the oscillation output waveform and the collector currentofreaches its maximum when the collector currentis close to the peak,and it reaches the minimumwhenin Fig.9show that thecollector shot noise is mixed mostly with the first and second harmonics of the oscillation frequency to contribute to the total phase noise.However,the collector shot noiseofwas performed.Todo this,theratioMARGARIT et al.:LOW-NOISE,LOW-POWER VCO767(a)(b)(c)Fig.8.(a)VCO output waveform.(b)Collector current of Q1.(c)Simulated functions h8;IIt768IEEE JOURNAL OF SOLID-STATE CIRCUITS,VOL.34,NO.6,JUNE 1999Fig.9.Frequency spectrum of h 8e (t; )(vertical axis in dBV).Fig.10.Phase noise (continuous line)and figure of merit (dashed line)versus feedback ratio n:TABLE IN OISE C ONTRIBUTIONS AT100-kHz O FFSET FROM AN 800-MHz C ARRIERAlthough the noise contribution from the tail current is not important at this offset frequency,it becomes the major noise source at offset frequencies less than 3kHz.The factor of two for some of the noise sources in Table I accounts for noise sources that are considered twice due to the circuit symmetry [5].The sum of these values gives a noise-to-signal ratio ofregion of the spectrum.SpectreRFpredicts a phase-noise level ofMARGARIT et al.:LOW-NOISE,LOW-POWER VCO769parison of the phase noise calculated with phase noise simulated in SpectreRF.Fig.12.Microphotograph of the VCO with AAC.However,the current version of SpectreRF did not predictthe43dBc and the third harmonic is106dBc/Hz at100-770IEEE JOURNAL OF SOLID-STATE CIRCUITS,VOL.34,NO.6,JUNE1999Fig.13.VCO outputspectrum.Fig.14.Measured phase noise.kHz offset for a carrier frequency of 800MHz,which is in agreement with the analysis presented in this paper (Fig.14).The VCO core consumes 1.6mA from a 2.7-V power supply.The remaining circuits used for the AAC (rectifier,voltage reference,and amplifier)consume 0.25mA.If better phase-noise performance is desired,only the current consumption inthe VCO core needs to be increased,while the consumption of the AAC circuits remains unchanged.V.C ONCLUSIONSIn this paper,the possibilities of developing a low-noise,low-power VCO with capabilities for wireless applicationsMARGARIT et al.:LOW-NOISE,LOW-POWER VCO 771have been explored.An automatic amplitude control circuit was implemented,which allows the choice of the optimum oscillator feedback ratio for noise performance without being constrained by startup considerations.At the same time,the automatic amplitude control allows proper VCO operation for a wide range of the resonator quality factor.A novel method was used to study the phase-noise performance of the VCO.The method predicts results that are close to the measurements and allows the designer to obtain detailed information about the processes that contribute to oscillator phase noise.A CKNOWLEDGMENTThe authors would like to thank Dr.C.Hull and R.Magoon for helpful discussions.R EFERENCES[1]J.L.Tham,M.Margarit,B.Pregardier, C.Hull,and F.Carr,“A2.7V 900MHz/1.9GHz dual-band transceiver IC for digital wireless communication,”in Proc.CICC ,1998,p.559.[2]J.L.Tham,“Integrated radio frequency LC voltage-controlled oscil-lators,”College of Engineering,University of California,Berkeley,Electronics Research Laboratory Memo.,1995.[3]P.Davis,P.Smith,E.Campbell,J.Lin,K.Gross,G.Bath,Y.Low,M.Lau,Y.Degani,J.Gregus,R.Frye,and K.Tai,“Si-on-Si integration of a GSM transceiver with VCO resonator,”in Proc.ISSCC 1998,vol.41,Feb.1998,p.248.[4] A.Hajimiri and T.H.Lee,“A general theory of phase noise in electricaloscillators,”IEEE J.Solid-State Circuits ,vol.33,pp.179–194,Feb.1998.[5] C.D.Hull and R.G.Meyer,“A systematic approach to the analysisof noise in mixers,”IEEE Trans.Circuits Syst.I ,vol.40,pp.909–919,Dec.1993.Mihai A.Margarit received the Dipl.Ing.degree in electrical engineering from the “Politehnica”Uni-versity Bucharest,Romania,in 1984.He currently is pursuing the Ph.D.degree in electrical engineering at Simon Fraser University,Burnaby,B.C.,Canada.Since 1984,he has worked in analog circuit design for the National Institute for Microelectron-ics,Bucharest,the Fraunhofer Institute,Erlangen,Germany,and Simon Fraser University,Vancouver,Canada.He is currently with Rockwell Semicon-ductor Systems,Newport Beach,CA,where he isa Senior Design Engineer working on high-frequency circuits for wireless communicationapplications.Joo Leong (Julian)Tham (S’88–M’96)received the B.S.degree in electrical engineering (with high-est honors)from the University of California,Santa Barbara,and the M.S.degree in electrical engineer-ing from the University of California,Berkeley.He has worked at Raytheon and Trimble Navi-gation.His previous work includes autocalibration systems and global positioning system receivers.From 1993to 1999,he was with Rockwell Semi-conductor Systems,Newport Beach,CA,where he was a Principal Design Engineer and Managerworking on radio-frequency integrated circuits for wireless communication applications.He currently is with Maxim Integrated Products,Sunnyvale,CA.His current interests are in the areas of high-frequency circuit design and integrated transceiver architectures.Mr.Tham is a member of Eta Kappa Nu,Tau Beta Pi,and the Golden Key Honor Society.He was named Rockwell Semiconductor Systems Engineer of the Year in1995.Robert G.Meyer (S’64–M’68–SM’74–F’81)was born in Melbourne,Australia,on July 21,1942.He received the B.E.,M.Eng.Sci.,and Ph.D.degrees in electrical engineering from the University of Melbourne in 1963,1965,and 1968,respectively.In 1968,he was an Assistant Lecturer in electrical engineering at the University of Melbourne.Since September 1968,he has been with the Department of Electrical Engineering and Computer Sciences,University of California,Berkeley,where he is now a Professor.His current research interests are high-frequency analog integrated-circuit design and device fabrication.He has been a Consultant on electronic circuit design for numerous companies in the electronics industry.He is a coauthor of Analysis and Design of Analog Integrated Circuits (New York:Wiley,1993)and Editor of Integrated Circuit Operational Amplifiers (New York:IEEE Press,1978).Dr.Meyer was President of the IEEE Solid-State Circuits Council and was an Associate Editor of the IEEE J OURNAL OF S OLID -S TATE C IRCUITS and of the IEEE T RANSACTIONS ON C IRCUITS AND S YSTEMS.M.Jamal Deen (S’81–M’86–SM’92)was born in Georgetown,Guyana.He received the B.Sc.degree in physics and mathematics from the University of Guyana in 1978and the M.S.and Ph.D.degrees in electrical engineering and applied physics from Case Western Reserve University,Cleveland,OH,in 1982and 1985,respectively.From 1978to 1980,he was an Instructor of physics at the University of Guyana.From 1980to 1983,he was a Research Assistant at Case Western Reserve University.He was a Research Engineer(1983–1985)and an Assistant Professor (1985–1986)at Lehigh University,Bethlehem,PA.In 1986,he joined the School of Engineering Science,Simon Fraser University,Vancouver,BC,Canada,as an Assistant Professor and since 1993has been a full Professor.He was a Visiting Scientist at the Herzberg Institute of Astrophysics,National Research Council,Ottawa,Ont.,Canada,in summer 1986,and he spent his sabbatical leave as a Visiting Scientist at Northern Telecom,Ottawa,in 1992–1993.He was also a Guest Professor in the Faculty of Electrical Engineering,Delft University of Technology,The Netherlands,in summer 1997and a CNRS scientist at the Physics of Semiconductor Devices Laboratory,Grenoble,France,in summer 1998.His current research interests include integrated devices and circuits;device physics,modeling,and characterization;and low-power,low-noise,high-frequency circuits.Dr.Deen is a member of Eta Kappa Nu,the American Physical Society,and the Electrochemical Society.He was a Fulbright-Laspau Scholar from 1980to 1982,an American Vacuum Society Scholar from 1983to 1984,and an NSERC Senior Industrial Fellow in 1993.。
2024年英文论文参考文献

2024年英文论文参考文献
英文论文参考文献 1
[1] J.F.Di Marzio.Android A Progammer's Guide.New York Mc-Graw-Hill,2008:105-111P
[2] Thompson T.The Android Mobile Phone Platform.The World of SoftwareDevelopment,2008,33(9):40-47P
[22]Corbett, C., Blackburn, J. and van Wassenhove, L. (1999), “Partnerships to improve supply chains”, MIT Sloan Management Review, Vol. 40 No. 4, pp. 71-82.
[24]Croom, S., Romano, P. and Giannakis, M. (2000), “Supply chain management: an analyticalframework for critical literature review”, European Journal of Purchasing Supply Management, Vol. 6, pp. 67-83.
International Journal of Electrical Power & Energy Systems

Integrating agroecology and landscape multifunctionality in Vermont: An evolving86Agricultural Systems, Volume 103, Issue 5, June 2010, Pages 327-341Sarah Taylor Lovell, S’ra DeSantis, Chloe A. Nathan, Meryl Breton Olson, V.Ernesto Méndez, Hisashi C. Kominami, Daniel L. Erickson, Katlyn S. Morris,William B. MorrisClose preview | Purchase PDF (1589 K) | Related articles | Related reference work articlesAbstract | Figures/Tables | ReferencesAbstractAgroecosystems cover vast areas of land worldwide and are known to have a large impacton the environment, yet these highly modified landscapes are rarely considered ascandidates for landscape design. While intentionally-designed agricultural landscapes couldserve many different functions, few resources exist for evaluating the design of thesecomplex landscapes, particularly at the scale of the whole-farm. The objective of this paper isto introduce an evolving framework for evaluating the design of agroecosystems based on acritical review of the literature on landscape multifunctionality and agroecology. We considerhow agroecosystems might be designed to incorporate additional functions while adhering toagroecology principles for managing the landscape. The framework includes an assessmenttool for evaluating farm design based on the extent of fine-scale land use features and theirspecific functions, to consider the present state of the farm, to plan for future conditions, or tocompare alternative futures for the design of the farm. We apply this framework to two farmsin Vermont that are recognized locally as successful, multifunctional landscapes. TheIntervale Center, an agricultural landscape located within the city limits, serves as anincubator for new farm startups and provides unique cultural functions that benefit the localcommunity. Butterworks Farm, a private operation producing organic yogurt and other foodproducts, achieves important ecological functions through an integrated crop-livestocksystem. These farms and many others in Vermont serve as models of a framework that integrates landscape multifunctionality and agroecology in the design of the landscape. In the discussion section, we draw from the literature and our work to propose a set of important themes that might be considered for future research.Article Outline1. Introduction2. Literature review2.1. Agroecology2.2. Landscape multifunctionality3. Framework for designing agroecosystems4. Methods4.1. Study site4.2. Semi-structured interviews4.3. Agroecosystem design assessment tool5. Results5.1. Regional characterization and context of Vermont agricultural landscape5.2. Case study 1: the Intervale5.2.1. Overview and site history5.2.2. Production functions5.2.3. Ecological functions5.2.4. Cultural functions5.2.5. Multifunctional landscape assessment5.3. Case study 2: Butterworks Farm5.3.1. Overview and site history5.3.2. Production functions5.3.3. Ecological functions5.3.4. Cultural functions5.3.5. Multifunctional landscape assessment6. Discussion6.1. Study limitations6.2. Future research6.3. Emerging themes6.3.1. Theme 1: policy-driven versus grass-roots initiatives6.3.2. Theme 2: assessment methods and tools6.3.3. Theme 3: synergies and integration of functions6.3.4. Theme 4: geography of agricultural systems6.3.5. Theme 5: alternative farm types7. ConclusionAcknowledgementsReferencesPlanning production on a single processor with sequence-dependent setups part 1:87Computers & Chemical Engineering, Volume 25, Issues 7-8, 15 August 2001,Pages 1021-1030Hong-Choon Oh, I. A. KarimiClose preview | Purchase PDF (154 K) | Related articles | Related reference work articlesAbstractAbstractProduction planning of processors located within in a facility or distributed across facilities isa routine and crucial industrial activity. So far, most attempts at this have treated planninghorizon as a decision variable, and have limited their scope to sequence-independentsetups. In this two-part paper, we present a new and improved methodology for solving thesingle machine economic lot scheduling problem (ELSP) with sequence-dependent setupsand a given planning horizon. We decompose the entire complex problem into twosubproblems; one involving lot sizing and the other involving lot sequencing and scheduling.In this part, we present a novel mixed integer nonlinear programming (MINLP) formulation forthe lot-sizing problem. Using a multi-segment separable programming approach, wetransform this MINLP into a MILP and propose one rigorous and two heuristic algorithms forthe latter. Based on a thorough numerical evaluation using randomly simulated largeproblems, we find that our best heuristic gives solutions within 0.01% of the optimal on anaverage and in much less time than the optimal algorithm. Furthermore, it works equally wellon problems with sequence-independent setups. Overall, our methodology is well suited forreal-life large-scale industrial problems.Advances in genetically engineered (transgenic) plants in pest management—an88Crop Protection, Volume 22, Issue 9, November 2003, Pages 1071-1086R. Mohan Babu, A. Sajeena, K. Seetharaman, M. S. ReddyClose preview | Purchase PDF (369 K) | Related articles | Related reference work articlesAbstract | Figures/Tables | ReferencesAbstractTransgenic plants are produced via Agrobacterium mediated transformation and other directDNA transfer methods. A number of transgenes conferring resistance to insects, diseasesand herbicide tolerance have been transferred into crop plants from a wide range of plantand bacterial systems. In the majority of the cases, the genes showing expression intransgenic plants are stably inherited into the progeny without detrimental effects on therecipient plant. More interestingly, transgenic plants under field conditions have alsomaintained increased levels of insect resistance. Now, transgenic crops occupy 44.2 millionhectares on global basis. During the last 15 years, transformations have been produced inmore than 100 plant species; notable examples include maize, wheat, soybean, tomato,potato, cotton, rice, etc. Amongst these herbicide tolerant and insect tolerant cotton, maizeand soybean carrying Bacillus thuringiensis(Bt) genes are grown on a commercial scale.Genetic transformation and gene transfer are routine in many laboratories. However,isolation of useful genes and their expression to the desired level to control insect pests stillinvolves considerable experimentation and resources. Developing pest resistant varieties byinsertion of a few or single specific gene(s) is becoming an important component of breeding. Use of endotoxin genes such as Bt and plant derived genes (proteinase inhibitors) to the desired levels offers new opportunities to control insects and strategies involving combination of genes. Transgenic technology should be integrated in a total system approach for ecologically friendly and sustainable pest management. Issues related to Intellectual property rights, regulatory concerns, and public perceptions for release of transgenics need to be considered. Providing wealth of information on gene expression in higher plants by switching the gene on and off as and when required, makes gene manipulation a more direct process for genetic improvement of crops.Article Outline1. Introduction2. Methods for producing transgenic plants2.1. Agrobacterium-mediated gene transfer2.2. Direct gene transfer2.3. Polyethylene glycol (PEG) mediated gene transfer2.4. Electroporation2.5. Microinjection2.6. Microprojectile bombardment2.7. Approaches for developing genetically engineered plants resistant to insects2.8. Bacillus thruingiensis (Bt) genes2.9. Genetic manipulation of Bt2.10. Plasmid curing and conjugal transfer2.11. Recombinant DNA technology2.12. Field trial testing of Bt crops2.13. Plant derived genes2.14. Proteinase inhibitor genes2.15. α-Amylase inhibitor genes2.16. Lectin genes2.17. Other novel genes2.18. Gene pyramiding (combination of multiple gene effect)2.19. Commercialized transgenic crops3. ConclusionReferences89Master plan for water framework directive activities in Ireland leading to River Basin Management Plans Original Research ArticleDesalination, Volume 226, Issues 1-3, 25 June 2008, Pages 134-142Ray Earle, Sean BlacklockeClose preview | Purchase PDF (621 K) | Related articles | Related reference work articlesAbstractAbstractThe water framework directive master plan (WFDMP) in Ireland is being developed jointly by the Department of the Environment, Heritage and Local Government (DEHLG), the Environmental Protection Agency (EPA), the River Basin District (RBD) competent authorities (namely lead Local Authorities) and stakeholders including the relevant public authorities. The WFDMP was recently adopted by the National Technical Coordination Group (NTCG) and has been uploaded onto the website (www.wfdireland.ie) as the fundamental document coordinating WFD related activities in Ireland leading to the River Basin Management Plans (RBMP). There are eight River Basin Districts (RBD) covering the entire island of Ireland and accordingly there will be eight River Basin Management Plans (RBMP). Key elements of the new ecological approach to adaptive management of water resources are in focus namely public participation and integrated water resources planning.The WFDMP sets out the overall work plan required to meet the Republic of Ireland’s obligations under the WFD and associated national Water Policy Regulations (SI No. 722 of 2003) which transposed the WFD into Irish law and very close co-operation with the UK authorities is essential to ensure harmonization for three of the RBDs that straddle the border with Northern Ireland (NI) with one RBD being entirely within NI. Having successfullycompleted Article 3 (designate RBD areas and Competent Authorities), 5 (Characterisation)and 6 (Register of Protected Areas) requirements, the following prerequisite deadlines andmilestones lie ahead leading to the production of the first River Basin Management Plans(RBMP) in 2009: (a) classification systems (including EQS for priority substances), (b)programme of monitoring, (c) timetable and work programme for production of RBMP, (d)Overview of the significant water management issues (SWMI) in RBDs (for purpose of publicinformation and consultation), (e) draft RBMP, (f) environmental objectives, (g) programmeof measures and (h) RBMPs.The paper will address the above milestones in detail and report on and provide a snapshotof Ireland’s position in implementing the WFD.Alleviating piracy through open source strategy: An exploratory study of business90The Journal of Strategic Information Systems, Volume 18, Issue 4, December2009, Pages 165-177T. Pykäläinen, D. Yang, T. FangClose preview | Purchase PDF (222 K) | Related articles | Related reference work articlesAbstract | Figures/Tables | ReferencesAbstractThis paper advances the existing knowledge of anti-piracy strategies by proposing an opensource strategy (OS strategy) to alleviate software piracy based on a qualitative,case-based, exploratory study of eight software firms operating in China. The paper showsthat the OS strategy is conditionally adoptable, depending on how users are willing to pay forservices (market conditions); how critical and complex software is required for upgrading andmodifications (software conditions); and how firms can avoid resources overloading and/orshortage (firm conditions). The paper also identifies several new indicators to assess theeffectiveness of the OS strategy against piracy. Managerial implications about how toimprove business in piracy-ridden environment are discussed.Article Outline1. Introduction2. Strategies against piracy2.1. Existing strategies against piracy and strategic effectiveness2.2. Open source strategy (OS strategy)3. Methodology3.1. Research design and sample characteristics3.2. Interview question, pre-test, and data collection3.3. Analysis methods3.4. Reliability and validity4. Findings4.1. Firms description4.2. Feasibility of OS strategy against piracy and conditions for effectiveness4.3. Indicators of the OS strategy’s effectiveness against piracy5. Discussions and conclusions5.1. Discussions5.2. Research contribution5.3. Implications for practice5.4. Limitations and directions for future researchReferences91Merging the acquisitions and serials department at the University of New Mexico: acase study Original Research ArticleLibrary Acquisitions: Practice & Theory, Volume 22, Issue 3, Autumn 1998,Pages 259-270Sever Bordeianu, Linda K. Lewis, Frances C. WilkinsonShow preview | Purchase PDF (59 K) | Related articles | Related reference work articles92Spatial analysis of recreational boating as a first key step for marine spatial planning in Mallorca (Balearic Islands, Spain)Original Research ArticleOcean & Coastal Management, Volume 54, Issue 3, March 2011, Pages241-249P. Balaguer, A. Diedrich, R. Sardá, M. Fuster, B. Cañellas, J. TintoréShow preview | Purchase PDF (991 K) | Related articles | Related reference work articlesResearch highlights►This paper provides an approximation of the capacity of the coastal zones (seabeds available for anchoring). ► The results can be a decision tool for the proper management of the coastal zone. ► The work is based on the use of GIS (Geographic Information Systems). ► The developed method is applicable to any coastal area and is considered useful for the future management.Monitoring the commitment and child-friendliness of governments: A new approach93Child Abuse & Neglect, Volume 34, Issue 1, January 2010, Pages 34-44Assefa BequeleShow preview | Purchase PDF (1599 K) | Related articles | Related reference work articlesPrediction of global solar irradiance based on time series analysis: Application to94ArticleSolar Energy, Volume 84, Issue 10, October 2010, Pages 1772-1781Luis Martín, Luis F. Zarzalejo, Jesús Polo, Ana Navarro, Ruth Marchante,Marco ConyShow preview | Purchase PDF (702 K) | Related articles | Related reference work articles你为企业“冲锋陷阵”还是“救险解围”?2010年的南非世界杯赛渐入佳境,各支幸存的球队即将在通向大力神杯的道路上展开最后冲刺,比赛正日趋于白热化。
Encyclopedia of Integer Sequences (or OEIS). The

The On-Line Encyclopedia of Integer SequencesN. J. A. SloaneThis article gives a brief introduction to the On-Line Encyclopedia of Integer Sequences (or OEIS). The OEIS is a database of nearly 90,000sequences of integers, arranged lexicographically. The entry for a sequence lists the initial terms (50 to 100, if avail-able), a description, formulae, programs to gener-ate the sequence, references, links to relevant web pages, and other information.To Consult the DatabaseSince 1996 an electronic version [20] has been ac-cessible via the Internet at the URL http://www. /~njas/sequences/. If a list of numbers is entered there, the reply will display the entries for all matching sequences.For example, suppose you were trying to count the ways to insert parentheses into a string of n letters so that the parentheses are balanced and there are at least two letters inside each pair of parentheses. The outer pair of parentheses is to be ignored. For n=3and 4 there are respectively 3 and 11 possibilities:n=3:abc,(ab)c,a(bc);n=4:abcd,(ab)cd,a(bc)d,ab(cd),(ab)(cd),(abc)d,a(bcd),((ab)c)d,(a(bc))d,a((bc)d),a(b(cd)).Further work shows that for n=1,...,5the num-bers are 1, 1, 3, 11, 45. Entering these into the web page produces nine matching sequences, but they are sorted, with the most probable match appear-ing first. Indeed, this entry tells you that these are the numbers (sequence A1003) arising from “Schröder’s second problem” and are also known as “super-Catalan numbers”.The reply (an abridged version is shown in Fig-ure 1) gives 21 references, ranging from Schröder (1870) [17] to articles published electronically in the last few years. There is an explicit formula:a(n)=1nn−2k=02n−k−2n−1n−2k,n>1;a recurrence:(n+1)a(n+1)=3(2n−1)a(n)−(n−2)a(n−1) when n>1,and a(1)=a(2)=1;programs to produce the sequence in Maple and Mathematica; and much more.There is no other reference work that will carry out this kind of search.The Encyclopedia can also be consulted via email. There are two addresses. Sending email to sequences@ with a line in the body of the message sayinglookup1131145will trigger the same search that the web page per-forms, only now the results are sent, almost im-mediately, via email. Superseeker (superseeker@ ) carries out a more sophisti-cated analysis and tries hard to find an explana-tion for the sequence, even if it is not in the data-base. If the simple lookup fails, Superseeker carries out many other tests, including:•applying over 130 transformations to the se-quence, including the binomial, Euler, Möbius, etc., transforms [1], and checking to see if the result is in the database;•applying Padé approximation methods to try, for example, to express the n th term as a rational function of n(using the “gfun” package of Salvy and Zimmermann [16], the “guesss” program ofNeil J. A. Sloane is with AT&T Shannon Labs, Florham Park, NJ. His email address is njas@.Derksen [6], and the “RATE” program of Krat-tenthaler [8]);•checking to see if changing one or two charac-ters produces a sequence in the database. Since Superseeker carries out a nontrivial amount of calculation, users are asked to submit only one sequence per hour.The electronic version of the Encyclopedia had its origins in the books [18] (1973) and [21] (1995). Disk space is cheap, and the present incarnation (excluding illustrations) contains about 72times as much data as the 1995 book. The history of the En-cyclopedia is described in more detail in [19].ApplicationsMost people use the Encyclopedia to identify a se-quence, as illustrated above. It has been around long enough that there is a good chance that your se-quence will be there. If not, you will see a message encouraging you to submit it.Most of these applications are unspectacular, akin to looking up a word in a dictionary (cf.[2]). One encounters a sequence in the middle of a cal-culation, perhaps124610121618222830… ,and one wants to know quickly what it is—prefer-ably a formula for the n-th term (in this case it is probably prime(n)−1, A6093) or a recurrence. Suc-cessful applications of this type usually go unre-marked. Some are more dramatic: there is a web page1that lists several hundred articles that ac-knowledge help from the OEIS. One quotation will serve to illustrate this. Emeric Deutsch of Poly-technic University, Brooklyn, said in a recent email message: “… your database is invaluable. For ex-ample, for a certain sequence a n, using Maple I found the first 100 or so indices i for which a i is odd. Only the OEIS could tell me that the sequence of these i’s is a known sequence related to the Thue-Morse sequence. Of course, this had to be fol-lowed by further reading and proof.”The other main application is to find out the current status of work on a problem, for example, the search for Mersenne primes (see A43), the enu-meration of Hadamard matrices (A7299), Latin squares (A315), or meanders (A5316), the latest in-formation about the decimal expansion of π(A796) or, better, its continued fraction expansion (A1203).Of course people trying to solve puzzles or in-telligence tests find the database useful. A5228is a classic:1371218263545566983… .There are also some less obvious applications. One is in simplifying complicated integer-valued expressions. You might, for example, have en-countered the sumnk=04n+12n−2kn+kk.There are powerful methods for evaluating such sums [12], [13], but it doesn’t take long to work out the first few terms: 1, 12, 240, 5376, and to look them up in the database. In this case you would have been lucky. The reply suggests that this is se-quence A6588, 4n3nn, and supplies, with refer-ences, the binomial coefficient identity you were hoping for.Another application is in proving inequalities. You might suspect that σ(n)<n√n for n>2, where σis the sum-of-divisors function (A203). If the initial terms of [n√n]−σ(n)(where []denotes the “floor” function) are submitted to the data-base, the reply suggests that this is A55682and points you to a reference that gives a proof of your inequality.1/~njas/sequences/ cite.html.Figure 1. Part of the reply when the sequence 1, 1, 3, 11, 45 is submitted to the On-Line Encyclopedia. Many references, links, and comments have been omitted to save space.I cannot resist mentioning sequence A57641,which gives the values ofH n +exp(H n )log(H n )−σ(n )for n ≥1, where H n is the harmonic number ni =11/i . Lagarias [9], extending earlier work of Robin [15], has shown that this sequence is non-negative if and only if the Riemann hypothesis holds!Although the database contains a number of sequences of both of the above types, I have not made a systematic search through reference works such as [7], [11], and it would be nice to get many more examples.The database can also be used to save space when referring to particular sequences. When in-troducing the Motzkin numbers, for example, in-stead of giving the definition, references, and the first few terms, it is simpler just to say “...the Motzkin numbers M n (sequence A1006of [20]).”One can also search the database for sequences that mention a particular name (Riemann, say),and there is a separate alphabetical index, useful for keeping track of all sequences on a certain topic—e.g., the entry for groups lists abelian (A688),primitive permutation (A19), transitive permutation (A2106), simple (A5180), total number (A1), and others.In the past year the main look-up page has been translated into twenty-eight languages, with the goal of making it easier to use throughout the world. The entries from the database still appear in English, but the headings in the replies and the error messages have also been translated.The DatabaseTo be included in the database a sequence should be integer valued, well defined, and interesting.The main sources are combinatorics, number theory, and recreational mathematics, but most branches of mathematics are represented (e.g.,A27623, the number of rings with n elements), and there are hundreds of entries from chemistry and physics (e.g., A8253, the coordination sequence for diamond: the number of carbon atoms that are n bonds away from a particular carbon atom).Sequences of rational numbers are entered as a linked pair giving numerators and denominators separately. The Bernoulli numbers B n form the pair A27641/A27642.Triangular arrays of numbers are read row-by-row, so that Pascal’s triangle gives A7318:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1, ….Square arrays are read by antidiagonals, so that the Nim-addition table012345...103254...230167...321076...............produces A3987:0,1,1,2,0,2,3,3,3,3,4,2,0,2,4,… .Most well-defined submissions get accepted,since an open-door policy seems the best. The amazing coincidences of the Monstrous Moonshine investigations [4], for example, make it difficult to say that a particular sequence, no matter how ob-scure, will never be of interest.Sequences that are discouraged are those that depend on an arbitrary and large parameter: primes of the form x 2+y 2+2003, say, whereas primes of the form x 2+y 2+1form a perfectly acceptable sequence (A79545).The Encyclopedia currently receives between 10,000and 12,000downloads per day. The rate of arrival of new sequences has remained constant at about 10,000per year for the past seven years,with roughly the same number of comments and updates. To keep this flood of information from get-ting out of control, people are asked to use a web form 2when submitting new sequences or com-ments.For most of its life the Encyclopedia has been maintained by the author, but in the past year a board of associate editors has been formed to help with the work. There is also a group of regular users who constantly send corrections and exten-sions and help maintain the accuracy of the entries.Even so, much remains to be done. There are more journals and e–print servers now than ever,and the trained eye sees integer sequences every-where. I still discover articles in the library or on the Web where authors have published sequences without sending them to the Encyclopedia. If you come across an integer sequence in your own work or elsewhere, please submit it to the Encyclopedia!Of course, accuracy is a major concern in main-taining the database. The entries in [18] and [21]were checked very thoroughly, and almost all the errors that have been discovered in those books were already present in the sources from which the sequences were taken. As the number of se-quences has increased in recent years, it has become more difficult to check them all. However, the num-ber of users has also increased, and a large num-ber of the entries carry a comment that the se-quence has been extended (or sometimes corrected and extended) by someone. Contributors see a re-minder that the standards are those of a2/~njas/sequences/Submit.html.mathematics reference work, and all submissions should be carefully checked. So, on the whole, users can be confident that the sequences are correct. The keywords “uned” and “obsc” indicate sequences that have not yet been edited or for which the de-finition is unclear. These serve both to warn users and to indicate places where volunteers can help.One of the pleasures of maintaining the database is seeing the endless flow of new sequences. I will end by mentioning a few recent examples: Home primes(A37274), [5]: a(n)is the prime reached when you start with n, concatenate its prime factors, and repeat until a prime is reached. (a(n)is defined to be −1if no prime is ever reached, although it is conjectured that this never happens). E.g., 8=2×2×2→222=2×3×37→2337=3×19×41→31941→···→(after13steps)3331113965338635107, a prime, so a(8)=3331113965338635107:123211523733311139653386351073117731122313....The EKG sequence(A64413), [10]: a(1)=1, a(2)=2, and, for n≥3, a(n)is the smallest natural number not in {a(k):1≤k≤n−1}with the prop-erty that gcd{a(n−1),a(n)}≥2:1246391281051518147212416202211….Lacing a shoe(A78601), [14]: Number of ways to lace a shoe that has n pairs of eyelets. The lace must follow a Hamiltonian path through the 2n eye-lets, and at least one of the neighbors of every eye-let must be on the other side of the shoe.1342108051840375840038283840052733721600....A “bootstrap” sequence(A79000), [3]: a(n)is taken to be the smallest positive integer greater than a(n−1)which is consistent with the assertion “n is a member of the sequence if and only if a(n) is odd.”1467891113151617181920212325272931….References[1]M. B ERNSTEIN and N. J. A. S LOANE, Some canonical se-quences of integers, Linear Alg. Appl.226–228(1995), 57–72; /abs/math.CO/ 0205301.[2]B. C IPRA, Mathematicians get an on-line fingerprintfile, Science265(22 July 1994), 473.[3]B.C LOITRE, N.J.A.S LOANE,and M.J.V ANDERMAST, Nu-merical analogues of Aronson’s sequence, J. Integer Sequences, to appear; / abs/math.NT/0305308.[4]J. H. C ONWAY and S. P. N ORTON, Monstrous moonshine,Bull. London Math. Soc.11(1979), 308–339.[5]P. D E G EEST, Home primes <100and beyond,published electronically at http://www./topic1.htm, 2003.[6]H. D ERKSEN, An algorithm to compute generalized Padé-Hermite forms, Report 9403, Dept. Math., Catholic Univ. Nijmegen, 1994, http://www.math.lsa./~hderksen/preprints/.[7]H. W. G OULD, Combinatorial Identities, Morgantown,WV, 1972.[8]C. K RATTENTHALER, RATE—A Mathematica guessingmachine, available electronically from http://euler.univ-lyon1.fr/home/kratt/rate/rate.html. [9]J. C. L AGARIAS, An elementary problem equivalent to theRiemann hypothesis, Amer. Math. Monthly109(2002), 534–543.[10] J. C. L AGARIAS, E. M. R AINS,and N. J. A. S LOANE, The EKGsequence, Experimental Math.11(2002), 437–446;/abs/math.NT/0204011.[11] D. S. M ITRINOVIC´, J. S ANDOR, and B. C RSTICI, Handbookof Number Theory, Kluwer, Dordrecht, 1996.[12] I. N EMES, M. P ETKOVSˇEK, H. S. W ILF, and D. Z EILBERGER, Howto do Monthly problems with your computer, Amer.Math. Monthly104(1997), 505–519.[13] M. P ETKOVSˇEK, H. S. W ILF, and D. Z EILBERGER, A=B,Peters, Wellesley, MA, 1996; http://www.cis./wilf/AeqB.html.[14] B. P OLSTER, What is the best way to lace your shoes?,Nature420(December5, 2002), 476.[15] G. R OBIN, Grandes valeurs de la fonction somme desdiviseurs et hypothèse de Riemann [Large values of the sum-of-divisors function and the Riemann hypothe-sis], J. Math. Pures Appl.63(1984), 187–213.[16] B. S ALVY and P. Z IMMERMANN, Gfun: A Maple packagefor the manipulation of generating and holonomic functions in one variable, ACM Trans. Math. Software 20(1994), 163–177; ftp://ftp.inria.fr/ INRIA/publication/publi-ps-gz/RT/RT-0143.ps.gz.[17] E. S CHRÖDER, Vier combinatorische Probleme [Fourcombinatorial problems], Z. Math. Phys.15(1870), 361–376.[18] N. J. A. S LOANE, A Handbook of Integer Sequences, Aca-demic Press, New York, 1973.[19] ———, My favorite integer sequences, Sequences andTheir Applications (Proceedings of SETA ’98), edited byC. Ding, T. Helleseth, and H. Niederreiter, Springer-Ver-lag, London, 1999, pp. 103–130; / abs/math.CO/0207175.[20] ———, The On-Line Encyclopedia of Integer Sequences,published electronically at http://www.research./~njas/sequences/, 2003.[21] N. J. A. S LOANE and S. P LOUFFE, The Encyclopedia of In-teger Sequences, Academic Press, 1995.。
integer的valueof的用法

integer的valueof的用法在编程中,我们常常需要处理整数。
在许多编程语言中,整数通常被表示为基本数据类型。
然而,这些整数类型可能并不总是能够满足我们的需求。
例如,如果我们需要处理非常大的整数,或者我们需要将浮点数转换为整数,那么我们需要使用一些特殊的函数或方法。
在许多编程语言中,包括Java、Python和JavaScript等,都有这样的方法。
在这些语言中,`Integer`类提供了一个名为`valueOf`的方法,用于将其他数据类型转换为整数。
`Integer`类的`valueOf`方法通常用于将字符串、数字、字节等数据类型转换为整数。
这个方法返回一个表示该值的`Integer`对象。
如果传递给该方法的参数无法转换为整数,那么将会抛出`NumberFormatException`异常。
二、使用示例下面是在Java中如何使用`Integer`类的`valueOf`方法的示例:```javaint num = 123;Integer integer = Integer.valueOf(num);System.out.println(integer); // 输出:123```在这个例子中,我们首先定义了一个整数变量`num`,然后使用`Integer.valueOf()`方法将其转换为`Integer`对象并赋值给变量`integer`。
最后,我们打印出这个对象,它实际上是一个整数。
三、使用场景使用`Integer`类的`valueOf`方法可以方便地将其他数据类型转换为整数。
这在处理大量数据时非常有用,尤其是当这些数据无法直接转换为整数时。
例如,在处理网络请求时,我们可能会从服务器接收一个字符串表示的数字。
相反,我们可以使用`Integer.valueOf()`方法将字符串转换为整数。
四、注意事项虽然使用`Integer.valueOf()`方法可以方便地将其他数据类型转换为整数,但有时候可能会出现问题。
植物生长和测量数据分析软件说明书

Package‘tgram’October14,2022Type PackageTitle Compute and Plot TracheidogramsVersion0.2-3Date2017-11-24Author Marcelino de la Cruz and Lucia DeSotoMaintainer Marcelino de la Cruz<**************************>DescriptionFunctions to compute and plot tracheidograms,as in De Soto et al.(2011)<doi:10.1139/x11-045>.Depends zooLicense GPL(>=2)LazyLoad yesNeedsCompilation noRepository CRANDate/Publication2017-11-2423:31:50UTCR topics documented:juniperus (2)standz.all (2)tgram (4)traq.profile (6)Index71juniperus Traqueid Measurements in Juniperus thuriferaDescriptionAn example of traqueid measurements to standarize with function tgram.Usagedata(juniperus)FormatA data frame with77observations on the following4variables.traqueidogram Numeric vector indicating the traqueidogram to which each measurement belongs lumen.wall A factor indicating if the measurement is lumen(l)or wall(w)order Position of the measurement in the ordered sequence within each traqueidogramwidth.um Width(micrometres)of each measurementExamplesdata(juniperus)cosa<-with(juniperus,standz.all(traq=width.um,series=traqueidogram,wl=lumen.wall,w.char="w",G=20))plot(cosa,type="l")standz.all Vaganov Normalized TracheidogramDescriptionThe function produces a normalized tracheidogram,i.e.a curve showing variations in cell param-eters as a function of the cell position within an annual ring,following the procedure of Vaganov (1990).Usagestandz.all(traq,series,wl=NULL,w.char=NULL,order=NULL,G=30)standz(tgl1,G=30)##S3method for class standz.allplot(x,which=NULL,...)Argumentstraq A vector with the ordered sequences of measurements for each tracheidogram.series A vector of indicator values(i.e.a factor)with each level indicating each unique tracheidogram.wl A vector indicating if the measurement is wall or lumen.w.char Character used in wl to indicate"wall".order Vector indicating the ordering of each measurement in each lumen or wall series within a tracheidogram.G Number of cells to get the original measurements normalized to.tgl1Vector with the ordered sequences of measurements of a single tracheidogram.x An object of class standz.all resulting from applying the standz.all function.which One of NULL,"w",or any other character.This produces the plot function to draw all the tracheidograms together,only the"wall"traqueidograms or only the"lumen"ones,respectively....Additional graphical parameters passed to link{plot}.Valuestandz returns a vector of length G with the normalized values.standz.all returns an object of class standz.all.Basically a list with the following elements:data.stdz A matrix with G columns and as many rows as unique wall and lumen tra-cheidograms were in the original data,each with the normalized values of eachtracheidogram.which.w Vector indicating which rows in data.stdz are"wall"tracheidograms.which.l Vector indicating which rows in data.stdz are"lumen"tracheidograms. Author(s)Marcelino de la Cruz Rot and Lucia DeSotoReferencesVaganov,E.A.1990.The tracheidogram method in tree-ring analysis and its application.In:CookE.R.,Kairiukstis L.A.,eds.Methods of dendrochronology:applications in the environmentalsciences.Kluwer Academic Publishers.Dordrecht,the Netherlands.pp.63-76.Examplesdata(juniperus)cosa<-with(juniperus,standz.all(traq=width.um,series=traqueidogram,wl=lumen.wall,w.char="w",G=20))plot(cosa,type="l")plot(cosa,type="l",which="w")plot(cosa,type="l",which="l",add=TRUE)standz(with(juniperus,width.um[traqueidogram==1&lumen.wall=="l"]),G=20)lines(1:20,standz(with(juniperus,width.um[traqueidogram==1&lumen.wall=="l"]),G=20),lwd=3)tgram Compute TracheidogramsDescriptionFunction to compute tracheidograms from microscopic measurements.Usagetgram(traq,val50=50,xlim=NULL,ylim=NULL,mw=1,plotit=TRUE)##S3method for class tgramplot(x,xlim=NULL,ylim=NULL,colores=c("red","green"),leyenda=c("lumen","double wall"),lwd=2,add=FALSE,traq.0=TRUE,bg.legend=NULL,...)Argumentstraq microscopic light profile.A vector with the light measurements or a data.frame or matrix with two columns.In this case,thefirst column contains pixel order(i.e.position along the x axis)and the second one contains the light(i.e."y")lectures.val50"y-value"at wich measurements should be made.mw integer.Width of the rolling window to smooth the original data.plotit logical.should the original data and the computed tracheidogram be drawn?xlim extent of the x-axis.A vector of length2.ylim extent of the y-axis.A vector of length2.x an object of class tgram,resulting from tgram function.colores a vector of length2,with the colors to draw the lumen and wall measurements, respectively.leyenda a vector of length2with the legend to appear in the plot.By default leyenda =c("lumen","double wall").lwd width of the lines in the legend.add logical.If TRUE,add to a current plot.traq.0logical.If TRUE,draw the original measurements.bg.legend background color for the legend....additional graphical parameters.DetailsThe purpouse of this fucntion is obtaining cell anatomical data from microscopic light measure-ments(see DeSoto et al.for details of data adquisition).The microscopic lectures arefirst smoothed with a rolling window(using function rollmean of package zoo,using the selected width mw.Then, the smoothed curve is"cut"at the treshold value val50and the distances among the intersection points are computed.This provides an ordered sequence of lumen diameters(LD)and double wall thikness(DWT)measurements.From this sequence some other anatomical measurements are com-puted.Radial cell wall thickness is computed as CWT[t]=1/2*(DWT[t]/2+DWT[t+1]/2).Tracheid diameter is computed as TD[t]=DWT[t]/2+LD[t]+DWT[t+1]/2.Valuetgram returns an object of class tgram,bassically a list withtraq original data.traq0if traq was a2column matrix,then traq0returns the same object.If traq wasa vector,traq0returns a two column matrix(first column with pixel positionand second with ligh lectures).cut.points two column matrix with the coordinates of the intersection of y=val50and the smoothed curve.what vector indicating if the computed distances are of lumen(1)or double wall(2).distances ordered sequence of the computed distances(both of lumen and double wall).LD ordered sequence of lumen diameters.DWT ordered sequence of double wall thickness.mw width of the rolling window employed to smooth the data.CWT ordered sequence of radial cell wall thikness’.TD ordered sequence of tracheid diameters.LD_CWT_ratio ordered sequence of LD/CWT ratio.Author(s)Marcelino de la Cruz Rot and Lucia DeSotoReferencesDeSoto,L.,De la Cruz,M.&Fonti,P.2011.Intra-annual pattern of tracheid size in the Mediter-ranean Juniperus thurifera as indicator for seasonal water stress.Canadian Journal of Forest Re-search41:1280-1294.6traq.profile Examplesdata(traq.profile)plot(tgram(traq.profile,mw=10),leyenda=c("lumen","double wall"),xlab="distance pixel",ylab="grey value",ylim=c(0,250),bg.legend="white")traq.profile Light Throughout a Microscopic Section of Juniperus WoodDescriptionA measurement of light intensity troughout a sequence of pixels in a microscopic section of Junipe-rus thurifera wood.Usagedata(traq.profile)FormatA data frame with883observations on the following2variables.X1Pixel position in the sequenceY1Light intensityExamplesdata(traq.profile)tgram(traq.profile,mw=10)Index∗datasetsjuniperus,2traq.profile,6∗manipstandz.all,2tgram,4∗smoothstandz.all,2tgram,4juniperus,2plot.standz.all(standz.all),2plot.tgram(tgram),4rollmean,5standz(standz.all),2standz.all,2tgram,4traq.profile,67。
上海大学新增核心期刊目录

上海大学新增核心期刊目录法学1 北大社会学学刊2 北大网络法学评论3 北方法学4 法律科学5 法学论坛6 法制与社会发展7 甘肃政法学院学报8 国家检察官学院学报9 互联网法律通讯10 环球法律评论11 经济社会学12 民商法研究13 南京大学法律评论14 清华社会学评论15 山东警察学院学报16 时代法学17 思想理论教育18 思想理论教育导刊19 思想政治教育20 云南法学21 政法丛刊22 知识产权法研究23 中国发明与专利24 中国社会研究25 中国司法26 中国刑事法杂志27 中央政法管理干部学院学报28 专利法研究29 转型与发展30 组织与制度文学1 安徽师范大学学报2 北方美术3 北京第二外语大学学报4 产品设计5 CG6 传媒7 DV @时代8 大舞台9 当代电视10 电视字幕·特技与动画11 电影12 雕塑13 东方丛刊14 杜甫研究学刊15 福建外语16 钢琴艺术17 古籍整理研究学刊18 广东外语外贸大学学报19 国画家20 国文化研究21 国学研究22 汉字文化23 河南大学学报24 湖北美术学院学报25 幻想26 建筑师27 今传媒28 景观设计29 剧作家30 满语研究31 美术大观32 美术学报33 美与时代34 美苑35 南方电视学刊36 泮溪传播学术论坛37 齐鲁艺苑38 山东师范大学学报39 山东外语教学40 山东艺术学院学报41 上海文化42 上海音乐学院学报43 设计44 设计新潮45 沈阳音乐学院学报46 世界传媒产业评论47 世界建筑导报48 世界文学评论49 市场观察50 视听界51 室内52 收藏家53 数码艺术54 天津美术学院学报55 天津外国语学院学报56 天津音乐学院学报57 外国文学研究动态58 外语艺术教育研究59 文献60 武汉音乐学院学报61 西安外国语学院学报62 西安音乐学院学报63 西北大学学报64 现代电影技术65 现代广告66 新美术67 新视觉艺术68 新闻采编69 新闻记者70 学术前沿71 学术研究72 艺术百家73 艺术科技74 艺术市场75 艺术探索76 艺术学丛刊77 艺苑——南艺学报78 音乐爱好者79 音乐生活80 音乐探索81 音乐天地82 音乐与表演——南京艺术学院学报83 英语研究84 语言科学85 语言文字学86 园林87 云南艺术学院学报88 中国报业89 中国藏学90 中国传媒报告91 中国典籍与文化92 中国广播电视93 中国广告94 中国美术研究95 中国诗学96 中国外语97 中国音乐教育98 中国园林99 中国韵文学刊100 中外军事影视101 正式出版的10万字以上的文学名著或有重大影响的理论著作的译作(仅限外语专业)历史学1 百年潮2 传统文化与现代化3 党的文献4 党史研究与教学5 档案与史学6 贵州文史丛刊7 军事历史8 上海党史与党建9 文化中国10 中共党史研究11 中国博物馆12 中国历史博物馆馆刊理学1 东北数学(英文版)2 Advances in Pure Mathematics (ISSN:2160-0368, 美国)3 Annals of Functional Analysis(ISSN:8752-2008, 伊朗)4 Bollettino dell'Unione Matematica Italiana(ISSN:1972-6724, 意大利)5 Computational Mathematics and modeling(ISSN:1046-283X, 施普林格出版社)6 Far East Journal of Mathematical Sciences (ISSN:0972-0871, 印度)7 复杂系统与复杂性科学8 化学分析计量9 International Journal of Pure and Applied Mathematics10 International Journal of Functional Informatics and Personalised Medicine11 International Journal of Mathematics and Mathematical Sciences(ISSN:0161-1712, 美国)12 International Journal of Nonlinear Science13 International Journal of Differential Equations(ISSN:1402-9251, 欣达维出版社)14 Journal for Algebra and Number Theory Academia (ISSN:0976-8475, 印度)15 Journal of Integer Sequences(ISSN:1530-7638, 加拿大)16 JP Journal of Algebra, Number Theory and Applications (ISSN:0972-5555,印度)17 理论数学(Pure Mathematics)(ISSN: 2160-7583, 美国)18 Pioneer Journal of Algebra, Number Theory and its Applications (ISSN:2231-1831, 印度)19 Ricerche di Matematiche(ISSN:0035-5038, 施普林格出版社)20 Southeast Asian Bulletin of Mathematics (ISSN 0129-2021 )21 Studies in Mathematical Sciences (ISSN:1923-8444, 加拿大)22 Surveys in Mathematics and Mathematical Sciences(ISSN:2277-551X, Pushpa Publishing House)23 Universal Journal of Mathematics and Mathematical Sciences(ISSN:2277-1417, Pushpa Publishing House)24 Vietnam Journal of Mathematics (ISSN 0866-7179, Springer)25 微分方程年刊(英文版)26 应用数学与计算数学学报(ISSN:1006-6330)工学1 Asian Journal of Control2 Biomed Environ Sci3 北京生物医学工程4 材料科学与工程学报5 材料科学与技术(英文版)6 蚕业科学7 测绘工程8 测控技术9 Cell Res10 Chem Res Chin Univ11 Chin J Cancer Res12 Chin J Chem Eng13 Chinese Journal of Electronics14 Chromatography B15 大地测量与地球动力学16 地下空间与工程学报17 电力技术18 电镀与精饰19 电镀与涂饰20 电光与控制21 电机控制学报22 电力传动自动化23 电力技术24 电力科学与工程25 电力系统及其自动化学报26 电路与系统学报27 电声技术28 电子测量技术29 电子测量与仪器学报30 电子器件31 电子显微学报32 电子学报(英文版)33 电子与信息学报34 动力学与控制学报35 毒理学杂志36 锻压机械37 Entomologia Sinica38 飞行器测控学报39 分析科学学报40 分析仪器41 分子细胞生物学报42 粉末冶金材料科学与工程43 Food Chemistry44 福建林业科技45 感光科学与光化学46 钢结构47 钢铁钒钛48 钢铁研究学报(英文版)49 高等学校化学研究50 高分子科学51 高分子通报52 Genomics Proteomics & Bioinformatics53 工程地质学报54 工程设计学报55 工程图学学报56 工业工程57 工业计量58 工业控制计算机59 供用电60 光电子技术61 光电子技术与信息62 光纤与电缆及其应用技术63 光学仪器64 贵金属65 果树学报66 High Technology Letters67 海洋湖沼通报68 焊接69 焊接技术70 航空材料学报71 航空制造技术72 合成化学73 核技术(英文版)74 湖泊科学75 化工科技76 化工自动化及仪表77 混凝土78 机械工程学报(英文版)79 机械工业自动化80 激光与光电子学进展81 继电器82 计量与测试技术83 计算机测量与控制84 计算机仿真85 计算机辅助工程86 计算机工程与科学87 计算机集成制造系统—CIMS88 计算机技术与发展89 计算机与应用化学90 J COMPUT SCI & TECH91 J Environ Sci92 J Forest Res S93 Journal of Computer Science and Technology94 Journal of Information and Computational Science95 Journal of Systems Engineering and Electronics96 检验医学97 建筑材料学报98 建筑科学99 交通运输工程学报100 金属热处理101 金属学报(英文版)102 科学通报(英文版)103 空间结构104 矿冶105 理化检验物理分册106 辽宁林业科技107 流体机械108 Nucl Sci Tech109 南京邮电学院学报110 Pedosphere111 Plasma Sci Technol112 Progress in Natural Science113 热处理114 上海金属115 生命的化学116 生物多样性117 生物工程进展118 生物数学学报119 生物信息学120 食品研究与开发121 食品与机械122 世界地震工程123 数据采集与处理124 数值计算与计算机应用125 水利水运工程学报126 水文地质工程地质127 四川动物128 特种橡胶制品129 微电机130 微电子学131 微计算机信息132 微计算机应用133 微型电脑应用134 无损检测135 无线通讯技术136 Science in China Series E-Technological Sciences 137 Science in China Series F-Information Sciences 138 武汉植物学研究139 物理测试140 西北植物学报141 稀有金属(英文版)142 系统仿真技术143 系统仿真学报144 系统工程与电子技术145 World J Gastroenterol146 现代隧道技术147 现代通信148 现代预防医学149 现代科学仪器150 信息安全与通信保密151 遥测遥控152 遥感技术与应用153 遥感信息154 冶金分析155 液晶与显示156 移动通信157 应用生态学报158 有色金属学报(英文版)159 宇航计测技术160 轧钢161 浙江林业科技162 真空电子技术163 振动工程学报164 中国电力165 中国辐射卫生166 中国焊接(英文版)167 中国化学168 中国化学工程学报(英文版)169 中国化学快报170 中国激光A171 中国集成电路172 中国胶粘剂173 中国空间技术174 中国实用内科杂志175 中国水产176 中国塑料177 中国物理快报178 中国稀土学报(英文版)179 中国现代应用药180 中国油料作物学报181 中国有色金属学报182 中国有色金属学会会刊(英文版) 183 中国有线电视184 中国职业医学185 中国种业186 中国铸造装备与技术187 中华医学遗传学杂志188 中华整形外科杂志189 中外公路190 铸造191 自动化仪表192 自动化与仪表193 自动化与仪器仪表管理学1 档案天地2 工业工程3 工业工程与管理4 管理工程学报5 管理科学6 管理评论7 航空档案8 湖北档案9 科研管理10 兰台内外11 南开管理评论12 山东档案13 陕西档案14 未来与发展15 预测16 云南档案17 运筹与管理18 中国管理科学下面是赠送的中秋节演讲辞,不需要的朋友可以下载后编辑删除谢谢中秋佳节演讲词推荐中秋,怀一颗感恩之心》老师们,同学们:秋浓了,月圆了,又一个中秋要到了!本周日,农历的八月十五,我国的传统节日——中秋节。
slope——精选推荐

Bounded-degree graphs can have arbitrarily largeslope numbersJ´a nos Pach∗and D¨o m¨o t¨o r P´a lv¨o lgyiR´e nyi Institute,Hungarian Academy of SciencesSubmitted:Oct21,2005;Accepted:Dec22,2005;Published:Jan7,2006Mathematics Subject Classification:05C62AbstractWe construct graphs with n vertices of maximum degree5whose every straight-linedrawing in the plane uses edges of at least n1/6−o(1)distinct slopes.A straight-line drawing of a graph G=(V(G),E(G))is a layout of G in the plane suchthat the vertices are represented by distinct points,the edges are represented by(possiblycrossing)line segments connecting the corresponding point pairs and not passing throughany other point that represents a vertex.If it creates no confusion,the vertex(edge)ofG and the point(segment)representing it will be denoted by the same symbol.Wade and Chu[WC94]defined the slope number sl(G)of G as the smallest number of distinctedge slopes used in a straight-line drawing of G.Dujmovi´c et al.[DSW04]asked whetherthe slope number of a graph of maximum degree d can be arbitrarily large.The followingshort argument shows that the answer is yes for d≥5.Define a“frame”graph F on the vertex set{1,...,n}by connecting vertex1to2by an edge and connecting every i>2to i−1and i−2.Adding a perfect matchingM between these n points,we obtain a graph G M:=F∪M.The number of different matchings is at least(n/3)n/2.Let G denote the huge graph obtained by taking the union of disjoint copies of all G M.Clearly,the maximum degree of the vertices of G isfive. Suppose that G can be drawn using at most S slopes,andfix such a drawing.For every edge ij∈M,label the points in G M corresponding to i and j by the slopeof ij in the drawing.Furthermore,label each frame edge ij(|i−j|≤2)by its slope.Notice that no two components of G receive the same labeling.Indeed,up to translationand scaling,the labeling of the edges uniquely determines the positions of the pointsrepresenting the vertices of G M.Then the labeling of the vertices uniquely determinesthe edges belonging to M.Therefore,the number of different possible labelings,which isS|F|+n<S3n,is an upper bound for the number of components of G.On the other hand, we have seen that the number of components(matchings)is at least(n/3)n/2.Thus,for any S we obtain a contradiction,provided that n is sufficiently large.With some extra care one can refine this argument to obtainTheorem.For any d≥5,there exist graphs G with n vertices of maximum degree d, whose slope numbers satisfy sl(G)≥n1d−2−o(1).Proof.Now instead of a matching,we add to the frame F in every possible way a(d−4)-regular graph R on the vertex set{1,...,n}.Thus,we obtain at least(cn/d)(d−4)n/2 different graphs G R:=F∪R,each having maximum degree at most d(here c>0 is a constant;see e.g.[BC78]).Suppose that each G R can be drawn using S slopes σ1<...<σS.Now we cannot insist that these slopes are the same for all G R,therefore, these numbers will be regarded as variables.Fix a graph G R=F∪R and one of its drawings with the above properties,in which vertex1is mapped into the origin and vertex2is mapped into a point whose x-coordinate bel every edge belonging to F by the symbolσk representing its slope.Furthermore,label each vertex j with a(d−4)-tuple of theσk s:with the symbols corresponding to the slopes of the d−4edges incident to j in R(with possible repetition). Clearly,the total number of possible labelings of the frame edges and vertices is at most S|F|+(d−4)n<S(d−2)n.Now the labeling itself does not necessarily identify the graph G R, because we do not know the actual values of the slopesσk.However,we can show that the number of different G R s that receive the same labeling cannot be too large.To prove this,first notice that for afixed labeling of the edges of the frame,the coordinates of every vertex i can be expressed as the ratio of two polynomials of degree at most n in the variablesσ1,...,σS.Indeed,letσ(ij)denote the label of ij∈F and let x(i)and y(i)denote the coordinates of vertex i.Since,by assumption,we have x(1)=y(1)=0and x(2)=1,we can conclude that y(2)=σ(12).We have the following equations for the coordinates of3:y(3)−y(1)=σ(13)(x(3)−x(1)),y(3)−y(2)=σ(23)(x(3)−x(2)).Solving them,we obtainx(3)=σ(12)−σ(23)σ(13)−σ(23),and so on.In particular,x(i)=Q i(σ1,...,σS)Q i Q j,we can decide whether the image of i is to the left of the image of j,to the right of it,or they have the same x-coordinate,provided that weknow the “sign pattern”of the polynomials P ij :=Q i Q j −Q i Q j and P ij :=Q i Q j ,i.e.,we know which of them are positive,negative,or zero.Thus,altogether we have 3 n 2 polynomials P ij ,P ij ,P ij (1≤i <j ≤n )in S variables,each of degree at most 2n .Forany fixed labeling of the frame edges and vertices,the sign pattern of these polynomials uniquely determines the graph G R .(Observe that if the label of a vertex i is a (d −4)-tuple containing the symbol σk ,then from the sign pattern of the above polynomials we can reconstruct the sequence of all vertices that belong to the line of slope σk passing through i ,from left to right.From this sequence,we can select all elements whose label contains σk ,and determine all edges of R along this line.)To conclude the proof,we need the Thom-Milnor theorem [BPR03]:Given N poly-nomials in S ≤N variables,each of degree at most 2n ,the number of sign patterns determined by them is at most (CNn/S )S ,for a suitable constant C >0.In our case,the number of graphs G R is at most the number of labelings (<S (d −2)n )times the maximum number of sign patterns of the polynomials P ij ,P ij ,P ij (1≤i <j ≤n ).By the Thom-Milnor theorem,this latter quantity is at most C 3 n 2n S,for a suitable constant C .Thus,the number of G R s is at most S (d −2)n (C 3n 3)S .Comparing this to the lower bound (cn/d )(d −4)n/2,stated in the first paragraph of the proof,we obtain that S ≥n 1d −2−o (1),as required.Acknowledgment.Bar´a t et al.[BMW05]independently found some similar,but slightly weaker results for the slope number.In particular,for d =5,they have a more complicated proof for the existence of graphs with maximum degree five and arbitrarily large slope numbers,that does not give any good explicit lower bound for the growth rate of the slope number,as the number of vertices tends to infinity.They have also established similar results for the geometric thickness ,defined as the smallest integer S with the property that the graph G admits a straight-line drawing,in which the edges can be colored by S colors so that no two edges of the same color cross each other [E04].Clearly,this number cannot exceed sl(G ).We are grateful to B.Aronov for his valuable remarks.References[BMW05]J.Bar´a t,J.Matouˇs ek,and D.R.Wood:Bounded-degree graphs have arbitrar-ily large geometric thickness,The Electronic bin.,13(2006),R3.[BPR03]S.Basu,R.Pollack,and M.-F.Roy:Algorithms in Real Algebraic Geometry ,Springer-Verlag,Berlin,2003.[BC78]E.A.Bender and E.R.Canfield:The asymptotic number of labeled graphs withgiven degree sequences,bin.Theory Ser.A 24(1978),296–307.[DSW04]V.Dujmovi´c ,M.Suderman,and D.R.Wood:Really straight graph drawings,in:Graph Drawing (GD ’04)(J.Pach,ed.),Lecture Notes in Computer Science 3383,Springer-Verlag,Berlin,2004,122–132.[E04]D.Eppstein:Separating thickness from geometric thickness,in:Towards a Theory of Geometric Graphs(J.Pach,ed.),Contemporary Mathematics342,Amer.Math. Soc.,2004,75–86.[WC94]G.A.Wade and J.-H.Chu:Drawability of complete graphs using a minimal slope set,The Computer J.37/2(1994),139–142.。
斐波那契数列
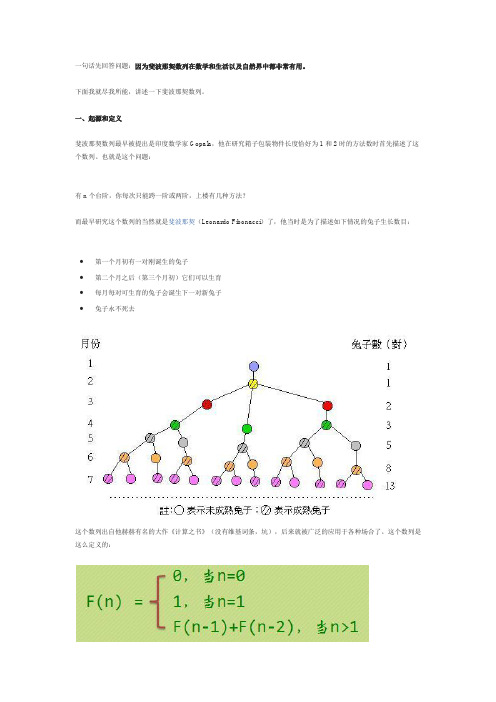
一句话先回答问题:因为斐波那契数列在数学和生活以及自然界中都非常有用。
下面我就尽我所能,讲述一下斐波那契数列。
一、起源和定义斐波那契数列最早被提出是印度数学家Gopala,他在研究箱子包装物件长度恰好为1和2时的方法数时首先描述了这个数列。
也就是这个问题:有n个台阶,你每次只能跨一阶或两阶,上楼有几种方法?而最早研究这个数列的当然就是斐波那契(Leonardo Fibonacci)了,他当时是为了描述如下情况的兔子生长数目:•第一个月初有一对刚诞生的兔子•第二个月之后(第三个月初)它们可以生育•每月每对可生育的兔子会诞生下一对新兔子•兔子永不死去这个数列出自他赫赫有名的大作《计算之书》(没有维基词条,坑),后来就被广泛的应用于各种场合了。
这个数列是这么定义的:The On-Line Encyclopedia of Integer Sequences® (OEIS®)序号为A000045 - OEIS(注意,并非满足第三条的都是斐波那契数列,卢卡斯数列(A000032 - OEIS)也满足这一特点,但初始项定义不同)二、求解方法讲完了定义,再来说一说如何求对应的项。
斐波那契数列是编程书中讲递归必提的,因为它是按照递归定义的。
所以我们就从递归开始讲起。
1.递归求解int Fib(int n){return n < 2 ? 1 : (Fib(n-1) + Fib(n-2));}这是编程最方便的解法,当然,也是效率最低的解法,原因是会出现大量的重复计算。
为了避免这种情况,可以采用递推的方式。
2.递推求解int Fib[1000];Fib[0] = 0;Fib[1] = 1;for(int i = 2;i < 1000;i++) Fib[i] = Fib[i-1] + Fib[i-2];递推的方法可以在O(n)的时间内求出Fib(n)的值。
但是这实际还是不够好,因为当n很大时这个算法还是无能为力的。
形式幂级数∏∞n=0(1-x2n)m系数的无界性(英文)

2024 年 3月第 61 卷第 2 期Mar. 2024Vol. 61 No. 2四川大学学报(自然科学版)Journal of Sichuan University (Natural Science Edition)形式幂级数∏n=0∞(1-x2n)m系数的无界性朱朝熹,赵伟(保密通信全国重点实验室,成都 610041)摘要: 设∏n=0∞(1-x2)为Prouhet-Thue-Morse序列的生成级数.设m≥2为正整数.令F m(x)=(F(x))m=(∏n=0∞()1-x2)m≔∑n=0∞t m(n)x n.2018年,Gawron,Miska和Ulas猜想:当m≥2时序列{t m(n)}∞n=1无界.对于m=3及m=2k的情形,他们通过研究t m(n)的2-adic赋值证明猜想部分成立.本文发展了一种新方法,即由序列{t m(n)}∞n=1的递推关系式得到一类反中心对称矩阵,然后通过计算其相应矩阵的特征值来证明猜想.利用这种方法,本文证明当m=5和6时猜想成立.此外,本文还给出了序列{t5(n)}∞n=1和{t6(n)}∞n=1的无界子列,以及{t5(n)}∞n=1的一个子列的2-adic 赋值表达式,进而证明了另一个关于{t5(n)}∞n=1的2-adic赋值的猜想部分成立.关键词: Prouhet-Thue-Morse 序列;无界性;特征值中图分类号: O156.2 文献标志码: A DOI:10.19907/j.0490-6756.2024.021003On the unboundedness of the coefficients of power series ∏n=0∞(1-x2n)mZHU Chao-Xi, ZHAO Wei(National Key Laboratory of Communication Security, Chengdu 610041, China)Abstract: Let∏n=0∞(1-x2) be the generating function of the Prouhet-Thue-Morse sequence.Let F m(x)=(F(x))m=(∏n=0∞()1-x2)m≔∑n=0∞t m(n)x n.In 2018,Gawron,Miska and Ulas proposed a conjecture on the unboundedness of the sequence{t m(n)}∞n=1 for m≥2. They also proved this conjecture for m=3and m=2k by studying the 2-adic of t m(n),where k is a positive integer.In this paper,we intro‑duce a new method for this conjecture. In this method, a class of anti-centrosymmetric matrices are firstly ob‑tained by studying the recursive relation of t m(n). Then the conjecture may be proved by calculating the ei‑genvalues of the matrices.In particular,we prove the conjecture for m=5and 6 by presenting unbounded sub-sequences of {t5(n)}∞n=1and{t6(n)}∞n=1. Meanwhile, we also partially prove another conjecture on the 2-adic values of t5(n) by calculating the 2-adic value of a sub-sequence of{t5(n)}∞n=1.Keywords: Prouhet-Thue-Morse sequence; Unboundedness; Eigenvalue(2010 MSC 11R09, 11R04)收稿日期: 2022-09-20基金项目: 保密通信重点实验室基金资助(61421030111012101)作者简介: 朱朝熹(1992―),男,重庆人,博士,主要研究方向为数论及密码学. E-mail: zhuxi0824@通讯作者: 赵伟. E-mail: zhaowei9801@第 61 卷四川大学学报(自然科学版)第 2 期1 IntroductionLet n ∈Z and s 2(n ) be the sum of binary digits function of n ,i.e .,if n =∑i =0s k i 2i, k i ∈{0,1} isthe unique expansion of n in base 2,then s 2(n )=∑i =0s k i .Write the Prouhet -Thue -Morse sequenceas t 1(n )=(-1)s ()n .The Prouhet -Thue -Morse se‑quence has many remarkable properties in combina‑torics on words ,analysis on manifolds ,number theory and even physics [1-6].In 2018,Gawron , Miska and Ulas [7] initiatedthe study of the sequence {t m (n )}∞n =1,which is gen‑erated by the coefficient of the power seriesF m (x )=(F (x ))m=(∏n =0∞()1-x 2)m≔∑n =0∞tm(n )xn.They obtained some interesting properties of{t m(n )}∞n =1 and pointed that the sequence{t m(n )}∞n =1is deeply involved into some partitionproblems [8-10].Particularly , they proposed the fol‑lowing two conjectures.Conjecture 1.1[7] Let m be a positive integerwith m ≥2.Then {t m (n )}∞n =1is unbounded.Conjecture 1.2[7] For each n ∈N ,we have ν2(t 5(4n +j))=4éêêêùúúúν2()n +12-(ν2(n +1) (mod 2)), j ∈{0,1,2,3},where ν2(n +1) is the 2-adic value of n +1,éêêêùúúúν2()n +12 stands for the minimal integer k such that k ≥ν2()n +12and (ν2(n +1) (mod 2)) is theminimal nonnegative residue of ν2(n +1) modulo 2.Meanwhile ,they also obtained the exact 2-adicvalue of the sequences {t 2(n )}∞n =1and {t 3(n )}∞n =1and further proved that Conjecture 1.1 is true for m =2k and m =3.When m =2,they presented aninteresting conclusion that the equation t 2(n )=k has infinity many solutions for n ∈N +,i.e .,everypositive integer can be found in the expansion of∏n =0∞()1-x 22,where k is a positive integer.In this paper ,we try to prove Conjecture 1.1for m =5,6 and show that Conjecture 1.2 is true for (n ,j )=(2k -1,3).In fact , we have the follow‑ing results :Theorem 1.3 The sequence {t m (n )}∞n =1is un‑bounded for m =5 and 6.As a result of Theorem 1.3,we can declaim that Conjecture 1.1 is true for m ≤6 and m =2k .As for Conjecture 1.2, we haveTheorem 1.4 Let k be a positive integer and n =2k -1.We haveν2(t 5(4n +3))=4éêêêêùúúúν2()n +12-(ν2(n +1) (mod 2)).2 Double -cyclic matricesWe introduce a class of double -cyclic matrices which play the key role in the proof of Conjec‑ture 1.1.Definition 2.1 Let n ≡0 (mod 2) be a posi‑tive integer and A =(a ij)n ×nbe a matrix of order n .If a ij =a i +2,j +2 holds for all integers i and j such that 1≤i ≤n -2 and 1≤j ≤n -1,then A is called a double -cyclic matrix.Lemma 2.2[7]Let m be a positive integer.Then t m (0)=1,t m (1)=-m and t m (2n )=∑j =0éëêêùûúúm 2C 2j m t m (n -j ),t m (2n +1)=-∑j =0éëêêùûúúm -12C 2j +1m t m ()n -j ,where we additionally define t m (n )=0 for n ≤0.If m ≡0(mod 2),then we have from Lemma2.2 thatæèççççççöø÷÷÷÷÷÷t m (2n +1)t m (2n )⋮t m (2n -m +2)=A m æèççççççöø÷÷÷÷÷÷t m (n )t m (n -1)⋮t m (n -m +1)(1)where第 2 期朱朝熹,等: 形式幂级数∏n =0∞(1-x 2)m系数的无界性第 61 卷A m ≔æèçççççççöø÷÷÷÷÷÷÷-C 1m⋯-C m -1mC 0m⋯C m -2m0-C 1m ⋯0 0 0C m m 0 0-C m -1m 0 0⋯⋯⋯C 0m ⋯⋱ ⋱⋱⋯0 -C 1mC m -2m C mm 0⋱⋱⋱-C 3m ⋯-C 1m⋯⋱0⋯0 C 0mC 2m ⋯C m -2mC m mOn the other hand , if m ≡1 (mod 2) then we haveA m ≔æèçççççççöø÷÷÷÷÷÷÷-C 1m⋯-C m -2m C 0m⋯C m -3m-C 1m ⋯-C mm 0 0C m -1m 0 0-C m -2m -C mm0⋯⋯⋯0 C 0m⋯⋱ ⋱⋱⋯0 -C 1mC m -3m C m -1m0⋱⋱⋱-C 3m⋯-C m -2m⋯⋱-C m m ⋯ 0 C 0mC 2m⋯C m -3mC m -1m One can check that the order of A m is 2[m 2].There are many interesting properties about A m .We present some of them as follows.Proposition 2.3 Let m =p kwith p being anodd prime and k being a positive integer.Thendet (A m )≡0 (mod 2).ProofLet r be an integer with 0≤r ≤m -12.We have C 2r m +C 2r +1m =C 2r +1m +1=m +12r +1C 2rm .Since m +1 is even , 2r +1 is odd and C 2rm is an in‑teger , then we haveC 2r m +C 2r +1m =C 2r +1m +1=m +12r +1C 2rm ≡0 (mod 2)(2)Denote by a 1 and a 2 the first and the second row vec‑tors of A m ,respectively.One hasa 1-a 2=(C 0m+C 1m,…,Cm -1m+C m m,0, 0.By (2),it follows that a 1-a 2≡()0,…,0 (mod 2).Therefore ,one can deduce that det (A m )≡0(mod 2).This completes the proof.Proposition 2.4 Let m =p k with p being an odd prime and k being a positive integer.Thendet (A m )≡±1 (mod p ).ProofLet r be an integer with 0<r <p k .Then C r m=p k r C r -1p -1≡0 (mod p ).It is clear thatC 0m =C m m =1≡1 (mod p ).Therefore ,we can findthat there is one and only one element in each row of A m is 1 or -1 modulo p .For the same reason there is one and only one element in each column of A m is 1 or -1 modulo p .Hence ,one can deduce that det (A m )≡±1 (mod p ).So Proposition 2.4 is proved.Since A m is an integer matrix ,then det (A m )must be an integer.By Proposition 2.3,one can de‑duce that det (A m )≠±1.By Proposition 2.4,onecan derive that det (A m )≠0.It then follows that |det (A m)|≥2.This infers there is at least one ofthe eigenvalues λ of A m such that |λ|>1.Proposition 2.5 Let m =p k with p being an odd prime and k being a positive integer.The eigen‑values of A m are pairwise different.Proof Let f (λ)=det (λE -A m ),where E isthe identity matrix.Then we need to prove the poly‑nomial f (λ) has no multiple roots.Noticing that iff (λ)hasmultipleroots ,thenf ˉ(λ)≔f ()λ (mod p ) still has multiple roots ,where f ˉ(λ) isa polynomial over the finite field F p .Now we prove that gcd (f ˉ(λ),-f ′(λ))=1,where -f ′ is the derivation of f ˉ. By the fact第 61 卷四川大学学报(自然科学版)第 2 期A m -λE =æèçççççççöø÷÷÷÷÷÷÷-C 1m-λ⋯-C m -2m C 0m ⋯ C m -3m0-C 1m ⋯-C mm 0 0C m -1m 00-C m -2m -C mm⋯⋯⋯0 C 0m⋯ ⋱ ⋱ ⋱⋯0 -C 1mC m -3m C m -1m0⋱⋱⋱-C 3m ⋯-C m -2m -λ⋯⋱-C mm⋯ 0 C 0mC 2m ⋯C m -3mC m -1m -λ=æèçççççççöø÷÷÷÷÷÷÷-λ⋯01⋯000⋯-1000000-10⋯⋯⋯1⋯ ⋱⋱⋱ ⋯00 0 00 ⋱ ⋱⋱0 ⋯-λ⋯⋱-1⋯ 0 1⋯0-λ (mod p ),one can derive that f ˉ(λ)=λm -1±1 by the defini‑tion of the determinant.It follows thatgcd (f ˉ(λ), f ˉ′(λ))=gcd (λm -1±1,(m -1)λm -2)=1,as desired.It follows that f ˉ()λ has no multiple roots.This finishes the proof.3 Proof of the main resultsProof of Theorem 1.3 Let d be a positive in‑teger.When m =6,we haveæèççççççççççççöø÷÷÷÷÷÷÷÷÷÷÷t 6(2d n +2d -1)t 6(2d n +2d -2)t 6(2d n +2d -3)t 6(2d n +2d -4)t 6(2d n +2d -5)t 6(2d n +2d-6)=A d 6æèççççççççççççöø÷÷÷÷÷÷÷÷÷÷÷t 6(n )t 6(n -1)t 6(n -2)t 6(n -3)t 6(n -4)t 6(n -5)(3)for any positive integer n by (1),whereA 6=æèççççççççççöø÷÷÷÷÷÷÷÷÷÷-6-20-6115150-6-20 0 0 01 0 0-6 0 0 0 1 150 0 -60 0 1151 0-20-6 01515 1.One can find that all the eigenvalues of A 6 are λ1=1, λ2=4-45, λ3=4+45,λ4=α+3889α-103, λ5=e 4πi 3α+3889αe 2πi 3-103,λ5=e 2πi 3α+3889αe 4πi 3-103,whereα=(+159227)13in the first quartile.Then there exist a matrix T such thatA 6=T æèççççççççççöø÷÷÷÷÷÷÷÷÷÷λ1000λ2000λ30 0 00 0 00 0000 00 0 00 0 0λ4000λ500λ6T -1(4)By (3) and (4),we haveæèççççççççççççöø÷÷÷÷÷÷÷÷÷÷÷t 6(2d n +2d -1)t 6(2d n +2d -2)t 6(2d n +2d -3)t 6(2d n +2d -4)t 6(2d n +2d -5)t 6(2d n +2d-6)=T æèççççççççççöø÷÷÷÷÷÷÷÷÷÷λd 1000λd 2000λd 30 0 00 0 0000 0 00 0 000 0λd 4000λd 5000λd 6T -1æèççççççççççççöø÷÷÷÷÷÷÷÷÷÷÷t 6(n )t 6(n -1)t 6(n -2)t 6(n -3)t 6(n -4)t 6(n -5)(5)It then follows thatt 6(2d -1)=f 1λd 1+f 2λd 2+f 3λd 3+f 4λd 4+f 5λd5+f 6λd 6(6)for some f i ∈C , i =1,2,3,4,5,6.One can check that |α|=3889 and the argument of α is close to π6.Hence one can derive that |λ6|>|λ5|>|λ4|>|λ3|>|λ2|>|λ1|=1.Since t 6(1)=1,we set d =1.Then we have 1=f 1λ1+f 2λ2+f 3λ3+f 4λ4+第 2 期朱朝熹,等: 形式幂级数∏n =0∞(1-x 2)m系数的无界性第 61 卷f 5λ5+f 6λ6.One can confirm that it is impossible for all of f i ,i =1,2,3,4,5,6,being zero.Let i be thelargest number such that f i ≠0.We havelim d →∞t 6(2d -1)λd i=f i ≠0.so we have the sequence {t 6(2d -1)}∞d =1is un‑bounded.When m = 5, by (1),we haveæèççççççöø÷÷÷÷÷÷t 5(2d n +2d -1)t 5(2d n +2d -2)t 5(2d n +2d-3)t 5(2d n +2d-4)=A d 5æèççççççöø÷÷÷÷÷÷t 5(n )t 5(n -1)t 5(n -2)t 5(n -3)(7)holds for any positive integer n , whereA 5=æèçççöø÷÷÷-5-10110-1 05 00-50 1 -10-1 105.One can find all the eigenvalues of A 5 is 8,4,-4,-8.Then there exist a matrixT =æèçççöø÷÷÷2-911-131-4-4-131-1192such thatA 5=T æèçççöø÷÷÷-800-400000 00 04008T -1(8)By (7) and (8), we haveæèççççççöø÷÷÷÷÷÷t 5(2d n +2d -1)t 5(2d n +2d -2)t 5(2d n +2d-3)t 5(2d n +2d-4)=T æèçççöø÷÷÷-800-400000 00 04008T -1æèççççççöø÷÷÷÷÷÷t 5(n )t 5(n -1)t 5(n -2)t 5(n -3)(9)By Lemma 2.2,we have t 5(0)=1,t 5(-1)=0,t 5(-2)=0,t 5(-3)=0. Let n =0.It then fol‑lows from (9) thatt 5(2d -1)=-1964d +3332(-4)d-1168d +124(-8)d(10)Clearly ,we have lim d →∞|t 5(2d -1)|=+∞.This com ‑pletes the proof of Theorem 1.3.Proof of Theorem 1.4 Let d =k +2.It fol‑lows from (10) thatt 5(4n +3)=t 5(2k +2-1)=4k +2×-1+99()-1k +2-6×2k +2+4()-2k +296(11)If k ≡0 (mod 2),then by the factν2(98)=1<3≤ν2(-6×2k +2+4(-2)k +2)it follows from (10) thatν2()t 5()4n +3=2(k +2)+ν2(-1+99×(-1)k +2-6×2k +2+4(-2)k +2)-ν2(96)=2k =4éêêêêùúúúν2()n +12-(ν2(n +1) (mod 2)).If k ≡1 (mod 2),then by the factν2(-100)=2<4≤ν2(-6×2k +2+4(-2)k +2)we haveν2(t 5(4n +3))=2(k +2)+ν2(-1+99×(-1)k +2-6×2k +2+4(-2)k +2)-ν2(96)=2k +1=4éêêêêùúúúν2()n +12-(ν2(n +1) (mod 2)),as desired.The proof is end.4 ConclusionsIn 2018,Gawron , Miska and Ulas proposed aconjecture that the sequence {t m (n )}∞n =1is un‑bounded for m ≥2.They also proved this conjec‑ture for m =3 and m =2k with k being positive inte‑ger by studying the 2-adic value of t m (n ).In this pa‑第 61 卷四川大学学报(自然科学版)第 2 期per,we obtained a class of anti-centrosymmetric ma‑trices A m by studying the recursive relation of t m(n) and introduce a new method to prove this conjecture for m=5and 6 by focusing on the eigenvalues of A m.Thus we conclude that the conjecture is true for m≤6.We also obtain the 2-adic value of a sub-sequence of {t5(n)}∞n=1.Finally,we should point that the anti-centrosymmetric matrices A m play im‑portant role in solving the conjecture and it is quite difficult to determine the eigenvalues for variable m. References:[1]Ding C,Helleseth T,Niederreiter H.Sequences and their applications [M].London: Springer, 1999.[2]Allouche J P,Shallit J.Automatic sequences:Theory,application,generalizations [M].Cam‑bridge: Cambridge University Press, 2003.[3]Gawron M.A note on the arithmetic properties of Stern polynomials [J].Pub Math Debr,2014,85: 453.[4]Mahler K.On a special functional equation [J].J London Math Soc, 1940, 15: 115.[5]Ulas M.On certain arithmetic properties of Stern polynomials [J].Pub Math Debr, 2011, 79: 55.[6]Ulas M.Arithmetic properties of the sequence of de‑grees of Stern polynomials and related results [J].IntJ Number Theory, 2012, 8: 669.[7]Gawron M, Miska P, Ulas M.Arithmetic properties of coefficients of power series expansion of∑n=0∞(1-x2)^t[J].Monatsh Math,2018,185: 307.[8]Bruijn N G.On Mahler′s partition problem [J].Indag Math, 1948, 10: 210.[9]Churchhouse R F.Congruence properties of the bi‑nary partition function [J].Proc Cambridge PhilSoc, 1969, 66: 371.[10]Gupta H.Proof of the Churchhouse conjecture con‑cerning binary partition [J].Proc Cambridge PhilSoc, 1971, 70: 53.。
斐波那契数列论文文献检索

7.题目:斐波那契数列通项公式的求法 作者:张新娟 作者单位:连云港职业技术学院基础课部,江苏连云港,222006 刊名:高等数学研究 英文刊名: STUDIES IN COLLEGE MATHEMATICS 年,卷(期): 2009 12(4) 分类号: O151.21 文摘:分别运用常用求数列通项的方法,子空间理论,矩阵理论, 函数方程理论,均可求出斐波那契数列的通项公式.
(Sho06)Sequences of Games A Tool for Taming Complexity in Security Proofs

Sequences of Games:A Tool for Taming Complexity in Security Proofs∗Victor Shoup†January18,2006AbstractThis paper is brief tutorial on a technique for structuring security proofs as sequences games.1IntroductionSecurity proofs in cryptography may sometimes be organized as sequences of games.In certain circumstances,this can be a useful tool in taming the complexity of security proofs that might otherwise become so messy,complicated,and subtle as to be nearly impossible to verify.This technique appears in the literature in various styles,and with various degrees of rigor and formality.This paper is meant to serve as a brief tutorial on one particular“style”of employing this technique,which seems to achieve a reasonable level of mathematical rigor and clarity,while not getting bogged down with too much formalism or overly restrictive rules.We do not make any particular claims of originality—it is simply hoped that others might profit from some of the ideas discussed here in reasoning about security.At the outset,it should be noted that this technique is certainly not applicable to all security proofs.Moreover,even when this technique is applicable,it is only a tool for organizing a proof—the actual ideas for a cryptographic construction and security analysis must come from elsewhere.1.1The Basic IdeaSecurity for cryptograptic primitives is typically defined as an attack game played between an adversary and some benign entity,which we call the challenger.Both adversary and challenger are probabilstic processes that communicate with each other,and so we can model the game as a probability space.Typically,the definition of security is tied to some particular event S.Security means that for every“efficient”adversary,the probability that event S occurs is“very close to”some specified“target probabilty”:typically,either0, 1/2,or the probability of some event T in some other game in which the same adversary is interacting with a different challenger.∗First public version:Nov.30,2004†Computer Science Dept.NYU.shoup@In the formal definitions,there is a security parameter:an integer tending to infinity,and in the previous paragraph,“efficient”means time bounded by a polynomial in the security parameter,and“very close to”means the difference is smaller than the inverse of any polynomial in the security parameter,for sufficiently large values of the security parameter. The term of art is negligibly close to,and a quantity that is negliglibly close to zero is just called negligible.For simplicity,we shall for the most part avoid any further discussion of the security parameter,and it shall be assumed that all algorithms,adversaries,etc.,take this value as an implicit input.Now,to prove security using the sequence-of-games approach,one prodceeds as follows. One constructs a sequence of games,Game0,Game1,...,Game n,where Game0is the original attack game with respect to a given adversary and cryptographic primitive.Let S0 be the event S,and for i=1,...,n,the construction defines an event S i in Game i,usually in a way naturally related to the definition of S.The proof shows that Pr[S i]is negligibly close to Pr[S i+1]for i=0,...,n−1,and that Pr[S n]is equal(or negligibly close)to the “target probability.”From this,and the fact that n is a constant,it follows that Pr[S]is negligibly close to the“target probability,”and security is proved.That is the general framework of such a proof.However,in constructing such proofs, it is desirable that the changes between succesive games are very small,so that analyzing the change is as simple as possible.From experience,it seems that transitions between successive games can be restricted to one of three types:Transitions based on indistinguishability.In such a transition,a small change is made that,if detected by the adversary,would imply an efficient method of distinguishing be-tween two distributions that are indistinguishable(either statistically or computationally). For example,suppose P1and P2are assumed to be computationally indistinguishable dis-tributions.To prove that|Pr[S i]−Pr[S i+1]|is negligible,one argues that there exists a distinguishing algorithm D that“interpolates”between Game i and Game i+1,so that when given an element drawn from distribution P1as input,D outputs1with probability Pr[S i], and when given an element drawn from distribution P2as input,D outputs1with prob-abilty Pr[S i+1].The indistinguishability assumption then implies that|Pr[S i]−Pr[S i+1]| is ually,the construction of D is obvious,provided the changes made in the transition are minimal.Typically,one designs the two games so that they could easily be rewritten as a single“hybrid”game that takes an auxilliary input—if the auxiallary input is drawn from P1,you get Game i,and if drawn from P2,you get Game i+1.The distinguisher then simply runs this single hybrid game with its input,and outputs1if the appropriate event occurs.Transitions based on failure events.In such a transition,one argues that Games i and i+1proceed identically unless a certain“failure event”F occurs.To make this type of argument as cleanly as possible,it is best if the two games are defined on the same underlying probability space—the only differences between the two games are the rules for computing certain random variables.When done this way,saying that the two games proceed identically unless F occurs is equivalent to saying thatS i∧¬F⇐⇒S i+1∧¬F,that is,the events S i∧¬F and S i+1∧¬F are the same.If this is true,then we can use thefollowing fact,which is completely trivial,yet is so often used in these types of proofs that it deserves a name:Lemma1(Difference Lemma).Let A,B,F be events defined in some probability dis-tribution,and suppose that A∧¬F⇐⇒B∧¬F.Then|Pr[A]−Pr[B]|≤Pr[F]. Proof.This is a simple calculation.We have|Pr[A]−Pr[B]|=|Pr[A∧F]+Pr[A∧¬F]−Pr[B∧F]−Pr[B∧¬F]|=|Pr[A∧F]−Pr[B∧F]|≤Pr[F].The second equality follows from the assumption that A∧¬F⇐⇒B∧¬F,and so in particular,Pr[A∧¬F]=Pr[B∧¬F].Thefinal inequality follows from the fact that both Pr[A∧F]and Pr[B∧F]are numbers between0and Pr[F].2So to prove that Pr[S i]is negligibly close to Pr[S i+1],it suffices to prove that Pr[F]is negligible.Sometimes,this is done using a security assumption(i.e.,when F occurs,the adversary has found a collision in a hash function,or forged a MAC),while at other times, it can be done using a purely information-theoretic argument.Usually,the event F is defined and analyzed in terms of the random variables of one of the two adjacent games.The choice is arbitrary,but typically,one of the games will be more suitable than the other in terms of allowing a clear proof.In some particularly challenging circumstances,it may be difficult to analyze the event F in either game.In fact,the analysis of F may require its own sequence of games sprouting offin a different direction,or the sequence of games for F may coincide with the sequence of games for S,so that Pr[F]finally gets pinned down in Game j for j>i+1.This technique is sometimes crucial in side-stepping potential circularities.Bridging steps.The third type of transition introduces a bridging step,which is typically a way of restating how certain quantities can be computed in a completely equivalent way. The change is purely conceptual,and Pr[S i]=Pr[S i+1].The reason for doing this is to prepare the ground for a transition of one of the above two types.While in principle,such a bridging step may seem unnecessary,without it,the proof would be much harder to follow.As mentioned above,in a transition based on a failure event,it is best if the two successive games are understood to be defined on the same underlying probability space. This is an important point,which we repeat here for emphasis—it seems that proofs are easiest to understand if one does not need to compare“corresponding”events across distinct and(by design)quite different probability spaces.Actually,it is good practice to simply have all the games in the sequence defined on the same underlying probability space.However,the Difference Lemma generalizes in the obvious way as follows:if A, B,F1and F2are events such that Pr[A∧¬F1]=Pr[B∧¬F2]and Pr[F1]=Pr[F2],then |Pr[A]−Pr[B]|≤Pr[F1].With this generalized version,one may(if one wishes)analyze transitions based on failure events when the underlying probability spaces are not the same.1.2Some Historical Remarks“Hybrid arguments”have been used extensively in cryptography for many years.Such an argument is essentially a sequence of transitions based on indistinguishability.An early example that clearly illustrates this technique is Goldreich,Goldwasser,and Micali’s paper [GGM86]on constructing pseudo-random functions(although this is by no means the ear-liest application of a hybrid argument).Note that in some applications,such as[GGM86], one in fact makes a non-constant number of transitions,which requires an additional,prob-abilistic argument.Although some might use the term“hybrid argument”to include proofs that use transi-tions based on both indistinguishability and failure events,that seems to be somewhat of a stretch of terminology.An early example of a proof that is clearly structured as a sequence of games that involves transitions based on both indistinguishability and failure events is Bellare and Goldwasser’s paper[BG89].Kilian and Rogaway’s paper[KR96]on DESX initiates a somewhat more formal ap-proach to sequences of games.That paper essentially uses the Difference Lemma,specialized to their particular setting.Subsequently,Rogaway has refined and applied this technique in numerous works with several co-authors.We refer the reader to the paper[BR04]by Bellare and Rogaway that gives a detailed introduction to the methodology,as well as references to papers where it has been used.However,we comment briefly on some of the differences between the technique discussed in this paper,and that advocated in[BR04]:•In Bellare and Rogaway’s approach,games are programs and are treated as purely syntactic objects subject to formal manipulation.In contrast,we view games as probability spaces and random variables defined over them,and do not insist on any particular syntactic formalism beyond that convenient to make a rigorous mathemat-ical argument.•In Bellare and Rogaway’s approach,transitions based on failure events are restricted to events in which an executing program explicitly sets a particular boolean variable to true.In contrast,we do not suggest that events need to be explicitly“announced.”•In Bellare and Rogaway’s approach,when the execution behaviors of two games are compared,two distinct probability spaces are involved,and probabilities of“corre-sponding”events across probability spaces must be compared.In contrast,we sug-gest that games should be defined on a common probability space,so that when discussing,say,a particular failure event F,there is literally just one event,not a pair of corresponding events in two different probability spaces.In the end,we think that the choice between the style advocated in[BR04]and that suggested here is mainly a matter of taste and convenience.The author has used proofs organized as sequences of games extensively in his own work [Sho00,SS00,Sho01,Sho02,CS02,CS03b,CS03a,GS04]and has found them to be an indispensable tool—while some of the proofs in these papers could be structured differently, it is hard to imagine how most of them could be done in a more clear and convincing way without sequences of games(note that all but thefirst two papers above adhere to the rule suggested here of defining games to operate on the same probability space).Other authorshave also been using very similar proof styles recently[AFP04,BK04,BCP02a,BCP02b, BCP03,CPP04,DF03,DFKY03,DFJW04,Den03,FOPS04,GaPMV03,KD04,PP03, SWP04].Also,Pointcheval[Poi04]has a very nice introductory manuscript on public-key cryptography that illustrates this proof style on a number of particular examples.The author has also been using the sequence-of-games technique extensively in teaching courses in cryptography.Many“classical”results in cryptography can be fruitfully analyzed using this technique.Generally speaking,it seems that the students enjoy this approach, and easily learn to use and apply it themselves.Also,by using a consistent framework for analysis,as an instructor,one can more easily focus on the ideas that are unique to any specific application.1.3Outline of the Rest of the PaperAfter recalling some fairly standard notation in the next section,the following sections illustrate the use of the sequence-of-games technique in the analysis of a number of classical cryptographic pared to many of the more technically involved examples in the literature of this technique(mentioned above),the applications below are really just “toy”examples.Nevertheless,they serve to illustrate the technique in a concrete way,and moreover,we believe that the proofs of these results are at least as easy to follow as any other proof,if not more so.All of the examples,except the last two(in§§7-8),are presented at an extreme level of detail;indeed,for these examples,we give complete,detailed descriptions of each and every game.More typically,to produce a more compact proof,one might simply describe the differences between games,rather than describing each game in its entirety(as is done in§§7-8).These examples are based mainly on lectures in courses on cryptography taught by the author.2NotationWe make use of fairly standard notation in what follows.In describing probabilistic processes,we writex c|←Xto denote the action of assigning to the variable x a value sampled according to the dis-tribution X.If S is afinite set,we simply write s c|←S to denote assignment to s of an element sampled from the uniform distribution on S.If A is a probabilistic algorithm and x an input,then A(x)denotes the output distribution of A on input x.Thus,we write y c|←A(x)to denote the action of running algorithm A on input x and assigning the output to the variable y.We shall writePr[x1c|←X1,x2c|←X2(x1),...,x n c|←X n(x1,...,x n−1):φ(x1,...,x n)]to denote the probability that when x1is drawn from a certain distribution X1,and x2is drawn from a certain distribution X2(x1),possibly depending on the particular choice ofx1,and so on,all the way to x n,the predicateφ(x1,...,x n)is true.We allow the predicate φto involve the execution of probabilistic algorithms.If X is a probability distribution on a sample space X,then[X]denotes the subset of elements of X that occur with non-zero probability.3ElGamal Encryption3.1Basic DefinitionsWefirst recall the basic definition of a public-key encryption scheme,and the notion of semantic security.A public-key encryption scheme is a triple of probabilistic algorithms(KeyGen,E,D). The key generation algorithm KeyGen takes no input(other than an implied security pa-rameter,and perhaps other system parameters),and outputs a public-key/secret-key pair (pk,sk).The encryption algorithm E takes as input a public key pk and a message m, selected from a message space M,and outputs a ciphertextψ.The decryption algorithm takes as input a secret key sk and ciphertextψ,and outputs a message m.The basic correctness requirement is that decryption“undoes”encryption.That is,for all m∈M,all(pk,sk)∈[KeyGen()],allψ∈[E(pk,m)],and all m ∈[D(sk,ψ)],we have m=m .This definition can be relaxed in a number of ways;for example,we may only insist that it is computationally infeasible tofind a message for which decryption does not “undo”its encryption.The notion of semantic security intuitively says that an adversary cannot effectively dis-tinguish between the encryption of two messages of his choosing(this definition comes from [GM84],where is called polynomial indistinguishability,and semantic security is actually the name of a syntactically different,but equivalent,characterization).This is formally defined via a game between an adversary and a challenger.•The challenger computes(pk,sk)c|←KeyGen(),and gives pk to the adversary.•The adversary chooses two messages m0,m1∈M,and gives these to the challenger.•The challenger computesb c|←{0,1},ψc|←E(pk,m b)and gives the“target ciphertext”ψto the adversary.•The adversary outputsˆb∈{0,1}.We define the SS-advantage of the adversary to be|Pr[b=ˆb]−1/2|.Semantic security means that any efficient adversary’s SS-advantage is negligible.3.2The ElGamal Encryption SchemeWe next recall ElGamal encryption.Let G be a group of prime order q,and letγ∈G be a generator(we view the descriptions of G andγ,including the value q,to be part of a set of implied system parameters).The key generation algorithm computes(pk,sk)as follows:x c|←Z q,α←γx,pk←α,sk←x.The message space for the algorithm is G.To encrypt a message m∈G,the encryption algorithm computes a ciphertextψas follows:y c|←Z q,β←γy,δ←αy,ζ←δ·m,ψ←(β,ζ).The decryption algorithm takes as input a ciphertext(β,ζ),and computes m as follows:m←ζ/βx.It is clear that decryption“undoes”encryption.Indeed,ifβ=γy andζ=αy·m,then ζ/βx=αy m/βx=(γx)y m/(γy)x=γxy m/γxy=m.3.3Security AnalysisElGamal encryption is semantically secure under the Decisional Diffie-Hellman(DDH) assumption.This is the assumption that it is hard to distinguish triples of the form (γx,γy,γxy)from triples of the form(γx,γy,γz),where x,y,and z are random elements of Z q.The DDH assumption is more precisely formulated as follows.Let D be an algorithm that takes as input triples of group elements,and outputs a bit.We define the DDH-advantage of D to be|Pr[x,y c|←Z q:D(γx,γy,γxy)=1]−Pr[x,y,z c|←Z q:D(γx,γy,γz)=1]|.The DDH assumption(for G)is the assumption that any efficient algorithm’s DDH-advantage is negligible.We now give a proof of the semantic security of ElGamal encryption under the DDH assumption,using a sequence of games.Game0.Fix an efficient adversary A.Let us define Game0to be the attack game against A in the definition of semantic security.To make things more precise and more concrete, we may describe the attack game algorithmically as follows:x c|←Z q,α←γxr c|←R,(m0,m1)←A(r,α)b c|←{0,1},y c|←Z q,β←γy,δ←αy,ζ←δ·m bˆb←A(r,α,β,ζ)In the above,we have modeled the adversary A is a deterministic algorithm that takes as input“random coins”r sampled uniformly from some set R.It should be evident that this algorithm faithfully represents the attack game.If we define S0to be the event that b=ˆb,then the adversary’s SS-advantage is|Pr[S0]−1/2|.Game1.[This is a transition based on indistinguishability.]We now make one small change to the above ly,instead of computingδasαy,we compute it asγz for randomly chosen z∈Z q.We can describe the resulting game algorithmically as follows: x c|←Z q,α←γxr c|←R,(m0,m1)←A(r,α)b c|←{0,1},y c|←Z q,β←γy,z c|←Z q,δ←γz,ζ←δ·m bˆb←A(r,α,β,ζ)Let S1be the event that b=ˆb in Game1.Claim1.Pr[S1]=1/2.This follows from the fact that in Game2,δis effectively a one-time pad,and as such,the adversary’s outputˆb is independent of the hidden bit b.To prove this more rigorously,it will suffice to show that b,r,α,β,ζare mutually independent, since from this,it follows that b andˆb=A(r,α,β,ζ)are independent.First observe that by construction,b,r,α,β,δare mutually independent.It will suffice to show that conditioned on anyfixed values of b,r,α,β,the conditional distribution ofζis the uniform distribution over G.Now,if b,r,α,βarefixed,then so are m0,m1,since they are determined by r,α; moreover,by independence,the conditional distribution ofδis the uniform distribution on G,and hence from this,one sees that the conditional distribution ofζ=δ·m b is the uniform distribution on G.Claim2.|Pr[S0]−Pr[S1]|= ddh,where ddh is the DDH-advantage of some efficient algorithm(and hence negligible under the DDH assumption).The proof of this is essentially the observation that in Game0,the triple(α,β,δ)is of the form(γx,γy,γxy),while in Game1,it is of the form(γx,γy,γz),and so the adversary should not notice the difference,under the DDH assumption.To be more precise,our distinguishing algorithm D works as follows:Algorithm D(α,β,δ)r c|←R,(m0,m1)←A(r,α)b c|←{0,1},ζ←δ·m bˆb←A(r,α,β,ζ)if b=ˆbthen output1else output0Algorithm D effectively“interpolates”between Games0and1.If the input to D is of the form(γx,γy,γxy),then computation proceeds just as in Game0,and thereforePr[x,y c|←Z q:D(γx,γy,γxy)=1]=Pr[S0].If the input to D is of the form(γx,γy,γz),then computation proceeds just as in Game1, and thereforePr[x,y,z c|←Z q:D(γx,γy,γz)=1]=Pr[S1].From this,it follows that the DDH-advantage of D is equal to|Pr[S0]−Pr[S1]|.That completes the proof of Claim2.Combining Claim1and Claim2,we see that|Pr[S0]−1/2|= ddh,and this is negligible.That completes the proof of security of ElGamal encryption.3.4Hashed ElGamalFor a number of reasons,it is convenient to work with messages that are bit strings,say,of length ,rather than group elements.Because of this,one may choose to use a“hashed”version of the ElGamal encryption scheme.This scheme makes use of a family of keyed“hash”functions H:={H k}k∈K,where each H k is a function mapping G to{0,1} .The key generation algorithm computes(pk,sk)as follows:x c|←Z q,k c|←K,α←γx,pk←(α,k),sk←(x,k).To encrypt a message m∈{0,1} ,the encryption algorithm computes a ciphertextψas follows:y c|←Z q,β←γy,δ←αy,h←H k(δ),v←h⊕m,ψ←(β,v).The decryption algorithm takes as input a ciphertext(β,v),and computes m as follows:m←H k(βx)⊕v.The reader may easily verify that decryption“undoes”encryption.As for semantic security,this can be proven under the DDH assumption and the as-sumption that the family of hash functions H is“entropy smoothing.”Loosely speaking, this means that it is hard to distinguish(k,H k(δ))from(k,h),where k is a random element of K,δis a random element of G,and h is a random element of{0,1} .More formally, let D be an algorithm that takes as input an element of K and an element of{0,1} ,and outputs a bit.We define the ES-advantage of D to be|Pr[k c|←K,δc|←G:D(k,H k(δ))=1]−Pr[k c|←K,h c|←{0,1} :D(k,h)=1]|.We say H is entropy smoothing if every efficient algorithm’s ES-advantage is negligible.It is in fact possible to construct entropy smoothing hash function families without ad-ditional hypothesis(the Leftover Hash Lemma may be used for this[IZ89]).However,these may be somewhat less practical than ad hoc hash function families for which the entropy smoothing property is only a(perfectly reasonable)conjecture;moreover,our definition also allows entropy smoothers that use pseudo-random bit generation techniques as well.We now sketch the proof of semantic security of hashed ElGamal encryption,under the DDH assumption and the assumption that H is entropy smoothing.Game0.This is the original attack game,which we can state algorithmically as follows:x c|←Z q,k c|←K,α←γxr c|←R,(m0,m1)←A(r,α,k)b c|←{0,1},y c|←Z q,β←γy,δ←αy,h←H k(δ),v←h⊕m bˆb←A(r,α,k,β,v)We define S0to be the event that b=ˆb in Game0.Game1.[This is a transition based on indistinguishability.]Now we transform Game0 into Game1,computingδasγz for random z∈Z q.We can state Game1algorithmically as follows:x c|←Z q,k c|←K,α←γxr c|←R,(m0,m1)←A(r,α,k)b c|←{0,1},y c|←Z q,β←γy,z c|←Z q,δ←γz,h←H k(δ),v←h⊕m bˆb←A(r,α,k,β,v)Let S1be the event that b=ˆb in Game1.We claim that|Pr[S0]−Pr[S1]|= ddh,(1) where ddh is the DDH-advantage of some efficient algorithm(which is negligible under the DDH assumption).The proof of this is almost identical to the proof of the corresponding claim for“plain”ElGamal.Indeed,the following algorithm D“interpolates”between Game0and Game1, and so has DDH-advantage equal to|Pr[S0]−Pr[S1]|:Algorithm D(α,β,δ)k c|←Kr c|←R,(m0,m1)←A(r,α,k)b c|←{0,1},h←H k(δ),v←h⊕m bˆb←A(r,α,k,β,v)if b=ˆbthen output1else output0Game 2.[This is also a transition based on indistinguishability.]We now transform Game1into Game2,computing h by simply choosing it at random,rather than as a hash. Algorithmically,Game2looks like this:x c|←Z q,k c|←K,α←γxr c|←R,(m0,m1)←A(r,α,k)b c|←{0,1},y c|←Z q,β←γy,z c|←Z q,δ←γz,h c|←{0,1} ,v←h⊕m bˆb←A(r,α,k,β,v)Observe thatδplays no role in Game2.Let S2be the event that b=ˆb in Game2.We claim that|Pr[S1]−Pr[S2]|= es,(2) where es the ES-advantage of some efficient algorithm(which is negligible assuming H is entropy smoothing).This is proved using the same idea as before:any difference between Pr[S1]and Pr[S2] can be parlayed into a corresponding ES-advantage.Indeed,it is easy to see that the fol-lowing algorithm D “interpolates”between Game1and Game2,and so has ES-advantage equal to|Pr[S1]−Pr[S2]|:Algorithm D (k,h)x c|←Z q,α←γxr c|←R,(m0,m1)←A(r,α,k)b c|←{0,1},y c|←Z q,β←γy,v←h⊕m bˆb←A(r,α,k,β,v)if b=ˆbthen output1else output0Finally,as h acts like a one-time pad in Game2,it is evident thatPr[S2]=1/2.(3) Combining(1),(2),and(3),we obtain|Pr[S0]−1/2|≤ ddh+ es,which is negligible,since both ddh and es are negligible.This proof illustrates how one can utilize more than one intractability assumption in a proof of security in a clean and simple way.4Pseudo-Random Functions4.1Basic DefinitionsLet 1and 2be positive integers(which are actually polynomially bounded functions in a security parameter).Let F:={F s}s∈S be a family of keyed functions,where each functionF s maps{0,1} 1to{0,1} 2.LetΓ1, 2denote the set of all functions from{0,1} 1to{0,1} 2.Informally,we say that F is pseudo-random if it is hard to distinguish a random functiondrawn from F from a random function drawn fromΓ1, 2,given black box access to such afunction(this notion was introduced in[GGM86]).More formally,consider an adversary A that has oracle access to a function inΓ1, 2,and suppose that A always outputs a bit.Define the PRF-advantage of A to be|Pr[s c|←S:A F s()=1]−Pr[f c|←Γ1, 2:A f()]=1|.We say that F is pseudo-random if any efficient adversary’s PRF-advantage is negligible.4.2Extending the Input Length with a Universal Hash FunctionWe now present one construction that allows one to stretch the input length of a pseudo-random family of functions.Let be a positive integer with > 1.Let H:={H k}k∈K be a family of keyed hash functions,where each H k maps{0,1} to{0,1} 1.Let us assume that H is an uh-universal family of hash functions,where uh is negligible.This means that for all w,w ∈{0,1} with w=w ,we havePr[k c|←K:H k(w)=H k(w )]≤ uh.There are many ways to construct such families of hash functions.Now define the family of functionsF :={F k,s}(k,s)∈K×S,where each Fk,s is the function from{0,1} into{0,1} 2that sends w∈{0,1} to F s(H k(w)).We shall now prove that if F is pseudo-random,then F is pseudo-random.Game0.This game represents the computation of an adversary given oracle access to a function drawn at random from F .Without loss of generality,we may assume that the adversary makes exactly q queries to its oracle,and never repeats any queries(regardless of the oracle responses).We may present this computation algorithmically as follows: k c|←K,s c|←Sr c|←Rfor i←1...q dow i←A(r,y1,...,y i−1)∈{0,1}x i←H k(w i)∈{0,1} 1y i←F s(x i)∈{0,1} 2b←A(r,y1,...,y q)∈{0,1}output bThe idea behind our notation is that the adversary is modeled as a deterministic al-gorithm A,and we supply its random coins r∈R as input,and in loop iteration i,the adversary computes its next query w i as a function of its coins and the results y1,...,y i−1 of its previous queries w1,...,w i−1.We are assuming that A operates in such a way that the values w1,...,w q are always distinct.Let S0be the event that the output b=1in Game0.Our goal is to transform this game into a game that is equivalent to the computation of the adversary given oracle access to a random element ofΓ ,2,so that the probability that b=1in the latter game is negligibly close to Pr[S0].Game1.[This is a transition based on indistinguishability.]We now modify Game0so that we use a truly random function from 1bits to 2bits,in place of F s.Intuitively, the pseudo-randomness property of F should guarantee that this modification has only a negligible effect on the behavior of the adversary.Algorithmically,Game1looks like this:。
依赖β beta的分块beta Bootstrap选择最佳块长度的包说明书

Package‘blocklength’October12,2022Type PackageTitle Select an Optimal Block-Length to Bootstrap Dependent Data(Block Bootstrap)Version0.1.5Maintainer Alec Stashevsky<***********************>Description A set of functions to select the optimal block-length for a dependent bootstrap(block-bootstrap).Includes the Hall,Horowitz,and Jing (1995)<doi:10.1093/biomet/82.3.561>cross-validation method and thePolitis and White(2004)<doi:10.1081/ETC-120028836>Spectral DensityPlug-in method,including the Patton,Politis,and White(2009)<doi:10.1080/07474930802459016>correction with a corresponding set of S3 plot methods.License GPL(>=2)Encoding UTF-8RoxygenNote7.1.2Suggests testthat,covr,parallel,knitr,rmarkdownImports tseries,statsURL https:///r/blocklength,https:///Alec-Stashevsky/blocklengthBugReports https:///Alec-Stashevsky/blocklength/issues VignetteBuilder knitrNeedsCompilation noAuthor Alec Stashevsky[aut,cre],Sergio Armella[ctb]Repository CRANDate/Publication2022-03-0223:50:02UTC12hhj R topics documented:hhj (2)plot.hhj (4)plot.pwsd (5)pwsd (6)Index8hhj Hall,Horowitz,and Jing(1995)"HHJ"Algorithm to Select the Opti-mal Block-LengthDescriptionPerform the Hall,Horowitz,and Jing(1995)"HHJ"cross-validation algorithm to select the optimal block-length for a bootstrap on dependent data(block-bootstrap).Dependent data such as stationary time series are suitable for usage with the HHJ algorithm.Usagehhj(series,nb=100L,n_iter=10L,pilot_block_length=NULL,sub_sample=NULL,k="two-sided",bofb=1L,search_grid=NULL,grid_step=c(1L,1L),cl=NULL,verbose=TRUE,plots=TRUE)Argumentsseries a numeric vector or time series giving the original data for which tofind the optimal block-length for.nb an integer value,number of bootstrapped series to compute.n_iter an integer value,maximum number of iterations for the HHJ algorithm to com-pute.pilot_block_lengtha numeric value,the block-length(l∗in HHJ)for which to perform initial blockbootstraps.sub_sample a numeric value,the length of each overlapping subsample,m in HHJ.hhj3 k a character string,either"bias/variance","one-sided",or"two-sided"de-pending on the desired object of estimation.If the desired bootstrap statistic isbias or variance then select"bias/variance"which sets k=3per HHJ.Ifthe object of estimation is the one-sided or two-sided distribution function,thenset k="one-sided"or k="two-sided"which sets k=4and k=5,respec-tively.For the purpose of generating symmetric confidence intervals around anunknown parameter,k="two-sided"(the default)should be used.bofb a numeric value,length of the basic blocks in the block-of-blocks bootstrap,see m=for tsbootstrap and Kunsch(1989).search_grid a numeric value,the range of solutions around l∗to evaluate within the MSE function after thefirst iteration.Thefirst iteration will search through all thepossible block-lengths unless specified in grid_step=.grid_step a numeric value or vector of at most length2,the number of steps to incre-ment over the subsample block-lengths when evaluating the MSE function.Ifgrid_step=1then each block-length will be evaluated in the MSE function.If grid_step>1,the MSE function will search over the sequence of block-lengths from1to m by grid_step.If grid_step is a vector of length2,thefirstiteration will step by thefirst element of grid_step and subsequent iterationswill step by the second element.cl a cluster object,created by package parallel,doParallel,or snow.If NULL,no parallelization will be used.verbose a logical value,if set to FALSE then no interim messages are output to the con-sole.Error messages will still be output.Default is TRUE.plots a logical value,if set to FALSE then no interim plots are output to the console.Default is TRUE.DetailsThe HHJ algorithm is computationally intensive as it relies on a cross-validation process using a type of subsampling to estimate the mean squared error(MSE)incurred by the bootstrap at various block-lengths.Under-the-hood,hhj()makes use of tsbootstrap,see Trapletti and Hornik(2020),to perform the moving block-bootstrap(or the block-of-blocks bootstrap by setting bofb>1)according to Kunsch (1989).Valuean object of class’hhj’ReferencesAdrian Trapletti and Kurt Hornik(2020).tseries:Time Series Analysis and Computational Finance.R package version0.10-48.Kunsch,H.(1989)The Jackknife and the Bootstrap for General Stationary Observations.The Annals of Statistics,17(3),1217-1241.Retrieved February16,2021,from http://www.jstor.org/stable/22417194plot.hhj Peter Hall,Joel L.Horowitz,Bing-Yi Jing,On blocking rules for the bootstrap with dependent data,Biometrika,V olume82,Issue3,September1995,Pages561-574,DOI:doi:10.1093/biomet/82.3.561Examples#Generate AR(1)time seriessim<-stats::arima.sim(list(order=c(1,0,0),ar=0.5),n=500,innov=rnorm(500))#Calculate optimal block length for serieshhj(sim,sub_sample=10)#Use parallel computinglibrary(parallel)#Make cluster object with2corescl<-makeCluster(2)#Calculate optimal block length for serieshhj(sim,cl=cl)plot.hhj Plot MSE Function for HHJ AlgorithmDescriptionS3Method for objects of class’hhj’Usage##S3method for class hhjplot(x,iter=NULL,...)Argumentsx an object of class’hhj’iter a vector of hhj()iterations to plot.NULL.All iterations are plotted by default....Arguments passed on to base::ploty the y coordinates of points in the plot,optional if x is an appropriate structure. ValueNo return value,called for side effectsplot.pwsd5 Examples#Generate AR(1)time seriessim<-stats::arima.sim(list(order=c(1,0,0),ar=0.5),n=500,innov=rnorm(500))#Generate hhj class object of optimal block length for serieshhj<-hhj(sim,sub_sample=10)##S3method for class hhjplot(hhj)plot.pwsd Plot Correlogram for Politis and White Auto−Correlation Implied Hy-pothesis TestDescriptionS3Method for objects of class’pwsd’See?plot.acf of the stats package for more customization options on the correlogram,from which plot.pwsd is basedUsage##S3method for class pwsdplot(x,c=NULL,main=NULL,ylim=NULL,...)Argumentsx an of object of class’pwsd’or’acf’c a numeric value,the constant which acts as the significance level for the impliedhypothesis test.Defaults to qnorm(0.975)for a two-tailed95%confidencelevel.Politis and White(2004)suggest c=2.main an overall title for the plot,if no string is supplied a default title will be popu-lated.See titleylim a numeric of length2giving the y-axis limits for the plot...Arguments passed on to base::ploty the y coordinates of points in the plot,optional if x is an appropriate structure. ValueNo return value,called for side effects6pwsdExamples#Use S3Method#Generate AR(1)time seriessim<-stats::arima.sim(list(order=c(1,0,0),ar=0.5),n=500,innov=rnorm(500))b<-pwsd(sim,round=TRUE,correlogram=FALSE)plot(b)pwsd Politis and White(2004)Spectral Density"PWSD"Automatic Block-Length SelectionDescriptionRun the Automatic Block-Length selection method proposed by Politis and White(2004)and cor-rected in Patton,Politis,and White(2009).The method is based on spectral density estimation via flat-top lag windows of Politis and Romano(1995).This code was adapted from b.star to add functionality and include correlogram support including an S3method,see Hayfield and Racine (2008).Usagepwsd(data,K_N=NULL,M_max=NULL,m_hat=NULL,b_max=NULL,c=NULL,round=FALSE,correlogram=TRUE)Argumentsdata an nxk data.frame,matrix,or vector(if k=1)where the optimal block-length will be computed for each of the k columns.K_N an integer value,the maximum lags for the auto-correlation,rho k,which to apply the implied hypothesis test.Defaults to max(5,log(N)).See Politis andWhite(2004)footnote c.M_max an integer value,the upper-bound for the optimal number of lags,M,to compute the auto-covariance for.See Theorem3.3(ii)of Politis and White(2004).pwsd7 m_hat an integer value,if set to NULL(the default),then m_hat is estimated as the smallest integer after which the correlogram appears negligible for K_N lags.Inproblematic cases,setting m_hat to an integer value can be used to override theestimation procedure.b_max a numeric value,the upper-bound for the optimal block-length.Defaults to ceiling(min(3*sqrt(n),n/3))per Politis and White(2004).c a numeric value,the constant which acts as the significance level for the impliedhypothesis test.Defaults to qnorm(0.975)for a two-tailed95%confidencelevel.Politis and White(2004)suggest c=2.round a logical value,if set to FALSE then thefinal block-length output will not be rounded,the default.If set to TRUE thefinal estimates for the optimal block-length will be rounded to whole numbers.correlogram a logical value,if set to TRUE a plot of the correlogram(i.e.a plot of R(k)vs.k)will be output to the console.If set to FALSE,no interim plots will be outputto the console,but may be plotted later using the corresponding S3method,plot.pwsd.Valuean object of class’pwsd’ReferencesAndrew Patton,Dimitris N.Politis&Halbert White(2009)Correction to"Automatic Block-Length Selection for the Dependent Bootstrap"by D.Politis and H.White,Econometric Review,28:4,372-375,DOI:doi:10.1080/07474930802459016Dimitris N.Politis&Halbert White(2004)Automatic Block-Length Selection for the Dependent Bootstrap,Econometric Reviews,23:1,53-70,DOI:doi:10.1081/ETC120028836Politis,D.N.and Romano,J.P.(1995),Bias-Corrected Nonparametric Spectral Estimation.Journal of Time Series Analysis,16:67-103,DOI:doi:10.1111/j.14679892.1995.tb00223.xTristen Hayfield and Jeffrey S.Racine(2008).Nonparametric Econometrics:The np Package.Journal of Statistical Software27(5).DOI:doi:10.18637/jss.v027.i05Examples#Generate AR(1)time seriessim<-stats::arima.sim(list(order=c(1,0,0),ar=0.5),n=500,innov=rnorm(500))#Calculate optimal block length for seriespwsd(sim,round=TRUE)#Use S3Methodb<-pwsd(sim,round=TRUE,correlogram=FALSE)plot(b)Indexb.star,6base::plot,4,5hhj,2plot.hhj,4plot.pwsd,5,7pwsd,6title,5tsbootstrap,38。
全球数学网址大全

全球数学网址大全数理逻辑、数学理论AILAhttp://www.disi.unige.it/aila/eindex.html意大利逻辑及其应用协会的主页,包括意大利数理逻辑领域的相关内容。
Algebra and Logic/title.cgi?2110《代数与逻辑》,《西伯利亚代数与逻辑期刊》的翻译版,荷兰的Kluwer学术出版社提供其在线服务。
alt.math.undergrad-Math Forum/epigone/alt.math.undergradMsth Forum上的大学生和研究生数学论坛,提供档案文件、论题等信息。
Annals of Pure and Applied Logic/~dmjones/hbp/apal/《纯逻辑与应用逻辑学年鉴》,麻省理工大学计算理论小组主页提供其过刊的浏览,荷兰的Elservier出版社提供其电子刊的在线服务。
Archive for Mathematical Logichttp://link.springer.de/link/service/journ...00153/index.htm《数学逻辑档案》,属于德国Springer出版公司在线电子期刊的一种。
Aristotle and the Paradoxes of Logic-Gilbert Voeten/nilog/files/arist...adoxes_of_l.htm亚里士多德及其逻辑理论研究。
BLC/~exr/blc/不列颠逻辑研讨会的主页,包括数学逻辑的相关研究,如相关网站及电子期刊。
Books:Professional&Technical:Professional Science: /exec/obidos/tg/brows...3600008-7001844浏览亚马逊网上专业和技术店中的数学畅销书,提供应用范畴,混沌与系统化;几何与拓扑;数学分析;数学物理学;数字规律;纯数学;数学变换等领域,包括数理逻辑方面的畅销书的在线预览。
OEIS

OEIS以下是百度的:OEIS全称为:The On-Line Encyclopedia of Integer Sequences™(OEIS™)是一个关于整数序列(数列)的专业型网站,是一个关于组合数学研究的重要的网站,里面包含了众多数列的研究成果,读者可以直接查询里面的内容,里面除了包含各种结论,还附有各个结论的论文出处,作者,著作时间等等信息,方便读者查询。
查询方法:一、输入名称:在搜索栏中,输入序列(数列)的名称,例如Catalan,即可查询到所有有关Catalan序列的信息,包括Catalan序列以及其他论文中涉及到Catalan序列的内容。
二、输入数字:对于一些不清楚名称的数列,OEIS也提供直查询方法。
在搜索栏中,输入数字列(数字之间用英文的逗号“,”分隔),例如1,2,3,6,11,23,47,106,235,输入的个数没有限制,但是数字越多,查询结果越精确,因为OEIS里面的序列太多了,所以如果数字太少,你会在很多结果中寻找自己所需要的序列,很费时间。
以A000055为例子搜索的时候输入A00005、M0791、N0299最终搜索的结果是一样的,后两个是第一个之前所存在的搜索。
出现的一段数据:是搜索出来的一个数列,关于这个数列有以下的相关信息:(list; graph; refs; listen; history; text; internal format)列表、图、涉及(在其他数列中所提及到A00005)、听(里面可以播放一些东西,没有明白)、记事本(关于这个数列的文本形式)、内部格式OFFSET:移动偏移量COMMENTS:解说,关于这个数列的一些解释说明,涉及到一些数列也会在这里面标注出来。
REFERENCES:参考,一些人研究及其姓名、研究时间会在这里面标注出来。
LINKS:链接,在REFERENCES出现的一部分人会在这里面给出链接网址,方便读者参考已有的研究成果。
FORMULA:公式,在这里面会给出推导公式EXAMPLE:关于这个数列举例说明MAPLE:(未看懂)MATHEMATICA:一些研究者给出的有关数学方便的知识(我理解的可能是一些已有的数学公式的定义)PROG:前卫,我理解的是最近一些人的一些研究成果,在这里给出了研究者的姓名以及链接,可以点进去进行参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Article 03.1.5Journal of Integer Sequences, Vol. 6 (2003),OBJECTS COUNTED BY THE CENTRAL DELANNOY NUMBERSROBERT A.SULANKEAbstract.The central Delannoy numbers,(d n)n≥0=1,3,13,63,321,1683,8989,48639,...(A001850of The On-Line Encyclopedia of Integer Sequences)will be defined so that d ncounts the lattice paths running from(0,0)to(n,n)that use the steps(1,0),(0,1),and(1,1).In a recreational spirit we give a collection of29configurations that these numberscount.1.IntroductionIn the late nineteenth century,Henri Delannoy[4]introduced what we now call the Delannoy array.For integers i and j,we define this array d i,j to satisfyd i,j=d i−1,j+d i,j−1+d i−1,j−1with the conditions d0,0=1and d i,j=0if i<0or j<0.The members of the se-quence(d i)i≥0:=(d i,i)i≥0=1,3,13,63,321,1683,8989,48639,...(A001850of Sloane[15]), are known as the(central)Delannoy numbers.d i,j:=i\j01234 011111 113579 215132541 3172563129 41941129321In Section3we will show that the generating function for the central Delannoy numberssatisfiesi≥0d i z i=1√1−6z+z2.(1)An alternative derivation of this is given by Stanley[16,Sect.6.3].These numbers satisfy the recurrence,(n+2)d n+2=3(2n+3)d n+1−(n+1)d n.(2) subject to d0=1and d1=3,as shown,e.g.,by Stanley[16,Sect.6.4]and the author[18].12We refer the question,“Why Delannoynumbers?”,to the survey on the life and works of Delannoy written by Banderier and Schwer [1].While the (central)Delannoy numbers are known through the books of Comtet [3]and Stanley [16],only a few examples of objects enumerated by these numbers have been found in the literature.These examples will appear and be referenced in the following sections.After Delannoy’s introduction of the numbers,essentially as counting unrestricted paths that use the steps (0,1),(1,0),and (1,1),they appear again in 1952,when Lawden [8],with-out citing Delannoy,found them to be the values of the Legendre polynomials with argument equaling 3.However,the definition of the Legendre polynomials does not appear to foster any combinatorial interpretation leading to enumeration.See also Moser and Zayachkowski[9].In the following section we give a catalog of 29configurations counted by the (central)Delannoy numbers,ordered primarily as they were collected.In keeping with Delannoy’s interest in recreational mathematics,this catalog is intended to constitute exercises inviting bijective,recursive,and generating functional proofs that the Delannoy numbers do indeed count the configurations.Each example is accompanied by an illustration of a set of configu-rations corresponding to d 2=13.Section 3contains intentionally incomplete notes regarding some bijective and generating functional verifications for the examples.The collector wishes to thank Cyril Banderier,Emeric Deutsch,Enrica Duchi,Ira Gessel,Sylviane Schwer,Lou Shapiro,and Renzo Sprugnoli for their contribution to this project.He also appreciates the referee’s generous critique.2.A catalog of configurationsIn the integer plane,we will take lattice paths to be represented as concatenations of the directed steps belonging to various specified sets.When the steps are weighted,the weight of a path is the product of the weights of its steps,and the weight of a path set is the sum of the weights of its paths.As noted in the remark following Example 3,the independent coloring of substructures on paths is equivalent to weighting.Throughout,we will denote the diagonal up and down steps as U :=(1,1)and D :=(1,−1).Example 1.A classic example is the set of paths from (0,0)to (2n,0)using the steps U ,D ,and (2,0).For the “tilted”version consider the path from (0,0)to (n,n )using the steps (0,1),(1,0),and (1,1).From this path model one can obtain a combinatorial proof that,for n ≥0,d n =n k =0n k n +k k .(3)Figure 1.The d 2=13unrestricted paths from (0,0)to (2n,0)using thesteps U ,D ,and (2,0).3Example 2.The Delannoy number d n is the weight of the set of paths from (0,0)to (n,0)using the steps U 2,D ,and (1,0)3,where the up step U 2and the horizontal step (1,0)3have weights 2and 3,respectively.Alternatively,d n counts the paths from (0,0)to (n,0)using the steps U ,D ,and (1,0),where the U steps are independently colored blue or red and the (1,0)steps are independently colored blue,red,or green.See the remark following Example3.Figure 2.Here 2+2+3·3=d 2Example ing the steps U and D ,we find d n to be the weighted sum of the paths from (0,0)to (2n,0)where within each path the right-hand turns,or peaks ,have weight 2.Consequently,one can obtain a combinatorial proof that,for n ≥0,n i =0n i 22i =d n .(4)Figure 3.The sum of the weights of the paths is 2+4+2+2+2+1=d 2.Remark:Often,as in Examples 3,we will consider paths with substructures –such as peaks,double ascents,etc.–which make a multiplicative contribution of 2to the weight of each path.Other such examples include 4,5,14,20,21,24,25,26,and 27.If momentarily the weights of the substructures is reduced to 1,then the weight of a set of such paths becomes a cardinality,namely the central binomial coefficient, 2n n .Indeed,in the figures for the above named examples,there will be 42 =6shapes in each illustration.However,when the substructures have weight 2,the weight of the set of such paths is a Delannoy number,which in turn is the cardinality of the paths of same shapes on which the substructures are independently colored Blue or Red.In this catalog we will usually omit versions of examples with Blue-Red substructures,which would yield 13shapes instead of 6shapes in the relevant illustrations.4ing the steps U and D,wefind that d n is the sum of the weights of the paths from(0,0)to(2n+1,1)that begin with an up step and where the intermediate vertices of double ascents have weight2.Figure4.The sum of the weights of the paths is4+2+2+2+1+2=d2.ing the steps U and D,wefind that d n is the weighted sum over the paths from(0,0)to(2n,0)where each U step which is oddly positioned along its path has weight 2.Figure5.The sum over the weights of the paths is2+4+2+2+1+2=d2.Example6.The product2n−1d n counts the set of all paths from(0,0)to(n,n)with steps of the form(x,y)where x and y are nonnegative integers,not both0.Figure6.Here2n−1d n=2·13,for n=2.5Example ing the steps U 2,D ,and (2,0)−1where the up step and the horizontal step have weights of 2and −1,respectively,d n is the sum of the weights of the paths running from (0,0)to (2n,0).1–2–2–244Figure 7.The sum over the paths is 13.Example 8.Here we consider a second moment for a path ing the steps U,D,and (2,0),for the elevated (Schr¨o der)paths running from (0,0)to (2n +2,0),we find that d n is the sum,over its paths,of the average of the positive squared heights of the lattice points traced by eachpath.Figure 8.Within each path the squared heights are additive.115+195+55+8+8+14=65=d 2.Example 9.We consider another second moment .Consider the elevated Schr¨o der paths running from (0,0)to (2n +2,0)where within each path the noninitial up step and the horizontal steps have weights 2and −1,respectively.Here d n is the sum of the weighted average of the positive squared heights of the lattice points traced by eachpath.–28–16–1657644Figure 9.The sum over the paths is 44+76+5+(−16)+(−16)+(−28)=d 2.6Example10.We consider one more second moment.Take the elevated paths running from (0,0)to(n+2,0)using the steps U,D,and(1,0),where the noninitial U steps have weight 2and the unit horizontal steps have weight3.Here d n is the sum of the weighted average of the positive squared heights of the lattice points traced by each path.Figure10.The sum over the paths is2(1+4+1)+3·3(1+1+1)=d2.Example11.Here we will define a zebra to be a parallelogram polyomino whose noninitial columns are either white or gray.For any zebra,its average diagonal thickness squared will be the average of the squares of the number of unit cells along each–45degree diagonal passing through the center of the cells.The sum,over all zebras of afixed perimeter2n+4, of the average diagonal thickness squared is the Delannoy number d n.Figure11.The sum of the average diagonal thickness squared is1+1+13+2(1+1+1)3+2(1+4+1)3+2(1+1+1)3+4(1+1+1)3=d2.Example12.The number d n counts the domino tilings of the Aztec diamond of width2n having an additional center row.Figure12.d2tilings.7 Example13.Consider counting matchings in the comb graph.For a comb with2n teeth, there are d n ways to have an n-set of non-adjacent edges.Figure13.The d22-matchings in the comb with2·2teeth.Example14.In a lattice path using the steps U and D,a long,is a maximal subpath having at least two steps,all of the same type.The number d n is the weighted sum over the paths running from(0,0)to(2n+1,1)which begin with a U step and whose nonfinal longs have the weight2.Figure14.The sum of the weights of the paths is2+2+4+2+1+2=d2. Example15.Consider the walks that begin at the origin and use the unit steps:east(E), west(W),and north(N).If these walks never start with W and are self-avoiding,that is, E and W are nonadjacent,then d n counts the walks with2n steps andfinal height n.Figure15.d2walks.8Example16.The number d n counts the ways to distribute n white and n black balls into r labeled urns where r takes on the values from n to2n and where each urn is nonempty and does not contain more than one ball of each color.(The balls are unlabeled and are ordered so that white precedes black when two are present in an urn.)Figure16.d2balls-in-urns distributions.Example17.The number d n counts the words from the alphabet{a,b,{a,b}}where the total occurrences of a and b in each word is n.{a,b}{a,b},{a,b}ab,{a,b}ba,a{a,b}b,b{a,b}a,ab{a,b},ba{a,b},aabb,abab,abba,baab,baba,bbaaFigure17.d2words.Example18.In Z n,d n counts the n-dimensional lattice points inside or on the hyperocta-hedron with vertices on the axes located a distance n from the origin.More specifically,for z=(z1,...,z n)∈R n,let||z||1denote the norm n i=1|z i|.Then d n=|{y∈Z n:||y||1≤n}|.Figure18.For n=2,d2=13is the number of lattice points inside thesquare region{(x,y):|x|+|y|≤2}.9 Example19.The number d n counts the set of paths using the three steps types,U,D,and (2,0),running from(0,0)to the line x=2n,and remaining weakly above the x-axis.Figure19.The paths running from(0,0)to the line x=4and remainingweakly above the x-axis.Example20.For the steps U and D,d n is the weighted sum of the paths running from (0,0)to the line x=2n and remaining weakly above the x-axis,where within each path the right-hand turns have weight2.Figure20.The sum of the weights of the paths is4+2+1+2+2+2=d2. Example21.For the steps U and D,d n is the weighted sum of the paths running from (0,0)to the line x=2n and remaining weakly above the x-axis,where within each path each long has weight2.Here a long is a maximal subpath of the same step type of length exceeding one.Figure21.The sum of the weights of the paths is1+4+2+2+2+2=d2.10Example 22.Consider the known array extending the large Schr¨o der numbers:namely,for integers i and j ,we define this array r i,j to satisfyr i,j =r i −1,j +r i,j −1+r i −1,j −1with the conditions r 0,0=1and r i,j =0if j <0or i <j .The members of the sequence (r i )i ≥0:=(r i,i )i ≥0=1,2,6,22,90...are known as the large Schr¨o der numbers.The central Delannoy number d n is the sum of the 2n +1-st diagonal,that is d n = i r i,2n −i .r i,j :=i \j0123401000011200021460031616220418306890Figure 22.An array of the extended large Schr¨o der numbers.Here 1+6+6=d 2.Example 23.Let T (n )denote the set of plane trees with 2n +1edges,with roots of odd degree,with the non-root vertices having degree 1(for the leaves),2,or 3,and with an even number of vertices of degree two between any two vertices of odddegree.Figure 23.The specified trees counted by d 2.Example 24.A high peak is the intermediate vertex of a UD pair with ordinate exceeding1.Let P (n,k )denote the set of paths using the steps U and D ,running from (0,0)to (n,0),remaining weakly above the x-axis,intersecting the x-axis k times,and having high peaks of weight2.Then the Delannoy number counts a union of sets:d n = n +1 i =1P (2n +2i,2i ) .11Figure 24.4+2+2+2+2+1=d 2.Example 25.A double ascent (or double rise )is just a consecutive UU pair.Let P (n,k )denote the set of paths using the steps U and D ,running from (0,0)to (n,0),remaining weakly above the x-axis,intersecting the x-axis k times,and having double ascents of weight2.Then the Delannoy number counts a union of sets:d n = n +1 i =1P (2n +2i,2i ).Figure 25.2+4+2+2+2+1=d 2.Example 26.Let P (n,k )denote the set of paths using the steps U and D ,running from (0,0)to (n,0),remaining weakly above the x-axis,intersecting the x-axis k times,and evenly positioned ascents of weight 2.Then the Delannoy number counts a union of sets:d n = n +1 i =1P (2n +2i,2i ).Figure 26.4+2+2+2+2+1=d 2.Example 27.On a path using the steps U and D ,a restricted long is a maximal subpath of a single step type having length exceeding 1,except when the subpath ends at the x-axis,in which case the length of the subpath must exceed 2.Let P (n,k )denote the set of paths using the steps U and D ,running from (0,0)to (n,0),remaining weakly above the x-axis,intersecting the x-axis k times and having restricted longs of weight 2.Then the Delannoy number counts a union of sets:d n = n +1 i =1P (2n +2i,2i ) .12Figure 27.2+4+2+2+2+1=d 2.Example 28.The central Delannoy number d n counts the matrices with 2rows and entries 0or 1such that there are exactly n 1’s in each row and at least one 1in each column.1111 110101 101110 110011 011110101011 011101 110000111010010110010110 01101001 0101101000111100 Figure 28.There are d 2such matrices.Example 29.The product 2n −1d n counts the matrices having two rows and nonnegative integer entries where each row sum is n and each column has at least one positive entry.2220020220 200011 020101 002110011200 101020 110002 2011 02111120 1102 Figure 29.2·d 2counts the set formed by these matrices and those of Figure 28.3.Notes regarding verificationsBefore reviewing the above examples,let us look at a mildly general lattice path model.For fixed positive integer h ,we will allow the three steps U t ,D ,and (h,0)s which are weighted by t ,1,and s ,respectively.For n ≥0,let U (n )denote the set of all unrestricted paths running from (0,0)to (n,0),and let C (n )denote the set of paths in U (n )constrained never to pass beneath the horizontal axis.We will use a well-known decomposition of path sets to derive formulas for the generating functions c (z ):= n ≥0|C (n )|z n and u (z ):= n ≥0|U (n )|z n .13 Since each path of C(n)must either(i)have zero length,(ii)start with an(h,0)step followed by a constrained path,or(iii)start with an U step followed by the translation of a constrained path,then by a D,andfinally by another constrained path we havec(z)=1+sz h c(z)+tz2c(z)2.Since every path in U(n)either(i)has zero length,(ii)begins with an(h,0)step followed by an unrestricted path,or(iii)begins with U(or with D)followed by a constrained path (or its reflection)which returns to the horizontal axis for thefirst time and then is followed by an unrestricted path,u(z)=1+sz h u(z)+2tz2c(z)u(z)Solving these two equations simultaneously yieldsu(z)=1(1−sz)−4tz=1√.If this formula is to agree essentially with the formula of(1),then either h=1or h=2.If h=1,then u(z)=1/ 1−2sz+(s2−4t)z2,and it must be that s=3and t=2.On the other hand,if h=2,then u(z)=1/ 1−(2s+4t)z2+s2z4,and thus either s=t=1or s=−1and t=2.We number the subsequent Notes to agree with the numbering of the examples of Section 2.Since the examples may serve as exercises and since they are ordered as collected,these notes may appear mildly haphazard.Note1The introductory discussion of this section gives the generating function for Example 1.One canfind an alternate derivation of the generating function and a recurrence in[20, Sect.6].Equation(3)can be obtained by considering all possible choices for the steps in the paths leading to(n,0).Note2That the Delannoy numbers count Example2follows from the initial discussion of this section.In Note5we will see how Example2is bijectively related to Example1via Examples3and5.Note3Replicate the paths from(0,0)to(2n,0)using the steps U and D by independently coloring their right-hand turns by blue or red.Replacing each consecutive blue UD by a (2,0)step describes a bijection with Example1.Note4We will indicate a bijection from Example4to a reflected Example3,reflected about the horizontal axis.The following proof is from the proof of[21,equation(5)].We will also tilt our lattice paths by45degrees for the following.Consider the steps N:=(0,1)and E:=(1,0).Let A(n)denote the set of all paths from (0,−1)to(n,n)which remain weakly above the horizontal axis except on thefirst step.A left turn is the intermediate point of a consecutive EN pair.Let A (n)(A d(n),resp.) denote the set of replicated paths formed from A(n)so each left turn(double ascent,resp.) is independently colored blue or red.14We have a bijectionF :A d (n )−→A (n )defined as follows:Let P ∈A d (n )be determined by the set (perhaps empty)of the coordinates of its left turns,namely {(x 1,y 1),...,(x k ,y k )}.Then (x 1,y 1),...,(x h ,y h ),...,(x n −k ,y n −k )are the left turns of the path F (P )∈A (n )(This was mistyped in [21].)where{x 1,...,x n −k }={1,...,n }−{x 1,...,x k }{y 1,...,y n −k }={0,...,n −1}−{y 1,...,y k }with x 1<x h <x n −k and y 1<y h <y n −k and the left turn at (x h ,y h )has the color blue (red,resp.)if,and only if,y h is the ordinate of the intermediate vertex of a blue (red,resp.)double ascent on P .See also Note 14.Note 5A.Each path in Example 5is sequence of consecutive oddly-evenly positioned step pairs.The morphism sending UU to U ,UD to (1,0)2,DU to (1,0)1,and DD to D (where its subscripts indicate the weights)determines a weight preserving bijection from Example 5to Example 2.B.We give a bijection from Example 5to Example 1,which constitutes a combinatorial solution for the Monthly problem [22].Our bijective proof is in the 45-degree tilted environ-ment.In the following we will encode each path from each of the two examples as a triple of subsets of integers of the form (X,Y,H )where X :={x 1,...,x h ,...,x i }⊂{1,...,n },Y :={y 1,...,y h ,...,y i }⊂{1,...,n },and H :={h 1,...,h j }⊂{1,...,i }where i and j depend on the path.Since there will be a unique encoding triple for each path from each model we will have a bijection.Let A (n )denote the set of lattice paths from (0,0)to (n,n )that permit four step types:the horizontal step (1,0),the uncolored step (0,1)where this vertical step may assume only even positions in a path,and the steps (0,1)red or (0,1)green where these vertical steps may assume only odd positions in a path.Any path in A (n )having i of its horizontal steps in the even positions,2x 1,...,2x h ,...,2x i ,having necessarily i of its vertical steps in the odd positions,2y 1−1,...,2y h −1,...,2y i −1,and having exactly j red steps in positions,2y h 1−1,...,2y h j −1,can be encoded as (X,Y,H ).Let D (n )denote the set of lattice paths from (0,0)to (n,n )that permit the three step types:(1,0),(0,1),and the diagonal,(1,1).By replacing each diagonal step with a blue (0,1)(1,0)step pair (i.e.,a blue right-hand turn ),we can match each path in D (n )having j diagonal steps and i −j uncolored right-hand turns with a marked path from (0,0)to (n,n )that uses the two steps,(1,0)and (0,1),and has marked right-hand turns.Each resulting marked path is determined by the coordinates of the intermediate vertices of its right-hand turns,say,(x 1−1,y 1),...,(x h −1,y h ),...(x i −1,y i ),where those turns corresponding to y h 1,...,y h j are colored blue.Hence,each path can be encoded as (X,Y,H ).See also Note 14.Note 6This example appears as exercise [16,6.16]where a generating function proof is indicated.A combinatorial proof,as requested in [16],appears in [21]and uses some of the bijections of these notes.15 Note7That the Delannoy numbers count this example follows from the initial discussion of Section3.Presently we have no ideas for bijective considerations.Note8A generating function argument,and consequently,the recurrence(2)for Example 8appear in[20].The cut and paste bijection of[10]gives an immediate bijection between this example and Example1.Note9The cut and paste bijection[10]gives an immediate bijection between this example and Example7.Note10The cut and paste bijection[10]gives an immediate bijection between this example and Example2.See Note11.Note11In[18]a zebra is defined as a parallelogram polyomino having all(not just the noninitial)columns colored either black or white.In[18]generation function methods show that the sum of the average of the squares of the diagonal thicknesses of all zebras of afixed perimeter is twice a Delannoy number.By extending the known bijection given in[5](See also[18,Sect.5].),we have a bijection between the configurations of Example11and those of Example10.Note12Sachs and Zernitz[11]discovered this example and its solution,giving them in terms of counting perfect matchings.Stanley[16,Exercise6.49]records Dana Randell’s restatement of the example and its solution in terms of Aztec diamonds.Note13For m=1,2,3,...,let COMB m denote the comb graph with m teeth.This graph has vertex set{1,2,...,2m}and edge set{{1,2},{3,4},...,{2m−1,2m}}∪{{2,4},{4,6},...,{2m−2,2m}}.In addition to the example for d n,Emeric Deutsch[6]discovered that the collection of sets of k pairwise nonadjacent edges of COMB m has cardinality d k,m−k.To see this one can establish a bijection from this collection to the collection of paths from(0,0)to(k,m−k) using the steps(0,1),(1,0),(1,1).In particular,this bijection maps a set with j edges of the type{2i,2i+2}to a path with j steps of type(1,1).Note14For Dyck paths(i.e.,paths running from(0,0)to(2n,0),using the steps U and D,and never running below the x-axis)there are many statistics which are distributed by the Narayana numbers[17]:namely,for1≤k≤n,1n n k−1 n k .The three classic statistics are(i)the number of peaks(This is immediately equivalent both to number of valleys plus one and to the number of double ascents plus one.),(ii)the number of ascents which are oddly positioned along the path,and(iii)the number of nonfinal longs plus one.(See Examples3,4,and5.The plus one term is unavoidable–it is in agreement with the need for both small and large Schr¨o der numbers.(See[19].)16For unrestricted paths,if one assign a weight of2to each object(or substructure)counted by those statistics,computes the weight of each path,and then sums over the paths of a given length,one arrives at the Delannoy number as in Examples3,4,5,and14.That the assignment of the weight2to each objects counted by certain statistics yields a Delannoy number is in agreement with equation(4).Kreweras and Moszkowski[7]introduced the number of nonfinal longs statistic for Dyck paths.Benchekroun and Moszkowski[2]then gave a bijective proof that this statistic indeed has the Narayana distribution:The number of Dyck paths of length2n,having k nonfinal longs is|D(n,k)|=1nn k n k+1 .(5)We use their proof to obtain a bijection between Example14and a modified Example3, modified as to be in terms of left-hand turns(i.e.,valleys,not peaks).To obtain the domain for this bijection we tilt the paths of Example14to run from(0,−1)to(n,n)weakly above the x-axis except on thefirst step and to use the steps(0,1)and(1,0).The codomain will be the set of paths from(0,0)to(n,n)with the unit steps(0,1)and(1,0).If(x1,y1),..., (x h,y h),...,(x j,y j)denote the locations of the next to thefinal lattice points on the long steps of a path in the domain,then(x1+1,y1),...,(x h+1,y h),...,(x j+1,y j−h)will be the locations of the left-hand turns of the image path.Note15Louis Shapiro[13]discovered this example.A bijection with the tilted version of Example1can be established recursively.Let W(x,y)denote the set of lattice walks of the Example15that have x+y steps andfinal height y.Let U(x,y)denote the set of lattice path running from(0,0)to(x,y)that use the steps E:=(1,0),N:=(0,1),and D:= (1,1).We define f:=W(x,y)→U(x,y)so that f(P E)=f(P)E,f(P W W)=f(P W)E, f(P NW)=f(P)D,and f(P N)=f(P)N.With the obvious boundary conditions for x=0 or y=0,f can be shown to be bijective.Note16This and the next example were found by Sylviane Schwer[12]and her interest in the Delannoy numbers resulted in[1].More generally,she considered unlabeled balls of m colors with p i balls having color i,for i=1...m.For =max(p1,p2,...,p m)and u=p1+p2+···+p m,she made available u− +1collections of urns where each collection has r urns,labeled by1,2,...,r,for ≤r≤u.With D(p1,p2,...,p m)denoting the ways to distribute the balls so that in each urn there is a ball and no two balls have the same color,she showed that D(p1,p2,...,p m)is isomorphic to the lattice paths in m-space that run from(0,0,...,0)to(p1,p2,...,p m)using the nonzero steps of the form( 1, 2,..., m) where i∈{0,1}.(See[14]for a discussion of multidimensional Delannoy numbers.)Note17Continuing from note16,Schwer formulated the enumeration of possible words which take as their alphabet nonempty subsets of some set X={x1,x2,...,x m}.If||f||x denotes the number of occurrences of x in the subsets forming a word f,then the Parikhvector of f is denoted by(||f||x1,||f||x2,...,||f||xm).The set of words with a Parikh vectorequal to(p1,p2,...,p m)has the cardinality of D(p1,p2,...,p m).Note18This example was found by M.Vassilev and K.Atanassov[23].See Math Rev.: 96b:05004.More generally,their paper proves that d p,q counts{y∈Z p:||y||1≤q}.17 Note19Let P(x0)denote the set of unweighted paths using the steps,(1,1)and(1,−1), beginning at(0,0),ending on the line x=x0,and remaining weakly above the x-axis.Then|P(2k)|=2k k .(6)To see(6),wefirst observe that the manner in which the paths of P(2k−1)can be appended to form paths of P(2k)implies|P(2k)|=2|P(2k−1)|.Likewise,|P(2k−1)|=2|P(2k−2)|−c k−2,where c k−2= 2k−2k−1 /k is the Catalan number counting the paths in P(2k−2)which terminate at(k−2,0).Since the central binomial coefficient satisfies 2k k =4 2k−2k−1 −2c k−2, (6)follows inductively.To verify this example we count the ways to insert n−k(2,0)-steps into any path of P(2k).Hence,k 2k k n+k n−k = k(2n)!k!k!(n−k)!= k n k n+k k =d n.Note20Example20follows by labeling the peaks of Example19red and replacing the (2,0)-steps by a blue(1,1)(1,−1)pair.It would be interesting tofind a bijection involving an even earlier example.Note21Let D(n,k)denote the set of lattice paths running from(0,0)to(n,0),using the steps U and D,never passing beneath the x-axis,and having k non-final longs.By Note 14,|D(n,k)|has the the Narayana distribution.Let L(n,k)denote the set of lattice paths running from(0,0),having n steps of types U and D,never passing beneath the x-axis,and having k longs.Since∪n>0D(n,k)can be decomposed with respect to the point offirst return to the x-axis,we have,for d:=d(x,t)= n≥0 k≥0|D(n,k)|t k x n,d=1+x2d+x2t(d−1+(t−1)x2d)(d−1)+x2(d+(t−1)x2d).(7) Here the next-to-the-last term corresponds to an intermediatefirst return to the x-axis;hence thefirst t is required to count the nonfinal long assumed by the D steps at that return.The (t−1)x2factors assure that initial double ascents followed by D steps are counted as being long.Since∪n>0L(n,k)can be decomposed with respect to whether or not paths return to the x-axis for a last time,we have,for := n≥0 k≥0|L(n,k)|t k x n,=1+x2 +x2t(d−1+(t−1)x2d) +x( +(t−1)x+(t−1)x2 ).(8) The factors t,(t−1)x,and(t−1)x2are required somewhat as indicated in the above paragraph.Equations(7)and(8)easily yield,with the middle formula discounting paths of odd length,n k|L(2n,k)|2k x n= (z,2)+ (−z,2)2=1√.Note22The reader can establish a simple bijection between the paths giving the counts in this array and the paths of Example19.。
