WECOST培训例题(new)

合集下载

非学科数学学培训三角函数的应用

自学资料一、解直角三角形的应用（方向角问题）【知识探索】1．方向角：以观测者的位置为中心，将正北或正南方向作为起始方向，旋转到目标的方向线所成的小于90°的角，通常表达成北（南）偏东（西）* 度.若正好为45°，则表示为西（东）南（北）．【错题精练】例1．如图，某轮船在海上以每小时40海里的速度向正西方向航行，上午八点在C处测得小岛A在北偏东30度方向，上午九点船到达B处，测得岛A在北偏东45度方向，求点C和小岛A之间的距离．第1页共14页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训例2．如图，某轮船在海上向正东方向航行，上午8:00在点A处测得小岛O在北偏东60°方向，之后轮船继续向正东方向行驶1.5行驶到达B处，这时小岛O在船的北偏东30°方向．（1）求轮船从A处到B处的航速；（2）如果轮船按原速继续向东航行，还需经过多少时间轮船才恰好位于小岛的东南方向？例3．如图，某渔船向正东方向以12海里/时的速度航行，在A处测得岛C在北偏东的60∘方向，1小时后渔船航行到B处，测得岛C在北偏东的30∘方向，已知该岛周围10海里内有暗礁．（1）B处离岛C有多远？（2）如果渔船继续向东航行，有无触礁危险？例4．如图，轮船沿正南方向以30海里/时的速度匀速航行，在M处观测到灯塔P在西偏南68°方向上，航行2小时后到达N处，观测灯塔P在西偏南46°方向上，若该船继续向南航行至离灯塔最近位置，则此时轮船离灯塔的距离约为（由科学计算器得到sin68°=0.9272，sin46°=0.7193，sin22°=0.3746，sin44°=0.6947）（）第2页共14页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训A. 22.48B. 41.68C. 43.16D. 55.63例5．气象台预报，一台风中心在位于某沿海城市A的南偏东30°方向且距A市300千米的海面B处，正以20千米/时的速度沿正北方向移动（如图所示）．在离台风中心250千米的范围内将受台风影响．（1）A城市是否会遭受台风影响？（2）若受影响，受影响的时间是多长？【举一反三】1．在一次夏令营活动中，小明同学从营地A出发，要到A地的北偏东60°方向的C处，他先沿正东方向走了200m到达B地，再沿B地北偏东30°方向走，恰好到达目的地C处，那么，由此可知，B，C两地相距为（）A. 100mB. 150mC. 200mD. 250m2．如图，一艘轮船以40海里/时的速度在海面上航行，当它行驶到A处时，发现它的北偏东30°方向有一灯塔B．轮船继续向北航行2小时后到达C处，发现灯塔B在它的北偏东60°方向．若轮船继续向北航行，那么当再过多长时间时轮船离灯塔最近？（）第3页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训A. 1小时B. 小时C. 2小时D. 小时3．在东西方向的海岸线l上有一长为1km的码头MN（如图），在码头西端M的正西19.5km处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°，且与A相距40km的B处；经过1小时20分钟，又测得该轮船位于A的北偏东60°，且与A相距km的C处．（1）求该轮船航行的速度（保留精确结果）；（2）如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸？请说明理由．4．钓鱼岛自古以来就是我国的神圣领土，为维护国家主权和海洋权利，我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理．如图，某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B，B船在A船的正东方向，且两船保持20海里的距离，某一时刻两海监船同时测得在A的东北方向，B 的北偏东15°方向有一我国渔政执法船C，求此时船C与船B的距离是多少．5．如图，有一艘渔船在捕鱼作业时出现故障，急需抢修，调度中心通知附近两个小岛A、B上的观测点进行观测，从A岛测得渔船在南偏东37°方向C处，B岛在南偏东66°方向，从B岛测得渔船在正西方向，已知两个小岛间的距离是72海里，A岛上维修船的速度为每小时20海里，B岛上维修船的速度为每小时28.8海里，为及时赶到维修，问调度中心应该派遣哪个岛上的维修船？第4页共14页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训二、解直角三角形的应用（坡度坡角问题）【知识探索】1．知识延伸*（1）如图，某大坝的横断面是梯形，其中是坝顶，是坝高，是迎水坡，是背水坡．（2）如图，工件燕尾槽的横断面是等腰梯形，叫做燕尾角，叫做外口，叫做里口，叫做燕尾槽深度．2．如图，坡面的铅垂高度()和水平宽度()的比叫做坡面的坡度（或坡比），记作，即．【注意】（1）坡度通常写成的形式，如1︰1.5；（2）在计算的过程中，可将坡度的形式化成最简整数比，借助勾股定理、锐角三角比快速求解三边之比．3．坡面与水平面的夹角叫做坡角,记作．坡度与坡角之间的关系:．【说明】（1）在有关斜坡的问题情境中，常用到坡度和坡角，需明确坡度和坡角的含义；（2）①坡角是指斜坡的坡面与水平面的夹角，是一个角度，有单位；②坡度等于坡角的正切值，是一个比值，没有单位．【错题精练】例1．在台风来临之前，有关部门用钢管加固树木（如图）．已知固定点A离地面的高度AC=m，钢管第5页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训第6页共14页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训与地面所成角∠ABC =∠α，那么钢管AB 的长为（）A. m cosα；B. msinα；C. mcosα；D. msinα．例2．如图，在平地上种植树木时，要求株距（相邻两树间的水平距离）为4m ．如果在坡比为i =1:43的山坡上种树，也要求株距为4m ，那么相邻两树间的坡面距离为（）A. 5m ；B. 6m ；C. 7m ；D. 8m ．例3．如图，某小型水库栏水坝的横断面是四边形ABCD ，DC ∥AB ，测得迎水坡的坡角α=30∘，已知背水坡的坡比为1.2：1，坝顶部宽为2m ，坝高为6m ，则坝底AB 的长为．例4．如图，某数学活动小组为测量学校旗杆AB 的高度，沿旗杆正前方2√3米处的点C 出发，沿斜面坡度i =1:√3的斜坡CD 前进4米到达点D ，在点D 处安置测角仪，测得旗杆顶部A 的仰角为37∘，量得仪器的高DE 为1.5米．已知A 、B 、C 、D 、E 在同一平面内，AB ⊥BC ，AB ∥DE ．求旗杆AB 的高度（参考数据：sin37∘≈35，cos37∘≈45，tan37∘≈34．计算结果保留根号）例5．某小区开展了“行车安全，方便居民”的活动，对地下车库作了改进．如图，这小区原地下车库的入口处有斜坡AC长为13米，它的坡度为i=1:2.4，AB⊥BC，为了居民行车安全，现将斜坡的坡角改为13°，即∠ADC＝13°（此时点B、C、D在同一直线上）．（1）求这个车库的高度AB；（2）求斜坡改进后的起点D与原起点C的距离（结果精确到0.1米）．（参考数据：sin13°≈0.225，cos13°≈0.974，tan13°≈0.231，cot13°≈4.331）例6．太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面△ABC如图2所示，BC=10米，∠ABC=∠ACB=36°，改建后顶点D在BA的延长线上，且∠BDC=90°，求改建后南屋面边沿增加部分AD的长．（结果精确到0.1米）（参考数据：sin18°≈0.31，cos18°≈0.95．tan18°≈0.32，sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）【举一反三】，则小车上升的高度是（）1．如图，一辆小车沿倾斜角为α的斜坡向上行驶13米，已知cosα=1213A. 5米；B. 6米；C. 6.5米；D. 12米．第7页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训2．斜坡的倾斜角为α，一辆汽车沿这个斜坡前进了500米，则它上升的高度是（）A. 500•sinα米B. 米C. 500•cosα米D. 米3．如图，某小型水库栏水坝的横断面是四边形ABCD，DC∥AB，测得迎水坡的坡角α=30∘，已知背水坡的坡比为1.2：1，坝顶部宽为2m，坝高为6m，则坝底AB的长为m．4．如图所示，某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高，其中迎水坡AB的坡角α=45∘，坡长AB=6√2米，背水坡CD的坡度i=1：√3（i为DF与FC的比值），则背水坡CD的坡长为米．5．小高发现电线杆AB的影子落在土坡的坡面CD和地面BC上，量得CD=12米，BC=20米，CD与地面成30°角，且此时测得1米杆的影长为2米，求电线杆的高度．（结果保留根号）三、解直角三角形的应用（仰角俯角问题）第8页共14页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训【知识探索】1．在测量时（如图），在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，视线在水平线下方的角叫做俯角．【注意】在仰角和俯角这两个概念中，需注意是视线与水平线所夹的角，而不是视线与铅垂线所成的角．【说明】从低处观察高处所形成的仰角与从高处观察低处所形成的俯角的角度相等．2．水平线：水平面上的直线以及和水平面平行的直线．铅垂线：垂直于水平面的直线，我们通常称为铅垂线．【错题精练】例1．如图，从点A看一山坡上的电线杆PQ，观测点P的仰角是45°，向前走6m到达B点，测得顶端点P 和杆底端点Q的仰角分别是60°和30°，则该电线杆PQ的高度（）A. 6+2√3；B. 6√3；C. 10−√3；D. 8+√3．例2．如图，广场上空有一个气球A，地面上点B、C在一条直线上，BC=22m．在点B、C分别测得气球A的仰角为30°、63°，求气球A离地面的高度．（精确到个位）（参考值：sin63∘≈0.9，cos63∘≈0.5，tan63∘≈2.0）第9页共14页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训例3．如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB=30m．（1）求∠BCD的度数．（2）求教学楼的高BD．（结果精确到0.1m，参考数据：tan20∘≈0.36，tan18∘≈0.32）例4．由地面上A点测得山顶电视塔顶点B和电视塔基地C点的仰角分别为60°和30°,已知山顶C到地平面的垂直高度为50米.求电视塔高BC.例5．如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为__________ m（结果不作近似计算）【举一反三】1．如图，一艘舰艇在海面下600米A处测得俯角为30°前下方的海底C处有黑匣子信号发出，继续在同一深度直线航行2000米后再次在B点处测得俯角为60°前下方的海底C处有黑匣子信号发出，求海底黑匣子C处距离海面的深度（结果保留根号）第10页共14页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训2．腾飞中学在教学楼前新建了一座“腾飞”雕塑（如图①）.为了测量雕塑的高度，小明在二楼找到一点C，利用三角板测得雕塑顶端A点的仰角为30°，底部B点的俯角为45°，小华在五楼找到一点D，利用三角板测得A点的俯角为60°（如图②）.若已知CD为10米，请求出雕塑AB的高度．（结果精确到0.1米，参考数据）．3．如图，山顶建有一座铁塔，塔高CD=30m，某人在点A处测得塔底C的仰角为20°，塔顶D的仰角为23°，此人距CD的水平距离AB为__________ m．（参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364，sin23°≈0.391，cos23°≈0.921，tan23°≈0.424）4．如图，小明为了测量小山顶的塔高，他在A处测得塔尖D的仰角为45°，再沿AC方向前进73.2米到达山脚B处，测得塔尖D的仰角为60°，塔底E的仰角为30°，求塔高．（精确到0.1米，）5．如图，为了测量某山AB的高度，小明先在山脚下C点测得山顶A的仰角为45°，然后沿坡角为30°的斜坡走100米到达D点，在D点测得山顶A的仰角为30°，山AB的高度为__________ 米．1．如图，在小山的东侧A点有一个热气球，由于受西风的影响，以30米/分的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则小山东西两侧A、B两点间的距离为__________ 米2．如图，某海监船向正西方向航行，在A处望见一艘正在作业渔船D在南偏西45°方向，海监船航行到B处时望见渔船D在南偏东45°方向，又航行了半小时到达C处，望见渔船D在南偏东60°方向，若海监船的速度为50海里/小时，则A，B之间的距离为__________ .3．如图，小敏同学想测量一棵大树的高度．她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°，已知小敏同学身高（AB）为1.6m，则这棵树的高度为（）（结果精确到0.1m，）．A. 3.5mB. 3.6mC. 4.3mD. 5.1m4．如图，热气球的探测器显示，从热气球A看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为60°，热气球A与高楼的水平距离为120m，这栋高楼BC的高度为A. 200B. 200C. 160D. 1605．河堤横断面如图所示，堤高BC=5米，迎水坡AB的坡比是1：√3（坡比是坡面的铅直高度BC与水平宽度AC之比），则AC的长是（）A. 5√3米；B. 10米；C. 15米；D. 10√3米．。

非学科数学学培训-一次函数的应用-(资料附答案)

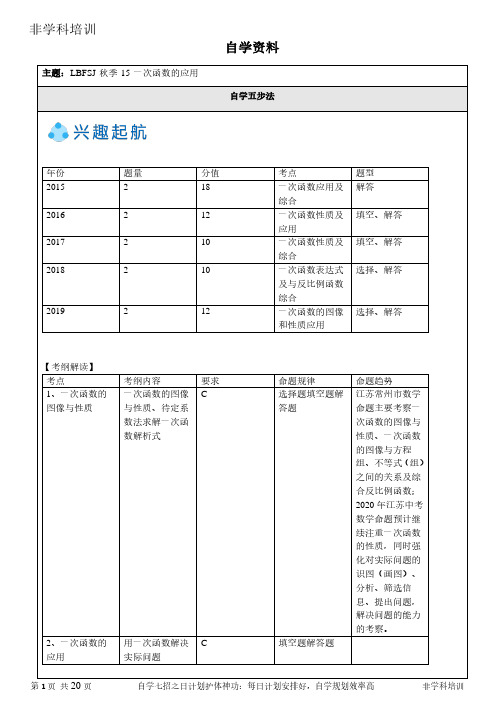
自学资料年份题量分值考点题型2015218一次函数应用及综合解答2016212一次函数性质及应用填空、解答2017210一次函数性质及综合填空、解答2018210一次函数表达式及与反比例函数综合选择、解答2019212一次函数的图像和性质应用选择、解答【考纲解读】考点考纲内容要求命题规律命题趋势1、一次函数的图像与性质一次函数的图像与性质、待定系数法求解一次函数解析式C选择题填空题解答题江苏常州市数学命题主要考察一次函数的图像与性质、一次函数的图像与方程组、不等式（组）之间的关系及综合反比例函数；2020年江苏中考数学命题预计继续注重一次函数的性质，同时强化对实际问题的识图（画图）、分析、筛选信息、提出问题，解决问题的能力的考察。

2、一次函数的应用用一次函数解决实际问题C填空题解答题第1页共20页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训【考点分析】2015年主要考察的是一次函数应用及综合2016年主要考察的是一次函数性质及应用2017年主要考察的是一次函数性质及综合2018年主要考察的是一次函数性质与反比例函数综合2019年主要考察的是一次函数图像性质以及双函数问题一、一次函数与一元一次方程【知识探索】1．因为任何一个以为未知数的一元一次方程都可以变形为（）的形式，所以解一元一次方程相当于在某个一次函数的函数值为0时，求自变量的值．【错题精练】例1．（2013春•高淳县期中）上学期，我们学习了解一元一次方程及用一元一次方程解决实际问题．本学期，我们又学习了解二元一次方程组，试用二元一次方程组及以前解决实际问题的经验解决下列问题：某校初一（1）班45名同学为“支援灾区”共捐款900元，捐款情况如下表：表中捐款10元和20元的人数不小心被墨水污染，看不清楚，请你确定表中的数据．【解答】【答案】略.例2．如图，直线y=x+2交x轴于点A，点C为直线y=x+2上一点，点D为点C关于y轴的对称点，点B（1，0）．（1）求出点A的坐标．（2）若点C的横坐标x=3，求点D的坐标．第2页共20页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训（3）当∠BCD为直角时，直接写出△BCD的面积= ．【答案】解：（1）令y=0，则x+2=0，解得x=﹣2，所以，A（﹣2，0）；（2）∵点C的横坐标x=3，∴y=3+2=5，∴点C的坐标为（3，5），∵点D为点C关于y轴的对称点，∴点D（﹣3，5）；（3）∵∠BCD为直角时，点D为点C关于y轴的对称点，∴点B、C的横坐标相同，都是1，∴y=1+2=3，∴点C的坐标为（1，3），∵点D为点C关于y轴的对称点，∴点D的坐标为（﹣1，3），∴BC=3，CD=1﹣（﹣1）=2，∴△BCD的面积=BC•CD=×3×2=3．故答案为：3．【举一反三】1．已知一次函数y=kx+b与y=﹣kx+b的图象，如图所示，且关于x的一元一次方程kx+b=0的解为x=﹣2．（1）求点C的坐标；（2）求△ABC的面积．第3页共20页自学七招之错题本锁骨术：巧用智能错题本，错题定期反复练非学科培训【解答】解：（1）∵关于x的一元一次方程kx+b=0的解为x=﹣2．∴直线y=kx+b与x轴的交点为（﹣2，0），由一次函数y=kx+b与y=﹣kx+b可知直线y=kx+b与直线y=﹣kx+b关于y轴对称，∴C（2，0）．（2）∵B（﹣2，0），C（2，0），A（0，1），∴S△ABC=×4×1=2．【答案】略2．作出函数y1=2x﹣2与y2=﹣2x+6的图象，利用图象解答下列问题：（1）方程组的解为；（2）y1＞0与y2＞0同时成立时x取何值范围是；（3）直线y1=2x﹣2的图象与y轴交于点A，直线y2=﹣2x+6的图象与y轴交于点B，两者相交于点C，求△ABC的三角形的面积；（4）在直线y1=2x﹣2的图象上存在异于点C的另一点P，使得△ABC与△ABP的面积相等，请求出点P的坐标．第4页共20页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训【答案】二、一次函数与一元一次不等式【知识探索】1．因为任何一个以为未知数的一元一次不等式都可以变形为（或）（）的形式，所以解一元一次不等式相当于在某个一次函数的值大于0（或小于0）时，求自变量的值．【错题精练】例1．如图，已知直线y1=﹣x+1与x轴交于点A，与直线y2=﹣x交于点B．第5页共20页自学七招之错题本锁骨术：巧用智能错题本，错题定期反复练非学科培训（1）求△AOB的面积；（2）求y1＞y2时x的取值范围．【答案】例2．如图，直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A（－1，0）和B（3，0）两点．则不等式组k1x+b>k2x+b>0的解集为．【答案】0<x<3．【举一反三】1．已知一次函数y=kx+b（k、b为常数，且k≠0）的图象（如图1）．（1）方程kx+b=0的解为x=2，不等式kx+b＜4的解集为；（2）正比例函数y=mx（m为常数，且m≠0）与一次函数y=kx+b相交于点P（如图2），则不等式组的解集为；第6页共20页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训（3）在（2）的条件下，比较mx与kx+b的大小（直接写出结果）．【答案】三、一次函数与二元一次方程组【知识探索】1．含有未知数和的两个二元一次方程组成的每个二元一次方程组，都对应两个一次函数，于是也对应两条直线．从“数”的角度看，解这样的方程组，相当于求自变量为何值时相应的两个函数值相等，以及这个函数值是多少；从“形”的角度看，解这样的方程组，相当于确定两条相应直线交点的坐标因此，我们可以用画一次函数图象的方法得到方程组的解．2．一般地，因为每个含有未知数和的二元一次方程都可以改写为（、是常数，且）的形式，所以每个这样的方程都对应一个一次函数，于是也对应一条直线，这条直线上每个点的坐标（，）都是这个二元一次方程的解．【错题精练】例1．如图，在平面直角坐标系xOy中，直线l1：y=﹣x+3与l2：交于点C，分别交x轴交于点A，B．（1）求点A，B，C的坐标；（2）求△ABC的面积；（3）在直线l1上是否存在点P，使△PBA是等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．第7页共20页自学七招之错题本锁骨术：巧用智能错题本，错题定期反复练非学科培训【答案】解：（1）A（3，0），B（﹣1，0）．C（2，1）．（2）S△ABC=1=2．（3）存在．①当AB为直角边时．如图，过点B作P1B⊥x轴，交l1于P1，∠P1BA=90°．易得△AP1B为等腰直角三角形，P1（﹣1，4）．②当AB为斜边时．如图，过点B作BP2⊥l1于P2，∠BP2A=90°．易得△AP2B为等腰直角三角形，P2（1，2）．（8分）综上，在直线l1上存在点P1（﹣1，4），P2（1，2），使△PBA是等腰直角三角形．例2．复习课中，教师给出关于x的函数y=−2mx+m−1（m≠0）．学生们在独立思考后，给出了5条关于这个函数的结论：①此函数是一次函数，但不可能是正比例函数；②函数的值y随着自变量x的增大而减小；③该函数图象与y轴的交点在y轴的正半轴上；④若函数图象与x轴交于A（a，0），则a＜0.5；⑤此函数图象与直线y=4x﹣3、y轴围成的面积必小于0.5．对于以上5个结论是正确有（）个．A. 4；B. 3；C. 2；D. 0．【答案】D．第8页共20页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训【举一反三】1．如图，在平面直角坐标系中，一条直线l与x轴相交于点A（2，0），与正比例函数y=kx（k≠0，且k为常数）的图象相交于点P（1，1）．（1）求k的值；（2）求△AOP的面积．（3）在x轴找一点M，使三角形AMP是等腰三角形．【答案】四、一次函数的简单应用【错题精练】例1．一辆快车和一辆慢车分别从甲、乙两地出发，匀速相向而行，相遇后继续前行，已知两车相遇时快车比慢车多行驶40千米，设行驶的路程为x（小时），两车之间的距离为y（千米），图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系．（1）根据图中信息，求线段AB所在直线的函数解析式和甲、乙两地之间的距离；（2）求两车速度及快车从甲地到乙地所需时间t；（3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图象．第9页共20页自学七招之错题本锁骨术：巧用智能错题本，错题定期反复练非学科培训【答案】解：（1）设y与x之间的函数关系为y=kx+b，由题意，得，解得：，∴y=﹣140x+280．当x=0时，y=280．答：线段AB所在直线的函数解析式为：y=﹣140x+280；甲、乙两地之间的距离为280km；（2）设慢车的速度为akm/h，就有快车的速度为（a+20）km/h，由题意，得（a+a+20）×2=280，解得：a=60，∴快车的速度为：60+20=80km/h，快车从甲地到乙地需要的时间为：80t=280，t=3.5．答：快车的速度为80km/h，慢车的速度为60km/h，快车从甲地到乙地所需时间t=3.5小时；（3）由题意，得快车到达乙地时，慢车离甲地的距离为：280﹣3.5×60=70．慢车到达甲地还需要的时间为：70÷60=h，慢车到达甲地时快车离甲地的距离为：280﹣×80=km，剩下的路程快车到达甲地还需要的时间为：÷80=h．根据条件画出图形，得第10页共20页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训例2．如图，在直角坐标系中，一次函数y=x+2的图象与x轴交于点A，与y轴交于点B，点C的坐标为（2，0），连接BC．（1）判断△ABC是不是等腰直角三角形，并说明理由；（2）若点P在线段BC的延长线上运动（P不与点C重合），连结AP，作AP的垂直平分线交y轴于点E，垂足为D，分别连结EA，EP；①当点P在运动时，∠AEP的度数是否变化？若变化，请说明理由；若不变，求出∠AEP的度数；②若点P从点C出发，运动速度为每秒1个单位长度，设△AOE的面积为S，点P的运动时间为t秒，求S关于t的函数关系式．【答案】解：（1）如图1，由一次函数y=x+2，则A（-2，0），B（0，2），C（2，0）．∴OA=OB=OC=2，AC=4，∴△AOB和△COB是等腰直角三角形，∴∠ABO=∠BAO=∠CBO=∠BCO=45°，∴AB=BC=2，∠ABC=90°∴△ABC为等腰直角三角形．（2）∠AEP的度数不变化；如图2，连接EC，∵E点在y轴上，且A、C关于y轴对称，∴E点在线段AC的垂直平分线上，即EA=EC；∵E点在线段AP的垂直平分线上，则EA=EP，∴EA=EP=EC，∴∠EAC=∠ECA，∠ECP=∠EPC；∵∠BCA=45°，即∠ACP=∠ECA+∠ECP=∠BAC+∠ABC=135°，∴∠EAC+∠EPC=135°，即∠EAC+∠EPC+∠ACP=270°，故∠AEP=360°-270°=90°，∴∠AEP的度数不会发生变化，为定值90°．（3）如图3，过E作EM⊥BP于M、过A作AN⊥BP于N；由（2）知：△CEP是等腰三角形，则有：例3．已知A、B两地之间的笔直公路上有一处加油站C（靠近B地），一辆客车和一辆货车分别从A、B两地从发，朝另一地前进，两车同时出发，均速行驶，如图所示是客车、货车离加油站C的距离y1，y2（千米）与行驶时间x（小时）之间的函数关系图像．（1）求客车和货车的速度；（2）图中点E代表的实际意义是什么，求点E的横坐标．【解答】（1）解：由题意知：货车速度：602=30（km/ℎ），客车速度：3606=60（km/ℎ）；（2）解：由题意知：E点代表两车在此处相遇，两地距离：60+360=420（km），设E点横坐标为t，∴30t+60t=420，∴t=143（小时）．【答案】（1）30km/ℎ，60km/ℎ；（2）143．例4．在等腰三角形ABC中，底边BC长为y，腰长AB长为x，若三角形ABC的周长为12．（1）求y关于x的函数表达式．（2）当腰长比底边的2倍多1时，求x的值．【解答】（1）解：y==12−2x；（2）解：x=5；【答案】（1）y==12−2x；（2）x=5．【举一反三】1．甲、乙两车分别从A地将一批物品运往B地，再返回A地，图6表示两车离A地的距离s（千米）随时间t（小时）变化的图象，已知乙车到达B地后以30千米/小时的速度返回．请根据图象中的数据回答：（1）甲车出发多长时间后被乙车追上？（2）甲车与乙车在距离A地多远处迎面相遇？（3）甲车从B地返回的速度多大时，才能比乙车先回到A地？【答案】解：（1）由图知，可设甲车由A地前往B地的函数解析式为s=kt，将（2.4，48）代入，解得k=20，所以s=20t，由图可知，在距A地30千米处，乙车追上甲车，所以当s=30千米时，（小时）．即甲车出发1.5小时后被乙车追上，（2）由图知，可设乙车由A地前往B地函数的解析式为s=pt+m，将（1.0，0）和（1.5，30）代入，得，解得，所以s=60t﹣60，当乙车到达B地时，s=48千米．代入s=60t﹣60，得t=1.8小时，又设乙车由B地返回A地的函数的解析式为s=﹣30t+n，将（1.8，48）代入，得48=﹣30×1.8+n，解得n=102，所以s=﹣30t+102，当甲车与乙车迎面相遇时，有﹣30t+102=20t解得t=2.04小时代入s=20t，得s=40.8千米，即甲车与乙车在距离A地40.8千米处迎面相遇；（3）当乙车返回到A地时，有﹣30t+102=0，解得t=3.4小时，甲车要比乙车先回到A地，速度应大于（千米/小时）．2．如图，已知直线y=﹣x上一点B，由点B分别向x轴、y轴作垂线，垂足为A、C，若A点的坐标为（0，5）．（1）若点B也在一反比例函数的图象上，求出此反比例函数的表达式．（2）若将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，求点E的坐标．【答案】1．已知一次函数y=kx+b+1（k≠0）的图像经过第一，二，四象限，且过点（3，－2），则b=（用含k的代数式表示）；k的取值范围是．．【答案】−3−3k，k＜−232．已知等腰三角形的周长是10，底边长y是腰长x的函数，则下列图象中，能正确反映y与x之间函数关系的图象是（）A.B.C.D.【答案】D3．观察图，可以得出不等式组{ax +b ＞0cx +d ＜0的解集是（）A. x ＜4；B. x ＜−1；C. −1＜x ＜0；D. −1＜x ＜4．【答案】B4．已知点（−4，y 1），（2，y 2）都在直线y =−12x +2上，则y 1，y 2大小关系是（）A. y 1>y 2B. y 1=y 2C. y 1<y 2D. 不能比较【答案】A5．在直角坐标系中，有两点A （﹣1，1），B （2，3）（1）若M 为y 轴上一点，且MA=MB ，求M 的坐标；（2）若N 为x 轴上一点，且NA+NB 最小，求N 的坐标．【答案】6．若一次函数y=kx+b的图象与x、y轴分别交于点A（4，0），B（0，6）．（1）求该一次函数的解析式；（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC+PD的最小值．【答案】（2）设点C关于点O的对称点为C′，连接C′D交OB于P′，连接P′C，则PC=PC′，∴PC+PD=PC′+PD=C′D，即PC+PD的最小值是C′D．连接CD，∵A（4，0），B（0，6），OA、AB的中点分别为C、D，∴D点坐标为：（2，3），C点坐标为：（2，0），∴CC′=4，CD=3，∴在Rt△DCC′中，C′D==5，即PC′+PD的最小值为5．7．如图1所示，在A，B两地之间有汽车站C，客车由A地驶往C站，货车由B地驶往A地，两车同时出发，匀速行驶．图2是客车、货车离C站的距离y1，y2（千米）与行驶时间x（小时）之间的函数图象．（1）①A，B两地的距离为千米；②货车的速度是千米/小时；（2）求点E的坐标，并说明点E的实际意义．【解答】（1）解：①A，B两地的距离为：360+80＝440（km）②货车的速度是40千米/小时；（2）解：∵货车的速度为80÷2＝40千米/小时，∴货车到达A地一共需要2+360÷40＝11小时．设y2=kx+b，代入点（2，0）、（11，360）得{2k+b=011k+b=360，解得：{k =40b =−80． ∴y 2=40x −80（x ≥2）．设y 1=mx +n ，代入点（6，0）、（0，360）得{6m +n =0n =360，解得：{m =−60n =360， ∴y 1=−60x +360．由y 1=y 2得，40x −80=−60x +360，解得x =4.4．当x =4.4时，y =96．∴E 点坐标为（4．4，96）．点E 的实际意义：行驶4．4小时，两车相遇，此时距离C 站96km ．【答案】（1）440，40；（2）96．8．一辆货车从甲地匀速驶往乙地，到达后用了半小时卸货，随即匀速返回，已知货车返回的速度是它从甲地驶往乙地的速度的1．5倍．货车离甲地的距离y （千米）关于时间x （小时）的函数图象如图所示．则a = ．（小时）【答案】5．● 如何梳理一个多元知识树呢？。

苏州造价培训函数习题

1. 二次函数2ax y =的图像与性质2. （1）抛物线23x y =的开口，对称轴是，顶点坐标是；（2）抛物线241x y -=的开口，对称轴是，顶点坐标是．3. 已知y=（m-2）x22m -是二次函数。

（1）求m 的值；（2）求顶点坐标和对称轴．（3）点A （m ，—16）在抛物线y=（m-2）x 22m -上吗？（4）若点B （n ，—8）在抛物线y=（m-2）x22m -上，求n.（3）当x= 时，函数y 的值最小，最小值是。

6. 由 y=x 2 怎样平移得到 y=（x+2）2的图象？由 y=x 2 怎样平移得到 y=（x-2）2的图象？7. 由 y=x 2 怎样平移得到 y=x 2+2图象？由 y=x 2 怎样平移得到 y=x 2-2图象？4. 抛物线y=2x 2中：(1)开口向___ ,顶点坐标是， (2)在对称轴的 (即当x_____时）y 随着x 的增大而增大；在对称轴的 (即当x___时）y 随着x 的增大而减小（4）该抛物线除顶点外，在x 轴的 _____方。

5．说说下列函数图象的开口方向、对称轴、顶点坐标、增减性、最值。

（1）232x y =(2)243x y -=（3）抛物线2)1(2++=x y 的性质2. 分别回答下列抛物线的开口方向，顶点坐标，对称轴，增减性，并说明x 取何值时函数的最大（小）值是多少3. 画出y=253212--x x 的大致图象。

并说明X 取何值时y 有最小值，这个最小值是多少？4. 根据下列条件，分别求出对应的二次函数的关系式．（1）已知抛物线的顶点为（—1，—2），且图像经过点（1，10）；（2）已知二次函数的图象经过点A （0，1）、B （2，4）、C （3，10）；（3）已知抛物线与x 轴交于点M （3，0）、（5，0），且图像经过点（0，1）；（4）已知抛物线与x 轴交于点M （-3，0）、（5，0），且最低点的纵坐标为516-；（5）已知抛物线对称轴是直线x ＝2，且经过(3，1)和(0，－5)两点。

维斯塔斯培训试题(有答案版本)

维斯塔斯培训选拔试题1、选择并翻译此题（2分，翻译1分，选择1分）What is the nominal output in MW for a V80.A:2.75MW B:2.0MW(USA1.8MW) C:1.65MW D:3.0MW(答案：V80的输出功率是多少？B)2、填空并翻译此题（5分，每空1分，排序1分）State with numbers 1-2-3-4,whloh components that are erected first 1 and last 4 on a WTG.______Nacelle _______Hub _______Blades _______Tower(答案：将1、2、3、4填写到空白处，顺序为安装顺序。

2 3 4 1 翻译：机舱轮毂叶片塔筒)3、填空并翻译此题（4分，前4空2分、后面空1分，翻译1分）Name the five components in a WTG？First letter given.B________、H_______、N_______、T________、F________.(答案：写出5个风机中的主要部件，第一个字母已经给出。

Blades 叶片、Hub 轮毂、Nacelle 机舱、Tower 塔筒、Foundation 基础)4、选择并翻译所选择的选项及题目：（单选）（5分翻译4分，选择1分。

）If you discover lager sized metal filings in the oil/filter than normal-what do you do?A:Let the turbine run and fix it on the next soheduled service.B:Contect your manager, take plotures notes, change the filter.C:Change oil and filterD.Discuss the problem with your colleagues.(答案：如果你发现有较大金属颗粒在油/过滤器中的时候，正常情况下你应该如何做？A：让风机继续运行，下次做维护时候修复B：照相、更换滤芯、联系你的经理C：更换油和滤芯D：和你的同事探讨这个问题选B)5、选择并翻译所选择的选项及题目。

营销中心线上培训试卷(汤臣倍健篇)

营销中心线上培训试卷（汤臣倍健篇）本试卷满分100分，共计40道题，每题2.5分，其中：单选题12个，多选题12个，判断题16个您的姓名： [填空题] *_________________________________一、单选题1.以下关于男士多维正确的是？ * [单选题] *A. 含有12种矿物质B. 含有4矿物质(正确答案)C. 含有4种维生素D. 含有8种维生素2.汤臣倍健多维中矿物质的添加形式正确的是？ * [单选题] *A. 碳酸锌B. 硫酸亚铁C. 硫酸锌D. 富马酸亚铁(正确答案)3.汤臣倍健鱼油软胶囊所含的主要成分的是？ * [单选题] *A. DPA和DHAB. DHA和EPA(正确答案)C.EPA和维生素ED.维生素E和DPA4.汤臣倍健藻油软胶囊的主要卖点定位是？ * [单选题] *A.植物DHA，出众记忆力(正确答案)B.全面补充记忆力C.脑力视力免疫力D.三效合一辅助降血脂5.77岁的老人比20岁年轻人心肌中的辅酶Q10减少了多少？ * [单选题] *A.67%B.57%(正确答案)C.83%D.45%6.氨糖软骨素钙的机理不包括（） * [单选题] *A. 氨糖消炎止痛，修补关节B骨碎补强肾、CPP促进钙的吸收C软骨素能锁钙(正确答案)D硫酸软骨素润增加关节滑液，减少关节摩擦7.汤臣倍健锌咀嚼片的不适宜人群是？ * [单选题] *A.4岁以下B.成人C.3岁以下(正确答案)D.5岁以下8.维生素C的RNI推荐摄入量是？ * [单选题] *A.14岁-50岁每天标准推荐摄入量是100mg,特殊人群孕中期到孕晚期+15mg,哺乳期+50mg(正确答案)B.14岁-50岁每天标准推荐摄入量是2000mg,特殊人群孕中期到孕晚期+15mg,哺乳期+30mgC.14岁-50岁每天标准推荐摄入量是1000mg,特殊人群孕中期到孕晚期+15mg,哺乳期+50mg9.氨糖软骨素钙的用量为？ * [单选题] *A.随餐，每日2次，每次1片B. 餐后半小时，每日2次，每次2片(正确答案)C. 随餐，每次1次，每次2片D.餐后半小时，每日1次，每次2片10.汤臣倍健雄赳赳益康胶囊不含有以下哪个成分？ * [单选题] *A绞股蓝B甘草(正确答案)C西洋参D红景天11.雄赳赳当中使用的马鹿茸采用哪里所产的原材料？ * [单选题] *A陕西B山东C宁夏D新疆(正确答案)12.每天补充多少( )mg褪黑素可以有效提升睡眠质量？ * [单选题] *A. 补充褪黑素(0.1-3mg/d)可以显著缩短睡眠潜伏期，延长睡眠时间，改善睡眠质量，调节人体生物钟，促进睡眠(正确答案)B. 补充褪黑素(0.1-5mg/d)可以显著缩短睡眠潜伏期，延长睡眠时间，改善睡眠质量，调节人体生物钟，促进睡眠C. 补充褪黑素(0.1-4mg/d)可以显著缩短睡眠潜伏期，延长睡眠时间，改善睡眠质量，调节人体生物钟，促进睡眠二、多选题1.汤臣倍健维生素C的主要功能过是( )？ * *A.增强免疫力(正确答案)B.促进胶原蛋白合成(正确答案)>C.促进铁/叶酸吸收(正确答案)D.解毒(正确答案)2.褪黑素的作用包括( )？ * *A.促睡眠(正确答案)B.显著缩短睡眠潜伏期(正确答案)C.延长睡眠时间调节人体生物钟(正确答案)3.鱼油软胶囊原料进口自( )？ * *A.丹麦B.挪威(正确答案)C.芬兰D.冰岛(正确答案)4.辅酶Q10的保健功能是( )？ * *A.心脏的发动机B.缓解体力疲劳(正确答案)C.营养心肌细胞D.增强免疫力(正确答案)5.以下表述中正确的是( )？ * *A.维生素对宠物猫狗是不可或缺性的(正确答案)B.VA参与脂肪代谢(正确答案)C.猫将植物中β胡萝卜素转化成VA能力比较弱(正确答案)d.猫狗不能合成VE，并且猫对VE缺乏十分敏感(正确答案)6.藻油软胶囊的用量为( ) * *A. 每天2次B. 每天1次(正确答案)C.每次二粒(正确答案)D.每次一粒7.汤臣倍健藻油软胶囊一般可以和以下哪些产品搭配( ) * *A．孕妇多种维生素B．儿童多种维生素(正确答案)C．牛初乳加钙(正确答案)D. 番茄红素8.番茄红素在泌尿系统具有哪些功能( )？ * *A改善下尿路症状(正确答案)B保护心脑血管C降低前列腺特异性抗原(正确答案)D抑制前列腺增生的发展(正确答案)9.氨糖软骨素钙一般可以和以下哪些药品或产品搭配食用（） * *A.万通筋骨贴(正确答案)B. 布洛芬(正确答案)C. 雄赳赳(正确答案)D. 大豆异黄酮(正确答案)10.以下关于汤臣倍健多维产品特色包括( ) ？* *A.人群专属(正确答案)B.含量适宜(正确答案)C.原料进口(正确答案)D.工艺先进(正确答案)11.汤臣倍健番茄红素维生素E软胶囊当中的原材料进口自哪些国家( )？ * *A德国(正确答案)B美国(正确答案)C法国(正确答案)D以色列(正确答案)12.宠物吃鱼油的功效包括哪些( )？【多选题】 * *A提高免疫力，减少宠物的过敏反应和掉毛情况(正确答案)B让宠物的毛色更有光泽，增毛(正确答案)C使宠物的皮肤更加健康(正确答案)D保护眼睛，是使宠物的眼睛更加明亮(正确答案)三、判断题1.褪黑素的发展趋势7岁以上为巅峰时期，7岁以下开始减少，年龄的增长、工作的压力、不良的生活习惯，会直接影响退黑色的分泌，促使褪黑素日益锐减( ) * [判断题] *B.错误2.汤臣倍健锌咀嚼片中的锌是柠檬酸锌( ) * [判断题] *A.正确(正确答案)B.错误3.人过35氨糖必须补，这个说法正确么( )？ * [判断题] *A.对(正确答案)B.错4.汤臣倍健番茄红素维生素E软胶囊的保健功能标注为抗氧化( )。

课程顾问培训考试试题题库

课程顾问培训考试试题题库课程顾问培训考试试题题库包含了一系列的测试题目，旨在评估课程顾问的专业知识、沟通技巧以及对教育行业的理解。

以下是一些模拟试题，供参考：一、选择题1. 作为课程顾问，以下哪项不是您的主要职责？A. 了解客户需求B. 推荐合适的课程C. 教授课程内容D. 跟进客户反馈2. 在与客户沟通时，以下哪种方式是不恰当的？A. 积极倾听B. 适时提问C. 打断客户讲话D. 保持专业态度3. 以下哪项不是课程顾问需要具备的素质？A. 良好的沟通能力B. 强烈的销售意识C. 丰富的行业知识D. 熟练的编程技能二、判断题1. 课程顾问需要对所有课程内容有深入的了解。

（）2. 课程顾问的工作只限于销售阶段，与售后服务无关。

（）3. 建立良好的客户关系对于课程顾问来说非常重要。

（）三、简答题1. 描述课程顾问在客户咨询过程中的一般流程。

2. 课程顾问如何平衡客户需求与课程设置之间的差异？3. 请举例说明课程顾问如何通过有效的沟通技巧提高客户满意度。

四、案例分析题背景信息：张女士是一位忙碌的职场人士，她希望提升自己的英语水平，但担心没有足够的时间参加常规的线下课程。

问题：1. 作为课程顾问，你将如何向张女士介绍适合她的课程？2. 请提出几种可能的解决方案，帮助张女士克服时间上的障碍。

五、论述题1. 论述课程顾问在教育行业中的重要性，并说明其对教育机构和客户双方的价值。

2. 描述课程顾问如何通过持续的专业发展提升自身的服务质量。

请注意，以上试题仅为示例，实际的课程顾问培训考试试题可能会根据具体的培训内容和机构要求有所不同。

考试时，考生需要根据所学知识和实际工作经验，认真作答。

天职国际别人的笔试

天职国际笔试一、数列题有✓假设1=5，2=15，3=215，4=2 145，那么5=（1）or 21485 ✓256,269,286,302（）307✓解法：256+2+5+6=269✓269+2+6+9=286✓286+2+8+6=302✓302+3+0+2=307✓102,96,108,84,132（）102-96=6108-84=24——（24=12*2）132-84=48——（48=24*2）？-132=96——（96=48*2）？=36✓13,11,16,8,（）,4,25,-1 13+11=16+8=20+4=25+ -1 =24✓3968 63 8 3 （2）✓2,4,3,5,6,8,7，_9✓827,635,443, _(17-14-11-8)✓21 28 33 42 43 60 （45）✓-2，1/2，4,2,16，（256）-2 1/2 4 2 164=(1/2)^(-2)2=4^(1/2)16=2^4✓ 2 ，4，9，23，64 （122）5=2*3-114=5*3-141=14*3-1122=41*3-1✓2,5,14,29,86，（17）2*2+1=55*3-1=1414*2+1=2929*3-1=8686*2+1=17✓12,16,22,30,39,49（61）✓1,2,4,9,,19,23，（64✓102,96,108,84, 132（36）✓44,15,177,576,(2259)177=3x(44+15)576=3x(177+15)3x(576+177)=2259✓1, 1/2, 6/11, 17/29, 23/381/1,2/4,6/11,17/29,46/76,();每个分数的分子为前一个分数的分子、分母之和,而分母为前一个分数的分母和自身分子的和再加1,所以（）＝122/199✓2,3,5,10,20,（40）;✓7,13,39,61,103, ;✓0,7,26,63,124,（215）;✓ 3 15 35 63 （99✓2,3,11,124,（15387）2、数学应用题●游泳池长30米，甲米每分钟，乙，问经过一分钟50秒，甲乙相遇多少次？1分50秒=11/6分两人一共行了：（+）×11/6 =90×11/6=165米一共行了165÷30=个全程两人共相遇了（5+1）÷2=3次●有一种挂历上面只印有月、日及星期,为了节约起见,可将此挂历留作日后.问公元1998年使用过的挂历,最早能在公元哪一年使用? 2007●32名学生需要到河对岸去野营，只有一条船，每次最多只能载4个人，其中需要一个人来划船，往返一次是5分钟如果9点整开始渡河，则9点17分至少有多少人在等待渡河？答案知道是19人●如果所有的W是T，就没有T是G，没有G是W。

全能培训题

x 全能培训题（4）1.点P （-2,-9)在第象限,它到x 轴距离是 ,到y 轴距离是 .2.点M 与x ,y 轴的距离分别是4,3,则点M 坐标是 .3.已知点M （3,a ),N (b ,-1),并且MN ∥y 轴,则a = ,b = .如点M ， N 在第二,四象限的平分线上,则a = ,b = .4.若点P(a ,b )在第二象限,则点P 1(1-a ,-b )在第象限.5.若点A ()b a ,在第四象限，则点()b a a b A --,1在第象限.6.已知点A (a ,3)和B (-2,b )关于x 轴对称,则a = ,b = .7.已知线段MN 的两个端点分别是()14--，M ，()1,0N ,将MN 平移后得到线段()////22N ，，M ，N M 则点的坐标为若-的坐标为 .8.已知点()()()0,0,1,2,0,6O B A ，则ABO ∆的面积是 .9.平行四边形的三个顶点坐标分别是（1，1），（2，2）和（3，-1），则第四个顶点坐标是 .10.已知点P ()y x ,关于原点对称的点在第一象限内，则点Q ()3,1-+-x y 关于x 轴对称的点在第象限。

11.在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右……的方向依次不断移动，每次移动1个单位长度，其行走路线如下图（1）填写下列各点坐标：4A ，8A ，12A 。

（2）写出点n A 4的坐标（n 为正整数）（3）指出蚂蚁从点100A 到点101A 的移动方向。

12.若P ()y x ,的坐标满足方程()0432=+++y x ，求点P 的坐标，并指出它的象限。

13.如图，这是某市部分简图，为了确定各建筑物的位置：（1）请你以火车站为原点建立平面直角坐标系．（2）写出市场、超市的坐标.（3）请将体育场、宾馆和火车站看作三点用线段连起来，得△ABC ，然后将此三角形向下平移4个单位长度,画出平移后的111A B C ∆，并求出其面积．14.四边形ABCD 的四个顶点A ，B ，C ，D 的坐标分别是（0，0），（-2，8），（-11，6），（-14，0），求（1）四边形ABCD 的面积，（2）如把原四边形ABCD各个顶点的纵坐标保持不变，横坐标增加2，所得的四边形面积又是多少？。

技术培训试题(有答案).doc

培训练习题姓名: 一、填空题：（每空1分）1、手工焊锡主要工具是电烙铁，正确的握烙铁方法是握笔法；焊接好后, 电烙铁以基于被焊体约45度角移开；在焊接时，应按照作业指导书或样板的要求进行焊接，焊接时要快，一般焊接时间应不超过秒。

2、打螺丝时，必须保证风（电）批咀与螺丝垂直于被打的螺一丝.及丝牙孔位；风批的档位常规：（L）为向左转,（R）为向右转。

3、电阻的字母代号R表示,单位是一欧姆,单位符号是一Q 。

4、电容的单位是一法拉,用字母F 表示，电解电容有极性之分, 长脚为十极,短脚为一极。

或在封装皮上标有黑色竖条为一极。

5、我厂现在用的电容有电解电容、瓷片电容、咪啦（绦纶）电容、轴向电容、独石电容等:6、晶体二极管由一个PN加上相应的电结做成的半导体器件，其主要特性是具有单向导电。

二极管由于用途的不同可分为整流、变容、顼关、稳压及发光二极管等。

7、晶体三极管的内部是由两个PN结和三个电极所构成，它们三个电极分别是集电极、发射极、基极、分别用字母表示为C极、E极、B 极。

三极管按类型可分为PNP管和NPN管两大类,按功能用途可分为放大管和开关管两大类,8、晶振的作用是用于稳定频率和选择频率,陶瓷滤波器与晶振元件一样。

9、A M的中频频率是一455KHz ；FM的中频频率是10.7MHZ 。

10、我厂现时生产的汽车收放机按电压可分12伏和24伏两种,按类型可分手动调谐数字显示和电子调谐数字显示及手动调谐指针示三类；显示屏又分为LED发光二极管显示及LCD 液晶显示。

选择题：（每小题1分）1、根据作业指导书或样板之要求，该焊元件末焊,焊成其它元件叫B、错焊。

A、焊反B、错焊C、漏焊2、加锡的顺序是—A、先加热后放焊锡°A、先加热后放焊锡B、先放锡后焊C、锡和烙铁咀同时3、根据我们厂的生产情况，在使用电烙铁焊接时要求电烙铁B、必须接地。

A、不用接地B、必须接地C、两者都可4、用风批打螺丝时，风批的力度应调到D实际需要。

非学科数学学培训期末复习之一次函数综合复习 (资料附答案)

自学资料一、一次函数综合复习【错题精练】例1．已知一次函数y=(m+1)x+2m−1（m≠−1）的图像过点（m，3）．（1）求一次函数的表达式；（2）若A（x1，t），B（x2，t+1）是该一次函数图像上的两点，比较x1与x2的大小．第1页共19页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训第2页共19页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训第3页共19页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训例4．已知直线y 1=kx +1（k <0）与直线y 2=nx （n >0）的交点坐标为（13，13n ），则不等式组nx −3<kx +1<nx 的解集为．【答案】13<x <43例5．如图，直线l 1：y =x +1与直线l 2：y =mx +n 相交于点P （1，b ），直线l 2与x 轴交于点A （4，0）．（1）求b 的值并直接写出关于x ，y 的方程组{y =x +1y =mx +n的解；（2）求直线l 2的表达式；（3）判断直线l 3：y =nx +m 是否也经过点P ？请说明理由．【解答】（1）解：∵点P （1，b ）在直线y =x +1上，∴b =1+1=2．∴点P 的坐标为（1，2）．∴方程组{y =x +1y =mx +n 的解为{x =1y =2．（2）解：∵点P （1，2），A （4，0）在直线y =mx +n 上，∴{m +n =24m +n =0．解得{m =−23n =83． ∴直线l 2的表达式：y =−23x +83．（3）解：∵点P （1，2）在直线l 2：y =mx +n 上，∴n +m =2．把x =1代入直线l 3：y =nx +m 得，y =n +m ．即x =1时，y =2．所以，直线l 3：y =nx +m 经过点P （1，2）．【答案】（1）b =2，{x =1y =2；（2）直线l 2的表达式：y =−23x +83；（3）经过．第4页共19页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训例6．如图，一次函数y =−34x +3的图象与x 轴和y 轴分别交于点A 和B ，再将△AOB 沿直线CD 对折，使点A 与点B 重合、直线CD 与x 轴交于点C ，与AB 交于点D ．（1）点A 的坐标为，点B 的坐标为；（2）求OC 的长度；（3）在x 轴上有一点P ，且△PAB 是等腰三角形，不需计算过程，直接写出点P 的坐标．【解答】（1）解：令y =0，则x =4；令x =0，则y =3，故点A 的坐标为（4，0），点B 的坐标为（0，3）．（2）解：设OC =x ，则AC =CB =4−x ，∵∠BOA =90∘，∴OB 2+OC 2=CB 2，32+x 2=(4−x )2，解得x =78，∴OC =78．（3）解：设P 点坐标为（x ，0），当PA =PB 时，√(x −4)2=√x 2+9，解得x =78；当PA =AB 时，√(x −4)2=√42+32，解得x =9或x =−1；当PB =AB 时，√x 2+32=√42+32，解得x =−4．∴P 点坐标为（78，0），（-4，0），（-1，0），（9，0）．【答案】（1）A 的坐标为（4，0），点B 的坐标为（0，3）（2）OC =78（3）（78，0），（-4，0），（-1，0），（9，0）例7．如图，一次函数y =−2x +4与x 轴，y 轴分别交于A ，B ，以线段AB 为直角边在第一象限内作Rt△ABC ，使AB =AC ．（1）求直线AC 的函数关系式；第5页共19页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训（2）若P （m ，3）在第二象限内，求当△PAB 与△ABC 面积相等时m 的值．【解答】（1）解：令x =0代入y =−2x +4中，∴y =4，∴B （0，4）令y =0代入y =−2x +4中，∴x =2，∴A （2，0）过点C 作CD ⊥x 轴于点D ，∵∠BAC =90∘，∴∠BAC =90∘，∴∠ABO =∠DAC ，在△ABO 与△CAD 中，{∠ABO =∠DAC∠BOA =∠CDA AB =AC，∴△ABO ≌△CAD （AAS ）∴CD =OA =2，AD =OB =4，∴OD =6，∴C （6，2）设直线AC 的解析式为y =kx +b ，∴{2k +b =06k +b =2， ∴解得：{k =12b =−1，∴直线AC 的解析式为：y =12x −1；（2）解：过点P 作PE ⊥x 轴于点E ，∴PE =3，OE =−m ，∵AB =AC =2√5，∴S △ABC =12AC ⋅AB =12×2√5×2√5=10， ∴S △APB =S △OAB +S △OPB −S △OPA=12AO ⋅BO +12OB ⋅OE −12OA ⋅PE=1−2m∴1−2m=10∴m=−92．【答案】（1）y=12x−1；（2）−92．例8．如图，一次函数y=−23x+b的图象与x轴、y轴分别交于点A、B，线段AB的中点为D（3，2）．将△AOB沿直线CD折叠，使点A与点B重合，直线CD与x轴交于点C．（1）求此一次函数的解析式；（2）求点C的坐标；（3）在坐标平面内存在点P（除点C外），使得以A、D、P为顶点的三角形与△ACD全等，请直接写出点P的坐标．【解答】（1）解：设A点坐标为（a，0），B点坐标为（0，b）．由线段AB的中点为D（3，2），得0+a2=3，0+b2=2．解得a=6，b=4．即A（6，0），B（0，4）．故一次函数解析式为y=−23x+4．（2）解：如图1：连接BC，设OC=x，则AC=CB=6−x．∵∠BOA=90∘，∴OB2+OC2=CB2，42+x2=(6−x)2．第6页共19页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训第7页共19页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训解得x =53．即C （53，0）．（3）解：①当△ACD ≌△APD 时，设P 1（c ，d ）．由D 是PC 的中点，得c+532=3，d+02=2．解得c =133，d =4．即P 1（133，4）（如图2）．②当△ACD ≌△DP 2A 时，做DE ⊥AC 与E ，P 2F ⊥AC 与F 点．则DE =2，CE =3−53=43．由△CDE ≌△AP 2F ，AF =CE =43，P 2F =DE =2，OF =6−43=143． ∴P 2（143，—2）．③当△ACD ≌△DP 3A 时，设P 3（e ，f ）．A 是线段P 2P 3的中点，得e+1432=6，f+(−2)2=0．解得e =223，f =2．即P 3（223，2）．综上所述：P 1（133，4），P 2（143，—2），P 3（223，2）．【答案】（1）一次函数解析式为y =−23x +4；（2）C （53，0）；（3）P 1（133，4）；P 2（143，—2）；P 3（223，2）．例9．现有甲骑电瓶车，乙骑自行车从湖州西山漾公园丝绸小镇门口出发沿同一路线匀速前往太湖龙之梦乐园，设乙行驶的时间为x （ℎ），甲、乙两人距出发点的路程S 甲、S 乙关于x 的函数图像如图①所示；甲、乙两人之间的路程差y 关于x 的函数图像如图②所示：请你解决以下问题（1）甲的速度是 km/ℎ；乙的速度是 km/ℎ；第8页共19页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训（2）对比图①、②可知：a = ，b = ；（3）乙出发多少时间，甲、乙两人路程差为7.5km ？【答案】（1）25，10；（2）10，56；（3）43或74．（1）解：25；10；（2）解：10；56；（3）解：由（2）可知：a =10，b =56，由（1）可知：当甲到达目的地时，甲的行驶时间为1ℎ，乙的行驶时间为1.5ℎ，此时a =10，设y =mx +n （m ≠0），当56≤ x ≤1.5时，函数y =mx +n （m ≠0）的图象经过（56，0），（1.5，10）两点，∴{56m +n =01.5m +n =10，解得：{m =1.5n =−12.5（56≤m ≤1.5）， ∴y =15x −12.5，56≤x ≤1.5，当1.5≤x ≤2.5时，函数y =mx +n （m ≠0）的图象经过（56，0），（2.5，0）两点，∴{56m +n =02.5m +n =0，解得：{m =−10n =25， ∴y =−10x +25（1.5≤x ≤2.5），由题意得：15x −12.5=7.5或−10x +25=7.5，解得：x =43或74，故乙出发43或74小时，甲、乙两人路程差为7.5km ．例10．某校的甲、乙两位老师同住一小区，该小区与学校相距2400米．甲从小区步行去学校，出发10分钟后乙再出发，乙从小区先骑公共自行车，途经学校义骑行若干米到达还车点后，立即步行走回学校．已知甲步行的速度比乙步行的速度每分钟快5米．设甲步行的时间为x（分），图1中线段OA和折线B−C−D分别表示甲、乙离开小区的路程y（米）与甲步行时间x（分）的函数关系的图象；图2表示甲、乙两人之间的距离s（米）与甲步行时间x（分）的函数关系的图象（不完整）．根据图1和图2中所给信息，解答下列问题：（1）求甲步行的速度和乙出发时甲离开小区的路程；（2）求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离；（3）在图2中，画出当25≤x≤30时s关于x的函数的大致图象．（温馨提示：请画在答题卷相对应的图上）【解答】（1）由题意，得：甲步行的速度是2400÷30=80（米/分），∴乙出发时甲离开小区的路程是80×10=800（米）．（2）设直线OA的解析式为：y=kx(k≠0)，∵直线OA过点A(30,2400)，∴30k=2400，解得k=80，∴直线OA的解析式为：y=80x．∴当x=18时，y=80×18=1440，∴乙骑自行车的速度是1440÷(18−10)=180（米/分）．∵乙骑自行车的时间为25−10=15（分），∴乙骑自行车的路程为180×15=2700（米）．当x=25时，甲走过的路程是y=80x=80×25=2000（米），∴乙到达还车点时，甲、乙两人之间的距离是2700−2000=700（米）．（3）乙步行的速度为：80-5=75（米/分），乙到达学校用的时间为：25+（2700-2400）÷75=29（分），当25≤x≤30时s关于x的函数的大致图象如图所示．【答案】（1）80米/分，800米；（2）180米/分，700米；（3）见解答．【举一反三】=kx−2k（k是常数，且k≠0）．1．设一次函数y1第9页共19页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训第10页共19页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训【解答】（1）解：由图可知，乙比甲先出发1小时，由C 点的几何意义可知：当t =3时，甲乙两人相距最远，即此时，甲已到达B 地，∴甲骑摩托车的速度为120÷（3－1）=60km/ℎ，由OA 段可知，乙的速度为20km/ℎ，设在乙出发t 小时后两人第一次相遇，即60(t −1)=20t ，解得：t =1.5；（2）解：设BC 段所在直线为y =kt +b （k ≠0），由（1）可知：B （1.5，0），C （3，60），将B ，C 两点坐标分别代入y =kt +b 中，得{1.5k +b =03k +b =0，解得：{k =40b =−60， ∴线段BC 所在直线的函数表达式为y =40t −60；（3）解：依题意可得，D （6，0），线段CD 所在直线表达式为y 2=−20t +120，把y =30，y =50分别代入y =40t −60，得t =2.25，t =2.75，再把y =30，y =50分别代入y 2=−20t +120，得t =4.5，t =3.5，∴当30≤y ≤50，2.25≤t ≤2.75和3.5≤t ≤4.5；（4）解：乙出发3小时后，乙行了60km ，甲到达B 地，此时原路返回，设经时间t 后，甲乙两人相距10km ，20(t −3)+10+60(t −3)=60或60(t −3)+20(t −3)−10=60，分别解得t =298或318．【答案】（1）1小时，1.5；（2）y =40t −60；（3）2.25≤t ≤2.75和3.5≤t ≤4.5；（4）298或318．4．在平面直角坐标系中，点A ，B ，C 分别在直线y =x −1，y =x ，y =x +2上，它们的横坐标分别为a ，b ，c ，若点A ，B ，C 不能构成三角形，则a ，b ，c 应满足的条件是．【答案】a =b =c 或a −1=b =c +2或2a +c =3b ．5．方成同学看到一则材料，甲开汽车，乙骑自行车从M 地出发沿一条公路匀速前往N 地，设乙行驶的时间为t （ℎ），甲乙两人之间的距离为y （km ），y 与t 的函数关系如图1所示，方成思考后发现了图1的部分正确信息，乙先出发1ℎ，甲出发0.5ℎ与乙相遇，…请你帮助方成同学解决以下问题：（1）分别求出线段BC ，CD 所在直线的函数表达式；（2）当20＜y ＜30时，求t 的取值范围；（3）分别求出甲、乙行驶的路程S 甲、S 乙与时间t 的函数表达式，并在图2所给的直角坐标系中分别画出它们的图象．【解答】（1）解：设直线BC 的函数解析式为y =kt +b ．把（1.5，0），（7 3，100 3 ）代入得：{1.5k +b =073k +b =1003．解得：{k =40b =−60． ∴直线BC 的解析式为：y =40t ﹣60．设直线CD 的函数解析式为y 1=k 1t +b 1．把（73，1003），（4，0）代入得：{4k 1+b 1=073k 1+b 1=1003．解得：{k 1=−20b 1=80． ∴直线CD 的函数解析式为：y =﹣20t +80．（2）解：设甲的速度为akm/ℎ ，乙的速度为bkm/ℎ．根据题意得；{0.5a =1.5b a (73−1)=73b +1003．解得：{a =60b =20． ∴甲的速度为60km/ℎ，乙的速度为20km/ℎ．∴OA 的函数解析式为：y =20t （0≤t ≤1），所以点A 的纵坐标为20．当20＜y ＜30时，即20＜40t ﹣60＜30，或20＜﹣20t +80＜30．解得：2＜t ＜94或52＜t ＜3．（3）解：根据题意得：s 甲=60t ﹣60（1≤t ≤73）．s乙=20t（0≤t≤4）．所画图象如图2所示：【答案】（1）直线CD的函数解析式为：y=﹣20t+80；（2）2＜t＜94或52＜t＜3；（3）略．1．如图，直线l与x轴，y轴分别交于M，N两点，且OM=ON=3．（1）求这条直线的函数表达式；（2）Rt△ABC与直线l在同一个平面直角坐标系内，其中∠ABC=90∘，AC=2√5，A（1，0），B（3，0），将△ABC沿着x轴向左平移，当点C落在直线l上时，求线段AC扫过的面积．【解答】（1）解：设该直线的函数表达式为y=kx+b（k≠0），∵OM=ON=3，且M、N分别在x轴负半轴、y轴负半轴上，∴M（－3，0），N（0，－3）．将M（－3，0）、N（0，－3）代入y=kx+b，{−3k+b=0b=−3，解得：{k=−1b=−3，∴这条直线的函数表达式为y=−x−3．（2）解：∵A（1，0），B（3，0），∴AB=2．∵∠ABC=90∘，AC=2√5，∴BC=4，∴C（3，4）．设平移后点A、C的对应点分别为A′、C′，当y=−x−3=4时，x=−7，∴C′（－7，4），∴CC′=10．∵线段AC扫过的四边形ACC′A′为平行四边形，∴S=CC′⋅BC=10×4=40．答：线段AC扫过的面积为40．【答案】（1）y=−x−3；（2）40．2．如图，直线y=kx+b经过点A（5，0），B（1，4）．（1）求直线AB的解析式；（2）若直线y=2x−4与直线AB相交于点C，求点C的坐标；（3）根据图象，写出关于x的不等式2x−4>kx+b的解集．【解答】（1）解：∵直线y=kx+b经过点A（5，0），B（1，4），∴．解得．∴直线AB的解析式为：y=−x+5；（2）解：∵若直线y=2x−4与直线AB相交于点C，∴．解得，∴点C（3，2）．（3）根据图象可得x>3．【答案】（1）y=−x+5；（2）点C（3，2）；（3）x>3．3．如图，已知直线y=x+1与y轴交于点A，一次函数y=kx+b的图象经过点B（0，－1），并且与x轴以及直线y=x+1分别交于点C、D．（1）求直线BD的函数表达式；（2）求四边形AOCD的面积；（3）在y轴上是否存在这样的点P，使得以P、B、D为顶点的三角形是等腰三角形．如果存在，求出点P 的坐标；如果不存在，说明理由．【解答】（1）解：∵点D 在y =x +1的图象上，∴当x =1时，y =2，即D （1，2）．∵函数y =kx +b 的图象经过点B （0，－1）、D （1，2），∴．解得：．∴直线BD 解析式为y =3x −1．（2）解：易知A （0，1），令y =0，得x =13．∴C （13，0）．连接OD ．则S 四边形AOCD =S △AOD +S △COD =12×1×1+12×13×2=56．（3）解：分三种情况考虑：当DP =DB 时，得到P （0，5）；当BP =BD 时，BD =√10，得到P （0，－1－√10）或P （0，－1+√10）；当PB =PD 时，设P （0，a ），则(a +1)2=12+(2−a )2，解得：a =23，即P （0，23）．∴存在．坐标分别为（0，5），（0，－1－√10），（0，23），（0，－1+√10）．【答案】（1）直线BD 解析式为y =3x −1；（2）56；（3）（0，5），（0，－1－√10），（0，23），（0，－1+√10）．4．如图，在平面直角坐标系中，O是坐标原点，正方形OABC的顶点A、C分别在x轴与y轴上，已知正方形边长为3，点D为x轴上一点，其坐标为（1，0），连接CD，点P从点C出发以每秒1个单位的速度沿折线C⟶B⟶A的方向向终点A运动，当点P与点A重合时停止运动，运动时间为t秒．（1）连接OP，当点P在线段BC上运动，且满足△CPO≌△ODC时，求直线OP的表达式；（2）连接PC，求△CPD的面积S关于t的函数表达式；（3）点P在运动过程中，是否存在某个位置使得△CPD为等腰三角形，若存在，直接写出点P的坐标，若不存在，说明理由．【解答】（1）解：∵四边形ABCO是正方形，∴∠COD=∠OCP．∵OC=CO，∴当CP=OD=1时，△CPO≌△ODC．∴P（1，3）．设直线OP的解析式为y=kx，则有3=k，∴直线OP的解析式为y=3x．（2）解：当点P在线段BC上时，如图1中，S=12⋅CP⋅CO=32t（0<t≤3）．当点P在线段AB上时，如图2中，BP=t−3，AP=3−(t−3)=6−t，S=3×3−12×1×3−12×3×(t−3)−12×2×(6−t)=−12t+6（3<t≤6）．综上所述，S={32t(0<t≤3)−12t+6(3<t≤6)．（3）解：如图3中，①当DC=DP1时，P1（2，3），②当DC=DP2时，AP2=√DP22−AD2=√6，∴P2（3，√6）．③当CD=CP3=√10时，BP3=√10−9=1，∴P3（3，2）．④当P4C=P4D时，设AP4=a，则有22+a2=32+(3−a)2，解得a=73，∴P4（3，73）．综上所述，满足条件的点P坐标为（2，3）或（3，√6）或（3，2）或（3，73）．【答案】见解答．5．如图，已知∠ABC=90∘，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连接AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连接QE并延长交射线BC于点F．（1）如图，当BP=BA时，∠EBF=°，猜想∠QFC=°；（2）如图，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明．（3）已知线段AB=4√3，设BP=x，点Q到射线BC的距离为y，求y关于x的函数关系式．【解答】（1）解：∵△ABE是等边三角形，∴∠ABE=60∘，∴∠EBF=30∘，猜想：∠QFC=60∘（在（2）中证明）；（2）证明：∠QFC=60∘．理由如下：不妨设BP＞AB，∵∠BAP=∠BAE+∠EAP=60∘+∠EAP，∠EAQ=∠QAP+∠EAP=60∘+∠EAP，∴∠BAP=∠EAQ，在△ABP和△AEQ中，{AB=AE∠BAP=∠EAQAP=AQ，∴△ABP≌△AEQ，∴∠AEQ=∠ABP=90∘，∴∠BEF=180∘−∠AEQ−∠AEB=180∘−90∘−60∘=30∘，∴∠QFC=∠EBF+∠BEF=30∘+30∘=60∘；（3）解：在图1中，过点F作FG⊥BE于点G，过点Q作QH⊥BC于点H，∵△ABE是等边三角形，∴BE=AB=4√3，由（1）得∠EBF=30∘，在Rt△BGF中，BG=12BE=2√3，∴FG=2，BF=4，∴EF=BF=4，∵△ABP≌△AEQ，∴QE=PB=x，∴QF=QE+EF=x+4，由（2）得∠QFC=60∘，∴在Rt△QHF中，∠FQH=30∘，，即y关于x的函数关系式是：y=√32x+2√3（x＞0）．【答案】（1）30；60；（2）略；（3）y=√3x+2√3（x＞0）．2● 通过观察一次函数的图象获取有用的信息是我们在日常生活中经常遇到的问题，要掌握这个重点在于对函数图象的观察和分析，观察函数图象时，首先要看分别代表的是什么，也就是观察图象反映的是哪两个变量之间的关系．观察图象获取信息时，一定要注意图象上的特殊点，这些特殊点对我们解决问题有很大的帮助．。

非学科数学学培训-三角形综合复习--(资料附答案)

自学资料一、直角三角形【知识探索】1．定理2：直角三角形斜边上的中线等于斜边的一半．（1）推论1：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；（2）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°．【说明】“推论”是从某一个定理直接推出的定理．【错题精练】例1．若直角三角形的两直角边长分别为5和12，则斜边上的中线长为__________【答案】 6.5例2．如图，在一个长6m、宽3m、高2m的房间里放进一根竹竿，则这根竹竿最长为（）第1页共24页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训A. 3m；B. 5m；C. 7m；D. 11m．【答案】C例3．在数学拓展课上，小明发现：若一条直线经过平行四边形对角线的交点，则这条直线平分该平行四边形的面积．如图是由5个边长为1的小正方形拼成的图形，P是其中4个小正方形的公共顶点，小强在小明的启发下，将该图形沿着过点P的某条直线剪一刀，把它剪成了面积相等的两部分，则剪痕的长度是（）A. 2√2；B. √5；； D. √10．C. 3√52【答案】D例4．如图，在△ABC中，AC=BC，∠ACB=90∘，点D在BC上，BD=3，DC=1，点P是AB上的动点，则PC+PD的最小值为（）A. 4；B. 5；C. 6；D. 7．【答案】B例5．如图一直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（）第2页共24页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训A. 2cm；B. 3cm；C. 4cm；D. 5cm．【答案】B例6．如图，四边形ABCD中，∠A=∠B=90度，E是AB上一点，且AE=BC，∠1=∠2（1）判断Rt△ADE与Rt△BEC是否全等？并说明理由；（2）证明AB＝AD＋BC；（3）判断△CDE是什么三角形？并说明理由.【解答】（1）证明：Rt△ADE≌Rt△BEC，∵∠1=∠2，∴DE=EC，在Rt△ADE和Rt△BEC中ED＝ECAE＝CB，∴Rt△ADE≌Rt△BEC（HL）；(2) 证明：∵Rt△ADE≌Rt△BEC，∴AD=EB，AE=BC，∴AB=AE+BE=AD+CB（3）△CDE是等腰直角三角形，∵Rt△ADE≌Rt△BEC，∴∠ADE=∠BEC，∵∠A=90°，∴∠AED+∠ADE=90°，∴∠AED+∠BEC=90°，∴∠DEC=90°，∴△DEC是等腰直角三角形第3页共24页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训【答案】(1)Rt△ADE≌Rt△BEC(3)△DEC是等腰直角三角形【举一反三】1．在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是__________ 。

wecost同望培训例题

同望WECOST培训例题(施工图预算—省道XXX一级公路)编制信息:建设项目基本信息：1、建设项目名称：省道XXX一级公路2、编制类型：施工图预算3、路线总长：51.282KM4、建设单位：XX市交通建设投资集团有限公司5、设计单位：XX市勘察设计院6、建管费汇总方式：以汇总后建安费为基数7、建管费汇总累计办法：08建管费部颁标准8、汇总累计费率系数：1造价文件基本信息1、文件名称：K0+000~K51+2822、计价依据：预算选择“08部颁预算计价依据”；清单选择“09公路工程清单计价依据”3、主定额：公路工程2008部颁预算定额4、工程类别：路线5、起止桩号：K0+000~K51+2826、设计长度：51.282KM7、公路等级：一级公路8、建设性质：新建9、路基宽度：23.5m10、平均养护月数：6个月11、车船税标准：贵州省养路费车船税标准（08）12、机械不变费用系数：113、建管费累进办法：08建管费部颁标准14、年造价上涨率：5%15、上涨计费年限：2取费程序的基本信息：工程所在地：贵州（贵阳）费率标准：贵州省补充规定08冬季施工：准一区；雨季施工：Ⅱ区4个月沿海地区、高原施工、风沙施工：不计行车干扰：不计夜间、安全文明、临时设施、施工辅助：计基本费用、职工探亲、职工取暖：不计财务费用、辅助生产、利润：计综合里程：4km；工地转移：100km纳税人所在地：市区规费费率：（养老保险费率：20%；失业保险费率：2%；医疗保险费率7.5%；工伤保险费率：1.2%；住房公积金费率：5%）- 1 -预算书内容：- 2 -- 3 -- 4 -- 5 -- 6 -- 7 -- 8 -- 9 -- 10 -补充预算定额数据表补充材料及补充机械注：工料机价格信息表见附件K0+000～K51+282单价文件清单报价—第五合同段注：1、导入清单见附件第五合同段工程量清单。

2、421-1 砼拌合站按砼用量比例分别分摊至405-1-b-4、405-1-b-5、410-1-b、410-1-c、410-2-c-1、410-2-c-2、410-2-d-2、410-2-f-1、410-5-d、410-6-a、410-6-e-2、415-2-c、420-1-a-4、420-1-a-5、420-3-a-6。

上海职业培训师题库

上海职业培训师题库选择题（单项选择）在职业培训中，为了提升学员的实践能力，通常采用哪种教学方法更为有效？A. 讲授法B. 案例分析C. 角色扮演D. 小组讨论关于职业培训课程的开发，以下哪个步骤不是必需的？A. 需求调研B. 课程设计C. 教材编写D. 学员背景审核在进行职业培训效果评估时，主要关注的是：A. 培训师的授课技巧B. 学员的出勤率C. 学员的学习成果D. 培训场地的设施职业培训师在授课过程中，为了增强互动性，常采用哪种技术或工具？A. 投影仪B. 问卷调查C. 互动白板D. 教材分发下列哪项不属于职业培训师应具备的核心能力？A. 专业知识B. 教学技巧C. 市场营销D. 学员管理能力填空题职业培训课程的开发应遵循“_________、_________、_________”的原则，以确保课程的有效性和针对性。

答案：需求导向、实用性、系统性在职业培训中，_________是评估培训效果的重要手段，通过它可以了解学员的学习进展和存在的问题。

答案：效果评估职业培训师在授课前，应充分准备_________，以确保课程内容丰富、条理清晰。

答案：教案或课件解答题简述职业培训师在课程设计过程中应考虑的主要因素。

答：职业培训师在课程设计过程中应考虑以下主要因素：需求调研：了解学员的实际需求和职业发展方向，确保课程内容与学员需求相匹配。

教学目标：明确课程旨在达到的学习成果，包括知识、技能和态度等方面的提升。

教学内容：根据教学目标，选择和组织相关的教学内容，确保内容的准确性和实用性。

教学方法：采用多种教学方法和手段，如讲授、案例分析、角色扮演、小组讨论等，以提高学员的参与度和学习效果。

评估方式：设计合理的评估方式，如测试、作业、项目等，以检验学员的学习成果和课程的实施效果。

分析职业培训师在提升学员实践能力方面可以采取的策略。

答：职业培训师在提升学员实践能力方面可以采取以下策略：案例教学：通过引入真实或模拟的工作案例，让学员在分析和解决问题的过程中提升实践能力。

专训1-二次函数综合应用及答案

1．如图，在直角坐标系角三角形，∠2＋bx－2二次函数与平行四边形的综合2．如图所示，在平面直角坐标系xOy中，正方形OABC的边长为C分别在y轴的负半轴和轴的正半轴上，抛物线＋bx＋c经过点A，12a＋5c＝求抛物线对应的函数表达式．AB边以2 cm/s的速度开始沿BC边以1移动．一点到达终点后另一点停止移S＝PQ2(cm2)，试写出之间的函数表达式，并写出t的取值范围．取得最小值时，在抛物线上是否存在点3．二次函数标原点，点AB，B，4．(中考·孝感)如图所示，已知正方形长为1，点E在边BC方形外角的平分线CF(1)图①中，若点两个三角形全等来证明方案，并指出是哪两个三角形全等(2)如图②，若点C 重合)．①AE＝EF是否总成立？请给出证明．②在如图②所示的平面直角坐标系中，当点到某处时，点F恰好落在抛物线此时点F的坐标．(第1题)如图，过点C 作CD ⊥x 90°.，CAD ＝90°，∴∠OAB ∠AOB ＝∠CDA AAS )，∴AO ＝CD ＝＝3，∴C(3，1)．∵点－2上，∴1＝12×32＋∴抛物线对应的函数表达式为y ＝根据题意知：A(0，－2)点在抛物线上，∴c ＝－2.，∴a ＝56.知抛物线的对称轴为直线∴抛物线对应的函数表达式为y ＝5①若点E 在线段BC 上滑动，AE ＝证明：如图②，在AB 上截取AM ＝BM ＝BE ，MBE 是等腰直角三角形，∴∠AME 135°.又∵CF 平分正方形的外角，，∴∠AME ＝∠ECF.而∠BAE ＋∠AEB AEB ＝90°，∴∠BAE ＝AME ≌△ECF ，∴AE ＝EF.②如图②，过点F 作FH ⊥x 轴于点H. FH ＝BE ＝CH.BH ＝a ，则FH ＝a －1，∴点F 的坐标为F 恰好落在抛物线y ＝－x 2＋x ＋1a ＋1，∴a 2＝2，∴a ＝2或－2()，∴a －1＝2－1.∴点F 的坐标为。

微畔中职数学题库

微畔中职数学题库1. 数列及其应用数列是指按照一定规律排列的一列数字，例如 1，3，5，7，9 就是一个奇数数列。

数列的应用广泛，涉及到数学、物理、经济、计算机等多个领域。

数列有多种分类方法，包括等差数列、等比数列、斐波那契数列、调和数列等。

在数列的求和问题中，我们通常会用到数列求和公式，例如对于等差数列，其求和公式为 Sn=n(a1+an)/2。

等比数列的求和公式为 Sn=a1(1-q^n)/(1-q)，其中a1表示首项，an表示末项，q表示公比，n表示项数。

2. 函数及其图像函数是指一个或多个自变量与因变量之间的映射关系，例如y=x+1 就是一个函数。

函数的图像是指函数所表示的曲线或者平面区域，图像的形态与函数的性质有着密切的关系。

常见的函数类型包括一次函数、二次函数、绝对值函数、指数函数、对数函数等。

在函数的图像问题中，我们通常会关注其性质如单调性、奇偶性、周期性等。

例如对于一次函数 y=kx+b，如果 k>0，则函数单调递增，如果 k<0，则函数单调递减，如果 k=0，则函数为常数函数。

对于二次函数 y=ax^2+bx+c，如果 a>0，则函数开口向上，如果 a<0，则函数开口向下，如果 a=0，则函数为一次函数。

3. 三角函数及其应用三角函数是指由正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数等六个函数组成的函数组。

它们同样广泛应用于科学、工程、数学等领域中。

在三角函数的应用中，我们通常会用到它们的周期性、对称性、奇偶性等。

例如正弦函数 y=Asin(Bx+C)+D 的图像在周期T=2π/B 的平移下不变，其对称轴为y=D，如果B>0，则函数最大值为A+D，最小值为 -A+D，如果 B<0，则函数最大值为 -A+D，最小值为 A+D。

余弦函数 y=Acos(Bx+C)+D 的特性同理。

4. 极限与导数极限是指函数在接近某个数值时的近似取值，是计算机、信号处理等领域的重要概念。

非学科数学学培训三角函数综合复习

自学资料一、解直角三角形综合复习【知识探索】1．三角函数：（1）特殊角的三角函数值的计算；（2）仰俯角的定义；（3）影子问题。

【错题精练】例1．如图1，为放置在水平桌面l上的台灯，底座的高AB为5cm．长度均为20cm的连杆BC，CD与AB 始终在同一水平面上．（1）旋转连杆BC，CD，使∠BCD成平角，∠ABC=150∘，如图2，求连杆端点D离桌面l的高度DE．（2）将（1）中的连杆CD绕点C逆时针旋转，使∠BCD=165∘，如图3，问此时连杆端点D离桌面l的高度是增加了还是减少？增加或减少了多少？（精确到0.1cm，参考数据：√2≈1.41，√3≈1.73）第1页共11页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训例2．如图，在⊙O中，AB=AC，弦AB⊥CD于点E，BF⊥AB交AD的延长线于点F，连结BD．（1）证明：BD=BF；，BF=5，求CF的长．（2）连结CF，若tan∠ACD=34例3．如图，汽车在一条南北走向的公路上以每小时60千米的速度匀速向北行驶，当汽车在A处时，某信号塔C在它的北偏西30°方向，汽车前行2分钟到达B处，此时信号塔C在它的北偏西45°方向．（1）求AB的距离；（2）求信号塔C到该公路的距离．（√3≈1.73，结果精确到0．1千米）．例4．如图，有一个底面直径与杯高均为15㎝的杯子里面盛了一些溶液，当它支在桌子上倾斜到液面与杯壁呈52∘才能将液体倒出，则此时杯子最高处距离桌面~cm．（sin52∘≈0.79，cos52∘≈0.62，tan52∘≈1.28）第2页共11页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训例5．如图1，点M、N分别是正方形ABCD的边AB、AD的中点，连接CN、DM．（1）判断CN、DM的数量关系与位置关系，并说明理由；（2）如图2，设CN、DM的交点为H，连接BH，求证：BH＝BC；（3）将△ADM沿DM翻折得到△A′DM，延长MA′交DC的延长线于点E，如图3，求cos∠DEM．例6．如图，在菱形ABCD中，AB=6，∠DAB=60°，AE分别交BC、BD于点E、F，CE=2，连接CF，以下结论：（1）tan∠DCF= ；（2）△ABF的面积为．例7．已知边长为3的正方形ABCD中，点E在射线BC上，且BE=2CE，连接AE交射线DC于点F，若△ABE沿直线AE翻折，点B落在点B1处．（1）如图1，若点E在线段BC上，求的长；（2）求sin∠DAB1的值；=x”，其它条件都不变，试写出△ABE翻折后与正方形ABCD公共（3）如果题设中“BE=2CE”改为“BECE部分的面积y与x的关系式及自变量x的取值范围（只要写出结论，不需写出解题过程）．例8．如图1，点D为直角三角形ABC的斜边AB上的中点，DE⊥AB交AC于E，连EB、CD，线段CD与第3页共11页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训第4页共11页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训BF 交于点F ，若AC =8，tanA =12，则CFDF = ；如图2，点D 为直角三角形ABC 的斜边AB 上的一点，DE ⊥AB 交AC 于E ，连EB 、CD ，线段CD 与BF 交于点F ，若AC =8，ADDB =13，tanA =12，则CF DF= ．例9．（1）将两块等腰直角三角板AOB 和COD 按如图①放置，其中∠AOB =∠COD =90∘，求证：AC =BD ．（2）将两块含30°的直角三角板AOB 和COD 按如图②放置，其中∠AOB =∠COD =90∘，∠OAB =∠OCD =30∘，求证：BD ⊥AC ．（3）将图②的三角板OCD 绕点O 旋转到点C ，D ，B 三点一线时如图③所示，若AB =14，CD =10，求sin∠AOC 的值．例10．如图，由12个形状、大小完全相同的小矩形组成一个大的矩形网格，小矩形的顶点称为这个矩形网格的格点，已知这个大矩形网格的宽为4，△ABC 的顶点都在格点．（1）求每个小矩形的长与宽；（2）在矩形网格中找出所有的格点E ，使△ABE 为直角三角形；（描出相应的点，并分别用E 1，E 2…表示）（3）求sin∠ACB 的值．例11．如图，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60∘，点M、N分别在AB、AD边上，若AM:MB=AN:ND=1:2．则cos∠MCN=．，则BD的长例12．如图，已知菱形ABCD，对角线AC，BD相交于点O．若tan∠BAC=13是．例13．如图，在矩形ABCD中，E是BC边上的点，AE＝BC，AE=BC，在AE上截取AF=BE.（1）求证：DF⊥AE；（2）如果BE：EC＝2：1，求tan∠CDF的值．例14．如图，以△ABC的一边AB为直径的半圆与其它两边AC，BC的交点分别为D、E，且第5页共11页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训．（1）试判断△ABC的形状，并说明理由．（2）已知半圆的半径为5，BC＝12，求sin∠ABD的值．【举一反三】1．如图，在平面直角坐标系中，抛物线y=ax2+bx+c与x轴交于点A，C，与y轴交于点B，已知点A 坐标为（8，0），点B为（0，8），点D为（0，3），tan∠DCO=3，直线AB和直线CD相交于点E．4（1）求抛物线的解析式，并化成y=a(x−m)2+k的形式；（2）设抛物线的顶点为G，请在直线AB上方的抛物线上求点P的坐标，使得S△ABP=S△ABG；（3）点M为直线AB上的一点，过点M作x轴的平行线分别交直线AB，CD于点M，N，连结DM，DN是否存在点M，使得△DMN为等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．2．矩形ABCD中，AD=2AB=2√2，E是AD的中点，Rt∠FEG顶点与点E重合，将∠FEG绕点E旋转，角的两边分别交AB，BC（或它们的延长线）于点M，N，设∠AME=α（0∘＜α＜90∘），有下列结论：，其中正确的是（）①BM=CN；②M+CN=√2；③S△EMN=1sin2αA. ①；B. ②③；C. ①③；D. ①②③．第6页共11页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训第7页共11页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训3．如图，点D （0,3）,O （0,0）,C （4,0）在⊙A 上，BD 是⊙A 的一条弦，则sin∠OBD =（）A. 12 B. 34 C. 45D. 354．已知在△ABC 中，∠CAB =90∘，AC =3，sin∠B =35，AD ⊥BC 于点D ，点E 为边AB 上一动点（不与点A 、B 重合），EC 与AD 交于点G ，点F 在边BC 上，EF ⊥CE ，若点E 为AB 的中点，则CGEF 的值为．5．如图，在△ABC 中，CD 是边AB 上的中线，∠B 是锐角，且sinB =√22，tanA =12，AC =3√5．（1）求∠B 的度数与AB 的值；（2）求tan∠CDB ．6．如图，有两张矩形纸片ABCD 和EFGH ，AB ＝EF ＝2cm ，BC ＝FG ＝8cm ．把纸片ABCD 交叉叠放在纸片EFGH 上，使重叠部分为平行四边形，且点D 与点G 重合．当两张纸片交叉所成的角α最小时，tanα等于（）第8页共11页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训A. 14； B. 12； C. 817；D. 815．7．已知：二次函数y =ax 2+2ax −4（a ≠0）的图象与x 轴交于点A ，B （A 点在B 点的左侧），与y 轴交于点C ，△ABC 的面积为12．（1）求二次函数图象的对称轴与它的解析式；（2）点D 在y 轴上，当以A 、O 、D 为顶点的三角形与△BOC 相似时，求点D 的坐标；（3）点D 的坐标为（−2，1），点P 在二次函数图象上，∠ADP 为锐角，且tan∠ADP =2，求点P 的横坐标．8．如图，在△ABC 中，CD 是边AB 上的中线，∠B 是锐角，sinB =√22，tanA =12，AC =√5，（1）求∠B 的度数和AB 的长．（2）求tan∠CDB 的值．9．如图，直线y =−2x +6与x 轴，y 轴分别交于A 、B 两点，点A 关于原点O 的对称点是点C ，动点E 从点A 出发以每秒1个单位的速度到点C ，点D 在线段OB 上满足tan∠DEO =2，过点E 作EF ⊥AB 于点F ，点A 关于点F 的对称点为点G ，以DG 为直径作圆M ，设点E 运动的时间为t 秒．（1）当点E在线段OA上运动，t=时，△AEF与△EDO的相似比为1:√5；（2）当圆M与y轴相切时，求t的值；（3）若直线EG与圆M交于点N，是否存在t使NG=√2，若存在，求出t的值；若不存在，说明理由．10．如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．（1）求证：BE=CE；（2）若BD=2，BE=3，求tan∠BAC的值．11．如图1，我们已经学过：点C将线段AB分成两部分，如果ACAB =BCAC，那么称点C为线段AB的黄金分割点．某校的数学拓展性课程班，在进行知识拓展时，张老师由黄金分割点拓展到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果S1S =S2S1，那么称直线l为该图形的黄金分割线．如图2，在△ABC中，∠A=36∘，AB=AC，∠C的平分线交AB于点D．（1）证明点D是AB边上的黄金分割点；（2）证明直线CD是△ABC的黄金分割线．第9页共11页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训12．如图，在△ABC中，已知∠A=α，∠B=β，AC=b，AB=c，则b，c，α，β之间关系正确的是（）A. bsinα=tanα(c−b⋅cosα)；B. b⋅sinα=tanα(c−b⋅tanβ)；C. b⋅sinβ=c−b⋅cosαtanβ；D. b⋅sinα=tanβ(c−b⋅cosα)．1．如图，抛物线与x轴交于A、B两点，以线段AB为直径的半圆与抛物线在第二象限的交点为C，与y轴交于D点，设∠BCD=α，则BOAO的值为（）A. sin2αB. cos2αC. tan2αD. tan−2α2．如图，在Rt△BAD中，延长斜边BD到点C，使DC=13BC，连接AC，若tanB=53，则tan∠CAD的值第10页共11页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训非学科培训第11页共11页自学七招之预习轻身术：预习习惯培养好，课堂轻松没烦恼非学科培训为．3．如图，在圆O 中，弦AB 、CD 相交于点E ，AB =CD =4，点D 在上，连接CO ，并延长CO 交线段AB 于F ，连接OA 、OB ，且tan∠C =12．（1）求证：△OFA ∽△EFC ；（2）当△AOF 是直角三角形的时候，求EF 的长；（3）记△COE ，△FOE ，△BOF 的面积为S 1，S 2，S 3，如果S 2是S 1和S 3的比例中项，求OF 的长．（请直接写出答案）。

QC七大手法培训测试题

QC七大手法培训测试题填空题（每空2.5分，共计100分）1、七大手法分别是____________、____________、____________、____________、____________、____________、____________。

2、何为计量型数据，举例如___________、____________、____________，何为计数型数据，举例如___________、____________、____________。

3、查检表在车间的应用举例如__________、___________、___________。

4、层别法就是针对部门别、人别、工作方法别、设备、地点等所收集的数据,按照___________分类统计的一种分析方法。

5、柏拉图定律是_____________________________________________。

6、在制作特性要因图时可以利用___________的方法进行追踪原因。

7、5W1H是指________、________、________、_________、_______。

8、头脑风暴的思考原则是___________、____________、___________、___________。

10、散布图是用来分析两组数据之间的___________。

11、直方图可以理解为是一种___________表。

12、管制图分为两大类，分别是_________________、_________________。

13、管制图是在___________的基础上加上中心线和3σ上下管制界限构成的。

13、七大手法的口诀是____________、____________、____________、____________、____________、____________、____________。

健身俱乐部培训资料教练考试题目

晋级考试题目
教练姓名：日期：目前级别：考试得分：
一．服务的概念:
答:
二．服务的三个特性：
三．被成为健身房的硬件, 被成为健身房的软件.
四．心理服务的特点
答:
五．柔韧度训练的目的是:
答：
六．抗阻力训练的目的:
答:
七．高血压人事抗阻力训练动作的注意事项
答:
八．孕期人事训练的注意事项
答:
九．七大营养素是什么:
答:
十．糖的分类：
十一．蛋白质的分类：
十二．体重为65公斤的成年人,其蛋白质的摄入量为: 克
十三．维生素的分类:
十四．无机盐的分类:
十五．膳食纤维的作用:
答：
十六．每日需要2500千卡的热量,其早中晚餐分别需要摄入多少蛋白质,脂肪和碳水化合物.
答：。

克维教育word模版 (4)

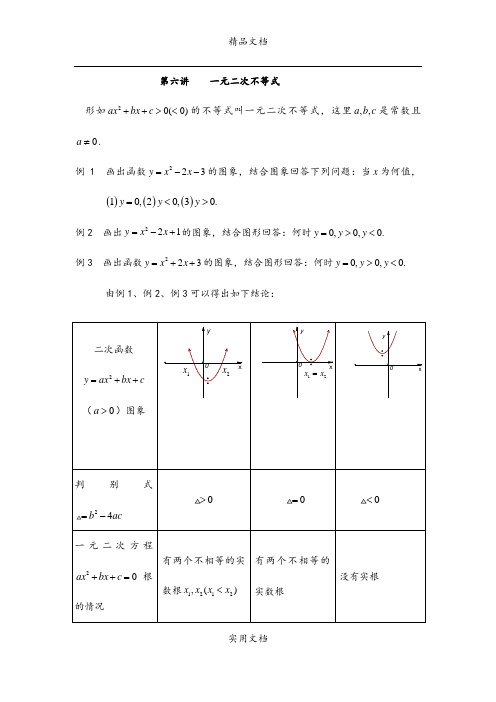
第六讲一元二次不等式形如20(0)ax bx c ++><的不等式叫一元二次不等式，这里,,a b c 是常数且0a ≠.例 1 画出函数223y x x =--的图象，结合图象回答下列问题：当x 为何值，()()()10,20,30.y y y =<>例2 画出221y x x =-+的图象，结合图形回答：何时0,0,0.y y y =>< 例3 画出函数223y x x =++的图象，结合图形回答：何时0,0,0.y y y =>< 由例1、例2、例3可以得出如下结论：2ax bx ++有两个不相等的实有两个不相等的没有实根［要点概括］1. 若0a <,将不等式20(0)ax bx c ++><两边同乘－1可化为0a >的情况来求解集。

2. 理解二次函数、一元二次方程、一元二次不等式之间的联系，培养数形结合的能力。

3. 当0a >，0>时，不等式20(0)ax bx c ++><的解集可总结为：大于零，取两根的两边；小于零，取两根之间。

0≤时的解集结合函数图象来记。

4. 不等式20(0)ax bx c ++≥≤的解集可类似求。

［例题精讲］例1 解下列不等式：（1）2280;x x --< （2）23100;x x +-> （3）2210;x x ++>（4）2690;x x ++≤ （5）210;x x -+-> （6）24140;x x -+-<例2 解下列不等式：（1）62;2x x +>+ （2）321;21x x +≥- 例3 解不等式246117.x x -<-+≤例4 解不等式322 3.x x +>-例5 解不等式2232 2.x x x -->+例6 解不等式22517 1.22x x x x --<-+- 例7 若不等式22221463x kx k x x -+<-+对一切实数x 恒成立，求实数k 的范围。