2015-2016北师大版九年级数学上册《菱形的性质与判定(三)》公开课课件

合集下载

九年级数学上册 1.1.3 菱形的性质与判定课件 (新版)北师大版

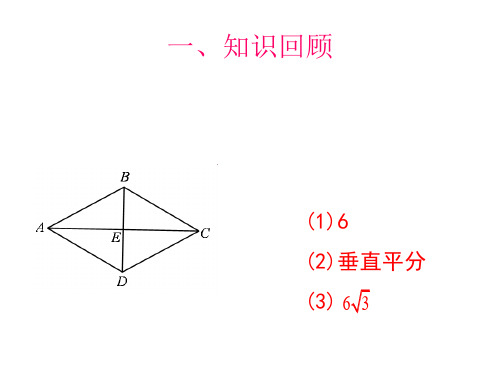
Rt△ABC=90°∠BAC=60°，BC的垂直平分
线分别交BC和AB于点D、E，点F在DE延长
线上，且AF=CE . • 求证：四边B 形ACEF是菱形.
D
E
F
C
图10
A
第3题图
九、布置ห้องสมุดไป่ตู้业
• 必做题：课本第 9 页习题1 .3 第2题； • 选做题：课本第9页习题1 .3 第3题.
谢谢大家！
• (必做题)1.如图所示，菱形ABCD的周长为 40cm，它的一条对角线BD长10cm，则 ∠ABC= °，AC= cm.
•
2.如图，四边形ABCD是菱形，对角线
AC和BD相交于点O，AC=4cm，BD=8cm，
则这个菱形的面积是 cm²．
•
第1题图
第2题图
• 3. （选做题六）、已效知果：如检图测，在菱形
•
(2)菱形ABCD的面积.
☆思路启迪：菱形的对角线有什么特点？
二、知识应用
• 1.典型例题(☆规范书写过程) •
☆思考：菱形面积是如何求出的？
三、总结提高
• 3.方法启迪 • (1)同学们在我们刚才完成的 • 例题中你有什么方法感悟或 • 者经验？
☆重• 大(发2)现求：菱菱形形面的积面的积方等法于有其几对种角？线乘积的一半.
四、变式练习
• 2.变式训练
•
如图所示，四边形ABCD是菱形，
• 其中对角线BD=12cm，AC=16cm.
• 求：(1)菱形的边长；
•
(2)求菱形一条边上的高.
答案:(1)10cm,(2)9.6cm
五、拓展应用
• 1.如图，两张等宽的纸条交叉重叠在一起，重叠部分ABCD是菱形吗？为什么？

北师大版九年级数学上册《菱形的性质与判定》优课件(共27张PPT)

菱形
有一组邻边相等的平行四边形
有一组邻边相等的平行四边形叫做菱形
A
∵四边形ABCD
是平行四边形
B
D
AB=BC
C
∴四边形ABCD
是菱形
感受生活
你能举出生活中你看到的菱形吗？
菱形就在我们身边
感受生活
三菱汽车标志欣赏
活动三：折一折剪一剪
如何利用折纸、剪切的方法，既快又准确地剪出一个菱形的纸片？
同理： DB平分∠ABC；
(2)在△DAC中,又∵AO=CO AC平分∠DAB和∠DCB
D
O
A
C
B
（1）菱形具有平行四边形的一切性质；
（2）菱形的四条边都相等；
（3）菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；
D
边菱形的两组对边平行且相等 A
O
C
菱形的四条边相等
B 数学语言
菱形的两组对角分别相等 ∵四边形ABCD是菱形
第一章特殊的平行四边形
第一节菱形
活动一：
边平行四
边形的性质：
对角线
平行四边形的对边平行；平行四边形的对边相等；
平行四边形的对角线互相平分；
角
平行四边形的对角相等；
平行四边形的邻角互补；
活动二：
在平行四边形中，如果内角大小保持不变仅改变边的长度，能否得到一个特殊的平行四边形？
平行四边形
邻边相等
BD 2 BO 34 . 64 花坛的面积
S 菱形 ABCD
1 AC • BD 2
346 . 4 m 2
活动四：做一做
1、菱形ABCD两条对角线BD、AC长分
别是6cm和8cm，求菱形的周长和面积。

新北师大版九年级数学上册《菱形的性质与判定》优质课课件(共20张PPT)

独立作业
驶向胜利的彼岸
老师期望: 你能写出规范的证明过程.
提高证明能力的源泉
6.已知:如图,AN⊥OB,BM⊥OA,垂足分别是N,M,OM=ON. 求证:PM=PN.
独立作业
N
B
P
驶向胜利的彼岸
O
M
A
老师期望: 你能写出规范的证明过程.
提高证明能力的源泉
独立作业
7.已知:如图,MN是线段AB的垂直 M 平分线,C,D是MN上的点. C 求证: (1)△ABC,△ABD是等腰三角形; (2)∠CAD=∠CBD. D
O A
D P
C
1 2
E B
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上 ∵ PD⊥OA,PE⊥OB , PD=PE ∴ ∠1=∠2(OP是角平分线或P在∠AOB的平分线上)
线段的垂直平分线定理定理：线段垂直平分线上的点到这条线段两个端点的距离相等
∵PC垂直平分AB (PC⊥AB,AC=BC或P在AB的垂直平分线上) ∴PA=PB 到一条线段两个端点距离相等的点, 在这条线段的垂直平分线上
1 BC AB 2
B
直角三角形的性质
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
直角三角形全等的判定定理: 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形斜边和一条直角边对应相等的两个直角三角形全等 (简称“HL”)
角平分线的定理定理:角平分线上的点到这个角两边的距离相等 ∵∠1=∠2,PD⊥OA,PE⊥OB ∴PD=PE
A
A F E C
O
O
C
B
B
D
提高证明能力的源泉

北师大数学九上课件1.1菱形的性质与判定(3)

初中数学课件
金戈铁骑整理制作
北师大版九年级(上)
1.1 菱形的性质与判定(3)
复习旧知
1、菱形的定义：有一组邻边相等的平行四边形叫做菱形。
2、菱形的特性： (1) 菱形的四条边相等； (2) 菱形的对角线互相平分。
3、菱形的判定： (1) 对角线互相垂直的平行四边形是菱形； (2) 四条边都相等的四边形是菱形。
A
E F
B
C
D
课堂小结
推论：菱形的面积等于其对角线乘积的一半。
2
∴
S菱形ABCD =
1 2
AC×
(OB+OD)
= 1 AC×BD
2
新知归纳
推论：菱形的面积等于其对角线乘积的一半。
新知探究
Ⅱ、已知：如图，菱形ABCD，作一个矩形，使得A、 B、C、D四点分别在矩形的四边上，且矩形的面积为菱形ABCD面积的2倍。
D
A
C
B
合作交流
ⅰ、如图，两张等宽的纸条交叉重叠在一起，重叠的部分ABCD是菱形吗？为什么？
F E
合作交流
ⅱ、已知：如图，在四边形ABCD中，AD=BC，点E、
F、G、H分别是AB、CD、AC、BD的中点.
求证：四边形EGFH是菱形.
F
C
D

G
H
A
E
B
范例讲解
例1、如图，四边形ABCD是边长为13cm的菱形，其中对
角线BD长10cm。求：
A
(1)对角线AC的长；
(2)菱形ABCD的面积. 解：(1) ∵四边形ABCD是菱形，
E
D
AC与BD交于点E
B
∴∠AED=90°

北师大版九年级数学上册1.1 菱形的性质与判定课件 (共41张PPT)

建立模型，探索新知
探究2：证明菱形的性质菱形的四条边相等，菱形的对角线互相垂直. 小组讨论：要严格证明这两个结论， 1. 有哪些“〞条件？ 2. “求证〞什么？ 3. “证明〞过程如何？
建立模型，探索新知
：如图，在菱形ABCD中，AB=AD，对角线 AC与BD相交于点O.
求证：〔1〕AB=BC=CD=AD；〔2〕AC⊥BD.
活动2 探究菱形的判定方法二用一长一短的两根细木条，在它们的中点处固定
一个小钉，做成一个可动的十字，四周围上一根橡皮筋，做成一个四边形.
示意图
建立模型，探索新知
〔1〕转动木条，这个四边形总有什么特征？你能证明你发现的结论吗？
建立模型，探索新知
〔2〕继续转动木条，观察什么时候橡皮筋围成的四边形变成菱形？
2 菱形的判定和面积
回忆复习，导入新课
菱形的定义：有一组邻边相等的平行四边形是菱形. 菱形的性质： ① 两条对角线互相垂直平分；
② 四条边都相等； ③ 每条对角线平分一组对角； ④ 菱形是一个中心对称图形，也是一
个轴对称图形.
回忆复习，导入新课
平行四边形的判定方法有哪些？边：两组对边分别平行的四边形是平行四边形；
1 BD AC 2
1 10 24 2
菱形的面积等于对角线之积的一半.
120(cm2 ).
归纳总结，提升认识
四条边都相等对角线互相垂直平分
归纳总结，提升认识
• 整节课你有什么感悟？ • 探索总结了什么规律？ • 对某些知识点你还有什么困惑？ • 你有什么新发现？ • 你学到了什么数学思想方法？
面积 =2 × △ABD的面积 2 1 BD AE 2 1 1012
2
2

北师大版九年级数学课件-菱形的性质与判定

图 20.3.1
如圖20.3.2，你還可以作一個兩條對角線互相垂直的平行四邊形．
图 20.3.2
和你的同伴交換一下，看看是否成了一個菱形．
由此可以得到判定菱形的一種方法：
對角線互相垂直的平行四邊形是菱形．
如圖20.3.3，平行四邊形ABCD中，對角線AC、BD互相垂直，我們可以證明：四邊形ABCD是菱形．
OE
F
B
C
想一想
你能說出這節課的心得和體會，讓大家與你分享嗎？
∴△AOE≌△COF
想一想
對於一個一般的四邊形，能否也可以找到判定它是不是菱形的方法呢？由菱形的另一條性質“四條邊都相等”，你可能會想到：如果一個四邊形的四條邊都相等，那它會不會一定是菱形？試著畫一畫，與周圍的同學討論，猜一猜結論是否成立．
由此我們得到了判定菱形的又一種方法：
四條邊都相等的四邊形是菱形．
1.下列條件中,不能判定四邊形ABCD為菱形的是
（ C ）．
Ａ. AC⊥BD ，AC與BD互相平分
Ｂ. AB=BC=CD=DA
Ｃ. AB=BC，AD=CD，且AC ⊥BD
Ｄ. AB=CD，AD=BC，AC ⊥BD
A
D
O
B
C
2.已知:如圖,在平行四邊形ABCD中,AE平分∠BAD,
與BC相交於點E,EF//AB,與AD相交於點F.
想一想
菱形的性質“兩條對角線互相垂直平分”中，“對角線
互相平分”是平行四邊形所具有的一般性質，而“對角線
垂直由”此是，菱可形以所得特到有一的個性猜質想。：“如果一個平行四邊形
的兩條對角線互相垂直，那麼這個平行四邊形等的細木棒，讓兩個木棒的中點重合並固定在一起，用筆和直尺畫出木棒四個端點的連線。我們知道，這樣得到的四邊形是一個平行四邊形．若轉動其中一個木棒，重複上面的做法，當兩個木棒之間的夾角等於90°時，得到的圖形是什麼圖形呢？

北师大版九年级数学上册《菱形的性质与判定(三)》公开课课件

重大发现：菱形的面积等于其对角线乘积的一半
3：已知菱形的周长为40，一条对角线长为16，则这个菱形的面积是 96 .
9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。20 21/7/29 2021/7/29Thur sday , July 29, 2021
4. 已知：如图，在菱形ABCD中，E、F分别是AB 和BC上的点，且BE=BF，Biblioteka 求证：(1)△ADE≌CDF；
(2) ∠DEF=∠DFE.
五、课堂小结
1.通过本节课的学习你有哪些收获，你还存在什么疑问？
2.请从以下三个方面进行总结：知识收获、方法收获、关注问题。 3.总结完成后请小组内进行交流。
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/7/292021/7/292021/7/292021/7/297/29/2021
14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年7月29日星期四2021/7/292021/7/292021/7/29
10、阅读一切好书如同和过去最杰出的人谈话。2021/7/292021/7/292021/7/297/29/2021 7:55:09 AM
11、一个好的教师，是一个懂得心理学和教育学的人。2021/7/292021/7/292021/7/29Jul-2129-Jul-21
12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/7/292021/7/292021/7/29Thursday, July 29, 2021

北师大版数学九上 1.1菱形的性质与判定(第3课时) 上课实用课件

E
P
M
(1)证明： ∵EF∥AB，PM∥AC， ∴四边形AEPM为平行四边形． ∵AD平分∠BAC， ∴∠CAD＝∠BAD. ∵EP∥AB，
∴∠BAD＝∠EPA. ∴∠CAD＝∠EPA. ∴EA＝EP. ∴四边形AEPM为菱形．
菱形性质复习性质判定应用性质判定练习
C
D F B
(2)当点P为EF的中点时，S菱形AEPM＝
.
1 2
EF·EN
菱形性质复习性质判定应用性质判定练习
E
P
A NM
C
D F B
1.如图，已知菱形ABCD的周长为24，对角线AC、BD交于点O，且AC+BD＝16，
则该菱形的面积等于（ D ）
B
A．6 B．8 C．14 D．28
A
O
C
2.如图，菱形ABCD中，过点D作DE⊥BA交BA的延长线于点E，DDF⊥BC交BC的
例2．如图，在四边形ABCD中，AB∥CD，AB≠CD，BD＝AC.
A
(1)求证：AD＝BC；
E
B
(2)若E，F，G，H分别是AB，CD，AC，BD的
H
G
中点，求证：线段EF与线段GH互相垂直平分．
证明：(1)如图，过点B作BM∥AC交DC的延长线
于点M，则∠ACD＝∠M. ∵AB∥CD，
A
E
∴四边形ABMC为平行四边形．
证明：∵AC⊥BD，∠FCA＝90°， ∴∠AEB＝∠ACF， ∴BD∥CF． ∵∠CBF＝∠DCB． ∴CD∥BF， ∴四边形DBFC是平行四边形； ∵BC平分∠DBF， ∴∠CBF＝∠CBD， ∵∠CBF＝∠DCB， ∴∠CBD＝∠DCB， ∴CD＝BD， ∴四边形DBFC是菱形．

北师大版九年级数学上册《菱形的性质与判定》优课件(共27张PPT)精选全文

22
2
S 菱形 ABCD
1 AC • BD 2
你有什么发现？
24
D
S菱A 形BCDAB •DE
A
O
C
E B
S菱形 ABCD12AC•BD
AB•DE 1 AC•BD 2
1 个定：有一组邻边相等的平行四边形叫菱形义 2个公式：S菱形=底×高
S菱形= 对角线乘积的一半
3 个特：特在“边、对角线、对称性” 性
相等的线段：AB=CD=AD=BC OA=OC OB=OD
5
6
B
O
34
C
相等的角：∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
等腰三角形有：△ABC △ DBC △ACD △ABD
直角三角形有：Rt△AOB Rt△BOC Rt△COD
他是这样做的：将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可.你知道其中的道理吗？
画出菱形的两条折痕, 并通过折叠手中的图形回答以下问题：
１、菱形是轴对称图形吗？ 2、菱形有几条对称轴？ 3、对称轴之间有什么关系？
4、你能看出图中哪些线段和角相等？
菱形ABCD中
A
12
D
7 8
BD 2 BO 34 . 64 花坛的面积
S 菱形 ABCD
1 AC • BD 2
346 . 4 m 2
活动四：做一做
1、菱形ABCD两条对角线BD、AC长分
别是6cm和8cm，求菱形的周长和面积。
分析： S菱形 ABCD4SAOB
D
4 1 OA • OB A

北师大版九年级数学上1.1 菱形的性质与判定(3) (共26张PPT)

用对角线能计算菱形的面积吗?
1
P9习题第2题
2 S S S 菱形ABCD = △ABD+ △BCD =
AC×BD
面积：S菱形=底×高=对角线乘积的一半
学以致用
已知菱形ABCD的两条对角线AC与BD相交于点 O,且AC=8cm,BD=6cm， A 求菱形的周长和面积．
解得:
D
O
C
B
菱形的周长为20cm ,面积为24cm2
（2）若AC=BD，则□ABCD是矩形；
（3）若∠ABC是直角，则□ABCD是菱形；（4）若∠BAO=∠DADO，则□ABCD是C 形。
O
A
B
3、选择：
（1）.下列命题中正确的是（ C）
A.一组邻边相等的四边形是菱形 B.三条边相等的四边形是菱形 C.四条边相等的四边形是菱形 D.四个角相等的四边形是菱形
复习回顾
菱形常用的判定方法：
1.有一组邻边相等的平行四边形是菱形. 2.对角线互相垂直的平行四边形是菱形. 3.有四条边相等的四边形是菱形.
【菱形的面积公式】菱形是特殊的平行四边形,
那么能否利用平行四边形
A
面积公式计算菱形的面积吗?
B
O
D
E
C
S菱形=BC. AE
思考:计算菱形的面积除了上述方法外,利
判定法一
文字语言
一组邻边相等的平行四边形是菱形
图形语言
A
D
B
C
符号语言
∵在□ABCD中
AB=AD ∴四边形ABCD是菱形
判定对角线互相垂直
法二
的平行四边形是菱形
判定
四边相等的四边形是菱形
法三

北师大版九年级数学上册1.1菱形的性质与判定第3课时(14张PPT)

菱形的性质与判定3
一、学习目标
1、菱形的性质定理的应用（菱形与等腰三角形、等边三角形、勾股定理）. 2、菱形的判定定理的应用（能结合题意选择合适的定理证明四边形是菱形）.
3、菱形面积的计算.
二、菱形的性质定理的应用
例1：如图，在菱形ABCD中，∠DAB=60°，两条对角线AC、BD相交于点O,若DB=4，求AC的长
（么1考）虑求用3这定、个义菱或四形者的定条每理一一边个；内相角的等度数的；四边形是菱形（定理二）
分析：根据菱形的周长可求得菱形的边长，证明：∵ ∠ACB=90°，∠BAC=60° 长，由此可求得AC的长．
长长，，由由注此此可可：求求得得其AACC的的中长长．．定义和定理一是在平行四边形的基础上证明的，分二析、：菱所先形根的以据性勾质如股定定理果理的求应已得用A知B的长是度，平再行四边形或容易证明是平行四边形那么考虑用定义或者定理一； ∴∠BAD=∠BCD=60°，∠ADC=∠ABC=60°×2=120°，
总结：
1、菱形具有平行四边形的性质，它又对角线互相垂直和四边相等.在做题时常常有菱形和等腰三角形、等边三角形以及勾股定理结合应用的问题，需注意．２、菱形的判定方法有三个，一个定义和两个判定定理，做题时需结合已知条件选取恰当的定理证明．３、菱形的面积等于底×高，也等于对角线乘积的一半，经常用等面积法解题．
分析：根据菱形的周长可求得菱形的边长，根据对角线和边长相等可得△ABD和△BDC 为等边三角形；根据勾股定理可求得AO的长，由此可求得AC的长．
解：（2）如图，∵四边形ABCD为菱形，
三、菱形的判定定理的应用
菱形的判定方法：长，由此可求得AC的长．
∴AD=AB=BC=DC=BD,△ABD和△BDC为等边三角形，