证明(三)-平行四边形复习讲义

合集下载

平行四边形性质和判定复习讲义

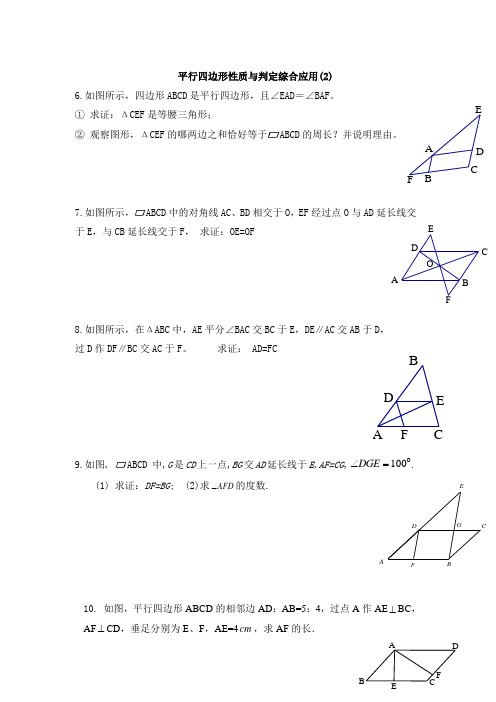
A BECFD ABOCDE AB E CFD ABCDF EG平行四边形性质与判定综合应用(2)6.如图所示，四边形ABCD 是平行四边形，且∠EAD ＝∠BAF 。

① 求证：ΔCEF 是等腰三角形；② 观察图形，ΔCEF 的哪两边之和恰好等于ABCD 的周长？并说明理由。

7.如图所示，ABCD 中的对角线AC 、BD 相交于O ，EF 经过点O 与AD 延长线交于E ，与CB 延长线交于F ，求证：OE=OF8.如图所示，在ΔABC 中，AE 平分∠BAC 交BC 于E ，DE ∥AC 交AB 于D ，过D 作DF ∥BC 交AC 于F 。

求证： AD=FC 9.如图,ABCD 中,G 是CD 上一点,BG 交AD 延长线于E ,AF=CG ,100=∠DGE .(1) 求证：DF=BG ; (2)求AFD ∠的度数.10. 如图，平行四边形ABCD 的相邻边AD ：AB=5：4，过点A 作AE ⊥BC ，AF ⊥CD ，垂足分别为E 、F ，AE=4cm ，求AF 的长．CDBAFOMNDCBANMQ PDCB AF E DBA11、如图，已知AC 是□ABCD 的一条对角线，BM ⊥AC 于M ，DN ⊥AC 于N ，求证：四边形BMDN 是平行四边形.12. 如图,在平行四边形ABCD 中,M,N 分别是OA,OC 的中点,O 为对角线AC 与BD 的交点,试问四边形BMDN 是平行四边形吗?说说你的理由.13、如图4.2-7,在平行四边形ABCD 中,AC 的平行线MN 交DA 的延长线于M,交DC 的延长线于N,交AB,BC 于P,Q.(1) 请指出图中平行四边形的个数,并说明理由. (2) MP 与QN 能相等吗?14、□ABCD 中，E 、F 在AC 上，AE=CF ，求证：四边形DEBF 是平行四边形.ABCDE15.如图，AC ∥ED ，点B 在AC 上且AB=ED=BC ,找出图中的平行四边形。

数学八年级下《平行四边形》复习课件

选择题:
2.平行四边形一边长为 10 ,则它的两条对角线可以是( C ) A、6 ,8 B、8, 12
C、8, 14
D、6, 14
如图， ABCD的周长为２０cm, O是对角线AC和BD的交点（１）若△ABC的周长是７cm,求 OC的长（２）若△OAB的周长比△OBC的周长短４cm，求AB的长
对角线: 4.对角线互相平分的四边形是平行四边形
角:
5.两组对角分别相等的四边形是平行四边形
（注：第５条不能直接应用）
A B C
D
两组对边分别平行
？
B
A
D C
2.平行四边形的识别方法：（1）∵AD//BC，AB//CD ∴四边形ABCD是平行四边形（2）∵AD// BC，AD=BC ∴四边形ABCD是平行四边形（3）∵AD=BC ，AB=DC ∴四边形ABCD是平行四边形（4）∵∠A=∠C，∠B=∠D ∴四边形ABCD是平行四边形（5）∵OA=OC，0B=0D ∴四边形ABCD是平行四边形
☆定义：两组对边分别平行的四边形是平行四边形。 ☆性质： 1、平行四边形对边平行且相等 2、平行四边形对角相等互补邻角 3、平行四边形对角线互相平分
4、平行四边形是中心对称图形
边： 1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形 3.一组对边平行且相等的四边形是平行四边形
已知E、F是
ABCD边AD、BC的中点
求证：BE=DF。
A E D
B
F
C
已知:点D、E、F分别在△ABC的边BC、 AB、AC上，且DE∥AF，DE=AF，G在 FD的延长线上，DG=DF。
求证：AG与ED互相平分。

平行四边形性质的复习课件

题目
在平行四边形ABCD中，若∠A 和∠B的度数之和为180°，则 ∠C的度数为 ()。
答案与解析
答案为“180°”。因为平行四边形的对角相等，即∠A + ∠B = 180°，所以∠A + ∠C = 180°
，从而得出∠C = 180°。
解答题
题目
已知平行四边形ABCD中，AE是BC边上的高，若AE = 3cm, AB = 4cm, AC = 5cm, 求 BC的长度。
对角线相等且互相垂直平分
正方形的对角线不仅长度相等，而且互相垂直平分，这是正方形的一个重要性质。
是特殊的矩形和菱形
正方形既是特殊的矩形也是特殊的菱形，因为它同时具备两者的所有性质。
CHAPTER 04
平行四边形在实际生活中的应用
建筑学中的应用
平行四边形在建筑设计中被广泛应用，如斜拉桥的钢索结构、吊车的悬挂系统等。
感谢您的观看
详细描述
在平行四边形中，相对的两边长度相等。这意味着如果你测量平行四边形的任意两边，它们的长度将是相同的。
对角线互相平分
总结词
平行四边形的对角线互相平分。
详细描述
在平行四边形中，对角线会相交于一点，并且被这条对角线平分的两个角是相等的。此外，对角线还将平行四边形分成两个相等的三角形。
CHAPTER 02
平行四边形的对边相等性质在服装设计和图案设计中也有应用，如对称和平衡等。
日常生活中的应用
平行四边形在日常生活中也随处可见，如门窗的设计、桌椅的摆放等。
平行四边形的对边相等性质在体育比赛中也有应用，如跳水、体操等项目的评分标准等。
平行四边形的对角线性质在包装和运输中也有应用，如纸箱的折叠和固定等。

八（下）数学：证明平行四边形的常用方法，总结全面，收藏复习

八（下）数学：证明平行四边形的常用方法，总结全面，收藏复习同学们好，在八年级数学下册第六单元，我们学习了平行四边形。

这一单元的知识，无论是在平时的考试中，还是在中考里，都属于重点内容之一。

特别是平行四边形的性质与判定，一定要作为重中之重去对待。

接下来老师就带大家一起来对这一块的知识进行一下复习：1.平行四边形的性质：平行四边形两组对边分别平行且相等；平行四边形两组对角分别相等；平行四边形两条对角线互相平分2.平行四边形的判定：两组对边分别平行的四边形是平行四边形；两组对边分别相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形。

接下来我们就一起来看看具体证明平行四边形的方法吧：方法一：利用两组对边分别平行判定平行四边形1第1题相对比较基础，由四边形ABCD是平行四边形，可得AD//BC,AD=BC,则BF//DE,再结合BF=DE,可判定四边形BEDF是平行四边形，根据平行四边形性质可得BE//DF,即ME//FN。

接着由BF=DE,AD=BC,可证AE=CF,结合AE//CF,从而可证四边形AECF是平行四边形，最后根据平行四边形的性质可得FM//EN,从而可证四边形FMEN是平行四边形。

方法二：利用两组对边分别相等判定平行四边形2方法三：利用一组对边平行且相等来判定平行四边形3方法四：利用对角线互相平分判定平行四边形4以上就是老师为大家分享的平行四边形判定常用的四种方法。

要证明一个四边形是平行四边形，同学们一定先要将判定方法熟记于心，才能根据具体的题目条件判断出使用的证明方法。

今天的内容分享就到这里，也欢迎大家下方留言或评论，来一起说说你们的想法或建议吧。

第二单元平行四边形的初步认识(期末复习讲义)二年级数学上册(苏教版)

苏教版二年级数学上册期末复习重难点知识点第二单元平行四边形的初步认识同学们，经过一个学期的学习，你一定进步了吧！今天，让我们共同回顾一下本学期的知识吧，并且通过完成这些练习，看看自己在哪些方面做得还真不错，以便继续发扬；哪些方面存在不足，需要在今后的学习中注意赶上。

每个人的成功都要经历无数次历练，无论成功还是失败对我们都十分重要。

加油！知识点一：认识多边形由几条边组成的封闭图形就是几边形，它们的每条边都是直直的。

知识点二：认识平行四边形1.平行四边形有四条边，它相对的两条边是相等的。

2.长方形变成了平行四边形，说明了四边形容易变形。

重点：初步认识四边形、五边形、六边形以及平行四边形等平面图形。

难点：通过对图形的折、剪、拼等活动，使学生体会图形的变换，开展空间观念。

考点一：多边形与平行四边形的认识由几条边组成的封闭图形就是几边形，它们的每条边都是直直的。

平行四边形有四条边，它相对的两条边是相等的。

考点二：多边形由4条直直的边组成的封闭图形是四边形；由5条直直的边组成的封闭图形是五边形；由6条直直的边组成的封闭图形是六边形；……一、选择题1．在下面图形上直直的剪一刀，一定不能将图形分成两个四边形的是（）。

A．B．C．2．下面的图形是平行四边形的是（）。

A．B．C．3．把分成三角形，最少能分成（）个。

A．3 B．4 C．5 D．64．下列图形中，哪一个是平行四边形？（）A．B．C．D．5．能围成平行四边形的是（）。

A．B．C．6．一张四边形纸剪去一个角，剩下的不可能是（）图形？A．四边形B．五边形C．六边形二、填空题7．有( )条线段；有( )条线。

11．图中一共有( )个四边形。

三、判断题13．平行四边形一定是四边形。

( )14．平行四边形剪掉一个角剩下的一定是四边形。

( )15．6根同样长的小棒可以摆成一个平行四边形。

( )16．两个完全相同的三角形一定能拼成一个平行四边形。

( )17．图中，一共有2个平行四边形。

人教版数学八年级下册第十八章平行四边形性质与判定专题复习辅导讲义

辅导讲义学员编号：年级：课时数：学员姓名：辅导科目：学科老师：授课类型T 平行四边形的概念、性质T 平行四边形的断定C中位线定理授课日期时段教学内容一、同步学问梳理学问点1：平行四边形的定义：两组对边分别平行的四边形是平行四边形．表示：平行四边形用符号“”来表示．如图，在四边形ABCD中，AB∥DC，AD∥BC，那么四边形ABCD是平行四边形．平行四边形ABCD，记作ABCD”，读作“平行四边形ABCD”．留意：平行四边形中对边是指无公共点的边，对角是指不相邻的角，邻边是指有公共端点的边，邻角是指有一条公共边的两个角．而三角形对边是指一个角的对边，对角是指一条边的对角．学问点2：平行四边形的性质：（1）边：平行四边形的对边平行且相等．（2）角：平行四边形的对角相等．邻角互补（3）对角线：平行四边形的对角线相互平分对称性：平行四边形是中心对称图形，两条对角线的交点是对称中心；二、同步题型分析题型1：平行四边形的边、角例1：已知，如图1，四边形ABCD为平行四边形，∠A＋∠C＝80°，平行四边形ABCD的周长为46 cm，且AB－BC＝3 cm，求平行四边形ABCD的各边长和各内角的度数．分析：由平行四边形的对角相等，邻角互补可求得各内角的度数；由平行四边形的对边相等，得AB＋BC＝23 cm，解方程组即可求出各边的长．解：由平行四边形的对角相等，∠A＋∠C＝80°，得∠A＝∠C＝40°又DC∥AB，∠D及∠A为同旁内角互补，∴∠D＝180°－∠A＝180°－40°＝140°．∴∠B＝140°．由平行四边形对边相等，得AB＝CD，AD＝BC．因周长为46 am，因此AB＋BC＝23 cm，而AB－BC＝3 cm，得AB＝13 cm，BC＝10 cm，∴CD＝13 am．AD＝10 cm．题后反思：留意充分利用性质解题．例2：如图2，在平行四边形ABCD中，E、F是直线BD上的两点，且DE＝BF，你认为AE＝CF吗？试说明理由．分析：本题主要考察平行四边形的性质．要证明AE＝CF，可以把两线段分别放在两个三角形里，然后证明两三角形全等．解：AE＝CF．理由：在平行四边形ABCD中，∵AB＝CD且AB∥CD．∴∠ABE＝∠CDF．∵DE＝BF，∴ DE＋BD＝BF＋BD，即BE＝DF：∴△ABE≌△CDF ∴ AE＝CF题后反思：利用平行四边形的性质解题时，一般要用到三角形全等学问，此题还可以证明其他三角形全等来证明两线段相等．题型2：平行四边形的周长例1：如图3，在平行四边形ABCD中，AC、BD相交于点O，作OE⊥BD于O，交CD于E，连接BE，若△BCE的周长为6，则平行四边形ABCD的周长为（ B ）图3A. 6B. 12C. 18D. 不确定分析：本题主要考察平行四边形的性质:对角线相互平分。

八年级下册数学平行四边形总复习讲义.doc

中心对称图形知识点1:平行四边形的定义两组对边分别平行的四边形叫做平行四边形，在四边形ABCD中，AB〃DC, AD〃BC,那么四边形ABCD是平行四边形。

定义的作用：（1）给出一种判定四边形是平行四边形的方法，如果所给四边形的两组对边分别平行，那么它一定是平行四边形；（2）给出了平行四边形的一个重要性质：两组对边分别平行。

知识点2：平行四边形的性质（1）定义性质：平行四边形的两组对边分别平行。

（2）性质:A、平行四边形的对角相等。

B、平行四边形的对边相等。

C、平行四边形的对角线互相平分。

（3）平行四边形是中心对称图形，平行四边形绕英对角线的交点旋转180后，与自身重合，我们说平行四边形是屮心对称图形，对称屮心为对角线的交点。

注意：边：对边平行，对边相等；角：对角相等，邻角互补；对角线：对角线互相平分。

知识点3：平行四边形的判定（1）定义：两组对边分别平行的四边形是平行四边形（2）定理1：两组对角分别相等的四边形是平行四边形（3）定理2：两组对边分别相等的四边形是平行四边形（4）定理3：对角线互相平分的四边形是平行四边形（5）定理4：一组对边平行且相等的四边形是平行四边形形形。

③是中心对称图形又是轴对称图__________________ I 形。

I ______________________________ 题型1:平行四边形的性质与判定例1：如图，oABCD +，ZB、ZC的平分线交于点O , BO和CD的延长线交于E ,求证：BO=OE例2：已知：如图，OABCD的对角线AC、BD相交于点0, EF过点0与AB、CD分別相交于点E、F.求证：OE = OF, AE=CF, BE=DF.例3：如图，CJ ABCD中，AE丄BD于E, CF丄BD于F, G、H分别为AD、. BC的中点，求证：EF和GH互相平分.B H C例4：如图，已知在"BCD中，E、F是对角线BD上的两点，BE=DF，点G、H分别在BA和DC 的延长线上，且AG=CH,连接GE、EH、HF、FG.(1)求证：四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上，其余条件不变，贝I」(1)中的结论是否成立？(不用说明理由)例5：如图，在口4BCQ中，点E在上，连接BE, DF〃BE交BC予点、F, AF与BE交与点M, CE 与DF交于点、N.求证：四边形MFNE是平行四边形.题型2：矩形性质与判定例1：如图，将矩形纸片ABCD沿对角线AC折柱，使点B落到点B，的位-置，AB与CD交于点E.(1)试找出一个与AAED全等的三角形，并加以证明；(2)若AB=8, DE=3, P为线段AC上的任意一点，PG丄AE于G, PH丄EC于H,试求PG+PH的值，并说明理由.例2：如图，矩形MCD中，AB=2, BC=3,对角线的垂直平分线分别交D, BC于点E、F,连结CE,则CE的长__________A E D例3：已知：如图，D ABCD屮,4C与BD交于0点,ZOAB=ZOBA.(1)求证：四边形ABCD为矩形；(2)作BELAC 于E, CF丄BD 于F,求证：BE=CF.例4：如图，在△初C中，D是3C边上的一点，E是/D的中点，过点力作的平行线交BE的延长线于F,且连结CF.(1)求证：D是3C的中点；(2)如果试猜测四边形ADCF的形状，并证明你的结论A F题型3：菱形性质与判定例1：如图，在菱形ABCD中，E、F分别是M、/C的中点，如果EF=2,那么菱形MCD 的周长是().(A)4 (B)8 (C)12 (D)16例2：如图，在菱形ABCD中，E是的中点，且DE丄4B, AB=4.求：(l)ZMC的度数；(2)菱形的面积.例3：如图，四边形ABCD +，AB//CD, /C 平分ABAD, CE//AD 交4B 于E.(1)求证：四边形AECD是菱形；(2)若点E是力3的中点，试判断MBC的形状，并说明理由.题型4：正方形性质与判定例1：如图，A. B、C三点在同一条直线上，AB二2BC,分别以MB, BC为边做正方形ABEF 和正方形BCMN,联结FN, EC.求证：FN二ECA B C例2：己知：如图，正方形ABCD中，点E、M、N分别在力从BC、/D边上，CE=MN, 乙MCE=35°,求ZANM的度数.。

八年级数学下册_平行四边形总复习课件_人教版

(3).下列性质中，平行四边形不一定具备的是（ C ）
(A)对角相等 (C )对角互补
(B)邻角互补 (D)内角和是360°
(4).下面判定四边形是平行四边形的方法中，
错误的是（ D ）。
(A)一组对边平行，另一组对边也平行； (B)一组对角相等，另一组对角也相等； (C )一组对边平行，一组对角相等； (D)一组对边平行，另一组对边相等
A
D
E
A 3x E 2x D x
2x
3x
3x
B
C
B
C
结束语
谢谢大家聆听！！！
23
F
A、６cm
B、12cm
E
C、18cm
D、24cm
B
D
C
（7）、平行四边形一边长为12cm，那么它的两条
对角线的长度可以是（ C ）
A、8cm和14cm
B、10cm 和14cm
C、18cm和20cm
D、10cm和34cm
（8）、四边形的四个内角的度数比是
2：2：3：1，则此四边形是( D )
A、任意四边形
B、任意梯形
C、等腰梯形
D、直角梯形
9.正方形具备而矩形不具备的特征是（D）
A. 四个角都是直角
B.对角线互相平分
C. 对角线相等
D.对角线互相垂直
10. 若菱形的两条对角线的长分别为4cm和6cm，则它
的面积为（ C）
A. 3cm2 B. 6cm2 C. 12cm2 D. 24cm2
11.如图所示，在平行四边形ABCD中，DB＝DC，
八年级数学下册_平行四边形总复习课件_人教版
平行四边形的对边平行边
平行四边形的对边相等

八年级数学下册《平行四边形》全章复习与巩固知识讲解

平行四边形全章复习与巩固知识讲解平行四边形全章复习与巩固；【学习目标】；1.掌握平行四边形、矩形、菱形、正方形的概念,了；2.探索并掌握平行四边形、矩形、菱形、正方形的有；些知识进行有关的证明和计算.；3.掌握三角形中位线定理.；【知识网络】；【要点梳理】；要点一、平行四边形；1．定义：两组对边分别平行的四边形叫做平行四边形；2．性质：（1）对边平行且相等；；（2）对角相等；邻角互补；；（平行四边形全章复习与巩固【学习目标】1. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.2. 探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算.3. 掌握三角形中位线定理.【知识网络】【要点梳理】要点一、平行四边形1．定义：两组对边分别平行的四边形叫做平行四边形.2．性质：（1）对边平行且相等；（2）对角相等；邻角互补；（3）对角线互相平分；（4）中心对称图形.3．面积：S平行四边形?底?高4．判定：边：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形．角：（4）两组对角分别相等的四边形是平行四边形；（5）两组邻角分别互补的四边形是平行四边形．边与角：（6）一组对边平行，一组对角相等的四边形是平行四边形；对角线：（7）对角线互相平分的四边形是平行四边形.要点诠释：平行线的性质：（1）平行线间的距离都相等；（2）等底等高的平行四边形面积相等.要点二、矩形1．定义：有一个角是直角的平行四边形叫做矩形.2．性质：（1）具有平行四边形的所有性质；（2）四个角都是直角；（3）对角线互相平分且相等；（4）中心对称图形，轴对称图形.3．面积：S矩形＝长?宽４．判定：（1) 有一个角是直角的平行四边形是矩形.（2）对角线相等的平行四边形是矩形.（3）有三个角是直角的四边形是矩形.要点诠释：由矩形得直角三角形的性质：（1）直角三角形斜边上的中线等于斜边的一半；（2）直角三角形中，30度角所对应的直角边等于斜边的一半．要点三、菱形1. 定义：有一组邻边相等的平行四边形叫做菱形.2．性质：（1）具有平行四边形的一切性质；（2）四条边相等；（3）两条对角线互相平分且垂直，并且每一条对角线平分一组对角；（4）中心对称图形，轴对称图形.3．面积：S菱形＝底?高＝对角线?对角线24．判定：（1）一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四边相等的四边形是菱形.要点四、正方形1. 定义：四条边都相等，四个角都是直角的四边形叫做正方形. 2．性质：（1）对边平行；（2）四个角都是直角；（3）四条边都相等；（4）对角线互相垂直平分且相等，对角线平分对角；（5) 两条对角线把正方形分成四个全等的等腰直角三角形；（6）中心对称图形，轴对称图形.3．面积：S正方形=边长×边长＝1×对角线×对角线24．判定：（1）有一个角是直角的菱形是正方形；（2）一组邻边相等的矩形是正方形；（3）对角线相等的菱形是正方形；（4）对角线互相垂直的矩形是正方形；（5）对角线互相垂直平分且相等的四边形是正方形；（6）四条边都相等，四个角都是直角的四边形是正方形.【典型例题】类型一、平行四边形1、如图，点D是△ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B重合）．以BD、BF为邻边作平行四边形BDEF，又APBE（点P、E在直线AB的同侧），如果BD＝1AB，那么△PBC的面积与△ABC面积之比为（） 41313A．B．C．D．4554【答案与解析】解：过点P作PH∥BC交AB于H，连接CH，PF，∵APBE，∴四边形APEB是平行四边形，∴PE∥AB，PE＝AB，∵四边形BDEF是平行四边形，∴EF∥BD，EF＝BD，即EF∥AB，∴P，E，F共线，1AB，∴PE＝AB＝4a，4则PF＝PE－EF＝3a，设BD＝a，∵BD＝∵PH∥BC，∴S△HBC?S△PBC，∵PF∥AB，∴四边形BFPH是平行四边形，∴BH＝PF＝3a，∵S△HBC:S△ABC＝BH：AB＝3a：4a＝3：4，∴S△PBC:S△ABC＝3：4．【总结升华】此题考查了平行四边形的判定与性质与三角形面积比的求解方法．此题难度较大，注意准确作出辅助线，注意等高三角形面积的比等于其对应底的比．举一反三：【变式】已知△ABC中，AB＝3，AC＝4，BC＝5，分别以AB、AC、BC为一边在BC边同侧作正△ABD、正△ACE和正△BCF，求以A、E、F、D四点为顶点围成的四边形的面积．【答案】证明：∵AB＝3，AC＝4，BC＝5，∴∠BAC＝90°∵△ABD、△ACE和△BCF为正三角形，∴AB＝BD＝AD，AC＝AE＝CE，BC＝BF＝FC ,∠1＋∠FBA＝∠2＋∠FBA＝60°∴∠1＝∠2易证△BAC≌△BDF（SAS），∴DF＝AC＝AE＝4，∠BDF＝90°同理可证△BAC≌△FEC∴AB＝AD＝EF＝3∴四边形AEFD是平行四边形（两组对边分别相等的四边形是平行四边形）∵DF∥AE，DF⊥BD延长EA交BD于H点，AH⊥BD，则H为BD中点∴平行四边形AEFD的面积＝DF×DH＝4×类型二、矩形3＝6. 22、如图，O是矩形ABCD的对角线的交点，E、F、G、H分别是OA、OB、OC、OD上的点，且AE＝BF＝CG＝DH．（1）求证：四边形EFGH是矩形；（2）若E、F、G、H分别是OA、OB、OC、OD的中点，且DG⊥AC，OF＝2cm，求矩形ABCD的面积．【答案与解析】（1）证明：∵四边形ABCD是矩形，∴OA＝0B＝OC＝OD，∵AE＝BF＝CG＝DH，∴AO－AE＝OB－BF＝CO－CG＝DO－DH，即：OE＝OF＝OG＝OH，∴四边形EFGH是矩形；（2）解：∵G是OC的中点，∴GO＝GC，∵DG⊥AC，∴∠DGO＝∠DGC＝90°，又∵DG＝DG，∴△DGC≌△DGO，∴CD＝OD，∵F是BO中点，OF＝2cm，∴BO＝4cm，∵四边形ABCD是矩形，∴DO＝BO＝4cm，∴DC＝4cm，DB＝8cm，?∴矩形ABCD的面积＝4×?．【总结升华】本题主要考查矩形的判定，首先要判定四边形是平行四边形，然后证明对角线相等．举一反三：【变式】如图，O为△ABC内一点，把AB、OB、OC、AC的中点D、E、F、G依次连接形成四边形DEFG．（1）四边形DEFG是什么四边形，请说明理由；（2）若四边形DEFG是矩形，点0所在位置应满足什么条件？说明理由．2【答案】解：（1）四边形DEFG是平行四边形．理由如下：∵D、G分别是AB、AC的中点，∴DG是△ABC的中位线；∴DG∥BC，且DG＝1BC； 21BC；2同理可证：EF∥BC，且EF＝∴DG∥EF，且DG＝EF；故四边形DEFG是平行四边形；（2）O在BC边的高上且A和垂足除外．理由如下：连接OA；同（1）可证：DE∥OA∥FG；∵四边形DEFG是矩形，∴DG⊥DE；∴OA⊥BC；即O点在BC边的高上且A和垂足除外．。

八年级数学平行四边形的复习ppt课件

五、其他重要定理
1. 四边形的内角和等于 360°. 2. n 边形的内角和等于 ( n – 2 ). 180°. 3. 任意多边形的外角和等于360°. 4. 关于中心对称的两个图形的性质：
（1）是全等形；（2）对称点的连线都经过对称中心并且被对称中心平分。
六、三角形中位线定理
A
如图，三角形ABC中，AD=DB，AE=EC，
四、对角线与特殊四边形的关系
1.对角线互相平分的四边形是平行四边形
A
D DD DDDDD D
B
2.对角线相等的平行四边形是矩形
AAAAAAA AA
C
DDDDDDDDD
BB
CCC
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
A
D
E
A
D
F
B
C
A
DF
B
E
FC
B
C
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
平行四边形
四边形
梯形
矩形菱形
正方形
等腰梯形
直角梯形
(A)一组对角相等。
(B)两条对角线互相平分。
(C )两条对角线互相垂直。 (D)一对邻角的和为180°。
7.下列图形中，既是轴对称图形又是中心对称图形的是（ C ） (A)等边三角形。(B)平行四边形。(C )菱形。(D)等腰梯形。
8.下列图形中，既是轴对称图形又是中心对称图形的是（ D ）

人教版数学八年级下册第十八章-平行四边形-专题复习辅导讲义

辅导讲义是”；是平行四边形，可以记做“ABDC1题图2．如图所示，在ABCD所示，在ABCD125．在ABCD 中，∠B-∠A=30°，则∠A ，∠B ，∠C ，∠D 的度数是（）．A ．95°，85°，95°，85°B ．85°，95°，85°，95°C ．105°，75°，105°，75°D ．75°，105°，75°，105° 6．在ABCD 中，∠A ：∠B ：∠C ：∠D 的值可以是（）．A ．1：2：3：4B ．3：4：4：3C ．3：3：4：4D ．3：4：3：4 7．如图所示，如果ABCD 的对角线AC ，BD 相交于点O ，•那么图中的全等三角形有（）．A ．1对B ．2对C ．3对D ．4对8．如图所示，若平行四边形ABCD 的周长为22cm ，AC ，BD 相交于点O ，•△AOD 的周长比△AOB 的周长小3cm ，则AD=_______，AB=_______．答案：4cm 7cm知识点3 平行四边形的面积 9．如图所示，ABCD 的对角线AC 的长为10cm ，∠CAB=30°，AB 的长为6cm.求ABCD 的面积．答案：30cm 210．如图所示，在ABCD 中，AB=10cm ，AB 边上的高DH=6cm ，BC=6cm ，求BC 边上的高DF 的长．答案：10cm知识点4 平行四边形的判定11．1已知：如图，ABCD 中，E 、F 分别是AD 、BC 的中点，求证：BE=DF ．提示：证明DE ∥BF ，DE=BF12．1已知：如图，ABCD 中，E 、F 分别是AC 上两点，且BE ⊥AC 于E ，DF ⊥AC 于F ．求证：四边形BEDF 是平行四边形．提示：证明BE ∥DF ，BE=DF13．1已知：如图ABCD 的对角线AC 、BD 交于点O ，E 、F 是AC 上的两点，并且AE=CF ．求证：四边形BFDE 是平行四边形．提示：证明OB=OD, OE=OF知识点5 三角形的中位线14．1如图，A 、B 两点被池塘隔开，在AB 外选一点C ，连结AC 和BC ，并分别找出AC 和BC 的中点M 、N ，如果测得MN=20 m ，那么A 、B 两点3题图 4题图7题图 8题图3的距离是 m ，理由是．答案：40 三角形两边的中点连线平行于第三边且等于第三边的一半15．1△ABC 中，D 、E 分别为AB 、AC 的中点，若DE ＝4，AD ＝3，AE ＝2，则△ABC 的周长为______．答案：1816．1已知：如图（1），在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．提示：连结BD ，利用中位线定理得：EH BD ，GFBD知识点6 矩形的定义与性质 17．已知在四边形ABCD 中，AB CD ，请添加一个条件，使四边形ABCD 是矩形，•加上的条件是_______．答案：AC=BD (答案不唯一) 18．如图所示，M 是ABCD 的边AD 的中点，且MB=MC ．求证：ABCD 是矩形．提示：证明△ABM ≌△DCM ，得到∠A=∠D ，又因为∠A+∠D=180°19．如图所示，矩形ABCD 的两条对角线相交于点D ，∠AOD=120°，AB=4cm ，求矩形的对角线的长．答案：8cm知识点7 直角三角形斜边中线的性质20．已知直角三角形两直角边的长分别为6cm 和8cm ，则斜边上的中线长．答案：5cm21．如图所示，在△ABC 中，∠ACB=90°，点D ，E 分别为AC ，AB 的中点，点F•在BC 的延长线上，且∠CDF=∠A ．求证：四边形DECF 为平行四边形．提示：AE=CE,得到角相等，推出DF ∥CE ，又DE ∥BF ，即证 22．如图所示，在△ABC 中，∠C=90°，AC=BC ，AD=BD ，PE ⊥AC 于点E ，PF⊥BC 于点F ，求证：DE=DF ．提示：连结CD ，证明△ADE ≌△CDF 知识点8 矩形的判定 23．下列说法中：（1）四个角都相等的四边形是矩形．（2）两组对边分别相等并且有一个角是直角的四边形是矩形．（3）对角线相等并且有一个角是直角的四边形是矩形．B=AC，推出．如图所示，在菱形ABCD4如图，ABCD．对角线互相平分．若正方形的一条对角线长为，则它的边长是求∠AFD的度数．56提示：证明△ABE ≌△BCF知识点12 正方形的判定43．有下列命题，其中真命题有（）． ①四边都相等的四边形是正方形； ②四个内角都相等的四边形是正方形；③有三个角是直角，且有一组邻边相等的四边形是正方形； ④对角线与一边夹角为45°的四边形是正方形．A ．1个B ．2个C ．3个D ．4个 44．如图所示，在△ABC 中，∠ABC=90°，BD 平分∠ABC ，DE ⊥BC ，DF ⊥AB. 求证：四边形BEDF 是正方形．提示：由角平分线的性质可推出：DE=DF ，又三个角为90°的四边形是矩形，所以推出四边形BEDF 是正方形．一、专题精讲专题1 动点问题例1 1如图所示，在矩形ABCD 中，AB=4cm ，BC=8cm 、点P 从点D 出发向点A 运动，同时点Q 从点B 出发向点C 运动，点P 、Q 的速度都是1cm/s ．(1）在运动过程中，四边形AQCP 可能是菱形吗？如果可能，那么经过多少秒后，四边形AQCP 是菱形？(2）分别求出菱形AQCP 的周长、面积．分析：（1）设经过x 秒后，四边形AQCP 是菱形，根据菱形的四边相等列方程即可求得所需的时间．（2）根据第一问可求得菱形的边长，从而不难求得其周长及面积．解答：解：（1）经过x 秒后，四边形AQCP 是菱形 ∴DP=xcm，AP=CP=AD-DP=（8-x ）cm ， ∵DP 2+CD 2=PC 2，∴16+x 2=（8-x ）2，解得x=3 即经过3秒后四边形是菱形．（2）由第一问得菱形的边长为5∴菱形AQCP的周长=5×4=20（cm）菱形AQCP的面积=5×4=20（cm2）点评：此题主要考查菱形的性质及矩形的性质的理解及运用．ABC’D’是菱形，并请说8ABCFD ∴BC′=21AC ．而∠ACB=30°， ∴AB=21AC ∴AB=BC′．∴四边形ABC′D′是菱形．点评：本题即考查了全等的判定及菱形的判定，注意对这两个判定定理的准确掌握．考查了学生综合运用数学的能力．重合，点D 落到分析：（1）根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′，AB=AD′，∠1=∠3，从而利用ASA 判定△ABE≌△AD′F；（2）四边形AECF 是菱形，我们可以运用菱形的判定，有一组邻边相等的平行四边形是菱形来进行验证．∴△ABE≌△AD′F（ASA）．（2）解：四边形AECF是菱形．证明：由折叠可知：AE=EC，∠4=∠5．∵四边形ABCD是平行四边形，∴AD∥BC．∴∠5=∠6．∴∠4=∠6．∴AF=AE．∵AE=EC，∴AF=EC．又∵AF∥EC，∴四边形AECF是平行四边形．∵AF=AE，∴平行四边形AECF是菱形．点评：此题考查了全等三角形的判定及菱形的判定方法，做题时要求学生对常用的知识点牢固掌握．分析：要证明HG与HB是否相等，可以把线段放在两个三角形中证明这两个三角形全等，或放在一个三角形中证明这个三角形是等腰三角形，而图中没有这样的三角形，因此需要作辅助线，构造三角形．910∴Rt△AGH≌Rt△ABH（HL），∴HG=HB．证法2：连接GB，∵四边形ABCD，AEFG都是正方形，∴∠ABC=∠AGF=90°，由题意知AB=AG，∴∠AGB=∠ABG，∴∠HGB=∠HBG，∴HG=HB．点评：解答本题要充分利用正方形的特殊性质．注意在正方形中的特殊三角形的应用，搞清楚矩形、菱形、正方形中的三角形的三边关系，可有助于提高解题速度和准确率．二、专题过关1. 如图所示，△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠BCA的外角平分线于点F.(1)求证：EO=FO(2)当点O运动到何处时，四边形AECF是矩形？并证明你的结论.分析：（1）根据平行线性质和角平分线性质及，由平行线所夹的内错角相等易证．（2）根据矩形的判定方法，即一个角是直角的平行四边形是矩形可证解答：（1）证明：∵CE平分∠ACB，∴∠1=∠2，又∵MN∥BC，∴∠1=∠3，∴∠3=∠2，∴EO=CO，同理，FO=CO ，∴EO=FO．（2）解：当点O 运动到AC 的中点时，四边形AECF 是矩形．∵EO=FO，点O 是AC 的中点．∴四边形AECF 是平行四边形，∵C F 平分∠BCA 的外角，∴∠4=∠5，又∵∠1=∠2，∴∠2+∠4=21×180°=90°．即∠ECF=90度，∴四边形AECF 是矩形．点评：本题涉及矩形的判定定理，解答此类题的关键是要突破思维定势的障碍，运用发散思维，多方思考，探究问题在不同条件下的不同结论，挖掘它的内在联系，向“纵、横、深、广”拓展，从而寻找出添加的条件和所得的结论．12图3【解法指导】欲证两条线段之和等于第三条线段，可通过截长补1415 分析：过F 作AB 、CD 的平行线FG ，由于F 是AD 的中点，那么G 是BC 的中点，即Rt△BCE 斜边上的中点，由此可得BC=2EG=2FG ，即△GEF、△BEG 都是等腰三角形，因此求∠B 的度数，只需求得∠B EG 的度数即可；易知四边形ABGF 是平行四边形，得∠EFG=∠AEF，由此可求得∠FEG 的度数，即可得到∠AEG 的度数，根据邻补角的定义可得∠BEG 的值，由此得解．解答：解：过F 作FG∥AB∥CD，交BC 于G ；则四边形ABGF 是平行四边形，所以AF=BG ，即G 是BC 的中点；连接EG ，在Rt△BEC 中，EG 是斜边上的中线，则BG=GE=FG=21BC ； ∵AE∥FG，∴∠EFG=∠AEF=∠FEG=54°，∴∠AEG=∠AEF+∠FEG=108°，∴∠B=∠BEG=180°-108°=72°．故选D ．点评：此题主要考查了平行四边形的性质、直角三角形的性质以及等腰三角形的判定和性质，正确地构造出与所求相关的等腰三角形是解决问题的关键．17。

人教版八年级数学下册第十八章《平行四边形》单元复习课件

第5题图
6.(人教8下P62改编)如图，在△ABC中，中线BD，CE相交
于O，F，G分别为BO，CO的中点，则四边形EFGD的形状
是平行四边形
.
第6题图
7.【例1】(全国视野)(2022丹东模拟)如图，在▱ABCD中，点
O是AD的中点，连接CO并延长交BA的延长线于点E，连接
AC，DE.求证：四边形ACDE是平行四边形.
AF于点G.
(1)求证：四边形ABCF是矩形；
(2)若EA＝EG，求证：ED＝EC.
或对角线相等.
2.如图，在Rt△ABC中，∠ACB＝90°，DE，DF是△ABC
的中位线，连接EF，CD.求证：EF＝CD.
证明：∵DE，DF是△ABC的中位线，
∴DE∥BC，DF∥AC，
∴四边形DECF是平行四边形，
∵∠ACB＝90°，∴四边形DECF
是矩形，
∴EF＝CD.
知识点三：菱形
(1)菱形的特殊性质：菱形的四条边相等、对角线互相垂直
＝
在Rt△ABG和Rt△AFG中，
，
＝
∴△ABG≌△AFG(HL).
(2)解：∵△ABG≌△AFG，∴BG＝FG，
设BG＝FG＝x，则GC＝6－x，
∵E为CD的中点，∴CE＝EF＝DE＝3，
∴EG＝3＋x，∴在Rt△CEG中，32＋(6－x)2＝(3＋x)2，
解得x＝2，∴BG＝2.
的中点，将△ADE沿AE对折至△AFE，延长EF交边BC于点
G，连接AG.
(1)求证：△ABG≌△AFG；
(2)求BG的长.
(1)证明：在正方形ABCD中，AD＝AB＝BC＝CD，
∠D＝∠B＝∠BCD＝90°，
∵将△ADE沿AE对折至△AFE，

北师大版八下第六章平行四边形复习讲义

一、平行四边形的定义及性质知识点1平行四边形的概念两组对边分别平行的四边形是平行四边形知识点2 平行四边形的性质（边，角，对角线，对称性）（1）边的性质：平行四边形的对边相等平行四边形的对边平行（2）角的性质：平行四边形的对角相等（3）对角线的性质：平行四边形的对角线互相平分（4）平行四边形是中心对称图形二、平行四边形的判定:知识点1 平行四边形的判定（1）两组对边分别平行的四边形是平行四边形（定义）（2）两组对边分别相等的四边形是平行四边形（3）对角线互相平分的四边形是平行四边形（4）一组对边平行且相等的四边形是平行四边形（注意：①必须是同一组对边平行且相等，也就是一组对边平行，另一组对边相等时，不一定是平行四边形。

②有两条边相等，并且另外两条边相等的四边形不一定是平行四边形）知识点2 两条平行线间的距离的定义若两条直线互相平行，则其中一条直线上任意两点到另一条直线的距离相等，这个距离称为平行线之间的距离，实际上平行线间的距离处处相等三、三角形的中位线1、三角形中位线的定义：连接三角线两边中点的线段叫做三角形的中位线2、三角形中位线定理：三角形的中位线平行于三角线的第三边，且等于第三边的一半（要区别三角形中位线和中线不要搞混淆了，说的是中位线与第三边的位置关系，中位线与第三边的数量关系）四、多边形的内角与外角和知识点一、多边形及正多边形1、多边形：在平面内，由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形2、多边形的分类：多边形按组成它的线段的条数分为三边形（三角形）、四边形、五边形……由n 条线段组成的多边形叫做n边形3、多边形的对角线：连接多边形不相邻的两个顶点的线段叫做多边形的对角线B C 4、正多边形：在平面内，内角都相等、边也都相等的多边形叫做正多边形知识点二、多边形的内角和与外角和1、多边形的内角和：n 变形的内角和等于（n-2）*180°（n ≥3）2、多边形的外角和：多边形的外角和等于360°3.多边形的对角线有： (3)2n n【巩固训练】一、平行四边形的概念及性质1. （2012浙江杭州3分）已知平行四边形ABCD 中，∠B=4∠A，则∠C=【】A ．18°B ．36°C ．72°D ．144°2. （2012四川自贡3分）如图，在平行四边形ABCD 中，AD=5，AB=3，AE 平分∠BAD 交BC 边于点E ，则线段BE ，EC 的长度分别为【】A ．2和3B ．3和2C ．4和1D ．1和43. （2012山东泰安3分）如图，在平行四边形ABCD 中，过点C 的直线CE⊥AB，垂足为E ，若∠EAD=53°，则∠BCE 的度数为【】A ．53°B ．37°C ．47°D ．123°4. （2012广西南宁3分）如图，在平行四边形ABCD 中，AB=3cm ，BC=5cm ，对角线AC ，BD 相交于点O ，则OA 的取值范围是【】A ．2cm ＜OA ＜5cmB ．2cm ＜OA ＜8cmC ．1cm ＜OA ＜4cmD ．3cm ＜OA ＜8cm5. （2012湖南永州3分）如图，平行四边形ABCD 的对角线相交于点O ，且AB≠AD，过O 作OE⊥BD 交BC 于点E ．若△CDE 的周长为10，则平行四边形ABCD 的周长为．6. （2012山东烟台3分）ABCD 中，已知点A （﹣1，0），B （2，0），D （0，1）．则点C 的坐标为．7、（2010青海西宁）在□ABCD 中，对角线AC 、BD 相交于点O ，如果AC=14，BD=8，AB=x ，那么x 的取值范围是 .8、（2010辽宁铁岭）.如图所示，平行四边形ABCD 的周长是18 cm ，对角线AC 、BD 相交于点O,若△AOD 与△AOB的周长差是5 cm ，则边AB 的长是________ cm.9. 如图2，在平行四边形ABCD 中，下列结论中错误．．的是（） A BCD C ．AB =CDD ． AC ⊥BD10．（2013黑龙江省哈尔滨市，7）如图，在ABCD 中，AD=2AB ，CE 平分∠BCD 交AD 边于点E ，且AE=3，12 A BC 图2则AB的长为( )．(A)4 (B)3 (C) 52(D)211、（2012四川巴中3分）不能判定一个四边形是平行四边形的条件是【】A. 两组对边分别平行B. 一组对边平行，另一组对边相等C. 一组对边平行且相等D. 两组对边分别相等12 （2012四川广元3分）若以A（-0.5，0），B（2，0），C（0，1）三点为顶点要画平行四边形，则第四个顶点不可能在【】A. 第一象限B. 第二象限C. 第三象限D. 第四象限13．(2013湖北荆门，7，3分)四边形ABCD中，对角线AC，BD相交于点O，给出下列四个条件：①AD∥BC②AD＝BC ③OA＝OC④OB＝OD从中任选两个条件，能使四边形ABCD为平行四边形的选法有( )A．3种 B．4种 C．5种 D．6种14、（2013四川泸州，6，2分）四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）A．AB//DC，AD//BC B．AB＝DC，AD＝BCC．AO＝CO，BO＝DO D．AB//DC，AD＝BC15. （2012广东佛山3分）依次连接任意四边形各边的中点，得到一个特殊图形（可认为是一般四边形的性质），则这个图形一定是【】A．平行四边形B．矩形C．菱形D．梯形16 （2012湖南怀化3分）如图，在ABCD中，AD=8，点E、F分别是BD、CD的中点，则EF= . 17．（2013江苏扬州，6，3分）一个多边形的每个内角均为108°，则这个多边形是（）．A．七边形 B．六边形 C．五边形 D．四边形18（2013广东湛江，5，4分）已知一个多边形的内角和是540°，则这个多边形是（）A．四边形 B．五边形 C．六边形 D．七边形19、（2013四川雅安，2，3分）五边形的内角和为（）A．720°B．540°C．360°D．180°20．（2013·泰安，8，3分）如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC 的外角，则∠1＋∠2＋∠3等于（）A．90°B．180°C．210°D．270°，这个多边形的边数是．22．（2013湖南娄底，16，4分）一个多边形的内角和是外角和的2倍，则这个多边形的边数为．23（2013湖南长沙，8， 3分）下列多边形中，内角和与外角和相等的是（）A.四边形B.五边形C.六边形D.八边形24、（2013·鞍山，22，6分）如图，E，F是四边形ABCD的对角线AC上两点，AF＝CE，DF＝BE，DF∥BE．求证：（1）△AFD≌△CEB；（2）四边形ABCD是平行四边形．25、（2013湖南郴州，23，8分）如图，已知BE∥DF，∠ADF=∠CBE，AF=CE，求证：四边形DEBF是平行四边形．求证：AE=CF ．27．(2012湖北孝感8分)我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形．如图，在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，依次连接各边中点得到中点四边形EFGH ．(1)这个中点四边形EFGH 的形状是；(2)证明你的结论．28、（08湖北恩施)如图，在平行四边形ABCD 中,∠ABC 的平分线交CD 于点E,∠ADC 的平分线交AB 于点F.试证明四边形DFBE 为平行四边形.29、（2010江苏宿迁）如图，在□ABCD 中，点E 、F 是对角线AC 上两点，且AE=CF ．求证：∠EBF=∠FD（对角线互相平分的四边形为平行四边形）30 （2010•滨州）如图，四边形ABCD ，E 、F 、G 、H 分别是AB 、BC 、CD 、 DA 的中点．请判断四边形EFGH 的形状？并说明为什么；31、已知平行四边形ABCD 的周长为36cm ，过D 作AB ，BC 边上的高DE 、DF ，且ABCD 的面积．cm ，，求平行四边形32、（2009•永州）如图，平行四边形ABCD ，E 、F 两点在对角线BD 上，且BE=DF ，连接AE ，EC ，CF ，FA ．求证：四边形AECF 是平行四边形．33、（2011•泸州）如图，已知D 是△ABC 的边AB 上一点，CE ∥AB ，DE 交AC 于点O ，且OA=OC ，猜想线段CD 与线段AE 的大小关系和位置关系，并加以证明．34、（2011•徐州）如图，在四边形ABCD 中，AB=CD ，BF=DE ，AE ⊥BD ，CF ⊥BD ，垂足分别为E ，F ．（1）求证：△ABE ≌△CDF ；（2）若AC 与BD 交于点O ，求证：AO=CO ．35、（2010湖南株洲）．（本题满分6分）如图，已知平行四边形ABCD ，DE 是ADC ∠的角平分线，交BC 于点E ．（1）求证：CD CE =；（2）若BE CE =，80B ∠=︒，求DAE ∠的度数．。

多边形证明(复习讲义)(三角形、平行四边形、矩形、正方形、菱形)(解析)-中考数学重难点题型专题汇总

题型四--多边形证明（三角形、平行四边形、矩形、正方形、菱形）（复习讲义）【考点总结|典例分析】考点01三角形全等及性质一、三角形的基础知识1．三角形的概念由三条线段首尾顺次相接组成的图形，叫做三角形．2．三角形的三边关系（1）三角形三边关系定理：三角形的两边之和大于第三边．推论：三角形的两边之差小于第三边．（2）三角形三边关系定理及推论的作用：①判断三条已知线段能否组成三角形；②当已知两边时，可确定第三边的范围；③证明线段不等关系．3．三角形的内角和定理及推论三角形的内角和定理：三角形三个内角和等于180°．推论：①直角三角形的两个锐角互余；②三角形的一个外角等于和它不相邻的两个内角的和；③三角形的一个外角大于任何一个和它不相邻的内角．4．三角形中的重要线段（1）三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线．（2）在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线．（3）从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）．（4）连接三角形两边中点的线段叫做三角形的中位线，三角形的中位线平行于第三边，且等于第三边的一半．二、全等三角形5．三角形全等的判定定理：（1）边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）；（2）角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）；（3）边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）；（4）对于特殊的直角三角形，判定它们全等时，还有HL定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL”）．6．全等三角形的性质：（1）全等三角形的对应边相等，对应角相等；（2）全等三角形的周长相等，面积相等；（3）全等三角形对应的中线、高线、角平分线、中位线都相等．7．等腰三角形的性质定理：等腰三角形的两个底角相等（简称：等边对等角）．推论1：等腰三角形顶角平分线平分底边并且垂直于底边，即等腰三角形的顶角平分线、底边上的中线、底边上的高重合．推论2：等边三角形的各个角都相等，并且每个角都等于60°．8．等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等．推论1：三个角都相等的三角形是等边三角形．推论2：有一个角是60°的等腰三角形是等边三角形．推论3：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．四、等边三角形（1）定义：三条边都相等的三角形是等边三角形．（2）性质：等边三角形的各角都相等，并且每一个角都等于60°．（3）判定：三个角都相等的三角形是等边三角形；有一个角等于60°的等腰三角形是等边三角形．五、直角三角形与勾股定理9．直角三角形定义：有一个角是直角的三角形叫做直角三角形．性质：（1）直角三角形两锐角互余；（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；（3）在直角三角形中，斜边上的中线等于斜边的一半．判定：（1）两个内角互余的三角形是直角三角形；（2）三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形．10．勾股定理及逆定理（1）勾股定理：直角三角形的两条直角边a、b的平方和等于斜边c的平方，即：a2+b2=c2．（2）勾股定理的逆定理：如果三角形的三条边a、b、c有关系：a2+b2=c2，那么这个三角形1.如图，AC 和BD 相交于点O ，OA =OC ，OB =OD ．(1)求证：∠A =∠C ；(2)求证：AB//CD ．【答案】证明：(1)在△AOB 和△COD 中，OA =OC ∠AOB =∠COD OB =OD ,∴△AOB≌△COD(SAS)，∴∠A =∠C ；(2)由(1)得∠A =∠C ，∴AB//CD ．2.如图，点B ，F ，C ，E 在同一条直线上，BF =EC ，AB =DE ，∠B =∠E.求证：∠A =∠D ．【答案】证明：∵BF =EC ，∴BF +CF =EC +CF ，即BC =EF ，在△ABC 和△DEF 中，AB =DE ∠B =∠E BC =EF ，∴△ABC≌△DEF(SAS)，∴∠A =∠D ．3.(2022·四川省宜宾市)已知：如图，点A、D、C、F在同一直线上，AB//DE，∠B=∠E，BC=EF.求证：AD=CF．【答案】证明：∵AB//DE，∴∠A=∠EDF．在△ABC和△DEF中，∠A=∠EDF∠B=∠EBC=EF，∴△ABC≌△DEF(AAS)．∴AC=DF，∴AC−DC=DF−DC，即：AD=CF．4.(2022·陕西省)如图，在△ABC中，点D在边BC上，CD=AB，DE//AB，∠DCE=∠A.求证：DE=BC．【答案】证明：∵DE//AB，∴∠EDC=∠B，在△CDE和△ABC中，∠EDC=∠BCD=AB∠DCE=∠A，∴△CDE≌△ABC(ASA)，∴DE =BC ．5.(2022·浙江省杭州市)如图，在Rt △ACB 中，∠ACB =90°，点M 为边AB 的中点，点E 在线段AM 上，EF ⊥AC 于点F ，连接CM ，CE.已知∠A =50°，∠ACE =30°．(1)求证：CE =CM ．(2)若AB =4，求线段FC 的长．【答案】(1)证明：∵∠ACB =90°，点M 为边AB 的中点，∴MC =MA =MB ，∴∠MCA =∠A ，∠MCB =∠B ，∵∠A =50°，∴∠MCA =50°，∠MCB =∠B =40°，∴∠EMC =∠MCB +∠B =80°，∵∠ACE =30°，∴∠MEC =∠A +∠ACE =50°，∴∠MEC =∠EMC ，∴CE =CM ；(2)解：∵AB =4，∴CE =CM =12AB =2，∵EF ⊥AC ，∠ACE =30°，∴FC =CE ⋅cos30°=3．6.（2021·云南中考真题）如图，在四边形ABCD 中，,,AD BC AC BD AC ==与BD 相交于点E ．求证：DAC CBD ∠=∠．【答案】见解析【分析】直接利用SSS 证明△ACD ≌△BDC ，即可证明．【详解】解：在△ACD 和△BDC 中，AD BC AC BD CD DC =⎧⎪=⎨⎪=⎩，∴△ACD ≌△BDC （SSS ），∴∠DAC=∠CBD ．【点睛】本题考查了全等三角形的判定和性质，解题的关键是根据题意灵活运用SSS 的方法．7.（2021·浙江绍兴市·中考真题）如图，在ABC 中，40A ∠=︒，点D ，E 分別在边AB ，AC 上，BD BC CE ==，连结CD ，BE．（1）若80ABC ∠=︒，求BDC ∠，ABE ∠的度数．（2）写出BEC ∠与BDC ∠之间的关系，并说明理由．【答案】（1）50BDC ∠=︒；20ABE ∠=︒；（2）110BEC BDC ∠+∠=︒，见解析【分析】（1）利用三角形的内角和定理求出ACB ∠的大小，再利用等腰三角形的性质分别求出BDC ∠，ABE ∠．（2）利用三角形的内角和定理、三角形外角的性质和等腰三角形的性质，求出用含ABE ∠分别表示BEC ∠，BDC ∠，即可得到两角的关系．【详解】（1）80ABC ∠=︒ ，BD BC =，50BDC BCD ∴∠=∠=︒．在ABC 中，180A ABC ACB ∠+∠+∠=︒，40A ∠=︒ ，60ACB ∠=︒∴，CE BC = ，60EBC ∴∠=︒．20ABE ABC EBC ∴∠=∠-∠=︒．（2）BEC ∠，BDC ∠的关系：110BEC BDC ∠+∠=︒．理由如下：设BEC α∠=，BDC β∠=．在ABE △中，40A ABE ABE α=∠+∠=︒+∠，CE BC = ，CBE BEC α∴∠=∠=．2402ABC ABE CBE A ABE ABE ∴∠=∠+∠=∠+∠=︒+∠，在BDC 中，BD BC =，2402180BDC BCD DBC ABE β∴∠+∠+∠=+︒+∠=︒．70ABE β︒∴=-∠．4070110ABE ABE αβ∴+=︒+∠+︒-∠=︒．110BEC BDC ∴∠+∠=︒．【点睛】本题主要通过求解角和两角之间的关系，考查三角形的内角和定理、三角形外角的性质和等腰三角形的性质．三角形的内角和等于180︒．三角形的外角等于与其不相邻的两个内角之和．等腰三角形等边对等角．8.（2021·浙江温州市·中考真题）如图，BE 是ABC 的角平分线，在AB 上取点D ，使DB DE =．（1）求证：//DE BC ．（2）若65A ∠=︒，45AED ∠=︒，求EBC ∠的度数．【答案】（1）见解析；（2）35°【分析】（1）直接利用角平分线的定义和等边对等角求出BED EBC ∠=∠，即可完成求证；（2）先求出∠ADE ，再利用平行线的性质求出∠ABC ，最后利用角平分线的定义即可完成求解．【详解】解：（1） BE 平分ABC ∠，∴ABE EBC ∠=∠．DB DE =，∴ABE BED ∠=∠，∴BED EBC ∠=∠，∴//DE BC ．（2） 65A ∠=︒，45AED ∠=︒，∴18070ADE A AED ∠=︒-∠-∠=︒．//DE BC ．∴70ABC ADE ∠=∠=︒．BE 平分ABC ∠，∴1352EBC ABC ∠=∠=︒，即35EBC ∠=︒．【点睛】本题综合考查了角平分线的定义、等腰三角形的性质、平行线的判定与性质等内容，解决本题的关键是牢记概念与性质，本题的解题思路较明显，属于几何中的基础题型，着重考查了学生对基本概念的理解与掌握．9.（2021·福建中考真题）如图，在ABC 中，D 是边BC 上的点，,⊥⊥DE AC DF AB ，垂足分别为E ，F ，且,DE DF CE BF ==．求证：B C ∠=∠．【答案】见解析【分析】由,⊥⊥DE AC DF AB 得出90DEC DFB ∠=∠=︒，由SAS 证明DEC DFB ≌，得出对应角相等即可．【详解】证明：∵,⊥⊥DE AC DF AB ，∴90DEC DFB ∠=∠=︒．在DEC 和DFB △中，,,,DE DF DEC DFB CE BF =⎧⎪∠=∠⎨⎪=⎩∴DEC DFB ≌，∴B C ∠=∠．【点睛】本小题考查垂线的性质、全等三角形的判定与性质、等基础知识，考查推理能力、空间观念与几何直观．10.（2021·四川乐山市·中考真题）如图，已知AB DC =，A D ∠=∠，AC 与DB 相交于点O ，求证：OBC OCB ∠=∠．【答案】证明见解析【分析】根据全等三角形的性质，通过证明ABO DCO △≌△，得OB OC =，结合等腰三角形的性质，即可得到答案．【详解】∵A D AOB DOC AB DC ∠=∠∠=∠=⎧⎪⎨⎪⎩，∴ABO DCO △≌△（AAS ），∴OB OC =，∴OBC OCB ∠=∠．【点睛】本题考查了全等三角形、等腰三角形的知识；解题的关键是熟练掌握全等三角形、等腰三角形的性质，从而完成求解．考点02相似六、相似三角形的判定及性质11．定义对应角相等，对应边成比例的两个三角形叫做相似三角形，相似三角形对应边的比叫做相似比．12．性质（1）相似三角形的对应角相等；（2）相似三角形的对应线段（边、高、中线、角平分线）成比例；（3）相似三角形的周长比等于相似比，面积比等于相似比的平方．13．判定（1）有两角对应相等，两三角形相似；（2）两边对应成比例且夹角相等，两三角形相似；（3）三边对应成比例，两三角形相似；（4）两直角三角形的斜边和一条直角边对应成比例，两直角三角形相似．【方法技巧】判定三角形相似的几条思路：（1）条件中若有平行线，可采用相似三角形的判定（1）；（2）条件中若有一对等角，可再找一对等角[用判定（1）]或再找夹边成比例[用判定（2）]；（3）条件中若有两边对应成比例，可找夹角相等；（4）条件中若有一对直角，可考虑再找一对等角或证明斜边、直角边对应成比例；（5）条件中若有等腰条件，可找顶角相等，或找一个底角相等，也可找底和腰对应成比例．七、相似多边形14．定义对应角相等，对应边成比例的两个多边形叫做相似多边形，相似多边形对应边的比叫做它们的相似比．15．性质（1）相似多边形的对应边成比例；（2）相似多边形的对应角相等；（3）相似多边形周长的比等于相似比，相似多边形面积的比等于相似比的平方．八、位似图形16．定义如果两个图形不仅是相似图形而且每组对应点的连线交于一点，对应边互相平行（或在同一条直线上），那么这样的两个图形叫做位似图形，这个点叫做位似中心，相似比叫做位似比．27．性质（1）在平面直角坐标系中，如果位似变换是以原点为中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或–k ；（2）位似图形上任意一对对应点到位似中心的距离之比等于位似比或相似比．18．找位似中心的方法将两个图形的各组对应点连接起来，若它们的直线或延长线相交于一点，则该点即是位似中心．19．画位似图形的步骤（1）确定位似中心；（2）确定原图形的关键点；（3）确定位似比，即要将图形放大或缩小的倍数；（4）作出原图形中各关键点的对应点；（5）按原图形的连接顺序连接所作的各个对应点．11.（2021·云南中考真题）如图，在ABC 中，点D ，E 分别是,BC AC 的中点，AD 与BE 相交于点F ，若6BF ，则BE 的长是______．【答案】9【分析】根据中位线定理得到DE=12AB，DE∥AB，从而证明△DEF∽△ABF，得到12DE EFAB BF==，求出EF，可得BE．【详解】解：∵点D，E分别为BC和AC中点，∴DE=12AB，DE∥AB，∴△DEF∽△ABF，∴12 DE EFAB BF==，∵BF=6，∴EF=3，∴BE=6+3=9，故答案为：9．【点睛】本题考查了三角形中位线定理，相似三角形的判定和性质，解题的关键是根据中位线的性质证明△DEF∽△ABF．12.（2020•盐城）如图，BC∥DE，且BC＜DE，AD＝BC＝4，AB+DE＝10．则AE AC的值．【分析】由平行线得三角形相似，得出AB•DE，进而求得AB，DE，再由相似三角形求得结果．【解析】∵BC∥DE，∴△ADE ∽△ABC ，∴AD AB =DE BC =AE AC ，即4AB =DE 4=AE AC ，∴AB •DE ＝16，∵AB+DE ＝10，∴AB ＝2，DE ＝8，∴AE AC =DE BC =84=2，故答案为：2．13.（2021·广东中考真题）如图，边长为1的正方形ABCD 中，点E 为AD 的中点．连接BE ，将ABE △沿BE 折叠得到,FBE BF 交AC 于点G ，求CG 的长．【答案】CG =【分析】根据题意，延长BF 交CD 于H 连EH ，通过证明()Rt EDH Rt EFH HL ≌、DHE AEB ∽得到34CH =，再由HGC BGA ∽得到()34CG AC CG =-，进而即可求得CG 的长．【详解】解：延长BF 交CD 于H 连EH ，∵FBE 由ABE △沿BE 折叠得到，∴EA EF =，90EFB EAB ∠=∠=︒，∵E 为AD 中点，正方形ABCD 边长为1，∴12EA ED ==，∴12ED EF ==，∵四边形ABCD 是正方形，∴90D EFB EFH ∠=∠=∠=︒，在Rt EDH △和Rt EFH 中，ED EF EH EH =⎧⎨=⎩，∴()Rt EDH Rt EFH HL ≌，∴DEH FEH ∠=∠，又∵AEB FEB ∠=∠，∴90DEH AEB ∠+∠=︒，∵90ABE AEB ∠+∠=︒，∴ABE DEH ∠=∠，∴DHE AEB ∽，∴12DH AE DE AB ==，∴14DH =，∴13144CH CD DH =-=-=，∵CH AB ∥，∴HGC BGA ∽，∴34CG CH AG AB ==，∴()3344CG AG AC CG ==-，∵1AB =，1CB =，90CBA ∠=︒，∴AC =，∴)34CG CG =，∴CG =．【点睛】本题主要考查了三角形全等的判定及性质、三角形相似的判定及性质以及正方形的性质，熟练掌握相关几何知识是解决本题的关键．14.（2020•长沙）在矩形ABCD 中，E 为DC 边上一点，把△ADE 沿AE 翻折，使点D 恰好落在BC 边上的点F ．（1）求证：△ABF ∽△FCE ；（2）若AB ＝23，AD ＝4，求EC 的长；（3）若AE ﹣DE ＝2EC ，记∠BAF ＝α，∠FAE ＝β，求tan α+tan β的值．【分析】（1）根据两角对应相等的两个三角形相似证明即可．（2）设EC ＝x ，证明△ABF ∽△FCE ，可得AB CF =BF EC ，由此即可解决问题．（3）首先证明tan α+tan β=BF AB +EF AF =BF AB +CF AB =BF+CF AB =BC AB ，设AB ＝CD ＝a ，BC ＝AD ＝b ，DE ＝x ，解直角三角形求出a ，b 之间的关系即可解决问题．【解答】（1）证明：∵四边形ABCD 是矩形，∴∠B ＝∠C ＝∠D ＝90°，由翻折可知，∠D ＝∠AFE ＝90°，∴∠AFB+∠EFC ＝90°，∠EFC+∠CEF ＝90°，∴∠AFB ＝∠FEC ，∴△ABF ∽△FCE ．（2）设EC＝x，由翻折可知，AD＝AF＝4，∴BF=AF2−AB2=16−12=2，∴CF＝BC﹣BF＝2，∵△ABF∽△FCE，∴AB CF=BF EC，∴2322，∴x=∴EC=（3）∵△ABF∽△FCE，∴AF EF=AB CF，∴tanα+tanβ=BF AB+EF AF=BF AB+CF AB=BF+CF AB=BC AB，设AB＝CD＝a，BC＝AD＝b，DE＝x，∴AE＝DE+2CE＝x+2（a﹣x）＝2a﹣x，∵AD＝AF＝b，DE＝EF＝x，∠B＝∠C＝∠D＝90°，∴BF=b2−a2，CF==2ax−a2，∵AD2+DE2＝AE2，∴b2+x2＝（2a﹣x）2，∴a2﹣ax=14b2，∵△ABF∽△FCE，∴AB CF=BF EC，−(a−x)2=a−x∴a2﹣ax=b2−a2•2ax−a2，∴14b2=b2−a2•整理得，16a4﹣24a2b2+9b4＝0，∴（4a2﹣3b2）2＝0，∴b a=233，∴tanα+tanβ=BC AB=考点03多边形十、多边形20．多边形的相关概念（1）定义：在平面内，由一些段线首尾顺次相接组成的封闭图形叫做多边形．（2）对角线：从n边形的一个顶点可以引(n–3)条对角线，并且这些对角线把多边形分成了(n–2)个三角形；n边形对角线条数为()32n n-．21．多边形的内角和、外角和（1）内角和：n边形内角和公式为(n–2)·180°；（2360°. 22．正多边形（1）定义：各边相等，各角也相等的多边形.（2）正n边形的每个内角为()2180nn-⋅，每一个外角为360n︒．（3）正n边形有n条对称轴.（4）对于正n边形，当n为奇数时，是轴对称图形；当n为偶数时，既是轴对称图形，又是中心对称图形．15.（2021·湖南岳阳市·中考真题）下列命题是真命题的是（）A．五边形的内角和是720︒B．三角形的任意两边之和大于第三边C．内错角相等D．三角形的重心是这个三角形的三条角平分【答案】B【分析】根据相关概念逐项分析即可．【详解】A 、五边形的内角和是540︒，故原命题为假命题，不符合题意；B 、三角形的任意两边之和大于第三边，原命题是真命题，符合题意；C 、两直线平行，内错角相等，故原命题为假命题，不符合题意；D 、三角形的重心是这个三角形的三条中线的交点，故原命题为假命题，不符合题意；故选：B ．【点睛】本题考查命题判断，涉及多边形的内角和，三角形的三边关系，平行线的性质，以及三角形的重心等，熟记基本性质和定理是解题关键．16.（2021·四川自贡市·中考真题）如图，AC 是正五边形ABCDE 的对角线，ACD ∠的度数是（）A ．72°B ．36°C ．74°D ．88°【答案】A【分析】根据正五边形的性质可得108B BCD ∠=∠=︒，AB BC =，根据等腰三角形的性质可得36BCA BAC ∠=∠=︒，利用角的和差即可求解．【详解】解：∵ABCDE 是正五边形，∴108B BCD ∠=∠=︒，AB BC =，∴36BCA BAC ∠=∠=︒,∴1083672ACD ∠=︒-︒=︒，故选：A ．本题考查正五边形的性质，求出正五边形内角的度数是解题的关键．17.（2021·四川资阳市·中考真题）下列命题正确的是（）A．每个内角都相等的多边形是正多边形B．对角线互相平分的四边形是平行四边形C．过线段中点的直线是线段的垂直平分线D．三角形的中位线将三角形的面积分成1∶2两部分【答案】B【分析】分别根据正多边形的判定、平行四边形的判定、线段垂直平分线的判定以及三角形中线的性质逐项进行判断即可得到结论．【详解】解：A.每个内角都相等，各边都相等的多边形是正多边形，故选项A的说法错误，不符合题意；B.对角线互相平分的四边形是平行四边形,说法正确，故选项B符合题意；C.过线段中点且垂直这条线段的直线是线段的垂直平分线，故选项C的说法错误，不符合题意；D.三角形的中位线将三角形的面积分成1∶3两部分，故选项D的说法错误，不符合题意．故选：B．【点睛】此题主要考查了对正多边形、平行四边形、线段垂直平分线的判断以及三角形中线性质的认识，熟练掌握正多边形、平行四边形、线段垂直平分线的判断是解答此题的关键．18．（2021·浙江丽水市·中考真题）一个多边形过顶点剪去一个角后，所得多边形的内角和为720 ，则原多边形的边数是__________．【答案】6或7【分析】求出新的多边形为6边形，则可推断原来的多边形可以是6边形，可以是7边形．【详解】解：由多边形内角和，可得（n-2）×180°=720°，∴n=6，∴新的多边形为6边形，∵过顶点剪去一个角，∴原来的多边形可以是6边形，也可以是7边形，故答案为6或7．【点睛】本题考查多边形的内角和；熟练掌握多边形的内角和与多边形的边数之间的关系是解题的关键．19．（2021·湖北黄冈市·中考真题）正五边形的一个内角是_____度．【答案】108【分析】根据正多边形的定义、多边形的内角和公式即可得．【详解】解：正五边形的一个内角度数为180(52)1085︒⨯-=︒，故答案为：108．【点睛】本题考查了正多边形的内角，熟练掌握多边形的内角和公式是解题关键．20．（2021·陕西中考真题）正九边形一个内角的度数为______．【答案】140°【分析】正多边形的每个内角相等，每个外角也相等，而每个内角等于180︒减去一个外角，求出外角即可求解．【详解】正多边形的每个外角360=n︒（n为边数），所以正九边形的一个外角360==409︒︒∴正九边形一个内角的度数为18040140︒-︒=︒故答案为：140°．【点睛】本题考查的是多边形的内角和，多边形的外角和为360︒，正多边形的每个内角相等，通过计算1个外角的度数来求得1个内角度数是解题关键．21．（2021·湖南中考真题）一个多边形的每个外角的度数都是60°，则这个多边形的内角和为______．【答案】720°【分析】多边形的外角和计算公式为：边数×外角的度数=360°，根据公式即可得出多边形的边数，然后再根据多边形的内角和公式求出它的内角和，n边形内角和等于(n-2)×180°．【详解】解：∵任何多边形的外角和是360°，此正多边形每一个外角都为60°，边数×外角的度数=360°，∴n=360°÷60°=6，∴此正多边形的边数为6，则这个多边形的内角和为(n-2)×180°，(6-2)×180°=720°，故答案为720°．【点睛】本题主要考查了多边形内角和及外角和定理，熟知“任何多边形的外角和是360°，n边形内角和等于(n-2)×180°”考点04平行四边形十一、平行四边形的性质23．平行四边形的定义两组对边分别平行的四边形叫做平行四边形，平行四边形用“ ”表示.24．平行四边形的性质（1）边：两组对边分别平行且相等．（2）角：对角相等，邻角互补．（3）对角线：互相平分．（4）对称性：中心对称但不是轴对称．25．注意：利用平行四边形的性质解题时一些常用到的结论和方法：（1）平行四边形相邻两边之和等于周长的一半．（2）平行四边形中有相等的边、角和平行关系，所以经常需结合三角形全等来解题．（3）过平行四边形对称中心的任一直线等分平行四边形的面积及周长．26．平行四边形中的几个解题模型（1）如图①，AE 平分∠BAD ，则可利用平行线的性质结合等角对等边得到△ABE 为等腰三角形，即AB=BE ．（2）平行四边形的一条对角线把其分为两个全等的三角形，如图②中△ABD ≌△CDB ；两条对角线把平行四边形分为两组全等的三角形，如图②中△AOD ≌△COB,△AOB ≌△COD ；根据平行四边形的中心对称性，可得经过对称中心O 的线段与对角线所组成的居于中心对称位置的三角形全等，如图②△AOE ≌△COF.图②中阴影部分的面积为平行四边形面积的一半．（3）如图③，已知点E 为AD 上一点，根据平行线间的距离处处相等，可得S △BEC =S △ABE +S △CDE .（4）如图④，根据平行四边形的面积的求法，可得AE ·BC=AF ·CD ．十二、平行四边形的判定（1）方法一（定义法）：两组对边分别平行的四边形是平行四边形.（2）方法二：两组对边分别相等的四边形是平行四边形.（3）方法三：有一组对边平行且相等的四边形是平行四边形.（4）方法四：对角线互相平分的四边形是平行四边形.（5）方法五：两组对角分别相等的四边形是平行四边形．十三、矩形的性质与判定27．矩形的性质：（1）四个角都是直角；（2）对角线相等且互相平分；（3）面积=长×宽=2S △ABD =4S △AOB ．（如图）28．矩形的判定：（1）定义法：有一个角是直角的平行四边形；（2）有三个角是直角；（3）对角线相等的平行四边形．十四、菱形的性质与判定29．菱形的性质：（1）四边相等；（2）对角线互相垂直、平分，一条对角线平分一组对角；（3）面积=底×高=对角线乘积的一半．30．菱形的判定：（1）定义法：有一组邻边相等的平行四边形；（2）对角线互相垂直的平行四边形；（3）四条边都相等的四边形．十五、正方形的性质与判定31．正方形的性质：（1）四条边都相等，四个角都是直角；（2）对角线相等且互相垂直平分；=4S△AOB．（3）面积=边长×边长=2S△ABD32．正方形的判定：（1）定义法：有一个角是直角，且有一组邻边相等的平行四边形；（2）一组邻边相等的矩形；（3）一个角是直角的菱形；（4）对角线相等且互相垂直、平分．十六、联系（1）两组对边分别平行；（2）相邻两边相等；（3）有一个角是直角；（4）有一个角是直角；（5）相邻两边相等；（6）有一个角是直角，相邻两边相等；（7）四边相等（8）有三个角都是直角．十七、中点四边形（1）任意四边形所得到的中点四边形一定是平行四边形.（2）对角线相等的四边形所得到的中点四边形是矩形.（3）对角线互相垂直的四边形所得到的中点四边形是菱形.（4.22.（2021·江苏扬州市·中考真题）如图，在ABC 中，BAC ∠的角平分线交BC 于点D ，//,//DE AB DF AC ．（1）试判断四边形AFDE 的形状，并说明理由；（2）若90BAC ∠=︒，且AD =，求四边形AFDE 的面积．【答案】（1）菱形，理由见解析；（2）4【分析】（1）根据DE∥AB，DF∥AC判定四边形AFDE是平行四边形，再根据平行线的性质和角平分线的定义得到∠EDA=∠EAD，可得AE=DE，即可证明；（2）根据∠BAC=90°得到菱形AFDE是正方形，根据对角线AD求出边长，再根据面积公式计算即可．【详解】解：（1）四边形AFDE是菱形，理由是：∵DE∥AB，DF∥AC，∴四边形AFDE是平行四边形，∵AD平分∠BAC，∴∠FAD=∠EAD，∵DE∥AB，∴∠EDA=∠FAD，∴∠EDA=∠EAD，∴AE=DE，∴平行四边形AFDE是菱形；（2）∵∠BAC=90°，∴四边形AFDE是正方形，∵AD=，=2，∴∴四边形AFDE的面积为2×2=4．【点睛】本题考查了菱形的判定，正方形的判定和性质，平行线的性质，角平分线的定义，解题的关键是掌握特殊四边形的判定方法．23.（2021·江苏连云港市·中考真题）如图，点C是BE的中点，四边形ABCD是平行四边形．（1）求证：四边形ACED是平行四边形；，求证：四边形ACED是矩形．（2）如果AB AE【答案】（1）见解析；（2）见解析【分析】（1）由平行四边形的性质以及点C是BE的中点，得到AD∥CE，AD=CE，从而证明四边形ACED是平行四边形；（2）由平行四边形的性质证得DC=AE，从而证明平行四边形ACED是矩形．【详解】证明：（1）∵四边形ABCD是平行四边形，∴AD∥BC，且AD=BC．∵点C是BE的中点，∴BC=CE，∴AD=CE，∵AD∥CE，∴四边形ACED是平行四边形；（2）∵四边形ABCD是平行四边形，∴AB=DC，∵AB=AE，∴DC=AE，∵四边形ACED是平行四边形，∴四边形ACED是矩形．【点睛】本题考查了平行四边形和矩形的判定和性质，正确的识别图形是解题的关键．24.（2021·四川广安市·中考真题）如图，四边形ABCD是菱形，点E、F分别在边AB、AD=．连接CE、CF．的延长线上，且BE DF求证：CE CF=．【答案】见解析【分析】根据菱形的性质得到BC=CD ，∠ADC=∠ABC ，根据SAS 证明△BEC ≌△DFC ，可得CE=CF ．【详解】解：∵四边形ABCD 是菱形，∴BC=CD ，∠ADC=∠ABC ，∴∠CDF=∠CBE ，在△BEC 和△DFC 中，BE DF CBE CDF BC CD =⎧⎪∠=∠⎨⎪=⎩，∴△BEC ≌△DFC （SAS ），∴CE=CF ．【点睛】本题考查了菱形的性质，全等三角形的判定和性质，解题的关键是根据菱形得到判定全等的条件．25.（2021·四川自贡市·中考真题）如图，在矩形ABCD 中，点E 、F 分别是边AB 、CD 的中点．求证：DE=BF．【答案】证明见试题解析．【分析】由矩形的性质和已知得到DF=BE ，AB ∥CD ，故四边形DEBF 是平行四边形，即可得到答案．【详解】∵四边形ABCD 是矩形，∴AB ∥CD ，AB=CD ，又E 、F 分别是边AB 、CD 的中点，∴DF=BE ，又AB ∥CD ，∴四边形DEBF 是平行四边形，∴DE=BF ．考点：1．矩形的性质；2．全等三角形的判定．26.（2021·四川遂宁市·中考真题）如图，在平行四边形ABCD 中，对角线AC 与BD 相交于点O ，过点O 的直线EF 与BA 、DC 的延长线分别交于点E 、F ．（1）求证：AE ＝CF ；（2）请再添加一个条件，使四边形BFDE 是菱形，并说明理由．【答案】（1）见解析；（2）EF ⊥BD 或EB ＝ED ，见解析【分析】（1）根据平行四边形的性质和全等三角形的证明方法证明AOE COF V V ≌，则可得到AE ＝CF ；（2）连接BF ，DE ，由AOE COF V V ≌，得到OE=OF ，又AO=CO ，所以四边形AECF 是平行四边形，则根据EF ⊥BD 可得四边形BFDE 是菱形．【详解】证明：（1）∵四边形ABCD 是平行四边形∴OA ＝OC ，BE ∥DF∴∠E ＝∠F在△AOE 和△COF 中E F AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴AOE COF V V ≌()AAS ∴AE ＝CF（2）当EF ⊥BD 时，四边形BFDE 是菱形，理由如下：如图：连结BF ，DE∵四边形ABCD 是平行四边形∴OB ＝OD∵AOE COFV V ≌∴OE OF=∴四边形BFDE 是平行四边形∵EF ⊥BD ，∴四边形BFDE 是菱形【点睛】本题主要考查了全等三角形的性质与判定、平行四边形的性质，菱形的判定等知识点，熟悉相关性质，能全等三角形的性质解决问题是解题的关键．。

中心对称图形-平行四边形复习讲义

图形的旋转在平面内，将一个图形绕一个定点转动一定角度，这样的图形运动叫旋转，这个定点称为旋转中心，旋转角度称为旋转角图形旋转的性质：1、旋转前、后图形全等2、对应点到旋转中心的距离相等3、每对对应点与旋转中心的连所成的叫彼此相等中心对称：把一个图形绕某点旋转180°，如果它能与另一个图形重合，那么这两个图形关于这一点城中心对称中心对称的性质：1.、具有旋转图形的所有性质2、对应点连线都经过对称中心，并且被对称中心平分中心对称图形把一个平面图形绕某一点旋转180°，如果旋转后的图形与原图形完全重合，那么这个图形式中心对称图形，这个点是对称中心平行四边形：两组对边分别平行的四边形叫平行四边形平行四边形的性质：1、平行四边形对边相等2、平行四边形对角相等3、平行四边形对角线互相平分平行四边形的判定：1、两组对边分别平行的四边形是平行四边形2、一组对边平行且相等的四边形是平行四边形3、两条对角线互相平分的四边形是平行四边形4、两组对边分别别相等的四边形是平行四边形矩形：有一个角是直角的平行四边形是矩形矩形的性质：1、所有平行四边形的性质2、对角线相等1、四个角都是直角1、有一个角是直角的平行四边形是矩形2、有3个角是直角的四边形正是矩形3、对角线相等的平行四边形是矩形菱形：有一组邻边相等的平行四边形是菱形菱形的性质：1、所有平行四边形的性质2、四边相等3、对角线相互垂直，且每条对角线平分一组对角菱形的判定：1、有一组邻边相等的平行四边形是菱形2、四边都相等的四边形是菱形3、对角线相互垂直的平行四边形是菱形正方形：有一组邻边相等且一个角为直角的平行四边形是正方形三角形中位线：连接三角形两边中点的线段叫三角形的中位线三角形中位线的性质：三角形中位线平行于第三边且等于它的一半例1.如图，BD是?ABCD的对角线，AE⊥BD于E，CF⊥BD于F，求证：四边形AECF 为平行四边形。

例2.如图，在平行四边形ABCD中，对角线交于点0，点E、F在直线AC上（不同于A、C），当E、F的位置满足的条件时，四边形DEBF是平行四边形．变式：如图，点E、F在?ABCD的对角线BD上，要使四边形AECF是平行四边形，还需添加一个条件．（只需写出一个结论，不必考虑所有情况）．例3：如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为()A. 30°B. 60°C. 90°D. 120°例4、如图，在△ABC中，AB=BC，BD平分∠ABC.四边形ABED是平行四边形，DE交BC于点F，连接CE.求证：四边形BECD是矩形。

九年级数学复习课导学案证明(三)(平行四边形)

C
2.在 ABCD 中，AC=4，BD=6，P 是 BD 上一点，过点 P 作 EF∥AC，
与 ABCD 的两边分别交于点 E、F。设 BP=x,EF=y,则能反映 y 与 x
之间关系的图象大致为（）
y 4
y 4
y 4
y 4
A D
Ep
3 6x A
3 6x B
2 6x 3
C
D
B x
FC
三、小结反馈
测出 MN=a 米，则 AB=____米
MA
CNB
2.已知：△ABC 的三条边长分别为 a,b,c，△ABC 的面积是 S。
它的三条中位线围成一个新△A1B1C1，这个新三角形的周长为
_______;面积为
若将△A1B1C1 的三条中位线又组成一
个新△A2B2C2 ，则这个小三角形的周长为_____面积为
底阁中学九年级数学复习课导学案----杨婷霞
课题复习目标
重点难点考点教法学法指导一、课前准备
证明（三）(平行四边形)
课型
复习课
课时 1
1、通过复习回忆平行四边形的性质定理和判定定理，进一步提高推理论证能力。
2、体会三角形的中位线性质及定理的应用、中点四边形的判定
3、体会证明过程中所运用的归纳、概括及转化等数学思想方法。
.
4、顺次连接矩形各边中点的连线所成的四边形是
.
5、DE 是△ABC 的中位线，M 是 DE 的中点，CM 的延长线交 AB 于点 N，
则 S△DMN:S 四边形 ANME=（）
A1:5
A
B1:4 C2:5 D2:7
N D ME
B
C