一、试作出图示各杆的轴力图。
工程力学部分习题答案,基本划出的习题一至十一章
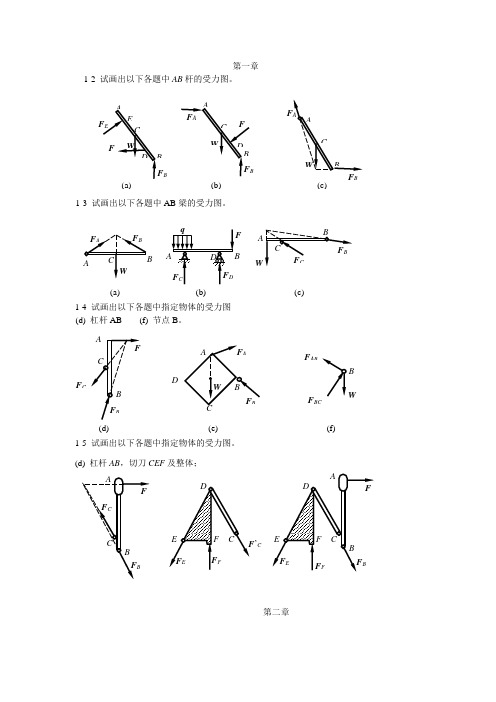
第一章 1-2 试画出以下各题中AB 杆的受力图。
1-3 试画出以下各题中AB 梁的受力图。
1-4 试画出以下各题中指定物体的受力图 (d) 杠杆AB (f) 节点B 。
1-5 试画出以下各题中指定物体的受力图。
(d) 杠杆AB ,切刀CEF 及整体;第二章(a)B (b)(c)B (a)F (b) (c)(d)F C D(e)WB(f)F ABF BC’C2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画 受力图,注意AC 、BC 都为二力杆(右上图)(2) 列平衡方程:12140 sin 600530 cos 6005207 164 o y AC o x BC AC AC BCF F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-7 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求平衡时力F 1和F 2的大小之间的关系。
解:(1)取铰链B 为研究对象,AB 、BC 均为二力杆,画受力图和封闭力三角形;1BC F =(2) 取铰链C 为研究对象,BC 、CD 均为二力杆,画受力图和封闭力三角形;F 1F F F BCF ABF 1 CF CDF 2F CB F CD22cos302oCB F F F == 由前二式可得:121222120.61 1.634BC CB F F F F F F or F F ==∴===2-8 无第三章3-2 在题图所示结构中二曲杆自重不计,曲杆AB 上作用有主动力偶,其力偶矩为M ,试求A 和C 点处的约束力。
解:(1) 取BC 为研究对象,受力分析,BC 为二力杆,画受力图;B C F F =(2) 取AB 为研究对象,受力分析,A 、B 的约束力组成一个力偶,画受力图;FC()''030 0.3540.354B B AC M M a a M F a MF F a=⨯+-===∴==∑3-5 四连杆机构在图示位置平衡。
工程力学答案第4章
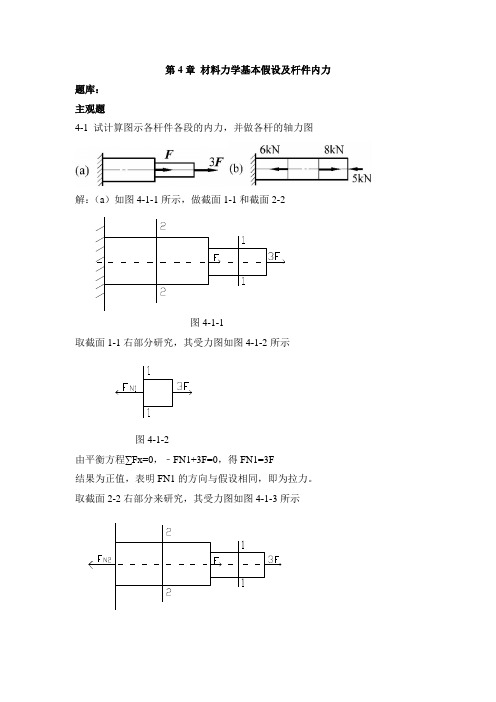
第4章材料力学基本假设及杆件内力题库:主观题4-1 试计算图示各杆件各段的内力,并做各杆的轴力图解:(a)如图4-1-1所示,做截面1-1和截面2-2图4-1-1取截面1-1右部分研究,其受力图如图4-1-2所示图4-1-2由平衡方程∑Fx=0,﹣FN1+3F=0,得FN1=3F结果为正值,表明FN1的方向与假设相同,即为拉力。
取截面2-2右部分来研究,其受力图如图4-1-3所示图4-1-3由平衡方程∑Fx=0,﹣FN2+F+3F=0得FN2=4F结果为正值,表明FN2的方向与假设相同,即为拉力轴力图如图4-1-4所示图4-1-4(b)如图4-1-5所示,做截面1-1、截面2-2和截面3-3图4-1-5取截面1-1右部分来研究,其受力图如图4-1-6所示图4-1-6由平衡方程∑Fx=0,﹣FN1﹣5KN=0,得FN1=-5KN结果为负值,表明FN1的方向与假设相反,即为压力。
取截面2-2右部分来研究,其受力图如图4-1-7所示图4-1-7由平衡方程∑Fx=0,﹣FN2+8KN-5KN=0,得FN2=3KN结果为正值,表明FN2的方向与假设相同,即为拉力。
取截面3-3右部分来研究,其受力图如图4-1-8所示图4-1-8由平衡方程∑Fx=0,﹣FN3﹣6KN+8KN-5KN=0,得FN3=-3KN 结果为负值,表明FN3的方向与假设相反,即为压力。
轴力图如图4-1-9所示:图4-1-9知识点:1.内力,截面法;2. 轴力和轴力图参考页: P72-73学习目标: 2(会用截面法计算法求轴力和轴力图)难度: 1提示一:该题考察知识点:3 内力,截面法;4轴力和轴力图提示二:无提示三:无提示四(同题解)题解:1、用截面法求解每个截面的内力;2、画出每个截面的内力图。
4-2 求图示各梁中指定截面上的剪力和建立图解:(a)计算1-1截面上的剪力Fs和弯矩M1用截面1-1把梁截开,取梁的左段为研究对象如图4-2-1所示图4-2-1由∑Fy=0得:Fs1=-qa(负剪力)由∑Mo1=0得:qa﹒a+M1=0,得M1=-qa2(负弯矩)计算2-2截面上的剪力Fs2和弯矩M2如图4-2-2所示,由∑Fy=0得:Fs2=-qa(负剪力)由∑Mo2=0得M2=-3qa2(负弯矩)图4-2-2计算3-3截面上的剪力Fs3和弯矩M3如图4-2-3所示,由∑Fy=0,-qa-qa-Fs3=0得:Fs3=-2qa(负剪力)由∑Mo3=0,qa﹒4a+qa﹒0.5a+ M3=0得M3=-4.5qa2(负弯矩)图4-2-3(b)计算支座范力选整体梁为研究对象,如图4-2-4所示·图4-2-4由∑MA=0,10KN﹒m+FB×2.5m=0得:FB = -4KN(↓)由∑Fy=0得:FA=-FB=4KN(↑)计算1-1截面上的剪力Fs1和弯矩M1用截面1-1把梁截开,取梁的左段为研究对象如图4-2-5所示图4-2-5由∑Fy=0,FA-Fs1=0,得FA=Fs1=4KN(正剪力)由∑Mo1=0得:-FA·1m+M1=0得M1=4KN·m(正弯矩)计算2-2截面上的剪力Fs2和弯矩M2,如图4-2-6所示图4-2-6由∑Fy=0,FB+Fs2=0,得-FB=Fs2=4KN(正剪力)由∑Mo2=0得:FB·1.5m-M2=0得M2=-6KN·m(负弯矩)(c)计算支座反力选整体梁为研究对象,如图4-2-7所示·图4-2-7由∑Fy=0,FA-5KN+FB=0得FA=3KN(↑)由∑MA=0得:FB·5m-5KN·3m+5KN·m=0得FB=2KN(↑)计算1-1截面上的剪力Fs1和弯矩M1取1-1截面左边部分为研究对象,如图4-2-8所示·图4-2-8由∑Mo1=0得:5KN·m + M1=0,得M1=-5KN·m(负弯矩)由∑Fy=0,FA-Fs1=0,得FA=Fs1=3KN(正剪力)计算2-2的剪力Fs2弯矩M2取2-2截面左边研究对象,如图4-2-9所示·图4-2-9由∑Mo2=0,5KN·m - FA·3m+M2=0,得M2=4KN·m(正弯矩)由∑Fy=0,FA-Fs2=0,得FA=Fs2=3KN(正剪力)计算3-3的剪力Fs3和弯矩M3取3-3截面右边研究对象,如图4-2-10所示图4-2-10由∑Mo3=0,FB·2m-M3=0,得M3=4KN·m(正弯矩)由∑Fy=0,FB+Fs3=0,得-FB=Fs3=-2KN(负剪力)(d)计算支座反力选整体梁为研究对象,如图4-2-11所示图4-2-11由∑MB=0得:qa·25a-FA·2a+qa·a=0,得FA=47qa (↑)由∑Fy=0,FA-2qa+FB=0得FB=41qa (↑)计算1-1截面上的剪力Fs1和弯矩M1取1-1截面左边部分为研究对象,如图4-2-12所示图4-2-12由图知 Fs1=0 M1=0 计算2-2的剪力Fs2弯矩M2取2-2截面左边研究对象,如图4-2-13所示图4-2-13由∑Mo2=0,qa·21a+ M2 =0得M2=-21qa 2(负弯矩)由∑Fy=0,-qa-Fs2=0,得Fs2=-qa(负剪力) 计算3-3的剪力Fs3和弯矩M3取3-3截面右边研究对象,如图4-2-14所示图4-2-14由∑Mo3=0,FB·a-M3=0,得M3=41qa 2(正弯矩)由∑Fy=0,-qa+FB+Fs3=0,得Fs3=43a (正剪力)知识点:1.内力,截面法;2. 轴力和轴力图 参考页: P72-73学习目标: 2(会用截面法计算法求轴力和轴力图) 难度: 1提示一:该题考察知识点:3 内力,截面法;4轴力和轴力图 提示二:无 提示三:无 提示四(同题解) 题解:1、用截面法求解每个截面的内力;2、画出每个截面的内力图。
(国家开放大学)机械设计基础形成性考核习题与答案
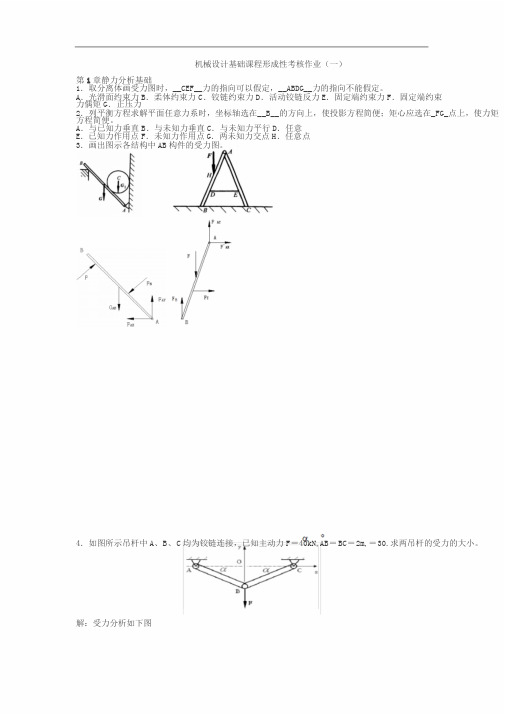
机械设计基础课程形成性考核作业(一)第1章静力分析基础1.取分离体画受力图时,__CEF__力的指向可以假定,__ABDG__力的指向不能假定。
A.光滑面约束力B.柔体约束力C.铰链约束力D.活动铰链反力E.固定端约束力F.固定端约束力偶矩G.正压力2.列平衡方程求解平面任意力系时,坐标轴选在__B__的方向上,使投影方程简便;矩心应选在_FG_点上,使力矩方程简便。
A.与已知力垂直B.与未知力垂直C.与未知力平行D.任意E.已知力作用点F.未知力作用点G.两未知力交点H.任意点3.画出图示各结构中AB构件的受力图。
4.如图所示吊杆中A、B、C均为铰链连接,已知主动力F=40kN,AB=BC=2m,=30.求两吊杆的受力的大小。
解:受力分析如下图列力平衡方程:Fx0又因为AB=BCF A sinF C sinF A FCFy02F A sinFFF A F B40KN2sin第2章常用机构概述1.机构具有确定运动的条件是什么?答:当机构的原动件数等于自由度数时,机构具有确定的运动2.什么是运动副?什么是高副?什么是低副?答:使两个构件直接接触并产生一定相对运动的联接,称为运动副。
以点接触或线接触的运动副称为高副,以面接触的运动副称为低副。
3.计算下列机构的自由度,并指出复合铰链、局部自由度和虚约束。
(1)n=7,P L=10,P H=0(2)n=5,P L=7,P H=0F3n2P L PF3n2P L P HH37210352711C处为复合铰链(3)n=7,P L=10,P H=0(4)n=7,P L=9,P H=1F3n2P L PF3n2P L P HH372103729112E、E’有一处为虚约束F为局部自由度C处为复合铰链第3章平面连杆机构1.对于铰链四杆机构,当满足杆长之和的条件时,若取_C_为机架,将得到双曲柄机构。
A.最长杆B.与最短杆相邻的构件C.最短杆D.与最短杆相对的构件2.根据尺寸和机架判断铰链四杆机构的类型。
《材料力学》第2章轴向拉(压)变形习题解答

其方向。 解:斜截面上的正应力与切应力的公式为:
ασσα20cos = αστα2sin 2 = 式中,MPa mm N A N 1001001000020===σ,把α的数值代入以上二式得:
[习题 2-7] 一根等直杆受力如图所示。已知杆的横截面面积 A 和材料的弹性模量 E 。试作轴力图,并求杆端点 D 的位移。 解: (1)作轴力图
[习题 2-9] 一根直径 mm d 16=、长 m l 3=的圆截面杆,承受轴 向拉力 kN F 30=,其伸长为 mm l 2.2=?。试求杆横截面上的应 力与材料的弹性模量 E 。 解:(1)求杆件横截面上的应力 MPa mm N A N 3.1491614.34 110302 23=???==σ (2)求弹性模量 因为:EA Nl l = ?, 所以:GPa MPa l l l A l N E 6.203)(9.2035902 .23000 3.149==?=??=???=σ。 [习题 2-10] (1)试证明受轴向拉伸(压缩)的圆截面杆横截 面沿圆周方向的线应变 s ε等于直径方向的线应变 d ε。 (2)一根直径为 mm d 10=的圆截面杆,在轴向力 F 作用下,直 径减小了 0.0025mm 。如材料 的弹性模量 GPa E 210=,泊松比 3.0=ν,试求该轴向拉力 F 。 (3)空心圆截面杆,外直径 mm D 120=,内直径 mm d 60=,材 料的泊松比 3.0=ν。当其轴向拉伸时,已知纵向线应变 001.0=, 试求其变形后的壁厚。 解:(1)证明 d s εε= 在圆形截面上取一点 A ,连结圆心 O 与 A 点,则 OA 即代表直 径方向。过 A 点作一条直线 AC 垂直于 OA ,则 AC 方向代表圆周方向。νεεε-==AC s(泊
《工程力学》第4次作业解答(杆件的内力计算与内力图).

《工程力学》第4次作业解答(杆件的内力计算与内力图)2008-2009学年第二学期一、填空题1.作用于直杆上的外力(合力)作用线与杆件的轴线重合时,杆只产生沿轴线方向的伸长或缩短变形,这种变形形式称为轴向拉伸或压缩。
2.轴力的大小等于截面截面一侧所有轴向外力的代数和;轴力得正值时,轴力的方向与截面外法线方向相同,杆件受拉伸。
3.杆件受到一对大小相等、转向相反、作用面与轴线垂直的外力偶作用时,杆件任意两相邻横截面产生绕杆轴相对转动,这种变形称为扭转。
4.若传动轴所传递的功率为P 千瓦,转速为n 转/分,则外力偶矩的计算公式为9549P M n=⨯。
5.截面上的扭矩等于该截面一侧(左或右)轴上所有外力偶矩的代数和;扭矩的正负,按右手螺旋法则确定。
6.剪力S F 、弯矩M 与载荷集度q 三者之间的微分关系是()()S dM x F x dx =、()()S dF x q x dx=±。
7.梁上没有均布荷载作用的部分,剪力图为水平直线,弯矩图为斜直线。
8.梁上有均布荷载作用的部分,剪力图为斜直线,弯矩图为抛物线。
9.在集中力作用处,剪力图上有突变,弯矩图上在此处出现转折。
10.梁上集中力偶作用处,剪力图无变化,弯矩图上有突变。
二、问答题1.什么是弹性变形?什么是塑性变形?解答:在外力作用下,构件发生变形,当卸除外力后,构件能够恢复原来的大小和形状,则这种变形称为弹性变形。
如果外力卸除后不能恢复原来的形状和大小,则这种变形称为塑性变形。
2.如图所示,有一直杆,其两端在力F 作用下处于平衡,如果对该杆应用静力学中“力的可传性原理”,可得另外两种受力情况,如图(b )、(c )所示。
试问:(1)对于图示的三种受力情况,直杆的变形是否相同?(2)力的可传性原理是否适用于变形体?解答:(1)图示的三种情况,杆件的变形不相同。
图(a )的杆件整体伸长变形,图(b )的杆件只有局部伸长变形,图(c )的杆件是缩短变形。
昆明理工大学工程力学应力状态答案

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( ) 1.2 内力只作用在杆件截面的形心处。
( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( ) 1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ) 1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( ) 1.9 同一截面上各点的切应力τ必相互平行。
( ) 1.10 应变分为正应变ε和切应变γ。
( ) 1.11 应变为无量纲量。
( ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ) 1.13 若物体内各点的应变均为零,则物体无位移。
( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( )1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ) 1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( )二、填空题1.1 材料力学主要研究 受力后发生的 ,以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ,变形特征是 。
1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
B题1.15图题1.16图1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所谓 ,是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 , , 。
材料力学课后作业

和弯矩方程绘制剪力图和弯矩图。
32、如图示,设q、a均为己知。求:梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
33、如图示,设q、a均为己知。求:梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
《材料力学》课后作业
1、试作图示各杆的轴力图。
2、求图示各杆 和 横截面上的轴力,并作轴力图。
答案:
3、 求图示阶梯状直杆横截面 、 和 上的轴力,并作轴力图。如横截面面积 , , ,求各横截面上的应力。
答案:
4、 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制成。下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个 的等边角钢。已知屋面承受集度为 的竖直均布荷载。求拉杆 和 横截面上的应力。
40、割刀在切割工件时,受到F=1KN的切削力作用,割刀尺寸如图所示,若割刀的许用弯曲正应力〔σ〕=200MPa。试校核割刀的弯曲正应力强度。
答案:σmax=200MPa
41、图示为一承受纯弯曲的铸铁梁,其截面为⊥形,材料的拉伸和压缩许用应力之比
〔σ+〕/〔σ-〕=1/4。求水平翼板的合理宽度b。
答案:b=510mm
答案:σA=σD=-163.5MPaσB=38.8 MPaσC=58.8 MPa
38、矩形截面的悬臂梁受集中力和集中力偶作用,如图所示。试求Ⅰ-Ⅰ截面和固定端Ⅱ-Ⅱ截面上A、B、C、D四点处的正应力。
答案:I-I截面:σA=-7.41MPaσB=4.94MPaσC=0σD=7.41MPa
I-I截面:σA=9.26MPaσB=-6.18MPaσC=0σD=-9.26MPa
试作图示各杆的轴力图

计 算 题( 第四章 )4.1 试作图示各杆的轴力图。
图题4. 14.2 图示等截面混凝土的吊柱和立柱,已知横截面面积A 和长度a ,材料的重度γ,受力如图示,其中10F Aaγ=。
试按两种情况作轴力图,并求各段横截面上的应力,⑴不考虑柱的自重;⑵考虑柱的自重。
图题4.24.3 一起重架由100×100mm 2 的木杆BC 和 直径为30m m 的钢拉杆AB 组成,如图所示。
现起吊一重物W F=40kN 。
求杆AB 和BC 中的正应力。
图题4.34.4 图示钢制阶梯形直杆,各段横截面面积分别为21100mm A =,2280mm A =,23120mm A =,钢材的弹性模量G P a E 200=,试求: (1)各段的轴力,指出最大轴力发生在哪一段,最大应力发生在哪一段; (2)计算杆的总变形;图题4.44.5 图示短柱,上段为钢制,长200m m ,截面尺寸为100×100mm 2;下段为 铝制,长300m m ,截面尺寸 为200×200mm 2。
当柱顶受F 力作 用时,柱子总长度减少了0.4mm 。
试求F 值。
已知:(E 钢=200GP a ,E 铝=70GPa )。
4.6 图示等直杆A C ,材料的容重为ρg , 弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
题4.5图 题4.6图4.7 两块钢板用四个铆钉连接,受力kN 4=F 作用,设每个铆钉承担4F 的力,铆钉的直径mm 5=d ,钢板的宽mm 50=b ,厚度mm 1=δ,连接按(a )、(b )两种形式进行,试分别作钢板的轴力图,并求最大应力max σ。
题4.7图4.8 用钢索起吊一钢管如图所示,已知钢管重kN 10=G F ,钢索的直径mm 40=d ,许用应力[]M P a 10=σ,试校核钢索的强度。
工程力学期末复习题参考答案
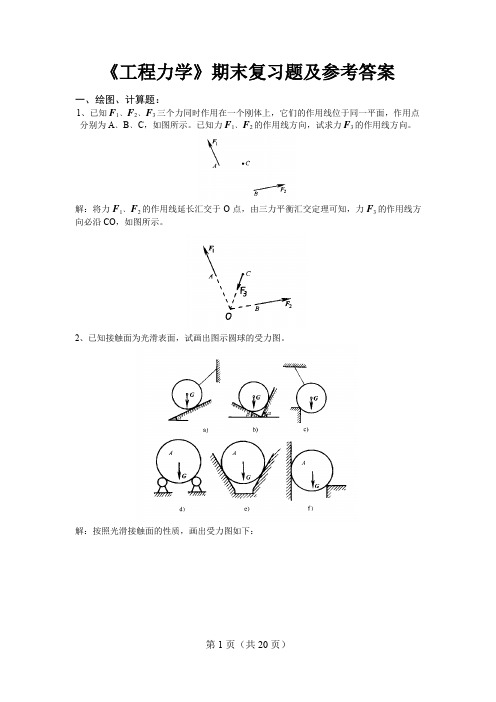
《工程力学》期末复习题及参考答案一、绘图、计算题:1、已知F1﹑F2﹑F3三个力同时作用在一个刚体上,它们的作用线位于同一平面,作用点分别为A﹑B﹑C,如图所示。
已知力F1﹑F2的作用线方向,试求力F3的作用线方向。
解:将力F1﹑F2的作用线延长汇交于O点,由三力平衡汇交定理可知,力F3的作用线方向必沿CO,如图所示。
2、已知接触面为光滑表面,试画出图示圆球的受力图。
解:按照光滑接触面的性质,画出受力图如下:3、试画出各分图中物体AB的受力图。
解:物体AB的受力图如图所示。
4、如图所示,简易起重机用钢丝绳吊起重量G=10kN的重物。
各杆自重不计,A、B、C三处为光滑铰链联接。
铰链A处装有不计半径的光滑滑轮。
求杆AB和AC受到的力。
解:画A处光滑铰链销钉受力图(见图),其中重物重力G垂直向下;AD绳索拉力F T沿AD方向,大小为G;AB 杆拉力F BA 沿AB 方向;AC 杆受压,推力F CA 沿CA 方向。
以A 为原点建立Axy 坐标系,由平衡条件得到如下方程:030sin 45sin ,0001=--=∑=T BA CA niix F F F F (a)030cos 45cos ,0001=--=∑=G F F F T CA ni iy (b)由(b)式得kN G F CA 4.2645cos )130(cos 00=+=,代入(a )式得kN F F F T CA BA 66.135.010707.04.2630sin 45sin 00=⨯-⨯=-=所以杆AB 受到的力kN F BA 66.13=,为拉力;杆AC 受到的力kN F CA 4.26=,为压力。
5、拖车的重量G =250kN ,牵引车对它的作用力F =50kN ,如图所示。
求当车辆匀速直线行驶时,车轮A 、B 对地面的正压力。
解:画拖车受力图,如图所示,拖车受6个力的作用:牵引力F ,重力G ,地面法向支撑力F NA 、F NB ,摩擦力F A 、F B 。
材料力学答案单辉祖版全部答案

第二章轴向拉压应力与材料的力学性能2-1试画图示各杆的轴力图。
题2-1图解:各杆的轴力图如图2-1所示。
图2-12-2试画图示各杆的轴力图,并指出轴力的最大值。
图a与b所示分布载荷均沿杆轴均匀分布,集度为q。
题2-2图(a)解:由图2-2a(1)可知,qxqaxF-=2)(N轴力图如图2-2a(2)所示,qaF2m ax,N=图2-2a(b)解:由图2-2b(2)可知,qaF=RqaFxF==R1N)(22R2N2)()(qxqaaxqFxF-=--=精选文档精选文档轴力图如图2-2b(2)所示,qa F =max N,图2-2b2-3 图示轴向受拉等截面杆,横截面面积A =500mm 2,载荷F =50kN 。
试求图示斜截面m -m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
题2-3图解:该拉杆横截面上的正应力为100MPa Pa 1000.1m10500N10508263=⨯=⨯⨯==-A F σ 斜截面m -m 的方位角,50-=α故有MPa 3.41)50(cos MPa 100cos 22=-⋅==ασσαMPa 2.49)100sin(MPa 502sin 2-=-⋅== αστα杆内的最大正应力与最大切应力分别为MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示,图中还同时画出了低应变区的详图。
试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
题2-5解:由题图可以近似确定所求各量。
220GPa Pa 102200.001Pa 10220ΔΔ96=⨯=⨯≈=εσEMPa 220p ≈σ, MPa 240s ≈σ精选文档MPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。
2-7 一圆截面杆,材料的应力-应变曲线如题2-6图所示。
若杆径d =10mm ,杆长 l =200mm ,杆端承受轴向拉力F = 20kN 作用,试计算拉力作用时与卸去后杆的轴向变形。
工程力学练习册习题答案解析

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F BC AB 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交 NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
材料力学作业

三、桥式起重机大梁上的小车的每个轮子对大梁的压力均为 ,试问小车在什么位置时梁内的弯矩为最大?其最大弯矩等于多少?最大弯矩的作用截面在何处?设小车的轮距为 ,大梁的跨度为 。
四、试利用微分关系作出图示各杆的剪力图和弯矩图。
五、已知简支梁的弯矩图如图所示,试作该梁的剪力图和载荷图。
材料力学作业
———————————————————————————————— 作者:
———————————————————————————————— 日期:
ﻩ
一、试作出图示各杆的轴力图。
二、图示结构中,1、2两杆的横截面直径分别为 和 ,试求两杆的应力。设两根横梁皆为刚体。
三、桁架的尺寸及受力如图所示,若 , 杆的横截面面积 ,试求 杆的应力。
四、在图示简易吊车中, 为钢杆, 为木杆。木杆 的横截面面积 ,许用应力 ;钢杆 的横截面面积 ,许用应力 。试求许可吊重 。
五、在低碳钢拉伸实验用的力与变形曲线及应力应变曲线中分别标出 、 、 和 、 、 ,并回答在 曲线中的 、 、 是否是构件中的真实应力,如果不是请另绘出强化阶段与颈缩阶段真实应力曲线的大致形状。
八、重量为 的直梁放置在水平刚性平面上,若受力后未提起的部分保持与平面密合,试求提起部分的长度。
一、在图示应力状态中,试用解析法和图解法求出指定截面上的应力及其主应力并画主单元体(应力单位为 )。
二、受力某点两平面上的应力如图示,求其主应力。应力单位为 。
六、简支梁的剪力图如图所示,已知梁上没有集中力偶作用,试作该梁的弯矩图和载荷图。
七、试作出图示平面刚架的内力图( 、 、 )。
一、把直径 的钢丝绕在直径 的轮缘上,已知材料的弹性模量 ,试求钢丝内的最大弯曲正应力。
(完整版)材料力学课后习题答案
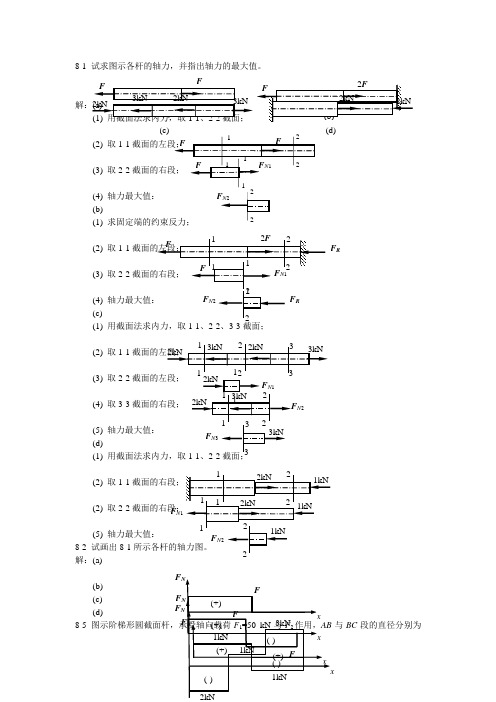
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
材料力学作业习题

第二章 轴向拉伸与压缩1、试求图示各杆1-1和2-2横截面上的轴力,并做轴力图。
(1) (2)2、图示拉杆承受轴向拉力F =10kN ,杆的横截面面积A =100mm 2。
如以α表示斜截面与横截面的夹角,试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力和切应力,并用图表示其方向。
3、一木桩受力如图所示。
柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变;(4)柱的总变形。
4、(1)试证明受轴向拉伸(压缩)的圆截面杆横截面沿圆周方向的线应变d ε,等于直径方向的线应变d ε。
(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0.0025mm 。
如材料的弹性摸量E =210GPa ,泊松比ν=0.3,试求轴向拉力F 。
(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0.3。
当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。
5、图示A和B两点之间原有水平方向的一根直径d=1mm的钢丝,在钢丝的中点C加一竖直荷载F。
已知钢丝产生的线应变为ε=0.0035,其材料的弹性模量E=210GPa,钢丝的自重不计。
试求:(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律);(2) 钢丝在C点下降的距离∆;(3) 荷载F的值。
6、简易起重设备的计算简图如图所示.一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度成,钢的许用应力]条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。
已知材料的许用应力[σ=170MPa,试选择杆AB,AD的角钢型号。
西南交大第二版材工程力学材料力学部分习题答案
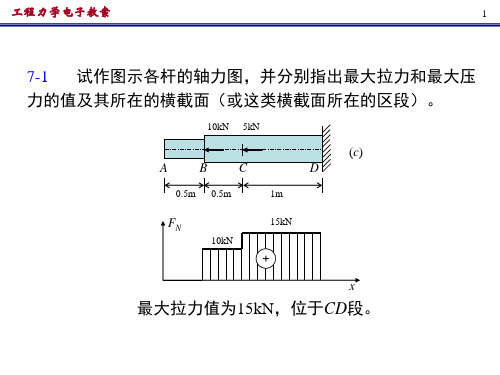
Ⅱ Ⅰ
l/2
l
l/2
1 0 3F 1 2A
Fl h 2 4 3 Fl 2 bh3 2bh2 12 2 0
3Fl 2bh2
Fl 2 3Fl 3 2 bh bh2 6 3 0
FAB A FAD
D
FAC
由分析可知: FN , AB 600kN , FN , AC 300 3kN
工程力学电子教案
6
2 AAB
FN , AB
600kN 35.3cm2 170MPa
B
AAB≥17.6cm2,AB杆应该选择 100×100×10的等边角钢。
2 AAD FN , AD
3
7-4 在图示结构中,各杆的横截面面积均为3000mm2。力F为 100kN。试求各杆横截面上的正应力。 解:假设各杆均被拉伸,对B点作 F 受力分析: B
FBC FAB F
B
3m
A
4m
C
2m
FN , AB 75kN, FN ,BC 125kN 由分析可知:
对C点作受力分析:
F'BC C FCD
3 20kN 2 10kN 1 20kN
a
3
a
2
a
1
10kN
解:
10kN 20kN
20 103 1 100MPa 6 200 10
10 103 2 50 MPa 6 200 10
10 103 3 50 MPa 6 200 10
工程力学电子教案
F
B
3m
A
4m
C
2m
试求图示各杆1-1
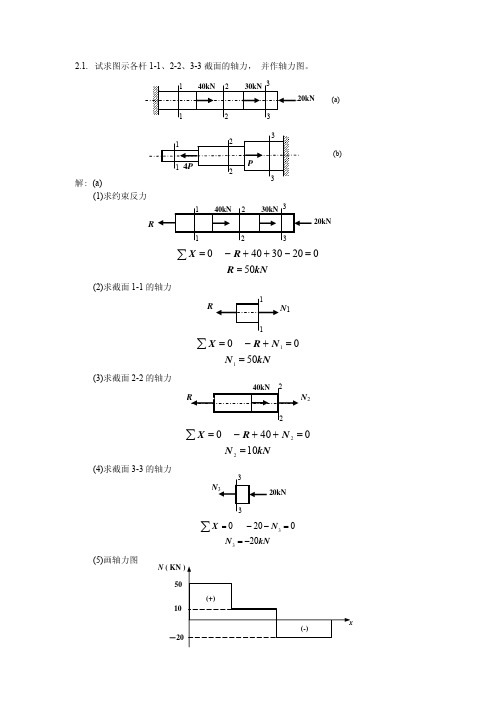
ACD ≥
N ×n
σs
(100 × 10 ) × 2 = 833mm =
3
2
240 × 106
(3) 测弹性模量 E 时,则 AB 杆内的最大应力为:
σ max =
所加最大拉力为
N max =σP AAB
⎛1 ⎞ N max = σ P × AAB = ( 200 × 106 ) × ⎜ × π × 0.012 ⎟ = 15.71kN ⎝4 ⎠
P 38 × 103 = = 63.33MPa A2 2 × 15 × 20 × 10−6
σ2 =
(3) 3-3 截面上的应力
σ3 =
P 38 × 103 = = 45.24 MPa A3 (50 − 22) × 15 × 2 × 10−6
(4) 最大拉应力在 1-1 截面上
σ max = σ 1 = 67.86MPa
S1 P
B
S1 α S2
α
S2
P
P = S1 = S2 = 23.1kN
(3) 由强度条件得三杆的横截面直径
d AB = d BC = d BD =
4 × ( 23.1 × 103 ) 4P = = 17.2mm π [σ ] π (100 × 106 )
2.10 图示简易吊车的杆BC为钢杆,杆AB为木杆, 。杆AB的横截面面积A1=100cm2,许用应力 [σ]1=7MPa;杆BC的横截面面积A2=6cm2,许用应力[σ]2=160MPa。求许可吊重P。
N1 ≤ [σ ]1 A1
(3) 由 BC 杆的强度条件
A × [σ ]2 ( 6 × 10 P≤ 2 = 2
(4) 许可吊重
N2 ≤ [σ ]2 A2
−4
工程力学作业答案
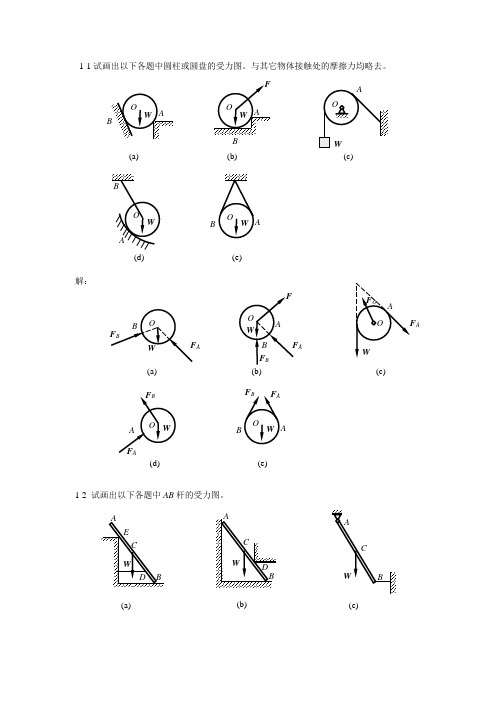
1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)98 解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b) CB(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
解:(a)(d)FC(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDC ’B2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos 6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)F 1F FDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。
答案与思考
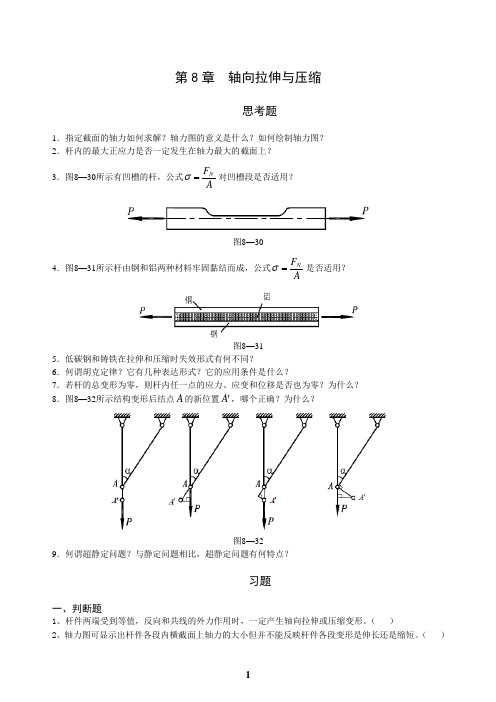
第8章 轴向拉伸与压缩思考题1.指定截面的轴力如何求解?轴力图的意义是什么?如何绘制轴力图?2.杆内的最大正应力是否一定发生在轴力最大的截面上?3.图8—30所示有凹槽的杆,公式A F N=σ对凹槽段是否适用?图8—304.图8—31所示杆由钢和铝两种材料牢固黏结而成,公式A F N=σ是否适用?图8—315.低碳钢和铸铁在拉伸和压缩时失效形式有何不同?6.何谓胡克定律?它有几种表达形式?它的应用条件是什么?7.若杆的总变形为零,则杆内任一点的应力、应变和位移是否也为零?为什么?8.图8—32所示结构变形后结点A 的新位置'A ,哪个正确?为什么?图8—329.何谓超静定问题?与静定问题相比,超静定问题有何特点?习题一、判断题1、杆件两端受到等值,反向和共线的外力作用时,一定产生轴向拉伸或压缩变形。
( )2、轴力图可显示出杆件各段内横截面上轴力的大小但并不能反映杆件各段变形是伸长还是缩短。
()3、一端固定的杆,受轴向外力的作用,不必求出约束反力即可画内力图。
( )4、求轴向拉伸或压缩杆件的轴力时,一般地说,在采用了截面法之后,是不能随意使用力的可传性原理来研究留下部分的外力平衡的。
( )5、对于轴向拉压杆,在与横截面成α角的斜截面上,只要在0900≤≤α范围内,斜截面上的正应力和切应力就不可能同时为零。
( )6、不论杆件的长短粗细如何,其绝对变形大小是可以完全反映这一杆件的变形程度的。
( )7、材料相同的两根等直杆,已知一根杆的伸长为0.001mm ,另一根杆的伸长为1mm ,则前者符合小变形假设,后者不符合小变形假设。
( )8、轴向拉伸或压缩杆作的轴向线应变和横向线应变符号一定是相反的。
( )9、同种材料制成的、但尺寸不同的试样,试验所得到的应力-应变曲线运动形状与试样 的尺寸是无关的。
( )10、铸铁这种脆性材料在拉伸或压缩试验时都不出现屈服,变形不大就突然断裂,其断口断面都近似垂直于轴线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、试作出图示各杆的轴力图。
二、桁架的尺寸及受力如图所示,若kN 300=F ,AB 杆的横截面面积2mm 6000=A ,试求AB 杆的应力。
解:设AB,BF,EF 三杆的轴力如图,则: 对桁架进行受力分析,有:
∑=0F M
84⨯=⨯F F N
6002=
=F F N kN 6000
106003⨯==A F N AB
σMPa=100MPa
a
三、在图示简易吊车中,BC 为钢杆,AB 为木杆。
木杆AB 的横截面面积21cm 100=A ,许用应力[]MPa 71=σ;钢杆BC 的横截面面积22cm 6=A 2[]F 。
解:设两杆轴力如图,对铰链B 进行受力分析,有:
[][]
[][][][]
[][]。
故许可吊重为杆:
对杆:
对4kN .40kN 482
2 BC kN
4.403
3AB 23{
30sin 30cos {22222
22
211111
11121
21221==
==
=
=======⇒==σσσσσσA F A F A F A F A F A F F
F F
F F F F F N N N N N N N οο
四、图示桁架,杆1、2的横截面积和材料均相同,在节点A 处受载荷F 作用。
从实验中测得1、2两杆的纵向线应变分别为41100.4-⨯=ε,42100.2-⨯=ε。
试确定载荷F 及其方位角θ的大小。
已知:221m m 200==A A ,G Pa 20021==E E 。
解:设AB,AC 两杆的轴力分别为,方向如图和21N N F F :
ο
οο9.103
124tg kN 2.214)312(kN 430sin )(sin kN
31230cos )(cos A kN 8AC kN 16AB 222222************==
=+==-==+=======θθθεσεσF F F F F F F A E A F A E A F N N N N N N 所以有:
进行受力分析有:
对铰链杆:
对杆:
对
五、图示结构中,AB 为刚体,杆1、杆2、杆3的材料和横截面面积均相同,在杆AB 的中点C 作用铅垂方向的载荷F ,试计算C 点的水平位移和铅垂位移。
已知:kN 20=F ,2321mm 100====A A A A ,mm 1000=l ,GPa 200=E 。
解:
F
30C A
B 2N F 1
N F
2
/l 2
/l l 2
3
1
C
A B
F
3N F
2N F
1
N F
1
l ∆
C
A
B
mm
5.0mm
5.00.5mm EA
00
2
112
312231=∆=∆=∆=∆==∆=∆=∆===l l l
l l l F F F F C C F N N N 垂直水平
六、设横梁ABCD 为刚体。
横截面面积为2mm 36.76的钢索绕过无摩擦的滑轮。
设kN 20=P ,试求钢索内的应力和C 点的垂直位移。
设钢索的弹性模量GPa 177=E 。
解:
(2sin601
)(21CC mm
367.1MPa 2.1513
1200
160060sin 80060sin 21111C 21∆+∆=+==∆==∆+∆=∆==
=
⨯=⨯+⨯⊥l l DD BB EA l
F l l l A
F P F P F F N N
N N N ο
οοσ
1
D
七、图示结构中,AB 为刚体,1、2杆的抗拉(压)刚度均为EA 。
试求两杆的轴力。
解:
F F F EA
a F l EA
a F l a
F a F a F l l N N N N N N 5
3
323323
2
212
1212121=
=⨯=
∆⨯=
∆⨯=⨯+⨯=∆∆联立解得:;
1
B
八、图示杆系的两杆同为钢杆,GPa 200=E ,C 061105.12-⨯=α。
两杆的横截面面积同为2cm 10=A 。
若BC 杆的温度降低C 200,而BD 杆的温度不变,试计算两杆的轴力。
解:
(压)
(拉)
联立解得:;kN 2.26kN 3.3030cos 230cos 30cos 21212
12121===∆⨯-
=∆=∆=∆N N N N N N F F EA l
F l EA a F l F F l l ο
οο
九、图示支架中的三根杆件材料相同,杆1的横截面面积为2mm 200,杆2的横截面面积为2mm 300,杆3的横截面面积为2mm 400。
若kN 30=P ,试求各杆内的应力。
解:
(压)
(拉)(拉)
故:
,,联立解得:,,86.6MPa 8MPa .268MPa .12664kN
.3404kN .8kN 36.25cos30030cos 30cos 30sin 30sin 30cos 30cos 3213
32
21
12
321
32132132131=======
∆=
∆=
∆=-+=+∆+∆=∆-∆σσσN N N N N N N N N N N F F F EA l F l EA l F l EA l F l F F F F F F l l l l ο
ο
ο
οοο
ο
枯藤老树昏鸦,小桥流水人家,古道西风瘦马。
夕阳西下,断肠人在天涯。
A。
