南通市2015届高三第二次调研数学测试题

合集下载

南通市2015届高三上学期期末考试数学试题(含答案)

江苏省南通市2015届高三上学期期末考试数学试题数学I一、填空题1.已知集合{2,1}A，{1,2,3}B ，则A B.2.已知复数z 满足341(i z i 为虚数单位)，则z 的模为.3.某中学共有学生2800人，其中高一年级970人，高二年级930人，高三年级900人．现采用分层抽样的方法，抽取280人进行体育达标检测，则抽取高二年级学生人数为.4.函数2()lg(23)f x x x 的定义域为. 5.右图是一个算法流程图，则输出的x 的值是. 6.同时抛掷两枚质地均匀的骰子(一种各面上分别标有1，2，3，4，5，6个点的正方体玩具)，观察向上的点数，则两个点数之积不小于4的概率为.7.底面边长为2，高为1的正四棱锥的侧面积为.8.在平面直角坐标系xOy 中，以直线2y x 为渐近线，且经过抛物线24yx 焦点的双曲线的方程是.9.在平面直角坐标系xOy 中，记曲线2(m yxxx R ，2)m在1x 处的切线为直线l ．若直线l 在两坐标轴上的截距之和为12，则m 的值为.10.已知函数()sin 26f x x．若()(0)2yf x 是偶函数，则.11.在等差数列{}n a 中，已知首项10a ，公差0d．若1260a a ，23100a a ，则155a a 的最大值为.12.已知函数(0)xyab b 的图像经过点(1,3)P ，如下图所示，则411a b的最小值为.13.如上图，圆O 内接ABC 中，M 是BC 的中点，3AC．若4AO AM ，则AB.开始y<50x ←2x+y 输出x结束YNy ←2x+yx ←1,y ←113yOxACBOM （第12题）（第13题）14.已知函数()f x 是定义在1,上的函数，且1|23|,12,()11(),2,22x x f x f x x　则函数2()3y x f x 在区间(1,2015)上的零点个数为.二、解答题15.在?ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．已知cos cos 2cos b Cc B a A ．（1）求角A 的大小；（2）若3AB AC，求ABC 的面积．16.如图，在直三棱柱111ABC A B C 中，AC BC ，14CC ，M 是棱1CC 上的一点．（1）求证：BC AM ；（2）若N 是AB 的中点，且CN ∥平面1AB M ，求CM 的长．ACBMNC 1B 1A 117.如图，在平面直角坐标系xOy 中，1F ，2F 分别是椭圆22221(0)x y a b ab的左、右焦点，顶点B 的坐标为0,b ，且12BF F 是边长为2的等边三角形．（1）求椭圆的方程；（2）过右焦点2F 的直线l 与椭圆相交于A ，C 两点，记2ABF ，2BCF 的面积分别为1S ，2S ．若122S S ，求直线l 的斜率．18.在长为20m ，宽为16m 的长方形展厅正中央有一圆盘形展台(圆心为点C )，展厅入口位于长方形的长边的中间．在展厅一角B 点处安装监控摄像头，使点B 与圆C 在同一水平面上，且展台与入口都在摄像头水平监控范围内(如图阴影所示)．（1）若圆盘半径为25m ，求监控摄像头最小水平视角的正切值；（2）若监控摄像头最大水平摄像视角为60，求圆盘半径的最大值．（注：水平摄像视角指镜头中心点水平观察物体边缘的视线的夹角．）Oxy BACF 1F 2BC入口16m20m19.若函数()y f x 在0x x 处取得极大值或极小值，则称0x 为函数()yf x 的极值点．已知函数3()3ln (f x axx xa aR )．（1）当0a 时，求()f x 的极值；（2）若()f x 在区间1(,)e e上有且只有一个极值点，求实数a 的取值范围．（注：e 是自然对数的底数）20.设数列{}n a 的前n 项和为n S ．若1122n na a (nN *)，则称{}n a 是“紧密数列”．（1）若数列{}n a 的前n 项和2134n S nn (nN *)，证明：{}n a 是“紧密数列”；（2）设数列{}n a 是公比为q 的等比数列．若数列{}n a 与{}n S 都是“紧密数列”，求q 的取值范围．数学Ⅱ附加题部分注意事项1．本试卷共2页，均为解答题（第21题～第23题，共4题）．本卷满分为40分，考试时间为30分钟.考试结束后，请将本试卷和答题卡一并交回．2．作答试题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其它位置作答一律无效．21．【选做题】本题包括A、B、C、D四小题，请选定其中两题．．．．．．．，并在相应的答题区域内作答．．．．．．．．．．．．．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．A．选修4－1：几何证明选讲（本小题满分10分）如图，已知AB是圆O的直径，CD是圆O的弦，分别延长AB，CD相交于点M，N为圆O上一点，AN＝AC，证明：∠MDN＝2∠OCA．B．选修4－2：矩阵与变换（本小题满分10分）已知矩阵273mM的逆矩阵127nMm，求实数m，n．C．选修4－4：坐标系与参数方程（本小题满分10分）在平面直角坐标xOy中，已知曲线C的参数方程为21,214x ty t（t为参数），曲线与直线l：12y x相交于A，B两点，求线段AB的长．D．选修4－5：不等式选讲（本小题满分10分）已知a，b，c均为正数．求证：111a b cbc ca ab a b c．OACBMDN【必做题】第22题、第23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．22.（本小题满分10分）如图，在四棱锥A-BCDE 中，底面BCDE 为平行四边形，平面ABE ⊥平面BCDE ，AB ＝AE ，DB ＝DE ，∠BAE ＝∠BDE ＝90o ．（1）求异面直线AB 与DE 所成角的大小；（2）求二面角B-AE-C 的余弦值．23.设n a 是满足下述条件的自然数的个数：各数位上的数字之和为n (nN *)，且每数位上的数字只能是1或2．（1）求1a ，2a ，3a ，4a 的值；（2）求证：51n a (nN *)是5的倍数．BAEDCASq12ABE ACE。

2015年3月2015届高三第二次全国大联考(江苏版)数学卷(原卷版)

【学科网学易大联考】2015年第二次全国大联考【江苏版】一、填空题（每题5分，满分70分，将答案填在答题纸上）1．已知复数z =201532i i-(i 是虚数单位)，则复数z 所对应的点位于复平面的第象限． 2．已知全集U=N ，集合{}10A x x =->，则=A C U ．3．若样本321,,a a a 的方差是2，则样本12322015,22015,22015a a a +++的方差是．4．已知双曲线22221y x a b-=的一个焦点与圆x 2+y 2－10x =05，则该双曲线的准线方程为．5．已知实数x ∈[3，9]，执行如右图所示的流程图，则输出的x 不小于55的概率为．6．若S n 为等差数列{a n }的前n 项和，S 9=－36，S 13=－104，则a 5与a 7的等比中项为． 7．定义在R 上的奇函数()f x ，对任意x ∈R 都有(2)()f x f x +=-，当(02)x ∈，时，()4x f x =，则(2015)f = ．8. 一个三棱柱恰好可放入一个正四棱柱的容体中，底面如图所示，其中三棱柱的底面AEF 是一个直角三角形，∠AEF = 90︒，AE = 2，EF = 1，三棱柱的高与正四棱柱的高均为1，则此正四棱柱的体积为．开始结束Yn ←1输入x 输出xn ←n +1 x ←2x +1n ≤3 N（第8题）FEDCBA9．已知函数y ＝sin ωx (ω＞0)在区间[0，2π]上为增函数，且图象关于点(3π，0)对称，则ω的取值集合为．.10．已知直线y =ax +3与圆22280x y x ++-=相交于A ，B 两点，点00(,)P x y 在直线y =2x 上，且P A =PB ,则0x的取值范围为． 11. 已知函数20151()sin 201521xf x x =++在[]2015,2015-上的最大值分别为,M m ，则M m += ．12．在ABC ∆中，2AC BC ⋅=且两中线AD 与BE 互相垂直，求ABC ∆面积的最大值． 13．设P (x ，y)为函数22y x =+(x >图象上一动点，记353712x y x y m x y +-+-=+--，则当m 最小时，点 P的坐标为．14．设椭圆和双曲线有公共焦点12F F ，，两曲线的一个公共点为P ，且123F PF π∠=，记12e e ，分别为椭圆和双曲线的离心率，则1211e e +的最大值为．二、解答题（本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤.）15．（本小题满分14分）如图，在xoy 平面上，点)0,1(A ，点B 在单位圆上，θ=∠AOB （πθ<<0） (I) 若点)54,53(-B ，求)42tan(πθ+的值；(II)若OC OB OA =+，四边形OACB 的面积用θS 表示，求OC OA S ⋅+θ的取值范围.16．（本小题满分14分）如图，长方体1111ABCD A B C D -中，底面1111A B C D 是正方形，E 是棱1AA 上任意一点，F 是CD 的中点． (I) 证明：BD 1EC ⊥； (II)若AF ∥平面C 1DE ，求1AEA A的值． D 1C 1B 1A 1FEDCBA17．（本小题满分14分）下图是一块平行四边形园地 ABCD ，经测量，AB = 20 m ，BC = 10 m ， ∠ABC = 120 °．拟过线段 AB 上一点 E 设计一条直路 EF （点 F 在四边形 ABCD 的边上，不计路的宽度），将该园地分为面积之比为 3:1 的左、右两部分分别种植不同花卉．设 EB = x ，EF = y （单位：m ）．（Ⅰ）当点 F 与点 C 重合时，试确定点 E 的位置；（Ⅱ）求 y 关于 x 的函数关系式；（Ⅲ）请确定点 E ，F 的位置，使直路 EF 长度最短．18．（本小题满分16分）如图，在平面直角坐标系 xOy 中，A ，B 是圆 O ：221x y +=与 x 轴的两个交点（点 B 在点 A 右侧），点(2,0)Q -， x 轴上方的动点 P 使直线 PA ，PQ ，PB 的斜率存在且依次成等差数列． (I) 求证：动点 P 的横坐标为定值；（II ）设直线 PA ，PB 与圆 O 的另一个交点分别为 S ，T ，求证：点 Q ，S ，T 三点共线．19．（本小题满分16分）设二次函数2()f x ax bx c =++的导函数为().f x '（Ⅰ）若 a = 1，c = 2 ，且在平面直角坐标系 xOy 中，直线 y =()f x '恰与抛物线 y = f (x ) 相切，求 b 的值；（II ）若 ,()()x R f x f x '∀∈≥恒成立，（ⅰ）求证： c ≥a > 0 ；（ⅱ）求222b ac +的最大值．20．（本小题满分16分）已知数列{}n a 的奇数项是首项为1的等差数列，偶数项是首项为2的等比数列，数列{}n a 前n 项和为n S ，且满足5459342,S a a a a a =+=+.(Ⅰ)求数列{}n a 的通项公式；(Ⅱ)若12m m m a a a ++=，求正整数m 的值； (Ⅲ)是否存在正整数m ，使得221mm S S -恰好为数列{}n a 中的一项？若存在，求出所有满足条件的m 值，若不存在，说明理由.数学Ⅱ 附加题部分【理】21.【选做题】本题包括A 、B 、C 、D 四小题，请选定其中两题．．．．．．．，并在相应的答题区域内作答．．．．．．．．．．．．．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．【选做题】（在A 、B 、C 、D 四小题中只能选做2题） A ．【选修4—1几何证明选讲】（本小题满分10分）如图，在△ABC 中，CM 是∠ACB 的平分线，△AMC 的外接圆O 交BC 于点N . 若AB =2AC ，求证：BN =2AM .B ．【选修4—2：矩阵与变换】（本小题满分10分）已知曲线C ，在矩阵M 1002⎡⎤=⎢⎥⎣⎦对应的变换作用下得到曲线1C ，1C 在矩阵N 0110-⎡⎤=⎢⎥⎣⎦对应的变换作用下得到曲线2218C y x =：，求曲线C 的方程．C.【选修4—4：坐标系与参数方程】（本小题满分10分）已知极坐标系的极点在直角坐标系的原点，极轴与x 轴的正半轴重合．曲线C 的极坐标方程为22312sin ρθ=+，直线l的参数方程为,1x y t ⎧=⎪⎨=+⎪⎩(t 为参数，t ∈R )．试在曲线C 上求一点M ，使它到直线l 的距离最大．D ．【选修4—5：不等式选讲】（本小题满分10分）求函数：y =最大值．【必做题】（第22题、第23题，每题10分，共20分.解答时应写出文字说明、证明过程或演算步骤） 22.（本小题满分10分）学校足球队进行罚点球训练，队员在一轮训练中最多可罚4次，并规定，一旦命中该队员即停止此轮练习，否则一直罚到第4次为止. 已知一选手罚点球的命中率为0.8，求一轮练习中，该选手的实际罚球次数X 的分布列，并求X 的数学期望. 23. （本小题满分10分）已知多项式5431111()52330f n n n n n =++-.(Ⅰ)求(1)f -及(2)f 的值；(Ⅱ)试探求对一切整数n ，()f n 是否一定是整数？并证明你的结论．MC NBO ·A。

江苏省南通市2024届高三第二次调研测试数学试题(含解析)

南通市2024届高三第二次调研测试数学注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上指定位置上，在其他位置作答一律无效.3.本卷满分为150分，考试时间为120分钟.考试结束后，将本试卷和答题卡一并交回.一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知单位向量1e ，2e 的夹角为120°，则122(2)-⋅=e e e （）A ．2-B ．0C ．1D ．22．在正方体1111ABCD A B C D -中，下列关系正确的是（）A ．1ADB C⊥B ．1A D BD⊥C ．11AC AC ⊥D ．11AC CD ⊥3．一组样本数据删除一个数后，得到一组新数据：10，21，25，35，36，40.若这两组数据的中位数相等，则删除的数为（）A ．25B ．30C ．35D ．404．已知函数()22,3,,3,2x x x f x x f x -⎧+≤⎪=⎨⎛⎫> ⎪⎪⎝⎭⎩则2(log 9)f =（）A ．83B ．103C ．809D ．8295．设0x >，0y >，122y x+=，则1x y+的最小值为（）A ．32B ．C ．32+D ．36．若函数()e 2ax f x x =+有大于零的极值点，则实数a 的取值范围为（）A ．2a >-B ．12a >-C ．2a <-D ．12a <-7．设抛物线2:4C y x =的焦点为F ，C 的准线与x 轴交于点A ，过A 的直线与C 在第一象限的交点为M ，N ，且||3||FM FN =，则直线MN 的斜率为（）A ．2B ．12C D ．238．若cos α，πcos()6α-，πcos()3α+成等比数列，则sin 2α=（）A ．4B ．C ．13D ．14-二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9．已知双曲线222:1(0)4x y C b b-=>的右焦点为F ，直线:0+=l x by 是C 的一条渐近线，P 是l 上一点，则（）A ．C 的虚轴长为B ．CC ．PF 的最小值为2D ．直线PF 的斜率不等于10．已知1()5P A =，1(|)4P B A =.若随机事件A ，B 相互独立，则（）A ．1()3P B =B ．1()20=P AB C ．4(|)5=P A B D ．4(5+=P A B 11．已知函数()f x ，()g x 的定义域均为R ，()f x 的图象关于点(2，0)对称，(0)(2)1g g ==，()()()()++-=g x y g x y g x f y ，则（）A ．()f x 为偶函数B ．()g x 为偶函数C ．(1)(1)--=--+g x g x D ．(1)(1)g x g x -=+三、填空题：本题共3小题，每小题5分，共15分.12．设R m ∈，i 为虚数单位.若集合{1,2(1)i}=+-A m m ，{2i,1,2}=-B ，且A B ⊆，则m ＝.13．在ABC 中，AB =1AC =，M 为BC 的中点，60MAC ∠=︒，则AM =.14．若正四棱锥的棱长均为2，则以所有棱的中点为顶点的十面体的体积为，该十面体的外接球的表面积为.四、解答题：本题共5小题，共77分.解答时应写出文字说明、证明过程或演算步骤.15．甲公司推出一种新产品，为了解某地区消费者对新产品的满意度，从中随机调查了1000名消费者，得到下表：满意不满意男44060女46040(1)能否有95%的把握认为消费者对新产品的满意度与性别有关；(2)若用频率估计概率，从该地区消费者中随机选取3人，用X 表示不满意的人数，求X 的分布列与数学期望.附：22()()()()()n ad bc K a b c d a c b d -=++++，n a b c d =+++.2()P K k ≥0.10.050.01k2.7063.8416.63516．设函数()sin()(0,0π)f x x ωϕωϕ=+><<.已知()f x 的图象的两条相邻对称轴间的距离为π2，且π1(42-=-f .(1)若()f x 在区间()0,m 上有最大值无最小值，求实数m 的取值范围；(2)设l 为曲线()y f x =在π6x =-处的切线，证明：l 与曲线()y f x =有唯一的公共点.17．如图，边长为4的两个正三角形ABC ，BCD 所在平面互相垂直，E ，F 分别为BC ，CD 的中点，点G 在棱AD 上，2AG GD =，直线AB 与平面EFG 相交于点H .(1)从下面两个结论中选一个证明：①//BD GH ；②直线HE ，GF ，AC 相交于一点；注：若两个问题均作答，则按第一个计分.(2)求直线BD 与平面EFG 的距离.18．已知数列{}n a 的前n 项和为n S ，14+=-n n n S a a ，11a =-.(1)证明：数列1{2}n n a a +-为等比数列；(2)设4(1)+=+n n a b n n ，求数列{}n b 的前n 项和；(3)是否存在正整数p ，q （6<<p q ），使得p S ，6S ，q S 成等差数列？若存在，求p ，q ；若不存在，说明理由.19．在平面直角坐标系xOy 中，已知椭圆Γ：22221(0)x y a b a b +=>>，直线l 与Γ相切，与圆O ：2223+=x y a 相交于A ，B 两点.当l 垂直于x 轴时，||AB =(1)求Γ的方程；(2)对于给定的点集M ，N ，若M 中的每个点在N 中都存在距离最小的点，且所有最小距离的最大值存在，则记此最大值为,()d M N .（ⅰ）若M ，N 分别为线段AB 与圆O 上任意一点，P 为圆O 上一点，当PAB 的面积最大时，求,()d M N ；（ⅱ）若,()d M N ，(,)d N M 均存在，记两者中的较大者为(,)H M N .已知(,)H X Y ，(,)H Y Z ，(,)H X Z 均存在，证明：(,)(,)(,)≥+H X Z H Y Z H X Y .1．A 【分析】根据数量积的运算律整理式子，结合数量积的定义，可得答案.【详解】()221221221221222cos1202122e e e e e e e e e ⎛⎫-⋅=⋅-=-=⨯--=- ⎪⎝⎭.故选：A.2．D 【分析】建立空间直角坐标系对选项一一判断即可得出答案.【详解】以D 为坐标原点，建立如图所示的空间直角坐标系，所以()()()()1,0,0,0,0,0,1,1,0,0,1,0A D B C ，()()()()11111,0,1,0,0,1,1,1,1,0,1,1A D B C ，()()11,0,0,1,0,1AD B C =-=-- ，()()11,0,1,1,1,0A D BD =----，()()()1111,1,1,1,1,1,0,1,1AC AC CD =-=--=- 对于A ，()11110AD B C ⋅=-⨯-=≠，故A 错误；对于B ，()11110A D BD ⋅=-⨯-=≠，故B 错误；对于C ，()()1111111110AC AC ⋅=-⨯-+⨯+⨯-=≠，故C 错误；对于D ，()()111011110AC CD ⋅=-⨯+⨯-+⨯-=，故D 正确.故选：D.3．B 【分析】根据给定条件，利用中位数的定义求解即得.【详解】依题意，新数据组有6个数，其中位数是2535302+=，显然原数据组有7个数，因此删除的数是中位数30.故选：B 4．B 【分析】由已知函数解析式，结合对数恒等式即可求解．【详解】由于2log 93>，所以22log 3222log 311110(log 9)(log 9)(log 3)232332f f f ===+=+=，故选：B 5．C 【分析】由不等式“1”的代换求解即可.【详解】因为122y x+=，所以112y x+=，因为0x >，0y >，所以111111222x x y xy y y xxy ⎛⎫⎛⎫+=++=+++ ⎪⎪⎝⎭⎝⎭3133322222222xy xy +=++≥++⨯=.当且仅当12112xy xy y x⎧=⎪⎪⎨⎪+=⎪⎩，即x y ⎧=⎪⎨⎪=⎩时取等.故选：C.6．C 【分析】求出函数的导数，求出极值点，利用极值点大于0，求出a 的范围．【详解】函数()e 2ax f x x =+，可得()e 2axf x a '=+，若()0,0a f x '≥>，此时()f x '单调递增，无极值点，故a<0，令()e 20axf x a '=+=，解得12ln()x a a=-，当12ln()x a a >-时，()0f x ¢>，当12ln()x a a<-时，()0f x '<，故12ln()x aa=-是()e 2ax f x x =+的极值点由于函数()e 2ax f x x =+有大于零的极值点，∴1222ln()0ln(001a a a a->⇒-<⇒<-<，解得2a <-．故选：C ．7．A 【分析】根据题意可设MN 直线方程为()1,0y k x k =+>，联立直线与抛物线方程，通过根与系数的关系及抛物线的焦半径公式，建立方程，即可求解，【详解】根据题意可得抛物线2:4C y x =的焦点(1,0)F ，准线方程为=1x -，则有(1,0)A -，设MN 直线方程为()1,0y k x k =+>，联立2(1)4y k x y x=+⎧⎨=⎩，可得()222240k x k x k +-+=，则()()()2222Δ24416110k k k k k =--⋅=--+>，得11k -<<，故01k <<，设()()112221,,,,0M x y N x y x x <<，21212242,1k x x x x k -+==，M 到准线距离为MM '，N 到准线距离为NN '，又||3||FM FN =，有3MM NN '='，即()12131x x +=+，得1223x x =+，()1222231x x x x ∴=+=，又210x x <<，解得211,33x x ==，212242133k x x k -∴+==+，又0k >，解得k =故选：A8．B 【分析】利用等比中项，结合三角恒等变换求解即得.【详解】由cos α，πcos()6α-，πcos(3α+成等比数列，得2co ππcos (cos(s 63ααα-=+，即1π111cos 2[1cos(2)]cos (cos )sin 22322224αααααα++-=-=⋅-，1111cos 22cos 2sin 2244444αααα++=+-，所以sin 2α=故选：B 【点睛】思路点睛：三角函数是以角为自变量的函数，因此解三角函数题，首先从角进行分析，善于用已知角表示所求角，即注重角的变换.角的变换涉及诱导公式、同角三角函数基本关系、两角和与差的公式、二倍角公式、配角公式等，选用恰当的公式是解决三角问题的关键，明确角的范围，对开方时正负取舍是解题正确的保证.9．AD 【分析】根据给定条件，求出双曲线的渐近线方程，求出b ，再逐项判断即得.【详解】双曲线222:14x y C b-=的渐近线方程为20bx y ±=，依题意，12b b -=-，解得b =，对于A ，C 的虚轴长2b =A 正确；对于B ，C 的离心率2e a ==，B 错误；对于C ，点F 到直线:0l x ==，即PF ，C错误；对于D ，直线:0l x =的斜率为2，而点F 不在l 上，点P 在l 上，则直线PF 的斜率不等于2，D 正确.故选：AD 10．BCD 【分析】根据条件概率公式和独立事件乘法公式即可判断ABC ，再根据()()()()P A B P A P B P AB +=+-即可判断D.【详解】对B ，()()11(),()1()4205P AB P AB P B A P AB P A ===∴=∣，B 正确；对A ，1()()()()5P AB P A P B P B ==，1()4P B ∴=，A 错误；对C ，411()()()545P AB P A P B ==⨯=，1()45()1()54P AB P AB P B ===∣，C 正确；对D ，()()()()P A B P A P B P AB +=+-()13134()()()54545P A P B P A P B =+-=+-⨯=，D 正确.故选：BCD.11．ACD 【分析】由赋值法，函数奇偶性，对称性对选项一一判断即可得出答案.【详解】令y y =-，则()()()()g x y g x y g x f y -++=-，注意到()g x 不恒为0，故()()f y f y =-，故A 正确；因为()f x 的图象关于点(2，0)对称，所以(2)0f =，令0,2x y ==，得(2)(2)(0)(2)0g g g f +-==，故()(2)12g g -=-≠，故B 错误；令1x y ==-，得(2)(0)(1)(1)0g g g f -+=--=，令1x y ==，得(2)(0)(1)(1)2g g g f +==，故(1),(1)0g f ≠，从而(1)0f -≠，故(1)0g -=,令=1x -，得(1)(1)0g y g y -++--=，化简得(1)(1)g y g y --=--+，故C 正确；令2y =，得(2)(2)0g x g x ++-=，而()(1)(3)1g x g x g x -=--=+，故D 正确.故选：ACD.【点睛】方法点睛：抽象函数的对称性常有以下结论（1）()()()f x a f b x f x +=-⇒关于2a bx +=轴对称，（2）()()()2f x a f b x c f x ++-=⇒关于,2a b c +⎛⎫⎪⎝⎭中心对称，12．1【分析】由集合的包含关系得两个集合中元素的关系，由复数的相等解m 的值.【详解】集合{1,2(1)i}=+-A m m ，{2i,1,2}=-B ，且A B ⊆，则有2(1)i 2i m m +-=-或2(1)i 2m m +-=，解得1m =.故答案为：113．32【分析】根据给定条件，取AC 的中点N ，利用余弦定理求解即得.【详解】在ABC 中，取AC 的中点N ，连接MN ，由M 为BC 的中点，得1722MN AB ==，在AMN 中，由余弦定理得2222cos MN AM AN AM AN CAM =+-⋅∠，则2711442AM AM =+-，即213022AM AM --=，而0AM >，所以32AM =.故答案为：3214．5265264π【分析】根据给定条件，利用割补法，结合锥体体积公式计算体积；建立空间直角坐标系，求出外接球半径即可求出表面积.【详解】正四棱锥P ABCD -的所有棱长为2，点,,,,,,,A B C D E F M N ''''是所在棱的中点，如图，显然2228PB PD BD +==，即有PB PD ⊥，则正四棱锥P ABCD -于是114133326P ABCD P A B C D V V ''''--=⨯==⨯⨯=，11112,2AMN S A '=⨯⨯= 到平面AMN的距离11223221A AMN d V '-==⨯⨯=，所以所求十面体的体积为4361264P ABCD P A B C D A AMN V V V V '''''---=----⨯==；令AC BD O = ，以直线,,OA OB OP 分别为,,x y z轴建立空间直角坐标系，如图，则(0,0,(0,(0,),0,A P B D，则A B ''，((,,0)2222M N -，设外接球球心(,,)O x y z '，半径R ，则O A R O B R O M R O N R =⎧⎪=⎪⎨=⎪⎪=''''⎩''，因此2222222222222222()()22()()22()()22()()22x y z R x y z R x y z R x y z R ⎧-++-=⎪⎪⎪+-+-=⎪⎪⎨⎪-+-+=⎪⎪⎪-+++=⎪⎩，解得20001x y z R =⎧⎪=⎪⎨=⎪⎪=⎩，所以十面体的外接球的表面积为4πS =.4π【点睛】关键点睛：求几何体的体积，将给定的几何体进行恰当的分割，转化为可求体积的几何体求解是关键.15．(1)有95%的把握认为消费者对新产品的满意度与性别有关(2)分布列见解析，期望3()10E X =【分析】（1）先利用所给数据表完善22⨯列联表，再利用2K 公式求出2K ，利用临界值表进行判定；（2）先求出不满意的概率为110，由二项分布求解概率，列表得到分布列，利用期望公式进行求解..【详解】（1）补全22⨯列联表如图所示：满意不满意总计男44060500女46040500总计9001001000221000(4404046060)40 4.444 3.8415005009001009K ⨯⨯-⨯==≈>⨯⨯⨯，故有95%的把握认为消费者对新产品的满意度与性别有关．（2）由题知，从该地区的消费者中随机抽取1人，不满意的概率为110，X 的所有可能取值为0，1，2，3，且3123972991243(0)(),(1)C ()10100010101000P X P X =====⨯=．2233912711(2)C (),(3)()10101000101000P X P X ==⨯⨯====，所以X 的分布列为：X0123P 7291000243100027100011000所以7292432713()0123100010001000100010E X =⨯+⨯+⨯+⨯=．16．(1)π7π1212m <≤(2)证明见解析【分析】（1）根据周期以及π1()42-=-f 可求解()πsin 23f x x ⎛⎫=+ ⎪⎝⎭，进而根据整体法即可求解，（2）求导，根据点斜式求解切线方程，进而构造函数()ππ2sin 263g x x x ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭，利用导数判断函数的单调性，即可求解.【详解】（1）由题意可得周期2ππ22T ω==⨯，故2ω=，ππ11()sin cos cos 4222f ϕϕϕ⎛⎫-=-+=-=-⇒= ⎪⎝⎭，由于()0,πϕ∈，故π3ϕ=，故()πsin 23f x x ⎛⎫=+ ⎪⎝⎭，当()0,x m ∈时，πππ2,2333x m ⎛⎫+∈+ ⎪⎝⎭，由于()f x 在区间()0,m 上有最大值无最小值，故ππ3π2232m <+≤，解得π7π1212m <≤，故π7π1212m <≤（2）()π2cos 23f x x ⎛⎫=+ ⎪⎝⎭'，πππ2cos 2633f ⎛⎫⎛⎫-=-+= ⎪ ⎝'⎪⎝⎭⎭，πππsin 0633f ⎛⎫⎛⎫-=-+= ⎪ ⎪⎝⎭⎝⎭，故直线l 方程为π26y x ⎛⎫=+ ⎪⎝⎭，令()ππ2sin 263g x x x ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭，则π()22cos 203g x x ⎛⎫=-+ '≥⎪⎝⎭，故()g x 在定义域内单调递增，又π06g ⎛⎫-= ⎪⎝⎭，因此()g x 有唯一的的零点π6-，故l 与曲线()y f x =有唯一的交点，得证.17．(1)证明见解析；【分析】（1）选择条件①，利用线面平行的判定性质推理即得；选择条件②，利用平面的基本事实推理即得.（2）以点E 为原点，建立空间直角坐标系，利用点到平面距离公式求解即得.【详解】（1）选择条件①，由E ,F 分别为BC ,CD 的中点，得//EF BD ，又BD ⊄平面,EFG EF ⊂平面EFG ，则//BD 平面EFG ，又BD ⊂平面ABD ，平面ABD ⋂平面EFG GH =，所以//BD GH .选择条件②，在ACD 中，2,AG GD F =为CD 中点，则GF 与AC 不平行，设GF AC K = ，则,K AC K GF ∈∈，又AC ⊂平面,ABC FG ⊂平面EFG ，于是K ∈平面,ABC K ∈平面EFG ，又平面ABC ⋂平面EFG HE =，因此K HE ∈，所以HE ,GF ,AC 相交于一点.（2）若第（1）问中选①，由（1）知，//BD 平面EFG ，则点B 到平面EFG 的距离即为BD 与平面EFG 的距离，若第（1）问中选②，由E ,F 分别为BC ,CD 的中点，则//EF BD ，又BD ⊄平面,EFG EF ⊂平面EFG ，于是//BD 平面EFG ，因此点B 到平面EFG 的距离即为BD 与平面EFG 的距离，连接EA ,ED ，由,ABC BCD 均为正三角形，E 为BC 的中点，得,EA BC ED BC ⊥⊥，又平面ABC ⊥平面BCD ，平面ABC ⋂平面,BCD BC AE =⊂平面ABC ，于是⊥AE 平面BCD ，又ED ⊂平面BCD ，则EA ED ⊥，以点E 为原点，直线,,EB ED EA 分别为,,x y z 轴建立空间直角坐标系，则(2,0,0),((0,33B F G -，(2,0,0),(1,EB EF ==-,(0,)33EG = ，设平面EFG 的一个法向量为(,,)n x y z = ,则0033EF n x EG n y ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，令1y =，得2)n =- ，设点B 到平面EFG 的距离为d ，则||||EB n d n ⋅== ，所以BD 与平面EFG 的距离为2.18．(1)证明见解析；(2)31182(1)n n +-+；(3)存在，5,8p q ==.【分析】（1）利用给定的递推公式，结合1,2n n n a S S n -=-≥及等比数列定义推理即得.（2）由（1）求出,n n a b ，再利用裂项相消法求和即可.（3）由（1）求出n S ，由已知建立等式，验证计算出p ，再分析求解q 即可.【详解】（1）N n *∈，14+=-n n n S a a ，当2n ≥时，114n n n S a a --=-，两式相减得1144n n n n n a a a a a -+=--+，即1144n n n a a a +-=-，则有11()222n n n n a a a a +--=-，当1n =时，1124S a a =-，则20a =，即21210a a -=≠，所以数列{}12n n a a +-是以1为首项，12为公比的等比数列.（2）由（1）得，11122n n n a a +--=，则11221n n n n a a -+-=，数列1{2}n n a -是等差数列，于是122n n a n -=-，解得122n n n a --=，则312111[]2(1)822(1)n n n n n b n n n n +-+==-++，所以{}n b 的前n 项和21311111111[(1()()]822222322(1)82(1)n n n n T n n n -+=-+-++-=-⨯⨯⨯++ .（3）由（1）知，11214222n n n n n n n S ----=-⨯=-，由6,,p q S S S 成等差数列，得51112222p q p q ---=--，整理得32216p q p q +=，由32216p q p q +=，得3216p p <，又*16,N p p ≤<∈，23412343222216=>>>，5p =不等式成立，因此5332216q q +=，即1232q q =，令2n n n d =，则11102n n n n d d ++--=≤,从而12345d d d d d =>>>> ，显然8132d =，即8q =，所以存在5,8p q ==，使得6,,p q S S S 成等差数列.【点睛】易错点睛：裂项法求和，要注意正负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消去的项，未被消去的项有前后对称的特点，实质上造成正负相消是此法的根源与目的．19．(1)2213x y +=；(2)（ⅰ）32；（ⅱ）证明见解析.【分析】（1）根据给定条件，求出a ，再结合离心率求出b 即得.（2）（ⅰ）在直线l 的斜率存在时，设出直线方程并与椭圆方程联立，借助判别式求出圆心O 到l 距离，列出PAB 的面积关系求解，再验证斜率不存在的情况；（ⅱ）利用新定义，结合对称性推理即得.【详解】（1）因为当l 垂直于x 轴时，||AB =:l x a =±与Γ相切，则=a =又椭圆ΓΓ的半焦距c 1b ==，所以Γ的方程为2213x y +=.（2）（i ）当l 的斜率存在时，设l 的方程为：y kx m =+，由2233y kx m x y =+⎧⎨+=⎩消去y 得：222(31)6330k x kmx m +++-=，由直线l 与椭圆Γ相切，得222(6)4(31)(33)0km k m ∆=-+-=，整理得2231m k =+，于是圆心O 到直线l 的距离[1,3)d =∈，则PAB 的面积为11(3)||(3)22PAB S d AB d ≤+⋅=+⋅设3()(3)(3),1f d d d d =-+≤<，求导得2()2(3)(32)f d d d '=+-，当312d ≤<时，()0f d '>，函数()f d 单调递增，当32d <<时，()0f d '<，函数()f d 单调递减，因此当32d =时，()f d 取得最大值，此时max ()4PAB S = ，当l 的斜率不存在时，由（1）知，13)2S ≤⨯⨯由221157016-+=->->>32d =.对于线段AB 上任意点E ，连接OE 并延长与圆O 交于点F ，则F 是圆上与E 最近的点，当E 为线段AB 的中点时，EF 取得最大值32，所以3(,)2d M N =.（ii ）因为(,),(,),(,)H X Y H Y Z H X Z 均存在，设点121212,,,,,X X X Y Y Y Z Z Z ∈∈∈，且111222(,),(,),(,)H X Z X Z H Y Z Y Z H X Y X Y ===，设2Y 是集合Y 中到2X 的最近点，根据对称性，不妨设22(,)(,)H X Y d X Y X Y ==，令点2X 到集合Z 的最近点为3Z ，点3Z 到集合Y 的最近点为3Y ，因为11X Z 是集合X 中所有点到集合Z 最近点距离的最大值，则1123X Z X Z ≥，因为12Y Z 是集合Y 中所有点到集合Z 最近点距离的最大值，则1233Y Z Y Z ≥，因此11122333(,)(,)H X Z H Y Z X Z Y Z X Z Y Z +=+≥+，而在坐标平面中，233323X Z Y Z X Y +≥，又点2Y 是集合Y 中到点2X 的最近点，则2322X Y X Y ≥，所以(,)(,)(,)≥+H X Z H Y Z H X Y .【点睛】关键点睛：本题第（2）问涉及新定义问题，反复认真读题，理解最小距离的最大值的含义是解题的关键.。

2015南通三模数学学科参考答案及评分建议 (2)

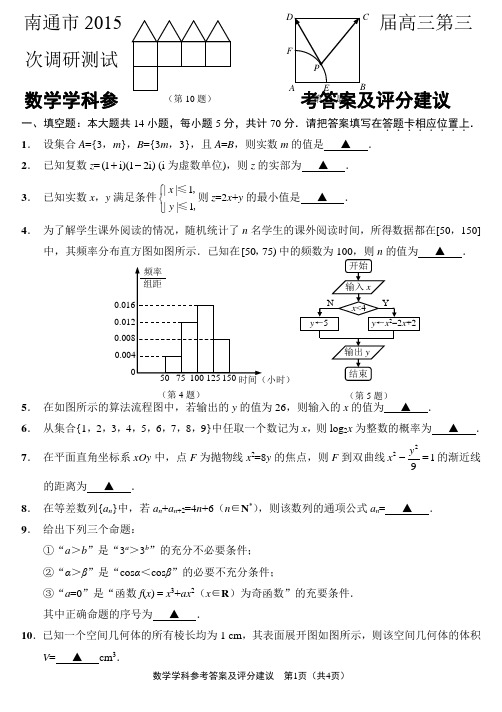
（第10题）C（第11题）（第5题）（第4题）南通市2015届高三第三次调研测试数学学科参考答案及评分建议一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1．设集合A ={3，m }，B ={3m ，3}，且A =B ，则实数m 的值是 ▲ ． 2．已知复数z =(1i)(12i)+-(i 为虚数单位)，则z 的实部为 ▲ ． 3．已知实数x ，y 满足条件||1||1x y ⎧⎨⎩≤≤,,则z =2x +y 的最小值是 ▲ ．4．为了解学生课外阅读的情况，随机统计了n 名学生的课外阅读时间，所得数据都在[50，150]中，其频率分布直方图如图所示．已知在[50 75)，5．在如图所示的算法流程图中，若输出的y 的值为26，则输入的x 的值为 ▲ ．6．从集合{1，2，3，4，5，6，7，8，9}中任取一个数记为x ，则log 2x 为整数的概率为 ▲ ．7．在平面直角坐标系xOy 中，点F 为抛物线x 2=8y 的焦点，则F 到双曲线2219y x -=的渐近线的距离为 ▲ ．8．在等差数列{a n }中，若a n +a n +2=4n +6（n ∈N *），则该数列的通项公式a n = ▲ ． 9．给出下列三个命题： ①“a ＞b ”是“3a ＞3b ”的充分不必要条件； ②“α＞β”是“cos α＜cos β”的必要不充分条件；③“a =0”是“函数f (x ) = x 3+ax 2（x ∈R ）为奇函数”的充要条件．其中正确命题的序号为 ▲ ．10．已知一个空间几何体的所有棱长均为1 cm ，其表面展开图如图所示，则该空间几何体的体积V = ▲ cm 3．11．如图，已知正方形ABCD 的边长为2，点E 为AB 的中点．以A 为圆心，AE 为半径，作弧交AD 于点F ．若P 为劣弧EF 上的动点，则PC PD 的最小值为 ▲ ．12．已知函数322301()5 1x x m x f x mx x ⎧++=⎨+⎩≤≤，，，＞.若函数f (x )的图象与x 轴有且只有两个不同的交点，则实数m 的取值范围为 ▲ ．13．在平面直角坐标系xOy 中，过点P （-5，a ）作圆x 2+y 2-2ax +2y -1=0的两条切线，切点分别为M (x 1，y 1)，N (x 2，y 2)，且2112211220y y x x x x y y -+-+=-+，则实数a 的值为 ▲ ． 14．已知正实数x ，y 满足24310x y x y+++=，则xy 的取值范围为 ▲ ．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域．．．．．．．内作答．解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）如图，在三棱柱ABC -A 1B 1C 1中，B 1C ⊥AB ，侧面BCC 1B 1为菱形．（1）求证：平面ABC 1⊥平面BCC 1B 1；（2）如果点D ，E 分别为A 1C 1，BB 1的中点，求证：DE ∥平面ABC 1．1（第15题）已知函数()sin()f x A x ωϕ=+（其中A ，ω，ϕ为常数，且A ＞0，ω＞0，22ϕππ-＜＜）的部分图象如图所示．（1）求函数f (x )的解析式；（2）若3()2f α=，求sin(2)6απ+的值．17．（本小题满分14分）如图，在平面直角坐标系xOy 中，椭圆22221x y a b+=(a ＞b ＞0)的两焦点分别为F 1(0)，F 20)，且经过点12)．（1）求椭圆的方程及离心率；（2）设点B ，C ，D 是椭圆上不同于椭圆顶点的三点，点B 与点D 关于原点O 对称．设直线CD ，CB ，OB ，OC 的斜率分别为k 1，k 2，k 3，k 4，且k 1k 2=k 3k 4． ①求k 1k 2的值； ②求OB 2+OC 2的值．（第17题）为丰富市民的文化生活，市政府计划在一块半径为200 m ，圆心角为120°的扇形地上建造市民广场．规划设计如图：内接梯形ABCD 区域为运动休闲区，其中A ，B 分别在半径OP ，OQ 上，C ，D 在圆弧PQ 上，CD ∥AB ；△OAB 区域为文化展示区，AB长为m ；其余空地为绿化区域，且CD 长不得超过．．．．200 m ．（1）试确定A ，B 的位置，使△OAB 的周长最大？（2）当△OAB 的周长最大时，设∠DOC =2θ，试将运动休闲区ABCD 的面积S 表示为θ的函数，并求出S 的最大值．19．（本小题满分16分）已知数列{a n }，{b n }中，a 1=1，22111(1)n n n n a b a a ++=-⋅，n ∈N *，数列{b n }的前n 项和为S n ．（1）若12n n a -=，求S n ；20．（本小题满分16分）已知函数1()ln f x a x x=--（a ∈R ）．（1）若a =2，求函数()f x 在(1，e 2)上的零点个数（e 为自然对数的底数）；BCDQ（第18题）O。

江苏省南通市市直中学2015届高三年级调研测试数学试题

江苏省南通市市直中学2015届高三年级调研测试数学试题一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位置上．．．．．．．．． 1．已知集合A ={－2，－1}，B ={－1，2，3}，则A B = ▲ ．2．若复数z 满足(1i)2i z +=，则复数z = ▲ ． 3．抛物线24y x =的焦点坐标为 ▲ ．4．函数22()cos sin f x x x =-的最小正周期为 ▲ ．5．从1，2，3，4这四个数中一次随机取两个数，则两个数的和是奇数的概率为 ▲ ． 6．某大学共有学生5600人，其中专科生1300人，本科生3000人，研究生1300人，现采用分层抽样的方法，抽取容量为280的样本，则抽取的本科生人数为 ▲ ． 7．如图所示的算法中，输出的结果是 ▲ ．8．若直线y x m =+与曲线ln y x =相切，则实数m 的值为 ▲ ．9．如图，各条棱长均为2的正三棱柱111ABC A B C -中，M 为11AC 的中点，则三棱锥1M AB C -的体积为 ▲ ．110．已知圆22:24200C x y x y +---=，直线l 过点P （3，1），则当直线l 被圆C 截得的弦长最短时，直线l 的方程为 ▲ ．11．已知等比数列{}n a 的前n 项和为n S ，且1324412a a a a S +=++=，，则数列{}n a 的公比q为 ▲ ．12．已知△ABC 中，∠C =90°，34CA CB ==，，D E 、分别为边CA CB 、上的点，且6BD CA ⋅=，8A E C B ⋅=，则AE BD ⋅= ▲ ．13．已知函数23 1 ()xa x f x x a x ⎧+>⎪=⎨+⎪⎩≤，，，1，若()f x 在R 上为增函数，则实数a 的取值范围是 ▲ ． 14．已知00x y >>，，且满足18102y x x y+++=，则2x y +的最大值为 ▲ ．二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答．解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）已知在△ABC 中，sin()2sin()A B A B +=-．（1）若π6B =，求A ；（2）若tan 2A =，求tan B 的值．16．（本小题满分14分）如图，在四棱锥P ABCD -中，底面ABCD 是矩形，PA CD ⊥．（1）求证：直线//AB 平面PCD ；（2）求证：平面PAD ⊥平面PCD ．17．（本小题满分14分）如图，海平面某区域内有A 、B 、C 三座小岛（视小岛为点），岛C 在A 的北偏东70°方向，岛B 在C 的南偏西40°方向，岛B 在A 的南偏东65°方向，且A 、B 两岛间的距离为3 n mile ．求A 、C 两岛间的距离．18．（本小题满分16分）已知椭圆222:1(2x y C a a +=（1）求椭圆C 的方程；（2）若P 是椭圆C 上任意一点，Q 为圆22:(2)1E x y +-=上任意一点，求PQ 的最大值．19．（本小题满分16分）已知无穷数列{}n a 满足：11a =，2132a a a =+，且对于任意*n ∈N ，都有0n a >，2124n n n a a a ++=+．（1）求234,,a a a 的值；（2）求数列{}n a 的通项公式．20．（本小题满分16分）已知函数()e x f x c =-，3211()(,,).32g x ax bx cx a b c =++∈R（1）若0ac <，求证：函数()y g x =有极值；（2）若0a b ==，且函数()y f x =与()y g x =的图象有两个相异交点，求证： 1.c >南通市市直中学高三年级调研测试数学参考答案与评分标准一、填空题：本大题共14小题，每小题5分，共70分． 1．{2,1,2,3--} 2．1i +3．(1,0)4．π5．236．150 7．11 8．1-9 10．250x y --= 11．1312．14- 13．[1,2]- 14．18二、解答题：本大题共6小题，共90分．15．解:（1）由条件，得 ππsin()2sin()66A A +=-．11cos cos )22A A A A +=-． …………………………………………3分化简，得 s i n c o s A A ．tan A ∴=6分又(0,π)A ∈， π3A ∴=． ………………………………………………………………7分（2）sin()2sin()A B A B +=-，sin cos cos sin 2(sin cos cos sin )A B A B A B A B ∴+=-．化简，得 3c o s s i n s i n c o AB A B =．…………………………………………………11分又 c o s c o s 0A B ≠，tan 3tan A B ∴=．又tan 2A =，2tan 3B ∴=．……………………………………………………………………………14分16．（1）证明:∵ABCD 为矩形，∴//AB CD ． ………………………………………………2分又DC ⊂面PDC ，AB ⊄面PDC ，……………………………………………………4分 ∴//AB 面PDC ． ……………………………………………………………………7分（2）证明: ∵ABCD 为矩形, ∴CD AD ⊥, ……………………………………………9分又P A ⊥CD ,PAAD A =， PA AD ⊂，平面PAD ,∴CD ⊥平面PAD ． …………………………………………………………………11分又CD ⊂面PDC ,∴面PAD ⊥面PCD ． ………………………………………14分17．解：由题意可知45,30CAB ACB ∠=∠=． …………………………………………………4分则105ABC ∠=． …………………………………………………………………………6分在三角形ABC 中，由正弦定理可得 sin30sin105AB AC=． ………………………………………………………………………8分 ∴ 6sin105AC = 6s i n (6045)=+6(sin60cos45cos60sin 45)=+6=3)2=． …………………………………………………………………12分答：A 、C 两岛间的距离为32 n mile ． …………………………………………14分18．解：（1）由题设知e =， ∴2222222226293c a b a e a a a --=====． …………………………………………………3分解得26a =．∴椭圆C 的方程为22162x y +=． ……………………………………………………6分（2）圆22:(2)1E x y +-=的圆心为(0,2)E ，点Q 在圆E 上，∴1PQ EP EQ EP +=+≤（当且仅当直线PQ 过点E 时取等号）．……………………9分设00(,)P x y 是椭圆C 上的任意一点，则2200162x y +=，即220063x y =-． ∴2222000=+(2)2(1)12EP x y y -=-++． ………………………………………………13分因为0y ⎡∈⎣，所以当01y =-时，2EP 取得最大值12，即1PQ ≤.所以PQ 的最大值为． …………………………………………………………16分19．解：（1）由条件，*212,4n n n n a a a ++∀∈=+N ，令1n =，得22134a a a +=． …………………………………………………………2分又2132a a a =+，且11a =，易求得233,5a a ==． ……………………………4分再令2n =，得23244a a a +=，求得47a =． …………………………………………6分（2）∵2124n n n a a a ++=+ (1) ∴22134+++=+n n n a a a (2) 由(1)-(2)得，2212213(4)(4)n n n n n n a a a a a a +++++-=+-+ 213n n n n a a a a +++=- ……………………………………………8分∴2211322n n n n n n a a a a a a ++++++=+ ∴11322()()n n n n n n a a a a a a ++++++=+ ∴21312n n n n n n a a a a a a +++++++=，∴数列21n n n a a a ++⎧⎫+⎨⎬⎩⎭为常数数列． ………………………12分 ∴21n n n a a a +++=1322.a a a += ∴212.n n n a a a +++= ∴数列{}n a 为等差数列． ……………………………………………………………14分又公差212d a a =-=， ∴21n a n =-．……………………………………………16分20．解：（1）由3211()32g x ax bx cx =++得2(),g x ax bx c '=++∵0ac <，∴2=40b ac ∆->且0a ≠． …………………………………………4分 ∴函数()g x '有两个零点，则可设为()=()()()g x a x x αβαβ'--<， ∴若123x x x αβ<<<<，则1223()()0()()0g x g x g x g x ''''⋅<⋅<，．∴()g x 有极值． ……………………………………………………………………6分（2）由e x c cx -=，得e 0x cx c --=，记()e x h x cx c =--，则()e x h x c '=-，由函数()y f x =与()y g x =的图象有两个相异交点知函数()h x 有两互异零点…9分若0()0,()c h x h x '⇒>≤单调递增，则()h x 最多1个零点，矛盾． …………11分 ∴0c >．此时，令()0h x '=，则ln x c =．列表：∴min ()(ln )ln 0h x h c c c ==-<， ∴1c >．………………………………………16分。

南通市高三第二次调研测试数学.docx

I ← 1While I < 7 S ← 2 I + 1 I ← I + 2 End While Print S（第4题）南通市2015届高三第二次调研测试数学学科参考答案及评分建议一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位．．．．．．置上．．． 1．命题“x ∃∈R ，20x >”的否定是“ ▲ ”．【答案】x ∀∈R ，20x ≤2．设1i i 1ia b +=+-(i 为虚数单位，a ，b ∈R )，则ab 的值为 ▲ ．【答案】03．设集合{}11 0 3 2A =-，，，，{}2 1B x x =≥，则A B = ▲ ．【答案】{}1 3-，4．执行如图所示的伪代码，则输出的结果为 ▲ ．【答案】115．一种水稻试验品种连续5年的平均单位面积产量(单位：t/hm 2) 如下：9.8，9.9，10.1，10，10.2，则该组数据的方差为 ▲ ．【答案】0.026．若函数()π()2sin 3f x x ω=+(0)ω>的图象与x 轴相邻两个交点间的距离为2，则实数ω的值为 ▲ ．【答案】π2BDC（第12题）A7．在平面直角坐标系xOy 中，若曲线ln y x =在e x =(e 为自然对数的底数)处的切线与直线30ax y -+=垂直，则实数a 的值为 ▲ ．【答案】e -8．如图，在长方体1111ABCD A B C D -中，AB =3 cm ，AD =2 cm ，1AA =1 cm ，则三棱锥11B ABD -的体积为 ▲ cm 3．【答案】19．已知等差数列{}n a 的首项为4，公差为2，前n 项和为n S ．若544k k S a +-=(k *∈N )，则k 的值为 ▲ ．【答案】710．设32()4(3)f x x mx m x n =++-+(m n ∈R ，)是R 上的单调增函数，则m 的值为 ▲ ．【答案】611．在平行四边形ABCD 中，AC AD AC BD ⋅=⋅3=，则线段AC 的长为 ▲ ．【答案】312．如图，在△ABC 中，3AB =，2AC =，4BC =，点D 在边BC 上，BAD ∠=45°，则tan CAD ∠的值为 ▲ ．【答案】8157+13．设x ，y ，z 均为大于1的实数，且z 为x 和y 的等比中项，则lg lg 4lg lg z zx y+的最小值为 ▲ ．【答案】9814．在平面直角坐标系xOy 中，圆1C ：22(1)(6)25x y ++-=，圆2C ：222(17)(30)x y r -+-=．若圆2C 上存在一点P ，使得过点P 可作一条射线与圆1C 依次交于点A ，B ，满足2PA AB =，则半径r 的取值范围是 ▲ ．AA 1 B不C不B 1不C 1不D 1不D不（第8题）A BC DMNQ（第15题）【答案】[]5 55，二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答. 解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）如图，在四面体ABCD 中，平面BAD ⊥平面CAD ，BAD ∠=90°．M ，N ，Q 分别为棱AD ，BD ，AC 的中点．（1）求证：//CD 平面MNQ ；（2）求证：平面MNQ ⊥平面CAD ．证明：（1）因为M ，Q 分别为棱AD ，AC 的中点，所以//MQ CD ， …… 2分又CD ⊄平面MNQ ，MQ ⊂平面MNQ ，故//CD 平面M． …… 6分（2）因为M ，N 分别为棱AD ，BD 的中点，所以//MN AB ，又90BAD ∠=°，故M ⊥． …… 8分因为平面BAD ⊥平面CAD ，平面BAD平面CAD AD =，且MN ⊂平面ABD ，所以MN ⊥平面ACD ． …… 11分又MN ⊂平面MNQ ，平面M ⊥平面C． …… 14分（注：若使用真命题“如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面”证明“MN ⊥平面ACD ”，扣1分．）16．（本小题满分14分）体育测试成绩分为四个等级：优、良、中、不及格．某班50名学生参加测试的结果如下：（1）从该班任意抽取1名学生，求这名学生的测试成绩为“良”或“中”的概率；（2）测试成绩为“优”的3名男生记为1a ，2a ，3a ，2名女生记为1b ，2b ．现从这5人中任选2人参加学校的某项体育比赛． ① 写出所有等可能的基本事件； ② 求参赛学生中恰有1名女生的概率．解：（1）记“测试成绩为良或中”为事件A ，“测试成绩为良”为事件1A ，“测试成绩为中”为事件2A ，事件1A ，2A 是互斥的. …… 2分由已知，有121923()()5050P A P A ==，． …… 4分因为当事件1A ，2A 之一发生时，事件A 发生，所以由互斥事件的概率公式，得1212192321()()()()505025P A P A A P A P A =+=+=+=． …… 6分（2）① 有10个基本事件：12()a a ，，13()a a ，，11()a b ，，12()a b ，，23()a a ，，21()a b ，，22()a b ，，31()a b ，，32()a b ，，12()b b ，．…… 9分② 记“参赛学生中恰好有1名女生”为事件B ．在上述等可能的10个基本事件中，等级优良中不及格人数519233事件B 包含了11()a b ，，12()a b ，，21()a b ，，22()a b ，，31()a b ，，32()a b ，．故所求的概率为63()105P B ==．答：（1）这名学生的测试成绩为“良”或“中”的概率为2125；（2）参赛学生中恰有1名女生的概率为35． ……14分（注：不指明互斥事件扣1分；不记事件扣1分，不重复扣分；不答扣1分．事件B 包含的6种基本事件不枚举、运算结果未化简本次阅卷不扣分．）17．（本小题满分14分）在平面直角坐标系xOy 中，已知向量=a (1，0)，=b (0，2).设向量=+x a (1cos θ-)b ， k =-y a 1sin θ+b ，其中0πθ<<.（1）若4k =，π6θ=，求x ⋅y 的值；（2）若x //y ，求实数k 的最大值，并求取最大值时θ的值.解：（1）（方法1）当4k =，π6θ=时，()123=-，x ，=y (44-，)，…… 2分则⋅=x y ()1(4)234443⨯-+-⨯=-． …… 6分（方法2）依题意，0⋅=a b ， …… 2分则⋅=x y ()()()223314242122⎡⎤+-⋅-+=-+⨯-⎢⎥⎣⎦a b a b a b()342144432=-+⨯-⨯=- ． …… 6分（2）依题意，()122cos θ=-，x ，()2sin k θ=-，y ，因为x //y ，所以2(22cos )sin k θθ=--，整理得，()1s i nc okθθ=-， …… 9分令()()sin cos 1f θθθ=-，则()()cos cos 1sin (sin )f θθθθθ'=-+- 22c o s c o s 1θθ=--()()2cos 1cos 1θθ=+-. …… 11分令()0f θ'=，得1cos 2θ=-或cos 1θ=，又0πθ<<，故2π3θ=.列表：故当2π3θ=时，min ()f θ=334-，此时实数k 取最大值439-. ……14分（注：第（2）小问中，得到()122cos θ=-，x ，()2sin k θ=-，y ，及k 与θ的等式，各1分．）18．（本小题满分16分）如图，在平面直角坐标系xOy 中，椭圆2222 1 ( 0 )y x a b a b+=>>的左顶点为A ，右焦点为(0)F c ，.00( )P x y ，为椭圆上一点，且PA PF ⊥.（1）若3a =，5b =，求0x 的值；（2）若00x =，求椭圆的离心率；xyO PAF （第18题）θ()2π0 3， 2π3()2π π3， ()f θ' - 0 +()f θ↘极小值334-↗（3）求证：以F 为圆心，FP 为半径的圆与椭圆的右准线2a x c=相切.解：（1）因为3a =，5b =，所以2224c a b =-=，即2c =，由PA PF ⊥得，0000132y yx x ⋅=-+-，即220006y x x =--+, …… 3分又2200195x y +=，所以2004990x x +-=，解得034x =或03x =-(舍去) ． …… 5分（2）当00x =时,220y b =，由PA PF ⊥得，001y ya c⋅=--，即2b a c =，故22a c ac -=， …… 8分所以210e e +-=，解得512e -=（负值已舍）． ……10分（3）依题意，椭圆右焦点到直线2a x c =的距离为2a c c -，且2200221x y a b+=，① 由PA PF ⊥得，00001y y x a x c⋅=-+-,即2200()y x c a x ca =-+-+, ② 由①②得，()2002()0a b ac x a x c ⎡⎤-⎢⎥++=⎢⎥⎣⎦，解得()2202a a ac c x c --=-或0x a=-(舍去). …… 13分所以()2200PF x c y =-+()22000()x c x c a x ca =--+-+0c a x a=-()222a a ac c c a a c --=+⋅2a c c =-，所以以F 为圆心，FP 为半径的圆与右准线2ax c=相切. …… 16分（注：第（2）小问中，得到椭圆右焦点到直线2a x c =的距离为2a c c-，得1分；直接使用焦半径公式扣1分．）19．（本小题满分16分）设a ∈R ，函数()f x x x a a =--．（1）若()f x 为奇函数，求a 的值；（2）若对任意的[2 3]x ∈，，()0f x ≥恒成立，求a 的取值范围；（3）当4a >时，求函数()()y f f x a =+零点的个数．解：（1）若()f x 为奇函数，则()()f x f x -=-，令0x =得，(0)(0)f f =-，即(0)0f =，所以0a =，此时()f x x x =为奇函数． …… 4分（2）因为对任意的[2 3]x ∈，，()0f x ≥恒成立，所以min ()0f x ≥．当0a ≤时，对任意的[2 3]x ∈，，()0f x x x a a =--≥恒成立，所以0a ≤； …… 6分当0a >时，易得22 () x ax a x a f x x ax a x a ⎧-+-<⎪=⎨--⎪⎩，，，≥在(2a ⎤-∞⎥⎦，上是单调增函数，在 2a a ⎡⎤⎢⎥⎣⎦，上是单调减函数，在[) a +∞，上是单调增函数，当02a <<时，min ()(2)2(2)0f x f a a ==--≥，解得43a ≤，所以43a ≤；当23a ≤≤时，min ()()0f x f a a ==-≥，解得0a ≤，所以a 不存在；当3a >时，{}{}min ()min (2)(3)min 2(2)3(3)0f x f f a a a a =----，=，≥，解得92a ≥，所以92a ≥；综上得，43a ≤或92a ≥． ……10分（3）设[]()()F x f f x a =+，令()t f x a x x a =+=-则()y f t ==t t a a --，4a >，第一步，令()0f t =t t a a ⇔-=，所以，当t a <时，20t at a -+=，判别式(4)0a a ∆=->，解得2142a a a t --=，2242a a a t +-=；当t a ≥时，由()0f t =得，即()t t a a -=，解得2342a a a t ++=；第二步，易得12302a t t a t <<<<<，且24a a <，① 若1x x a t -=，其中2104a t <<，当x a <时，210x ax t -+=，记21()p x x ax t =-+，因为对称轴2a x a =<，1()0p a t =>，且21140a t ∆=->，所以方程210t at t -+=有2个不同的实根；当x a ≥时，210x ax t --=，记21()q x x ax t =--，因为对称轴2a x a =<，1()0q a t =-<，且22140a t ∆=+>，所以方程210x ax t --=有1个实根，从而方程1x x a t -=有3个不同的实根；② 若2x x a t -=，其中2204a t <<，由①知，方程2x x a t -=有3个不同的实根；③ 若3x x a t -=，当x a >时，230x ax t --=，记23()r x x ax t =--，因为对称轴2a x a =<，3()0r a t =-<，且23340a t ∆=+>，所以方程230x ax t --=有1个实根；当x a ≤时，230x ax t -+=，记23()s x x ax t =--，因为对称轴2a x a =<，3()0s a t =>，且2334a t ∆=-，2340a t ->⇔324160a a --<， ……14分记32()416m a a a =--，则()(38)0m a a a '=->，故()m a 为(4 )+∞，上增函数，且(4)160m =-<，(5)90m =>，所以()0m a =有唯一解，不妨记为0a ，且0(45)a ∈，，若04a a <<，即30∆<，方程230x ax t -+=有0个实根；若0a a =，即30∆=，方程230x ax t -+=有1个实根；若0a a >，即30∆>，方程230x ax t -+=有2个实根，所以，当04a a <<时，方程3x x a t -=有1个实根；当0a a =时，方程3x x a t -=有2个实根；当0a a >时，方程3x x a t -=有3个实根．综上，当04a a <<时，函数[]()y f f x a =+的零点个数为7；当0a a =时，函数[]()y f f x a =+的零点个数为8；当0a a >时，函数[]()y f f x a =+的零点个数为9． …… 16分（注：第（1）小问中，求得0a =后不验证()f x 为奇函数，不扣分；第（2）小问中利用分离参数法参照参考答案给分；第（3）小问中使用数形结合，但缺少代数过程的只给结果分．）20．（本小题满分16分）设{}n a 是公差为d 的等差数列，{}n b 是公比为q (1q ≠)的等比数列．记n n n c a b =+．（1）求证：数列{}1n n c c d +--为等比数列；（2）已知数列{}n c 的前4项分别为4，10，19，34．① 求数列{}n a 和{}n b 的通项公式；② 是否存在元素均为正整数的集合A ={1n ，2n ，…，} k n (4k ≥，k *∈N )，使得数列1n c ，2n c ，…，k n c 为等差数列？证明你的结论．解：（1）证明：依题意，()()111n n n n n n c c d a b a b d +++--=+-+- ()()11n n n n a a d b b ++=--+-(1)0n b q =-≠， …… 3分从而2111(1)(1)n n n n n n c c d b q q c c d b q ++++---==---，又211(1)0c c d b q --=-≠，所以{}1n n c c d +--是首项为1(1)b q -，公比为q 的等比数列． …… 5分（2）① 法1：由（1）得，等比数列{}1n n c c d +--的前3项为6d -，9d -，15d -，则()29d -=()()615d d --，解得3d =，从而2q =， …… 7分且11114 3210 a b a b +=⎧⎨++=⎩，，解得11a =，13b =，所以32n a n =-，132n n b -=⋅． …… 10分法2：依题意，得1111211311410219334a b a d b q a d b q a d b q +=⎧⎪++=⎪⎨++=⎪⎪++=⎩，，，， …… 7分消去1a ，得1121132116915d b q b d b q b q d b q b q +-=⎧⎪+-=⎨⎪+-=⎩，，，消去d ，得2111321112326b q b q b b q b q b q ⎧-+=⎪⎨-+=⎪⎩，，消去1b ，得2q =，从而可解得，11a =，13b =，3d =，所以32n a n =-，132n n b -=⋅． …… 10分② 假设存在满足题意的集合A ，不妨设l ，m ，p ，r A ∈()l m p r <<<，且l c ，m c ，p c ，r c 成等差数列，则2m p l c c c =+，因为0l c >，所以2m p c c >， ① 若1p m >+，则2p m +≥，结合①得，112(32)32(32)32m p m p --⎡⎤-+⋅>-+⋅⎣⎦13(2)232m m ++-+⋅≥，化简得，8203m m -<-<， ②因为2m ≥，m *∈N ，不难知20m m ->，这与②矛盾，所以只能1p m =+，同理，1r p =+，所以m c ，p c ，r c 为数列{}n c 的连续三项，从而122m m m c c c ++=+，即()11222m m m m m m a b a b a b +++++=+++，故122m m m b b b ++=+，只能1q =，这与1q ≠矛盾，所以假设不成立，从而不存在满足题意的集合A ． ……16分（注：第（2）小问②中，在正确解答①的基础上，写出结论“不存在”，就给1分．）南通市2015届高三第二次调研测试数学Ⅱ（附加题）A．[选修4-1：几何证明选讲]（本小题满分10分）如图，从圆O外一点P引圆的切线PC及割线PAB，C为切点．求证：AP BC AC CP⋅=⋅．证明：因为PC为圆O的切线，所以P∠=，……3分又CPA CPB∠=∠，故△C∽△BCP，……7分所以AC APBC PC=，即AP BC AC CP⋅=⋅．……10分B．[选修4-2：矩阵与变换]（本小题满分10分）设23⎡⎤⎢⎥⎣⎦是矩阵232a⎡⎤=⎢⎥⎣⎦M的一个特征向量，求实数a的值．解：设23⎡⎤⎢⎥⎣⎦是矩阵M属于特征值λ的一个特征向量，B ACPO（第21 - A题）则232a ⎡⎤⎢⎥⎣⎦23λ⎡⎤=⎢⎥⎣⎦23⎡⎤⎢⎥⎣⎦， …… 5分故262 123 a λλ+=⎧⎨=⎩，，解得4 1. a λ⎧⎨=⎩=，…… 10分C ．[选修4-4：坐标系与参数方程]（本小题满分10分）在极坐标系中，设直线π3θ=与曲线210cos 40ρρθ-+=相交于A ，B 两点，求线段AB中点的极坐标．解：（方法1）将直线π3θ=化为普通方程得，3y x =，将曲线210c o s 40ρρθ-+=化为普通方程得，221040x y x +-+=, …… 4分联立2231040y x x y x ⎧=⎪⎨+-+=⎪⎩，并消去y 得，22520x x -+=，解得112x =，22x =，所以AB中点的横坐标为12524x x +=，纵坐标为532， …… 8分化为极坐标为()5π 23，． …… 10分（方法2）联立直线l 与曲线C 的方程组2π310cos 40θρρθ⎧=⎪⎨⎪-+=⎩，，…… 2分消去θ，得2540ρρ-+=，解得11ρ=，24ρ=， …… 6分所以线段AB 中点的极坐标为()12π 23ρρ+，，即()5π 23，． …… 10分（注：将线段AB 中点的极坐标写成()5π 2π ()23k k +∈Z ，的不扣分．）D ．[选修4-5：不等式选讲]（本小题满分10分）设实数a ，b ，c 满足234a b c ++=，求证：22287a b c ++≥．证明：由柯西不等式，得()()222222123ab c ++++≥()223a b c ++， …… 6分因为234a b c ++=，故22287a b c ++≥， …… 8分当且仅当123a b c ==，即27a =，47b =，67c =时取“=”． ……10分【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）如图，在平面直角坐标系x O y 中，点(84)A -，，(2)P t ，(0)t <在抛物线22y p x =(0)p >上．（1）求p ，t 的值；（2）过点P 作PM 垂直于x 轴，M 为垂足，直线AM 与抛物线的另一交点为B ，点C 在直线AM 上．若PA ，PB ，PC 的斜率分别为1k ，2k ，3k ，且By OC M1232k k k +=，求点C 的坐标．解：（1）将点(84)A -，代入22y px =，得1p =， …… 2分将点(2)P t ，代入22y x =，得2t =±，因为0t <，所以2t =-． …… 4分（2）依题意，M 的坐标为(20)，，直线AM 的方程为2433y x =-+，联立224332y x y x⎧=-+⎪⎨⎪=⎩，并解得B ()112，， …… 6分所以113k =-，22k =-，代入12k kk +=得，376k =-， …… 8分从而直线PC 的方程为7163y x =-+，联立24337163y x y x ⎧=-+⎪⎨⎪=-+⎩，并解得C ()823-，． …… 10分23．（本小题满分10分）设A ，B 均为非空集合，且A B =∅，AB ={ 123，，，…，}n (n ≥3，n *∈N )．记A ，B 中元素的个数分别为a ，b ，所有满足“a ∈B ，且b A ∈”的集合对(A ，B )的个数为n a ．（1）求a 3，a 4的值；（2）求n a ．解：（1）当n =3时，AB ={1，2，3}，且AB =∅，若a =1，b =2，则1B ∈，2A ∈，共01C 种；若a =2，b =1，则2B ∈，1A ∈，共11C 种，所以a 3=01C 11+ C 2=； …… 2分当n =4时，A B ={1，2，3，4}，且A B =∅，若a =1，b =3，则1B ∈，3A ∈，共02C 种；若a =2，b =2，则2B ∈，2A ∈，这与AB =∅矛盾；若a =3，b =1，则3B ∈，1A ∈，共22C 种，所以a 4=02C 22+ C 2=． …… 4分（2）当n 为偶数时，A B ={1，2，3，…，n }，且A B =∅，若a =1，b 1n =-，则1B ∈，1n -A ∈，共02C n -（考虑A ）种；若a =2，b 2n =-，则2B ∈，2n -A ∈，共12C n -（考虑A ）种； ……若a =12n -，b 12n =+，则12n -B ∈，12n +A ∈，共222C n n --（考虑A ）种；若a =2n ，b 2n =，则2n B ∈，2n A ∈，这与AB =∅矛盾；若a 12n =+，b 12n =-，则12n +B ∈，12n -A ∈，共22C n n -（考虑A ）种； ……若a =1n -，b 1=，则1n -B ∈，1A ∈，共（考虑A ）22C n n --种，所以a n =02C n -+12C n -+…+222C n n --+22C nn -+…+122222C2C n n n n n -----=-； …… 8分当n 为奇数时，同理得，a n =02C n -+12C n -+…+222C 2n n n ---=，综上得，θ ()2π0 3，2π3 ()2π π3，f θ'f θ334-122222C 2 .n n n n n n a n ----⎧⎪-=⎨⎪⎩，为偶数，，为奇数 …… 10分。

2015年江苏省南通市高三二模考试数学试题含答案

（第4题）南通市2015届高三第二次调研测试数学学科参考答案及评分建议一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位．．．．．．置上．．． 1．命题“x ∃∈R ，20x >”的否定是“ ▲ ”．【答案】x ∀∈R ，20x ≤2．设1i i 1ia b +=+-(i 为虚数单位，a ，b ∈R )，则ab 的值为 ▲ ．【答案】03．设集合{}11 0 3 2A =-，，，，{}2 1B x x =≥，则AB = ▲ ．【答案】{}1 3-，4．执行如图所示的伪代码，则输出的结果为 ▲ ．【答案】115．一种水稻试验品种连续5年的平均单位面积产量(单位：t/hm 2) 如下：9.8，9.9，10.1，10，10.2，则该组数据的方差为 ▲ ．【答案】0.026．若函数()π()2sin 3f x x ω=+(0)ω>的图象与x 轴相邻两个交点间的距离为2，则实数ω的值为 ▲ ．【答案】π27．在平面直角坐标系xOy 中，若曲线ln y x =在e x =(e 为自然对数的底数)处的切线与直线 30ax y -+=垂直，则实数a 的值为 ▲ ．【答案】e -8．如图，在长方体1111ABCD A B C D -中，AB =3 cm ，AD =2 cm ，1AA =1 cm ，则三棱锥11B ABD -的体积为 ▲ cm 3．【答案】1AA 1 B不CB 1不C 1不D 1不D不（第8题）BDC（第12题）AA BCDMNQ9．已知等差数列{}n a 的首项为4，公差为2，前n 项和为n S ．若544k k S a +-=(k *∈N )，则k 的值为 ▲ ．【答案】710．设32()4(3)f x x mx m x n =++-+(m n ∈R ，)是R 上的单调增函数，则m 的值为 ▲ ．【答案】611．在平行四边形ABCD 中，AC AD AC BD ⋅=⋅3=，则线段AC 的长为 ▲ ．12．如图，在△ABC 中，3AB =，2AC =，4BC =，点D 在边BC 上，BAD ∠=45°，则tan CAD ∠的值为 ▲ ．13．设x ，y ，z 均为大于1的实数，且z 为x 和y 的等比中项，则lg lg 4lg lg z zx y+的最小值为 ▲ ．【答案】9814．在平面直角坐标系xOy 中，圆1C ：22(1)(6)25x y ++-=，圆2C ：222(17)(30)x y r -+-=．若圆2C 上存在一点P ，使得过点P 可作一条射线与圆1C 依次交于点A ，B ，满足2PA AB =，则半径r 的取值范围是 ▲ ．【答案】[]5 55，二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答. 解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）如图，在四面体ABCD 中，平面BAD ⊥平面CAD ，BAD ∠=90°．M ，N ，Q 分别为棱AD ，BD ，AC 的中点．（1）求证：//CD 平面MNQ ；（2）求证：平面MNQ ⊥平面CAD ．证明：（1）因为M ，Q 分别为棱AD ，AC 的中点，所以//MQ CD ， …… 2分又CD ⊄平面MNQ ，MQ ⊂平面MNQ ，故//CD 平面M． …… 6分（2）因为M ，N 分别为棱AD ，BD 的中点，所以//MN AB ，又90BAD ∠=°，故MN AD ⊥． …… 8分因为平面BAD ⊥平面CAD ，平面BAD平面CAD AD =，且MN ⊂平面ABD ，所以MN ⊥平面ACD ． …… 11分又MN ⊂平面MNQ ，平面MNQ ⊥平面CAD ． …… 14分（注：若使用真命题“如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面”证明“MN ⊥平面ACD ”，扣1分．）16．（本小题满分14分）体育测试成绩分为四个等级：优、良、中、不及格．某班50名学生参加测试的结果如下：（1）从该班任意抽取1名学生，求这名学生的测试成绩为“良”或“中”的概率；（2）测试成绩为“优”的3名男生记为1a ，2a ，3a ，2名女生记为1b ，2b ．现从这5人中任选2人参加学校的某项体育比赛． ① 写出所有等可能的基本事件；② 求参赛学生中恰有1名女生的概率．解：（1）记“测试成绩为良或中”为事件A ，“测试成绩为良”为事件1A ，“测试成绩为中”为事件2A ，事件1A ，2A 是互斥的. …… 2分由已知，有121923()()5050P A P A ==，． ……4分因为当事件1A ，2A 之一发生时，事件A 发生，所以由互斥事件的概率公式，得1212192321()()()()P A P A A P A P A =+=+=+=． ……6分（2）① 有10个基本事件：12()a a ，，13()a a ，，11()a b ，，12()a b ，，23()a a ，，21()a b ，，22()a b ，，31()a b ，，32()a b ，，12()b b ，． ……9分② 记“参赛学生中恰好有1名女生”为事件B ．在上述等可能的10个基本事件中，事件B 包含了11()a b ，，12()a b ，，21()a b ，，22()a b ，，31()a b ，，32()a b ，．故所求的概率为63()105P B ==．答：（1）这名学生的测试成绩为“良”或“中”的概率为2125；（2）参赛学生中恰有1名女生的概率为35． ……14分（注：不指明互斥事件扣1分；不记事件扣1分，不重复扣分；不答扣1分．事件B 包含的6种基本事件不枚举、运算结果未化简本次阅卷不扣分．）17．（本小题满分14分）在平面直角坐标系xOy 中，已知向量=a (1，0)，=b (0，2).设向量=+x a (1cos θ-)b ，k =-y a 1sin θ+b ，其中0πθ<<.（1）若4k =，π6θ=，求x ⋅y 的值；（2）若x //y ，求实数k 的最大值，并求取最大值时θ的值.解：（1）（方法1）当4k =，πθ=时，(12=，x ，=y (44-，)， ……2分则⋅=x y (1(4)244⨯-+-⨯=- …… 6分（方法2）依题意，0⋅=a b ， …… 2分则⋅=x y (()(22142421⎡⎤+⋅-+=-+⨯⎢⎥⎣⎦a b a b a b(421443=-+⨯⨯=． ……6分（2）依题意，()122cos θ=-，x ，()2sin k θ=-，y ，因为x //y ，所以2(22cos )k θθ=--，整理得，()1sin cos 1k θθ=-， ……9分令()()sin cos 1f θθθ=-，则()()cos cos 1sin (sin )f θθθθθ'=-+- 22cos cos 1θθ=--()()2cos 1cos 1θθ=+-. …… 11分令()0f θ'=，得1cos θ=-或cos 1θ=，又0πθ<<，故2π3θ=.列表：故当2πθ=时，min ()f θ=，此时实数k取最大值. ……14分（注：第（2）小问中，得到()122cos θ=-，x ，()2sin k θ=-，y ，及k 与θ的等式，各1分．）18．（本小题满分16分）如图，在平面直角坐标系xOy 中，椭圆2222 1 ( 0 )y x a b a b+=>>的左顶点为A ，右焦点为(0)F c ，.00( )P x y ，为椭圆上一点，且PA PF ⊥.（1）若3a =，b 0x 的值；（2）若00x =，求椭圆的离心率；（3）求证：以F 为圆心，FP 为半径的圆与椭圆的右准线2a x c=相切.解：（1）因为3a =，b =2224c a b =-=，即2c =，由PA PF ⊥得，0000132y y x x ⋅=-+-，即220006y x x =--+, …… 3分又2200195x y +=，所以2004990x x +-=，解得034x =或03x =-(舍去) ． ……5分（2）当00x =时,220y b =，由PA PF ⊥得，001y y a c⋅=--，即2b a c =，故22a c ac -=， …… 8分（第18题）所以210e e +-=，解得e ． ……10分（3）依题意，椭圆右焦点到直线2a x c =的距离为2a c c -，且2200221x y a b+=，① 由PA PF ⊥得，00001y y x a x c⋅=-+-,即22000()y x c a x ca =-+-+, ② 由①②得，()2002()0a b ac x a x c ⎡⎤-⎢⎥++=⎢⎥⎣⎦，解得()2202a a ac c x c --=-或0x a =-(舍去). ……13分所以PF ==0c a x =-()222a a ac c c a a c --=+⋅2a c c =-，所以以F 为圆心，FP 为半径的圆与右准线2a x c=相切. …… 16分（注：第（2）小问中，得到椭圆右焦点到直线2a x c=的距离为2a c c -，得1分；直接使用焦半径公式扣1分．）19．（本小题满分16分）设a ∈R ，函数()f x x x a a =--．（1）若()f x 为奇函数，求a 的值；（2）若对任意的[2 3]x ∈，，()0f x ≥恒成立，求a 的取值范围；（3）当4a >时，求函数()()y f f x a =+零点的个数．解：（1）若()f x 为奇函数，则()()f x f x -=-，令0x =得，(0)(0)f f =-，即(0)0f =，所以0a =，此时()f x x x =为奇函数． …… 4分（2）因为对任意的[2 3]x ∈，，()0f x ≥恒成立，所以min ()0f x ≥．当0a ≤时，对任意的[2 3]x ∈，，()0f x x x a a =--≥恒成立，所以0a ≤； …… 6分当0a >时，易得22 () x ax a x a f x x ax a x a ⎧-+-<⎪=⎨--⎪⎩，，，≥在(a ⎤-∞⎥⎦，上是单调增函数，在2a a ⎡⎤⎢⎥⎣⎦，上是单调减函数，在[) a +∞，上是单调增函数，当02a <<时，min ()(2)2(2)0f x f a a ==--≥，解得43a ≤，所以43a ≤；当23a ≤≤时，min ()()0f x f a a ==-≥，解得0a ≤，所以a 不存在；当3a >时，{}{}min ()min (2)(3)min 2(2)3(3)0f x f f a a a a =----，=，≥，解得92a ≥，所以92a ≥；综上得，43a ≤或92a ≥． ……10分（3）设[]()()F x f f x a =+，令()t f x a x x a =+=-则()y f t ==t t a a --，4a >，第一步，令()0f t =t t a a ⇔-=，所以，当t a <时，20t at a -+=，判别式(4)0a a ∆=->，解得1t ，2t =；当t a ≥时，由()0f t =得，即()t t a a -=，解得3t =第二步，易得12302a t t a t <<<<<，且24a a <，① 若1x x a t -=，其中2104a t <<，当x a <时，210x ax t -+=，记21()p x x ax t =-+，因为对称轴2a x a =<，1()0p a t =>，且21140a t ∆=->，所以方程210t at t -+=有2个不同的实根；当x a ≥时，210x ax t --=，记21()q x x ax t =--，因为对称轴2a x a =<，1()0q a t =-<，且22140a t ∆=+>，所以方程210x ax t --=有1个实根，从而方程1x x a t -=有3个不同的实根；② 若2x x a t -=，其中2204a t <<，由①知，方程2x x a t -=有3个不同的实根；③ 若3x x a t -=，当x a >时，230x ax t --=，记23()r x x ax t =--，因为对称轴2a x a =<，3()0r a t =-<，且23340a t ∆=+>，所以方程230x ax t --=有1个实根；当x a ≤时，230x ax t -+=，记23()s x x ax t =--，因为对称轴2a x a =<，3()0s a t =>，且2334a t ∆=-，2340a t ->⇔324160a a --<， …… 14分记32()416m a a a =--，则()(38)0m a a a '=->，故()m a 为(4 )+∞，上增函数，且(4)160m =-<，(5)90m =>，所以()0m a =有唯一解，不妨记为0a ，且0(45)a ∈，，若04a a <<，即30∆<，方程230x ax t -+=有0个实根；若0a a =，即30∆=，方程230x ax t -+=有1个实根；若0a a >，即30∆>，方程230x ax t -+=有2个实根，所以，当04a a <<时，方程3x x a t -=有1个实根；当0a a =时，方程3x x a t -=有2个实根；当0a a >时，方程3x x a t -=有3个实根．综上，当04a a <<时，函数[]()y f f x a =+的零点个数为7；当0a a =时，函数[]()y f f x a =+的零点个数为8；当0a a >时，函数[]()y f f x a =+的零点个数为9． …… 16分（注：第（1）小问中，求得0a =后不验证()f x 为奇函数，不扣分；第（2）小问中利用分离参数法参照参考答案给分；第（3）小问中使用数形结合，但缺少代数过程的只给结果分．）20．（本小题满分16分）设{}n a 是公差为d 的等差数列，{}n b 是公比为q (1q ≠)的等比数列．记n n n c a b =+．（1）求证：数列{}1n n c c d +--为等比数列；（2）已知数列{}n c 的前4项分别为4，10，19，34． ① 求数列{}n a 和{}n b 的通项公式；② 是否存在元素均为正整数的集合A ={1n ，2n ，…，} k n (4k ≥，k *∈N )，使得数列1n c ，2n c ，…，k n c 为等差数列？证明你的结论．解：（1）证明：依题意，()()111n n n n n n c c d a b a b d +++--=+-+- ()()11n n n n a a d b b ++=--+-(1)0n b q =-≠， …… 3分从而2111(1)n n n n n n c c d b q q ++++---==，又211(1)0c c d b q --=-≠，所以{}1n n c c d +--是首项为1(1)b q -，公比为q 的等比数列． …… 5分（2）① 法1：由（1）得，等比数列{}1n n c c d +--的前3项为6d -，9d -，15d -，则()29d -=()()615d d --，解得3d =，从而2q =， …… 7分且11114 3210 a b a b +=⎧⎨++=⎩，，解得11a =，13b =，所以32n a n =-，132n n b -=⋅． …… 10分法2：依题意，得1111211311410219334a b a d b q a d b q a d b q +=⎧⎪++=⎪⎨++=⎪⎪++=⎩，，，， …… 7分消去1a ，得1121132116915d b q b d b q b q d b q b q +-=⎧⎪+-=⎨⎪+-=⎩，，，消去d ，得2111321112326b q b q b b q b q b q ⎧-+=⎪⎨-+=⎪⎩，，消去1b ，得2q =，从而可解得，11a =，13b =，3d =，所以32n a n =-，132n n b -=⋅． ……10分② 假设存在满足题意的集合A ，不妨设l ，m ，p ，r A ∈()l m p r <<<，且l c ，m c ，p c ，r c 成等差数列，则2m p l c c c =+，因为0l c >，所以2m p c c >， ① 若1p m >+，则2p m +≥，结合①得，112(32)32(32)32m p m p --⎡⎤-+⋅>-+⋅⎣⎦13(2)232m m ++-+⋅≥，化简得，8203m m -<-<， ②因为2m ≥，m *∈N ，不难知20m m ->，这与②矛盾，所以只能1p m =+，同理，1r p =+，所以m c ，p c ，r c 为数列{}n c 的连续三项，从而122m m m c c c ++=+，即()11222m m m m m m a b a b a b +++++=+++，故122m m m b b b ++=+，只能1q =，这与1q ≠矛盾，所以假设不成立，从而不存在满足题意的集合A ． ……16分（注：第（2）小问②中，在正确解答①的基础上，写出结论“不存在”，就给1分．）南通市2015届高三第二次调研测试数学Ⅱ（附加题）A ．[选修4-1：几何证明选讲]（本小题满分10分）如图，从圆O 外一点P 引圆的切线PC 及割线PAB ，C 为切点．求证：AP BC AC CP ⋅=⋅．证明：因为PC 为圆O 的切线，P所以P∠=， …… 3分又CPA CPB ∠=∠，故△C∽△BCP ， …… 7分所以AC AP BC PC=，即AP BC AC CP ⋅=⋅． …… 10分B ．[选修4-2：矩阵与变换]（本小题满分10分）设23⎡⎤⎢⎥⎣⎦是矩阵232a ⎡⎤=⎢⎥⎣⎦M 的一个特征向量，求实数a 的值．解：设23⎡⎤⎢⎥⎣⎦是矩阵M 属于特征值λ的一个特征向量，则232a ⎡⎤⎢⎥⎣⎦23λ⎡⎤=⎢⎥⎣⎦23⎡⎤⎢⎥⎣⎦， …… 5分故262 123 a λλ+=⎧⎨=⎩，，解得4 1. a λ⎧⎨=⎩=，……10分C ．[选修4-4：坐标系与参数方程]（本小题满分10分）在极坐标系中，设直线π3θ=与曲线210cos 40ρρθ-+=相交于A ，B 两点，求线段AB 中点的极坐标．解：（方法1）将直线π3θ=化为普通方程得，y =，将曲线210cos 40ρρθ-+=化为普通方程得，221040x y x +-+=, …… 4分联立221040y x y x ⎧=⎪⎨+-+=⎪⎩，并消去y 得，22520x x -+=，解得112x =，22x =，所以AB 中点的横坐标为12524x x +=，…… 8分化为极坐标为()5π 23，．…… 10分（方法2）联立直线l 与曲线C 的方程组2π310cos 40θρρθ⎧=⎪⎨⎪-+=⎩，，…… 2分消去θ，得2540ρρ-+=，解得11ρ=，24ρ=， …… 6分所以线段AB 中点的极坐标为()12π 23ρρ+，，即()5π 23，． …… 10分（注：将线段AB 中点的极坐标写成()5π 2π ()23k k +∈Z ，的不扣分．）D ．[选修4-5：不等式选讲]（本小题满分10分）设实数a ，b ，c 满足234a b c ++=，求证：22287a b c ++≥．证明：由柯西不等式，得()()222222123a b c ++++≥()223a b c ++， …… 6分因为234a b c ++=，故22287a b c ++≥， …… 8分当且仅当a b c ==，即2a =，4b =，6c =时取“=”． ……10分【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）如图，在平面直角坐标系xOy 中，点(84)A -，，(2)P t ，(0)t <在抛物线22y px =(0)p >上．（1）求p ，t 的值；（2）过点P 作PM 垂直于x 轴，M 为垂足，直线AM 与抛物线的另一交点为B ，点C 在直线AM 上．若PA ，PB ，PC 的斜率分别为1k ，2k ，3k ，且1232k k k +=，求点C 的坐标．解：（1）将点(84)A -，代入22y px =，得1p =， …… 2分将点(2)P t ，代入22y x =，得2t =±，因为0t <，所以2t =-． …… 4分（2）依题意，M 的坐标为(20)，，直线AM 的方程为24y x =-+，联立224332y x y x⎧=-+⎪⎨⎪=⎩，并解得B ()112，， …… 6分所以11k =-，22k =-，代入1232k k k +=得，376k =-， ……8分从而直线PC 的方程为7163y x =-+，（第22题）联立243371y x y x ⎧=-+⎪⎨⎪=-+⎩，并解得C ()82-，． ……10分23．（本小题满分10分）设A ，B 均为非空集合，且A B =∅，AB ={ 123，，，…，}n (n ≥3，n *∈N )．记A ，B 中元素的个数分别为a ，b ，所有满足“a ∈B ，且b A ∈”的集合对(A ，B )的个数为n a ．（1）求a 3，a 4的值；（2）求n a ．解：（1）当n =3时，AB ={1，2，3}，且AB =∅，若a =1，b =2，则1B ∈，2A ∈，共01C 种；若a =2，b =1，则2B ∈，1A ∈，共11C 种，所a 3=01C 11+ C 2=；当n =4时，A B ={1，2，3，4}，且A B =∅，若a =1，b =3，则1B ∈，3A ∈，共02C 种；若a =2，b =2，则2B ∈，2A ∈，这与AB =∅矛盾；若a =3，b =1，则3B ∈，1A ∈，共22C 种，所以a 4=02C 22+ C 2=． …… 4分（2）当n 为偶数时，A B ={1，2，3，…，n }，且A B =∅，若a =1，b 1n =-，则1B ∈，1n -A ∈，共02C n -（考虑A ）种；若a =2，b 2n =-，则2B ∈，2n -A ∈，共12C n -（考虑A ）种； ……(()2π π3，f θ'f θ若a =12n -，b 12n =+，则12n -B ∈，12n +A ∈，共222C nn --（考虑A ）种；若a =2n ，b 2n =，则2n B ∈，2n A ∈，这与AB =∅矛盾；若a 1n =+，b 1n =-，则1n +B ∈，1n -A ∈，共2C nn -（考虑A ）种； ……若a =1n -，b 1=，则1n -B ∈，1A ∈，共（考虑A ）22C n n --种，所以a n =02C n -+12Cn -+…+222C n n --+22Cn n -+…+122222C2Cn n n n n -----=-； ……8分当n 为奇数时，同理得，a n =02C n -+12C n -+…+222C 2n n n ---=，综上得，12222C 2 .n n n n n n a n ----⎧⎪-=⎨⎪⎩，为偶数，，为奇数 …… 10分。

南通中学2015届高三第二次月考数学试卷

南通中学2015届高三第二次月考数学试卷（教师版）参考公式：锥体的体积公式 13V Sh =，其中S 表示锥体的底面积，h 表示锥体的高. 柱体的体积公式 V Sh =，其中S 表示柱体的底面积，h 表示柱体的高.一、填空题：（本大题共14小题，每小题5分，共计70分．请把答案填写在答卷纸相应的位置上．）1．设复数1z 、2z 在复平面内的对应点关于虚轴对称，12z i =+（i 为虚数单位），则12z z ⋅= ▲ .5- 2．从甲、乙、丙、丁4位同学中随机选出2名代表参加学校会议，则甲被选中的概率是 ▲ .123．根据如图所示的伪代码，可知输出的S 的值为 ▲ .134．为了调查城市 2.5PM 的值，按地域把长三角地区36个城市分成甲、乙、丙三组，对应的城市数分别为6、12、18.若用分层抽样的方法抽取12个城市，则乙组中应抽取的城市数为 ▲ .4 5．设集合{}1,2M =、{}2N a =，则“1a =”是“N M ⊆”的 ▲ 条件．充分不必要条件（从“充分不必要”、 “必要不充分”、“充分且必要”、“既不充分也不必要”中择一填写）6．有一段演绎推理：大前提：整数是自然数；小前提：3-是整数；结论：3-是自然数.这个推理显然错误，则错误的原因是 ▲ 错误.（从“大前提”、“小前提”、“结论”中择一填写）. 大前提7．关于x 的不等式22230(0)x ax a a --<<的解集为12(,)x x ，且2112x x -=，则实数a 的值等于 ▲ .3-8．已知抛物线28y x =的焦点是双曲线22213x y a -=（0a >）的右焦点，则双曲线的右准线方程为 ▲ .12x =9．设x 、y 满足约束条件010x y a x y ++≥⎧⎨-+≤⎩，且ay x z -=的最小值为7，则实数=a ▲ .3-10．在ABC ∆中，点M 是BC 的中点，角120A ︒=，2AB AC ⋅=-，则||AM 的最小值为 ▲ .设AB c =、AC b =，由1AB AC ⋅=-，120A ︒=得4bc =，倍长AM 至D ，则60ABD ︒∠=，由余第3题弦定理得22224AD b c bc bc bc bc =+-≥-==，即22AM AD =≥，1AM ≥即||AM 最小值为1.11．已知圆22:(3)(4)1C x y -+-=和两点(,0)A m -、(,0)B m （0m >），若圆上存在一点P ，使得90APB ︒∠=，则m 的最小值为 ▲ .显然2AB m =，因为90APB ︒∠=，所以12OP AB m ==，所以要求m 的最小值即求圆C 上点P 到原点O 的最小距离，因为5OC =，所以min ()4OP OC r =-=，即m 的最小值为4.12．如图为函数2()1xf x x =+的部分图像，ABCD 是矩形，A 、B 在图像上，将此矩形（AB 边在第一象限）绕x 轴旋转得到的旋转体的体积的最大值为 ▲ ./22(1)(1)()0(1)x x f x x -+-==+得1x =为极大值点，且1(1)2f =，设A 、B 的纵坐标为1(0)2k k <<，则由21xk x =+得 20kx x k -+=，1A B x x k+=，1A B x x ⋅=，所以||A B AB x x =-==2V k ππ===2π4π≤，当且仅当k ==”，此时0∆>，故旋转体体积的最大值为4π. 13．设数列{}n a 为等差数列，数列{}n b 为等比数列．若12a a >，12b b >，且2i i b a =（1i =，2，3），则数列{}n b 的公比为 ▲ .方法1：设1a ，2a ，3a 依次为a d -，a ，a d +，因为12a a >，所以0d <，因为12b b >，所以01q <<，又2213b b b =，所以422222()()()a a d a d a d =-+=-，则222a d a =-或222a a d =-（舍），所以d =.若d =，则222222222111()()1)31b a a a q b a a a d ======+=+>-（舍）；若d =，则222222222111()()1)1b a a a q b a a a d ======-<-，所以3q =- 方法2:易知422213a a a =，则2213a a a =±，若2213a a a =，则123a a a ==（舍），若2213a a a =-，则21313()2a a a a +=-且10a <，所以22113360a a a a ++=，所以23311()610a a a a +⋅+=，则313a a =-±又2223332111()b a aq b a a ===且01q <<，所以3q =-.14．已知函数()af x x x=-，且对任意的(0,1)x ∈，都有()(1)1f x f x ⋅-≥恒成立，则实数a 的取值范围是 ▲ .因为2(1)(1)(1)11a a x f x x x x ---=--=--，所以对任意(0,1)x ∈，都有22(1)11a x a x x x---⋅≥-即22()[(1)](1)a x a x x x -⋅--≥-恒成立，整理得222(1)(21)(1)()0x x a x x a a -+--+-≥，令(1)x x t -=，则104t <≤，问题等价于22(21)()0t a t a a +-+-≥对104t <≤恒成立，令 22()(21)()g t t a t a a =+-+-，因为22(21)4()10a a a ∆=---=>，所以211241()04a g -⎧-≥⎪⎪⎨⎪≥⎪⎩或 2102(0)0a g -⎧-≤⎪⎨⎪≥⎩，即21416830a a a ⎧≤⎪⎨⎪--≥⎩或2120a a a ⎧≥⎪⎨⎪-≥⎩，所以141344a a ora ⎧≤⎪⎪⎨⎪≤-≥⎪⎩或1201a a ora ⎧≥⎪⎨⎪≤≥⎩，所以 14a ≤-或1a ≥.另解1：由22(21)()0t a t a a +-+-≥得()[(1)]0t a t a +⋅++≥，所以1t a ≥-+或t a ≤-，由题意得10a -+≤或14a -≥即14a ≤-或1a ≥. 另解2：由22(21)()0t a t a a +-+-≥得()[(1)]0a t a t +⋅++≥，所以1a t ≥-+或a t ≤-，因为104t <≤，所以3(1)14t ≤--<或104t -≤-<，由题意得14a ≤-或1a ≥. 另解3：()[(1)]11a a x x x x ---≥-，设1x m x n =⎧⎨-=⎩，则01011m n m n <<⎧⎪<<⎨⎪+=⎩，又2212m n mn +=-，所以 ()()1a am n m n--≥即2()10a n m a mn mn m n -++-≥，即2(21)(1)0a mn a mn mn +-+-≥，即 ()(1)0a mn a mn ++-≥，所以a mn ≤-或1a mn ≥-+，因为104mn <≤，所以由题意得14a ≤- 或1a ≥.二、解答题：（本大题共6小题，共计90分，解答时应写出必要的文字说明、证明过程或演算步骤）15．（本题满分14分）如图所示，A 、B 分别是单位圆与x 轴、y 轴正半轴的交点，点P 在单位圆上，AOP θ∠=（0θπ<<），点C 坐标为(2,0)-，平行四边形OAQP 的面积为S ．（Ⅰ）求t OA OQ S =⋅+的最大值；（Ⅱ）若CB ∥OP ，求sin(2)3πθ-．【解析】（Ⅰ）∵(1,0)OA =，(cos ,sin )P θθ，∴(1cos ,sin )OQθθ=+，∴1cos OA OQ θ⋅=+，而12||||sin sin 2S OA OP θθ=⋅⋅⋅⋅=，所以1cos sin 1)4t OA OQ S πθθθ=⋅+=++=++，………………………………4分∵0θπ<<，∴当4πθ=时，t OA OQ S =⋅+取得最大值为1+；………………………7分（Ⅱ）(2,1)CB =，(cos ,sin )OP θθ=，由CB ∥OP 得cos 2sin θθ=，又0θπ<<，结合22sin cos 1θθ+=得sin θ=，cos θ=4sin 25θ=，3cos 25θ=，……………………11分所以sin(2)3πθ-sin 2coscos 2sin33ππθθ=⋅-⋅=．……………………………………14分 16．（本题满分14分）如图，矩形ABCD 中，3AB =，4BC =，E 、F 分别在线段BC 和AD 上，EF ∥AB ，将矩形ABEF 沿EF 折起，记折起后的矩形为MNEF ，且平面MNEF ⊥平面ECDF ．（Ⅰ）求证：NC ∥平面MFD ；（Ⅱ）求四面体CDFN 体积的最大值．（翻折前）（翻折后）ABCDEF【解析】（Ⅰ）∵四边形MNEF ，EFDC 都是矩形，∴MN ∥EF ∥CD ，MN EF CD ==，∴四边形MNCD 是平行四边形，∴NC ∥MD ，又∵NC ⊄平面MFD ，MD ⊂平面MFD ，∴NC ∥平面MFD ；………………………………………………………………………………………………7分（Ⅱ）由（Ⅰ）易证NE ⊥平面FEC ，设NE x =，则4EC x =-，其中04x <<．∴四面体CDFN 的体积为11(4)32CDFN NCDF NFEC EFC V V V S NE x x ∆===⋅=-21(4)[]222x x +-≤⋅=，当且仅当4x x =-，即2x =时取“=”，故四面体CDFN 体积最大值为2．…………………………………………14分17．（本题满分14分）如图，P 为某湖中观光岛屿，AB 是沿湖岸南北方向道路，Q 为停车场，103PQ =km ，某旅游团浏览完岛屿后，乘游船回停车场Q ，已知游船以10/km h 的速度沿方位角θ的方向行驶，3sin 5θ=．游船离开观光岛屿3分钟后，因事耽搁没有来得及登上游船的游客甲，为了及时赶到停车地点Q 与旅游团会合，立即决定租用小艇先到达湖岸南北大道M 处，然后乘景区电动出租车到停车场Q 处（假设游客甲到达湖滨大道后幸运地一点未耽搁便乘上了电动出租车）．游客甲乘小艇行驶的方位角是α，电动出租车的速度为70/3km h ．（Ⅰ）设4sin 5α=，问小艇的速度为多少/km h 时，游客甲才能与游船同时到达点Q ；（Ⅱ）设小艇速度为10/km h ，请你替该游客设计小艇行驶的方位角α，当角α的余弦值是多少时，游客甲能按计划以最短时间到达Q ．【解析】（Ⅰ）方法一：如图，作PNAB ⊥，N 为垂足，3sin 5θ=，4sin 5α=，在Rt PNQ ∆中，103sin 235PN PQ θ=⋅=⋅=（km ）， cos QN PQ θ=⋅=1048353⋅=（km ）．在Rt PNM ∆中， 234tan 23PN MN α===（km ）．76QM QN MN =-=， 5cos 2NM PM α==，………………………………………4分设游船从P 到Q 所用时间为1t h ，游客甲从P 经M 到Q 所用时间为2t h ，则1101310103PQ t ===（h ）， BM设小艇的速度为1/v km h ，则2111755162707022033PM MQ t v v v =+=+=+（h ），由已知得21120t t +=，即15111220203v ++=，∴1757v =，∴小艇的速度为75/7km h 时，游客甲才能与游船同时到达Q ； ………………………………………………8分（Ⅰ）方法二：如图，∵3sin 5θ=，4sin 5α=，∴4cos 5θ=，3cos 5α=，sin sin()QPM αθ∠=-= sin cos cos sin αθαθ⋅-⋅725=，由正弦定理得sin()sin()QM QP αθπα=--，所以76QM =， sin sin()PM PQ θπα=-，所以52PM =．下同方法一；（Ⅱ）在Rt PNM ∆中，∵2sin sin PN PM αα==（km ），2cos tan sin PN MN ααα==（km ）． ∴82cos 3sin QM QN MN αα=-=-（km ），所以143cos 70105sin 3535sin 3PM QM t ααα=+=+-173cos 435sin 35αα-=⨯+． ………………………………………………………………………11分 ∵2/2213sin (73cos )cos 37cos 35sin 35sin t αααααα---=⨯=⋅，∴令/0t =得3cos 7α=．当3cos 7α<时， /0t >；当3cos 7α>时，/0t <．∵cos y α=在)2,0(πα∈上是减函数，∴当方位角α满足 3cos 7α=时，t 最小，即游客甲能按计划以最短时间到达Q ． ………………………………14分 18．（本题满分16分）已知函数21()ln 2f x x a x =-⋅（a R ∈），2()24g x x mx =-+（m R ∈）．（Ⅰ）若函数()f x 在2x =处的切线方程为y x b =+，求实数a 与b 的值；（Ⅱ）求()f x 的单调减区间；（Ⅲ）当1a =时，若对任意的1[1,2]x ∈，存在2[1,2]x ∈，使得12()()f x g x ≥，求实数m 的取值范围．【解析】（Ⅰ）/()a fx x x =-，由/(2)212a f =-=得2a =，∴21()2ln 2f x x x =-，(2)22ln 2f =-，即切点为(2,22ln 2)-，代入方程y x b =+得2ln 2b =-；……………………………………5分（Ⅱ）()f x 的定义域为(0,)+∞，2/()a x af x x x x-=-=，①当0a ≤时，/()0f x >在(0,)+∞上恒成立，∴()f x 无减区间；②当0a >时，由/()0f x <得0x <<，此时，()f x 减区间为；…………………………………………………………10分（Ⅲ）由题意可得[1,2]x ∈时，min min ()()f x g x ≥． ……………………………………………12分 ∵1a =时，/1(1)(1)()0x x f x x x x +-=-=>，()f x 在[1,2]x ∈为增函数，∴min 1()(1)2f x f ==， 222()24()4g x x mx x m m =-+=-+-．①当1m <时，()g x 在区间[1,2]上递增，所以min 1()(1)522g x g m ==-≤，由1522m -≤解得94m ≥，舍去；②当12m ≤≤时，2min 1()()42g x g m m ==-≤，解得m ≤m ≥2m ≤≤；③当2m >时，()g x 在区间[1,2]上递减，所以min 1()(2)842g x g m ==-≤，由1842m -≤解得158m ≥，∴2m >.综上，m ≥. …………………………………………………………………………16分 19．（本题满分16分）已知直线220x y -+=经过椭圆2222:1x y C a b+=（0a b >>）的左顶点A 和上顶点D ．椭圆C 的右顶点为B ，点E 是椭圆C 上位于x 轴上方的动点，直线AE 、BE 与直线:l103x =分别交于M 、N 两点．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）求线段MN 长度的最小值；（Ⅲ）当线段MN 的长度最小时，椭圆C 上是否存在这样的点T ，使得TBE ∆的面积为15？若存在，确定点T 的个数；若不存在，请说明理由．【解析】（Ⅰ）令0x=得1y =，所以(0,1)D ，所以1b =，令0y =得2x =-，所以(2,0)A -，所以2a =，所以椭圆C 的标准方程为2214x y +=；……………………………………………………………5分（Ⅱ）显然直线AE 的斜率存在且为正数，设直线AE 的方程为(2)y k x =+（0k >），联立得(2)103y k x x =+⎧⎪⎨=⎪⎩，解得1016(,)33k M ，由22(2)44y k x x y =+⎧⎨+=⎩得2222(14)161640k x k x k +++-=，显然16∆=，由求根公式得222814k x k -==+或222814k x k --==+（舍），所以 222284(,)1414k k E k k -++，从而直线BE 的方程为1(2)4y x k =--，联立得1(2)4103y x kx ⎧=--⎪⎪⎨⎪=⎪⎩，解得 101(,)33N k -，所以1618333k MN k =+≥=，当且仅当14k =时取“=”，因此，线段 MN 长度的最小值为83；………………………………………………………………………10分（Ⅲ）由（Ⅱ）知，14k =时线段MN 的长度最小，此时64(,)55E，BE =，因为TBE ∆的面积为S =15，所以点T 到直线BE的距离为2S d BE ==，因为直线BE 的方程为20x y +-=，设过点T 且与直线BE 平行的直线m 的方程为0x y t ++=(2)t ≠-=，解得32t =-或52t =-，当32t =-时，直线m 的方程为302x y +-=，联立得 2230244x y x y ⎧+-=⎪⎨⎪+=⎩，消去y 得251250x x -+=，显然判别式0∆>，故点T 有2个；当52t =-时，直线 m 的方程为502x y +-=，联立得2250244x y x y ⎧+-=⎪⎨⎪+=⎩，消去y 得2520210x x -+=，显然判别式0∆<，故点T 不存在．所以，椭圆C 上存在两个点T ，使得TBE ∆的面积为15．…………………………………………16分 20．（本题满分16分）已知等差数列{}n a 的前n 项和为n S ，若423S S =，221n n a a =-．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）对任意的m N *∈，将数列{}n a 中落入区间2(2,2)mm内的项的个数记为{}m b ．①求数列{}m b 的通项公式； ②记2122m m m c b -=-，数列{}m c 前m 项的和为m T ，求出所有使得等式111m m t T t T t c +-=-+成立的正整数m ，t ．【解析】（Ⅰ）设公差为d ，首项为1a ，则由423S S =得114(41)2(21)43[2]22a d a d ⋅-⋅-+⋅=+⋅，即123d a =；由221n n a a =-得21n n a nd a +=-，∴1n a nd =+，将123d a =代入1n a nd =+得1213n na a =+，令1n =得13a =，从而2d =，故21n a n =+；…………4分（Ⅱ）①令22212m m n <+<，则121112222m m n ---<<-，即121221m m n --≤≤-，∴21122m m m b --=-；………………………………………………………………………………8分 ②2211221()222m m m m m c b ---===-，显然数列{}m c 是首项为2，公比为12的等比数列，前m 项的和为m T 14(1)2m =⋅-，由111m m t T t T t c +-=-+取倒数得11m m t m T c t c T t ++-=+-，即111m t m c c T t++=+-，即 1221()12()12(4)()2m t m t ---=--化简得221(4)242m t t -=-⋅-即1(4)242m t t --⋅-=，即1(4)242m t t --⋅=+， ∵1240t -+>，∴(4)20mt -⋅>，∴4t <，又t N *∈，∴1t =或2t =或3t =．……………12分当1t =时，由1(4)242mt t --⋅=+得325m ⋅=，显然无正整数解；当2t =时，由1(4)242m t t --⋅=+得226m ⋅=，即23m =，显然无正整数解；当3t =时，由1(4)242mt t --⋅=+得28m =，显然3m =为正整数解．综上，存在符合条件的正整数3t =，3m =．…………………………………………………………………………………………………16分Ⅱ 附加题部分21．【选做题】B ．（选修4—2：矩阵与变换）（本题满分10分）已知1002M ⎡⎤=⎢⎥⎣⎦，10201N ⎡⎤⎢⎥=⎢⎥⎣⎦，设曲线sin y x =在矩阵MN 对应的变换作用下得到曲线F ，求F 方程．【解析】由题设得11100022020102MN ==⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，设所求曲线F 上任意一点的坐标为(,)x y ，x y sin = 上任意一点的坐标为),(y x ''，则MN ⎥⎦⎤⎢⎣⎡''y x ＝⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡''⎥⎥⎦⎤⎢⎢⎣⎡y x y x 20021，解得⎪⎩⎪⎨⎧='='y y x x 212，把⎪⎩⎪⎨⎧='='y y x x 212代入x y '='sin ，化简得x y 2sin 2=，所以，曲线F 的方程为x y 2sin 2=.C ．（选修4-4：坐标系与参数方程）（本题满分10分）已知直线l 的参数方程为21222x t y t⎧=-+⎪⎪⎨⎪=⎪⎩（为参数），曲线C 的极坐标方程是2sin 1sin θρθ=-，以极点为原点，极轴为轴正方向建立直角坐标系，点(1,0)M -，直线与曲线C 交于A 、B 两点．（Ⅰ）写出直线l 的极坐标方程与曲线C 的普通方程；（Ⅱ）求线段MA 、MB 长度之积MA MB ⋅的值．【解析】（Ⅰ）直线l cos()14πθ+=-，曲线C 的普通方程为2y x =；（Ⅱ）将1x y ⎧=-+⎪⎪⎨⎪=⎪⎩代入2y x =得220t -+=，12||2MA MB t t ⋅==．另解：显然直线:10l x y -+=，联立得210x y y x-+=⎧⎨=⎩，消去y 得210x x --=，所以112x =、21522x =-，不妨设1535(,)2222A --，1535(,)2222B ++，则352()22MA =-、 32(2MB =+，所以332(2(222MA MB ⋅=-+=．【选做题】22．（本题满分10分）如图，在空间直角坐标系O xyz -中，正四棱锥P ABCD -的侧棱长与底面边长都为点M 、N 分别在线段PA 、BD 上，且13PM BN PA BD ==．（Ⅰ）求证：MN AD ⊥；（Ⅱ）求MN 与平面PAD 所成角的正弦值．【解析】（Ⅰ）∵正四棱锥P ABCD -的侧棱长与底边长都为，∴3OA =，3OP =，则(3,0,0)A ，(0,3,0)B 、(0,3,0)D -，(0,0,3)P ，所以(1,0,2)M ，(0,1,0)N ，(1,1,2)0MN =--≠，(3,3,0)0AD =--≠，∴(1)(3)1(3)(2)00MN AD ⋅=-⋅-+⋅-+-⋅=，所以MN AD ⊥；（Ⅱ）设平面PAD 的一个法向量为(,,)n x y z =，(3,0,3)AP =-，由00n AD n AP ⎧⋅=⎪⎨⋅=⎪⎩得330330x y x z --=⎧⎨-+=⎩，取1z =，则1x =，1y =-，即(1,1,1)n =-，则cos ,||||n MN n MN n MN ⋅<>==⋅ =MN 与平面PAD 所成角为θ，sin |cos ,|n MN θ=<>=，MN 与平面PAD 所成． 23．（本题满分10分）在平面直角坐标系xOy 中，已知点(2,2)M ，P 是动点，且POM ∆的三边所在直线的斜率满足OM OP PM k k k +=．（Ⅰ）求点P 的轨迹C 的方程；（Ⅱ）点N 在直线41y x =-上，过N 作（Ⅰ）中轨迹C 的两切线，切点分别为A 、B ，若ABN ∆ 是直角三角形，求点N 的坐标．【解析】（Ⅰ）设(,)P x y ，由OM OP PM k k k +=得212y y x x -+=-，即22x y =，所以P 点的轨迹C 的方程是22x y =(0x ≠且2)x ≠；（Ⅱ）因为212y x =，所以'y x =，设2111(,)2A x x ，2221(,)2B x x （12x x ≠），(,)N a b ，则1AN k x =， 2BN k x =，由于AN 是曲线的切线，所以211112x b x x a-=-，即211220x ax b -+=，同理222220x ax b -+=，两式相减得121212()()2()0x x x x a x x +---=，又12x x ≠，故122x x a +=．1︒ 若AN BN ⊥，则1AN BNk k =-，所以121x x =-，由⎧⎪⎨⎪⎩211222122202201x ax b x ax b x x -+=-+==-得 221212()2()40x x a x x b +-++=即2121212[()2]2()40x x x x a x x b +--++=即2(2)22240a a a b +-⋅+=，所以12b =-，又41b a =-，所以18a =，此时11(,)82N -； 2︒ 若AN AB ⊥，则1AN ABk k =-，即222112111221x x x x x -⋅=--，化简得121()20x x x ++=，即。

江苏省2015届高三下学期高考南通密数学试题含解析

一、填空题:本大题共14个小题，每小题5分,共70分。

1。

设,a b R ∈,231a bii i+=+-，其中i 是虚数单位，则a b += ．【答案】6 【解析】试题分析：23(23)(1)55,161a bii a bi i i a bi i a b a b i+=+⇒+=+-⇒+=+⇒==⇒+=- 考点:复数相等2.已知集合{}P x x a =≤，{}sin ,Q y y R θθ==∈．若P Q ⊇,则实数a 的取值范围是．【答案】[1,)+∞ 【解析】试题分析：sin P Q a θ⊇⇒≤恒成立,因此max(sin )1a θ≥=考点：集合包含关系,不等式恒成立3.为了了解一片经济林的生长情况,随机测量了其中100株树木的底部周长（单位：cm ),所得数据如图．则在这100株树木中，底部周长不小于100cm 的有株．【答案】70 【解析】试题分析：底部周长不小于100cm 的概率为1(0.010.02)100.7-+⨯=，所以底部第3题图周长不小于100cm的有0.710070⨯=株考点：频率分布直方图4.设向量(1,)a m=，(1,2)b m=-，且a b ≠,若()a b a-⊥，则实数m=．【答案】1【解析】试题分析:2()(2,2)(1,)032021a b a m m m m m m m-⊥⇒--⋅=⇒-+=⇒==或，又a b ≠，所以2, 1.m m≠=考点：向量垂直，向量数量积5。

如图所示的流程图的运行结果是．【答案】20【解析】试题分析：第一次循环：5,4S a==，第二次循环:20,34S a==<，结束循环,输出20.S=考点：循环结构流程图6。

将边长为a的正方形ABCD沿对角线AC折起,使BD a=，则三棱锥D ABC-的体积为．【答案】3【解析】试题分析：取AC中点M，则DM BM==，222+DM BM BD=，即DM BM⊥，因第5题图为,DM AC ⊥,所以DM ABC ⊥面,三棱锥D ABC -的体积为23111.332ABCDM S a ∆⋅=⨯ 考点：三棱锥体积7。

江苏省南通市2014届高三第二次调研测试数学试题(解析版)

江苏省南通市2014届高三第二次调研测试数学试题（解析版）一、填空题（每题5分，满分70分，将答案填在答题纸上）1.已知集合{}{}31A x x x x =<-≥，则A =R ð ▲ ．2.某学校有8个社团，甲、乙两位同学各自参加其中一个社团，且他俩参加各个社团的可能性相同，则这两位同学参加同一个社团的概率为 ▲ ．3.复数i 1iz =-（其中i 为虚数单位）的模为 ▲ ．4.从编号为0，1，2，…，79的80件产品中，采用系统抽样的方法抽取容量是5的样本，若编号为28的产品在样本中，则该样本中产品的最大编号为 ▲ ．考点：系统抽样5.根据如图所示的伪代码，最后输出的a 的值为 ▲ ．6.若12log 11a a <-，则a 的取值范围是 ▲ ．7.若函数32()f x x ax bx =++为奇函数，其图象的一条切线方程为3y x =-b 的值为 ▲ ．8.设l，m表示直线，α表示平面，m是α内任意一条直线．则“l m⊥”成立⊥”是“lα的▲条件．（在“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选填一个）9.在平面直角坐标系xOy中，设A是半圆O：222x≥）上一点，直线OA的倾斜+=（0x y角为45°，过点A作x轴的垂线，垂足为H，过H作OA的平行线交半圆于点B，则直线AB 的方程是▲．10.在△ABC中，D是BC的中点，AD＝8，BC＝20，则AB AC⋅的值为▲．11.设x，y，z是实数，9x，12y，15z成等比数列，且1x ，1y，1z成等差数列，则x zz x+的值是▲．12.设π6是函数()()sin2f x xϕ=+的一个零点，则函数()f x在区间()02π，内所有极值点之和为▲．13.若不等式(mx－1)［3m 2－( x + 1)m－1］≥0对任意(0)m∈+∞，恒成立，则实数x的值为▲．14.设实数a，b，c满足a2＋b2≤c≤1，则a＋b＋c的最小值为▲．三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.）15.在△ABC中，已知916AB AC AB BC⋅=⋅=-，．求：（1）AB的值；（2）sin()sinA BC-的值．试题解析：（1）因为916⋅=⋅=-，，…………………………… 4分AB AC AB BC16.在四棱锥P－ABCD中，AB∥DC，AB⊥平面PAD， PD＝AD，AB＝2DC，E是PB的中点．求证：（1）CE∥平面PAD；（2）平面PBC⊥平面PAB．EF CD，于是四边形DCEF是平行四边形，空气中释放的浓度y （单位：毫克/立方米）随着时间x (单位：天)变化的函数关系式近似为161048154102x x y x x ⎧-⎪-=⎨⎪-<⎩，≤≤，，≤．若多次喷洒，则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和．由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时，它才能起到净化空气的作用．（1）若一次喷洒4个单位的净化剂，则净化时间可达几天?（2）若第一次喷洒2个单位的净化剂，6天后再喷洒a （14a ≤≤）个单位的药剂，要使接下来的4天中能够持续有效净化，试求a 的最小值（精确到0.11.4）．18.在平面直角坐标系xOy 中，设曲线C 1：1(0)x y a b a b +=>>所围成的封闭图形的面积为C 1上的点到原点O ．以曲线C 1与坐标轴的交点为顶点的椭圆记为C 2．（1）求椭圆C 2的标准方程；（2）设AB 是过椭圆C 2中心O 的任意弦，l 是线段AB 的垂直平分线．M 是l 上的点（与O 不重合）．①若MO ＝2OA ，当点A 在椭圆C 2上运动时，求点M 的轨迹方程； ②若M 是l 与椭圆C 2的交点，求△AMB 的面积的最小值①由l是线段AB的垂直平分线，可转化为：0⋅=，又由MO＝2OA，可转化得到：OA OM=，这2OM OA所以22222222888(1)181818A Ak kOA x yk k k+=+=+=+++，222232(1)418kAB OAk+==+.19.设数列{a n }的首项不为零，前n 项和为S n ，且对任意的r ，t ∈N *，都有()2rt S r S t=．（1）求数列{a n }的通项公式（用a 1表示）；（2）设a 1=1，b 1=3，()1*2n n b b S n n -=∈N ≥，，求证：数列{}3log n b 为等比数列；（3）在（2）的条件下，求121nk n k k b T b -==-∑消的方法，可得：()211122222111112313131k k n nnk n k k k b T b ----====-=-----∑∑．20.设函数()e ()x f x ax a a =-+∈R ，其图象与x 轴交于1(0)A x ，，2(0)B x ，两点，且x 1＜x 2．（1）求a 的取值范围；（2）证明：0f '<（()f x '为函数()f x 的导函数）；（3）设点C 在函数()y f x =的图象上，且△ABCt =，求(1)(1)a t --的值．所以(ln)(2ln)0a>．.=-<，即2ef a a a数学Ⅱ（附加题）21.A．选修4—1：几何证明选讲如图，△ABC内接于圆O，D为弦BC上一点，过D作直线DP // AC，交AB于点E，交圆O在A 点处的切线于点P ．求证：△P AE ∽△BDE ．21.B ．选修4—1：矩阵与变换已知二阶矩阵M 有特征值1λ=及对应的一个特征向量111⎡⎤=⎢⎥-⎣⎦e ，且M 11⎡⎤⎢⎥⎣⎦＝31⎡⎤⎢⎥⎣⎦．求矩阵M ．21.C．选修4—4：坐标系与参数方程在平面直角坐标系xOy中，设动点P，Q都在曲线C：12cos2sinxyθθ=+⎧⎨=⎩，（θ为参数）上，且这两点对应的参数分别为θ＝α与θ＝2α(0＜α＜2π)，设PQ的中点M与定点A(1，0)间的距离为d，求d的取值范围．21.D ．选修4—5：不等式选讲已知：2a x ∈≥，R ．求证：|1|||x a x a -++-≥3．所以|1|||3x a x a -++-≥． (10)分考点：含有绝对值不等式的运用22.在长方体ABCD —A 1B 1C 1D 1中，112AD AA AB ==，点E 是棱AB 上一点．且AE EB λ=．（1）证明：11D E A D ⊥；（2）若二面角D 1—EC —D 的大小为π4，求λ的值．一点，所以λ＞0，故所求的λ值为2 33－1．所以()11211(101)01D E A D λλ⋅=-⋅--=+，，，，．23.设数列{a n }共有n （3n n ∈N ≥，）项，且11n a a ==，对每个i (1≤i ≤1n -，i ∈N )，均有{}11122i i a a +∈，，．（1）当3n =时，写出满足条件的所有数列{a n }（不必写出过程）；（2）当8n =时，求满足条件的数列{a n }的个数．第 21 页共 21 页因为{}211122a a ∈，，，{}321122a a ∈，，，即{}21122a ∈，，，{}211122a ∈，，，。

2015年江苏省南通市高三二模考试数学试题及答案

南通市2015届高三第二次调研测试数学学科一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位置上．．．．．．．．． 1．命题“x ∃∈R ，20x >”的否定是“ ▲ ”．【答案】x ∀∈R ，20x ≤2．设1i i 1ia b +=+-(i 为虚数单位，a ，b ∈R )，则ab 的值为 ▲ ．【答案】03．设集合{}11 0 3 2A =-，，，，{}2 1B x x =≥，则AB = ▲ ．【答案】{}1 3-，4．执行如图所示的伪代码，则输出的结果为 ▲ ．【答案】115．一种水稻试验品种连续5年的平均单位面积产量(单位：t/hm 2)如下：9.8，9.9，10.1，10，10.2，则该组数据的方差为 ▲ ．【答案】0.026．若函数()π()2sin 3f x x ω=+(0)ω>的图象与x 轴相邻两个交点间的距离为2，则实数ω的值为▲ ．【答案】π27．在平面直角坐标系xOy 中，若曲线ln y x =在e x =(e 为自然对数的底数)处的切线与直线30ax y -+=垂直，则实数a 的值为 ▲ ．【答案】e -8．如图，在长方体1111ABCD A B C D -中，AB =3 cm ，AD =2 cm ，1AA =1 cm ，则三棱锥11B ABD -的体积为 ▲ cm 3．【答案】19．已知等差数列{}n a 的首项为4，公差为2，前n 项和为n S ．若544k k S a +-=(k *∈N )，则k 的值为 ▲ ．【答案】710．设32()4(3)f x x mx m x n =++-+(m n ∈R ，)是R 上的单调增函数，则m 的值为 ▲ ．AA 1B不CB 1不C 1不D 1不D（第8题）I ← 1While I < 7 S ← 2 I + 1 I ← I + 2 End While Print S（第4题）【答案】611．在平行四边形ABCD 中，AC AD AC BD ⋅=⋅3=，则线段AC 的长为 ▲ ．解1：()3a b a +=，()()3a b a b +-=，（1）×2-（2解2：AC BD ⋅-0AC AD ⋅=，得()0AC BD AD ⋅-=，即0AC BA ⋅=，射影得AC AD ⋅=2AC =3，AC =．12．如图，在△ABC 中，3AB =，2AC =，4BC =，点D在边BC 上，BAD ∠=45°，则tan CAD ∠的值为 ▲ ．13．设x ，y ，z 均为大于1的实数，且z 为x 和y 的等比中项，则lg lg 4lg lg z zx y+的最小值为 ▲ ．【答案】9814．在平面直角坐标系xOy 中，圆1C ：22(1)(6)25x y ++-=，圆2C ：222(17)(30)x y r -+-=．若圆2C 上存在一点P ，使得过点P 可作一条射线与圆1C 交于点A ，B ，满足2PA AB =，则半径r 的取值范围是 ▲ ．【答案】[]5 55，设00(,)P x y ，11(,)A x y ，22(,)B x y ．则由2PA AB =得10232x x x -=，10232y y y -=．将A ，B 坐标代入圆1C 的方程，得222112220011(1)(6)5,21210()()().333x y x y x y ⎧++-=⎪⎨-+-+-=⎪⎩此方程组有解等价于两方程对应的两圆有公共点，于是10105533-≤≤+，整理得525≤≤有解．令d=525d ≤≤有解．BDC（第12题）A当点1C 在圆2C 外时，min 30d r =-，max 30d r =+；当点1C 在圆2C 内时，min 30d r =-，max 30d r =+．于是305r +≥，|30|25r -≤，解得555r ≤≤．二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答.解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）如图，在四面体ABCD 中，平面BAD ⊥平面CAD ，BAD ∠=90°．M ，N ，Q 分别为棱AD ，BD ，AC 的中点．（1）求证：//CD 平面MNQ ；（2）求证：平面MNQ ⊥平面CAD ．证明：（1）因为M ，Q 分别为棱AD ，AC 的中点，所以//MQ CD ． ……2分又CD ⊄平面MNQ ，MQ ⊂平面MNQ ，故//CD 平面MNQ ． ……6分（2）因为M ，N 分别为棱AD ，BD 的中点，所以//MN AB ．又90BAD ∠=°，故MN AD ⊥． ……8分因为平面BAD ⊥平面CAD ，平面BAD平面CAD AD =，且MN ⊂平面ABD ，所以MN ⊥平面ACD ． ……11分又MN ⊂平面MNQ ，平面MNQ ⊥平面CAD ． ……14分（注：若使用真命题“如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面”证明“MN ⊥平面ACD ”，扣1分．）16．（本小题满分14分）体育测试成绩分为四个等级：优、良、中、不及格．某班50名学生参加测试的结果如下：（1）从该班任意抽取1名学生，求这名学生的测试成绩为“良”或“中”的概率；（2）测试成绩为“优”的3名男生记为1a ，2a ，3a ，2名女生记为1b ，2b ．现从这5人中任选2人参加学校的某项体育比赛． ①写出所有等可能的基本事件；A BCDMNQ（第15题）②求参赛学生中恰有1名女生的概率．解：（1）记“测试成绩为良或中”为事件A ，“测试成绩为良”为事件1A ，“测试成绩为中”为事件2A ，事件1A ，2A 是互斥的. ……2分由已知，有121923()()5050P A P A ==，． ……4分因为当事件1A ，2A 之一发生时，事件A 发生，所以由互斥事件的概率公式，得1212192321()()()()505025P A P A A P A P A =+=+=+=． ……6分（2）①有10个基本事件：12()a a ，，13()a a ，，11()a b ，，12()a b ，，23()a a ，，21()a b ，，22()a b ，，31()a b ，，32()a b ，，12()b b ，． ……9分②记“参赛学生中恰好有1名女生”为事件B ．在上述等可能的10个基本事件中，事件B包含了11()a b ，，12()a b ，，21()a b ，，22()a b ，，31()a b ，，32()a b ，．故所求的概率为63()105P B ==．答：（1）这名学生的测试成绩为“良”或“中”的概率为2125；（2）参赛学生中恰有1名女生的概率为35． ……14分（注：不指明互斥事件扣1分；不记事件扣1分，不重复扣分；不答扣1分．事件B 包含的6种基本事件不枚举、运算结果未化简本次阅卷不扣分．）17．（本小题满分14分）在平面直角坐标系xOy 中，已知向量=a (1，0)，=b (0，2).设向量=+x a (1cos θ-)b ，k =-y a 1θ+b ，其中0πθ<<．（1）若4k =，π6θ=，求x ⋅y 的值；（2）若x //y ，求实数k 的最大值，并求取最大值时θ的值．解：（1）（方法1）当4k =，π6θ=时，(12=，x ，=y (44-，)， ……2分则⋅=x y (1(4)244⨯-+-⨯=- ……6分（方法2）依题意，0⋅=a b ， ……2分则⋅=x y (()(22142421⎡⎤+-⋅-+=-+⨯⎢⎥⎣⎦a b a b a b(421443=-+⨯⨯=． ……6分（2）依题意，()122cos θ=-，x ，()2sin k θ=-，y ，因为x //y ，所以2(22cos )k θθ=--，整理得，()1sin cos 1kθθ=-， ……9分令()()sin cos 1f θθθ=-，则()()cos cos 1sin (sin )f θθθθθ'=-+-22c o s c o s 1θθ=-- ()()2cos 1cos 1θθ=+-. ……11分令()0f θ'=，得1cos 2θ=-或cos 1θ=，又0πθ<<，故2π3θ=．列表：故当2π3θ=时，min ()f θ=，此时实数k 取最大值 ……14分（注：第（2）小问中，得到()122cos θ=-，x ，()2sin k θ=-，y ，及k 与θ的等式，各1分）18．（本小题满分16分）如图，在平面直角坐标系xOy 中，椭圆2222 1 ( 0 )y x a b a b+=>>的左顶点为A ，右焦点为(0)F c ，．00( )P x y ，为椭圆上一点，且PA PF ⊥．（1）若3a =，b 0x 的值；（2）若00x =，求椭圆的离心率；（3）求证：以F 为圆心，FP 为半径的圆与椭圆的右准线2a x c=相切．解：（1）因为3a =，b =2224c a b =-=，即2c =．由PA PF ⊥得，0000132y y x x ⋅=-+-，即22006y x x =--+． ……3分又22001x y +=，所以204990x x +-=，解得034x =或03x =-(舍去)． ……5分（2）当00x =时，220y b =，由PA PF ⊥得，001y y a c⋅=--，即2b ac =，故22a c ac -=， ……8分所以210e e +-=，解得e ． ……10分（3）依题意，椭圆右焦点到直线2a x c =的距离为2a c c -，且2200221x y a b+=．① 由PA PF ⊥得，00001y y x a x c⋅=-+-，即2200()y x c a x ca =-+-+． ② 由①②得，22000()()()0x a b x a a x c ⎡⎤+---=⎣⎦，解得()2202a a ac c x c --=-（0x a =-舍去）. ……13分所以PF ==0c a x a =-()222a a ac c c a a c --=+⋅2a c c =-，所以以F 为圆心，FP 为半径的圆与右准线2a x c=相切． ……16分（注：第（3）小问中，得到椭圆右焦点到直线2a x c =的距离为2a c c-，得1分；直接使用焦半径（第18题）公式扣1分）19．（本小题满分16分）设a ∈R ，函数()f x x x a a =--．（1）若()f x 为奇函数，求a 的值；（2）若对任意的[2 3]x ∈，，()0f x ≥恒成立，求a 的取值范围；（3）当4a >时，求函数()()y f f x a =+零点的个数．解：（1）若()f x 为奇函数，则()()f x f x -=-，令0x =得，(0)(0)f f =-，即(0)0f =，所以0a =，此时()f x x x =为奇函数． ……4分（2）因为对任意的[2 3]x ∈，，()0f x ≥恒成立，所以min ()0f x ≥．当0a ≤时，对任意的[2 3]x ∈，，()0f x x x a a =--≥恒成立，所以0a ≤；……6分当0a >时，易得22 () x ax a x a f x x ax a x a ⎧-+-<⎪=⎨--⎪⎩，，，≥在(2a ⎤-∞⎥⎦，上是单调增函数，在 a a ⎡⎤⎢⎥⎣⎦，上是单调减函数，在[) a +∞，上是单调增函数．当02a <<时，min ()(2)2(2)0f x f a a ==--≥，解得43a ≤，所以43a ≤；当23a ≤≤时，min ()()0f x f a a ==-≥，解得0a ≤，所以此时a 不存在；当3a >时，{}{}min ()min (2)(3)min 2(2)3(3)0f x f f a a a a ==----，，≥，解得92a ≥，所以92a ≥；综上得，43a ≤或92a ≥． ……10分（3）设[]()()F x f f x a =+．令()t f x a x x a =+=-，则()y f t ==t t a a --，4a >．第一步，()0f t =t t a a ⇔-=，所以，当t a <时，20t at a -+=，判别式(4)0a a ∆=->，解得1t =2t =；当t a ≥时，由()0f t =得，即()t t a a -=，解得3t 第二步，易得12302a t t a t <<<<<，且24a a <． ①若1x x a t -=，其中2104a t <<，当x a <时，210x ax t -+=，记21()p x x ax t =-+，因为对称轴2a x a =<，1()0p a t =>，且21140a t ∆=->，所以方程210t at t -+=有2个不同的实根；当x a ≥时，210x ax t --=，记21()q x x ax t =--，因为对称轴a x a =<，1()0q a t =-<，且22140a t ∆=+>，所以方程210x ax t --=有1个实根，从而方程1x x a t -=有3个不同的实根；②若2x x a t -=，其中2204a t <<，由①知，方程2x x a t -=有3个不同的实根；③若3x x a t -=，当x a >时，230x ax t --=，记23()r x x ax t =--，因为对称轴2a x a =<，3()0r a t =-<，且23340a t ∆=+>，所以方程230x ax t --=有1个实根；当x a ≤时，230x ax t -+=，记23()s x x ax t =--，因为对称轴2a x a =<，3()0s a t =>，且2334a t ∆=-，2340a t ->⇔324160a a -->， ……14分记32()416m a a a =--，则()(38)0m a a a '=->，故()m a 为(4 )+∞，上增函数，且(4)160m =-<，(5)90m =>，所以()0m a =有唯一解，不妨记为0a ，且0(45)a ∈，，若04a a <<，即30∆<，方程230x ax t -+=有0个实根；若0a a =，即30∆=，方程230x ax t -+=有1个实根；若0a a >，即30∆>，方程230x ax t -+=有2个实根．所以，当04a a <<时，方程3x x a t -=有1个实根；当0a a =时，方程3x x a t -=有2个实根；当0a a >时，方程3x x a t -=有3个实根．综上，当04a a <<时，函数[]()y f f x a =+的零点个数为7；当0a a =时，函数[]()y f f x a =+的零点个数为8；当0a a >时，函数[]()y f f x a =+的零点个数为9． ……16分（注：第（1）小问中，求得0a =后不验证()f x 为奇函数，不扣分；第（2）小问中利用分离参数法参照参考答案给分；第（3）小问中使用数形结合，但缺少代数过程的只给结果分）20．（本小题满分16分）设{}n a 是公差为d 的等差数列，{}n b 是公比为q (1q ≠)的等比数列．记n n n c a b =+．（1）求证：数列{}1n n c c d +--为等比数列；（2）已知数列{}n c 的前4项分别为4，10，19，34． ①求数列{}n a 和{}n b 的通项公式；②是否存在元素均为正整数的集合A ={1n ，2n ，…，} k n (4k ≥，k *∈N )，使得数列1n c ，2n c ，…，k n c 为等差数列？证明你的结论．解：（1）依题意，()()111n n n n n n c c d a b a b d +++--=+-+-()()11n n n n a a d b b ++=--+-(1)0n b q =-≠， ……3分从而2111(1)(1)n n n n n n c c d b q q c c d b q ++++---==---，所以{}1n n c c d +--是首项为1(1)b q -，公比为q 的等比数列． ……5分（2）①法1：因数列{}n c 的前4项分别为4，10，19，34，故{}1n n c c d +--的前3项为6d -，9d -，15d -，由（1）得，{}1n n c c d +--是等比数列，则()29d -=()()615d d --，解得3d =，从而2q =， ……7分且11114 3210 a b a b +=⎧⎨++=⎩，，解得11a =，13b =，所以32n a n =-，132n n b -=⋅． ……10分法2：依题意，得1111211311410219334a b a d b q a d b q a d b q +=⎧⎪++=⎪⎨++=⎪⎪++=⎩，，，， ……7分消去1a ，得1121132116915d b q b d b q b q d b q b q +-=⎧⎪+-=⎨⎪+-=⎩，，，消去d ，得2111321112326b q b q b b q b q b q ⎧-+=⎪⎨-+=⎪⎩，，消去1b ，得2q =，从而可解得，11a =，13b =，3d =，所以32n a n =-，132n n b -=⋅． ……10分 ②假设存在满足题意的集合A ，不妨设l ，m ，p ，r A ∈()l m p r <<<，且l c ，m c ，p c ，r c 成等差数列，则2m p l c c c =+，因为0l c >，所以2m p c c >，（*）若1p m >+，则2p m +≥，结合（*）得，112(32)32(32)32m p m p --⎡⎤-+⋅>-+⋅⎣⎦13(2)232m m ++-+⋅≥，化简得，8203m m -<-<，（**）因为2m ≥，m *∈N ，不难知20m m ->，这与（**）矛盾，所以只能1p m =+．同理，1r p =+．所以m c ，p c ，r c 为数列{}n c 的连续三项，从而122m m m c c c ++=+，即()11222m m m m m m a b a b a b +++++=+++，故122m m m b b b ++=+，由132n n b -=⋅得45=，矛盾，所以假设不成立，从而不存在满足题意的集合A ． ……16分（注：第（2）小问②中，在正确解答①的基础上，写出结论“不存在”，就给1分）南通市2015届高三第二次调研测试数学Ⅱ（附加题）A ．[选修4-1：几何证明选讲]（本小题满分10分）如图，从圆O 外一点P 引圆的切线PC 及割线PAB ，C 为切点．求证：AP BC AC CP ⋅=⋅．证明：因为PC 为圆O 的切线，所以PCA CBP ∠=∠， ……3分又CPA CPB ∠=∠，故△CAP ∽△BC P ， ……7分所以AC AP =，即AP BC AC CP ⋅=⋅． ……10分B ．[选修4-2：矩阵与变换]（本小题满分10分）设23⎡⎤⎢⎥⎣⎦是矩阵232a ⎡⎤=⎢⎥⎣⎦M 的一个特征向量，求实数a 的值．解：设23⎡⎤⎢⎥⎣⎦是矩阵M 属于特征值λ的一个特征向量，则232a ⎡⎤⎢⎥⎣⎦23λ⎡⎤=⎢⎥⎣⎦23⎡⎤⎢⎥⎣⎦， ……5分故262 123 a λλ+=⎧⎨=⎩，，解得4 1. a λ⎧⎨=⎩=，……10分C ．[选修4-4：坐标系与参数方程]（本小题满分10分）在极坐标系中，设直线π3θ=与曲线210cos 40ρρθ-+=相交于A ，B 两点，求线段AB 中点的极坐标．解：（方法1）将直线π3θ=化为普通方程得，y =，将曲线210cos 40ρρθ-+=化为普通方程得，221040x y x +-+=， ……4分联立221040y x y x ⎧=⎪⎨+-+=⎪⎩，并消去y 得，22520x x -+=，解得112x =，22x =，P（第21 - A 题）所以AB 中点的横坐标为12524x x +=……8分化为极坐标为()5π 23，． ……10分（方法2）联立直线l 与曲线C 的方程组2π310cos 40θρρθ⎧=⎪⎨⎪-+=⎩，，……2分消去θ，得2540ρρ-+=，解得11ρ=，24ρ=， ……6分所以线段AB 中点的极坐标为()12π 23ρρ+，，即()5π 23，． ……10分（注：将线段AB 中点的极坐标写成()5π 2π ()23k k +∈Z ，的不扣分）D ．[选修4-5：不等式选讲]（本小题满分10分）设实数a ，b ，c 满足234a b c ++=，求证：2228a b c ++≥．证明：由柯西不等式，得()()222222123a b c ++++≥()223a b c ++， ……6分因为234a b c ++=，故22287a b c ++≥， ……8分当且仅当123a b c ==，即27a =，47b =，67c =时取“=”． ……10分【必做题】第22题、第23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）如图，在平面直角坐标系xOy 中，点(84)A -，，(2)P t ，(0)t <在抛物线22y px =(0)p >上．（1）求p ，t 的值；（2）过点P 作PM 垂直于x 轴，M 为垂足，直线AM 与抛物线的另一交点为B ，点C 在直线AM 上．若PA ，PB ，PC 的斜率分别为1k ，2k ，3k ，且1232k k k +=，求点C 的坐标．解：（1）将点(84)A -，代入22y px =，得1p =， ……2分将点(2)P t ，代入22y x =，得2t =±，因为0t <，所以2t =-． ……4分（2）依题意，M 的坐标为(20)，，直线AM 的方程为2433y x =-+，（第22题）联立224332y x y x⎧=-+⎪⎨⎪=⎩，并解得B ()112，， ……6分所以113k =-，22k =-，代入1232k k k +=得，376k =-， ……8分从而直线PC 的方程为7163y x =-+，联立24337163y x y x ⎧=-+⎪⎨⎪=-+⎩，并解得C ()823-，． ……10分23．（本小题满分10分）设A ，B 均为非空集合，且AB =∅，AB ={ 123，，，…，}n (n ≥3，n *∈N )．记A ，B 中元素的个数分别为a ，b ，所有满足“a ∈B ，且b A ∈”的集合对(A ，B )的个数为n a ．（1）求a 3，a 4的值；（2）求n a 的表达式．解：（1）当n =3时，AB ={1，2，3}，且AB =∅．若a =1，b =2，则1B ∈，2A ∈，共01C 种；若a =2，b =1，则2B ∈，1A ∈，共11C 种．所以a 3=01C 11+ C 2=； ……2分当n =4时，A B ={1，2，3，4}，且A B =∅．若a =1，b =3，则1B ∈，3A ∈，共02C 种；若a =2，b =2，则2B ∈，2A ∈，这与AB =∅矛盾；若a =3，b =1，则3B ∈，1A ∈，共22C 种．所以a 4=02C 22+ C 2=． ……4分（2）当n 为偶数时，A B ={1，2，3，…，n }，且A B =∅．若a =1，b 1n =-，则1B ∈，1n -A ∈，共02C n -（考虑A ）种；若a =2，b 2n =-，则2B ∈，2n -A ∈，共12C n -（考虑A ）种； ……若a =12n -，b 12n =+，则12n -B ∈，12n +A ∈，共22C nn --（考虑A ）种；若a =2n ，b 2n =，则2n B ∈，2n A ∈，这与AB =∅矛盾；若a 12n =+，b 12n =-，则12n +B ∈，12n -A ∈，共22C nn -（考虑A ）种； ……若a =1n -，b 1=，则1n -B ∈，1A ∈，共（考虑A ）22C n n --种．所以a n =02Cn -+12Cn -+…+222C n n --+22Cn n -+…+122222C2Cn n n n n -----=-． ……8分当n 为奇数时，同理得，a n =02C n -+12C n -+…+222C 2n n n ---=．综上得，122222C 2 .n n n n n n a n ----⎧⎪-=⎨⎪⎩，为偶数，，为奇数 ……10分。

数学_2014-2015学年江苏省南通市某校高三(上)第二次学情调研数学试卷(理科)(含答案)

2014-2015学年江苏省南通市某校高三（上）第二次学情调研数学试卷（理科）一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．1. 若集合A ={0, 1}，集合B ={0, −1}，则A ∪B =________．2. 复数Z 满足(1+i)Z =|1−i|，是Z 的虚部为________．3. 抛物线y =−4x 2的准线方程是________．4. 若ac >0且bc <0，直线ax +by +c =0不通过第________象限．5. 椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右顶点分别是A ，B ，左、右焦点分别是F 1，F 2．若|AF 1|，|F 1F 2|，|F 1B|成等比数列，则此椭圆的离心率为________．6. 已知一个圆锥的侧面展开图是一个半径为3，圆心角为23π的扇形，则此圆锥的体积为________．7. △ABC 中，若sin(π−A)=35，tan(π+B)=125，则cosC ＝________．8.如图所示为函数f(x)=2sin(ωx +ϕ)(ω>0, π2≤ϕ≤π)的部分图象，其中A ，B 两点之间的距离为5，那么f(−1)=________．9. 若双曲线x 2a 2−y 2b 2=λ(λ≠0)的一条渐近线方程是y =2x ，则离心率e 的值为________． 10. 下列有关命题的说法正确的是________．①命题“若x 2=1，则x =1”的否命题为：“若x 2=1，则x ≠1”；②已知x >0时，(x −1)f′(x)<0，若△ABC 是锐角三角形，则f(sinA)>f(cosB)； ③命题“若x =y ，则sinx =siny”的逆否命题为真命题；④命题“∃x ∈R 使得x 2+x +1<0”的否定是：“∀x ∈R 均有x 2+x +1>0”．11. 已知A(−2, 0)，B(2, 0)，点P 在圆(x −3)2+(y −4)2=r 2(r >0)上，满足PA 2+PB 2=40，若这样的点P 有两个，则r 的取值范围是________．12. 定义在R 上的函数f(x)满足：f′(x)>1−f(x)，f(0)=6，f′(x)是f(x)的导函数，则不等式e x f(x)>e x +5（其中e 为自然对数的底数）的解集为________．13. O 为△ABC 的外接圆圆心，AB =10，AC =4，∠BAC 为钝角，M 是边BC 的中点，则AM →⋅AO →=________．14. 已知函数y =f(x)是定义域为R 的偶函数．当x ≥0时，f(x)={516x 2(0≤x ≤2)(12)x +1(x >2)，若关于x 的方程[f(x)]2+af(x)+b =0，a ，b ∈R 有且仅有6个不同实数根，则实数a 的取值范围是________．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15. 已知向量a →=(sinx, 34)，b →=(cosx, −1)． (1)当a → // b →时，求cos 2x −sin2x 的值；(2)设函数f(x)=2(a →+b →)⋅b →，已知在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若a =√3，b =2，sinB =√63，求 f(x)+4cos(2A +π6)（x ∈[0, π3]）的取值范围．16.在正四面体ABCD 中，点F 在CD 上，点E 在AD 上，且DF:FC =DE:EA =2:3．证明：（1）EF // 平面ABC ；（2）直线BD ⊥直线EF ．17. 某小区想利用一矩形空地ABCD 建造市民健身广场，设计时决定保留空地边上的一个水塘（如图中阴影部分），水塘可近似看作一个等腰直角三角形，其中AD =60m ，AB =40m ，且△EFG 中，∠EGF =90∘，经测量得到AE =10m ，EF =20m ．为保证安全同时考虑美观，健身广场周围准备加设一个保护栏．设计时经过点G 作一条直线交AB ，DF 于M ，N ，从而得到五边形MBCDN 的市民健身广场．（1）假设DN =x(m)，试将五边形MBCDN 的面积y 表示为x 的函数，并注明函数的定义域；（2）问：应如何设计，可使市民健身广场的面积最大？并求出健身广场的最大面积． 18. 已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1，F 2，短轴两个端点为A ，B ，且四边形F 1AF 2B 是边长为2的正方形．(1)求椭圆的方程；(2)若C ，D 分别是椭圆长的左、右端点，动点M 满足MD ⊥CD ，连接CM ，交椭圆于点P ．证明：OM →⋅OP →为定值．(3)在(2)的条件下，试问x 轴上是否存异于点C 的定点Q ，使得以MP 为直径的圆恒过直线DP ，MQ 的交点，若存在，求出点Q 的坐标；若不存在，请说明理由． 19. 已知函数f(x)=x ⋅lnx ，g(x)=ax 3−12x −23e ．（1）求f(x)的单调增区间和最小值；（2）若函数y =f(x)与函数y =g(x)在交点处存在公共切线，求实数a 的值；（3）若x ∈(0, e 2]时，函数y =f(x)的图象恰好位于两条平行直线l 1:y =kx ；l 2:y =kx +m 之间，当l 1与l 2间的距离最小时，求实数m 的值．20. 已知函数f(x)=ax 2+bx +1(a ，b 为实数，a ≠0，x ∈R)，F(x)={f(x),x >0−f(x),x <0．（1）若f(−1)=0，且函数f(x)的值域为[0, +∞)，求F(x)的表达式；（2）设mn <0，m +n >0，a >0，且函数f(x)为偶函数，判断F(m)+F(n)是否大于0？（3）设g(x)=lnx+1e x，当a =b =1时，证明：对任意实数x >0，[F(x)−1]g′(x)<1+e −2（其中g′(x)是g(x)的导函数）．第Ⅱ卷（理科加试）（总分40分，考试时间30分钟）21. 将曲线y =2sin4x 经矩阵M 变换后的曲线方程为y =sinx ，求变换矩阵M 的逆矩阵． 22. 以直角坐标系的原点O 为极点，x 轴的正半轴为极轴，且两个坐标系取相等的长度单位．已知直线l 的参数方程为{x =1+tcosαy =tsinα (t 为参数，0<α<π)，曲线C 的极坐标方程为ρsin 2θ=4cosθ．（1）求曲线C 的直角坐标方程；（2）设直线l 与曲线C 相交于A 、B 两点，当α变化时，求|AB|的最小值． 23. 已知动圆过定点F(0, 2)，且与定直线L:y =−2相切．（1）求动圆圆心的轨迹C 的方程；（2）若AB 是轨迹C 的动弦，且AB 过F(0, 2)，分别以A 、B 为切点作轨迹C 的切线，设两切线交点为Q ，证明：AQ ⊥BQ ．24. 设x =3是函数f(x)=(x 2+ax +b)e 3−x ，(x ∈R)的一个极值点．（1）求a 与b 的关系式（用a 表示b ），并求f(x)的单调区间；（2）设a >0，g(x)=(a 2+254)e x，若存在ξ1，ξ2∈[0, 4]，使得|f(ξ1)−g(ξ2)|<254成立，求实数a 的取值范围．2014-2015学年江苏省南通市某校高三（上）第二次学情调研数学试卷（理科）答案1. {−1, 0, 1}2. −√223. y =116 4. 四 5. √556.2√23π 7. 1665 8. 2 9. √5或√52 10. ②③ 11. (1, 9) 12. (0, +∞) 13. 2914. (−52, −94)∪(−94, −1) 15. 解：(1)∵ a → // b →， ∴ 34cosx +sinx =0，∴ tanx =−34，cos 2x −sin2x =cos 2x −2sinxcosxsin 2x +cos 2x=1−2tanx 1+tan 2x=85.(2)f(x)=2(a →+b →)⋅b →=√2sin(2x +π4)+32，由正弦定理得，asinA =bsinB ，可得sinA =√22， ∵ a <b ， ∴ A <B , ∴ A =π4，f(x)+4cos(2A +π6)=√2sin(2x +π4)−12，∵ x ∈[0,π3]，∴ 2x +π4∈[π4,11π12]，所以√32−1≤f(x)+4cos(2A +π6)≤√2−12.16. 证明：（1）因为点F 在CD 上，点E 在AD 上，且DF:FC =DE:EA =2:3，… 所以EF // AC ，… 又EF ⊄平面ABC ， AC ⊂平面ABC ，所以EF // 平面ABC ．…（2）取BD 的中点M ，连AM ，CM ，因为ABCD 为正四面体，所以AM ⊥BD ，CM ⊥BD ，… 又AM ∩CM =M ，所以BD ⊥平面AMC ，… 又AC ⊂平面AMC ，所以BD ⊥EF ，… 又EF // AC ，所以直线BD ⊥直线EF ．…17. 当DN =20m 时，得到的市民健身广场面积最大，最大面积为2000m 2．18. 解：(1)∵ 四边形F 1AF 2B 是边长为2的正方形， ∴ F 1F 2=2OA =2√2， ∴ b =c =√2， ∴ a 2=b 2+c 2=4, ∴ 椭圆方程为x 24+y 22=1；(2)C(−2, 0)，D(2, 0)，设M(2, y 0)，P(x 1, y 1)，则OP →=(x 1,y 1)，OM →=(2,y 0) 直线CM:y =y 04(x +2)，即y =y 04x +12y 0，代入椭圆方程x 2+2y 2=4，得(1+y 028)x 2+12y 02x +12y 02−4=0.∵ x 1=−124(y 02−8)y 02+8，∴ x 1=−2(y 02−8)y 02+8，∴ y 1=8yy 02+8，∴ OP →=(−2(y 02−8)y 02+8，8yy 02+8).∴ OP →⋅OM →=−4(y 02−8)y 02+8+8y 02y 02+8=4y 02+32y 02+8=4（定值）.(3)设存在Q(m, 0)满足条件，则MQ ⊥DP ，MQ →=(m −2,−y 0)，DP →=(−4y 02y 02+8,8y 0y 02+8)则由MQ →⋅DP →=0得 −4y 02y 02+8(m −2)−8y 02y 02+8=0，从而得m =0.∴ 存在Q(0, 0)满足条件.19. 解：（1）因为f ′(x)=lnx +1，由f ′(x)>0，得x >1e ，所以f(x)的单调增区间为(1e ，+∞)，又当x ∈(0,1e)时，f ′(x)<0，则f(x)在(0,1e)上单调减，当x ∈(1e ，+∞)时，f ′(x)>0，则f(x)在(1e ，+∞)上单调增，所以f(x)的最小值为f(1e)=−1e．（2）因为f ′(x)=lnx +1，g′(x)=3ax 2−12，设公切点处的横坐标为x ∘，则与f(x)相切的直线方程为：y =(lnx ∘+1)x −x ∘，与g(x)相切的直线方程为：y =(3ax ∘2−12)x −2ax ∘3−23e ，所以{lnx ∘+1=3ax ∘2−12−x ∘=−2ax ∘3−23e ，解之得x ∘lnx ∘=−1e ，由（1）知x ∘=1e，所以a =e 26．（3）若直线l 1过(e 2, 2e 2)，则k =2，此时有lnx ∘+1=2（x ∘为切点处的横坐标），所以x ∘=e ，m =−e ，当k >2时，有l 2:y =(lnx ∘+1)x −x ∘，l 1:y =(lnx ∘+1)x ，且x ∘>2，所以两平行线间的距离d =√1+(lnx +1)2，令ℎ(x)=xlnx −(lnx ∘+1)x +x ∘，因为ℎ′(x)=lnx +1−lnx ∘−1=lnx −lnx ∘，所以当x <x ∘时，ℎ′(x)<0，则ℎ(x)在(0, x ∘)上单调减；当x >x ∘时，ℎ′(x)>0，则ℎ(x)在(x ∘，e 2)上单调增，所以ℎ(x)有最小值ℎ(x ∘)=0，即函数f(x)的图象均在l 2的上方，令t(x)=x 2ln 2x+2lnx+2，则t′(x)=2xln 2x+4xlnx+4x−2xlnx−2x(ln 2x+2lnx+2)2=2xln 2x+2xlnx+2x (ln 2x+2lnx+2)2>0，所以当x >x ∘时，t(x)>t(x ∘)，所以当d 最小时，x ∘=e ，m =−e ． 20. 解：（1）因为f(−1)=0，所以a −b +1=0，因为f(x)的值域为[0, +∞)，所以{a >0△=b 2−4a =0，所以b 2−4(b −1)=0⇒b =2，a =1，所以f(x)=(x +1)2，所以F(x)={(x +1)2，&x >0−(x +1)2，&x <0；（2）因为f(x)是偶函数，所以b =0，即f(x)=ax 2+1，又a >0，所以F(x)={ax 2+1，&x >0−ax 2−1，&x <0，因为mn <0，不妨设m >0，则n <0，又m +n >0，所以m >−n >0，此时F(m)+F(n)=am 2+1−an 2−1=a(m 2−n 2)>0，所以F(m)+F(n)>0；（3）因为x >0，所以F(x)=f(x)=ax 2+bx +1，又a =b =1，则F(x)−1=x 2+x ，因为g(x)=lnx+1e x，所以g ′(x)=1x−lnx−1e x则原不等式证明等价于证明“对任意实数x >0，(x 2+x)⋅1x−lnx−1e x<1+e −2，即1+x e x⋅(1−xlnx −x)<1+e −2．先研究 1−xlnx −x ，再研究1+x e x．①记m(x)=1−xlnx −x ，x >0，m′(x)=−lnx −2，令m′(x)=−lnx −2=0，得x =e −2，当x ∈(0, e −2)时，m′(x)>0，m(x)单增；当x ∈(e −2, +∞)时，m′(x)<0，m(x)单减．所以，m(x)的最大值m(e −2)=1+e −2，即1−xlnx −x ≤1+e −2． ②记n(x)=1+x e x，x >0，n′(x)=−xe x <0，所以n(x)在(0, +∞)单减，所以，n(x)<n(0)=1，即1+x e x<1．综上①、②知，g(x)=1+x e x(1−xlnx −x)≤1+x e x(1+e −2)<1+e −2．即原不等式得证，对任意实数x >0，[F(x)−1]g ′(x)<1+e −2． 21. 解：设将曲线y =sinx 变换为y =2sin4x 对应的变换矩阵为N =[ab cd]，由[a b cd][xy ]=[x′y′]，则{x′=ax +byy′=cx +dy， ∵ 将曲线y =sinx 变换为y =2sin4x ，对应的坐标关系为： {x =4x′y =y′2，∴ {x′=x4y′=2y，∴ { a =14b =0c =0d =2，矩阵N =[14002]．变换矩阵M 的逆矩阵为[14002]．22. 解：（1）由ρsin 2θ=4cosθ，得(ρsinθ)2=4ρcosθ， ∴ 曲线C 的直角坐标方程为y 2=4x ．（2）将直线l 的参数方程代入y 2=4x ，得t 2sin 2α−4tcosα−4=0．设A 、B 两点对应的参数分别为t 1、t 2，则t 1+t 2=4cosαsin 2α，t 1t 2=−4sin 2α，∴ |AB|=|t 1−t 2|=√(t 1+t 2)2−4t 1t 2=√(4cosαsin 2α)2+16sin 2α=4sin 2α，当α=π2时，|AB|的最小值为4．23. 解：（1）依题意，圆心的轨迹是以F(0, 2)为焦点，L:y =−2为准线的抛物线上因为抛物线焦点到准线距离等于4，所以圆心的轨迹是x 2=8y（2）∵ 直线AB 与x 轴不垂直，设AB:y =kx +2．A(x 1, y 1)，B(x 2, y 2)．由{y =kx +2y =18x 2.可得x 2−8kx −16=0，x 1+x 2=8k ，x 1x 2=−16抛物线方程为y =18x 2，求导得y′=14x ．所以过抛物线上A 、B 两点的切线斜率分别是 k 1=14x 1，k 2=14x 2，k 1⋅k 2=14x 1⋅14x 2=116x 1⋅x 2=−1所以，AQ ⊥BQ 24. 解：（1）∵ f(x)=(x 2+ax +b)e 3−x∴ f′(x)=(2x +a)e 3−x −(x 2+ax +b)e 3−x =−[x 2+(a −2)x +b −a]e 3−x ，由题意得：f′(3)=0，即32+3(a −2)+b −a =0，b =−2a −3， ∴ f(x)=(x 2+ax −2a −3)e 3−x 且f′(x)=−(x −3)(x +a +1)e 3−x 令f′(x)=0得x 1=3，x 2=−a −1．∵ x=3是函数f(x)=(x2+ax+b)e3−x，(x∈R)的一个极值点∴ x1≠x2，即a≠−4故a与b的关系式b=−2a−3，(a≠−4)．①当a<−4时，x2=−a−1>3，由f′(x)>0得单增区间为：(3, −a−1)；由f′(x)<0得单减区间为：(−∞, 3)，(−a−1, +∞)；②当a>−4时，x2=−a−1<3，由f′(x)>0得单增区间为：(−a−1, 3)；由f′(x)<0得单减区间为：(−∞, −a−1)，(3, +∞)．（2）由（1）知：当a>0时，x2=−a−1<0，f(x)在[0, 3]上单调递增，在[3, 4]上单调递减，∴ f(x)min=min{f(0),f(4)}=−2(a+3)e3，f(x)max=f(3)=a+6．∴ f(x)在[0, 4]上的值域为[−2(a+3)e3, a+6]．又g(x)=(a2+254)e x，在x∈[0, 4]上单调递增，∴ g(x)在x∈[0, 4]上的值域为[a2+254，(a2+254)e4]．由于(a2+254)−(a+6)=(a−12)2≥0，∴ 若存在ξ1，ξ2∈[0, 4]，使得|f(ξ1)−g(ξ2)|<254成立，必需{a>0(a2+254)−(a+6)<254，解得0<a<3．∴ a的取值范围是(0, 3)．。