理论力学第二章例题
理论力学(机械工业出版社)第二章平面力系习题解答

第二章 习 题2-1 试计算图2-55中力F 对点O 之矩。
图2-55(a) 0)(=F O M (b) Fl M O =)(F (c) Fb M O -=)(F (d) θsin )(Fl M O =F(e) βsin )(22b l F M O +=F(f) )()(r l F M O +=F2-2 一大小为50N 的力作用在圆盘边缘的C 点上,如图2-56所示。
试分别计算此力对O 、A 、B 三点之矩。
图2-56mN 25.6m m N 625030sin 2505060cos 30sin 5060sin 30cos 50⋅=⋅=︒⨯⨯=︒⨯︒-︒⨯︒=R R M Om N 075.17825.1025.630cos 50⋅=+=⨯︒+=R M M O A m N 485.9235.325.615sin 50⋅=+=⨯︒+=R M M O B2-3 一大小为80N 的力作用于板手柄端,如图2-57所示。
(1)当︒=75θ时,求此力对螺钉中心之矩;(2)当θ为何值时,该力矩为最小值;(3) 当θ为何值时,该力矩为最大值。
图2-57(1)当︒=75θ时,(用两次简化方法)m N 21.20mm N 485.59.202128945.193183087.21sin 8025075sin 80⋅=⋅=+=⨯︒⨯+⨯︒⨯=O M (2) 力过螺钉中心 由正弦定理)13.53sin(250sin 30θθ-︒= 08955.03/2513.53cos 13.53sin tan =+︒︒=θ ︒=117.5θ(3) ︒=︒+︒=117.95117.590θ2-4 如图2-58所示,已知N 200N,300N,200N,150321='====F F F F F 。
试求力系向O 点的简化结果,并求力系合力的大小及其与原点O 的距离d 。
图2-58kN64.1615110345cos kN64.4375210145cos 321R321R-=+-︒-=∑='-=--︒-=∑='F F F F F F F F F F y y x x主矢RF '的大小 kN 54.466)()(22R =∑+∑='y x F F F 而 3693.064.43764.161tan RR ==''=x y F F α ︒=27.20α m N 44.21162.0511.045cos )(31⋅=-⨯+⨯︒=∑=F F M M O O Fmm 96.45m 04596.054.466/44.21/R==='=F M d O2-5 平面力系中各力大小分别为kN 60kN,260321===F F F ,作用位置如图2-59所示,图中尺寸的单位为mm 。
理论力学02习题课

M F d 1 2 F d 2ABC 2
平面内两个力偶,如果力偶矩相等,则两个力偶等效
8
主要内容和方法
平面力偶系的合成和平衡条件
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系
平面力偶系合成结果还是一个力偶,其力偶矩为各力偶矩的 代数和。
M FR d F1d F2 d M1 M 2
例题7:在刚体的A、B、C、D四点作用 有四个大小相等的力,此四力沿四个边 恰好组成封闭的力多边形,如图所示.此 刚体是否平衡?选择其中一对平行力, 同时改变方向,此刚体是否平衡? 答:图示情况下刚体不平衡,依然存在顺时针方向力矩,选择其 中一对平行力,同时改变方向,此时刚体平衡。
14
典型题目
例题8:在下面各图中,力或力偶对点A的矩都相等,它们引起的支座 约束力是否相同?
解:
F 0 F F 0 M 0 F l M 0
x A B A B
M M FA ; FB l l
23
作业题
2-12已知梁上作用有力偶,重量不计,在下面三种情况下,计算 之作的约束力
解:
F 0 F cos F cos 0 M 0 F l cos M 0
Fx 0 F FA
2 5 0 FA F 2 5
Fy 0 FD FA
19
1 1 0 FD F 2 5
支座A点的约束力与假设的方向相反
作业题
2-6如图所示,输电线重量沿AB均匀分布,求电线中点和两 端拉力 f 1m, AB 40m, P 400 N
0 M 2 F cos r2 0 M1 r cos r2 M 1 2 cos r1 r1
理论力学(周衍柏 第二版)第2章习题解答

把⑥代入⑦得,
R1 = m1m2 cosθ g ⑧ m2 + m1 sin 2 θ
水平面对劈的反作用力 R2 。仍用隔离法。因为劈在垂直水皮方向上无加速度, 所以
R2 − m2 g − R1 cosθ = 0 ⑨
于是
R2 = m2 ( m1 + m2 ) g ⑩ m2 + m1 sin 2 θ
6
2.5解 因为质点组队某一固定点的动量矩 J = ∑ ri × mi v i
m 相对于地固连的坐标系 Oxy 的绝对速度
V绝对 = V相 + V牵
V相 为 m 相对 M 的运动速度
② u = aθ
故水平方向 vx = u cosθ − V ③ 竖直方向
v y = usiaθ ④
在 m 下滑过程中,只有保守力(重力)做功,系统机械能守恒: (以地面为重力零势能面)
8
mga cos α = mga cos θ +
(M + M ′) − M 2 μg M′ u− 2mM M
2
2.16 雨滴落下时,其质量的增加率与雨滴的表面积成正比例,求雨滴速度与时间的关系。 2.17 设用某种液体燃料发动的火箭, 喷气速度为 2074 米/秒, 单位时间内所消耗的燃料为 原始火箭总质量的 1 。如重力加速度 g 的值可以认为是常数,则利用此种火箭发射人造太
i =1 n
所以对于连续物体对某一定点或定轴,我们就应该把上式中的取和变为积分。如 图 2.5.1 图所示薄圆盘,任取一微质量元,
O
dθ
dr
dm = ρ ⋅ rdθdr
ρ=
所以圆盘绕此轴的动量矩 J
J =
M πa 2
∫∫ r × ( dm v ) = ∫∫ r ⋅ ρ rdrd
理论力学第二章习题答案

理论力学第二章习题答案理论力学是物理学中研究物体运动规律和相互作用的分支学科,它以牛顿运动定律为基础,通过数学方法来描述物体的运动和力的作用。
本章习题答案将帮助学生更好地理解和掌握理论力学的基本概念和计算方法。
习题1:考虑一个质量为m的物体在重力作用下自由下落。
忽略空气阻力,求物体下落过程中的速度和位移。
答案:物体自由下落时,受到的力只有重力,大小为mg,方向向下。
根据牛顿第二定律,F=ma,可以得到加速度a=g。
物体的速度v随时间t变化,可以使用公式v=gt计算。
物体的位移s随时间变化,可以使用公式s=1/2gt^2计算。
习题2:一个质量为m的物体在水平面上以初速度v0开始运动,受到一个大小为k的恒定摩擦力作用。
求物体停止前所经过的距离。
答案:物体在水平面上运动时,受到的摩擦力与物体的位移成正比,即F=-kx。
根据牛顿第二定律,F=ma,可以得到加速度a=-k/m。
物体的位移x随时间t变化,可以使用公式x=v0t - 1/2(k/m)t^2计算。
当物体速度减至0时,物体停止,此时t=2v0/k,代入公式得到x=2v0^2/k。
习题3:一个质量为m的物体在斜面上,斜面与水平面的夹角为θ。
物体受到一个向上的拉力F,使得物体沿斜面匀速上升。
求拉力F的大小。
答案:物体沿斜面匀速上升时,拉力F与重力分量mgsinθ和摩擦力μmgcosθ平衡。
根据平衡条件,F=mgsinθ + μmgcosθ。
如果摩擦系数为μ,可以进一步简化为F=mg(sinθ + μcosθ)。
习题4:考虑一个质量为m的物体在竖直平面内做圆周运动,圆心位于物体的正下方。
物体的运动由一个弹簧连接到圆心,弹簧的劲度系数为k。
求物体在圆周运动中的角速度。
答案:物体在圆周运动中,受到弹簧力和重力的作用。
根据牛顿第二定律,向心力Fc=mv^2/r=ma,其中r为圆的半径。
由于物体做圆周运动,向心力由弹簧力和重力的垂直分量提供。
因此,Fc=kx - mgcosθ,其中x为弹簧的伸长量,θ为物体与竖直方向的夹角。
理论力学作业卷答案(第二章)

16 2 4 2 m/ s 2 9 3 100 2 10 2 2 r1 1 0.3 m/ s 2 9 3
at R 20 rad s 2
鼓轮轮缘上一点的加速度
10(m/ s 2 ) at v an v 2 R 20t 2 (m/ s 2 )
2 a at2 an 10 1 4t 4 (m/ s 2 )
v R 20t rad s
题2-6图
题2-7图
题2-10图
题
第
2ቤተ መጻሕፍቲ ባይዱ
页共 21
页
n1
Ⅲ Ⅰ Ⅱ
2
v AB vBC vCD vDA a AB aCD 0
n1
30
r1 1 0.3
10 m/ s 3
W
题2-8图
2-6
升降机装置由半径为 R =50cm 的鼓轮带动,如图所示。被升降物体的运动方程为 x=5t2 (t 以 s
aBC r2 2 2 0.75
计,x 以 m 计) 。求鼓轮的角速度和角加速度,并求在任意瞬时,鼓轮轮缘上一点的全加速度的大小。 aDA 解: 轮缘上一点的速度与切向加速度为 2-10 车床的走刀架机构如图所示。已知各齿轮的齿数为 z1 =40,z2 =84 ,z3 =28 ,z4 =80 ,主轴转速 10t (m/ s) vx n1 =120r/min,丝杠螺距 t=12mm 试求走刀速度 v 2 。 a 2 10(m/ s ) at v 从而,鼓轮的角速度与角加加速度为
1
10 rad/ s 3 r i12 1 2 2 r1 30 r1 30 10 4 1 rad/ s r2 75 3 3
《理论力学》第二章作业答案

xyPTF22036O152-⋅图[习题2-3]动学家估计,食肉动物上颚的作用力P 可达800N ,如图2-15示。
试问此时肌肉作用于下巴的力T 、F 是多少? 解:解:0=∑xF036cos 22cos 00=-F T22cos 36cos F T =0=∑yF036sin 22sin 00=-+P F T 80036sin 22sin 22cos 36cos 000=+F F )(651.87436sin 22tan 36cos 80000N F =+=)(179.76322cos 36cos 651.87422cos 36cos 000N F T ===182-⋅图B[习题2-6] 三铰拱受铅垂力P F 作用,如图2-18所示。
如拱的重量不计,求A 、B 处支座反力。
解:0=∑x F0cos 45cos 0=-θB A R RB A R l l l R 22)23()2(222+=B A R R 10121=B A R R 51=0=∑yF0sin 45sin 0=-+P B A F R R θP B A F R l l l R =++22)23()2(2321P B A F R R =+10321的受力图轮A P B B F R R =+⨯1035121P B F R =104P P B F F R 791.0410≈=31623.0101)23()2(2cos 22≈=+=l l l θ0565.71≈θ P P P A F P F R 354.04241051≈=⨯=方向如图所示。
[习题2-10] 如图2-22所示,一履带式起重机,起吊重量kN F P 100=,在图示位置平衡。
如不计吊臂AB 自重及滑轮半径和摩擦,求吊臂AB 及揽绳AC 所受的力。
解:轮A 的受力图如图所示。
0=∑x F030cos 20cos 45cos 000=--P AC AB F T R的受力图轮A 603.869397.07071.0=-AC AB T R AC AB T R 3289.1476.122+=0=∑yF030sin 20sin 45sin 000=---P P AC AB F F T R010*******.07071.0=---AC AB T R 1503420.07071.0=-AC AB T R1503420.0)3289.1476.122(7071.0=-+⨯AC AC T T 1503420.09397.06023.86=-+AC AC T T 3977.635977.0=AC T )(069.106kN T AC ≈)(432.263069.1063289.1476.1223289.1476.122kN T R AC AB =⨯+=+=解法二:用如图所示的坐标系。
理论力学(刘又文 彭献)答案第2章

答:不对。因为其中一个平面上的 3 个投影方程,完全可由其他两组方程导 出,故独立平衡方程数只有 6 个。
13.均质杆 AB、AC,铅垂架在粗糙水平面上,并处于临界平衡状态,如图 2.9 所示。研究整体,其受力为平面一般力系,则可解出 3 个未知量。对吗?
可由其导出,它们与上述 6 个方程互不独立;如果使用整体及其中一刚体的共 6
个平衡方程,则另一刚体的 3 个平衡方程也可由其导出。故该系统的独立平衡方
程只有 6 个。 9. 如 图 2.6 所 示 为 两 铰 拱 , A 、 B 支 座 处 有 4 个 未 知 约 束 力 , 可 由
∑ Fx = 0, ∑ Fy = 0, ∑ M A = 0, ∑ M B = 0,共 4 个平衡方程联立解出。对吗?
答:不对。平面一般力系,只有 3 个独立平衡方程,第 4 个方程一定是前 3
个的某种线性组合,是不独立的。该结构为超静定,4 个未知量不可由平衡方程
全部求出。
10.某力系中,各力的作用线平行于某一平面,则独立平衡方程的个数是 3。
对吗?
答:不对。平行于某平面的力线不一定共面,也不一定平行。如图 2.7 所示,
吗?
答:不对。当 A、B 两矩心与汇交点共线,且力系对于 AB 轴对称时,如图
∑ ∑ 2.3 所示汇交力系中, F1 = F2 ,虽有 MA = 0, MB = 0,但该力系并不平衡。
∑ ∑ ∑ 5.平面一般力系,满足 MA =0, MB =0, Fx = 0,则一定平衡。对吗?
答:不对。应补充 AB 不垂直 x 轴的条件,否则条件不充分。如图 2.3 所示 情形,力系虽满足上述三个方程,但并不平衡。
理论力学第二章习题答案

理论力学第二章习题答案理论力学第二章习题答案理论力学是物理学的基础学科之一,它研究物体的运动规律以及力的作用原理。
在理论力学的学习过程中,习题是检验学生理解和掌握程度的重要方式之一。
下面将为大家提供理论力学第二章的习题答案,希望对大家的学习有所帮助。
1. 一个质点在匀速直线运动中,它的加速度是多少?答:在匀速直线运动中,速度保持不变,所以加速度为0。
2. 一个质点的速度随时间的变化规律为v=3t+2,求它在t=2s时的速度。
答:将t=2s代入速度变化规律中,得到v=3*2+2=8m/s。
3. 一个质点做匀加速直线运动,它的初速度为2m/s,加速度为3m/s²,求它在t=4s时的位移。
答:根据匀加速直线运动的位移公式s=vt+1/2at²,将初速度v=2m/s,时间t=4s,加速度a=3m/s²代入,得到s=2*4+1/2*3*4²=8+24=32m。
4. 一个质点做匀加速直线运动,它的初速度为4m/s,位移为20m,加速度为2m/s²,求它的末速度。
答:根据匀加速直线运动的末速度公式v²=u²+2as,将初速度u=4m/s,位移s=20m,加速度a=2m/s²代入,得到v²=4²+2*2*20=16+80=96,所以末速度v=√96≈9.8m/s。
5. 一个质点做直线运动,它的速度随时间的变化规律为v=2t²+3t,求它在t=3s时的加速度。
答:加速度是速度对时间的导数,所以将速度变化规律v=2t²+3t对时间t求导,得到加速度a=dv/dt=4t+3。
将t=3s代入,得到a=4*3+3=15m/s²。
6. 一个质点做直线运动,它的速度随时间的变化规律为v=5t²+2t,求它在t=2s 时的加速度。
答:同样地,将速度变化规律v=5t²+2t对时间t求导,得到加速度a=dv/dt=10t+2。
基础知识-理论力学(二)_真题(含答案与解析)-交互

基础知识-理论力学(二)(总分105, 做题时间90分钟)单项选择题(下列选项中,只有一项符合题意)1.将大小为100N的力,沿x、y方向分解(见图4-1-1),若F在x轴上的投影为50N,而沿x方向的分力的大小为200N,则F在y轴上的投影为( )。
A.0 B.50N C.200N D.100NSSS_SIMPLE_SINA B C D分值: 1答案:A[解析] 由力F在x轴上的投影为50N,沿x轴的分力为200N可得:力F作用方向与x轴夹角是60°,与y轴夹角是90°,从而可得:F在y轴上的投影为0。
2.如图4-1-2所示,三力矢F1、F2、F3的关系是( )。
A.F1+F2+F3=0 B.F3=F1+F2C.F2=F1+F3D.F1=F2+F3 SSS_SIMPLE_SINA B C D分值: 1答案:D[解析] 力的计算要满足矢量的运算法则。
3.如图4-1-3所示,等边三角板ABC,边长a,沿其边缘作用大小均为F的力,方向如图所示,则此力系简化为( )。
SSS_SIMPLE_SINA B C D分值: 1答案:A[解析] 在此平面汇交力系中,各力在水平向和竖向的投影之代数和都等于0,故汇交力系平衡,FR=0。
因为过A、C点的力都经过A点,故只有过B点的力对A点有弯矩作用,力臂为a,故MA =Fa。
4.某平面任意力系向O点简化后,得到如图4-1-4所示的一个力R和一个力偶矩为M的力偶,则该力系的最后合成结果是( )。
A.作用在O点的一个合力B.合力偶C.作用在O的左边某点的一个合力D.作用在O点右边某点的一个合力SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] 由平面任意力系简化原理判断。
5.三铰拱上作用有大小相等,转向相反的二力偶,其力偶矩大小为M,如图4-1-5所示。
略去自重,则支座A的约束力大小为( )。
SSS_SIMPLE_SINA B C D分值: 1答案:B[解析] 正对称结构在正对称力作用下,只有正对称的力,而C点是铰接,故只有轴向力,这样,取左边一半分析,根据力矩平衡以及在x,y方向受力平衡得6.简支梁受分布荷载作用如图4-1-6所示,支座A、B的约束为( )。
理论力学机械工业出版社课后习题答案第二章2-24

2-32 图示平面机构由圆盘、连杆和滑块组成,连杆的两端分别与圆盘和滑块铰接,已知圆盘的半径为r ,r AB 32=,滑块以匀速度B v沿倾角为60◦ 的滑道向下运动,圆盘相对于水平地面作纯滚动,试求图示位置(连杆AB 处于水平位置)圆盘的角速度和角加速度。
(习题难度:易)解:(1) 运动分析:圆盘C 作纯滚动;杆AB 作平面运动;滑块B 沿斜面作直线平移。
(2) 速度分析:如图(a)圆盘C :点P 1为圆盘的速度瞬心C C A r A P v ωω=⋅=1?(A P 1⊥) 杆AB :点P 2为杆AB 的速度瞬心C C A ABr r A P v ωωω2122===(顺时针) C C AB B r r B P v ωωω=⋅=⋅=2122 ⇒rvB C AB 22==∴ωω(顺时针)(3) 加速度分析:如图(b)圆盘C :tn AC AC C A a a a a ++= 杆AB :t n 0BA BA A B a a a a ++==题2-32图题2-32图(a)则 tn t n 0BABAACACCB a a a a a a++++== 大小 C r α? 2C r ω C r α? 232AB r ω AB r α32?方向 ← C A → AC ⊥ A B → BA ⊥沿AB 方向投影得到 nt n 60cos 60sin 0BAAC AC C a a a a -+--= ⇒ 223221230ABC C C r r r r ωαωα-⋅+⋅--= ⇒ 22)2(322123)(0rv r r r v r r B C B C -⋅+⋅--=αα ⇒题2-32图(b)。
理论力学第二章课后习题答案

理论力学第二章课后习题答案·12·理论力系第2章平面汇交力系与平面力偶系一、是非题(恰当的在括号内踢“√”、错误的踢“×”)1.力在两同向平行轴上投影一定相等,两平行相等的力在同一轴上的投影一定相等。
2.用解析法求平面呈报力系的合力时,若挑选出相同的直角坐标轴,其税金的合力一定相同。
(√)3.在平面汇交力系的平衡方程中,两个投影轴一定要互相垂直。
(×)4.在维持力偶矩大小、转为维持不变的条件下,可以将例如图2.18(a)右图d处为平面力偶m移至例如图2.18(b)所示e处,而不改变整个结构的受力状态。
(×)(a)图2.185.如图2.19所示四连杆机构在力偶m1m2的作用下系统能保持平衡。
6.例如图2.20右图皮带传动,若仅就是包角发生变化,而其他条件均维持维持不变时,并使拎轮旋转的力矩不能发生改变。
(√图2.19图2.201.平面呈报力系的均衡的充要条件就是利用它们可以解言的约束反力。
2.三个力汇交于一点,但不共面,这三个力3.例如图2.21右图,杆ab蔡国用数等,在五个力促进作用下处在平衡状态。
则促进作用于点b的四个力的合力fr=f,方向沿4.如图2.22所示结构中,力p对点o的矩为plsin。
5.平面呈报力系中作力多边形的矢量规则为:各分力的矢量沿着环绕着力多边形边界的某一方向首尾相接,而合力矢量沿力多边形半封闭边的方向,由第一个分力的起点指向最后一个分力的终第面汇交力系与平面力偶图2.21图2.226.在直角坐标系中,力对坐标轴的投影与力沿坐标轴分解的分力的大小但在非直角坐标系中,力对坐标轴的投影与力沿坐标轴分解的分力的大小不相等。
1.例如图2.23右图的各图为平面呈报力系所作的力多边形,下面观点恰当的就是(c)。
(a)图(a)和图(b)就是平衡力系则(b)图(b)和图(c)就是平衡力系则(c)图(a)和图(c)就是平衡力系则(d)图(c)和图(d)就是平衡力系则f2f2f1(a)(b)(c)2.关于某一个力、分力与投影下面说法正确的是(b)。
理论力学答案第二章
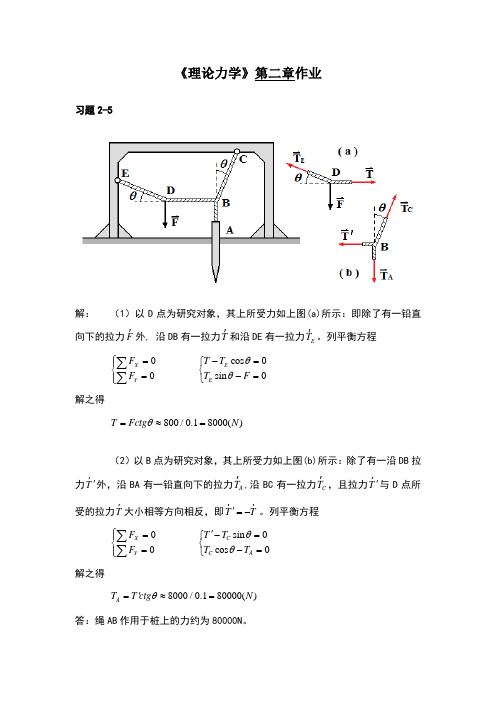
《理论力学》第二章作业习题2-5解:(1)以D点为研究对象,其上所受力如上图(a)所示:即除了有一铅直向下的拉力Fr外, 沿DB有一拉力Tr和沿DE有一拉力ETr。
列平衡方程XYFF⎧=⎪⎨=⎪⎩∑∑cos0sin0EET TT Fθθ-=⎧⎨-=⎩解之得800/0.18000()T Fctg Nθ=≈=(2)以B点为研究对象,其上所受力如上图(b)所示:除了有一沿DB拉力T'r外,沿BA有一铅直向下的拉力ATr,沿BC有一拉力CTr,且拉力T'r与D点所受的拉力Tr大小相等方向相反,即T T'=-r r。
列平衡方程XYFF⎧=⎪⎨=⎪⎩∑∑sin0cos0CC AT TT Tθθ'-=⎧⎨-=⎩解之得8000/0.180000()AT T ctg Nθ'=≈=答:绳AB作用于桩上的力约为80000N。
习题2-6 解:(1) 取构件BC 为研究对象,其受力情况如下图(a)所示:由于其主动力仅有一个力偶M ,那末B 、C 处所受的约束力B F r 、C F r必定形成一个阻力偶与之平衡。
列平衡方程()0B M F =∑r0C M F l -=所以 C M F l=(2) 取构件ACD 为研究对象,其受力情况如上图(b)所示:C 处有一约束力C F 'r与BC 构件所受的约束力C F r 互为作用力与反作用力关系,在D 处有一约束力D F r 的方向向上,在A 处有一约束力A F r,其方向可根据三力汇交定理确定,即与水平方向成45度角。
列平衡方程0X F =∑sin 450o A C F F '-=所以 222A C C M F F F l'=== 2Ml(b)所示。
习题2-7解:(1) 取曲柄OA 为研究对象,其受力情况如下图(a)所示:由于其主动力仅有一个力偶M ,那末O 、A 处所受的约束力O F ρ、BA F ρ必定形成一个阻力偶与之平衡。
理论力学机械工业出版社课后习题答案第二章2-19

2-27 图示系统处于同一铅垂平面内,曲柄O 1A 以匀角速度ω绕轴O 1作顺时针转动,齿轮A 焊接于曲柄O 1A 上而成为一体,齿轮C 铰接于杆AB 上,两齿轮的半径都为r ,且相互啮合,O 1A = O 2B = 2r ,O 1O 2 = AB = 4r ,试求图示位置齿轮C 的最低点D 的速度和加速度。
(习题难度:中难)解:(1) 运动分析:杆O 1A (齿轮A )和杆O 2B 作定轴转动;杆AB 作平移;齿轮C 作平面运动。
(2) 速度分析:如图(a)杆O 1A (齿轮A ):题2-27B题2-27图(a)ωr v A 2=(A O 1⊥)r r r r AM A O AM A O M O 7120cos 44120cos 222212211=-+=⋅⋅-+=ωωr M O v M 71=⋅=(M O 1⊥) 杆AB :)2(ωr v v v A B C ===(A O 1⊥) 齿轮C :由齿轮C 上的点M 的速度M v 和点C 的速度C v可确定速度瞬心为点P ,如图。
ωωω===r r PC v C C 22 或 ωωω===rr PM v M C 77(逆时针) r r r r CD PC CD PC PD 325150cos 44150cos 222222+=-+=⋅⋅-+=PD ⊥,方向如图所示)(3) 加速度分析:如图(b) 杆O 1A (齿轮A ):2n2ωr a a AA ==(1//)221n7ωωr M O a a M M =⋅==(1//MO )2211323727120sin sin ωωθr r r r MO AO a a a M M My -=⋅⋅-=⋅-=-=杆AB :)2(2ωr a a A C ==(1//AO ) 齿轮C : tn MCMCCMa a a a++=大小 ? 22ωr 2C r ω C r α?方向 ? 1//AO → ↓题2-27图(b)沿y 轴投影得到(注意:齿轮啮合点的加速度在两个齿轮轮廓线的切线方向的加速度投影相等)t30cos MCC My a a a --= ⇒ C r r r αωω-⋅-=-232322 ⇒ 0=C α tn D C D CCDa a a a ++=大小 ? 22ωr 2C r ω 0=C r α方向 ? 1//AO ↑ →沿x 轴投影得到沿y 轴投影得到。
理论力学第二章思考题及习题答案

第二章思考题2.1一均匀物体假如由几个有规则的物体并合(或剜去)而成,你觉得怎样去求它的质心? 2.2一均匀物体如果有三个对称面,并且此三对称面交于一点,则此质点即均匀物体的质心,何故?2.3在质点动力学中,能否计算每一质点的运动情况?假如质点组不受外力作用,每一质点是否都将静止不动或作匀速直线运动?2.4两球相碰撞时,如果把此两球当作质点组看待,作用的外力为何?其动量的变化如何?如仅考虑任意一球,则又如何?2.5水面上浮着一只小船。
船上一人如何向船尾走去,则船将向前移动。
这是不是与质心运动定理相矛盾?试解释之。
2.6为什么在碰撞过程中,动量守恒而能量不一定守恒?所损失的能量到什么地方去了?又在什么情况下,能量才也守恒?2.7选用质心坐标系,在动量定理中是否需要计入惯性力?2.8轮船以速度V 行驶。
一人在船上将一质量为m 的铁球以速度v 向船首抛去。
有人认为:这时人作的功为()mvV mv mV v V m +=-+222212121 你觉得这种看法对吗?如不正确,错在什么地方? 2.9秋千何以能越荡越高?这时能量的增长是从哪里来的?2.10在火箭的燃料全部燃烧完后,§2.7(2)节中的诸公式是否还能应用?为什么? 2.11多级火箭和单级火箭比起来,有哪些优越的地方?第二章思考题解答2.1.答:因均匀物体质量密度处处相等,规则形体的几何中心即为质心,故先找出各规则形体的质心把它们看作质点组,然后求质点组的质心即为整个物体的质心。
对被割去的部分,先假定它存在,后以其负质量代入质心公式即可。
2.2.答:物体具有三个对称面已足以确定该物体的规则性,该三平面的交点即为该物体的几何对称中心,又该物体是均匀的,故此点即为质心的位置。
2.3.答:对几个质点组成的质点组,理论上可以求每一质点的运动情况,但由于每一质点受到周围其它各质点的相互作用力都是相互关联的,往往其作用力难以预先知道;再者,每一质点可列出三个二阶运动微分方程,各个质点组有n 3个相互关联的三个二阶微分方程组,难以解算。
理论力学题库第二章-范本模板

理论力学题库——第二章一、 填空题1. 对于一个有n 个质点构成的质点系,质量分别为123,,,...,...i n m m m m m ,位置矢量分别为123,,,...,...i n r r r r r ,则质心C 的位矢为 。
2. 质点系动量守恒的条件是 。
3. 质点系机械能守恒的条件是 .4. 质点系动量矩守恒的条件是 。
5. 质点组 对 的微商等于作用在质点组上外力的矢量和,此即质点组的 定理。
6. 质心运动定理的表达式是 .7. 平面汇交力系平衡的充分必要条件是合力为零.8.各质点对质心角动量对时间的微商等于 外力对质心的力矩 之和。
9. 质点组的角动量等于 质心角动量 与各质点对质心角动量之和。
10. 质点组动能的微分的数学表达式为: ∑∑∑===⋅+⋅==n i i i i n i i e i n i i i r d F r d F v m d dT 1)(1)(12)21( ,表述为质点组动能的微分等于 内 力和 外 力所作的 元功 之和。
11. 质点组动能等于 质心 动能与各质点对 质心 动能之和。
12. 柯尼希定理的数学表达式为: ∑='+=ni i i C r m r m T 12221 ,表述为质点组动能等于 质心 动能与各质点对 质心 动能之和。
13. 2-6。
质点组质心动能的微分等于 内、外 力在 质心系 系中的元功之和。
14. 包含运动电荷的系统,作用力与反作用力 不一定 在同一条直线上.15. 太阳、行星绕质心作圆锥曲线的运动可看成质量为 折合质量 的行星受太阳(不动)的引力的运动。
16. 两粒子完全弹性碰撞,当 质量相等 时,一个粒子就有可能把所有能量转移给另一个粒子.17. 设木块的质量为m 2 , 被悬挂在细绳的下端,构成一种测定子弹速率的冲击摆装置.如果有一质量为m 1的子弹以速率v 1 沿水平方向射入木块,子弹与木块将一起摆至高度为h处,则此子弹射入木块前的速率为:2/11211)2(gh m m m +=v 。
理论力学第二章答案

[
]
代入完整保守体系的拉格朗日方程,并化简得
&& θ + sinθ ⋅ cosθ ⋅ ω 2 = 0
2.9 用拉格朗日方程写出习题1.27的运动微分方程 解:体系为自由度为2的完整约束体系,取x,y为广义坐标
m & & T = (x2 + y2) 2
则
V =−
e2 4 πε 0
⋅
1 x2 + y2 1 x2 + y2
ϕ +ϕ ϕ +ϕ m1g sinϕ1 − k cos 1 2 ⋅ (l − 2R) ⋅ sin 1 2 = 0 2 2 m g sinϕ − k cosϕ1 + ϕ2 ⋅ (l − 2R) ⋅ sinϕ1 + ϕ2 = 0 2 2 2 2
o
ϕ1 ϕ2
m2
m1
2.23 质量为m,电荷为q的粒子在轴对称电场 中运动。写出粒子的拉格朗日函数和运动微分方程。 v v v v 解: 由题中 E = E 0 e r ,B = B 0 k 令 ϕ = E 0 ln R v 1 v A = B 0 R eθ 2 v v 在柱坐标系中,有: = 1 mv 2 − q ϕ + q A ⋅ V , L 2 d ∂L ∂L − =0 代入: & dt ∂ q α ∂ qα
o
2.6 用拉格朗日程写出习题1.20的运动微分方程 解:如图,取底面圆心处为坐标原点,建立柱坐标系,质点到 v &v v v & eϕ + ze z & 轴距为R,则: υ = R er + Rϕ & & 由几何关系 R = ( R2 + z ⋅ tan α ), R = z ⋅ tan α
