单位根检验-课件(PPT·精选)
单位根检验PPT课件

AR(1)过程 {yt}为一随机步游过程。
14
单位根检验:定义
❖ 看图识平稳 :15源自单位根检验:定义❖ 看图识平稳 :
16
单位根检验:定义
❖ 看图识平稳 :
17
单位根检验:定义
❖ I(d)过程:有时原始序列是非平稳过程,但对 原始序列经过d次差分后可变为平稳过程,则 原序列记为I(d)过程;
12
单位根检验:定义
❖ AR(1)过程是平稳序列吗?
❖ 定理:若| |1,则AR(1)过程是平稳过程。因
为
(1)
Eyt
1
(2)cov(
yt
,
yt
h
)
2 |h| 1 2
var(
yt
)
1
2
2
(3) (t, h) |h|
❖ 证明过程略
13
单位根检验:定义
❖ 如果 | |1 ,AR(1)过程 {yt}还是平稳过程吗? 为什么?
❖ 经济时间序列多为I(1)或I(2)过程; ❖ 显然,I(0)过程是平稳序列 。
18
单位根检验:定义
❖ 当回归模型中含有非平稳的I(d)序列时,常规 的统计推断都不再成立,因此必须检验被解 释变量和解释变量是不是平稳的。标准的检 验方法是“单位根检验”。
19
单位根检验:定义
❖ 一个随机过程的平稳性取决于其特征方程的 根的值。若所有的根都位于单位圆之外,则 该过程是平稳的。若某个(些)根的值位于单位 圆上或单位圆内,则该过程是非平稳的。若 特征方程的根取值为1,则称其为单位根。对 单位根的检验(即对随机过程单整阶数的检验) 也就是对随机过程平稳性的检验。
单位根检验的EViews操作课件

如何进一步学习时间序列分析的相关知识
01
阅读时间序列分析相关的专业书籍和学术论文,深入理解时间 序列分析的基本原理和方法。
02
学习EViews软件的使用方法,掌握各种时间序列分析工具和命
令。
参加时间序列分析相关的课程和培训,与专业人士交流学习,
03
提高自己的分析能力。
THANKS FOR WATCHING
设,认为数据不存在单位根。
03
根据单位根检验结果,可以进一步进行其他相关分析和建 模。
04
单位根检验的EViews操 作实例
单个时间序列数据的单位根检验
01
打开EViews软件,选择 “File”菜单中的“New”选 项,创建一个新的工作文件。
02
在工作文件中,选择 “Quick”菜单中的“Empty Group”选项,创建一个空的 工作组。
单位根检验的原理
单位根检验基于ADF(Augmented Dickey-Fuller)检验和PP(Phillips-Perron )检验等统计方法,通过构建适当的回归模型并检验其残差是否具有单位根来确 定时间序列数据是否平稳。
如果残差存在单位根,则说明时间序列数据是非平稳的,即存在一个单位根;如 果残差不存在单位根,则说明时间序列数据是平稳的。
02
EViews软件介绍
EViews软件的特点
界面友好
01
EViews软件采用直观的图形界面,方便用户进行数据处理和统
计分析。
功能强大
02
EViews提供了丰富的数据处理、模型估计、统计分析和预测功
能,满足各种研究需求。
兼容性好
03
EViews支持多种数据格式和软件接口,方便与其他软件进行数
单位根检验PPT课件

❖ R-squared
0.379331
Mean dependent var
0.001161
❖ Adjusted R-squared 0.350463
S.D. dependent var
0.217449
❖ S.E. of regression 0.175250
是在相互独立的序列进行的实际回归中,经R2常 伴随着 高的 ,并且 系数显著。这种现象就
称为为伪回归(虚假回归)现象。
3
虚假回归(伪回归) :定义
❖ 虚假回归:两个没有任何逻辑联系的序列进行回 归 , 含 有很 高 的 R2, 因 为 两个 序 列 都与 时俱 进 (具有时间趋势,随时间推移而发生变化)。例 子,考研人数与手机数量。
❖ 可以通过数学推导证明; ❖ 已知随机步游是非平稳的,当 | |1 时,
AR(1)过程 {yt}为一随机步游过程。
14
单位根检验:定义
❖ 看图识平稳 :
15
单位根检验:定义
❖ 看图识平稳 :
16
单位根检验:定义
❖ 看图识平稳 :
17
单位根检验:定义
❖ I(d)过程:有时原始序列是非平稳过程,但对 原始序列经过d次差分后可变为平稳过程,则 原序列记为I(d)过程;
31
单位根检验:DF和ADF检验
❖ DF和ADF检验在Eviews中的实现: ❖ 选择Quick/Series Statistics/Unit Root test,
输入序列名即可。 ❖ Lagged differences 为0即为DF检验 ❖ Lagged differences 不为0即为ADF检验
ADF检验为保证方程中的为白噪声,设随机过
平稳性和单位根检验 ppt课件

3.49
3.12
2.79
2.38
500
3.48 ppt课件3.11
2.78
2.38
38
>500
3.46
3.11
2.78
2.38
• 一个简单的检验过程:
– 同时估计出上述三个模型的适当形式,然后通过 ADF临界值表检验零假设H0:=0。
–例如:如果有两列时间序列数据表现出一致的变化趋势 (非平稳的),即使它们没有任何有意义的关系,但进 行回归也可表现出较高的可决系数。
ppt课件
5
2、平稳性的定义
• 假定某个时间序列是由某一随机过程(stochastic
process)生成的,即假定时间序列{Xt}(t=1, 2, …)
的每一个数值都是从一个概率分布中随机得到,如果
扩展实验
① x=0.5*x(-1)+u
② x=1+0.5*x(-1)+u
③ x=1.5*x(-1)+u
④ x=1+1.5*x(-1)+u
⑤ x=1+t+1.5*x(-1)+u
ppt课件
15
二、单整、趋势平稳与差分平稳
ppt课件
16
1、单整(integrated Serial)
• 如果一个时间序列经过一次差分变成平稳的, 就称原序列是一阶单整(integrated of 1)序列, 记为I(1)。
随机游走,非平稳
对该式回归,如果确实 发现ρ=1,则称随机变
量Xt有一个单位根。
X t ( 1) X t1 t X t1 t
等价于通过该式判断 是否存在δ=0。
• 通过上式判断Xt是否有单位根,就是时间序列 平稳性的单位根检验。
第4章 单位根检验(讲稿)

第4章单位根检验4.1 DF分布由于虚假回归问题的存在,在回归模型中应避免直接使用非平稳变量。
因此检验变量的平稳性是一个必须解决的问题。
在第二章中介绍用相关图判断时间序列的平稳性。
这一章则给出严格的统计检验方法,即单位根检验。
1)检验模型在介绍检验方法之前,先讨论所用统计量的分布。
给出三个简单的自回归数据生成过程(d.g.p.),y t = β y t-1 + u t , (4.1)y t = μ + β y t-1 + u t , (4.2)y t = μ + α t + β y t-1 + u t ,(4.3)y0 = 0, u t~ IID(0, σ2)其中μ称作位移项(漂移项),α t称为趋势项。
显然,对于以上三个模型:当|β| < 1时,y t 是平稳的,当|β| = 1时,y t 是非平稳的。
2)检验统计量分布以模型(4.1)为例,(1)若β = 0,统计量,(1)ˆ0ˆ()~ˆ()T t t s βββ--= (4.4) 的极限分布为标准正态分布。
(2)若| β | < 1,统计量,)ˆ(ˆ)ˆ(ββββs t -= (4.5) 渐进服从标准正态分布。
根据中心极限定理,当T → ∞ 时,)ˆ(ββ-TT → N (0, σ 2 (1- β 2 ) ) (4.6) (3)那么在 | β | = 1条件下,统计量)ˆ(βt 服从什么分布呢?当 | β | = 1时,变量非平稳,上述极限分布发生退化(方差为零)。
①DF 统计量检验单位根的一个统计量是DF 统计量。
DF 统计量的表达式与通常意义的t 统计量完全相同。
∑=---=-==T t t u y s s t DF 12/121)(1ˆ)ˆ(1ˆ)ˆ(ββββ∑∑∑=-=-=-=Tt t T t t t uT t t y y u s y 1211112/121)( =∑∑=-=-T t t u T t t t y s y u 12/12111)( (4.16) 当T → ∞ 时,DF = )ˆ(1ˆββs - ⇒ 2/11022))(()1)1()(2/1(di i W W ⎰- (4.17)同理,对于模型 (4.2) 和 (4.3) 的DF 统计量的极限分布也是Wiener 过程的函数。
范文eviews讲解单位根检验.ppt

14
例10.4中I?的水平变量的所有方法的单位根检验结果:
只有此处小于 0.05,说明除此 法外都认为非
平稳
各种方法的结果(除Breitung检验 外)都接受原假设, I?
存在单位根,是非平稳的。 精选整理
15
例10.4中I?的一阶差分变量的所有方法的单位根检验结果:
所有P值均小于 0.05,说明平稳
单位根检验
第一节 单序列单位根检验 第二节 面板数据单位根检验
精选整理一 序列单位根检验在时间序列分析中的地位 二 序列单位根检验软件相关操作
三 不同检验结果后续分析思路
四 协整检验
精选整理
2
一 序列单位根检验在时间序列分析中的地位
时间序列总体分析思路
时间序列
◎原假设:6种方法中除KPSS外是:不稳定(存在单位根) ◎判定规则
P规则:小于临界值则接受H1 临界值法
具体:左则单边: ①ADF② DFGLS ③ PP⑥ NP 接受(原假设)域 统计值大于临界值
右则单边: ④ KPSS ⑤ ERS 接受(原假设)域 统计值小于临界值
备注:只要软件提供了P值就直接按P规则 做判定;除非没有提供的情况 下 才动用临界值法
备注:只要软件提供了P值就直接按P规则
做判定;除非没有提供的情况下 才动用 临界值法
精选整理
7
三 不同检验结果后续分析思路
分析思路 差分平稳
精选整理
8
不同检验结果后续分析思路
时间序列总体分析思路
时间序列
平稳性检验 原:不平稳
若是平稳序列
非平稳序列
单序列 多序列
考虑差分平稳
ARMA 多元回归分析 差分平稳I(d) 不平稳
单位根检验操作PPT课件

方法2: 用自相关系数图判断
中国GDP时间序列的自相关系数不是很快地(如滞后期K=2,3
趋于零,即缓慢下降,再次表明序精选列是非平稳的.
7
方法3: 单位根检验
Quick Series Statistics
Unit Root Test
精选
8
输入变量名(本例:GDP)
精选
9
选择ADF检验 / Level(水平序列)/ Trend and Intercept (趋势项和漂移项)/ 滞后期数:2
(A)DF检验
PP检验
(2)检验对象
Level(水平序列)
1st difference(一阶差分序列)
2nd difference(二阶精差选分序列)
2
(3)检验式中应包括的附加项 Intercept(漂移项) Trend and Intercept(趋势项和漂移项) None(无附加项)
(4)检验式中因变量的滞后差分项的个数。
• 所以,对于一般的序列,采用画图的方法就可以了。
• 至于你检验出现的这种情况则是正常现象,因为检验序列显著性水平的T 统计量在原假设下的渐进分布依赖于单位根检验的不同形式。
精选
18
精选
3
例 根据《中国统计年鉴2004》,得到我国1978—2003年的
GDP序列,检验其是否为平稳序列。 中国1978—2003年度GDP序列
精选
4
精选
5
方法1: 用时序图判断
由GDP的时序图初步判断序列是不平稳的(可以看出该序列可能 存在趋势项,若需用ADF检验则选精选择第三种模型进行检验)。 6
• 滞后阶数的问题。最佳滞后阶数主要根 据AIC SC准则判定,当你选择好检验方 式,确定好常数项、趋势项选择后,在 lagged differences栏里可以从0开始尝试, 最大可以尝试到7。你一个个打开去观察, 看哪个滞后阶数使得结论最下方一栏中 的AIC 和SC值最小,那么该滞后阶数则 为最佳滞后阶数。
第4章单位根检验(讲稿)(★)

第4章单位根检验(讲稿)(★)第一篇:第4章单位根检验(讲稿)第4章单位根检验4.1 DF分布由于虚假回归问题的存在,在回归模型中应避免直接使用非平稳变量。
因此检验变量的平稳性是一个必须解决的问题。
在第二章中介绍用相关图判断时间序列的平稳性。
这一章则给出严格的统计检验方法,即单位根检验。
1)检验模型在介绍检验方法之前,先讨论所用统计量的分布。
给出三个简单的自回归数据生成过程(d.g.p.),yt = β yt-1 + ut ,(4.1) yt = μ + β yt-1 + ut ,(4.2)yt = μ + α t + β yt-1 + ut ,(4.3)y0 = 0, ut ~ IID(0, σ)其中μ称作位移项(漂移项),α t称为趋势项。
显然,对于以上三个模型:当|β| < 1时,yt 是平稳的,当|β| = 1时,yt 是非平稳的。
2)检验统计量分布以模型(4.1)为例,(1)若β= 0,统计量,2ˆ-0βˆ)t(β=t~(T-1)(4.4)ˆs(β)的极限分布为标准正态分布。
(2)若|β| < 1,统计量,ˆ-ββˆ)=t(βˆ)(4.5)s(β渐进服从标准正态分布。
根据中心极限定理,当T →∞时,ˆ-β)→ N(0, σ 2(1-β 2))(4.6)T(βTˆ)t(β(3)那么在|β| = 1条件下,统计量服从什么分布呢?当|β| = 1时,变量非平稳,上述极限分布发生退化(方差为零)。
①DF统计量检验单位根的一个统计量是DF统计量。
DF统计量的表达式与通常意义的t统计量完全相同。
ˆ-1ˆ-1ββˆ)=DF=t(β=Tˆs(β)s(y2)-1/2u∑t-1t=1 2=(∑yt-1)t=1T21/2∑uytt=1Tt=1Tt-12suT y∑t-1∑utyt-1= 当T →∞时,DF =ˆ-1βˆ)s(βsu(∑yt-12)1/2t=1t=1T(4.16)⇒(1/2)(W(1)2-1)(W(i)di)0⎰121/2(4.17)同理,对于模型(4.2)和(4.3)的DF统计量的极限分布也是Wiener过程的函数。
时间序列的平稳性和单位根检验.共65页PPT

谢谢!
•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
时间序列的平稳性和单位根检验.
•
26、我们像鹰一样,生来就是自由的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理,即使延续时 间再长 ,也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
第13讲 单位根检验
第13讲 单位根检验由于虚假回归问题的存在,在回归模型中应避免直接使用不存在协积关系的非平稳变量。
因此检验变量的平稳性是一个必须解决的问题。
在第二章中介绍用相关图判断时间序列的平稳性。
这一章则给出序列平稳性的严格的统计检验方法,即单位根检验。
在介绍单位根检验之前,先认识四种典型的非平稳随机过程。
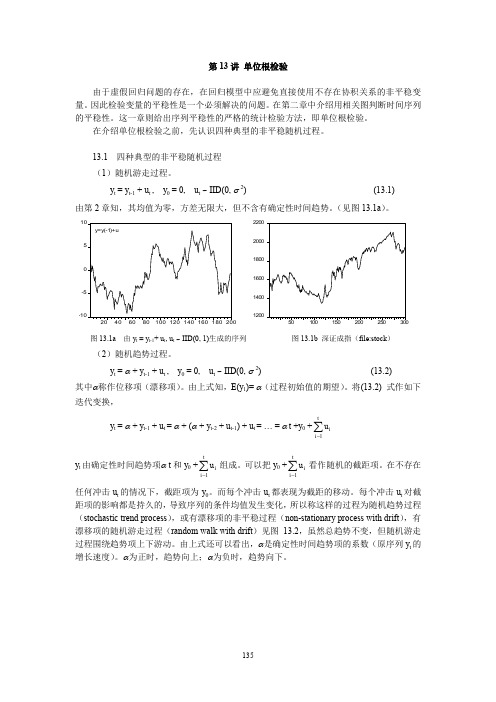
13.1 四种典型的非平稳随机过程(1)随机游走过程。
y t = y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) (13.1) 由第2章知,其均值为零,方差无限大,但不含有确定性时间趋势。
(见图13.1a )。
-10-551020406080100120140160180200y=y(-1)+u120014001600180020002200图13.1a 由y t = y t -1+ u t , u t ~ IID(0, 1)生成的序列 图13.1b 深证成指(file:stock )(2)随机趋势过程。
y t = α + y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) (13.2) 其中α称作位移项(漂移项)。
由上式知,E(y 1)= α(过程初始值的期望)。
将(13.2) 式作如下迭代变换,y t = α + y t -1 + u t = α + (α + y t -2 + u t -1) + u t = … = α t +y 0 +∑-ti i u 1y t 由确定性时间趋势项α t 和y 0 +∑-ti i u 1组成。
可以把y 0 +∑-ti i u 1看作随机的截距项。
在不存在任何冲击u t 的情况下,截距项为y 0。
而每个冲击u t 都表现为截距的移动。
每个冲击u t 对截距项的影响都是持久的,导致序列的条件均值发生变化,所以称这样的过程为随机趋势过程(stochastic trend process ),或有漂移项的非平稳过程(non-stationary process with drift ),有漂移项的随机游走过程(random walk with drift )见图 13.2,虽然总趋势不变,但随机游走过程围绕趋势项上下游动。
第五章单位根检验

Yt (1 )Yt1 ut 即 Yt Yt1 ut
Yt 1 (1 )Yt1 ut 即 Yt 1 Yt1 ut
Yt 1 2t (1 )Yt1 ut 即 Yt 1 2t Yt1 ut
大样本下的检验
• 较弱的同方差假设:Var (ut|xt) = 2, 对所有 t。[比 较:Var(ut|X) = Var(ut) = 2 ]
• 较弱的序列不相关的假设:E(utus| xt, xs) = 0 , t s。 [比较:Corr(ut,us| X)=0, t s]
• 在以上假设的基础上,我们就可以得到渐进正态 分布和通常标准差,以及正确的t ,F和LM统计量
• (1)渐进t检验。该种方法是首先选择一个较大 的m值,然后用t检验确定系数是否显著,如果是 显著的,则选择滞后项数为m;如果不显著,则减 少m直到对应的系数值是显著的。
• (2)信息准则。常用的信息准则有AIC信息准则 、SC信息准则,一般而言,我们选择给出了最小 信息准则值的m值
• 然而,在零假设(序列非平稳)下,即使在大样 本下t统计量也是有偏误的(向下偏倚),通常的t 检验无法使用。
性,如1980与1985无关
0.50 0.25 0.00 -0.25
whitenoise
0
50
100
150
200
250
300
350
400
450
500
1.0 ACF-whitenoise
0.5
0.0
-0.5
0
5
10
• For a random walk the correlogram does not die out. High autocorrelation for large values of k
第十章(一) 伪回归和单位根检验PPT课件

二、时间序列数据的平稳性
8
时间序列的平稳性概念:
▪ 所谓时间序列的平稳性,是指时间序列的统计规 律不会随时间的推移而发生变化。
▪ 直观上,一个平稳的时间序列可以看做一条围绕 其均值上下波动的曲线。
▪ 只有序列平稳时,之前的经典建模方法和检验过 程才能采用。
9
时间序列的平稳性概念:
假定某个时间序列是由某一随机过程 (stochastic process)生成的,即假定时间序列 {Xt}(t=1, 2, …)的每一个数值都是从一个概率分布 中随机得到,如果满足下列条件:
1.000 0.480 5.116 0.018 5.123 -0.069 5.241 0.028 5.261 -0.016 5.269 -0.219 6.745 -0.063 6.876 0.126 7.454 0.024 7.477 -0.249 10.229 -0.404 18.389 -0.284 22.994 -0.088 23.514 -0.066 23.866 0.037 24.004 0.105 25.483 0.093 27.198
Xt= 1Xt-1+2Xt-2…+kXt-k 该随机过程平稳性条件将在第二节中介绍。
14
三、平稳性检验的图示判断
15
▪ 给出一个随机时间序列,首先可通过该 序列的时间路径图来粗略地判断它是否 是平稳的。
▪ 一个平稳的时间序列在图形上往往表现 出一种围绕其均值不断波动的过程;
▪ 而非平稳序列则往往表现出在不同的时 间段具有不同的均值(如持续上升或持 续下降)。
Xt=Xt-1+t
这里, t是一个白噪声。
11
容易知道该序列有相同的均值:E(Xt)=E(Xt-1) 为了检验该序列是否具有相同的方差,可假设Xt的 初值为X0,则易知 X1=X0+1 X2=X1+2=X0+1+2 …… Xt=X0+1+2+…+t 由于X0为常数,t是一个白噪声,因此Var(Xt)=t2 即Xt的方差与时间t有关而非常数,它是一非平稳序列。
平稳性和单位根检验71页PPT

平稳性和单位根检验
6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
