剪力图和弯矩图
工程力学弯曲强度1(剪力图与弯矩图

05 剪力图与弯矩图的计算与分析
CHAPTER
剪力与弯矩的计算方法
要点一
剪力计算
根据受力分析,通过力的平衡原理计算剪力。在梁的截面 上,剪力方向与梁的轴线垂直,大小等于通过截面形心的 剪切面上的剪力。
要点二
弯矩计算
弯矩是描述梁弯曲变形的量,其计算方法包括截面法、力 矩分配法等。弯矩的计算需要考虑梁的长度、截面尺寸、 材料属性以及外力分布等因素。
在工程实践中,许多结构和设备都需 要承受弯曲负荷,如桥梁、建筑、车 辆等,因此弯曲强度的研究具有重要 意义。
弯曲强度的基本原理
弯曲强度的基本原理包括剪力和弯矩 的分析。剪力是指在弯曲过程中垂直 于轴线的力,而弯矩则是指弯曲过程 中产生的力矩。
剪力和弯矩的分析是确定结构在弯曲 负荷下的应力和变形的重要手段,也 是进行结构设计和优化的基础。
谢谢
THANKS
剪力图与弯矩图的受力分析
剪力图
通过绘制剪力随梁长度变化的曲线图,可以直观地表示 出梁在不同位置受到的剪力大小和方向。根据剪力图, 可以分析梁在受力过程中的稳定性以及剪切破坏的可能 性。
弯矩图
弯矩图表示弯矩随梁长度变化的曲线图,可以用来分析 梁在不同位置的弯曲变形程度以及弯曲应力分布情况。 通过弯矩图,可以判断梁在受力过程中是否会发生弯曲 失稳或弯曲破坏。
CHAPTER
剪力图与弯矩图在结构设计中的应用
结构设计是工程中非常重要的环节,剪力图 与弯矩图是进行结构设计的关键工具。通过 分析剪力和弯矩的分布和大小,可以确定结 构的受力情况和变形趋势,从而优化结构设 计,提高结构的稳定性和安全性。
在进行结构设计时,需要综合考虑多种因素 ,如载荷、材料属性、连接方式等。剪力图 与弯矩图可以帮助工程师更好地理解和分析
2.3.2剪力图和弯矩图

二、剪力图和弯矩图的绘制方法
如图所示,坐标原点对应梁的左端点截面。
x轴对应梁的杆轴线,从梁左端点开始;y轴对应剪力
值或弯矩值:(注意:箭头可以省略不画)
剪力正值画在x轴上方,负值画在x轴下方,并标出正
3、弯矩极值点:剪力为0的点,对应弯矩值取极值
4、集中力作用点:剪力图发生突变,突变方向和集中力方 向一致,突变值等于集中力的值,弯矩图有转折
5、集中力偶作用点:剪力图不受影响,弯矩图有突变,突 变方向和集中力偶符号相反,突变值等于集中力偶矩的值。
四、剪力图和弯矩图的绘图步骤
1、求支座反力 2、荷载图、剪力图、弯矩图三图上下对齐 3、分段定性 4、根据荷载走向作出Fs图 5、根据Fs图作出M图
A
B
FAy=ql/2
l
q
FBy=ql/2 M中=ql2/8
A
B
(3)计算可得出:
FAy=ql
l
MA=ql2/2
M1
A
B (4)计算可得出:
FAy=FBy=0
l
M=-M1
1、无荷载区段:剪力图是水平线,弯矩图是斜直线(如剪 力图为0,弯矩图为水平线)
2、向下的均布荷载区段:剪力图是下斜直线,弯矩图是下 凸的抛物线
第二章 静定结构内力分析
第三节 单跨静定梁的内力分析 (剪力图和弯矩图)
授课教师:工计会组 靳玉红
一、剪力图和弯矩图的定义
在一般情况下,梁各个截面上的剪力值和弯矩值是不 同的,它们随着截面位置的不同而变化。
由于在进行梁的强度计算时,需要知道梁在外力作用 下所产生的最大内力及最大内力所在的截面位置,以及全 梁的内力随截面位置变化的情况。通常用相应的图形来表 示内力沿梁长度方向的变化规律,这种表示剪力和弯矩变 化规律的图形称为剪力图和弯矩图。
剪力、弯矩方程与剪力、弯矩图

截面位置对剪力和弯矩的影响
总结词
截面位置对剪力和弯矩具有显著影响。不同的截面位置会导致剪力和弯矩的大小和方向发生变化。
详细描述
在结构分析中,截面位置是影响剪力和弯矩的重要因素之一。不同的截面位置会导致剪力和弯矩的大小和方向发 生变化,从而影响结构的整体受力性能。例如,在梁中选取不同的截面位置进行支撑或固定,会对梁的剪力和弯 矩产生显著影响。
05 剪力、弯矩与材料力学性 能的关系
材料弹性对剪力和弯矩的影响
弹性材料在剪力和弯矩作用下会发生弹性变形,变形量与外力成正比,当外力去 除后,材料能够恢复原状。
弹性材料的剪切模量和弯曲刚度决定了剪力和弯矩的大小,剪切模量越大,材料 抵抗剪切变形的能力越强;弯曲刚度越大,材料抵抗弯曲变形的能力越强。
根据绕顺时针方向观察确定,使上侧 纤维受拉时为正。
02 剪力方程与弯矩方程
剪力图与弯矩图的绘制
1
剪力图和弯矩图是表示梁上剪力和弯矩随截面位 置变化的图形。
2
这些图的绘制基于剪力方程和弯矩方程的计算结 果,通过将计算得到的剪力和弯矩值标在图中相 应的位置上,并连接成线。
3
剪力图和弯矩图的绘制有助于直观地了解梁在不 同截面位置的受力状态和应力分布情况。
弯矩
在梁或结构中,由于弯曲而产生 的力矩,表示弯曲变形的大小。
剪力与弯矩在力学中的作用
剪力
主要影响结构的剪切变形,对梁的剪切承载能力有重要影响 。
弯矩
主要影响结构的弯曲变形,对梁的弯曲承载能力有重要影响 。
剪力与弯矩的符号规定
剪力正方向
根据右手定则确定,从杆件的受压一 侧指向受拉一侧。
弯矩正方向
02
材料强度越高,抵抗剪力和弯矩等外力的能力越强, 所能承受的剪力和弯矩越大。
剪力以及弯矩剪力图以及弯矩图

剪力图和弯矩图在工程管理中的应用
结构设计:用于计 算结构受力确定结 构尺寸和材料
施工管理:用于 指导施工确保施 工质量和安全
维护管理:用于 评估结构状态制 定维护计划
优化设计:用于 优化结构设计降 低成本和能耗
剪力图和弯矩图的注意 事项
绘制剪力图和弯矩图时应注意的事项
确保数据准确无误 注意单位换算确保单位一致 绘制过程中注意比例尺和坐标轴的设置 绘制完成后检查图例、标题、标注等是否清晰明确
添加副标题
剪力和弯矩剪力图以及弯矩 图
汇报人:
目录
CONTENTS
01 添加目录标题
02 剪力和弯矩的基本 概念
03 剪力图和弯矩图的 绘制
04 剪力图和弯矩图的 解读
05 剪力图和弯矩图的 应用
06 剪力图和弯矩图的 注意事项
添加章节标题
剪力和弯矩的基本概念
剪力和弯矩的定义
剪力:作用在物体表面上的力使物体发生剪切变形 弯矩:作用在物体表面上的力使物体发生弯曲变形 剪力图:表示剪力在物体表面上的分布情况 弯矩图:表示弯矩在物体表面上的分布情况
剪力和弯矩的计算方法
剪力:作用在物体上的力使物体发生剪切变形 弯矩:作用在物体上的力使物体发生弯曲变形 剪力计算方法:根据力的平衡原理利用剪力公式进行计算 弯矩计算方法:根据力的平衡原理利用弯矩公式进行计算
剪力和弯矩的单位和符号
剪力:单位为牛顿(N) 符号为F
弯矩:单位为牛顿·米 (N·m)符号为M
证结构安全
剪力图和弯矩图在施工中的应用
确定结构受力情况: 通过剪力图和弯矩图 可以了解结构的受力 情况为施工提供依据。
优化施工方案:根据 剪力图和弯矩图可以 优化施工方案提高施 工效率和质量。
剪力图和弯矩图

内力图:为了形象直观地表示内力沿截面位置变化的规律,通常将内力随截面位置变化的情况绘成图形,这种图形叫内力图。
它包括轴力图、扭矩图、剪力图和弯矩图。
内力图(图)外伸梁的剪力图和弯矩图内力图的规律:1、在无荷载作用区,当剪力图平行于x轴时,弯矩图为斜直线。
当剪力图为正时,弯矩图斜向右下;当剪力图为负时,弯矩图斜向右上。
2在均布荷载作用下的规律是:荷载朝下方,剪力往右降,弯矩凹朝上。
3、在集中力作用处,剪力图发生突变,突变的绝对值等于集中力的大小;弯矩图发生转折。
4、在集中力偶作用处弯矩图发生突变,突变的绝对值等于该集中力偶的力偶矩;剪力图无变化。
5、在剪力为零处有弯矩的极值弯矩图:弯矩图是一条表示杆件不同截面弯矩的曲线。
这里所说的曲线是广义的,它包括直线、折线和一般意义的曲线。
弯矩图是对构件弯矩的图形表示,弯矩图画在受拉侧,无须标正负号。
特性:弯矩图的绘制主要有两个关键点:一是要准确画出曲线的形状,即确定弯矩图的图形特征:二是确定曲线的位置,即在已知曲线的形状、大小之后确定平面曲线的位置,这就要求先确定曲线上任意两点的位置,此处所指两点的位置即指某两个截面处的弯矩值。
可见,弯矩图的绘制主要指完成以下两项工作:(1)确定图形特征及特征值;(2)得出某两个截面处的弯矩值。
基础:1、熟悉单跨梁在各种荷载独立作用下的弯矩图特征:比如悬臂梁在一个集中荷载作用下.其弯矩图的特征是一个直角三角形;悬臂梁在均布荷载作用于全长上时,其弯矩图为一个曲边三角形等。
单跨梁在一种荷载作用下的弯矩图。
2、杆件某段两端点弯矩值的确定杆件某段两端点弯矩值一般有下面三种情况:(1)无铰梁段:一般要先算出粱段两端截面处的弯矩值。
(2)梁段中间有一个铰:因已知无外力偶矩的铰处弯矩为零,只须另算一处截面的弯矩即可。
(3)梁段中间有两个铰:这两铰处的弯矩都为零,可直接按简支梁弯矩图特征画出弯矩图。
剪力图和弯矩图(基础)

轴,。
以表(a)(c)(1)(2) (3)≤ (4) 以剪力图是平行于轴的直线。
段的剪力为正,故剪力图在轴上方;段剪力为负,故剪力图在轴之下,如图8-12(b )所示。
由式(2)与式(4)可知,弯矩都是的一次方程,所以弯矩图是两段斜直线。
根据式(2)、(4)确定三点,, ,由这三点分别作出段与段的弯矩图,如图8-12(c )。
例8-4 简支梁受集度为的均布载荷作用,如图8-13(a )所示,作此梁的剪力图和弯矩图。
图8-13解 (1)求支反力 由载荷与支反力的对称性可知两个支反力相.即(2)列出剪力方程和弯矩方程 以梁左端为坐标原点,选取坐标系如图所示。
距原点为的任意横截面上的剪力和弯矩分别为x C l x AC x BC x x 0=x 0)(=x M a x =l Fabx M =)(l x =0)(=x M AC BC AB q A x解 (1)求支反力 由静力平衡方程,得(2)列剪力方程和弯矩方程 由于集中力作用在处,全梁内力不能用一个方程来表示,故以为界,分两段列出内力方程段0<≤ (1)0≤< (2)段 ≤< (3)≤≤(4) (3) 画剪力图和弯矩图 由式(1)、(3)画出剪力图,见图8-14(b );由式(2)(4)画出弯矩图,见图8-14(c )。
二、弯矩、剪力与分布载荷集度之间的微分关系在例8-4中,若将的表达式对取导数,就得到剪力。
若再将的∑=0)(x M A ∑=0)(x M B m C C AC l mF x F A Q ==)(x a xl m x F x M A ==)(x a BC l mF x F A Q ==)(a x l mx l mm x F x M A -=-=)(a x l )(x M x )(x F Q )(x F Q表达式对取导数,则得到载荷集度。
这里所得到的结果,并不是偶然的。
实际上,在载荷集度、剪力和弯矩之间存在着普遍的微分关系。
现从一般情况出发加以论证。
材料力学-5-弯矩图与剪力图

从所得到的剪力图和 弯矩图中不难看出:
在集中力作用点两 侧截面上的剪力是不相 等的,而在集中力偶作 用处两侧截面上的弯矩 是不相等的,其差值分 别为集中力与集中力偶 的数值。
例题5
q
A
4a FAy
梁由一个固定铰链支座和一个辊轴支座所
支承,但是梁的一端向外伸出,这种梁称为外 伸梁(overhanging beam)。梁的受力以及各部 分尺寸均示于图中。
工程中的弯曲构件
工程中可以看作梁的杆件是很多的:
桥式吊车的大梁 可以简化为两端饺支 的简支梁。在起吊重 量(集中力FP)及大梁自 身重量(均布载荷q)的 作用下,大梁将发生弯 曲。
工程中可以看作梁的杆件是很多的:
石油、化工设备中各种直立式反应塔,底部与地面固定 成一体,因此,可以简化为一端固定的悬臂梁。在风力载荷 作用下,反应塔将发生弯曲变形。
Nanjing University of Technology
材料力学 课堂教学(5)
2020年8月12日
第5章 梁的弯曲问题(1)-剪力图与弯矩图
杆件承受垂直于其轴线的外力或位于其轴线所在平面内的 力偶作用时,其轴线将弯曲成曲线,这种受力与变形形式称为 弯曲(bending)。
主要承受弯曲的杆件称为梁(beam)。
得到梁的剪力方程和弯 矩方程分别为:
M(x)
FQ x=FRA qx=ql-qx 0 x 2l
FRA x
M x=qlx-qx2
0 x 2l
2
这一结果表明,梁上的剪力方程是x的线性函数;弯矩方程是x的 二次函数。
载荷集度、剪力、弯矩之间的 微分关系
绘制剪力图和弯矩图有两种方法:
第一种方法是:根据剪力方程和弯矩方程,在FQx和M-x坐标系中绘制出相应的图线,便得到所需要的 剪力图与弯矩图。
剪力图和弯矩图-课件(PPT-精)

02 剪力图和弯矩图的绘制
绘制步骤
确定受力点
首先确定梁的受力点,通常为 梁的两端或支撑点。
分析受力
分析梁所受的剪力和弯矩,确 定剪力和弯矩的大小和方向。
绘制剪力图和弯矩图
根据分析结果,在梁上标出剪 力和弯矩的大小和方向,并绘 制剪力图和弯矩图。
标注数据
在剪力图和弯矩图上标注相关 数据,如剪力和弯矩的大小、
3
优化施工图设计
通过分析剪力图和弯矩图,可以发现施工图设计 中的不足之处,并进行优化改进,提高施工图设 计的合理性和可行性。
在施工过程中的应用
监控施工过程
在施工过程中,通过实时监测剪 力图和弯矩图的动态变化,可以 及时发现施工中的问题,采取相
应的措施进行调整和处理。
评估施工效果
根据剪力图和弯矩图的监测结果, 可以对施工效果进行评估,判断 施工是否符合设计要求和质量标
计算公式
剪力Q=F*sin(a),其中F为外力,a为 外力与杆件轴线的夹角;弯矩M=F*d, 其中F为外力,d为外力作用点到杆件 固定端的距离。
计算步骤
注意事项
在计算过程中应注意单位的统一,并 考虑杆件的固定端约束条件。
先确定杆件上各点的外力大小和方向, 然后根据公式计算各点的剪力和弯矩, 最后绘制剪力图和弯矩图。
THANKS FOR WATCHING
感谢您的观看
实例3
一斜梁在水平载荷作用下的剪力图 和弯矩图解读。
04 剪力图和弯矩图的应用
在结构设计中的应用
评估结构的承载能力
通过分析剪力图和弯矩图,可以确定结构在不同受力情况下的承 载能力,从而确保结构的安全性和稳定性。
优化结构设计
通过调整剪力图和弯矩图的分布和大小,可以优化结构设计,降低 材料消耗,提高结构的经济性和环保性。
剪力图和弯矩图(史上最全面)

1.25 1
q=2kN/m
+
x
_
1
26
§4–5 按叠加原理作弯矩图
一、叠加原理: 多个载荷同时作用于结构而引起的内力等于每个载荷单独
作用于结构而引起的内力的代数和。
Q ( P 1 P 2 P n ) Q 1 ( P 1 ) Q 2 ( P 2 ) Q n ( P n )
9
[例1]贮液罐如图示,罐长L=5m,内径 D=1m,壁厚t =10mm,
钢的密度为: 7.8g/cm³,液体的密度为:1g/cm³,液面高 0.8m,外伸端长 1m,试求贮液罐的计算简图。
解:
q — 均布力
10
§4–2 梁的剪力和弯矩
一、弯曲内力:
a
[举例]已知:如图,P,a,l。 A
求:距A端x处截面上内力。 l
Q Q(x) M M (x)
剪力方程 弯矩方程
2. 剪力图和弯矩图:
剪力图
Q Q(x) 的图线表示
弯矩图
M M (x) 的图线表示
16
[例2] 求下列各图示梁的内力方程并画出内力图。
MO
YO YO
MO
L
P
解:①求支反力
Q(x) M(x)
x
YOP; M OPL ②写出内力方程
Q(x) M(x)
利用内力和外力的关系及特殊点的内力值来作图的方法。
38
三、 叠加原理: 多个载荷同时作用于结构而引起的内力等于每个载荷单
独作用于结构而引起的内力的代数和。
Q ( P 1 P 2 P n ) Q 1 ( P 1 ) Q 2 ( P 2 ) Q n ( P n )
M ( P 1 P 2 P n ) M 1 ( P 1 ) M 2 ( P 2 ) M n ( P n )
剪力图和弯矩图教程解读
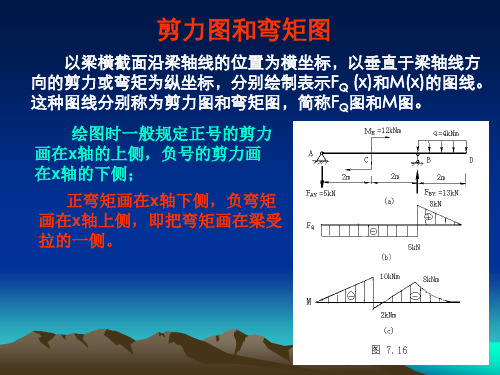
q=5kN/m
A
19.75kN
2kN
C
8m
B
1m 2kN
( Q)
+
x=3.95m
-
+
20.25kN 2kNm
( M)
+
39kNm
解得
RA 1 m 4 P 2qa 10kN 3 a
1 2 P 5a RB 3a m q2a 0 2
(2)画内力图: CA段: q=0, 剪力图为水平直线; 弯矩图为斜值线。
QC QA P 3kN
DB段:q<0, 剪力图为斜直线; 弯矩图为抛物图为抛物线。
d 2 M ( x) (2)当q(x)朝下时, 2 q( x) 0 M图为上凹下凸。 dx 2 d M ( x) 当q(x)朝上时, dx2 q( x) 0 M图为上凸下凹。
(3) 在集中力作用处,M图发生转折。如果集中力向下,则M 图向下转折;反之,则向上转折。 (4) 在集中力偶作用处,M图产生突变,顺时针方向的集中力偶 使突变方向由上而下;反之,由下向上。突变的数值等于该集 中力偶矩的大小。 3. 弯矩图与剪力图的关系 (1)任一截面处弯矩图切线的斜率等于该截面上的剪力。 (2) 当FQ图为斜直线时,对应梁段的M图为二次抛物线。当FQ 图为平行于x轴的直线时,M图为斜直线。 (3) 剪力等于零的截面上弯矩具有极值;反之,弯矩具有 极值的截面上,剪力不一定等于零。左右剪力有不同正、负 号的截面,弯矩也具有极值。
(a<x<l) (0≤x≤l)
3.作剪力图和弯矩图
例题4 简支梁受集中力偶作用,如图示,试画梁的剪力图和弯矩图。 解:1.求约束反力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
4 4
2m
2m
2m
FA
FB
FS1 = −4KN
(−),
M1 = −8KN.m (−)
FS 2 = −4kN(−), M2 = 4kN.m
在集中力偶两侧的相邻横截面上, 剪力相同而弯矩发生突变, 在集中力偶两侧的相邻横截面上 剪力相同而弯矩发生突变 且突变值等于外集中力偶之矩. 且突变值等于外集中力偶之矩
A
a
m
P
B
m x
∑y = 0
可得
F A − FS = 0
FA
y
m
FS = FA
FS 称为 剪力
A
x
FS
C m
x
a
由平衡方程
P
m
∑mC = 0
M − FAx = 0
可得 M = FAx
A
m x
B
内力偶 M 称为 弯矩
y
FA
m C
FS
x
A
x
m
M
a
P
结论 梁在弯曲变形时, 梁在弯曲变形时, 横截面上的内力有 两个, 两个,即, 剪力 FS
∑F y = 0, −F A − FS1 = 0 ∑MC = 0, F A× 2 + M1 = 0
FS1 = −4KN (−), M1 = −8KN.m (−)
2KN 12KN.m
1 1 2 2 3 3
A
B
4 4
2m
2m
2m
FA
12KN.m
2
FB M2
FA
2
FS1 = −4KN (−), M1 = −8KN.m (−)
梁的变形计算问题,早在13世纪纳莫尔( 梁的变形计算问题,早在13世纪纳莫尔(Nemore J 13世纪纳莫尔 de)已经提出,此后雅科布·伯努利 丹尼尔·伯努利 伯努利、 de)已经提出,此后雅科布 伯努利、丹尼尔 伯努利 Bernoulli)、欧拉( )、欧拉 L) (Daniel Bernoulli)、欧拉(Euler L)等人都曾经研 究过这一问题。1826年纳维在他材料力学讲义中得出了正 究过这一问题。1826年纳维在他材料力学讲义中得出了正 确的挠曲线微分方程式及梁的弯曲强度的正确公式, 确的挠曲线微分方程式及梁的弯曲强度的正确公式,为梁 的变形与强度计算问题奠定了正确的理论基础。 的变形与强度计算问题奠定了正确的理论基础。
FA
A
m
B
m x
y
m C
弯矩 M
FS
x
A
x
m
M
y
取右段梁为研究对象。 取右段梁为研究对象。
FA
m C
FS
x
其上剪力的指向和弯矩 的转向则与取右段梁为 研究对象所示相反。 研究对象所示相反。
A
x
m
M
P
m
FB
M
FS m
B
2、FS 和 M 的正负号的规定 、 (1)剪力 FS 的符号 ) 的错动为 剪力 FS 使 梁的微段发生 “ 左上右下 ” 的错动为 正。 考虑的脱离体有顺时针转动趋势的剪力为 有顺时针转动趋势的剪力为正 或使 考虑的脱离体有顺时针转动趋势的剪力为正。
俄罗斯铁路工程师儒拉夫斯基(ЖуравскийДИ) 俄罗斯铁路工程师儒拉夫斯基(ЖуравскийДИ) 1855年得到横力弯曲时的切应力公式 30年后 年得到横力弯曲时的切应力公式。 年后, 于1855年得到横力弯曲时的切应力公式。30年后,他的同胞别 斯帕罗夫(ВеспаловД)开始使用弯矩图, 斯帕罗夫(ВеспаловД)开始使用弯矩图,被认为是 历史上第一个使用弯矩图的人。 弯矩图的人 历史上第一个使用弯矩图的人。
2KN 12KN.m
1 1 2 2 3 3
A
B
4 4
2m
2m
2m
FA
12KN.m
3
FB M3
FA
3
FS3
横截面上的内力(假设剪力和弯矩为正 剪力和弯矩为正)。 求 3-3 横截面上的内力(假设剪力和弯矩为正)。
∑F = 0 ∑M = 0
y C
− FA − FS3 = 0 FA × 4 + M3 −12 = 0
内 容 提 要
剪力和弯矩 • 剪力图和弯矩图
§9— 1
剪力和弯矩 • 剪力图和弯矩图
在外力作用下主要发生弯曲变形的杆件称为梁。 在外力作用下主要发生弯曲变形的杆件称为梁。 一、梁的剪力( FS )和弯矩 ( M ) 的定义与计算 梁的剪力( 1、用截面法求横截面上的内力 、
a
m
P
A
m x
B
用截面法假想地在 横截面mm处把梁分 处把梁分 横截面 为两段,先分析梁左段。 为两段,先分析梁左段。 由平衡方程得
◆ 横截面上的
弯矩 在数值上等于此横截面的 左侧 或 右侧 梁
外力(包括外力偶) 段上的 外力(包括外力偶)对该截面形心的力矩之代数和 。外 力矩的正负号规定与弯矩的正负号规定相同。 力矩的正负号规定与弯矩的正负号规定相同。 弯矩符号:当横截面上的弯矩使考虑的脱离体凹向上弯曲( 弯矩符号:当横截面上的弯矩使考虑的脱离体凹向上弯曲(下 半部受拉,上半部受压) 半部受拉,上半部受压)时,横截面上的弯矩为正;反之凹向 横截面上的弯矩为正; 下弯曲(上半部受拉,下半部受压)为负。 下弯曲(上半部受拉,下半部受压)为负。 不论在截面的 左侧 或 右侧 向上的外力均将引起 的弯矩, 的弯矩。 正值 的弯矩,而向下 的外力则引起 负值 的弯矩。
+
FS FS
dx
左下右上” 的错动为 剪力 FS 使 梁的微段发生 “ 左下右上” 的错动为负。 或使 考虑的脱离体有逆时针转动趋势的剪力为负。 考虑的脱离体有逆时针转动趋势的剪力为负 有逆时针转动趋势的剪力为
FS FS
dx
(2)弯矩符号 ) 横截面上的弯矩使考虑的脱离体下边受拉, 横截面上的弯矩使考虑的脱离体下边受拉,上边受压时为 正 。 上的弯矩使考虑的脱离体下边受拉
(受压) 受压)
+
M
M
(受拉) 受拉)
横截面上的弯矩使考虑的脱离体上边受拉, 横截面上的弯矩使考虑的脱离体上边受拉,下边受压时为 负。 上的弯矩使考虑的脱离体上边受拉
(受拉) 受拉)
-
(受压) 受压)
例题: 横截面上的剪力和弯矩。 例题:求外伸梁 1-1,2-2,3-3,4-4 横截面上的剪力和弯矩。 , , ,
平截面假设是材料力学计算理论的重要基础之一。 平截面假设是材料力学计算理论的重要基础之一。雅科 是材料力学计算理论的重要基础之一 布·伯努利于1695年提出了梁弯曲的平截面假设,由此可以证明 伯努利于1695年提出了梁弯曲的平截面假设, 伯努利于1695年提出了梁弯曲的平截面假设 中性层)的曲率和弯矩成正比。此外他还得到了梁的挠曲 梁(中性层)的曲率和弯矩成正比。此外他还得到了梁的挠曲 线微分方程。但由于没有采用曲率的简化式, 线微分方程。但由于没有采用曲率的简化式,且当时尚无弹性 模量的定量结果,致使该理论并没有得到广泛的应用。 模量的定量结果,致使该理论并没有得到广泛的应用。
第9章 弯
曲
§9-1 剪力和弯矩 •剪力图和弯矩图 剪力图和弯矩图 §9-2 剪力图和弯矩图的进一步研究 §9-3 弯曲正应力 §9-4 求惯性矩的平行移轴公式 §9-5 弯曲切应力 §9-6 梁的强度条件 §9-7 挠度和转角 §9-8 弯曲应变能 §9-9 斜弯曲 §9-10 超静定梁
材料力学发展大事记 —梁的弯曲问题 梁的弯曲问题 在《关于力学和局部运动的两门新科学的对话和数学证 一书中,伽利略讨论的第二个问题是梁的弯曲强度问 明》一书中,伽利略讨论的第二个问题是梁的弯曲强度问 按今天的科学结论, 题。按今天的科学结论,当时作者所得的弯曲正应力公式 并不完全正确, 并不完全正确,但该公式已反映了矩形截面梁的承载能力 分别为截面的宽度和高度)成正比, 和bh2(b、h分别为截面的宽度和高度)成正比,圆截面梁 承载能力和d 为横截面直径)成正比的正确结论。 承载能力和d3(d为横截面直径)成正比的正确结论。对于 空心梁承载能力的叙述则更为精彩,他说,空心梁“能大 空心梁承载能力的叙述则更为精彩,他说,空心梁“ 大提高强度而无需增加重量, 大提高强度而无需增加重量,所以在技术上得到广泛的应 在自然界就更为普遍了。 用。在自然界就更为普遍了。这样的例子在鸟类的骨骼和 各种芦苇中可以看到,它们既轻巧, 各种芦苇中可以看到,它们既轻巧,而又对弯曲和断裂具 有相当高的抵抗能力” 有相当高的抵抗能力”。
熟练掌握 简便法
利用上述结论来计算某一截面上的内力是非常简便的, 利用上述结论来计算某一截面上的内力是非常简便的, 此时不需画脱离体的受力图和列平衡方程, 此时不需画脱离体的受力图和列平衡方程,只要梁上的 外力已知, 外力已知,任一截面上的内力均可根据梁上的外力逐项 写出。因此,这种求解内力的方法称为简便法。 写出。因此,这种求解内力的方法称为简便法 简便法。
2KN 12KN.m
1 2 2 3 3
A
1
B
4 4
2m
2m
2m
FA
FB
解:求支座反力,取整体为研究对象 求支座反力,
F A = 4KN (↓), FB = 6KN (↑)
2KN 12KN.m
1 2 2 3 3
A
1
B
4 4
2m
2m
2m
FA
1
FB M1
FA
1
FS1
横截面上的内力(假设剪力和弯矩为正 剪力和弯矩为正)。 求 1-1 横截面上的内力(假设剪力和弯矩为正)。
求剪力和弯矩的简便方法
◆ 横截面上的 剪力 在数值上等于此横截面的 左侧 或 右 侧 梁段上所有竖向 外力(包括斜向外力的竖向分力)的 外力(包括斜向外力的竖向分力) 外力正负号的规定与剪力正负号的规定相同。 代数和 。外力正负号的规定与剪力正负号的规定相同。
