2020-2021 六年级数学比例和反比例 培优题
2020-2021 六年级数学比例和反比例 培优题

2020-2021 六年级数学比例和反比例培优题一、比例和反比例1.如果10千克菜籽可以榨6.5千克菜油,那么有这种菜籽360千克,可以榨多少千克油?(用比例解)【答案】解:设可以榨x千克油。
10:6.5=360:x10x=6.5×360x=2340÷10x=234答:可以榨油234千克。
【解析】【分析】菜籽的重量和榨油的质量的比值是不变的,二者成正比例,设出未知数,根据正比例关系列出比例,解比例求出可以榨油的重量即可。
2.服装厂要加工一批服装,一共有4500套,头5天加工了750套,照这样计算,一共要多少天才能加工完这批报装?(用比例解)【答案】解:设一共要x天才能加工完这批服装。
750:5=4500:x750x=5×4500x=22500÷750x=30答:一共要30天才能加工完这批服装。
【解析】【分析】每天加工服装的套数不变,加工的总数与天数成正比例关系;设出未知数,根据每天加工的套数不变列出比例,解比例即可解决问题。
3.一辆汽车在公路上行驶,行驶的时间和路程如下图。
(1)这辆车10小时行驶多少千米?(2)行驶600千米要多少时?【答案】(1)解:10×80=800(千米)答:这辆车10小时行驶800千米。
(2)解:600÷80=7.5(小时)答:行驶600千米要7.5时。
【解析】【分析】(1)由时间路程图可知,1小时行驶的路程是80千米,即汽车的速度是80千米/小时,再由“路程=速度×时间”进行计算;(2)由(1)可知汽车的速度,再由“时间=路程÷速度”进行计算。
4.为了保护环境,净化空气,六年级同学要去植树,原计划每小时植树40棵,3小时植完。
实际每小时比原计划多植树20棵,实际提前几小时完成任务?【答案】1小时【解析】【解答】解:设实际提前x小时完成任务40:(40+20)=(3-x):360×(3-x)=1203-x=2x=1答:实际提前1小时完成任务【分析】同学要植树的总棵数是一定的,每小时植树棵数与时间成反比。
2020-2021六年级数学培优试卷(比例 )

2020-2021六年级数学培优试卷(比例 )一、比例1.下面()能和:4组成比例。
A. 5:10B.C.【答案】 C【解析】【解答】:4=÷4=;选项A,5:10=5÷10=,≠,不能组成比例;选项B,:=÷=,≠,不能组成比例;选项C,:=÷=,=,能组成比例。
故答案为:C。
【分析】表示两个比相等的式子叫比例,判断两个比是否能组成比例,用前项÷后项=比值,分别求出比值,如果比值相等,就能组成比例,否则,不能组成比例,据此解答。
2.把一个底3cm,高2cm的三角形,按3:1放大画在图上,放大后的三角形面积是()平方厘米.A. 9B. 18C. 27D. 54【答案】 C【解析】【解答】解:3×3=9(cm),2×3=6(cm),面积:9×6÷2=27(平方厘米)。
故答案为:C。
【分析】用三角形的底和高分别乘3即可求出放大后三角形的底和高,用底乘高除以2即可求出放大后三角形的面积。
3.与18:15能组成比例的一个比是()A. 6:30B. :C. 0.25 :D. 5:6【答案】 A【解析】【解答】解:18:15=1.2,A、6:30=0.2,不能组成比例;B、=1.2,能组成比例;C、0.25:=0.75,不能组成比例;D、5:6=,不能组成比例。
故答案为:B。
【分析】计算出每个比的比值,与18:15的比值相等的比才能组成一个比例。
4.一个零件长2毫米,在图纸上的长是5厘米,这幅图纸的比例尺是________.【答案】 25:1【解析】【解答】解:5厘米=50毫米,50:2=25:1。
故答案为:25:1。
【分析】1厘米=10毫米;比例尺=图上距离:实际距离;求比例尺时,单位要统一。
5.甲、乙两地之间的距离是240千米,在一幅地图上量得两地的图上距离是3厘米,这幅地图的比例尺是________。
【答案】 1:8000000【解析】【解答】3厘米:240千米=3厘米:24000000厘米=(3÷3):(24000000÷3)=1:8000000。
2020-2021六年级数学培优试卷(比例 )

2020-2021六年级数学培优试卷(比例 )一、比例1.把一个长5毫米的零件画在图纸上是1分米,这张图纸的比例尺是()。
A. 5:1B. 200:1C. 20:1【答案】 C【解析】【解答】1分米:5毫米=100毫米:5毫米=(100÷5):(5÷5)=20:1。
故答案为:C。
【分析】已知图上距离与实际距离,要求比例尺,用图上距离:实际距离=比例尺,据此列式解答。
2.下面能与6:组成比例的是()A. :6B. 3:C. 9:D. 3:【答案】 B【解析】【解答】解:6:=18;A、,不能组成比例;B、=18,能组成比例;C、,不能组成比例;D、=27,不能组成比例。
故答案为:B。
【分析】比例是表示两个比相等的式子,所以比值相等的两个比才能组成比例。
3.下面()能和:4组成比例。
A. 5:10B.C.【答案】 C【解析】【解答】:4=÷4=;选项A,5:10=5÷10=,≠,不能组成比例;选项B,:=÷=,≠,不能组成比例;选项C,:=÷=,=,能组成比例。
故答案为:C。
【分析】表示两个比相等的式子叫比例,判断两个比是否能组成比例,用前项÷后项=比值,分别求出比值,如果比值相等,就能组成比例,否则,不能组成比例,据此解答。
4.应用比例的基本性质,下面()组中的两个比可以组成比例。
A. 和B. 0.2:10和2:50C. 和【答案】 C【解析】【解答】解:×==×,能组成比例。
故答案为:C。
【分析】根据比列的基本性质,假设两个比可以组成比例,如果两内项之积等于两外项之积,即可组成比例。
5.下列各组中两个比能组成比例的是()。
A. 和B. 40:10和1:4C. 1.2:0.4和:D. :2和:5【答案】 C【解析】【解答】解:A、:2=,,不能组成比例;B、40:10=4,1:4=0.25,不能组成比例;C、1.2:0.4=3,,能组成比例;D、,,不能组成比例。
2020-2021 六年级数学比例 培优题

2020-2021 六年级数学比例培优题一、比例1.下面()能和:4组成比例。
A. 5:10B.C.【答案】 C【解析】【解答】:4=÷4=;选项A,5:10=5÷10=,≠,不能组成比例;选项B,:=÷=,≠,不能组成比例;选项C,:=÷=,=,能组成比例。
故答案为:C。
【分析】表示两个比相等的式子叫比例,判断两个比是否能组成比例,用前项÷后项=比值,分别求出比值,如果比值相等,就能组成比例,否则,不能组成比例,据此解答。
2.下面各比中,能与:6组成比例的是()A. 2.5:16B. 0.1:C. 3:2.4D. :4【答案】 D【解析】【解答】解:;A、2.5:16=2.5÷16=0.15625,不能组成比例;B、,不能组成比例;C、3:2.4=1.25,不能组成比例;D、,能组成比例。
故答案为:D。
【分析】比例是表示两个比相等的式子,因此比值相等的两个比才能组成比例。
3.下面各比中与:组成比例的比是()。
A. 3:4B. 4:3C. 1:12【答案】 B【解析】【解答】:=÷=,选项A,3:4=3÷4=,≠,不能组成比例;选项B,4:3=4÷3=,=,能组成比例;选项C,1:12=1÷12=,≠,不能组成比例。
故答案为:B.【分析】判断两个比是否能组成比例,可以求出比值,用前项÷后项=比值,如果比值相等,就能组成比例,否则不能组成比例.4.在下面各比中,能与∶组成比例的是( )。
A. 4∶3B. 3∶4C. ∶3【答案】 A【解析】【解答】解::=4:3。
故答案为:A。
【分析】根据比例的定义,比值相等的两个比可以构成比例。
5.人的体重和身高( )。
A. 不成比例B. 成正比例C. 成反比例【答案】 A【解析】【解答】解:人的体重和身高虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例。
2020-2021比例 培优题

2020-2021比例培优题一、比例1.下面能与6:组成比例的是()A. :6B. 3:C. 9:D. 3:【答案】 B【解析】【解答】解:6:=18;A、,不能组成比例;B、=18,能组成比例;C、,不能组成比例;D、=27,不能组成比例。
故答案为:B。
【分析】比例是表示两个比相等的式子,所以比值相等的两个比才能组成比例。
2.如果甲数的等于乙数的,那么甲数:乙数等于()A. 6:15B. 10:9C. 15:6D. 9:10【答案】 D【解析】【解答】如果甲数×=乙数×,则甲数:乙数=:=():()=9:10。
故答案为:D。
【分析】根据条件先列出等式,然后根据比例的基本性质,相乘的两个数同时作外项或内项,写出比例,然后化简即可。
3.把一个底3cm,高2cm的三角形,按3:1放大画在图上,放大后的三角形面积是()平方厘米.A. 9B. 18C. 27D. 54【答案】 C【解析】【解答】解:3×3=9(cm),2×3=6(cm),面积:9×6÷2=27(平方厘米)。
故答案为:C。
【分析】用三角形的底和高分别乘3即可求出放大后三角形的底和高,用底乘高除以2即可求出放大后三角形的面积。
4.如果5a=6b,那么a:b=()。
A. 5:6B. 6:5C. 3:2D. 2:3【答案】 B【解析】【解答】解:a:b=6:5。
故答案为:B。
【分析】根据比例的基本性质,把a和5看作两个外项,b和6看作两个内项即可。
5.3,4,9,12四个数组成的比例是( )。
A. 3∶4=12∶9B. 3∶4=9∶12C. 4∶3=9∶12【答案】 B【解析】【解答】解:A、两个比的比值不相等,不能组成比例;B、两个比的比值相等,能组成比例;C、两个比的比值不相等,不能组成比例。
故答案为:B。
【分析】表示两个比相等的式子叫做比例,只有两个比值相等的比才能组成比例。
6.一个长方形广场长是200m,在设计图上长5cm,这幅图的比例尺为________,图上长方形面积为20cm2,实际有________m2.【答案】 1:4000;32000【解析】【解答】5cm:200m=5cm:20000cm=(5÷5):(20000÷5)=1:4000;20÷5=4(cm);4÷=4×4000=16000(cm)=160(m);200×160=32000(m2)。
2020-2021比例和反比例 培优题

2020-2021比例和反比例培优题一、比例和反比例1.把一瓶果汁平均分成若干杯,分的杯数和每杯的果汁量如下表。
分的杯数/杯6543每杯的果汁量/mL100120()200(2)分的杯数和每杯的果汁量有什么关系?为什么?(3)如果把这些果汁平均分成10杯,每杯的果汁量是多少毫升?【答案】(1)150(2)解:成反比例,因为每杯的果汁量×分的杯数=果汁总量。
(3)解:6×100÷10=60(毫升)答:每杯的果汁量是60毫升。
【解析】【解答】解:(1)100×6÷4=150(mL)【分析】(1)这瓶果汁的总量不变,用总量除以4即可求出每杯的容量;(2)根据正反比例关系的意义确定这两个量的关系;(3)用果汁总量除以10即可求出每杯果汁的容量。
2.一幅地图上,用3cm的线段表示实际距离900km。
一条长480km的高速公路,在这幅地图上是多少厘米?(用比例解)【答案】解:设该条公路在这幅地图上是x厘米.900km=90000000cm,480km=48000000cm,90000000x=3×48000000x=1.6答:该条公路在这幅地图上是1.6厘米.【解析】【分析】设这条公路在这幅图上是x厘米,根据图上距离与实际距离的比不变列出比例,解比例求出图上距离即可.3.100克海水可以晒出3克盐。
照这样计算。
多少吨海水可以晒出1.2吨盐?【答案】解:设x吨海水可以晒出1.2吨盐,3:100=1.2:x3x=1.2×100x=120÷3x=40答:40吨海水可以晒出.【解析】【分析】晒出盐的质量与海水的质量比是不变的,因此设海水的吨数是x吨,根据这个比不变列出比例解答即可.4.30kg花生仁能榨出花生油12kg。
照这样计算,要榨出48t花生油,需要花生仁多少吨? 【答案】解:设需要花生仁x吨,12:30=48:x12x=30×48x=1440÷12x=120答:需要花生仁120t.【解析】【分析】花生油的出油率是不变的,花生仁的质量和花生油的质量成正比例,设出未知数,根据出油率不变列出比例解答即可.5.x、y、z是三个相关联的量且都不等于0,有x=yz。
2020-2021六年级数学培优试卷(比例 )

2020-2021六年级数学培优试卷(比例 )一、比例1.下面各比中,能与:6组成比例的是()A. 2.5:16B. 0.1:C. 3:2.4D. :4【答案】 D【解析】【解答】解:;A、2.5:16=2.5÷16=0.15625,不能组成比例;B、,不能组成比例;C、3:2.4=1.25,不能组成比例;D、,能组成比例。
故答案为:D。
【分析】比例是表示两个比相等的式子,因此比值相等的两个比才能组成比例。
2.人的体重和身高( )。
A. 不成比例B. 成正比例C. 成反比例【答案】 A【解析】【解答】解:人的体重和身高虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例。
故答案为:A。
【分析】判断两种量成正比例还是反比例的办法:当这两种相关联的量中相对应的两个数的商一定时,这两个数就成正比例关系;反之,当这两个数的积一定时,这两个数就成反比例关系。
3.在一张图纸上有400:1这样的一个比例。
这个比例告诉我们的是( )。
A. 图上距离是实际距离的B. 实际距离是图上距离的400倍C. 这张图纸是将实物放大到400倍画出来的【答案】 C【解析】【解答】在一张图纸上有400:1这样的一个比例,这个比例告诉我们的是:这张图纸是将实物放大到400倍画出来的.故答案为:C.【分析】根据对比例尺的认识可知,400:1这个比例尺表示图上距离是实际距离的400倍,据此解答.4.已知a:b=c:d,若将b乘5,使比例不成立的条件是( )。
A. a乘5B. c除以5C. d除以5【答案】 C【解析】【解答】因为 a:b=c:d ;所以bc=ad;bx5xc=ax5xd;bx5xc÷5=bc=ad故答案为:C【分析】由比例的基本性质可知,bc=ad,若将b乘5,等式左边扩大到原来的5倍,若d 除以5,等式的右边缩小到原来的.因此,等式不成立,即比例也不成立。
5.要把实际距离缩小到原来的,应选择的比例尺为()。
2020-2021 六年级数学比例 培优题

2020-2021 六年级数学比例培优题一、比例1.应用比例的基本性质,下面()组中的两个比可以组成比例。
A. 和B. 0.2:10和2:50C. 和【答案】 C【解析】【解答】解:×==×,能组成比例。
故答案为:C。
【分析】根据比列的基本性质,假设两个比可以组成比例,如果两内项之积等于两外项之积,即可组成比例。
2.与18:15能组成比例的一个比是()A. 6:30B. :C. 0.25 :D. 5:6【答案】 A【解析】【解答】解:18:15=1.2,A、6:30=0.2,不能组成比例;B、=1.2,能组成比例;C、0.25:=0.75,不能组成比例;D、5:6=,不能组成比例。
故答案为:B。
【分析】计算出每个比的比值,与18:15的比值相等的比才能组成一个比例。
3.能与∶组成比例的是()。
A. ∶B. 6∶5C. 5∶6【答案】B【解析】【解答】:=÷=×6=;选项A,:=÷=×5=;选项B,6:5=6÷5=;选项C,5:6=5÷6=;能与:组成比例的是6:5.故答案为:B.【分析】根据比例的意义:表示两个比相等的式子叫比例。
要求比值,用前项÷后项=比值,据此分别求出各选项的比值,然后与原题对比,与原题中的比的比值相等的才能组成比例,据此解答.4.在比例尺是1:600000的地图上,量的甲、乙两地之间的距离是15厘米,甲乙两地的实际距离是________千米.【答案】 90【解析】【解答】解:15÷=9000000厘米=90千米,所以甲乙两地的实际距离是90千米。
故答案为:90。
【分析】实际距离=图上距离÷比例尺,然后进行单位换算即可,即1千米=100000厘米。
5.在比例尺是1:50000的图纸上,量及两点之间的距离是18厘米,这两点的实际距离是________千米.【答案】 9【解析】【解答】解:18÷=900000厘米=9千米,所以这两点的实际距离是9千米。
2020-2021六年级数学培优试卷(比例和反比例 )

2020-2021六年级数学培优试卷(比例和反比例 )一、比例和反比例1.服装厂加工一批服装,计划每天加工120套,50天可以完成。
实际每天加工了150套,多少天可以加工完?(用比例解)【答案】解:设x天可以加工完。
150x=120×50x=6000÷150x=40答:40天可以加工完。
【解析】【分析】这批服装的总数不变,每天加工的套数与加工的天数成反比例,设出未知数,根据总套数不变列出比例,解比例求出实际加工的天数即可。
2.表中x和y是两个成比例的量,观察表格并填完整。
X36181210y51020X361812109y510151820空位中x和y的值。
3.一个滴水的水龙头滴水的时间和所浪费的水量如下表:滴水时间/分1020304050浪费水量/L0.61.21.82.43.0(1)在上图中描出表示滴水时间和相应浪费水量的点,然后把它们按顺序连起来。
(2)根据图象进行分析:滴水25分钟浪费的水有________L,滴水________分钟就会浪费2.7L的水。
滴水时间和浪费的水量成________比例。
(3)针对这一现象,你想说点什么呢?【答案】(1)解:(2)1.5;45;正(3)解:要珍惜水资源,注意节约用水。
(合理即可)【解析】【解答】(2)滴水25分钟浪费的水有1.5L,滴水45分钟就会浪费2.7L水;滴水时间和浪费的水量成正比例。
故答案为:(2)1.5;45;正。
【分析】(1)先描出对应的点,然后连接成一条线即可;(2)找出25分钟对应的点,然后确定浪费的水量;找出2.7L对应的点,然后确定对应的时间,根据图像可以直接判断两个量成正比例;(3)说出自己合理的观点即可。
4.补充表格。
药粉/克1246810水/克200400;2000【解析】【解答】因为200:1=200÷1=200,400:2=400÷2=200,所以水的质量:药粉的质量=200,则水的质量分别为:4×200=800(克),6×200=1200(克),8×200=1600(克),10×200=2000(克),根据计算,填空如下:【分析】根据题意可知,先求出水的质量与药粉质量的比,水的质量:药粉的质量=200,它们的比值一定,水和药粉的质量成正比例,用药粉的质量×200=水的质量,据此计算填空即可.5.a÷b=35,那么a与b成________比例关系,如果 = ,那么a与b成________比例关系.【答案】正;反【解析】【解答】解:a÷b=35,a与b的商一定,a与b成正比例关系;,则ab=35,所以a与b从反比例关系。
六年级数学比例和反比例培优题(20211109215922)

六年级数学比率和反比率培优题一、比率和反比率1.把一瓶果汁均匀分红若干杯,分的杯数和每杯的果汁量以下表。
分的杯数/杯 6 5 43每杯的果汁量/mL 100 120 () 200(1)请把上表增补完好。
(2)分的杯数和每杯的果汁量有什么关系?为何?(3)假如把这些果汁均匀分红 10 杯,每杯的果汁量是多少毫升?【答案】( 1) 150(2)解:成反比率,因为每杯的果汁量×分的杯数=果汁总量。
(3)解: 6×100÷10=60(毫升)答:每杯的果汁量是60 毫升。
【分析】【解答】解:(1) 100×6÷4=150( mL)【剖析】( 1)这瓶果汁的总量不变,用总量除以 4 即可求出每杯的容量;(2)依据正反比率关系的意义确立这两个量的关系;(3)用果汁总量除以 10 即可求出每杯果汁的容量。
2.学校买来一批课外书,准备散发到各班。
假如每班发15 本,能够发给24 个班,假如每班发 10 本,能够发给多少个班?(列比率解答)【答案】解:设能够散发给x 个班。
10x=15 × 24x=36答:能够发给36 个班。
【分析】【剖析】依据题意,这批课外书的总数不变,设假如每班发10 本,能够发给x 个班,则依据总数=每班散发数目×班数列出方程,求解方程即可。
3.妈妈有一辆自行车, A 和 B 是自行车的两个齿轮(如图),骑车时用脚驱动 A 带动 B,进而使自行车行进。
(1)这辆自行车,齿轮 A 有 50 个齿,齿轮 B 有 20 个齿。
当齿轮 A 转动 1 圈时,齿轮B转动多少圈?(2)这辆自行车的车轮直径约是 60cm,妈妈每日上班的行程大概是 3000m。
妈妈骑车上班大概要置多少圈(即齿轮 A 转动的圈数) ?(计算时π取 3,最后结果保存整数)【答案】( 1)解: 50×1÷20=2(.5圈)答:齿轮 B 转动 2.5 圈。
2020-2021比例和反比例 培优题
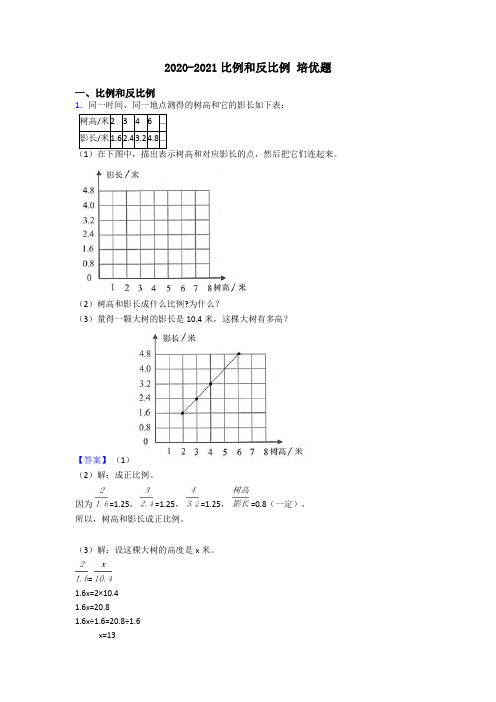
2020-2021比例和反比例培优题一、比例和反比例1.同一时间、同一地点测得的树高和它的影长如下表:树高/米2346…影长/米1.62.43.24.8…(2)树高和影长成什么比例?为什么?(3)量得一颗大树的影长是10.4米,这棵大树有多高?【答案】(1)(2)解:成正比例。
因为 =1.25, =1.25, =1.25, =0.8(一定),所以,树高和影长成正比例。
(3)解:设这棵大树的高度是x米。
=1.6x=2×10.41.6x=20.81.6x÷1.6=20.8÷1.6x=13答:这棵大树的高度是13米。
【解析】【分析】(1)观察统计图可知,横轴表示树高,竖轴表示影长,据此先描点,再连线,据此作图;(2)分别用树高:影长,求出比值,当比值一定时,成正比例,据此判断;(3)根据题意可知,设这棵大树的高度是x米,用树高:影长=树高:影长,据此列正比例解答.2.某工程队要铺设一条公路,前20天已铺设了2.8千米,照这样计算,剩下的4.2千米,还要多少天才能铺完?(用比例解)【答案】解:设还要x天才能铺完。
2.8∶20=4.2∶xx=30答:还要30天才能铺完。
【解析】【分析】照这样计算的意思就是每天铺的长度不变,铺的长度与天数成正比例,先设出未知数,根据每天铺的长度不变列出比例解答即可。
3.用一批纸张装订毕业纪念册,如果每本40页,可以装订50本。
如果现在用这批纸装订了100本,每本装订多少页?(用比例解)【答案】设每本装订x页。
100x=40×50x=20答:每本装订20页。
【解析】【分析】这批纸的总数一定,每本的页数与可以装订的本数成反比例,先设出未知数,再根据总页数一定列出比例,解比例求出每本装订的页数即可。
4.“浪漫一身”服装厂制作一批新款女式短裙,每条用布料1.2米,制作100条、200条、300条这样的短裙各需用布料多少米?将相应的米数填在表中。
2020-2021比例和反比例 练习题(培优)_

2020-2021比例和反比例练习题(培优)_一、比例和反比例1.下表中x与y两种量成反比例,请把表格填写完整。
X33060y40.312X33040601y40.40.30.212应的两个数的积一定,这两种量叫做成反比例的量,它们的关系叫做反比例关系,据此先求出x与y的积,然后用积÷一个量=另一个量,据此解答。
2.小兰看一本故事书,每天看10页,12天看完,若每天看15页,几天可以看完?【答案】解:设x天可以看完。
10×12=15x解得x=8答:8天可以看完。
【解析】【分析】已知每天看的页数×对应看完的天数=预计每天看的页数×对应预计看完的天数。
等式的性质2:等式两边同时乘(或除以)一个相同的数或式子,两边依然相等。
3.补充表格。
药粉/克1246810水/克200400;2000【解析】【解答】因为200:1=200÷1=200,400:2=400÷2=200,所以水的质量:药粉的质量=200,则水的质量分别为:4×200=800(克),6×200=1200(克),8×200=1600(克),10×200=2000(克),根据计算,填空如下:【分析】根据题意可知,先求出水的质量与药粉质量的比,水的质量:药粉的质量=200,它们的比值一定,水和药粉的质量成正比例,用药粉的质量×200=水的质量,据此计算填空即可.4.下面两幅图分别表示了人民币与美元和欧元的兑换情况。
(1)依据上图,写出100元人民币兑换的美元和欧元的钱数.(结果保留一位小数)人民币美元欧元100元________元________元(2)王叔叔用6000欧元兑换美元,能兑换多少美元?【答案】(1)16.7;12.5(2)解:300:400=3:46000÷3×4=8000(美元)答:能兑换8000美元。
2020-2021 六年级数学比例 培优题

2020-2021 六年级数学比例培优题一、比例1.下面()能和:4组成比例。
A. 5:10B.C.【答案】 C【解析】【解答】:4=÷4=;选项A,5:10=5÷10=,≠,不能组成比例;选项B,:=÷=,≠,不能组成比例;选项C,:=÷=,=,能组成比例。
故答案为:C。
【分析】表示两个比相等的式子叫比例,判断两个比是否能组成比例,用前项÷后项=比值,分别求出比值,如果比值相等,就能组成比例,否则,不能组成比例,据此解答。
2.下面不能组成比例的是( )。
A. 10∶12=35∶42B. 4∶3=60∶45C. 20∶10=60∶20【答案】 C【解析】【解答】解:因为12×35=420,10×42=420,所以10:12和35:42能组成比例;因为3×60=180,4×45=180,所以4:3和60:45能组成比例;因为10×60=600,20×20=400,所以20、10、60、20不能组成比例。
故答案为:C。
【分析】比例的基本性质:比例的内项之积等于比例的外项之积。
3.把一个直径4毫米的手表零件,画在图纸上的直径是8厘米,这幅图纸的比例尺是( )。
A. 1:2B. 2:1C. 1:20D. 20 2 1【答案】 D【解析】【解答】解:8厘米=80毫米,比例尺是80:4=20:1。
故答案为:D。
【分析】把图上距离换算成毫米,然后写出图上距离与实际距离的比并把比化成后项是1的比就是这幅图的比例尺。
4.图上2厘米代表实际距离60千米,甲、乙两地相距120千米,画在这幅图上,应画()厘米。
A. 4B. 6C. 8D. 10【答案】 A【解析】【解答】解:120÷60=2,2×2=4(厘米),应画4厘米。
故答案为:A。
【分析】可以计算出两地的距离是60千米的多少倍,那么图上距离也就是2厘米的多少倍。
2020-2021 六年级数学比例和反比例 培优题

2020-2021 六年级数学比例和反比例培优题一、比例和反比例1.工人铺一条路,用边长4分米的方砖铺需要500块,如果改用边长5分米的方砖铺,需要多少块?【答案】解:设需要x块,4×4×500=5×5×x25x=8000x=320答:如果改用边长5分米的方砖铺地,需要320块。
【解析】【分析】此题主要考查了反比例应用题,这条路的总面积是一定的,每块砖的面积与铺的块数成反比例,据此列比例解答.2.一辆汽车在公路上行驶,行驶的时间和路程如下图。
(1)这辆车10小时行驶多少千米?(2)行驶600千米要多少时?【答案】(1)解:10×80=800(千米)答:这辆车10小时行驶800千米。
(2)解:600÷80=7.5(小时)答:行驶600千米要7.5时。
【解析】【分析】(1)由时间路程图可知,1小时行驶的路程是80千米,即汽车的速度是80千米/小时,再由“路程=速度×时间”进行计算;(2)由(1)可知汽车的速度,再由“时间=路程÷速度”进行计算。
3.沙场有一堆沙子,每天运50车,需要24天运完。
如果在15天内完成,每天要运多少车? (用比例解答)【答案】解:设每天要运x车。
15x=50×24x=80答:每天要运80车。
【解析】【分析】设出每天要运x车,根据总量不变列出比例关系,求出未知数,解答即可。
4.一列火车行驶720km需要3小时。
照这样计算,从甲地到乙地的铁路长约1200千米,这列火车需要行驶几小时? (用比例解答)【答案】解:设需要行驶x小时。
=x=5答:需要行驶5小时。
【解析】【分析】设这列火车需要行x小时,根据火车速度不变列出正比例关系,求出未知数,解答即可。
5.补充表格。
药粉/克1246810水/克200400;2000【解析】【解答】因为200:1=200÷1=200,400:2=400÷2=200,所以水的质量:药粉的质量=200,则水的质量分别为:4×200=800(克),6×200=1200(克),8×200=1600(克),10×200=2000(克),根据计算,填空如下:【分析】根据题意可知,先求出水的质量与药粉质量的比,水的质量:药粉的质量=200,它们的比值一定,水和药粉的质量成正比例,用药粉的质量×200=水的质量,据此计算填空即可.6.一个修路队,原计划每天修400米,15天可以修完.结果12天就完成任务,实际每天修多少米?(用比例解)【答案】解:实际每天修x米,12x=400×1512x=6000x=500答:实际每天修500米。
2020-2021六年级数学培优试卷(比例和反比例).docx

2020-2021 六年级数学培优试卷 ( 比例和反比例 )一、比例和反比例1.一个会议室用边长为 4 分米的方砖铺地,需要750 块。
如果改用边长为 5 分米的方砖铺地,需要多少块? (用比例解答 )【答案】解:设需要x 块。
5× 5× x=4 × 4× 750x=480答:需要 480 块。
【解析】【分析】设出需要 5 分米的地砖 x 块,根据总面积不变列出比例关系,求出未知数,解答即可。
2.某工程队要用长8m 的新水管替换长5m 的旧水管,原来已铺的旧水管有124 根,现在有 75 根新水管,够用吗 ?(用比例知识解答)【答案】解:设新水管需要 x 根。
8x=124 ×5x=77.577.5>75答: 75 根新水管不够用。
【解析】【分析】可以设新水管需要x 根,题目中存在的等量关系是旧水管的根数×旧水管的长度 =新水管的长度×新水管的根数,即可解得新水管需要的根数,然后于75 作比较,如果比 75 大,说明不够,如果比75 小,说明够了。
3.从甲地到乙地,小华用了 5 小时,小红用了 3 小时。
小华和小红所用的时间的比是________,他们的速度比是________。
【答案】5∶ 3; 3∶5【解析】【解答】解:小华和小红所用的时间的比是5: 3,他们的速度比是3: 5。
故答案为: 5: 3;3: 5。
【分析】路程一定,速度和时间成反比。
4.圆柱的高一定,圆柱的体积和底面积成________比例;圆柱的侧面积一定,底面周长和高成 ________比例。
【答案】正;反【解析】【解答】解:圆柱的体积÷底面积=高(一定),圆柱的体积和底面积成正比例;圆柱的底面周长×高 =侧面积(一定),圆柱的底面周长和高成反比例。
故答案为:正;反。
【分析】根据圆柱的体积公式和侧面积公式分别判断圆柱的体积和底面积、圆柱的底面周长和高的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例。
2020-2021六年级数学培优试卷(比例 )

2020-2021六年级数学培优试卷(比例 )一、比例1.把一个长5毫米的零件画在图纸上是1分米,这张图纸的比例尺是()。
A. 5:1B. 200:1C. 20:1【答案】 C【解析】【解答】1分米:5毫米=100毫米:5毫米=(100÷5):(5÷5)=20:1。
故答案为:C。
【分析】已知图上距离与实际距离,要求比例尺,用图上距离:实际距离=比例尺,据此列式解答。
2.应用比例的基本性质,下面()组中的两个比可以组成比例。
A. 和B. 0.2:10和2:50C. 和【答案】 C【解析】【解答】解:×==×,能组成比例。
故答案为:C。
【分析】根据比列的基本性质,假设两个比可以组成比例,如果两内项之积等于两外项之积,即可组成比例。
3.小洋家的客厅长5米,宽3.8米,画在练习本上,选比例尺( )比较合适。
A. 1∶10B. 1∶100C. 1∶1000【答案】 B【解析】【解答】解:应用A的比例尺画图可得:画长=500厘米×=50厘米、画宽=380厘米×=38厘米,显然不合适,故A错;应用B的比例尺画图可得:画长=500厘米×=5厘米、画宽=380厘米×=3.8厘米,合适,故B对;应用C的比例尺画图可得:画长=500厘米×=0.5厘米、画宽=380厘米×=0.38厘米,显然不合适,故C错。
故答案为:B。
【分析】图上距离=实际距离×比例尺。
4.已知a:b=c:d,若将b乘5,使比例不成立的条件是( )。
A. a乘5B. c除以5C. d除以5【答案】 C【解析】【解答】因为 a:b=c:d ;所以bc=ad;bx5xc=ax5xd;bx5xc÷5=bc=ad故答案为:C【分析】由比例的基本性质可知,bc=ad,若将b乘5,等式左边扩大到原来的5倍,若d除以5,等式的右边缩小到原来的.因此,等式不成立,即比例也不成立。
2020-2021六年级数学培优试卷(比例 )

2020-2021六年级数学培优试卷(比例 )一、比例1.在比例尺是1:100000的平面图上,实际距离是1000m,在图上是()A. 1mB. 1dmC. 1cm【答案】 C【解析】【解答】1000m=100000cm,100000×=1(cm)。
故答案为:C。
【分析】根据1m=100cm,先将实际距离的单位m化成cm,然后用实际距离×比例尺=图上距离,据此列式解答。
2.如果甲数的等于乙数的,那么甲数:乙数等于()A. 6:15B. 10:9C. 15:6D. 9:10【答案】 D【解析】【解答】如果甲数×=乙数×,则甲数:乙数=:=():()=9:10。
故答案为:D。
【分析】根据条件先列出等式,然后根据比例的基本性质,相乘的两个数同时作外项或内项,写出比例,然后化简即可。
3.把一个底3cm,高2cm的三角形,按3:1放大画在图上,放大后的三角形面积是()平方厘米.A. 9B. 18C. 27D. 54【答案】 C【解析】【解答】解:3×3=9(cm),2×3=6(cm),面积:9×6÷2=27(平方厘米)。
故答案为:C。
【分析】用三角形的底和高分别乘3即可求出放大后三角形的底和高,用底乘高除以2即可求出放大后三角形的面积。
4.若5x=2y,则x:y=________:________。
【答案】 2;5【解析】【解答】解:5x=2y,则x:y=2:5。
故答案为:2;5。
【分析】把5和x看作外项,2和y看作内项,然后根据比例的基本性质写出比例即可,比例中两个内项的积等于两个外项的积。
5.甲、乙两地之间的距离是240千米,在一幅地图上量得两地的图上距离是3厘米,这幅地图的比例尺是________。
【答案】 1:8000000【解析】【解答】3厘米:240千米=3厘米:24000000厘米=(3÷3):(24000000÷3)=1:8000000。
2020-2021六年级数学培优试卷(比例 )

2020-2021六年级数学培优试卷(比例 )一、比例1.已知AB=K, =D,(ABCD都是大于0的自然数),那么下列比例中正确的是()A. B. C. D.【答案】 D【解析】【解答】解:是正确的。
故答案为:D。
【分析】AB=K,=D,那么=D,所以AB=CD,据此作答即可。
2.一个计算机芯片的实际尺寸是8mm×8mm,按一定比例所画的图如下图,图中所用的比例尺是()。
A. 1:5B. 25:1C. 2:1D. 5:1【答案】 D【解析】【解答】4cm:8mm=40mm:8mm=(40÷8):(8÷8)=5:1故答案为:D.【分析】已知图上距离和实际距离,求比例尺,用图上距离:实际距离=比例尺,据此解答.3.某校园长240米、宽180米,把平面图画在一张只有3分米长、2分米宽的长方形纸上,那么选择( )作比例尺比较合适。
A. 1:100B. 1:1000C. 1:2000D. 1:5000【答案】 B【解析】【解答】240米=2400分米,3分米:2400分米=3:2400=1:800;180米=1800分米,2分米:1800分米=2:1800=1:900;1:800和1:900接近1:1000.故答案为:B【分析】比例尺是图上距离与实际距离的比,长方形纸长3分米、宽2分米,与校园实际长240米、宽180米的比分别是1:800、1:900,用这两个比例尺中的任何一个来画图,都不合适,因此选择1;1000画出的图大小合适。
4.把一个直径4毫米的手表零件,画在图纸上的直径是8厘米,这幅图纸的比例尺是( )。
A. 1:2B. 2:1C. 1:20D. 20 2 1【答案】 D【解析】【解答】解:8厘米=80毫米,比例尺是80:4=20:1。
故答案为:D。
【分析】把图上距离换算成毫米,然后写出图上距离与实际距离的比并把比化成后项是1的比就是这幅图的比例尺。
5.在比例尺是1:50000的图纸上,量及两点之间的距离是18厘米,这两点的实际距离是________千米.【答案】 9【解析】【解答】解:18÷=900000厘米=9千米,所以这两点的实际距离是9千米。
2020-2021六年级数学培优试卷(比例 )

2020-2021六年级数学培优试卷(比例 )一、比例1.把线段比例尺改写成数字比例尺为()。
A. 1:200B. 1:2000C. 1:20000【答案】 C【解析】【解答】2cm:400m=2cm:40000cm=1:20000故答案:C【分析】通过比例尺的关系式:比例尺=图上距离:实际距离,找出线段比例尺中的图上距离和代表的实际距离,写出它们的比并进行化简。
2.人的体重和身高( )。
A. 不成比例B. 成正比例C. 成反比例【答案】 A【解析】【解答】解:人的体重和身高虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例。
故答案为:A。
【分析】判断两种量成正比例还是反比例的办法:当这两种相关联的量中相对应的两个数的商一定时,这两个数就成正比例关系;反之,当这两个数的积一定时,这两个数就成反比例关系。
3.两个城市之间的直线距离是450千米,在一幅比例尺是1:4000000的地图上,这两个城市的图上距离是()。
A.0.1125厘米B.1.125厘米C.11.25厘米D.1125厘米.【答案】 C【解析】【解答】解:450千米=45000000厘米,45000000×=11.25(厘米)。
故答案为:C。
【分析】把450千米换算成厘米,然后用实际距离乘比例尺求出图上距离即可。
4.在一幅地图上,1厘米表示实际距离1千米,这幅地图的比例尺是()。
A. 1:1千米B. 1:1000C. 1:100000D. 1:1000米【答案】 C【解析】【解答】解:1千米=100000厘米,比例尺是1:100000。
故答案为:C。
【分析】图上距离与实际距离的比叫做比例尺,把1千米换算成厘米,然后写出图上距离与实际距离的比就是这幅图的比例尺。
5.在比例尺是1∶5000000的地图上,量得甲、乙两地距离6.4厘米,甲乙两地实际距离相距________千米。
【答案】 320【解析】【解答】32000000厘米=320千米故答案为:320【分析】应用实际距离=图上距离÷比例尺,据此代入数据即可列式解答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020-2021 六年级数学比例和反比例培优题
一、比例和反比例
1.如果10千克菜籽可以榨6.5千克菜油,那么有这种菜籽360千克,可以榨多少千克油?(用比例解)
【答案】解:设可以榨x千克油。
10:6.5=360:x
10x=6.5×360
x=2340÷10
x=234
答:可以榨油234千克。
【解析】【分析】菜籽的重量和榨油的质量的比值是不变的,二者成正比例,设出未知数,根据正比例关系列出比例,解比例求出可以榨油的重量即可。
2.铁路工人铺一条铁轨,计划每天铺400米,18天完成,实际每天比计划多铺50米,实际多少天完成?
【答案】解:400×18÷(400+50)=16(天)
答:实际16天完成。
【解析】【解答】解:设实际x天完成。
(400+50)x=400×18
x=7200÷450
x=16
答:实际16天完成。
【分析】铁轨的总长度不变,每天铺的长度与铺的天数成反比例,设出未知数,根据铁轨的总长度不变列出比例,解比例求出未知数的值即可。
3.服装厂要加工一批服装,一共有4500套,头5天加工了750套,照这样计算,一共要多少天才能加工完这批报装?(用比例解)
【答案】解:设一共要x天才能加工完这批服装。
750:5=4500:x
750x=5×4500
x=22500÷750
x=30
答:一共要30天才能加工完这批服装。
【解析】【分析】每天加工服装的套数不变,加工的总数与天数成正比例关系;设出未知数,根据每天加工的套数不变列出比例,解比例即可解决问题。
4.如果竹竿左右两边拴上重物A和B,竹竿平衡。
已知A物体重180g,B物体重多少克?
【答案】解:180×5÷3=300(克)
答:B物体重300克。
【解析】【分析】观察可知,重物A距离支点5格,重物B距离支点3格,根据重物A的质量×重物A离支点的距离=重物B的质量×重物B离支点的距离,重物的质量和距离成反比例,据此用重物A的质量×重物A离支点的距离÷重物B离支点的距离=重物B的质量,据此列式解答.
5.沙场有一堆沙子,每天运50车,需要24天运完。
如果在15天内完成,每天要运多少车? (用比例解答)
【答案】解:设每天要运x车。
15x=50×24
x=80
答:每天要运80车。
【解析】【分析】设出每天要运x车,根据总量不变列出比例关系,求出未知数,解答即可。
6.一个滴水的水龙头滴水的时间和所浪费的水量如下表:
滴水时间/分1020304050
浪费水量/L0.61.21.82.43.0
(1)在上图中描出表示滴水时间和相应浪费水量的点,然后把它们按顺序连起来。
(2)根据图象进行分析:滴水25分钟浪费的水有________L,滴水________分钟就会浪费2.7L的水。
滴水时间和浪费的水量成________比例。
(3)针对这一现象,你想说点什么呢?
【答案】(1)解:
(2)1.5;45;正
(3)解:要珍惜水资源,注意节约用水。
(合理即可)
【解析】【解答】(2)滴水25分钟浪费的水有1.5L,滴水45分钟就会浪费2.7L水;滴水时间和浪费的水量成正比例。
故答案为:(2)1.5;45;正。
【分析】(1)先描出对应的点,然后连接成一条线即可;
(2)找出25分钟对应的点,然后确定浪费的水量;找出2.7L对应的点,然后确定对应的时间,根据图像可以直接判断两个量成正比例;
(3)说出自己合理的观点即可。
7.操场边一棵小树的高度是1.5米,影子长度是0.8米,一棵大树的影子长度是4.8米,这棵大树的高度是________米。
【答案】9
【解析】【解答】解:设这棵大树的高度是x米,
=
0.8x=4.8×1.5
0.8x=7.2
0.8x÷0.8=7.2÷0.8
x=9
故答案为:9.
【分析】此题主要考查了正比例应用题,用大树的树高:大树的影长=小树的树高:小树的影长,据此列比例解答.
8.如果ab=c,(a、b、c均不为0)那么当a一定时,b和c成________,当b一定时,a 和c成________,当c一定时,a和b成________。
【答案】正比例;正比例;反比例
【解析】【解答】如果ab=c,(a、b、c均不为0)那么当a一定时,b和c成正比例,
当b一定时,a和c成正比例,当c一定时,a和b成反比例.
故答案为:正比例;正比例;反比例.
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
两种相关联的量,一种量变化,另一种量也随着变化,这两种量中相对应的两个数的积一定,这两种量叫做成反比例的量,它们的关系叫做反比例关系,据此判断.
9.图上距离一定,实际距离和比例尺成正比例。
()
【答案】正确
【解析】【解答】因为实际距离×比例尺=图上距离(一定),当图上距离一定,实际距离和比例尺成反比例,原题说法错误.
故答案为:错误.
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,据此判断.
10.如果y=15x,x和y成________比例;如果y= ,x和y成________比例。
【答案】正
;反
【解析】【解答】如果y=15x,那么,(一定),故x和y成正比例;
如果y= ,那么,xy=15(一定),故x和y成反比例。
故答案为:正;反。
【分析】如果(一定),即两个数的比值一定,则这两个数成正比例;如果xy=k (一定),即两个数的积一定,则这两个数成反比例。
把本题中的两个式子变形为x与y 的比或积的形式,再来判断。
11.A× =2× (A≠0,B≠0),则A和B成________比例。
【答案】反
【解析】【解答】解:由A×=2×(A≠0,B≠0)可得,AB=6,所以A和B成反比例。
故答案为:反。
【分析】判断两种量成正比例还是反比例的办法:当这两种相关联的量中相对应的两个数的商一定时,这两个数就成正比例关系;反之,当这两个数的积一定时,这两个数就成反比例关系。
12.一个圆柱和一个圆锥等底等高,体积相差100dm3,圆锥的体积是()dm3
A. 50
B. 100
C. 150
D.
【答案】 A
【解析】【解答】100÷2=50(dm3)
故答案为:A.
【分析】等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱比圆锥的体积大2倍,用体积差÷2=圆锥的体积,据此列式解答.
13.在下图中,以直线为旋转轴,可以得到圆柱的是()。
A. B. C. D.
【答案】 A
【解析】【解答】在下图中,以直线为旋转轴,可以得到圆柱的是.
故答案为:A.
【分析】根据对圆柱特征的理解可知,一个长方形以长或宽为旋转轴,旋转一周形成的图形是圆柱体,据此解答.
14.一块直角三角板,两条直角边的长度分别是4cm和3cm,分别绕两条直角边旋转一周,都可得到一个圆锥体。
这两个圆锥的体积比是()。
A. 4:3
B. 1:1
C. 16:9
D. 9:16
【答案】 A
【解析】【解答】解:(π×4²×3×):(π×3²×4×)=16π:12π=4:3。
故答案为:A。
【分析】第一个圆锥的底面半径是4cm,高是3cm;第二个圆锥的底面半径是3cm,高是4cm;分别计算出两个圆锥的体积并写出体积的最简比即可。
15.圆柱的侧面展开图是一个正方形,那么这个圆柱的高是它底面半径的()倍。
A. 3.14
B. π
C. 6.28
D. 2π
【答案】 D
【解析】【解答】圆柱的侧面展开图是一个正方形,那么这个圆柱的高是它底面半径的:2πr÷r=2π倍.
故答案为:D.
【分析】如果一个圆柱的侧面展开图是一个正方形,那么这个圆柱的高与底面周长相等,据此列式解答.。
