历年自主招生考试数学试题大全-2011年北约自主招生数学试题Word版缺答案
自主招生数学试题及答案

自主招生数学试题及答案一、选择题(每题5分,共20分)1. 若函数f(x) = x^2 - 4x + 3,求f(2)的值。
A. 1B. 3C. 5D. 7答案:B2. 已知等差数列{a_n}的首项a_1 = 3,公差d = 2,求a_5的值。
A. 13B. 15C. 17D. 19答案:A3. 计算定积分∫(0到1) x^2 dx的值。
A. 1/3B. 1/2C. 2/3D. 1答案:B4. 设A = {1, 2, 3},B = {3, 4, 5},求A∩B的值。
A. {1, 2}B. {3}C. {4, 5}D. 空集答案:B二、填空题(每题5分,共20分)5. 已知函数f(x) = 2x - 1,求f(-1)的值。
答案:-36. 计算等比数列1, 2, 4, ...的第5项。
答案:167. 已知圆的半径为5,求圆的面积。
答案:25π8. 已知向量a = (3, 4),向量b = (-4, 3),求向量a与向量b的点积。
答案:-7三、解答题(共60分)9. 已知函数f(x) = x^3 - 6x^2 + 11x - 6,求f(x)的导数。
答案:f'(x) = 3x^2 - 12x + 1110. 已知直线l1: y = 2x + 1和直线l2: y = -x + 3,求两直线的交点坐标。
答案:交点坐标为(1, 3)11. 已知圆心在原点,半径为5的圆,求圆的方程。
答案:x^2 + y^2 = 2512. 已知函数f(x) = x^2 - 6x + 8,求函数的最小值。
答案:函数的最小值为2,当x = 3时取得。
2011北约华约自主招生联考笔试试题

2011北约华约自主招生联考笔试试题2011北约华约自主招生联考笔试试题华约试题英语:考题回放:第一项,完型填空,20个空,每空1.5分,共30分;第二项,文章填空,从一篇文章中抽出五个短句,要求考生将抽出的短句填在合适的位置上,每空3分;第三项,将一篇英语短文翻译并概括为200字左右的中文,20分;第四项,翻译,将五个与教育相关的中文句子翻译为英文;第五项,作文,以第四项翻译的内容为背景,请考生谈谈自己的看法。
语文:-《阅读和写作》阅读部分(50分)一、现代文阅读:杨福家的《哥本哈根精神》二、现代文阅读:老舍的《五九》三、古代诗文阅读1.辛弃疾《清平乐校检山园,书所见》2.《南齐书良政》断句3.翻译《论语泰伯》《韩非子外储说右下》4.写作部分(50分)你对忧患意识是怎样认识的?请写一篇文章,谈谈你的思想和认识,角度自选,立意自定,标题自拟;不要编造虚假事实论据,不要套作,不得抄袭。
文科:考题回忆版:1、根据材料论述法国农民与法兰西第三共和国间的关系。
2、北极冰川融化对国际贸易的影响(11分)北极冰川融化对生态环境的影响(10分)。
3、论述题(10分),给定三段材料,大致内容为:网络在线阅读的弊端在于内容冗杂,使阅读的有效性降低。
它的浏览方式使得读者无法进行更深层次的思考。
网络在线阅读方式的出现所引发的争议在打印机打印取代传统手写等过程中同样有过。
请结合材料分析,人们利用网络在线阅读得到的比失去的要多。
4.阅读材料,回答问题。
材料一“各级领导干部要自觉贯彻群众路线、切实转变作风,多做顺民意、解民忧、得民心的实事,坚决纠正损害群众利益的行为。
”——胡锦涛材料二某地政府官员以破坏了政府办公楼的“风水”为由要强行拆除一座楼房,遭到抵制后说出了“跟政府作对就是恶”的话,在网络上被称为“最雷人官话”之一。
在现实生活中,政府的具体行为并非总是与民众的意愿一致,有时甚至会产生矛盾冲突。
从人民与政府的关系来看,为什么不能说“跟政府作对就是恶”?理科:物理70分,化学30分。
解题--由一道北约2011年自主招生题所想到的-周欣孟

由一道北约2011年自主招生题所想到的周欣孟 重庆市巴蜀中学2011年北大等十三校联考(北约)自主招生数学试卷: 第七题:求1213120111x x x x -+-+-++-的最小值。
追本溯源,这就是一个折线函数问题。
折线函数:定义:绝对值里是一次多项式的函数称为折现函数。
函数1()nii i f x ax b ==-∑(1230,1,2,3,,;i n a i n b b b b >=<<<<)当x →+∞时,显然()f x →+∞; 当x →-∞时,显然()f x →+∞;那么,我们需要讨论函数1()nii i f x ax b ==-∑是否能取得最小值。
(思路:去掉绝对值符号,观察一次项系数的正负,判断单调性得出最值)网上解析:(1)当1x b ≤时,11()n nii ii i f x a x a b ===-+∑∑,此时()f x 在1(,]b -∞为单调递减函数;(2)当n x b >时,11()n nii ii i f x a x a b ===-∑∑,此时()f x 在(,)nb +∞为单调递增函数;(3)当1(1,2,3,,1)i i b x b i n +<≤=-时,1111()()()in n ij jj jj jj j i j i j f x a a x a b a b ==+=+==-+-∑∑∑∑;①当11injjj j i aa ==+<∑∑时,()f x 在1(,]i i b b +为单调递减函数;②当11injjj j i aa ==+>∑∑时,()f x 在1(,]i i b b +为单调递增函数;③当11injjj j i aa==+=∑∑时,()f x 在1(,]i i b b +为常数函数。
所以能得到如下结论: (i )当11k ni ii i k a a==+<∑∑且112k niii i k a a +==+>∑∑时,则1k x b+=时,()f x 取得最小值;分析:特别地a. 若12nii a a=>∑,则()f x 在12(,]b b 为单调递增函数,所以:对1,2,3,,1i n ∀=-,都有不等式11inj j j j i a a ==+>∑∑恒成立,故:对1,2,3,,1i n ∀=-,()f x 在1(,]i i b b +为单调递增函数,此时,min1()()f x f b =;特别地b. 若11n in i aa -=<∑,则()f x 在1(,]n nb b -为单调递减函数,所以:对1,2,3,,1i n ∀=-,都有不等式11i nj j j j i a a ==+<∑∑恒成立,故:对1,2,3,,1i n ∀=-,()f x 在1(,]i i b b +为单调递减函数,此时,当min()()n f x f b =;c. 若11k ni ii i k a a==+<∑∑,则对1,2,3,,i k ∀=都有()f x 在1(,]i i b b +为单调递减函数,若112k n iii i k a a +==+>∑∑,则对1,2,,1i k k n ∀=++-都有()f x 在1(,]i i b b +为单调递增函数,此时,min1()()k f x f b +=(ii )当11k ni ii i k a a==+=∑∑时,则对01[,]k k x b b +∀∈,min0()()f x f x =.由此可知,北大那题可以直接算出单调区间改变的临界条件: 题目:求1213120111x x x x -+-+-++-的最小值。
2011年北京市四中自主招生考试数学试卷

2011年北京市四中自主招生考试数学试卷参考答案与试题解析一、选择题(共6小题,每小题5分,满分30分)1.(5分)已知<cosA<sin80°,则锐角A的取值范围是()=,2222.或﹣1.时,4.(5分)代数式的最小值为()++=13(时,=0、性质:5.(5分)掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1至6六个数.连续掷两次,..种,所以概率是;+99=计算即可.二、填空题(共6小题,每小题5分,满分30分)7.(5分)多项式6x3﹣11x2+x+4可分解为(x﹣1)(3x﹣4)(2x+1).8.(5分)已知点P(x,y)位于第二象限,并且y≤2x+6,x、y为整数,则点P的个数是6.9.(5分)(2002•黄石)已知⊙O的半径OA=1,弦AB、AC的长分别是、,则∠BAC的度数是15°或75°.AC=,AB=,AOE==AOD==,10.(5分)方程(2007x)2﹣2006×2008x﹣1=0的较大根为a,方程x2+2006x﹣2007=0的较小根为b,则a﹣b=2008..11.(5分)已知x=,则x3+12x的算术平方根是2.=a=b=a=b.则.212.(5分)(2008•昆明)如图,Rt△ABC中,∠BCA=90°,∠BAC=30°,AB=6.△ABC以点B为中心逆时针旋转,使点C旋转至AB边延长线上的C′处,那么AC边转过的图形(图中阴影部分)的面积是9π.AB=3﹣三、解答题(共5小题,满分60分)13.(12分)现将一个表面涂满红色的正方体的每条棱十等分,此正方体分割成若干个小正方体.在这些小正方体中,求:(1)两面涂有红色的小正方体的个数;(2)任取一个小正方体,各面均无色的小正方体的概率;(3)若将原正方体每条棱n等分,只有一面涂有红色的小正方体的个数.P==0.51214.(12分)已知x、y均为实数,且满足xy+x+y=17,x2y+xy2=66,求:代数式x4+x3y+x2y2+xy3+y4的值.或15.(12分)在直角△ABC中,∠C=90°,直角边BC与直角坐标系中的x轴重合,其内切圆的圆心坐标为P(0,1),若抛物线y=kx2+2kx+1的顶点为A.求:(1)求抛物线的对称轴、顶点坐标和开口方向;(2)用k表示B点的坐标;(3)当k取何值时,∠ABC=60°?2,16.(12分)如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上的任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.(1)求证:RQ是⊙O的切线;(2)求证:OB2=PB•PQ+OP2;(3)当RA≤OA时,试确定∠B的取值范围.17.(12分)平面上有n个点(n≥3,n为自然数),其中任何三点不在同一直线上.证明:一定存在三点,以这三点作为顶点的三角形中至少有一个内角不大于.和当两种情况进行讨论.根据三角形的内角和定理就可以证出.时,连接中必有一个角不大于;时,∠,个角中,必有一个角不大于,则。
2011年清华自主招生数学试题和答案解析

2011年高水平大学自主招生选拔学业能力测试数学注意事项:1. 答卷前,考试务必将自己的姓名、准考证号填写在答题卡上。
2. 将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题3分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设复数z 满足|z|<1且15|z+|2z=,则|z |=( ) A 45 B 34 C 23 D 12解析:设|z |a bi =+代入15|z+|2z =整理得22221174a b a b ++=+,又|z |<1,所以2214a b +=,|z |=12=(2)在正四棱锥P-ABCD 中,M 、N 分别为PA 、PB 的中点,且侧面与底面所成二面角的正切.则异面直线DM 与AN 所成角的余弦值为( ) A13 B 16 C 18 D 112解析:设2AB =,容易算出2PB =,以底面中心为原点建立空间坐标系,1111(1,1,0),(1,1,0),(,,(,,222222D A M N ------,由1cos 6|DM AN ||DM ||AN |θ⋅==⋅uuu u r uuu ruuuu r uuu r (3)过点(1,1)-的直线l 与曲线3221y x x x =--+相切,且(1,1)-不是切点,则直线l 的斜率是( )A 2B 1C 1-D 2-解析:32221(),()322y x x x f x f x x x '=--+==--,设切点(),()t f t ,()()()y f t f t x t '-=-,把(1,1)-代入且1t ≠-得到1t =,所以2k =-(4)若23A B π+=,则22cos cos A B +的最小值和最大值分别为( )A.312-, B.1322,C.11D.112, 解析:2222211cos cos cos cos ()1cos(2)323A B A A A ππ+=+-=++,选B (5)如图,1O e 和2O e 外切于点C ,1O e ,2O e 又都和O e 内切,切点分别为,A B . 设AOB ACB αβ∠=∠=,,则( ) A cos sin02αβ+= B sin cos02αβ-=C sin 2sin 0βα+=D sin 2sin 0βα-= 解析:连接12O O 过点C ,设12CAO CBO ∠=∠∠=∠,,12O C O C 、,则+1+2=+21+22=βαπ∠∠∠∠,即2=βαπ-,只有D 是错的。
2011年北约自主招生数学试题(精校word版,无答案)-历年自主招生考试数学试题大全

1、按住c trl学(北约13校)自主选拔录取联合考试
数学试题
请注意:文科考生做1至5题,理科考生做3至7题.每题20分,共100分.
1.已知平行四边形的其中两条边长为3和5,一条对角线长为6,求另一条对角线长.
2.求过抛物线 和 的交点的直线方程.
3.在等差数列 中, ,数列 的前 项和为 ,求数列 的最小项,并指出其值为何?
4.在 中, ,求证: .
5.是否存在四个正实数,使得他们的两两乘积为2,3,5,6,10,16?
6. 和 是平面上两个不重合的固定圆, 是平面上的一个动圆, 与 , 都相切,则 的圆心的轨迹是何种曲线?说明理由.
7.求 的最小值.
历年自主招生考试数学试题大全
专题下载链接:/a760682.html
2011年综合性大学(北约)自主选拔录取联合考试数学试题及答案

2011年综合性大学(北约)自主选拔录取联合考试数学试题请注意:文科考生做1至5题,理科考生做3至7题,每题20分,共100分.1.已知平行四边形的其中两条边长为3和5,一条对角线长为6,求另一条对角线的长.2.求过抛物线2221y x x =--和2523y x x =-++的交点的直线方程.3.在等差数列{}n a 中,3713,3,a a =-=数列{}n a 的前n 项和为n S ,求数列{}n S 的最小项,并指出其值为何.4.在ABC ∆中,2a b c +≥,求证:60C ∠≤ .5.是否存在四个正实数,使得它们的两两乘积为2,3,5,6,10,16?6.1C 和2C 是平面上两个不重合的固定圆,C 是平面上的一个动圆,C 与12,C C 都相切,则C 的圆心的轨迹是何种曲线?说明理由.7.求()|1||21||20111|f x x x x =-+-++- 的最小值.参考答案1.x =【解】设另一条对角线的长度为x .由22222(35)6,x +=+解得x =. 2.【解】联立两方程,消去2,x 得6710x y +-=.此方程即为所求. 3.最小值为-66.【解法1】425,n a n =-由10,,0.n n a a +≤⎧⎨≥⎩即4250,.4(1)250.n n -≤⎧⎨+-≥⎩解得212544n ≤≤. 因为*,n N ∈所以当6n =时,n S 最小,最小值为66-. 【解法2】因为22235292232(),48n S n n n =-=--因为*,n N ∈所以当6n =时,n S 最小,最小值为66-. 4.由正弦定理sin sin sin a b c ABC==知,2sin sin 2sin 2sincos 2sin 22A B A B a b c A B C C +-+≥⇔+≥⇔≥又因为sin sin()cos ,sin 2sincos 222222A B C C C C C +π=-==,所以,cos cos 2sin cos2222CA B C C-≥,又因为022C π<<时,cos02C >所以11sin cos2222C A B-≤≤(当A B =时取等号),而022C π<<所以30,2C ≤即60C ≤.5.【解】假设存在满足条件的四个正实数,,,a b c d ,不妨,a b c d <<<则有,.ab ac ad bc bd cd <<<< (1)若ad bc <,则有2,3,5,6,10,16ab ac ad bc bd cd ====== 所以,23,b c a a==.由6bc =得1,2,3,5a b c d ====.所以15,cd =与16cd =矛盾.(2)若,ad bc >则有2,3,5,6,10,16.ab ac bc ad bd cd ====== 所以236,,b c d a a a===.由5bc =,得265a =,由16cd =,得298a =,矛盾.综上所述,假设不存立,所以不存在四个正实数,它们两两乘积分别为2,3,5,6,10,16. 6.【解】设圆心12,C C 的半径分别为12,r r ; (1)若12r r =.①若两圆相离,则C 的圆心轨迹为线段12C C 的垂直平分线;②若两圆相切,则C 的圆心轨迹为线段12C C 的垂直平分线(即两圆的内分切线)和直线12C C ,去掉切点;③若两圆相交,则C 的圆心轨迹为线段12C C 的垂直平分线和以12,C C 为焦点,长轴长为12r r +的椭圆,去掉交点. (2)若12r r ≠①若两圆外离,则C 的圆心轨迹为以12,C C 为焦点,长轴长为12||r r -的双曲线的一支(小圆圆心在开口内);②若两圆外切,则C 的圆心轨迹为以12,C C 为焦点,长轴长为12||r r -的双曲线的一支(小圆圆心在开口内)和直线12C C ,去掉切点;③若两圆相交,则C 的圆心轨迹为以12,C C 为焦点,长轴长为12||r r -的双曲线的一支(小圆圆心在开口内)和以12,C C 为焦点,长轴长为12r r +的椭圆,去掉交点.④若两圆内切,则C 的圆心轨迹为以12,C C 为焦点,长轴长为12r r +的椭圆和直线12C C ,去掉切点; ⑤若两圆内含,则C 的圆心轨迹为以12,C C 为焦点,长轴长为12r r +的椭圆. 依据椭圆、双曲线的定义即可证明,这儿不再赘述. 7.491832711【解】首先设1212,()||||||.n n a a a f x x a x a x a ≤≤≤=-+-++-则由绝对值几何意义知,n 为奇数时,当12n x a +=时,()f x 有最小值;当n 为偶数时,当x 取[,1]22n n aa+上任何值时,()f x 有最小值.回到原题, 20111111111()|1|||||||||||||||2233320112011f x x x x x x x x x =-+-+-+-+-+-++-++-个以上和式共有2012201112201120230662⨯+++== 个点.设12345620230661111,,,,,232011a a a a a a a =======所以20230661011533.2=下面求10115331011534,a a 的值.设10115331,a t =则121011533,12(1)1011533,t t +++≥+++-< 可得1422t =,且1011533101153411422a a ==.故11422x =时,()f x 最小.111111491()112114221423120111832142214221422142214221422711f =-+-⨯++-⨯+⨯-+⨯-=。
2011北约自主招生文科数学试题

2011北约自主招生文科数学试题1、(三函\解几)已知平行四边形的两边长分别为3和5,一条对角线长为6,求另一条对角线长。
2、(解几\方程)求过抛物线Y=2X^2-2X-1与Y=-5X^2+2X+3的交点的直线方程。
3、(数列)在等差数列{an(n下标)}中,a3=-13,a7=3,Sn(n下标)为其前n项和。
问数列{Sn(n下标)}的哪一项最小?并求出最小项值。
4、(三函\不等式)在三角形ABC中,若a+b》=(大于等于)2c,证明:C《=(小于等于)60度。
5、(数论)是否存在四个正实数,使得两两之积分别为2、3、5、6、10、16?参考思路:1、可以用余弦定理:先利用已知三边求出平行四边形一角的余弦值,则另一角的余弦值可知(互为相反数),再求未知对角线;也可以利用解几中的重要结论:平行四边形的两对角线平方和等于四边平方和(不过要先建立坐标系证明该结论)。
2、最容易想到的方法自然是联立两抛物线方程,解出交点坐标,用两点式或点斜式表示……好吧,我承认这样做有点难算,不过其实也不算太难啦(最后化简结果似乎是不含根式的)。
当然,也可以先设直线方程Y=kX+b,与两抛物线分别联立,再对比所得交点的系数,从而得解(我的一位同学就是这样做的)。
3、常规题。
先求公差,再求通项,再求前n项和,最后利用二次函数的性质解之(注意n为正整数),或利用an《=0且a(n+1)>=0解之(n和n+1下标)。
4、可以考虑反证法;不然就用余弦定理表示出cosC,把式子分子中的a、b利用原题中的不等式换成c,再用基本不等式,中间经过若干步转换,最后化简为cosC》=0.5,于是得证。
5、尚未解出。
数论问题对高中文科生来说还是难了一点……面试题1、最刁钻的问题:火车开车前为什么会先退一步然后再前进?在采访了物理老师之后,得出的结论是:通常情况下,火车各节车厢之间的挂钩拉得很紧,牵引力必须克服整列火车与铁轨的最大静摩擦力才能启动。
自主招生北约数学试题及解答(2010-2014)

2010年“北约”自主招生数学试题及解答1.(仅文科做)02απ<<,求证:sin tan ααα<<. 【解析】 不妨设()sin f x x x =-,则(0)0f =,且当02x π<<时,()1cos 0f x x '=->.于是()f x 在02x π<<上单调增.∴()(0)0f x f >=.即有sin x x >. 同理可证()tan 0g x x x =->.(0)0g =,当02x π<<时,21()10cos g x x'=->.于是()g x 在02x π<<上单调增。
∴在02x π<<上有()(0)0g x g >=。
即tan x x >。
注记:也可用三角函数线的方法求解.2.AB 为边长为1的正五边形边上的点.证明:AB.(25分) 【解析】 以正五边形一条边上的中点为原点,此边所在的直线为x 轴,建立如图所示的平面直角坐标系.⑴当,A B 中有一点位于P 点时,知另一点位于1R 或者2R 时有最大值为1PR ;当有一点位于O 点时,1max AB OP PR =<;⑵当,A B 均不在y 轴上时,知,A B 必在y 轴的异侧方可能取到最大值(否则取A 点关于y 轴的对称点A ',有AB A B '<).不妨设A 位于线段2OR 上(由正五边形的中心对称性,知这样的假设是合理的),则使AB 最大的B 点必位于线段PQ 上.且当B 从P 向Q 移动时,AB 先减小后增大,于是max AB AP AQ =或;对于线段PQ 上任意一点B ,都有2BR BA ≥.于是22max AB R P R Q == 由⑴,⑵知2max AB R P =.不妨设为x .下面研究正五边形对角线的长.I HG FE 1111x x-1如右图.做EFG ∠的角平分线FH 交EG 于H . 易知5EFH HFG GFI IGF FGH π∠=∠=∠=∠=∠=. 于是四边形HGIF 为平行四边形.∴1HG =. 由角平分线定理知111EFEH x FG x HG ===-.解得x =3.AB 为21y x =-上在y 轴两侧的点,求过AB 的切线与x 轴围成面积的最小值.(25分)【解析】 不妨设过A 点的切线交x 轴于点C ,过B 点的切线交x 轴于点D ,直线AC 与直线BD 相交于点E .如图.设1122(,),(,)B x y A x y ,且有222211121,1,0y x y x x x =-=->>.由于2y x '=-,于是AC 的方程为2222x x y y =--;① BD 的方程为1122x x y y =--. ②联立,AC BD 的方程,解得121221(,1)2()y y E x x x x ---. 对于①,令0y =,得222(,0)2y C x -;对于②,令0y =,得112(,0)2y D x -. 于是221212121222112222y y x x CD x x x x --++=-=-. 121(1)2ECD S CD x x ∆=-.不妨设10x a =>,20x b -=>,则 2222111111()(1)(22)44ECD a b S ab a b a b ab a b a b∆++=++=+++++1111()(2)(2)44a b ab ab ab ab=+++⋅++≥ ③0s >,则有331111111(2)(.....)223399ECD S s s s s s s s s∆=++=++++++ 6个 9个1243691616111116)]8()2393s s s ⋅⋅[⋅(⋅()=⋅≥3218)3=⋅(= ④又由当12x a x b s ===-==∴min ()ECD S ∆ 注记:不妨设311()(2)2g s s s s=++,事实上,其最小值也可用导函数的方法求解. 由2211()(32)2g s s s'=+-知当2103s <<时()0g s '<;当213s <时()0g s '>.则()g s 在(0,上单调减,在)+∞上单调增.于是当s =时()g s 取得最小值. 4.向量OA 与OB 已知夹角,1OA =,2OB =,(1)OP t OA =-,OQ tOB =,01t ≤≤.PQ在0t 时取得最小值,问当0105t <<时,夹角的取值范围.(25分) 【解析】 不妨设OA ,OB 夹角为α,则1,2OP t OQ t =-=,令 222()(1)42(1)2cos g t PQ t t t t α==-+-⋅-⋅2(54cos )(24cos )1t t αα=++--+. 其对称轴为12cos 54cos t αα+=+.而12()54x f x x +=+在5(,)4-+∞上单调增,故12cos 1154cos 3αα+-+≤≤. 当12cos 1054cos 3αα++≤≤时,012cos 1(0,)54cos 5t αα+=∈+,解得223αππ<<. 当12cos 1054cos αα+-<+≤时,()g t 在[0,1]上单调增,于是00t =.不合题意. 于是夹角的范围为2[,]23ππ. 5.(仅理科做)存不存在02x π<<,使得sin ,cos ,tan ,cot x x x x 为等差数列.(25分) 【解析】 不存在;否则有(cos sin )(cos sin )cos sin cot tan sin cos x x x x x x x x x x-+-=-=, 则cos sin 0x x -=或者cos sin 1sin cos x x x x+=.若cos sin 0x x -=,有4x π=1,1不成等差数列;若cos sin 1sin cos x x x x+=,有2(sin cos )12sin cos x x x x =+.解得有sin cos 1x x =. 而11sin cos sin 2(0,]22x x x =∈,矛盾!2011年“北约”自主招生数学试题及解答2012年“北约”自主招生数学试题及解答2013年北约自主招生数学试题与答案1.1A. 2B. 3C. 5D. 6解析:显然,多项式23()(2)(1)2f x x x ⎡⎤=---⎣⎦和11 5. 若存在一个次数不超过4的有理系数多项式432()g x ax bx cx dx e =++++,其两根分别为1,,,,a b c d e 不全为0,则:420(42)(2020a c e ga c eb d b d ++=⎧=++++=⇒⎨+=⎩(1(7)(232(630g a b c d e a b c d a b c =-+----+++++=702320a b c d e a b c d +---=⎧⇒⎨+++=⎩即方程组:420(1)20(2)70(3)2320(4)630(5)a c eb d a bcde a b c d a b c ++=⎧⎪+=⎪⎪+---=⎨⎪+++=⎪++=⎪⎩,有非0有理数解. 由(1)+(3)得:110a b c d ++-= (6) 由(6)+(2)得:1130a b c ++= (7) 由(6)+(4)得:13430a b c ++= (8) 由(7)-(5)得:0a =,代入(7)、(8)得:0b c ==,代入(1)、(2)知:0d e ==.于是知0a b c d e =====,与,,,,a b c d e 不全为0矛盾.所以不存在一个次数不超过4的有理系数多项式()g x11为两根的有理系数多项式的次数最小为5.2. 在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车占一格,共有几种停放方法? A. 720 B. 20 C. 518400 D. 14400解析:先从6行中选取3行停放红色车,有36C 种选择.最上面一行的红色车位置有6种选择;最上面一行的红色车位置选定后,中间一行的红色车位置有5种选择;上面两行的红色车位置选定后,最下面一行的红色车位置有4种选择。
2008-2011北京大学(北约)自主招生数学试题(全附答案)
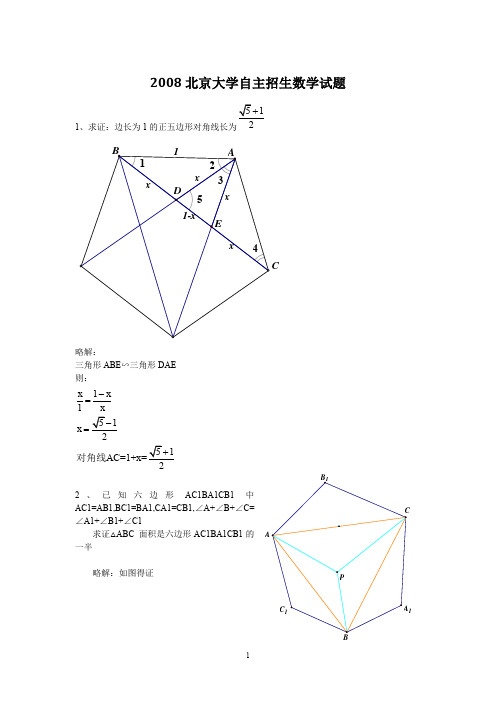
5
答案: 1、 不妨设角 ADC 为 a,那么角 ABC=π-a。 由余弦定理可得 AC=根号(9+16-24cosa)=根号(1+4+4cosa) 从而可解出 cosa=5/7.即有 sina=2(根号 6)/7. 代入 cosa=5/7,可得 AC=根号(55/7). 所以圆的半径就是 AC/2sina. 2、设 13=a1+md,25=a1+nd,41=a1+kd. 那么我们可得 a1+(m+499(k+m-2n))d=2009. 而实际上这道题是有漏洞的,因为 (m+499(k+m-2n))可能是负的,也就是当这是递减的等差数列的时候,那么 2009 就不在这个 数列中了。 3、 挺简单,设 a=tanx+(根 3),b=cotx+(根号 3),假设均为有理数。 那么由(a-(根号 3) ) (b-(根号 3) )=1 可得(a+b)根号 3=ab+2.若 a+b 非零,除过来就矛盾了。 所以必有 a+b=0,此时 ab+2 也是 0. 显然与 a,b 是有理数矛盾。 4、b=0 的时候可知得有|a|≤1.,此时 a+b≤1.下面考虑 b 不等于 0 的情况。 代入+1 和-1 后得出的式子可以化成|a|≤b+1.....(1)(必有 b≥-1) 对称轴的位置是 x=-a/4b.当对称轴在[-1,1]外的时候 那么 1≤|-a/4b|≤(b+1)/4|b|. 分类讨论后就可以得出 b≤1/3.此时 a+b≤b+1+b≤5/3. 若对称轴在[-1,1]内,则可得 a^2≤8(b-b^2)......(2) 这里注意到(b+1)^2-8(b-b^2)=(3b-1)^2≥0.故只需要(2)式成立,就必有 (1)式也成立。此时用柯西不等式 (a+b-1/2)^2≤(a^2+8(b-1/2)^2)(1+1/8)≤9/4 那么就有了 a+b≤2.等号成立的充要条件是 a=4/3,b=2/3,易验证这是成立的. 比较三种情况,显然 2 是 a+b 的最大值, 5、设优秀有 a 人,及格 b 人,不及格 c 人。 则 a+b+c=333 ① 6a+4b+0c≤1000(这里都取各层次里的最少人,故用小于等于) 即 6a+4b≤1000 即 3a+2b≤500 由①得 2a+2b=666-2c 即 a+666-2c≤500 即 a+166≤2c 若 a≥167 则这 167 人至少共解出 167*6=1002 道题,矛盾 故 a≤166 故 a+166≤166+166≤2c 即 c≥166 所以 c≥166≥a 即不及格得人数大于等于优秀的人数
自主招生考试数学试卷及参考答案

自主招生考试数学试卷及参考答案(总9页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--22第2自主招生考试 数学试题卷亲爱的同学:欢迎你参加考试!考试中请注意以下几点:1.全卷共三大题,满分120分,考试时间为100分钟。
2.全卷由试题卷和答题卷两部分组成。
试题的答案必须做在答题卷的相应位置上。
做在试题卷上无效。
3.请用钢笔或圆珠笔在答题卷密封区上填写学校、姓名、试场号和准考证号,请勿遗漏。
4.答题过程不准使用计算器。
祝你成功!一、选择题(本题共6小题,每小题5分,共30分.在每小题的四个选项中,只有一个符合题目要求)1.如果一直角三角形的三边为a 、b 、c ,∠B=90°,那么关于x 的方程a(x 2-1)-2cx+b(x 2+1)=0的根的情况为A 有两个相等的实数根B 有两个不相等的实数根C 没有实数根D 无法确定根的情况2.如图,P P P 123、、是双曲线上的三点,过这三点分别作y 轴的垂线,得三个三角形P A O P A O P A O 112233、、,设它们的面积分别是S S S 123、、,则 A S S S 123<< B S S S 213<< C S S S 132<<D S S S 123==3.如图,以BC 为直径,在半径为2圆心角为900的扇形内作半圆,交弦AB 于点D ,连接CD ,则阴影部分的面积是33第5A π-1B π-2C 121-πD 221-π4.由325x y a x y a x y a m-=+⎧⎪+=⎪⎨>⎪⎪>⎩得a>-3,则m 的取值范围是A m>-3B m ≥-3C m ≤-3D m<-3 5.如图,矩形ABCG (AB <BC )与矩形CDEF 全等,点B 、C 、D 在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是 A 0 B 1 C 2 D 36.已知抛物线y=ax 2+2ax+4(0<a<3),A (x 1,y 1)B(x 2,y 2)是抛物线上两点,若x 1<x 2,且x 1+x 2=1-a,则A y 1< y 2B y 1= y 2C y 1> y 2D y 1与y 2的大小不能确定二、填空题(本题共6小题,每小题5分,共30分.把答案填写在题中横线上)7. 二次函数y =ax 2+(a -b )x —b 的图象如图所示,44那么化简222||a ab b b -+-的结果是______▲________.8. 如图所示,在正方形 ABCD 中,AO ⊥BD 、OE 、FG 、HI 都垂直于 AD ,EF 、GH 、IJ 都垂直于AO ,若已知 S ΔA JI =1, 则S 正方形ABCD = ▲9.将一个棱长为8、各个面上均涂有颜色的正方体,锯成64个同样大小的小正方体,其中所有恰有2面涂有颜色的小正方体表面积之和为 ▲ 10.用黑白两种颜色正方形的纸片按黑色纸片数逐渐加l 的规律拼成一列图案:(1)第4个图案中有白色纸片 ▲ 张 (2)第n 个图案中有白色纸片 ▲ 张(3)从第1个图案到第100个图案,总共有白色纸片 ▲ 张第10题 第7题第8题5511.如图所示,线段AB 与CD 都是⊙O 中的弦,其中108,,36,O O AB AB a CD CD b ====,则⊙O 的半径R= ▲12.阅读下列证明过程: 已知,如图四边形ABCD 中,AB =DC ,AC =BD ,AD ≠BC ,求证:四边形ABCD 是等腰梯形.读后完成下列各小题.(1)证明过程是否有错误?如有,错在第几步上,答: ▲ . (2)作DE ∥AB 的目的是: ▲ .(3) 判断四边形ABED 为平行四边形的依据是: ▲ . (4)判断四边形ABCD 是等腰梯形的依据是 ▲ .(5)若题设中没有AD ≠BC ,那么四边形ABCD 一定是等腰梯形吗为什么 答 ▲ .自主招生考试第11题第12题66数学标准答案一、选择题(本题共6小题,每小题5分,共30分.在每小题的四个选项中,只有一个符合题目要求)二、填空题(本题共6小题,每小题5分,共30分.把答案填写在题中横线上)7. ______-1__________ 8. 256 9. 57610.(1) 13 (2) 3n+1 (3) 15250 11. a b12.(1)没有错误 (2)为了证明AD ∥BC(3) 一组对边平行且相等的四边形是平行四边形(4)梯形及等腰梯形的定义 (5) 不一定,因为当AD =BC 时,四边形ABCD 是矩形 三、解答题(本题共5小题,共60分.解答应写出必要的计算过程、推演步骤或文字说明)13.(本小题10分)某公园门票每张10元,只供一次使用,考虑到人们的不同需求,也为了吸引更多游客,该公园除保留原有的售票方法外,还推出一种“购个人年票”的售票方法(个人年票从购买之日起,可供持票者使用一年)。
独家2011年“北约”“华约”自主招生考试试题分析

2011年“北约”“华约”自主招生考试试题分析
在去年和今年的AAA测试中,都出现了一道和其他学科联系的题目,2010年五校联考出了一个生物背景的题目,2011年的七校联考则出了一个不折不扣的物理问题:
一个均匀的质量为a的杯子,里面装满水,水的质量为b,问里面装多少水的时候重心最低?
从物理意义上来分析,这个题目很显然,当重心落在水面上的时候是重心最低的时候,数学强调的是推导意义,因此只要抽象出基本的数学模型,用最简单的函数知识就可以解决。
类似于这样的问题,其实母体仍然出现在高考当中,只是较之高考,更加强调一般性问题的解决,更加强调在数学层面上的分析和推导,这和北约方数学试题的第6个题思路不谋而合。
平面上给定两个定圆,一个动圆和两个定圆相切,求动圆圆心的轨迹,并证明。
这个题目有两个关键点,一个是处理相切时的状态,得到点之间的距离关系;一个是注意在定圆的不同位置关系下和动圆的不同相切(内切和外切)状态下有不同的结论。
本题可以分很多种情况,不妨解释其中的一种:
这个问题其实在高考复习阶段,很多练习中会有一个到两个的具体例子,但是很多同学对这个问题并没有重视,这个题目就是从特殊情况(练习中的例子)到一般情况的一个拓展,学生如果平时不注重分析,这个题目往往会无法下手或者考虑情况不全,从这个意义上来说,自主招生并不是要一味求难求偏,而更强调在平时学习中能够“多想一点,多走一步”,这样的积极主动学习会给自主招生这类考试带来极大的益处。
北约自主招生能力测试数学试题(含参考答案

综合性大学自主选拔录取联合考试自然科学基础——理科试卷数学部分(北约)一、选择题(每小题8分,合计48分)1.圆心角为3π的扇形的面积为6π,则它围成的圆锥的表面积为( B ).A .B .7πC .D .解:由2166S R ππ==扇形得6R =,由263r ππ=⨯得1r =,故它围成的圆锥的表面积为267r πππ+=.2.将10个人分为3组,一组4人,另两组各3人,共有( C )种分法.A .1070B .2014C .2100D .4200解:433106321002C C C N ==. 3.已知2()2()()33a b f a f b f ++=,(1)1f =,(4)7f =,则(2014)f =( A ). A .4027 B .4028 C .4029 D .4030 解:421(4)2(1)(2)()333f f f f +⨯+===,124(1)2(4)(3)()533f f f f +⨯+===,猜想*()21()f n n n N =-∈,假设()21f n n =-对3(1)n k k ≤≥都成立,则(31)3(1)2(1)2(31)1f k f k f k +=+-=+-,(32)3(2)2(2)2(32)1f k f k f k +=+-=+-,(33)3(3)2(3)2(33)1f k f k f k +=+-=+-,所以*()21()f n n n N =-∈.4.若2()lg(2)f x x ax a =-+的值域为R ,则a 的取值范围是( D ).A .01a ≤≤B .C .D .0a ≤或1a ≥解:由题知,{}2(0,)2y y x ax a +∞⊆=-+,故2(2)40a a ∆=--≥,解得:0a ≤或1a ≥.5.已知1x y +=-,且x 、y 均为负实数,则1xy xy+有( B ). A .最大值174 B .最小值174 C .最大值174- D .最小值174-解:1()()x y =-+-≥104xy <≤,而函数1()f t t t=+在(0,1)上单调递减,在(1,)+∞单调递增,故1()()4f xy f ≥,即1174xy xy +≥,当且仅当12x y ==-时取等号. 6.已知22()arctan14x f x C x +=+-在(,)44ππ-上为奇函数,则C =( B ). A .0 B .arctan 2- C .arctan 2 D .不存有解:由()0f x =得arctan(2)arctan 2C =-=-,此时()()f x f x +-22arctan14x x +=-22arctan 214x C x -+++4arctan()2arctan 203=--=,故arctan 2C =-符合题意.二、解答题(每题18分,共72分)7.证明:0tan3R ∉.证明:设0tan 3Q ∈,则0tan 6tan12tan 24tan 30tan(624)Q Q Q Q ∈⇔∈⇔∈⇔=+∈,这与0tan 303Q =矛盾. 8.已知实系数二次函数()f x 和()g x ,若方程()()f x g x =和3()()0f x g x +=都只有一个偶重根,方程()0f x =有两个不等的实根,求证:方程()0g x =没有实根. 解:设2()f x ax bx c =++,2()g x dx ex f =++,0ad ≠,所以2()4()()b e a d c f -=--,2(3)4(3)(3)b e a d c f +=++,所以223124b e ac df +=+,又240b ac ->,所以22()44(4)0g x e df b ac ∆=-=--<,所以方程()0g x =没有实根.9.已知1a ,2a ,…,13a 成等差数列,{}113i j k M a a a i j k =++≤<<≤,问:0,72,163是否能够同时在M 中?并证明你的结论.解:设该数列的公差为d ,∴p ∃,q ,*r N ∈,130a pd +=,173()2a p q d ++=,1163()3a p q r d +++=,∴2111q r =,∴21q ≥,11p ≥,又0123p ≥++=,∴35p q r ++≥, 又12111033p q r ++≤++=,与上式矛盾,故0,72,163不能够同时在M 中.10.i x (1i =,2,…,n )为正实数,且11nii x==∏,求证:1)1)nn i i x =≥∏.解:由AM GM -不等式得:11(n i n =≥,11(ni n =≥两式相加得:1≥,故1)1)nn i i x =≥∏.。
2011年北约数学试题

2011年北约自主招生数学试题1、已知平行四边形两边长分别是3和5,一条对角线是6.求另一条对角线的长度.2、求过抛物线22221,523y x x y x x =--=-++两交点的直线方程.3、等差数列1237,,13, 3..n a a a a n S ⋅⋅⋅=-=满足这个数列的前项和为数列12,⋅⋅⋅S S 中哪一项最小?并求出这个最小值.4、在2,60.ABC a b c C ∆+≥∠≤中,如果证明5、是否存在四个正实数,它们两两乘积分别是2,3,5,6,10,16.6、设12C C 和是平面上两个不重合的固定圆周.设C 是该平面上的一个动圆,它与12C C 和均相 切.问:C 的圆心轨迹是何种曲线?证明你的结论.7、求12120111.x x x -+-+⋅⋅⋅+-的最小值2【参考答案】1、解答:设平行四边形为ABCD ,且6,3,5===AC BC AB ,易得:51cos -=∠ABC ,所以151cos =∠BAC ,24,321515322592==⨯⨯⨯-+=BD BD . 2、解答:设两条抛物线额交点为),(),,(2211y x B y x A ,联立两条抛物线的方程⎩⎨⎧++-=--=32512222x x y x x y ,消去2x 得:167+-=x y ,B A ,两点的坐标均满足这个方程,所以直线AB 的方程为0176=-+y x .3、解答:方法一:因为公差4437=-=a a d ,所以03,01,21761>=<-=-=a a a ,所以6S 最小,最小值666-=S ; 方法二:8234232322222-⎪⎭⎫ ⎝⎛-=-=n n n S n ,当6=n 时,n S 的最小值为666-=S . 4、解答:方法一、在ABC ∆中,由余弦定理得: 21848233222cos 22222222=≥-+=⎪⎭⎫ ⎝⎛+-+≥-+=ab ab ab ab b a ab b a b a ab c b a C ,因为函数x y cos =在),0(π上单调递减,所以3π≤C . 方法二、依题意得:2cos 2sin 42cos 2sin 2sin 2sin sin B A B A B A B A C B A ++≥-+⇔≥+, 212cos ≤+B A ,因为函数x y cos =在),0(π上单调递减,所以33232πππ≤⇒≥+⇒≥+C B A B A . 5、解答:假设存在满足题意的四个正实数d c b a ,,,,且假定d c b a <<<<0,依题意得:16,10,3,2====cd bd ac ab ,由前两个式子得32=c b ,由后两个式子得85=c b ,矛盾,所以不存在满足题意的四个数.6、解答:设⊙1C 的半径为1r ,⊙2C 的半径为2r ,⊙C 的半径为r ,且假定21r r ≥.(1)当21r r =时,①若⊙1C 与⊙2C 外离,当⊙C 与⊙1C 、⊙2C 均外切或均内切时,点C 的轨迹是21C C 的中垂线;当⊙C 与⊙1C 、⊙2C 一个外切一个内切时,点C 的轨迹是以21,C C 为焦点,实轴长为21r r +的双曲线; ②若⊙1C 与⊙2C 外切,当⊙C 与⊙1C 、⊙2C 均外切或均内切时,点C 的轨迹是21C C 的中垂线(除去21C C 的中点);当⊙C 与⊙1C 、⊙2C 一个外切一个内切时,点C 的轨迹是直线21C C (除去21C C 的中点); ③若⊙1C 与⊙2C 相交,此时⊙C 必与⊙1C 、⊙2C 均外切或均内切,点C 的轨迹是两圆公共弦在圆外部分的两条射线.(2)当21r r >时,①若⊙1C 与⊙2C 外离,当⊙C 与⊙1C 、⊙2C 均外切或均内切时,点C 的轨迹是以21,C C 为焦点,实轴长为21r r -的双曲线;当⊙C 与⊙1C 、⊙2C 一个外切一个内切时,点C 的轨迹是以21,C C 为焦点,实轴长为21r r +的双曲线;②若⊙1C 与⊙2C 外切,当⊙C 与⊙1C 、⊙2C 均外切或均内切时,点C 的轨迹是以21,C C 为焦点,实轴长为21r r -的双曲线(除去⊙1C 与⊙2C 的切点);当⊙C 与⊙1C 、⊙2C 一个外切一个内切时,点C 的轨迹是直线21C C (除去点21,C C 及⊙1C 与⊙2C 的切点这三个点);③若⊙1C 与⊙2C 相交,当⊙C 与⊙1C 、⊙2C 均外切或均内切时,点C 的轨迹是以21,C C 为焦点,实轴长为21r r -的双曲线(除去⊙1C 与⊙2C 的两个交点);当⊙C 与⊙1C 、⊙2C 一个外切一个内切时,点C 的轨迹是以21,C C 为焦点,长轴长为21r r +的椭圆(除去⊙1C 与⊙2C 的两个交点);④若⊙1C 与⊙2C 内切,当⊙C 与⊙1C 、⊙2C 均外切或均内切时,点C 的轨迹是直线21C C (除去⊙1C 与⊙2C 的切点);当⊙C 与⊙1C 、⊙2C 一个外切一个内切时,点C 的轨迹是以21,C C 为焦点,长轴长为21r r +的椭圆(除去⊙1C 与⊙2C 的两个切点);⑤若⊙1C 内含⊙2C ,且不同心,当⊙C 与⊙1C 内切、与⊙2C 外切时,点C 的轨迹是以21,C C 为焦点,长轴长为21r r +的椭圆;当⊙C 与⊙1C 、⊙2C 均内切时,点C 的轨迹是以21,C C 为焦点,长轴长为21r r -的椭圆;⑥若⊙1C 内含⊙2C ,且同心,当⊙C 与⊙1C 内切、与⊙2C 外切时,点C 的轨迹是以1C 为圆心,半径为221r r +的圆;当⊙C 与⊙1C 、⊙2C 均内切时,点C 的轨迹是以1C 为圆心,半径为221r r -的圆. 7、解答:首先设12n a a a ≤≤≤,12()||||||n f x x a x a x a =-+-++-.由绝对值的最高理论知, n 为奇数时,当12n x a +=时,()f x 有最小值;n 为偶数时,当122,n n x a a +⎡⎤∈⎢⎥⎣⎦任何值时,()f x 有最小值. 于是分解之,20111111111()|1|||||||||||||||2233320112011f x x x x x x x x x =-+-+-+-+-+-++-++-个, 共有: 201220111+2+2011==20230662⨯个断点(包括多重). 设123456111,,,23a a a a a a ======202306612011a =. 因为202306610115332=. 现在求1011533a 和1011534a 的值.设10115331a t =,则121011533t +++≥, 1211011533t +++-<.可得1422t =.且1011533101153411422a a ==,故11422x =时,()f x 的值最小.111111491()112114221423120111832.142214221422142214231422711f =-+-⨯++-⨯+⨯-++⨯-=。
2011年北约华约理工联盟自主招生部分试题汇总

2011 自主招生试题1.语文:第一题是10道选词填空题,考的是不同词汇之间的辨析,比如端倪和端睨,果腹和裹腹等等,难度较低。
第二道题是古文题题目很短:州郡遇圣节锡宴,率命猥妓数十群舞于庭,作“天下太平”字,殊为不经。
而唐《乐府杂录》云:“舞有字,以舞人亚身于地,布成字也。
”王建《宫词》云:“罗衫叶叶绣重重,金凤银鹅各一丛。
每遇舞头分两向,太平万岁字当中。
”则此事由来久矣。
让说明是什么社会现象并联系实际谈谈看法。
感觉应该是从表面太平这种虚假政绩来谈论,为了政绩而粉饰太平的现象。
第三道题是古文翻译,没有短句而且异常的长,是韩非子中的一段话:古者先王尽力于亲民,加事于明法。
彼法明,则忠臣劝;罚必,则邪臣止。
忠劝邪止而地广主尊者,秦是也;群臣朋党比周以隐正道行私曲而地削主卑者,山东是也。
乱弱者亡,人之性也;治强者王,古之道也。
越王勾践恃大朋之龟与吴战而不胜,身臣入宦于吴;反国弃龟,明法亲民以报吴,则夫差为擒。
故恃鬼神者慢于法,恃诸侯者危其国。
第四道是阅读:我们失去了和自然交流的语言不久前我在鄯善迪坎儿村,见一大棵梭梭树长在路旁。
我从小认识梭梭,见了亲切的很,就像看见一个亲人站在那儿。
我对这个村庄也一下有了兴趣。
一棵本来只能当烧柴的梭梭,在村里枝条完好地长了这么多年,一直长到老,谁在护着它呢。
迪坎儿村紧挨沙漠,走进一户人家,门前一渠沟水流,葡萄藤蔓覆盖了整个院落。
转到屋后,发现后墙已经被流沙淹埋掉大半,沙漠从这户人家的后墙根,一望无际地远去,没有一点绿色。
我生活的新疆地域辽阔,大块地存有一些自然风光,除了几个国家级的野生动物保护区,在相对疏松的村镇之间,连绵的农田间隙,还有幸能看到荒野草原、沙漠戈壁,这些暂时没被人侵占的地方,长野草野树,或寸草不生,任风沙吹刮。
不像内地中原,城市村庄紧凑相连,农田密布,整个大地住满人长满人吃的粮食,没有一块闲地供野草生长,更别说有野生动物了。
自然退居到偏远边疆和那些不易人居的荒芜山岭。
2008-2011北京大学(北约)自主招生数学试题(全附答案)

形
=
舞ACBABA慧CB麓AC =/缓二C
。,
。/
l/
Dk
:::.?日 \、E。.・。
\I,・’
,‘1
.。.
BA 。,
。
口2丁,62丁,
.al一口2
bI—b2
B A +£ A B C +£C .,二 C
即证{一(口I+口2+bI+62)一(口l+d2+口,+
a 口l a 口2
2丁+口,
2丁一口'
【百189】+1=13分,而北方最高分的最大值为6+n
万方数据
14
中’?善i:.7(200s年第2期・高中版)
南方球队内部比赛总得分CⅢ2
,12
・解题研究・
=136,
一l=11分<13分,
.・.
冠军在南方队
北方球队内部比赛总得分c2=28,
北方胜南方得分=30—28=2, 北方球队最高得分=7+2=9, 因为9×17=153<270, 所以南方球队中至少有一支得分超过9分. 冠军在南方球队中.综上所述,冠军是一支南方 球队. 点评这道试题要注意突破口的选择,也需要 耐心和比较强的推理、分析能力. 5.(理科)0一xyz坐标系内xoy平面系内0≤,,≤ 2一石2绕),轴旋转一周构成一个不透光立体在点 (1,0,1)设置一光源,在xoy平面内有一以原点为圆 心的圆c被光照到的长度为2霄,求曲线C上未被照 到的长度.
c:+。+n(肛+9)≥召,c:≤A,
即3n2—22n一36。<0.
‘.・
’B=9A,
.・.c:+9+n(,l+9)≥B=9A1>9c:,
(1)
,’2
又总分为乞Ⅲ有10I乞小钴厶(1)得厅=6或8.
2011年北京市四中自主招生考试数学试卷

2011年北京市四中自主招生考试数学试卷
5、掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1至6六个数.连续掷两次,掷得面向上的点数之和是3的倍数的概率为()
6、1×2+2×3+3×4+…+99×100()
8、已知点P(x,y)位于第二象限,并且y≤2x+6,x、y为整数,则点P的个数是_______.
9、已知⊙O的半径OA=1,弦AB、AC的长分别是,则∠BAC的度数是______.
三、解答题(共5小题,满分60分)
13、现将一个表面涂满红色的正方体的每条棱十等分,此正方体分割成若干个小正方体.在这些小正方体中,求:
(1)两面涂有红色的小正方体的个数;
(2)任取一个小正方体,各面均无色的小正方体的概率;
(3)若将原正方体每条棱n等分,只有一面涂有红色的小正方体的个数.。
2011年华约自主招生数学试题(精校word版,有参考答案)

2011年“华约”自主招生数学试题一、选择题1.设复数z满足|z|<1且15||2zz+=则|z| =()A.45B.34C.23D.12【答案】D【解析】由15||2zz+=得25||1||2z z+=,已经转化为一个实数的方程.解得|z| =2(舍去),12.2.在正四棱锥P-ABCD中,M、N分别为P A、PB.则异面直线DM与AN所成角的余弦为()A.13B.16C.18D.112【答案】D【解析】本题有许多条件,可以用“求解法”,即假设题中的一部分要素为已知,利用这些条件来确定其余的要素.本题中可假设底面边长为已知(不妨设为2),利用侧面与底面所成二面角可确定其他要素,如正四棱锥的高等.然后我们用两种方法,一种是建立坐标系,另一种是平移其中一条线段与另一条在一起.解法一:如图1,设底面边长为2.如图建立坐标系,则A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),P(0,0),则1111(,(,2222M N-,312132(,,),(,,)222222DM AN =-=-.设所成的角为θ,则1cos 6DM AN DM ANθ==.3.已知1223+--=x x x y ,过点(-1, 1)的直线l 与该函数图象相切,且(-1, 1)不是切点,则直线l 的斜率为 ( ) A .2B .1C .-1D .-2【答案】C【解析】显然(-1, 1)在1223+--=x x x y 的图象上.设切点为)12,(020300+--x x x x , 2232--='x x y ,所以223020--=x x k .另一方面,)1(1)12(002030---+--=x x x x k )2(00-=x x 223020--=x x .所以x 0=1,所以1-=k .选C . 4.若222cos cos 3A B A B π+=+,则的最小值和最大值分别为 ( ) A .321-,32B .12 ,32C .321-,321+D .12 ,221+【答案】B【解析】首先尽可能化简结论中的表达式22cos cos A B +,沿着两个方向:①降次:把三角函数的平方去掉;②去角:原来含两个角,去掉一个. 解:221cos 21cos 21cos cos 1(cos 2cos 2)222A B A B A B +++=+=++ 11cos()cos()1cos()2A B A B A B =++-=--,可见答案是B【答案】B【解析】题目中的条件是通过三个圆来给出的,有点眼花缭乱.我们来转化一下,就可以去掉三个圆,已知条件变为:ΔO O 1 O 2边O 1 O 2上一点C ,OO 1、OO 2延长线上分别一点A 、B ,使得O 1A =O 1C ,O 2B =O 2C . 解法一:连接12O O ,C 在12O O 上,则1221OO O OO O πα∠+∠=-,111212O AC O CA OO O ∠=∠=∠,222112O BC O CB OO O ∠=∠=∠,故1212211()22O CA O CB OO O OO O πα-∠+∠=∠+∠=, 12()2O CA O CB παβπ+=-∠+∠=,sin cos 2αβ=. 解法二:对于选择填空题,可以用特例法,即可以添加条件或取一些特殊值,在本题中假设两个小圆的半径相等,则12212OO O OO O πα-∠=∠=,1212124O CA O CB OO O πα-∠=∠=∠=,12()2O CA O CB παβπ+=-∠+∠=,sin cos2αβ=.6.已知异面直线a ,b 成60°角.A 为空间一点则过A 与a ,b 都成45°角的平面 ( ) A .有且只有一个B .有且只有两个C .有且只有三个D .有且只有四个【答案】D【解析】已知平面过A ,再知道它的方向,就可以确定该平面了.因为涉及到平面的方向,我们考虑它的法线,并且假设a ,b 为相交直线也没关系.于是原题简化为:已知两条相交直线a ,b 成60°角,求空间中过交点与a ,b 都成45°角的直线.答案是4个. 7.已知向量3131(0,1),(,),(,),(1,1)2222a b c xa yb zc ==--=-++=则222x y z ++的最小值为( ) A .1B .43C .32D .2【答案】B【解析】由(1,1)xa yb zc ++=得1)111222y z y z y z y z x x ⎧⎧+=-=⎪⎪⎪⎪⎨⎨+⎪⎪--=-=⎪⎪⎩⎩, 由于222222()()2y z y z x y z x ++-++=+,可以用换元法的思想,看成关于x ,y + z ,y -z三个变量,变形2(1)y z y z x ⎧-=⎪⎨⎪+=-⎩,代入222222()()2y z y z x y z x ++-++=+222228242(1)343()3333x x x x x =+-+=-+=-+,答案B 8.AB 为过抛物线y 2=4x 焦点F 的弦,O 为坐标原点,且135OFA ∠=,C 为抛物线准线与x 轴的交点,则ACB ∠的正切值为 ( ) A.B.5C.3D.3【答案】A【解析】解法一:焦点F (1,0),C (-1,0),AB 方程y = x – 1,与抛物线方程y 2 = 4x联立,解得A B (3+2+ (3-2- ,,于是22CA CB k k ==,tan 1CA CB CA CBk k ACB k k -∠==+ A 解法二:如图,利用抛物线的定义,将原题转化为:在直角梯形ABCD 中,∠BAD = 45°,EF ∥DA ,EF = 2,AF = AD ,BF = BC ,求∠AEB .tan tan 2DE GF AEF EAD AD AF ∠=∠===.类似的,有tan tan BEF EBC ∠=∠=2AEB AEF BEF AEF ∠=∠+∠=∠,tan tan 2AEB AEF ∠=∠= A【答案】DA .存在某种分法,所分出的三角形都不是锐角三角形B .存在某种分法,所分出的三角形恰有两个锐角三角形C .存在某种分法,所分出的三角形至少有3个锐角三角形D .任何一种分法所分出的三角形都恰有1个锐角三角形 【答案】D【解析】我们先证明所分出的三角形中至多只有一个锐角三角形.如图,假设ΔABC 是锐角三角形,我们证明另一个三角形ΔDEF (不妨设在AC 的另一边)的(其中的边EF 有可能与AC 重合)的∠D 一定是钝角.事实上,∠D ≥ ∠ADC ,而四边形ABCD 是圆内接四边形,所以∠ADC = 180°-∠B ,所以∠D 为钝角.这样就排除了B ,C .下面证明所分出的三角形中至少有一个锐角三角形.假设ΔABC 中∠B 是钝角,在AC 的另一侧一定还有其他顶点,我们就找在AC 的另一侧的相邻(指有FEDBCA DBCA公共边AC ) ΔACD ,则∠D = 180°-∠B 是锐角,这时如果或是钝角,我们用同样的方法继续找下去,则最后可以找到一个锐角三角形.所以答案是D . 二、解答题解:(I )tan tan tan tan()tan tan 1A BC A B A B +=-+=-,整理得tan tan tan tan tan tan A B C A B C =++(II )由已知3tan tan tan tan A C A B C =++,与(I )比较知tan 33B B π=,=.又11222sin 2sin 2sin 23sin 3A C B π+===,sin 2sin 2sin 2sin 23A C A C +=sin()cos()cos 2()cos 2()3A C A C A C A C +-=--+而3sin()sin 2A C B +==,1cos 2()cos 22A C B +==-,代入得2cos 2()13cos()A C A C -+=-,24cos ()3cos()10A C A C ----=,1cos()14A C -=-,,6cos 12A C -=,12.已知圆柱形水杯质量为a 克,其重心在圆柱轴的中点处(杯底厚度及重量忽略不计,且水杯直立放置).质量为b 克的水恰好装满水杯,装满水后的水杯的重心还有圆柱轴的中点处. (I )若b = 3a ,求装入半杯水的水杯的重心到水杯底面的距离与水杯高的比值; (II )水杯内装多少克水可以使装入水后的水杯的重心最低?为什么? 解:不妨设水杯高为1.(I )这时,水杯质量:水的质量=2 :3.水杯的重心位置(我们用位置指到水杯底面的距离)为12,水的重心位置为14,所以装入半杯水的水杯的重心位置为11237242320+=+(II)当装入水后的水杯的重心最低时,重心恰好位于水面上.设装x克水.这时,水杯质量:水的质量=a:x.水杯的重心位置为12,水的重心位置为2xb,水面位置为xb,于是122xa x xba x b+=+,解得x a=-13.已知函数21()(1)1()2xf x f fax b===+2,,3.令111()2n nx x f x+==,.(I)求数列{}nx的通项公式;(II )证明12112nx x xe+>.解:由12(1)1()1()21xf f a b f xx=====+2,得,3(I)方法一:先求出123412482359x x x x====,,,,猜想11221nn nx--=+.用数学归纳法证明.当n = 1显然成立;假设n = k成立,即11221kk kx--=+,则122()121kkk k kkxx f xx+===++,得证.方法二:121+=+nnn xxx取倒数后整理得)11(21111-=-+nnxx,所以)11()21(1111-=--xxnn所以12111+=-nx(II)方法一:证明12112nex x x+>.事实上,12111112(1)(1)(1)242nnx x x+=+++.我们注意到2212(1)12(1)nna a a a+<++<+,,,(贝努利(Bernoulli)不等式的一般形式:nxx n+≥+1)1(,x),1(+∞-∈)于是122121212111112(1)2(1)2(1)2222n n nn n nnex x x-+++-+<+=+<+<方法二:原不等式en<+++⇔)211()211)(211(21)]211()211)(211ln[(2<+++⇔n1)211ln()211ln()211ln(2<++++++⇔n构造函数)0()1ln()(>-+=x xx x g01111)(<+-=-+='xxx x g ,所以0)0()(=<g x g 所以)0()1ln(><+x x x令n x 21=则n n 21)211ln(<+ 1211212121)211ln()211ln()211ln(22<-=+++<++++++n n n14.已知双曲线221222:1(0,0),,x y C a b F F a b -=>>分别为C 的左右焦点.P 为C右支上一点,且使21212=,3F PF F PF π∠∆又的面积为.(I )求C 的离心率e ;(II )设A 为C 的左顶点,Q 为第一象限内C 上的任意一点,问是否存在常数λ(λ>0),使得22QF A QAF λ∠=∠恒成立.若存在,求出λ的值;若不存在,请说明理由.解:(I )如图,利用双曲线的定义,将原题转化为:在ΔP F 1 F 2中,21212=3F PF F PF π∠∆,的面积为,E 为PF 1上一点,PE = PF 2,E F 1 =2a ,F 1 F 2 = 2c ,求ca.设PE =PF 2=EF 2=x ,F F 2x ,1221211(222F PF S PF FF x a ∆==+=, 224120x ax a +-=,2x a =.ΔE F 1F 2为等腰三角形,1223EF F π∠=,于是2c =,ce a==. (II ) 21=λ此解法可能有误15.将一枚均匀的硬币连续抛掷n 次,以p n 表示未出现连续3次正面的概率. (I )求p 1,p 2,p 3,p 4;(II )探究数列{ p n }的递推公式,并给出证明;(III )讨论数列{ p n }的单调性及其极限,并阐述该极限的概率意义.解析:(I )显然p 1=p 2=1,878113=-=p ;又投掷四次连续出现三次正面向上的情况只有:正正正正或正正正反或反正正正,故161316314=-=p .(II )共分三种情况:①如果第n 次出现反面,那么前n 次不出现连续三次正面的概率121-⨯n P ;②如果第n 次出现正面,第n -1次出现反面,那么前n 次不出现连续三次正面和前n -2次不出现连续三次正面是相同的,所以这个时候不出现连续三次正面的概率是241-⨯n P ;③如果第n 次出现正面,第n -1次出现正面,第n -2次出现反面,那么前n 次不出现连续三次正面和前n -3次不出现连续三次正面是相同的,所以这个时候不出现连续三次正面的概率是381-⨯n P .综上,=n P +⨯-121n P +⨯-241n P 381-⨯n P .(4≥n ),④ (III )由(II )知=-1n P +⨯-221n P +⨯-341n P 481-⨯n P ,(5≥n )⑤,④-12×⑤,有=n P --1n P 4161-⨯n P (5≥n ) 所以5≥n 时,p n 的单调递减,又易见p 1=p 2>p 3>p 4>….3≥n 时,p n 的单调递减,且显然有下界0,所以p n 的极限存在.对=n P --1n P 4161-⨯n P 两边同时取极限可得0lim =-∞→n n p .其统计意义:当投掷的次数足够多时,不出现连续三次正面向上的次数非常少,两者比值趋近于零.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年综合性大学(北约13校)自主选拔录取联合考试
数学试题
请注意:文科考生做1至5题,理科考生做3至7题.每题20分,共100分.
1.已知平行四边形的其中两条边长为3和5,一条对角线长为6,求另一条对角线长.
2.求过抛物线2221y x x =--和2523y x x =-++的交点的直线方程.
3.在等差数列{}n a 中,3713,3a a =-=,数列{}n a 的前n 项和为n S ,求数列{}n S 的最小项,并指出其值为何?
4.在ABC ∆中,2a b c +≥,求证:060C ∠≤.
5.是否存在四个正实数,使得他们的两两乘积为2,3,5,6,10,16?
6.1C 和2C 是平面上两个不重合的固定圆,C 是平面上的一个动圆,C 与1C ,2C 都相切,则C 的圆心的轨迹是何种曲线?说明理由.
7.求()121........20111f x x x x =-+-++-的最小值.。
