第2讲 应力状态基本概念
知识点应力状态理论和强度理论

知识点9:应力状态理论和强度理论一、应力状态理论(一)应力状态的概念1.一般情况下,受力构件内各点的应力是不同的,且同一点的不同方位截面上应力也不相同。
过构件内某一点不同方位上总的应力情况,称为该点的应力状态。
2.研究一点的应力状态,通常是围绕该点截取一个微小的正六面体(即单元体)来考虑。
单元体各面上的应力假设是均匀分布的,并且每对互相平行截面上的应力,其大小和性质完全相同,三对平面上的应力代表通过该点互相垂直的三个截面上的应力。
当单元体三个互相垂直截面上的应力已知时,可通过截面法确定该点任一截面上的应力。
截取单元体时,应尽可能使其三个互相垂直截面的应力为已知。
3.单元体上切应力等于零的截面称为主平面,主平面上的正应力称为主应力。
过受力构件内任一点,一定可以找到一个由三个相互垂直主平面组成的单元体,称为主单元体。
它的三个主应力通常用σ1,σ2和σ3来表示,它们按代数值大小顺序排列,即σ1>σ2>σ3。
4.一点的应力状态常用该点的三个主应力来表示,根据三个主应力的情况可分为三类:只有一个主应力不等于零时,称为单向应力状态;有两个主应力不等于零时,称为二向应力状态(或平面应力状态);三个主应力都不等于零时,称为三向应力状态。
其中二向和三向应力状态称为复杂应力状态,单向应力状态称为简单应力状态。
5.研究一点的应力状态是对构件进行强度计算的基础。
(二)平面应力状态的分析1.分析一点的平面应力状态有解析法和图解法两种方法,应用两种方法时都必须已知过该点任意一对相互垂直截面上的应力值,从而求得任一斜截面上的应力。
2.应力圆和单元体相互对应,应力圆上的一个点对应于单元体的一个面,应力圆上点的走向和单元体上截面转向一致。
应力圆一点的坐标为单元体相应截面上的应力值;单元体两截面夹角为α,应力圆上两对应点中心角为2α;应力圆与σ轴两个交点的坐标为单元体的两个主应力值;应力圆的半径为单元体的最大切应力值。
3.在平面应力状态中,过一点的所有截面中,必有一对主平面,也必有一对与主平面夹角为45︒的最大(最小)切应力截面。
高等材料力学课件第二章应力状态

应变与应力之间的关系
应变和应力之间存在着密切的关系。应变是材料变形程度的度量,而应力是 材料受力的表现。了解应变与应力之间的关系可以帮助我们更好地分析和控 制材料的行为。
应力的平面转动
应力的平面转动是指在不同的坐标系下,应力分量的变化。通过对应力的平 面转动进行研究,我们可以更好地理解材料在不同坐标系下的受力情况应力。掌握主应力和主应力方 向的概念可以帮助我们识别和分析材料的受力情况。
应力状态的分类
应力状态可以分为三种基本形式:平面应力、轴对称应力和空间应力。通过分类应力状态,我们可以更好地理解材 料在不同条件下的受力行为。
平面应力和轴对称应力
平面应力是指只存在于某一平面上的应力,而轴对称应力是指具有旋转对称 性的应力。通过研究平面应力和轴对称应力,我们可以更好地分析材料在不 同维度上的受力情况。
平面应力下的摩尔-库仑方程
摩尔-库仑方程是描述平面应力下材料力学行为的重要方程。通过掌握摩尔-库仑方程,我们可以更好地分析和预测 材料在平面应力下的受力行为。
高等材料力学课件第二章 应力状态
在本章中,我们将深入探讨应力的概念和定义,重点介绍主应力和主应力方 向的概念,以及应力状态的分类以及平面应力和轴对称应力的特点。
应力的定义和概念
了解应力是理解材料行为的关键。应力是材料内部的力,是单位面积上的力。通过深入研究应力的定义和概念,我 们可以更好地理解材料的力学行为。
应力状态的概念

应力状态与强度理论\应力状态的概念
应力状态的概念
1.1 一点处的应力状态
在工程中,只知道杆件横截面上的应力是不够的。例如,在铸 铁试件压缩时,沿与轴线大约成45°左右的斜截面发生破坏(如 图),这是由于在与轴线成45°的斜截面上存在最大切应力所引起 的。
目录
应力状态与强度理论\应力状态的概念
力的影响。
为了分析破坏现象以及解决复杂受力构件的强度问题,必须首
先研究通过受力构件内一点处所有截面上应力的变化规律。我们把
通过受力构件内一点处不同方位的截面上应力的大小和方向情况,
称为一点处的应力状态。
目录
应力状态与强度理论\应力状态的概念
1.2 应力状态的表示
为了研究受力构件内一点处的应力状态,可围绕该点取出一个 微小的正六面体,称为单元体,并分析单元体六个面上的应力。由 于单元体的边长无限小,可以认为在单元体的每个面上应力都是均 匀分布的;且在单元体内相互平行的截面上应力都是相同的。
力状态。例如从地层深处某点取出的单元体,它在三个方向都受到 压力的作用,处于空间应力状态(如图)。
目录
应力状态与强度理论\应力状态的概念 若平面应力状态的单元体中,正应力都等于零,仅有切应力作
用,称为纯剪切应力状态,例如图所示的应力状态。
目录
应力状态与强度理论\应力状态的概念 应力状态也可以按主应力的情况分类。若单元体的三个主应力
如果知道了单元体的三个互相垂直平面上的应力,则其他任意 截面上的应力都可以通过截面法求得(详见8.2.1),那末该点处的 应力状态就可以确定了。因此,可用单元体的三个互相垂直平面上 的应力来表示一点处的应力状态。
目录
应力状态与强度理论\应力状态的概念
材料力学应力状态分析

材料力学应力状态分析材料力学是研究物质内部力学性质和行为的学科,其中应力状态分析是材料力学中的重要内容之一。
应力状态分析是指对材料内部受力情况进行分析和研究,以揭示材料在外力作用下的应力分布规律和应力状态特征,为工程设计和材料选用提供依据。
本文将从应力状态的基本概念、分类和分析方法等方面展开讨论。
首先,我们来介绍一下应力状态的基本概念。
应力是指单位面积上的力,是描述物体内部受力情况的物理量。
在材料力学中,通常将应力分为正应力和剪应力两种基本类型。
正应力是指垂直于截面的应力,而剪应力是指平行于截面的应力。
在实际工程中,材料往往同时受到多种应力的作用,因此需要对应力状态进行综合分析。
其次,我们将对应力状态进行分类。
根据应力的作用方向和大小,可以将应力状态分为拉应力状态、压应力状态和剪应力状态三种基本类型。
拉应力状态是指材料内部受到拉力作用的状态,压应力状态是指材料内部受到压力作用的状态,而剪应力状态是指材料内部受到剪切力作用的状态。
这三种应力状态在工程实践中都具有重要的意义,需要我们进行深入的分析和研究。
接下来,我们将介绍应力状态分析的方法。
应力状态分析的方法有很多种,常用的有应力分析法、应变分析法和能量方法等。
应力分析法是通过应力分布的计算和分析来揭示应力状态的特征,应变分析法则是通过应变分布的计算和分析来揭示应力状态的特征,而能量方法则是通过能量原理和平衡条件来揭示应力状态的特征。
这些方法各有特点,可以根据具体情况选择合适的方法进行分析。
最后,我们需要注意的是,在进行应力状态分析时,需要考虑材料的本构关系、边界条件和载荷情况等因素,以确保分析结果的准确性和可靠性。
同时,还需要注意应力状态分析的结果对工程实践的指导意义,以便更好地指导工程设计和材料选用。
总之,材料力学应力状态分析是一个复杂而重要的课题,需要我们进行深入的研究和分析。
只有深入理解应力状态的特征和规律,才能更好地指导工程实践,为实际工程问题的解决提供科学依据。
应力状态概念

应力状态概念一、应力的定义和分类1. 应力的定义应力是力对物体单位面积的作用。
即使物体本身并不发生运动,仍然可以存在应力。
应力的量纲是力除以面积,单位常用帕斯卡(Pa)来表示。
2. 应力的分类根据作用力的特点和方向,应力可以分为以下几种类型:•拉应力(tensile stress):作用力是拉伸物体的方向,使物体变长。
•压应力(compressive stress):作用力是压缩物体的方向,使物体变短。
•剪应力(shear stress):作用力是平行于物体表面的方向,使物体发生形变。
•弯应力(bending stress):作用力使物体弯曲。
二、应力与强度1. 应力与材料的强度应力与材料的强度密切相关。
强度是指材料所能承受的最大应力。
当材料的应力超过其强度时,材料就会发生破坏。
2. 不同材料的强度差异不同材料具有不同的强度特性。
一般而言,金属材料的强度较高,而塑料等非金属材料的强度较低。
三、应力的计算方法1. 基本应力计算方法基本应力的计算方法根据材料的受力情况而定。
对于不同的受力情况,我们采用不同的计算方法。
•拉伸应力的计算公式为:stress = force / area•压缩应力的计算公式为:stress = -force / area•剪切应力的计算公式为:stress = force / area•弯曲应力的计算公式为:stress = M * y / I其中,force表示受力大小,area表示受力区域的面积,M表示弯矩,y表示弯曲点到中性轴的距离,I表示截面的惯性矩。
2. 组合应力的计算方法组合应力是指不同方向的应力同时作用在材料上的情况。
对于组合应力,我们需要将不同方向的应力进行合成。
•对于平面应力状态下的组合应力,可以使用莫尔圆的方法进行计算。
•对于空间应力状态下的组合应力,可以使用三维应力变换公式进行计算。
四、应力的效应1. 弹性效应当施加的应力作用在材料上时,材料会产生弹性变形。
过一点所方向面上应力的集合,称为这一点的应力状态

应力是指物体内部受到的力的作用,它可以通过单位面积上的力来描述。
在工程力学中,应力是非常重要的物理量,它与物体的形状、材料特性和外部力的作用密切相关。
本文将围绕应力的概念展开讨论,针对其在材料力学中的应用进行深入分析。
一、应力的定义和分类1.1 应力的概念应力是单位面积上的力,常用符号表示为σ,其计算公式为力F除以面积A,即σ=F/A。
在物体内部,由于外部力的作用,各处都会受到应力的作用,这种应力称为内应力。
而外部施加在物体表面上的力也会导致应力的产生,这种应力称为外部应力。
1.2 应力的分类根据应力的作用方向和大小,可以将应力分为正应力、剪切应力和法向应力三种类型。
正应力是垂直于物体截面的应力,常用符号表示为σn。
而沿着截面方向的应力称为剪切应力,常用符号表示为τ。
另外,法向应力是指作用在物体某一点上的应力。
二、应力状态的描述2.1 应力张量在三维空间中,一个点的应力状态可以由一个3x3的对称矩阵来描述,这个对称矩阵称为应力张量。
应力张量的分量代表了在不同方向上的应力情况,可以通过数学方法进行求解和分析。
2.2 应力状态的表示一个点处的应力状态可以通过应力张量的特征值和特征向量来表示。
特征值代表了应力状态的大小,特征向量则代表了应力作用的方向。
通过对特征值和特征向量的分析,可以判断物体处于何种应力状态,从而进行相应的力学分析和设计。
三、应力的应用3.1 工程材料的性能应力是描述物体受力情况的重要参数,它直接影响着材料的强度、刚度和韧性等性能。
在工程中,通过对材料的应力状态进行分析,可以评估材料的可靠性和安全性,为工程设计提供参考依据。
3.2 结构的稳定性对结构件的受力状态进行分析,可以判断结构在外部载荷作用下的稳定性。
通过对结构的应力分布和应力集中区域的分析,可以预测结构是否会发生破坏或失稳现象,为结构设计和改进提供重要参考。
3.3 力学设计在工程实践中,需要根据实际的力学要求来设计各种零部件和结构件。
应力状态的概念

应力状态的概念
应力状态的概念是指个体在不同生活、工作或学习环境中所承受的各种压力和心理负荷的总和。
它是一种心理感受,描述了人们在面对压力时的心理、情绪和生理反应。
应力状态通常来源于各种不同的因素,如工作压力、学习压力、人际关系压力、经济压力等。
在应力状态下,人们往往感到紧张、焦虑、不安甚至抑郁。
长时间处于高度应力状态下,对个体的身心健康和社交功能都可能产生负面影响。
应力状态既可以是短暂的,也可以是持久的。
短期的应力状态可能是由于特定事件或任务引起的,如考试前的紧张感或工作任务的临时性压力。
而持久的应力状态往往与长期处于高度竞争的环境中、工作生活压力大、人际关系紧张等因素有关。
应力状态不仅仅在个体的心理和情绪层面产生影响,还可能导致身体上的一系列生理反应。
常见的生理反应包括失眠、食欲改变、心跳加快、血压升高等。
这些生理反应进一步加剧了个体在应力状态下的不适和负面影响。
理解和管理应力状态对于个体的健康和幸福至关重要。
通过采取积极的应对策略,如健康的生活方式、良好的时间管理、寻求支持和与他人沟通,可以帮助个体更好地应对应力状态,保护身心健康,促进个人发展和生活质量的提高。
第二章_应力讲解

第二章 应力分析研究弹性力学问题要从三方面规律(条件):平衡、几何、物理来建立,本章就是研究第一个规律:平衡规律。
第1节 内力和外力1.1 外力:物体承受外因而导致变形,外因可以是热力作用、化学力作用、电磁力作用和机械力作用;另一方面从量纲分类,外力主要为体积力和表面积力。
我们讨论的外力是属于机械力中的体力和面力的范围。
1. 外部体力:作用在物体单位体积(质量)上的力如重力(惯性力)。
量纲:力/(长度)3。
求V 中任意点P 上承受体力采用极限方法:X X 2X X 2第2节 应力和应力张量2.1 应力当变形体受外力作用时,要发生变形,同时引起物体内部各点之间相互作用力(抵抗力)——内力,为了描述物体内任意点P 的内力可采取如下方法:过P 点设一个截面S 将V 分为两部分:(作用力与反作用力)FF -l n n x ==1、m n n y ==2、n n n z ==3。
即n t m t l t n t n t n t n t t z y x i i n )()()(3)3(2)2(1)1()()( ++=++==,,1S n P B C S A B C ∆∆∆∆==0)()(=++-V f S t S t i i n ∆∆∆而 S n S t t i i i i ∆∆=-=-,)()(代入上式,并忽略高阶微量 0)()(=-S n t S t i i n ∆∆或 )()(i i n t n t =展开为 3)3(2)2(1)1()(n t n t n t t n++= 或n t m t l t t z y x n )()()()( ++=2.1 应力张量每个坐标面上的应力矢量又可以沿三个坐标面分解三个分量,比如坐标面法线为x 1jxj j j z xz y xy x xx x e e e e e e e e t t σσσσσσσσ==++=++==1313212111)()1(x 2x 1 x 1(x)x 3,,32S n PAB S n PAC ∆=∆∆=∆同理,得j yj j j z yz y yy x yx y e e e e e e e e t t σσσσσσσσ==++=++==2323222121)()2(jzj j j z zz y zy x zx z e e e e e e e e t t σσσσσσσσ==++=++==3333232131)()3(将法线方向n 取为单位长度,则将式(3.25)代入式(3.26),得3.3.2.讨论:) ( 333333222222253.l p l p l p l p ⎪⎪⎪⎭⎪⎬====σσσσ) (2631232221.l l l =++7)=1 ()()+() (23322222311.p p p σσσ+(1):如果以p 1,p 2,p 3为坐标轴建立直角坐标系,则在此坐标系中,上式为一椭球面方程,主半轴分别为σ1,σ2,σ3,称为应力椭球面。
材料学应力状态概述

材料学应力状态概述材料学中的应力状态是指材料内部受力的分布情况。
材料在受到外力作用时,会产生内部的应力。
了解和分析材料的应力状态对于材料的设计、加工和使用具有重要意义。
下面将对应力状态进行概述。
首先,应力可以分为拉应力、压应力和剪应力。
拉应力是材料内部发生拉伸的力,压应力是材料内部发生压缩的力,剪应力则是材料内部发生剪切的力。
这三种应力是材料在受力时最基本的应力形式。
其次,应力的分布是在材料内部的各个点上的应力大小和方向的变化。
根据应力的分布情况,可以分为均匀应力和非均匀应力。
均匀应力指的是受力材料内部各个点上的应力大小和方向完全相同,各点上的应力分布是均匀的。
非均匀应力指的是受力材料内部各个点上的应力大小和方向不同,各点上的应力分布是不均匀的。
另外,应力在材料内部是沿着不同的方向作用的。
这些不同的方向包括垂直于所受力的方向和与所受力垂直的方向。
对于材料来说,所受力的方向所产生的应力称为正应力,与所受力垂直的方向所产生的应力称为剪应力。
正应力可以进一步分为法向应力和切向应力,法向应力是垂直于材料截面的应力,切向应力是与材料截面相切的应力。
此外,还可以对应力进行分类。
静态应力是指材料在受力过程中保持相对静止的应力状态。
静态应力包括恒定应力和准静态应力。
动态应力是指材料在受力过程中发生明显变化的应力状态,动态应力通常产生在材料的瞬间或短暂受力下。
动态应力包括冲击应力、脉冲应力和循环载荷应力等。
最后,应力状态的分析是通过应力张量来描述的。
应力张量是一个描述应力状态的二阶对称张量。
对于各向同性材料,应力张量可以由其法向应力和切向应力来表示。
其中,法向应力的大小等于平均应力的大小,切向应力的大小则与法向应力的大小相关。
总之,材料学中的应力状态是指材料内部受力的分布情况。
根据应力的形式、分布和方向可以将应力分为拉应力、压应力和剪应力,均匀应力和非均匀应力,以及正应力和剪应力。
根据应力的性质可以将应力分为静态应力和动态应力。
第2讲 应力状态基本概念

其中li、mi、ni为新坐标轴在原坐标系下的方向余弦。
x x' y' z'
2013-7-12
y m1 m2 m3
z n1 n2 n3
32
l1 l2 l3
Lesson 20
y
y'
uy' uy o ux' u
ux
x'
2013-7-12 33
Lesson 20
10.3.2 应力张量
在斜面上的应力分析中,我们得到
SOAC S ABC cosn, y ds m
n z
SOBA S ABC cosn, z ds n
2013-7-12
g a
x
21
方向余弦有: l 2
m n 1
2 2
Lesson 20
由于变形体处于平衡状态,对于任意体素都有 三个方向的受力平衡,即
X 0
而 所以
2 2 Sn 12l 2 2 m2 3 n2
1 2 2 l 2m2 2 3 2 m2n2 3 1 2 n2l 2
2 n
2013-7-12 25
Lesson 20
综上可知,变形体内任意点的应力状态可以通 过该点且平行于坐标面的三个微分面上的九个 应力分量来表示。
2013-7-12 22
Lesson 20
整理后可得方程
S nx x l yx m zx n S ny xy l y m zy n S nz xz l yz m z n
(※)
用矩阵表示为
S nx x yx zx l S ny xy y zy m S yz z n nz xz
公共基础知识应力基础知识概述

《应力基础知识概述》一、引言应力作为物理学和工程学中的一个重要概念,在众多领域中都有着广泛的应用。
从材料科学到土木工程,从机械制造到航空航天,应力的理解和控制对于确保结构的安全性和可靠性至关重要。
本文将对应力的基础知识进行全面的阐述和分析,包括基本概念、核心理论、发展历程、重要实践以及未来趋势。
二、应力的基本概念(一)定义应力是指物体由于受到外力作用而产生的内部抵抗力。
当物体受到外力时,其内部的分子和原子会发生相对位移,从而产生一种抵抗外力的力,这种力就是应力。
应力的单位是帕斯卡(Pa),1帕斯卡等于 1 牛顿每平方米(N/m²)。
(二)分类1. 正应力:垂直于作用面的应力分量,又称为法向应力。
正应力可以是拉应力或压应力,当物体受到拉伸作用时,产生拉应力;当物体受到压缩作用时,产生压应力。
2. 切应力:平行于作用面的应力分量,又称为剪应力。
切应力的作用是使物体发生剪切变形。
(三)应力状态物体内部某一点的应力状态可以用三个正应力和三个切应力来表示。
这六个应力分量可以组成一个应力张量,通过应力张量可以全面地描述物体内部某一点的应力状态。
三、应力的核心理论(一)胡克定律胡克定律是描述弹性材料应力与应变关系的基本定律。
对于线弹性材料,在弹性限度内,应力与应变成正比,即σ=Eε,其中σ为应力,ε为应变,E 为弹性模量。
弹性模量是材料的一种固有属性,它反映了材料抵抗变形的能力。
(二)圣维南原理圣维南原理指出,如果把物体的一小部分边界上的面力变换为分布不同但静力等效的面力,那么近处的应力分布将有显著的改变,但是远处所受的影响可以忽略不计。
这个原理在工程实际中非常有用,可以简化复杂结构的应力分析。
(三)莫尔圆莫尔圆是一种用于分析平面应力状态的工具。
通过莫尔圆可以直观地表示出一点的正应力、切应力以及主应力的大小和方向。
莫尔圆的绘制方法是将一点的两个相互垂直的正应力和切应力作为直角坐标系中的两个坐标,然后根据一定的几何关系绘制出一个圆。
材料力学之应力状态知识讲解

1
m main =xx 2y
(x 2y)2x2y=
26MPa 96MPa
1=26 MP , a2=0, 3=96 MPa
26
例题 5 图示单元体。
已知: x =-40MPa ,y =60MPa ,xy=-50MPa 。 试求: ef 截面上的应力情况及主应力和主单元体的方位。
(1) 求 ef 截面上的应力
P A
B
C
A A
A
B B C
C
C C
从A、B、C三点截取 7
例题 1 画出如图所示梁 S 截面的应力状态单元体.
F
S平面
l/2 l/2
5 4 3 2
1
8
5
S平面
5
4
4
3
3
2
2
1
1
x1
1
x1 x2
2
x2
2
2
3
3
3
9
例题2 画出如图所示梁的危险截面上, 危险点的应力状态
yy
单元体。
1
4
FS
2
z
3
z2 xT 3
45°
所以 0= -45°与 max 对应
1
(2)求主应力
m m= a in x x 2y(x 2y)2x 2= y
1 = , 2 = 0 , 3 = - 30
§8-3 平面应力状态分析-图解法
一.莫尔圆
将斜截面应力计算公式改写为
= xx 2 2yys=i2n x 2yxcycoo22 s sxysi2n
把上面两式等号两边平方, 然后相加便可消去 , 得
(x 2y)2 2=( x 2y)2x 2y
材料力学8-1-应力状态概述

06
实际应用中的应力分析
机械零件的应力分析
机械零件在制造、使用过程中会受到各种力的作用,产生应力。对机械零件进行 应力分析,可以预测其承载能力和疲劳寿命,避免因应力过大而导致的断裂、变 形等问题。
例如,对发动机中的连杆、曲轴等关键零件进行应力分析,可以优化其结构,提 高发动机性能和可靠性。
晶体点阵在受力过程中发生的畸变。
应力和应变的关系
01
应力和应变之间的关系由胡克定 律描述,即应力与应变成正比, 比例系数为弹性模量。
02
在弹性范围内,材料遵循胡克定 律,即应力与应变成线性关系。
弹性模量
01
弹性模量是描述材料抵抗弹性变形能力的物理量,其
ห้องสมุดไป่ตู้
值取决于材料的种类和温度。
02
弹性模量是材料常数,用于计算在弹性范围内应力与
桥梁和建筑结构的应力分析
桥梁和建筑结构在设计和施工过程中需要进行应力分析,以 确保其安全性和稳定性。通过对桥梁和建筑结构的应力分析 ,可以了解结构的受力状况,优化设计方案,降低施工风险 。
例如,对大型桥梁的桥墩、桥跨结构进行应力分析,可以确 定合理的支撑结构形式和材料,提高桥梁的安全承载能力。
压力容器的应力分析
应力是描述物体内部受力状态 的物理量,与物体受力作用面 积有关。
应力大小与受力作用面积的倒 数成正比,即应力与受力作用 面积的乘积是一个常数。
分类:正应力和剪应力
正应力
垂直于受力作用面的应力,通常表 示为σ。
剪应力
平行于受力作用面的应力,通常表 示为τ。
应力单位
1
应力的国际单位是帕斯卡(Pa),1 Pa = 1 N/m^2。
举例
《应力状态理论》课件

VS
地质工程
在地质工程领域,应力状态理论对于研究 地壳应力分布、地震成因及岩土工程稳定 性等方面具有重要意义。通过将应力状态 理论与地质工程实践相结合,可以更好地 防范地质灾害和提高工程安全性。
感谢您的观看
THANKS
应力状态的重要性
工程应用
应力状态理论在工程领域中具有广泛应用,如结构分析、材料力学、岩石力学等,是解决实际工程问题的重要 基础。
学科发展
应力状态理论的发展推动了相关学科的进步,如断裂力学、损伤力学等,为解决复杂工程问题提供了更全面的 理论支持。
应力状态的历史与发展
早期研究
早期的应力状态研究主要集中在静力学领域,如弹性力学和塑性力学等,主要研究物体在受力作用下的平衡问题 。
多物理场耦合研究
在实际应用中,应力状态往往与温度、磁场等其他物理场存在耦合效应。未来研究应关注多物理场耦 合对应力状态的影响,建立更为完善的理论体系。
应力状态理论在其他领域的应用拓展
生物医学工程
在生物医学工程领域,应力状态理论在 骨骼、牙齿、血管等生物组织的生长、 修复和疾病防治等方面具有重要应用价 值。通过研究生物组织的应力状态,可 以为生物医学工程提供新的设计思路和 治疗方案。
应力的基本性质
应力的基本性质包括对称性、反对称性和转轴性。这 些性质反映了应力分布的内在规律,对于理解物体受 力状态和变形机制具有重要意义。
应力的基本性质包括对称性、反对称性和转轴性。对 称性是指对于任何点,其对称点的应力状态是相同的 ;反对称性则是指对于任何点,其对称点的应力状态 是相反的;转轴性则是指当坐标系旋转时,应力分量 的值会发生变化,但各向同性和各向异性状态不变。 这些性质反映了应力分布的内在规律,对于理解物体 受力状态和变形机制具有重要意义。
塑性变形与轧制技术:应力状态

二、应力图示
2、面应力状态
M1最有利于金属塑性的发挥; M3最不利,但能产生—些很小的塑性变形; M1介于二者之间。 面应力状态在金属压力加工的各种方法中,只见于某些个
别情况,如薄板的冲压、弯曲等。
二、应力图示
3、体应力状态
平辊轧制(- - -)、平锤头锻造(- - -) 、模孔挤压(- - -) 、拉拔 (+ - -)、带张力轧制带钢(+ - -)等都属于体应力状态。
主应力状态
( σ1 σ2 σ3 )
二、应力图示
应力图示:定性的表示所研究的点或物 体的某部分在各主轴方向上有无主应力 存在以及主应力方向如何的图。
表示方法:在三个互相垂直的面上用箭 头定性的表示有无主应力的存在。
主应力分拉应力(箭头向外)和压应力 (箭头向内)。
拉应力易导致金属的破坏;压应力利于 减小或抑制破坏的发生与发展。
二、应力图示
九种可能的应力图示: 线应力状态2种; 平面应力状态3种; 体应力状态4种。
应力状态图示 a—线应力状态;b—面应力状态;c—体应力状态
二、应力图示
1、线应力状态
(1)拉伸 型棒材、薄板拉伸矫直时离夹头稍远一点的部分、拉伸试
样未开始缩颈时的应力状态均为拉应力状态。 (2)压缩 受压表面无摩擦或摩擦很小忽略不计时才出现。
谢谢大家!
一、应力状态
3、应力状态的表示
用主应力来表示应力状态。
三个主应力分别用符号σ1、σ2、σ3表示,
规定σ1是最大主应力,σ3是最小主应力, σ2是中间主应力。按代数值进行排列, σ1>σ2>σ3,如( σ1 σ2 σ3 )。 主应力作用的平面称为主平面。 沿着主应力方向产生的变形称为主变形。
材料力学-弹性力学:什么是应力状态 ?

结束!谢谢!
孙嘉粲 2016年3月
y
x
pz=nσz+lτxz+mτyz
4、空间应力状态求正应力
z
σn
P
o
τn
y
x
σN=lpx+mpy+npz τN=sqrt(px2+py2+pz2-σN2)
参考文献:
【1】徐芝纶. 弹性力学(第4版)上册[M]. 北京: 高等教育出版社, 2006。 【2】闫晓军、胡殿印等编. 弹性力学[M]. 北京:清 华大学出版社, 2015。 【3】戴葆青等编. 材料力学教程[M]. 北京:北京航 空航天大学出版社, 2004。 【4】傅衣铭、熊慧而. 材料力学[M]. 湖南·长沙:湖 南大学出版社, 2007. (完)
3、应力状态的分类—三向应力状态(或空间应力状态)
z
pz P py
ox p
x
y
3、应力状态的分类—三向应力状态(或空间应力状态)
z
pz
y
yz
xz x xy
py
yx p o x
y
zx
zy z
x
4、空间应力状态求正应力
z
xz x xy
y
yz yx p o x zx z
集合
受力构件中某一点处 各不相同截面上的应力变化 情况。
也是就是说:研究一点的应力状态,就是研究
2、应力状态的定义
z σn
n =(A,B,C)
P
τn
o
y
x
2、应力状态的定义——单元体
σ1
σ3 σ2 dx
σ2
σ1
σ3
︑ 应 力 状 态 的 定 义 应 力 分 量
应力状态概念

应力状态概念应力状态概念引言应力是物理学中的一个重要概念,它是描述物体内部相互作用的力的状态。
在工程学中,了解材料的应力状态对于设计和制造可靠的结构至关重要。
因此,本文将介绍应力状态的概念、分类、计算方法以及其在工程学中的应用。
一、应力状态的概念1.1 定义应力是指物体内部各点之间相互作用的力。
在物理学中,它通常表示为σ(sigma),单位为牛顿/平方米(N/m²)或帕斯卡(Pa)。
应力可以分为正应力和剪切应力两种类型。
1.2 正应力正应力是指垂直于截面方向作用的拉伸或压缩效果。
当一个物体受到拉伸或压缩时,会产生正向的内部拉伸或压缩效果。
这种效果被称为正向应力。
1.3 剪切应力剪切应力是指沿截面方向作用于物体上两个平面之间相互滑动产生的效果。
这种效果被称为剪切效果。
二、应力状态分类2.1 一维状态一维状态下,物体只受到沿一个方向的力作用。
这种情况下,应力状态可以被描述为单一的正向应力或压缩应力。
2.2 二维状态在二维状态下,物体受到两个方向的力作用。
这种情况下,应力状态可以被描述为正向应力和剪切应力的组合。
2.3 三维状态在三维状态下,物体受到三个方向的力作用。
这种情况下,应力状态可以被描述为正向应力、剪切应力和法向应力的组合。
三、应力计算方法3.1 应变-位移法在工程学中,常用的计算方法是利用弹性模量和材料的截面面积来计算正向应变和剪切变形。
然后通过材料的弹性模量来计算出相应的正向和剪切应力。
3.2 等效应力法等效应力法是将不同类型的应力转化为等效正向或剪切应力进行计算。
该方法通常适用于复杂载荷条件下的结构分析。
四、应用案例4.1 桥梁结构分析在桥梁工程中,了解桥梁结构所受到的各种载荷条件下的应力状态是至关重要的。
通过应力分析,可以确定桥梁的最大负载能力,以及设计更加安全可靠的结构。
4.2 航空航天工程在航空航天工程中,了解材料应力状态对于设计和制造可靠的飞行器至关重要。
通过应力分析,可以确定各个零部件所受到的最大载荷,并且设计出更加安全可靠的结构。
应力、主应力和应力状态
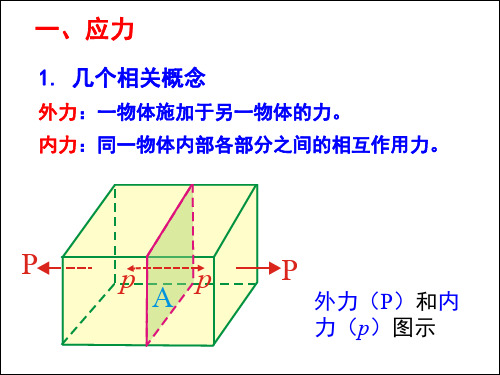
1. 几个相关概念
外力:一物体施加于另一物体的力。 内力:同一物体内部各部分之间的相互作用力。
P
pA p
P
外力(P)和内
力(p)图示
一、应力 1. 几个相关概念
固有内力:物体未受外力时,内部各质点 间已经存在的相互作用力,即自然状态粒 子结合力,它们使各质点处于相对平衡状 态,使物体保持固定的形状。 附加内力:物体受到外力作用时,内部质 点之间的相互作用力相应地改变,内力的 改变量称为附加内力。它阻止物体继续变 形并力图恢复其原来的形状。构造地质学 研究中非常关注附加内力。
一、应力
2. 应力
在物体内部某截面(如图中n截面)上的某点
(如m点)处截取一微小面积F,设其上的作
用力为P,则将 lim P dP P
F0 F dF
P
称为n截面上m点处的应力,
也可以称为m点处n截面上 n
的应力。
m
应力的特点:①是一个矢量;
②与材料内部特定的截面相关
一、应力 2. 应力 应力的分解
应力P 是矢量,可以分解为垂直于截面 n 的正应力或直应力()和平行于截面 n 的剪应力或切应力()。
P
规定:正应力挤压为正, n
m
拉伸为负。
二、 主应力、主方向、主平面与应力状态
应力状态:材料内部某点处所有截面上的应力集合。
为了表述一点处的应力状态,以考察点为中心,截 取一个体积趋于零的立方体,该立方体的六个表面
1
力状态或平面应力状态、
3
三轴应力状态。
2
主应力示意图
上只有正应力而没有剪
2
应力作用。此时的三对
3
正应力称之为3
用1、2和3表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用矩阵表示为
S nx x yx zx l S ny xy y zy m S yz z n nz xz
2013-7-12 14
Lesson 20
应力莫尔(Mohr)圆
z
max
1 2 3
y
O1
O2
O3
3
2 3
2
2
1
1 3
2
x
1 2 3
1 2
2
O1:l=0,m、n 变化(σ,τ)轨迹 O2:m=0,l、n 变化(σ,τ)轨迹 O3:n=0,m、l 变化(σ,τ)轨迹
17
Lesson 20
一点的应力向量不仅取决于该 点的位置,还取决于截面的方位。
2013-7-12
18
Lesson 20
通过变形体内任意点垂直坐标轴截取三个相互垂直的截面 和与坐标轴成任意角度的倾斜截面,这四个截面构成一个 四面体素
2013-7-12 19
Lesson 20
y z n
Sn
Snz B Sny
2013-7-12 34
Lesson 20
变形体内任意点的应力状态可以通过该点且平 行于坐标面的三个微分面上的九个应力分量来 表示。
x
y z
xy yx yz zy
zx xz
根据这九个应力分量的特点,我们可以采用一 种新的方法来表示它们,如下表所示。
一点的应力向量不仅取决于该 点的位置,还取决于截面的方位。
2013-7-12
12
Lesson 20
如果截面的法向与 某坐标轴重合,则 该截面上的切应力 还可以沿其余两坐 标轴分解。
2013-7-12
13
Lesson 20
对于包含某 点的微六面 体体素上, 每一面素上 作用有三个 应力分量, 其中一个正 应力,两个 切应力。
2013-7-12
35
Lesson 20
x 面
y 面
z 面 x方向 y方向
x yx zx xy y zy xz yz z
z方向
2013-7-12
36
Lesson 20
去掉表中虚线,则变成矩阵,并可用一个符 号表示该矩阵。
4
Lesson 20
重力
体积力
惯性力
电磁力
……
特点:分布在物体体积的外力,它作 用在物体内部的每一个质点上
外力
作用力(主动力)
表面力
约束反力
正压力
特点:分布在物 体表面的外力
摩擦力
2013-7-12 5
Lesson 20
塑性加工时,由于体积力与加工中的作用力 比较起来很小,在实际工程计算中一般可以 忽略。但在高速加工时,金属塑性流动的惯 性力应该考虑。 一般塑性加工只分析作用力、正压力、摩擦 力的作用状态。
塑性力学
第二讲 Lesson Two
Lesson 20
塑性力学主要学习内容
应力状态分析 应变状态分析 变形力学方程 滑移线场理论 工程法 上界定理
塑性加工力学 基础部分
塑性加工力学问题 求解方法部分
2013-7-12
2
第二讲 应力状态分析 Lesson Two
Lesson 20
其中li、mi、ni为新坐标轴在原坐标系下的方向余弦。
x x' y' z'
2013-7-12
y m1 m2 m3
z n1 n2 n3
32
l1 l2 l3
Lesson 20
y
y'
uy' uy o ux' u
ux
x'
2013-7-12 33
Lesson 20
10.3.2 应力张量
在斜面上的应力分析中,我们得到
Y 0
Z 0
在x方向: S nx ds x ds l yx ds m zx ds n 0 在y方向: Sny ds xy ds l y ds m zy ds n 0 在z方向: Snz ds xz ds l yz ds m z ds n 0
2013-7-12 23
Lesson 20
把微分斜面上的合应力Sn,向法线n方向投影,便可求 出微分斜面上的正应力,或将Snx、Sny、Snz分别投影到 法线n上,也同样得到微分斜面上的正应力,即
n S nx l S ny m S nz n
将Snx、Sny、Snz带入上式得
C
n
n x xy yx
o
Snx
xz
zx
ds
y
yz zy
z
A
x
2013-7-12
20
Lesson 20
该微分斜面面积为ds,外法线方向的方向余弦 为: cos(n,x)=l 、cos(n,y)=m 、cos(n,z)=n 三个垂直坐标面的面积可以表示为:
SOBC S ABC cosn, x ds l
而 所以
2 2 Sn 12l 2 2 m2 3 n2
1 2 2 l 2m2 2 3 2 m2n2 3 1 2 n2l 2
2 n
2013-7-12 25
Lesson 20
综上可知,变形体内任意点的应力状态可以通 过该点且平行于坐标面的三个微分面上的九个 应力分量来表示。
650 40 350 5 n S 14 3 3 9 3
2 2 n 2
2013-7-12
31
Lesson 20
应力坐标变换公式
x yx zx l1 xy y zy l2 yz z l3 xz m1 m2 m3 n1 x yx zx l1 n2 xy y zy m1 n3 xz yz z n1 l2 m2 n2 l3 m3 n3
2013-7-12
6
Lesson 20
2013-7-12
7
Lesson 20
作用力 塑性加工设备的可动工具部分对工件 所作用的力。又称主动力。 可以实测或理论计 算,用于验算设备强度和设备功率。 正压力 沿工具和工件接触面法向阻碍工件整 体移动或金属流动的力,其方向垂直于接触面, 并指向工件。 摩擦力 沿工具和工件接触面切向阻碍金属流 动的力,其方向平行于接触面,并与金属质点 流动方向或流动趋势相反。
2013-7-12
28
Lesson 20
课堂练习
已知变形体某点应力状态如图所示,当斜面法 线方向与三个坐标轴夹角余弦 l m n 1 3 时,求该斜面上的全应力S,全应力在坐标轴 上的分量Sx、Sy、Sz及斜面上的法线应力n和切 应力n。
2013-7-12
29
Lesson 20
解:首先确定各应力分量x=10、 y=10、 z=0、 xy=yx= 5、 xz=zx=5、 yz=zy=0 (单位MPa) 。由
1 1 1 5 5 3 3 3 1 1 1 S y xyl y m zy n 5 10 0 3 3 3 1 1 1 S z xzl yz m z n 5 0 0 3 3 3 S x xl yxm zx n 10
2013-7-12
max
1 3
2
15
Lesson 20
2013-7-12
16
Lesson 20
10.2 斜面上任一点应力状态分析
要想了解一点的应力状态必须知道过该点任 意截面上的应力分布。但是过该点的截面有 无穷多个,我们没有办法一一列举。为此必 须采用其他方式进行描述。
2013-7-12
2013-7-12 22
Lesson 20
整理后可得方程
S nx x l yx m zx n S ny xy l y m zy n S nz xz l yz m z n
(※)
用矩阵表示为
S nx x yx zx l S ny xy y zy m S yz z n nz xz
主要内容
Main Content
应力状态基本概念 斜面上任一点应力状态分析 应力张量 主应力及主切应力
2013-7-12
3
Lesson 20
基本假设
变形体是连续的,不存在微观结构,是宏观 的,材料是均匀的,各向同性。 变形体性能及变形行为存在随机现象,性能 是确定的。
2013-7-12
n x l 2 y m2 z n 2 2 xylm 2 yz mn 2 zx nl
微分面上的剪应力为
2 2 2 n Sn n
2013-7-12
24
Lesson 20
若坐标轴为主轴,则与坐标轴垂直的截面上的切应 力为零,则由 n x l 2 y m2 z n 2 2 xylm 2 yz mn 2 zx nl 可得 n 1l 2 2m2 3n2
SOAC S ABC cosn, y ds m
n z
SOBA S ABC cosn, z ds n
