正交检验的极差分析和方差分析 ppt课件
正交检验的极差分析和方差分析

为满足此要求,一般考虑用最小偏差平方和原则, 也就是使观测值与真值的偏差平方和达到最小.
4.2.2 参数点估计
由(4-4)可知,上述偏差平方和 令下列各偏导数为零
(i=1,2,…,k)
4.2.2 参数点估计
由
解得 由
解得
(4-7) (4-8)
4.2.2 参数点估计
并由此得 的估计量
至此,求得参数 的估计量
容易看出,自由度之间也有类似于分解定理的关系
(4-13)
4.2.4 显著性检验
参数 假设 检验 的假 设条 件
观测值(i=1,2,…,k;j=1,2,…,m) 相互独立
在水平Ai条件下, Yij(j=1,2,…m) 服从正态分布N
4.2.4 显著性检验
要判断在因素A的k个水平条件下真值之间是否 有显著性差异,
(4-9)
4.2.2 参数点估计
按照上述原则求参数估计量的方法称为最小二
乘法,
称为最小二乘估计量.
我们还可以证明 。
分别是参数
的无偏估计量
将 和 分别用它们的估计量代替,可以得到试验 误差 的估计量 ,
(4-10)
4.2.3 分解定理 自由度
为了由观测值的偏差中分析出各水平的效应,我们 研究三种偏差: , 和 .
8.2.1 数学模型和数据结构
为了便于比较和分析因素A的水平Ai对指标影响 的大小,通常把 再分解为
(i=1,2,…,k)
(4-5)
其中,
称为一般平均(Grand Mean),它是比
较作用大小的一个基点;
4.2.1 数学模型和数据结构
并且称 为第i个水平Ai的效应.它表示水平的真值比一般
水平差多少。满足约束条件
正交检验的极差分析和方差分析教材

正交检验的极差分析和方差分析教材正交检验的极差分析和方差分析引言:正交检验的极差分析和方差分析是统计学中常用的两种分析方法。
它们被广泛应用于实验设计和数据分析中,可以帮助我们判断变量之间的差异是否显著,并且确定是哪些因素对变量影响最为显著。
本文将重点介绍正交检验的极差分析和方差分析的基本原理和应用方法。
一、正交检验的极差分析1.1 基本原理正交检验的极差分析是通过观察不同水平的自变量对因变量的影响,推断不同水平之间的差异是否显著的一种方法。
它基于方差分析的原理,通过计算不同水平之间的平均差和标准差,判断不同水平之间的差异是否超过了预期的随机误差范围,从而得出结论。
1.2 应用方法首先,确定研究的自变量和因变量,并确定自变量的水平。
然后,通过随机抽样的方式获取样本数据,并计算每个水平下的极差。
接下来,计算整体样本数据的均值和方差,以及不同水平之间的平均差和标准差。
最后,使用统计方法,比较差异是否显著,并进一步推断不同水平之间的差异。
1.3 实例分析以某品牌洗衣机的不同水平温度对洗涤效果(洗涤时间)为例,通过极差分析探究不同水平温度下洗涤效果是否存在显著差异。
首先,选择3个不同水平的温度:40℃、60℃和80℃。
然后,使用这3个水平的温度进行多次洗涤实验,每次实验记录洗涤时间。
接下来,计算每个水平下的极差,并计算整体样本数据的均值和方差。
最后,使用正交检验的极差分析方法,比较不同水平之间的差异是否显著。
二、方差分析2.1 基本原理方差分析是通过比较不同组之间的方差大小,来判断不同组之间的差异是否显著的一种方法。
它基于总体方差和组内方差之间的关系,通过计算F统计量来比较差异是否显著。
2.2 应用方法首先,确定研究的自变量和因变量,并确定不同组别。
然后,通过随机抽样的方式获取样本数据,并计算每个组别的均值和方差。
接下来,计算总体样本数据的均值和方差,以及组内方差和组间方差。
最后,使用统计方法,计算F统计量,并比较差异是否显著。
第章正交试验设计的极差分析

第章正交试验设计的极差分析集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]第7章 正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
单指标正交试验设计及其极差分析极差分析法简称R 法。
它包括计算和判断两个步骤,其内容如图7-1所示。
值。
最优组合R j =max(jm j j K K K ,,,21 )-min(jm j j K K K ,,,21 )R j 反映了第j 列因素的水平变动时,试验指标的变动幅度。
R j 越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j 的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6-2来说明单指标正交试验结果的极差分析方法。
一、 确定因素的优水平和最优水平组合例6-2 为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6-2中,不考虑因素间的交互作用(因例6-2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6-5所示,试验方案则示于表6-6中。
试验结果的极差分析过程,如表7-1所示.表6-4 因素水平表表6-6 试验方案及结果试验指标为液化率,用y i表示,列于表6-6和表7-1的最后一列。
表7-1 试验方案及结果分析计算示例:因素A 的第1水平A 1所对应的试验指标之和及其平均值分别为:K A1=y 1+y 2+y 3=0+17+24=41,=1A K 31K A1=同理,对因素A 的第2水平A 2和第3水平A 3,有K A2=y 4+y 5+y 6=12+47+28=87,=2A K 31K A2=29K A3=y 7+y 8+y 9=1+18+42=61,=3A K 31K A3=由表7-1或表6-6可以看出,考察因素A 进行的三组试验中(A 1,A 2,A 3),B 、C 、D 各水平都只出现了一次,且由于B 、C 、D 间无交互作用,所以B 、C 、D 因素的各水平的不同组合对试验指标无影响,因此,对A 1、A 2和A 3来说,三组试验的试验条件是完全一样的。
正交检验的极差分析和方差分析讲课讲稿

按照上述原则求参数估计量的方法称为最小二
乘法,
,
i称,为最i 小二乘估计量.
我们还可以证明 , i分, 别i 是参数
量。
的,无i ,偏i估计
将和 分i 别用它们的估计量代替,可以得到试验 误差 的 ij估计量 , e ij
第四章 方差分析
4.2.2 参数点估计
由
解得 由
解得
S 2 (Y i j) i0
ˆ 1 km
Yij (4Y-7)
S
i
m
2 (Yij
j1
i)0
ˆi
1m mj1Yij
Y(4i-8Y)
第四章 方差分析
4.2.2 参数点估计
并由此得 的i 估计量
ˆi ˆˆi Yi
至此,求得参数 ,的i ,估i计量
F型
9.3
8.7
7.2
10.1
第四章 方差分析
4.1 方差分析的基本概念和原理
研究的指标:维修时间记作Y, Y~N(,2)
控制因素是生产线的型号,分为6个水平即A,
B,C,D,E,F,每个水平对应一个总体Yi(i=1,2,…,
6)。
第四章 方差分析
4.1 方差分析的基本概念和原理
现在的试验就是进行调查,每种型号调查4台,相当于
第四章 方差分析
4.2 单因素试验的方差分析
➢ 数学模型和数据结构 ➢ 参数点估计 ➢ 分解定理 自由度 ➢ 显著性检验 ➢ 多重分布与区间估计
第四章 方差分析
4.2.1 数学模型和数据结构
在单因素试验中,为了考察因素A的k个水平A1, A2,…,Ak对Y的影响(如k种型号对维修时间的影响), 设想在固定的条件Ai下作试验.所有可能的试验结果 组成一个总体Yi,它是一个随机变量.可以把它分解为
高级篇 第二章 正交试验设计及统计分析方差分析PPT课件

m个,每个水平作r次重复r=n/m。
当m=2时, SjS = n 1 ( K 1-jK 2) j2( j= 1, 2, ., ..k)
总自由度:
dfT=n-1
因素自由度:
df= j m1 ,m为因素水平个
3.2.2 不考虑交互作用等水平正交试验方差分析
例:自溶酵母提取物是一种多用途食品配料。为探 讨啤酒酵母的最适自溶条件,安排三因素三水平正 交试验。试验指标为自溶液中蛋白质含量(%)。 试验因素水平表见表10-22,试验方案及结果分 析见表10-23。试对试验结果进行方差分析。
(2)自由度分解:
dTfd因 f 素 d空 f 列 误(列(
(3)方差:M因 S= 素Sd因 因 Sf 素 素 , M误 S= 差Sd误 误 Sf 差 差
(4)构造F统计量:
F因素=
MS因素 MS误差
(5)列方差分析表,作F检验
若计算出的F值F0>Fa,则拒绝原假设,认为 该因素或交互作用对试验结果有显著影响;若 F0≼Fa,则认为该因素或交互作用对试验结果 无显著影响。
1 2 3 3 1 2 2 3 1 20.74 21.87 22.97 430.15 478.30 527.62
试验结果 yi 6.25 4.97 4.54 7.53 5.54 5.5 11.4 10.9 8.95
T65.58
(1)计算
计算各列各水平的K值
计算各列各水平对应数据之和K1j、K2j、K3j及其平
3.2.1 正交试验结果的方差分析
方差分析基本思想是将数据的总变异分解成因 素引起的变异和误差引起的变异两部分,构造F统 计量,作F检验,即可判断因素作用是否显著。
第7章-正交试验设计的极差分析

第7章正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
7.1单指标正交试验设计及其极差分析极差分析法简称R法。
它包括计算和判断两个步骤,其内容如图7-1所示。
图7-1 R法示意图图中,K m为第j列因素m水平所对应的试验指标和,K jm为K m的平均值。
由K m 的大小可以判断j因素的优水平和各因素的水平组合,即最优组合。
R为第j 列因素的极差,即第j列因素各水平下平均指标值的最大值与最小值之差:R二max(心,耳,,爲)-min(心,兀,,爲)R反映了第j列因素的水平变动时,试验指标的变动幅度。
R越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6 - 2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6 -2中,不考虑因素间的交互作用(因例6 - 2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6 - 5所示,试验方案则示于表6 - 6中。
试验结果的极差分析过程,如表7 - 1所示.表6-4 因素水平表表6-6 试验方案及结果试验指标为液化率,用y表示,列于表6 - 6和表7 - 1的最后一一表7-1试验方案及结果分析计算示例:因素A的第1水平A i所对应的试验指标之和及其平均值分别为:1K\i=y i+y2+y3=0+17+24=41, K AI = — K Ai=13.73同理,对因素A的第2水平A和第3水平A,有1K A2=y4+y5+y6=12+47+28=87 K A2=-K A2=2931K A3=y7+y8+y9=1 + 18+42=61 , K A3K A3=20.33由表7 - 1或表6 - 6可以看出,考察因素A进行的三组试验中(A,A2,A3), B、C D各水平都只出现了一次,且由于B C、D间无交互作用,所以B、C D因素的各水平的不同组合对试验指标无影响,因此,对A、A和A来说,三组试验的试验条件是完全一样的。
正交检验的极差分析和方差分析(教学课堂)

(Yij i )2
(Yij i )2
i1 j1
令下列各偏导数为零
S 0,
S 0
i
(i=1,2,…,k)
特选课堂
2
第四章 方差分析
4.1 方差分析的基本概念和原理
表 4-1 对6种型号生产线维修时数的调查结果
序号 型号
A型 B型 C型 D型 E型 F型
1
9.5 4.3 6.5 6.1 10.0 9.3
2
8.8 7.8 8.3 7.3 4.8 8.7
特选课堂
3
11.4 3.2 8.6 4.2 5.4 7.2
第四章 方差分析
4.2.1 数学模型和数据结构
其中:
i 纯属Ai作用的结果,称为在Ai条件下Yi的真值(也称为
在Ai条件下Yi的理论平均). i是实验误差(也称为随机误差)。
i ~ N (0, 2 ) (4-2)
Yi ~ N (i , 2 )
其中, 和 都是未知参数(i=1,2,…,k).
i 2
i 1
Mean),它是比
较作用大小的一个基点;
特选课堂
14
第四章 方差分析
4.2.1 数学模型和数据结构
并且称
i i
为第i个水平Ai的效应.它表示水平的真值比一般
水平差多少。满足约束条件
1 2 k 0
(4-6)
可得
Yij i ij ;
i 0
i=1,2,…,k ;j=1,2,…,m
…
Ykj
…
Ykm
特选课堂
合计
T1 T2
…
Ti
…
Tk
平均
Y1 Y2
…
Yi
第7章 正交试验设计的极差分析资料

第7章正交试验设计的极差分析第7章 正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
7.1 单指标正交试验设计及其极差分析极差分析法简称R 法。
它包括计算和判断两个步骤,其内容如图7-1所示。
图7-1 R 法示意图图中,K jm 为第j 列因素m 水平所对应的试验指标和,K jm 为K jm 的平均值。
由K jm 的大小可以判断j 因素的优水平和各因素的水平组合,即最优组合。
R j 为第j 列因素的极差,即第j 列因素各水平下平均指标值的最大值与最小值之差:R j =max(jm j j K K K ,,,21 )-min(jm j j K K K ,,,21 )R j反映了第j列因素的水平变动时,试验指标的变动幅度。
R j 越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6-2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2 为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6-2中,不考虑因素间的交互作用(因例6-2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6-5所示,试验方案则示于表6-6中。
试验结果的极差分析过程,如表7-1所示.表6-4 因素水平表表6-6 试验方案及结果试验指标为液化率,用y i表示,列于表6-6和表7-1的最后一列。
表7-1 试验方案及结果分析计算示例:因素A 的第1水平A 1所对应的试验指标之和及其平均值分别为:K A1=y 1+y 2+y 3=0+17+24=41, 1A K 31K A1=13.7同理,对因素A 的第2水平A 2和第3水平A 3,有K A2=y 4+y 5+y 6=12+47+28=87, 2A K 31K A2=29 K A3=y 7+y 8+y 9=1+18+42=61, 3A K 31K A3=20.3由表7-1或表6-6可以看出,考察因素A 进行的三组试验中(A 1,A 2,A 3),B 、C 、D 各水平都只出现了一次,且由于B 、C 、D 间无交互作用,所以B 、C 、D 因素的各水平的不同组合对试验指标无影响,因此,对A 1、A 2和A 3来说,三组试验的试验条件是完全一样的。
正交试验中的极差分析与方差分析

因素 4 回火温 $ 保温时 %工体质 试验指标
试验
度 (!) 间(min) 量( kg) (弹性)
1
440
3
7.5
2
440
4
9.0
3
440
5
10.5
4
460
3
9.0
5
460
4
10.5
6
460
5
7.5
7
500
3
10.5
8
500
4
7.5
9
500
5
9.0
步骤3 :试验并列出试验结果分析计算表. 列 出 方 案 表 之 后 ,就可以根 据 方 案 表 进 行 试 验 .试 验 过 程 中 ,我们应特别注意:试验的次序尽可能随机化 以减少因素间相互影响造成较大的误差;除了我们需要 考 查 的 因 素 ,其 他 的 试 验 条 件 在 整 个 实 验 过 程 中 尽 量 保 持 相 同 ,增大结论的可靠性;准确记录好每一次试验的 数据. 试 验结束后,对试验数据进行简单的分析计算,列 出实验结果分析表,详见表3.
表 1 因素水平表
水平 " 回40
2
460
3
500
#保温时间 (min) 3 4 5
$工件质量 (kg) 7.5 9.0 10!5
高中 版 十 . ?龙 * 7 31
数坛 在线
教育纵横
2017年 5 月
步骤2 :设计试验方案. 根 据 已 经 制 作 完 成 的 因 素 水 平 表 ,考 虑 试 验 条 件 和 实际的可操作性,选择一张适合的三水平正交表(" 9(34), 因这张表最多可以考查4个 因素对试验结果的影响,而 此 次 试 验 我 们 只 考 查 3个 因 素 对 试 验 的 影 响 ,所以我们 可任意选择表中的3列进行表头设计并制作试验方案表 安 排 试 验 ,见 表 2.
第7章-正交试验设计的极差分析
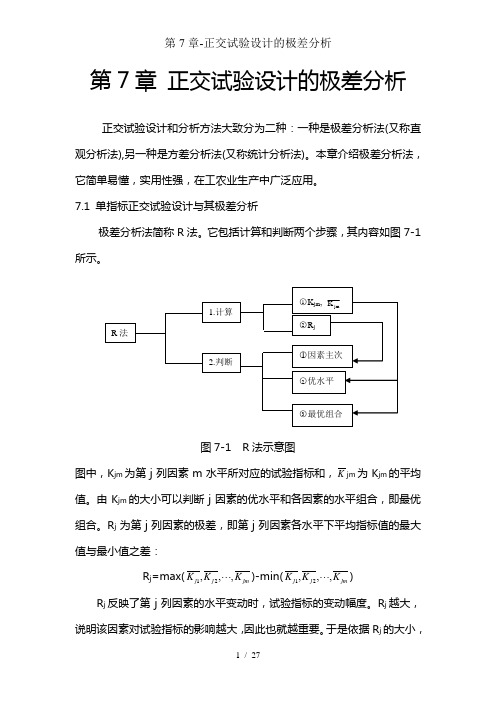
第7章 正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
7.1 单指标正交试验设计与其极差分析极差分析法简称R 法。
它包括计算和判断两个步骤,其内容如图7-1所示。
图7-1 R 法示意图图中,K jm 为第j 列因素m 水平所对应的试验指标和,K jm 为K jm 的平均值。
由K jm 的大小可以判断j 因素的优水平和各因素的水平组合,即最优组合。
R j 为第j 列因素的极差,即第j 列因素各水平下平均指标值的最大值与最小值之差:R j =max(jm j j K K K ,,,21 )-min(jm j j K K K ,,,21 )R j 反映了第j 列因素的水平变动时,试验指标的变动幅度。
R j 越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j 的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6-2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2 为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6-2中,不考虑因素间的交互作用(因例6-2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6-5所示,试验方案则示于表6-6中。
试验结果的极差分析过程,如表7-1所示.表6-4 因素水平表酶解温度(C)C表6-6 试验方案与结果试验指标为液化率,用y i表示,列于表6-6和表7-1的最后一列。
表7-1 试验方案与结果分析=189.0计算示例:因素A 的第1水平A 1所对应的试验指标之和与其平均值分别为:K A1=y 1+y 2+y 3=0+17+24=41,=1A K 31K A1=13.7 同理,对因素A 的第2水平A 2和第3水平A 3,有K A2=y 4+y 5+y 6=12+47+28=87,=2A K 31K A2=29 K A3=y 7+y 8+y 9=1+18+42=61,=3A K 31K A3=20.3 由表7-1或表6-6可以看出,考察因素A 进行的三组试验中(A 1,A 2,A 3),B 、C 、D 各水平都只出现了一次,且由于B 、C 、D 间无交互作用,所以B 、C 、D 因素的各水平的不同组合对试验指标无影响,因此,对A 1、A 2和A 3来说,三组试验的试验条件是完全一样的。
交检验的极差分析和方差分析

2 保持设备和工具清洁
定期对检验设备和工具进行清洁和维护,确保其准确性 和可靠性。
3 准确记录检验结果
对检验结果进行详细记录,包括样本编号、检验项目、 检验结果等,以便后续分析和追溯。
4 及时处理异常情况
在检验过程中发现任何异常情况,应立即停止检验并报 告相关人员进行处理。
05
极差和方差在交检验中应用案例
假设检验
方差分析可用于假设检验,比较不同组数据的方差是否有显著差 异,以判断因素对结果是否有显著影响。
优缺点分析
01
优点
02
方差分析能够量化数据的离散程度,提供客观的评价标准。
03
通过方差分析,可以发现过程中的异常波动,及时采取措施 进行改进。
优缺点分析
• 方差分析适用于各种类型的数据,具有广 泛的应用范围。
3
过程能力分析
极差可用于计算过程能力指数$C_{pk}$, 该指数反映了过程满足产品质量要求的能 力。较小的极差意味着过程波动较小,过 程能力较强。
优缺点分析
01
优点
02
计算简便:极差的计算非常简单,只需找出数据中的最大 值和最小值。
03
对异常值敏感:极差能够反映数据中的异常波动,有助于 及时发现潜在问题。
优缺点分析
01
缺点
02
方差分析对数据的要求较高,需要满足一定的前提条件,如正态分布、 方差齐性等。
03
在实际应用中,方差的计算可能受到异常值的影响,导致结果不准确。
04
方差分析只能提供数据离散程度的描述,不能提供具体的改进方向或 措施。
04
交检验流程与操作规范
交检验前准备工作
确定检验目的和对象
极差在质量控制中应用
极差分析方差分析假设检验

用).正交表的表示方法:一般的正交表记为L n (M k ),n 是表的行数, 也就是要安排的 试验次数;k 是表中的列数,表示因素的个数;m 是各因素 的水平数; 常见的正交表:2水平的有 L 4(23), L 8(27), L 12(211), L 16(215)等; 3水平的有 L 9(34), L 27(313)等;4水平的有 L 15(45); 5水平的有 L 25(56);利用正交表进行试验的步骤:1) 明确试验目的,确定要考核的试验指标;2) 根据试验目的,确定要考察的因素和各因素的水平;要通过对实际问题的具体分析选出主要因素,略去次要因素;3) 选用合适的正交表,安排试验计划;4) 根据安排的计划进行试验,测定各试验指标;5) 对试验结果进行计算分析,得出合理的结论并验证。
列号试验号123411111212223133342123解:如果每个因素的每个水平都互相搭配着进行全面试验,必 须做试验33=27次。
现在我们使用L 9(34)正交表来安排试验。
我们按选定的9个试验进行试验,并将每次试验测得的铁水温度记录下来:为了便于分析计算,我们把这些温度值和正交表列在一起组成一个新表。
另外,由于铁水温度数值较大,我们把每一个铁水温度的值都减去1350,得到9个较小的数,这样使计算简单。
极差分析方法某炼铁厂为提高铁水温度,需要通过试验选择最好的生产方案 经初步分析,主要有3个因素影响铁水温度,它们是焦比、风 压和底焦高度, 每个因素都 考虑3个水平,具体情况见表。
问 对这3个因素的3个水平如何安排,才能获得最高的铁水温度?因素重要性顺序:级差越大,影响越大。
实验指标:铁水温度越高越好查找试验结果最高的水平。
最终优化方案:C2A3B29组实验中C因素为2水平的是第2、4、9组。
第2、4、9组中只有第9组的A因素为第3水平。
但是B因素也为3水平,并非最优方案。
尽管如此,第9组温度仍然是所有实验结果里最好的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ykj
… M 合计 平均
…
Y1m
T1
Y1
…
Y2m
T2
…
…
…
Y2
…
…
Yim
Ti
Yi
…
…
…
…
…
Ykm
Tk
Y14k
第四章 方差分析
4.2.1 数学模型和数据结构
表中:
Yi m1(i=jm11,2Y,i…j ,k)
(4-3)
Yij表示在Ai条件下第j次试验的结果,用式子表示就是
Yij (ii=1,2i,j…,k j=1,2,…,m) (4-4)
第四章 方差分析
4.1 方差分析的基本概念和原理
表 4-1 对6种型号生产线维修时数的调查结果
序号
1
2
3
4
型号
A型Βιβλιοθήκη 9.58.811.4
7.8
B型
4.3
7.8
3.2
6.5
C型
6.5
8.3
8.6
8.2
D型
6.1
7.3
4.2
4.1
E型
10.0
4.8
5.4
9.6
F型
9.3
8.7
7.2
10.1
2020/11/13
两部分
Yi i i
(4-1)
2020/11/13
12
第四章 方差分析
4.2.1 数学模型和数据结构
其中:
纯i 属Ai作用的结果,称为在Ai条件下Yi的真值(也称为
在Ai条件下Yi的理论平均). 是i 实验误差(也称为随机误差)。
i ~N(0,2) (4-2)
Yi ~N(i,2)
其中, 和 都是未知参数(i=1,2,…,k).
y 1与 y,2
C
2 6
与y 1
,…y 3
与
y, 1
与y 6 ,…y ,2
与y 3 ,共有y(5
1y 56 )对。
2020/11/13
8
第四章 方差分析
4.1 方差分析的基本概念和原理
上 述 方 法 存 在 的 问 题
2020/11/13
工作量大 置信度低
将这15对平均数一一进 行比较检验
即使每对都进行了比较,并 且都以0.95的置信度得出 每对均值都相等的结论,但 是由此要得出这6个型号的 维修时间的均值都相等。
2020/11/13
10
第四章 方差分析
4.2 单因素试验的方差分析
➢ 数学模型和数据结构 ➢ 参数点估计 ➢ 分解定理 自由度 ➢ 显著性检验 ➢ 多重分布与区间估计
2020/11/13
11
第四章 方差分析
4.2.1 数学模型和数据结构
在单因素试验中,为了考察因素A的k个水平A1, A2,…,Ak对Y的影响(如k种型号对维修时间的影响), 设想在固定的条件Ai下作试验.所有可能的试验结果 组成一个总体Yi,它是一个随机变量.可以把它分解为
第四章 方差分析
➢方差分析解决的主要问题是什么? ➢单因素方差分析与双因素方差分析
原理的相同点与不同点? ➢正交实验设计的基本原理是什么?
2020/11/13
1
第四章 方差分析
4.1 方差分析的基本概念和原理
[例题] 某公司计划引进一条生产线.为了选择一条质量优
良的生产线以减少日后的维修问题,他们对6种型号的 生产线作了初步调查,每种型号调查4条,结果列于表81。这些结果表示每个型号的生产线上个月维修的小 时数。试问由此结果能否判定由于生产线型号不同而 造成它们在维修时间方面有显著差异?
5
第四章 方差分析
4.1 方差分析的基本概念和原理
研究的指标:维修时间记作Y, Y~N(,2)
控制因素是生产线的型号,分为6个水平即A,
B,C,D,E,F,每个水平对应一个总体Yi(i=1,2,…,
6)。
2020/11/13
6
第四章 方差分析
4.1 方差分析的基本概念和原理
现在的试验就是进行调查,每种型号调查4台,相当于
2020/11/13
2
精品资料
第四章 方差分析
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
这一结论的置信度仅是
(0.95)150.4632
9
第四章 方差分析
4.1 方差分析的基本概念和原理
方差分析的基本原理 :
(1)将数据总的偏差平方和按照产生的原因分解成:
(总的偏差平方和)=
(由因素水平引起的偏差平方和)+(试验误差 平方和)
(2)上式右边两个平方和的相对大小可以说明因素的不
同水平是否使得各型号的平均维修时间产生显著性差 异,为此需要进行适当的统计假设检验.
注意:
每次试验结果只能得到Yij,而(4-4)式中的 和i 都 ij 不能
直接观测到。
2020/11/13
15
第四章 方差分析
8.2.1 数学模型和数据结构
为了便于比较和分析因素A的水平Ai对指标影响
的大小,通常把 再i 分解为
i (i=1,2,i…,k)
(4-5)
其中,
1 k
k
称为i 一般平均(Grand
的无偏 2估计量.
须使参数 ,1,2,的..估..k,计值能使在水平Ai下求得
每个总体中抽取一个容量为4的样本,得到的数据记作yij(i
=1,2,…,6;j=1,2,3,4),即为下表数据。
计算各样本平均数 y 如i 下:
型号
yi
表 8-2
A
B
C
D
E
F
9.4 5.5 7.9 5.4 7.5 8.8
2020/11/13
7
第四章 方差分析
4.1 方差分析的基本概念和原理
两个总体平均值比较的检验法 把样本平均数两两组成对:
17
第四章 方差分析
4.2.1 数学模型和数据结构
要 解 决 的 问 题
2020/11/13
找出参数 ,1,2,....k, 和的2 估计量
分析观测值的偏差
检验各水平效应 1,2,...,k 有无显著差异
18
第四章 方差分析
4.2.2 参数点估计
用最小二乘法求参数 ,1,2,的..估..k,计量,然后寻求
i 1
Mean),它是比
较作用大小的一个基点;
2020/11/13
16
第四章 方差分析
4.2.1 数学模型和数据结构
并且称
i i
为第i个水平Ai的效应.它表示水平的真值比一般
水平差多少。满足约束条件
12( 4 -6k)0
可得
Yiji ij;
i 0
i=1,2,…,k ;j=1,2,…,m
2020/11/13
i 2
2020/11/13
13
第四章 方差分析
4.2.1 数学模型和数据结构
假定在水平Ai下重复做m次试验,得到观测值
Yi1,Yi2,...Y,im
1
2
A1
Y11
Y12
A2
Y21
Y22
…
…
…
Ai
Yi1
Yi2
…
…
…
Ak
Yk1
Yk2
2020/11/13
表 4-3
…
j
…
Y1j
…
Y2j
…
…
…
Yij
…
…
…
