第二章 控制系统状态空间表达式的解
合集下载
现代控制理论_控制系统状态空间表达式的解
第二章 控制系统状态空 间表达式的解
2.1.线性定常连续系统状态方程的解
1.齐次状态方程的解表示了系统在初始条件作用 下的自由运动，又称为零输入解；
2.系统状态的变化实质上是从初始状态开始的状 态转移，而转移规律取决于 eAt ，eA(t-t ) 故称其 为状态转移矩阵.一般用 ( t ) e At 来表示。 A( t t ) ( t t0 ) e 3.求齐次状态解的关键是求转移矩阵 eAt
At
x( t ) e
x(t0 ) e A Bu( )d
t0
t t0
t
x( t ) e
A( t t0 )
x(t0 ) e A( t ) Bu( )d
t
也就是 x(t ) (t t0 ) x(t0 ) t (t )Bu( )d
d At At e x ( t ) e Bu dt
e At Ax x
在区间[t0,t]上积分
e
At
x( t )
t t0
e A Bu( )d
t0
t
e
即
e
At
x( t )
t t0
e A Bu( )d
t0
At0
t
s 3 1 1 2 s s s 3 2
s 1 s 2 s s 1 s 2 1
s3 s 1 s 2 2 s 1 s 2
s 1 ( sI A) 1 s 2
Φ(t ) L
1
sI A
1
(1 t )e t t te
2.1.线性定常连续系统状态方程的解
1.齐次状态方程的解表示了系统在初始条件作用 下的自由运动，又称为零输入解；
2.系统状态的变化实质上是从初始状态开始的状 态转移，而转移规律取决于 eAt ，eA(t-t ) 故称其 为状态转移矩阵.一般用 ( t ) e At 来表示。 A( t t ) ( t t0 ) e 3.求齐次状态解的关键是求转移矩阵 eAt
At
x( t ) e
x(t0 ) e A Bu( )d
t0
t t0
t
x( t ) e
A( t t0 )
x(t0 ) e A( t ) Bu( )d
t
也就是 x(t ) (t t0 ) x(t0 ) t (t )Bu( )d
d At At e x ( t ) e Bu dt
e At Ax x
在区间[t0,t]上积分
e
At
x( t )
t t0
e A Bu( )d
t0
t
e
即
e
At
x( t )
t t0
e A Bu( )d
t0
At0
t
s 3 1 1 2 s s s 3 2
s 1 s 2 s s 1 s 2 1
s3 s 1 s 2 2 s 1 s 2
s 1 ( sI A) 1 s 2
Φ(t ) L
1
sI A
1
(1 t )e t t te
状态空间表达式的解
2020/6/4
***状态转移矩阵的基本性质**** 性质1：组合性质
e A e A t e A ( t ) ( t) () ( t )
性质2： e A ( t t) e 0 I ( t t ) ( t ) ( t ) I
性质3： 转移矩阵的逆意味着时间的逆转
e A 1 t e A t ( t) 1 ( t)
【例2－8】求下列状态方程在单位阶跃函数作用下的输出：
解：根据上面的式子
其中
， K=1
2020/6/4
在例2－6中已求的：
2020/6/4
其状态轨迹图可以MABLAB方便地绘出，如图所示： %Example Example 2-8 grid; xlabel('时间轴'); ylabel('x代表x1，----*代表x2'); t=0:0.1:10; x1=0.5-exp(-t)+0.5*exp(-2*t); x2=exp(-t)-exp(-2*t); plot(t,x1,'x',t,x2,'*') end
两边同时在
区间积分，得：
两边同时左乘 即：
并整理得：
2020/6/4
当初始时刻为t0=0时,初始状态x(t0)=x(0)时,其解为:
x (t) (t)x (0 ) 0 t (t )B() u d ，
当初始时刻为t0时,初始状态x(t0)时,其解为:
t
x (t) (t t0)x (t0 )t0 (t)B ()u d
1 t
1 t 2 ... 2!
(n
1 - 1)!
t
n1
0
1
t
...
(n
1 - 2)!
现代控制理论 刘豹
求下列系统在t=0.2,0.4秒时的状态转移阵
0 2 2 A 1 3,..B 0
matlab的m文件文本如下： A=[0 -2 ;1 -3]; B=[2; 0]; fait02=expm(A*0.2) fait04=expm(A*0.4)
2-6 应用Matlab的系统运动分析
求下列系统在u=1(t)时的状态响应和输出响应
第二章 控制系统状态空间表达式的解 图解内容
连 续
x(t) Ax(t) Bu(t) x(0) x0,u(t)
时 y(t) Cx(t) Du (t)
间
x(t)
离散化
离
x(0) x0,u(k)
散 x(k 1) Ax(k) Bu(k)
x(k)
时
间
第二章 控制系统状态空间表达式的解
主要内容
(1 e2T e2T
)
H
(T
)
1 2
(T 1
e 2T 2
e 2T
1
2
分析选择不同的采样周期T.的影响
2-4 连续时间状态方程的离散化
0.5
0.45 0.4
0.35
continous discrete 1 discrete 0.5
0.3
0.25
0.2
0.15
0.1
0.05
0
0
0.5
2(t t0 )
e(t t0 )
2e2(t t0
)
0 t0 0, x(0) 1
t1
0.2, e At
0.97 0.3
0.15 0.52
x1 x(0.2) eAt1 x(0)
t2
0.4, eAt2
0.89 0.44
0 2 2 A 1 3,..B 0
matlab的m文件文本如下： A=[0 -2 ;1 -3]; B=[2; 0]; fait02=expm(A*0.2) fait04=expm(A*0.4)
2-6 应用Matlab的系统运动分析
求下列系统在u=1(t)时的状态响应和输出响应
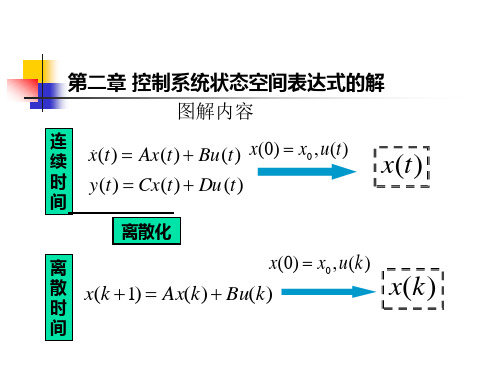
第二章 控制系统状态空间表达式的解 图解内容
连 续
x(t) Ax(t) Bu(t) x(0) x0,u(t)
时 y(t) Cx(t) Du (t)
间
x(t)
离散化
离
x(0) x0,u(k)
散 x(k 1) Ax(k) Bu(k)
x(k)
时
间
第二章 控制系统状态空间表达式的解
主要内容
(1 e2T e2T
)
H
(T
)
1 2
(T 1
e 2T 2
e 2T
1
2
分析选择不同的采样周期T.的影响
2-4 连续时间状态方程的离散化
0.5
0.45 0.4
0.35
continous discrete 1 discrete 0.5
0.3
0.25
0.2
0.15
0.1
0.05
0
0
0.5
2(t t0 )
e(t t0 )
2e2(t t0
)
0 t0 0, x(0) 1
t1
0.2, e At
0.97 0.3
0.15 0.52
x1 x(0.2) eAt1 x(0)
t2
0.4, eAt2
0.89 0.44
线性控制理论 第2章 状态空间表达式的求解
Φ(t1 t2 ) e A(t1 t2 ) 1 2 1 k 2 I A(t1 t2 ) A (t1 t2 ) A (t1 t2 ) k 2! k! 1 2 2 1 2 2 ( I At1 A t1 )(I At2 A t2 ) 2! 2! Φ(t1 )Φ(t2 )
12t 2 0 2 2 2 t 1 2! 0 2 2 n t
1 2 2 1 t t 0 1 1 2! 1 2 2 1 2 t 2 t 2! 1 2 2 0 1 n t n t 2!
1
1 2 1 m 1 t t 2! (m 1)! t （2-21） 1 2 1 t 2! t 1 mm
证明 因
12 1 1 0 1 2 ,A A 0 1 1 1 mm 21
x(t ) Φ(t ) x(0),t 0
上式表明齐次状态方程的解，在初始状 态确定情况下，由状态转移矩阵惟一确定，
即状态转移矩阵包含了系统自由运动的全部
信息，完全表征了系统的动态特性。
定义2.1
线性定常系统状态转移矩阵 Φ(t t0 ) 是
满足矩阵微分方程和初始条件
(t t ) AΦ (t t ), t t Φ 0 0 0 Φ (t0 t0 ) I
(2-3)
(t ) b1 2b2t kbk t x
( k 1)
k
Ax (t ) A(b0 b1t b2t bk t )
2ቤተ መጻሕፍቲ ባይዱ
比较上式两边t的同次幂可得
12t 2 0 2 2 2 t 1 2! 0 2 2 n t
1 2 2 1 t t 0 1 1 2! 1 2 2 1 2 t 2 t 2! 1 2 2 0 1 n t n t 2!
1
1 2 1 m 1 t t 2! (m 1)! t （2-21） 1 2 1 t 2! t 1 mm
证明 因
12 1 1 0 1 2 ,A A 0 1 1 1 mm 21
x(t ) Φ(t ) x(0),t 0
上式表明齐次状态方程的解，在初始状 态确定情况下，由状态转移矩阵惟一确定，
即状态转移矩阵包含了系统自由运动的全部
信息，完全表征了系统的动态特性。
定义2.1
线性定常系统状态转移矩阵 Φ(t t0 ) 是
满足矩阵微分方程和初始条件
(t t ) AΦ (t t ), t t Φ 0 0 0 Φ (t0 t0 ) I
(2-3)
(t ) b1 2b2t kbk t x
( k 1)
k
Ax (t ) A(b0 b1t b2t bk t )
2ቤተ መጻሕፍቲ ባይዱ
比较上式两边t的同次幂可得
第2章 控制系统状态空间表达式的解
第二章控制系统状态空间表达式的解§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）本章要点：状态转移矩阵§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）令和t2. 矩阵指数函数的计算方法⎤⎡λλ 2. A的特征值存在重根§2－1 线性定常齐次状态方程的解（自由解）⎤⎡−1112σ§2－1 线性定常齐次状态方程的解（自由解）证明：由指数函数矩阵的定义有：§2－1 线性定常齐次状态方程的解（自由解）k§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）§2－1 线性定常齐次状态方程的解（自由解）（1) 用拉氏变换法计算§2－1 线性定常齐次状态方程的解（自由解）⎤⎡01用凯莱－哈密尔顿法计算系统矩阵的矩阵指数函数一. 状态转移矩阵的定义二. 状态转移矩阵的性质§2－2 状态转移矩阵§2－2 状态转移矩阵§2－3 线性定常系统非齐次方程的解作变量变换：t一. 时变系统状态方程解的特点§2－5 连续时间状态空间表达式的离散化五. 状态转移矩阵的计算§2－5 连续时间状态空间表达式的离散化§2－5 连续时间状态空间表达式的离散化§2－5 连续时间状态空间表达式的离散化§2－5 连续时间状态空间表达式的离散化§2－5 连续时间状态空间表达式的离散化§2－5 连续时间状态空间表达式的离散化§2－6 离散时间系统状态方程的解。
第2章-控制系统状态空间表达式的解教学提纲
即
上式左乘
，得：
注意式（5）等式右边第二项，其中：
（5）
两个拉氏变换函数的积是一个卷积的拉氏变换，即 以此代入式（5），并取拉氏反变换，即得 ：
在特定控制作用下，如脉冲函数、阶跃函数和斜坡函数的激励下，则 系统的解式（2）可以简化为以下公式：
1.脉冲响应
即当
时
2.阶跃响应
即当
时
（6）
3.斜坡响应
1．若 A 为对角线矩阵，即 (5)
则 (6)
2.若 A 能够通过非奇异变换予以对角线化，即
则 (7)
3.若 A 为约旦矩阵
则 (8)
4.若 (9)
2.2.4 1.根据
的计算 的定义直接计算
2.变换 A 为约旦标准型 （1）A 特征根互异
其中 T 是使 A 变换为对角线矩阵的变换阵。由式（7），有：
第2章-控制系统状态空间表达式 的解
幂级数形式，即 (4)
代入式(1)得：
(5)
既然式(4)是式(1)的解，则式(5)对任意时刻 都成立，故 的同次 幂项的系数应相等，有：
在式(4)中，令
，可得：
将以上结果代入式(4)，故得： (6)
等式右边括号内的展开式是 即
于是式(6)可表示为：
矩阵，它是一个矩阵指数函数，记为 ， (7)
再用 的正确性。
代替
即在代替 的情况下，同样可以证明式2)
2.2 矩阵指数函数——状态转移矩阵
2.2.1 状态转移矩阵 齐次微分方程(1)的自由解为：
或
2.2.2 状态转移矩阵(矩阵指数函数)的基本性质 1．性质一
或
(1)
这就是组合性质，它意味着从 转移到0，再从0转移到 的组合。
第二章 控制系统的状态空间表达式的解
e
A( t2 −t1 ) At1
e
= e At2
（2-12）
状态转移矩阵（矩阵指数函数） 二 、状态转移矩阵（矩阵指数函数）的基本性质
1 、性质一 或
Φ ( t ) Φ (τ ) = Φ ( t + τ )
e At e Aτ1 = e
A( t +τ )
（2-13）
这就是组合性质，它意味着从－τ转移到0，再从0转移到t的组合，即
) （0）到x（t）的转移矩阵，而 Φ ( t − t0 ) = e A( t −t0表示x（t0）到x（t）的 • 转移矩阵。这样， x = Α的解，又可表示为 x ( t ) = Φ ( t ) x ( 0 ) 或 x
At
转移，所以 e At 也称为状态转移矩阵，通常记为Φ（t）。Φ ( t ) = e At− t0 ) x ( t0 )
状态转移矩阵（或矩阵指数）有以下关系
Φ ( t − t0 ) Φ ( t1 ) = Φ ( t2 )
或 这种关系称为组合性质。 利用状态转移矩阵，可以从任意指定的初始时刻的状态矢量x（t0），求得任 意时刻t的状态矢量x（t）。换言之，矩阵微分方程的解，在时间上可以任意 分段求取，这是动态系统用状态空间表示法的又一优点
3tet + 2et − e 2t 3tet + 5et − 4e 2t 3tet + 8et − 8e 2t −tet − et + e 2t −tet − 2et + 2e 2t −tet − 3et + 4e 2t
−2tet + e 2t = 2(e 2t − tet − et ) −2tet − 4et + 4e 2t
现代控制理论-第二章-控制系统的状态空间表达式的解
t
t2
2、状态转移矩阵的基本性质
(1) Φ(0) I (2) Φ (t) AΦ(t) Φ(t)A Φ (0) A (3) Φ(t1 t2 ) Φ(t1)Φ(t2 ) Φ(t2 )Φ(t1) (4) Φ1(t) Φ(t), Φ1(t) Φ(t) 证明： I Φ(0) Φ(t t) Φ(t)Φ(t) Φ(t)Φ(t) 推论： x(t) Φ(t)x(0) x(0) Φ1(t)x(t) Φ(t)x(t)
3、几个特殊的矩阵指数函数
（1）设A diag[，1,即2 ,A为, 对n ]角阵且具有互异元素时，有
e1t
0
(t)
e2t
0
e
nt
（2）若A能通过非奇异变换为对角阵时，即 P-1AP Λ
Φ(t) PΦ(t)P1
e1t
x1
x2
0 0
1 x1
0
x2
x(t) eAtx(0) I At 1 A2t 2 1 Akt k x(0)
2!
k!
A2
0 0
10 00
1 0 0 0
0 0
A3
直接求解法：根据定义 标准型法求解：对角线标准型和约当标准型 拉氏反变换法
1）根据状态转移矩阵的定义求解：
eAt I At 1 A2t 2 1 Akt k
2!
k!
对所有有限的t值来说，这个无穷级数都是收敛的 。
求出的解不是解析形式，适合于计算机求解。
例：求解系统状态方程的解 解：
第二章 控制系统状态空间表达式的解
16
第二章 控制系统状态空间表达式的解
状态转移矩阵的计算
e At et T 0 0 tet et 0 1 T e 2t 0 0 tet et 0 0 0 2 1 0 2 3 1 2 t e 1 2 1 3tet 2et 2e 2t 3tet 5et 4e 2t 3tet 8et 8e 2t tet et e 2t t t 2t te 2e 2e tet 3et 4e 2t
n 1 e n t 0 (t ) 1 (t ) n 2 (t )2 ( t ) n n 1 n
23
第二章 控制系统状态空间表达式的解
状态转移矩阵的计算
n, n-1, n-2, · · · ， 互不相同时，通过下式
t ( t ) 1 0 e 1 t 1 (t ) 1 2 e
1
A为标准型，所以变换阵可以有特征根直接写出
2 1 1 1
e
At
e t T 0
1 e t 0 1 1 T 2t e 1 2 0 e t e 2 t t 2t e 2e
用（t-t0)代替t, 可得到t0不为0时的解
x(t ) e A(t t0 ) x0 , t t0
关键问题：求矩阵的指数函数
6
第二章 控制系统状态空间表达式的解
2.2 矩阵指数函数—状态转移矩阵
齐次微分方程的自由解
x(t ) e x0 或
At
x(t ) e A(t t0 ) x0
3
第二章 控制系统状态空间表达式的解
第二章 控制系统状态空间表达式的解
状态转移矩阵的计算
e At et T 0 0 tet et 0 1 T e 2t 0 0 tet et 0 0 0 2 1 0 2 3 1 2 t e 1 2 1 3tet 2et 2e 2t 3tet 5et 4e 2t 3tet 8et 8e 2t tet et e 2t t t 2t te 2e 2e tet 3et 4e 2t
n 1 e n t 0 (t ) 1 (t ) n 2 (t )2 ( t ) n n 1 n
23
第二章 控制系统状态空间表达式的解
状态转移矩阵的计算
n, n-1, n-2, · · · ， 互不相同时，通过下式
t ( t ) 1 0 e 1 t 1 (t ) 1 2 e
1
A为标准型，所以变换阵可以有特征根直接写出
2 1 1 1
e
At
e t T 0
1 e t 0 1 1 T 2t e 1 2 0 e t e 2 t t 2t e 2e
用（t-t0)代替t, 可得到t0不为0时的解
x(t ) e A(t t0 ) x0 , t t0
关键问题：求矩阵的指数函数
6
第二章 控制系统状态空间表达式的解
2.2 矩阵指数函数—状态转移矩阵
齐次微分方程的自由解
x(t ) e x0 或
At
x(t ) e A(t t0 ) x0
3
第二章 控制系统状态空间表达式的解
大学课件(可做考研参考)：第2章_控制系统状态空间表达式的解
0 0 0，则e At 1 2
e t
0
0
0
0
tet et 0
0 0
0 0 e2t
0 0
0 0 te2t e2t 0
0
t
0 2e 2t
2! te2t
e2t
1 1 0 0 0
et tet 0 0 0
0 1 0 0 0
0
et
0
0
0
若A＝0 0 3 0 0， 则eAt 0 0 e3t 0 0
比 较 系 数 得：b1
Ab0
Ax 0；b 2
1 2
Ab1
1 2
A
Ax
0
1A 2!
2
x
0
b3
1 3
Ab2
3
1 2
A !
A2
x
0
1A 3!
3
x
0;
bk
1 k
Abk1
k
(
1 k-
1
)
A !
Ak
-1x
0
1A k!
k
x
0;
即 x(t)
x0
A x0t
1A 2!
2
x
0
t2
1A 3!
3
x
0
t3
1A k!
k
x0
tk
Φ (t) eAt，初 始 时 刻t0为0
或
Φ ( t t0 ) eA(tt0 )，初 始 时 刻 为 任 意 时 刻t0
则： x(t)Φ(t)x(0) 状态由x(0)转移到x(t)
或 x(t)Φ(t t0 )x(t0 ) 状态由x(t0)转移到x(t)
第二章-控制系统状态空间表达式的解
拉氏变换法(5/9)
为讨论方便,引入能描述系统状态转移特性的线性定常连续 系统的状态转移矩阵如下: (t)=eAt
因此,有如下关系式 x(t)=(t)x0=(t-t0)x(t0)
(t - t0 ) e A(t t0 )
由上述状态转移矩阵定义和齐次状态方程的解,系统状 态转移矩阵有如下关系 (t)=L-1[(sI-A)-1]
2 k 1 I A A A 1 1 1 L [( sI A) ] L 2 3 ... k ... s s s s A2t 2 Ak t k I At ... ... 2! k! e At
拉氏变换法(4/9)
因此,基于上述(sI-A)-1的拉氏反变换,该齐次方程的解为 x(t)=L-1[(sI-A)-1]x0 = eAt x0
因此, 状态x(t)的解可写为
A2 2 Ak k x (t ) I At t ... t ... x0 2! k!
该方程右边括号里的展开式是n×n维矩阵函数。 由于它类似于标量指数函数的无穷级数展开式,所 以称为矩阵指数函数,且记为
e
At
A2 2 Ak k I At t ... t ... 2! k!
如果所设解是方程的真实解,则对任意t,上式均成立。 因此,使t有相同幂次项的各项系数相等,即可求得
A q1 q0 , 1! A A2 q2 q1 q0 , 2 2! A Ak , qk qk 1 q0 k k!
级数展开法(4/5)
若初始时刻t0=0,初始状态x(0)=x0,则可确定 q0=x(0)=x0
概述(2/4)
本章先讨论用状态空间模型描述的线性系统的定量分析问 题,即状态空间模型--状态方程和输出方程的求解问题。
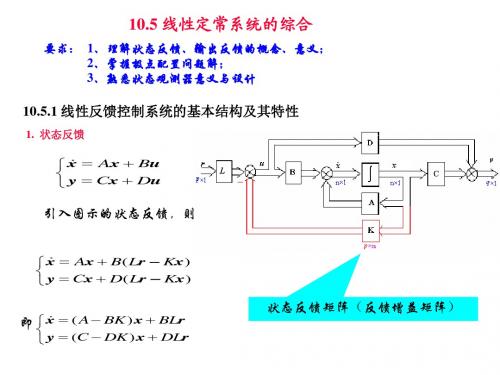
第二章控制系统状态空间表达式的解要求1、掌握状态空间表达式的
③ 比较 f ( )、f (* ) ④ 解得K 例 已知
G(s)
得n个方程
10 ，试设计状态试系统的闭环极点为-2，-1±j。 s( s 1)( s 2)
0 0 x 0 y 10 1 0 0 0 u 0 1 x 2 3 1 0 0 x
带输出反馈的传递函数阵（L=I，D=0）
GH ( s ) C[ sI ( A BHC )]1 LB [ I G0 ( s ) H ]1 G0 ( s ) G0 ( s )[ I HG0 ( s )]1
受控系统传递函数阵（D=0）
G0 (s) C (sI A)1 B
1. SISO系统极点配置
定理
对Σ0（A,B,C）任意配置极点 Σ0完全能控。
给定极点确定状态反馈增益K的步骤： ① 加入 K [ K0
K1 Kn1 ]
② 求 f () I ( A BK )
* * f * ( ) ( 1* )( 2 )( n )
故受控系统可以任意配置极点以及观测器的特征值。 令 G ( g1 g2 g3 )T ，则
1 ( ) I ( A GC) I f 3 0 0 g1 g 2 [0 1 1 2 0 g 3 0
K [k1 k2 k3 ]
20 G 25 12
令
，则
1 0 0 1 f ( ) I ( A BK ) I 3 1 1 0 [ k1 k2 k3 ] 0 2 0 0 k1 1 k2 k3 3 1 1 3 k1 2 (k1 3k2 3) 2k1 6k3 2
第二章状态空间表达式的解
了从初始时刻的状态向量x0，到任意t时刻的状态向量x(t)的一种 At 向量变换关系，变换矩阵就是矩阵指数函数e 。它不是一个常数 矩阵，其元素是时间t的函数，所以是一个 n n 时变函数矩阵。从 时间角度看，意味着它使状态向量随着时间的推移，不断地在状 态空间上作转移，所以变换矩阵也称为状态转移矩阵，通常记为 (t ) 。有 (t ) e At 和 (t t 0 ) e A(t t0 ) 。
通常，由这一方法只能得到数值结果，一般难 以获得其解析形式函数表达式。
例：已知
0 1 A - 2 - 3
分别用上述四种方法求
e
At
1 2 2 1 k k (1)由 e I At A t A t 2! k!
At
则
1 0 0 1 1 0 1 2 e t t 0 1 - 2 - 3 2! - 2 - 3
对于A的特征值有重根的情况下，例如特征 2 6 ,, n 时，有 值为 （三重根），（二重根）， 1
a 0 (t ) 0 a (t ) 1 0 a 2 (t ) 1 a3 (t ) 0 a 4 (t ) 1 a5 (t ) 1 a n 1 (t ) 1 0 1 1 21
At
2
3 2 7 3 2 3 1 t t t t t 2 6 7 3 7 2 5 3 2 2t 3t t 1 3t t t 3 2 2
矩阵指数函数的计算方法
2．变换A为对角线规范型或约旦规范型
e At L1[(sI A) 1 ]
例：已知
0 1 A - 2 - 3
通常，由这一方法只能得到数值结果，一般难 以获得其解析形式函数表达式。
例：已知
0 1 A - 2 - 3
分别用上述四种方法求
e
At
1 2 2 1 k k (1)由 e I At A t A t 2! k!
At
则
1 0 0 1 1 0 1 2 e t t 0 1 - 2 - 3 2! - 2 - 3
对于A的特征值有重根的情况下，例如特征 2 6 ,, n 时，有 值为 （三重根），（二重根）， 1
a 0 (t ) 0 a (t ) 1 0 a 2 (t ) 1 a3 (t ) 0 a 4 (t ) 1 a5 (t ) 1 a n 1 (t ) 1 0 1 1 21
At
2
3 2 7 3 2 3 1 t t t t t 2 6 7 3 7 2 5 3 2 2t 3t t 1 3t t t 3 2 2
矩阵指数函数的计算方法
2．变换A为对角线规范型或约旦规范型
e At L1[(sI A) 1 ]
例：已知
0 1 A - 2 - 3
控制系统状态空间表达式的解
关键问题： 关键问题：状态转移矩阵 eAt ?
2.2 矩阵指数函数 状态转移矩阵 定义 矩阵指数函数---状态转移矩阵
一.状态转移矩阵 : 齐次状态方程解x(t ) = e At x(0)或 齐次状态方程解x 反映从初态x x(t) = e A(t − t 0 )x(t 0 )反映从初态x(0) 或x(t 0 )到终态x(t)的向 量转移, 到终态x 量转移,
(λ1I − A)p1 = 0 1 −1 1 − 2 5 − 2 (λ1I − A)p2 = −p1 求T = [p1 p2 p3 ] = 1 0 2, T−1 = − 2 3 −1 1 1 4 1 −2 1 (λ3I − A)p3 = 0
2.2 矩阵指数函数 状态转移矩阵 求法 矩阵指数函数---状态转移矩阵 求法2
2 0 补例A 补例A = ; − 2 − 4 λ −2 2 λI− A = =λ + 4λ+ 4 = 0, 2 λ+ 4 λ = −2,只对应一独立特征向量 . 1,2
(λ − A)p1 = 0 I 由 1 求出 : (λ − A)p2 = −p1 I 2 1 −1 −1 − 2 1 − 2 1 ,J = T = [p1 p2 ] = , = T −1 −1/2 2 2 0 − 2
At
2.2 矩阵指数函数 状态转移矩阵定义 矩阵指数函数---状态转移矩阵
x10 已知x 例:已知x(0) = 和Φ(t1 )则 x 20 x11 x(t1 ) = = Φ(t1 )x(0); x 21
若已知Φ(t 2 ), 若已知Φ x12 则x(t 2 ) = = Φ(t 2 )x(0); x 22
若知x 若知x(t 1 )和Φ(t 2 − t1 ) 则x(t 2 ) = Φ(t 2 − t1 )x(t 1 ) = Φ(t 2 − t1 )Φ(t 1 )x(0)
第二章控制系统状态空间表达式的解
b1 2b2t 3b3t 2 kbkt k1
a(b0 b1t b2t 2 bkt k )
（1） （2） （3）
2.1 线性定常齐次状态方程的解（自由解）
等式两边t 的同次幂的系数相等，因此有
b1 ab0
b2 bk
1 2
1 k
ab1
abk
1 2!
a
2b0
1 k!
a
（5）
将（5）式代入（1）式
2.1 线性定常齐次状态方程的解（自由解）
b1 2b2t 3b3t 2 kbkt k 1
A(b0 b1t b2t 2 bkt k )
等式两边t 同次幂的系数相等，因此有
b1 Ab0
b2 bk
1 2
1 k
Ab1
Abk
1 2!
A2b0
1 k!
2.1 线性定常齐次状态方程的解（自由解）
1、线性定常系统的运动
1）、自由运动：线性定常系统在没有控制作用，即u＝0时， 由初始状态引起的运动称自由运动。
u0
x
( A, B)
齐次状态方程的解： x Ax , x(t) |t0 x(0)
2）、强迫运动：线性定常系统在控制u作用下的运动，称
为强迫运动。
e1t
0
e At Te AtT1 T
T 1
0
ent
其中： T为使A化为对角线标准型的非奇异变换矩阵。
求状态转移矩阵的步骤：
1）先求得A阵的特征值 。i
2）求对应于 的i 特征向量 ，p并i 得到T阵及T的逆阵。
3）代入上式即可得到状态转移矩阵的值。
即：A det(I A) 0 i (i I A)pi 0 pi T
0 0 0 0 1
a(b0 b1t b2t 2 bkt k )
（1） （2） （3）
2.1 线性定常齐次状态方程的解（自由解）
等式两边t 的同次幂的系数相等，因此有
b1 ab0
b2 bk
1 2
1 k
ab1
abk
1 2!
a
2b0
1 k!
a
（5）
将（5）式代入（1）式
2.1 线性定常齐次状态方程的解（自由解）
b1 2b2t 3b3t 2 kbkt k 1
A(b0 b1t b2t 2 bkt k )
等式两边t 同次幂的系数相等，因此有
b1 Ab0
b2 bk
1 2
1 k
Ab1
Abk
1 2!
A2b0
1 k!
2.1 线性定常齐次状态方程的解（自由解）
1、线性定常系统的运动
1）、自由运动：线性定常系统在没有控制作用，即u＝0时， 由初始状态引起的运动称自由运动。
u0
x
( A, B)
齐次状态方程的解： x Ax , x(t) |t0 x(0)
2）、强迫运动：线性定常系统在控制u作用下的运动，称
为强迫运动。
e1t
0
e At Te AtT1 T
T 1
0
ent
其中： T为使A化为对角线标准型的非奇异变换矩阵。
求状态转移矩阵的步骤：
1）先求得A阵的特征值 。i
2）求对应于 的i 特征向量 ，p并i 得到T阵及T的逆阵。
3）代入上式即可得到状态转移矩阵的值。
即：A det(I A) 0 i (i I A)pi 0 pi T
0 0 0 0 1
第2章_控制系统状态空间表达式的解
A(t t0 )
此处，e A t或e A ( tt0 )称为矩阵指数函数(指数为矩阵) ，该函数
在形式上为n n矩阵，矩阵中的元素部 分或全部为t的函数。
2.2
矩阵指数函数与状态转移矩阵
主要学习和掌握内容： 1、学习和掌握状态转移矩阵的概念； 2、学习和掌握状态转移矩阵的重要性质； 3、学习和掌握状态转移矩阵的四种求解方法 （后3种可获得解析解）： (1) 根据定义计算(非解析解形式) (2) 非奇异变换法（对角线阵法或约当阵法） (3) 反拉氏变换法 (4) 凯莱-哈密顿定理法
2.若A能通过非奇异 变换(变换阵为T)对 角线化，即T1AT Λ，则 0 λ 2t 可通过变换 e At 1 Λ t 1 T T e T Φ (t) e 阵T求A阵状 态转移矩阵 λnt e 1 2 2 1 1 2 2 1 Λt 1 证明:Λ T AT，e I Λt Λ t I T ATt T A Tt 2! 2! 1 1 2 2 1 1 A t T ( I At A t )T T e T， 左乘T右乘T 即得: 2! At Λ t 1 e λ1t T 0
因此，线性定常系统的 自由解即为系统齐次状 态方程的解。
(1) 推导：设标量微分方程x ax，x(0) x 0(初始时刻t0 0) 的解为 x(t) b 0 b1t b 2 t2 bk tk bk tk； ( bi 为待定系数)
k 0
当t 0时，x(0) b 0 x 0；将假设解代入微分方程x ax，有： x b1 2b2 t 3b3 t2 kbk tk 1 (k 1)bk 1tk ax ab0 ab1t ab2 t2 abk 1tk 1 abk tk 1 1 1 比较等式两边系数得：b1 ab0 ax0；b2 ab1 aax0 a 2 x 0 2 2 2! 1 1 1 b3 ab2 aa2 x 0 a 3 x 0； 3 3 2! 3! 1 1 1 bk abk 1 aak -1x 0 a k x 0； k k(k - 1)! k!
此处，e A t或e A ( tt0 )称为矩阵指数函数(指数为矩阵) ，该函数
在形式上为n n矩阵，矩阵中的元素部 分或全部为t的函数。
2.2
矩阵指数函数与状态转移矩阵
主要学习和掌握内容： 1、学习和掌握状态转移矩阵的概念； 2、学习和掌握状态转移矩阵的重要性质； 3、学习和掌握状态转移矩阵的四种求解方法 （后3种可获得解析解）： (1) 根据定义计算(非解析解形式) (2) 非奇异变换法（对角线阵法或约当阵法） (3) 反拉氏变换法 (4) 凯莱-哈密顿定理法
2.若A能通过非奇异 变换(变换阵为T)对 角线化，即T1AT Λ，则 0 λ 2t 可通过变换 e At 1 Λ t 1 T T e T Φ (t) e 阵T求A阵状 态转移矩阵 λnt e 1 2 2 1 1 2 2 1 Λt 1 证明:Λ T AT，e I Λt Λ t I T ATt T A Tt 2! 2! 1 1 2 2 1 1 A t T ( I At A t )T T e T， 左乘T右乘T 即得: 2! At Λ t 1 e λ1t T 0
因此，线性定常系统的 自由解即为系统齐次状 态方程的解。
(1) 推导：设标量微分方程x ax，x(0) x 0(初始时刻t0 0) 的解为 x(t) b 0 b1t b 2 t2 bk tk bk tk； ( bi 为待定系数)
k 0
当t 0时，x(0) b 0 x 0；将假设解代入微分方程x ax，有： x b1 2b2 t 3b3 t2 kbk tk 1 (k 1)bk 1tk ax ab0 ab1t ab2 t2 abk 1tk 1 abk tk 1 1 1 比较等式两边系数得：b1 ab0 ax0；b2 ab1 aax0 a 2 x 0 2 2 2! 1 1 1 b3 ab2 aa2 x 0 a 3 x 0； 3 3 2! 3! 1 1 1 bk abk 1 aak -1x 0 a k x 0； k k(k - 1)! k!
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
从而 称为状态转移矩阵
1 22 1 k k e = I + At + A t + L + A t + L 2! k!
At
x(t ) = e At x0
x(t ) = e A( t −t0 ) x0 这个解反映了从初始时刻的状态向量 x0 ，到任意时 刻的状态向量 x(t ) 的一种变换关系，变换矩阵就是 e At 称为状态转移矩阵，通常记为 φ (t ) 矩阵指数， 几个特殊的矩阵指数函数 1. 若A为对角线矩阵 2. 若A能通过非奇异变换变换成对角线矩阵 3. 若A为约旦矩阵
二、φ (t ) 或 e
1. 根据
At
的计算
e
At
或 φ (t )的定义直接计算
例： 试求如下线性定常系统的状态转移矩阵
& x1 0 x = − 2 &2
At
1 x1 −3 x 2
2 2 3
1 0 0 1 0 1 t 0 1 3 Φ (t ) = e = + −2 −3 t + −2 −3 2! + −2 −3 t + L 0 1 3 7 t − t2 − t3 +L 1− t 2 + t3 +L 2 6 = −2t + 3t 2 − 7 t 3 + L 1 − 3t + 7 t 2 − 5 t 3 + L 3 2 2
t 0 0
At
t
− Aτ
t
Bu (τ ) dτ
x(t ) = e x0 + ∫ e A(t −τ ) Bu (τ )dτ
0
2 1 e −t e = −2 −2 0
At
x &2
得 λ1 = −1 λ2 = −2
T
−1
1 1 2 = −1 −1
e −t − e −2t −e −t + 2e −2t
从而
0 1 1 2 2e −t − e −2t = −2 t e −1 −1 −2e−t + 2e −e + 2e
三、非齐次状态方程的解
状态方程 可写成 即
& x = Ax + Bu
& e (x − Ax) = e Bu
− At − At
d − At [e x(t )] = e − At Bu (t ) dt e
− At
从而得
x(t ) = ∫ e
3. 利用拉氏反变换求解 & x(t ) = Ax(t ) 对齐次微分方程 sX ( s) − x(0) = AX ( s) 两边求拉氏变换 X ( s ) = ( sI − A) x0 得： x (t ) = L−1[( sI − A) −1 ] x0 所以 e At = L−1[( sI − A) −1 ] 即 & 1 x1 x1 0 = 例： &
x2 − 2 −3 x 2
−1 s + 3
解：
s ( sI − A) = 2
s 1 ( sI − A) = ( s + 1)( s + 2) −2
−1
1
s + 3
2e − t − e −2t e At = L−1[( sI − A) −1 ] = −2e −t + 2e −2t
第二章
控制系统状态空间表达式的解
一、线性定常齐次状态方程的解(自由解)
& 齐次状态方程 x(t ) = Ax(t ) x (t )＝b0 + b1t + b2t 2 + L + bk t k + L 设解为： 代入齐次状态方程得：
1 22 1 k k x (t ) = ( I + At + A t + L + A t + L) x0 2! k!
2. 变换A为约旦标准型 （1）特征根互异 由于A是一个任意矩阵，将A变换成约旦标准型（对 角线型），得： ∧ = T −1 AT 而 eAt = Te∧tT −1 & 例： x1 = 0 1 x1 解 由
− 2 −3 x 2 λ −1 λI − A = = λ 2 + 3λ + 2 = 0 2 λ +3 APi = λi Pi 得 T = 2 1 −2 −2