高二BC段文科数学周测试卷(2)

合集下载

2021-2022年高二下学期周考(3.20)数学(文)试题含答案

2021-2022年高二下学期周考（3.20）数学（文）试题含答案注意事项： 1. 答第I 卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2. 每题选出答案后，用2B 铅笔把答题卡对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，在改涂在其他答案标号。

一．选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.不等式的解集为（）A. B.C. D.2.若，则下列不等式中正确的是A. B.C. D.3.极坐标系中，有三条曲线1sin 3cos ,3,0-+--θρθρπθθ围城的图形的面积是A. B. C. D.4.已知点M 的球坐标为（1，），则它的直角坐标系为（）A.（1，）B.C.D.5．已知点P 的极坐标是（1，），则过点P 且垂直极轴的直线方程是（）A. B. C. D.6.直线和直线的位置关系（）A. 垂直B.平行C.相交但不垂直D.重合7.若不等式在R 上有解，则实数a 的取值范围是（）A.a<3B.a>3C. a<1D.a>18.在极坐标中，圆的垂直于极轴的两条切线方程分别为（）A.和B.和C.和D. 和9.直线（t 为参数）的倾斜角是（）A. B. C. D.10.不等式对任意实数x 恒成立，则实数a 的取值范围是（）A. B. C. D.11.把方程xy=1化为以t 参数的参数方程是（） A.⎪⎩⎪⎨⎧==-2121t y t x B.⎪⎩⎪⎨⎧==t y t x sin 1sin C.⎪⎩⎪⎨⎧==t y t x cos 1cos D.⎪⎩⎪⎨⎧==t y t x tan 1tan 12.若函数=的最小值为3，则实数a 的值为（）A.5或8B.-1或5C.-1或-4D.-=4或8注意事项：第II 卷所有题目的答案考生需用黑色签字笔答在“数学”答题卡指定的位置。

二．填空题（本大题共4个小题，每小题5分，共20分。

高考数学文科测试卷(二)

2012高三文科限时训练(2)一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填在答题卡上）1．已知集合M ＝2{0}x x x -<，N ＝{2}x x <，则A ．M N =∅B ．M N M =C ．M N M =D ． M N R = 2．等比数列{}n a 中，44a =，则17a a 等于A ．4B ．8C ．16D ．32 3．若命题:11,:2p x q x -≤≤>-，则p 是q 的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知向量(3,4)a = ，(sin ,cos )b θθ=，且a b ⊥ ，则tan θ等于 A ．34B ． 34-C ．43D ．43-5．已知函数3()2x f x +=，1()fx -是()f x 的反函数，则1(16)f -的值为A ．2-B ．1-C ．4D ．16．在△ABC 中，角A B C ，，的对边分别为a b c ，，，若222a cb +-=，则角B 的值为 A ．6π B ． 3π C ．6π或56π D ．3π或23π7．若实数x y ，满足1002x y x y -+⎧⎪>⎨⎪⎩≤，，≤则y x 的取值范围是（）A ．(02)，B ．(]02，C ．(2)+，∞D ．[)2+，∞ 8．20(23)x -的展开式中，各项系数的和为A ．1B ．－1C ．202D ．2059．4张卡片上分别写有数字1，2，3，4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为 A ．13B ．12C ．23D ．3410．设A B C △是正三角形，则以A B ，为焦点且过B C 的中点的双曲线的离心率为（） A ．21+B ．31+C ．221+ D ．231+11．已知a 1＞a 2＞a 3＞0，则使得2(1)1(123)i a x i -<=，，都成立的x 取值范围是（） A ．110a ⎛⎫ ⎪⎝⎭，B ．120a ⎛⎫ ⎪⎝⎭，C ．310a ⎛⎫⎪⎝⎭，D ．320a ⎛⎫ ⎪⎝⎭，12．已知函数①()ln f x x =；②co s ()xf x e =；③()x f x e =；④()c o s f x x=．其中对于()f x 定义域内的任意一个自变量1x ，都存在定义域内的唯一一个自变量2x ，使得1=成立的函数是A ．①②④B ．②③C ．③D ．④二、填空题（每题５分，共２０分，请将答案填在答题卡上） 13．曲线324y x x =-+在点(13)，处的切线的倾斜角为。

高二文科数学一周一练0516

高二文科数学一周一练（5月16日）一、填空题：（每题8分，共32分）1，如图，在正方形ABCD 中，E 为AB 中点，BF ⊥CE 于F ，那么S △BFC :S 正方形ABCD =___________________2.如图所示，已知在△ABC 中，∠C=90°，正方形DEFC 内接于△ABC ，DE ∥AC ，EF ∥BC ， AC=1，BC=2，则AF ∶FC= .3. 如图，EF ∥BC ，FD ∥AB ，AE=1.8cm, BE=1.2cm, CD=1.4cm ．则BD= .4. ΔABC 中，点D 为BC 中点，点E 在CA 上，且CE=21EA ，AD ，BE 交于点F ，则AF:FD= ．5. 点D 在AB 上，当∠ ＝∠ 时，△ACD ∽△ABC 。

6. 在Rt △ ABC 中， ∠ABC=90°0，BD ⊥AC 于D ，若 AB=6，AD=2 ，则AC=______， BD=________，BC=_________.7,如图，平行四边形ABCD 中，AE:EB=1:2, △AEF 的面积等于6cm 2，则△CDF 的面积等于_____;平行四边形 ABCD 的面积等于________.8．在四边形ABCD 中，∠A=135°，∠B=∠D=90°， BC=32，AD=2，则四边形ABCD 的面积是_______.A F E 第4题D BC A AB DC 第5题ABCDFE第3题第6题第1题第2题第7题第8题三、解答题（共36分）：9、如图，平行四边形ABCD 中，E 是CD 延长线上的一点，BE 与AD 交于点F ，DE=21CD 。

（1）求证：△ABF ∽△CEB（2）若△DEF 的面积是2，求平行四边形ABCD 的面积10.已知：如图，在ABC ∆中，,36,AB AC A BD =∠=︒是角平分线. 求证：2AD DC AC =⋅．11.有一块三角形的土地，它的底边BC ＝100米，高AH ＝80米。

【2020最新】人教版最新高考文科数学复习试卷(2)及参考答案

教学资料范本【2020最新】人教版最新高考文科数学复习试卷(2)及参考答案编辑：__________________时间：__________________(附参考答案) 数学（文史类）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。

（1） i 是虚数单位，复数=534ii +- （A ）（B ）1i -1i -+（C ）（D ）1i +1i --【解析】复数，选C.i ii i i i i i +=+=+-++=-+1171717)4)(4()4)(35(435【答案】C（2）设变量x,y 满足约束条件,则目标函数z=3x-2y的最小值为⎪⎩⎪⎨⎧≤-≥+-≥-+01042022x y x y x（A ）-5 （B ）-4 （C ）-2 （D ）3【解析】做出不等式对应的可行域如图，由得，由图象可知当直线经过点时，直线的截距最大，而此时最小为，选 B.yx z 23-=223z x y -=223z x y -=)2,0(C 223zx y -=y x z 23-=423-=-=y x z 【答案】B（3）阅读右边的程序框图，运行相应的程序，则输出S 的值为（A ）8 （B ）18 （C ）26 （D ）80【解析】第一次循环，第二次循环，第三次循环，第四次循环满足条件输出，选 C.2,2330==-=n S 3,83322==-+=n S 4,2633823==-+=n S 26=S 【答案】C（4）已知，则a ，b ，c 的大小关系为120.2512,(),2log 22a b c -===（A ）c<b<a （B ）c<a<b （C ）b<a<c （D ）b<c<a【解析】因为，所以，，所以，选 A.122.02.022)21(<==-b a b <<114log 2log 2log 25255<===c a b c <<【答案】A（5）设xR ，则“x>”是“2x2+x-1>0”的∈12 （A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件【解析】不等式的解集为或，所以“”是“”成立的充分不必要条件，选A.0122>-+x x 21>x 1-<x 21>x 0122>-+x x【答案】A（6）下列函数中，既是偶函数，又在区间（1,2）内是增函数的为（A ） cos 2y x =，xR ∈（B ） xy 2log =，xR 且x ≠0∈（C ） 2x xe e y --=，xR ∈ （D ）31y x =+，xR ∈【解析】函数为偶函数，且当时，函数为增函数，所以在上也为增函数，选B.x y 2log =0>x x x y 22log log ==)2,1( 【答案】B（7）将函数（其中>0）的图像向右平移个单位长度，所得图像经过点，则的最小值是()sin f x x ω=ω4π)0,43(πω（A ）（B ）1 C ）（D ）21353【解析】函数向右平移得到函数，因为此时函数过点，所以，即所以,所以的最小值为2，选 D.4π)4sin()4(sin )4()(ωπωπωπ-=-=-=x x x f x g )0,43(π0)443(sin =-ππω,2)443(πωπππωk ==-Z k k ∈=,2ωω 【答案】D（8）在△ABC 中， A=90°，AB=1，设点P ，Q 满足=，=(1-)， R 。

高二下学期数学第二次周练试卷(文科A卷)含答案

高二数学第二次周练试卷（文科A 卷）（试卷总分：100分考试时间：80分钟）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若P 是平面α外一点，则下列命题正确的是( )A ．过P 只能作一条直线与平面α相交B ．过P 可作无数条直线与平面α垂直C ．过P 只能作一条直线与平面α平行D ．过P 可作无数条直线与平面α平行2．一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是( )A ．异面B ．相交C ．平行D ．不能确定 3．设l 为直线，α，β是两个不同的平面．下列命题中正确的是( )A ．若l ∥α，l ∥β，则α∥βB ．若l ⊥α，l ⊥β，则α∥βC ．若l ⊥α，l ∥β，则α∥βD ．若l ⊥β，l ∥α，则l ⊥β 4．下列关于直棱柱的描述不正确的是( )A ．侧棱都相等，侧面是矩形B ．底面与平行于底面的截面是全等的多边形C ．侧棱长等于棱柱的高D ．有两个矩形的侧面的棱柱是直棱柱 5．一个棱柱是正四棱柱的条件是( )A ．底面是菱形且有一个顶点处的两条棱互相垂直B ．底面是正方形，两个侧面垂直于底面C ．底面是正方形有两个侧面是矩形D ．底面是正方形，每个侧面都是全等矩形的四棱柱 6.设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂（） A ．若l β⊥，则αβ⊥ B ．若αβ⊥，则l m ⊥ C ．若//l β，则//αβ D ．若//αβ，则//l m 7.某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（） A ．1 B ．2 C ．3 D ．28．如图，BCDE 是一个正方形，AB ⊥平面BCDE ，则图中(侧面，底面)互相垂直的平面共有( )A ．4组B ．5组C ．6组D ．7组9．如图，在正方体ABCD －A 1B 1C 1D 1中，点P 在侧面BCC 1B 1内运动，并且总保持AP ⊥BD 1，则动点P 在( )A ．线段B 1C 上 B ．线段BC 1上C ．BB 1中点与CC 1中点的连线上D ．B 1C 1中点与BC 中点的连线上10．已知矩形ABCD ，AB ＝1，BC ＝ 2.将△ABD 沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中( )A ．存在某个位置，使得直线AC 与直线BD 垂直B ．存在某个位置，使得直线AB 与直线CD 垂直C ．存在某个位置，使得直线AD 与直线BC 垂直D ．对任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直二、填空题：(本大题共4小题，每小题4分，共16分.)11．在正方体ABCD －A 1B 1C 1D 1中，E 、F 、G 分别是D 1A 1、A 1B 1、B 1C 1的中点，则面AEF 与平面GBD 的关系为________．12．如图，△A ′O ′B ′是水平放置的△AOB 的直观图，其中O ′B ′＝O ′A ′＝2cm ，则原△AOB 的面积为________cm 2.13.设P 是ABC ∆外一点，则使点P 在此三角形所在平面内的射影是ABC ∆的垂心的条件为________________________(填一种即可).14．若四面体ABCD 的三组对棱分别相等，即AB ＝CD ，AC ＝BD ，AD ＝BC ，则________(写出所有正确结论的编号)．①四面体ABCD 每组对棱相互垂直； ②四面体ABCD 每个面的面积相等；③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大于90°而小于180°； ④连接四面体ABCD 每组对棱中点的线段相互垂直平分；⑤从四面体ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长．姓名班级学号得分一、选择题（本大题共10个小题，每小题5分，共50分）题号1 2 3 4 5 6 7 8 9 10 总分答案11． 12．13． 14．三、解答题（34分）15．如图，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD、PC的中点，求证：(1)PA⊥底面ABCD；(2)BE∥平面PAD；(3)平面BEF⊥平面PCD.16．如图，三棱台DEF ABC -中，2AB DE G H =，，分别为AC BC ，的中点. （I ）求证：//BD 平面FGH ；（II ）若CF BC AB BC ⊥⊥，，求证：平面BCD ⊥平面EGH .17.一个正方体的平面展开图及该正方体的直观图的示意图如图所示. (Ⅰ)请按字母F ，G ，H 标记在正方体相应地顶点处(不需要说明理由) (Ⅱ)判断平面BEG 与平面ACH 的位置关系.并说明你的结论. (Ⅲ)证明：直线DF ⊥平面BEGA B FHED C G CD EAB号题1 2 3 4 5 6 7 8 9 10案答DC BD D AC B A B二、填空题11. 平行 12. 4 13. AC PB BC PA ⊥⊥, 14. ②④⑤三、解答题15. (1)因为平面PAD ⊥底面ABCD ，且PA 垂直于这两个平面的交线AD ，所以PA ⊥底面ABCD . (2)因为AB ∥CD ，CD ＝2AB ，E 为CD 的中点，所以AB ∥DE ，且AB ＝DE .所以四边形ABED 为平行四边形．所以BE ∥AD .又因为BE 平面PAD ，AD 平面PAD ，所以BE ∥平面PAD .(3)因为AB ⊥AD ，而且ABED 为平行四边形，所以BE ⊥CD ，AD ⊥CD . 由(1)知PA ⊥底面ABCD .所以PA ⊥CD .所以CD ⊥平面PAD .所以CD ⊥PD . 因为E 和F 分别是CD 和PC 的中点，所以PD ∥EF .所以CD ⊥EF ，又因为CD ⊥BE ，BE ∩EF ＝E ，所以CD ⊥平面BEF . 所以平面BEF ⊥平面PCD . 16. I ）证法一：连接,.DG CD 设CD GF M ⋂=,连接MH ，在三棱台DEF ABC -中，2AB DE G =，分别为AC 的中点，可得//,DF GC DF GC =，所以四边形DFCG 是平行四边形，则M 为CD 的中点，又H 是BC 的中点，所以//HM BD ,又HM ⊂平面FGH ，BD ⊄平面FGH ，所以//BD 平面FGH . 证法二：在三棱台DEF ABC -中，由2,BC EF H =为BC 的中点，可得//,,BH EF BH EF =所以HBEF 为平行四边形，可得//.BE HF 在ABC ∆中，G H ，分别为AC BC ，的中点，所以//,GH AB 又GH HF H ⋂=，所以平面//FGH 平面ABED ，因为BD ⊂平面ABED ，所以//BD 平面FGH .(II)证明：连接HE .因为G H ，分别为AC BC ，的中点，所以//,GH AB 由,AB BC ⊥得GH BC ⊥，又H 为BC 的中点，所以//,,EF HC EF HC =因此四边形EFCH 是平行四边形，所以//.CF HE又CF BC ⊥，所以HE BC ⊥.又,HE GH ⊂平面EGH ，HE GH H ⋂=，所以BC ⊥平面EGH ，又BC ⊂平面BCD ，所以平面BCD ⊥平面.EGH 17(Ⅰ)点F ，G ，H 的位置如图所示 (Ⅱ)平面BEG ∥平面ACH .证明如下因为ABCD －EFGH 为正方体，所以BC ∥FG ，BC ＝FG又FG ∥EH ，FG ＝EH ，所以BC ∥EH ，BC ＝EH 于是BCEH 为平行四边形所以BE ∥CH又CH ⊂平面ACH ，BE ⊄平面ACH ，所以BE ∥平面ACH 同理BG ∥平面ACH 又BE ∩BG ＝B 所以平面BEG ∥平面ACH(Ⅲ)连接FH 因为ABCD －EFGH 为正方体，所以DH ⊥平面EFGH 因为EG ⊂平面EFGH ，所以DH ⊥EG又EG ⊥FH ，EG ∩FH ＝O ，所以EG ⊥平面BFHD 又DF ⊂平面BFDH ，所以DF ⊥EG 同理DF ⊥BG 又EG ∩BG ＝G 所以DF ⊥平面BEG .F。

高二下学期经典完整数学周测试卷及答案详解

高二年级下学期数学周测试卷及答案案详解（答案附后）姓名：班级：学号: 得分：一、填空题（请把正确的答案写在题后的横线上，每小题5分，共80分）1.已知函数f （x ）=ax 3﹣2x 的图象过点P （﹣1，4），则曲线y=f （x ）在点P 处的切线方程为．2.函数()f x 在()-∞+∞，单调递减，且为奇函数．若()11f =-，则满足()121f x --≤≤的x 的取值范围是；3.已知双曲线22221x y C a b-=：（0a >，0b >）的一条渐近线方程为y =，且与椭圆221123x y +=有公共焦点．则C 的方程为； 4．已知椭圆2222:1x y C a b+=（0a b >>）的左、右顶点分别为1A ，2A ，且以线段1A 2A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为；5．△ABC 的内角A 、B 、C 的对边分别为a 、b 、c 。

已知sin sin (sin cos )0B A C C +-=，a =2，c C = ；6.已知π(0)2a ∈，,tan α=2，则πcos ()4α-=__________；7.从分别写有1,2,3,4,5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为__________； 8.函数()cos sin =2+fx x x 的最大值为； .9．设函数10()20x x x f x x +≤⎧=⎨>⎩，，，，则满足1()()12f x f x +->的x 的取值范围是__________；10.若复数(1i)(i)a -+在复平面内对应的点在第二象限，则实数a 的取值范围是；11.已知点P 在圆22=1x y +上，点A 的坐标为(-2,0)，O 为原点，则AO AP ⋅的最大值为_________．12.已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==，则,,a b c 的大小关系为；13.已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为；14.若a ，b ∈R ，0ab >，则4441a b ab++的最小值为； .15.用数字1，2，3，4，5，6，7，8，9组成没有重复数字，且至多有一个数字是偶数的四位数，这样的四位数一共有___________个.（用数字作答）16.已知12,e e 12-e 与12λ+e e 的夹角为60，则实数λ的值是 .二、解答题（20分）17．已知函数f (x )=（x e x-（12x ≥）. （Ⅰ）求f (x )的导函数；（Ⅱ）求f (x )在区间1[+)2∞，上的取值范围.高二年级下学期数学周测试卷（6月）参考答案1.【解答】解：函数f （x ）=ax 3﹣2x 的图象过点P （﹣1，4），可得﹣a +2=4，解得a=﹣2，则f （x ）=﹣2x 3﹣2x ，f （x ）的导数为f′（x ）=﹣6x 2﹣2，则曲线y=f （x ）在点P 处的切线斜率为﹣8，可得曲线y=f （x ）在点P 处的切线方程为y ﹣4=﹣8（x +1），即为8x +y +4=0．故答案为：8x +y +4=0．2.【解答】因为()f x 为奇函数，所以()()111f f -=-=，于是()121f x --≤≤等价于()()()121f f x f --≤≤|又()f x 在()-∞+∞，单调递减121x ∴--≤≤3x ∴1≤≤即[]13，3.【解答】∵双曲线的一条渐近线方程为y =，则b a =又∵椭圆221123x y +=与双曲线有公共焦点，易知3c =，则2229a b c +==②由①②解得2,a b =C 的方程为22145x y -=，4.【解析】∵以12A A 为直径为圆与直线20bx ay ab -+=相切，∴圆心到直线距离d 等于半径，∴d a==又∵0,0a b >>，则上式可化简为223a b =∵222b a c =-，可得()2223a a c =-，即2223c a =∴，c e a ==5.【解析】由题意sin()sin (sin cos )0A C A C C ++-=得sin cos cos sin sin sin sin cos 0A C A C A C A C ++-=，即sin (sin cos )sin()04C A A C A π+=+=，所以34A π=.由正弦定理sin sin a c A C =得23sin sin 4C π=，即1sin 2C =，得6C π=6、7.【解析】如下表所示，表中的点横坐标表示第一次取到的数，纵坐标表示第二次取到的数总计有25种情况，满足条件的有10种所以所求概率为102255=。

高二文科数学试题

高二阶段性检测文科数学试题说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分150分，考试用时120分钟。

注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目写在答题卡上。

2．每小题选出答案后，用HB 或者2B 铅笔把答题卡上的对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试题卷上。

第Ⅰ卷（选择题，共50分）一、本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中只有一个是符合题目要求的选项。

1．如果命题“p q 或”和命题“p q 且”都为真，则有A ．p q 真假B ．p q 假真C ．p q 真真D ．p q 假假2．若b a >，则下列不等式中恒成立的是A ．1>ba B ．b a lg lg > C ．b a 22> D ．22b a > 3．已知{}n a 是等差数列，且2581148a a a a +++=，则67a a +=A ．12B ．16C ．20D ．244. 已知命题p ：,20x x R ∀∈>，那么命题p ⌝为A. ,20xx R ∃∈< B. ,20x x R ∀∈< C. ,20x x R ∃∈≤ D. ,20xx R ∀∈≤5.原点和点（1，1）在直线a y x =+两侧，则a 的取值范围是A ．20<<aB ．0<a 或2>aC ．0=a 或2=aD ．20≤≤a 6.在ABC ∆中,角,,A B C 所对的边分别是,,a b c ，若cos b C a>，则ABC ∆的形状是A ．等腰三角形B ．锐角三角形C ．钝角三角形D ．直角三角形7．设123)(+-=a ax x f ，若存在)1,1(0-∈x ，使0)(0=x f ，则实数a 的取值范围是A ．511<<-aB ．1-<aC ．或1-<a 51>aD ．51>a 8. 一船向正北航行，看见正西方向相距10海里的两个灯塔恰好与它在一条直线上，继续航行半小时后，看见一灯塔在船的南偏西060，另一灯塔在船的南偏西075，则这艘船的速度是每小时A ．5海里B ．53海里C ．10海里D ．103海里9．数列{}n a 满足：12121,2,(3)n n a n a a a a n n N --===≥∈且，则2014a =A ．1B ．2C ．12D ．20142- 10．直角三角形的斜边长为m ，则其内切圆半径的最大值为A ．m 22B ．m 212-C ．m 2D ．m )12(-第Ⅱ卷（非选择题,共100分）二、填空题：本大题共5小题，每小题5分，共25分。

2020-2021学年度高二文科数学10月份周练试卷附答案

（2）求证： ∥平面．
20．已知直线l：kx-y+1+2k=0(k∈R)
(1)证明：直线l过定点；
(2)若直线l不经过第四象限，求实数k的取值范围；
(3)若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，求S的最小值及此时直线l的方程．
21.在边长为的正方形中，分别为的中点，分别为的中点，现沿折叠，使三点重合，重合后的点记为，构成一个三棱锥．
(1)请判断与平面的位置关系，并给出证明；
(2)证明：平面；
(3)求三棱锥B-AEN的体积．
22.如图，在四棱锥P-ABCD中，AB//CD，且．
（1）证明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC，，且四棱锥P-ABCD的体积为，求该四棱锥的侧面积．
1-5.DCABC 6-10.CAAAA 11-12.CB
要使直线l不经过第四象限必须且只需，
故k∈[0, )；
(3)由直线l交x轴负半轴于点A，交y轴正半轴于点B知：k>0，
由直线l:kx-y+1+2k=0中，令则，
再令，则，所以有：
（当且仅当时，取等号），
所以，S的最小值为4，此时l的方程为：x-2y+4=0．
21.
22.
三、解答题
17．已知直线，．
(．
18.如图，ABCD是正方形，O是正方形的中心，PO 底面ABCD，E是PC的中点．
求证：（1）PA∥平面BDE；
（2）平面PAC 平面BDE．
19．如图，在直三棱柱中，分别为棱的中点，且．
（1）求证：平面平面；
13.x－2y＋4＝014. 15.3x＋4y＝0或x＋y＋1＝016.

2021年高二下学期数学周练试题(文科实验班3.6) 含答案

2021年高二下学期数学周练试题（文科实验班3.6）含答案一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．如果复数为纯虚数，那么实数的值为（）A ．-2B ．1C ．2D ．1或-22．若大前提是：任何实数的平方都大于0，小前提是：，结论是：，那么这个演绎推理（） A ．大前提错误 B ．小前提错误 C ．推理形式错误 D ．没有错误 3．若P=+，Q=+（a≥0），则P ，Q 的大小关系是（）A.P ＞QB.P=QC.P ＜QD.由a 的取值确定 4．设，则（）A ．都不大于－4B ．都不小于－4C ．至少有一个不大于－4D ．至少有一个不小于－45．某部门为了了解青年人喜欢户外运动是否与性别有关，运用2×2列联表进行独立性检验，经计算K 2=7.069，则所得到的统计学结论为：有（）把握认为“喜欢户外运动与性别有关”．A.0.1%B.1%C.99%D.99.9% 6．以下五个命题:①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；②样本方差反映了样本数据与样本平均值的偏离程度；③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；④在回归直线方程中，当解释变量x 每增加一个单位时，预报变量增加0.1个单位；⑤在一个2×2列联表中，由计算得k 2=13.079，则其两个变量间有关系的可能性是90%以上．其中正确的是（）A.①③⑤B.①③④C.②③④⑤D.②④ 7．对具有线性相关关系的变量x ，y 有一组观测数据（x i ，y i ）（ i=1，2，…，8），其回归直线方程是=x+a 且x 1+x 2+…+x 8=6，y 1+y 2+…+y 8=3，则实数a 的值是（） A. B. C. D.8．已知，由不等式221442,3,22x x x x x x x +≥=+=++≥=我们可以得出推广结论：，则（）A ．B ．C ．D ．9．给出以下数阵，按各数排列规律，则的值为（）122353416164565655nA． B． C．326 D．10．已知整数的数对列如下:（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4），，则第60个数对是（）A．（3，8） B．（4，7） C．（4，8） D．（5，7）11．观察下面关于循环小数化分数的等式：.......31182352159590.3,1.18,0.352,0.0005993991199910009999000======⨯=，据此推测循环小数，可化成分数（）A． B． C． D．12．面积为S的平面凸四边形的第条边的边长记为，此四边形内任一点P到第条边的距离记为，若，则．类比以上性质，体积为V的三棱锥的第个面的面积记为，此三棱锥内任一点Q 到第个面的距离记为，若，则等于（）A． B． C． D．二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上）13．数（i是虚数单位）的实部是．14．已知边长分别为a、b、c的三角形ABC面积为S，内切圆O半径为r，连接OA、OB、OC，则三角形OAB、OBC、OAC的面积分别为、、，由得，类比得四面体的体积为V，四个面的面积分别为,则内切球的半径R= ．15．如图，第n个图形是由正n + 2 边形“扩展”而来，，则在第n个图形中共_ 有个顶点．（用n表示）16．观察下列等式:，，2323456(1)136763x x x x x x x x++=++++++，242345678(1)1410161916104x x x x x x x x x x++=++++++++，由以上等式推测:对于，若则．三、解答题（本大题共6小题，第17小题10分，其余每小题12分，共70分.解答时应写出必要的文字说明、证明过程或演算步骤）17．（本小题满分10分）为考察某种药物预防禽流感的效果，进行动物家禽试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本.（1）根据所给样本数据完成下面2×2列联表；（2）请问能有多大把握认为药物有效？18．（本小题满分12分）已知a ，b ，c ，d ∈（0，＋∞），求证ac ＋bd ≤． 19．（本小题满分12分）已知，试证明至少有一个不小于1． 20．（本小题满分12分）设（1）计算：的值；（2）猜想具备的一个性质，并证明． 21．（本小题满分12分）数列满足，．（1）求证：；（2）设，求不超过的最大整数． 22．（本小题满分12分）图（1）、（2）、（3）、（4）分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”，按同样的方式构造图形，设第个图形包含个“福娃迎迎”．（1）求出；（2）利用合情推理的“归纳推理思想”归纳出与的关系式（不需证明）；（3）根据你得到的关系式求的表达式．不得禽流感得禽流感总计服药不服药总计丰城中学xx 学年度下学期高二数学（文）周考试卷答案1—6 AACCCC 7—12 BDDDDB 13． 14． 15． 16．（2）假设检验问题H ：服药与家禽得禽流感没有关系由P()＝0.10 所以大概90％认为药物有效 18. 解：证明：法一：（分析法）欲证ac ＋bd ≤，只需证（ac ＋bd ）2≤（a 2＋b 2）（c 2＋d 2），即证a 2c 2＋2abcd ＋b 2d 2≤a 2c 2＋b 2d 2＋a 2d 2＋b 2c 2，即证2abcd ≤a 2d 2＋b 2c 2，即证0≤（bc －ad ）2，而a ，b ，c ，d ∈（0，＋∞），0≤（bc －ad ）2显然成立，故原不等式成立．法二：（综合法）（a 2＋b 2）（c 2＋d 2）＝a 2c 2＋b 2d 2＋a 2d 2＋b 2c 2≥a 2c 2＋b 2d 2＋2abcd＝（ac ＋bd ）2，所以≥ac ＋bD ． 19．解: 假设均小于1，即，则有而22112232()3322a b c x x x ++=-++=-+≥，矛盾．所以原命题成立20. 解: （1）33633213331311331331)1()0(10=-+-=+++=+++=+f f 同理，可得（2）猜想：当时，证明：设，33)3233(332333)33(333233)33)(33()33)(33(21212121212112=++++=+++++=++++=+x x x x x x x x x x x x x x 时，21. 解: （1）因为，故1)1()1()1()()()(1222221112211>+-++-+-=+-++-+-=-----a a a a a a a a a a a a n n n n n n n ，于是．（2）解：，于是所以于是113)1111()1111()1111(2014201420133221--=---++---+---=a a a a a a a m 当时，，于是，故，所以，所以不超过m 的最大整数是2．22. 解: （1）f （1）=1,f （2）=5,f （3）=13,f （4）=25,f （5）=25+4×4=41．（2）f （2）-f （1）=4=4×1．f （3）-f （2）=8=4×2,f （4）-f （3）=12=4×3, f（5）-f （4）=16=4×4,由上式规律得出f （n+1）-f （n ）=4n ．（3） f （2）-f （1）=4×1, f（3）-f （2）=4×2, f（4）-f （3）=4×3, f（n-1）-f （n-2）=4·（n-2）, f （n ）-f （n-1）=4·（n-1） f （n ）-f （1）=4[1+2+ +（n-2）+（n-1）]=2（n-1）·n,f （n ）=2n 2-2n+1（）f （1）=1也满足上式，f （n ）=2n 2-2n+1 26907 691B 椛\n39855 9BAF 鮯38878 97DE 韞28777 7069 灩28331 6EAB溫hy26460 675C 杜32627 7F73 罳n 39493 9A45 驅-。

2021年高二下学期数学周练试题(文科实验班3.13) 含答案

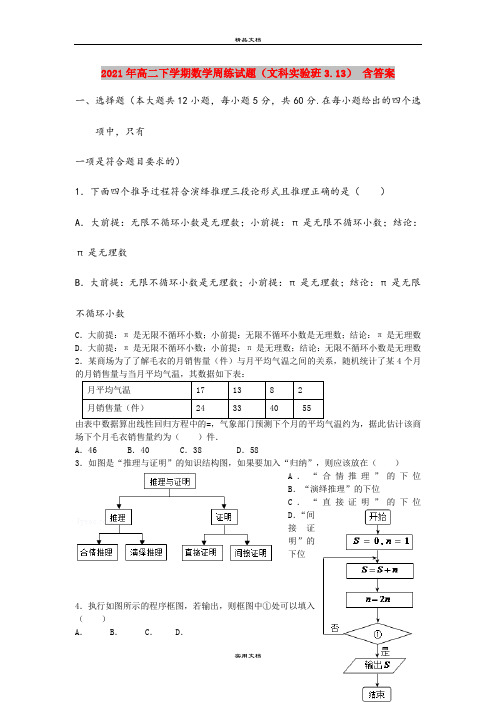
2021年高二下学期数学周练试题（文科实验班3.13）含答案一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．下面四个推导过程符合演绎推理三段论形式且推理正确的是（）A．大前提：无限不循环小数是无理数；小前提：π是无限不循环小数；结论：π是无理数B．大前提：无限不循环小数是无理数；小前提：π是无理数；结论：π是无限不循环小数C．大前提：π是无限不循环小数；小前提：无限不循环小数是无理数；结论：π是无理数D．大前提：π是无限不循环小数；小前提：π是无理数；结论：无限不循环小数是无理数2．某商场为了了解毛衣的月销售量（件）与月平均气温之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：月平均气温171382月销售量（件）243340 55由表中数据算出线性回归方程中的=，气象部门预测下个月的平均气温约为，据此估计该商场下个月毛衣销售量约为（）件．A．46 B．40 C．38 D．583．如图是“推理与证明”的知识结构图，如果要加入“归纳”，则应该放在（）A．“合情推理”的下位B．“演绎推理”的下位C．“直接证明”的下位D．“间接证明”的下位4．执行如图所示的程序框图，若输出，则框图中①处可以填入（）A． B． C． D．5．想沏壶茶喝．洗烧开水的壶、灌入凉水需2分钟，洗茶壶、茶杯需2分钟，拿茶叶需1分钟，烧开水需15分钟，沏茶需1分钟．最省时的操作时间是（）A．20分钟 B．19分钟 C．18分钟 D．17分钟6．用反证法证明命题“若，，则三个实数中最多有一个小于零”的反设内容为（）A．三个实数中最多有一个不大于零B．三个实数中最多有两个小于零 C．三个实数中至少有两个小于零D．三个实数中至少有一个不大于零7．在复平面内，复数为虚数单位），对应的的点在第三象限的充要条件是（）A. B. C. D.8．下面关于复数的四个命题：，，的共轭复数为，在复平面内对应点位于第四象限．其中真命题为（）A．、 B．、 C．、 D．、9．复数Z与点Z对应，为两个给定的复数，，则决定的Z的轨迹是（）A.过的直线B. 以Z为端点的圆C.双曲线的一支D.线段的中垂线10．由于工业化城镇化的推进，大气污染日益加重，空气质量逐步恶化，雾霾天气频率增大，大气污染可引起心悸、胸闷等心脏病症状．为了解某市患心脏病是否与性别有关，在某医院患心脏病不患心脏病合计男20525女101525合计302050参考临界值表：p（p2≥k）0.150.100.050.0250.0100.0050.001K 2.072 2.706 3.841 5.024 6.6357.87910.828问有多大的把握认为是否患心脏病与性别有关．答：（）A.95%B. 99.5%C. 99%D.99.9%11．如图，第（1）个图案由1个点组成，第（2）个图案由3个点组成，第（3）个图案由7个点组成，第（4）个图案由13个点组成，第（5）个图案由21个点组成，，依次类推，根据图案中点的排列规律，第100个图形由多少个点组成（）A．B．C．D．12．设2222222211111111 111112233420142015 S=+++++++++大于S的最大整数［S］等于（）A.xxB.xxC.xxD.xx二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上）13．若，，，，则_____________．14．已知复数且，则的范围为_____________．15．在△ABC 中，若D 为BC 的中点，则有，将此结论类比到四面体中，在四面体 A-BCD 中，若G 为△BCD 的重心，则可得一个类比结论：_____________．16．凸函数的性质定理为：如果函数在区间上是凸函数，则对于区间内的任意，有1212()()()()n nf x f x f x x x x f nn++++++≤,已知函数在区间上是凸函数，则在中，的最大值为_____________．三、解答题（本大题共6小题，第17小题10分，其余每小题12分，共70分.解答时应写出必要的文字说明、证明过程或演算步骤）17．（本小题满分10分）已知复数（是虚数单位），函数．（1）若,求实数的值; （2）解不等式． 18．（本小题满分12分）已知正数、、满足，求证：． 19．（本小题满分12分）已知求证． 20．（本小题满分12分）已知正数成等差数列，且公差，用反证法求证：不可能是等差数列。

2021年高二上学期数学周练试卷(文科实验班1.10) 含答案

2021年高二上学期数学周练试卷（文科实验班1.10）含答案一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．若椭圆的离心率为，则双曲线的渐近线方程为（）A ．B ．C ．D ．2．给出下列关于互不相同的直线和平面的四个命题，其中正确命题的个数是（）（1），点则与m 不共面；（2）是异面直线，且则；（3）若则；（4）若，则，（5）若，，则A ．1个B ．2个C ．3个D ．4个3．设点、、为球的球面上三点，为球心，若球的表面积为，且是边长为的正三角形，则三棱锥的体积为（）A ．12B ．C ．D ．4．一个圆锥被过顶点的平面截去了较少的一部分几何体，余下的几何体的三视图如下，则余下部分的几何体的体积为（）A ．B ．C ．D ．5．已知正四棱柱中,, 为的中点，则点到平面的距离为（）A ．1B ．C ．D ．26．下列命题中正确的是（）A ．若为真命题，则为真命题B ．“，”是“”的充分必要条件C ．命题“若，则或”的逆否命题为“若或，则”D ．命题，使得，则，使得7．已知(){}(){},(3)34,7(5)80x y m x y m x y x m y ++=-+--==∅，则直线与坐标轴围成的三角形面积是（）A ．1B ．2C ．3D ．48．直线R ）与椭圆恒有公共点，则的取值范围是（）A．（0，1） B．（0，5） C． D．9．对任意的实数,若表示不超过的最大整数,则“”是“”的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件10．若函数不是单调函数，则实数的取值范围是（）A． B． C． D．11．已知函数对任意的满足（其中是函数的导函数），则下列不等式成立的是（）A． B． C． D．12．设函数的导函数为，对任意R都有成立，则（）A． B．C． D．的大小不确定二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上）13．过点的直线与圆相交于两点，则的最小值为___________．14．已知直线与曲线相切，则的值为___________．15．已知是双曲线的左、右焦点，若点关于直线的对称点也在双曲线上，则该双曲线的离心率为___________．16．以下四个关于圆锥曲线的命题中：①设为两个定点，为非零常数，，则动点的轨迹为双曲线；②过定圆上一定点作圆的动弦，则弦中点P的轨迹为椭圆；③方程的两根可分别作为椭圆和双曲线的离心率；④双曲线与椭圆有相同的焦点．其中真命题的序号为___________．（写出所有真命题的序号）三、解答题（本大题共6小题，第17小题10分，其余每小题12分，共70分.解答时应写出必要的文字说明、证明过程或演算步骤）17．（本小题满分10分）设：实数满足，其中，命题：实数满足（1）若，且为真，求实数的取值范围；（2）若是的必要不充分条件，求实数的取值范围．18．（本小题满分12分）如图，直三棱柱中，，分别是，的中点，．（1）证明：平面；（2）当时，求三棱锥的体积．19．（本小题满分12分）在直角坐标系xOy中，圆C：，圆心为C，圆C与直线的一个交点的横坐标为2．（1）求圆C的标准方程；（2）直线与垂直，且与圆C交于不同两点A、B，若，求直线的方程．20．（本小题满分12分）统计表明，某种型号的汽车在匀速行驶中每小时的耗油量（升）关于行驶速度（千米/小时）的函数解析式可以表示为：3138(0120)12800080y x x x =-+<≤，已知甲、乙两地相距100千米（1）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？（2）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？21．（本小题满分12分）已知抛物线C ：y 2=4x ，点M （m ，0）在x 轴的正半轴上，过点M 的直线l 与抛物线C 相交于A ，B 两点，O 为坐标原点．（1）若m=1，且直线l 的斜率为1，求以AB 为直径的圆的方程；（2）是否存在定点M ，使得不论直线l 绕点M 如何转动，恒为定值？22．（本小题满分12分）已知函数：．（1）讨论函数的单调性；（2）若对于任意的，若函数在区间上有最值，求实数的取值范围．丰城中学xx 学年度上学期高二数学（文）周考试卷答案1—6 ACBDAD 7—12 BCBCAC13． 4 14． 2 15． 16．③④17. 解：（1）化简p ：集合化简q ：集合依题意有为真，（2）若是的必要不充分要条件，则且逆命题不成立，即。

高二文科数学周考试卷含答案

高二文科数学周考试卷一、选择题(共12小题,每小题5.0分,共60分)1.下列说法：①从投影角度看，三视图是在平行投影下画出的；②平行投影的投影线互相平行，中心投影的投影线交于一点；③空间图形经过中心投影后，直线变成直线，但平行线有可能变成相交直线；④如果一个三角形的平行投影仍是三角形，那么它的中位线的平行投影，一定是这个三角形的平行投影的中位线．其中正确的有 ()A． 1个B． 2个C． 3个D． 4个2.能保证直线与平面平行的条件是()A．直线与平面内的一条直线平行B．直线与平面内的某条直线不相交C．直线与平面内的无数条直线平行D．直线与平面内的所有直线不相交3.空间四点A、B、C、D共面而不共线，那么这四点中()A．必有三点共线B．必有三点不共线C．至少有三点共线D．不可能有三点共线4.一个样本的数据在60左右波动，各个数据都减去60后得到一组新数据，算得其平均数是6，则这个样本的平均数是()A． 6.6 B． 6 C． 66 D． 605.过点P(1,1)的直线，将圆形区域{(x，y)|x2＋y2≤4}分成两部分，使得这两部分的面积之差最大，则该直线的方程为()A．x＋y－2＝0 B．y－1＝0C．x－y＝0 D．x＋3y－4＝06.已知两条平行直线l1：3x＋4y＋5＝0，l2：6x＋by＋c＝0间的距离为3，则b＋c等于()A．－12 B． 48 C． 36 D．－12或487.光线从点A(－3,5)射到x轴上，经反射后经过点B(2,10)，则从A到B光线通过的距离是() A． 5B． 2C． 5D． 108.直线(a－2)y＝(3a－1)x－1恒过()A．第一象限B．第二象限C．第三象限D．第四象限9.一名小学生的年龄和身高(单位：cm)的数据如下表：由散点图可知，身高y与年龄x之间的线性回归方程为＝8.8x＋，预测该学生10岁时的身高为()A．154 cm B．153 cm C．152 cm D．151 cm10.如图所示，程序的输出结果为S＝132，则判断框中应填()A．i≥10?B．i≥11?C．i≤11?D．i≥12?11.已知某几何体的三视图如图所示，则该几何体的体积为()A．B．C．D．12.已知圆x2＋y2－2x－4y＋a＝0上有且仅有一个点到直线3x－4y－15＝0的距离为1，则实数a的取值范围为()A．B．－4C．－4或－20 D．－11二、填空题(共4小题,每小题5.0分,共20分)13.已知直线l1：ax－3y＋1＝0，l2：2x＋(a＋1)y＋1＝0.若l1⊥l2，则实数a的值等于____________．14.奶粉添加三聚氰胺问题引起全社会关注，某市质量监督局为了保障人民的饮食安全，要对超市中奶粉的质量进行专项抽查．已知该市超市中各种类型奶粉的分布情况如下：老年人专用奶粉300种，普通奶粉240种，婴幼儿奶粉360种．现采用分层抽样的方法抽取150种进行检验，则这三种型号的奶粉依次应抽取________．15.已知直线y＝x＋b与x轴、y轴的交点分别为A、B，如果△AOB的面积(O为坐标原点)不大于1，那么b的取值范围是________．16.由动点P向圆x2＋y2＝1引两条切线PA、PB，切点分别为A、B且∠APB＝60°，则动点P的轨迹方程为________．三、解答题17.已知点P(－4,2)和直线l：3x－y－7＝0.求：(1)过点P与直线l平行的直线方程一般式；(2)过点P与直线l垂直的直线方程一般式．18.已知圆C：(x－1)2＋(y－2)2＝25，直线l：(2m＋1)x＋(m＋1)y－7m－4＝0.(1)求证：直线l过定点并判断该定点与圆的位置关系(2)当m为何值时，直线l被圆C截得的弦最长19.如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y （吨标准煤）的几组对应数据．（1）请求出y关于x的线性回归方程=a+bx；（2）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤，试根据（1）中求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？（参考数值：3×2.5+4×3+5×4+6×4.5=66.5）参考公式：20.某学校为了了解学生的日平均睡眠时间(单位：h)，随机选择了n名同学进行调查，下表是这n 名同学的日平均睡眠时间的频率分布表：(1)求n的值；(2)若a＝20，试确定x、y、z、m的值；(3)统计方法中，同一组数据常用该组区间的中点值(例如[4,5)的中点值4.5)作为代表．若据此计算的这n名学生的日平均睡眠时间的平均值为6.68.求a、b的值．21.如图，在长方体ABCD－A1B1C1D1中，E为线段BC的中点，AB＝1，AD＝2，AA1＝.(1)证明：DE⊥平面A1AE；(2)求点A到平面A1ED的距离．22.已知点P（2，0）及圆C：x2+y2﹣6x+4y+4=0．（1）设过P的直线l1与圆C交于M、N两点，当|MN|=4时，求以MN为直径的圆Q的方程；（2）设直线ax﹣y+1=0与圆C交于A，B两点，是否存在实数a，使得过点P（2，0）的直线l2垂直平分弦AB？若存在，求出实数a的值；若不存在，请说明理由．答案解析1.【答案】C2.【答案】D 【解析】A 不正确，因为由直线与平面内的一条直线平行，不能推出直线与平面平行，直线有可能在平面内；B 不正确，因为由直线与平面内的某条直线不相交，不能推出直线与平面平行，直线有可能在平面内，也可能和平面相交；C 不正确，因为由直线与平面内的无数条直线平行，不能推出直线与平面平行，直线有可能在平面内；D 正确，因为由直线与平面内的所有直线不相交，依据直线和平面平行的定义可得直线与平面平行．故选D. 3.【答案】B 【解析】A 、B 、C 、D 共面而不共线，这四点可能有三点共线，也可能任意三点不共线，A 错误；如果四点中没有三点不共线，则四点共线，矛盾，故B 正确；当任意三点不共线时，也满足条件，故C 错误，当其中三点共线，第四个点不共线时，也满足条件，故D 错误，故选B.4.【答案】C 【解析】样本中的数据都减去60后得到一组新数据，新数据的平均数是6，那么这个样本的平均数是6＋60＝66.5.【答案】A 【解析】要使直线将圆形区域分成两部分的面积之差最大，通过观察图形(图略)，显然只需该直线与直线OP 垂直即可，又已知P (1,1)，则所求直线的斜率为－1，又该直线过点P (1,1)，易求得该直线的方程为x ＋y －2＝0.故选A.6. 【答案】D 将l 1：3x ＋4y ＋5＝0改写为6x ＋8y ＋10＝0，因为两条直线平行，所以b ＝8. 由＝3，解得c ＝－20或c ＝40.所以b ＋c ＝－12或48，故选D.7. 【答案】C【解析】A 点关于x 轴的对称点是C （-3，-5），故/BC/即为所求距离，由两点间距离公式得C 8. 【答案】A 【解析】直线(a －2)y ＝(3a －1)x －1，即a (3x －y )－x ＋2y －1＝0，由，，求得，，故直线(a －2)y ＝(3a －1)x －1恒过定点（，），故直线(a －2)y ＝(3a －1)x －1恒过第一象限，故选A. 9.【答案】B 【解析】由题意，＝7.5，＝131，代入线性回归方程＝8.8x ＋，得131＝8.8×7.5＋，可得＝65，∴ ＝8.8x ＋65. ∴当x ＝10时，＝8.8×10＋65＝153.10.【答案】B 【解析】对于选项可以逐个验证，当判断框中填写i ≥10？时，输出结果为S ＝1 320；当判断框中填写i ≥11？时，输出结果为S ＝132；当判断框中填写i ≤11？时，输出结果为S ＝1；当判断框中填写i ≥12？时，输出结果为S ＝12.11.【答案】B 【解析】由三视图可知，几何体表示的是三棱柱去掉三棱锥，三棱柱的体积V1＝S△ABE·EF＝×4×4×4＝32，三棱锥的体积V2＝×S△BFG×EF＝××2×4×4＝，因此该几何体V1－V2＝32－＝，故选B.12.【答案】B【解析】化圆的方程为(x－1)2＋(y－2)2＝5－a，由题易知直线与圆相离，则有－＝1，解得a＝－4，故选B.13.【答案】－3【解析】∵直线l1：ax－3y＋1＝0，l2：2x＋(a＋1)y＋1＝0，且l1⊥l2，∴＝－1，∴a＝－3.14.【答案】50种，40种，60种【解析】抽样比为＝，∴300×＝50,240×＝40,360×＝60.15.【答案】[－1,0)∪(0,1]【解析】令x＝0，得y＝b，令y＝0，得x＝－2b，∵△AOB的面积(O为坐标原点)不大于1，∴△AOB的面积S＝|b|×|－2b|＝|b|2≤1，∵b＝0时，A、O、B三点重合，构不成三角形，∴b≠0，∴－1≤b＜0或0＜b≤1.16.【答案】x2＋y2＝4【解析】由题意得满足条件的图形，如图所示．∵∠APB＝60°，∴∠OPB＝30°，即|OP|＝2|OB|＝2.∴点P的轨迹是以原点为圆心，半径长为2的圆，其方程为x2＋y2＝4.17.【答案】(1)设过点P与直线l平行的直线方程为3x－y＋m＝0，把P(－4,2)代入可得，－4×3－2＋m＝0，解得m＝14.∴过点P与直线l平行的直线方程一般式为3x－y＋14＝0.(2)设过点P与直线l垂直的直线方程为x＋3y＋n＝0，把P(－4,2)代入可得，－4＋3×2＋n＝0，解得n＝－2.∴过点P与直线l垂直的直线方程一般式为x＋3y－2＝0.18.【答案】(1)证明把直线l的方程整理成m(2x＋y－7)＋(x＋y－4)＝0，由于m的任意性，有解得∴直线l恒过定点D(3,1)．把点D(3,1)的坐标代入圆C的方程，得左边＝5＜25＝右边，∴点D(3,1)在圆C内．(2)解当直线l经过圆心C(1,2)时，被截得的弦最长(等于圆的直径长)，此时，直线l的斜率k l＝k CD，由直线l的方程得k l＝－，由点C、D的坐标得k CD＝＝－.∴－＝－，解得m＝－，∴当m＝－时，直线l被圆C截得的弦最长．19.【答案】解（1）由对照数据，计算得=4.5，=3.5，∴===0.7，=﹣b=0.35，∴所求线性回归方程为=0.7x+0.35；（2）由（1）求出的线性回归方程，估计生产100吨甲产品的生产能耗为0.7×100+0.35=70.35（吨），∴估计生产100吨甲产品的生产能耗为70.35吨．20.【答案】解：(1)样本容量n＝＝50.(2)x＝0.20×50＝10，y＝0.4，z＝0.24，m＝4.(3)n＝50，P(i＝3)＝，P(i＝4)＝，平均时间为 4.5×0.08＋5.5×0.2＋6.5×＋7.5×＋8.5×0.08＝6.68，即13a＋15b＝454.①又4＋10＋a＋b＋4＝50，即a＋b＝32，②由①②解得，a＝13，b＝19.21.【答案】(1)证明因为A1A⊥平面ABCD，DE⊂平面ABCD，所以A1A⊥DE.因为E为BC的中点，BE＝EC＝AB＝CD＝1，所以AE＝DE＝.又因为AD＝2，所以AE2＋DE2＝AD2，所以AE⊥DE.又AE⊂平面A1AE, A1A⊂平面A1AE，且AE∩A1A＝A，所以DE⊥平面A1AE.(2)解设点A到平面A1ED的距离为d，－＝××××＝.因为A1A⊥平面ABCD，所以AA1⊥AE，又AA1＝AE＝，所以A1E＝2.由(1)知DE⊥平面A1AE，所以DE⊥A1E，∴△＝×2×＝，∴－＝×d＝，∴d＝1.22.（1）由于圆C：x2+y2﹣6x+4y+4=0的圆心C（3，﹣2），半径为3，|CP|=，而弦心距d=，所以d=|CP|=，所以P为MN的中点，所以所求圆的圆心坐标为（2，0），半径为|MN|=2，故以MN为直径的圆Q的方程为（x﹣2）2+y2=4；（2）把直线ax﹣y+1=0即y=ax+1．代入圆C的方程，消去y，整理得（a2+1）x2+6（a﹣1）x+9=0．由于直线ax﹣y+1=0交圆C于A，B两点，故△=36（a﹣1）2﹣36（a2+1）＞0，即﹣2a＞0，解得a＜0．则实数a的取值范围是（﹣∞，0）．设符合条件的实数a存在，由于l2垂直平分弦AB，故圆心C（3，﹣2）必在l2上．所以l2的斜率k PC=﹣2，∴k AB=a=，由于，故不存在实数a，使得过点P（2，0）的直线l2垂直平分弦AB．。

2021年高二数学下学期周练试题(文科实验班,3.6)

2021年高二数学下学期周练试题（文科实验班，3.6）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．如果复数为纯虚数，那么实数的值为（）A．-2 B．1 C．2 D．1或-22．若大前提是：任何实数的平方都大于0，小前提是：，结论是：，那么这个演绎推理（）A．大前提错误 B．小前提错误 C．推理形式错误 D．没有错误3．若P=+，Q=+（a≥0），则P，Q的大小关系是（）A.P＞QB.P=QC.P＜QD.由a的取值确定4．设，则（）A．都不大于－4 B．都不小于－4C．至少有一个不大于－4 D．至少有一个不小于－45．某部门为了了解青年人喜欢户外运动是否与性别有关，运用2×2列联表进行独立性检验，经计算K2=7.069，则所得到的统计学结论为：有（）把握认为“喜欢户外运动与性别有关”．附：（独立性检验临界值表）A.0.1%B.1%C.99%D.99.9%6．以下五个命题:①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；②样本方差反映了样本数据与样本平均值的偏离程度；③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；④在回归直线方程中，当解释变量x每增加一个单位时，预报变量增加0.1个单位；⑤在一个2×2列联表中，由计算得k2=13.079，则其两个变量间有关系的可能性是90%以上．其中正确的是（）A.①③⑤B.①③④C.②③④⑤D.②④7．对具有线性相关关系的变量x，y有一组观测数据（x i，y i）（ i=1，2，…，8），其回归直线方程是=x+a且x1+x2+…+x8=6，y1+y2+…+y8=3，则实数a的值是（）A. B. C. D.8．已知，由不等式32221144422,33,2222x x x x x x x x x x x x+≥⋅=+=++≥⋅⋅=我们可以得出推广结论：，则（）A ．B ．C ．D ．9．给出以下数阵，按各数排列规律，则的值为（）122353416164565655n A ． B ． C ．326 D ． 10．已知整数的数对列如下:（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4），，则第60个数对是（） A ．（3，8） B ．（4，7） C ．（4，8） D ．（5，7） 11．观察下面关于循环小数化分数的等式：. (3118235215959)0.3,1.18,0.352,0.0005993991199910009999000======⨯=，据此推测循环小数，可化成分数（）A ．B ．C ．D ． 12．面积为S 的平面凸四边形的第条边的边长记为，此四边形内任一点P 到第条边的距离记为，若，则．类比以上性质，体积为V 的三棱锥的第个面的面积记为，此三棱锥内任一点Q 到第个面的距离记为，若，则等于（）A ．B ．C ．D ．二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上）13．数（i 是虚数单位）的实部是．14．已知边长分别为a 、b 、c 的三角形ABC 面积为S ，内切圆O 半径为r ，连接OA 、OB 、OC ，则三角形OAB 、OBC 、OAC 的面积分别为、、，由得，类比得四面体的体积为V ，四个面的面积分别为,则内切球的半径R= ． 15．如图，第n 个图形是由正n + 2 边形“ 扩展 ” 而来，，则在第n 个图形中共_ 有个顶点．（用n 表示）16．观察下列等式: ，，2323456(1)136763x x x x x x x x ++=++++++，242345678(1)1410161916104x x x x x x x x x x ++=++++++++，由以上等式推测:对于，若则．三、解答题（本大题共6小题，第17小题10分，其余每小题12分，共70分.解答时应写出必要的文字说明、证明过程或演算步骤）17．（本小题满分10分）为考察某种药物预防禽流感的效果，进行动物家禽试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本.（1）根据所给样本数据完成下面2×2列联表；（2）请问能有多大把握认为药物有效？ 18．（本小题满分12分）已知a ，b ，c ，d ∈（0，＋∞），求证ac ＋bd ≤． 19．（本小题满分12分）已知，试证明至少有一个不小于1． 20．（本小题满分12分）设（1）计算：的值；（2）猜想具备的一个性质，并证明． 21．（本小题满分12分）数列满足，．（1）求证：；（2）设，求不超过的最大整数． 22．（本小题满分12分）图（1）、（2）、（3）、（4）分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”，按同样的方式构造图形，设第个图形包含个“福娃迎迎”．不得禽流感得禽流感总计服药不服药总计（1）求出；（2）利用合情推理的“归纳推理思想”归纳出与的关系式（不需证明）；（3）根据你得到的关系式求的表达式．丰城中学xx 学年度下学期高二数学（文）周考试卷答案1—6 AACCCC 7—12 BDDDDB 13． 14． 15． 16．（2）假设检验问题H ：服药与家禽得禽流感没有关系由P()＝0.10 所以大概90％认为药物有效 18. 解：证明：法一：（分析法）欲证ac ＋bd ≤，只需证（ac ＋bd ）2≤（a 2＋b 2）（c 2＋d 2），即证a 2c 2＋2abcd ＋b 2d 2≤a 2c 2＋b 2d 2＋a 2d 2＋b 2c 2，即证2abcd ≤a 2d 2＋b 2c 2，即证0≤（bc －ad ）2，而a ，b ，c ，d ∈（0，＋∞），0≤（bc －ad ）2显然成立，故原不等式成立．法二：（综合法）（a 2＋b 2）（c 2＋d 2）＝a 2c 2＋b 2d 2＋a 2d 2＋b 2c 2≥a 2c 2＋b 2d 2＋2abcd＝（ac ＋bd ）2，所以≥ac ＋bD ． 19．解: 假设均小于1，即，则有而22112232()3322a b c x x x ++=-++=-+≥，矛盾．所以原命题成立20. 解: （1）33633213331311331331)1()0(10=-+-=+++=+++=+f f 同理，可得（2）猜想：当时，证明：设，33)3233(332333)33(333233)33)(33()33)(33(21212121212112=++++=+++++=++++=+x x x x x x x x x x x x x x 时，21. 解: （1）因为，故1)1()1()1()()()(1222221112211>+-++-+-=+-++-+-=-----a a a a a a a a a a a a n n n n n n n ，于是．（2）解：，于是所以于是113)1111()1111()1111(2014201420133221--=---++---+---=a a a a a a a m 当时，，于是，故，所以，所以不超过m 的最大整数是2．22. 解: （1）f （1）=1,f （2）=5,f （3）=13,f （4）=25,f （5）=25+4×4=41．（2）f （2）-f （1）=4=4×1．f （3）-f （2）=8=4×2,f （4）-f （3）=12=4×3, f（5）-f （4）=16=4×4,由上式规律得出f （n+1）-f （n ）=4n ．（3） f （2）-f （1）=4×1, f（3）-f （2）=4×2, f（4）-f （3）=4×3, f（n-1）-f （n-2）=4·（n-2）, f （n ）-f （n-1）=4·（n-1） f （n ）-f （1）=4[1+2+ +（n-2）+（n-1）]=2（n-1）·n,f （n ）=2n 2-2n+1（）f （1）=1也满足上式，f （n ）=2n 2-2n+1 @*@ 27463 6B47 歇930673 77D1 矑37370 91FA 釺40496 9E30 鸰32374 7E76 繶 28440 6F18 漘k31119 798F 福。

高二年级文科数学双周测试卷

高二年级文科数学双周测试卷（实验班附加题必做；其它班附加题选做）一、选择题：（每小题5分；共60分）1.老师为研究男女同学数学学习的差异情况；对某班50名同学（其中男同学30名；女同学20名）采取分层抽样的方法；抽取一个样本容量为10的样本进行研究；某女同学甲被抽到的概率为（） A.150 B.110 C.15 D.142. 若曲线4y x =的一条切线l 与直线480x y +-=垂直；则l 的方程为（） A ．430x y --= B ．450x y +-= C ．430x y -+= D ．430x y ++=()x f ；(R x ∈)上任一点(0x ；()0x f )处的切线斜率为k=()()20012+-x x ；则该函数的单调递减区间为( ) A [)∞+- 1 B (]2 ∞- C ()1-∞- 和（1 2） D [)∞+ 2()521x -的展开式中第二项小于第一项；且不小于第三项；则x 的取值范围是( )A ．x >－110 B ．x ≥－14 C ．－14≤x ≤0 D ．－110<x ≤0 5.点P 在曲线y = +-x x 323上移动时；过点P 的切线的倾斜角的取值范围是( )A ． [0；π）B 、（0；2π）∪[34π；π）C ．[0；2π）∪（2π；34π]D 、[0；2π）∪[34π；π）6.电视台连续播放5个广告；其中3个不同的商业广告和2个不同的奥运宣传广告；要求最后播放的必须是奥运宣传广告；且2个奥运宣传广告不能连续播放；则不同的播放方式有（） A ．120种 B ．48种 C ．36种 D ．18种 7.某风景区有一个三色风车如图（红、黄、蓝每一部分各占风车所在圆的31）；已知风车设定的程序是向左转或向右转（每次均转120°即停）；而且逆时针方向转的概率是顺时针方向转的概率的2倍；如图；假设红色在下边；则转三次之后蓝色在下边的概率是（）A ．92 B ．31 C ．94 D ．278 8.只用1；2；3三个数字组成一个四位数；规定这三个数必须同时使用；且同一数字不能相邻出现；这样的四位数有（）9.已知++++++=++++++2122102,)1()1()1(a a x a x a x a a x x x n n n 1-+n a),1,(29>∈-=n N n n 那么6)1(y +的展开式中含n y 项的系数是（）A.15B.20C.6D.109.nx x x x x f )1()1()1()1(1)(32++⋯+++++++= ；则)0('f 等于( )A.nB.1-nC.!nD.21n （n ＋1） 11.设函数f (x )在定义域内可导；y =f (x )的图象如图1所示；则导函数y =f '(x )的图象可能为（）12.将号码分别为1、2…9的九个小球放入一个袋中；这些小球仅号码不同；其余完全相同；甲从袋中摸出一个球；其号码为a ；放回后；乙从此袋中再摸出一个球；其号码为b ；则便不等式0102>+-b a 成立的事件发生的概率等于（）A ．8152 B ．8159 C ．8161 D ．8160 二、填空题：（每小题4分；共16分）13.()()811+-x x 的展开式中；5x 的系数为()101+x 的展开式中；任取一项；则该项的系数为奇数的概率为＿＿＿15.将4个颜色互不相同的球全部放入编号为1和2的两个盒子里；使得放入每个盒子里的球的个数不小于该盒子的编号；则不同的放球方法有16.若函数()321f x ax a =-+在区间[]1,1-上无实数根；则函数31()()(34)5g x a x x =--+的递减区间是题号 12345678910111213141516答案三、解答题：17.(本小题10分)有6件产品；其中含有3件次品；现逐个抽取检查不放回；求：（1）前4次恰好抽出2件次品的概率；（2）第五次恰好查出全部次品的概率18. (本小题10分)已知（nx x)1324+展开式中倒数第三项的系数为45。

高二数学上学期第二次双周练试题文-人教版高二全册数学试题

2016—2017学年上学期2015级第二次双周练文数试卷命题人：审题人：考试时间：2016年10月11日一、选择题（共12个小题，每小题5分,共60分，在每小题给出的四个选项中，只有一项符合题目要求） 1. 已知圆C 的圆心坐标为()2,3-，且点(1,1)--在圆上，则圆C 的方程为（）A ．224680x y x y +-++=B ．224680x y x y +-+-=C ．22460x y x y +--=D ．22460x y x y +-+=2. 经过两点A (4 ,2y ＋1)，B (2，－3)的直线的倾斜角为34π，则y =( ) A.－1 B.－3 C.0 D.23. 在等差数列{}n a 中，36852=++a a a ，27963=++a a a ，则数列{}n a 的前10项和=10S （） A.220 B.210 C.110 D.105 4．圆25)4()1(22=-++y x 被直线0434=--y x 截得的弦长是（） A. 3B. 4C.6D. 85．圆C 1：x 2＋y 2＋4x －4y ＋7＝0和圆C 2：x 2＋y 2－4x －10y ＋13＝0的公切线有( ) A ．1条 B ．2条 C ．3条 D ．4条6．圆012222=+--+y x y x 上的点到直线2=-y x 的距离最大值是（）A ．2B ．221+C ．221+D ．21+ 7. 一几何体的三视图如下，则它的体积是（）A ．333a π+B . 3712a πC . 331612a π+D . 373a π正视图侧视图俯视图aaaa2a2a2a8．若直线01=-+by ax (其中0>a 且0>b )平分圆224210x y x y +---=的周长，则ba 21+的最小值为A.16B. 8C. 4D. 29. 已知A(-2,1)，B(1,2).点C 为直线x y 31=上的动点，则BC AC +的最小值为 A.22 B. 32 C.52 D.7210．阅读如图所示的程序框图，运行相应的程序，输出的结果为A.4B.5C.6D.711．ABC ∆的外接圆圆心为O ，半径为2，0=++OC OB OA ，且AB OA =，则CB 在CA 方向上的投影为A ．1B ．2C 3．312．已知圆C ：0248622=+--+y x y x 和两点A )0,(m -，B )0,m （)0>m （，若圆C 上存在点P ，使得0=⋅BP AP ，则m 的最大值与最小值之差为A.1B.2C.3D.4二、填空题（共4个小题，每小题5分，共20分，把答案填写在答题卡相应的位置。

2021年高二下学期第二次段考数学试卷(文科)含解析

2021年高二下学期第二次段考数学试卷（文科）含解析一.填空题（本大题共14小题，每小题5分，共70分，请将答案填写在答题卷相应的位置上）1．已知幂函数y=f（x）的图象过点（，），则f（4）的值为．2．已知集合A={1，2，3，4，5}，B={1，3，5，7，9}，C=A∩B，则集合C的子集的个数为．3．函数f（x）=的定义域为．4．由命题“∃x∈R，x2+2x+m≤0”是假命题，求得实数m的取值范围是（a，+∞），则实数a= ．5．函数f（x）=，则f（f（﹣1））的值为．6．如果实数x，y满足线性约束条件，则z=x+y﹣2的最小值等于．7．函数f（x）=log|x|在（0，+∞）上单调递减，则f（﹣2）f（a+1）（填a“＜”，“=”，“＞”之一）．8．“a＞1”是“函数f（x）=a•x+cosx在R上单调递增”的条件．（空格处请填写“充分不必要条件”、“必要不充分条件”、“充要条件”或“既不充分也不必要条件”）9．设奇函数y=f（x）（x∈R），满足对任意t∈R都有f（t）=f（1﹣t），且时，f （x）=﹣x2，则的值等于．10．已知正数a，b，c满足4a﹣2b+25c=0，则lga+lgc﹣2lgb的最大值为．11．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=（）|x﹣1|+m，若函数f（x）有5个零点，则实数m的取值范围是．12．已知关于x的不等式x2﹣4x+t≤0的解集为A，若（﹣∞，t]∩A≠∅，则实数t的取值范围是．13．设定义域为（0，+∞）的单调函数f（x），对任意的x∈（0，+∞），都有f[f（x）﹣log2x]=6，若x0是方程f（x）﹣f′（x）=4的一个解，且x0∈（a，a+1）（a∈N*），则实数a=．14．已知f（x）=（x+1）|x|﹣3x．若对于任意x∈R，总有f（x）≤f（x+a）恒成立，则常数a的最小值是．二．解答题：（本大题共6小题，共90分.请在答题纸指定区域作答，解答时应写出必要的文字说明、证明过程或演算步骤）15．命题p：实数x满足x2﹣4ax+3a2＜0（其中a＞0），命题q：实数x满足（1）若a=1，且p∧q为真，求实数x的取值范围；（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．16．已知函数g（x）=是奇函数，f（x）=log4（4x+1）+mx是偶函数．（1）求m+n的值；（2）设h（x）=f（x）+x，若g（x）＞h[log4（2a+1）]对任意x≥1恒成立，求实数a的取值范围．17．如图，某水域的两直线型岸边l1，l2成定角120°，在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩．现某渔民准备经过该固定桩安装一直线型隔离网BC （B，C分别在l1和l2上），围出三角形ABC养殖区，且AB和AC都不超过5公里．设AB=x 公里，AC=y公里．（1）将y表示成x的函数，并求其定义域；（2）该渔民至少可以围出多少平方公里的养殖区？18．设A=[﹣1，1]，B=[﹣2，2]，函数f（x）=2x2+mx﹣1，（1）设不等式f（x）≤0的解集为C，当C⊆（A∩B）时，求实数m的取值范围；（2）若对任意x∈R，都有f（1﹣x）=f（1+x）成立，试求x∈B时，函数f（x）的值域；（3）设g（x）=2|x﹣a|﹣x2﹣mx（a∈R），求f（x）+g（x）的最小值．19．已知函数f（x）=e x，g（x）=ax+b（a，b∈R）．（1）设h（x）=xg（x）+1．①若a≠0，则a，b满足什么条件时，曲线y=f（x）与y=h（x）在x=0处总有相同的切线？②当a=1时，求函数F（x）=单调区间；（2）若集合{x|f（x）＜g（x）}为空集，求ab的最大值．20．已知函数f（x）=e x，g（x）=lnx+1，（1）求函数h（x）=f（x﹣1）﹣g（x）在区间[1，+∞）上的最小值；（2）已知1≤y＜x，求证：e x﹣y﹣1＞lnx﹣lny；（3）设H（x）=（x﹣1）2f（x），在区间（1，+∞）内是否存在区间[a，b]（a＞1），使函数H（x）在区间[a，b]的值域也是[a，b]？请给出结论，并说明理由．xx学年江苏省南通市如皋中学高二（下）第二次段考数学试卷（文科）参考答案与试题解析一.填空题（本大题共14小题，每小题5分，共70分，请将答案填写在答题卷相应的位置上）1．已知幂函数y=f（x）的图象过点（，），则f（4）的值为2．【考点】幂函数的概念、解析式、定义域、值域．【分析】设幂函数y=f（x）=xα，根据f（x）的图象过点（，），求得α的值，可得函数f（x）的解析式，从而求得f（4）的值．【解答】解：设幂函数y=f（x）=xα，∵f（x）的图象过点（，），∴=，∴α=，∴f（x）=∴f（4）==2，故答案为：2．2．已知集合A={1，2，3，4，5}，B={1，3，5，7，9}，C=A∩B，则集合C的子集的个数为8．【考点】交集及其运算．【分析】由A与B，求出两集合的交集确定出C，即可作出判断．【解答】解：∵A={1，2，3，4，5}，B={1，3，5，7，9}，∴C=A∩B={1，3，5}，则集合C的子集个数为23=8，故答案为：83．函数f（x）=的定义域为（0，1）∪（1，2）．【考点】函数的定义域及其求法．【分析】由对数式的真数大于0，分式的分母不等于0联立不等式组求得答案．【解答】解：要使原函数有意义，则，解得：0＜x＜2，且x≠1．∴函数f（x）=的定义域为：（0，1）∪（1，2）．故答案为：（0，1）∪（1，2）．4．由命题“∃x∈R，x2+2x+m≤0”是假命题，求得实数m的取值范围是（a，+∞），则实数a= 1．【考点】命题的真假判断与应用；四种命题的真假关系．【分析】存在x∈R，使x2+2x+m≤0”是假命题，其否命题为真命题，即是说“∀x∈R，都有x2+2x+m＞0”，根据一元二次不等式解的讨论，可知△=4﹣4m＜0，所以m＞1，则a=1．【解答】解：存在x∈R，使x2+2x+m≤0”是假命题，∴其否命题为真命题，即是说“∀x∈R，都有x2+2x+m＞0”，∴△=4﹣4m＜0，∴m＞1，m的取值范围为（1，+∞）．则a=15．函数f（x）=，则f（f（﹣1））的值为﹣2．【考点】函数的值．【分析】由﹣1≤0，得f（﹣1）=，由此能求出f（f（﹣1））的值．【解答】解：∵f（x）=，∴f（﹣1）=，∴f（f（﹣1））=f（）==﹣2．故答案为：﹣2．6．如果实数x，y满足线性约束条件，则z=x+y﹣2的最小值等于﹣3．【考点】简单线性规划．【分析】作出可行域，变形目标函数，平移直线y=﹣x可得当直线经过点A（﹣2，1）时，z 取最小值，代值计算可得．【解答】解：作出线性约束条件所对应的可行域（如图），变形目标函数可得y=﹣x+2+z，平移直线y=﹣x可知，当直线经过点A（﹣2，1）时，截距2+z取最小值，z取最小值，代值计算可得z的最小值为z=﹣2+1﹣2=﹣3故答案为：﹣3．7．函数f（x）=log a|x|在（0，+∞）上单调递减，则f（﹣2）＜f（a+1）（填“＜”，“=”，“＞”之一）．【考点】对数函数的图象与性质．【分析】由对数函数的性质得0＜a＜1，1＜a+1＜2，由此能求出结果．【解答】解：∵函数f（x）=log a|x|在（0，+∞）上单调递减，∴0＜a＜1，1＜a+1＜2，∴|﹣2|＞|a+1|，∴f（﹣2）=log a2＜f（a+1）=log a（a+1）．故答案为：＜．8．“a＞1”是“函数f（x）=a•x+cosx在R上单调递增”的充分不必要条件条件．（空格处请填写“充分不必要条件”、“必要不充分条件”、“充要条件”或“既不充分也不必要条件”）【考点】必要条件、充分条件与充要条件的判断．【分析】由条件利用充分条件、必要条件、充要条件的定义进行判断，可得结论．【解答】解：由“a＞1”，可得f′（x）=1﹣sinx＞0，故“函数f（x）=a•x+cosx在R上单调递增”，故充分性成立．由“函数f（x）=a•x+cosx在R上单调递增”，可得f′（x）=1﹣sinx≥0，a≥1，不能得到“a＞1”，故必要性不成立，故答案为：充分不必要条件．9．设奇函数y=f（x）（x∈R），满足对任意t∈R都有f（t）=f（1﹣t），且时，f（x）=﹣x2，则的值等于．【考点】函数的值；函数解析式的求解及常用方法．【分析】由题设知f（3）=f（1﹣3）=f（﹣2）=﹣f（2）=﹣[f（1﹣2）]=﹣f（﹣1）=f（1）=f（0）=0. = = = = =﹣．所以=﹣．【解答】解：∵奇函数y=f（x）（x∈R），满足对任意t∈R都有f（t）=f（1﹣t），且时，f（x）=﹣x2，∴f（3）=f（1﹣3）=f（﹣2）=﹣f（2）=﹣[f（1﹣2）]=﹣f（﹣1）=f（1）=f（0）=0．=====﹣．∴=﹣．故答案为：﹣．10．已知正数a，b，c满足4a﹣2b+25c=0，则lga+lgc﹣2lgb的最大值为﹣2．【考点】对数的运算性质；不等关系与不等式．【分析】将4a﹣2b+25c=0变形为：4a+25c=2b，利用基本不等式可得：2b；lga+lgc﹣2lgb=，即可求解．【解答】解：由题意：4a﹣2b+25c=0，变形为：4a+25c=2b，∵4a+25c，当且仅当4a=25c时，取等号．∴2b；即b2≥100ac那么：lga+lgc﹣2lgb=lg≤lg=lg10﹣2=﹣2故答案为：﹣2．11．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=（）|x﹣1|+m，若函数f （x）有5个零点，则实数m的取值范围是．【考点】函数奇偶性的性质．【分析】问题转化为y=﹣m和g（x）=（x＞0），的交点个数，画出函数g（x）的图象，从而求出m的范围即可．【解答】解：f（x）是奇函数，f（x）有5个零点，x=0是1个，只需x＞0时有2个零点即可，当x＞0时，f（x）=（）|x﹣1|+m，问题转化为y=﹣m和g（x）=（x＞0），的交点个数即可，函数画出g（x）的图象，如图示：，结合图象只需＜﹣m＜1，即﹣1＜m＜﹣，故答案为：．12．已知关于x的不等式x2﹣4x+t≤0的解集为A，若（﹣∞，t]∩A≠∅，则实数t的取值范围是[0，4] ．【考点】一元二次不等式的解法．【分析】根据题意，问题等价于二次函数f（x）=x2﹣4x+t，在区间（﹣∞，t]内至少存在一个数c 使得f（c）≤0，利用否定命题：对于区间（﹣∞，t]内的任意一个x都有f（x）＞0，求出t的取值范围，再求对应原命题的实数t的取值范围．【解答】解：关于x的不等式x2﹣4x+t≤0的解集为A，且（﹣∞，t]∩A≠∅，等价于二次函数f（x）=x2﹣4x+t，在区间（﹣∞，t]内至少存在一个数c 使得f（c）≤0，其否定是：对于区间（﹣∞，t]内的任意一个x都有f（x）＞0，∴①或②；由①得，解得t＜0；由②得，解得t＞4；即t＜0或t＞4；∴二次函数f（x）在区间（﹣∞，t]内至少存在一个实数c，使f（c）≤0的实数t的取值范围是[0，4]．故t的取值范围是[0，4]．故答案为：[0，4]．13．设定义域为（0，+∞）的单调函数f（x），对任意的x∈（0，+∞），都有f[f（x）﹣log2x]=6，若x0是方程f（x）﹣f′（x）=4的一个解，且x0∈（a，a+1）（a∈N*），则实数a=1．【考点】导数的运算；对数函数图象与性质的综合应用．【分析】由题意可得f（x）﹣log2x为定值，设为t，代入可得t=4，进而可得函数的解析式，化方程有解为函数F（x）=f（x）﹣f′（x）﹣4=log2x﹣有零点，易得F（1）＜0，F（2）＞0，由零点的判定可得答案．【解答】解：根据题意，对任意的x∈（0，+∞），都有f[f（x）﹣log2x]=6，又由f（x）是定义在（0，+∞）上的单调函数，则f（x）﹣log2x为定值，设t=f（x）﹣log2x，则f（x）=t+log2x，又由f（t）=6，可得t+log2t=6，可解得t=4，故f（x）=4+log2x，f′（x）=，又x0是方程f（x）﹣f′（x）=4的一个解，所以x0是函数F（x）=f（x）﹣f′（x）﹣4=log2x﹣的零点，分析易得F（1）=﹣＜0，F（2）=1﹣=1﹣＞0，故函数F（x）的零点介于（1，2）之间，故a=1，故答案为：114．已知f（x）=（x+1）|x|﹣3x．若对于任意x∈R，总有f（x）≤f（x+a）恒成立，则常数a的最小值是．【考点】函数恒成立问题．【分析】写出分段函数解析式，画出图形，把a的最小值转化为求线段MN的最大值，然后利用基本不等式求解．【解答】解：f（x）=（x+1）|x|﹣3x=，作出分段函数图象如图：作平行于x轴的直线l与f（x）有3个交点，设最左边的点为M，最右边的点为N，则a的最小值为线段MN长度的最大值，设直线l：y=t，则MN=3+==3+．当且仅当1+t=4﹣t，即t=是上式取“=”．故答案为：．二．解答题：（本大题共6小题，共90分.请在答题纸指定区域作答，解答时应写出必要的文字说明、证明过程或演算步骤）15．命题p：实数x满足x2﹣4ax+3a2＜0（其中a＞0），命题q：实数x满足（1）若a=1，且p∧q为真，求实数x的取值范围；（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．【考点】复合命题的真假；必要条件、充分条件与充要条件的判断．【分析】（1）先通过解不等式及不等式组求出命题p，q，并代入a=1得到命题p：1＜x＜3，命题q：2＜x≤3，而p∧q为真，所以求出p真q真时x的取值范围，再求交集即可；（2）先写出￢p：x≤a，或x≥3a，a＞0，￢q：x≤2，或x＞3，而根据￢p是￢q的充分不必要条件可得，解该不等式组即得a的取值范围．【解答】解：（1）解x2﹣4ax+3a2＜0，a＞0，得：a＜x＜3a；∴命题p：a＜x＜3a，a＞0；命题q：2＜x≤3；∴a=1时，命题p：1＜x＜3，p∧q为真；∴p真q真；∴；∴2＜x＜3；∴实数x的取值范围为（2，3）；（2）￢p：x≤a，或x≥3a，a＞0；￢q：x≤2，或x＞3；∴若￢p是￢q的充分不必要条件，则：；∴1＜a≤2；∴实数a的取值范围为（1，2]．16．已知函数g（x）=是奇函数，f（x）=log4（4x+1）+mx是偶函数．（1）求m+n的值；（2）设h（x）=f（x）+x，若g（x）＞h[log4（2a+1）]对任意x≥1恒成立，求实数a的取值范围．【考点】对数函数图象与性质的综合应用；函数奇偶性的性质．【分析】（1）由g（x）为定义在R上的奇函数，得g（0）=0，解得n=1；再根据偶函数满足f（﹣x）=f（x），比较系数可得m=﹣，由此即可得到m+n的值．（2）由（1）得h（x）=log4（4x+1），易得h[log4（2a+1）]=log4（2a+2）．而定义在R上的增函数g（x）在x≥1时的最小值为g（1）=，从而不等式转化成＞log4（2a+2），由此再结合真数必须大于0，不难解出实数a的取值范围．【解答】解：（1）由于g（x）为奇函数，且定义域为R，∴g（0）=0，即，…∵，∴，∵f（x）是偶函数，∴f（﹣x）=f（x），得mx=﹣（m+1）x恒成立，故，综上所述，可得；…（2）∵，∴h[log4（2a+1）]=log4（2a+2），…又∵在区间[1，+∞）上是增函数，∴当x≥1时，…由题意，得，因此，实数a的取值范围是：．…17．如图，某水域的两直线型岸边l1，l2成定角120°，在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩．现某渔民准备经过该固定桩安装一直线型隔离网BC （B，C分别在l1和l2上），围出三角形ABC养殖区，且AB和AC都不超过5公里．设AB=x 公里，AC=y公里．（1）将y表示成x的函数，并求其定义域；（2）该渔民至少可以围出多少平方公里的养殖区？【考点】基本不等式在最值问题中的应用．【分析】（1）由S △ABD +S △ACD =S △ABC ，将y 表示成x 的函数，由0＜y ≤5，0＜x ≤5，求其定义域；（2）S=xysinA=sin120°=（≤x ≤5），变形，利用基本不等式，即可得出结论．【解答】解：（1）由S △ABD +S △ACD =S △ABC ，得，所以x +y=xy ，所以y=又0＜y ≤5，0＜x ≤5，所以≤x ≤5，所以定义域为{x |≤x ≤5}；（2）设△ABC 的面积为S ，则结合（1）得：S=xysinA=sin120°=（≤x ≤5）=（x ﹣1）++2≥4，当仅当x ﹣1=，x=2时取等号．故当x=y=2时，面积S 取最小值\平方公里．答：该渔民总共至少可以围出平方公里的养殖区．18．设A=[﹣1，1]，B=[﹣2，2]，函数f （x ）=2x 2+mx ﹣1，（1）设不等式f （x ）≤0的解集为C ，当C ⊆（A ∩B ）时，求实数m 的取值范围；（2）若对任意x ∈R ，都有f （1﹣x ）=f （1+x ）成立，试求x ∈B 时，函数f （x ）的值域；（3）设g （x ）=2|x ﹣a |﹣x 2﹣mx （a ∈R ），求f （x ）+g （x ）的最小值．【考点】函数的值域；函数的最值及其几何意义．【分析】（1）可先求出A ∩B=[﹣1，1]，并求出f （0）=﹣1，从而根据f （x ）≤0的解集为C ，而C ⊆（A ∩B ），这样即可判断函数f （x ）有两个零点，从而得出，这样便可求出实数m 的取值范围；（2）根据f （1﹣x ）=f （1+x ）便可得出f （x ）的对称轴为x=1，从而可求出m ，进而得出f （x ），配方即可求出f （x ）在[﹣2，2]上的最大、最小值，即得出其值域；（3）可令h （x ）=f （x ）+g （x ），并去绝对值号得出，从而可看出需讨论a ：a ≤﹣1，﹣1＜a ＜1，以及a ≥1，对于每种情况判断h （x ）的单调性，根据单调性即可求出每种情况下h （x ）的最小值，即求出f （x ）+g （x ）的最小值．【解答】解：（1）由A=[﹣1，1]，B=[﹣2，2]，知：A ∩B=[﹣1，1]；且二次函数f （x ）的开口向上，f （0）=﹣1；由题意知不等式f （x ）≤0的解集为C ，当C ⊆（A ∩B ）时，函数f （x ）必有两零点，且两零点均在区间[﹣1，1]内；故只需：，解得﹣1≤m ≤1；∴实数m 的取值范围为[﹣1，1]；（2）对任意x ∈R ，都有f （1﹣x ）=f （1+x ）成立；∴函数f （x ）的图象关于直线x=1对称；∴，解得m=﹣4；∴函数f（x）=2（x﹣1）2﹣3，x∈[﹣2，2]；∴x=﹣2时，f（x）取最大值15，x=1时，f（x）取最小值﹣3；∴函数f（x）在区间B上的值域为[﹣3，15]；（3）令h（x）=f（x）+g（x）；则；①当a≤﹣1时，函数h（x）在区间（﹣∞，﹣1）是减函数，（﹣1，+∞）是增函数，此时h （x）min=h（﹣1）=﹣2a﹣2；②当﹣1＜a＜1时，函数h（x）在区间（﹣∞，a）是减函数，（a，+∞）是增函数，此时；③当a≥1时，函数f（x）在区间（﹣∞，1）是减函数，（1，+∞）是增函数，此时h（x）min=2a﹣2；综上：当a≤﹣1时，f（x）min=﹣2a﹣2，当﹣1＜a＜1时，当a≥1时f（x）min=2a﹣2．19．已知函数f（x）=e x，g（x）=ax+b（a，b∈R）．（1）设h（x）=xg（x）+1．①若a≠0，则a，b满足什么条件时，曲线y=f（x）与y=h（x）在x=0处总有相同的切线？②当a=1时，求函数F（x）=单调区间；（2）若集合{x|f（x）＜g（x）}为空集，求ab的最大值．【考点】利用导数研究曲线上某点切线方程．【分析】（1）①分别利用导数求出y=f（x）与y=h（x）在x=0的切线方程，根据两切线重合可求出a，b满足的条件；②先求出函数F（x）的解析式，然后求出导函数F′（x），令F′（x）=0，讨论根的大小，从而求出函数的单调减区间；（2）由集合{x|f（x）＜g（x）}为空集，可知不等式f（x）≥g（x）对任意x∈R恒成立，即y=f（x）﹣g（x）≥0恒成立．【解答】解：（1）h（x）=ax2+bx+1①∵f′（x）=e x，∴f′（0）=1，又f（0）=1，∴y=f（x）在x=0处的切线方程为y=x+1…又∵h′（x）=2ax+b，∴h′（0）=b，又h（0）=1，∴y=h（x）在x=0处的切线方程为y=bx+1，所以当a≠0，a∈R且b=1时，曲线y=f（x）与y=h（x）在x=0处总有相同的切线．…（2）由a=1，，∴，∴，…由F′（x）=0，得x1=1，x2=1﹣b，∴当b＞0时，函数y=F（x）的减区间为（﹣∞，1﹣b），（1，+∞）；增区间为（1﹣b，1）；当b=0时，函数y=F（x）的减区间为（﹣∞，+∞）；当b＜0时，函数y=F（x）的减区间为（﹣∞，1），（1﹣b，+∞），增区间为（1，1﹣b），…（2）由集合{x|f（x）＜g（x）}为空集，可知不等式f（x）≥g（x）对任意x∈R恒成立，即y=f（x）﹣g（x）≥0恒成立．…当a≤0时，函数y=e x﹣ax﹣b在R上单调递增，y≥0不恒成立，所以a＞0，此时y′=e x﹣a=0，解得x=lna，当x＜lna时，y′＜0，函数单调递减，当x＞lna时，y′＞0，函数单调递增，所以要使y=f（x）﹣g（x）≥0恒成立，只需y min=a﹣alna﹣b≥0，…所以b≤a﹣alna，ab≤a2﹣a2lna，a＞0，令G（x）=x2﹣x2lnx，x＞0，则G′（x）=2x﹣2xlnx﹣x=x（1﹣2lnx），令G′（x）=0解得，当时，G′（x）＞0，函数G（x）单调递增，当时，G′（x）＜0，函数G（x）单调递减，所以当时，函数G（x）=x2﹣x2lnx取得最大值，所以，所以ab的最大值为．…20．已知函数f（x）=e x，g（x）=lnx+1，（1）求函数h（x）=f（x﹣1）﹣g（x）在区间[1，+∞）上的最小值；（2）已知1≤y＜x，求证：e x﹣y﹣1＞lnx﹣lny；（3）设H（x）=（x﹣1）2f（x），在区间（1，+∞）内是否存在区间[a，b]（a＞1），使函数H（x）在区间[a，b]的值域也是[a，b]？请给出结论，并说明理由．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【分析】（1）求出函数的导数，结合x的范围，求出函数的单调区间，从而求出函数的最小值即可；（2）问题转化为只需证明：，即证明：xy﹣y2+y﹣x≥0，而xy﹣y2+y﹣x=y（x﹣y）﹣（x﹣y）=（x﹣y）（y﹣1），从而证出结论；（3）假设存在，得到方程（x﹣1）2e x=x有两个大于1的不等实根，设函数G（x）=（x﹣1）2e x﹣x（x＞1），根据函数的单调性得到G（x）在（1，+∞）上仅有一个零点，得到矛盾，从而判断结论．【解答】解：（1）h（x）=e x﹣1﹣lnx﹣1（x≥1），，∵x∈[1，+∞），∴∴，∴函数h（x）在区间[1，+∞）上单调递增，∴h（x）min=h（1）=0．…（2）由（1）知，当x≥1时，e x﹣1﹣1≥lnx且当x=1时取等号，∵1≤y＜x，∴x﹣y+1＞1∴e x﹣y+1﹣1﹣1＞ln（x﹣y+1），要证明e x﹣y﹣1＞lnx﹣lny，只需证明：ln（x﹣y+1）≥lnx﹣lny，只需证明：，…即证明：xy﹣y2+y﹣x≥0，而xy﹣y2+y﹣x=y（x﹣y）﹣（x﹣y）=（x﹣y）（y﹣1），∵1≤y＜x，∴x﹣y＞0，y﹣1≥0，∴xy﹣y2+y﹣x=（x﹣y）（y﹣1）≥0，得证．∴当1≤y＜x时，e x﹣y﹣1＞lnx﹣lny．…（3）H（x）=（x﹣1）2f（x），H′（x）=（x2﹣1）e x假设存在区间[a，b]（a＞1），使函数H（x）在区间[a，b]的值域也是[a，b]，当x＞1时，H′（x）＞0，所以函数在区间（1，+∞）单调递增，故，即方程（x﹣1）2e x=x有两个大于1的不等实根，…设函数G（x）=（x﹣1）2e x﹣x（x＞1），则G′（x）=（x2﹣1）e x﹣1，G′′（x）=（x2+2x﹣1）e x，当x＞1时，G′′（x）＞0，即函数G′（x）=（x2﹣1）e x﹣1在区间（1，+∞）单调递增，又G′（1）=﹣1＜0，G′（2）=3e2﹣1＞0，所以存在唯一的x0∈（1，2）使得G′（x0）=0，当x∈（1，x0）时，G′（x）＜0，函数G（x）递减，当x∈（x0，+∞）时，G′（x）＞0，函数G（x）递增，所以函数G（x）有极小值G（x0）＜G（1）=﹣1，G（2）=e2﹣2＞0，所以函数G（x）在（1，+∞）上仅有一个零点，这与方程（x﹣1）2e x=x有两个大于1的不等实根矛盾，故不存在区间[a，b]（a＞1），使函数H（x）在区间[a，b]的值域也是[a，b]．…xx年12月1日x27263 6A7F 橿32452 7EC4 组23606 5C36 尶38703 972F 霯8n28433 6F11 漑&35216 8990 覐28880 70D0 烐35131 893B 褻j。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高二BC 段文科数学周测试卷（2）
一、选择题（每小题5分，共50分） 1.函数x
x f 1)(=
的导数是（ C ）
A.2x
B.x
C.2
1x
- D.
2
1x
2.曲线2x y =在0=x 处的（ B ）
A.切线的斜率为1
B.切线的方程为0=y
C.切线方程为x y 2=
D.没有切线
3.已知曲线2
4
x
y =的一条切线的斜率为12
，则切点的横坐标为（ A ） A ．1
B ．2
C ．3
D ．4
4.已知10)(2+-=x x f ，则)(x f 在2
3=
x 处的瞬时变化率是（ D ）
A ．3
B ．2
C ．-2
D ．-3 5.曲线1323+-=x x y 在点（1，－1）处的切线方程为（ B ）
A ．43-=x y
B ．23+-=x y
C ．34+-=x y
D ．54-=x y
6.已知函数x x x f 3)(3+=，则该函数的单调增区间是（ C ）
A ．),1(),1,(+∞--∞
B ．),1()1,(+∞⋃--∞
C ．),(+∞-∞
D ．)1,1(-
7．函数x x y 33
-=的极大值为m ，极小值为n ，则n m +为（ A ）
A ．0
B ．1
C ．2
D ．4
8．函数)(x f 的定义域为开区间),(b a ，导函数)(x f '在),(b a 内的图象如图所示，则函数)(x f 在开区间),(b a 内有极小值点
（ A ） A ． 1个
B ． 2个
C ． 3个
D ． 4个
9．曲线x y e =在点2
(2)e ，处的切线与坐标轴所围三角形的面积为（ D ）
Ａ．2
94e
Ｂ．2
2e
Ｃ．2
e
Ｄ．
2
2
e
10．如图是函数32
()f x x bx cx d =+++的大致图象，则2212x x +等于（ C ）
A ．
3
2 B ．
3
4 C ．
3
8 D ．
3
12
二、填空题（每小题5分，共20分）
11.()f x '是3
1()213
f x x x =
++的导函数，则(1)f '-的值是 3 。

12.若函数ax x x f -=3)(在1=x 处取极值，则=a 3 13.已知函数)(x f y =的图象在M （1，f （1））处的切线方程是x
y 21=
+2，
='-)1()1(f f _______2_______.
14．函数x x x f ln )(=的单调递增区间是 ____)1
,0(e
_________
三、解答题 15.已知函数52
131)(2
3
+-
=
x x x f ，求该函数的单调区间
16．已知函数2)()(c x x x f -=在2=x 处有极大值，求c 的值
17．已知函数()c bx ax x x f +++=23，当1-=x 时，取得极大值7；当3=x 时，取得极
小值．求这个极小值及c b a ,,的值．
18．已知函数f （x ）=ax 4
+bx 2
+c 的图象经过点（0，1），且在x =1处的切线方程是2-=x y （1）求y =f （x ）的解析式；（2）求y =f （x ）的单调递增区间.
19．设函数
()b f x ax x
=-
，曲线()y f x =在点(2,(2))f 处的切线方程为74120x y --=。

（1）求()y f x =的解析式；（2）证明：曲线()y f x =上任一点处的切线与直线0
x =和直线y x =所围成的三角形面积为定值，并求此定值。

20．已知函数3
2
1(),3
f x x ax bx =
++且'(1)0f -=
（I ）试用含a 的代数式表示b ；（Ⅱ）求()f x 的单调区间。

x
参考答案：
17. 解：()b ax x x f ++=23'2。

据题意，－1，3是方程0232=++b ax x 的两个根，由韦达定理得 ⎪⎪⎩
⎪⎪⎨
⎧
=
⨯--=+-3313
231b a ∴9,3-=-=b a
∴()c x x x x f +--=9323 ∵()71=-f ，∴2=c
极小值()25239333323-=+⨯-⨯-=f ∴极小值为－25，9,3-=-=b a ，2=c 。

18．解：（1）由题意知f （0）=1，f '（1）=1，f （1）=－1.
∴⎪⎩
⎪
⎨⎧-=++=+=.1,124,1c b a b a c ∴c =1，a =
2
5，b =－
2
9，
f （x ）=
2
5x 4－2
9x 2+1.
（2）∵f '（x ）=10x 3－9x ，由10x 3－9x >0，得x ∈（－
10
103，0）∪（
10
103，+∞），
则f （x ）的单调递增区间为（－10
103，0）和（10
103，+∞）.
19．解：（Ⅰ）方程74120x y --=可化为734
y x =
-．当2x =时，12
y =
．
又2()b f x a x '=+，于是1222
744
b a b a ⎧
-=⎪⎪⎨⎪+=⎪⎩，，
, 解得13.a b =⎧⎨=⎩，故3()f x x x =-．
（Ⅱ）设00()P x y ，为曲线上任一点，由23
1y x
'=+知曲线在点00()P x y ，处的切线方程
为
002031()y y x x x ⎛⎫-=+- ⎪⎝⎭，即00200331()y x x x x x ⎛⎫⎛⎫
--=+- ⎪ ⎪
⎝
⎭⎝⎭．令0x =得0
6
y x =-
，从而得切线与直线0x =的交点坐标为060x ⎛⎫- ⎪⎝
⎭，．
令y x =得02y x x ==，从而得切线与直线y x =的交点坐标为00(22)x x ，．
所以点00()P x y ，处的切线与直线0x =，y x =所围成的三角形面积为
016262x x
-=．
故曲线()y f x =上任一点处的切线与直线0x =，y x =所围成的三角形的面积为定值，此定值为6．
20．解：（I ）依题意，得2'()2f x x ax b =++
由'(1)120f a b -=-+=得21b a =-
（Ⅱ）由（I ）得3
2
1()(21)3
f x x ax a x =
++-
故2'()221(1)(21)f x x ax a x x a =++-=++- 令0)(='x f ，则1x =-或12x a =-
① 当1a >时，121a -<-
当x 变化时，'()f x 与()f x 的变化情况如下表：
由此得，(12,1)a --
② 由1a =时，121a -=-，此时，'()0f x ≥恒成立，且仅在1x =-处'()0f x =，
故函数()f x 的单调区间为R
③ 当1a <时，121a ->-，同理可得函数()f x 的单调增区间为(,1)-∞-和
(12,)a -+∞，
单调减区间为(1,12)a --
综上得：
当1a >时，函数()f x 的单调增区间为(,12)a -∞-和(1,)-+∞，单调减区间为
(12,1)a --；
当1a =时，函数()f x 的单调增区间为R ；
当1a <时，函数()f x 的单调增区间为(,1)-∞-和(12,)a -+∞，单调减区间为
(1,12)a --。