11-压杆稳定
第十一章压杆的稳定 - 工程力学

第十一章压杆的稳定承受轴向压力的杆,称为压杆。
如前所述,直杆在轴向压力的作用下,发生的是沿轴向的缩短,杆的轴线仍然保持为直线,直至压力增大到由于强度不足而发生屈服或破坏。
直杆在轴向压力的作用下,是否发生屈服或破坏,由强度条件确定,这是我们已熟知的。
然而,对于一些受轴向压力作用的细长杆,在满足强度条件的情况下,却会出现弯曲变形。
杆在轴向载荷作用下发生的弯曲,称为屈曲,构件由屈曲引起的失效,称为失稳(丧失稳定性)。
本章研究细长压杆的稳定。
§11.1 稳定的概念物体的平衡存在有稳定与不稳定的问题。
物体的平衡受到外界干扰后,将会偏离平衡状态。
若在外界的微小干扰消除后,物体能恢复原来的平衡状态,则称该平衡是稳定的;若在外界的微小干扰消除后物体仍不能恢复原来的平衡状态,则称该平衡是不稳定。
如图11.1所示,小球在凹弧面中的平衡是稳定的,因为虚箭头所示的干扰(如微小的力或位移)消除后,小球会回到其原来的平衡位置;反之,小球在凸弧面上的平衡,受到干扰后将不能回复,故其平衡是不稳定的。
(a) 稳定平衡图11.1 稳定平衡与不稳定平衡上述小球是作为未完全约束的刚体讨论的。
对于受到完全约束的变形体,平衡状态也有稳定与不稳定的问题。
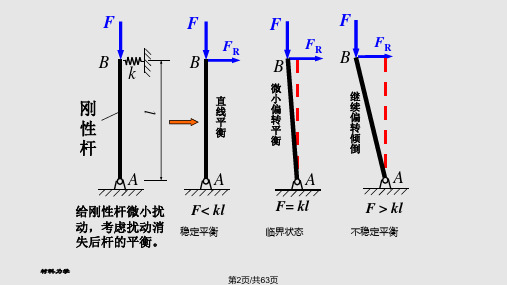
如二端铰支的受压直杆,如图11.2(a)所示。
当杆受到水平方向的微小扰动(力或位移)时,杆的轴线将偏离铅垂位置而发生微小的弯曲,如图11.2(b)所示。
若轴向压力F较小,横向的微小扰动消除后,杆的轴线可恢复原来的铅垂平衡位置,即图11.2(a),平衡是稳定的;若轴向压力F足够大,即使微小扰动已消除,在力F 作用下,杆轴线的弯曲挠度也仍将越来越大,如图11.2(c)所示,直至完全丧失承载能力。
在F =F cr 的临界状态下,压杆不能恢复原来的铅垂平衡位置,扰动引起的微小弯曲也不继续增大,保持微弯状态的平衡,如图11.2(b)所示,这是不稳定的平衡。
如前所述,直杆在轴向载荷作用下发生的弯曲称为屈曲,发生了屈曲就意味着构件失去稳定(失稳)。
第11章压杆稳定
材料力学
第29页/共63页
二、折减因数法
s
F A
[s w ]
s cr
nst
scr、nst与压杆柔度有关,[sw]是的 函数。
[sw]=j [s ]
[s ]——强度许用应力 j —— 折减因数 j 1
稳定条件
与柔度有关
s FP j[s ] 工作应力不大于
A
稳定许用应力
注 不必由柔度判断压杆属何种性质的杆,简化计算。 意
强度 条件
sr
[s ]
s0
n
相当应力不大 于许用应力
极限应力
s0
s
{
s
sb
塑性材料 脆性材料
极限应力和安全因数只与材料有关,与实 际应力状态无关,即强度许用应力为常数。
材料力学
第27页/共63页
稳定 条件
s
F A
[s
w
]
s0
nst
s cr
nst
工作应力不大于稳定许用应力。
极限应力(临界应力)和稳定安全因数不仅 与材料有关,而且与实际压杆的长度、约束 条件、横截面尺寸和形状有关,即与实际压 杆的柔度有关,所以稳定许用应力不是常数。
z
ml
iz
1 940 14.43
65.1
第36页/共63页
F A
z
材料力学
l1 z
B l1
y Fx
z
h
b
F x
x-z 面内,两端固定
绕y轴发生失稳
m = 0.5
iy
b 23
20 23
5.77 mm
y
ml
iy
0.5 880 5.77
76.3
工程力学压杆稳定

MA=MA =0 相当长为2l旳两端简支杆
Fcr
EI 2
(2l ) 2
l
F
0.5l
两端固定 EI 2
Fcr (0.5l) 2
图形比拟:失稳时挠曲线 上拐点处旳弯矩为0,故可设想 此处有一铰,而将压杆在挠曲 线上两个拐点间旳一段看成为 两端铰支旳杆,利用两端铰支 旳临界压力公式,就可得到原 支承条件下旳临界压力公式。
两端铰支
= 1
一端固定,一端自由 = 2
一端固定,一端铰支 = 0.7
两端固定
= 0.5
§11-4中小揉度杆旳临界压力
一、临界应力与柔度
cr
Fcr A
对细长杆
cr
2 EI (l)2 A
2 Ei2 ( l ) 2
2E ( l )2
记 l
i
i
cr
2E 2
––– 欧拉公式
:柔度,长细比
[cr] = [] < 1,称为折减系数
[ cr ] [ ]
根据稳定条件
F Fcr nst
F A
Fcr Anst
cr
nst
[ cr : 工作压力
: 折减系数
A: 横截面面积
[]:材料抗压许用值
解:首先计算该压杆柔度,该丝杆可简化为图示
下端固定,上端自由旳压杆。
=2
F
l=0.375m
i I d A4
l l 2 0.375 75
i d 0.04 / 4 4
查表, = 0.72
F
A
80 103
0.72 0.042
88.5106 88.5MPa [ ] 160MPa
4
故此千斤顶稳定性足够。
静力学11、压杆稳定

Fcr
2 EI l2
μ= 1
2 EI Fcr (0.7l)2
μ= 0.7
2 EI Fcr (0.5 l ) 2
μ= 0.5
2EI Fcr (2l )2
μ= 2
2 EI Fcr l 2
μ= 1
§11.4 欧拉公式的适用范围.经验公式
一、欧拉临界应力公式及使用范围
1.细长压杆的临界应力:临界力除以压杆横截面面积
0
Pcr d EI
k
2d
将边界条件代入统一微分方程的通解得:
式 0
如 图
k 0
1 0 k2
0 1 0
1 0 0
0 0 k
2
C1
C C
2 3
0
sinkL
coskL L 1
k 2 sinkL k 2 coskL 0 0
1 0
Cd4
有非零解的充要条件为:系数行列式值为零;
解得压杆失稳特征方程为:coskL 0
解: (1) 2 E I
Pcr ( l)2
2E d4
64
( l)2
1 16
2E I正
(2)
Pcr 正 Pcr 圆
( l)2 2E I圆
d2 2
a4 4
I正 I圆
12
d4
12
d4
3
( l)2
64
64
例5:五根直径都为 d的细长圆杆铰接构
成平面正方形杆系ABCD,如各杆材料相 同,弹性模量为E。求图 (a)、(b)所示两种 载荷作用下杆系所能承受的最大荷载。
60
2. cr=S时: 强度破坏,采用强度公式。
≤ S—粗短杆(小柔度杆);
表 1 直线公式的系数 a 和 b
第11章 压杆稳定性问题

相等,则此压杆的临界压力又为多少?
(压杆满足欧拉公式计算条件)
h
动脑又动笔
解: 一端固定,一端自由,长度因数 μ=2 在应用欧拉公式时,截面的惯性
矩应取较小的I 值。
Iy 1 3 1 hb 90 403 mm 4 48 104 mm 4 12 12
b
F
l
1 3 1 I z bh 40 903 mm 4 243 104 mm 4 12 12
理解长细比、临界应力和临界应力总图的概念,熟 悉各类压杆的失效形式。
§11–1 压杆稳定性的基本概念
① 强度 衡量构件承载能力的指标 ② 刚度 ③ 稳定性 工程中有些构件具有足够的强度、刚度,却不一定能安全 可靠地工作。 杆件在各种基本变形下的强度和刚度问题在前述各章节中 已作了较详细的阐述,但均未涉及到稳定性问题。事实上, 杆件只有在受到压力作用时,才可能存在稳定性的问题。
屈曲曲线是偏离原直线轴线不远的微弯状态。
F F EI L
M d2w 2 EI dx
§11–2 细长压杆的临界荷载—欧拉临界力
一、两端铰支压杆的临界力
多大的轴向压力才会使压杆失稳?
d2w EI 2 Fw 0 dx
y
M EI x w L
记
F
k2
F EI
F
F
x
d2w 2 k w0 2 dx
§11–3长细比的概念 三类不同压杆的判断
三、临界应力总图
cr
S
P
cr s
cr a b
2E cr 2
粗短杆 s
s s a
b
中长杆
P
细长杆
工程力学11-压杆的稳定性分析与设计解析

11.1.3 三种类型压杆的临界状态 压杆的分类:
细长杆 ——当F >Fcr时容易发生弹性屈曲 当F≤Fcr时不发生屈曲
中长杆 ——当F >Fcr时发生屈曲,但不再是弹性的
粗短杆 ——不会发生屈曲,失效属于强度破坏
《工程力学》
11.2
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
长细比概念三类不同压杆判断
11.3.2 三类不同压杆的区分
ห้องสมุดไป่ตู้
因,屈曲在弹性范围内导出
故有:
scr =
Fcr A
≤[sp]
在比例极限内有效
稳定平衡构形到屈曲(不稳定平衡构形)是一个 过程。
介于这个过程之间的平衡构形——临界平衡构形
或称:“临界状态” 临界载荷
处于临界状态时,杆件所受的施压载荷
称:“临界载荷”,或临界力,Fcr
《工程力学》
11.1
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
令:当材料达到比例极限时的长细比为“lp” 当材料屈服极限时的长细比为“ls”
细长杆 中长杆 粗短杆
—— l ≥ lp —— lp >l ≥ ls —— l < ls
细长压杆的临界载荷
第11章压杆稳定

压杆截面如图所示。两端为柱形铰链约束,
若绕 y 轴失稳可视为两端固定,若绕 z 轴失稳可视为 两端铰支。已知,杆长l=1m ,材料的弹性模量
E=200GPa,sp=200MPa。求压杆的临界应力。
解:
iy 1 3 ( 0 . 03 0 . 02 ) Iy 12 0.0058m A 0.03 0.02
3.压杆失稳:
弹性杆件 稳定直线平衡
F Fcr
F Fcr
F Fcr
F Fcr
微小扰动 恢复直线平衡 不稳定直线平衡
F Fcr
弯曲 除去扰动
v
弯曲
微小扰动
新的弯曲平衡 随遇平衡
除去扰动
F Fcr 除直线平衡形式外,无穷小邻域内,可能微弯平衡
压杆从直线平衡形式到弯曲平衡形式的转变,称为失稳
一、两端铰支的细长压杆:
x
Fcr
F M(x)=Fw
l m w B m
m
x
m
B y F
x
y
Fcr
压杆任一 x 截面沿 y 方向的位移 w f ( x ) 该截面的弯矩
M ( x ) Fw
杆的挠曲线近似微分方程
EIw '' M ( x ) Fw
2
( a)
m
F 令k 得 w '' k 2 w 0 (b) EI
16
4.压杆的临界压力: 稳 定 平 衡 临界状态
过 渡
临界压力:Fcr
不 即:使压杆保持在微 稳 弯状态下平衡的最小 定 轴向力。 平 衡
F Fcr —稳定平衡状态 F Fcr —临界平衡状态 F Fcr —不稳定平衡状态
材料力学-第11章 压杆稳定new

引言
压杆稳定的利用 - 柔性电子器件
材料力学-第11章 压杆稳定
引言
基本概念
F
压杆失稳(屈曲): 受压杆件由直线平衡状态变为弯曲平衡状态 临界载荷:
使得受压杆件由直线平衡态转为弯曲平衡态的临界力
材料力学-第11章 压杆稳定 受压杆件为什么会失稳?
F
引言
杆件压力超过临界载荷时,弯曲构型具有更 小的应变能
Fcr
π 2 EI
l
2
这一表达式称为欧拉公式。其中l为不同压杆屈曲后挠曲线上正弦 半波的长度,称为有效长度(effective length);
为反映不同支承影响的系数,称为长度因数(coefficient of
1ength),可由屈曲后的正弦半波长度确定。
材料力学-第11章 压杆稳定
FPcr
π 2 EI
l
2
需要注意的是, 临界载荷公式只有在压杆的微弯 曲状态下仍然处于弹性状态时才是成立的。
材料力学-第11章 压杆稳定
§11-3 两端非铰支细长压杆的临界载荷
例题
图示四根压杆,已知杆件横截面和材料完全相同。 试:将压杆按承载能力大小排序
5m
7m
(a)
(b)
3m
(c)
§11-3 两端非铰支细长压杆的临界载荷 长度因数 由屈曲后的正弦半波长度确定
欧拉公式可写为:
2 EI
正弦半波长
2
两端铰支 =1.0
一端自由, 一端固定 =2.0
一端铰支, 一端固定 =0.7
两端固定 =0.5
材料力学-第11章 压杆稳定
§11-3 两端非铰支细长压杆的临界载荷
F
Fcr
第 11 章 压杆的稳定性问题

直线形状平衡 稳定的
第 11 章 压杆的稳定性问题 2.不稳定性
F F>Fpcr
压杆稳定性的基本概念
直线平衡平衡状态转变为弯曲平 衡状态,扰动除去后,不能够恢 复到直线平衡状态,则称原来的 直线平衡状态是不稳定的。
FP<FPcr :在扰动作用下,
直线形状平衡 不稳定的
第 11 章 压杆的稳定性问题
第 11 章 压杆的稳定性问题
P
A
(a )
三类不同压杆的判断
h
y
b
h
B
y
P 解:正视图平 面弯曲截面绕 z 轴转。 3 P
x
P
z
l
A bh 1.0
iz Iz A
bh Iz 12
h 2 3
z
l
iz
1 2300 2
60
3
132.8 P 100
σp σe σs
压杆稳定性的基本概念
三、三种类型压杆的不同临界状态
σ
σb
ε
第 11 章 压杆的稳定性问题 欧拉临界力 §11-2 细长压杆的临界载荷---欧拉临界力
一、两端铰支的细长杆
F x F x
F
l M w x w w
压杆
微弯下平衡
内力与变形
第 11 章 压杆的稳定性问题
x
欧拉临界力
M =F w EI w〞= - M =-F w
欧拉临界力
二、其他刚性支承细长压杆临界载荷的通用公式
方法1: 同欧拉公式, 微分方程 + 边界条件 方法2: 相当长度法 在压杆中找出长度相当于两端铰支的 一段(即两端曲率为零或弯矩为零),该 段失稳曲线为半波正弦曲线,该段临界力 即压杆的临界力。
山东建筑大学期末工程力学第11章压杆稳定

对于等直杆
F N max [ ] max A
例题:一长为300 mm的钢板尺,横截面尺寸为 20mm 1mm 。钢 的许用应力为[ ]=196 MPa。按强度条件计算得钢板尺所能承受的 轴向压力为
一, 两端为绞支(球形绞支),长为 l 的 细长 压杆。
当 F 达到 FCr 时,压杆的特点是:保持微弯形式的平衡。
x
F cr
x
w
l
l 2
m w m
F cr
M ( x) F cr w
m m
x
o w o
x
w
F cr
FCr
x
w
m
M ( x) F cr w
m
x
o w
FCr
压杆任一 x 截面沿 w 方向的位移为 w = f (x) 该截面的弯矩为
E F cr cr A ( l / i )
l
i
称为压杆的柔度(长细比)。集中地反映了压杆的长度,杆端约
束,截面尺寸和形状对临界应力的影响。
2 E 2
cr
cr
E 2
2
越大,相应的 cr 越小,压杆越容易失稳。
F Cr A Cr
x
y
2 EI F cr 2 ( l )
z
2 EI y ( F Cr ) y ( l )2 y
2 EI z ( F Cr ) z ( l )2 z
F Cr {( F Cr ) y,( F Cr ) z}min
材料力学-11压杆稳定

π D4 d4 4
D2 d2 64
D2 d 2
17mm
4
μl i
1(1100) 64.7
17
235钢
2EI
Fcr crA Fcr (l)2 ?
2E 2
(D2 d2)
4
226.14 721090(522 4424)
(1) P
F M Fw
w
d 2w
M
dx2
EI
Fw EI
d2w F
dx2
w0 EI
令: k2 F EI
d2w dx2
k2w
0
二阶线性、 常系数齐次
F Fcr 方程解 wAsin B kc xoskx
x
2019/11/22
11
wAsin B kc xoskx
② 边界条件: w(0)0 w(l )0
2 EI
Fcr (2l )2
Euler公式 (固端-自由)
15
[例1] 试由挠曲微分方程,导出下述细长压杆临界力公式
l
Fcr P
解: 1. 挠曲线近似微分方程:
EI,,w M(x) PwMe
Me x x P
令: k2 P w,, k2w Me
EI
EI
M PwMe wAs ik nx Bcoksx M e
S
P
λ μl i
a s
2E
临界应力总图
b
P
2019/11/22
24
§4 压杆的稳定校核
Stability Condition
为保证压杆有足够的稳定性——安全工作
(工作荷载)F
11-压杆稳定

EI
x
F
x
w"k 2w k 2 M 0
M
F
w c cos kx d sin kx M0
F
边界条件为:
M0
M0
F
F
x 0, w w' 0;
x L, w w' 0
c M ,d 0 F
coskL 1 ( kL 2n ),sin kL 0 ( kL n )
实际的受压杆件由于: 1. 其轴线并非理想的直线而存在初弯曲, 2. 作用于杆上的轴向压力有“偶然”偏心, 3. 材料性质并非绝对均匀,
因此在轴向压力作用下会发生弯曲变形,且由此引起的 侧向位移随轴向压力的增大而更快地增大。
5
11.2 两端铰支中心受压直杆的欧拉公式
思路: 假设压杆在某个压力Pcr作用下在曲线状态平衡, 然后设法去求挠曲函数。若: (1)求得的挠曲函数≡0,说明只有直线平衡状态; (2)求得不为零的挠曲函数,说明压杆的确能够 在曲线状态下平衡,即出现失稳现象。
(1)直线型经验公式: cr a b 式中:a 和b 是与材料有关的常数,单位与应力相同。
①p<<u 时: cr ab cr a b u
②u< 时:
cr u
a u
b
0
p 的杆为大柔度杆,其临界应力用欧拉公式求。
0 p 的杆为中柔度杆,其临界应力用经验公式求。
0 的杆为小柔度杆,以极限应力u作为临界应力。27
11.5 超过比例极限时压杆的临界应力 临界应力
③临界应力总图
cr cr
u
u
cr ab
材料力学第11章 压杆稳定

长度系数
一端固定,另一端自由 两端铰支
2 1
一端固定,另一端铰支
2 0.7
3
两端固定
1 0.5
2
第十一章 压杆稳定
§11.3 欧拉公式的使用范围 临界应力总图
一、欧拉临界应力公式及其使用范围 二、中柔度压杆的临界应力 三、小柔度压杆的临界应力 四、临界应力总图
§11.3 欧拉公式的使用范围 临界应力总图
2E 2
O 小 0 中 p 大
柔柔
柔
度度
度
压压
压
杆杆
杆
可见:压杆的临界应力随着其柔度的增大而减小
§11.3 欧拉公式的使用范围 临界应力总图
例1 图示用No.28a工字钢制成的立柱,两端固定,
试求立柱的临界压力。
解:1.求
F
查表:i imin iy 2.50 cm, A 55.4 cm2
ymax
欧拉公式适用于小变形情况
§11.2 细长压杆临界压力的欧拉公式
二、其他约束下细长压杆的临界压力
解法:比较变形法
1.一端固定、另一端自由
Fcr
Fcr
2EI
Fcr (2l)2
l
l
l
Fcr
§11.2 细长压杆临界压力的欧拉公式
二、其他约束下细长压杆的临界压力
解法:比较变形法
2.两端固定
b=20
b 2.57 MPa
h=45
cr a b y 289.6 MPa
Fcr cr A 261 kN y
n
Fcr F
4.35
nst
∴ 连杆安全
l 1=800
11压杆稳定

(2)若在x-z平面内 失稳,μ=0.5,柔度为:
y
L i
L Iz / A L Iy / A
1 700 73.7 6.5104 / 720
0.5 580 39.9 3.8 104 / 720
所以连杆将在x—y平面内失稳,其许用压力应由lz决定。
x
P
x
P
580700
580 L
y
y z
P
zP
(2)确定许用压力:
由表查得硅钢:a=578MPa,b=3.744MPa, s=353MPa,计算有关的p和s为:
p
2E
p
2 2.1105
93 240
s
a s
b
578 353 60 3.744
可见连杆为中柔度杆。其临界载荷为:
Pcr A(a b) 218 kN
由此得连杆的许用压力为:
[Pcr
]
Pcr [nw
w
Fyl Fcr
sin kx 4.49
coskx 1
x l
利用此方程还可以进一步求得该
压杆在上列临界力作用下挠曲线
上的拐点在 x = 0.3l 处(图b)。
(b)
试由挠曲线近似微分方程,导出下述细长压杆
的临界力公式。
P
P
M0
x
解:挠曲线近似微分方程为:
EIw'' M (x) Pw M 0
w Asin kx Bcoskx (b)
利用的边界条件:x=0,w=0 和 x=l,w=0。
即:
A A
0 sin
B kl
0 B cosk
l
0
0
1
0
sin kl coskl
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①p<<u 时: crab cr a bu
②u< 时:
au cru b
0
p 的杆为大柔度杆,其临界应力用欧拉公式求。
0 p的杆为中柔度杆,其临界应力用经验公式求。
0 的杆为小柔度杆,以极限应力u作为临界应力。27
11.5 超过比例极限时压杆的临界应力 临界应力
③临界应力总图
cr cru
F
F
F<F cr
F=F cr
F>F cr
F'
F
F
F
F
F
稳 定 平 衡——压杆 能 恢复到原(直线)状态的平衡 不稳定平衡——压杆不能恢复到原(直线)状态的平衡
11.1 压杆稳定性的概念
从另一个角度来看,此处中心受压杆的临界力又可理解 为:杆能保持微弯状态时的轴向压力。
显然,理想中心压杆是有偶然偏心等因素的实际压杆的 一种抽象。
ymax
Fcr
y0m / F 1
y
1 ) .当 F F cr, ym ax仅 为 y0m 的 若 干 分 之 一 ; 2) .当 F0.5F cr, ym axy0m ;
3) .当 F F cr, ym ax迅 速 增 长 , 一 旦 FF cr, ym ax
例题
解: 截面惯性矩
临界力
按强度条件,屈服压力
33
稳定计算的一般步骤:
① 分别计算各个弯曲平面内的柔度y 、z , 从而得到max;
② 计算s 、p ,根据max确定计算压杆临
界压力的公式,小柔度杆cr= s,中柔
度杆cr=
ab,大柔度杆
cr
2E 2
③ 计算Fcr= crA,利用稳定条件
F cr F
n st
进行稳定计算。
11.6 压杆的稳定校核及提高稳定性的措施
作业:9-1,9-2,9-4
23
11.4 临界应力 欧拉公式的应用范围
在推导细长中心压杆临界力的欧拉公式时,应用了材料 在线弹性范围内工作时的挠曲线近似微分方程,可见欧拉公
式只可应用于压杆横截面上的应力不超过材料的比例极限p
的情况。
细长中心压杆在临界力Pcr作用时可在直线状态下维持
不稳定的平衡,故其时横截面上的应力可按cr=Pcr /A来计
19
在总压力F作用下,立柱微弯时可能有下列三种情况:
20
(a)每根立柱作为两端固定的压杆分别失稳:
(b)两根立柱一起作为下端固定而上端自由的体系在自 身平面内失稳
失稳时整体在面内弯曲,则1,2两杆组成一组合截面。
21
(c)两根立柱一起作为下端固定而上端自由的体系在面外失稳
故面外失稳时 最小
=
22
算,亦即
cr P A cr π l2E 2A I π l2 /E i2π 2 2 E
(a)
24
11.4 临界应力 欧拉公式的应用范围
式中,cr称为临界应力;iI/A为压杆横截面对于失稳
时绕以转动的形心主惯性轴的惯性半径;l /i为压杆的相当
长度与其横截面惯性半径之比,称为压杆的长细比
(slenderness)或柔度,记作,即
6
11.2 两端铰支中心受压直杆的欧拉公式
x
Pcr
y
y
mm y
xO y
(a)
本节以两端球形铰支(简称两端铰支) 的细长中心受压杆件(图a)为例,按照对 于理想中心压杆来说临界力就是杆能保 持微弯状态时的轴向压力这一概念,来 导出求临界力的欧拉(L.Euler)公式。
l
7
11.2 两端铰支中心受压直杆的欧拉公式
11 压杆稳定
1
11 压杆稳定
11.1 压杆稳定的概念 11.2 两端铰支中心受压直杆的欧拉公式 11.3 不同约束条件下压杆的欧拉公式 11.4 临界应力 欧拉公式的应用范围 11.5 超过比例极限时压杆的临界应力
临界应力总图 11.6 压杆的稳定校核及提高稳定性的措施
2
11.1 压杆稳定性的概念
通常把≥p的压杆,亦即能够应用欧拉公式求临界力Fcr 的压杆,称为大柔度压杆或细长压杆,而把<p的压杆,亦
即不能应用欧拉公式的压杆,称为小柔度压杆。
26
11.5 超过比例极限时压杆的临界应力 临界应力
超过比例极限时压杆临界应力的经验公式
(1)直线型经验公式: c rab
式中:a 和b 是与材料有关的常数,单位与应力相同。
11.2 两端铰支中心受压直杆的欧拉公式
此时杆的挠曲线方程可如下导出。前已求得B=0,且取 kl=,压杆的挠曲线表达式可写成
v Asinπx l
注意到当x= l /2 时 v=d,故有 A=d。从而知,对应于kl=,
亦即对应于Pcr=2EI/l 2,挠曲线方程为
v d sin π x
l 可见此时的挠曲线为半波正弦曲线。
支承情况
两端铰支
一端固定 另端铰支
两端固定
一端固定 两端固定但可沿 另端自由 横向相对移动
l l 0.7l l 0.5l
l 2l l 0.5l
Pcr
Pcr
Pcr
Pcr
Pcr
失
稳 时
B
B
B
挠
D
曲
线 形
C
C
状
A
A
A
C— 挠曲 C、D— 挠
线拐点 曲线拐点
临界力Pcr 欧拉公式
Pcr
2 EI l2
Pcr
(0.27El)I2Pcr
约束情况下的相当长度 l。
16
11.3 不同约束条件下压杆的欧拉公式
运用欧拉公式计算临界力时需要注意: (1)当杆端约束情况在各个纵向平面内相同时(例如球形铰),
欧拉公式中的 I 应是杆的横截面的最小形心主惯性矩 Imin。 (2)当杆端约束在各个纵向平面内不同时,欧拉公式中所取用
的I应与失稳(或可能失稳)时的弯曲平面相对应。
2EI
(0.5l ) 2
Pcr
2 EI (2l ) 2
长度系数μ μ=1 μ0.7 μ=0.5 μ=2
2EI
Pcr l 2
μ=1 15
11.3 不同约束条件下压杆的欧拉公式
表中列出了几种典型的理想杆端约束条件下,等截面细长
中心受压直杆的欧拉公式。从表中可见,杆端约束越强,压杆
的临界力也就越高。
l
i
根据欧拉公式只可应用于cr≤p的条件,由式(a)知该应
用条件就是
cr
π2E
2
p
亦即
π2E p
或写作 p
25
11.4 临界应力 欧拉公式的应用范围
可见 p
π 2 E 就是可以应用欧拉公式的压杆最小柔度。 p
对于Q235钢,按照 E=206 GPa,p =200 MPa,有
p π 2p E π2 220 0 10 16 60 P 90 Paa100
(2) 折减因数法
[ n s c]tr []s t[] 即 []
式中: [st]—稳定许用应力; []—许用压应力;
<1—折 减系 数 ,与 柔度
和材料有关, 可查规范。
35
11.6 压杆的稳定校核及提高稳定性的措施
580 700 580
l
例1 确定图示连杆的许用压力[P]st。已知连杆横截面面积
u
crab
P
2E
cr
2
0
a
u
b
P 2E
P
L i
28
11.5 超过比例极限时压杆的临界应力 临界应力
③临界应力总图
cr
cra1b12
u
p
cr
2E 2
O
p
29
11.5 超过比例极限时压杆的临界应力 临界应力
9-7 如果杆分别由下列材料制成:
试求可用欧拉公式计算临界力的压杆的最小柔度。
30
杆的边界条件:
v
x0
0
代入通解得:
v x l 0
(a)
kl Pcr L n
EI
(b) B 0
(n 1,2
)
A sik n lB co k ls0 sik n l0 临界力为最小压力:
Pcr
n2 2EI
l2
(n 1,2 )
Pcr
2 EI l2
—
欧拉公式
8
11.2 两端铰支中心受压直杆的欧拉公式
c 的杆为非细长压杆,以抛物线经验公式计算临界应32力。
11.6 压杆的稳定校核及提高稳定性的措施
1.压杆的稳定校核
(1)安全因数法
N An s ctr []st或 P n P c strP st
三类问题:确定许用载荷、稳定性校核、截面尺寸 设计
确定nst,除考虑确定安全系数的一般原则外,还 应考虑压杆初挠度、荷载偏心等因素影响,故 nst >n。
10
*初弯曲(初偏心、材质不均匀)对临界力的影响:
初弯曲位移函数:
y0 y0m sin l x
x截面上的弯矩:
M (x)F(y0y)
挠曲线近似微分方程: E IyF (y0y)
边界条件:
x 0 ,y 0 ;x l,y 0
挠曲线方程:
y y0m sinx
y0m
Fcr /F1 l
l
x l 2
时,有最大附加弯矩:
工程中有些构件具有足够的强度、刚度,却不一定能安全 可靠地工作。压杆的承载能力不仅取决于构件的强度和刚度, 还与其稳定性有关。
不稳定平衡
微小扰动就使小球远 离原来的平衡位置
稳定平衡
微小扰动使小球离开原
来的平衡位置,但扰动撤销
后小球回复到平衡位置
