2009年浙江省慈溪中学提前招生数学试题
慈溪中学提前招生自然试卷(含答案)
自 然说明:I. 本卷考试时间100分钟,满分100分。
II. 本卷分试题(共6页)和答卷(共4页),答案必须做在答题卷上。
III. 本卷可能用到的相对原子质量:(H —1、C —12、O —16、S —32、Cl —35.5、Mg —24、Fe —56、Na —23、Al —27、K —39、Zn —65、Cu —64、Ag —108 Ba —137)试 题一、选择题(共10小题,每小题3分,共30分。
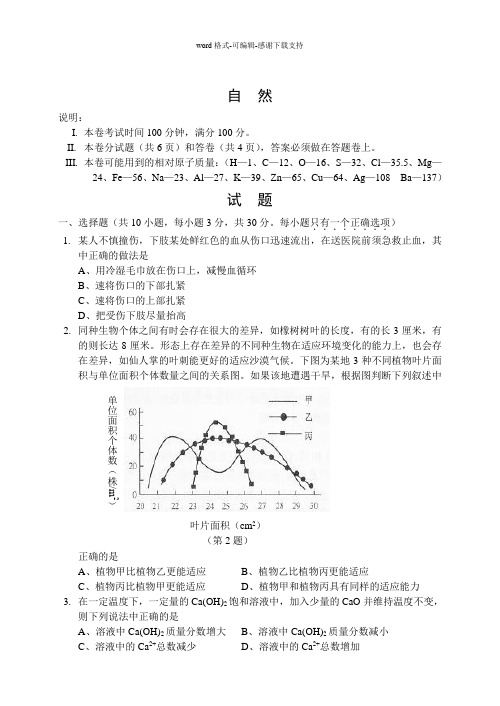
每小题只有一个正确选项........) 1. 某人不慎撞伤,下肢某处鲜红色的血从伤口迅速流出,在送医院前须急救止血,其中正确的做法是A 、用冷湿毛巾放在伤口上,减慢血循环B 、速将伤口的下部扎紧C 、速将伤口的上部扎紧D 、把受伤下肢尽量抬高2. 同种生物个体之间有时会存在很大的差异,如橡树树叶的长度,有的长3厘米,有的则长达8厘米。
形态上存在差异的不同种生物在适应环境变化的能力上,也会存在差异,如仙人掌的叶刺能更好的适应沙漠气候。
下图为某地3种不同植物叶片面积与单位面积个体数量之间的关系图。
如果该地遭遇干旱,根据图判断下列叙述中正确的是A 、植物甲比植物乙更能适应B 、植物乙比植物丙更能适应C 、植物丙比植物甲更能适应D 、植物甲和植物丙具有同样的适应能力3. 在一定温度下,一定量的Ca(OH)2饱和溶液中,加入少量的CaO 并维持温度不变,则下列说法中正确的是A 、溶液中Ca(OH)2质量分数增大B 、溶液中Ca(OH)2质量分数减小C 、溶液中的Ca 2+总数减少D 、溶液中的Ca 2+总数增加叶片面积(cm 2)(第2题)单位面积个体数(株/m 2)4. 有三种有机物C 2H 6O 、C 2H 4和C 6H 12组成的混合物,已知碳元素的质量分数为a%,则混合物中氧元素的质量分数为A 、10%B 、1-67a %C 、100-67a % D 、98(100-67a )%5. 在用氢气还原氧化铜实验中,根据氢气在本实验中的作用,生成的铜与消耗氢气的质量M 、m 关系图像正确的是6. 下述关系式中既表示物理量的概念的数学定义表达式,又体现该物理量与其它物理量之间的内在联系规律的是A 、P=W/tB 、ρ=m/νC 、p=F/SD 、I=U/R7. 下列有关凸透镜成像的说法中,正确的是A 、人们在电影院看到银幕上的画面,对人眼而言是物而不是像,对放映机镜头而言才是像B 、用黑纸遮住凸透镜的上半部分,则光屏上只能成一半的像C 、物体沿主轴从6倍焦距移到2倍焦距处的过程中,像移动的速度大于物体移动的速度,并且像逐渐变小D 、幻灯机的幻灯片总是倒插在焦点与镜头之间8. 如图所示,甲乙丙三个相同的小钢球从相同高度以相同的速度分别沿所示的方向抛出,若不计空气阻力,则关于小球落地时的速度与落地过程所需的时间的叙述正确的是(第8题)A 、落地速度甲最小,落地也最晚B 、乙的落地速度大小与落地时间都居中C 、落地的速度大小与所需的时间都一样D 、落地速度大小都一样,但丙最早落地9. 如图所示,甲、乙两只完全相同的金属球,甲用细线悬挂在天花板上,乙放在水平面上。
100测评网中考数学2009宁波重点中学保送生招生考试试卷及答案
OC B A D(1)(2)(3)2009宁波重点中学保送生招生考试数学试卷一、选择题(每小题3分,共36分)1、如图是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( )(A )25 (B )66 (C )91 (D )1202、有如下结论(1)有两边及一角对应相等的两个三角形全等;(2)菱形既是轴对称图形又是中心对称图形;(3)对角线相等的四边形是矩形;(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧。
其中正确结论的个数为( )(A )1个 (B )2个 (C )3个 (D )4个3、在1000个数据中,用适当的方法抽取50个作为样本进行统计,频数分布表中,54.5~57.5这一组的频率是0.12,那么,估计总体数据落在54.5~57.5之间的约有 ( )(A )6个 (B )12个 (C )60个 (D )120个4、如图,⊙O 中,弦AD ∥BC ,DA =DC ,∠AOC =160°,则∠BCO 等于( ).(A )20° (B )30° (C )40° (D )50°5.若直角三角形的两条直角边长为a 、b ,斜边长为c ,斜边上的高为h ,则有( )A 、ab=h ;B 、a 1+b 1=h 1 ;C 、21a +21b =21h; D 、a 2 +b 2=2h 2 6.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A 、B 、C 均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是A B C D7.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察图中每正方形(实线)四条边上的整点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点的个数共有…………………………( )A 、35个B 、40个C 、45个D 、50个8.用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正多边形的边数为x 、y 、z ,则zy x 111++的值为( ) (A )1 (B )32 (C )21 (D )31 9.13个小朋友围成一圈做游戏,规则是从某一个小朋友开始按顺时针方向数数,数到第13,该小朋友离开;这样继续下去.,直到最后剩下一个小朋友.小明是1号,要使最后剩下的是小明自己,他应该建议从( )小朋友开始数起?A 、7号B 、8号C 、13号D 、2号10、在1+11+111+……+111……111(最后一项2009个1)的和之中,数字1共出现了( )次. A 、224 B 、225 C 、1004 D 、100511、一只船有一个漏洞,水以均匀速度进入船内。
2009年宁波某区某校自主招生数学试卷

2009年宁波某区某校自主招生数学试卷一、填空题(每小题3分,共18分)1、因式分解 3221218a a a -+= .2、一个锐角的正切值为2,那么这个锐角的正弦值为 .3、数轴上点A 与B 的距离为5,点A 表示-3,则点B 表示的数是 .4、如图,△ABC 中∠BAC=90°,D 、E 在BC 上,AC=DC ,AB=EB ,∠DAE= 度.5、如图,湖边有一个高30米的塔AD ,在塔上看见湖面上空有一只热汽球B ,仰角45º,观测热气球在湖面镜像C 的俯角为60º,则热气球距湖面的高度为 米.6、已知a 、b 、c 是正整数,a <b <c ,且有13111210a b c ++=,那么满足条件的数组(a ,b ,c)有 组.二、选择题(每小题3分,共18分)7、已知二次函数91232-+-=x x y ,那么y 的最大值是 ( )A .0B .-9C .3D .128、如图,半径为8的⊙O 剪去一个直角扇形,剩下的部分围成一个圆锥的侧面,这个圆锥的底面半径等于 ( )A .6B .8C .10D .129、如图Rt △ABC 中,∠C=90°,AC=8,BC=6,∠A 和∠B 的平分线交于D ,则D 到AB 的距离DE 的长是 ( )A .2B .2.5C .3D .3.510、如图,将一张矩形纸片按如下方法折叠,那么∠BGA 的度数是 ( )A .30°B .45°C .60°D .75°11、有下列4个命题:①两个直角三角形有一个锐角和一条直角边相等,那么这两个三角形全等;②两个三角形有两条边和其中一边上的高对应相等,那么这两个三角形全等;③两个三角形有三个角和两条边分别相等,那么这两个三角形全等;④两个三角形有两边和其中一边的对角对应相等,那么这两个三角形一定有全等和不全等两种情况. 其中假命题的个数是 ( )A .1个B .2个C .3个D .4个(第4题) (第5题) (第9题)(第8题)12、已知x m =是方程01322=--x x 的根,则代数式222(21)39m m --的值是 ( ) A .1 B .2 C.3+ D.3三、解答题(13~15每题6分,16、17每题8分,18题10分,共44分)13、解方程 212121111x x x x x +--=+-+-.14、某建筑商为建一个高档商品房,需要进大批量的砖.确定砖好坏的指标是抗冲击强度,建房时要求每块砖的抗冲击强度尽可能的大,否则可能因为一块砖的质量影响整幢房子的质量.现有甲、乙两家砖瓦厂各10块砖的抗冲击强度如下表:(单位:kg )(1) 请把上表填写完整;(2) 为了保证商品房的质量,这个建筑商会在甲、乙两家砖瓦厂中选哪一家厂的砖?为什么?15、某草莓种植农户,用暖棚种了冬季草莓。
浙江省宁波市2009年中考数学试题含答案

宁波市2009年初中毕业生学业考试考生须知:1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷Ⅰ、答题卷Ⅱ.试题卷共6页,有三个大题,26个小题,满分120分,考试时间为120分钟.2.请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上.3.答题时,把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B 铅笔涂黑、涂满.将试题卷Ⅱ答案用黑色字迹钢笔或签字笔书写,答案必须按照题号顺序在答题卷Ⅱ各题目规定区域内作答,做在试题卷上或超出答题卷区域书写的答案无效.4.允许使用计算器,但没有近似计算要求的试题,结果都不能用近似数表示.抛物线2y ax bx c =++的顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.试题卷Ⅰ一、选择题(每题3分,共36分,在每题给出的四个选项中,只有一项符合题目要求)1.以下四个数中,比0小的数是( ) A .23BC .πD .1-2.等腰直角三角形的一个底角的度数是( ) A .30° B .45° C .60° D .90°3.一个不透明的布袋装有4个只有颜色不同的球,其中2个红球,1个白球,1个黑球,搅匀后从布袋里摸出1个球,摸到红球的概率是( ) A .12B .13C .14D .164.据《宁波市休闲旅游基地和商务会议基地建设五年行动计划》,预计到2012年,宁波市接待游客容量将达到4640万人次.其中4640万用科学记数法可表示为( ) A .90.46410⨯B .84.6410⨯C .74.6410⨯D .646.410⨯5x 的取值范围是( ) A .2x ≠ B .2x > C .x ≤2 D .2x ≥6.如图是由4个立方块组成的立体图形,它的俯视图是( )A .B .C .D . 7.以下调查适合作普查的是( ) A .理解在校大学生的主要娱乐方式 B .理解宁波市居民对废电池的处理情况 C .日光灯管厂要检测一批灯管的使用寿命(第6题)D .对甲型H1N1流感患者的同一车厢的乘客实行医学检查 8.以方程组21y x y x =-+⎧⎨=-⎩的解为坐标的点()x y ,在平面直角坐标系中的位置是( )A .第一象限B .第二象限C .第三角限D .第四象限9.如图,∠1,∠2,∠3,∠4是五边形ABCDE 的外角,且∠1=∠2=∠3=∠4=70°,则∠AED 的度数是( ) A .110° B .108° C .105° D .100°10.反比例函数ky x=在第一象限的图象如下图,则k 的值可能是( ) A .1 B .2 C .3 D .411.如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N 分别是边AB 、AD 的中点,连接OM 、ON 、MN ,则以下表达准确的是( ) A .△AOM 和△AON 都是等边三角形B .四边形MBON 和四边形MODN 都是菱形C .四边形AMON 与四边形ABCD 是位似图形 D .四边形MBCO 和四边形NDCO 都是等腰梯形 12.如图,点A 、B 、C 在一次函数2y x m =-+的图象上,它们的横坐标依次为1-,1,2,分别过这些点作x 轴与y 轴的垂线,则图中阴影局部的面积之和是( ) A .1 B .3C .3(1)m -D .3(2)2m -试题卷Ⅱ二、填空题(每题3分,共18分) 13.实数8的立方根是 . 14.不等式组6020x x -<⎧⎨->⎩的解是 .15.甲、乙、丙三名射击手的20次测试的平均成绩都是8环,方差分别是20.4S =甲(环2),2 3.2S =乙(环2),21.6S =丙(环2),则成绩比较稳定的是 .(填“甲”“乙”“丙”12 3 4 D C B A E (第9题)D B CA NMO (第11题) (第12题)中的一个)16.如图,在坡屋顶的设计图中,AB AC =,屋顶的宽度l 为10米,坡角α为35°,则坡屋顶高度h 为 米.(结果精确到0.1米)17.如图,梯形ABCD 中,AD BC ∥,7040B C ∠=∠=°,°,作DE AB ∥交BC 于点E ,若3AD =,10BC =,则CD 的长是 .18.如图,A ⊙、B ⊙的圆心A 、B 在直线l 上,两圆的半径都为1cm ,开始时圆心距4cm AB =,现A ⊙、B ⊙同时沿直线l 以每秒2cm 的速度相向移动,则当两圆相切时,A ⊙运动的时间为 秒.三、解答题(第19~21题各6分,第22题10分,第23~24题各8分,第25题10分,第26题12分,共66分)19.先化简,再求值:(2)(2)(2)a a a a -+--,其中1a =-.20.如图,点A ,B 在数轴上,它们所对应的数分别是4-,2235x x +-,且点A 、B 到原点的距离相等,求x 的值.21.(1)如图1,把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星,则这个六角星的边数是 .C (第16题)AB C DE (第17题)(第18题) (第20题)(2)如图2,在5×5的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为一边向外作正方形,并去掉居中的那条线段.请你把得到的图形画在图3中,并写出这个图形的边数.(3)现有一个正五边形,把正五边形的各边三等分,分别以居中那条线段为一边向外作正五边形,并去掉居中的那条线段,得到的图形的边数是多少?22.2009年宁波市初中毕业生升学体育集中测试项目包括体能(耐力)类项目和速度(跳跃、力量、技能)类项目.体能类项目从游泳和中长跑中任选一项,速度类项目从立定跳远、50米跑等6项中任选一项.某校九年级共有200名女生在速度类项目中选择了立定跳远,现从这200名女生中随机抽取10名女生实行测试,下面是她们测试结果的条形统计图.(另附:九年级女生立定跳远的计分标准)(1)求这10名女生在本次测试中,立定跳远距离..的极差和中位数,立定跳远得分..的众数和平均数.(2)请你估计该校选择立定跳远的200名女生中得满分的人数.23.如图,抛物线254y ax ax a =-+与x 轴相交于点A 、B ,且过点(54)C ,. (1)求a 的值和该抛物线顶点P 的坐标;10名女生立定跳远距离条形统计图 女生序号 (第22题)九年级女生立定跳远计分标准 (注:不到上限,则按下限计分,满分为10分) (图1) (第21题) (图2) (图3)(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.24.已知,如图,O ⊙的直径AB 与弦CD 相交于E ,BC BD =,O ⊙的切线BF 与弦AD 的延长线相交于点F . (1)求证:CD BF ∥;(2)连结BC ,若O ⊙的半径为4,3cos 4BCD ∠=,求线段AD 、CD 的长.25.2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009(第23题) 5,4)(第24题)年投入“需方”的资金将比2008年提升30%,投入“供方”的资金将比2008年提升20%. (1)该市政府2008年投入改善医疗卫生服务的资金是多少万元? (2)该市政府2009年投入“需方”和“供方”的资金各多少万元?(3)该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年增长率.26.如图1,在平面直角坐标系中,O 为坐标原点,点A 的坐标为(80)-,,直线BC 经过点(86)B -,,(06)C ,,将四边形(图1)OABC 绕点O 按顺时针方向旋转α度得到四边形OA B C ''',此时直线OA '、直线B C ''分别与直线BC 相交于点P 、Q .(1)四边形OABC 的形状是 , 当90α=°时,BPBQ的值是 ; (2)①如图2,当四边形OA B C '''的顶点B '落在y 轴正半轴时,求BPBQ的值; ②如图3,当四边形OA B C '''的顶点B '落在直线BC 上时,求OPB '△的面积. (3)在四边形OABC 旋转过程中,当0180α<≤°时,是否存有这样的点P 和点Q ,使12BP BQ =若存有,请直接写出点P 的坐标;若不存有,请说明理由.参考答案及评分标准) (图3)(图2)x(备用图)(第26题)三、解答题(共66分)注:1.阅卷时应按步计分,每步只设整分;2.如有其它解法,只要准确,都可参照评分标准,各步相对应给分.19.解:原式2242a a a =--+ ········································································ 2分24a =-. ················································································· 4分 当1a =-时, 原式2(1)4=⨯--6=- ····································································································· 6分 20.解:由题意得,22435x x +=-, ································································································ 3分 解得115x =. ································································································ 5分经检验,115x =是原方程的解.∴x 的值为115. ···················································6分21.(1)12. ························································1分 (2)这个图形的边数是20. ·········· 4分(其中画图2分) (3)得到的图形的边数是30. ································6分22.(1)立定跳远距离的极差20517431(cm)=-=. ··········································· 2分 立定跳远距离的中位数199197198(cm)2+==. ·················································· 4分 根据计分标准,这10名女生的跳远距离得分分值分别是: 7,9,10,10,10,8,10,10,9. 所以立定跳远得分的众数是10(分), ································································ 6分 立定跳远得分的平均数是9.3(分). ·································································· 8分 (2)因为10名女生中有6名得满分,所以估计200名女生中得满分的人数是620012010⨯=(人). ······································································································ 10分23.解:(1)把点(54)C ,代入抛物线254y ax ax a =-+得,252544a a a -+=, ····················································································· 1分 解得1a =. ·································································································· 2分∴该二次函数的解析式为254y x x =-+.22595424y x x x ⎛⎫=-+=-- ⎪⎝⎭∴顶点坐标为5924P ⎛⎫- ⎪⎝⎭,. ·············································································· 4分 (2)(答案不唯一,合理即准确)如先向左平移3个单位,再向上平移4个单位, ··················································· 6分 得到的二次函数解析式为225917342424y x x ⎛⎫⎛⎫=-+-+=++ ⎪ ⎪⎝⎭⎝⎭,即22y x x =++. ························································································· 8分 24.解:(1)直径AB 平分CD ,∴AB CD ⊥. ······························································································ 1分BF 与O ⊙相切,AB 是O ⊙的直径,AB BF ∴⊥. ······························································································ 2分 CD BF ∴∥. ······························································································ 3分 (2)连结BD ,AB 是O ⊙的直径,90ADB ∴∠=°, 在Rt ADB △中,3cos cos 4A C ∠=∠=,428AB =⨯=.3cos 864AD AB A ∴=∠=⨯=. ····································································· 5分 AB CD ⊥于E , 在Rt AED △3cos cos 4A C ∠=∠=,sin 4A ∠=.sin 6DE AD A ∴=∠== ···························································· 7分 直径AB 平分CD ,2CD DE ∴== ··················································································· 8分25.解:(1)该市政府2008年投入改善医疗服务的资金是:600012504750-=(万元) ··········································································· 2分 (2)设市政府2008年投入“需方”x 万元,投入“供方”y 万元,由题意得4750(130%)(120%)6000.x y x y +=⎧⎨+++=⎩,解得30001750.x y =⎧⎨=⎩,····························································································· 4分∴2009年投入“需方”资金为(130%) 1.330003900x +=⨯=(万元),2009年投入“供方”资金为(120%) 1.217502100y +=⨯=(万元).答:该市政府2009年投入“需方”3900万元,投入“供方”2100万元. ·················· 6分 (3)设年增长率为x ,由题意得26000(1)7260x +=, ··················································································· 8分解得10.1x =,2 1.1x =-(不合实际,舍去)答:从2009~2011年的年增长率是10%. ·························································· 10分 26.解:(1)矩形(长方形); ·········································································· 1分47BP BQ =. ···································································································· 3分 (2)①POC B OA ''∠=∠,PCO OA B ''∠=∠90=°,COP A OB ''∴△∽△. CP OC A B OA ∴=''',即668CP =,92CP ∴=,72BP BC CP =-=. ···································································· 4分 同理B CQ B C O '''△∽△,CQ B C C Q B C '∴=''',即10668CQ -=, 3CQ ∴=,11BQ BC CQ =+=. ··································································· 5分 722BP BQ ∴=. ······························································································· 6分 ②在OCP △和B A P ''△中,90OPC B PA OCP A OC B A ''∠=∠⎧⎪'∠=∠=⎨⎪''=⎩,°,, (AAS)OCP B A P ''∴△≌△. ·········································································· 7分 OP B P '∴=.设B P x '=,在Rt OCP △中, 222(8)6x x -+=,解得254x =. ··········································· 8分 125756244OPB S '∴=⨯⨯=△. ··········································································· 9分 (3)存有这样的点P 和点Q ,使12BP BQ =. ················································· 10分点P的坐标是19P ⎛⎫- ⎪⎝⎭,2764P ⎛⎫- ⎪⎝⎭,. ················································· 12分 对于第(3)题,我们提供如下详细解答,对学生无此要求. 过点Q 画QH OA '⊥于H ,连结OQ ,则QH OC OC '==,12POQ S PQ OC =△,12POQ S OP QH =△, PQ OP ∴=.设BP x =,12BP BQ =, 2BQ x ∴=,① 如图1,当点P 在点B 左侧时,3OP PQ BQ BP x ==+=,在Rt PCO △中,222(8)6(3)x x ++=,解得11x=,21x =(不符实际,舍去). 9PC BC BP ∴=+=19P ⎛⎫∴-- ⎪⎝⎭.②如图2,当点P 在点B 右侧时,OP PQ BQ BP x ∴==-=,8PC x =-.在Rt PCO △中,222(8)6x x -+=,解得254x =. PC BC BP ∴=-257844=-=, 2764P ⎛⎫∴- ⎪⎝⎭,.综上可知,存有点19P ⎛⎫- ⎪⎝⎭,2764P ⎛⎫- ⎪⎝⎭,,使12BP BQ =.。
2009年浙江省宁波市中考试卷答案
2009年浙江省宁波市中考 数学试卷参考答案及评分标准一、选择题(每小题3分,共36分)二、填空题(每小题3分,共18分) 三、解答题(共66分)注:1.阅卷时应按步计分,每步只设整分;2.如有其它解法,只要正确,都可参照评分标准,各步相应给分.19.解:原式2242a a a =--+ ··················································································· 2分24a =-. ······························································································ 4分当1a =-时, 原式2(1)4=⨯--6=- ····················································································································· 6分20.解:由题意得,22435x x +=-, ··············································································································· 3分 解得115x =. ··············································································································· 5分经检验,115x =是原方程的解.∴x 的值为115.····························································6分21.(1)12. ·······························································1分 (2)这个图形的边数是20. ·············4分(其中画图2分) (3)得到的图形的边数是30. ·····································6分22.(1)立定跳远距离的极差20517431(cm )=-=. ··············································· 2分 立定跳远距离的中位数199197198(cm )2+==. ························································· 4分 根据计分标准,这10名女生的跳远距离得分分值分别是: 7,9,10,10,10,8,10,10,9.所以立定跳远得分的众数是10(分), ········································································ 6分 立定跳远得分的平均数是9.3(分). ··········································································· 8分 (2)因为10名女生中有6名得满分,所以估计200名女生中得满分的人数是620012010⨯=(人).······················································································································10分23.解:(1)把点(54)C ,代入抛物线254y ax ax a =-+得,252544a a a -+=, ·································································································· 1分解得1a =. ················································································································· 2分∴该二次函数的解析式为254y x x =-+.22595424y x x x ⎛⎫=-+=-- ⎪⎝⎭∴顶点坐标为5924P ⎛⎫- ⎪⎝⎭,.·························································································· 4分 (2)(答案不唯一,合理即正确)如先向左平移3个单位,再向上平移4个单位, ··························································· 6分 得到的二次函数解析式为225917342424y x x ⎛⎫⎛⎫=-+-+=++ ⎪ ⎪⎝⎭⎝⎭,即22y x x =++. ······································································································· 8分 24.解:(1) 直径A B 平分,∴A B C D ⊥. ············································································································ 1分 BF 与O ⊙相切,A B 是O ⊙的直径,AB BF ∴⊥. ············································································································· 2分 C D B F ∴∥. ············································································································· 3分(2)连结B D ,A B 是O ⊙的直径, 90AD B ∴∠=°,在R t AD B △中,3cos cos 4A C ∠=∠=,428A B =⨯=.438cos ⨯=∠⋅=∴A AB AD . ···················································································· 5分A B C D ⊥于E ,在R t AED △3cos cos 4A C ∠=∠=,sin 4A ∠=.sin 64D E AD A ∴=∠=⨯=····································································· 7分 直径A B 平分,2C D D E ∴== ································································································ 8分25.解:(1)该市政府2008年投入改善医疗服务的资金是:600012504750-=(万元) ······················································································ 2分(2)设市政府2008年投入“需方”x 万元,投入“供方”y 万元,由题意得4750(130%)(120%)6000.x y x y +=⎧⎨+++=⎩,解得30001750.x y =⎧⎨=⎩, ··········································································································· 4分∴2009年投入“需方”资金为(130%) 1.330003900x +=⨯=(万元),2009年投入“供方”资金为(120%) 1.217502100y +=⨯=(万元).答:该市政府2009年投入“需方”3900万元,投入“供方”2100万元.····················· 6分(3)设年增长率为x ,由题意得26000(1)7260x +=, ································································································ 8分 解得10.1x =,2 1.1x =-(不合实际,舍去)答:从2009~2011年的年增长率是10%. ····································································10分 26.解:(1)矩形(长方形); ·················································································· 1分 47BP BQ=. ··················································································································· 3分(2)① P O C B O A ''∠=∠,P C O O A B ''∠=∠90=°,C O P A O B ''∴△∽△. C P O C A B O A ∴=''',即668C P =,92C P ∴=,72B P BC C P =-=. ·············································································· 4分同理B CQ B C O '''△∽△, C Q B C C QB C '∴=''',即10668C Q -=,3CQ ∴=,11BQ BC CQ =+=. ············································································· 5分 722BP BQ∴=. ·············································································································· 6分②在O C P △和B A P ''△中, 90O PC B PA O C P A O C B A ''∠=∠⎧⎪'∠=∠=⎨⎪''=⎩,°,, (AAS)OCP B A P ''∴△≌△. ····················································································· 7分 O P B P '∴=.设B P x '=,在R t O C P △中, 222(8)6x x -+=,解得254x =.·················································· 8分125756244O PB S '∴=⨯⨯=△. ······················································································· 9分(3)存在这样的点P 和点Q ,使12B P B Q =. ·························································10分点P 的坐标是19P ⎛⎫--⎪⎝⎭,2764P ⎛⎫- ⎪⎝⎭,. ··························································12分 对于第(3)题,我们提供如下详细解答,对学生无此要求. 过点Q 画QH OA '⊥于H ,连结O Q ,则QH OC OC '==,OC PQ S POQ ⋅=∆21,OC PQ S POQ⋅∆21,PQ OP ∴=.设B P x =,12BP BQ =,2BQ x ∴=,① 如图1,当点P 在点B 左侧时,3OP PQ BQ BP x ==+=,在R t PC O △中,222(8)6(3)x x ++=,解得11x =+,21x =-9P C B C B P ∴=+=+,19P ⎛⎫∴--⎪⎝⎭.②如图2,当点P 在点B 右侧时,OP PQ BQ BP x ∴==-=,8P C x =-.在R t PC O △中,222(8)6x x -+=,解得254x =.PC BC BP ∴=-257844=-=,2764P ⎛⎫∴- ⎪⎝⎭,.综上可知,存在点19P ⎛⎫--⎪⎝⎭,2764P ⎛⎫- ⎪⎝⎭,,使12B P B Q =.。
2009年浙江宁波中考数学模拟试卷(一)(二)

(3)研究小组在进一步探究中发现:过点 任作一条直线交 于点 ,再过点 作直线 ,交 于点 ,连接 (如图3),则直线 也是 的黄金分割线.
请你说明理由.
(4)如图4,点 是 的边 的黄金分割点,过点 作 ,交 于点 ,显然直线 是 的黄金分割线.请你画一条 的黄金分割线,使它不经过 各边黄金分割点.
17.如图,在由24个边长都为1的小正三角形组成的网格中,点P是正六边形的一个顶点,以点P为直角顶点作直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边长。
18.正 的边长为 ,边长为 的正 的顶点 与点 重合,点 分别在 , 上,将 沿着边 顺时针连续翻转(如图所示),直至点 第一次回到原来的位置,则点 运动路径的长为 .(结果保留 )
某某某某2009年中考数学模拟试卷(一)
参考答案
1-5:CACCD 6-10:AC ABD 11-12:DB
13:15: 17:
19: 或 ,45°< <90°或90°< <135°
20.解:原式
当 时,
原式
21.解:
主视图左视图
23解:(1) ,
这次考察中一共调查了60名学生.
(2) ,
,
在扇形统计图中,“乒乓球”
3.08年我市深入实施环境污染整治,某经济开发区域经的40家化工企业中已关停、整改32家,每年排放的污水减少了167000吨。将167000用科学计数法表示为( )
A、167×103×104C×105×106
4.在下列各电视台的台标图案中,是轴对称图形的是()
A B C D
5.a是实数,且x>y,则下列不等式中,正确的是( )
浙江宁波2009年中考数学模拟试卷(二)

浙江宁波2009年中考数学模拟试卷(二)一、选择题(本题有12小题,每题3分,共36分)1.下列算式中,正确的是A.a 2÷aa 1·=a 2 B.2a 2-3a 3=-a C.(a 3b )2=a 6b 2 D.-(-a 3)2=a 6 2.如图所示,AB ∥ED ,∠E =27°,∠C =52°,则∠EAB 的度数为( ) A :25° B :63° C :79° D :101°3.的大小应 ( )A.在9.1~9.2之间B.在9.2~9.3之间C.在9.3~9.4之间D.在9.4~9.5之间 4.若点P (a ,b )到x 轴的距离是2,到y 轴的距离是4,则这样的点P 有 ( )A.1个 B.2个 C.3个 D.4个5.如图(1)放置的一个机器零件,若其主视图如图(2),则其俯视图是 ( )6.已知⊙O 1的半径r 为3cm ,⊙O 2的半径R 为4cm ,两圆的圆心距O 1O 2为1cm ,则这两圆的位置关系是( )(A )相交 (B )内含 (C )内切 (D )外切7.红丝带是关注艾滋病防治问题的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如图所示。
红丝带重叠部分形成的图形是 ( ) A. 正方形 B.等腰梯形 C.菱形 D.矩形8. 调查表明,2008年资阳市城镇家庭年收入在2万元以上的家庭户数低于40%. 据此判断,下列说法正确的是( )A. 家庭年收入的众数一定不高于2万B. 家庭年收入的中位数一定不高于2万C. 家庭年收入的平均数一定不高于2万(A ) (B ) (C ) (D )( 2)( 1) (第5题)D. 家庭年收入的平均数和众数一定都不高于2万9. 若小唐同学掷出的铅球在场地上砸出一个直径约为10 cm 、深约为2 cm 的小坑,则该铅球的直径约为( )A. 10 cmB. 14.5 cmC. 19.5 cmD. 20 cm10.如下图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t ,正方形除去圆部分的面积为S (阴影部分),则S 与t 的大致图象为( )11.如图,将半径为2cm 的圆形纸片折叠后,圆弧恰好 经过圆心O ,则折痕AB 的长为( )A.2cmC.D.12.如图,把矩形纸条ABCD 沿EF GH ,同时折叠,B C,两点恰好落在AD 边的P 点处,若90FPH =∠,8PF =,6PH=,则矩形ABCD 的边BC 长为( ) A.20 B.22 C.24 D.30二、填空题(本题共有7小题,每题3分,共21分)13、函数x y 21-=的自变量x 的取值笵围是 。
2009年浙江省宁波市数学中考真题(word版含答案)

10.反比例函数 y
k 在第一象限的图象如图所示,则 k 的值可能是( x
A.1 B.2 C.3 D.4 11.如图,菱形 ABCD 中,对角线 AC、BD 相交于点 O,M、N 分别是边 AB、AD 的中点, 连接 OM、ON、MN,则下列叙述正确的是( ) A.△AOM 和△AON 都是等边三角形 y B.四边形 MBON 和四边形 MODN 都是菱形 A C.四边形 AMON 与四边形 ABCD 是位似图形 D.四边形 MBCO 和四边形 NDCO 都是等腰梯形 12.如图,点 A、B、C 在一次函数 y 2 x m 的图象上,它们的 横坐标依次为 1 ,1,2,分别过这些点作 x 轴与 y 轴的垂线,则图 中阴影部分的面积之和是( A.1 B.3 ) D.
y x 2 的解为坐标的点 ( x,y ) 在平面直角坐标系中的位置是( y x 1
)
A.第一象限 B.第二象限 C.第三角限 D.第四象限 9.如图,∠1,∠2,∠3,∠4 是五边形 ABCDE 的外角,且∠1=∠2=∠3=∠4=70°,则∠ AED 的度数是( ) A.110° B.108° C.105° D.100° D E 1 4 C 3 B A 2 (第 9 题) y M 2 1 x O 1 2 (第 10 题) B O C (第 11 题) ) A N D
1 O
B C 1 2 x
C. 3(m 1)
3 (m 2) 2
(第 12 题)
试题卷Ⅱ
二、填空题(每小题 3 分,共 18 分) 13.实数 8 的立方根是 . 14.不等式组
x 6 0 的解是 x 2 0
.
2 15.甲、乙、丙三名射击手的 20 次测试的平均成绩都是 8 环,方差分别是 S甲 , 0.4(环 2)
2009年浙江省宁波市中考数学试卷

2009年浙江省宁波市中考数学试卷一、选择题(共12小题,每小题3分,满分36分)1.(3分)下列四个数中,比0小的数是()A.B.C.πD.﹣12.(3分)等腰直角三角形的一个底角的度数是()A.30°B.45°C.60°D.90°3.(3分)一个不透明的布袋装有4个只有颜色的球,其中2个红色,1个白色,1个黑色,搅匀后从布袋里摸出1个球,摸到红球的概率是()A.B.C.D.4.(3分)据《宁波市休闲基地和商务会议基地建设五年行动计划》,预计到2012年,宁波市接待游客容量将达到4 640万人,其中4 640万用科学记数法可表示为()A.0.464×109B.4.64×108C.4.64×107D.46.4×107 5.(3分)若使二次根式在实数范围内有意义,则x的取值范围是()A.x≥2B.x>2C.x<2D.x≤26.(3分)如图是由4个立方块组成的立体图形,它的俯视图是()A.B.C.D.7.(3分)下列调查适合作普查的是()A.了解在校大学生的主要娱乐方式B.了解宁波市居民对废电池的处理情况C.日光灯管厂要检测一批灯管的使用寿命D.对甲型H1N1流感患者的同一车厢乘客进行医学检查8.(3分)以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是()A.第一象限B.第二象限C.第三象限D.第四象限9.(3分)如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是()A.110°B.108°C.105°D.100°10.(3分)反比例函数y在第一象限的图象如图所示,则k的值可能是()A.1B.2C.3D.411.(3分)如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD 的中点,连接OM、ON、MN,则下列叙述正确的是()A.△AOM和△AON都是等边三角形B.四边形MBON和四边形MODN都是菱形C.四边形AMON和四边形ABCD都是位似图形D.四边形MBCO和四边形NDCO都是等腰梯形12.(3分)如图,点A,B,C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是()A.1B.3C.3(m﹣1)D.二、填空题(共6小题,每小题3分,满分18分)13.(3分)8的立方根是.14.(3分)不等式组<>的解是.15.(3分)甲、乙、丙三名射击手的20次测试的平均成绩都是8环,方差分别是S甲2=0.4(环2),S乙2=3.2(环2),S丙2=1.6(环2),则成绩比较稳定的是.16.(3分)如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10米,坡角α为35°,则坡屋顶的高度h为米.(结果精确到0.1米)17.(3分)如图,梯形ABCD中,AD∥BC,∠B=70°,∠C=40°,作DE∥AB交BC 于点E,若AD=3,BC=10,则CD的长是.18.(3分)如图,⊙A、⊙B的圆心A、B在直线l上,两圆半径都为1cm,开始时圆心距AB=4cm,现⊙A、⊙B同时沿直线l以每秒2cm的速度相向移动,则当两圆相切时,⊙A 运动的时间为秒.三、解答题(共8小题,满分66分)19.(6分)先化简,再求值:(a﹣2)(a+2)﹣a(a﹣2),其中a=﹣1.20.(6分)如图,点A,B在数轴上,它们所对应的数分别是﹣4,,且点A、B到原点的距离相等,求x的值.21.(6分)(1)如图1,把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星,则这个六角星的边数是;(2)如图2,在5×5的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为一边向外作正方形,去掉居中的那条线段,请把得到的图画在图3中,并写出这个图形的边数.(3)现有一个正五边形,把正五边形的各边三等分,分别以居中的那条线段为边向外作正五边形,并去掉居中的那条线段,得到的图的边数是多少?22.(10分)2009年宁波市初中毕业生升学体育集中测试项目包括体能(耐力)类项目和速度(跳跃、力量、技能)类项目.体能类项目从游泳和中长跑中任选一项,速度类项目从立定跳远、50米跑等6项中任选一项.某校九年级共有200名女生在速度类项目中选择了立定跳远,现从这200名女生中随机抽取10名女生进行测试,下面是她们测试结果的条形图.(另附:九年级女生立定跳远的计分标准)九年级女生立定跳远计分标准:(注:不到上限,则按下限计分,满分10分)(1)求这10名女生在本次测试中,立定跳远距离的极差,立定跳远得分的众数和平均数;(2)请你估计该校选择立定跳远的200名女生得满分的人数.23.(8分)如图抛物线y=ax2﹣5ax+4a与x轴相交于点A、B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标.(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.24.(8分)已知:如图,⊙O的直径AB与弦CD相交于E,,⊙O的切线BF与弦AD的延长线相交于点F.(1)求证:CD∥BF.(2)连接BC,若⊙O的半径为4,cos∠BCD,求线段AD、CD的长.25.(10分)2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011)》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高30%,投入“供方”的资金将比2008年提高20%.(1)该市政府2008年投入改善医疗卫生服务的资金是多少万元?(2)该市政府2009年投入“需方”和“供方”的资金是多少万元?(3)该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年增长率.26.(12分)如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为(﹣8,0),直线BC经过点B(﹣8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′,此时直线OA′、B′C′分别与直线BC相交于P、Q.(1)四边形OA′B′C′的形状是,当α=90°时,的值是;(2)①如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求的值;②如图3,当四边形OA′B′C′的顶点B′落在直线BC上时,求△OPB′的面积;(3)在四边形OABC旋转过程中,当0°<α≤180°时,是否存在这样的点P和点Q,使BP BQ?若存在,请直接写出点P的坐标;若不存在,请说明理由.2009年浙江省宁波市中考数学试卷参考答案与试题解析一、选择题(共12小题,每小题3分,满分36分)1.(3分)下列四个数中,比0小的数是()A.B.C.πD.﹣1【解答】解:∵﹣1<0,∴只有D符合条件.故选:D.2.(3分)等腰直角三角形的一个底角的度数是()A.30°B.45°C.60°D.90°【解答】解:等腰直角三角形一个底角的度数=(180°﹣90°)÷2=45°.故选B.3.(3分)一个不透明的布袋装有4个只有颜色的球,其中2个红色,1个白色,1个黑色,搅匀后从布袋里摸出1个球,摸到红球的概率是()A.B.C.D.【解答】解:因为只有四个球,红球有2个,所以从布袋里摸出1个球摸到红球的概率红球的个数.球的总个数故选:A.4.(3分)据《宁波市休闲基地和商务会议基地建设五年行动计划》,预计到2012年,宁波市接待游客容量将达到4 640万人,其中4 640万用科学记数法可表示为()A.0.464×109B.4.64×108C.4.64×107D.46.4×107【解答】解:4 640万=46 400 000=4.64×107.故选C.5.(3分)若使二次根式在实数范围内有意义,则x的取值范围是()A.x≥2B.x>2C.x<2D.x≤2【解答】解:根据题意得:x﹣2≥0,求得x≥2.故选:A.6.(3分)如图是由4个立方块组成的立体图形,它的俯视图是()A.B.C.D.【解答】解:根据俯视图的画法可知:该俯视图左列由2个正方形,右列由1个正方形组成,故选B.7.(3分)下列调查适合作普查的是()A.了解在校大学生的主要娱乐方式B.了解宁波市居民对废电池的处理情况C.日光灯管厂要检测一批灯管的使用寿命D.对甲型H1N1流感患者的同一车厢乘客进行医学检查【解答】解:A、B项因为数目太大,而不适合进行普查,只能用抽查,C、因具有破坏性,也只能采用抽查的方式.D、了解某甲型H1N1确诊病人同机乘客的健康状况,精确度要求高、事关重大,必须选用普查.故选:D.8.(3分)以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:根据题意,可知﹣x+2=x﹣1,∴x,∴y.∵x>0,y>0,∴该点坐标在第一象限.故选:A.9.(3分)如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是()A.110°B.108°C.105°D.100°【解答】解:根据五边形的内角和公式可知,五边形ABCDE的内角和为(5﹣2)×180°=540°,根据邻补角的定义可得∠EAB=∠ABC=∠BCD=∠CDE=180°﹣70°=110°,所以∠AED=540°﹣110°×4=100°.故选:D.10.(3分)反比例函数y在第一象限的图象如图所示,则k的值可能是()A.1B.2C.3D.4【解答】解:如图,当x=2时,y,∵1<y<2,∴1<<2,解得2<k<4,所以k=3.故选:C.11.(3分)如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD 的中点,连接OM、ON、MN,则下列叙述正确的是()A.△AOM和△AON都是等边三角形B.四边形MBON和四边形MODN都是菱形C.四边形AMON和四边形ABCD都是位似图形D.四边形MBCO和四边形NDCO都是等腰梯形【解答】解:根据位似图形的定义可知A、O与OM和AM的大小却无法判断,所以无法判断△AMO和△AON是等边三角形,故错误;B、无法判断BM是否等于OB和BM是否等于OC,所以也无法判断平行四边形MBON和MODN是菱形,故错误;C、四边形MBCO和四边形NDCO是位似图形,故此选项正确;D、.无法判断四边形MBCO和NDCO是等腰梯形,故此选项错误;故选:C.12.(3分)如图,点A,B,C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是()A.1B.3C.3(m﹣1)D.【解答】解:由题意可得:A点坐标为(﹣1,2+m),B点坐标为(1,﹣2+m),C点坐标为(2,m﹣4),D点坐标为(0,2+m),E点坐标为(0,m),F点坐标为(0,﹣2+m),G点坐标为(1,m﹣4).所以,DE=EF=BG=2+m﹣m=m﹣(﹣2+m)=﹣2+m﹣(m﹣4)=2,又因为AD=BF=GC=1,所以图中阴影部分的面积和等于2×1×3=3.故选:B.二、填空题(共6小题,每小题3分,满分18分)13.(3分)8的立方根是2.【解答】解:8的立方根为2,故答案为:2.14.(3分)不等式组<>的解是2<x<6.【解答】解:由x﹣6<0解得x<6 ①,由x﹣2>0解得x>2 ②,取①、②的公共部分得2<x<6.15.(3分)甲、乙、丙三名射击手的20次测试的平均成绩都是8环,方差分别是S甲2=0.4(环2),S乙2=3.2(环2),S丙2=1.6(环2),则成绩比较稳定的是甲.【解答】解:根据方差的定义,方差越小数据越稳定,因为S甲2=0.4(环2),S乙2=3.2(环2),S丙2=1.6(环2),方差最小的为甲,所以本题中成绩比较稳定的是甲.故填甲.16.(3分)如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10米,坡角α为35°,则坡屋顶的高度h为 3.5米.(结果精确到0.1米)【解答】解:在直角三角形ABD中,tan35°解得h=5tan35°≈3.5.17.(3分)如图,梯形ABCD中,AD∥BC,∠B=70°,∠C=40°,作DE∥AB交BC 于点E,若AD=3,BC=10,则CD的长是7.【解答】解:∵DE∥AB,∴∠DEC=∠B=70°,而∠C=40°,∴∠CDE=70°,∴CD=CE.又∵AD∥BE,AB∥DE,∴四边形ABED是平行四边形.∴BE=AD=3,又∵BC=10,∴CE=CB﹣BE=10﹣3=7,∴CD=CE=7.18.(3分)如图,⊙A、⊙B的圆心A、B在直线l上,两圆半径都为1cm,开始时圆心距AB=4cm,现⊙A、⊙B同时沿直线l以每秒2cm的速度相向移动,则当两圆相切时,⊙A 运动的时间为或秒.【解答】解:本题所说的两圆相切,应分为两圆第一次相遇时的相切和两圆继续移动,即将相离时的相切两种情况.第一种情况两圆所走的路程为4﹣2=2cm;第二种情况两圆所走的路程为4+2=6cm.不妨设圆A运动的时间为x秒,根据题意可得方程2x+2x=2或2x+2x=6,解得x或.三、解答题(共8小题,满分66分)19.(6分)先化简,再求值:(a﹣2)(a+2)﹣a(a﹣2),其中a=﹣1.【解答】解:(a﹣2)(a+2)﹣a(a﹣2),=a2﹣4﹣a2+2a,=2a﹣4,当a=﹣1时,原式=2×(﹣1)﹣4=﹣6.20.(6分)如图,点A,B在数轴上,它们所对应的数分别是﹣4,,且点A、B到原点的距离相等,求x的值.【解答】解:由题意得,|﹣4|,解得,经检验是原方程的解,∴x的值为.21.(6分)(1)如图1,把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星,则这个六角星的边数是12;(2)如图2,在5×5的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为一边向外作正方形,去掉居中的那条线段,请把得到的图画在图3中,并写出这个图形的边数.(3)现有一个正五边形,把正五边形的各边三等分,分别以居中的那条线段为边向外作正五边形,并去掉居中的那条线段,得到的图的边数是多少?【解答】解:(1)把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星(如图所示),故此多边形的边数是:12.(2)这个图形的边数是20.(3)得到的图形的边数是30.22.(10分)2009年宁波市初中毕业生升学体育集中测试项目包括体能(耐力)类项目和速度(跳跃、力量、技能)类项目.体能类项目从游泳和中长跑中任选一项,速度类项目从立定跳远、50米跑等6项中任选一项.某校九年级共有200名女生在速度类项目中选择了立定跳远,现从这200名女生中随机抽取10名女生进行测试,下面是她们测试结果的条形图.(另附:九年级女生立定跳远的计分标准)九年级女生立定跳远计分标准:(注:不到上限,则按下限计分,满分10分)(1)求这10名女生在本次测试中,立定跳远距离的极差,立定跳远得分的众数和平均数;(2)请你估计该校选择立定跳远的200名女生得满分的人数.【解答】解:(1)从小到大排列出距离为:174,183,189,196,197,199,200,200,201,205,得分为7,8,9,9,10,10,10,10,10,10.∴立定跳远距离的极差=205﹣174=31(cm).所以立定跳远得分的众数是10(分),立定跳远的平均数为(7+8+9+9+10+10+10+10+10+10)=9.3(分).(2)因为10名女生中有6名得满分,所以估计200名女生中得满分的人数是200120(人).23.(8分)如图抛物线y=ax2﹣5ax+4a与x轴相交于点A、B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标.(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.【解答】解:(1)把点C(5,4)代入抛物线y=ax2﹣5ax+4a,得25a﹣25a+4a=4,解得a=1.∴该二次函数的解析式为y=x2﹣5x+4.∵y=x2﹣5x+4=(x)2,∴顶点坐标为P(,).(2)如先向左平移3个单位,再向上平移4个单位.得到的二次函数解析式为y=(x3)24=(x)2,即y=x2+x+2.24.(8分)已知:如图,⊙O的直径AB与弦CD相交于E,,⊙O的切线BF与弦AD的延长线相交于点F.(1)求证:CD∥BF.(2)连接BC,若⊙O的半径为4,cos∠BCD,求线段AD、CD的长.【解答】(1)证明:∵直径AB平分,∴AB⊥CD.∵BF与⊙O相切,AB是⊙O的直径,∴AB⊥BF.∴CD∥BF.(2)解:连接BD,BC.∵AB是⊙O的直径,∴∠ADB=90°.在Rt△ADB中,∵cos∠BAF=cos∠BCD,AB=4×2=8.∴AD=AB•cos∠BAF=86.∵AB⊥CD于E,在Rt△AED中,cos∠BAF=cos∠BCD,sin∠BAF.∴DE=AD•sin∠BAF=6.∵直径AB平分,∴CD=2DE=3.25.(10分)2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011)》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高30%,投入“供方”的资金将比2008年提高20%.(1)该市政府2008年投入改善医疗卫生服务的资金是多少万元?(2)该市政府2009年投入“需方”和“供方”的资金是多少万元?(3)该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年增长率.【解答】解:(1)该市政府2008年投入改善医疗服务的资金是:6000﹣1250=4750答:该市政府2008年投入改善医疗卫生服务的资金是4750万元.(2)设市政府2008年投入“需方”x万元,投入“供方”y万元,由题意得,解得∴2009年投入“需方”资金为(1+30%)x=1.3×3000=3900(万元),2009年投入“供方”资金为(1+20%)y=1.2×1750=2100(万元).答:该市政府2009年投入“需方”3900万元,投入“供方”2100万元.(3)设年增长率为m,由题意得6000(1+m)2=7260,解得m1=0.1,m2=﹣2.1(不合实际,舍去)答:从2009~2011年的年增长率是10%.26.(12分)如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为(﹣8,0),直线BC经过点B(﹣8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′,此时直线OA′、B′C′分别与直线BC相交于P、Q.(1)四边形OA′B′C′的形状是矩形,当α=90°时,的值是;(2)①如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求的值;②如图3,当四边形OA′B′C′的顶点B′落在直线BC上时,求△OPB′的面积;(3)在四边形OABC旋转过程中,当0°<α≤180°时,是否存在这样的点P和点Q,使BP BQ?若存在,请直接写出点P的坐标;若不存在,请说明理由.【解答】解:(1)图1,四边形OA′B′C′的形状是矩形;根据题意,即是矩形的长与宽的比,则.(2)①图2∵∠POC=∠B′OA′,∠PCO=∠OA′B′=90°,∴△COP∽△A′OB′.∴,即,∴CP,BP=BC﹣CP.同理△B′CQ∽△B′C′O,∴,即,∴CQ=3,BQ=BC+CQ=11.∴,∴;②图3,在△OCP和△B′A′P中,∠∠′′,∴△OCP≌△B′A′P(AAS).∴OP=B′P.设B′P=x,在Rt△OCP中,(8﹣x)2+62=x2,解得x.∴S△OPB′.(3)存在这样的点P和点Q,使BP BQ.点P的坐标是P1(﹣9,6),P2(,6).【对于第(3)题,我们提供如下详细解答,对学生无此要求】过点Q画QH⊥OA′于H,连接OQ,则QH=OC′=OC,∵S△POQ PQ•OC,S△POQ OP•QH,∴PQ=OP.设BP=x,∵BP BQ,∴BQ=2x,如图4,当点P在点B左侧时,OP=PQ=BQ+BP=3x,在Rt△PCO中,(8+x)2+62=(3x)2,解得,(不符实际,舍去).∴PC=BC+BP=9,∴P1(﹣9,6).如图5,当点P在点B右侧时,∴OP=PQ=BQ﹣BP=x,PC=8﹣x.在Rt△PCO中,(8﹣x)2+62=x2,解得x.∴PC=BC﹣BP,∴P2(,6),综上可知,存在点P1(﹣9,6),P2(,6),使BP BQ.。
2009年宁波市初中毕业生学业考试中考数学试卷及答案

宁波市2009年初中毕业生学业考试数 学 试 题考生须知:1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷Ⅰ、答题卷Ⅱ.试题卷共6页,有三个大题,26个小题,满分120分,考试时间为120分钟.2.请将姓名、准考证号分别填写在试题卷和答题卷的规定位置上.3.答题时,把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B 铅笔涂黑、涂满.将试题卷Ⅱ答案用黑色字迹钢笔或签字笔书写,答案必须按照题号顺序在答题卷Ⅱ各题目规定区域内作答,做在试题卷上或超出答题卷区域书写的答案无效.4.允许使用计算器,但没有近似计算要求的试题,结果都不能用近似数表示.抛物线2y ax bx c =++的顶点坐标为2424b ac b aa ⎛⎫-- ⎪⎝⎭,.试题卷Ⅰ一、选择题(每小题3分,共36分,在每小题给出的四个选项中,只有一项符合题目要求)1.下列四个数中,比0小的数是( ) A .23BC .πD .1-2.等腰直角三角形的一个底角的度数是( ) A .30° B .45° C .60° D .90° 3.一个不透明的布袋装有4个只有颜色不同的球,其中2个红球,1个白球,1个黑球,搅匀后从布袋里摸出1个球,摸到红球的概率是( ) A .12B .13C .14D .164.据《宁波市休闲旅游基地和商务会议基地建设五年行动计划》,预计到2012年,宁波市接待游客容量将达到4640万人次.其中4640万用科学记数法可表示为( ) A .90.46410⨯B .84.6410⨯C .74.6410⨯D .646.410⨯5x 的取值范围是( )A .2x ≠B .2x >C .x ≤2D .2x ≥ 6.如图是由4个立方块组成的立体图形,它的俯视图是( )A .B .C .D . 7.下列调查适合作普查的是( ) A .了解在校大学生的主要娱乐方式(第6题)B .了解宁波市居民对废电池的处理情况C .日光灯管厂要检测一批灯管的使用寿命D .对甲型H1N1流感患者的同一车厢的乘客进行医学检查 8.以方程组21y x y x =-+⎧⎨=-⎩的解为坐标的点()x y ,在平面直角坐标系中的位置是( )A .第一象限B .第二象限C .第三角限D .第四象限9.如图,∠1,∠2,∠3,∠4是五边形ABCDE 的外角,且∠1=∠2=∠3=∠4=70°,则∠AED 的度数是( ) A .110° B .108° C .105° D .100°10.反比例函数ky x=在第一象限的图象如图所示,则k 的值可能是( ) A .1 B .2 C .3 D .411.如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N 分别是边AB 、AD 的中点,连接OM 、ON 、MN ,则下列叙述正确的是( ) A .△AOM 和△AON 都是等边三角形B .四边形MBON 和四边形MODN 都是菱形C .四边形AMON 与四边形ABCD 是位似图形 D .四边形MBCO 和四边形NDCO 都是等腰梯形12.如图,点A 、B 、C 在一次函数2y x m =-+的图象上,它们的横坐标依次为1-,1,2,分别过这些点作x 轴与y 轴的垂线,则图中阴影部分的面积之和是( ) A .1B .3C .3(1)m -D .3(2)2m -试题卷Ⅱ二、填空题(每小题3分,共18分) 13.实数8的立方根是 .14.不等式组6020x x -<⎧⎨->⎩的解是 .15.甲、乙、丙三名射击手的20次测试的平均成绩都是8环,方差分别是20.4S =甲(环2),12 3 4 D C B A E (第9题)D B CA NM O (第11题) (第12题)2 3.2S =乙(环2),2 1.6S =丙(环2),则成绩比较稳定的是 .(填“甲”“乙”“丙”中的一个)16.如图,在坡屋顶的设计图中,AB AC =,屋顶的宽度l 为10米,坡角α为35°,则坡屋顶高度h 为 米.(结果精确到0.1米)17.如图,梯形ABCD 中,AD BC ∥,7040B C ∠=∠=°,°,作DE AB ∥交BC 于点E ,若3AD =,10BC =,则CD 的长是 . 18.如图,A ⊙、B ⊙的圆心A 、B 在直线l 上,两圆的半径都为1cm,开始时圆心距4cm AB =,现A ⊙、B ⊙同时沿直线l 以每秒2cm 的速度相向移动,则当两圆相切时,A ⊙运动的时间为 秒.三、解答题(第19~21题各6分,第22题10分,第23~24题各8分,第25题10分,第26题12分,共66分)19.先化简,再求值:(2)(2)(2)a a a a -+--,其中1a =-.20.如图,点A ,B 在数轴上,它们所对应的数分别是4-,2235x x +-,且点A 、B 到原点的距离相等,求x 的值.21.(1)如图1,把等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个六角星,则这个六角星的边数是 .(2)如图2,在5×5的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为一边向外作正方形,并去掉居中的那条线段.请你把得到的图形画在图3中,并写出这个图形的边数.(3)现有一个正五边形,把正五边形的各边三等分,分别以居中那条线段为一边向外作正五边形,并去掉居中的那条线段,得到的图形的边数是多少?C (第16题)AB C D(第17题) (第18题)A B (第20题) (图1) (第21题)(图2) (图3)22.2009年宁波市初中毕业生升学体育集中测试项目包括体能(耐力)类项目和速度(跳跃、力量、技能)类项目.体能类项目从游泳和中长跑中任选一项,速度类项目从立定跳远、50米跑等6项中任选一项.某校九年级共有200名女生在速度类项目中选择了立定跳远,现从这200名女生中随机抽取10名女生进行测试,下面是她们测试结果的条形统计图.(另附:九年级女生立定跳远的计分标准)(1)求这10名女生在本次测试中,立定跳远距离..的极差和中位数,立定跳远得分..的众数和平均数.(2)请你估计该校选择立定跳远的200名女生中得满分的人数.23.如图,抛物线254y ax ax a =-+与x 轴相交于点A 、B ,且过点(54)C ,.(1)求a 的值和该抛物线顶点P 的坐标;(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.10名女生立定跳远距离条形统计图 女生序号 (第22题)九年级女生立定跳远计分标准 (注:不到上限,则按下限计分,满分为10分) (第23题) 5,4)24.已知,如图,O ⊙的直径AB 与弦CD 相交于E ,BC BD =,O ⊙的切线BF 与弦AD 的延长线相交于点F . (1)求证:CD BF ∥;(2)连结BC ,若O ⊙的半径为4,3cos 4BCD ∠=,求线段AD 、CD 的长.25.2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高30%,投入“供方”的资金将比2008年提高20%. (1)该市政府2008年投入改善医疗卫生服务的资金是多少万元? (2)该市政府2009年投入“需方”和“供方”的资金各多少万元?(3)该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年增长率.26.如图1,在平面直角坐标系中,O 为坐标原点,点A 的坐标为(80)-,,直线BC 经过点(86)B -,,(06)C ,,将四边形OABC 绕点O 按顺时针方向旋转α度得到四边形OA B C ''',此时直线OA '、直线B C ''分别与直线BC 相交于点P 、Q . (1)四边形OABC 的形状是 ,当90α=°时,BPBQ的值是 ; (2)①如图2,当四边形OA B C '''的顶点B '落在y 轴正半轴时,求BPBQ的值; ②如图3,当四边形OA B C '''的顶点B '落在直线BC 上时,求OPB '△的面积.(第24题)(图1)(3)在四边形OABC 旋转过程中,当0180α<≤°时,是否存在这样的点P 和点Q,使12BP BQ =?若存在,请直接写出点P 的坐标;若不存在,请说明理由.)(图3)(图2)(备用图)(第26题)宁波市2009年初中毕业生学业考试 数学试题参考答案及评分标准一、选择题(每小题3分,共36分)三、解答题(共66分)注:1.阅卷时应按步计分,每步只设整分;2.如有其它解法,只要正确,都可参照评分标准,各步相应给分.19.解:原式2242a a a =--+ ·········································································· 2分24a =-. ················································································· 4分 当1a =-时, 原式2(1)4=⨯--6=- ····································································································· 6分 20.解:由题意得,22435x x +=-, ··································································································· 3分 解得115x =. ································································································ 5分经检验,115x =是原方程的解.∴x 的值为115. ··················································· 6分21.(1)12. ·························································· 1分 (2)这个图形的边数是20. ·················· 4分(其中画图2分) (3)得到的图形的边数是30. ···································· 6分22.(1)立定跳远距离的极差20517431(cm)=-=. ············································· 2分 立定跳远距离的中位数199197198(cm)2+==. ·················································· 4分 根据计分标准,这10名女生的跳远距离得分分值分别是: 7,9,10,10,10,8,10,10,9.所以立定跳远得分的众数是10(分), ····································································· 6分 立定跳远得分的平均数是9.3(分). ····································································· 8分(2)因为10名女生中有6名得满分,所以估计200名女生中得满分的人数是620012010⨯=(人). ···················································································· 10分 23.解:(1)把点(54)C ,代入抛物线254y ax ax a =-+得,252544a a a -+=, ······················································································· 1分 解得1a =. ·································································································· 2分∴该二次函数的解析式为254y x x =-+.22595424y x x x ⎛⎫=-+=-- ⎪⎝⎭∴顶点坐标为5924P ⎛⎫- ⎪⎝⎭,. ·············································································· 4分(2)(答案不唯一,合理即正确)如先向左平移3个单位,再向上平移4个单位, ························································ 6分 得到的二次函数解析式为225917342424y x x ⎛⎫⎛⎫=-+-+=++ ⎪ ⎪⎝⎭⎝⎭,即22y x x =++. ························································································· 8分 24.解:(1)直径AB 平分CD ,∴AB CD ⊥. ······························································································ 1分BF 与O ⊙相切,AB 是O ⊙的直径,AB BF ∴⊥. ······························································································ 2分 CD BF ∴∥. ······························································································ 3分 (2)连结BD ,AB 是O ⊙的直径, 90ADB ∴∠=°, 在Rt ADB △中,3cos cos 4A C ∠=∠=,428AB =⨯=.3cos 864AD AB A ∴=∠=⨯=. ····································································· 5分AB CD ⊥于E , 在Rt AED △3cos cos 4A C ∠=∠=,sin A ∠=.sin 6DE AD A ∴=∠== ···························································· 7分直径AB 平分CD,2CD DE ∴== ··················································································· 8分25.解:(1)该市政府2008年投入改善医疗服务的资金是:600012504750-=(万元) ··············································································· 2分 (2)设市政府2008年投入“需方”x 万元,投入“供方”y 万元, 由题意得4750(130%)(120%)6000.x y x y +=⎧⎨+++=⎩,解得30001750.x y =⎧⎨=⎩,····························································································· 4分∴2009年投入“需方”资金为(130%) 1.330003900x +=⨯=(万元),2009年投入“供方”资金为(120%) 1.217502100y +=⨯=(万元).答:该市政府2009年投入“需方”3900万元,投入“供方”2100万元. ······················· 6分 (3)设年增长率为x ,由题意得26000(1)7260x +=, ······················································································ 8分解得10.1x =,2 1.1x =-(不合实际,舍去)答:从2009~2011年的年增长率是10%. ···························································· 10分 26.解:(1)矩形(长方形); ················································································· 1分47BP BQ =. ···································································································· 3分 (2)①POC B OA ''∠=∠,PCO OA B ''∠=∠90=°,COP A OB ''∴△∽△. CP OC A B OA ∴=''',即668CP =,92CP ∴=,72BP BC CP =-=. ······································································ 4分 同理B CQ B C O '''△∽△,CQ B C C Q B C '∴=''',即10668CQ -=, 3CQ ∴=,11BQ BC CQ =+=. ····································································· 5分 722BP BQ ∴=. ······························································································· 6分②在OCP △和B A P ''△中,90OPC B PA OCP A OC B A ''∠=∠⎧⎪'∠=∠=⎨⎪''=⎩,°,, (AAS)OCP B A P ''∴△≌△. ·········································································· 7分 OP B P '∴=.设B P x '=,在Rt OCP △中, 222(8)6x x -+=,解得254x =. ················································ 8分 125756244OPB S '∴=⨯⨯=△. ··········································································· 9分 (3)存在这样的点P 和点Q ,使12BP BQ =. ······················································· 10分点P的坐标是19P ⎛⎫- ⎪⎝⎭,2764P ⎛⎫- ⎪⎝⎭,. ··················································· 12分 对于第(3)题,我们提供如下详细解答,对学生无此要求. 过点Q 画QH OA '⊥于H ,连结OQ ,则QH OC OC '==,12POQ S PQ OC =△,12POQ S OP QH =△, PQ OP ∴=.设BP x =,12BP BQ =, 2BQ x ∴=,① 如图1,当点P 在点B 左侧时,3OP PQ BQ BP x ==+=,在Rt PCO △中,222(8)6(3)x x ++=,解得11x =+,21x =(不符实际,舍去). 9PC BC BP ∴=+=+19P ⎛⎫∴-- ⎪⎝⎭.②如图2,当点P 在点B 右侧时,OP PQ BQ BP x ∴==-=,8PC x =-.在Rt PCO △中,222(8)6x x -+=,解得254x =. PC BC BP ∴=-257844=-=, 2764P ⎛⎫∴- ⎪⎝⎭,. 综上可知,存在点19P ⎛⎫-- ⎪⎝⎭,2764P ⎛⎫- ⎪⎝⎭,,使12BP BQ =.。
宁波重点中学保送生招生考试数学试卷及答案

12.如图,把 Rt ABC 依次绕顶点沿水平线翻转两次,若
么 AC 边从开始到结束所扫过的图形的面积为(
)
C 90 , AC
3 , BC 1,那
7
A.
4
7
B.
12
9
C.
4
二、填空题(每小题 3 分 , 共 18 分)
13.已知 a、 b、 c 均为非零实数,满足:
25
D.
12
b c a c a b a b c ( a b)(b c)(c a)
开展成平面,则展开图不可能是
、 a2 +b2=2h 2 A、 B 、 C 均是棱的中点,现将纸盒剪
A
B
C
D
7.在平面直角坐标系中,横坐标、纵坐标都为整数的
点称为整点,观察图中每正方形(实线)四条边上的整
点的个数,请你猜测由里向外第 10 个正方形(实线)
四条边上的整点的个数共有…………………………(
所以,∠ ABC=∠ MCP.
而∠ ABC=∠ APC,则∠ APC=∠ MCP,有 MP=CM.
④
AN
由式③、④得
CN
AM
.
CM
22:设取红球、白球、黄球分别为 x, y, z 个 , 0≤ x≤2,0≤ y≤3,0≤ z≤5则10﹤5 x+ 2y + z ﹤15, x+ y + z=5,分类: ① 当 x=0时, y 不存在 ② 当 x=1时,1﹤ y﹤6,取 y=2,3 ③ 当 x=2时,-3﹤ y﹤2,取 y =0,1 取法总数为110种
的图像与线段 AB 只有一个交点,则 a 的取值范围是
。
17.一个六边形的六个内角都是 120 度,连续四边的长为 1, 3, 4, 2,则该六边形的周长
浙江省慈溪中学初中保送生招生考试数学试卷及参考答案

浙江省慈溪中学20XX 年初中保送生招生考试数学试卷(本卷考试时间90分钟,满分130分.)一、选择题(每题6分,共30分)1.将正方形ABCD 折叠,使顶点A 与CD 边上的点M 重合,折痕交AD 于E ,交BC 于F ,边AB 折叠后与BC 边交于点G(如图). 如果DM :MC=3:2,则DE :DM :EM=()(A)7:24:25 (B)3:4:5 (C)5:12:13(D)8:15:172.假期里王老师有一个紧急通知,要用电话尽快通知给50个同学,假设每通知一个同学 需要1分钟时间,同学接到电话后也可以相互通知,那么要使所有同学都接到通知最快需要的时间为()(A)8分钟 (B)7分钟 (C)6分钟. (D)5分钟3.已知:二次函数y=2x +2x+a(a 为大于0的常数),当x=m 时的函数值y 1<0; 则当x=m+2时的函数值y 1与0的大小关系为()(A)y 2>0 (B)y 2<0 (C)y 2=O (D)不能确定4.记S=121221121212008200720072007-++++++则S 所在的范围为()(A)0<S<1 (B)1<S<2 (C)2<S<3 (D)3<S<45.如图,点A 是函数y=x 1的图象上的点,点B 、 C的坐标分别为B(-2,-2)、C(2,2).试利用性质:“函数y=x1的图象上任意一点A 都满足|AB-AC|=22”求解下面问题:“作∠BAC 的内角平分线AE ,过B 作AE 的垂线交AE 于F ,已知当点A 在函数y=x1的图象上运动时,点F 总在一条曲线上运动,则这条曲线为() (A)直线 (B)抛物线 (C)圆 (D)反比例函数的曲线6.已知关于x 的不等式(2a-b)x≥a -2b 的解是x>25, 则关于x 的不等式ax+b<0的解为.7.已知右边方格纸中的每个小方格是边长为1的正方形,A 、B 两点在小方格的顶点上,位置如图所示.在小方格的顶点上确定一点C ,连结AB 、AC 、BC ,使△ABC 的面积为3个平方单位.则这样的点C 共有个.8.直角坐标系中,点A(0,0),B(2,0),C(0,23),若有一三角形与△AB C 全等,且有一条边与BC 重合,那么这个三角形的另一个顶点坐标是________.9.n 个单位小立方体叠放在桌面上,所得几何体的主视图和俯视图均如图所示.那么n 的最大值与最小值的和是_______.10.对大于或等于2的自然数m 的n 次幂进行如右图方式的“分裂”,仿此,36的“分裂”中最大的数是.11.甲,乙,丙3人用擂台赛形式进行训练,每局2人进行单打比赛,另1人当裁判,每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时发现甲共打了12局,乙共打了21局,而丙共当裁判8局.那么,整个比赛的第10局的输方一定是_____.12.△ABC 和△DEF 是两个等腰直角三角形,∠A=∠D =90°,△DEF 的顶点E 位于边BC 的中点上.(1)如图1,设DE 与AB 交手点M ,EF 与AC 交于点N ,求证:△BEM∽△CNE;(2)如图2,将△DEF 绕点E 旋转,使得DE 与BA 的延长线交于点M ,EF 与AC 交于点N ,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形?并证明你的结论.13.已知函数y=2x +(b-1)x+c(b ,c 为常数),这个函数的图象与x 轴交于两个不同的点A(1x ,0)和B(2x ,0).若x 1,x 2满足12x x >1(1)求证: 2b ≥2(b+2c);(2)若t<1x ,试比较2t +bt+c 与1x 的大小,并加以证明。
慈溪中学保送生招生考试数学模拟试卷及参考答案

慈溪中学保送生招生考试数学模拟试卷(考试时间90分钟,满分130分)一、 选择题(每小题6分,共30分)1、 下列图中阴影部分面积与算式2131242-⎛⎫-++ ⎪⎝⎭的结果相同的是( )2、 如图,∠ACB =60○,半径为2的⊙O 切BC 于点C ,若将⊙O 在CB上向右滚动,则当滚动到⊙O 与CA 也相切时,圆心O 移动的水平距离为( )A 、 2πB 、 πC 、 32D 、 43、 如果多项式212x px ++可以分解成两个一次因式的积,那么整数p 的值可取( )个A 、 4B 、 5C 、 6D 、 84、 小明、 小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多( )道A 、 15B 、 20C 、 25D 、 305、 已知BD 是ABC V 的中线,AC=6,且∠ADB=45°,∠C=30°,则AB=( )A 、B 、 32C 、D 、 6二、 填空题(每小题6分,共36分)6、 满足方程532=-++x x 的x 的取值范围是 .7、 已知三个非负实数c b a ,,满足: 523=++c b a 和132=-+c b a ,若c b a m 73-+=,则m 的最小值为 .8、 如图所示: 设M 是ABC ∆的重心(即M 是中线AD 上一点,且AM=2MD ),过M 的直线分别交边AB 、AC 于P 、Q 两点,且n QCAQm PB AP ==,,则=+nm 11 .9、 在平面直角坐标系中,横坐标与纵坐标都是整数的点(y x ,)称为整点,如果将二次函数43982-+-=x x y 的图像与x 轴所围成的封闭图形染成红色,则此红色区域内部及其边界上的整点个数有 个.10、 如图所示: 在平面直角坐标系中,OCB ∆的外接圆与y 轴交于)2,0(A ,,60︒=∠OCB ︒=∠45COB ,则=OC .11、 如图所示: 两个同心圆,半径分别是3462和,矩形ABCD 边AB 、 CD分别为两圆的弦,当矩形ABCD 面积取最大值时,矩形ABCD 的周长是 .三、 解答题(每小题16分,共64分) 12、 九年级(1)、 (2)、 (3)班各派4名代表参加射击比赛,每队每人打两枪,射中内环得50分,射中中环得35分,射中外环得25分,脱靶得0分.统计比赛结果,(1)班8枪全中,(2)班1枪脱靶,(3)班2枪脱靶,但三个班的积分完全相同,都是255分.第8题图 第11题图第10题图13、 设二次函数c bx ax y ++=2的图像开口向下,顶点落在第二象限.(1)确定ac b b a 4,,2-的符号,简述理由.(2)若此二次函数图象经过原点,且顶点在直线0=+y x 上,顶点与原点的距离为23,求抛物线的解析式. 14、 如图,四边形ABCD 为圆内接四边形,对角线AC 、 BD 交于点E ,延长DA 、 CB 交于点F ,且∠CAD=60°,DC=DE ,求证:(1)AB=AF(2)A 为△BEF 的外心(即△BEF 外接圆的圆心)15、 在平面直角坐标中,边长为1的正方形OABC 的两顶点A 、 C 分别在y 轴、 x轴的正半轴上,点O 在原点. 现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线y x =上时停止旋转. 旋转过程中,AB 边交直线y x =于点M ,BC 边交x 轴于点N (如图1).(1)求边AB 在旋转过程中所扫过的面积;(2)设△MBN 的周长为p ,在旋转正方形OABC 的过程中,p 值是否有变化? 请证明你的结论;(3)设MN=m ,当m 为何值时△OMN 的面积最小,最小值是多少? 并直接写出此时△BMN 内切圆的半径.图1参考答案一、 选择题: BCCBC3、 p 值可取±7,±8,±13;4、 如图,设a 是容易题;b ,c ,d 是中档题; m ,n ,p 是难题. 则由题意可得:6060322218060a b c m a bd n a b c d m n p a c d p +++=⎧⎪+++=⇒++++++=⎨⎪+++=⎩又100a b c d m n p ++++++= 所以280a b c d +++= 设所求x m n p a =++-则28020a b c d m n p a x x ++++++-=+⇒= 5、二、 填空题: 6、 23x -≤≤; 7、 57-; 37730,7110,32711a cbc c m c =-≥=-≥⇒≤≤=- 8、 1; 过B 、 C 分别作PQ 的平行线即可 9、 25; 0y =时,12313,22x x ==; 225(4)4y x =--+; 当x=2时,满足条件的点有3个,当x=3时,满足条件的点有6个,当x=4时,满足条件的点有7个,当x=5时,满足条件的点有6个,当x=6时,满足条件的点有3个 10、 3 11、 16+dcb apnm如图,设AB=CD=a ,AD=BC=b , DE=CF=c ,则有222222()9624()192a b c bc a b c ⎧+-==⎪⇒=⇒⎨++==⎪⎩所以,2224()96a b b+-=,又S ab = 可得: 4221445760b b S -++= 由204608S S ≥⇒≤⇒≤V 当S =8b a == 三、 解答题:12、理由如下: 可设t 枪脱靶,x 枪射中内环,y 枪射中中环,则有(8)x y t ---枪射中外环,所以503525(8)255x y x y t ++---=化简得152()(1)2y t x t x =+-++- 对于(1)班,10,52(1)2t y x x ==-+-,x 为奇数,只能取x=1,得y=3;对于(2)班,11,72(2)2t y x x ==-+-,x 为偶数,只能取x=2,得y=3;对于(3)班,12,92(3)2t y x x ==-+-,x 为奇数,只能取x=3,得y=3; -------7分(视情况给分)13、 解: (1)开口向下,所以0a <; -------------2分顶点在第二象限,所以22020,40404b ab b ac ac b a⎧-<⎪⎪⇒<->⎨-⎪>⎪⎩--------------4分 (2)由题意可得c=0,-----------------------------------8分此时顶点坐标为2(,)24b b a a --,因顶点在直线0x y +=上,所以20224b b b a a--=⇒=----------------------------11分此时顶点坐标为11(,)a a -,由2211183a a a+=⇒=-----------------------14分 抛物线的解析式为232y x x =------------------------------16分 14、 证明:(1)∠ABF=∠ADC=120°-∠ACD=120°-∠DEC =120°-(60°+∠ADE )=60°-∠ADE---------4分 而∠F=60°-∠ACF-------6分 因为∠ACF=∠ADE---------7分所以∠ABF=∠F ,所以AB=AF--------8分 (2)四边形ABCD 内接于圆,所以∠ABD=∠ACD ,--------------------------------------------------------------------10分 又DE=DC ,所以∠DCE=∠DEC=∠AEB ,------------12分 所以∠ABD=∠AEB ,所以AB=AE ; --------------------------------------------------14分 所以AB=AF=AE ,即A 是三角形BEF 的外心-----------16分15、 解: (1)如图,OAB OAA OBB OAA S S S S S '''=+--V V 阴扇形扇形=22454513603608OBB OAA S S πππ''-=-⨯=扇形扇形 ---------------------------------6分(2)p 值无变化----------------------------7分 证明: 延长BA 交y 轴于E 点, 在OAE OCN V V 与中,9090AOE CON AON OAE OCN OA OC ∠=∠=︒-∠⎧⎪∠=∠=︒⎨⎪=⎩所以,OAE V ≌OCN V所以,OE=ON ,AE=CN--------------------------8分 在OME OMN V V 与中45OE ON MOE MON OM OM =⎧⎪∠=∠=︒⎨⎪=⎩所以,OME V ≌OMN V所以,MN==ME=AM+AE=AM+CN------------------------9分所以,P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2--------------------10分 (3)设,1,,1AM n BM n CN m n BN m n ==-=-=-+则, 因为,OME V ≌OMN V , 所以,1122MON MOE S S OA EM m ==⨯=V V -----------------------11分 在Rt BMN V 中,222BM BN MN +=所以,2222(1)(1)20n m n m n mn m -+-+=⇒-+-=所以,24(2)022m m m m =--≥⇒≥≤-V 或---------------13分所以,当2m =时,OMN V 的面积最小-------------------14分Rt BMN V的内切圆半径为32BM BN MN+-=-分。
慈溪中学2009年保送生招生考试

慈溪中学2009年保送生招生考试科学说明:I.本卷考试时间100分钟,满分130分。
II.本卷分试题(共7页)和答卷(共4页),答案必须做在答题卷上。
III.本卷可能用到的相对原子质量:H-1,C-12,O-16,Na-23,O-16,s-32,K-39。
试题一、选择题(每小题4分,共9小题,共36分。
每小题只有一个正确选项)1.据报道,三鹿奶粉中含有一种叫做三聚氰胺(C3N6H6)的物质,长期食用会致使婴儿生殖、泌尿系统损害,造成膀胱、。
肾部结石等后果。
请问三聚氰胺被人体吸收后到达肾脏,至少要经过心脏几次( )A.0 B.1 C.2 D.32.下列有关物品保存的说法中,正确的说法有几种( )①种子入库前必须进行干燥处理,目的是降低含水量,以减少营养物质的消耗和避免种子发芽霉变②蔬菜保鲜效果较好的条件是低温、低氧、干燥③用自来水洗净的鸡肉置一包装袋中并抽成真空,不冷冻也可保持数年不变质④天然织物保存特别需要防潮,因为其中含有大量的纤维素、蛋白质,一旦受潮,衣物上就会有霉菌等寄生微生物出现。
A.1 B.2 C.3 D.43.如图为太阳系八大行星示意图,各行星以椭圆轨道运行,太阳在椭圆轨道的焦点上。
对于太阳系中地球位置和地球上冬冷夏热原因的叙述正确的是()A.地球处于图中4号位置。
B.夏天地球距太阳近,冬天地球距太阳远。
C.夏季时,太阳光线直射于地面,日照时间长;冬季时,太阳光线斜射于地面,曰照时问短。
D.夏季时,大气层变薄太阳光线易透过;冬季时,大气层变厚太阳光线不易透过。
4.下列各组物质,从物质分类的角度看,前者从属于后者的一组是() A.碱、碱性氧化物B.酸、含氧酸C.盐、酸式盐D.有机物、化合物5.在AB+2CD===AD2+C2B中,50gAB和20gCD恰好完全反应生成10gAD2。
若l0gAB 和10gCD反应,生成C2B的质量是( )A.12g B.2g C.5g D.17.1g6.在试管中加入过量的块状碳酸钙,加入一定量的稀盐酸,充分反应,有少量气泡产生。
