2009年安徽高考理科数学
近五年安徽省高考数学理科试卷分析

近五年安徽省高考数学理科试卷分析一、整体评价近五年安徽高考数学试题从整体上看,贯彻了“整体维持稳定,深化能力立意,踊跃改革创新”的指导思想,试卷内容上表现新课程观念,对基础知识、大体技术和数学思想方式都有较全面的考查。
二、试卷特点1、试卷结构维持稳定,近五年来一直是10道选择题、5道填空题、6道解答题的结构;2、试卷分值稳定,选择、填空每题5分,解答题共75分;3、试卷难易安排稳定,大体是由易到难,给学生一个循序渐进的进程。
三、具体分析2021年是安徽省高考自主命题的第六年,是安徽省进入新课程改革高考的第三年,处在由大纲高考到新课标高考的过渡期的最后一年。
11年的数学命题迈出了“稳中求变,变中求新,新中求活,突出应用,切近现实,交汇融合,凸显能力”的命题改革前进步伐,理科数学难度有所增大。
11年的理科试卷相对于以前做了很大的变更。
(1)第(16)题一改往年的做法,不是三角函数题,而是函数与导数整合的题目;(2)第(17)题的立体几何,考的是线线平行与表面积问题,并无依照常规考二面角的求解问题;(3)第(19)题设置的是不等式的证明题,为历年罕有;(4)第(21)题的解析几何直接要求动点的轨迹方程,回归到解析几何的本质却不涉及到韦达定理。
这份卷子学生感觉题目难,根本原因是学生缺乏数学思维。
为了扭转当前这种只重视做题数而不重视数学思维能力培育的不良教学局面,11年的数学试卷进行了创造性的改革,考查的不是学生会不会套用常常利用题型,而是重在考查学生会不会思维,有无良好的思维习惯和创新的精神。
2021高考试卷就比较符合正常思维。
对于选择题第(1)题考查复数的计算,是简单第(2)题考查函数的解析式,主要看学生对函数解析式的理解,第(3)题考查程序框图及算法,利用列举法可以取得答案,第(4)题考查等比数列的性质和指数对数的运算,需要学生有转化能力,属于中等难度的题。
第(5)题频率散布直方图,方差和平均数的计算,第(6)题考查线面的垂直关系和充要条件的概念,要求学生有必然的空间想象能力和逻辑思维能力。
2007年理科数学安徽省高考真题含答案

(1) 在下列函数中,反函数是其自身的函数为,选D。 (2) 设l,m,n均为直线,其中m,n在平面内,“l”,则“lm且ln”,反之若“lm 且ln”,当m//n时,推不出“l”,∴ “l”是“lm且ln”的充分不必要条件,选 A。
(3)若对任意R,不等式≥ax恒成立,当x≥0时,x≥ax,a≤1,当x<0时,- x≥ax,∴a≥-1,综上得,即实数a的取值范围是≤1,选B。 (4)若a为实数,=-i,则,a=-,选B。
2007年普通高等学校招生全国统一考试(安徽卷)
数 学(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2 页,第Ⅱ卷第3至第4页。全卷满分150分,考试时间120分钟。 考生注意事项:
1. 答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、 姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、 科类”与本人座位号、姓名、科类是否一致。
(Ⅰ)证明: A B C D . . 与平行,与平行, 于是与共面,与共面. (Ⅱ)证明:, , ,. 与是平面内的两条相交直线.
平面. 又平面过. 平面平面. (Ⅲ)解:. 设为平面的法向量, ,. 于是,取,则,. 设为平面的法向量, ,. 于是,取,则,. . 二面角的大小为. 解法2(综合法): (Ⅰ)证明:平面,平面. ,,平面平面.
(A)0
(B)1
(C)2
(D)3
(7)如果点在平面区域上,点在曲线上,那么 的最小值为
(A)
(B)
(C) (D)
(8)半径为1的球面上的四点是正四面体的顶点,则与两点间的球面距
离为
(A) (B) (C)(D)
(9)如图,和分别是双曲线的两个焦点,和是以为圆心,以为半径的圆
2009年高考安徽数学(理科)试题及参考答案

熟悉建筑结构抗震基本知识地震基本知识地震俗称地动,是一种具有突发性的自然现象。
地震按其发生的原因,主要有火山地震、陷落地震、人工诱发地震以及构造地震。
构造地震破坏作用大,影响范围广是房屋建筑抗震研究的主要对象。
在建筑抗震设计中,所指的地震是由于地壳构造运动(岩层构造状态的变动)使岩层发生断裂、错动而引起的地面振动,这种地面振动称为构造地震,简称地震。
地壳深处发生岩层断裂、错动的地方称为震源。
震源正上方的地面称为震中。
震中附近地面运动最激烈,也是破坏最严重的地区,叫震中区或极震区。
地面上某处到震源的距离叫震源距。
震源至地面的距离称为震源深度。
一般把震源深度小于60Km的地震称为浅源地震;60~300Km称为中源地震;大于300Km 成为深源地震。
中国发生的绝大部分地震均属于浅源地震。
地震波地震引起的振动以波的形式从震源向四周传播,这种波就称为地震波。
地震波按其在地壳传播的位置不同,分为体波和面波。
体波是在地球内部由震源向四周传播的波,分为纵波(P波)和横波(S波)。
纵波(P波)是由震源向四周传播的压缩波,介质质点的振动方向与波的传播方向一致,引起地面垂直振动,周期短、振幅小、波速快。
横波(S波)传播的是由震源向四周传播的剪切波,介质质点的振动方向与波的传播方向垂直,引起地面水平振动,周期长、振幅大、波速慢。
面波是体波经地层界面多次放射、折射形成的次生波。
面波的质点振动方向比较复杂,既引起地面水平振动又引起地面垂直振动。
当地震发生时,纵波首先到达,使房屋产生上下颠簸,接着横波到达,使范围产生水平摇晃,一般是当面波和横波都到达时,房屋振动最为激烈。
震级地震的震级是衡量一次地震大小的等级,用符号M表示。
地震的震级M,一般称为里氏震级。
1935年由里希特首先提出了震级的定义。
当震级相差一级,地面振动振幅增加约10倍,而能量增加近32倍。
一般说来,M<2的地震,人们感觉不到,称为微震;M=2~4的地震称为有感地震;M>5的地震,对建筑物就要引起不同程度的破坏,统称为破坏性地震;M>7的地震称为强烈地震或大地震;M>8的地震称为特大地震。
2009年安徽省高考数学试卷(理科)及答案
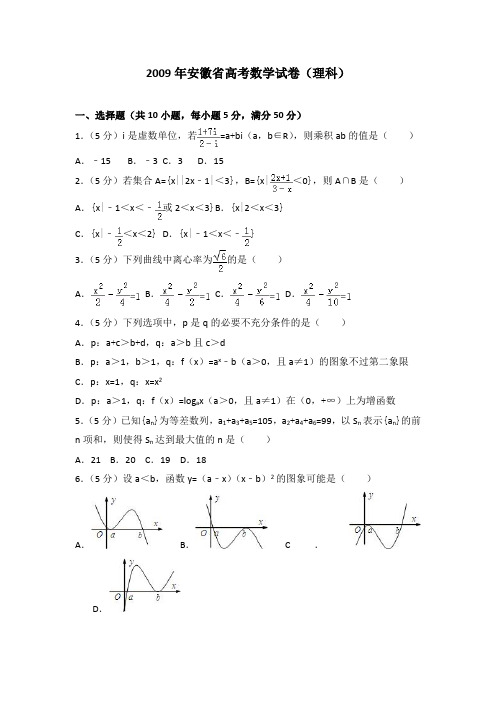
2009年安徽省高考数学试卷(理科)一、选择题(共10小题,每小题5分,满分50分)1.(5分)i是虚数单位,若=a+bi(a,b∈R),则乘积ab的值是()A.﹣15 B.﹣3 C.3 D.152.(5分)若集合A={x||2x﹣1|<3},B={x|<0},则A∩B是()A.{x|﹣1<x<﹣或2<x<3}B.{x|2<x<3}C.{x|﹣<x<2}D.{x|﹣1<x<﹣}3.(5分)下列曲线中离心率为的是()A.B.C.D.4.(5分)下列选项中,p是q的必要不充分条件的是()A.p:a+c>b+d,q:a>b且c>dB.p:a>1,b>1,q:f(x)=a x﹣b(a>0,且a≠1)的图象不过第二象限C.p:x=1,q:x=x2D.p:a>1,q:f(x)=log a x(a>0,且a≠1)在(0,+∞)上为增函数5.(5分)已知{a n}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以S n表示{a n}的前n项和,则使得S n达到最大值的n是()A.21 B.20 C.19 D.186.(5分)设a<b,函数y=(a﹣x)(x﹣b)2的图象可能是()A.B.C.D.7.(5分)若不等式组所表示的平面区域被直线y=kx+分为面积相等的两部分,则k的值是()A.B.C.D.8.(5分)已知函数f(x)=sinwx+coswx(w>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是()A.[kπ﹣,kπ+],k∈Z B.[kπ+,kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ+,kπ+],k∈Z9.(5分)已知函数f(x)在R上满足f(1+x)=2f(1﹣x)﹣x2+3x+1,则曲线y=f(x)在点(1,f(1))处的切线方程是()A.x﹣y﹣2=0 B.x﹣y=0 C.3x+y﹣2=0 D.3x﹣y﹣2=010.(5分)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于()A.B.C.D.二、填空题(共5小题,每小题5分,满分20分)11.(5分)若随机变量X~N(μ,σ2),则P(X≤μ)=.12.以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为(ρ∈R),它与曲线(α为参数)相交于两点A和B,则|AB|=.13.(5分)程序框图(即算法流程图)如图所示,其输出结果是.14.(5分)给定两个长度为1的平面向量和,它们的夹角为120°.如图所示,点C在以O为圆心,以1半径的圆弧AB上变动.若=x+y,其中x,y∈R,则x+y的最大值是.15.(5分)对于四面体ABCD,下列命题正确的序号是.①相对棱AB与CD所在的直线异面;②由顶点A作四面体的高,其垂足是△BCD的三条高线的交点;③若分别作△ABC和△ABD的边AB上的高,则这两条高所在直线异面;④分别作三组相对棱中点的连线,所得的三条线段相交于一点;⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.三、解答题(共6小题,满分75分)16.(12分)在△ABC中,sin(C﹣A)=1,sinB=.(Ⅰ)求sinA的值;(Ⅱ)设AC=,求△ABC的面积.17.(12分)某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A 到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是.同样也假定D受A、B和C感染的概率都是.在这种假定之下,B、C、D中直接受A感染的人数x就是一个随机变量.写出x的分布列(不要求写出计算过程),并求x的均值(即数学期望).18.(13分)如图所示,四棱锥F﹣ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.(1)求二面角B﹣AF﹣D的大小;(2)求四棱锥E﹣ABCD与四棱锥F﹣ABCD公共部分的体积.19.(12分)已知函数f(x)=x﹣+a(2﹣lnx),(a>0),讨论f(x)的单调性.20.(13分)点P(x0,y0)在椭圆(a>b>0)上,x0=acosβ,y0=bsinβ,0<.直线l2与直线l1:垂直,O为坐标原点,直线OP的倾斜角为α,直线l2的倾斜角为γ(Ⅰ)证明:点P是椭圆与直线l1的唯一交点;(Ⅱ)证明:tanα,tanβ,tanγ构成等比数列.21.(13分)首项为正数的数列{a n}满足a n+1=(a n2+3),n∈N+.(1)证明:若a1为奇数,则对一切n≥2,a n都是奇数;(2)若对一切n∈N+都有a n+1>a n,求a1的取值范围.2009年安徽省高考数学试卷(理科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)(2009•安徽)i是虚数单位,若=a+bi(a,b∈R),则乘积ab的值是()A.﹣15 B.﹣3 C.3 D.15【分析】先根据两个复数相除的除法法则化简,再依据两个复数相等的充要条件求出a和b的值,即得乘积ab的值.【解答】解:∵===﹣1+3i=a+bi,∴a=﹣1,b=3,∴ab=﹣1×3=﹣3.故选B.2.(5分)(2009•安徽)若集合A={x||2x﹣1|<3},B={x|<0},则A∩B 是()A.{x|﹣1<x<﹣或2<x<3}B.{x|2<x<3}C.{x|﹣<x<2}D.{x|﹣1<x<﹣}【分析】集合A中的绝对值不等式可利用讨论2x﹣1的正负得到一个不等式组,求出不等式组的解集即可得到集合A;集合B中的其他不等式可转化为2x+1与x ﹣3同号即同时为正或同时为负得到两个不等式组,分别求出解集即可得到集合B,求出两集合的交集即可.【解答】解:∵|2x﹣1|<3,∴﹣3<2x﹣1<3,即,∴﹣1<x<2,又∵<0,∴(2x+1)(x﹣3)>0,即或,∴x>3或x<﹣,∴A∩B={x|﹣1<x<﹣}.故选D3.(5分)(2009•安徽)下列曲线中离心率为的是()A.B.C.D.【分析】通过验证法可得双曲线的方程为时,.【解答】解:选项A中a=,b=2,c==,e=排除.选项B中a=2,c=,则e=符合题意选项C中a=2,c=,则e=不符合题意选项D中a=2,c=则e=,不符合题意故选B4.(5分)(2009•安徽)下列选项中,p是q的必要不充分条件的是()A.p:a+c>b+d,q:a>b且c>dB.p:a>1,b>1,q:f(x)=a x﹣b(a>0,且a≠1)的图象不过第二象限C.p:x=1,q:x=x2D.p:a>1,q:f(x)=log a x(a>0,且a≠1)在(0,+∞)上为增函数【分析】由题意根据必要条件、充分条件和充要条件的定义对ABCD四个选项进行一一判断,从而求解.【解答】解:A、∵q:a>b且c>d,∴a+c>b+d,∴q⇒p,但p推不出q,p 是q的必要不充分条件,故A正确;B、∵p:a>1,b>1,∴f(x)=a x﹣b(a>0,且a≠1)的图象不过第二象限,但若b=1,a>1时f(x)的图象也不过第二象限,q推不出p,∴p是q的充分不必要条件,故B错误;C、∵x=1,∴x=x2,但当x=0时,x=x2,也成立,q推不出p,∴p是q的充分不必要条件,故C错误;D、∵a>1,∴f(x)=log a x(a>0,且a≠1)在(0,+∞)上为增函数,p是q 的充要条件,故D错误;故选A.5.(5分)(2009•安徽)已知{a n}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以S n表示{a n}的前n项和,则使得S n达到最大值的n是()A.21 B.20 C.19 D.18【分析】写出前n项和的函数解析式,再求此式的最值是最直观的思路,但注意n取正整数这一条件.【解答】解:设{a n}的公差为d,由题意得a1+a3+a5=a1+a1+2d+a1+4d=105,即a1+2d=35,①a2+a4+a6=a1+d+a1+3d+a1+5d=99,即a1+3d=33,②由①②联立得a1=39,d=﹣2,∴S n=39n+×(﹣2)=﹣n2+40n=﹣(n﹣20)2+400,故当n=20时,S n达到最大值400.故选:B.6.(5分)(2009•安徽)设a<b,函数y=(a﹣x)(x﹣b)2的图象可能是()A.B.C.D.【分析】根据所给函数式的特点,知函数值的符号取决于x的值与a的值的大小关系,当x≥a时,y≤0,当x≤a时,y≥0,据此即可解决问题.【解答】解:∵y=(a﹣x)(x﹣b)2∴当x≥a时,y≤0,故可排除A、D;又当x≤a时,y≥0,故可排除C;故选B.7.(5分)(2009•安徽)若不等式组所表示的平面区域被直线y=kx+分为面积相等的两部分,则k的值是()A.B.C.D.【分析】先根据约束条件:,画出可行域,求出可行域顶点的坐标,再利用几何意义求面积即可.【解答】解:满足约束条件:,平面区域如图示:由图可知,直线恒经过点A(0,),当直线再经过BC的中点D (,)时,平面区域被直线分为面积相等的两部分,当x=,y=时,代入直线的方程得:k=,故选A.8.(5分)(2009•安徽)已知函数f(x)=sinwx+coswx(w>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是()A.[kπ﹣,kπ+],k∈Z B.[kπ+,kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ+,kπ+],k∈Z【分析】先把函数化成y=Asin(ωx+φ)的形式,再根据三角函数单调区间的求法可得答案.【解答】解:f(x)=sinwx+coswx=2sin(wx+),(w>0).∵f(x)的图象与直线y=2的两个相邻交点的距离等于π,恰好是f(x)的一个周期,∴=π,w=2.f(x)=2sin(2x+).故其单调增区间应满足2kπ﹣≤2x+≤2kπ+,k∈Z.kπ﹣≤x≤kπ+,故选C.9.(5分)(2009•安徽)已知函数f(x)在R上满足f(1+x)=2f(1﹣x)﹣x2+3x+1,则曲线y=f(x)在点(1,f(1))处的切线方程是()A.x﹣y﹣2=0 B.x﹣y=0 C.3x+y﹣2=0 D.3x﹣y﹣2=0【分析】对等式两边进行求导数,通过赋值求切线斜率;对等式赋值求切点坐标;据点斜式写出直线方程.【解答】解:∵f(1+x)=2f(1﹣x)﹣x2+3x+1∴f′(1+x)=﹣2f′(1﹣x)﹣2x+3∴f′(1)=﹣2f′(1)+3∴f′(1)=1f(1+x)=2f(1﹣x)﹣x2+3x+1∴f(1)=2f(1)+1∴f(1)=﹣1∴切线方程为:y+1=x﹣1即x﹣y﹣2=0故选A10.(5分)(2009•安徽)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于()A.B.C.D.【分析】先用组合数公式求出甲乙从这6个点中任意选两个点连成直线的条数共有C62,再用分步计数原理求出甲乙从中任选一条共有225种,利用正八面体找出相互平行但不重合共有共12对,代入古典概型的概率公式求解.【解答】解:甲从这6个点中任意选两个点连成直线,共有C62=15条,乙也从这6个点中任意选两个点连成直线,共有C62=15条,甲乙从中任选一条共有15×15=225种不同取法,因正方体6个面的中心构成一个正八面体,有六对相互平行但不重合的直线,则甲乙两人所得直线相互平行但不重合共有12对,这是一个古典概型,所以所求概率为=,故选D.二、填空题(共5小题,每小题5分,满分20分)11.(5分)(2009•安徽)若随机变量X~N(μ,σ2),则P(X≤μ)=.【分析】由正态分布的图象规律知,其在x=μ左侧一半的概率为,故得P(ζ≤μ)的值.【解答】解:∵ζ服从正态分布N(μ,σ2),根据正态密度曲线的对称性可得∴曲线关于x=μ对称,P(X≤μ)=选填:.12.(2009•安徽)以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为(ρ∈R),它与曲线(α为参数)相交于两点A和B,则|AB|=.【分析】把参数方程、极坐标方程化为直角坐标方程,求出弦心距,再利用弦长公式求得弦长|AB|的值.【解答】解:直线的极坐标方程为(ρ∈R),化为直角坐标方程为x﹣y=0.曲线(α为参数)的普通方程为(x﹣1)2+(y﹣2)2=4,表示以(1,2)为圆心,半径等于2的圆.求得弦心距d==,故弦长为2=2=,故答案为.13.(5分)(2009•安徽)程序框图(即算法流程图)如图所示,其输出结果是127.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算a值,并输出满足条件a>100的第一个a值,模拟程序的运行过程,用表格将程序运行过程中变量a的值的变化情况进行分析,不难给出答案.【解答】解:程序在运行过程中各变量的值如下表示:a 是否继续循环循环前1/第一圈 3 是第二圈7 是第三圈15 是第四圈31 是第五圈63 是第六圈127 否故最后输出的a值为:127故答案为:12714.(5分)(2009•安徽)给定两个长度为1的平面向量和,它们的夹角为120°.如图所示,点C在以O为圆心,以1半径的圆弧AB上变动.若=x+y,其中x,y∈R,则x+y的最大值是2.【分析】根据题意,建立坐标系,设出A,B点的坐标,并设∠AOC=α,则向量,且=x+y,由向量相等,得x,y的值,从而求得x+y 的最值.【解答】解:建立如图所示的坐标系,则A(1,0),B(cos120°,sin120°),即B(﹣,).设∠AOC=α,则=(cosα,sinα).∵=x+y=(x,0)+(﹣,y)=(cosα,sinα);则,解得,∴x+y=sinα+cosα=2sin(α+30°).∵0°≤α≤120°.∴30°≤α+30°≤150°.∴x+y有最大值2,当α=60°时取最大值2.答案:215.(5分)(2009•安徽)对于四面体ABCD,下列命题正确的序号是①④⑤.①相对棱AB与CD所在的直线异面;②由顶点A作四面体的高,其垂足是△BCD的三条高线的交点;③若分别作△ABC和△ABD的边AB上的高,则这两条高所在直线异面;④分别作三组相对棱中点的连线,所得的三条线段相交于一点;⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.【分析】①根据三棱锥的结构特征判断.②根据对棱不一定相互垂直判断.③可由正四面体时来判断.④由棱中点两两连接构成平行四边形判断.⑤根据两边之和大于第三边判断.【解答】解:①根据三棱锥的结构特征知正确.②因为只有对棱相互垂直才行,所以不一定,不正确.③若分别作△ABC和△ABD的边AB上的高,若是正四面体时,则两直线相交,不正确.④因为相对棱中点两两连接构成平行四边形,而对棱的中点的连接正是平行四边形的对角线,所以三条线段相交于一点,故正确.⑤设图中CD是最长边.BC+BD>CD,AC+AD>CD若AC+BC≤CD 且AD+BD≤CD则AC+AD+BC+BD≤CD+CD,矛盾则命题成立.故答案为:①④⑤三、解答题(共6小题,满分75分)16.(12分)(2009•安徽)在△ABC中,sin(C﹣A)=1,sinB=.(Ⅰ)求sinA的值;(Ⅱ)设AC=,求△ABC的面积.【分析】(I)利用sin(C﹣A)=1,求出A,C关系,通过三角形内角和结合sinB=,求出sinA的值;(II)通过正弦定理,利用(I)及AC=,求出BC,求出sinC,然后求△ABC 的面积.【解答】解:(Ⅰ)因为sin(C﹣A)=1,所以,且C+A=π﹣B,∴,∴,∴,又sinA>0,∴(Ⅱ)如图,由正弦定理得∴,又sinC=sin(A+B)=sinAcosB+cosAsinB=∴17.(12分)(2009•安徽)某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是.同样也假定D受A、B和C感染的概率都是.在这种假定之下,B、C、D中直接受A感染的人数x 就是一个随机变量.写出x的分布列(不要求写出计算过程),并求x的均值(即数学期望).【分析】由题意知X的可能取值为1,2,3,分别求出相应的概率,由此能求出x的分布列和x的均值.【解答】解:由题意知X的可能取值为1,2,3,随机变量X的分布列是X123PX的均值为EX=1×+2×+3×=.18.(13分)(2009•安徽)如图所示,四棱锥F﹣ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.(1)求二面角B﹣AF﹣D的大小;(2)求四棱锥E﹣ABCD与四棱锥F﹣ABCD公共部分的体积.【分析】(1)连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足,连接BG、DG,根据定义可知∠BGD为二面角B﹣AF﹣D的平面角,在三角形BGD 中求出此角即可;(2)连接EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E﹣ABCD 与四棱锥F﹣ABCD的公共部分为四棱锥H﹣ABCD,过H作HP⊥平面ABCD,P•HP求解即可.为垂足,然后求出HP,利用体积公式V=S菱形ABCD【解答】解:(1)解:连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足,连接BG、DG.由BD⊥AC,BD⊥CF得BD⊥平面ACF,故BD⊥AF.于是AF⊥平面BGD,所以BG⊥AF,DG⊥AF,∠BGD为二面角B﹣AF﹣D的平面角.由FC⊥AC,FC=AC=2,得∠FAC=,OG=.由OB⊥OG,OB=OD=,得∠BGD=2∠BGO=.(2)解:连接EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E﹣ABCD与四棱锥F﹣ABCD的公共部分为四棱锥H﹣ABCD.过H作HP⊥平面ABCD,P为垂足.因为EA⊥平面ABCD,FC⊥平面ABCD,所以平面ACEF⊥平面ABCD,从而P∈AC,HP⊥AC.由+=+=1,得HP=.=AC•BD=,又因为S菱形ABCD故四棱锥H﹣ABCD的体积V=S•HP=.菱形ABCD19.(12分)(2009•安徽)已知函数f(x)=x﹣+a(2﹣lnx),(a>0),讨论f (x)的单调性.【分析】先求出函数的定义域,然后求出导函数,设g(x)=x2﹣ax+2,二次方程g(x)=0的判别式△=a2﹣8,然后讨论△的正负,再进一步考虑导函数的符号,从而求出函数的单调区间.【解答】解:f(x)的定义域是(0,+∞),.设g(x)=x2﹣ax+2,二次方程g(x)=0的判别式△=a2﹣8.①当△=a2﹣8<0,即时,对一切x>0都有f′(x)>0,此时f(x)在(0,+∞)上是增函数.②当△=a2﹣8=0,即时,仅对有f′(x)=0,对其余的x>0都有f′(x)>0,此时f(x)在(0,+∞)上也是增函数.③当△=a2﹣8>0,即时,方程g(x)=0有两个不同的实根,,0<x1<x2.x(0,x1)x1(x1,x2)x2(x2,+∞)f'(x)+0_0+f(x)单调递增↗极大单调递减↘极小单调递增此时f(x)在上单调递增,在是上单调递减,在上单调递增.20.(13分)(2009•安徽)点P(x0,y0)在椭圆(a>b>0)上,x0=acosβ,y0=bsinβ,0<.直线l2与直线l1:垂直,O为坐标原点,直线OP的倾斜角为α,直线l2的倾斜角为γ(Ⅰ)证明:点P是椭圆与直线l1的唯一交点;(Ⅱ)证明:tanα,tanβ,tanγ构成等比数列.【分析】(Ⅰ)由,得y=,从而x=acosβ,由此能证明直线l1与椭圆有唯一交点P.(Ⅱ)tanα==tanβ,由此得ta nαtanγ=tan2β≠0,从而能证明tanα,tanβ,tanγ构成等比数列.【解答】解:(Ⅰ)由,得y=,代入椭圆,得,将,代入上式,得x2﹣2acosβx+a2cos2β=0,从而x=acosβ,∴有唯一解,即直线l1与椭圆有唯一交点P.(Ⅱ)tanα==tanβ,l1的斜率为tan=,由此得tanαtanγ=tan2β≠0,∴tanα,tanβ,tanγ构成等比数列.21.(13分)(2009•安徽)首项为正数的数列{a n}满足a n+1=(a n2+3),n∈N+.(1)证明:若a1为奇数,则对一切n≥2,a n都是奇数;(2)若对一切n∈N+都有a n+1>a n,求a1的取值范围.【分析】(1)首先在n=1时,知a1为奇数,再利用归纳法证明对一切n≥2,a n 都是奇数;(2)先求出a n+1﹣a n的表达式,利用函数思想求解不等式a n+1﹣a n>0,求出a n 取值范围,利用归纳法求出a1的取值范围.【解答】(1)证明:已知a1是奇数,假设a k=2m﹣1是奇数,其中m为正整数,则由递推关系得a k+1==m(m﹣1)+1是奇数.根据数学归纳法,对任何n≥2,a n都是奇数.(2)法一:由a n+1﹣a n=(a n﹣1)(a n﹣3)知,a n+1>a n当且仅当a n<1或a n >3.另一方面,若0<a k<1,则0<a k+1<=1;若a k>3,则a k+1>=3.根据数学归纳法得,0<a1<1⇔0<a n<1,∀n∈N+;a1>3⇔a n>3,∀n∈N+.综上所述,对一切n∈N+都有a n+1>a n的充要条件是0<a1<1或a1>3.法二:由a2=>a1,得a12﹣4a1+3>0,于是0<a1<1或a1>3.a n+1﹣a n=﹣=,因为a1>0,a n+1=,所以所有的a n均大于0,因此a n+1﹣a n与a n﹣a n﹣1同号.根据数学归纳法,∀n∈N+,a n+1﹣a n与a2﹣a1同号.因此,对一切n∈N+都有a n+1>a n的充要条件是0<a1<1或a1>3.。
2010年安徽省高考数学试卷(理科)答案与解析

2010年安徽省高考数学试卷(理科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)(2010•安徽)i是虚数单位,=()A.﹣i B.i C.D.【考点】复数代数形式的乘除运算.【分析】通常分子与分母同时乘以分母的共轭复数,然后利用复数的代数运算,结合i2=﹣1得结论.【解答】解:===+,故选B.【点评】本题考查复数的分式形式的化简问题,主要是乘除运算,是基础题.2.(5分)(2010•安徽)若集合A={x|x≥},则∁R A=()A.(﹣∞,0]∪(,+∞)B.(,+∞)C.(﹣∞,0]∪[,+∞)D.[,+∞)【考点】补集及其运算;对数函数的单调性与特殊点.【专题】计算题.【分析】欲求A的补集,必须先求集合A,利用对数的单调性求集合A,然后得结论,【解答】解:∵x≥,∴x≥,∴0<x,∴∁R A=(﹣∞,0]∪(,+∞).故选A.【点评】本题主要考查补集及其运算,这里要注意对数中真数的范围,否则容易出错.3.(5分)(2010•安徽)设向量,则下列结论中正确的是()A.B.C.与垂直D.【考点】向量的模;数量积判断两个平面向量的垂直关系.【专题】计算题.【分析】本题考查的知识点是向量的模,及用数量积判断两个平面向量的垂直关系,由,我们易求出向量的模,结合平面向量的数量坐标运算,对四个答案逐一进行判断,即可得到答案.【解答】解:∵,∴=1,=,故不正确,即A错误∵•=≠,故B错误;∵﹣=(,﹣),∴(﹣)•=0,∴与垂直,故C正确;∵,易得不成立,故D错误.故选C【点评】判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”.4.(5分)(2010•安徽)若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)﹣f(4)=()A.1 B.2 C.﹣2 D.﹣1【考点】函数奇偶性的性质;函数的周期性.【专题】计算题.【分析】利用函数奇偶性以及周期性,将3或4的函数值问题转化为1或2的函数值问题求解即可.【解答】解:∵若f(x)是R上周期为5的奇函数∴f(﹣x)=﹣f(x),f(x+5)=f(x),∴f(3)=f(﹣2)=﹣f(2)=﹣2,f(4)=f(﹣1)=﹣f(1)=﹣1,∴f(3)﹣f(4)=﹣2﹣(﹣1)=﹣1.故选D.【点评】本题考查函数奇偶性的应用,奇(偶)函数的定义:一般地,如果对于函数f (x)的定义域内任意一个x,都有f(﹣x)=﹣f(x))(或f(﹣x)=f(x)),那么函数f(x)是奇(偶)函数.5.(5分)(2010•安徽)双曲线方程为x2﹣2y2=1,则它的右焦点坐标为()A.B.C.D.【考点】双曲线的简单性质.【专题】计算题.【分析】把双曲线方程化为标准方程可分别求得a和b,进而根据c=求得c,焦点坐标可得.【解答】解:双曲线的,,,∴右焦点为.故选C【点评】本题考查双曲线的焦点,把双曲线方程先转化为标准方程,然后利用c2=a2+b2求出c即可得出交点坐标.但因方程不是标准形式,很多学生会误认为b2=1或b2=2,从而得出错误结论.6.(5分)(2010•安徽)设abc>0,二次函数f(x)=ax2+bx+c的图象可能是()A.B.C.D.【考点】函数的图象.【专题】综合题;分类讨论.【分析】当a>0时,二次函数开口向上,判断C、D中c的符号,再确定b的符号,判断C、D的正误,当a<0时,同样的方法判断A、B的正误.【解答】解:当a>0时,因为abc>0,所以b、c同号,由(C)(D)两图中可知c<0,故b<0,∴,即函数对称轴在y轴右侧,C不正确,选项(D)符合题意.显然a<0时,开口向下,因为abc>0,所以b、c异号,对于A、由图象可知c<0,则b>0,对称轴,A不正确;对于 B,c>0,对称轴,B选项不正确.故选D.【点评】根据二次函数图象开口向上或向下,分a>0或a<0两种情况分类考虑.另外还要注意c值是抛物线与y轴交点的纵坐标,还要注意对称轴的位置或定点坐标的位置等.是常考题.7.(5分)(2010•安徽)设曲线C的参数方程为(θ为参数),直线l的方程为x﹣3y+2=0,则曲线C上到直线l距离为的点的个数为()A.1 B.2 C.3 D.4【考点】圆的参数方程.【专题】计算题;压轴题.【分析】由题意将圆C和直线l先化为一般方程坐标,然后再计算曲线C上到直线l距离为的点的个数.【解答】解:化曲线C的参数方程为普通方程:(x﹣2)2+(y+1)2=9,圆心(2,﹣1)到直线x﹣3y+2=0的距离,直线和圆相交,过圆心和l平行的直线和圆的2个交点符合要求,又,在直线l的另外一侧没有圆上的点符合要求,故选B.【点评】解决这类问题首先把曲线C的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系,这就是曲线C上到直线l距离为,然后再判断知,进而得出结论.8.(5分)(2010•安徽)一个几何体的三视图如图,该几何体的表面积是()A.372 B.360 C.292 D.280【考点】由三视图求面积、体积.【专题】计算题;压轴题.【分析】三视图很容易知道是两个长方体的组合体,得出各个棱的长度.即可求出组合体的表面积.【解答】解:该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和.S=2(10×8+10×2+8×2)+2(6×8+8×2)=360.故选B.【点评】把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体,得出各个棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和.9.(5分)(2010•安徽)动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是()A.[0,1]B.[1,7]C.[7,12]D.[0,1]和[7,12]【考点】函数单调性的判断与证明.【专题】压轴题.【分析】由动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似,由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在[0,12]变化时,点A的纵坐标y关于t(单位:秒)的函数的单调性的变化,从而得单调递增区间.【解答】解:设动点A与x轴正方向夹角为α,则t=0时,每秒钟旋转,在t∈[0,1]上,在[7,12]上,动点A的纵坐标y关于t都是单调递增的.故选D.【点评】本题主要考查通过观察函数的图象确定函数单调性的问题.10.(5分)(2010•安徽)设{a n}是任意等比数列,它的前n项和,前2n项和与前3n项和分别为X,Y,Z,则下列等式中恒成立的是()A.X+Z=2Y B.Y(Y﹣X)=Z(Z﹣X)C.Y2=XZ D.Y(Y﹣X)=X(Z﹣X)【考点】等比数列.【专题】压轴题.【分析】取一个具体的等比数列验证即可.【解答】解:取等比数列1,2,4,令n=1得X=1,Y=3,Z=7代入验算,只有选项D满足.故选D【点评】对于含有较多字母的客观题,可以取满足条件的数字代替字母,代入验证,若能排除3个选项,剩下唯一正确的就一定正确;若不能完全排除,可以取其他数字验证继续排除.二、填空题(共5小题,每小题5分,满分25分)11.(5分)(2010•安徽)命题“对任何x∈R,使得|x﹣2|+|x﹣4|>3”的否定是存在x∈R,使得|x﹣2|+|x﹣4|≤3.【考点】命题的否定.【专题】阅读型.【分析】全称命题的否定是特称命题,只须将全称量词“任何”改为存在量词“存在”,并同时把“|x﹣2|+|x﹣4|>3”否定.【解答】解:全称命题的否定是特称命题,∴命题“对任何x∈R,使得|x﹣2|+|x﹣4|>3”的否定是:存在x∈R,使得|x﹣2|+|x﹣4|≤3.故填:存在x∈R,使得|x﹣2|+|x﹣4|≤3.【点评】本题主要考查了命题的否定,属于基础题之列.这类问题常见错误是,没有把全称量词改为存在量词,或者对于“>“的否定改成了”<“,而不是“≤”.12.(5分)(2010•安徽)(﹣)6展开式中,x3的系数等于15.【考点】二项式系数的性质.【专题】计算题.【分析】根据题意,易得其二项展开式,分析可得,当r=2时,有C62•()4•(﹣)2=15x3,即可得答案.【解答】解:根据题意,易得其二项展开式的通项为T r+1=C6r•()6﹣r•(﹣)r,当r=2时,有C62•()4•(﹣)2=15x3,则x3的系数等于15,故答案为15.【点评】本题考查二项式定理的应用,注意二项式的展开式的形式,特别要区分某一项的系数与二项式系数.13.(5分)(2010•安徽)设x,y满足约束条件,若目标函数z=abx+y(a>0,b>0)的最大值为8,则a+b的最小值为4.【考点】简单线性规划的应用.【专题】压轴题.【分析】本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件,画出满足约束条件的可行域,再根据目标函数z=abx+y(a>0,b>0)的最大值为8,求出a,b的关系式,再利用基本不等式求出a+b的最小值.【解答】解:满足约束条件的区域是一个四边形,如下图4个顶点是(0,0),(0,2),(,0),(1,4),由图易得目标函数在(1,4)取最大值8,即8=ab+4,∴ab=4,∴a+b≥2=4,在a=b=2时是等号成立,∴a+b的最小值为4.故答案为:4【点评】用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.14.(5分)(2010•安徽)如图所示,程序框图(算法流程图)的输出值x为12【考点】程序框图.【专题】图表型;算法和程序框图.【分析】模拟执行程序框图,依次写出每次循环得到的x的值,当x=12时满足条件x>8,退出循环,输出x的值为12.【解答】解:模拟执行程序框图,可得x=1满足条件x是奇数,x=2不满足条件x是奇数,x=4,不满足条件x>8,x=5满足条件x是奇数,x=6,不满足条件x>8,x=7满足条件x是奇数,x=8,不满足条件x>8,x=9满足条件x是奇数,x=10,不满足条件x是奇数,x=12,满足条件x>8,退出循环,输出x的值为12.【点评】本题主要考查了循环结构的程序框图,正确依次写出每次循环得到的x的值是解题的关键,属于基础题.15.(5分)(2010•安徽)甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以A1,A2和A3表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是②④(写出所有正确结论的编号).①;②;③事件B与事件A1相互独立;④A1,A2,A3是两两互斥的事件;⑤P(B)的值不能确定,因为它与A1,A2,A3中哪一个发生有关.【考点】互斥事件的概率加法公式.【专题】压轴题.【分析】本题是概率的综合问题,掌握基本概念,及条件概率的基本运算是解决问题的关键.本题在A1,A2,A3是两两互斥的事件,把事件B的概率进行转化P(B)=P(B|•A1)+P(B•A2)+P(B•A3),可知事件B的概率是确定的.【解答】解:易见A1,A2,A3是两两互斥的事件,.故答案为:②④【点评】概率的综合问题,需要对基本概念和基本运算能够熟练掌握.三、解答题(共6小题,满分75分)16.(12分)(2010•安徽)设△ABC是锐角三角形,a,b,c分别是内角A,B,C所对边长,并且.(Ⅰ)求角A的值;(Ⅱ)若,求b,c(其中b<c).【考点】余弦定理的应用;两角和与差的正弦函数.【专题】计算题.【分析】(1)先根据两角和与差的正弦公式展开得到角A的正弦值,再由角A的范围确定角A的值.(2)先根据向量数量积的运算和角A的值得到cb=24,再由a=2和余弦定理可求出b,c的值.【解答】解:(1)因为sin2A=(()+sin2B==所以sinA=±.又A为锐角,所以A=(2)由可得,cbcosA=12 ①由(1)知A=,所以cb=24 ②由余弦定理知a2=b2+c2﹣2bccosA,将a=2及①代入可得c2+b2=52③③+②×2,得(c+b)2=100,所以c+b=10因此,c,b是一元二次方程t2﹣10t+24=0的两根解此方程并由c>b知c=6,b=4【点评】本题主要考查两角和与差的正弦公式和余弦定理的应用.属基础题.17.(12分)(2010•安徽)设a为实数,函数f(x)=e x﹣2x+2a,x∈R.(Ⅰ)求f(x)的单调区间与极值;(Ⅱ)求证:当a>ln2﹣1且x>0时,e x>x2﹣2ax+1.【考点】利用导数研究函数的极值;利用导数研究函数的单调性;利用导数求闭区间上函数的最值.【专题】导数的综合应用.【分析】(Ⅰ)由f(x)=e x﹣2x+2a,x∈R,知f′(x)=e x﹣2,x∈R.令f′(x)=0,得x=ln2.列表讨论能求出f(x)的单调区间区间及极值.(Ⅱ)设g(x)=e x﹣x2+2ax﹣1,x∈R,于是g′(x)=e x﹣2x+2a,x∈R.由(1)知当a>ln2﹣1时,g′(x)最小值为g′(ln2)=2(1﹣ln2+a)>0.于是对任意x∈R,都有g′(x)>0,所以g(x)在R内单调递增.由此能够证明e x>x2﹣2ax+1.【解答】(Ⅰ)解:∵f(x)=e x﹣2x+2a,x∈R,∴f′(x)=e x﹣2,x∈R.令f′(x)=0,得x=ln2.于是当x变化时,f′(x),f(x)的变化情况如下表:x (﹣∞,ln2)ln2 (ln2,+∞)f′(x)﹣0 +f(x)单调递减2(1﹣ln2+a)单调递增故f(x)的单调递减区间是(﹣∞,ln2),单调递增区间是(ln2,+∞),f(x)在x=ln2处取得极小值,极小值为f(ln2)=e ln2﹣2ln2+2a=2(1﹣ln2+a),无极大值.(Ⅱ)证明:设g(x)=e x﹣x2+2ax﹣1,x∈R,于是g′(x)=e x﹣2x+2a,x∈R.由(1)知当a>ln2﹣1时,g′(x)最小值为g′(ln2)=2(1﹣ln2+a)>0.于是对任意x∈R,都有g′(x)>0,所以g(x)在R内单调递增.于是当a>ln2﹣1时,对任意x∈(0,+∞),都有g(x)>g(0).而g(0)=0,从而对任意x∈(0,+∞),g(x)>0.即e x﹣x2+2ax﹣1>0,故当a>ln2﹣1且x>0时,e x>x2﹣2ax+1.【点评】本题考查函数的单调区间及极值的求法和不等式的证明,具体涉及到导数的性质、函数增减区间的判断、极值的计算和不等式性质的应用.解题时要认真审题,仔细解答.18.(12分)(2010•安徽)如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H为BC的中点.(1)求证:FH∥平面EDB;(2)求证:AC⊥平面EDB;(3)求二面角B﹣DE﹣C的大小.【考点】直线与平面平行的判定;直线与平面垂直的判定;与二面角有关的立体几何综合题.【专题】综合题.【分析】(1)设AC于BD交于点G,则G为AC的中点,连接EG,GH,又H为BC的中点,可得四边形EFHG为平行四边形,然后利用直线与平面平行判断定理进行证明;(2)因为四边形ABCD为正方形,有AB⊥BC,又EF∥AB,可得EF⊥BC,要证FH⊥平面ABCD,FH⊥平面ABCD,从而求解.(3)在平面CDEF内过点F作FK⊥DE交DE的延长线与k,可知∠FKB为二面角B﹣DE ﹣C的一个平面角,然后设EF=1,在直角三角形中进行求证.【解答】证明:(1)设AC于BD交于点G,则G为AC的中点,连接EG,GH,又H为BC的中点,∴GH∥AB且GH=AB,又EF∥AB且EF=AB,∴EF∥GH且EF=GH,∴四边形EFHG为平行四边形∴EG∥FH,而EG⊂平面EDB,∴FH∥平面EDB.(2)由四边形ABCD为正方形,有AB⊥BC,又EF∥AB,∴EF⊥BC而EF⊥FB,∴EF⊥平面BFC,∴EF⊥FH,∴AB⊥FH,又BF=FC,H为BC的中点,∴FH⊥BC∴FH⊥平面ABCD,∴FH⊥BC,FH⊥AC,又FH∥EG,∴AC⊥EG又AC⊥BD,EG∩BD=G,∴AC⊥平面EDB,(3)EF⊥FB,∠BFC=90°,∴BF⊥平面CDEF,在平面CDEF内过点F作FK⊥DE交DE的延长线与k,则∠FKB为二面角B﹣DE﹣C的一个平面角,设EF=1,则AB=2,FC=,DE=,又EF∥DC,∴∠KEF=∠EDC,∴sin∠EDC=sin∠KEF=,∴FK=EFsin∠KEF=,tan∠FKB==,∴∠FKB=60°,∴二面角B﹣DE﹣C为60°.【点评】此题考查直线与平面平行的判断及平面与平面垂直的判断,此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.19.(13分)(2010•安徽)已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率.(1)求椭圆E的方程;(2)求∠F1AF2的平分线所在直线l的方程;(3)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【专题】综合题;圆锥曲线的定义、性质与方程.【分析】(1)设出椭圆方程,根据椭圆E经过点A(2,3),离心率,建立方程组,求得几何量,即可得到椭圆E的方程;(2)求得AF1方程、AF2方程,利用角平分线性质,即可求得∠F1AF2的平分线所在直线l的方程;(3)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,设出直线BC方程代入,求得BC中点代入直线2x﹣y﹣1=0上,即可得到结论.【解答】解:(1)设椭圆方程为∵椭圆E经过点A(2,3),离心率∴,∴a2=16,b2=12∴椭圆方程E为:;(2)F1(﹣2,0),F2(2,0),∵A(2,3),∴AF1方程为:3x﹣4y+6=0,AF2方程为:x=2设角平分线上任意一点为P(x,y),则.得2x﹣y﹣1=0或x+2y﹣8=0∵斜率为正,∴直线方程为2x﹣y﹣1=0;(3)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,∴∴直线BC方程为代入得x2﹣mx+m2﹣12=0,∴BC中点为代入直线2x﹣y﹣1=0上,得m=4.∴BC中点为(2,3)与A重合,不成立,所以不存在满足题设条件的相异的两点.【点评】本题考查椭圆的标准方程,考查直线方程,考查对称性,考查学生分析解决问题的能力,属于中档题.20.(13分)(2010•安徽)设数列a1,a2,…,a n,…中的每一项都不为0.证明:{a n}为等差数列的充分必要条件是:对任何n∈N,都有++…+=.【考点】等差数列的性质;必要条件、充分条件与充要条件的判断;数学归纳法.【专题】证明题;压轴题.【分析】先证必要性;设数列a n的公差为d,若d=0,则所述等式显然成立.若d≠0,则==.再用数学归纲法证明充分性:对任何n∈N,都有++…+=,{a n}是公差为d的等差数列.【解答】证明:先证必要性设数列a n的公差为d,若d=0,则所述等式显然成立.若d≠0,则===.再证充分性:用数学归纳法证明:①设所述的等式对一切n∈N都成立,首先在等式①两端同时乘a1a2a3,即得a1+a3=2a2,所以a1,a2,a3成等差数列,记公差为d,则a2=a1+d.②假设a k=a1+(k﹣1)d,当n=k+1时,观察如下二等式=②,=,将②代入③得,在该式两端同时乘a1a k a k+1,得(k﹣1)a k+1+a1=ka k,把a k=a1+(k﹣1)d代入后,整理得a k+1=a1+kd.由数学归纳法原理知对任何n∈N,都有++…+=.所以,{a n}是公差为d的等差数列.【点评】本题考查等差数列、数学归纳法与充要条件等有关知识,考查推理论证、运算求解能力.21.(13分)(2010•安徽)品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.现设n=4,分别以a1,a2,a3,a4表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令X=|1﹣a1|+|2﹣a2|+|3﹣a3|+|4﹣a4|,则X是对两次排序的偏离程度的一种描述.(Ⅰ)写出X的可能值集合;(Ⅱ)假设a1,a2,a3,a4等可能地为1,2,3,4的各种排列,求X的分布列;(Ⅲ)某品酒师在相继进行的三轮测试中,都有X≤2,①试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);②你认为该品酒师的酒味鉴别功能如何?说明理由.【考点】离散型随机变量及其分布列;分布列对于刻画随机现象的重要性.【专题】压轴题.【分析】(1)X的可能取值集合为{0、2、4、6、8},在1、2、3、4中奇数与偶数各有两个,a2,a4中的奇数个数等于a1,a3中的偶数个数,得到|1﹣a1|+|3﹣a3|与|2﹣a2|+|4﹣a4|的奇偶性相同,得到结论.(2)可以用列表或者树状图列出1、2、3、4的一共24种排列,计算每种排列下的X的值,算出概率,写出分布列.(3)做出三轮测试都有X≤2的概率,记做P,做出概率的值和已知量进行比较,得到结论,【解答】解:(1)X的可能取值集合为{0、2、4、6、8}∵在1、2、3、4中奇数与偶数各有两个,∴a2,a4中的奇数个数等于a1,a3中的偶数个数,∴|1﹣a1|+|3﹣a3|与|2﹣a2|+|4﹣a4|的奇偶性相同,∴X=(|1﹣a1|+|3﹣a3|)+(|2﹣a2|+|4﹣a4|)必为偶数,X的值非负,且易知其值不大于8,∴X的可能取值集合为{0、2、4、6、8}(2)可以用列表或者树状图列出1、2、3、4的一共24种排列,计算每种排列下的X的值,在等可能的假定下,得到P(X=0)=P(X=2)=P(X=4)=P(X=6)=P(X=8)=(3)①首先P(X≤2)=P(X=0)+P(X=2)==将三轮测试都有X≤2的概率记做P,有上述结果和独立性假设得P==,②由于P=<是一个很小的概率,这表明仅凭随机猜测得到三轮测试都有X≤2的结果的可能性很小,∴我们认为该品酒师确实有良好的鉴别功能,不是靠随机猜测.【点评】本题主要考查分布列和期望的简单应用,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.。
2010年安徽高考理科数学真题及答案

2010年安徽高考理科数学真题及答案本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分.考试用时120分钟. 注意事项:1.答卷前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致.务必在答题卡背面规定的地方填写姓名和座位号后两位.2.答第I 卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3.答第Ⅱ卷时,必须使用0.5毫米黑色黑水签字笔在答题卡上书写,要求字体工整、笔迹清晰.作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色签际笔描清楚.必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效. 4.考试结束,务必将试题卷和答题卡一并上交. 参考公式: 如果事件A 与B 互斥,那么 如果A 与B 是两个任意事件,,那么)()()(B P A P B A P +=+0)(≠A P 如果事件A 与B 相互独立,那么)|()()(A B P A P AB P =)()()(B P A P AB P ≠第Ⅰ卷(选择题 共50分) 一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)是虚数单位,i =+ii 33(A )(B ) (C ) (D )12341-i 12341-i 6321+i 6321-(2)若集合,则}21log |{21≥=x x A =A C R (A ) (B ) ⎪⎪⎭⎫⎝⎛+∞⋃-∞,22]0,(⎪⎪⎭⎫⎝⎛+∞,22(C ) (D ) ⎪⎪⎭⎫⎢⎣⎡+∞⋃-∞,22]0,(⎪⎪⎭⎫⎢⎣⎡+∞,22(3)设向量,则下列结论中正确的是)21,21(),0,1(==b a(A ) (B ) (C )垂直 (D ) ||||b a =22=⋅b a b b a 与-b a //(4)若是R 上周期为5的奇函数,且满足则= )(x f ,2)2(,1)1(==f f )4()3(f f -(A )-1(B )1(C )-2 (D )2(5)双曲线方程为,则它的右焦点坐标为1222=-y x(A ) (B ) (C ) (D ))0,22()0,25()0,26()0,3((6)设,二次函数的图象可能是 0>abc c bx ax x f ++=2)((7)设曲线C 的参数方程为(为参数),⎩⎨⎧+-=+=θθsin 31cos 32y x θ直线的方程为,则曲线C 到直线的距l 023=+-y x l 离为的点的个数为 10107 (A )1 (B )2 (C )3 (D )4(8)一个几何全体的三视图如图,该几何体的表面积为 (A )280 (B )292(C )360 (D )372(9)动点在圆上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.),(y x A 122=+y x 已知定时t=0时,点A 的坐标是,则当时,动点A 的纵坐标y 关于)23,21(120≤≤t t (单位:秒)的函数的单调递增区间是(A )[0,1] (B )[1,7] (C )[7,12](D )[0,1]和[7,12]、(10)设是任意等比数列,它的前n 项和,前2n 项和与前3n 项和分别为X ,Y ,Z ,则}{n a 下列等式中恒成立的是(A )(B )Y Z X 2=+)()(X Z Z X Y Y -=-(C )(D )XZ Y=2)()(X Z X X Y Y -=-(在此卷上答题无效)绝密★启用并使用完毕前2010年普通高等学校招生全国统一考试(安徽卷)数 学(理科)第Ⅱ卷(非选择题 共100分)考生注意事项: 请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置. (11)命题“对任何”的否定是 .3|4||2|,>-+-∈x x R x (12)的展开式中,的系数等于 . 6⎪⎪⎭⎫ ⎝⎛-x y y x 3x (13)设满足约束条件若目标函数的最大值y x ,⎪⎩⎪⎨⎧≥≥≤--≥+-,0,0,048,022y x y x y x )0,0(>>+=b a y abx z 为8,则的最小值为 .b a +(14)如图所示,程序框图(算法流程图)的输出值 . =x (15)甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球,先从甲罐中随机取出一球放入乙罐, 分别以A 1,A 2和A 3表示由甲罐取出的球是红球,白球和黑球 的事件;再从乙罐中随机取出一球,以B 表示由乙罐取出的球 是红球的事件,则下列结论中正确的是 (写出所有正确结 论的编号). ①; 52)(1=B P ②;115)|(1=A B P ③事件B 与事件A 1相互独立; ④A 1,A 2,A 3是两两互斥的事件;⑤的值不能确定,因为它与A 1,A 2,A 3中究竟哪一个发生有关.)(B P 三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤,解答写在答题卡上的指定区域内. (16)(本小题满分12分)设是锐角三角形,分别是内角A ,B ,C 所对边长,并且ABC ∆c b a ,,.sin )3sin()3sin(sin 22B B B A +-+=ππ(Ⅰ)求角A 的值;(Ⅱ)若,求(其中).72,12==⋅a AC AB c b ,c b <(17)(本小题满分12分)设a 为实数,函数 .,22)(R x a x e x f x∈+-= (I )求的单调区间与极值;)(x f (II )求证:当时,012ln >->x a 且.122+->ax x e x(18)(本小题满分13分)如图,在多面体ABCDEF 中,四边形ABCD 是正方形,EF//AB ,EF ⊥FB ,AB=2EF ,BF=FC ,H 为BC 的中点.,90︒=∠BFC (I )求证:FH//平面EDB ; (II )求证:AC ⊥平面EDB ;(III )求二面角B—DE—C 的大小.(19)(本小题满分13分)已知椭圆E 经过点A (2,3),对称轴为坐标轴,焦点F 1,F 2在x 轴上,离心率 .21=e (I )求椭圆E 的方程;(II )求的角平分线所在直线的方程;21AF F ∠l (III )在椭圆E 上是否存在关于直线对称的相异两点?若存在,请找出;若不存在,l 说明理由.(20)(本小题满分12分)设数列中的每一项都不为0.,,,21 a a ,n a证明,为等差数列的充分必要条件是:对任何,都有}{n a N n ∈ .1111113221++=+++n n n a a n a a a a a a(21)(本小题满分13分)品酒师需要定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序,经过一段时间,等其记忆淡忘之后,再让其品尝这n 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.现设n=4,分别以表示第一次排序时被排为1,2,3,4的四种酒在第二次4321,,,a a a a 排序时的序号,并令.|4||3||2||1|4321a a a a X -+-+-+-=则X 是对两次排序的偏离程度的一种描述. (I )写出X 的可能值集合;(II )假设等可能地为1,2,3,4的各种排列,求X 的分布列; 4321,,,a a a a (III )某品酒师在相继进行的三轮测试中,都有,2≤X (i )试按(II )中的结果,计算出现这种现象的概率(假定各轮测试相互独立); (ii )你认为该品酒师的酒味鉴别功能如何?说明理由.参考答案一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)B (2)A (3)C (4)A (5)C (6)D (7)B (8)C (9)D (10)D二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置. (11)存在 ,-2-4|3x x x ∈≤R 使得||+|(12)15(若只写,也可)2466C C 或(13)4 (14)12 (15)②④三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤,解答写在答题卡上的指定区域内. (16)(本小题满分12分)本题考查两角和的正弦公式,同角三角函数的基本关系,特殊角的三角函数值,向量的数量积,利用余弦定理解三角形等有关知识,考查综合运算求解能力. 解:(I )因为2211sin sin sin )sin 22A B B B B B =+-+222313cos sin sin ,444sin ,.3B B B A A A π=-+===所以又为锐角所以 (II )由可得12AB AC ⋅=①cos 12.cb A = 由(I )知所以,3A π=②24cb =由余弦定理知及①代入,得2222cos ,a c b cb A a =+==将③+②×2,得,所以()100c b 2+=10.c b +=因此,c ,b 是一元二次方程的两个根.210240t t -+=解此方程并由6, 4.c b c b >==知(17)(本小题满分12分)本题考查导数的运算,利用导数研究函数的单调区间,求函数的极值和证明函数不等式,考查运算能力、综合分析和解决问题的能力. (I )解:由()22,()2,.xxf x e x a x f x e x '=-+∈=-∈R R 知令的变化情况如下表:()0,ln 2.,(),()f x x x f x f x ''==得于是当变化时故的单调递减区间是,单调递增区间是,()f x (,ln 2)-∞(ln 2,)+∞处取得极小值,()ln 2f x x =在极小值为ln 2(ln 2)2ln 222(1ln 2).f ea a =-+=-+ (II )证:设2()21,,xg x e x ax x =-+-∈R 于是()22,.xg x e x a x '=-+∈R 由(I )知当ln 21,()(ln 2)2(1ln 2)0.a g x g a ''>-=-+>时最小值为,()0,()x g x g x '∈>R R 于是对任意都有所以在内单调递增,于是当 ln 21,(0,),()(0),a x g x g >-∈+∞>时对任意都有而 (0)0,(0,),()0.g x g x =∈+∞>从而对任意即22210,2 1.xxe x ax e x ax -+->>-+故(18)(本小题满分13分)本题考查空间线面平行、线面垂直、面面垂直的判断与证明,考查二面角的求法以及利用向量知识解决几何问题的能力,同时考查空间想象能力、推理论证能力和运算能力.[综合法](1)证:设AC 与BD 交于点G ,则G 为AC 的中点,连EG ,GH , 又H 为BC 的中点, 11//,//,//.22GH AB EF AB EF GH ∴∴又 ∴四边形EFHG 为平行四边形,∴EG//FH ,而EG 平面EDB ,∴FH//平面EDB.⊂ (II )证:由四边形ABCD 为正方形,有AB ⊥BC ,又EF//AB ,∴EF ⊥BC.而EF ⊥FB ,∵EF ⊥平面BFC ,∴EF ⊥FH ,∴AB ⊥FH. 又BF=FC ,H 为BC 的中点,∴FH ⊥BC. ∴FH ⊥平面ABCD ,∴FH ⊥AC , 又FH//BC ,∴AC=EG.又AC ⊥BD ,EG BD=G ,∴AG ⊥平面EDB.⋂ (III )解:EF ⊥FB ,∠BFC=90°,∴BF ⊥平面CDEF ,在平面CDEF 内过点F 作FK ⊥DE 交DE 的延长线于K , 则∠FKB 为二面角B—DE—C 的一个平面角.设EF=1,则AB=2,,又EF//DC ,∴∠KEF=∠EDC ,∴sin ∠EDC=sin ∠∴FK=EFsin ∠,tan ∠FKB=∴∠FKB=60° BFFK=∴二面角B—DE—C 为60°. [向量法]∵四边形ABCD 为正方形,∴AB ⊥BC ,又EF//AB ,∴EF ⊥BC. 又EF ⊥FB ,∴EF ⊥平面BFC. ∴EF ⊥FH ,∴AB ⊥FH.又BF=FC ,H 为BC 的中点,∴FH ⊥BC ,∴FH ⊥平面ABC.以H 为坐标原点,轴正向,轴正向,HB x 为HF z为建立如图所示坐标系.设BH=1,则A (1,—2,0),B (1,0,0), C (—1,0,0),D (—1,—2,0),E (0,—1,1), F (0,0,1).(I )证:设AC 与BD 的交点为G ,连GE ,GH ,则(0,1,0),(0,0,1),(0,0,1)//.G CE HF HF GE -∴==∴又平面EDB ,HF 不在平面EDB 内,∴FH ∥平面EBD ,GE ⊂ (II )证:(2,2,0),(0,0,1),0,.AC GE AC GE AC GE =-=⋅=∴⊥又AC ⊥BD ,EG ∩BD=G ,∴AC ⊥平面EDB.(III )解:(1,1,1),(2,2,0).BE BD =--=--设平面BDE 的法向量为111(1,,),n y z =则1111110,120,BE n y z BD n y ⋅=--+=⋅=--=111222222121212121,0,(1,1,0).(0,2,0),(1,1,1),(1,,),0,0,(1,0,1),1cos ,,||||2,60,y z n CD CE CDE y z CD y ∴=-==-=-=-=⋅===-⋅<>===⋅∴<>=n n n n n n n n n n n即设平面的法向量为则故即二面角B—DE—C 为60°. (19)(本小题满分13分)本题考查椭圆的定义及标准方程,椭圆的简单几何性质,直线的点斜式方程与一般方程,点到直线的距离公式,点关于直线的对称等基础知识;考查解析几何的基本思想、综合运算能力、探究意识与创新意识.解:(I )设椭圆E 的方程为22221x y a b +=2222222211,,2,3,221.43c e a c b a c e a x y c e ====-=∴+=由即得椭圆方程具有形式将A (2,3)代入上式,得22131,2,c c c+==解得∴椭圆E 的方程为221.1612x y += (II )解法1:由(I )知,所以12(2,0),(2,0)F F -直线AF 1的方程为: 3(2),3460,4y x x y =+-+=即直线AF 2的方程为:2.x =由点A 在椭圆E 上的位置知,直线l 的斜率为正数. 设上任一点,则(,)P x y l 为|346||2|.5x y x -+=-若(因其斜率为负,舍去). 346510,280x y x x y -+=-+-=得所以直线l 的方程为: 210.x y --=解法2:121212121(2,3),(2,0),(2,0),(4,3),(0,3).114(4,3)(0,3)(1,2).535||||2,:32(1),210.A F F AF AF AF AF AF AF k l y x x y -∴=--=-∴+=--+-=-∴=∴-=---=即 (III )解法1:假设存在这样的两个不同的点1122(,)(,),B x y C x y 和2121121200001,.2(,),,,22BC y y BC l k x x x x y y BC M x y x y -⊥∴==-++== 设的中点为则由于M 在l 上,故 ①00210.x y -+=又B ,C 在椭圆上,所以有222211221 1.16121612x y x y +=+=与两式相减,得222221210,1612x x y y --+=即12211221()()()()0.1612x x x x y y y y +-+-+=将该式写为, 122112211108262x x y y y y x x +-+⋅+⋅⋅=-并将直线BC 的斜率和线段BC 的中点,表示代入该表达式中, BC k 得② 0000110,320.812x y x y -=-=即①×2—②得,即BC 的中点为点A ,而这是不可能的. 202,3x y ==∴不存在满足题设条件的点B 和C. 解法2:假设存在, 1122(,),(,)B x y C x y l 两点关于直线对称则1,.2BC l BC k ⊥∴=-221,1,21612x y BC y x m =-++=设直线的方程为将其代入椭圆方程得一元二次方程 2222134()48,120,2x x m x mx m +-+=-+-=即则是该方程的两个根,12x x 与由韦达定理得12,x x m +=于是 121213()2,22m y y x x m +=-++=∴B ,C 的中点坐标为 3(,).24m m 又线段BC 的中点在直线 321,1, 4.4m y x m m =-∴=-=上得即B ,C 的中点坐标为(2,3),与点A 重合,矛盾.∴不存在满足题设条件的相异两点.(20)(本小题满分12分)本题考查等差数列、数学归纳法与充要条件等有关知识,考查推理论证、运算求解能力.证:先证必要性设数列则所述等式显然成立,{},0,n a d d =的公差为若若,则0d ≠ 122313212112233122311111111111()1111111(()()(1111(n n n n n n n n n n n a a a a a a a a a a a a d a a a a a a d a a a a a a a a d a a d a a ++++++++++---=+++=-+-++--=-= 11.n n a a +=再证充分性.证法1:(数学归纳法)设所述的等式对一切都成立,首先,在等式n +∈N ① 122313112a a a a a a +=两端同乘成等差数列,123132123,2,,,a a a a a a a a a +=即得所以记公差为21,.d a a d =+则假设时,观察如下二等式1(1),1k a a k d n k =+-=+当② 12231121111,k k k a a a a a a a a --+++= , ③ 122311111111k k k k k k a a a a a a a a a a -++++++= 将②代入③,得 111111,k k k k k k a a a a a a ++-+=在该式两端同乘11111,,(1).k k k a a a k a a ka ++-+=得将111(1),,.k k a a k d a a kd +=+-=+代入其中整理后得由数学归纳法原理知,对一切1(1),n n a a n d +∈=+-N 都有所以的等差数列.{}n a d 是公差为证法2:[直接证法]依题意有① 1223111111,n n n n a a a a a a a a +++++= ② 12231121211111.n n n n n n a a a a a a a a a a +++++++++= ②—①得, 12121111n n n n n n a a a a a a +++++=-在上式两端同乘112111,(1),n n n n a a a a n a na ++++=+-得同理可得 ③11(1),n n a na n a +=--③—④得122()n n n na n a a ++=+即是等差数列,211,{}n n n n n a a a a a +++-=-所以(21)(本小题满分13分)本题考查离散型随机变量及其分布列,考查在复杂场合下进行计数的能力,能过设置密切贴近生产、生活实际的问题情境,考查概率思想在现实生活中的应用,考查抽象概括能力、应用与创新意识.解:(I )X 的可能值集合为{0,2,4,6,8}.在1,2,3,4中奇数与偶数各有两个,所以中的奇数个数等于中的偶数个23,a a 13,a a数,因此的奇偶性相同,1334|1||3||2||4|a a a a ++--+-与从而必为偶数.2324(|1||3|)(|2||4|)X a a a a =-+++-+-X 的值非负,且易知其值不大于8.容易举出使得X 的值等于0,2,4,6,8各值的排列的例子.(II )可用列表或树状图列出1,2,3,4的一共24种排列,计算每种排列下的X 值,在等可能的假定下,得到X 0 2 4 6 8P 124324724924424(III )(i )首先,将三轮测试都有41(2)(0)(2)246P X P X P X ≤==+===2X ≤的概率记做p ,由上述结果和独立性假设,得311.2166p == (ii )由于是一个很小的概率,这表明如果仅凭随机猜测得到三轮测152161000p =<试都有的结果的可能性很小,所以我们认为该品酒师确实有良好的味觉鉴别功2X ≤能,不是靠随机猜测.。
安徽2009年高考分数线一览表

安徽2009年高考分数线一览表高考是每年的一项重要考试,对于考生来说,了解分数线情况是非常重要的。
下面是安徽省2009年高考分数线一览表,供考生参考。
文科类分数线:
一本分数线:文科561分
二本分数线:文科491分
三本分数线:文科460分
高职高专分数线:文科380分
理科类分数线:
一本分数线:理科596分
二本分数线:理科531分
三本分数线:理科487分
高职高专分数线:理科396分
文科和理科的分数线都是根据考生的成绩来排定的,不同类别的学校有不同的录取分数线要求。
考生要根据自己的实际情况,合理安排志愿填报。
对于文科生而言,若成绩达到一本分数线及以上,就可以选择理想的大学;成绩达到二本分数线及以上,可以选择较好的大学;成绩达到三本分数线及以上,可以选择普通的大学;成绩未达到三本分数线但达到高职高专分数线,可以选择高职高专院校。
对于理科生而言,若成绩达到一本分数线及以上,可以选择重点理工类大学;成绩达到二本分数线及以上,可以选择普通理工类大学;成绩达到三本分数线及以上,可以选择理科综合大学;成绩未达到三本分数线但达到高职高专分数线,可以选择高职高专院校。
总之,考生应该根据自己的实际情况,合理评估自己的成绩,并选择适合自己的学校和专业。
同时,也要注意填报志愿的时限,确保准确无误地填报志愿。
祝愿所有考生在高考中取得优异成绩,实现自己的理想!。
2009年-2014年安徽高考数学文、理科试题均分与难度

2013年高考数学文、理科试题均分与难度
题号 均分 难度 均分 文科 难度 理科 选择题 填空题 16题 17题 18题 19题 20题 21题 50分 25分 12分 12分 12分 13分 13分 13分 28.27 9.31 8.55三角 4.78导数 5.91解几 2.13立几 0.63数列 1.51概率 0.57 0.372 0.71 0.4 0.49 0.16 0.05 0.12 31.43 6.42 5.59三角 7.08统计 3.64立几 5.33数列 1.76导数 3.47解几 0.63 0.257 0.47 0.59 0.3 0.41 0.14 0.27 总计 61.08 0.407 64.72 0.446
2014年高考数学文、理科试题均分与难度 2013年高考数学文、理科试题均分与难度
2012年高考数学文、理科试题均分与难度
2011年高考数学文、理科试题均分与难度
2010年高考数学文、理科试题均分与难度
2009年高考数学文、理科试题均分与难度
2014年高考数学文、理科试题均分与难度
题号 均分 难度 均分 文科 难度 理科 选择题 填空题 16题 17题 18题 19题 20题 21题 50分 25分 12分 12分 12分 13分 13分 13分 35.38 8.7 7.99三角 7.83概率 4.49导数 2.74解几 1.03立几 0.41数列 0.71 0.348 0.666 0.653 0.374 0.211 0.079 0.032 33.32 8.72 5.96三角 7.95统计 4.60数列 2.93立几 2.14导数 2.70解几 0.666 0.349 0.497 0.663 0.383 0.225 0.165 0.208 总计 68.57 0.457 68.32 0.455
2009年安徽数学高考试卷 评析与复习对策 安庆一中 程

程乐根,生于1960年8月,大学本科,理 学士,中国数学会会员、中国社会心理学 学会会员、首批国家级骨干教师培训班学 员、中国奥林匹克高级教练、全国优秀教 师、安徽省数学会常务理事、安徽省特级 教师、省政府特殊津贴专家、安庆市有突 出贡献专家、首批安庆市名师、首届感动 安庆十大教育人物,现任安庆一中省理科 实验班主教练。
3、三角题:文理科三角题都考了三角形, 对理科考生而言,不少人可能会将已知条件 展开,那就很难做出来了。文科考生不会这 样,直接告诉了C-A=π/2,第二小题尽管 不难,但要依赖于第一小题的正确结果。 估计全省平均分:文理科均在7分左右。
4、概率统计题:理科概率虽不难,但对于 中等偏下水平的同学,若对问题实质把握不 清,或列举能力较差,就会做错,好在没有 运算量。文科考了茎叶图虽然不难,但考生 分析问题不一定全面,回答问题不一定把握 的很准,从而造成失分。 估计:理科平均分在6分左右,文科平均分 在4分左右。
7、解析几何题:2009年文理科解析几何 题也完全不同,但都明显降低了运算量,理 科考生多半是用△-判别式法做的,但过程 有点繁,不少考生会中途而废。第二小题考 生可能会忽视tanβ≠0这一点,可能因此失分。 对文科考生而言,第二小题是有难度的,主 要是不知道用什么方法做,因此得分不高。 估计全省平均分:理科在6分左右,文科在4 分左右。
6、函数题:文理科应属姊妹题,理科的函数 题尽管只有一个问,但考生容易忽视对数的 真数“x>0”这个隐含条件,以及忽略了分 类讨论,这些地方都容易丢分。文科的函数 题是作为最后一题呈现的,比理科多一个问, 中等偏下水平的学生一般做不到此题。即便 做到了,也会出现和理科考生一样的情况。 估计此题全省平均分:理科会在6分左右, 文科会在5分左右。
近六年安徽高考数学考点分布

向量、平面区域
含参数的绝对值函数的最值、分类讨论
10
排列组合:立几中排列组合与古典概率
数列:等比数列前n项和
函数:三次图象与性质
排列组合:组合数的计算
函数极值
平面向量、
集合
11
正态分布:求
全称命题否定
算法:流程图
线性规划:求目标函数的取值范围
二项式定理:已知指定项的系数求参数
算法:流程图
充要条件、
对数不等式
3
解析几何:求双曲线离心率
平面向量:基本运算
解析几何:求双曲线实轴长
算法:流程图
立体几何:三公理
算法:流程图
数列
4
综合知识与充要条件
函数性质:周期、奇偶、求值
线性规划:求目标函数最值
数列:等比数列
函数:性质、充要条件
极坐标与参数方程:求圆心到直线的距离
5
数列:等差数列前n项和
复数的四则混合运算
集合运算
集合运算
集合运算
全称命题的否定
3
线性规划:可行域面积
平面向量:基本运算
解析几何:双曲线实轴长
对数运算:换底公式
充要条件
抛物线的准线方程
4
不等式与充要条件
解析几何:求直线方程
解析几何:直线过圆心
全称命题否定
算法:流程图
算法:流程图
5
数列:等差数列前20项和
数列:求数列项
对数函数与对数运算
数列:
等比数列与三角函数综合
统计概率:
求概率
求分布列和期望
二次不等式求解,导数的计算和应用
独立事件概率、离散型随机变量的分布列和数学期望
2009年高考安徽数学(理科)试题及参考答案

2009年高考安徽数学(理科)试题及参考答案合肥市大学生生命教育调查与分析摘要: 当前大学生生命意识的淡薄反映了家庭、高校和社会生命教育的缺乏。
大学生生命教育缺失的原因是多方面的,有家庭、学校和社会多重因素。
要扎实有效地推进生命教育,需要学校教育充分与社会、家庭教育相结合,与生活经验结合,再回归于日常生活的实践关键词: 合肥市大学生;生命教育;重要性;策略;一、生命教育研究的缘起生命教育是通过认识生命的起源、发展和终结,从而认识生命、理解生命、欣赏生命和尊重生命,进而珍惜有限生命,建立起乐观、积极的人生观,促进受教育者价值观、生理心理、社会适应能力的全面均衡发展的教育。
生命教育理应成为教育不可或缺的一部分。
1968 年,美国学者杰·唐纳·华特士首次提出了生命教育的思想。
他倡导并实践生命教育,引导学生正确认识人的价值、人的生命,理解生活的真正意义,培养学生的人文精神和对终极信仰的追求,养成他们的关爱情怀。
而西方国家明确标举“生命教育”概念的是1979 年在澳洲成立的“生命教育中心”。
它不仅包括教育学生正确认识自己的生命、珍惜自己的生命,还教育学生关爱他人、尊重他人的生命,保护动物、珍爱动物的生命。
在我国,生命教育已经引起了中小学教育工作者的重视,并在中小学生中进行了初步实践,取得了一定成效。
我国港台地区已进行了多年生命教育理论与实践的探索,台湾教育机构更是将2001 年定为“生命教育年”。
台湾地区媒体更是将“生命教育”课定位于一生最重要的一门课。
自20世纪90年代以来,中国大陆也全面实施素质教育,倡导以人为本和尊重、关心、理解、信任每一个人,从某种意义上讲,这是开展生命教育的开端。
近年来,在各级党和政府特别是教育部门的重视下,各种有关促进青少年生命健康成长为主题的活动轰轰烈烈地开展,并取得了许多可喜的成绩。
上海、辽宁、江苏、四川、山东、黑龙江、吉林等省市富有创造性地开展了生命教育科研、教学实践、教材编制、教学大纲试行等活动。
2009年高考安徽数学(理科)试题及参考答案

绝密★启用前2009年普通高等学校招生全国统一考试(安徽卷)数学(理科) 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷第1至第2页。
第II 卷第3至第4页。
全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2.答第I 卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮檫干净后,在选涂其他答案标号。
3.答第II 卷时,必须使用用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在标号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.考试结束,务必将试题卷和答题卡一并上交。
参考公式:如果事件A 、B 互斥,那么 S 表示底面积,h 表示底面上的高()()()P A B P A P B +=+ 棱柱体积 V Sh=如果事件A B 、相互独立,那么 棱锥体积 13V Sh =()()()P A B P A P B •=•第I 卷(选择题 共50分)一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)i 是虚数单位,若17(,)2ia bi ab R i+=+∈-,则乘积ab 的值是 (A )-15 (B )-3 (C )3 (D )15[解析]17(17)(2)1325i i i i i +++==-+-,∴1,3,3a b ab =-==-,选B 。
(2)若集合{}21|21|3,0,3x A x x B xx ⎧+⎫=-<=<⎨⎬-⎩⎭则A ∩B 是 (A ) 11232x x x ⎧⎫-<<-<<⎨⎬⎩⎭或 (B) {}23x x <<(C ) 122x x ⎧⎫-<<⎨⎬⎩⎭ (D)112x x ⎧⎫-<<-⎨⎬⎩⎭[解析]集合1{|12},{|3}2A x x B x x x =-<<=<->或,∴1{|1}2A B x x =-<<-选D(3)下列曲线中离心率为62的是(A )22124x y -= (B )22142x y -= (C )22146x y -= (D )221410x y -=[解析]由62e =得222222331,1,222c b b a a a =+==,选B(4)下列选项中,p 是q 的必要不充分条件的是(A )p:a c +>b+d , q:a >b 且c >d (B )p:a >1,b>1 q:()(01)xf x a b a a =->≠,且的图像不过第二象限(C )p: x=1, q:2x x=(D )p:a >1, q: ()log (01)a f x x a a =>≠,且在(0,)+∞上为增函数[解析]:由a >b 且c >d ⇒a c +>b+d ,而由a c +>b+d a >b 且c >d ,可举反例。
2010年安徽省高考数学试卷(理科)及答案
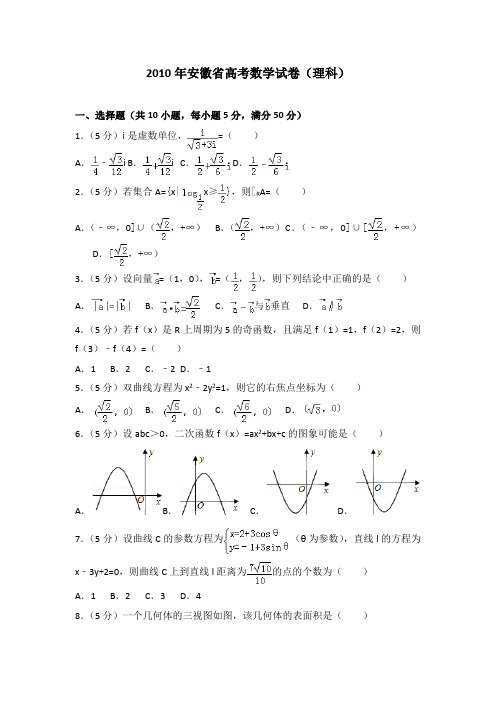
2010年安徽省高考数学试卷(理科)一、选择题(共10小题,每小题5分,满分50分)1.(5分)i是虚数单位,=()A.﹣i B.i C. D.2.(5分)若集合A={x|x≥},则∁R A=()A.(﹣∞,0]∪(,+∞)B.(,+∞)C.(﹣∞,0]∪[,+∞)D.[,+∞)3.(5分)设向量=(1,0),=(,),则下列结论中正确的是()A.B.C.与垂直D.4.(5分)若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)﹣f(4)=()A.1 B.2 C.﹣2 D.﹣15.(5分)双曲线方程为x2﹣2y2=1,则它的右焦点坐标为()A.B.C.D.6.(5分)设abc>0,二次函数f(x)=ax2+bx+c的图象可能是()A.B.C.D.7.(5分)设曲线C的参数方程为(θ为参数),直线l的方程为x﹣3y+2=0,则曲线C上到直线l距离为的点的个数为()A.1 B.2 C.3 D.48.(5分)一个几何体的三视图如图,该几何体的表面积是()A.372 B.360 C.292 D.2809.(5分)动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是()A.[0,1]B.[1,7]C.[7,12] D.[0,1]和[7,12]10.(5分)设{a n}是任意等比数列,它的前n项和,前2n项和与前3n项和分别为X,Y,Z,则下列等式中恒成立的是()A.X+Z=2Y B.Y(Y﹣X)=Z(Z﹣X)C.Y2=XZ D.Y(Y﹣X)=X(Z﹣X)二、填空题(共5小题,每小题5分,满分25分)11.(5分)命题“对任何x∈R,使得|x﹣2|+|x﹣4|>3”的否定是.12.(5分)(﹣)6展开式中,x3的系数等于.13.(5分)设x,y满足约束条件,若目标函数z=abx+y(a>0,b>0)的最大值为8,则a+b的最小值为.14.(5分)如图所示,程序框图(算法流程图)的输出值x为15.(5分)甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以A1,A2和A3表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B 表示由乙罐取出的球是红球的事件,则下列结论中正确的是(写出所有正确结论的编号).①;②;③事件B与事件A1相互独立;④A1,A2,A3是两两互斥的事件;⑤P(B)的值不能确定,因为它与A1,A2,A3中哪一个发生有关.三、解答题(共6小题,满分75分)16.(12分)设△ABC是锐角三角形,a,b,c分别是内角A,B,C所对边长,并且.(Ⅰ)求角A的值;(Ⅱ)若,求b,c(其中b<c).17.(12分)设a为实数,函数f(x)=e x﹣2x+2a,x∈R.(Ⅰ)求f(x)的单调区间与极值;(Ⅱ)求证:当a>ln2﹣1且x>0时,e x>x2﹣2ax+1.18.(12分)如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF ⊥FB,AB=2EF,∠BFC=90°,BF=FC,H为BC的中点.(1)求证:FH∥平面EDB;(2)求证:AC⊥平面EDB;(3)求二面角B﹣DE﹣C的大小.19.(13分)已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x 轴上,离心率e=.(1)求椭圆E的方程;(2)求∠F1AF2的平分线所在直线l的方程;(3)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.20.(13分)设数列a1,a2,…,a n,…中的每一项都不为0.证明:{a n}为等差数列的充分必要条件是:对任何n∈N,都有++…+=.21.(13分)品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.现设n=4,分别以a1,a2,a3,a4表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令X=|1﹣a1|+|2﹣a2|+|3﹣a3|+|4﹣a4|,则X是对两次排序的偏离程度的一种描述.(Ⅰ)写出X的可能值集合;(Ⅱ)假设a1,a2,a3,a4等可能地为1,2,3,4的各种排列,求X的分布列;(Ⅲ)某品酒师在相继进行的三轮测试中,都有X≤2,①试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);②你认为该品酒师的酒味鉴别功能如何?说明理由.2010年安徽省高考数学试卷(理科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)(2010•安徽)i是虚数单位,=()A.﹣i B.i C. D.【分析】通常分子与分母同时乘以分母的共轭复数,然后利用复数的代数运算,结合i2=﹣1得结论.【解答】解:===+,故选B.2.(5分)(2010•安徽)若集合A={x|x≥},则∁R A=()A.(﹣∞,0]∪(,+∞)B.(,+∞)C.(﹣∞,0]∪[,+∞)D.[,+∞)【分析】欲求A的补集,必须先求集合A,利用对数的单调性求集合A,然后得结论,【解答】解:∵x≥,∴x≥,∴0<x,∴∁R A=(﹣∞,0]∪(,+∞).故选A.3.(5分)(2010•安徽)设向量=(1,0),=(,),则下列结论中正确的是()A.B.C.与垂直D.【分析】本题考查的知识点是向量的模,及用数量积判断两个平面向量的垂直关系,由,我们易求出向量的模,结合平面向量的数量坐标运算,对四个答案逐一进行判断,即可得到答案.【解答】解:∵,∴=1,=,故不正确,即A错误∵•=≠,故B错误;∵﹣=(,﹣),∴(﹣)•=0,∴与垂直,故C正确;∵,易得不成立,故D错误.故选C4.(5分)(2010•安徽)若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)﹣f(4)=()A.1 B.2 C.﹣2 D.﹣1【分析】利用函数奇偶性以及周期性,将3或4的函数值问题转化为1或2的函数值问题求解即可.【解答】解:∵若f(x)是R上周期为5的奇函数∴f(﹣x)=﹣f(x),f(x+5)=f(x),∴f(3)=f(﹣2)=﹣f(2)=﹣2,f(4)=f(﹣1)=﹣f(1)=﹣1,∴f(3)﹣f(4)=﹣2﹣(﹣1)=﹣1.故选D.5.(5分)(2010•安徽)双曲线方程为x2﹣2y2=1,则它的右焦点坐标为()A.B.C.D.【分析】把双曲线方程化为标准方程可分别求得a和b,进而根据c=求得c,焦点坐标可得.【解答】解:双曲线的,,,∴右焦点为.故选C6.(5分)(2010•安徽)设abc>0,二次函数f(x)=ax2+bx+c的图象可能是()A.B.C.D.【分析】当a>0时,二次函数开口向上,判断C、D中c的符号,再确定b的符号,判断C、D的正误,当a<0时,同样的方法判断A、B的正误.【解答】解:当a>0时,因为abc>0,所以b、c同号,由(C)(D)两图中可知c<0,故b<0,∴,即函数对称轴在y轴右侧,C不正确,选项(D)符合题意.显然a<0时,开口向下,因为abc>0,所以b、c异号,对于A、由图象可知c<0,则b>0,对称轴,A不正确;对于B,c>0,对称轴,B选项不正确.故选D.7.(5分)(2010•安徽)设曲线C的参数方程为(θ为参数),直线l的方程为x﹣3y+2=0,则曲线C上到直线l距离为的点的个数为()A.1 B.2 C.3 D.4【分析】由题意将圆C和直线l先化为一般方程坐标,然后再计算曲线C上到直线l距离为的点的个数.【解答】解:化曲线C的参数方程为普通方程:(x﹣2)2+(y+1)2=9,圆心(2,﹣1)到直线x﹣3y+2=0的距离,直线和圆相交,过圆心和l平行的直线和圆的2个交点符合要求,又,在直线l的另外一侧没有圆上的点符合要求,故选B.8.(5分)(2010•安徽)一个几何体的三视图如图,该几何体的表面积是()A.372 B.360 C.292 D.280【分析】三视图很容易知道是两个长方体的组合体,得出各个棱的长度.即可求出组合体的表面积.【解答】解:该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和.S=2(10×8+10×2+8×2)+2(6×8+8×2)=360.故选B.9.(5分)(2010•安徽)动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是()A.[0,1]B.[1,7]C.[7,12] D.[0,1]和[7,12]【分析】由动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似,由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在[0,12]变化时,点A的纵坐标y关于t(单位:秒)的函数的单调性的变化,从而得单调递增区间.【解答】解:设动点A与x轴正方向夹角为α,则t=0时,每秒钟旋转,在t∈[0,1]上,在[7,12]上,动点A的纵坐标y关于t都是单调递增的.故选D.10.(5分)(2010•安徽)设{a n}是任意等比数列,它的前n项和,前2n项和与前3n项和分别为X,Y,Z,则下列等式中恒成立的是()A.X+Z=2Y B.Y(Y﹣X)=Z(Z﹣X)C.Y2=XZ D.Y(Y﹣X)=X(Z﹣X)【分析】取一个具体的等比数列验证即可.【解答】解:取等比数列1,2,4,令n=1得X=1,Y=3,Z=7代入验算,只有选项D满足.故选D二、填空题(共5小题,每小题5分,满分25分)11.(5分)(2010•安徽)命题“对任何x∈R,使得|x﹣2|+|x﹣4|>3”的否定是存在x∈R,使得|x﹣2|+|x﹣4|≤3.【分析】全称命题的否定是特称命题,只须将全称量词“任何”改为存在量词“存在”,并同时把“|x﹣2|+|x﹣4|>3”否定.【解答】解:全称命题的否定是特称命题,∴命题“对任何x∈R,使得|x﹣2|+|x﹣4|>3”的否定是:存在x∈R,使得|x﹣2|+|x﹣4|≤3.故填:存在x∈R,使得|x﹣2|+|x﹣4|≤3.12.(5分)(2010•安徽)(﹣)6展开式中,x3的系数等于15.【分析】根据题意,易得其二项展开式,分析可得,当r=2时,有C62•()4•(﹣)2=15x3,即可得答案.=C6r•()6﹣r•(﹣)【解答】解:根据题意,易得其二项展开式的通项为T r+1r,当r=2时,有C62•()4•(﹣)2=15x3,则x3的系数等于15,故答案为15.13.(5分)(2010•安徽)设x,y满足约束条件,若目标函数z=abx+y (a>0,b>0)的最大值为8,则a+b的最小值为4.【分析】本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件,画出满足约束条件的可行域,再根据目标函数z=abx+y(a>0,b>0)的最大值为8,求出a,b的关系式,再利用基本不等式求出a+b的最小值.【解答】解:满足约束条件的区域是一个四边形,如下图4个顶点是(0,0),(0,2),(,0),(1,4),由图易得目标函数在(1,4)取最大值8,即8=ab+4,∴ab=4,∴a+b≥2=4,在a=b=2时是等号成立,∴a+b的最小值为4.故答案为:414.(5分)(2010•安徽)如图所示,程序框图(算法流程图)的输出值x为12【分析】模拟执行程序框图,依次写出每次循环得到的x的值,当x=12时满足条件x>8,退出循环,输出x的值为12.【解答】解:模拟执行程序框图,可得x=1满足条件x是奇数,x=2不满足条件x是奇数,x=4,不满足条件x>8,x=5满足条件x是奇数,x=6,不满足条件x>8,x=7满足条件x是奇数,x=8,不满足条件x>8,x=9满足条件x是奇数,x=10,不满足条件x是奇数,x=12,满足条件x>8,退出循环,输出x的值为12.15.(5分)(2010•安徽)甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以A1,A2和A3表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是②④(写出所有正确结论的编号).①;②;③事件B与事件A1相互独立;④A1,A2,A3是两两互斥的事件;⑤P(B)的值不能确定,因为它与A1,A2,A3中哪一个发生有关.【分析】本题是概率的综合问题,掌握基本概念,及条件概率的基本运算是解决问题的关键.本题在A1,A2,A3是两两互斥的事件,把事件B的概率进行转化P (B)=P(B|•A1)+P(B•A2)+P(B•A3),可知事件B的概率是确定的.【解答】解:易见A1,A2,A3是两两互斥的事件,.故答案为:②④三、解答题(共6小题,满分75分)16.(12分)(2010•安徽)设△ABC是锐角三角形,a,b,c分别是内角A,B,C所对边长,并且.(Ⅰ)求角A的值;(Ⅱ)若,求b,c(其中b<c).【分析】(1)先根据两角和与差的正弦公式展开得到角A的正弦值,再由角A 的范围确定角A的值.(2)先根据向量数量积的运算和角A的值得到cb=24,再由a=2和余弦定理可求出b,c的值.【解答】解:(1)因为sin2A=(()+sin2B==所以sinA=±.又A为锐角,所以A=(2)由可得,cbcosA=12 ①由(1)知A=,所以cb=24 ②由余弦定理知a2=b2+c2﹣2bccosA,将a=2及①代入可得c2+b2=52③③+②×2,得(c+b)2=100,所以c+b=10因此,c,b是一元二次方程t2﹣10t+24=0的两根解此方程并由c>b知c=6,b=417.(12分)(2010•安徽)设a为实数,函数f(x)=e x﹣2x+2a,x∈R.(Ⅰ)求f(x)的单调区间与极值;(Ⅱ)求证:当a>ln2﹣1且x>0时,e x>x2﹣2ax+1.【分析】(Ⅰ)由f(x)=e x﹣2x+2a,x∈R,知f′(x)=e x﹣2,x∈R.令f′(x)=0,得x=ln2.列表讨论能求出f(x)的单调区间区间及极值.(Ⅱ)设g(x)=e x﹣x2+2ax﹣1,x∈R,于是g′(x)=e x﹣2x+2a,x∈R.由(1)知当a>ln2﹣1时,g′(x)最小值为g′(ln2)=2(1﹣ln2+a)>0.于是对任意x ∈R,都有g′(x)>0,所以g(x)在R内单调递增.由此能够证明e x>x2﹣2ax+1.【解答】(Ⅰ)解:∵f(x)=e x﹣2x+2a,x∈R,∴f′(x)=e x﹣2,x∈R.令f′(x)=0,得x=ln2.于是当x变化时,f′(x),f(x)的变化情况如下表:x(﹣∞,ln2)ln2(ln2,+∞)f′(x)﹣0+f(x)单调递减2(1﹣ln2+a)单调递增故f(x)的单调递减区间是(﹣∞,ln2),单调递增区间是(ln2,+∞),f(x)在x=ln2处取得极小值,极小值为f(ln2)=e ln2﹣2ln2+2a=2(1﹣ln2+a),无极大值.(Ⅱ)证明:设g(x)=e x﹣x2+2ax﹣1,x∈R,于是g′(x)=e x﹣2x+2a,x∈R.由(1)知当a>ln2﹣1时,g′(x)最小值为g′(ln2)=2(1﹣ln2+a)>0.于是对任意x∈R,都有g′(x)>0,所以g(x)在R内单调递增.于是当a>ln2﹣1时,对任意x∈(0,+∞),都有g(x)>g(0).而g(0)=0,从而对任意x∈(0,+∞),g(x)>0.即e x﹣x2+2ax﹣1>0,故当a>ln2﹣1且x>0时,e x>x2﹣2ax+1.18.(12分)(2010•安徽)如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H为BC的中点.(1)求证:FH∥平面EDB;(2)求证:AC⊥平面EDB;(3)求二面角B﹣DE﹣C的大小.【分析】(1)设AC于BD交于点G,则G为AC的中点,连接EG,GH,又H为BC的中点,可得四边形EFHG为平行四边形,然后利用直线与平面平行判断定理进行证明;(2)因为四边形ABCD为正方形,有AB⊥BC,又EF∥AB,可得EF⊥BC,要证FH⊥平面ABCD,FH⊥平面ABCD,从而求解.(3)在平面CDEF内过点F作FK⊥DE交DE的延长线与k,可知∠FKB为二面角B﹣DE﹣C的一个平面角,然后设EF=1,在直角三角形中进行求证.【解答】证明:(1)设AC于BD交于点G,则G为AC的中点,连接EG,GH,又H为BC的中点,∴GH∥AB且GH=AB,又EF∥AB且EF=AB,∴EF∥GH且EF=GH,∴四边形EFHG为平行四边形∴EG∥FH,而EG⊂平面EDB,∴FH∥平面EDB.(2)由四边形ABCD为正方形,有AB⊥BC,又EF∥AB,∴EF⊥BC而EF⊥FB,∴EF⊥平面BFC,∴EF⊥FH,∴AB⊥FH,又BF=FC,H为BC的中点,∴FH⊥BC∴FH⊥平面ABCD,∴FH⊥BC,FH⊥AC,又FH∥EG,∴AC⊥EG又AC⊥BD,EG∩BD=G,∴AC⊥平面EDB,(3)EF⊥FB,∠BFC=90°,∴BF⊥平面CDEF,在平面CDEF内过点F作FK⊥DE交DE的延长线与k,则∠FKB为二面角B﹣DE﹣C的一个平面角,设EF=1,则AB=2,FC=,DE=,又EF∥DC,∴∠KEF=∠EDC,∴sin∠EDC=sin∠KEF=,∴FK=EFsin∠KEF=,tan∠FKB==,∴∠FKB=60°,∴二面角B﹣DE﹣C为60°.19.(13分)(2010•安徽)已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=.(1)求椭圆E的方程;(2)求∠F1AF2的平分线所在直线l的方程;(3)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.【分析】(1)设出椭圆方程,根据椭圆E经过点A(2,3),离心率,建立方程组,求得几何量,即可得到椭圆E的方程;(2)求得AF1方程、AF2方程,利用角平分线性质,即可求得∠F1AF2的平分线所在直线l的方程;(3)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,设出直线BC方程代入,求得BC中点代入直线2x﹣y﹣1=0上,即可得到结论.【解答】解:(1)设椭圆方程为∵椭圆E经过点A(2,3),离心率∴,∴a2=16,b2=12∴椭圆方程E为:;(2)F1(﹣2,0),F2(2,0),∵A(2,3),∴AF1方程为:3x﹣4y+6=0,AF2方程为:x=2设角平分线上任意一点为P(x,y),则.得2x﹣y﹣1=0或x+2y﹣8=0∵斜率为正,∴直线方程为2x﹣y﹣1=0;(3)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,∴∴直线BC方程为代入得x2﹣mx+m2﹣12=0,∴BC中点为代入直线2x﹣y﹣1=0上,得m=4.∴BC中点为(2,3)与A重合,不成立,所以不存在满足题设条件的相异的两点.20.(13分)(2010•安徽)设数列a1,a2,…,a n,…中的每一项都不为0.证明:{a n}为等差数列的充分必要条件是:对任何n∈N,都有++…+=.【分析】先证必要性;设数列a n的公差为d,若d=0,则所述等式显然成立.若d≠0,则==.再用数学归纲法证明充分性:对任何n∈N,都有++…+=,{a n}是公差为d的等差数列.【解答】证明:先证必要性设数列a n的公差为d,若d=0,则所述等式显然成立.若d≠0,则===.再证充分性:用数学归纳法证明:①设所述的等式对一切n∈N都成立,首先在等式①两端同时乘a1a2a3,即得a1+a3=2a2,所以a1,a2,a3成等差数列,记公差为d,则a2=a1+d.②假设a k=a1+(k﹣1)d,当n=k+1时,观察如下二等式=②,=,将②代入③得,在该式两端同时乘a1a k a k+1,得(k﹣1)a k+1+a1=ka k,把a k=a1+(k﹣1)d代入后,整理得a k+1=a1+kd.由数学归纳法原理知对任何n∈N,都有++…+=.所以,{a n}是公差为d的等差数列.21.(13分)(2010•安徽)品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.现设n=4,分别以a1,a2,a3,a4表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令X=|1﹣a1|+|2﹣a2|+|3﹣a3|+|4﹣a4|,则X是对两次排序的偏离程度的一种描述.(Ⅰ)写出X的可能值集合;(Ⅱ)假设a1,a2,a3,a4等可能地为1,2,3,4的各种排列,求X的分布列;(Ⅲ)某品酒师在相继进行的三轮测试中,都有X≤2,①试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);②你认为该品酒师的酒味鉴别功能如何?说明理由.【分析】(1)X的可能取值集合为{0、2、4、6、8},在1、2、3、4中奇数与偶数各有两个,a2,a4中的奇数个数等于a1,a3中的偶数个数,得到|1﹣a1|+|3﹣a3|与|2﹣a2|+|4﹣a4|的奇偶性相同,得到结论.(2)可以用列表或者树状图列出1、2、3、4的一共24种排列,计算每种排列下的X的值,算出概率,写出分布列.(3)做出三轮测试都有X≤2的概率,记做P,做出概率的值和已知量进行比较,得到结论,【解答】解:(1)X的可能取值集合为{0、2、4、6、8}∵在1、2、3、4中奇数与偶数各有两个,∴a2,a4中的奇数个数等于a1,a3中的偶数个数,∴|1﹣a1|+|3﹣a3|与|2﹣a2|+|4﹣a4|的奇偶性相同,∴X=(|1﹣a1|+|3﹣a3|)+(|2﹣a2|+|4﹣a4|)必为偶数,X的值非负,且易知其值不大于8,∴X的可能取值集合为{0、2、4、6、8}(2)可以用列表或者树状图列出1、2、3、4的一共24种排列,计算每种排列下的X的值,在等可能的假定下,得到P(X=0)=P(X=2)=P(X=4)=P(X=6)=P(X=8)=(3)①首先P(X≤2)=P(X=0)+P(X=2)==将三轮测试都有X≤2的概率记做P,有上述结果和独立性假设得P==,②由于P=<是一个很小的概率,这表明仅凭随机猜测得到三轮测试都有X≤2的结果的可能性很小,∴我们认为该品酒师确实有良好的鉴别功能,不是靠随机猜测.。
2009年高考安徽数学(理科)试题及参考答案

解析几何易错题集一、选择题:1. 若双曲线22221x y a b-=-的离心率为54,则两条渐近线的方程为A0916X Y ±= B 0169X Y ±= C 034X Y ±= D 043X Y±= 2. 椭圆的短轴长为2,长轴是短轴的2倍,则椭圆的中心到其准线的距离是AB C D 3. 过定点(1,2)作两直线与圆2222150x y kx y k ++++-=相切,则k 的取值范围是A k>2B -3<k<2C k<-3或k>2D 以上皆不对4.设双曲线22221(0)x y a b a b-=>>的半焦距为C ,直线L 过(,0),(0,)a b 两点,已知原点到直线L,则双曲线的离心率为A 2B 2C D5.已知二面角βα--l 的平面角为θ,PA α⊥,PB β⊥,A ,B 为垂足,且PA=4,PB=5,设A 、B 到二面角的棱l 的距离为别为y x ,,当θ变化时,点),(y x 的轨迹是下列图形中的A B C D6.若曲线y =与直线(2)y k x =-+3有两个不同的公共点,则实数 k 的取值范围是A 01k ≤≤B 304k ≤≤C 314k -<≤ D 10k -<≤ 7. P(-2,-2)、Q(0,-1)取一点R(2,m)使︱PR ︱+︱RQ ︱最小,则m=( )A21 B 0 C –1 D -348.能够使得圆x 2+y 2-2x+4y+1=0上恰好有两个点到直线2x+y+c=0距离等于1的一个值为( )A 2 B5 C 3 D 359. P 1(x 1,y 1)是直线L :f(x,y)=0上的点,P 2(x 2 ,y 2)是直线L 外一点,则方程f(x,y)+f(x 1,y 1)+f(x2,y 2)=0所表示的直线( )A 相交但不垂直B 垂直C 平行D 重合10.已知圆()3-x 2+y 2=4 和 直线y=mx 的交点分别为P 、Q 两点,O 为坐标原点, 则︱O P ︱·︱OQ ︱=( ) A 1+m 2B215m + C 5 D 1011.在圆x 2+y 2=5x 内过点(25,23)有n 条弦的长度成等差数列,最短弦长为数列首项a 1,最长弦长为a n ,若公差d ∈⎥⎦⎤⎝⎛31,61,那么n 的取值集合为( )A {}654、、B {}9876、、、C {}543、、D {}6543、、、12.平面上的动点P 到定点F(1,0)的距离比P 到y 轴的距离大1,则动点P 的轨迹方程为( ) A y 2=2x B y 2=2x 和 ⎩⎨⎧≤=00x y C y 2=4x D y 2=4x 和⎩⎨⎧≤=0x y 13.设双曲线22a x -22b y =1与22by -22a x =1(a >0,b >0)的离心率分别为e 1、e 2,则当a 、 b变化时,e 21+e 22最小值是( )A 4 B 42 C 2 D 214.双曲线92x -42y =1中,被点P(2,1)平分的弦所在直线方程是( )A 8x-9y=7B 8x+9y=25C 4x-9y=16D 不存在 15.已知α是三角形的一个内角,且sin α+cos α=51则方程x 2sin α-y 2cos α=1表示( ) A 焦点在x 轴上的双曲线 B 焦点在y 轴上的双曲线 C 焦点在x 轴上的椭圆 D 焦点在y 轴上的椭圆16.过抛物线的焦点F 作互相垂直的两条直线,分别交准线于P 、Q 两点,又过P 、Q 分别作抛物线对称轴OF 的平行线交抛物线于M ﹑N 两点,则M ﹑N ﹑F 三点A 共圆B 共线C 在另一条抛物线上D 分布无规律 17.曲线xy=1的参数方程是( )A x=t 21 B x=Sin α C x=cos α D x=tan α y=t21- y=csc α y=See α y=cot α18.已知实数x ,y 满足3x 2+2y 2=6x ,则x 2+y 2的最大值是( ) A 、29B 、4C 、5D 、2 19.双曲线x 2n -y 2=1(n>1)的焦点为F 1、F 2,,P 在双曲线上 ,且满足:|PF 1|+|PF 2|=2n+2 ,则ΔPF 1F 2的面积是 A 、1 B 、2 C 、4 D 、1220.过点(0,1)作直线,使它与抛物线x y 42=仅有一个公共点,这样的直线有( )A.1条B.2条C. 3条D. 0条21.(已知动点P (x ,y )满足 ,则P 点的轨迹是 ( )A 、直线 B 、抛物线 C 、双曲线 D 、椭圆22.在直角坐标系中,方程()()02312=--+-+y x x y x 所表示的曲线为( ) A .一条直线和一个圆 B .一条线段和一个圆 C .一条直线和半个圆 D .一条线段和半个圆23.设坐标原点为O ,抛物线22y x =与过焦点的直线交于A 、B 两点,则OA OB ⋅=( )A .34 B .34- C .3 D .-3 24.直线134=+y x 与椭圆191622=+y x 相交于A 、B 两点,椭圆上的点P 使PAB ∆的面积等于12,这样的点P 共有( )个A .1 B .2 C .3 D .425.过点(1,2)总可作两条直线与圆2222150x y kx y k ++++-=相切,则实数k 的取值范围是( )A 2k > B 32k -<< C 3k <-或2k > D 都不对 26.已知实数x ,y 满足250x y ++=A B C . D .27.若直线y x b =+与曲线224(0)x y y +=≥有公共点,则b 的取值范围是A . [2,2]-B . [0,2]C .D . [-28.设f(x )= x 2+ax+b ,且1≤f (-1)≤2,2≤f (1)≤4,则点(a ,b )在aOb 平面上的区域的面积是 A .12 B .1 C .2 D .9229.当x 、y 满足约束条件0,,20x y x x y k ≥⎧⎪≤⎨⎪++≤⎩(k 为常数)时,能使3z x y =+的最大值为12的k 的|1143|)2()1(522-+=-+-y x y x值为 A .-9 B .9 C .-12 D .1230.已知关于t 的方程20t tx y ++=有两个绝对值都不大于1的实数根,则点(,)P x y 在坐标平面内所对应的区域的图形大致是31.能够使得圆222410x y x y +-++=上恰有两个点到直线20x y c ++=距离等于1的c 的一个值为( ) A .2C .3 D. 32.抛物线y=4x 2的准线方程为( )A 、x=-1B 、y=-1C 、x=161-D 、y=161- 33.对于抛物线C :y 2=4x ,称满足y 02<4x 0的点M(x 0,y 0)在抛物线内部,若点M(x 0,y 0)在抛物线内部,则直线l :y 0y=2(x+x 0)与曲线C ( )A 、恰有一个公共点B 、恰有两个公共点C 、可能有一个公共点也可能有2个公共点D 、无公共点 34.直线l 过点,那么直线l 倾斜角α的取值范围是( )。
2003年安徽高考理科数学

2003年安徽高考理科数学
2003年安徽高考理科数学是指2003年安徽省高考理科的数学试卷,主要考察高中数学的知识和技能。
2003年安徽高考理科数学其内容一般会包括但不限于以下方面:
1.代数:包括方程、不等式、函数、数列等内容。
2.几何:如平面几何、立体几何、解析几何等。
3.三角函数与复数:如三角函数的性质、图像和变换,复数的运算等。
4.概率与统计:涉及概率论初步,统计初步等内容。
5.微积分初步:包括极限、导数等。
以下是试卷中的具体题目示例:
1.选择题:已知函数f(x)的定义域为(-1,1),则函数f(x+1/2)的定义域是()
2. A.(-3/2,-1/2) B.(-3/2,1/2) C.(-1/2,3/2) D.(-2,0)
3.解答题:已知数列{ an } 是公差不为0的等差数列,a1=1,且a1,a2,
a5成等比数列,求数列 { an } 的通项公式。
总结来说,“2003年安徽高考理科数学”是一份测试考生对高中数学知识的掌握和运用能力的试卷,要求考生具有扎实的数学基础和较高的逻辑推理能力。
安徽省高考理科数学试题及答案

普通高等学校招生全国统一考试(安徽卷)数学(理科)参考公式:如果事件A 与B 互斥,那么()()()P A B P A P B +=+; 标准差:222121[()()()n s x x x x x x n=-+-++-其中121()n x x x x n=+++.一、选择题:本大题共10个小题;每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的。
(1)设i 是虚数单位,则复数21ii-在复平面内所对应的点位于 (A )第一象限 (B )第二象限(C )第三象限(D )第四象限211ii i=-+-,选B. (2)下列函数中,既是偶函数又存在零点的是(A )y cos x = (B )y sin x = (C )y ln x = (D )21y x =+ 选A.(3)设:12p x <<,:21xq > ,则p 是q 成立的(A )充分不必要条件 (B )必要不充分条件(C )充分必要条件 (D )既不充分也不必要条件 选A.4、下列双曲线中,焦点在y 轴上且渐近线方程为2y x =±的是( )(A )2214y x -= (B )2214x y -= (C )2214y x -= (D )2214x y -= 选.5、已知m ,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是( ) (A )若α,β垂直于同一平面,则α与β平行 (B )若m ,n 平行于同一平面,则m 与n 平行(C )若α,β不平行,则在α内不存在与β平行的直线(D )若m ,n 不平行,则m 与n 不可能垂直于同一平面 选D.6、若样本数据1x ,2x ,⋅⋅⋅,10x 的标准差为8,则数据121x -,221x -,⋅⋅⋅,1021x -的标准差为( )(A )8 (B )15 (C )16 (D )32若样本数据1x ,2x ,⋅⋅⋅,10x 的方差为2S ,数据121x -,221x -,⋅⋅⋅,1021x -的方差为20S ,则2204S S =,所以所求标准差为16,选C.7、一个四面体的三视图如图所示,则该四面体的表面积是( ) (A )13+(B )23+(C )122+(D )22侧(左)视图111122如图,面ABC ⊥面ABD ,2AC BC AD BD ====,2AB =,E 是AB 的中点,选B.三角形,已知向量a ,b8、C ∆AB 是边长为2的等边满足2a AB =,C 2a b A =+,则下列结论正确的是( )(A )1b = (B )a b ⊥ ()4C a b -⊥B(C )1a b ⋅= (D )因为C ∆AB 是边长为2的等边三角形,所以C 2(2)4cos 602a a b AB⋅A =⋅+==,即2(2)21a a b a a b ⋅+=+⋅=,又|||2|2a AB ==,所以||1a =,因此1a b ⋅=- ;因为BC AC AB b =-=,所以||2b =,因此2(4)C (4)40a b a b b a b b -⋅B =-⋅=⋅-=,所以选D.另:可画图,得(A)(B)(C)均错,选D. 9、函数()()2ax bf x x c +=+的图象如图所示,则下列结论成立的是( )(A )0a >,0b >,0c < (B )0a <,0b >,0c > (C )0a <,0b >,0c < (D )0a <,0b <,0c < 由()()2ax bf x x c +=+的定义域知0c ->,即0c <;由(0)0f >知0b >;()()22222ax bx ac bcf x x c --+-'=+,则22220ax bx ac bc --+-=有一解为c -,另一解为0(0,)x c ∈- ;而22220ax bx ac bc --+-<的解为0x x c <<-,所以0a ->,即0a <;选C.10、已知函数()()sin f x x ωϕ=A +(A ,ω,ϕ均为正的常数)的最小正周期为π,当23x π=时,函数()f x 取得最小值,则下列结论正确的是( ) (A )()()()220f f f <-< (B )()()()022f f f <<-(C )()()()202f f f -<< (D )()()()202f f f <<-作图知,选(A)二、填空题:本大题共5小题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年普通高等学校招生全国统一考试(安徽卷)
数学(理科)试题
本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷1至2页。
第II 卷3 至4页。
全卷满分150分,考试时间120分钟。
考生注意事项:
1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名,座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2.答第I 卷时、每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮檫干净后,在选涂其他答案标号。
3.答第II 卷时,必须用直径0.5毫米黑色黑水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后在用0.5毫米的黑色墨色签字笔清楚。
必须在标号所指示的答题区域作答,超出答题卡区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.考试结束,务必将试题卷和答题卡一并上交。
参考公式:
S 表示底面积,h 表示底面的高
如果事件A 、B 互斥,那么 棱柱体积 V S h =
P(A+B)=P(A)+P (B) 棱锥体积 13V S h =
第I 卷 (选择题 共50分)
一.选择题:本大题10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)i 是虚数单位,若17(,)2i a bi a b R i
+=+∈-,则乘积ab 的值是( ) (A )-15 (B )-3 (C )3 (D )15
(2)若集合{}21|21|3,0,3x A x x B x x ⎧+⎫=-<=<⎨⎬-⎩⎭
则A ∩B 是( )
(A ) 11232x x x ⎧⎫-<<-<<⎨⎬⎩⎭或 (B) {}
23x x << (C) 122x x ⎧⎫-<<⎨⎬⎩⎭
(D) 112x x ⎧⎫-<<-⎨⎬⎩
⎭
(3( )
(A )22124x y -= (B )22142x y -= (C )22146x y -= (D )221410
x y -=
(4)下列选项中,p 是q 的必要不充分条件的是( )
(A )p:a c +>b+d , q:a >b 且c >d
(B )p:a >1,b>1, q:()(10)x f x a b a =-≠>的图像不过第二象限
(C )p: x=1, q:2
x x =
(D )p:a >1, q: ()log (10)a f x x a =≠>在(0,)+∞上为增函数
(5)已知{}n a 为等差数列,1a +3a +5a =105,246a a a ++=99.以n S 表示{}n a 的前n 项和,则使得n S 达到最大值的n 是( )
(A )21 (B )20 (C )19 (D ) 18
(6)设a <b,函数2()()y x a x b =--的图像可能是( )
(7)若不等式组03434x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域被直线43y kx =+分为面积相等的两部分,则k 的值是( ) (A )73 (B ) 37 (C )43 (D ) 34
(8
)已知函数()cos (0)f x x x ωωω=+>,()y f x =的图像与直线2y =的两个相邻交点的距离等于π,则()f x 的单调区间是( )
(A )5[,],1212
k k k Z ππππ-+∈ (B )511[,],1212k k k Z ππππ++∈ (C )[,],36k k k Z ππππ-+∈ (D )2[,],63
k k k Z ππππ++∈ (9)已知函数()f x 在R 上满足2()2(2)88f x f x x x =--+-,则曲线()y f x =在点(1,(1))f 处的切线
方程是( )
(A )21y x =- (B )y x = (C )32y x =- (D )23y x =-+
(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( )
(A )175 (B ) 275 (C )375 (D )475
二.填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应
位置。
(11)若随机变量X ~2(,)μσ,则()P X μ≤=________.
(12)以直角坐标系的原点为极点,x 轴的正半轴为极轴,并在两种坐标系中取相同
的长度单位。
已知直线的极坐标方程为()4R πθρ=∈,它与曲线12cos 22sin x y αα
=+⎧⎨=+⎩(α为参数)相交于两点A 和B ,则|AB|=_______.
(13) 程序框图(即算法流程图)如图所示,其输出结果是
_______.
(14)给定两个长度为1的平面向量OA 和OB ,它们的夹角为120o
. 如图所示,点C 在以O 为圆心的圆
弧上变动.若,OC xOA yOB =+其中,x y R ∈,则x y +的最大值是=________. (15)对于四面体ABCD ,下列命题正确的是_________(写出所有正确命题的编
号)。
○
1相对棱AB 与CD 所在的直线异面; ○
2由顶点A 作四面体的高,其垂足是∆BCD 的三条高线的交点; ○
3若分别作∆ABC 和∆ABD 的边AB 上的高,则这两条高所在的直线异面; ○
4分别作三组相对棱中点的连线,所得的三条线段相交于一点; ○5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
三.解答题:本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤。
解答写在答题卡的指定区域内。
(16)(本小题满分12分)
在∆ABC 中,sin(C-A)=1, sinB=
13。
(I )求sinA 的值;
(II)设∆ABC 的面积。
(17)(本小题满分12分)某地有A 、B 、C 、D 四人先后感染了甲型H1N1流感,其中只有A 到过疫区.B 肯定是受A 感染的。
对于C ,因为难以断定他是受A 还是受B 感染的,于是假定他受A 和受B 感染的概率都是12。
同样也假定D 受A 、B 和C 感染的概率都是13。
在这种假定之下,B 、C 、D 中直接..受A 感染的人数X 就是一个随机变量。
写出X 的分布列(不要求写出计算过程),并求X 的均值(即数学期望).
(18)(本小题满分13分)如图,四棱锥F-ABCD 的底面ABCD 是菱形,其对角线AC=2,
AE 、CF 都与平面ABCD 垂直,AE=1,CF=2。
(I )求二面角B-AF-D 的大小;
(II )求四棱锥E-ABCD 与四棱锥F-ABCD 公共部分的体积。
(19)(本小题满分12分) 已知函数2()(2ln ),0f x x a x a x
=-+->,讨论()f x 的单调性.
(20)(本小题满分13分) 点00(,)P x y 在椭圆22
221(0)x y a b a b
+=>>上,00cos ,sin ,0.2x a y b πβββ==<<直线2l 与直线00122:1x y l x y a b
+=垂直,O 为坐标原点,直线OP 的倾斜角为α,直线2l 的倾斜角为γ. (I )证明: 点P 是椭圆22
221x y a b
+=与直线1l 的唯一交点; (II )证明:tan ,tan ,tan αβγ构成等比数列。
(21)(本小题满分13分)
首项为正数的数列{}n a 满足211(3),.4n n a a n N ++=+∈ (I )证明:若1a 为奇数,则对一切2,n n a ≥都是奇数; (II )若对一切n N +∈都有1n n a a +>,求1a 的取值范围。
