验证性因子分析
验证性因子分析..

9
单因子模型(测量模型)
父母社 经地位
λ1 X1 δ1 λ2 X2 δ2 λ3 X3 δ3
观测变量 潜在变量 路 相 径 关
10
Table 1 相关系数矩阵
X1 X2 X3 Y1 Y2
X1 1.0000 0.5902 0.5461 0.2852 0.2701
X2
X3
Y1
Y2
1.0000 0.4509 1.0000 0.2377 0.2349 1.0000 0.2269 0.2203 0.6759 1.0000
13
Slight ____
Slight ____
Quite ____
Exremely ____ Limited Selection
2 验证性因子分析的基本过程
理论构建 模型设定 模型识别 模型估计 模型评价 模型修正
14
φ12
ξ1
ξ2
X1
x2
x3
y2
y2
δ1
δ2
δ3
δ4
δ5
RMR 残差平方根
反应理论假设模型 整体残差
<0.05, 越接近0越好
CFA可计算模型拟合优度指标,以验证因子模型是否 适合样本资料的相关结构; 通过CFA,可检查因子结构与可靠度 (测量信度); CFA可提供信度及效度(收敛效度与区分效度)分析。 如上例:相关系数高,可知测量结果应具有一致性。
11
(二)评价信度与构念效度
CFA可以使用模型拟合优度统计量(如χ2)与相关拟 合优度指标(GFI、AGFI)来衡量变量的信度与 (reliability)与效度(validity)。
0.5461 corr ( X 1 , X 3 ) corr (111 1 , 311 3 ) 1131 0.714
信度效度分析结构方程模型验证性因子分析

信度效度分析结构方程模型验证性因子分析信度效度分析结构方程模型是一种统计方法,用于评估一个测量工具(如问卷或量表)的信度和效度。
验证性因子分析是使用结构方程模型的一种方法,用于验证假设的因素结构。
本文将介绍信度效度分析结构方程模型和验证性因子分析的步骤和应用,以及一些相关的注意事项。
首先,我们将介绍信度效度分析结构方程模型的步骤。
该模型可以用于评估测量工具的信度和效度,以确定它是否能够准确地测量所需的概念。
1.确定研究目的和研究问题:在进行分析之前,需要明确研究目的和研究问题。
这将有助于确定所需的测量工具和相关的概念。
2.收集数据:然后,需要收集与研究问题相关的数据。
这可以通过调查问卷、观察或其他适当的方法来实现。
3. 选择合适的统计软件:进行信度效度分析结构方程模型分析时,选择合适的统计软件是很重要的。
一些常用的软件包括AMOS、Mplus和LISREL。
4.构建测量模型:根据所选择的测量工具,构建一个测量模型。
这个模型将包括所需的概念和相关的测量项目。
5. 评估信度:评估信度是评估测量工具的一致性和稳定性。
常用的信度分析方法包括内部一致性(如Cronbach's α系数)和重测信度(如测试-重新测试法)。
6.评估效度:评估效度是评估测量工具的有效性和准确性。
常用的效度分析方法包括内部效度(如因子分析)和外部效度(与其他测量工具或标准进行比较)。
7.进行结构方程模型:一旦信度和效度得到评估,可以进行结构方程建模。
这将用于验证因素结构和模型拟合。
8.评估模型拟合:评估模型拟合是验证性因子分析的关键一步。
常用的指标包括χ²值、自由度、比例指数(CFI)、增量拟合指数(IFI)、均方根误差逼近指数(RMSEA)等。
9.修正模型:如果模型拟合不佳,需要进行适当的修正。
这可能包括删除不显著的路径、修正误差项相关性等。
10.解释和报告结果:最后,需要解释和报告分析结果。
这将包括变量之间的关系、可信度和效度的指标以及任何必要的修正。
验证性因子分析

• 一、基本原理 • 二、基本概念 • 三、实例分析
一、基本原理
• 结构方程模式(Structural Equation Models, 简称SEM),早期称为线性结构方程模式 (Linear Structural Relationships,简称 LISREL)或称为共变量结构分析 (Covariance Structure Analysis)。
1
2
31 41
X3
X4
3
4
外生变量与内生变量
• 外生变量(exogenous observable)是指那 些在模型或系统中,只起解释变量作用的变量, 即作为自变量存在的部分。
• 内生变量(endogenous variables)是指模型 中被影响或解释的变量
• 无论外生变量还是内生变量都可能是潜在变量
• 主要目的在于检验潜在变量(Latent variables) 和外显变量(Manifest variable, 又称观察变量)之关系与数个潜在变量间的因 果关系。
• 它结合了因素分析(factor analysis)与路径 分析(path analysis),包涵测量与结构模式。
Amos统計模式
常用图标
• 潜变量或因子
• 观察变量或指标
• 单向影响/效应 • 弧形:相关关系 • 内生潜变量未被解释的部
分 • 测量误差
模式组成
測量模 式
δ1
X1
ξ1
δ2
X2
δ3
X3
ξ2
δ4
X4
结构模式
Y1
ε1
ξ3
Y2
ε2
常用评价指标
指标(侯杰泰列举39种) Chi-Square
AMOS做验证性因子分析

AMOS做验证性因子分析验证性因子分析(Confirmatory factor analysis, CFA)是一种统计方法,用于检验研究者构建的理论或假设模型是否与实际数据相吻合。
它是一种多变量分析方法,用于测量和验证潜在因子对观察指标的关系。
在本文中,将介绍如何使用AMOS软件进行验证性因子分析,并说明其步骤和解释结果的方法。
验证性因子分析的步骤如下:1.准备数据:首先,需要准备清洁和格式化的数据集。
确保变量的测量是连续的,并检查是否存在缺失值。
如果存在缺失值,可以选择删除缺失值或使用合适的方法进行缺失值处理。
2.建立模型:在AMOS软件中,创建新项目并选择“新模型”的选项。
在模型中添加指标和潜变量,并指定它们之间的因子关系。
可以使用路径图或列表方式指定模型。
3. 参数估计:在参数估计部分,选择适当的估计方法,如最大似然估计(Maximum Likelihood, ML)或广义最小二乘估计(Generalized Least Squares, GLS)。
这些方法可以根据数据集的特点来选择。
4. 模型拟合度检验:进行模型拟合度检验是确认模型的重要步骤。
通过比较实际数据与模型预测数据的吻合程度来评估模型的拟合度。
常用的拟合度指标包括卡方检验值(chi-square)、规范拟合指数(NFI)、增量拟合指数(IFI)和根均方误差逼近指数(RMSEA)。
5.修正模型:如果模型拟合度不佳,需要对模型进行修正。
可以根据修正指标的建议来调整模型,例如删除不明显或不显著的路径,增加或修改潜变量之间的关系。
6.解释结果:解释模型结果是验证性因子分析的重要任务之一、通过对模型参数和估计值的解读来解释实际数据与模型之间的关系。
还可以进行模型比较,比较不同模型之间的差异和优劣。
验证性因子分析的结果通常包括了对模型拟合度的评估和模型参数的解释。
模型拟合度指标可以告诉我们模型与实际数据的吻合程度,例如卡方检验值的显著性、NFI、IFI和RMSEA等指标。
数学模型中的因子分析法

数学模型中的因子分析法因子分析是一种常用的数学模型,用于解释多个变量之间的关系和发现潜在的因素。
它是一种降维技术,旨在将众多变量转化为较少数量的无关因子。
因子分析在统计学、心理学和市场研究等领域广泛应用,可用于数据降维、消除多重共线性、提取潜在特征、构建模型等等。
在因子分析中,有两种主要类型:探索性因子分析(Exploratory Factor Analysis,EFA)和验证性因子分析(Confirmatory Factor Analysis,CFA)。
探索性因子分析用于发现数据中的潜在因素,而验证性因子分析则用于验证已经提出的因素模型是否符合实际数据。
探索性因子分析的步骤如下:1.提出假设:确定为什么要进行因子分析以及预期结果,用于指导后续的数据分析。
2.数据准备:收集和整理要进行因子分析的数据,确保数据的可用性和准确性。
3.因子提取:通过主成分分析或最大似然法等方法,提取出能够解释数据变异最大的因子。
4.因子旋转:因子旋转是为了使提取出的因子更易于解释和理解。
常用的旋转方法有正交旋转和斜交旋转等。
5.因子解释和命名:对于每个提取出的因子,需要根据变量的载荷矩阵和旋转后的载荷矩阵进行解释和命名。
载荷矩阵表示每个因子与每个变量之间的关系。
6.结果评估:对于提取出的因子,需要进行信度和效度的评估。
信度评估包括内部一致性和稳定性等指标;效度评估包括构造效度和相关效度等指标。
验证性因子分析通常用于验证已经提出的因子模型是否符合实际数据。
其步骤包括:1.提出假设:确定已存在的因子模型,并对其进行理论和实际的验证。
2.选择分析方法:确定适合验证性因子分析的模型拟合方法,如最大似然法或广义最小二乘法等。
3.构建模型:将因子模型转化为测量模型,并建立测量方程。
4.模型拟合:对构建的测量模型进行拟合,评估模型的拟合度,如χ²检验、准则拟合指数(CFI)等。
5.修正模型:根据拟合域冒去改进模型的拟合,如剔除不显著的路径、修正测量方程等。
验证性因子分析

验证性因子分析验证性因子分析(Confirmatory Factor Analysis, CFA)是一种统计方法,用于检验和验证一个已经构建的多维量表的因子结构和因子载荷是否与预测一致。
其基本原理是在预设的因子结构前提下,通过对观察数据进行分析,确定相关因子的因子载荷是否显著,从而确定因子结构的准确性。
验证性因子分析需要先有理论基础并构建出一个已经测试过的多维量表,然后使用CFA模型对观察数据进行分析。
在该分析中,先构建一个因子模型,并设定各个因子与测量变量之间的关系,然后通过最大似然估计或贝叶斯估计等方法,根据数据对模型的适配度进行统计检验,判断模型是否能够很好地解释数据。
在验证性因子分析中,通常通过以下指标来评估模型的适配度:1. 卡方检验(Chi-Square Test):检验观察数据与模型之间的拟合程度,通常考虑的是卡方值和自由度的比值。
较小的卡方值和较大的自由度比值表示较好的拟合程度。
2. 均方根误差逼近指标(Root Mean Square Error of Approximation, RMSEA):此指标反映模型误差的程度,一般认为RMSEA值在0.05以下表示较好的拟合程度。
3. 标准化拟合指数(Comparative Fit Index, CFI)和增量拟合指数(Incremental Fit Index, TLI):这两个指标反映模型与数据的拟合程度,值越接近1表示拟合效果越好。
4. 标准化残差(Standardized Residuals):这个指标可以用来检验模型的统计显著性,较小的标准化残差表示模型比较合理。
通过分析以上指标,我们可以根据验证性因子分析的结果来评估模型的适配度,并判断因子结构是否与预期一致。
如果模型的适配度较好,即各个指标都在接受范围内,说明构建的因子结构是恰当的;如果拟合度较差,我们可能需要重新考虑因子结构或修改测量工具。
验证性or探索性因子分析傻傻分不清?

写在前面:同样都是因子分析,探索性因子分析与验证性因子分析有什么不同?探索性因子分析:基于降维的思想,将错综复杂的众多变量聚合成少数几个独立的公共因子,在乎的是多个测试项是否能组成一个或多个理论变量,其理论变量是未知的,例如30 个题目里面能生成多少个理论变量,即最合适的因子个数是多少。
验证性因子分析:事前已知理论变量,强调多个测试项是否能否代表某个理论变量,例如检验购买频率、主观评估、消费比例是否真的可以反映忠诚度。
也就是我们预先的理论架构是否是好的,题目设置是否是好的,收集到的数据能否体现想要的结果,实际上也就是一种效度检验。
探索性因子分析更适合于在没有理论支持的情况下对数据的试探性分析。
验证性因子分析充分利用了先验信息,在已知因子的情况下检验所搜集的数据资料是否按事先预定的结构方式产生作用。
同时,两种因子分析缺少任何一个,因子分析都将是不完整的。
一般来说,如果研究者没有坚实的理论基础支撑,有关观测变量内部结构一般先用探索性因子分析,产生一个关于内部结构的理论,再在此基础上用验证性因子分析,这样的做法是比较科学的,但这必须要用两组分开的数据来做。
如果研究者直接把探索性因子分析的结果放到统一数据的验证性因子分析中,研究者就仅仅是拟合数据,而不是检验理论结构。
如果样本容量足够大的话,可以将数据样本随机分成两半,合理的做法就是先用一半数据做探索性因子分析,然后把分析取得的因子用在剩下的一半数据中做验证性因子分析。
今天我们主要来详细讲解一下验证性因子分析1 背景下表是理科班的100 名同学的语文、数学、英语、物理、生物、化学成绩。
研究者想要验证他们的语文、英语成绩是否可以反映理科班的文科成绩水平;他们的数学、物理、生物、化学成绩是否可以反映理科班的理科成绩水平。
2 分析步骤2.1 模型构建首先对样本进行频数统计,验证性因子分析要求总样本数据(行数)最少是全部题目(列数)的5倍以上,最好10倍以上,且一般情况下至少需要200个样本;2.2 删除不合理测量项通过因子载荷系数对因子内测量变量进行筛选,一般来说,测量变量通过显著性检验(< 0.05或0.01),并且标准化载荷系数值大于0.7,可表明测量变量符合因子要求,条件差距太大可以考虑删除变量;2.3 模型评价根据平均公因子方差抽取量(AVE)与组合信度(CR)结果可以分析因子内的测量指标的提取度,一般来说AVE要求高于0.5,且越接近1代表测量指标提取程度越高,CR要求高于0.72.4 分析总结3 软件实现3.1 案例操作3.2 结果解释3.21 因子基本汇总表样本数据集共有因子数量2 个,变量数6 个,样本数量200个,满足验证性因子分析基本数据要求。
cfa检验方法考题

cfa检验方法考题摘要:一、CFA检验方法简介1.CFA基本概念2.CFA检验方法分类二、CFA检验方法的应用1.金融市场中的应用2.企业财务中的应用三、CFA检验方法的关键步骤1.数据收集与整理2.建立模型3.模型检验与应用四、CFA检验方法的有效性评估1.评估指标2.评估方法五、提高CFA检验方法应用能力的策略1.加强理论知识学习2.注重实践操作3.深入了解行业与应用场景正文:一、CFA检验方法简介CFA(Confirmatory Factor Analysis,验证性因子分析)是一种常用的统计分析方法,主要用于检验潜在变量(latent variable)与观测变量(observed variable)之间的关系。
CFA通过构建因子模型,分析观测变量背后的潜在因子结构,从而为研究变量间的内在联系提供依据。
CFA检验方法主要分为两类:一类是因子分析(Factor Analysis),另一类是结构方程模型(Structural Equation Modeling,SEM)。
因子分析主要关注观测变量之间的关联性,而结构方程模型则进一步探讨了潜在变量与观测变量之间的关系。
二、CFA检验方法的应用1.金融市场中的应用在金融市场中,CFA检验方法被广泛应用于资产定价、投资组合优化、市场微观结构分析等方面。
例如,研究者可以通过CFA检验方法评估股票收益率与风险因子之间的关系,从而为投资策略的制定提供依据。
2.企业财务中的应用在企业财务领域,CFA检验方法可以帮助企业分析经营业绩、财务状况和市场竞争力。
例如,企业可以通过CFA检验方法检验营销投入与销售额之间的关系,以便制定更有效的市场营销策略。
三、CFA检验方法的关键步骤1.数据收集与整理在进行CFA检验之前,首先需要收集与研究主题相关的观测变量数据。
数据来源可以包括问卷调查、实验数据、企业财务报表等。
在收集数据后,需要对数据进行整理,确保数据质量。
2.建立模型根据研究目的和理论假设,选择合适的因子模型进行构建。
验证性因子分析思路总结

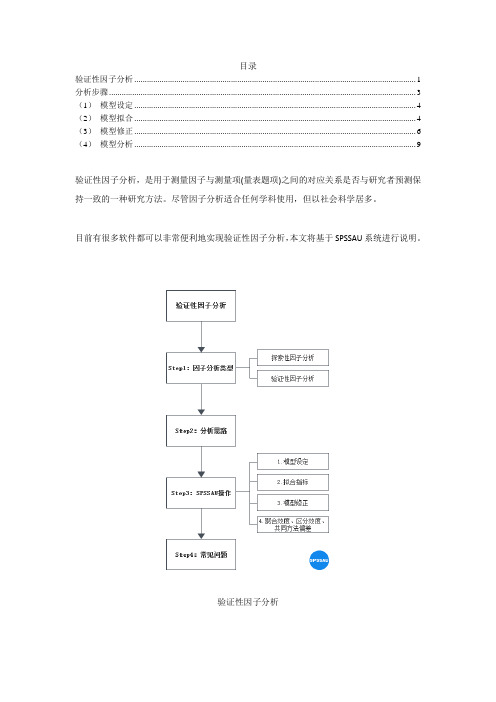
目录验证性因子分析 (1)分析步骤 (3)(1)模型设定 (4)(2)模型拟合 (4)( 3 )模型修正 (6)(4)模型分析 (9)验证性因子分析,是用于测量因子与测量项(量表题项)之间的对应关系是否与研究者预测保持一致的一种研究方法。
尽管因子分析适合任何学科使用,但以社会科学居多。
目前有很多软件都可以非常便利地实现验证性因子分析,本文将基于SPSSAU系统进行说明。
验证性因子分析Step1:因子分析类型因子分析可分为两种类型:探索性因子分析(EFA)和验证性因子分析(CFA)。
探索性因子分析,主要用于浓缩测量项,将所有题项浓缩提取成几个概括性因子,达到减少分析次数,减少重复信息的目的。
验证性因子分析与探索性因子分析相似,两者区别只在于探索性因子分析(EFA)用于探索因子与测量项之间的对应关系,验证性因子分析(CFA)用于验证结果与理论预期是否一致。
Step2:分析思路在实际研究中,验证性因子分析常会与结构方程模型、路径分析等方法联系到一起,对于不熟悉概念的研究人员容易搞混这些方法,下表对这几种方法进行简单说明:探索性因子分析(EFA)验证性因子分析(CFA )研究测量关系研究测量关系回归分析研究自变量对一个因变量的影响关系路径分析研究多个自变量与多个因变量之间的影响关系适用于非经典量表适用于经典量表y 为定量数据可先用CFA/EFA 确定因子与研究项关系,再进行路径分析结构方程模型包括两部分:结构方程模型研究影响关系及测量关系验证性因子分析和路径分析探索性因子分析:验证因子与分析项的对应关系,索性因子分析。
验证性因子分析:验证因子与分析项的对应关系,性因子分析。
确认测量关系后,后续可进行路径分析系。
检验量表效度,非经典量表通常用探检验量表效度,成熟量表通常用验证/ 线性回归分析研究具体的影响关路径分析:用于研究多个自变量与多个因变量影响关系;如果因变量只有一个,可以使用线性回归分析。
结构方程模型SEM:包括测量关系和影响关系。
因子分析中的因子结构验证方法(九)

因子分析是一种常用的统计方法,用于研究变量之间的关联性和组织结构。
在因子分析中,因子结构验证是一个重要的步骤,它可以帮助研究者确认所提取的因子是否合理和可靠。
本文将介绍因子分析中的因子结构验证方法,包括探索性因子分析和验证性因子分析,以及常用的验证方法和步骤。
探索性因子分析是一种用于发现潜在结构的方法,它可以帮助研究者识别数据中的潜在因子,并确定它们之间的关系。
在进行探索性因子分析时,研究者通常会使用主成分分析或最大似然估计等方法来提取因子。
一旦因子被提取出来,就需要进行因子旋转和因子解释,以便理解因子之间的关系。
而在验证性因子分析中,研究者会基于以前的理论或假设,提出一个关于因子结构的模型,并使用数据来检验这个模型的拟合程度。
在进行因子结构验证时,研究者可以使用许多不同的方法和指标来评估模型的拟合程度。
其中最常用的指标包括卡方拟合指数(Chi-square goodness of fit test)、比较拟合指数(Comparative Fit Index,CFI)、均方根误差逼近度(Root Mean Square Error of Approximation,RMSEA)等。
这些指标可以帮助研究者判断模型的拟合程度,从而决定是否接受或拒绝模型。
此外,研究者还可以使用残差矩阵、模型修正指数(Model Modification Indices),以及因子载荷等指标来评估模型的拟合程度。
另外,研究者还可以使用因子结构验证图来帮助理解因子模型。
因子结构验证图可以清晰地展现因子之间的关系,帮助研究者更直观地理解因子结构。
通过因子结构验证图,研究者可以清楚地看到因子之间的相关性,以及因子与观察变量之间的关系。
这有助于研究者更好地理解因子结构,并决定是否需要对模型进行修正。
在进行因子结构验证时,研究者需要注意一些常见的问题。
首先,研究者需要确保样本量足够大,以便保证模型的稳健性。
其次,研究者需要仔细检查数据的偏度和峰度,以确保因子分析的合理性。
spssau 验证性因子分析

验证性因子分析目录1验证性因子分析基本说明 (2)2 如何使用SPSSAU进行验证性因子操作 (3)3 验证性因子不达标如何办? (9)第1点:效度不达标 (9)第2点:factor loading值过大或过小 (10)第3点:拟合指标不达标 (10)验证性因子分析(confirmatory factor analysis, CFA)是结构方程模型的一种最常见的应用。
验证性因子分析(confirmatory factor analysis, CFA)通常可用于四种用途,一是针对成熟量表进行效度分析,包括结构效度,聚合(收敛效度)和区分效度;二是验证性因子分析可用于组合信度的分析;三是验证性因子分析还可用于进行共同方法偏差CMV检验。
四是使用验证性因子分析进行权重计算;CFA的功能应用如下:验证性因子分析功能如果是使用CFA进行结构效度验证,即测量因子与对应项之间的对应关系情况是否良好,一般查看标准化factor loading即因子载荷系数值即可,如果所有的项标准化factor loading值大于0.7即说明结构效度良好。
当然,如果某项的factor loading值较小,那么可删除该项后再次分析。
如果使用CFA进行聚合效度验证,那么其是测量本应该在同一因子的项确实在该因子里面;其具体测量方式是要求A VE值大于0.5即可;如果出现A VE明显的小于0.5,此时可考虑移项一些载荷系数值较低项后再次分析。
如果使用CFA进行区分效度验证,那么其是测量不应该同一因子的项确实不在同一因子下面;测量方式有两种,第一种是看A VE平方根号值与相关系数值进行PK,如果说A VE平方根号值全部大于相关系数值,意味着聚合性明显更强,说明具有区分效度;区分效度时还有一种测量方式是使用HTMT值,该指标一般小于0.9即可,但该指标要求相对较严格,使用较少。
如果使用CFA进行信度分析,那么使用组合信度系数CR值测量即可,一般CR值大于0.7即可。
验证性因子分析思路总结
目录验证性因子分析 (1)分析步骤 (3)(1)模型设定 (4)(2)模型拟合 (4)(3)模型修正 (6)(4)模型分析 (9)验证性因子分析,是用于测量因子与测量项(量表题项)之间的对应关系是否与研究者预测保持一致的一种研究方法。
尽管因子分析适合任何学科使用,但以社会科学居多。
目前有很多软件都可以非常便利地实现验证性因子分析,本文将基于SPSSAU系统进行说明。
验证性因子分析Step1:因子分析类型因子分析可分为两种类型:探索性因子分析(EFA)和验证性因子分析(CFA)。
探索性因子分析,主要用于浓缩测量项,将所有题项浓缩提取成几个概括性因子,达到减少分析次数,减少重复信息的目的。
验证性因子分析与探索性因子分析相似,两者区别只在于探索性因子分析(EFA)用于探索因子与测量项之间的对应关系,验证性因子分析(CFA)用于验证结果与理论预期是否一致。
Step2:分析思路在实际研究中,验证性因子分析常会与结构方程模型、路径分析等方法联系到一起,对于不熟悉概念的研究人员容易搞混这些方法,下表对这几种方法进行简单说明:探索性因子分析(EFA)研究测量关系适用于非经典量表验证性因子分析(CFA)研究测量关系适用于经典量表回归分析研究自变量对一个因变量的影响关系y为定量数据路径分析研究多个自变量与多个因变量之间的影响关系可先用CFA/EFA确定因子与研究项关系,再进行路径分析结构方程模型研究影响关系及测量关系结构方程模型包括两部分:验证性因子分析和路径分析●探索性因子分析:验证因子与分析项的对应关系,检验量表效度,非经典量表通常用探索性因子分析。
●验证性因子分析:验证因子与分析项的对应关系,检验量表效度,成熟量表通常用验证性因子分析。
确认测量关系后,后续可进行路径分析/线性回归分析研究具体的影响关系。
●路径分析:用于研究多个自变量与多个因变量影响关系;如果因变量只有一个,可以使用线性回归分析。
●结构方程模型SEM:包括测量关系和影响关系。
验证性因子分析报告

验证性因子分析报告引言验证性因子分析(CFA)是一种统计方法,用于评估测量模型的适配性和建立因子与观测变量之间的关系。
本报告旨在介绍CFA的步骤和思考过程,以及如何解释和应用CFA结果。
步骤一:确定研究目的和假设在进行CFA之前,首先需要明确研究目的和假设。
研究目的可以是验证一个已有的理论模型,或者建立一个新的测量模型。
假设可以是具体的关系假设或者差异假设。
步骤二:选择合适的测量工具和样本第二步是选择合适的测量工具和样本。
测量工具可以是问卷调查、观察或者其他形式的测量工具。
样本的选择应该具有代表性,并且具备足够的样本量以支持结果的可靠性。
步骤三:建立测量模型建立测量模型是CFA的核心步骤。
首先,确定要测量的潜在因子,并选择合适的观测变量。
然后,建立一个初始模型,将观测变量与潜在因子进行关联。
在建立模型时,需要考虑因子间的相关性以及观测变量的量表信度。
步骤四:评估模型适配性一旦建立了测量模型,接下来需要评估模型的适配性。
常用的适配性指标包括卡方检验、比较合适度指数(CFI)、增量合适度指数(IFI)和根均方误差逼近指数(RMSEA)。
这些指标可以帮助研究者判断模型是否与实际数据拟合良好。
步骤五:检验因子负荷和因子间关系一旦模型的适配性得到确认,接下来需要检验因子负荷和因子间的关系。
因子负荷指观测变量与潜在因子之间的关系强度,可以通过标准化回归系数来度量。
因子间关系可以通过检验路径系数或者相关系数来判断。
步骤六:解释和应用CFA结果最后一步是解释和应用CFA的结果。
根据因子负荷和因子间关系的方向和强度,可以对测量模型进行解释,并验证研究假设。
此外,CFA结果还可以用于改进测量工具或者探索其他相关问题。
结论验证性因子分析是一种强大的统计方法,可以用于评估测量模型的适配性和建立因子与观测变量之间的关系。
通过明确研究目的和假设,选择合适的测量工具和样本,建立测量模型,评估模型适配性,检验因子负荷和因子间关系,并解释和应用CFA结果,研究者可以得出可靠的结论,并推动理论和实践的发展。
验证性因子分析

验证性因子分析
验证性因子分析(CFA)是一种用于检验和验证研究模型的统计分析方法。
它是基于因子分析的一种方法,通过考察特征因子和变量之间的关系来评估研究模型的拟合程度。
在进行CFA之前,首先需要构建研究模型。
研究模型是通过将观察变量组织成潜在变量的形式来描述和解释数据之间的关系。
潜在变量表示无法直接观测或测量的概念或构造,例如抽象的概念、心理特征或态度。
CFA的步骤如下:
1. 设定研究模型:根据研究问题和理论基础,确定研究模型的结构和变量之间的关系。
研究模型通常由潜在变量和观察变量组成。
2. 收集数据:收集足够数量的数据来进行CFA分析。
数据可以通过问卷调查、实验或其他适当的方法来收集。
3. 选择统计软件:选择适用于CFA分析的统计软件,例如SPSS、AMOS或LISREL等。
4. 进行模型拟合度检验:使用CFA软件分析数据,并计算出模型的拟合度指标。
常用的拟合度指标包括χ²值、DF(自由度)、CFI (相对拟合指数)、RMSEA(均方根误差逼近指数)等。
5. 修正模型:根据拟合度指标和相关统计量对模型进行修正。
如果模型的拟合度不佳,可以尝试添加或删除某些路径、允许关联错误项、修正模型规范等,以提高模型的拟合度。
6. 验证模型:对修正后的模型进行再次分析,检验拟合度指标是否得到了改善。
如果模型的拟合度满足要求,则可以认为模型通过了验证。
需要注意的是,CFA只能检验给定模型的拟合程度,而不能确定模型的因果关系。
因此,在进行CFA之前,需要有明确的研究假设和理论基础,以便根据统计结果对研究模型进行解释和解释。
各因子模型结构效度判断依据

各因子模型结构效度判断依据因子模型是一种常用的研究方法,用于分析测量数据的内部结构,包括依据数据中的各种因素来解释观察到的变异。
因子模型结构效度判断依据主要包括因子分析、验证性因子分析和多组因素分析。
因子分析是一种常用的数据降维方法,通过将一组观测变量转化为较小数量的潜在变量(因子)来解释原始数据的变异。
因子分析的结构效度判断依据主要包括以下几个方面:1.充分性:因子分析应保证提取到的因子解释了足够的变异。
通常来说,如果前几个因子可以解释了总变异的70%以上,那么认为该因子提取是充分的。
2.简洁性:因子分析旨在提取少量的因子来解释观测变量的变异。
因此,模型的简洁性是一个重要的判断依据。
一般来说,应该避免提取过多的因子,而应该选择解释变异最多的前几个因子。
3.解释力:因子分析应该能够提供对观测变量的解释。
这意味着提取到的因子应该与实际变量的内在结构相关联。
因此,在因子分析之后,需要进行因子负载量分析,以确认因子和观测变量之间的关系是否符合预期。
验证性因子分析是一种用来验证因子模型的有效性和适应性的方法。
它基于因子分析,并进一步引入了模型拟合指标以评估模型的适配程度。
验证性因子分析的结构效度判断依据主要包括以下几个方面:1.模型拟合度:验证性因子分析的重要任务是检验模型是否能够很好地适应数据。
模型拟合度指标主要包括卡方检验、拟合优度指标(如比较拟合指标CFI、增量拟合指标IFI等)和残差分析。
只有在模型拟合达到较好水平的情况下,才能认为模型具有较好的结构效度。
2.各因子负载量:验证性因子分析还需要检验各因子与观测变量之间的关系。
在因子负载量分析中,需要检验观测变量与其所属因子之间的相关性是否较高,同时需要排除其他因子对所属观测变量的影响。
3.因子间相关性:验证性因子分析还需要检验因子之间的相关性。
如果各因子之间的相关性较低,那么可以认为因子分析的结构效度较好,各因子之间是相互独立的。
多组因素分析是一种用于比较不同样本之间因子结构的方法,通常应用于不同群体、不同性别或不同文化背景的比较研究中。
验证性因子分析的讲解

结构方程模型另一方法——PLS
偏最小平方模型PLS(Wald,1982) 《模型构建方法与结构方程建模——与张建平同志
商讨》一文中旨在将结构方程模型与LISREL的 概念区分开而具体介绍
当研究目的是理论检验且先验理论知识充足时, 更宜采用LISREL;当研究目的是因果预测应用, 且理论知识非常缺乏时,则PLS更加适合。
数表示) Σ(Θ^):根据样本估计出Θ^后得到的协方差矩阵
目的
S——Σ Σ(Θ^)——Σ(Θ) 估计出参数,使得Σ(Θ^)逼近S,即使得Σ(Θ)
逼近Σ
参数估计 模型识别 模型评价等具体细节原理 教材CH9
应用举例
《外资企业跨文化适应模式分析结构方程建模》
谢谢
Байду номын сангаас
基本思想的差异
EFA
CFA
主要是为了找出影响观测 变量的因子个数,以及各 个因子和各个观测变量之 间的相关程度
主要目的是决定事前定义 因子的模型拟合实际数据 的能力
CFA原理分析
教材P170 参数:λij,ξi的方差、协方差φij,δ的方差θii Θ:全体位置参数组成的向量 Θ^: Θ的估计 Σ:X在总体中真实的协方差矩阵(9.3) S:X在样本的协方差矩阵(可代替Σ ) Σ(Θ):由模型推出的整体协方差矩阵(9.4由各参
效度检验最详细讲解

效度检验
验证性因子分析(confirmatory factor analysis, CFA)是用于测量因子与测量项(量表题项)之间的对应关系是否与研究者预测保持一致的一种研究方法。
与验证性因子分析CFA相对应的为探索性因子分析,二者的区别在于,验证性因子分析(CFA)用于验证对应关系,探索性因子分析(EFA)用于探索因子与测量项(量表题项)之间的对应关系。
应用情形:如果是成熟的量表,研究者可同时使用验证性因子分析CFA,和探索性因子分析(简称因子分析,EFA)用于验证量表的效度。
如果量表的权威性较弱,通常使用探索性因子分析(EFA)进行探索因子,或者效度检验分析。
验证性因子分析CFA的主要目的在于进行效度验证,同时还可以进行共同方法偏差CMV的分析。
效度有很多种,比如内容效度,结构效度,聚合(收敛)效度,区分效度等。
各个名称的区别说明如下:
如果并非经典量表,通常情况下研究人员会使用探索性因子分析(EFA)进行效度验证,该验证方法一般称作结构效度分析,同时还会使用内容效度进行分析即用文字描述量表的来源设计过程等,用于论证研究量表的有效性。
当然如果还想进一步深入分析,亦可使用CFA进行深入研究。
如果是经典量表需要进行效度验证,其内容效度确认无疑,而且使用探索性因子分析(EFA)进行分析时,也具有良好的结构效度。
所以研究人员更偏好于使用CFA进行深入分析,即进行聚合(收敛)效度和区分效度分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k
k
k
12
模型拟合优度检验
n n 1 ln( LF ) [ln S tr( SS )] [ln S p] 2 2
n ln( LR ) ln tr S 1 2
H0: Reduced model is indifferent from full model Ha: two models are significantly different Set α=0.2
11
模型的评价
• 一个好的模型就是参数的估计值使得模型隐含的方差协方 差矩阵 (k ) 与样本导出的方差协方差矩阵S充分地接近, 或满足事先给定的标准。 • 令F=F(S, ( ) ) • 它是一个非负函数。F=0,当且仅当S= ( ) ,即模型完全 拟合数据。F被称为拟合函数,它的具体公式取决于方法。 • 验证性因子分析的总体拟合优度的统计假设是: H0:S= ( ) ,即数据完全拟合。 H1:S ( ) ,即数据不完全拟合。
均方根
GFI拟合优度指数 不受样本大小影响, >0.95:good level (goodness of fit index) 可用于不同模型之 >0.90:acceptable level 间的比较。 AGFI 调整后拟合优 度指数 >0.90:good level >0.80:acceptable level
10
模型的参数估计
• 1、估计因子载荷
逐步迭代: k g (k ), k 1,2,... 直到 ( k ) 与S充分的接近。 最后得到的估计为模型的一个非标准参数估计
• 2、 计算标准因子载荷
标准因子载荷消除了纲量的影响,可以用来比较指标对潜在因 子的相对重要性。绝对值越大,指标对潜在因子的贡献越大。 1) 令每个因子的方差为1; 2) 将每个因子与因子载荷在之上的变量间的λ值任选一个, 并固定为1
探索性因子分析与验证性因子分析
• 验证性因子分析
1)定义因子模型 2)搜集数据 3)获得协方差矩阵或相关系数矩阵 4)模型估计 5)模型评价 6)模型修正和再定义
6
验证性因子分析
• CFA属于结构方程模型 (SEM with latent variables)的 子模型,CFA分析的数学原理与统计程序,都是SEM的特殊 应用。 • CFA:必须有特定理论依据或概念构架作为基础,然后藉由 数学语言来确认该理论所导出的计量模型是否合理适当。 • CFA的参数估计采用“最大似然估计”,而非矩阵分解,其 优点在于 – 提供模型拟合优度统计量 – 提供参数估计的标准误
RMR 残差平方根
反应理论假设模型 整体残差
<0.05, 越接近0越好
15
拟合残差和标准拟合残差
• 拟合残差矩阵:样本导出的方差协方差矩阵减去模型拟合 的方差协方差矩阵。 • 拟合残差:拟合残差矩阵中的元素。
• 标准拟合残差:拟合残差除以它的标准误。
• 一个大的正的拟合残差表明模型低估了对应的一对观察变
• 所有的固定参数的修正指标都不大(<3.841); • 所有的标准拟合残差都很小(<1.96);
19
操作软件
• LISREL是一套用于SEM分析的统计专 用软件。采用LISREL 8.7版 • 其它:
• AMOS(SPSS) • EQS • SAS CALIS • EQS • Mplus
20
例题
3
探索性因子分析与验证性因子分析
• 验证性因子分析 (1)公共因素之间可以相关也可以无关 (2)观测变量可以只受某一个或几个公共因素的影响而不 必受所有公共因素的影响 (3)特殊因素之间可以有相关,还可以出现不存在误差因 素的观测变量 (4)公共因素和特殊因素之间相互独立 (5)观测变量与潜变量之间的关系事先假定的 (6)潜在变量的个数在数据分析前确定的 (7)模型通常要求是可识别的
26
21
• 量表结构域变量命名:
• 每一个条目是一个可观测变量,每一个维度相当于一个潜 变量,社会支持、特质应对则相当于更高层次的潜变量。 • 以上表为例,对某特定人群,随机抽样239名个体,问卷 调查相关社会心理因素,采用验证性因子分析评价社会支 持量表的构念效度。
22
• 社会支持量表共10个条目,分3个维度,即3个潜在因子, 可分别拟合单因子模型和多因子模型。下表给出了多因子 验证性因子分析的最大似然估计结果及部分拟合指数。 • 发现除SSS2外,其他条目的非标准解均具有统计学意义。 决定系数是衡量观察变量度量潜在变量可靠性的指标,除 SSS2外,其他各观测变量的决定系数均较高,SSS2对该维 度的贡献较小,该量表第2个条目为:
9
模型的参数估计
• 在验证性因素分析中常用的参数估计的方法: 未加权最小二乘法(ULS)、广义最小二乘估计(GLS)、 极大似然估计(ML)、工具变量法(IV) 、两阶段最小 平方法(TSLS)、广义加权最小平方法(WLS)、对角加 权最小平方(DWLS) • 最常用的参数估计的方法: 极大似然估计 、广义最小二乘法 • 样本导出的方差协方差矩阵S: 由原始数据计算出来的关于p个观察变量的方差协方差矩 阵。由于它不受任何条件限制,所以称之为非限制性方差 协方差矩阵。它表示了原始变量之间的关联程度。
4
探索性因子分析与验证性因子分析
• 2. 分析步骤 • 探索性因子分析 1)收集观测变量并 2)获得协方差阵(或相关系数矩阵) 3)确定因子个数:Kaiser准则、Screen检验 4)提取因子:主成分法、最小二乘法、最大似然法 5)因子旋转: 因子载荷阵的不唯一性,可对因子进行旋转,使因子结 构朝合理方向趋近。 旋转方法:正交、斜交旋转等,常用方差最大化正交旋 转 6)解释因子结构:依据因子载荷作出解释,并赋予因子含义 7)因子得分:公共因子代表原始变量,利于描述研究对象的 特征 5
2
探索性因子分析与验证性因子分析
• 1.模型假设
• 探索性因子分析的假设: (1)所有的公共因素都相关(或都无关) (2)所有的公共因素直接影响所有的观测变量 (3)特殊因素之间相互独立 (4)所有观测变量只受一个特殊因素的影响 (5)公共因素和特殊因素相互独立 (6)观测变量与潜在变量之间的关系不是事先假定的 (7)潜在变量的个数不是在分析前确定的
改,然后重新估计未知参数和重新进行模型的总体评价,
直到模型的总体检验合格并且所有的参数估计满足要求为 止。
17
修正指标和预期估计
• 如果将模型中的一个固定参数(取值为0的参数)改变为 自由参数(需要估计的参数)。并令其他的参数保持不变, 重新估计模型,则修正后的模型与修正前的模型的卡方值 的差称为是这个固定参数的修正指标。
• 无论潜变量还是显变量均可分为内生变量与外生变量。内 生变量指由模型内变量作用所影响的变量,在一个假设的 因果模型中被看做是效应变量或因变量。外生变量是那些 影响模型中其他变量的变量,在模型中为起因变量或自变 量。通常我们用X表示外生变量,Y表示内生变量。外生变 量和内生变量分别用ξ(Ksi)和η(Eta)表示。 • 以社会心理行为研究中的社会支持评定量表(social support scale,SSS)与特质应对方式问卷(trait coping style questionnaire,TCSQ)为例,SSS量表包含3个维度, 10个条目,TCSQ量表包括2个维度,20个条目。
量之间的协相关性;而一个大的负的拟合残差表明模型高
估了对应的一对观察变量之间的协相关性。一个拟合好的 模型,它的所有标准拟合残差都应当很小。
16
模型的修正和再估计
• 不论模型的总体评价失败与否,都需要对模型中所有未知 参数的估计值是否具有统计意义和实际的解释意义进行逐 个检查。如果有不满足要求的,就需要对初始模型进行修
零假设: the proposed model fits as well as a perfect model
14
评价指数
RMSEA近似误差
说明
被认为是评价模型拟合 效果的最具信息标准的 指标。对模型中自由参 数的数目敏感,即受模 型复杂性影响较大。
数值(0~1)
<0.05拟合好 0.08~0.10一般 >0.10拟合不好
• 也就是说,修正指标近似的等于修正后的模型的卡方值的 减少量,并且称修正后的模型中原固定参数对应的估计值 为原固定参数的期望参数估计。 • 一个大的修正指标表明它对应的固定参数是有必要修正的。
18
一个好的最后模型应该满足这样几个条件:
• 模型总体上很好的拟合了原始数据,主要拟合指标都满足 要求; • 所有因子载荷和结构系数的估计值在统计意义上不等于零, 且具有实际解释意义(正确的符号和数值大小);
对n极为敏感
2[ln( LR ) ln( LF )] n[ln tr( S 1 ) ln S p] ~ 2
13
评价指标
2[ln( LR ) ln( LF )] ~
2
指标 χ2 卡方值
说明 χ2易受样本量大小影响,当样本 量较大时,易导致拒绝零假设, 因此建议与其它指标同时评价。
• 该条目取值为3、4的占到93.5%,区分度(r=0.113)偏低 ,建议对该条目的第1、2选项进一步修订。
23
24
• 修正指数:
25
从标准解可见:对于第一个潜在 变量的主观支持,SSS5(从家庭成员 得到的支持和照顾)的因子载荷最大, 说明该条目对主观支持的度量最好。 对于第二个潜在变量的客观支持,指 标SSS6(过去您遇到紧急情况时,曾 经得到的经济支持和解决实际问题的 帮助来源)与SSS7(过去您遇到紧急 情况时,曾经得到的安慰和关心的来 源)的因子载荷最大。第三个潜变量 支持利用度,指标SSS中主 观支持与客观支持,主观支持与支持 利用度表现出较强的关联性。
x x '
