鲁棒控制与鲁棒控制器设计-文档资料
控制系统中的鲁棒性与鲁棒优化控制

控制系统中的鲁棒性与鲁棒优化控制一、引言鲁棒性与鲁棒优化控制在控制系统中起着重要的作用。
鲁棒性是指控制系统对于外部扰动和系统参数变化的稳定性。
鲁棒优化控制是在保持鲁棒性的前提下,通过调整控制器参数实现最优控制。
本文将从鲁棒性的定义与评估、鲁棒控制设计基础、鲁棒优化控制等方面进行探讨。
二、鲁棒性的定义与评估在控制系统中,外部扰动和系统参数变化是难以避免的。
因此,控制系统的鲁棒性成为了一个关键的性能指标。
鲁棒性的定义是指控制系统在外部扰动和系统参数变化的条件下仍然能够保持稳定的能力。
评估鲁棒性通常可以通过鲁棒稳定边界来实现。
鲁棒稳定边界是指控制系统在外部扰动和系统参数变化的范围内仍然能够保持稳定的区域。
三、鲁棒控制设计基础为了提高控制系统的鲁棒性,可以采用鲁棒控制设计基础方法。
鲁棒控制设计基础方法包括鲁棒稳定性分析和鲁棒控制器设计两个主要步骤。
1.鲁棒稳定性分析鲁棒稳定性分析是控制系统鲁棒性设计的第一步。
它通过分析系统的传递函数,确定系统存在哪些参数的变化和外部扰动的范围是导致系统不稳定的原因。
常用的鲁棒稳定性分析方法有小增益鲁棒分析、大增益鲁棒分析等。
2.鲁棒控制器设计鲁棒控制器设计是控制系统鲁棒性设计的关键步骤。
通过选取合适的鲁棒控制器结构和调整控制器参数,可以实现对系统的鲁棒性能的改善。
常用的鲁棒控制器设计方法有H∞控制、μ合成控制等。
四、鲁棒优化控制鲁棒优化控制是在保持系统鲁棒性的前提下,通过调整控制器参数实现最优控制性能的方法。
在实际控制系统中,鲁棒优化控制能够有效地提高系统的鲁棒性和控制性能。
1.鲁棒优化控制基本原理鲁棒优化控制的基本原理是在目标函数中同时考虑系统控制性能和鲁棒性能,并通过调整控制器参数来实现最优化。
常用的鲁棒优化控制方法有线性二次调节器(LQR)和H∞最优控制。
2.鲁棒优化控制实践实际应用中,鲁棒优化控制可以通过离线和在线两种方式实现。
离线方式包括离线参数调整和离线优化方法,通过对控制系统的模型进行分析和优化来获取最优的控制器参数。
控制系统中的鲁棒性分析与设计

控制系统中的鲁棒性分析与设计在控制系统中,鲁棒性是指控制系统对于参数变化、外部干扰、测量噪声等不确定性因素的稳定性和性能表现。
鲁棒性分析与设计主要目的是提高控制系统的稳定性、鲁棒性和性能,以适应实际工程环境中的不确定性。
1. 鲁棒性分析鲁棒性分析是控制系统设计的重要环节。
它可以帮助工程师评估以及量化控制系统对于参数变化、干扰和噪声的容忍程度。
以下是一些常用的鲁棒性分析方法:1.1 系统感度函数分析系统感度函数是用来描述控制系统输出对于参数变化的敏感程度。
通过分析系统感度函数,可以确定系统的脆弱性和稳定性。
系统感度函数分析常用于评估系统的稳定性边界、参数不确定性边界和鲁棒性边界。
1.2 线性矩阵不等式(LMI)方法线性矩阵不等式方法是一种基于数学理论的鲁棒性分析方法。
它通过建立一系列矩阵不等式,来刻画控制系统的稳定性和性能。
LMI方法在控制系统设计中被广泛应用,它不仅可以评估系统的鲁棒性,还可以用于设计鲁棒控制器。
1.3 干扰分析干扰是控制系统中常见的不确定因素,对系统的性能和稳定性产生重要影响。
干扰分析可以帮助工程师了解系统对于不同干扰的响应,并根据需要采取相应的措施来改进系统鲁棒性。
常用的干扰分析方法包括频域分析、时域分析和能量分析等。
2. 鲁棒性设计鲁棒性设计旨在采取控制策略和控制器结构,使得控制系统对于不确定性因素具有较好的稳定性和性能。
以下是一些常见的鲁棒性设计方法:2.1 鲁棒控制器设计鲁棒控制器设计是指根据鲁棒性需求,设计出满足控制系统鲁棒性要求的控制器。
常用的鲁棒控制器设计方法包括H∞控制、μ合成、鲁棒PID控制等。
这些方法都是基于数学理论,可用于设计满足鲁棒性和性能要求的控制器。
2.2 鲁棒优化设计鲁棒优化设计是指结合鲁棒控制与优化方法,兼顾控制系统的稳定性和性能。
通过优化设计,可以在满足鲁棒性要求的前提下,使系统的性能指标达到最优。
鲁棒优化设计方法包括H∞优化、线性二次调节器和状态反馈等。
控制系统鲁棒性设计

控制系统鲁棒性设计控制系统鲁棒性设计是指在考虑到系统动态特性和不确定因素的情况下,设计出具有良好鲁棒性的控制系统。
鲁棒性设计的目标是使系统能够在不确定因素的干扰下仍然能够保持稳定性和性能。
本文将从鲁棒性设计的概念、重要性以及实现鲁棒性设计的方法三个方面对控制系统鲁棒性设计进行探讨。
一、鲁棒性设计的概念鲁棒性是指系统对于参数变化、外部干扰以及模型不准确性等因素的容忍度。
在控制系统中,不同的干扰和参数变化可能会导致系统动态特性和稳定性发生变化,鲁棒性设计的目标就是保证系统的性能不受这些因素的影响而变差。
二、鲁棒性设计的重要性鲁棒性设计在控制系统中具有重要的意义。
首先,现实世界中的系统往往存在着各种不确定因素,如参数变化、外部干扰等,如果控制系统在面对这些不确定因素时不能保持稳定性和性能,则无法满足实际应用的需求。
其次,控制系统的设计往往是建立在一定的模型假设下进行的,而这些模型存在不准确性,因此需要通过鲁棒性设计来保证系统的稳定性和性能。
最后,鲁棒性设计可以提高系统对于异常情况的响应能力,确保系统在面对未知情况时仍能正常工作。
三、实现鲁棒性设计的方法实现鲁棒性设计的方法主要包括模型不确定性分析、鲁棒控制器设计以及鲁棒性性能评估等。
1. 模型不确定性分析在鲁棒性设计中,模型的不确定性是一个重要的考虑因素。
通过对系统模型的不确定性进行分析,可以了解到系统模型的不确定部分,从而进一步确定鲁棒控制设计中需要关注的方面。
2. 鲁棒控制器设计鲁棒控制器设计是实现鲁棒性设计的关键步骤。
鲁棒控制器的设计需要考虑到系统的不确定性和干扰,通过引入校正项或者使用鲁棒控制策略,可以使得控制系统对于不确定因素的变化具有一定的容忍度,从而保证系统的稳定性和性能。
3. 鲁棒性性能评估鲁棒性性能评估是评价控制系统鲁棒性设计效果的重要手段。
通过对控制系统的鲁棒稳定性和鲁棒性能进行评估,可以判断控制系统对于不确定因素的容忍度以及系统性能的表现。
鲁棒控制与鲁棒控制器设计说明共95页

1
0
、
倚
南
窗
以
寄
傲
,
审
ቤተ መጻሕፍቲ ባይዱ
容
膝
之
易
安
。
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
Thank you
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
鲁棒控制与鲁棒控制器设计说明
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
频域角度下的鲁棒控制器设计与鲁棒性分析

频域角度下的鲁棒控制器设计与鲁棒性分析鲁棒控制器设计与鲁棒性分析是自动控制领域中的重要研究课题之一。
在实际工程应用中,系统常常会受到不确定性、非线性以及外部干扰等多种影响,而鲁棒控制器设计旨在提高系统的稳定性和性能,并使其对这些影响具有一定的抵抗能力。
本文将从频域角度出发,介绍鲁棒控制器设计的基本原理和方法,并针对所设计的鲁棒控制器进行鲁棒性分析。
一、鲁棒控制器设计的基本原理和方法鲁棒控制器设计的目标是使系统具有鲁棒稳定性和性能,即能够保持系统的稳定性和满足一定的性能要求。
鲁棒控制器设计的基本步骤可以分为以下几个方面:1.系统建模:首先需要对待控制系统进行建模,包括系统的数学描述和参数估计。
常用的系统建模方法有传递函数模型、状态空间模型等。
2.鲁棒性分析:在设计鲁棒控制器之前,需要对系统的不确定性和干扰进行分析,以确定系统的不确定性边界。
常用的鲁棒性分析方法有离散化鲁棒性分析、频域鲁棒性分析等。
3.设计鲁棒控制器:在确定系统的不确定性边界后,可以采用鲁棒控制器的设计方法进行控制器的设计。
常用的鲁棒控制器设计方法有H∞控制、μ-合成控制等。
4.性能评价与优化:设计出鲁棒控制器后,需要对其进行性能评价和优化。
常用的性能评价指标包括稳定裕度、性能指标等。
二、鲁棒控制器的频域设计方法频域设计方法是一种常用的鲁棒控制器设计方法,其基本思想是通过频域分析来获取系统的频率特性,从而设计出具有鲁棒性能的控制器。
常用的频域设计方法包括基于Bode图的设计方法、基于Nyquist图的设计方法等。
1.基于Bode图的设计方法:Bode图是描述系统的频率特性的一种图形表示方法,通过绘制系统的幅频响应曲线和相频响应曲线,可以直观地了解系统的频率响应。
基于Bode图的设计方法通过在Bode图上设定一定的稳定裕度要求,设计出满足要求的控制器。
2.基于Nyquist图的设计方法:Nyquist图是描述系统的稳定性和相位裕度的一种图形表示方法,通过绘制系统的开环传递函数的极点和零点的轨迹,可以对系统的稳定性进行分析。
最优控制问题的鲁棒H∞控制设计

最优控制问题的鲁棒H∞控制设计最优控制理论在工程系统控制中具有重要的应用价值。
然而,传统的最优控制方法在系统模型存在不确定性或外部干扰的情况下可能无法有效应对。
为了克服这一问题,鲁棒控制方法被引入到最优控制中,并且在实际应用中取得了显著的成果。
本文将探讨最优控制问题的鲁棒H∞控制设计方法及其应用领域。
一、鲁棒控制概述鲁棒控制是一种针对不确定性或外部干扰具有克服能力的控制方法。
其目标是在不确定性环境中实现系统稳定性和性能要求。
最常见的鲁棒控制方法之一是H∞控制,该方法通过优化问题来设计控制器,以抑制系统中不确定性的影响。
二、最优控制问题最优控制问题旨在通过选择最佳控制策略来实现系统的最优性能。
在没有不确定性时,可以使用动态规划、变分法等方法求解最优控制问题。
然而,在实际应用中,系统往往存在参数不确定性或外部干扰,导致最优控制问题变得更加复杂。
因此,需要引入鲁棒控制方法来解决这些问题。
三、鲁棒H∞控制设计方法鲁棒H∞控制方法是一种常用的鲁棒控制方法,其基本思想是在保证系统稳定性的前提下,优化系统对外部干扰的抑制能力。
鲁棒H∞控制设计问题可以被描述为一个优化问题,目标是最大化系统的H∞性能指标,并且确保控制器对系统模型不确定性具有鲁棒性。
为了实现鲁棒H∞控制设计,可以采用两种常用的方法:线性矩阵不等式(LMI)方法和基于频域分析的方法。
LMI方法通过求解一组线性矩阵不等式来得到控制器参数,从而实现系统的鲁棒H∞控制设计。
基于频域分析的方法则通过频域特性分析来设计控制器,以实现系统对不确定性的鲁棒性。
四、鲁棒H∞控制设计的应用领域鲁棒H∞控制设计方法在工程领域有广泛的应用。
它可以应用于飞行器姿态控制、机器人控制、智能电网控制等多个领域。
以飞行器姿态控制为例,鲁棒H∞控制设计可以有效提高飞行器对外部干扰的鲁棒性,并且保证姿态跟踪性能。
在机器人控制领域,鲁棒H∞控制设计可以提高机器人对环境不确定性的抑制能力,以实现精确的轨迹跟踪。
鲁棒控制与鲁棒控制器设计

9
高等应用数学问题的MATLAB求解——MATLAB语
言与应用——MATLAB语言与应用——MATLAB语
言与应用——MATLAB语言与应用
2020/7/15东北大学Fra bibliotek息学院10
【例7-2】
高等应用数学问题的MATLAB求解——MATLAB语
言与应用——MATLAB语言与应用——MATLAB语
言与应用——MATLAB语言与应用
言与应用——MATLAB语言与应用——MATLAB语
言与应用——MATLAB语言与应用
2020/7/15
东北大学信息学院
5
【例7-1】
高等应用数学问题的MATLAB求解——MATLAB语
言与应用——MATLAB语言与应用——MATLAB语
言与应用——MATLAB语言与应用
2020/7/15
东北大学信息学院
若想在对象模型的输出端恢复环路传递函数,则
高等应用数学问题的MATLAB求解——MATLAB语
言与应用——MATLAB语言与应用——MATLAB语
言与应用——MATLAB语言与应用
2020/7/15
东北大学信息学院
20
【例7-5】 对【例7-3】选定一个 q 向量,设计 LTR 控制器,并绘制出不同 q 值下环路传递函数 的 Nyquist 图。
高等应用数学问题的MATLAB求解——MATLAB语
言与应用——MATLAB语言与应用——MATLAB语
言与应用——MATLAB语言与应用
2020/7/15
东北大学信息学院
21
7.2 鲁棒控制问题的一般描述
2020/7/15
东北大学信息学院
18
高等应用数学问题的MATLAB求解——MATLAB语
鲁棒控制与鲁棒控制器设计

精品PPT
【例5】带有双积分器的非最小相位受控对象
设计系统的最优
,选择加权函数
并选择极点漂移为 控制器。
精品PPT
精品PPT
3、新鲁棒控制工具箱 及应用
3.1 不确定系统的描述
精品PPT
【例6】典型二阶开环传函 选定标称值为
构造不确定系统模型。
精品PPT
对叠加型不确定性 对乘积型的不确定性
假定系统对象模型的状态方程为 的状态方程模型为
状态方程模型为
的模型表示为
,加权函数 的
,而非正则的
式中
精品PPT
这时鲁棒控制问题可以集中成下面三种形式:
灵敏度问题
并不指定
稳定性与品质的混合鲁棒问题
假定
为空
一般的混合灵敏度问题
要求三个加权函数都存在。
精品PPT
1.3 鲁棒控制系统的 MATLAB 描述
精品PPT
【例8】
精品PPT
假设系统的不确定部分为乘积型的,且已知 ,并已知不确定参数的变化范围为 ,设计固定的 控制器
精品PPT
4、 总结
小增益定理以及基于范数的鲁棒控制三种形式: 控制、 控制及最优 控制器,三种鲁棒控制问题,即灵
敏度问题、稳定性与品质的混合鲁棒问题及一般混合灵 敏度问题。 基于范数的鲁棒控制问题的 MATLAB 描述方法和鲁棒 控制器的计算机辅助设计的理论与求解方法。 新版本的鲁棒控制工具箱将三种著名的方法,统一到一 个框架下,给出了统一的模型描述与设计函数。
鲁棒控制工具箱的设计方法
精品PPT
2.1 鲁棒控制工具箱的 设计方法
鲁棒控制器的状态方程表示
其中 X 与 Y 由下面的两个代数 Riccati 方程求解
控制理论系统鲁棒控制器设计方法

控制理论系统鲁棒控制器设计方法鲁棒控制器设计方法是控制理论系统中的重要研究方向之一。
通过设计有效的鲁棒控制器,可以在不确定性和外部干扰的情况下保持系统的稳定性和性能。
本文将介绍一种常用的鲁棒控制器设计方法——H∞控制器设计方法,以及其在实际应用中的一些问题和挑战。
H∞控制器设计方法是鲁棒控制器设计中广泛应用的一种方法。
该方法通过鲁棒性性能指标H∞范数来描述系统的稳定性和性能,并通过优化过程来设计出满足要求的控制器。
在H∞控制器设计中,系统的不确定性和外部干扰被建模为带有加性扰动的系统。
通过引入权重函数,可以对系统的不同频率范围进行加权,从而实现对不确定性和干扰的控制。
在H∞控制器设计方法中,首先需要对系统进行数学建模。
这包括确定系统的状态方程、输入和输出方程以及系统的不确定性和外部干扰。
然后,根据系统的性能要求和鲁棒性要求,选择适当的H∞范数来描述系统的稳定性和性能指标。
一般来说,H∞范数越小,表示系统对不确定性和干扰更鲁棒。
接下来,通过优化过程来设计H∞控制器。
优化过程的目标是找到满足要求的控制器参数,使得系统的H∞范数最小。
这个过程通常通过数值优化方法来实现,例如线性矩阵不等式(LMI)方法。
通过计算和迭代,可以得到满足系统性能要求的控制器参数。
然而,H∞控制器设计方法在实际应用中面临一些挑战和问题。
首先,系统的建模可能存在不确定性和误差,这会影响控制器设计的准确性和性能。
其次,优化过程可能会面临计算复杂度的问题,尤其是在系统的维度较大的情况下。
此外,控制器的实时实施和稳定性问题也需要考虑。
针对这些问题和挑战,研究人员提出了一些改进和解决方法。
例如,可以使用系统辨识方法来改善系统的建模精度,从而提高控制器设计的准确性。
同时,优化算法的改进和并行计算技术的使用也可以显著提高控制器设计的效率。
此外,针对具体应用领域的特点,可以设计和应用一些特殊的鲁棒控制策略,例如基于自适应控制和模糊控制的方法。
鲁棒控制器设计1讲解
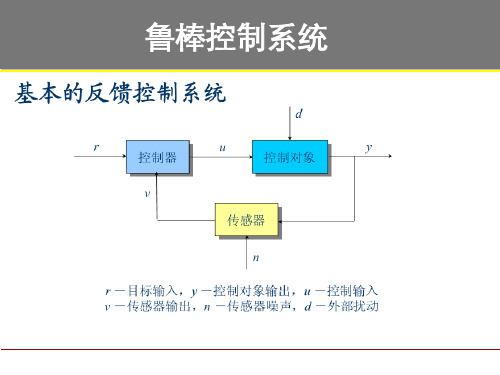
鲁棒控制系统
鲁棒控制系统设计
希望
T (s) Y (s) 1 R(s)
系统的伯德图平整,具有无限带宽的0db增益并且相角始终为零
r1
4,5, r2
[3,4], r3
[2,3]
取k=1,此时闭环传递函数的分母为
其中
s4 r3s3 r2s2 r1s 1 s3 2s2 2s 1 s4 p3s3 p2s2 p1s 2 p1 [2,3], p2 [5,6], p3 [3,4]
此时上面的闭环系统稳定当且仅当下面的四个多项式稳定
T (s) Y (s) Gc (s)G1(s)G2 (s) R(s) 1 Gc (s)G1(s)G2 (s)
Y(s)
G2 (s)
D(s) 1 Gc (s)G1(s)G2 (s)
鲁棒控制系统
T (s) 对D(s) 的灵敏度
SGT
1
1 Gc (s)G1(s)G2 (s)
要想降低系统的灵敏度S,就应该提高环路开环增益L(jw)
鲁棒控制系统
常用乘性摄动来描述受控对象的不确定性 乘性摄动更符合直觉 在低频段对象模型精确,乘性摄动较小 在高频段对象模型不够精确,乘性摄动较大
鲁棒控制系统
具有不确定参数的系统
假设系统的特征多项式为
其系数满足
f (s) ansn an1sn1 a1s a0
ai ai ai , i 0,1,, n,0 [ai , ai ]
鲁棒控制系统
鲁棒控制系统
鲁棒控制系统
鲁棒性分析
《鲁棒控制与鲁棒控制器设计》

《鲁棒控制与鲁棒控制器设计》鲁棒控制是指在系统存在不确定性和外部干扰的情况下仍然能够保证系统稳定性和性能的控制方法。
在现实生活中,控制系统往往会受到各种不确定因素的影响,如参数变化、外部扰动、测量误差等。
鲁棒控制的目标就是在这些不确定性的情况下,保持系统的稳定性和性能。
鲁棒控制器设计是实现鲁棒控制的关键环节。
其设计目标是要求控制器能够在不确定性和外部干扰的情况下仍然能够保持系统的稳定性和性能。
鲁棒控制器设计的方法有很多种,下面介绍两种常见的设计方法:1.H∞鲁棒控制H∞鲁棒控制是一种基于频域的鲁棒控制方法。
它通过最小化系统输入输出的γ范数来设计控制器,使系统对不确定性和外部干扰具有鲁棒稳定性和鲁棒性能。
H∞鲁棒控制的设计流程一般包括以下几个步骤:首先,建立系统模型,获取系统的传递函数;然后,根据系统模型设计一个传递函数为V的鲁棒性能权值V;接着,利用V来计算问题的解;最后,根据问题的解设计出最优的鲁棒控制器。
2.μ合成鲁棒控制μ合成鲁棒控制是一种基于频域分析的鲁棒控制方法。
它通过合成满足一定性能要求的不确定性权值函数,来设计鲁棒控制器。
μ合成鲁棒控制的基本思想是先构造正向控制律,使得系统的输出能够满足给定性能要求;然后,构造反向控制律,抵消系统的不确定性和外界干扰,使得系统具有鲁棒稳定性。
以上是两种常见的鲁棒控制器设计方法,它们都能够有效地确保系统在不确定性和外部干扰的情况下仍能保持稳定性和性能。
在实际应用中,根据具体系统的特点和需求,可以选择合适的鲁棒控制器设计方法来解决问题。
总结起来,鲁棒控制器设计是鲁棒控制的关键环节之一、通过合适的设计方法,能够使系统在面对不确定性和外部干扰的情况下仍然能够保持稳定性和性能。
在实际应用中,我们应根据具体情况选择合适的鲁棒控制器设计方法,以满足系统的要求。
直流电动机的鲁棒控制设计

直流电动机的鲁棒控制设计直流电动机的鲁棒控制设计直流电动机的鲁棒控制设计一、引言直流电动机在整个电力拖动应用中,占有十分重要的地位。
相对于交流电动机,直流电动机的调速性能更为优越,在大范围、高精度调速要求的应用中,成为首选。
因此,研究直流电动机的调速具有十分重要的意义。
由于电机的参数和模型受到其应用环境的影响,常规的 PID控制在电机参数发生变化的时候,将变得不可靠。
文中将鲁棒控制技术应用到电机调速系统中,可有效地避免电动机模型及外加载荷的变化对系统的影响,增加系统的可靠性。
文中设计了鲁棒控制器,给出了直流电动机的数学模型,并将设计的鲁棒控制器应用在直流电动机模型上,对其进行了计算机仿真实验,给出了仿真结果。
二、鲁棒控制器的设计 1、鲁棒控制鲁棒控制理论是在空间通过某些性能指标的无穷范数优化而获得具有鲁棒性能控制器的一种控制理论。
范数为矩阵函数在开右半平面的最大奇异值的上界,其物理意义是它代表系统获得的最大能量增益。
近年鲁棒控制方法得到迅速发展,特别是对模型具有不确定性及干扰能量为有限信号的系统,应用控制理论设计的控制器进行控制,使系统具有很强的鲁棒性。
2、系统的能控性和能观性研究能控性和能观性是控制器设计中比较基本的一步。
( 1)状态能控性状态能控性的含义是系统控制输入支配状态变量的能力。
状态能控性的定义:如果对任何初始状态任何时间,和任何最终状态,存在着一个输入使成立,则动态系统是状态可控。
反之,则系统的该状态不能控的。
若全体状态变量均满足要求,则称为系统是完全可控的。
能控性判据:系统可控的充分必要条件是的秩为 n, n是状态个数。
( 2)状态能观性状态能观性的含义是系统控制输出支配状态变量的能力。
状态能观的定义:如果对任何时刻,输入信号和在之间的输入,初始状态能被确定,则动态系统,是状态能观的。
反之,系统是状态不能观的。
若通过输出量的测量值确定所有状态变量,则系统是完全状态能观的。
状态能观判据:系统能观的充分必要条件是是满秩的,即秩为 n。
鲁棒控制与鲁棒控制器设计共40页文档

46、法律有权打破平静。——马·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
——MATLAB语言与应用
2020/6/6
东北大学信息学院
2
7.1 线性二次型 Gauss 控制
7.1.1 线性二次型 Gauss 问题
假设对象模型的状态方程表示为
为白噪声信号,分别表示模型的不确定 性与输出信号的量测噪声。
——MATLAB语言与应用
2020/6/6
东北大学信息学院
3
定义最优控制的指标函数为
——MATLAB语言与应用
2020/6/6
东北大学信息学院
36
变换出系统矩阵 P
——MATLAB语言与应用
2020/6/6
东北大学信息学院
37
【例7-7】用【例7-6】中的对象模型和加权函数, 得出其系统矩阵模型 P
——MATLAB语言与应用
2020/6/6
东北大学信息学院
38
7.3
鲁棒控制器的
——MATLAB语言与应用
2020/6/6
东北大学信息学院
16
▪ 先求解标准的 LQ 问题,然后应用 LTR 技术
——MATLAB语言与应用
2020/6/6
东北大学信息学院
17
——MATLAB语言与应用
2020/6/6
东北大学信息学院
18
【例7-4】 对【例7-3】不同的 q 值应用 LTR 技术
分数阶微积分的定义
——MATLAB语言与应用
2020/6/6
东北大学信息学院
64
当系数简单表示
——MATLAB语言与应用
2020/6/6
东北大学信息学院
65
编写求取给定函数的分数阶微分函数
——MATLAB语言与应用
2020/6/6
东北大学信息学院
66
Riemann-Liouville 定义为目前最常用的分数阶微积分定义
2020/6/6
东北大学信息学院
47
7.3.2 基于线性矩阵不等式 工具箱的设计方法
问题转 换成线性矩阵 不等式的最优 化问题
——MATLAB语言与应用
2020/6/6
东北大学信息学院
48
【例7-11】采用【例7-6】中增广的系统模型,用 LMI 工具箱的相关函数设计最优 控制器
——MATLAB语言与应用
70
7.5.2 分数阶线性系统频域 与时域分析
单变量线性系统的分数阶传递函数一般形式为
——MATLAB语言与应用
2020/6/6
东北大学信息学院
71
分数阶系统的频域分析
——MATLAB语言与应用
2020/6/6
东北大学信息学院
72
分数阶系统的时域分析
——MATLAB语言与应用
2020/6/6
——MATLAB语言与应用
2020/6/6
东北大学信息学院
40
控制器存在的前提条件为
足够小, 且满足
;
控制器 Riccati 方程的解为 正定矩阵;
观测器 Riccati 方程的解为 正定矩阵;
。该式说明两个 Riccati 方程的积
矩阵的所有特征值均小于 。
——MATLAB语言与应用
2020/6/6
都是良定的,
即如果系统的回路传递函数的范数小于 1,则闭 环系统将总是稳定的。
——MATLAB语言与应用
2020/6/6
东北大学信息学院
25
7.2.2 鲁棒控制器的结构
闭环系统中引入的增广对象模型
其对应的增广状态方程为
——MATLAB语言与应用
2020/6/6
东北大学信息学院
26
闭环系统传递函数为
③ 分数阶微积分算子为线性的,即对任意常数 , 有
——MATLAB语言与应用
2020/6/6
东北大学信息学院
69
④ 分数阶微积分算子满足交换律,并满足叠加关系 ⑤ 函数分数阶微分的 Laplace 变换为
特别地,若函数 及其各阶导数的初值均为 0,则
——MATLAB语言与应用
2020/6/6
东北大学信息学院
东北大学信息学院
41
【例7-8】对【例7-6】中的增广的系统模型,分别 设计
——MATLAB语言与应用
2020/6/6
东北大学信息学院
42
绘制在控制器作用下系统的开环 Bode 图和 闭环阶跃响应曲线
——MATLAB语言与应用
2020/6/6
东北大学信息学院
43
【例7-9】
加权矩阵
并设置
设计最优 控制器,并绘制出该控制器作用下的 阶跃响应曲线和开环系统的奇异值曲线。
——MATLAB语言与应用
2020/6/6
东北大学信息学院
27
鲁棒控制的目的是设计出一个镇定控制器
使得闭环系统
的范数取
一个小于 1 的值,亦即
鲁棒控制问题的三种形式:
最优控制问题 其中需求解
;
最优控制问题 其中需求解
;
控制问题 需要得出一个控制器满足
——MATLAB语言与应用
2020/6/6
东北大学信息学院
计算机辅助设计
鲁棒控制工具箱的设计方法 基于线性矩阵不等式工具箱的设计方法 基于 分析与综合工具箱的 控制器设计 基于回路成型技术的鲁棒控制器设计
——MATLAB语言与应用
2020/6/6
东北大学信息学院
39
7.3.1 鲁棒控制工具箱的 设计方法
鲁棒控制器的状态方程表示
其中
X 与 Y 由下面的两个代数 Riccati 方程求解
第7 章
鲁棒控制与鲁棒控制器 设计
薛定宇 著
《控制系统计算机辅助设计—— MATLAB语言与应用》 清华大学出版社
——MATLAB语言与应用
2020/6/6
东北大学信息学院
1
主要内容
线性二次型 Gauss 控制
鲁棒控制问题的一般描述
鲁棒控制器的计算机辅助设计
新鲁棒控制工具箱及应用
分数阶控制系统分析与设计
——MATLAB语言与应用
2020/6/6
东北大学信息学院
19
——MATLAB语言与应用
2020/6/6
东北大学信息学院
20
应用 MATLAB 求解 LQG/LTR 问题
若想使得系统在输入端恢复环路传递函数,则
若想在对象模型的输出端恢复环路传递函数,则
——MATLAB语言与应用
2020/6/6
28
加权灵敏度问题的控制结构框图
加权函数
,使得
均正则。
即传递函数在
时均应该是有界的。
——MATLAB语言与应用
2020/6/6
东北大学信息学院
29
假定系统对象模型的状态方程为 的状态方程模型为
状态方程模型为
的模型表示为
,加权函数 的
,而非正则的
式中
——MATLAB语言与应用
2020/6/6
东北大学信息学院
——MATLAB语言与应用
2020/6/6
东北大学信息学院
23
7.2.1 小增益定理
(a) 标准反馈控制结构
(b) 小增益定理示意图
——MATLAB语言与应用
2020/6/6
东北大学信息学院
24
• 小增益定理
假设
为稳定的,则当且仅当小增益条件 满足时
图 (b) 中所示的系统对所有稳定的 且是内部稳定的。
2020/6/6
东北大学信息学院
6
【例7-1】
——MATLAB语言与应用
2020/6/6
东北大学信息学院
7
LQG 控制器设计的分离原理
——MATLAB语言与应用
2020/6/6
东北大学信息学院
8
基于观测器的 LQG 调节器设计
——MATLAB语言与应用
2020/6/6
东北大学信息学院
9
由 Kalman 滤波器方程 可以写出基于观测器的 LQG 调节器为
——MATLAB语言与应用
2020/6/6
东北大学信息学院
4
7.1.2 使用 MATLAB 求解 LQG 问题
带有 Kalman 滤波器的 LQG 结构
——MATLAB语言与应用
2020/6/6
东北大学信息学院
5
Kalman 滤波器的增益矩阵
式中
, 满足下面的 Riccati 代数方程
——MATLAB语言与应用
——MATLAB语言与应用
2020/6/6
东北大学信息学院
67
Caputo 分数阶微分定义为
Caputo 分数阶积分定义为
——MATLAB语言与应用
2020/6/6
东北大学信息学院
68
分数阶微积分的性质
① 解析函数 的分数阶导数
对
都是解析的。
②
为整数时,分数阶微分与整数阶微分的
值完全一致,且
。
——MATLAB语言与应用
2020/6/6
东北大学信息学院
10
——MATLAB语言与应用
2020/6/6
东北大学信息学院
11
【例7-2】
——MATLAB语言与应用
2020/6/6
东北大学信息学院
12
7.1.3 带有回路传输恢复的 LQG 控制
LQG/LTR 控制器设计算法
直接状态反馈系统的开环传递函数为
东北大学信息学院
61
【例7-15】
——MATLAB语言与应用
2020/6/6
东北大学信息学院
62
假设系统的不确定部分为乘积型的,且已知 ,并已知不确定参数的变化范围为 ,设计固定的 控制器
