吉林省职高对口升学数学高考适应性考试试题七(含答案)

合集下载

职高数学试卷高考答案

一、选择题（每题5分，共50分）1. 下列各数中，有理数是（）A. √9B. √-1C. πD. √4/3答案：D2. 已知函数f(x) = 2x - 1，则f(-3)的值为（）A. -7B. -5C. 5D. 7答案：A3. 下列各式中，正确的是（）A. 3x^2 + 2x + 1 = (3x + 1)^2B. 4x^2 - 4x + 1 = (2x - 1)^2C. 9x^2 - 6x + 1 = (3x - 1)^2D. 16x^2 - 8x + 1 = (4x - 1)^2答案：B4. 在直角坐标系中，点A(2, 3)关于x轴的对称点为（）A. (2, -3)B. (-2, 3)C. (2, -3)D. (-2, -3)答案：A5. 已知等差数列{an}的前n项和为Sn，且a1 = 3，S5 = 55，则公差d为（）A. 5B. 4C. 3D. 2答案：D6. 下列函数中，奇函数是（）A. y = x^2B. y = |x|C. y = x^3D. y = x^4答案：C7. 下列各对数中，正确的是（）A. log2(8) = 3B. log2(16) = 4C. log2(4) = 2D. log2(2) = 1答案：D8. 在三角形ABC中，角A、B、C的对边分别为a、b、c，若a = 5，b = 7，c = 8，则三角形ABC的面积为（）A. 14B. 15C. 16D. 17答案：B9. 下列各式中，正确的是（）A. sin(α + β) = sinα + sinβB. cos(α + β) = cosα + cosβC. tan(α + β) = tanα + tanβD. cot(α + β) = cotα + cotβ答案：A10. 已知等比数列{an}的首项a1 = 2，公比q = 3，则第5项an为（）A. 54B. 162C. 243D. 729答案：B二、填空题（每题5分，共50分）1. 已知函数f(x) = 3x - 2，则f(2)的值为______。

对口高考数学试卷真题答案

1. 下列各式中，正确的是（）A. （a+b）^2 = a^2 + 2ab + b^2B. （a-b）^2 = a^2 - 2ab + b^2C. （a+b）^3 = a^3 + 3a^2b + 3ab^2 + b^3D. （a-b）^3 = a^3 - 3a^2b + 3ab^2 - b^3答案：C解析：根据立方公式，（a+b）^3 = a^3 + 3a^2b + 3ab^2 + b^3，（a-b）^3 = a^3 - 3a^2b + 3ab^2 - b^3，所以选C。

2. 若m、n是方程x^2 - 2x - 3 = 0的两个根，则（m+n）^2的值为（）A. 8B. 10C. 12D. 14答案：A解析：根据一元二次方程的根与系数的关系，m+n = -(-2)/1 = 2，所以（m+n）^2 = 2^2 = 4，选项A符合题意。

3. 已知函数f(x) = x^2 - 4x + 3，若f(x) = 0，则x的值为（）A. 1B. 2C. 3D. 4答案：C解析：根据一元二次方程的求根公式，x = (-(-4) ± √((-4)^2 -4×1×3))/(2×1) = (4 ± √4)/2 = 2 ± 1，所以x的值为2或3，选项C符合题意。

4. 已知等差数列{an}的公差为d，首项为a1，第n项为an，则an = （）A. a1 + (n-1)dB. a1 - (n-1)dC. a1 + ndD. a1 - nd答案：A解析：根据等差数列的通项公式，an = a1 + (n-1)d，所以选A。

5. 已知函数f(x) = x^2 + kx + 1，若f(x)在x=1时取得最小值，则k的值为（）A. -2B. -1C. 0D. 1答案：B解析：根据二次函数的性质，对称轴为x = -k/2，所以当x=1时，对称轴上的函数值最小，即f(1) = 1 + k + 1 = 2 + k，令2 + k = 0，解得k = -1，选项B符合题意。

对口高考数学模拟试卷含答案

对口高考数学模拟试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试用时120分钟.第Ⅰ卷（选择题共50分）参考公式：如果事件A 、B 互斥，那么柱体(棱柱、圆柱)的体积公式P （A+B ）=P （A ）+P （B ） h V S =柱体如果事件A 、B 相互独立，那么其中S 表示柱体的底面积，P （A ·B ）=P （A ）·P （B ）h 表示柱体的高一、单项选择题：（每一小题仅有一个正确答案，请将正确答案的代号填入答题表内。

每小题5分，共计60分）1．下列关系中正确的是 ( )A. φ∈0B.a ∈{a}C.{a,b}∈{b,a}D. φ=}0{ 2．不等式21≥-xx 的解集为（）A ． )0,1[-B ． ),1[+∞-C ． ]1,(--∞D ． ),0(]1,(+∞--∞3．对任意实数,,a b c 在下列命题中，真命题是（）A ． ""ac bc >是""a b >的必要条件B ． ""ac bc =是""a b =的必要条件C ． ""ac bc >是""a b >的充分条件D ． ""ac bc =是""a b =的充分条件4．若平面向量与向量)2,1(-=的夹角是o 180，且53||=，则=（）A ． )6,3(-B ． )6,3(-C ． )3,6(-D ． )3,6(-5．设P 是双曲线19222=-y ax 上一点，双曲线的一条渐近线方程为023=-y x ，1F 、2F 分别是双曲线的左、右焦点。

若3||1=PF ，则=||2PF （）A ． 1或5B ． 6C ． 7D ．96、原点到直线y=kx+2的距离为2，则k 的值为（）A. 1B. -1C. ±1D. ±77、若135sin )cos(cos )sin(=+-+αβααβα，且β是第二象限角，则βcos 的值为（） A ．1312 B ．1312- C ．53 D ．53-8、在等差数列{a n }中,a 1+a 2+a 3+a 4+a 5=15 , a 3= ( ) A. 2 B. 3 C. 4 D. 5 9、已知函数b a x f x +=)(的图象经过点)3,1(，又其反函数)(1x f-的图象经过点)0,2(，则函数)(x f 的表达式是（）姓名准考证号座位号A ．12)(+=x x fB ．22)(+=x x fC ．32)(+=x x fD ．42)(+=x x f 10、已知向量a 与b ，则下列命题中正确的是（）A. 若|a |>|b |，则a >bB. 若|a |=|b |，则a =bC. 若a =b ，则a ∥bD. 若a ≠b ，则a 与b 就不是共线向量11．下列函数中为偶函数的是（）A ．f(x)=1-x 3 B.f(x)=2x-1 C.f(x)=x 2+2 D.f(x)=x 312. 一商场有三个大门,商场内有两部上楼的电梯,一顾客从商场外到商场二楼购物,不同的走法共有( )A.5种B.6种C.8种D.9种第Ⅱ卷（非选择题共100分）二、填空题：（本大题共4小题，每小题4分，共16分.答案填在题中横线上）11．一个圆柱的底面半径和高都与一个球的直径相等，则该圆柱与该球的体积比为____________。

吉林省对口高考试题及答案

吉林省对口高考试题及答案吉林省对口高考试题及答案是许多高中生关注的热门话题，这些题目意在考察吉林省高中学生的综合素质和学科知识。

吉林省教育厅按照统一的考试大纲，制定了相应的试题，旨在评估学生的学业水平和学力发展情况。

在考试科目方面，通常包括语文、数学、英语等主要学科。

其中，语文试题要求学生运用所学的词汇、语法、修辞手法等技巧进行阅读和写作。

数学试题则注重学生的逻辑思维和数学运算能力，要求学生能灵活运用各种数学方法解决实际问题。

而英语试题则考察学生的听力、阅读、口语和写作等综合语言能力。

这些对口高考试题的难度各异，要求学生不仅要对基础知识掌握熟练，还需要具备良好的思维能力和解题技巧。

因此，备考期间学生需要有针对性地进行复习练习，不断巩固知识点，并培养自己的问题解决能力。

对于有些学生来说，吉林省对口高考试题及答案的公布是一种机会和挑战。

通过了解试题及答案，他们可以更好地了解自己在各学科上的薄弱环节，并有针对性地进行针对性的学习。

同时，通过对试题及答案的分析，学生也能够深入了解考试对学生综合能力的评价标准。

这对于他们未来的学习规划和职业选择都具有重要意义。

基于此，吉林省对口高考试题及答案的公开就成了学生、家长和老师们争相关注的焦点。

然而，需要指出的是，吉林省对口高考试题及答案的公布并不应被作为单一的评价标准。

学生的学习成绩和综合素质还应该综合考虑其他因素，例如平时表现、实践能力和创新能力等。

因此，学生和家长们在面对吉林省对口高考试题及答案时，也要保持理性和客观，不应把所有的期望寄托在试题的公布上。

综上所述，吉林省对口高考试题及答案的公布对学生学习和发展具有一定的指导意义。

它可以帮助学生了解自己学科上的不足，并提供复习方向；同时也让学生接触到评价标准，为未来学习和职业规划做好准备。

然而，我们不能把对口高考试题及答案看作是唯一的评价标准，还需要综合其他因素进行评估。

希望吉林省对口高考试题及答案的公布能够给学生带来实际的帮助，促进各方面的全面发展。

吉林职高对口升学数学高考复习模拟试题七(含答案)

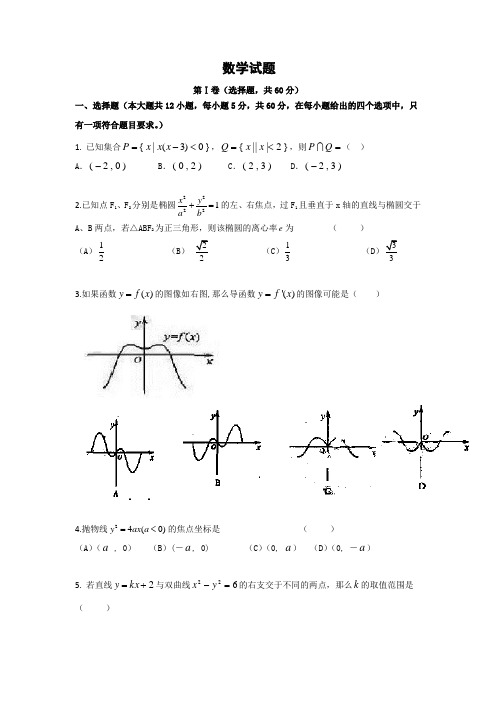
数学试题第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目要求。

）1. 已知集合}0)3(|{<-=x x x P ，}2|||{<=x x Q ，则=Q P （） A ．)0,2(- B ．)2,0(C ．)3,2(D ．)3,2(-2.已知点F 1、F 2分别是椭圆22221x y a b+=的左、右焦点，过F 1且垂直于x 轴的直线与椭圆交于A 、B 两点，若△ABF 2为正三角形，则该椭圆的离心率e 为（）（A ）12 （B ） 22 （C ）13（D ）333.如果函数()y f x =的图像如右图,那么导函数'()y f x =的图像可能是（）4.抛物线24(0)y ax a =<的焦点坐标是（）（A ）（a , 0）（B ）(－a , 0) （C ）（0, a ）（D ）（0, －a ）5. 若直线2+=kx y 与双曲线622=-y x 的右支交于不同的两点，那么k 的取值范围是（）（A ）（315,315-）（B ）（315,0）（C ）（0,315-）（D ）（1,315--）6.已知命题tan 1p x R x ∃∈=：，使，其中正确的是（）(A) tan 1p x R x ⌝∃∈≠：，使(B) tan 1p x R x ⌝∃∉≠：，使 (C) tan 1p x R x ⌝∀∈≠：，使(D) tan 1p x R x ⌝∀∉≠：，使7.双曲线22221x y a b-=（a ＞0，b ＞0）的两个焦点为F 1、F 2，若P 为其上一点，且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为（）（A ）（1,3）（B ）(]1,3 （C ）()3,+∞ （D ）[)3,+∞8.函数y =的值域为（）A 、[]0,2B 、[]0,4C 、(],4-∞D 、[)0,+∞9.对具有线性相关关系的变量x ，y 有一组观测数据（x i ，y i )(i=1，2，…，8)，其回归直线方程是ax y +=31：，且x 1+x 2+x 3+…+x 8=2(y 1+y 2+y 3+…+y 8)=6，则实数a 的值是（）A. 161B. 81C. 41D. 2110. 设曲线220x y -=与抛物线24y x =-的准线围成的三角形区域（包含边界）为D ，),(y x P 为D 内的一个动点，则目标函数52+-=y x z 的最大值为（）A ．4B ．5C ．8D ．1211.已知βα,是两个不同的平面，m ，n 是两条不同的直线，给出下列命题：①若βαβα⊥⊂⊥，则m m ,； ②若βαββαα//,////,,则，n m n m ⊂⊂；③如果ααα与是异面直线，那么、n n m n m ,,⊄⊂相交； ④若.////,//,βαβαβαn n n n m n m 且，则，且⊄⊄=⋂ 其中正确的命题是（） A ．①② B ．②③ C ．③④ D ．①④12.设3212a=log 2b=log 3c=log 5，，,则（）A ．c ﹤b ﹤aB ．a ﹤c ﹤b C. c ﹤a ﹤b ．D ．b ﹤c ﹤a第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4个小题，每小题5分，共20分）13.已知实数x 、y 满足不等式组52600x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩，则34z x y =+的最大值是________。

2020届中职数学对口升学复习测试题含答案(集合不等式函数指数对数数列)

2020届中职数学对口升学总复习测试题（集合不等式函数指数对数数列测试题）一、选择：1.已知{|5},5M x x a =≤=则下列关系中正解的是（）A.a M ⊆B.a M ∈C.{}a M ∈D.{}M a ∈ 2.21x 0x x >->是的（）条件A.充分不必要B.必要不充分C.充要条件D.以上都不对3.下列函数在(,)-∞+∞上是增函数的是（）A.21y x =+B.y =C.y=3xD.y=sinx 4.二次函数y=215322y x x =---的顶点坐标是（）A.(3,2)B.(-3,-2)C.(-3,2)D.(3,-2)5.下列函数是偶函数的是（）A.3y x =B.42y x x =+C.y=sinxD.y=x+16.函数f(x)=sinxcosx 是（）A.2T π=的奇函数B.2T π=的偶函数C.T π=的奇函数D.T π=的偶函数7.已知a,b,c 成等差数列且a+b+c=18，则b=( )A.6B.8C.9D.188.已知集合U={1,2,3,4,5},M={1,2,3},N={3,4},则()U M C N ⋂=( )A.{2,4}B.{1,2}C.{0,1}D.{0,1,2,3} 9.若12()log (3)f x x =-，则f(7)=( )A.1B.-2C.0D.510.等差数列1,5,9...,前10项的和是（）A.170B.180C.190D.200二、填空（每小题4分，共32分）11.cos 225︒=_____________12.数学2lg(43)y x x =+-的定义域为_______________ 13.sin80cos 20cos80sin 20︒︒︒︒-=________14.若2()log (3)f x x =-，则f(5)=_________15.比较大小：2330.2___2.3-- 16.在等比数列中，已知1352,8,a ___a a ===则17.在ABC ∆中,2,45,___a b A C ︒===∠=则 18.3322log log _____927-= 三、解答题（共38分）19. (1)求值.222222650(93)-︒-⨯++⨯(4分)(2)求解不等式2321()22x x -->(4分)20.(6分)已知等差数列{}n a 的公差d=1，若131,,a a 成等比数列，求1a .21.(6分)已知函数22y x x =-+,求值域.22.(6分)如果集合A=2{|20}x x ax -+=只有一个元素，求a 的值.23.(6分)求函数sin(2)3y x π=-的单调递增区间. 24.(6分)已知 1sin cos 5θθ-=，求sin cos θθ的值.姓名__________________总分______________一、选择题(本大题共10个小题，每小题4分，共40分)二、填空题：（本大题共8小题，每小题4分，共32分）11、12、13、14、15、16、17、18、三、解答题：（本大题共28分）19、（1）（2）20、21、22、23、24、参考答案：1-10 BACCB CABBC11.; 12. (-1,4) ; 13. 14. 1;15. >; 16. 32 ; 17. 105︒18.119.（1）43；（2）（-1，3）；20.112a=-或；21.7 [,)4+∞；22.a=±23.5[,] 1212k kππππ-++；24.12 25 -。

数学对口高考试题及答案

数学对口高考试题及答案第一节：选择题1. 设函数$f(x)=\frac{1}{x}$，则$f\left( \frac{1}{2} \right)=$_________。

A. $-2$B. $2$C. $-\frac{1}{2}$D. $\frac{1}{2}$答案：D. $\frac{1}{2}$2. 设$a$、$b$、$c$满足条件$a+b+c=0$，则$\frac{a^3+b^3+c^3}{3abc}=$_________。

A. $-1$B. $3$C. $1$D. $-3$答案：A. $-1$3. 曲线$y=ax^2+bx+c$（a>0）与$x$轴交于两点$A$、$B$，交与$y$轴交于点$C$，且$S_{\bigtriangleup ABC}=15$，则该曲线的表达式为_________。

A. $y=2x^2+3x-1$B. $y=2x^2-3x+1$C. $y=2x^2-3x-1$D.$y=2x^2+3x+1$答案：C. $y=2x^2-3x-1$第二节：填空题1. 利用对数表，计算$log_520$的值为_________。

答案：$1.5$2. 已知函数$f(x)=\log_2{x}$，则方程$f\left( x^{2^{x}} \right)+1=f^{-1}(x)$的解为_________。

答案：$x=0$ or $x=1$3. 设$x^2+ax+b=0$，其中$a$，$b$为实数，$x_1$、$x_2$是其两个根。

若$x_1+\frac{1}{x_2}=3$，$x_2+\frac{1}{x_1}=2$，则$a$、$b$的值分别是_________。

答案：$a=-4$，$b=10$第三节：解答题1. 已知函数$f(x)=\frac{1}{x-1}$，函数$g(x)=x^2-5$，求复合函数$f(g(x))$的定义域。

解答：首先找出复合函数$f(g(x))$的表达式：$f(g(x))=\frac{1}{(x^2-5)-1}=\frac{1}{x^2-6}$。

职中对口数学试卷高考模拟

一、选择题（本大题共10小题，每小题4分，共40分）1. 下列各数中，绝对值最小的是（）A. -3B. -2C. 0D. 12. 若m，n是方程x^2 - (m+n)x + mn = 0的两根，则m+n的值是（）A. 0B. 1C. 2D. m+n3. 下列函数中，是奇函数的是（）A. y = x^2B. y = |x|C. y = x^3D. y = x^44. 在直角坐标系中，点P(2,3)关于x轴的对称点是（）A. (2,-3)B. (-2,3)C. (-2,-3)D. (2,3)5. 若等差数列{an}的首项为2，公差为3，则第10项a10的值是（）A. 29B. 28C. 27D. 266. 下列各式中，正确的是（）A. a^2 = b^2，则a = bB. a^2 = b^2，则a = ±bC. a^2 = b^2，则a = ±b，b = ±aD. a^2 = b^2，则a = b，b = a7. 若等比数列{an}的首项为1，公比为2，则第n项an的值是（）A. 2nB. 2n-1C. 2^nD. 2^(n-1)8. 在△ABC中，若∠A=60°，∠B=45°，则∠C的度数是（）A. 75°B. 120°C. 45°D. 60°9. 下列函数中，是反比例函数的是（）A. y = 2xB. y = x^2C. y = 1/xD. y = x^310. 若sinα = 1/2，则cosα的值是（）A. √3/2B. -√3/2C. 1/2D. -1/2二、填空题（本大题共5小题，每小题5分，共25分）11. 已知函数y = -x^2 + 4x - 3，则该函数的对称轴是________。

12. 若等差数列{an}的首项为a1，公差为d，则第n项an = ________。

13. 在直角坐标系中，点P(-2,1)关于原点的对称点是________。

2017年吉林省高等职业教育对口招生统一考试数学试题

2017年吉林省高等职业教育对口招生数学试题一．选择题：本大题共12小题，每小题5分，共60分1.设集合{}12|<≤-=x x A ，集合{}21|≤≤-=x x B ，则A B=( )A. [)1,2-B.[]2,2-C. [)1,1-D.（-∞，-2）∪（2，∞） 2,设4log 2≤x ，则x 的取值范围是（）A ．(]16,∞-B ．(]16,0C ． [)+∞,16D ． (]8,03.设函数32)1()(2++-=mx x m x f ，满足2)1(=-f 则)(x f 是（）A.奇函数，在区间（-∞，0）内单调递减B.奇函数，在区间)0,(-∞内单调递增C.偶函数，在区间()0,∞-内单调递减D.偶函数，在区间()0,∞-内单调递增 4.已知31sin -=α，且α是第三象限的角，则αtan =( ) A.42-B ．42 C.22- D ．22 5.等差数列{}n a 中，31-=a ，195100=a ，则=+983a a ( ) A.190 B ．192 C.194 D ．196 6.已知向量),1(m a =，向量)5,3(-=b ，若7=⋅b a ，则=m （）A ．32-B ．32C ．-2D ．2 7.过点（2，3），且与直线y=32+x 平行的直线的方程为（）A.042=-+y xB. 042=+-y xC.012=--y xD.012=+-y x 8.圆122=+y x 上的点到直线3x-4y+20=0的距离的最小径是（）A.3B.4C.1D.59. 若直线//a 平面α，直线//b 平面α，则a 与b 的位置关系是（） A ．平行 B.相交 C.异面 D.以上均有可能 10.)2(3x x -的展开式中，第4想的二项式系数是（）A.35B.560C.-560D.28011.三对夫妻坐成一排照相，每对夫妻必须相邻，则不同的坐法种数为（） A.720 B.48 C.6 D.1212.“a ，b ，c 成等比例数列 ”是“ac b =2”的（）A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件二、填空题：本大题共4小题，每小题4分，共16分. 13.函数x x y -++=251的定义域为 .（用区间作答） 14计算：=++325081log 2017_________. 15.已知指数函数y=)(x f ，且278)3(=f ，则其解析式)(x f = . 16.若4sin cos 4cos 2sin 3=-+aa aa ，则αtan =_______.三．解答题：本大题共6小题，共74分。

2023年吉林省吉林市普通高校对口单招数学自考模拟考试(含答案)

2023年吉林省吉林市普通高校对口单招数学自考模拟考试(含答案)一、单选题(10题)1.若集合A = {1，2}，集合B={1}，则集合A与集合B的关系是（）A.B.A=BC.B∈AD.2.某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种，现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是（）A.4B.5C.6D.73.某商品降价10%，欲恢复原价，则应提升（）A.10%B.20%C.D.4.已知互为反函数，则k和b的值分别是（）A.2，B.2，C.-2，D.-2，5.圆心为（1，1)且过原点的圆的方程是（）A.(x-l)2+(y-1)2=1B.(x+1)2+(y+1)2=1C.(x+1)2+(y+1)2=2D.(x-1)2+(y-1)2=26.由数字0，1，2，3，4，5组成没有重复数字的六位数，其中个位数小于十位数的共有（）A.210B.360C.464D.6007.A.2B.3C.4D.58.若a0.6<a<a0.4，则a的取值范围为（）</aA.a＞1B.0＜a＜1C.a＞0D.无法确定9.函数在（-，3）上单调递增，则a的取值范围是（）A.a≥6B.a≤6C.a＞6D.-810.若函数f(x)=x2+mx+1有两个不同的零点，则实数m的取值范围是（）A.(-1,1)B.(-2,2)C.(-∞，-2)∪(2，+∞)D.(-∞，-l)∪(l，+∞)二、填空题(10题)11.设平面向量a=(2，sinα)，b=(cosα，1/6），且a//b，则sin2α的值是_____.12.己知0<a<b<1，则0.2a 0.2b。

13.拋物线的焦点坐标是_____.14.15.16.要使的定义域为一切实数，则k的取值范围_____.17.i为虚数单位，1/i+1/i3+1/i5+1/i7____.18.己知三个数成等差数列，他们的和为18，平方和是116，则这三个数从小到大依次是_____.19.若logx=1，则x=_____.220.过点(1，-1),且与直线3x-2y+1=0垂直的直线方程为。

数学对口招生考试适应性训练及答案1

数学对口招生考试适应性训练（一）（训练时间120分，总成绩150分）班级座号姓名一、选择题（各4分，共60分）：1、若集合{}22+-==x y y A ，{}x x y y B 22-==，则B A I = （） A 、(]2,∞- B 、[)+∞-,1 C 、[]2,1- D 、()+∞∞-,2、在实数范围内，若关于x 的不等式)0(02≠<++a c bx ax 无解，则（） A 、0<a 且042>-ac b B 、0<a 且042≤-ac b C 、0>a 且042≤-ac b D 、0>a 且042>-ac b3、设R c b a ∈,,，命题甲：b a >，命题乙：44bc ac >，则甲是乙的（） A 、充分必要 B 、必要充分 C 、充要条件 D 、既不充分又不必要4、若()b x x f +=21的反函数为()51-=-ax x f ，那么b a ,的值分别是（） A 、25,2==b a B 、2,25==b a C 、5,21-==b a D 、21,5=-=b a5、三个数 22.0，2.0log 2，2.02 之间的大小关系是 ( )A 、22.0<2.02<2.0log 2 B 、22.0<2.0log 2<2.02C 、2.0log 2<22.0<2.02D 、 2.0log 2<2.02<22.06、函数()x x x f 2=是（） A 、偶函数，又是增函数 B 、偶函数，又是减函数 C 、奇函数，又是增函数 D 、奇函数，又是减函数7、函数()1log 21-=x y 的定义域是（）A 、()+∞,1B 、()+∞,2C 、(]2,1D 、()2,18、()︒+︒+︒︒20tan 10tan 320tan 10tan 等于（）A 、33B 、1C 、3D 、6 9、在等差数列{}n a 中，若155=S ，则3a 为（）A 、3B 、4C 、5D 、610、若cm P P 121=，点1P P 在、2P 延长线上，cm PP 22=，则点P 分21P P 所成的比是（）A 、2B 、-2C 、23 D 、23- 11、实数b a ,满足0>ab ，方程b ax y +=和by x 22-=的图形是（）12、过坐标原点与圆()1222=+-y x 相切的直线的斜率是（）A 、33B 、3C 、33±D 、3±13、已知二面角βα--l 内一点P 到二面角的两个面α、β的距离分别为PB PA ,，且2===AB PB PA ，则二面角的度数是（）A 、︒60B 、︒120C 、︒60或︒120D 、︒15014、100张奖券中,有4张中奖券,从中抽取2张,则2张都是中奖券的概率（） A 、501B 、251C 、8251D 、4950115、()ny x +的展开中，第5项的二项式系数与第8项的二项式系数相等，则n= ( ) A 、10 B 、11 C 、12 D 、13 二、填空题（各6分，共30分）：16、不等式组⎪⎩⎪⎨⎧<-≥-7112x x 的解集用区间表示为17、经过A(2,-1),B(-2,3)两点的直线方程是 18、函数x x y 22cos sin -=的最小正周期是19、短轴长为 5 ,离心率为23 的椭圆的两个焦点为F 1,F 2,过F 1作直线交椭圆于A,B.则△ABF 2的周长为20、在ABC ∆中，已知7,3,120==︒=∠BC AB BAC ，则AC = . 21、三个运动员打破某项记录的概率都是0.1，那么一次比赛中记录未被打破的概率是 .三、解答题：22、（8分）计算：()3log 060cos 3131313120sin 09.0271⎪⎭⎫⎝⎛+︒-+-⎪⎭⎫⎝⎛︒-π23、（8分）已知二次函数当1-=x 时，有最值4，且它的图象过点（1，6），求这个二次函数.24、（10分）证明：21tan 212sin 2cos 112sin +=+++αααα25、（10分）已知正方形ABCD ，边长为4，过A 作平面ABCD 的垂线AM ，其长为3，求点M 到正方形ABCD 的边CD 及对角线BD 的距离.MABCD26、（12分）将进货单价为8元的商品按10元一个销售时，每天可卖出100个，若这种商品的销售价格每个上涨1元，则日销售量就减少10个。

职中对口数学试卷高考答案

一、选择题（每题4分，共20分）1. 已知函数f(x) = 2x - 3，若f(x+1) = 2，则x的值为（）A. 1B. 2C. 3D. 4答案：B解析：将x+1代入函数f(x)中，得到f(x+1) = 2(x+1) - 3 = 2x - 1。

由题意知f(x+1) = 2，所以2x - 1 = 2，解得x = 2。

2. 在△ABC中，若∠A = 60°，∠B = 45°，则∠C的度数为（）A. 75°B. 90°C. 105°D. 120°答案：D解析：三角形内角和为180°，所以∠C = 180° - ∠A - ∠B = 180° - 60° - 45° = 75°。

3. 下列函数中，定义域为全体实数的是（）A. y = 1/xB. y = √(x-1)C. y = x²D. y = |x|答案：C解析：A项的定义域为x ≠ 0，B项的定义域为x ≥ 1，D项的定义域为全体实数，但y = |x|不是多项式函数。

只有C项的定义域为全体实数，且y = x²是一个多项式函数。

4. 已知等差数列{an}的首项a1 = 2，公差d = 3，则第10项a10的值为（）A. 27B. 30C. 33D. 36答案：D解析：等差数列的通项公式为an = a1 + (n-1)d，代入a1 = 2，d = 3，n = 10，得到a10 = 2 + (10-1)×3 = 2 + 27 = 29。

故选D。

5. 若复数z满足|z-1| = |z+1|，则z的几何意义是（）A. z在实轴上B. z在虚轴上C. z在y=x的直线上D. z在y=-x的直线上答案：A解析：复数z在复平面上的几何意义为z对应的点。

|z-1|表示z对应的点到点(1,0)的距离，|z+1|表示z对应的点到点(-1,0)的距离。

数学对口招生考试适应性训练及答案3

数学对口招生考试适应性训练(三)（训练时间120分钟，总成绩150分）班级姓名一、单项选择题（将正确答案的序号填入括号内；每小题4分，共48分）：1、设全集I={1，2，3，4，5，6，7，8}，集合M={3，4，5}，N={1，3，6}，则集合P={2，7，8}可表示成（）A. M∪N B . C I (M∪N) C. C I (M∩N) D . M∩N2、不等式x 2+6x+9＞0的解集是（）A.空集B.全体实数C.{x|x≠--3}D.{x|x ＜–3或x ＞3}3、已知ab ＞0，则“x=ab ”是“a, x, b 成等比数列”的（） A.充分非必要条件 B.必要非充分条件C.充要条件D.既非充分也非必要条件4、函数y=2cos 4x －2sin 4x 的最小正周期是（）A.πB. 2πC.4πD.2π5、设抛物线y=x 2＋ax －2的对称轴方程为x=1，则该抛物线顶点坐标为（）A.（1，－3）B.（1，－1）C.（1，0） D （―1，―3 ）6、下列函数为偶函数的是（）A. y=－xB. y=xsinxC. y=xcosxD. y=x 2+x7、设角α的终边过点P （－5，12），则cot α+sin α等于（） A.137B. －137C.15679D.－156798、抛物线y=2px 2的准线方程为（）A. x=－21B. y=－21C. x=－p 81D. y=－p 819、如果有5本不同的书籍，有一个人要借2本，借法有（）A. 10种B. 20种C. 25种D. 32种10、点M （2，4）与点N （3，3）关于下列直线中对称的是（）A. x －y=0B. x ＋y=0C. x ＋y －1=0D. x －y ＋1=011、椭圆25x 2+9y 2=225的一个焦点与短轴的一个顶点的距离是（）A. 5B. 6C. 8D. 1012、下列命题正确的是（）A.过平面外一点有且仅有一个平面和这个平面平行；B.过平面外一点有且仅有一个平面和这个平面垂直；C.所有平行的直线必定都在同一个平面内；D.平面α的斜线a 在平面上的射影是直线b ，如果c⊥b，则c⊥a。

对口升学数学试题及答案

对口升学数学试题及答案一、选择题（每题3分，共30分）1. 下列函数中，哪一个是奇函数？A. $ f(x) = x^2 $B. $ f(x) = x^3 $C. $ f(x) = x^4 $D. $ f(x) = \frac{1}{x} $答案：B2. 已知等差数列的首项为2，公差为3，求该数列的第5项。

A. 17B. 14C. 11D. 8答案：A3. 计算以下极限：\[ \lim_{x \to 0} \frac{\sin x}{x} \]A. 0B. 1C. 2D. 3答案：B4. 以下哪个选项是二项式定理的展开式？A. $ (a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k $B. $ (a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^k b^{n-k} $C. $ (a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k $D. $ (a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^k b^{n-k} $答案：B5. 已知函数 $ f(x) = ax^2 + bx + c $ 的图像与x轴有两个交点，且这两个交点的横坐标之和为-4，求b的值。

A. 4B. -4C. 2D. -2答案：B6. 计算以下定积分：\[ \int_{0}^{1} x^2 dx \]A. $ \frac{1}{3} $B. $ \frac{1}{2} $C. $ \frac{1}{4} $D. $ \frac{1}{6} $答案：A7. 已知圆的方程为 $ (x-2)^2 + (y-3)^2 = 9 $，求该圆的半径。

A. 3B. 4C. 5D. 6答案：A8. 计算以下二重积分：\[ \iint_{D} (x^2 + y^2) dxdy \]其中D是由x=0，y=0，x+y=1构成的区域。

2022年吉林省吉林市普通高校对口单招数学一模测试卷(含答案)

2022年吉林省吉林市普通高校对口单招数学一模测试卷(含答案)班级:________ 姓名:________ 考号:________一、单选题(20题)1.若等差数列{a n}中，a1=2，a5=6,则公差d等于（）A.3B.2C.1D.02.三角函数y=sinx2的最小正周期是( )A.πB.0.5πC.2πD.4π3.若函数f（x-）=x2+，则f（x+1）等于（）A.（x+1）2+B.（x-）2+C.（x+1）2+2D.（x+1）2+14.函数y=|x|的图像( )A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于y=x直线对称5.袋中有大小相同的三个白球和两个黑球，从中任取两个球，两球同色的概率为（）A.1/5B.2/5C.3/5D.4/56.等差数列{a n}中，若a2+a4+a9+a11=32，则a6+a7=()A.9B.12C.15D.167.A.第一象限角B.第二象限角C.第一或第二象限角D.小于180°的正角8.已知平面向量a=(1,3），b(-1,1），则ab=A.(0,4)B.(-1,3)C.0D.29.椭圆9x2+16y2=144短轴长等于（）A.3B.4C.6D.810.A.B.C.11.集合M={a，b}，N={a+1，3}，a,b为实数，若M∩N={2}，则M∪N=()A.{0,1,2}B.{0,1,3}C.{0,2,3}D.{1,2,3}12.已知集合M={0，1，2,3}，N={1,3,4}，那么M∩N等于（）A.{0}B.{0,1}C.{1,3}D.{0，1，2,3,4}13.以点（2,0)为圆心，4为半径的圆的方程为（）A.(x-2)2+y2=16B.(x-2)2+y2=4C.(x+2)2+y2=46D.(x+2)2+y2=414.在等差数列{a n}中，若a3+a17=10，则S19等于( )A.65B.75C.85D.9515.设f（x）是定义在R上的偶函数，当x≤0时，f(x)=2x2-x，则f(-1)=()A.-3B.-1C.1D.316.下列函数为偶函数的是A.B.C.D.17.A.10B.5C.2D.1218.A.B.C.D.19.设a，b为实数，则a2=b2的充要条件是（）A.a=bB.a=-bC.a2=b2D.|a|=|b|20.A.πB.C.2π二、填空题(10题)21.22.若△ABC 中，∠C=90°,,则= 。

2022年吉林省吉林市普通高校高职单招数学测试题(含答案)

2022年吉林省吉林市普通高校高职单招数学测试题(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.设a=log32，b=log52，c=log23，则（）A.a＞c＞bB.b＞c＞aC.c＞b＞aD.c＞a＞b2.若a>b.则下列各式正确的是A.-a>-bB.C.D.3.已知集合A={x|x＞2}，B={x|1＜x＜3}，则A∩B=()A.{x|x＞2}B.{x|x＞1}C.{x|2＜x＜3}D.{x|1＜x＜3}4.若x2-ax+b＜0的解集为（1，2)，则a+b=( )A.5B.-5C.1D.-15.已知等差数列{a n}的前n项和为S n,a4=2，S10=10,则a7的值为（）A.0B.1C.2D.36.椭圆离心率是()A.B.C.5/6D.6/57.用简单随机抽样的方法从含有100个个体的总体中依次抽取一个容量为5的样本，则个体m被抽到的概率为（）A.1/100B.1/20C.1/99D.1/508.5人站成一排，甲、乙两人必须站两端的排法种数是（）A.6B.12C.24D.1209.若函数f(x)=x2+mx+1有两个不同的零点，则实数m的取值范围是（）A.(-1,1)B.(-2,2)C.(-∞，-2)∪(2，+∞)D.(-∞，-l)∪(l，+∞)10.A.6B.7C.8D.911.实数4与16的等比中项为A.-8B.C.812.在△ABC中，“x2=1” 是“x =1” 的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件13.A.B.C.14.若不等式x2+x+c＜0的解集是{x|-4＜x＜3}，则c的值等于（）A.12B.-12C.11D.-1115.下列函数是奇函数且在区间(0, 1)内是单调递增的是( )A.y = xB.y = lgxC.y = e xD.y = cosx16.在正方体ABCD-A1B1C1D1中，二面角D1-AB-D的大小是( )A.30°B.60°C.45°D.90°17.已知sin2α＜0,且cosa＞0,则α的终边在（）A.第一象限B.第二象限C.第三象限D.第四象限18.已知a∈(π，3/2π)，cosα=-4/5，则tan(π/4-α)等于（）A.7B.1/7C.-1/7D.-719.A=，是AB=的（）A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件20.已知的值（）A.B.C.D.二、填空题(20题)21.22.1+3+5+…+（2n-b）=_____.23.己知三个数成等差数列，他们的和为18，平方和是116，则这三个数从小到大依次是_____.24.若集合，则x=_____.25.某机电班共有50名学生，任选一人是男生的概率为0.4,则这个班的男生共有名。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数学试题第I 卷一、选择题:本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．抛物线24y x =的焦点为（）（A ）（0,1）（B ）（1,0）（C ）(0,1)- （D ）(1,0)-2．已知(2,0)M -，(2,0)N ，||3|PM PN|-=，则动点P 的轨迹是（）（A ）双曲线（B ）圆（C ）椭圆（D ）抛物线3. 已知命题p ：R ∀∈x ,cos 1≤x ，则p ⌝是（）（A ）∈∃0x R,1cos 0≥x （B ）∈∀x R,1cos ≥x（C ）∈∀x R,1cos >x （D ）∈∃0x R,1cos 0>x4. 已知函数()f x 的导函数()f x '的图象如图所示，那么函数()f x 的图象最有可能的是（）5．设,R a b ∈，那么“>1ab ”是“>>0a b ”的( )（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件6．可导函数在闭区间的最大值必在（）取得（A ）极值点（B ）导数为0的点（C ）极值点或区间端点（D ）区间端点7. )()()(0000lim x f x x f x x f x '=∆-∆+→∆，其中x ∆（）（A ）恒取正值或恒取负值（B ）有时可以取0（C ）恒取正值（D ）可以取正值和负值，但不能取08．下列说法正确的是（）（A ）0R x ∃∈，00x e ≤（B ）对,a b ∀>则2ab =,22min ()4a b +=（C ）1a >，1b >是1ab >的充分条件（D ）0a b +=的充要条件是1ab =-9．设等比数列{}n a 的公比2q =，前n 项和为n S ，则24a S 的值为（）（A ）154 （B ）152 （C ）74 （D ）72 10．已知12(1,0),(1,0)F F -是椭圆的两个焦点，过1F 的直线l 交椭圆于,M N 两点，若2MF N∆的周长为8，则椭圆方程为（）（A ）13422=+y x （B ）13422=+x y （C ）1151622=+y x （D ）1151622=+x y 11．函数32()f x x bx cx d =+++的大致图象如图所示，则2212x x +等于（）（A ）89 （B ）109 （C ）169 （D ）28912. 直线kx y =交双曲线22:143x y C -=于,A B 两点，P 为双曲线C 上异于,A B 的任意一点，则直线,PA PB 的斜率之积为( ) （A ）43 （B ）34（C ）233 （D ）32 第II 卷二、填空题:本大题共4小题，每小题5分，共20分．13．双曲线22149x y -=的渐近线方程是 . 14. n S 为等差数列{}n a 的前n 项和，266a a +=，则=7S .15．曲线ln y x =在点（1,0）处的切线方程为 .16. 已知双曲线:C 2221(0,1)y x b b b-=>≠的左右焦点为12F F ，，过点1F 的直线与双曲线C 左支相交于,A B 两点，若22||||2||AF BF AB +=，则||AB 为 .三、解答题：本大题共小6题,共70分,解答应写出文字说明、证明过程或演算步骤.17．（本小题满分10分）已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，A 为B ，C 的等差中项.(Ⅰ)求A ；(Ⅱ)若a ＝2，△ABC 的面积为3，求b ，c 的值.18．(本小题满分12分)不等式260x x --≤解集为M ,不等式2280x x +->解集为N ，不等式22320x ax a -+<)0(>a 解集为P .(Ⅰ) 求M N ；(Ⅱ)若“M N ”是“P ”的充分条件，求实数a 的取值范围.19．(本小题满分12分)已知函数32()23128f x x x x =--+.(Ⅰ)求函数()f x 的单调区间；(Ⅱ)若[2,3]x ∈-，求函数()f x 的值域.20．（本小题满分12分）已知离心率2e =的椭圆2222:1(0)x y C a b a b +=>>一个焦点为（-1,0).(Ⅰ)求椭圆C 的方程；(Ⅱ) 若斜率为1的直线l 交椭圆C 于,A B 两点,且||3AB =，求直线l 方程.21．（本小题满分12分）已知抛物线的顶点在坐标原点O ，对称轴为x 轴，焦点为F ,抛物线上一点A 的横坐标为2，且16=⋅OA FA 。

（Ⅰ）求抛物线的方程；（Ⅱ）过点)0,8(M 作直线l 交抛物线于B ，C 两点,求证:OC OB ⊥ .22．（本小题满分12分）已知函数21()ln 2f x x a x =+（0a <）. （Ⅰ）若1a =-，求函数()f x 的极值；（Ⅱ）若0x ∀>，不等式()0f x ≥恒成立，求实数a 的取值范围.参考答案一、选择题1．B ；2．A ；3.D ；4. A ；5．B ；6．C ；7. D ；8．C ；9．B ；10．A ；11．C ；12. B .二、填空题 13.x y 23±=；14.21；15.1y x =-；16.4．三、解答题17.解：(Ⅰ)∵A 为B ，C 的等差中项， 2A B C =+，2分 ······································∵A B C π++=,∴A ＝π3. ········································································· 4分 (Ⅱ)△ABC 的面积S ＝12bc sin A ＝3，故bc ＝4. ················································· 6分而a 2＝b 2＋c 2－2bc cos A ，故b 2＋c 2＝8. ·························································· 8分解得b ＝c ＝2. ························································································· 10分18.解：(Ⅰ)∵ 260x x --≤，∴{|23}M x x =-≤≤. ··································· 2分∵2280x x +->，∴{|2N x x =>或4}x <-. ········································ 4分 ∴实数M N 为{|23}x x <≤. ····························································· 5分(Ⅱ)由22430x ax a -+<得()(2)0x a x a --<，又0a >,∴{|2}P x a x a =<<, ···················································· 7分又“M N ”是“P ”的充分条件，∴ ⎩⎨⎧>≤,32,2a a . ···································· 9分 ∴实数a 的取值范围]2,23(. ························································· 12分 19.解：(Ⅰ)2()=6612f x x x --， . 当()0f x >，时，2x >或1x <-； ····························································· 2分当()0f x <，时， 12x -<<. ·································································· 4分 ∴函数()f x 的单调增区间为(,1)-∞-和(2,)+∞；函数()f x 的单调减区间为(1,2)-。