时滞系统的状态反馈和基于观测器的输出反馈设计
现在控制理论第五章状态反馈与状态观测器

(5-5)
引出的反馈系数,则
变换后k的0, 状态, 反kn馈1系统动态方程为 :
x1, ,xn
式中:
xAbkxbv
y Cx
0
1
0
0
0
1
Abk
0
0
0
a0k0 a1k1 a2k2
(5-6)
(5-7)
0
0
1
an1kn1
I A (5 -b 9)k n a n 1 k n 1 n 1 a 2 k 2 2 a 1 k 1 1
过 行
待设 矩阵
计的 ,负
参 反
y Cx 馈至系统的参考输入,于是存在
01 式中v为纯量, 为 为 维行矩阵,为 环状态阵,
维向量, 为
维矩阵, 为
维向量, 为
维矩阵。
为闭环特征多项式。
维向量, 为闭
02 用状态反馈使闭环极点配置在任意位置上的充要条件是:受控对象能 控
03
证明 :0
若1式
(
k0, ,kn1
k
能控的多输入-多输出系统,经如上类似分析可知,
实现闭环极点任意配置的状态反馈阵 K为 pn维 。
若受控对象不稳定,只要有能控性,完全可由状态反馈配置极点使系统稳定。 状态变量受控情况下,引入状态反馈表示增加一条反馈通路,它能改变反馈所 包围环节的传递特性,即通过改变局部回路的极点来改变闭环极点配置。不能 控状态变量与控制量无关,即使引入状态反馈,对闭环极点位置也不会产生任 何影响,这是因为传递函数只与系统能控、能观测部分有关的缘故。若不能控 状态变量是稳定的状态变量,那么系统还是能稳定的,否则,系统不稳定。
0
1
0
A
h
几类随机系统的输出反馈控制的开题报告

几类随机系统的输出反馈控制的开题报告本文将探讨几类随机系统的输出反馈控制,包括线性时间不变系统、非线性系统、时滞系统和分布式参数系统。
这些系统具有不同的特点和挑战,需要采用不同的控制策略来达到良好的控制效果。
本文将简要介绍这些系统的基本性质,并讨论一些有效的输出反馈控制方法。
一、线性时间不变系统线性时间不变系统是最常见的控制对象之一,它在自然界和人工系统中广泛存在。
这种系统的输出反馈控制是相对简单的,可以采用常见的控制方法如比例积分微分(PID)控制器和线性二次调节(LQR)控制器来设计。
此外,还有基于状态反馈的强化学习方法,如深度神经网络来实现高精度控制。
二、非线性系统非线性系统具有更复杂的行为和更强的不确定性。
输出反馈控制是更加困难的问题。
一般来说,非线性系统需要考虑非线性控制理论,如滑模控制、自适应控制、反馈线性化等。
这些方法利用系统的非线性特性来设计特定的控制方法,以达到良好的控制效果。
此外,还有一些现代控制理论,如基于反馈线性化的方法,如多参数自适应控制等。
三、时滞系统时滞系统是一类具有内部延迟的系统,在现实应用中也非常常见。
对于时滞系统的控制,可以采用状态反馈控制、动态输出反馈控制等方法来引入时滞信息。
此外,还有一些专门针对时滞系统设计的控制方法,如李亚普诺夫K增益法和滞后补偿法等控制策略。
四、分布式参数系统分布式参数系统是一类复杂的系统,具有高度的空间耦合和复杂的动态行为。
输出反馈控制针对这一类系统的设计较为困难,需要考虑系统的多个空间点之间的相互作用。
在这种情况下,可以采用传统的分布式参数系统的方法,如有限元方法,以及先进的控制策略,如模态控制和反演模型控制。
总之,针对随机系统的输出反馈控制方法需要考虑系统特定的性质和挑战,采用相应的控制方法来达到良好的控制效果。
在未来的研究中,还需开发更高效和实用的控制技术来适应不断发展的工业需求。
第六章状态反馈与状态观测器
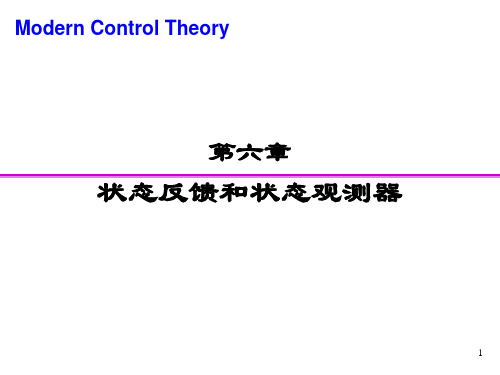
y 0 1x
1)判断原系统的能控性,能观性。 0 1 rankb Ab rank 2 能控 1 0
C 0 1 rank rank 2 CA 1 0
能观
13
6.1 状态反馈和输出反馈
2)引入状态反馈: u v Kx
则: x ( A bK ) x bV 可得:
Modern Control Theory
第六章
状态反馈和状态观测器
1
第六章 状态反馈和状态观测器
目前为止,我们已经:
建立了系统的状态空间模型
提出了基于状态空间模型的系统的运动分析
探讨了系统的性能:稳定性、能控性、能观性 “认识了世界” ⇒ 如何来“改变世界”?! 设计控制系统! 系统的控制方式----反馈?:开环控制、闭环控制
– 极点位置(系统矩阵的特征值)
通过反馈控制器的设计,可使得闭环系 统的极点位于预先给定的期望位置。
16
6.2 极点配置问题
定义:通过选择反馈增益矩阵K,将闭环系统的 极点恰好配置在根平面上所期望的位置,以获 得所希望的动态性能。
极点配置的方法:
一、采用状态反馈
(Ⅰ)定理:线性定常系统可通过线性状态反馈 任意地配置其全部极点的充要条件 是:此被控系统状态完全能控。
不改变 系统的 能控性 和能观 性
状态反馈 — 效果佳
都不改变 系统维数 (因为两种 反馈形式均 输出反馈 — 实现方便 但能力有限
未增加新的 状态变量)
15
6.2 极点配置问题
• 系统性能:稳态性能和动态性能
– 稳态性能:稳定性、静态误差 – 动态性能:调节时间、响应速度...
• 影响系统稳定性、动态性能的因素:
现代控制实验状态反馈器和状态观测器的设计

现代控制实验状态反馈器和状态观测器的设计现代控制实验中,状态反馈器和状态观测器是设计系统的重要组成部分。
状态反馈器通过测量系统的状态变量,并利用反馈回路将状态变量与控制输入进行耦合,以优化系统的性能指标。
状态观测器则根据系统的输出信息,估计系统的状态变量,以便实时监测系统状态。
本文将分别介绍状态反馈器和状态观测器的设计原理和方法。
一、状态反馈器的设计:状态反馈器的设计目标是通过调整反馈增益矩阵,使得系统的状态变量在给定的性能要求下,达到所需的一组期望值。
其设计步骤如下:1.系统建模:通过对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
通常表示为:ẋ=Ax+Buy=Cx+Du其中,x为系统状态向量,u为控制输入向量,y为系统输出向量,A、B、C、D为系统的状态矩阵。
2.控制器设计:根据系统的动态性能要求,选择一个适当的闭环极点位置,并计算出一个合适的增益矩阵。
常用的设计方法有极点配置法、最优控制法等。
3.状态反馈器设计:根据控制器设计得到的增益矩阵,利用反馈回路将状态变量与控制输入进行耦合。
状态反馈器的输出为:u=-Kx其中,K为状态反馈增益矩阵。
4.性能评估与调整:通过仿真或实验,评估系统的性能表现,并根据需要对状态反馈器的增益矩阵进行调整。
二、状态观测器的设计:状态观测器的设计目标是根据系统的输出信息,通过一个状态估计器,实时估计系统的状态变量。
其设计步骤如下:1.系统建模:同样地,对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
2.观测器设计:根据系统的动态性能要求,选择一个合适的观测器极点位置,以及一个合适的观测器增益矩阵。
常用的设计方法有极点配置法、最优观测器法等。
3.状态估计:根据观测器设计得到的增益矩阵,通过观测器估计系统的状态变量。
状态观测器的输出为:x^=L(y-Cx^)其中,L为观测器增益矩阵,x^为状态估计向量。
4.性能评估与调整:通过仿真或实验,评估系统的状态估计精度,并根据需要对观测器的增益矩阵进行调整。
线性时滞系统基于观测器的最优输出跟踪控制器近似设计

线性时滞系统基于观测器的最优输出跟踪控制器近似设计唐功友;李超;高洪伟
【期刊名称】《控制理论与应用》
【年(卷),期】2008(25)1
【摘要】研究线性时滞系统的最优输出跟踪控制器近似设计过程.首先根据原系统最优输出跟踪控制问题构造了两个分别具有已知初始条件和终端条件的微分方程迭代序列,并证明它们一致收敛于原问题的最优解.然后通过对该解序列的有限次迭代,得到最优输出跟踪控制问题的一个近似解,进一步给出一个计算近似最优输出跟踪控制律的算法.最后通过构造降维参考输入观测器解决了最优输出跟踪控制器中前馈项的物理可实现问题.仿真结果表明该方法是有效的,且易于实现.
【总页数】5页(P120-124)
【作者】唐功友;李超;高洪伟
【作者单位】中国海洋大,学信息科学与工程学院,山东,青岛,266100;中国海洋大,学信息科学与工程学院,山东,青岛,266100;中国海洋大,学信息科学与工程学院,山东,青岛,266100
【正文语种】中文
【中图分类】TP13
【相关文献】
1.受扰非线性时滞系统近似最优跟踪控制 [J], 唐功友;胡乃平;赵艳东
2.基于观测器的控制时滞线性系统的最优跟踪控制 [J], 张城明;唐功友;白玫
3.采用观测器的双线性系统最优跟踪控制器设计 [J], 唐功友;赵艳东;胡乃平
4.基于观测器的受扰非线性系统近似最优跟踪控制 [J], 唐功友;高德欣;张宝琳
5.受正弦扰动的线性时滞系统的最优输出跟踪控制 [J], 唐功友;胡乃平;赵艳东因版权原因,仅展示原文概要,查看原文内容请购买。
北航_自控实验报告_状态反馈和状态观测器

北航_自控实验报告_状态反馈和状态观测器摘要:本实验通过对一个质点的运动进行实时控制的实验研究,了解了状态反馈和状态观测器的原理和应用。
通过实验验证了状态反馈和状态观测器在控制系统中的重要性和有效性。
1引言状态反馈和状态观测器是控制系统中常用的两种控制方法,可以实现对系统状态的准确估计和实时控制。
在实际控制应用中,状态反馈和状态观测器广泛应用于电力系统、轨道交通系统等领域。
本实验通过对一个质点运动的控制,以实验方式掌握状态反馈和状态观测器的原理和应用。
2实验目的2.1理解状态反馈和状态观测器的原理;2.2 学会使用Matlab编程实现状态反馈和状态观测器;2.3通过实验验证状态反馈和状态观测器的有效性。
3实验内容与方法3.1实验设备本实验所需设备和材料有:计算机、Matlab软件。
3.2系统建模通过对质点的运动进行建模,得到系统的状态空间方程,用于状态反馈和状态观测器的设计。
3.3状态反馈设计根据系统建模和状态反馈的原理,设计状态反馈控制器,并进行仿真实验。
3.4状态观测器设计根据系统建模和状态观测器的原理,设计状态观测器,并进行仿真实验。
4实验结果与分析4.1状态反馈实验结果在进行状态反馈实验时,观察到质点运动的稳定性得到了明显提高,达到了预期的控制效果。
4.2状态观测器实验结果在进行状态观测器实验时,观察到对系统状态的估计准确性得到了明显提高,状态观测器的设计能够很好地预测系统状态变化。
5结论本实验通过对一个质点运动进行实时控制的实验研究,学习并实践了状态反馈和状态观测器的原理和应用。
通过实验验证了状态反馈和状态观测器在控制系统中的重要性和有效性。
实验结果表明,状态反馈和状态观测器能够有效改善系统的稳定性和估计准确性,达到了实时控制的目的。
[1]袁永安.现代控制理论与技术[M].北京:中国电力出版社。
[2]何国平,刘德海.控制系统设计与应用[M].北京:中国电力出版社。
[3]王晓红.状态反馈和状态观测在电力系统控制中的应用[J].电网技术,2024。
状态反馈控制器与状态观测器

测控系统课程设计题目:状态反馈控制器与状态观测器——方案B1 2院(系)机电及自动化学院专业测控技术与仪器(辅助)学号姓名级别 2 0 0 9指导老师2012年6月摘要在经典控制系统设计中,对于一个简单的SISO (单输入单输出)闭环系统而言,控制器部分只有简单的增益环节c K ,因此系统仅有唯一的控制参数c K 可供调整。
对于N 维控制系统,控制器需要至少N 个独立变量来调整系统所需根极点的位置,状态反馈控制器则可以将系统的所有状态变量X 都进行反馈,将系统的根极点调整到需要的位置。
而状态反馈控制的实现前提就是要求系统的所有状态变量可测,此时,利用系统某种数学形式的仿真来估计状态值,即系统的状态观测设计,就可以保证系统带全观测的状态反馈控制顺利实现。
本文主要介绍了带全观测器的状态反馈控制器。
关键词:状态反馈,状态观测AbstractThe classical control system design, for a simple SISO (SISO) closed loop system, a controller part is only the simple gain link, therefore only one control parameter can be adjusted. For the N control system, the controller needs at least N independent variable to adjust the system required root pole position, a state feedback controller can be a system of all state variables in X feedback, the system root poles are adjusted to the needs of the location of. While the state feedback control is the premise requirement system realizes all the state variables can be measured, this time using a mathematical form, system simulation to estimate the state value, namely the system state observer design, can guarantee system with full state feedback control for the smooth realization of observation. This paper mainly introduces the observer-based state feedback controller.Key words : state feedback, state observer目录1. 状态反馈控制器 ................................................................................................... - 4 -1.1状态反馈的定义 ................................................................................................ - 4 -1.2状态反馈控制器 ................................................................................................ - 4 -1.3完全可控性........................................................................................................... - 5 -1.4状态反馈控制器的极点配置...................................................................... - 6 -2.状态观测器设计 ...................................................................................................... - 7 -2.1系统状态观测器定义...................................................................................... - 7 -2.2完全可观性........................................................................................................... - 9 -2.3观测器增益的确定 ......................................................................................... - 10 -3.带全观测器的状态反馈控制 ...................................................................... - 10 -3.1仿真程序及分析 .............................................................................................. - 10 -3.2程序运行结果.................................................................................................... - 12 -4.学习小结....................................................................................................................... - 13 - 参考文献 ........................................................................................................................... - 13 -1. 状态反馈控制器1.1状态反馈的定义经典控制:只能用系统输出作为反馈控制器的输入; 现代控制:由于状态空间模型刻画了系统内部特征,故而还可用系统内部状态作为反馈控制器的输入。
正弦干扰下时滞系统的状态预测观测器与前馈-反馈预测控制器设计

系统的时滞项移至系统 闭 环 结 构 之 外&从 而 其 优 化 控 制 规 律 完 全 可 以 按 无 时 滞 系 统 进 行 设 计.时
域 分 析 表 明&设 计 的 预 测 控 制 器 对 外 部 正 弦 干 扰 有 较 强 的 鲁 棒 性&得 到 的 结 果 关 于 二 次 型 平 均 性
能指标是次优的.
4’*49和 4:&注意到
E- "9’>’?@A#"’$8 B’%G
!=/ -"99>9?@A#"9$8B9% I-J!
#’:%
C
F- "9D>D?@A#"D$8 BD%H
其中 J/K@LM3"’9*"99*C"9D<&将#’(%代入#N%*得到 4’5)#$%/4’O5#$%-4’P4’65#$%84’#Q-P49%!#$%-4’P4:!"
问题的充分必要条件导致求解下列两点边值问题
7"Y%&)*+"%&)>Z[%&)’./%&)
6>
$
[%&)*
R"%&)’
+L[%&)
%\])
8-%&> ()* > S> G,L[%&)
边界条件为
"%3)* 431[%N )* 3
%\^)
其中 Z*,S>G,L:两点边值问题%\])的第 F式是物理不可实现的:所以从理论上讲1这一问题
摘 要- 研究控制变量含有时滞的线性系统在外部正弦干扰下的最优减振预测控制问题.利用
基于时域观测器的系统状态估计与反馈控制设计

基于时域观测器的系统状态估计与反馈控制设计概述:本文将讨论基于时域观测器的系统状态估计与反馈控制设计。
我们将详细介绍时域观测器的原理和设计方法,并探讨其在系统状态估计和反馈控制中起到的作用。
同时,我们还将讨论如何利用时域观测器来实现系统状态估计和反馈控制,并基于实例进行说明。
1. 时域观测器的原理时域观测器是一种用于估计系统状态的技术。
它通过测量系统的输出和输入信号,利用系统的数学模型对状态进行估计。
时域观测器的原理基于系统的状态方程和输出方程,通过对观测误差进行修正来实现状态估计。
2. 时域观测器的设计方法时域观测器的设计方法主要包括两个步骤:观测器增益的选择和观测器误差的修正。
观测器增益的选择可以通过最优化方法来实现,例如线性二次调节(LQR)方法。
观测器误差的修正可以通过状态误差修正器进行实现,例如卡尔曼滤波器。
3. 系统状态估计与时域观测器系统状态估计是指在没有直接测量系统状态的情况下,通过观测系统的输出和输入信号来估计系统的状态。
时域观测器可以作为一种常用的状态估计方法。
它利用系统的模型以及观测误差的修正来实现状态估计,并具有较好的性能和稳定性。
4. 反馈控制与时域观测器反馈控制是指通过对系统状态的测量和估计,根据某种控制策略对系统的输出进行调节和控制。
时域观测器能够提供对系统状态的估计,从而在反馈控制中发挥关键作用。
通过利用时域观测器估计的状态信息,我们可以设计合适的反馈控制器,实现对系统的稳定性、精度和鲁棒性的提高。
5. 实例分析:基于时域观测器的控制系统为了更好地理解基于时域观测器的系统状态估计和反馈控制设计,我们以一个控制系统为例进行分析。
假设我们要设计一个机器人的控制系统,根据外部环境的变化和用户的指令,控制机器人的运动。
首先,我们需要建立机器人的数学模型,包括系统的状态方程和输出方程。
然后,通过选择合适的观测器增益,并利用状态误差修正器对观测误差进行修正,实现对机器人状态的估计。
状态反馈和状态观测器

01
02
03
经典控制理论方法
采用频率响应法、根轨迹 法等经典控制理论方法进 行控制器参数整定。
现代控制理论方法
利用最优控制、鲁棒控制 等现代控制理论方法进行 控制器设计。
智能优化算法
应用遗传算法、粒子群算 法等智能优化算法进行控 制器参数寻优。
仿真验证与实验结果分析
仿真验证
利用MATLAB/Simulink等仿真工具对设计的控制系统进行仿真 验证,观察系统性能。
性能评估
除了稳定性外,状态反馈控制系统的性能还包括动态响应、稳态精度、鲁棒性等方面。通过对 这些性能指标的评估,可以全面了解系统的控制效果,为进一步优化控制策略提供指导。
应用领域与案例分析
应用领域
状态反馈控制技术广泛应用于航空航天、机器人、自动化生 产线等领域。在这些领域中,系统的动态性能和稳定性要求 较高,状态反馈控制能够提供更加精确和可靠的控制方案。
化和环境变化,提高状态估计的准确性和实时性。
THANKS
感谢观看
基于状态观测器的控制系统
03
设计
控制系统结构框架搭建
确定被控对象
01
明确被控对象的动态特性和输入输出关系,建立被控对象的数
学模型。
设计状态观测器
02
根据被控对象的数学模型,设计状态观测器以估计系统状态。
构建控制系统
03
将状态观测器与控制器相结合,构建基于状态观测器的控制系
统。
控制器参数整定方法论述
姿态和位置反馈
利用姿态传感器和位置传感器获取机器人的姿态和位置信 息,通过状态反馈控制机器人的平衡和定位精度。
力和力矩反馈
在机器人末端执行器上安装力传感器,实时监测机器人与 环境之间的交互力和力矩,通过状态反馈实现机器人的柔 顺控制和自适应能力。
状态反馈和状态观测器1
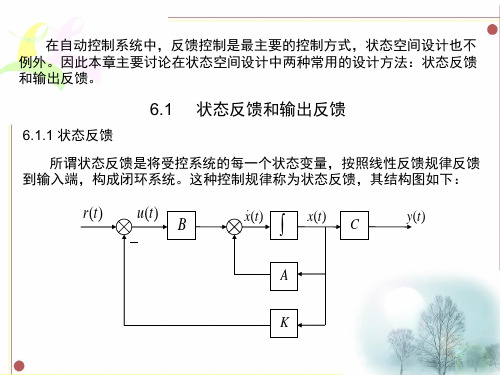
1 6)(s
12)
s3
1 18s 2
72s
综合指标为: % 5%;tS 0.5s,ep 0,试用状态反馈实现上述指标。
解:将极点配置为一对主导极点和一个非主导极点;根据二阶
系统的性能指标,求出 0.707,n 10。取 0.707,n 10
则,主导极点为:
s1,2 0.707 j7.07
状态反馈闭环系统的状态空间表达式为
x (A BK )x Br
y Cx
简记为 K (A BK ), B,C。该系统的闭环传递函数阵为
GK (s) CsI (A BK ) 1 B
经过状态反馈后,系数矩阵C和B没有变化,仅仅是系统矩阵A发生了变
化,变成了 (A BK )。也就是说状态反馈矩阵K的引入,没有增加新的状态
证明: 假定开环系统能控,A,b可为能控标准形
0 1 0 0
A
0
0
1
0
1
a0
a1
a
n
1
K K0 K1 Kn1
0 0 则 bK K0 K1
0
K
n
1
0
b
0
1
0
10
0
[A bK]
0
01
1
(a0 K0 ) (a1 K1)
(an1 Kn1)
sn rn1sn1 r0 0
实际系统与希望系统的特征方程的系数应当相一致。
3、状态反馈阵K的计算步骤 1)判断A,b能控性 2)写出实际的闭环特征方程(传递阵的分母为0的方程)
SI [A bK] 0
3)根据要配置的特征根,写出希望的特征方程
f (s) (s 1)(s n ) 0
4)对应实际的与希望的特征方程,求出K。
现代控制理论状态反馈和状态观测器的设计实验报告

本科实验报告课程名称: 现代控制理论实验项目: 状态反馈与状态观测器得设计实验地点: 中区机房专业班级:自动化学号:学生姓名:指导教师:年月日现代控制理论基础一、实验目得(1)熟悉与掌握极点配置得原理。
(2)熟悉与掌握观测器设计得原理。
(3)通过实验验证理论得正确性。
(4)分析仿真结果与理论计算得结果。
二、实验要求(1)根据所给被控系统与性能指标要求设计状态反馈阵K。
(2)根据所给被控系统与性能指标要求设计状态观测器阵L。
(3)在计算机上进行分布仿真。
(4)如果结果不能满足要求,分析原因并重复上述步骤。
三、实验内容(一)、状态反馈状态反馈就是将系统得状态变量乘以相应得反馈系数,然后反馈到输入端与参考输入叠加形成控制作为受控系统得控制输入,采用状态反馈不但可以实现闭环系统得极点任意配置,而且也就是实现解耦与构成线性最优调节器得主要手段。
1、全部极点配置给定控制系统得状态空间模型,则经常希望引入某种控制器,使得该系统得闭环极点移动到某个指定位置,因为在很多情况下系统得极点位置会决定系统得动态性能。
假设系统得状态空间表达式为(1)其中引入状态反馈,使进入该系统得信号为(2)式中r为系统得外部参考输入,K为矩阵、可得状态反馈闭环系统得状态空间表达式为(3)可以证明,若给定系统就是完全能控得,则可以通过状态反馈实现系统得闭环极点进行任意配置。
假定单变量系统得n个希望极点为λ1,λ2,…λn, 则可以求出期望得闭环特征方程为(sλ1)(sλ2)…(sλn)=这就是状态反馈阵K可根据下式求得K= (4)式中,就是将系统期望得闭环特征方程式中得s换成系统矩阵A后得矩阵多项式。
例1已知系统得状态方程为采用状态反馈,将系统得极点配置到1,2,3,求状态反馈阵K、、其实,在MATLAB得控制系统工具箱中就提供了单变量系统极点配置函数acker,该函数得调用格式为K=acker(A,b,p)式中,p为给定得极点,K为状态反馈阵。
《现代控制理论》线性定常系统的反馈结构及状态观测器

《现代控制理论》线性定常系统的反馈结构及状态观测器现代控制理论中,线性定常系统的反馈结构及状态观测器是控制系统中的关键部分。
反馈结构和状态观测器的设计对于控制系统的性能和稳定性有着重要的影响。
本文将从反馈结构和状态观测器的定义、功能和设计方法等方面进行详细介绍。
首先,我们来介绍反馈结构。
反馈结构是控制系统中最常见的一种控制方式,通过将系统的输出信号与期望值进行比较,计算出控制量,并作为输入信号对系统进行控制,以实现对系统输出的调节。
在线性定常系统中,反馈结构一般由比例控制器、积分控制器和微分控制器组成,通过调节这些控制器的参数,可以实现对系统性能的优化。
其中,比例控制器用于调节系统的过渡过程,积分控制器用于消除系统的稳态误差,微分控制器用于抑制系统的振荡和提高系统的动态响应速度。
通过适当选择和调节这些控制器的参数,可以使系统的性能指标如超调量、响应时间等得到满足。
接下来我们来介绍状态观测器。
状态观测器是用于估计和反馈系统状态的一种装置,通过测量系统的输出信号和输入信号,以及系统的数学模型,来估计系统的状态。
状态观测器在控制系统中起到了关键的作用,可以实现对系统状态的估计和补偿,从而提高系统的稳定性和性能。
在线性定常系统中,状态观测器一般由状态估计器和状态补偿器组成。
状态估计器根据系统的输出信号和输入信号,以及系统的数学模型,通过运算得到系统的状态估计值,以反馈给系统进行控制。
状态补偿器则根据系统的状态估计值和期望值,以及系统的数学模型,通过运算得到控制量,以控制系统的输出。
关于反馈结构和状态观测器的设计方法,一般可以采用经典控制理论方法和现代控制理论方法。
经典控制理论方法主要包括根轨迹法、频率响应法等。
根轨迹法可以通过绘制系统的根轨迹图来分析系统的稳定性和性能,并通过调节控制器参数来满足系统的性能指标。
频率响应法则通过分析系统的频率特性来设计合适的频率补偿器,以达到系统的优化。
现代控制理论方法则主要包括状态空间法和最优控制方法。
现代控制理论状态反馈和状态观测器的设计实验报告

现代控制理论状态反馈和状态观测器的设计实验报告本次实验是关于现代控制理论中状态反馈与状态观测器的设计与实现。
本次实验采用MATLAB进行模拟与仿真,并通过实验数据进行验证。
一、实验目的1、学习状态反馈控制的概念、设计方法及其在实际工程中的应用。
3、掌握MATLAB软件的使用方法。
二、实验原理1、状态反馈控制状态反馈控制是指将系统状态作为反馈控制的输出,通过对状态反馈控制器参数的设计,使系统的状态响应满足一定的性能指标。
状态反馈控制的设计步骤如下:(1) 确定系统的状态方程,即确定系统的状态矢量、状态方程矩阵和输出矩阵;(2) 设计状态反馈控制器的反馈矩阵,即确定反馈增益矩阵K;(3) 检验状态反馈控制器性能是否满足要求。
2、状态观测器(1) 确定系统的状态方程;(2) 设计观测器的状态估计矩阵和输出矩阵;(3) 检验观测器的状态估计精度是否符合标准。
三、实验内容将简谐信号加入单个质点振动系统,并对状态反馈控制器和状态观测器进行设计与实现。
具体实验步骤如下:1、建立系统状态方程:(1)根据系统的物理特性可得单自由度振动系统的运动方程为:m¨+kx=0(2)考虑到系统存在误差、干扰等因素,引入干扰项,得到系统状态方程:(3)得到系统状态方程为:(1)观察系统状态方程,可以发现系统状态量只存在于 m 行 m 到 m 行 n 之间,而控制量只存在于 m 行 1 到 m 行 n 之间,满足可控性条件。
(2)本次实验并未给出状态变量的全部信息,只给出了系统的一维输出,因此需要设计状态反馈器。
(3)我们采用极点配置法进行状态反馈器设计。
采用 MATLAB 工具箱函数,计算出极点:(4) 根据极点求解反馈矩阵,得到状态反馈增益矩阵K:(1)通过矩阵计算得到系统的可观性矩阵:(2)由若干个实测输出建立观测器,可将观测器矩阵与可观测性矩阵组合成 Hankel 矩阵,求解出状态观测器系数矩阵:(3)根据系统的状态方程和输出方程,设计观测方程和状态估计方程,如下:4、调试控制器和观测器(1)经过上述设计步骤,将反馈矩阵和观测矩阵带入 MATLAB 工具箱函数进行仿真。
状态反馈观测 设计

状态反馈观测设计状态反馈观测是一种控制系统中常用的技术,可以用于估计系统的状态并根据估计值进行控制调节。
在状态反馈观测设计中,我们需要确定观测器的结构和参数,以及观测误差的影响。
首先,观测器的结构是状态反馈观测设计的核心问题之一。
观测器的结构是指观测器的状态和输出方程的形式。
常用的观测器结构有全阶观测器、降阶观测器和高阶观测器等。
全阶观测器是指观测器的状态和系统的状态维数相同,适用于系统状态完全可观测的情况。
降阶观测器是指观测器的状态维数小于系统的状态维数,适用于系统状态不完全可观测的情况。
高阶观测器是指观测器的状态维数大于系统的状态维数,适用于系统状态超定观测的情况。
其次,观测器的参数是观测器设计的另一个重要问题。
观测器的参数包括观测器的增益矩阵和误差权重矩阵等。
观测器的增益矩阵可以通过线性矩阵不等式(LMI)或者频域设计方法来确定。
误差权重矩阵用于权衡观测器输出误差和观测器状态的变化量。
观测器的参数选择不当可能会导致观测器的不稳定性或性能不佳,因此需要通过优化方法或者经验法则来确定。
最后,观测误差对系统性能的影响也需要考虑在内。
观测误差是指观测器输出与系统状态的真实值之间的差异。
观测误差的存在会导致控制器对系统状态的估计值产生偏差,从而影响系统的性能。
观测误差的大小与观测器的参数选择、系统的可观测性和外部干扰等因素有关。
为了减小观测误差对系统性能的影响,可以采取一些措施,如增加观测器的增益、提高系统的可观测性、降低外部干扰的影响等。
总结起来,状态反馈观测设计是一项复杂而重要的任务,需要考虑观测器的结构和参数选择以及观测误差对系统性能的影响。
通过合理选择观测器的结构和参数,可以实现对系统状态的准确估计,并根据估计值进行控制调节,从而提高控制系统的性能和稳定性。
几类时滞不确定系统的观测器及反馈控制设计

几类时滞不确定系统的观测器及反馈控制设计基于观测器的控制设计问题是时变时滞不确定非线性系统的重要研究课题,吸引了很多研究学者的关注.而目前大部分的研究集中于系统的渐近稳定性,忽略了系统的瞬态性能,对此,本文旨在对几类时滞不确定系统进行观测器及反馈控制设计并研究其有限时间有界性,取得了一些新的成果,具体如下:首先,本文研究了单边Lipschitz时滞不确定奇异系统的观测器设计的稳定性分析问题,基于系统的非线性满足单边Lipschitz条件和二次内部有界条件,通过构造新的Lyapunov-Krasovskii泛函,应用Schur补引理,詹森不等式,自由权矩阵技术得到单边Lipschitz时滞不确定奇异系统的观测器稳定的新充分条件,并且通过变量变换得出观测器增益的设计方法.最后数值仿真结果证实了提出方法的有效性.其次,本文研究了具有时变时滞和参数不确定的伪单边Lipschitz非线性系统的基于观测器控制的有限时间有界问题.伪单边Lipschitz条件比单边Lipschitz 条件更泛化,保守性更低.主要通过构造新的Lyapunov-Krasovskii泛函,利用杨氏关系式等线性矩阵不等式方法,设计基于观测器的控制,保证闭环系统的有限时间有界性,得出有限时间有界的一个充分条件,进一步实现控制器和观测器增益的同时计算,最后仿真结果验证了该方法的有效性.最后,本文研究了带有不确定参数的时滞随机系统的基于观测器的有限时间H∞控制问题.通过设计基于观测器的控制使得闭环系统有限时间随机有界,再考虑控制输出和外部干扰之间的关系,给出了随机系统的基于观测器的有限时间H∞控制器的定义,通过构造新的Lyapunov-Krasovskii泛函,应用Schur补引理等线性矩阵不等式技术得出随机系统基于观测器的有限时间H∞控制的新判据,在此基础上并给出观测器和控制器增益的设计方法,最后通过数值仿真结果显示其有效性.。
时滞系统的输出反馈滑模控制的一种奇异系统方法

时滞系统的输出反馈滑模控制的一种奇异系统方法
刘月;马树萍
【期刊名称】《自动化学报》
【年(卷),期】2013(39)5
【摘要】利用一种奇异系统方法讨论了时滞系统的输出反馈滑模控制问题.时滞系统的非线性项满足范数有界约束.首先,将滑动模态与线性切换面作为一个奇异时滞系统,基于奇异时滞系统的稳定性理论,给出滑动模态稳定及切换面存在的线性矩阵不等式(Linear matrix inequality,LMI)充分条件.然后,给出使得系统闭环渐近稳定的静态输出反馈滑模控制器的设计方法,此控制器保证闭环系统有限时间到达切换面.最后,用数值算例验证本文方法的有效性和正确性.
【总页数】8页(P594-601)
【作者】刘月;马树萍
【作者单位】山东大学数学学院济南250100;山东大学数学学院济南250100【正文语种】中文
【相关文献】
1.基于观测器输出反馈奇异时滞系统的同时H控制 [J], 李瑞杰;包俊东
2.不确定时滞系统的静态输出反馈滑模控制 [J], 姚合军
3.时变时滞离散模糊奇异系统的H∞滑模控制 [J], 付丽;柏建军
4.不确定性时变时滞奇异摄动控制系统的输出反馈控制器设计 [J], 王永超
5.变时滞不确定奇异系统的输出反馈H_∞控制(英文) [J], 王军庆;王天成;高在瑞
因版权原因,仅展示原文概要,查看原文内容请购买。
