第二章电路的分析方法
合集下载
(完整版)第二章电路分析方法
第二章电路的分析方法电路分析是指在已知电路构和元件参数的情况下，求出某些支路的电压、电流。
分析和计算电路可以应用欧姆定律和基尔霍夫定律，但往往由于电路复杂，计算手续十分繁琐。
为此，要根据电路的构特点去寻找分析和计算的简便方法。
2．1 支路电流法支路电流法是分析复杂电路的的基本方法。
它以各支路电流为待求的未知量，应用基尔霍夫定律（KCL 和KVL ）和欧姆定律对结点、回路分别列出电流、电压方程，然后解出各支路电流。
下面通过具体实例说明支路电流法的求解规律。
例2-1】试用支路电流法求如图2-1 所示电路中各支路电流。
已知U S1 130V ，U S2 117V ，R1 1 ，R2 0.6 ，R 24 。
【解】该电路有3 条支路（b=3），2个结点（n=2）,3 个回路（L=3 ）。
先假定各支路电流的参考方向和回路的绕行方向如图所示。
因为有3 条支路则有3 个未知电流，需列出3 个独立方程，才能解得3个未知量。
根据KCL 分别对点A、B 列出的方程实际上是相同的，即结点A、B 中只有一个结点电流方程是独立的，因此对具有两个结点的电路，只能列出一个独立的KCL 方程。
再应用KVL 列回路电压方程，每一个方程中至少要包含一条未曾使用过的支路（即没有列过方程的支路）的电流或电压，因此只能列出两个独立的回路电压方程。
根据以上分析，可列出3 个独立方程如下：结点A I1 I2 I 0回路ⅠI1R1 I2R2 U S1 U S2回路ⅡI2 R2 IR U S2I1 10A， I2 5A， I=5A 联立以上3 个方程求解，代入数据解得支路电流通过以上实例可以总出支路电流法的解题步骤是：1．假定各支路电流的参考方向，若有n个点，根据KCL 列出（n－１）个结点电流方程。
２．若有b 条支路，根据KVL 列（b－n＋１）个回路电压方程。
为了计算方便，通常选网孔作为回路。
5 3．解方程组，求出支路电流。
【例 2-2】如图 2-2 所示电路，用支路电流法求各支路电流。
第二章电路的分析方法（答案）
第⼆章电路的分析⽅法（答案）第⼆章电路的分析⽅法本章以电阻电路为例，依据电路的基本定律，主要讨论了⽀路电流法、弥尔曼定理等电路的分析⽅法以及线性电路的两个基本定理：叠加定理和戴维宁定理。
1．线性电路的基本分析⽅法包括⽀路电流法和节点电压法等。
（1）⽀路电流法：以⽀路电流为未知量，根据基尔霍夫电流定律（KCL）和电压定律(KVL)列出所需的⽅程组，从中求解各⽀路电流，进⽽求解各元件的电压及功率。
适⽤于⽀路较少的电路计算。
（2）节点电压法：在电路中任选⼀个结点作参考节点，其它节点与参考节点之间的电压称为节点电压。
以节点电压作为未知量，列写节点电压的⽅程，求解节点电压，然后⽤欧姆定理求出⽀路电流。
本章只讨论电路中仅有两个节点的情况，此时的节点电压法称为弥尔曼定理。
2 ．线性电路的基本定理包括叠加定理、戴维宁定理与诺顿定理，是分析线性电路的重要定理，也适⽤于交流电路。
（1）叠加定理：在由多个电源共同作⽤的线性电路中，任⼀⽀路电压（或电流）等于各个电源分别单独作⽤时在该⽀路上产⽣的电压（或电流）的叠加（代数和）。
①“除源”⽅法（a）电压源不作⽤：电压源短路即可。
（b）电流源不作⽤：电流源开路即可。
②叠加定理只适⽤于电压、电流的叠加，对功率不满⾜。
（2）等效电源定理包括戴维宁定理和诺顿定理。
它们将⼀个复杂的线性有源⼆端⽹络等效为⼀个电压源形式或电流源形式的简单电路。
在分析复杂电路某⼀⽀路时有重要意义。
①戴维宁定理：任何⼀个线性含源的⼆端⽹络，对外电路来说，可以⽤⼀个理想电压源和⼀个电阻的串联组合来等效代替，其中理想电压源的电压等于含源⼆端⽹络的开路电压，电阻等于该⼆端⽹络中全部独⽴电源置零以后的等效电阻。
②诺顿定理：任何⼀个线性含源的⼆端⽹络，对外电路来说，可以⽤⼀个理想电流源和⼀个电阻的并联组合来等效代替。
此理想电流源的电流等于含源⼆端⽹络的短路电流，电阻等于该⼆端⽹络中全部独⽴电源置零以后的等效电阻。
3 ．含受控源电路的分析对含有受控源的电路，根据受控源的特点，选择相应的电路的分析⽅法进⾏分析。
第2章 电路分析基础(张永瑞)(第三版)
为 i1, i2, i3, 其参考方向标示在图上。就本例而言，问题是如
何找到包含未知量 i1, i2, i3 的 3个相互独立的方程组。
第二章 电路的基本分析方法
图 2.1-2 支路电流法分析用图
第二章 电路的基本分析方法
根据KCL，对节点 a 和 b 分别建立电流方程。设流出
节点的电流取正号，则有
第二章 电路的基本分析方法
解出支路电流之后，再要求解电路中任何两点之间的电 压或任何元件上消耗功率那就是很容易的事了。例如， 若再要求解图 2.1-2 电路中的 c 点与 d 点之间电压ucd 及 电压源 us1所产生的功率 Ps1，可由解出的电流i1、i2、i3 方 便地求得为
ucd R1i1 R2i2 ps1 us1i1
i1 i2 i3 0
(2.1-7)
(2.1-7)式即是图2.1-2 所示电路以支路电流为未知量的足够的 相互独立的方程组之一，它完整地描述了该电路中各支路电 流和支路电压之间的相互约束关系。应用克莱姆法则求解 (2.1-7)式。系数行列式Δ和各未知量所对应的行列式Δj(j=1, 2,
个节点列KCL方程时，规定流出节点的电流取正号，流入节
点的电流取负号，每一个支路电流在n个方程中一定出现两 次， 一次为正号(+ij), 一次为负号(-ij), 若把这n个方程相加，
它一定是等于零的恒等式，即
第二章 电路的基本分析方法
( i ) [( i ) ( i )] 0
第二章 电路的基本分析方法
2.1.2 独立方程的列写
一个有n个节点、b条支路的电路，若以支路电流作未知
变量， 可按如下方法列写出所需独立方程。
(1) 从 n 个节点中任意择其n-1个节点，依KCL列节点电
电工学 第二章 电路的分析方法
返回
例4、用叠加原理求图示电路中的I。 1mA 4kΩ + 10V － 2kΩ I 2kΩ
2kΩ
解:
电流源单独作用时 电压源单独作用时: 10 2 44 mA 1 257mA II 1 mA .0.25mA 4 2 [2+4//2] 4 4 2 [(2+2)//2] 2 I=I′+I″= 1.507mA
返回
第三节 电压源与电流源的等 效变换
等效变换的概念 二端电阻电路的等效变换 独立电源的等效变换 电源的等效变换 无源二端网络的输入电阻 和等效电阻
返回
一、等效变换的概念
1、等效电路
两个端口特性相同，即端口对外的 电压电流关系相同的电路，互为等效电 路。
返回
2、等效变换的条件 对外电路来说，保证输出电压U和 输出电流I不变的条件下电压源和电流 源之间、电阻可以等效互换。
1 1 2 2 S
－US＋R2I2＋R3I3＋R4I4 ＝0
返回
第二节 叠加原理
叠加原理
原理验证
几点说明
返回
一、叠加原理
在由多个 独立电 源共同 作用的 线性 电路中,任一支路的电流(或电压)等于各 个独立电源分别单独作用在该支路中产 生的电流(或电压)的叠加(代数和) 。
不作用的恒压源短路,不作用的恒流 源开路。
US2单独作用
= 4/3A
返回
三、几点说明
叠加原理只适用于线性电路。
电路的结构不要改变。将不作用的恒压
源短路，不作用的恒流源开路。
最后叠加时要注意电流或电压的方向:
若各分电流或电压与原电路中电流或
电压的参考方向一致取正，否则取负。 功率不能用叠加原理计算。
例4、用叠加原理求图示电路中的I。 1mA 4kΩ + 10V － 2kΩ I 2kΩ
2kΩ
解:
电流源单独作用时 电压源单独作用时: 10 2 44 mA 1 257mA II 1 mA .0.25mA 4 2 [2+4//2] 4 4 2 [(2+2)//2] 2 I=I′+I″= 1.507mA
返回
第三节 电压源与电流源的等 效变换
等效变换的概念 二端电阻电路的等效变换 独立电源的等效变换 电源的等效变换 无源二端网络的输入电阻 和等效电阻
返回
一、等效变换的概念
1、等效电路
两个端口特性相同，即端口对外的 电压电流关系相同的电路，互为等效电 路。
返回
2、等效变换的条件 对外电路来说，保证输出电压U和 输出电流I不变的条件下电压源和电流 源之间、电阻可以等效互换。
1 1 2 2 S
－US＋R2I2＋R3I3＋R4I4 ＝0
返回
第二节 叠加原理
叠加原理
原理验证
几点说明
返回
一、叠加原理
在由多个 独立电 源共同 作用的 线性 电路中,任一支路的电流(或电压)等于各 个独立电源分别单独作用在该支路中产 生的电流(或电压)的叠加(代数和) 。
不作用的恒压源短路,不作用的恒流 源开路。
US2单独作用
= 4/3A
返回
三、几点说明
叠加原理只适用于线性电路。
电路的结构不要改变。将不作用的恒压
源短路，不作用的恒流源开路。
最后叠加时要注意电流或电压的方向:
若各分电流或电压与原电路中电流或
电压的参考方向一致取正，否则取负。 功率不能用叠加原理计算。
第二章 电路的分析方法
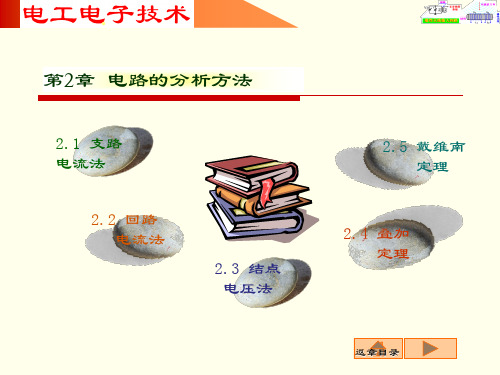
电路分析基础
回路电流法求解电路的步骤
选取自然网孔作为独立回路,在网孔中标出各回路电流
的参考方向,同时作为回路的绕行方向; 支路上的互阻压降由相邻回路电流而定;
建立各网孔的KVL方程,注意自电阻压降恒为正,公共 联立求解方程式组,求出各假想回路电流. .
它们与回路电流之间的关系,求出各支路电流.
返节目录
电路分析基础
思考 练习
用结点电压法求解下图所示电路,与回路电流法相比较, 能得出什么结论? US3 R I A+ - 3 3 B
IS1 I1
R1
I4
R4
I5
R5
I2
R2
IS2
此电路结点n=3,用 结点电压法求解此电 路时,只需列出3-1=2 个独立的结点电压方 程式:
U S3 1 1 1 1 ( + + )V A V B = I S1 + R1 R 3 R 4 R3 R3 ( U 1 1 1 1 + + )V B V A = I S2 S3 R 2 R3 R5 R3 R3
返节目录
电路分析基础
结点电压法应用举例
用结点电压法求解结点n=2的复杂电路时,显然只需 列写出2-1=1个结点电压方程式,即: US
例
① I2 R2 + US2 _ I3 R3 I4 R4
-
V1 =
∑R ∑
S
I1 R1 + US1 _
1 R
+
US4
此式称弥尔曼 定理.是结点 电压法的特例
直接应用弥尔曼定理求V1
返节目录
电路分析基础
第1节 支路电流法
定义
以支路电流为未知量,根据基尔霍夫两定律列出必 要的电路方程,进而求解客观存在的各支路电流的方 法,称支路电流法 支路电流法.
第二章(1)电路基本分析方法
I3
U s1
R1
R2
I2
②
U s3
R3
①
1
3
2
②
2.1.1 电路图与拓扑图
②
R2
① R3
R4
R5
③
R6 ④
U s1
R1
实际电路图
②
2
4
①
5
③
3
6
④
1
对应的线图
线图是由点（节点）和线段（支路）组成，反映实际 电路的结构（支路与节点之间的连接关系）。
有向图
如果线图各支路规定了一个方向（用 箭头表示，一般取与电路图中支路电流 方向一致），则称为有向图。
回路2：I3×R3＋US3－I4×R4＋I2×R2=0
回路3：I4×R4＋I6×R6－I5×R5=0
网孔回路电压方程必为独立方程。
网孔回路电压方程数=b（支路数）－n（节点数）＋1
解出支路电流
4>. 由n1个节点电流方程和bn+1个网孔电压方程（共b
个方程）可解出b个支路电流变量。
R3
I 3
U s3
第二章(1) 电路基本分析方法
本章内容
1.网络图论初步 2.支路电流法 3.网孔电流法 4.回路电流法 5.节点电压法
2.1 网络图论的概念
图的概念：对于一个由集中参数元件组成的电网络，
若用线段表示支路，用黑圆点表示节点，由此得到一
个由线条和点所组成的图形，称此图为原电网络的拓
扑图，简称为图。
I1 ①
－ I1 ＋ I2 － I3 =0
I1 －10＋3× I2 =0 3×I2 ＋2× I3 －13=0
解得： I1 =1A， I2 =3A， I3 =2A
电工学
列电流方程 (N-1个)
节点a：
I6
I 3 I 4 I1
R6
I5
c
节点b： 节点c： 节点d：
I1 I 6 I 2
I 2 I5 I3
d
+
E3
R3
I 4 I6 I5
节点数 N=4 支路数 B=6
（取其中三个方程）
b
I2 I1 a I3 I4 I6 R6 c
列电压方程 (选取网孔)
2. 实际电压源
电压源模型 伏安特性
I
U E U
IRO
RO
+
-
E
I
Ro越大 斜率越大
U E IRo
恒压源中的电流由外电路决定
I + E _ Uab b 例
设: E=10V 则： 当R1接入时 ： I=5A
a
2 R1
2
R2
当R1 R2 同时接入时： I=10A
恒压源特性小结
I
+
a
R
E
abda: E4 I 4 R4 I1 R1 I 6 R6
I5
bcdb: 0 I 2 R2 I 5 R5 I 6 R6
d
+
E3
adca :
R3
E3 E4 I 3 R3 I 4 R4 I 5 R5
电压、电流方程联立求得：
I1 ~ I 6
支路电流法小结
解题步骤
1 结论 对每一支路假设 1. 假设未知数时，正方向可任意选择。 一未知电流 2. 原则上，有B个支路就设B个未知数。 （恒流源支路除外） 2 列电流方程： 若电路有N个节点，
_
电路的分析方法
WXH
例题 求图示电路的电流I。
I
I
电阻的串并联等效变换
WXH
R1
R5
R3
R1
R5
R3
E R2
E
R4
R2
R4
9
2020年3月26日星期四
WXH
例题 求图示电路的电流I。
I
I
电阻的串并联等效变换
WXH
R1
R5
R3
R1
R5
R3
E
E
R2
R4
R2
R4
10
2020年3月26日星期四
§2-2 电阻的星形联接和三角形联接的等效变换
R12
R1
R2
R1R 2 R3
R 23
R2
R3
R 2R 3 R1
R 31
R3
R1
R 3R1 R2
12
2020年3月26日星期四
WXH
△→ Y
电阻的星形联接和三角形联接的等效变换
WXH
R1
R12
R12R 31 R 23 R31
R2
R12
R12R 23 R 23 R31
R3
R12
R 23R 31 R 23 R31
6
解：（1）求开路电压
等效电路
UOC=4×2－18=－10V I= -1A
（2）求等效电阻R0
R0= 4
也可以用电源等效变 换法求得。
（3）画出等效电路
44
2020年3月26日星期四
戴维宁定理与诺顿定理
WXH
WXH
例题： 电路如图所示，试求电路I。
4 18V +
I 2A 6
电工技术 第二章电路的分析方法
戴维南定理和诺顿定理
总结词
戴维南定理和诺顿定理是两种等效电源定理，它们可 以将复杂电路简化为一个等效的电源和一个电阻的串 联或并联形式，从而简化电路分析。
详细描述
戴维南定理将一个线性有源二端网络等效为一个电压 源和一个电阻的串联形式，其中电压源的电压等于二 端网络的开路电压，电阻等于网络内部所有独立源为 零时的等效电阻。诺顿定理则将有源二端网络等效为 一个电流源和一个电阻的并联形式，其中电流源的电 流等于网络的短路电流，电阻与戴维南定理中的电阻 相同。这两种定理在电路分析中有着广泛的应用。
最大功率传输定理
总结词
最大功率传输定理是关于电路中最大功率传输的条件和规律的定理。它表明在一定的电源内阻和负载 电阻条件下，负载电阻可以吸收的最大功率是一定的，且该最大功率发生在负载电阻等于电源内阻时 。
详细描述
最大功率传输定理是分析功率传输问题的基础，它可以帮助我们了解在给定电源内阻和负载电阻的情 况下，如何选择合适的负载电阻以获得最大的功率传输效率。这对于电子设备和系统的设计具有重要 的指导意义。
非线性电容和电感电路的分析
总结词
非线性电容和电感电路是指电容和电感值随电压或电流变 化的电路，其分析方法主要包括等效法和状态变量法。
详细描述
等效法是通过简化电路来分析非线性电容和电感电路的方 法，而状态变量法则通过建立状态方程来求解非线性电容 和电感电路的解。
总结词
在分析非线性电容和电感电路时，需要注意非线性元件的 特性变化和电路的稳定性，以确定电路的工作状态和性能 。
电路的基本物理量
电流
单位时间内通过导体横截面的电荷量， 用符号“I”表示，单位为安培（A）。
电阻
表示导体对电流阻碍作用的物理量， 用符号“R”表示，单位为欧姆 （Ω）。
电工技术--第二章 电路的分析方法
I1
A
R1 Us1 R2
I2
R3 Us2 B
I3
A
I1 '
A
I2' I1"
R1 Us1
R2
R1
R2
I2"
R3
I3'
+
R3 Us2
I3 "
B
B
A
I1
R1 R2
A
I2
R3
A
I2'
R3
I1' I3
R1
R2
I1" I3'
R1
R2
I2"
R3
Us1 Us2
=
Us1
+
Us2
I3"
B
B
B
解： I1
U S1 R 2R 3 R1 + R2 + R3
例1 ：
I1 R1 I3
a
I2 R2 R3 2 +
对结点 a： I1+I2–I3=0 对网孔1： I1 R1 +I3 R3=E1 E2 对网孔2： I2 R2+I3 R3=E2
+ E1
-
1
-
b
联立求解各支路电流
例：试求各支路电流。
a
c
支路中含有恒流源 I3 注意：当支路中含有恒流源 时，若在列KVL方程时，所选 回路中不包含恒流源支路
+
U -
I RL
Ro Uo
+
+ _
I RL
网络
U B
B 有源二端网络
戴维南等效电路
任意一个线性有源二端网络对外都可等 效为等效电压源。
A
R1 Us1 R2
I2
R3 Us2 B
I3
A
I1 '
A
I2' I1"
R1 Us1
R2
R1
R2
I2"
R3
I3'
+
R3 Us2
I3 "
B
B
A
I1
R1 R2
A
I2
R3
A
I2'
R3
I1' I3
R1
R2
I1" I3'
R1
R2
I2"
R3
Us1 Us2
=
Us1
+
Us2
I3"
B
B
B
解： I1
U S1 R 2R 3 R1 + R2 + R3
例1 ：
I1 R1 I3
a
I2 R2 R3 2 +
对结点 a： I1+I2–I3=0 对网孔1： I1 R1 +I3 R3=E1 E2 对网孔2： I2 R2+I3 R3=E2
+ E1
-
1
-
b
联立求解各支路电流
例：试求各支路电流。
a
c
支路中含有恒流源 I3 注意：当支路中含有恒流源 时，若在列KVL方程时，所选 回路中不包含恒流源支路
+
U -
I RL
Ro Uo
+
+ _
I RL
网络
U B
B 有源二端网络
戴维南等效电路
任意一个线性有源二端网络对外都可等 效为等效电压源。
电工技术(第三版席时达)教学指导、习题解答第二章.docx
第二章电路分析方法【引言】①电路分析是指在已知电路结构和元件参数的条件下，确定各部分电压与电流之间的关系。
②电路按结构形式分简单电路——单回路电路。
用欧姆定律即可解决。
复杂电路——不能用串并联的方法将多个回路化简为单回路的电路③ 分析和计算电路原则上可以应用欧姆定律和基尔霍夫定律解决，但往往由于电路复杂，计算手续十分繁琐，还需用到一些其他方法，以简化计算。
本章介绍三种最常用的电路分析方法：支路电流法、叠加定理和戴维宁定理。
学习目的和要求1．掌握用支路电流法分析电路的方法。
2.掌握用叠加定理分析电路的方法3.掌握用戴维南定理分析电路的方法。
2-1支路电流法【讲授】计算复杂电路的各种方法中，最基本的方法是支路电流法。
一、内容：以支路电流为待求量，利用基尔霍夫两条定律，列出电路的方程式，从而解出支路电流。
【说明】因基尔霍夫定律适用于任何电路，故支路电流法是分析复杂电路的一种最基本方法，可以在不改变电路结构的情况下求解任何电路。
〔例 2-1-1 〕试用支路电流法求例1-2-3 的两台直流发电机并联电路中的负载电流I 及每台发电机的输出电流I1和 I2。
〔解〕（ 1）假定各支路电流的参考方向如图2-1-1所示。
根据基尔霍夫电流定律列出结点电流方程。
对于结点 A 有12－ I=0（ 1）I +I对于结点 B 有－I 12－ I +I=0【说明】①这两个方程中只有一个是独立的。
另一个可由图 2-1-1②一个独立的电流方程中至少应包含一个在其它方程中没有出现过的新支路电流。
一般情况下，如果电路有 n 个结点，则按基尔霍夫电流定律列出的独立方程数为n-1。
至于选那几个结点列方程，则是任意的。
③本例中选结点 A 的电流方程作为独立方程，把它记作式（ 1 ）。
（2）根据基尔霍夫电压定律，列出回路的电压方程。
对于回路Ⅰ有I1R1－ I2R2+U S2－ U S1=0（ 2）对于回路Ⅱ有I 2 2S2（ 3）R +IR－ U =0本例中共有三条支路，也就是有三个待求电流I1、I 2和I，因而有三个方程即可求解。
第二章 电路分析的等效变换法
i3 Y u31Y R2 u23Y R1 R1 R2 R2 R3 R3 R1
R1R2 R2R3 R3R1 R12 R3 R1R2 R2R3 R3R1 R23 R1 R1R2 R2R3 R3R1 R31 R2
i1 =u12 /R12 – u31 /R31
+
+
5V
_
5V
_
_
2.3.2 电流源的串并联 并联： 可等效成一个理想电流源 i S º iS1 iS2 iSk º 串联: º 2A 2A 2A º º 电流相同的理想电流源 才能串联。但每个电流 iS
º iS= iSk （注意参考方向） º
源的端电压无法确定。 º
2. 3. 3 电压源与电流源的串并联 Is
º
º
º
º
º
º
º
º
º
º
º
º
2.3 电源的等效变换
2.3.1 电压源的串并联 + uS1 _ + uSn _ º
º + uS _
º
串联: uS= uSk ( 注意参考方向。一致， 取+；否则，取 - 。) 并联: 电压相同的电压源才 能并联。但每个电压 源的电流无法确定。 º
º I
º
I
º + 5V º
=G1u2+G2u2+ +Gnu2
=p1+ p2++ pn 故可以直接用等效电阻计算并联电路“内部”的总功率。 （对照前面：“对外等效”，对内不一定等效。）
2.1.3 电阻的串并联 要求：弄清楚串、并联的概念。 计算举例： 例1.
4 º 2
3 Req = 4∥(2+3∥6) = 2
R1R2 R2R3 R3R1 R12 R3 R1R2 R2R3 R3R1 R23 R1 R1R2 R2R3 R3R1 R31 R2
i1 =u12 /R12 – u31 /R31
+
+
5V
_
5V
_
_
2.3.2 电流源的串并联 并联： 可等效成一个理想电流源 i S º iS1 iS2 iSk º 串联: º 2A 2A 2A º º 电流相同的理想电流源 才能串联。但每个电流 iS
º iS= iSk （注意参考方向） º
源的端电压无法确定。 º
2. 3. 3 电压源与电流源的串并联 Is
º
º
º
º
º
º
º
º
º
º
º
º
2.3 电源的等效变换
2.3.1 电压源的串并联 + uS1 _ + uSn _ º
º + uS _
º
串联: uS= uSk ( 注意参考方向。一致， 取+；否则，取 - 。) 并联: 电压相同的电压源才 能并联。但每个电压 源的电流无法确定。 º
º I
º
I
º + 5V º
=G1u2+G2u2+ +Gnu2
=p1+ p2++ pn 故可以直接用等效电阻计算并联电路“内部”的总功率。 （对照前面：“对外等效”，对内不一定等效。）
2.1.3 电阻的串并联 要求：弄清楚串、并联的概念。 计算举例： 例1.
4 º 2
3 Req = 4∥(2+3∥6) = 2
第二章电路分析方法和定理
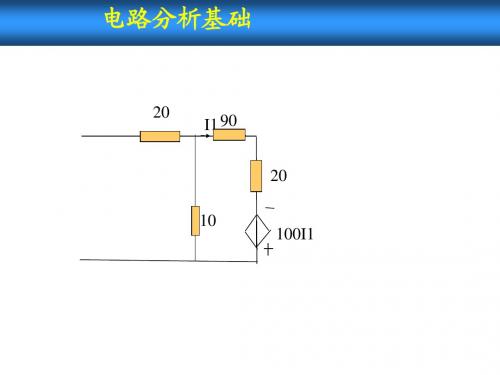
电路分析基础
用回路法求各支路电流。 用回路法求各支路电流。 I1 R1 + US1 _ I2 R2 Ia + US2 _ I3 Ib R3 Ic I4 R4 + US4 _
解： (1) 设独立回路电流 顺时针 设独立回路电流(顺时针 顺时针)
(2) 列 KVL 方程 (R1+R2)Ia = US1- US2 -R2Ib -R2Ia + (R2+R3)Ib - R3Ic = US2 -R3Ib + (R3+R4)Ic = -US4 (3) 求解回路电流方程，得 Ia , Ib , Ic 求解回路电流方程， (4) 求各支路电流： I1=Ia , I2=Ib-Ia , I3=Ic-Ib , I4=-Ic 求各支路电流： -
电路分析基础
2.2 网孔电流法 (net current method )
网孔电流法： 网孔电流法：以网孔电流为未知量列写电路方程分析电路 的方法。 的方法。 A I1 R1 Us1 D R2 Us2 B I2 R3 Us3 C
电路分析基础
2.2 网孔电流法 (net current method )
电路分析基础
回路法的一般步骤： 回路法的一般步骤： (1) 选定 -(n-1)个独立回路，并确定其绕行方向； 选定l=b- - 个独立回路 并确定其绕行方向； 个独立回路， (2) 对l个独立回路，以回路电流为未知量，由自、 个独立回路， 个独立回路 以回路电流为未知量，由自、 互电阻列标准回路方程 方程； 互电阻列标准回路方程； (3) 求解上述方程，得到 个回路电流； 求解上述方程，得到l个回路电流 个回路电流； (4) 求各支路电流 用回路电流表示 ； 求各支路电流(用回路电流表示 用回路电流表示)； (5) 其它分析。 其它分析。 网孔电流法：对平面电路，若以网孔为独立回路， 网孔电流法：对平面电路，若以网孔为独立回路，此 时回路电流也称为网孔电流， 时回路电流也称为网孔电流 ， 对应的分 析方法称为网孔电流法。 析方法称为网孔电流法。
第二章 电路的分析方法之 电源等效变换法
Rki Rk
u Req
Rk Req
uu
说明电压与电阻成正比，因此串3;+
u-1 u_ u+2
º
两个电阻的分压：
R1
u1
R1 R1 R2
u
R2
u2
R2 R1 R2
u
注意方向 !
二、电阻的并联
I1
I2
In
R1
R2
…… Rn
R
1 1 1 ...... 1 n 1
_
º
º
iS
R
º
i is1 u R1 is2 u R2 is1 is2 (1 R1 1 R2 )u is u R
任意 元件
º+
iS
uR
等效电路
º
iS
_
对外等效！
º
º与理想电流源串联的元件可去
并联的多个电流源可以合并为一个电流源
任何元件与理想电流源串联，对外部电路而言， 只相当于该理想电流源独立作用的情况。(与理 想电流源串联的元件可去)
I1 6
R1
+E _
R2
9V
4 1
ID
R5 2
ID 0.5I1
I1 6 4
R1
E+ _
R2 1
9V
2
+
_ ED
ED 2ID I1 V
I1 6
R1
E+ _
R2
9V
4 2
1 + _
ED
ED 2ID I1 V
I1 6
R1 E + R2
_ 9V 1
6 ID’
I D'
ED 6
电路分析基础第二章
- R2il1+ (R2 +R3) il2 =uS2
令
R11=R1+R2 — 回路1的自电阻。等于回路1中所有电阻之和。 R22=R2+R3 — 回路2的自电阻。等于回路2中所有电阻之和。
自电阻总为正。 R12= R21= –R2 — 回路1、回路2之间的互电阻。 当两个回路电流流过相关支路方向相同时，互电阻取正 号；否则为负号。
(2) 列 KVL 方程
(R1+R2)Ia
-R2Ib
= US1- US2
-R2Ia + (R2+R3)Ib
- R3Ic = US2
-R3Ib + (R3+R4)Ic = -US4
对称阵，且 互电阻为负
(3) 求解回路电流方程，得 Ia , Ib , Ic
(4) 求各支路电流： I1=Ia , I2=Ib-Ia , I3=Ic-Ib , I4=-Ic
0 : 无关
特例：不含受控源的线性网络 Rjk=Rkj , 系数矩阵为对称阵。 （平面电路， Rjk均为负(当回路电流均取顺(或逆)时针方向)）
回路法的一般步骤： (1) 选定l=b-(n-1)个独立回路，并确定其绕行方向； (2) 对l个独立回路，以回路电流为未知量，列写其 KVL方程； (3) 求解上述方程，得到l个回路电流； (4) 求各支路电流(用回路电流表示)；
-Ib+3Ic=3U2
增补方程: ② U2=3(Ib-Ia)
4Ia-3Ib=2
解得 Ia=1.19A
受控电压源
③ -12Ia+15Ib-Ic=0 9Ia-10Ib+3Ic=0
Ib=0.92A Ic=-0.51A
看作独立电 压源列方程
第二章电路的分析方法
G1G3 G1 G2 G3
对于由三个相等的电阻组成的三端电阻网络 △→Y的等效变换 Y→△的等效变换
RY
1 R 3
R 3RY
例：如图所示网络，已知R1＝R3＝R4＝6Ω，
R2＝R5＝R6＝2Ω，试求端钮a 、b间的等效电阻R0。
6Ω
R5 R4 R6
a
6Ω
a
6Ω 6Ω 6Ω
R1
I1 I2
R1 Im1
- US1+
解：
R3 - US3+
- US2+ R4 Im2 R5 I5
( R1 R3 ) Im1 R3 Im3 U S1 U S 3 U S 2 (R4 R5 ) Im2 R4 Im3 U S 2 U S 4
Im3 US4 R6 I6 +
R3 Im1 R4 Im2 (R3 R4 R6 ) Im3 U S 3 U S 4
I 1
a R 2
I 2 +
解： 当电流源出现在边缘时，不列写该网孔 的方程 －R1IS1＋（R1＋R3）Im2－R3Im3＝0
I1 s
I 4
R 1
I 3
R 3
E 2 -
b
－R3Im2＋（R2＋R3）Im3＝－E2
U 1 1 1 1 1 )U n1 U n2 U n3 I S1 S 6 R1 R4 R6 R4 R6 R6 U 1 1 1 1 1 U n1 ( )U n 2 U n3 S 2 R4 R2 R4 R5 R5 R2
两式相减得： R0‘IS －E －(R0‘－R0)I ＝0
R0＝R0‘ E＝R0‘IS 2 电压源变换为电流源 用同样的分析方法可知
第二章 电路的分析方法
3. 联立求解得： I、I1、I 2、I 3、I 4、I G
支路电流法的优缺点:
优点：支路电流法是电路分析中最基本的 方法之一。只要根据基尔霍夫定律、欧 姆定律列方程，就能得出结果。
缺点：电路中支路数多时，所需方程的个 数较多，求解不方便。
a
支路数 =4
b
需列4个方程式
2.5、节点电压法
节点电压的概念：
U –
R1
R2
● 各电阻两端的电压相同；
11 1
等效：
R R1 R2
电流分配关系：
或：G G1 G2
G为电导，单位S
I
+ U –
● 并联电阻上电流与电阻大小成反比。
两电阻并联时的分流公式：
R
I1
R2 R1 R2
I
I2
R1 R1 R2
I
电阻等效变换举例：
利用串并联变换 I
利用对称性(相同电位短接）
2、列写方程步骤： A
E1
1 E2
2
-
-
I3 R3
R1 I1
R2 I2
B
1）在图中标注各支路电流及正方向； 2）选定回路（可按网孔）并标注绕行方向； 3）由节点：列写（n-1）个独立的节点电流方程； 4）由回路：列写 b-(n-1) 个独立的回路电压方程； 5）联立求解出各支路电流； 6）进而求去其它电量。
以支路电流为自变量列写的KCL方程和KVL方程， 联立求解的方法。
求出各支路电流之后，进而可以求出其他量。
注意：
●若电路中有 b 条支路（b个支路电流未知数），共需列b个独 立方程才能求解。 ●若电路中有n个节点，
用KCL可列（n-1）个独立的电流方程。 用KVL可列 b-(n-1) 个独立的电压方程(即“网孔数”)。
支路电流法的优缺点:
优点：支路电流法是电路分析中最基本的 方法之一。只要根据基尔霍夫定律、欧 姆定律列方程，就能得出结果。
缺点：电路中支路数多时，所需方程的个 数较多，求解不方便。
a
支路数 =4
b
需列4个方程式
2.5、节点电压法
节点电压的概念：
U –
R1
R2
● 各电阻两端的电压相同；
11 1
等效：
R R1 R2
电流分配关系：
或：G G1 G2
G为电导，单位S
I
+ U –
● 并联电阻上电流与电阻大小成反比。
两电阻并联时的分流公式：
R
I1
R2 R1 R2
I
I2
R1 R1 R2
I
电阻等效变换举例：
利用串并联变换 I
利用对称性(相同电位短接）
2、列写方程步骤： A
E1
1 E2
2
-
-
I3 R3
R1 I1
R2 I2
B
1）在图中标注各支路电流及正方向； 2）选定回路（可按网孔）并标注绕行方向； 3）由节点：列写（n-1）个独立的节点电流方程； 4）由回路：列写 b-(n-1) 个独立的回路电压方程； 5）联立求解出各支路电流； 6）进而求去其它电量。
以支路电流为自变量列写的KCL方程和KVL方程， 联立求解的方法。
求出各支路电流之后，进而可以求出其他量。
注意：
●若电路中有 b 条支路（b个支路电流未知数），共需列b个独 立方程才能求解。 ●若电路中有n个节点，
用KCL可列（n-1）个独立的电流方程。 用KVL可列 b-(n-1) 个独立的电压方程(即“网孔数”)。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R2 U R1+ R2
I
I3 I’
U R3 R’
I
U
R
1 R
1 R3
1 R'
❖ 并联 两个或更多个电阻联接在两个公共的节点之间的联接方法。
分流公式： I3 = U/ R3 =
I’ = I R2 =
R’ I
R3+ R’ R1 I R3+ R’
对于复杂电路（如下图）仅通过串、并联无法求
解，必须经过一定的解题方法，才能算出结果。 如： I2
输出电流 I 可变 ----变
化
I 的大小、方向均
量 由外电路决定
端电压Uab 可变 -----
Uab 的大小、方向 均由外电路决定
例a Is
R
Uab=?
I
_
E
+
电压源中的电流 如何决定？电流 源两端的电压等 于多少？
b
原则：Is不能变，E 不能变。
电压源中的电流 I= IS
恒流源两端的电压 Uab IR E
Uab' Is I' Ro'
Is Ro' I' Ro'
E I Ro Is Ro' I' Ro'
E I s Ro'
Ro Ro'
电压源
I a
RO +
Uab
E-
b
Is E Ro Ro ' Ro
Is
E Is Ro' Ro Ro'
电流源
I'
a
Uab'
RO'
b
* 电压源的串并联
❖ 串联
+ uS1_
+ uS2_
+º us us1 us2 usk
+ +º
uS
等效电路
_
uS _ _
º
º
❖ 并联
I º
+
+
uS1_
uS2_
us us1 us2
º
相同的电压源才能并联,
电源中的电流不确定。
* 电流源的串并联
❖ 串联
is is1 is2 isn isk
º iS
2.1.3 电压源与电流源等效变换
* 电压源与电流源之间
Ia
RO
+
Uab
E
b
IS
I' a
RO'
Uab'
b
等效互换的条件：对外的电压电流相等。
即：
I=I' Uab = Uab'
❖ 等效公式
I a
RO + E
Uab
-
b
I' a
RO' Uab'
IS
b
Uab E I Ro
若
则
I=I'
Uab = Uab'
? I 10 2 7 A 2
? I 10 4 3 A 2
I1
I6
I3 I4
R6 I5
+E3
R3
2.1 电源的两种模型及其等效变换
2.1.1 电压源 * 理想电压源
❖定 义
Ia
两端电压总能保持定值或一定的时间函数 ，其值与流过它的电流 i 无关的元件，也称做 恒压源。
+
E_
Uab
b
❖ 电路符号
Uab 伏安特性
❖ 伏安特性曲线
E
I
❖特 点
例
Ia
（1）RO= 0
Uab
b
❖ 伏安特性曲线
❖ 电路符号
Uab
伏
安
I
特 性
IS
❖特 点
例
I
（1）RO=
（2）输出电 流不变，其值恒等于电流
源电流 IS
（3）输出电压由外电路决定
两端可否被短路或断路？
Is
U
R 设: IS=1 A
则: R=0 时， U =0 V R=10 时， U =10 V
若 R= 时， U = ！
（2）输出电 压不变，其值恒等于电动
势。 即 Uab E
（3）电源中的电流由外电路决定
E
+ _
Uab
2 R1
R2
2
设: E=10V
因为: I E
R
b
则： • 当R1接入时 ： I=5A
• 当 R1 R2 同时接入时： I=10A
• 若直接用导线连接，即R =0： I= 。
短路！ 恒压源不能短接！
电工技术基础
专业基础课
第二章
电路的分析方法
对于简单电路，通过串、并联关系即可求解。
I
I
R1
U1
U R3
R2
U2
U R3 R’
❖ 串联 两个或更多个电阻一个接一个地顺序连接，这些电阻通过同一
电流。R’ = R1 + R2
分压公式： U1 = I R1 =
U2 = I R2 =
R1 U R1+ R2
恒流源不能开路！
* 电流源模型 Ia
Uab
IS
RO
b
I I S Uab Ro
Uab
外
特
性
Is I RO越大 特性越陡
可由稳流电子设备产生，如晶体管的集电极电流与负载无关； 光电池在一定光线照射下光电池被激发产生一定值的电流等
晶体三极管
Ic
Ic
Ib c
Uce
+
be
+
E -
-
Ib
Uce
Ic Ib
E Ro
E 0
（不存在）
I=?
R5
应
R1 R2
R3 I
+ E1 -
+
- E3
R4
Is
用 举 例
I1 E1 R1
R1 R2
R5 I
I3 E3
I1
I3 R3 R4
Is
R3
(接上页) R5
R1 R2
I
I1
I3 R3 R4
Is
R5
I1+I3
I
R4 Is
R1//R2//R3
(接上页)
R5
I1+I3
I R4
R1//R2//R3
IS
R5
Rd
I
R4
+ - Ed
+ E4 -
Ed I1 I3 R1 // R2 // R3
Rd R1 // R2 // R3 E4 I S R4
I Ed E4 Rd R5 R4
讨论题
+ 10V -
I
2 2A
I ?
? 哪 I 10 5 A
个
2
答 案 对
º iS
iS1 iS2
iSn
等效电路
º
❖ 并联
º
iS1
iS2
is
is is1 is2
相同的电流源才能串联,每 个电源两端电压不确定。
总结
(1)
“等效”是指“对外”等效（等效互换前后对外伏--
安特性一致），对内不等效。
aI
I' a
RO
Is
+
Uab RL
-E b
RO'
Uab' b RL
例如：
RL
时 对内不等效
对外等效
RO中不消耗能量 RO'中则消耗能量
U ab U ab E I I 0
(2) 注意转换前后 E 与 Is 的方向
a
I
RO
Is
+
E
-b
a I
RO -
Is
E +b
I'
a
RO' b
I' a
RO' b
(3) 恒压源和恒流源不能等效互换
a I +EbI' a来自Uab' Is
b
IS
* 电压源模型
考
虑
I
内
阻
RO
+
U
E
-
U E IRo
伏安特性
U E
I
Ro越大 斜率越大
实际电压源也不允许短路。因其内阻小，若 短路，电流很大，可能烧毁电源。
2.1.2 电流源
* 理想电流源
❖定 义
Ia
输出电流总能保持定值或一定的时间函 数，其值与它的两端电压u 无关的元件，也称 做恒流源。
+
E_
当 I b 确定后，I c 就基本确定了。在 IC 基本恒定的范围 内 ，I c 可视为恒流源 (电路元件的抽象) 。
总结
恒压源
恒流源
I
a
不 变
_+E
Uab
Uab = E （常数）
Is
量
b
Ia
Uab b
I = Is （常数）
Uab的大小、方向均为恒定， I 的大小、方向均为恒定，
外电路负载对 Uab 无影响。 外电路负载对 I 无影响。
I
I3 I’
U R3 R’
I
U
R
1 R
1 R3
1 R'
❖ 并联 两个或更多个电阻联接在两个公共的节点之间的联接方法。
分流公式： I3 = U/ R3 =
I’ = I R2 =
R’ I
R3+ R’ R1 I R3+ R’
对于复杂电路（如下图）仅通过串、并联无法求
解，必须经过一定的解题方法，才能算出结果。 如： I2
输出电流 I 可变 ----变
化
I 的大小、方向均
量 由外电路决定
端电压Uab 可变 -----
Uab 的大小、方向 均由外电路决定
例a Is
R
Uab=?
I
_
E
+
电压源中的电流 如何决定？电流 源两端的电压等 于多少？
b
原则：Is不能变，E 不能变。
电压源中的电流 I= IS
恒流源两端的电压 Uab IR E
Uab' Is I' Ro'
Is Ro' I' Ro'
E I Ro Is Ro' I' Ro'
E I s Ro'
Ro Ro'
电压源
I a
RO +
Uab
E-
b
Is E Ro Ro ' Ro
Is
E Is Ro' Ro Ro'
电流源
I'
a
Uab'
RO'
b
* 电压源的串并联
❖ 串联
+ uS1_
+ uS2_
+º us us1 us2 usk
+ +º
uS
等效电路
_
uS _ _
º
º
❖ 并联
I º
+
+
uS1_
uS2_
us us1 us2
º
相同的电压源才能并联,
电源中的电流不确定。
* 电流源的串并联
❖ 串联
is is1 is2 isn isk
º iS
2.1.3 电压源与电流源等效变换
* 电压源与电流源之间
Ia
RO
+
Uab
E
b
IS
I' a
RO'
Uab'
b
等效互换的条件：对外的电压电流相等。
即：
I=I' Uab = Uab'
❖ 等效公式
I a
RO + E
Uab
-
b
I' a
RO' Uab'
IS
b
Uab E I Ro
若
则
I=I'
Uab = Uab'
? I 10 2 7 A 2
? I 10 4 3 A 2
I1
I6
I3 I4
R6 I5
+E3
R3
2.1 电源的两种模型及其等效变换
2.1.1 电压源 * 理想电压源
❖定 义
Ia
两端电压总能保持定值或一定的时间函数 ，其值与流过它的电流 i 无关的元件，也称做 恒压源。
+
E_
Uab
b
❖ 电路符号
Uab 伏安特性
❖ 伏安特性曲线
E
I
❖特 点
例
Ia
（1）RO= 0
Uab
b
❖ 伏安特性曲线
❖ 电路符号
Uab
伏
安
I
特 性
IS
❖特 点
例
I
（1）RO=
（2）输出电 流不变，其值恒等于电流
源电流 IS
（3）输出电压由外电路决定
两端可否被短路或断路？
Is
U
R 设: IS=1 A
则: R=0 时， U =0 V R=10 时， U =10 V
若 R= 时， U = ！
（2）输出电 压不变，其值恒等于电动
势。 即 Uab E
（3）电源中的电流由外电路决定
E
+ _
Uab
2 R1
R2
2
设: E=10V
因为: I E
R
b
则： • 当R1接入时 ： I=5A
• 当 R1 R2 同时接入时： I=10A
• 若直接用导线连接，即R =0： I= 。
短路！ 恒压源不能短接！
电工技术基础
专业基础课
第二章
电路的分析方法
对于简单电路，通过串、并联关系即可求解。
I
I
R1
U1
U R3
R2
U2
U R3 R’
❖ 串联 两个或更多个电阻一个接一个地顺序连接，这些电阻通过同一
电流。R’ = R1 + R2
分压公式： U1 = I R1 =
U2 = I R2 =
R1 U R1+ R2
恒流源不能开路！
* 电流源模型 Ia
Uab
IS
RO
b
I I S Uab Ro
Uab
外
特
性
Is I RO越大 特性越陡
可由稳流电子设备产生，如晶体管的集电极电流与负载无关； 光电池在一定光线照射下光电池被激发产生一定值的电流等
晶体三极管
Ic
Ic
Ib c
Uce
+
be
+
E -
-
Ib
Uce
Ic Ib
E Ro
E 0
（不存在）
I=?
R5
应
R1 R2
R3 I
+ E1 -
+
- E3
R4
Is
用 举 例
I1 E1 R1
R1 R2
R5 I
I3 E3
I1
I3 R3 R4
Is
R3
(接上页) R5
R1 R2
I
I1
I3 R3 R4
Is
R5
I1+I3
I
R4 Is
R1//R2//R3
(接上页)
R5
I1+I3
I R4
R1//R2//R3
IS
R5
Rd
I
R4
+ - Ed
+ E4 -
Ed I1 I3 R1 // R2 // R3
Rd R1 // R2 // R3 E4 I S R4
I Ed E4 Rd R5 R4
讨论题
+ 10V -
I
2 2A
I ?
? 哪 I 10 5 A
个
2
答 案 对
º iS
iS1 iS2
iSn
等效电路
º
❖ 并联
º
iS1
iS2
is
is is1 is2
相同的电流源才能串联,每 个电源两端电压不确定。
总结
(1)
“等效”是指“对外”等效（等效互换前后对外伏--
安特性一致），对内不等效。
aI
I' a
RO
Is
+
Uab RL
-E b
RO'
Uab' b RL
例如：
RL
时 对内不等效
对外等效
RO中不消耗能量 RO'中则消耗能量
U ab U ab E I I 0
(2) 注意转换前后 E 与 Is 的方向
a
I
RO
Is
+
E
-b
a I
RO -
Is
E +b
I'
a
RO' b
I' a
RO' b
(3) 恒压源和恒流源不能等效互换
a I +EbI' a来自Uab' Is
b
IS
* 电压源模型
考
虑
I
内
阻
RO
+
U
E
-
U E IRo
伏安特性
U E
I
Ro越大 斜率越大
实际电压源也不允许短路。因其内阻小，若 短路，电流很大，可能烧毁电源。
2.1.2 电流源
* 理想电流源
❖定 义
Ia
输出电流总能保持定值或一定的时间函 数，其值与它的两端电压u 无关的元件，也称 做恒流源。
+
E_
当 I b 确定后，I c 就基本确定了。在 IC 基本恒定的范围 内 ，I c 可视为恒流源 (电路元件的抽象) 。
总结
恒压源
恒流源
I
a
不 变
_+E
Uab
Uab = E （常数）
Is
量
b
Ia
Uab b
I = Is （常数）
Uab的大小、方向均为恒定， I 的大小、方向均为恒定，
外电路负载对 Uab 无影响。 外电路负载对 I 无影响。