材料力学 第八章 课件
合集下载
材料力学(I)第八章更新版

§8–2 两相互垂直平面内的弯曲—— 斜弯曲
变形后,杆件的轴线弯成一空间曲线称为斜弯曲。斜弯
曲可分解为两个平面弯曲。
分解荷载
z
x
Pz
Py
Py
z
x+
Py y
Py P cos
Pz P sin
大家要学会化繁为简,各 个攻破!
z x Pz y
将复杂的问题细分成一个个简单的小问题 z
x
x
Py
Pz x
max m in
P A
Pe Wz
[
];
三、双向偏心拉伸(压缩)的应力计算
外力作用线与杆轴线平行,且作用点不在截面的任何一个
形心主轴上,而且位于Z、Y轴的距离分别为 和ey 的e某z 一
点K处。这类偏心称为双向偏心拉(压)。下图为双向偏心
拉伸:
x zp ey
ez y
x zP ey
ez y
在双向偏心拉(压)时,杆件横截面上任一点正应力计算方
限切应力除以安全因数确定。
(2) 挤压的实用计算 在实用计算中,连接件与被连接件之间的挤压应力
(bearing stress)是按某些假定进行计算的。
对于螺栓连接和铆钉连接,挤压面是半个圆柱形面(图 b),挤压面上挤压应力沿半圆周的变化如图c所示,而最大
挤压应力bs的值大致等于把挤压力Fbs除以实际挤压面(接触
z0
o
z
d
f c
P
y
Mz y My z
Iz
Iy
中性轴的位置
P cos
Iz
y0
P sin
Iy
z0
0
tg y0 Iz tg
z0 I y
材料力学(I)第八章-铆钉连接的计算

第 8 章 组合变形及连接部分的计算
§8-6 铆钉连接的计算
1
铆钉连接主要有三种方式: 1.搭接(图a),铆钉受单剪; 2.单盖板对接(图b),铆钉受单剪; 3.双盖板对接(图c),铆钉受双剪。
2
铆钉组承受横向荷载
实际铆钉组中位于 两端的铆钉所传递的力 要比中间的铆钉所传递 的力大。
为了简化计算,假设: (1) 如果作用于连接上的力其作用线通过铆钉组 中所有铆钉横截面的形心,而且各铆钉的材料和直径 均相同,则认为每个铆钉传递相等的力。 (2) 不考虑弯曲的影响。 铆钉连接与螺栓连接的计算方法相同。
i 1
2.754 103 N 2.754 kN
22
例题 8-10
F F
'' 2 '' 5
M e r2
2 r i i 1 6
2.928kN
F F
'' 3 '' 4
M e r3
2 r i i 1 6
4.344kN
Fi 的方向垂直于ri。
23
例题 8-10
将Fi'和Fi''按矢量合成以得出每一铆钉所受的力 Fi。图b中示出了1,2,3三个铆钉所受力的情况。 经比较按矢量合成后的力F1,F2,…,F6 知,铆钉 1和6所受力最大,F1=F6=4.41 kN。
24
例题 8-10
5. 此连接为搭接,铆钉受单剪,故受力最大的铆 钉1和6剪切面上的切应力为
F1 4.41 103 N 6 t1 t 6 14 10 Pa 14 MPa A s1 π (0.02 m)2 4
257
例题 8-10
解: 1. 将外力F向铆
§8-6 铆钉连接的计算
1
铆钉连接主要有三种方式: 1.搭接(图a),铆钉受单剪; 2.单盖板对接(图b),铆钉受单剪; 3.双盖板对接(图c),铆钉受双剪。
2
铆钉组承受横向荷载
实际铆钉组中位于 两端的铆钉所传递的力 要比中间的铆钉所传递 的力大。
为了简化计算,假设: (1) 如果作用于连接上的力其作用线通过铆钉组 中所有铆钉横截面的形心,而且各铆钉的材料和直径 均相同,则认为每个铆钉传递相等的力。 (2) 不考虑弯曲的影响。 铆钉连接与螺栓连接的计算方法相同。
i 1
2.754 103 N 2.754 kN
22
例题 8-10
F F
'' 2 '' 5
M e r2
2 r i i 1 6
2.928kN
F F
'' 3 '' 4
M e r3
2 r i i 1 6
4.344kN
Fi 的方向垂直于ri。
23
例题 8-10
将Fi'和Fi''按矢量合成以得出每一铆钉所受的力 Fi。图b中示出了1,2,3三个铆钉所受力的情况。 经比较按矢量合成后的力F1,F2,…,F6 知,铆钉 1和6所受力最大,F1=F6=4.41 kN。
24
例题 8-10
5. 此连接为搭接,铆钉受单剪,故受力最大的铆 钉1和6剪切面上的切应力为
F1 4.41 103 N 6 t1 t 6 14 10 Pa 14 MPa A s1 π (0.02 m)2 4
257
例题 8-10
解: 1. 将外力F向铆
《材料力学》课程讲解课件第八章组合变形

强度条件(简单应力状态)——
max
对有棱角的截面,最大的正应力发生在棱角点处,且处于单向应力状态。
max
N A
M zmax Wz
M ymax Wy
x
对于无棱角的截面如何进行强度计算——
1、确定中性轴的位置;
y
F z
M z F ey M y F ez
ez F ey z
y
zk yk z
y
x
1、荷载的分解
F
Fy F cos
Fz F sin
z
2、任意横截面任意点的“σ”
x
F
y
(1)内力: M z (x) Fy x F cos x
M y (x) Fz x F sin x
(2)应力:
Mz k
M z yk Iz
My k
M y zk Iy
(应力的 “+”、“-” 由变形判断)
F
1, 首先将斜弯曲分解
为两个平面弯曲的叠加 Fy F cos
z
L2
L2
Fz F sin
z
2, 确定两个平面弯曲的最大弯矩
y
Mz
Fy L 4
M
y
Fz L 4
3, 计算最大正应力并校核强度
max
My Wy
Mz Wz
217.8MPa
查表: Wy 692.2cm3
4, 讨论 0
y
Wz 70.758cm3
的直径为d3,用第四强度理论设计的直径为d4,则d3 ___=__ d4。
(填“>”、“<”或“=”)
因受拉弯组合变形的杆件,危险点上只有正应力,而无切应力,
r3 1 3 2 4 2
r4
材料力学2-第八章-组合变形PPT课件

x
z
xቤተ መጻሕፍቲ ባይዱ
m Pz
Py
y
LP
Pz
zj
Py P
y
② 应力
My引起的应力:
MyzMzcojs
Iy
Iy
M z引起的应力:
MzyMysijn
Iz
Iz
合应力: M(zcoj sysijn)
Iy
Iz
m
x
z
x
m Pz
Py
y
LP
Pz
zj
Py P
y
③ 中性轴方程 M(z0cojsy0sijn)0 中性轴
Iy
Iz
D2
tg y0 Iz ctgj
均布力作用, []=12MPa,许可挠度为L/200 ,E=9GPa,试选
择截面尺寸并校核刚度。
解:① 外力分析—分解q
yq
z
26°34´
q
A
B
L
qyqsin 80 0.0 44 375 N8/m
q z q co 8 s 0 0 .8 0 9 74 N 15 /m
Mzmaxqy8L235838240N 3m Myma xqz8L271 83 5280N4m
az
中性轴
1 yP y0 zPz0 0
iz2
iy2
ay
截面核心
已知 ay, az 后 ,
z
1
yPa y
i
2 z
0
1
z
Pa
i
2 y
z
0
P(zP,yP)
可求 P力的一个作用点 (zP,yP)
y
利用以上关系可确定截面核心的边界
例3 分别确定圆截面与矩形截面的截面核心.
材料力学第八章组合变形

例题: 图示吊车大梁,由32a热轧普通工字钢制成,许 用应力 [σ]=160MPa ,L=4m 。起吊的重物重量F =80kN,且作用在梁的中点,作用线与y轴之间的夹角α =5°,试校核吊车大梁的强度是否安全。
F
Fy F cos 50
L2
L2
解:1. 外力分解
Fy F cos 80 cos 50 79.7kN Fz F sin 80 sin 50 6.96kN
材料力学
Mechanics of Materials
例:图示梁,已知F1=800N,F2=1650N,截面宽度 b=90mm,高度h=180mm。求:
1、梁上的max及所在位置; 2、若改为a=130mm的正方形截面,梁上的max; 3、若改为d=130mm圆形截面,梁上的max。
F2
F1 z
32
32 6
d3
72.6mm
取 d 73mm
构件在荷载的作用 下如发生两种或两种以 上基本形式的变形,且 几种变形所对应的应力 (和变形)属于同一数 量级,则构件的变形称 为组合变形。
❖组合变形的分析方法 线弹性小变形范围内,采用叠加原理
材料力学
Mechanics of Materials
二.组合变形分析方法 条件:线弹性小变形
组合 变形
0.642q 106 31.5 103
0.266q 106 237 103
160MPa
q 7.44kN / m
材料力学
Mechanics of Materials
M zD 0.456q
M zA 0.266q
z
M yD 0.444q
M yA 0.642q
A截面
y
max
材料力学:第八章-应力应变状态分析

斜截面: // z 轴; 方位用 a 表示;应力为 sa , ta
正负符号规定:
切应力 t - 使微体沿顺时针 旋转为正 方位角 a - 以 x 轴为始边、逆时针旋转 为正
斜截面应力公式推导 设α斜截面面积为dA, 则eb侧面和bf 底面面积分别为dAcosα, dAsinα
由于tx 与 ty 数值相等,同时
sa+90 ,ta+90
E
sa+90 ,ta+90
结论: 所画圆确为所求应力圆
应力圆的绘制与应用3
应力圆的绘制
已知 sx , tx , sy ,
画相应应力圆
t
先确定D, E两点位置, 过此二点画圆即为应力圆
Ds x ,t x , E s y ,t y
t
C OE
s 2 , 0
s 1 , 0
应力圆绘制 作D, E连线中垂线,与x轴相交即为应力圆圆心
tb sb
t
sa
O
C
ta
D
sa ,ta
t
s
E
sb ,tb
O
D
sa ,ta
C
s
E
sb ,tb
由|DC|=|CE|,可得sC值:
sC
s
2 β
+
t
2 β
s
2 α
+
t
2 α
2 sα sβ
点、面对应关系
转向相同, 转角加倍 互垂截面, 对应同一直径两端
应变状态
构件内一点处沿所有方位的应变总况或集合, 称为该点处的 应变状态
研究方法
环绕研究点切取微体, 因微体边长趋于零, 微体趋于所研究 的点, 故通常通过微体, 研究一点处的应力与应变状态
正负符号规定:
切应力 t - 使微体沿顺时针 旋转为正 方位角 a - 以 x 轴为始边、逆时针旋转 为正
斜截面应力公式推导 设α斜截面面积为dA, 则eb侧面和bf 底面面积分别为dAcosα, dAsinα
由于tx 与 ty 数值相等,同时
sa+90 ,ta+90
E
sa+90 ,ta+90
结论: 所画圆确为所求应力圆
应力圆的绘制与应用3
应力圆的绘制
已知 sx , tx , sy ,
画相应应力圆
t
先确定D, E两点位置, 过此二点画圆即为应力圆
Ds x ,t x , E s y ,t y
t
C OE
s 2 , 0
s 1 , 0
应力圆绘制 作D, E连线中垂线,与x轴相交即为应力圆圆心
tb sb
t
sa
O
C
ta
D
sa ,ta
t
s
E
sb ,tb
O
D
sa ,ta
C
s
E
sb ,tb
由|DC|=|CE|,可得sC值:
sC
s
2 β
+
t
2 β
s
2 α
+
t
2 α
2 sα sβ
点、面对应关系
转向相同, 转角加倍 互垂截面, 对应同一直径两端
应变状态
构件内一点处沿所有方位的应变总况或集合, 称为该点处的 应变状态
研究方法
环绕研究点切取微体, 因微体边长趋于零, 微体趋于所研究 的点, 故通常通过微体, 研究一点处的应力与应变状态
材料力学 第八章
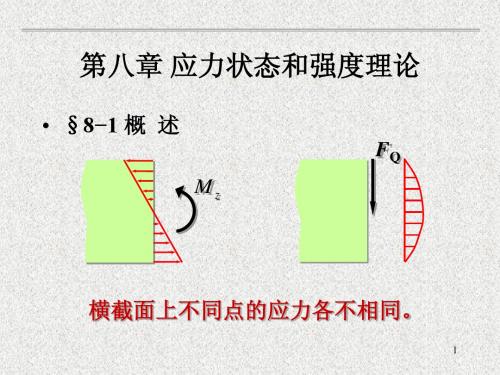
σ max σ min σ x σ y
(8−9)
即对于同一个点所截取的不同方位的单元体,其相互 垂直面上的正应力之和是一个不变量,称之为第一弹性应 力不变量。可利用此关系来校核计算结果。
14
用类似的方法,可以讨论切应力的极值和它们所在 的平面。将式(8—4)对取导数:
d τα (σ x σ y ) cos 2α 2τ x sin 2α dα
不可能总是通过直接试验的方法来确定材料的极限 应力。通过应力状态分析来探求材料破坏的规律,确定 引起材料破坏的决定因素,从而建立相应的强度条件, 即强度理论。
5
§8−2 平面应力状态的应力分析—解析法
一、斜截面应力
图(a)所示平面应力单元体常用平面图形(b)来表示。 现欲求垂直于平面xy的任意斜截面ef上的应力。
例题8−2 图示为某构件某一点的应力
20
σ1
35.8° 30 30
状态,试确定该点的主应力的大小及
方位。 解:由图可知:
σ x 30 MPa , σ y 20 MPa, τ x 30 MPa
σ3
单位:MPa
将其代入式(8−6)有:
2 σ m ax 30 20 55.4MPa 30 20 2 30 σ m in 2 2 5.4MPa
0min表示),则可按下述规则进行判定:
(1) 若 x> y ,则有 |0max|<45° (2) 若 x< y ,则有 |0max|>45°
45 ( τ x 0) 45 ( τ x 0)
(3) 若 x = y ,则有
(8−7)
α 0 max
σ α σ x cos2 α σ y sin 2 α 2τ x sin α cos α τ α (σ x σ y ) sin α cos α τ x (cos2 α sin 2 α)
材料力学第八章

D2 E2 O2
某实际应力状态:与 包络线相切,1>3, 3 1 有正负。 E3O3 O1O3 D3O3 D1O1 OO1 OO3 E2O2 O1O2 D2O2 D1O1 OO1 OO2 1 3 [ c ] [ t ] D3O3 D2O2 D1O1 2 2 2 1 3 [ c ] [ t ] OO3 OO2 OO1 2 2 2
最大拉应力1,与应力状态无关; 1.断裂原因: 2.强度准则: 1 u / nb 1 [ ] 断裂判据: 1 u 1 b 3.u由单向拉伸断裂条件确定: u b nb [ ] 4.应用情况:符合脆性材料的多向拉断试验,或 压应力不超过拉应力情况,如铸铁单向拉伸和 扭转;不能用于无拉应力的应力状态。
1.屈服原因: 形状改变比能uf,与应力状态无关;
2.强度准则:
1 uf ufu / ns ( 1 2 )2 ( 2 3 )2 ( 3 1 )2 [ ] 2
屈服判据:
1 uf ufu ( 1 2 )2 ( 2 3 )2 ( 3 1 )2 s 2
4.应用情况: 符合表面润滑石料的轴压破坏,某些 脆性材料压应力很大时的双向拉压状态。
§8-2
断裂准则
一、最大切应力理论(第三强度理论,Tresca准则) 不论材料处于何种应力状态,引起材料屈服的 原因是最大切应力max达到共同极限值s。
1.屈服原因: 最大切应力max,与应力状态无关; 2.强度准则: max s / ns 1 3 [ ]
[t]、[c]:许可拉、压应力; [ t ] 1 3 [ t ] 如[t]=[c],退化为最大切 [ c ] 应力准则。
《材料力学》第八章组合变形

解 (1)外力分析,确定变形类型—拉弯组合;
(2)内力分析,确定危险截面—整个轴;
M=600(kN·cm) FN=15(kN)
(3)应力计算,确定危险点—a、b点;
P产生拉伸正应力: t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲:的正应力:wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知: P=2kN,L求=:1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2.画弯矩图,确定危险截面--固定端截面。 3.画应力分布图,确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中,在计算中,往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉(压)的组合怎么处理?
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm,材料为45钢, [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的,转速为n=966r/min。带轮的直径为D=132 mm,
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为:M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y),
与弯矩Mz、My对应的正应力分别为σ’和σ”,故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸(或压缩)的组合、扭转与弯曲的组合 的强度计算。
重点: 弯曲与拉伸(或压缩)的组合,扭转与弯曲的组合。
(2)内力分析,确定危险截面—整个轴;
M=600(kN·cm) FN=15(kN)
(3)应力计算,确定危险点—a、b点;
P产生拉伸正应力: t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲:的正应力:wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知: P=2kN,L求=:1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2.画弯矩图,确定危险截面--固定端截面。 3.画应力分布图,确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中,在计算中,往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉(压)的组合怎么处理?
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm,材料为45钢, [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的,转速为n=966r/min。带轮的直径为D=132 mm,
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为:M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y),
与弯矩Mz、My对应的正应力分别为σ’和σ”,故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸(或压缩)的组合、扭转与弯曲的组合 的强度计算。
重点: 弯曲与拉伸(或压缩)的组合,扭转与弯曲的组合。
材料力学第8章

裂缝综合理论计算公式: 裂缝综合理论计算公式
我国现行《规范》采用此式, 我国现行《规范》采用此式,但 式中系数K 通常由各国自行确定。 式中系数 1 、 K2通常由各国自行确定。
l m = K 2 c + K1 ⋅
d
ρ
根据对试验资料的统计分析,并考虑不同构件受力特征的影响, 根据对试验资料的统计分析,并考虑不同构件受力特征的影响,对于 公式为, 常用的带肋钢筋,我国《规范》 常用的带肋钢筋,我国《规范》给出的平均裂缝间距 lm 公式为,
裂缝综合理论
1,根据粘结 滑移理论裂缝宽度的验算 ,根据粘结 滑移理论: 粘结—滑移理论: 8.2
混凝土 拉应力 钢筋 应力 粘结应力
由图( )可见, 为粘结应力传递长度, 由图(b)可见,图中 l 为粘结应力传递长度,在裂缝两侧 l 范 所以不可能再产生新的裂缝。 围内混凝土的拉应力总是小于 ft ,所以不可能再产生新的裂缝。
则在其间还会存在σ 如果两条裂缝的间距大于 2 l ,则在其间还会存在 ct≥ ft 则在其间还会存在 区段,就会产生新的裂缝; 的混凝土 区段,就会产生新的裂缝 如果两条裂缝的间距小于 2 l ,则由于粘结应力传递长 度不够,裂缝间混凝土处处 度不够,裂缝间混凝土处处σct < ft ,因此将不会再出现新 的裂缝。故裂缝间距最终将稳定在 l ~ 2 l 之间,可近似取 之间, 的裂缝。 裂缝的平均间距 l m =1. 5 l。 。 由于混凝土材料的不均匀性,裂缝的出现、 由于混凝土材料的不均匀性,裂缝的出现、分布和开展 具有很大的离散性,裂缝间距和宽度也是不均匀的。 具有很大的离散性,裂缝间距和宽度也是不均匀的。但大量 的试验统计分析表明, 的试验统计分析表明,裂缝间距和宽度的平均值具有一定规 律性。 律性。
我国现行《规范》采用此式, 我国现行《规范》采用此式,但 式中系数K 通常由各国自行确定。 式中系数 1 、 K2通常由各国自行确定。
l m = K 2 c + K1 ⋅
d
ρ
根据对试验资料的统计分析,并考虑不同构件受力特征的影响, 根据对试验资料的统计分析,并考虑不同构件受力特征的影响,对于 公式为, 常用的带肋钢筋,我国《规范》 常用的带肋钢筋,我国《规范》给出的平均裂缝间距 lm 公式为,
裂缝综合理论
1,根据粘结 滑移理论裂缝宽度的验算 ,根据粘结 滑移理论: 粘结—滑移理论: 8.2
混凝土 拉应力 钢筋 应力 粘结应力
由图( )可见, 为粘结应力传递长度, 由图(b)可见,图中 l 为粘结应力传递长度,在裂缝两侧 l 范 所以不可能再产生新的裂缝。 围内混凝土的拉应力总是小于 ft ,所以不可能再产生新的裂缝。
则在其间还会存在σ 如果两条裂缝的间距大于 2 l ,则在其间还会存在 ct≥ ft 则在其间还会存在 区段,就会产生新的裂缝; 的混凝土 区段,就会产生新的裂缝 如果两条裂缝的间距小于 2 l ,则由于粘结应力传递长 度不够,裂缝间混凝土处处 度不够,裂缝间混凝土处处σct < ft ,因此将不会再出现新 的裂缝。故裂缝间距最终将稳定在 l ~ 2 l 之间,可近似取 之间, 的裂缝。 裂缝的平均间距 l m =1. 5 l。 。 由于混凝土材料的不均匀性,裂缝的出现、 由于混凝土材料的不均匀性,裂缝的出现、分布和开展 具有很大的离散性,裂缝间距和宽度也是不均匀的。 具有很大的离散性,裂缝间距和宽度也是不均匀的。但大量 的试验统计分析表明, 的试验统计分析表明,裂缝间距和宽度的平均值具有一定规 律性。 律性。
刘鸿文主编 材料力学 第八章 PPT课件

§8-3 斜 弯 曲
挠度:
f
f
2 y
f
2 z
fz
fy
Fy l 3 3EI z
fz
Fz l 3 3EI y
tan fz Iz tan
fy Iy
f
fy 矩形 I y I z 正方形 I y I z
斜弯曲
平面弯曲
目录
§8-4 弯曲与扭转的组合
弯曲与扭转组合变形是机械工程中最常见的情况,
• 叠加法的应用条件: (1)线弹性材料,加载在弹性范围内,即服从胡克定律; (2)小变形,保证内力与诸外载荷加载次序无关。
组合变形构件危险点的应力状态
单向应力状态:例如,拉伸(或压缩)与弯曲的组合、偏心拉 伸(或压缩)等;
复杂应力状态:例如,弯曲与扭转的组合、拉伸(或压缩)与 扭转的组合、拉伸(或压缩)与弯曲与扭转的组合变形等;
F 350 F
F 350
M
y1 z0 y
FN
z1
150
A 15000 mm2 z0 75mm z1 125mm I y 5.31107 mm4
50 (2)立柱横截面的内力
FN F
M F 350 75103
50
150
425F 103 N m
目录
§8-2 拉伸或压缩与弯曲的组合
A 15000 mm2 I y 5.31107 mm4
z0 75mm z1 125mm
FN F
M 425 103 F N.m
(3)立柱横截面的最大应力
F 350
M FN
t.max
Mz0 Iy
材料力学 第八章

边界条件: x 0
xL
y1 0
y2 0
L
Fb 2 x C1 2L
x连Βιβλιοθήκη 条件:xay1 y2
Fb 3 x C1 x D1 6L
Fb 2 F x ( x a ) 2 C2 2L 2
1 2
Fb 2 C1 ( L b 2 ) C2 , 6L
yC , B
1、载荷分解
q
ql
ql2
2查表:单独载荷作用下
q
5ql yC1 384EI
yC 2
B2
4
ql3 B1 , 24EI
yC1
ql
B1
(ql)l 3 48EI
(ql) l 2 ql3 , 16EI 16EI
yC2
ql2
B2
yC 3
3ql 4 48EI
图所示。试求 ( x), y( x)
和
A 。
Fa L
FAy
FBy
1、求支座反力
FAy
Fb , L
FBy
2、分段列出梁的弯矩方程 AC段 (0 x a)
Fb M 1 ( x) FA x x, L
BC段 (a x L)
Fb M 2 ( x) x F ( x a), L
1 y
y '' ( x )
'2
( x)
3
2
M ( x) EI z
y ( x) ( x) 0
'
1 y ' 2 ( x) 1
故得挠曲线近似微分方程:
M ( x) y' ' EI
材料力学第八章

FN F zF z F yF y A Iy Iz
式中 A为横截面面积;
C
y
Iy , Iz 分别为横截面对 y 轴和 z 轴的惯性矩;
(zF,yF ) 为力 F 作用点的坐标;
(z,y)为所求应力点的坐标.
四、中性轴的位置
FN F zF z F yF y A Iy Iz
z
z
F/A
y
FzF/Wy
z FyF/Wz y
y
FN
(a)
My
(b)
Mz
(c)
(5)对于周边具有棱角的截面,其危险点必定在截面的棱角处, 并可根据杆件的变形来确定
最大拉应力 tmax 和最大压应力 cmin 分别在截面的棱角 D1 D2 处。无需先确定中性轴的位置,直接观察确定危险点的位置 即可
i ay yF
中性轴
2 z
2 iy az zF
(3)中性轴与外力作用点分别处于截面形心的相对两侧
z (yF , zF )
O
az ay
y
z
中性轴
O
外力作用点
z
D1(y1,z1) y
中性轴
y
D2(y2,z2)
(4)中性轴将横截面上的应力区域分为拉伸区和压缩区 横截面上最大拉应力和最大压应力分别为D1 , D2 两切点
C
Fx 0 Fy 0
FNAB F
FRAx 0.866F FRAy 0.5 F
A 1.2m F
30°
B
D 1.2m
FRAy
FNAB
30°
Fy
B
AB杆为平面弯曲与轴向压缩组合变形 中间截面为危险截面.最大压应力 FRAx A 发生在该截面的上边缘 F
材料力学刘鸿文第六版最新课件第八章 组合变形

667 667
F c 160 106 171300N
934 934
许 可 压 力 为 F 45000N 45kN
§8-2 拉伸或压缩与弯曲的组合
例2图 示一夹具。在夹紧零件时, 夹 具受到的P = 2KN的力作用 。已知: 外力作用线与夹具竖杆轴线间的距离
e = 60 mm, 竖杆横截面的尺寸为b = 10 mm ,h = 22 mm,材料许用应力 [] = 170 MPa 。 试校核此夹具竖杆 的强度。
4、拉(压)弯组合变形下的强度计算
拉弯组合变形下的危险点 处于单向应力状态
t ,max
Fl Wy
F A
[ t ]
c ,max
Fl Wy
F A
[ c ]
4、中性轴位置
由中性轴上各点的正应力均为零;
FN
My
Байду номын сангаас
|z| 0
A
Iy
| z | FN I y A M y
+_
(-z y)
y -_
z
_
_
+
|z|
第三组
圆截面、弯扭组合变形
§8-4 扭转与弯曲的组合
扭转+双向弯曲
求合弯矩
M
2
M
2 y
M
2 z
§8-4 扭转与弯曲的组合
例题1 传动轴左端的轮子由电机带动,传入的扭转力偶矩
Me=300Nm。两轴承中间的齿轮半径R=200mm,径向啮合 力F1=1400N,轴的材料许用应力〔σ 〕=100MPa。试按 第三强度理论设计轴的直径d。
§8-1 组合变形和叠加原理
基本变形 构件只发生一种变形;
轴向拉压、扭转、平面弯曲、剪切;
F c 160 106 171300N
934 934
许 可 压 力 为 F 45000N 45kN
§8-2 拉伸或压缩与弯曲的组合
例2图 示一夹具。在夹紧零件时, 夹 具受到的P = 2KN的力作用 。已知: 外力作用线与夹具竖杆轴线间的距离
e = 60 mm, 竖杆横截面的尺寸为b = 10 mm ,h = 22 mm,材料许用应力 [] = 170 MPa 。 试校核此夹具竖杆 的强度。
4、拉(压)弯组合变形下的强度计算
拉弯组合变形下的危险点 处于单向应力状态
t ,max
Fl Wy
F A
[ t ]
c ,max
Fl Wy
F A
[ c ]
4、中性轴位置
由中性轴上各点的正应力均为零;
FN
My
Байду номын сангаас
|z| 0
A
Iy
| z | FN I y A M y
+_
(-z y)
y -_
z
_
_
+
|z|
第三组
圆截面、弯扭组合变形
§8-4 扭转与弯曲的组合
扭转+双向弯曲
求合弯矩
M
2
M
2 y
M
2 z
§8-4 扭转与弯曲的组合
例题1 传动轴左端的轮子由电机带动,传入的扭转力偶矩
Me=300Nm。两轴承中间的齿轮半径R=200mm,径向啮合 力F1=1400N,轴的材料许用应力〔σ 〕=100MPa。试按 第三强度理论设计轴的直径d。
§8-1 组合变形和叠加原理
基本变形 构件只发生一种变形;
轴向拉压、扭转、平面弯曲、剪切;
材料力学第八章

(a)
(b)
图8-5
设有一矩形截面杆,如图 8-6(a)所示,在顶端作用一偏心压力 F ,其作 用点 A 与横截面形心 C 的距离 AC ,用 e 表示,称为偏心距。
(a) (b)
(c) 图8-6
( d)
(e)
轴向压力 FN F 所对应的压应力沿截面宽度均匀分布,如图 8-6(c)所示。 其值为
r3 2 4 2 r4 2 3 2
[ ]
[ ]
(8-5)
如果将 M /W 和 T /Wp 代入上式,并考虑到对于圆截面有Wp 2W ,则强
度条件可改写为
r3 r4
M 2 T 2 [ ]
W
M 2 0.75T 2 W
[ ]
(8-6)
式中, M 和 T 分别代表圆轴危险截面上的弯矩和扭矩; W 代表圆形截面的抗 弯截面系数。
材料力学
第八章 组合变形
一 组合变形的概念与实例
二
弯曲与拉伸(压缩)的组合
三
弯曲与扭转的组合
第一节 组合变形的概念与实例
工程实际中,有些杆件在外力作用下往往同时存在着两种或两种以上 的基本变形。这类变形形式称为组合变形。
图8-1
图8-2
第二节 弯曲与拉伸(压缩)的组合
一、杆件同时受到轴向力和横向力的作用
在危险截面上,由轴向力引起的压应力为
FN A
21.65 3.08 103
kN/m2
7.03103
kN/m2
7.03 MPa
在危险截面的上、下边缘各点,由弯矩引起的最大弯曲正应力为
Mm W
a
x
1
16. . 85
2154 0k
N
/
m2
材料力学第八章.
8
例题 8-5
图a所示钢制实心圆轴其上的两个齿轮上作用有切向力 和径向力,齿轮C 的节圆(齿轮上传递切向力的点构成的 圆)直径dC=400 mm,齿轮D的节圆直径dD=200 mm。已知 许用应力 [ ]=100 MPa。试按第四强度理论求轴的直径。
9
例题 8-5
解: 1. 轴的受力图和内力图 将作用在齿轮上的切向力向轴的 形心简化,传动轴的受力图如图 b所示,在水平荷载作用下,轴 将在xy平面内弯曲,弯矩Mz图如 图c所示;在竖直荷载作用下, 轴将在xz平面内弯曲,弯矩My图 如图d所示;弯矩图均画在受拉 侧,不注明正负。在两个力偶矩 作用下,轴产生扭转,扭矩T图 如图e所示。
或
r 4 [ ]
6
究竟按哪个强度理论计算相当应力,在不同设计规范中并不 一致。注意到发生扭-弯变形的圆截面杆,其危险截面上危 险点处:
M , W
2
T T Wp 2W
2
为便于工程应用,将上式代入式(a)、(b)可得:
r3
M T 4 W 2W M T 3 W 2W
r4
2
M 0.75T [ ] W
2 2 2
即 亦即
(1064 N m ) 0.75( 1000 N m) 100 106 Pa W 1372 N m 6 100 10 Pa 3 πd / 32
3
于是得
13
d
32 1372 N m 0.0519 m 51.9 mm 6 π(100 10 Pa)
11
1064N m
例题 8-5
C截面的总弯矩为
M C (568N m )2 ( 227N m )2 616.7N m M B MC
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BUAA
MECHANICS OF MATERIALS
2
2
一般受力状态的应力圆 y
x y y x 圆心坐标: 半径:
(
x y
, 0)
y
R
(
x
)
2
2 x
x y B A
A
x
(A, A)
(0, )
B
o
(B, B)
2(-)
o
(0, )
Page11
BUAA
MECHANICS OF MATERIALS
y
x
y
y
n
x
2
y
x
2
y
cos( 2 ) x sin ( 2 )
x
x
x
2
y
sin ( 2 ) x cos( 2 )
x
y
当x
y
0
第八章
§8-1 引言
应力、应变状态分析
问题:构件上A点的应力是多少?
F
A
F
F
A
F
F
A
F
Page3
BUAA
MECHANICS OF MATERIALS
应力的定义:
F K
切应力
K
A
p 正应力
p
F A
p lim
F A
A 0
K处的应力
A内的平均应力
应力的单位:Pa,常用Mpa
y
x
2
y
cos( 2 ) x sin ( 2 )
x
2
y
sin ( 2 ) x cos( 2 )
Page14
BUAA
MECHANICS OF MATERIALS
应力圆的绘转角加倍。
Page17
BUAA
MECHANICS OF MATERIALS
作业:8-2(c),8-6,8-8(c)
Page18
一点处的应力与该点所处的截面方位有关
不同方位截面的应力彼此不独立
Page4
BUAA
MECHANICS OF MATERIALS
应力状态:受力构件内一点的各个侧面上的应力情况称为应力状态。
如何描述一点处的应力?
研究构件内一点的应力状态时,通常是围绕该点
取出一个微小立方体(简称微体)作为研究对象
Page15
BUAA
MECHANICS OF MATERIALS 圆心坐标: 半径:
R
几种简单受力状态的应力圆
(
x
2
y
, 0)
(
x
2
y
)
2
2 x
单向受力状态
x x
纯剪切受力状态
y x R=x
双向等拉
R=x/2
o
x/2
o
o
Page16
时,此时对应单向应力状态
2
x co s
x
sin 2
2
当 x
y
0
时,此时对应纯剪切应力状态
x cos 2
x sin 2
Page12
BUAA
MECHANICS OF MATERIALS
§8-3 应 力 圆
x
x
x
y d A sin ( ) co s( ) y d A sin ( ) sin ( ) 0
F
x
t
0
dA x dA cos( ) cos( ) x dA cos( ) sin ( )
y dA sin ( ) sin ( ) y dA sin ( ) cos( ) 0
BUAA
MECHANICS OF MATERIALS
本学期教学安排
一、教学内容:材料力学(Ⅰ) 第8、9、10章 材料力学(Ⅱ) 第11~14,17章 二、作业:每周(二)5:00之前交作业。
三、答疑时间:周(二)下午4:00~5:00, 地点(一)210; 平时可以和老师预约答疑。
三、考试:理论考试70%,平时10%,实验20%, 小论文,设计或改进材力实验加分(1∽10分)
H( , ) D 2 x 2
0
x
x
o y E
C y
x
y
O C C H co s( 2 0 2 ) O C C D co s( 2 0 2 ) O C C D (co s 2 0 co s 2 sin 2 0 sin 2 )
T F T F
Page7
BUAA
MECHANICS OF MATERIALS
梁横截面上同时存在剪力和弯矩时
其余各处
a, c 点处: 单向应力
b 点处: 纯剪切
Page8
BUAA
MECHANICS OF MATERIALS
工字梁:
d
a 点处: 纯剪切; c , d 点处: 单向应力;
b 点处: , 联合作用
y
已知x , y, x , y, 求任意斜截面的应力 ?
dz
x
z
Page10
BUAA
MECHANICS OF MATERIALS
分析方法:微体中取分离体,对分离体求平衡。 y
x y
F
n
n
0
y
d A x d A co s( ) sin ( ) x d A co s( ) co s( )
y
dx dy
单向应力状态
dz
x
, 纯剪切状态
z
Page5
BUAA
MECHANICS OF MATERIALS
杆件的基本变形形式:
轴向拉伸与压缩
扭转
纯弯
单向应力状态: max []
纯剪切状态: max []
Page6
BUAA
MECHANICS OF MATERIALS
螺旋桨轴:
Page13
R
(
x
2
y
)
2
2 x
BUAA
MECHANICS OF MATERIALS
(
应力圆的绘制及应用 y
x y y x
x
2
y
, 0)
R
(
x
2
y
)
2
2 x
x
o y E
C y
D x
x
y
x
2
(x+ y)/2 (x- y)/2 x
Tel: 82338489 E-Mail: huweiping@
Page1
BUAA
MECHANICS OF MATERIALS
本 讲 内 容
第八章 应力、应变状态分析
§8-1 §8-2 §8-3
引言 平面应力状态应力分析 应力圆
Page2
BUAA
MECHANICS OF MATERIALS
y x x
dA
x
2
y
x
2
y
cos( 2 ) x sin ( 2 )
x
2
y
y y
sin ( 2 ) x cos( 2 )
符号规定:—拉伸为正;—使微体顺时针转者为正 —以x轴为始边,指向沿逆时针转者为正
2
y
x
2
y
cos( 2 ) x sin ( 2 )
x
2
(
y
sin ( 2 ) x cos( 2 )
x
2
y
)
2
2
(
x
2
y
)
2
2 x
—坐标系下的圆方程
圆心坐标: 半径:
(
x
2
y
, 0)
R o (x+ y)/2
复杂应力状态下,如何建立强度条件 ?
max [] max []
Page9
BUAA
MECHANICS OF MATERIALS
§8-2 平面应力状态应力分析
y
y x
y
dx x dz dy x
微体仅有四个面作用有应力;
应力作用线均平行于不受力表面;
x
平面应力状态
z
y
(x+ y)/2 (x- y)/2 x
H C H sin ( 2 2 0 )
C D co s 2 0 sin 2 C D sin 2 0 co s 2
H
x
2
y
x
2
x
2
y
y
co s 2 x sin 2
sin 2 x co s 2
