九年级数学上册 4.2 平行线分线段成比例课件 (新版)北师大版(1)
北师大数学九上《4.2平行线分线段成比例》[袁老师]【市一等奖】优质课
![北师大数学九上《4.2平行线分线段成比例》[袁老师]【市一等奖】优质课](https://img.taocdn.com/s3/m/5cd63a2c6bd97f192379e912.png)
教学目标知识目标理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用。
能力目标通过应用,培养识图能力和推理论证能力。
情感与价值观目标(1)、培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值。
(2)、在进行探索的活动过程中发展学生的探索发现归纳意识并养成合作交流的习惯。
2学生知识状况分析学生在本章前两课时的学习中,通过对相似图形的直观感知,体会到可以用对应线段长度的比来描述两个形状相同的平面图形的大小关系。
从而认识了线段的比,成比例线段。
通过对方格纸中成比例线段的探究,了解了合比性质与等比性质,并在探究活动中积累了一定的合作交流的经验,培养了提出问题与解决问题的能力。
同时学生通过对合比性质与等比性质的演绎证明,也进一步发展了逻辑推理能力。
3教学任务分析本节课采用在方格纸中探究的方式,引导学生得出平行线分线段成比例及其推论。
平行线分线段成比例定理是研究相似形的最重要和最基本的理论,是《课程标准》图形的性质及其证明中列出的九个基本事实之一。
在知识技能方面,要求学生理解并掌握平行线分线段成比例定理及其推论,并会灵活应用。
学生经历运用平行线分线段成比例及其推论解决问题的过程,在观察、计算、讨论、推理等活动获取知识。
让学生经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和特殊到一般的思想方法。
进一步发展学生的说理和简单推理的意识及能力;进一步体会数学与现实生活的紧密联系。
4重点难点教学重点:平行线分线段成比例定理和推论及其应用。
教学难点:平行线分线段成比例定理及推论的灵活应用,平行线分线段成比例定理的变式。
5教学过程5.1 第一学时5.1.1教学活动活动1【导入】复习旧知,引入新课内容:教师提问:什么是成比例线段?成比例线段的有哪些性质?目的:(1)复习成比例线段的内容,回顾成比例线段的性质。
效果:学生能够很熟练的运用活动2【活动】小组活动,探究定理1. 探究活动一:内容:如图(1)小方格的边长都是1,直线a ∥b∥ c ,分别交直线m,n于A1,A2,A3,B1,B2,B3 。
4.2平行线分线段成比例 课件(共16张PPT) 北师大版数学九年级上册

AF交BC于点D,若BF=3EF,则 =
.
.
( B)
.
.
点拨:过点E作 //交 BC 于点H,则
=
.
∵BE 是 △ 的中线, ∴ = , ∴ = .
∵ //, = , ∴
=
= , ∴
1 2 1 2
3 .计算
与
的值,你有什么发现?
2 3 2 3
如果不通过测量,我们要将一条长为5厘米的细线分成两部
分,使得这两部分之比为2:3.我们如何运用所学知识解决
这个问题呢?
知识讲解
自主探究
1.请同学们阅读课本82-83页内容.
2.思考并完成课本82页导入的内容中的问题可以得出什么结论?
例2:如图,已知AD为△ABC的角平分线,DE//AB交
AC于E,如果
= ,那么BD:BC等于(
D
)
A.3:5 B. 5:3 C.8:5 D. 3:8
点拨: ∵ //, ∴
=
=
,∴
=
.
【题型三】平行线分线段成比例与三角形中位线的综合应用
例3:如图,BE是△BC的中线,点F在BE上,延长
平行的直线,用它们截两条直线,然后测量被截
的每段线段的长度,观察并计算是否满足本节课
所学的基本事实.
清楚哪些线段是对应的,切勿写反.
注意:在应用基本事实和推论时,我们需要注意的是:对应线段成比例,一
北师大版九上数学4.2平行线分线段成比例知识点精讲
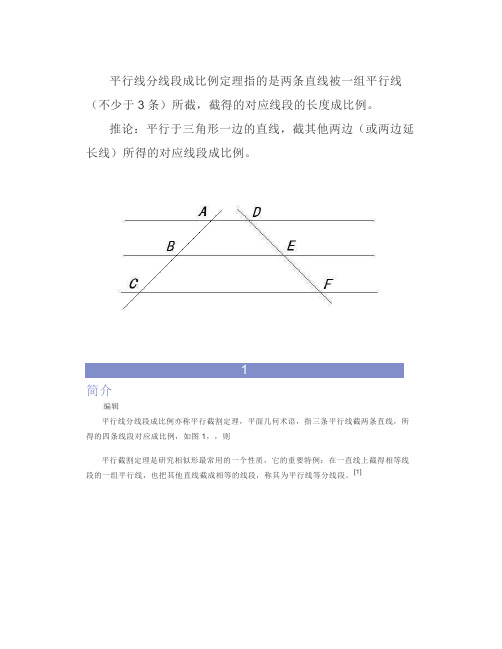
平行线分线段成比例定理指的是两条直线被一组平行线(不少于3条)所截,截得的对应线段的长度成比例。
推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例。
1简介编辑平行线分线段成比例亦称平行截割定理,平面几何术语,指三条平行线截两条直线,所得的四条线段对应成比例,如图1,,则平行截割定理是研究相似形最常用的一个性质,它的重要特例:在一直线上截得相等线段的一组平行线,也把其他直线截成相等的线段,称其为平行线等分线段。
[1]图12定理证明编辑设三条平行线与直线 m 交于 A、B、C 三点,与直线 n 交于 D、E、F 三点。
连结AE、BD、BF、CE根据平行线的性质可得 S△ABE=S△DBE, S△BCE=S△BEF,∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得:AB/BC=DE/EF。
由更比性质、等比性质得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF。
3定理推论编辑过一点的一线束被平行线截得的对应线段成比例。
平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
推广:过一点的一线束被平行线截得的对应线段成比例。
定理推论:①平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
②平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
01平行线分线段成比例的基本事实1.基本事实:两条直线被一组平行线所截,所得的对应线段成比例。
2.符号表示:如图02平行线分线段成比例的基本事实的推论1.推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例。
2.符号表示:如图【知识梳理】1. 平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
北师大版九年级数学上册--第四章 4.2《平行线分线段成比例》第1课时 课件

返回
第四章 图形的相似
4.2 平行线分线段成比例 第1课时 平行线分线段成比例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点 1 平行线分线段成比例的基本事实
1.两条直线被一组平行线所截,所得的对应线段
_成__比__例___.如图,若直线
l1∥l2∥l3,则__BA_CB____DE_FE__或
__AA_CB___DD_FE____或__BA_CC___DE__FF__.
返回
2.(中考·杭州)如图,已知直线a∥b∥c,直线m分别交
直线a,b,c于点A,B,C,直线n分别交直线a,b,
c于点D,E,F,若 AB 1 ,则
BC 2
DE EF
等于(
B
)
1
A. 3
1
B. 2
C.
2 3
D.1
返回
3.如图,已知直线a∥b∥c,直线m,n与a,b,c分
别相交于点A,C,E,B,D,F,若AC=4,CE
又∵AD∥CE,∴
AB AE
BD DC
.
.③
∴ AB BD .
AE DC
(1)上述证明过程中,步骤①②③处的理由分别是什么?
(写出两条即可)
解:步骤①处的理由是两直线平行,同位角相 等;两直线平行,内错角相等.步骤②处的理 由是等角对等边.步骤③处的理由是平行线分 线段成比例的基本事实.(写出两条即可)
三角形内角平分线定理:三角形任意两边之比等
于它们夹角的平分线分对边之比.
已知:如图,在△ABC中,AD是角平分线.
求证:AB BD .
北师大版九年级数学上册第四章图形的相似4.2平行线分线段成比例(教案)

(2)逆向思维的培养:在解决逆向问题,即已知线段比例求平行线问题时,学生往往感到困难。
举例:已知在三角形ABC中,AB/AC = 2/3,点D在BC上,使得AD//BC,求BD/DC的比例。
其次,在新课讲授环节,我采用了理论介绍、案例分析、重点难点解析的方式,逐步引导学生掌握平行线分线段成比例定理。在这个过程中,我发现图示和实际案例的分析对于学生理解这一概念非常有帮助。但在讲解过程中,我应该更加注意语言的简洁明了,避免让学生产生混淆。
在实践活动环节,我安排了分组讨论、实验操作和成果展示。通过这个环节,学生们的动手能力和团队合作能力得到了锻炼。但我也注意到,部分学生在操作过程中还存在一些问题,如对尺度的把握不准确等。因此,在以后的教学中,我可以增加一些关于几何作图的技巧讲解,提高学生们的实践能力。
北师大版九年级数学上册第四章图形的相似4.2平行线分线段成比例(教案)
一、教学内容
本节课选自北师大版九年级数学上册第四章“图形的相似”中的4.2节“平行线分线段成比例”。教学内容主要包括以下两点:
1.探索并掌握平行线分线段成比例定理,即:如果两条直线平行,那么它们所分得的对应线段成比例。
2.学会运用平行线分线段成比例定理解决相关问题,如:求线段比例、相似三角形等。通过对该定理的理解和应用,培养学生空间想象能力和解决问题的能力。
在学生小组讨论环节,我鼓励学生们提出自己的观点和想法,并进行交流。这个环节的效果还不错,学生们积极参与讨论,课堂氛围活跃。但我也注意到,部分学生过于依赖教材,缺乏独立思考的能力。为了培养学生的创新思维,我可以在今后的教学中多设置一些开放性的问题,引导学生进行深度思考。
2023-2024学年北师大版九年级数学上册教案:4.2 平行线分线段成比例

2023-2024学年北师大版九年级数学上册教案:4.2 平行线分线段成比例一. 教材分析《2023-2024学年北师大版九年级数学上册》第4.2节“平行线分线段成比例”主要介绍了平行线分线段成比例的性质。
通过这一节的学习,学生能够理解并掌握平行线分线段成比例的定理,并能够运用该定理解决实际问题。
本节内容是初中数学的重要知识点,对于学生来说具有较高的难度,需要通过大量的练习来巩固。
二. 学情分析九年级的学生已经掌握了平行线的性质,对于线段的比例也有一定的理解。
但是,将平行线与线段的比例联系起来,对于他们来说还有一定的难度。
因此,在教学过程中,需要通过具体的实例,引导学生理解并掌握平行线分线段成比例的性质。
三. 教学目标1.了解平行线分线段成比例的定理,并能够运用该定理解决实际问题。
2.培养学生的逻辑思维能力和解决问题的能力。
3.提高学生的数学素养,使他们在数学学习上有所突破。
四. 教学重难点1.平行线分线段成比例的定理的理解和运用。
2.如何将平行线与线段的比例联系起来,形成系统性的认识。
五. 教学方法采用问题驱动的教学方法,通过具体的实例,引导学生发现并总结平行线分线段成比例的定理。
同时,结合小组讨论和练习,巩固所学知识,提高学生的实际应用能力。
六. 教学准备1.准备相关的教学材料,如PPT、实例等。
2.准备练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)通过一个实际问题,引导学生思考平行线与线段的比例之间的关系。
例如,假设有一块土地,被两条平行线和一条横线分成四个部分,如何求出每个部分的面积比例。
2.呈现(10分钟)通过具体的实例,呈现平行线分线段成比例的定理。
引导学生发现并总结定理的内容。
3.操练(10分钟)让学生分组讨论,运用平行线分线段成比例的定理解决实际问题。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)给出一些练习题,让学生独立完成,巩固所学知识。
教师选取部分题目进行讲解,分析解题思路。
九年级数学北师大版上册 第4章《4.2平行线分线段成比例》教学设计 教案

课题 4.2 平行线分线段成比例 单元 第四单元 学科数学年级九学习 目标1.理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用。
2.通过应用,培养识图能力和推理论证能力。
3.培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值。
重点 平行线分线段成比例定理和推论及其应用。
难点 平行线分线段成比例定理及推论的灵活应用,平行线分线段成比例定理的变式。
教学过程教学环节 教师活动学生活动 设计意图 导入新课教师提问:(1)什么叫比例线段?四条线段 a 、b 、c 、d 中,如果 a :b=c :d ,那么这四条线段a 、b 、c 、d 叫做成比例的线段,简称比例线段.(2)比例的基本性质? 如果a cb d= ,那么ad=bc. 如果ad=bc (a, b, c, d 都不等于0),那么a cb d= 学生思考回答问题。
复习成比例线段的内容,回顾上节课通过方格纸探究成比例线段性质的过程。
讲授新课如下图,小方格的边长均为1,直线l 1 ∥ l 2 ∥ l 3 , 分别交直线m ,n 于格点A 1,A 2, A 3, B 1,B 2, B 3.(1)计算121212122323232313131313A AB B A A B B A A B B 与,与,与A A B B A A B B A A B B的值,你有什么发现?(2)将l 2向下平移到如图的位置,直线m,n 与l 2的交点分别为A 2,B 2,你在问题(1)中发现的结论还成立吗?如果将l 2平移到其他位置呢?学生通过观察、度量、计算、猜测、验证、推理与交流等数学活动,得出结论。
让学生通过观察、度量、计算、猜测、验证、推理与交流等数学活动,达到对平行线分线段成比例定理的意会、感悟。
学生在以前的学习中,尤其是本章前两节的探究也是通过表格中的多边形来完成的。
所以学生有种熟悉(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?试着在纸上画一画!想一想:你能得到什么结论?平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.温馨提示:1. 一组平行线两两平行,被截直线不一定平行;2. 所有的成比例线段是指被截直线上的线段,与这组平行线上的线段无关;几何语言表示:如图,∵l3∥ l4∥ l5AB DE AB DE BC EF∴=,=,=BC EF AC DF AC DF【做一做】如左下图,直线a∥b ∥ c,分别交直线m,n于点A1,A2,A3,B1,B2,B3,过点A1作直线n的平行线,分别交直线b,c于点C2,C3(如右下图). 右下图中有哪些成比例线段?让学生在探究得出结论的基础上,对平行线分线段成比例定理的有进一步的理解。
九年级数学北师大版上册 第4章《4.2平行线分线段成比例》教学设计 教案

4.2平行线分线段成比例◇教学目标◇【知识与技能】理解掌握平行线分线段成比例定理及其推论.【过程与方法】探索并掌握基本事实‘两条直线被一组平行线所截,所得的对应线段成比例’及其推论.【情感、态度与价值观】进一步体会由特殊到一般的归纳推理的思想和方法.◇教学重难点◇【教学重点】理解掌握平行线分线段成比例定理及其推论.【教学难点】正确理解平行线分线段成比例定理.◇教学过程◇一、情境导入如图,任意画两条直线l1,l2,再画三条与l1,l2相交的平行线l3,l4,l5,分别度量l3,l4,l5在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,AB∶BC与DE∶EF相等吗?任意平移l5,再度量AB,BC,DE,EF的长度,AB∶BC与DE∶EF相等吗?二、合作探究探究点1平行线分线段成比例定理典例1如图,直线l1∥l2∥l3,若AB=3,BC=4,则DEDF的值是()A.73B.37C.43D.47[解析]因为l1∥l2∥l3,且AB=3,BC=4,所以DEDF =ABAC=ABAB+BC=37.[答案] B如图,F是▱ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是()A.EDEA =DFABB.DEBC=EFFBC.BCDE =BFBED.BFBE=BCAE[答案] C探究点2平行线分线段成比例定理的推论典例2如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,若线段DE=5,则线段BC的长为()A.7.5B.10C.15D.20[解析]∵DE∥BC,∴△ADE∽△ABC,∴ADAB =DEBC.∵BD=2AD,∴ADAB=13.∵DE=5,∴5BC=13,∴BC=15.[答案] C在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使以A,D,E 三点为顶点的三角形与△ABC相似,则AE的长为()A.16B.14C.16或14D.16或9[答案] D三、板书设计平行线分线段成比例1.平行线分线段成比例定理2.平行线分线段成比例的推论◇教学反思◇通过本节课的学习,学生做到了以下几个方面:首先,探索并掌握基本定理“两条直线被一组平行线所截,所得的对应线段成比例”及其推论;其次,会应用该性质及其推论进行简单的推理计算并且进一步体会由特殊到一般的归纳推理的思想和方法.。
《平行线分线段成比例》课件 初中数学湘教版九年级上册

A₂,C₂. 由于a∥b∥c, l₃∥ l₂ ,因此由 B
B₁ b
“夹在两平行线间的平行线段相等”可知, C C₂
C₁ c
A₂B=A₁B₁, BC₂=B₁C₁.
l₁ l
l₂
₃
新知讲解
在△BAA₂和△BCC₂中, ∠ABA₂=∠CBC₂, BA=BC, ∠BAA₂= ∠BCC₂ . 因此,△BAA₂≌△BCC₂. 从而 BA₂=BC₂. 所以,A₁B₁=B₁C₁.
3.2 平行线分线段成比例
湘教版九年级上册
教学目标
1. 能推导并记住基本事实:“两条直线被一组平行线所截, 所得的对应线段成比例”.
2. 能探究、理解结论:“平行于三角形一边的直线截其他两 边,所得的对应线段成比例”.
3. 能利用本节基本事实和结论列出比例式解决相关问题. 4. 培养学生用数形结合思想解决问题的能力.
B
A
D
E
C
新知讲解
如图,过点A作直线MN,使MN∥DE. M
∵ MN∥BC, D
∴ MN∥DE∥BC.
因此AB,AC被一组平行线MN,DE,BC所截, B 则由平行线分线段成比例可得,
,
.
A
N
E
C
,
.
同时还可以得到
新知讲解
由此,得到以下结论: 平行于三角形一边的直线截其他两边,
所得的对应线段成比例.
由于 a∥d∥b∥e∥f ∥c, 所以 A₁D₁=D₁B₁=B₁E₁=E₁F₁ = F₁C₁.
从而 = ,
即.
A D B E F C
l₁
A₁ a D₁ d B₁ b E₁ e F₁ f
C₁ c
l₂
新知讲解
【北师大版】数学九(上)平行线分线段成比例同步练习本(课件版)

A.
C.
=
=
B.
D.
=
=
11. 如图,在△ABC 中,DE⫽BC,DE 分别与 AB,AC 相交
于点 D, E,若 AE = 4,EC = 2,则 AD∶AB 的值
为
2∶3
.
1
12. 如图,△ABC 中有菱形 AMPN,如果
= ,
AC 所在的直线于点 E,求 CE 的长.
解:如图 1,当点 D 在边 AB 上时,
∵AB = 6,AC = 9,AD = 2,
∴BD = AB - AD = 4. ∵DE⫽BC,
∴ =
4
,即6 =
9
. 解得 CE = 6.
如图 2,当点 D 在边 BA 的延长线上时,
∵AB = 6,AC = 9,AD = 2,
15. 如图,
E 为 AC 的中点,
点 F 在 AB 上,
且 AF∶AB = 2∶5,
EF 与 BC 的延长线交于点 D,求 EF∶ED 的值.
解:如图,作 EG⫽BC 交 AB 于点 G.
∵E 为 AC 中点,EG⫽BC,
∴AG = BG.
∵AF∶AB = 2∶5,即 AF∶FB = 2∶3,
AE
3
AC
4
DE⫽BC.若 = ,AD = 9,则 AB =
12
.
5. 如图,在▱ABCD 中,E 是边 AD 的中点,EC 交对角线 BD 于
点
F
1∶2
,
.
则
北师版数学九年级上册42平行线分线段成比例(1课时)教案与反思金品

2 平行线分线段成比例知人者智,自知者明。
《老子》原创不容易,【关注】,不迷路!一、基本目标1.理解平行线分线段成比例定理及其推论;2.会熟练运用平行线分线段成比例定理及其推论计算线段的长度.二、重难点目标【教学重点】平行线分线段成比例定理及推论的掌握与应用.【教学难点】运用平行线分线段成比例定理及其推论进行计算.环节1 自学提纲、生成问题【5 min阅读】阅读教材P82~P84的内容,完成下面练习.【3 min反馈】1.基本事实:两条直线被一组平行线所截,所得的对应线段成比例.2.推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.3.如图,直线AB//CD//EF,则ACBD=CEDF,ACAE=BDBF,AECE=BFDF.环节2 合作探究,解决问题活动1 小组讨论(师生对学)【例1】已知l1∥l2∥l3,AB=3,DE=2,EF=4,求BC的长.【互动探索】(引发学生思考)根据平行线分线段成比例定理得到AB BC =DE EF,即3BC =24,然后根据比例的性质计算. 【解答】∵l 1∥l 2∥l 3, ∴AB BC =DE EF ,即3BC =24,∴BC =6. 【互动总结】(学生总结,老师点评)两条直线被一组平行线所截,所得的对应线段成比例.“对应线段”是指两条平行线所截得的线段,如AB 与DE 是对应线段、BC 与EF 是对应线段、AC 与DF 是对应线段.“对应线段成比例”是指同一直线上的两条线段的比等于另一条直线上与它们对应的线段的比.【例2】如图,DE ∥FG ∥BC ,AD ∶DF ∶FB =2∶3∶4,如果EG =4,则AC 的长为多少?【互动探索】(引发学生思考)根据平行线分线段成比例定理列出比例式,分别求出AE 、GC 的长,计算即可.【解答】∵DE ∥FG ∥BC ,∴AE ∶EG ∶GC =AD ∶DF ∶FB =2∶3∶4.∵EG =4,∴AE =2×43=83,GC =4×43=163, ∴AC =AE +EG +GC =12.【互动总结】(学生总结,老师点评)平行于三角形一边的直线与其他两边相交,截得的对应线段比例,这是平行线分线段成比例的推论.平行线分线段成比例的推论是在平行线分线段成比例的基础上得到的,是通过作辅助线构造平行四边形,并利用了平行四边形对边相等的性质证得的.活动2 巩固练习(学生独学)1.如图,△ABC 中,D 、E 分别在AB 、AC 上,且DE ∥BC ,若AE ∶EC =1∶2,AD=6,则AB的长为( A )A.18 B.12C.9 D.32.如图,在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且ADDB=3∶5,那么CF∶FB=( D )A.5∶8 B.3∶8C.3∶5 D.5∶33.如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.若ABC=错误!,DE=4,则EF的长是6.4.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,若ABBC=23,DE=6,则EF=9.活动3 拓展延伸(学生对学)例3】如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:(1)当AFAD=12时,AEAC=13;(2)当AFAD=13时,AEAC=15;(3)当AFAD=14时,AEAC=17;…猜想:当AFAD=1n+1时,AEAC=?并说明理由.【互动探索】要求当AFAD=1n+1时,AEAC的值为多少,我们可以通过作辅助线,利用平行线分线段成比例定理,证得AEAG=AFAD=1n+1,得到EG=nAE,证明EG=CG,AC=(2n+1)AE,即可解决问题.【解答】猜想:当AFAD=1n+1时,AEAC=12n+1.理由如下:如图,过点D作DG∥BE,交AC于点G.则AEAG=AFAD=1n+1,∴AEEG=1n,EG=nAE.∵AD是△ABC的中线,∴EG=CG,AC=(2n+1)AE,∴AEAC=12n+1.【互动总结】(学生总结,老师点评)通过作平行线,利用平行线分线段成比例的基本事实的推论证明三角形中线段的比例,解题的关键是作辅助线,构造平行线,灵活运用平行线分线段成比例定理来分析、判断、推理或解答.环节3 课堂小结,当堂达标(学生总结,老师点评)对应线段成比例⎩⎨⎧ 基本事实→两条直线被一组平行线所截,所得的对应线段成比例推论→平行于三角形一边的直线与其他两边相交,截得的对应线段成比例请完成本课时对应训练!【素材积累】 每个人对未来都有所希望和计划,立志是成功的起点,有了壮志和不懈的努力,就能向成功迈进。
2023-2024学年北师大版九年级数学上册教学设计:4.2 平行线分线段成比例

2023-2024学年北师大版九年级数学上册教学设计:4.2 平行线分线段成比例一. 教材分析平行线分线段成比例是北师大版九年级数学上册的教学内容,本节课主要通过探究平行线分线段成比例的定理,让学生理解并掌握平行线分线段成比例的性质及应用。
教材通过丰富的例题和练习,引导学生探究并发现平行线分线段成比例的规律,培养学生的逻辑思维能力和解决问题的能力。
二. 学情分析九年级的学生已经掌握了平行线的性质,对图形的变换和推理已经有了初步的认识。
但是,对于平行线分线段成比例的定理,他们可能还比较陌生,需要通过实例和练习来逐步理解和掌握。
因此,在教学过程中,教师需要关注学生的认知基础,通过引导和激励,激发学生的学习兴趣和积极性。
三. 教学目标1.理解平行线分线段成比例的定理及证明过程。
2.能够运用平行线分线段成比例的定理解决实际问题。
3.培养学生的逻辑思维能力和解决问题的能力。
四. 教学重难点1.教学重点:平行线分线段成比例的定理及证明过程。
2.教学难点:理解平行线分线段成比例的证明方法。
五. 教学方法1.引导探究法:通过引导学生观察、思考、讨论,让学生自主发现平行线分线段成比例的规律。
2.实例教学法:通过丰富的例题和练习,让学生理解和掌握平行线分线段成比例的定理。
3.问题解决法:引导学生运用平行线分线段成比例的定理解决实际问题,培养学生的应用能力。
六. 教学准备1.教学课件:制作课件,展示平行线分线段成比例的例题和练习。
2.教学素材:准备相关的例题和练习题,用于巩固和拓展学生的知识。
七. 教学过程1.导入(5分钟)教师通过展示实际问题,引导学生思考平行线分线段成比例的现象,激发学生的学习兴趣。
2.呈现(10分钟)教师通过课件展示平行线分线段成比例的例题,引导学生观察和分析,让学生自主发现平行线分线段成比例的规律。
3.操练(10分钟)教师给出相关的练习题,让学生独立完成,巩固对平行线分线段成比例的理解。
4.巩固(10分钟)教师通过课件讲解平行线分线段成比例的证明过程,让学生理解和掌握定理。
九年级数学 平行线分线段成比例 知识点精讲 教案 课件

九年级数学平行线分线段成比例知识点精讲平行线分线段成比例定理平行线分线段成比例定理指的是两条直线被一组平行线(不少于3条)所截,截得的对应线段的长度成比例。
推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例。
1简介编辑平行线分线段成比例亦称平行截割定理,平面几何术语,指三条平行线截两条直线,所得的四条线段对应成比例,如图1,,则平行截割定理是研究相似形最常用的一个性质,它的重要特例:在一直线上截得相等线段的一组平行线,也把其他直线截成相等的线段,称其为平行线等分线段。
[1]图12定理证明编辑设三条平行线与直线m 交于A、B、C 三点,与直线n 交于D、E、F 三点。
连结AE、BD、BF、CE根据平行线的性质可得S△ABE=S△DBE,S△BCE=S△BEF,∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得:AB/BC=DE/EF。
由更比性质、等比性质得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF。
3定理推论编辑过一点的一线束被平行线截得的对应线段成比例。
平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
推广:过一点的一线束被平行线截得的对应线段成比例。
定理推论:①平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
②平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
01平行线分线段成比例的基本事实1.基本事实:两条直线被一组平行线所截,所得的对应线段成比例。
2.符号表示:如图02平行线分线段成比例的基本事实的推论1.推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例。
