小升初数学专题——解决问题的策略
小升初第七讲解决问题的策略

第七讲解决问题的策略——转化法1.使学生初步学着运用转化的策略分析问题,灵活确定解决问题的思路,根据问题特点确定具体的转化方法.2.理解转化策略的价值,丰富学生的策略意识,初步掌握转化的方法和技巧.3.让学生知道怎样转化是学生学习的难点.1.使学生通过回顾曾经运用转化策略解决问题的过程,从策略的角度进一步体会知识之间的联系,感受转化策略在解决问题时的价值.2.学生通过回顾曾经运用转化策略解决问题的过程,从策略的角度进一步体会知识之间的联系,感受转化策略的应用价值.3.学生进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,主动克服在解决问题中遇到的困难,获得成功的体验,提高学好数学的信心.世界上很多著名的数学问题都是转化为你已知的知识来解决的.曹冲称象转化成称石头,阿基米德检测纯金王冠转化成测量水的体积,泰勒斯测量金字塔高度转化成测量人的影长,欧拉解决七桥问题转化成一笔画问题.学校食堂买来4把炒勺,5个高压锅共付832元,已知每个高压锅的价钱是炒勺的12倍,每个高压锅和每个炒勺各多少元?1、用大小两辆汽车运煤,大汽车运了9次,小汽车运了10次,一共运了132吨,大汽车3次运的煤等于小汽车4次运的,大、小汽车的载重量各是多少吨?2、少先队员植树,如果每人种5棵树,还多3棵树;如果其中2人每人种4棵树,其余每人种6棵,就恰好种完.少先队员有多少人?甲、乙、丙三人各有钱若干元,甲的钱数是乙的53,丙的钱数比甲多41,求丙的钱数是乙的几分之几?题目中的单位“1”不相同,所以关键在与如何转化单位“1”的量.1、某中学的初中部三个年级中,初一的学生数是初二学生数的910 ,初二的学生数是初三学生数的114倍,这个学校里初三的学生数占初中部学生数的几分之几?2、甲数的34 等于乙数的25,甲数是乙数的几分之几?乙数是甲数的几分之几?甲、乙两人在银行共存钱若干元,已知甲的存款数的41等于乙存款数的51,又知乙比甲多存了24元,求甲、乙两人各存款多少元?1、为了迎接“六一”国际儿童节,玩具厂四月份计划生产玩具12000件,实际上半月生产7000件,要超额全月计划的15%,下半月还要生产多少件?2、甲的年龄比乙的年龄少61,乙的年龄比丙的年龄多31,甲比丙大4岁,求丙的年龄是多少岁?一条小水渠,甲乙两队合修,10天可以完成,如果甲队先修4天,乙队接着6天,则能完成这条水渠的157,如果乙队单独修这条小水渠,需几天完成?1、一堆水泥,上午运走它的72,下午运走它的215还多4吨,最后还剩下16吨,这堆水泥原有多少吨?2、六年级原有学生240人,其中女生占157,后来又转进几名女生,这时女生占全年级人数的3115,后来转进几名女生?乘汽车从甲城到乙城去,原计划215小时,由于途中36千米的道路不平,走这段不平的道路时,速度相当于原来的43,因此晚到51小时,求甲、乙两城之间的距离.1、某校六年级有2个班,共有学生76人,有11人保送重点中学.六(1)班保送人数占未保送人数的51,六(2)班保送人数占未保送人数的71,求两个班各保送了多少人?2、甲、乙两个专业户,去年全年的收入,甲是乙的3倍.甲用全年收入的51支援了办学,又用了全年收入的25%购买了科技书刊.如果甲再给乙6500元,这样甲剩下的钱就和乙剩下的钱相等了.求甲去年的全年收入是多少元?五点过多少分时,时针与分针离“5”的距离相等,并且在“5”的两边?本道题目可以换一个角度进行思考,用转化思想,把追及问题变为相遇问题.1、钟面上4点过几分时,时针和分针与“3”的距离相等,并且在“3”的两边?2、张华5点多起床,一看钟,“6”它恰好在时针和分针的正中间(即两针到“6”的距离相等),这时是5点几分?芳芳3点多钟开始看书,时针和分针正好重合在一起,5点多钟看完书时,时针与分针正好又重合在一起.芳芳看了多长时间书?1、星期天,王甜2点多钟开始做作业,此时时针与分针正好重合在一起,5点多钟看完书时,时针与分针正好又重合在一起.王甜看了多长时间书?2、兰兰下午3点到4点之间.当时针和分针正好重合在一起时,开始做作业,当做完作业时,时针与分针刚好在一条直线上,兰兰做了多少时间的作业?1、有两枝蜡烛.当第一枝燃去54,第二枝燃去32时,它们剩下的部分一样长.这两枝蜡烛原来长度的比是?2、甲乙两人生产同样的一种零件,原计划每天共生产70件,实际甲每天多做30个,乙每天的生产量是原来的3倍,这样,两人一天一共生产零件220个,甲、乙原计划每天各生产零件多少个?3、乙的年龄相当于甲的65,甲的年龄相当于丙的34,已知乙比丙大4岁,求甲的年龄.4、甲、乙两人从东、西两城相向而行,甲行了全程的115正好与乙相遇.已知甲每小时行4.5千米,乙行完全程需要215小时,求甲、乙两城相距多少千米?5、甲、乙两站相距610千米,两站之间有丙站,快车从甲站开往丙站,已经行驶了90千米,慢车从乙站开往丙站,已行驶了它的全部路程的83.这时丙站正好处在快慢两车之间中点的位置上,求甲站到丙站的距离.6、钟面上3点过几分,时针和分针所在的射线与中心到“3”字的连线所成的角度相等?7、爷爷散步不到1小时,结束时他发现手表上时针、分针的位置正好与开始时时针、分针的位置交换了一下.爷爷散步用了多少时间?1、甲数=12345×6789 乙数=123456×789 ,那么甲、乙两数比较大的是哪个?2、王老师每天从家到单位时,前31的路程骑车,后32的路程乘车,从单位回家时,前83的时间骑车,后85的时间乘车,结果去单位的时间比回家的时间多用132小时,已知王老师骑车每小时行8千米,乘车每小时行16千米,那么王老师从家到单位有多远呢?3、学校阅览室例有36名学生在看书,其中女生占49,后来又有几名女生来看书,这时女生人数占所有看书人数的919,问后来又有几名女生来看书?4、六点整时针与分针反向成一条线,下一次时针与分针反向成一条线是几点几分?5、一只手表每小时慢4分,标准时间4点半时,把此表与标准时间对准,现在标准时间是十一点半.问经过多少时间后,这只表才能走到十一点半?1、孙雯家有两个旧挂钟,一个每天快20分钟,另一个每天慢30分钟,晚上7点时将这两个旧挂钟同时调到标准时间,问它们何时再同时显示标准时间?2、一昼夜快4分的手表,如果要在下午3时调拨到几时几分,才能使第二天上午9时指向正确的时刻?3、李家和王家共养了521头牛,李家牛群中有67%是母牛,而王家的牛群中仅有131是母牛,李家和王家各养了多少牛?1、《大圣增桃考少年》月宫蟠桃两百多,赠与杯赛表庆贺;每堆十个少三枚,十二成堆多七个;聪明的你快做答,大圣赠桃多少个?。
小学六年级数学第六单元《解决问题的策略》的教案

小学六年级数学第六单元《解决问题的策略》的教案一、教学目标1.让学生通过自主探究、合作交流,掌握解决问题的策略,提高解决问题的能力。
2.培养学生运用数学知识解决实际问题的意识,提高学生的数学素养。
二、教学重难点1.教学重点:引导学生掌握解决问题的策略,学会运用策略解决实际问题。
2.教学难点:培养学生独立思考、合作交流的能力,提高解决问题的效率。
三、教学过程1.导入新课利用生活中的实际问题,引发学生对解决问题的兴趣,为新课的学习打下基础。
2.自主探究(1)一个长方形的长是12厘米,宽是5厘米,求长方形的面积。
(2)小华有10个苹果,小明有8个苹果,小刚有5个苹果,他们一共拥有多少个苹果?(3)小明的年龄是小红的2倍,小红比小明小3岁,求小明和小红的年龄。
学生在自主探究过程中,可以运用已学的数学知识,如加法、减法、乘法、除法等,尝试解决问题。
3.合作交流(1)在解决问题的过程中,你们运用了哪些策略?(2)这些策略在解决问题中起到了什么作用?(3)如何将所学策略应用到其他实际问题中?(1)画图表示:将问题用图形表示,直观地看出问题的解决方法。
(2)列表表示:将问题中的信息整理成表格,便于分析和解决问题。
(3)列式计算:运用数学公式、法则进行计算,解决问题。
(4)转换问题:将问题转换为已知的数学问题,运用已学知识解决问题。
(5)逻辑推理:通过逻辑推理,找出解决问题的方法。
5.实践应用(1)一个正方形的边长是8厘米,求正方形的面积。
(2)小王买了3本书,每本书的价格是25元,他一共花费了多少元?(3)小丽的年龄是小强的3倍,小强比小丽小4岁,求小强和小丽的年龄。
学生完成后,相互检查,教师点评。
6.课堂小结7.课后作业(1)复习本节课所学内容,巩固解决问题的策略。
(2)完成课后练习题,提高解决问题的能力。
四、教学反思教师根据学生的课堂表现和作业完成情况,反思教学过程中的优点和不足,为下一节课的教学做好准备。
小升初专题 第30讲 解决问题的策略

1.最优化问题。
2.逆推问题。
3.最大与最小值问题。
1.某校足球队计划买50个足球,采购员看了甲、乙、丙三家商店,他们给出的足球单价都是25元,促销方式如下表:甲店乙店丙店“买十送二”“打八折”满100元返还现金20元请你帮采购员算一算,去哪家商店购买比较合算? (请写出计算过程)2.一个农夫提着一篮子鸡蛋去卖,第一次卖掉了全部的一半多2个,第二次卖掉了剩下的一半多2个,第三次还是卖掉了剩下的一半多2个,最后篮子里还剩下3个鸡蛋,问农夫篮子里原有多少个鸡蛋?第30讲解决问题的策略3. 有三种型号的钢板A.B.C分别由3、3、4个1×1的小正方形组成,现有A型钢板7块,需购进B.C两种型号的钢板若干块,不重叠、无缝隙地拼成5×5的正方形钢板2块,已知B 型钢板每块500元,C型钢板每块400元,请考虑B.C两种型号的钢板各购多少块,才能使所花的钱最少?计算出最省钱的方案。
A B C4.有一条可以坐20人的木船要载35名同学从岸边C处到湖中的A、B两岛參观(如图),参观A岛需要30分钟,参观B岛需要20分,C与A岛间船行需要10分钟,C与B岛间船行需要12分钟,A岛与B岛间船行需要6分钟,问:35名同学观完两岛后返回岸边C处最少需要多少时间?A BC5.甲、乙、丙三人各有糖果若干颗,甲从乙处取来一些糖果,使原来的糖果增加了一倍,乙从丙处取来一些糖果,使留下的糖果增加了一倍,最后丙从甲处取来一些糖果,使留下的糖果也增加了一倍.这时三人的糖果一样多,开始时,丙有32颗糖果,那么乙原来有多少颗糖果?6.某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代为租赁5年.5年期满后由开发商以比原商铺标价高20%的价格进行回购。
投资者可在以下两种购铺方案中作出选择:方案一:投资者按商铺标价一次性付清款项,每年可以获得的租金为商铺标价的10%;方案二:投资者按商铺标价的八五折一次性付清款项,2年后每年可以获得的租金为商铺标价的10%,但要缴纳租金的10%作为管理费用。
2020年深圳市小升初数学总复习:解决问题的策略

2 解决问题的策略(2)
基础素养课课清
2 解决问题的策略(2)
基础素养课课清
25 16 9 68 25 17 8 66 25 18 7 64 25 19 6 62
18
7
2 解决问题的策略(2)
基础素养课课清
2 解决问题的策略(2)
基础素养课课清
2 解决问题的策略(2)
谢谢!
能力素养步步赢
1 解决问题的策略(1)
能力素养步步赢
1 解决问题的策略(1)
创新素养个个行
1 解决问题的策略(1)
创新素养个个行
点拨:如果丙说4号是英国人是对的,那么丁说的都不对。所 以丙说3号是美国人是对的,甲说1号是法国人是对的,丁说4 号是韩国人是对的,乙说2号是英国人是对的。 解答:1号是法国人,2号是英国人,
能力素养步步赢
2 解决问题的策略(2)
能力素养步步赢
10
10
130 少15角
9
11
133 少12角
8
12
136 少9角
7
13
139 少6角
5
15
145
0
2 解决问题的策略(2)
能力素养步步赢
5 15
2 解决问题的策略(2)
能力素养步步赢
1个梨子=3个橘子 2个梨子=3根香蕉 2个橘子=1根香蕉 1个橘子重240÷2=120g
2020年深圳市小升初数学 解决问题的策略
4.解决问题的策略 基础素养课课清 1 解决问题的策略(1)
3×3=9件
1 解决问题的策略(1)
基础素养课课清
李老师教语文, 张老师教数学, 王老师教英语。
(小升初培优讲义)专题37 解决问题的策略-六年级一轮复习(知识点精讲+达标检测)(教师版)

专题37解决问题的策略(1)对应法:对应是数学中各类数量间最常见的存在形式。
有一个量,必然有一个与之对应的量或串。
(2)转化法:当题中出现多个单位“1”时,我们可以把不同的单位“1”转化成统一的单位“1”,再进行分析、思考、解答。
(3)假设法:假设法是数学中思考问题的一种常用方法和解题策略。
有些数量关系比较隐蔽或数量之间以建立直接联系的问题,如果对某一个已知数量或未知数量作特定的假设,可以使题中的数量关系于明朗化,从而找到解题的途径。
(4)分数可以转化成比,把比当分数。
(5)抓住不变量的方法:一些较复杂的分数问题中,会出现许多数量前后发生变化的。
这时的解题思维是:在这些变化中抓住不变的量,将不变的量作为标准,有目的地转化数量关系,来找到解题的线索。
不变的量可能是某一部分量,也可以是和、差不变,视题目具体情况而定。
(6)还原法:有些数学问题的答案需要从最后的结果出发,运用加法与减法、乘法与除法的互逆关系,从后往前一步步地推算,逐步使问题得到解决。
能够运用还原法的问题的基本件征是:叙述某一未知量,经过一系列的已知变化,最后成为另一个已知数量,要求出原来的未知量。
[提示]还原的基本途径是从最后一个已知数开始,逐步逆推回去。
原来加的,还原时就诚;原来诚的,还原时就加;原来秦的,还原时就除;原来除的,还原时就乘。
(7)方程法:在解任何问题时,列方程都是一种不能忽视的备用方法。
【例1】某校选出男教师的111和12名女教师参加合唱比赛,剩下的男教师人数是剩下的女教师人数的2倍,已知学校共有男、女教师156名。
男教师有多少名?【点拨分析】此题中数量变化多样,条件复杂,我们可利用列表的方法来帮助分析、解答。
通过分析可得出女教师减少12名后所占的分率(或份数)。
而156名是教师总数,当女教师减少12名后,总数也相应地减少12名,是(156-12)名,它是原有男教师和变化后女数师的人数和。
【答案】解法一(156-12)÷[(1−111)÷2+1]=99(名)解法二(156-12)÷(11+11−1)2×11=99(名)答:男教师有99名。
小学苏教版六年级上册数学《解决问题的策略》校内公开课教案

小学苏教版六年级上册数学《解决问题的策略》校内公开课教案一. 教材分析《解决问题的策略》是小学苏教版六年级上册数学的一章节,主要让学生掌握一些解决问题的方法和策略,培养学生的逻辑思维能力和解决问题的能力。
本节课的内容主要包括分析问题、制定计划、执行计划和检验结果四个方面。
通过本节课的学习,学生能理解问题的本质,学会用有序的方法解决问题,并能对解决问题的过程进行反思和总结。
二. 学情分析六年级的学生已经具备了一定的数学基础,掌握了基本的四则运算和几何知识。
在学习本节课之前,学生已经学习了分数、小数和百分数等知识,对解决问题有一定的认识。
但是,学生在解决实际问题时,往往缺乏条理性和计划性,解决问题的方法不够科学和有效。
因此,在本节课的学习中,需要引导学生从实际问题出发,学会分析问题、制定计划和执行计划,以提高解决问题的能力。
三. 教学目标1.让学生理解问题的本质,学会用有序的方法解决问题。
2.培养学生的逻辑思维能力和解决问题的能力。
3.让学生能对解决问题的过程进行反思和总结,提高解决问题的效果。
四. 教学重难点1.重难点:分析问题、制定计划、执行计划和检验结果四个方面的方法和策略。
2.难点:如何引导学生从实际问题出发,学会分析问题、制定计划和执行计划,以及如何对解决问题的过程进行反思和总结。
五. 教学方法1.讲授法:讲解问题的分析方法、制定计划的方法和执行计划的方法。
2.案例分析法:分析实际问题,引导学生学会分析问题、制定计划和执行计划。
3.小组讨论法:让学生在小组内讨论问题,培养学生的合作意识和解决问题的能力。
4.总结反思法:让学生对解决问题的过程进行总结和反思,提高解决问题的效果。
六. 教学准备1.准备相关的问题案例,用于分析和讨论。
2.准备问题解决的计划和策略,用于讲解和指导。
3.准备黑板和粉笔,用于板书和总结。
七. 教学过程1.导入(5分钟)利用一个实际问题,引导学生思考如何解决这个问题,从而引出本节课的主题。
解决问题的策略1-6年级知识点

解决问题的策略1-6年级知识点解决问题的策略1-6年级知识点:一、数学问题:1. 加减法问题:- 加减法口诀:根据年级不同,可以适当调整口诀的难度。
例如,一年级可以使用简单的口诀:"加法是往右加,减法是往左减";二年级可以使用稍复杂的口诀:"同加同减不变化,差异相差相加"。
- 进位和借位:解决加法或减法中的进位和借位问题,可以使用宝箱进出法等具体方法。
2. 乘除法问题:- 乘法口诀表:要求学生熟记乘法口诀表,能够灵活运用。
- 乘法分配律和除法简便运算:对于较复杂的乘除法,可以通过运用乘法的分配律和除法的简便运算方法,简化计算过程。
- 约分和分数计算:能够进行分数的约分和加减乘除的计算,理解分数的意义。
二、语文问题:1. 阅读理解问题:- 预测法和猜词猜意:通过标题、插图等来预测文章的内容;遇到不认识的生字或陌生词语时,可以猜测词义或意思。
- 分段阅读和标记法:将长篇文章分段读,读完一段后,可以用自己的语言表达段落的大意,并在文章上标记重点内容。
2. 写作问题:- 写作框架和思维导图:学会使用写作框架和制作思维导图来提升写作能力。
例如,对于记叙文,可以将故事按照“开头-事件-结尾”的框架进行组织;对于说明文,可以使用思维导图来整理要点和组织思路。
- 词语的选择和句式的变换:学会使用丰富多样的词语和句式,提升文章的表达力。
三、英语问题:1. 单词拼写问题:- 认真拼写:培养学生认真抄写和默写单词的习惯,注意单词形式和拼写规则。
- 同音异形词和易错词:学习同音异形词和易错词的拼写和用法。
2. 语法问题:- 语法规则记忆和运用:学习常见的语法规则,能够正确运用到写作和句子构造中。
以上只是一些解决问题的策略和相关参考内容,具体的问题解决方法需要根据具体的问题来确定。
在解决问题的过程中,还需要培养学生主动思考、自主学习和沟通交流的能力,引导学生形成问题解决的思维和方法。
小升初数学系列课件-第26课时 解决问题的策略 (通用版,含答案) (共57张PPT)

☞思路点拨 本题考查用转化法解决问题的策略。由于足球 和篮球的价钱都不 知道,而且买的个数也不相等 ,用转化的方法, 把买两种球转化为买一种球,根据“每个足球的价钱是篮球的 1.5 倍”可以知道,买 1 个足球就可买 1.5 个篮球,那么买 4 个足 球的钱就可以买 6 个篮球,从而可知,买篮球和足球的 540 元就 相当于买 3+6=9 个篮球的钱,用 540÷9=60(元)求出每个篮球 的钱,再用 60×1.5=90(元)求出每个足球的钱。
7.假设法 (1)解题时,对 题目中的某个 条件或者某 个情节,做一 些特定 的 假设,再 利用假设 与题目的 已知条件 所产生的 差异或矛 盾,使 题 目的数量 关系变得 简单、清 晰起来, 以便找到 解题的途 径,这 种解题方法叫做假 设法。 (2)假设的内容 主要有①将题 目中不相同 的数量条件, 假设为 相 同的数量 条件;② 对题目中 比较复杂 的情节, 进行新的 调整; ③针对解题的需要 ,假设出一个具体的数量,或假设一 些新的 情节。
小升初数学课件
2.画示意图 在解决问题时有时候需要采取一些手段来帮助分析题意,最 常用的手段就是画示意图。示意图能直观形象地表达数量关系, 使人一目了然,以便较快找到解题的途径,对解答条件隐蔽、复 杂疑难的问题,能起到化难为易的作用。
温馨提示: 在解答有关平面图形面积的问题时,可以依据题目中的条件, 用示意图的方式呈现题目的原意,这样有利于对题目的理解。
老人的年龄 → 加上14 → 除以3 → 减去26 → 乘25 →
100岁 用倒推法思考: 老人的年龄 ← 减去14 ← 乘3 ← 加上26 ← 除以25 ←
100岁
【解】 100÷25=4,4+26=30,30×3=90,90-14=76(岁) 答:这个老人今年 76 岁。
小升初数学总复习归类精讲-第四章解决问题(三)解决问题的策略 全国通用

解决问题的策略课标要求1.掌握画图、倒推、列举、假设、转化等常用的解决问题的策略,能选择合适的策略,解决相应的实际问题,提高思维水平及解题技巧。
考点1 画图的策略1.一个长方形草坪,长90米,扩建后长增加了20米,面积增加了1400平方米。
原来这个草坪的面积是多少平方米(先在图上画一画,再解答)?2.正方形的边长增加3厘米,则面积增加51平方厘米。
原来正方形的周长是多少厘米?现在正方形的面积是多少平方厘米(先画图,再解答)?3.把一条长100厘米的彩带剪成三段,第二段是第一段的2倍,第三段比第二段长10厘米。
第一段彩带长多少厘米(先把线段补充完整,再解答)?第一段:第二段:第三段:4.一个书架有上、下两层,下层书的本数是上层书本数的。
如果把上层的书搬30本放到下层,那么两层书的本数同样多。
原来上、下两层各有多少本书(先把线段图补充完整,再解答)?上层:下层:5. 盒子里有黑、白两种颜色的围棋子共170枚,拿出白棋子的 ,再拿出8枚黑棋子,则剩下的白棋子和黑棋子一样多。
盒子里原来有白棋子多少枚(先把线段补充完整,再解答)?考点2 倒推的策略6. 夏培培在计算一道两位数的加法算式时,由于粗心,将其中一个加数个位上的8看成了3,把另一个加数十位上的1看成了7,结果所得的和是128。
这道加法算式的正确答案是( )。
7. 芳芳收集了一些邮票,她拿出邮票的一半还多2枚送给了齐齐,自己还有40枚,芳芳原来有( )枚邮票。
8. 科学家进行一次实验,实验开始时做第1次记录,以后每隔,5小时做一次记录,他做第11次记录时,时钟正好指向9时整,则第一次记录时,时钟指向( )时整。
9. 小红看一本书,第一天读了全书的一半多3页,第二天读了剩下的一半少3页,第三天读完了余下的48页。
这本书共有多少页?10. 有三堆橘子共48个,先从第一堆中拿出与第二堆个数相等的橘子放入第二堆,再从第二堆中拿出与第三堆个数相等的橘子放入第三堆,最后又从第三堆中拿出与这时第一堆个数相等的橘子放入第一堆。
小升初数学难题的解题技巧

小升初数学难题的解题技巧小升初这段时间,对孩子们来说,就像是爬山,不仅有风景,还有不少坎坷。
而数学题目呢,就像是山路上的石头,需要一点一点地捡起来,才能顺利登顶。
今天,我们就来聊聊那些能够帮助你顺利通过数学难题的小技巧,让你在考试中游刃有余。
1. 理解题意,打好基础在面对数学难题时,第一步就是搞清楚题意。
这就像是你去探险前要了解路线一样重要。
1.1 认真审题别小看这一点,很多时候题目看似简单,但其中可能藏着“陷阱”。
所以,审题的时候要特别仔细,搞清楚题目在问什么,条件是什么。
比如,有些题目可能会用“至少”、“至多”这些词,搞清楚这些词的含义对于解题至关重要。
1.2 用自己的话复述把题目用自己的话说一遍,看看是不是理解对了。
比如,题目说小明有10元钱,每次花5元,那么他最多能买几次东西,你可以把这句话换成“10元除以5元等于多少”,这样是不是更清晰呢?2. 分步解决,逐步推进一旦搞清楚题目后,就可以进入解题阶段。
别想着一步登天,逐步推进才是关键。
2.1 拆分问题复杂的问题,往往可以拆分成几个小问题。
比如,你要解一道涉及面积的题目,可以先求出长和宽,再算面积。
一步一步来,不要让大题目吓到你。
2.2 列出方程列方程是解决问题的好方法。
用代数的方式把问题化简,往往能让问题变得清晰。
比如,设未知数,然后用等式表示条件,这样解起来就能条理清晰。
3. 实战练习,积累经验知识掌握了,还要通过大量的练习来巩固。
就像打游戏一样,练得多了,自然水平就提高了。
3.1 多做习题数学的学习离不开做题。
做题的过程中,你会遇到各种各样的问题,这些都是你积累经验的好机会。
每做一道题,都要总结一下,看看自己有没有哪个地方还可以改进。
3.2 查漏补缺做题时难免会遇到错误,这时候就要认真分析错误的原因。
是不是某个知识点没掌握牢?还是审题不仔细?找到问题所在,及时调整,才能不断进步。
4. 心态调整,保持冷静最后,面对难题的时候,心态也非常重要。
苏教版小学数学六年级上册第四单元《解决问题的策略》

苏教版小学数学六年级上册第四单元《解决问题的策略》一. 教材分析《解决问题的策略》是苏教版小学数学六年级上册第四单元的内容。
本节课的主要任务是让学生掌握解决问题的基本策略,学会运用画图、列表等方法来分析问题、解决问题。
通过本节课的学习,学生能够提高自己的数学思维能力,培养解决实际问题的能力。
二. 学情分析六年级的学生已经具备了一定的数学基础,对于简单的问题解决能力已经有了一定的掌握。
但是,学生在面对复杂问题时,往往缺乏条理清晰的解决策略,对于如何将问题简化、如何进行分析等方法还不够熟练。
因此,在教学过程中,需要引导学生学会运用合适的方法来解决问题。
三. 说教学目标1.知识与技能目标:学生能够掌握解决问题的基本策略,学会运用画图、列表等方法来分析问题、解决问题。
2.过程与方法目标:学生通过自主探究、合作交流,培养解决实际问题的能力。
3.情感态度与价值观目标:学生增强对数学学科的兴趣,培养积极解决问题的态度。
四. 说教学重难点1.教学重点:学生掌握解决问题的基本策略,学会运用画图、列表等方法来分析问题、解决问题。
2.教学难点:学生如何将复杂问题简化,如何运用合适的策略进行问题分析。
五. 说教学方法与手段本节课采用“问题驱动”的教学方法,引导学生通过自主探究、合作交流的方式来解决问题。
同时,利用多媒体手段,展示相关问题的图像和数据,帮助学生更直观地理解问题。
六. 说教学过程1.导入:通过一个实际问题,引发学生思考,激发学生解决问题的兴趣。
2.自主探究:学生通过画图、列表等方式,尝试解决导入问题。
3.合作交流:学生分享自己的解决方法,讨论哪种方法更加有效,为什么。
4.讲解与演示:教师对学生的解决方法进行讲解,并通过多媒体手段进行演示。
5.练习与巩固:学生进行相关的练习题,巩固所学的方法。
6.总结与拓展:学生总结本节课所学的解决问题的策略,尝试解决更加复杂的问题。
七. 说板书设计板书设计要清晰、简洁,能够突出本节课的重点内容。
(完整版)小升初数学复习-解决问题的策略(含练习题及答案)
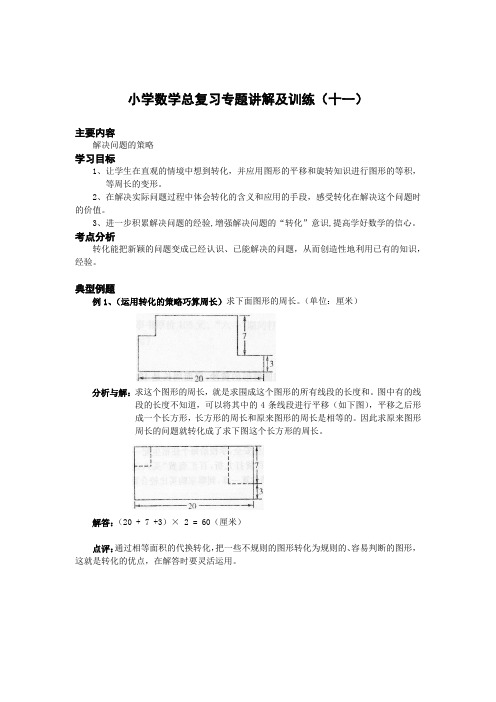
小学数学总复习专题讲解及训练(十一)主要内容解决问题的策略学习目标1、让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形。
2、在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。
3、进一步积累解决问题的经验,增强解决问题的“转化”意识,提高学好数学的信心。
考点分析转化能把新颖的问题变成已经认识、已能解决的问题,从而创造性地利用已有的知识,经验。
典型例题例1、(运用转化的策略巧算周长)求下面图形的周长。
(单位:厘米)分析与解:求这个图形的周长,就是求围成这个图形的所有线段的长度和。
图中有的线段的长度不知道,可以将其中的4条线段进行平移(如下图),平移之后形成一个长方形,长方形的周长和原来图形的周长是相等的。
因此求原来图形周长的问题就转化成了求下图这个长方形的周长。
解答:(20 + 7 +3)× 2 = 60(厘米)点评:通过相等面积的代换转化,把一些不规则的图形转化为规则的、容易判断的图形,这就是转化的优点,在解答时要灵活运用。
例2、(将复杂的图形转化成简单的图形后计算面积)如图1是一块长方形草地,长方形的长是16米,宽是10米。
中间有两条道路,一条是长方形,一条是平行四边形。
草地部分的面积有多大?图1 图2分析与解:求草地部分的面积,可以用大长方形的面积减去两条道路的面积,但要考虑两条道路的重叠部分,因此计算比较复杂。
可以将图1转化成图2,两条道路转化到了长方形草地的边上,很明显,图2草地部分(阴影部分)的面积和图1相等,现在求草地的面积转化成了求长方形的面积,计算比较简单。
解答:(16 - 2 )×(10 - 2) = 112(平方米)答:草地部分的面积是112平方米。
例3、(辨析)下面图形的周长可以转化成长15厘米、宽9厘米的长方形来计算,即周长是(15 + 9)× 2 = 48(厘米)。
分析与解:如下图,将长2厘米的线段移到上面,转化成了一个长方形,但还多两条3厘米的线段。
小升初数学知识点精讲(解决问题的策略)

正解:(25+1)×2=52(张)
归纳总结
先分类
不遗漏;
时要
考
重复
再列举
如果一件事物经过一番变化, 重点已5经倒知推 道了结果,要求原来的
数像量这,种那由么现我在们倒就退可回以去从,求这原个来
结的在果问倒开题过始来,这倒推种推想方,的法运时我用候们“要称倒注之过意为来变倒 推化想法顺”,序的和策变略化进方行式解。题。
题1 画图法
源题解析
① ②③④⑤⑥
长/m 11 10 9 8 7 6
宽/m 1 2 3 4 5 6
面积 /m2
11 20 27 32 35 36
易错1
易错点拨
小军收集了一些画片,他拿出画片的一半还多1张送给小明,自己还剩25 张。小军原有多少张画片?
原有( )张
÷2
()
+-11
25张
×2
-+11
错解(25-1)×2=48(张) 解析:拿出一半多1张应该是加1
学校举行足球比赛,一共有6个球队参加。如果每两个球 队要踢一场球,一共要踢多少场球?
5+4+3+2+1
题2列表法 说一说小明10周岁前体重是如何随年龄增长而变化。
年龄
出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/千克 3.5 7.0
10.5
14.0Biblioteka 21.0 31.5题3 列举
爷爷用24根1米长的栅栏围成一个长方形羊圈,爷爷有几种围法?围 成的面积最大是多少平方米? 24 ÷ 2=12(m)
解决问题的策略
重点1 画图法
重点透视
列举出所有搭配方法 表示变化的量之间的关系 分析问题中的数量关系
小学四年级数学第八单元《解决问题的策略》教案

小学四年级数学第八单元《解决问题的策略》教案一、教学目标1.让学生掌握解决问题的基本策略,如画图、列表、猜想与尝试等。
2.培养学生分析问题、解决问题的能力。
3.培养学生合作交流、自主探究的精神。
二、教学内容1.解决问题的策略:画图、列表、猜想与尝试。
2.解决实际问题,提高解题能力。
三、教学重点与难点1.教学重点:掌握解决问题的策略,提高解题能力。
2.教学难点:灵活运用策略解决问题,培养解题思维。
四、教学过程1.导入新课师:同学们,我们在日常生活中会遇到很多问题,那么你们知道如何解决问题吗?今天,我们就来学习解决问题的策略。
2.策略一:画图师:请大家看这个题目,小华有10个苹果,他每天吃2个,几天能吃完?生1:5天能吃完。
师:你是怎么想的?生1:我用10除以2,得5。
师:很好!如果我们用画图的方式来表示这个问题,会怎么做呢?生2:我们可以画10个苹果,每天吃掉2个,直到吃完。
(1)小明有18个球,他每天玩3个,几天能玩完?(2)小红买了12个铅笔,她每天用2个,几天能用完?3.策略二:列表物品|数量|单价(元)|总价(元)-苹果|5|2|香蕉|3|3|葡萄|2|4|师:请大家帮小红算一下,她妈妈一共花了多少钱?生3:我可以把每种水果的总价算出来,然后相加。
物品|数量|单价(元)|总价(元)-铅笔|10|1|橡皮|5|0.5|作业本|3|3|求小刚一共花了多少钱?物品|数量|单价(元)|总价(元)-书包|1|50|文具盒|2|10|笔袋|3|5|求小王一共花了多少钱?4.策略三:猜想与尝试师:有时候,我们遇到的问题可能没有现成的解决方法,这时我们可以尝试猜想。
请大家看这个题目,小华有20个球,他想把这些球分给几个同学,每个同学分几个球,才能保证每个人都能得到相同数量的球?生4:我可以先猜一下,然后把20个球分给几个同学,看能不能平均分配。
(1)小王有18个糖果,他想把这些糖果分给几个同学,每个同学分几个糖果,才能保证每个人都能得到相同数量的糖果?(2)小芳有24个饼干,她想把这些饼干分给几个同学,每个同学分几个饼干,才能保证每个人都能得到相同数量的饼干?物品|数量|单价(元)|总价(元)-饼干|10|2|面包|5|3|牛奶|3|4|求小红的妈妈一共花了多少钱?五、课后反思本节课通过讲解三种解决问题的策略,让学生在实际操作中掌握方法,提高解题能力。
小升初数学系列课件-第26课时 解决问题的策略 l (通用版,含答案 ) (共57张PPT)

【解】 草地面积=(16-2)×(10-2)=112(平方米) 答:有草部分(阴影部分)的面积有 112 平方米。 方法总结: 本题启发我们,求不规则图形的面积首先要把不规则图形转 化成规则图形,再求面积,数学上把这种方法叫做等积变换。要 想有这种“转化”的本领,首先要提高对图形的观察能力。
小升初数学PPT课件
老人的年龄 → 加上14 → 除以3 → 减去26 → 乘25 →
100岁 用倒推法思考: 老人的年龄 ← 减去14 ← 乘3 ← 加上26 ← 除以25 ←
100岁
【解】 100÷25=4,4+26=30,30×3=90,90-14=76(岁) 答:这个老人今年 76 岁。
【例 6】 学校买了 3 个篮球和 4 个足球,共花了 540 元,每个足球的价钱是篮球的 1.5 倍,每个足球和每个篮球各 多少元?
第26课时 解决问题的策略
考点 解决问题的常用策略
1.列表法 (1)对于数量关系比较隐蔽或复杂的应用题,我们可以用表格 的形式对题中的条件进行分类处理并整理一些对解题有用的信 息,使条件与问题间的关系条理化、明朗化,从而获得准确的解 题思路,这种方法叫做列表法。 (2)列表法便于发现数量之间的联系,容易寻找规律。
( 1)原来题目中叙述的运算 ,在倒推列式计算时 ,要全部变 化 。如题目 中是除法 ,那么在 倒推列式 计算时, 要改为乘 法;题 目中是减法,在倒推列式计算时,要改成加法。
( 2)在倒推解题时,按 照题目的叙述顺序进行倒推 ,一般不 列综合算式进行计 算。根据题意,我们可以列出下面的 流程图:
8.转化法 (1)在解决问题中有时候会遇到题中的已知条件标准不统一, 数量关系不明确, 通过转化的思想可以使数量关系明确 ,轻松 解题。 (2)转化的类型有①转化已知条件;②转化“单位 1”;③转 化叙述方式。
第二十讲 小升初—解决问题的策略(专项复习)人教版六年级下册数学

第20讲解决问题的策略知识点回顾:例1:鸡、兔同笼共100只,鸡脚只数比兔脚只数多20只,请问:鸡兔各有多少只?练习1:1.鸡和兔同时放在一只笼子里,上面有29个头,下面有92只脚,笼中鸡、兔各有多少只?例2:小朋友分小红花,如果每人分4朵,则剩下20朵;如果每人分5朵,则差5朵。
求小朋友的人数和小红花的朵数分别是多少?练习2:1.幼儿园老师给小朋友分糖果,每个小朋友分3颗糖,就多出50颗糖;每个小朋友分5颗,就少10颗。
那么有几个小朋友?有多少颗糖?2.四年级一班同学去划船,他们租了一些船,如果每船4人则多出6人,如果每船5人则船上有4个空位,问有多少个同学?多少条船?例3:小明到水果店去买梨和苹果,用全部的钱可买3千克梨和12千克苹果,或者可买6千克梨和8千克苹果。
如果全部的钱只买梨或只买苹果,各可买多少千克?练习3:1.建筑工地用5辆大车和4辆小车一次运来砂石42.5吨,每辆大车比每辆小车多运4吨。
每辆大车和每辆小车各运砂石多少吨?课堂同步练习:1.小明设计的猜年龄程序是:刘爷爷按这种程序输出的结果是100。
请计算六刘爷爷的年龄。
2.停车场上停有三轮摩托车和两轮摩托车共23辆,小明数了一下,这些摩托车一共有60个轮子,停车场上三轮摩托车和两轮摩托车各多少辆?3.小红买了4个苹果和5个梨子共用了6元钱,小林买了同样6个苹果和5个梨子共用7元钱。
1个苹果和1个梨子各多少元?4.100个和尚吃100个馒头,大和尚每人吃4个,小和尚每4人吃1个,问大和尚和小和尚各吃了多少个馒头?5.学校买回一批跳绳分给全校各班级,如果每班分8根,就余下54根,如果每班分10根,就余下20根。
这个学校有多少个班?买回了跳绳多少根?6.有一段路长720米,在路的一边每隔3米种1棵树,并且两端都要种,一共要种多少棵树?7.70本书和38支钢笔平均奖给三好学生。
结果书多出5本,钢笔差1支。
评出的三好学生最多有多少人?8.关于汽车号码的编排,你知道哪些?从停车场里这几辆汽车的车牌号中,你能了解哪些信息?(1)请你说一说上面三辆车分别来自哪个省市?(2)观察身边经过的汽车牌号,记录下来,做一个简单的统计,它们来自哪些省、市和地区,你发现了什么?9.有两个相同的直角三角形重叠在一起(如下图,单位:厘米),求阴影部分的面积。
小升初数学系列课件-第26课时 解决问题的策略 l (通用版,含答案 ) (共57张PPT)

【例 4】 鸡兔同笼,有 20 个头,54 条腿,鸡兔各有
多少只? ☞思路点拨 本题考查用列举法解决问题的策略。“鸡兔同
笼”问题的解决方法很多,可以用假设法,也可以用方程解,这 里教给大家另外一种方法,即用列举法来求。
【解】 根据题意可画表如下:
头(个)
鸡(只)
兔(只)
20
1
19
20
2
18
20
3
老人的年龄 → 加上14 → 除以3 → 减去26 → 乘25 →
100岁 用倒推法思考: 老人的年龄 ← 减去14 ← 乘3 ← 加上26 ← 除以25 ←
100岁
【解】 100÷25=4,4+26=30,30×3=90,90-14=76(岁) 答:这个老人今年 76 岁。
【例 6】 学校买了 3 个篮球和 4 个足球,共花了 540 元,每个足球的价钱是篮球的 1.5 倍,每个足球和每个篮球各 多少元?
17
…
…
…
20
13
7
答:鸡有 13 只,兔有 7 只。
腿(条) 78 76 74 … 54
【例 5】 有一位老人说:“把我的年龄加上 14 后除以 3,再减去 26,最后用 25 乘,恰巧是 100 岁。”这位老人今年多 少岁?
☞思路点拨 本题考查用倒推法解决问题的策略。求这位老 人今年多少岁,我们只能从最后的条件入手,从后向前倒着推, 在倒推的时候需要注意两点:
【解】 4÷2×3=6(小时)(乙 4 小时的工作量, 甲需要 6 小时) 6+4=10(小时)(甲单独生产 800 个零件需要 10 小时) 800÷10=80(个)(甲每小时生产 80 个) 答:甲每小时生产 80 个零件。 方法总结: 通过替换,把两个人合做变成一个人独做,简化了数量关系, 使问题变得简单。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学总复习专题——解决问题的策略主要内容
解决问题的策略
学习目标
1、让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进
行图形的等积,等周长的变形。
2、在解决实际问题过程中体会转化的含义和应用的手段,感受转
化在解决这个问题时的价值。
3、进一步积累解决问题的经验,增强解决问题的“转化”意识,提
高学好数学的信心。
考点分析
转化能把新颖的问题变成已经认识、已能解决的问题,从而创造性地利用已有的知识,经验。
典型例题
例1、(运用转化的策略巧算周长)求下面图形的周长。
(单位:厘米)
分析与解:求这个图形的周长,就是求围成这个图形的所有线段的长度和。
图中有的线段的长度不知道,可以将其中的4条线段进行平移(如下
图),平移之后形成一个长方形,长方形的周长和原来图形的周长
是相等的。
因此求原来图形周长的问题就转化成了求下图这个长方
形的周长。
解答:(20 + 7 +3)× 2 = 60(厘米)
点评:通过相等面积的代换转化,把一些不规则的图形转化为规则的、容易判断的图形,这就是转化的优点,在解答时要灵活运用。
例2、(将复杂的图形转化成简单的图形后计算面积)
如图1是一块长方形草地,长方形的长是16米,宽是10米。
中间有两条道路,一条是长方形,一条是平行四边形。
草地部分的面积有多大?
图1 图2
分析与解:求草地部分的面积,可以用大长方形的面积减去两条道路的面积,但要考虑两条道路的重叠部分,因此计算比较复杂。
可以将图1转
化成图2,两条道路转化到了长方形草地的边上,很明显,图2草地
部分(阴影部分)的面积和图1相等,现在求草地的面积转化成了
求长方形的面积,计算比较简单。
解答:(16 - 2 )× (10 - 2) = 112(平方米)
答:草地部分的面积是112平方米。
例3、(辨析)下面图形的周长可以转化成长15厘米、宽9厘米的长方形来计算,
即周长是(15 + 9)× 2 = 48(厘米)。
析与解:如下图,将长2厘米的线段移到上面,转化成了一个长方形,但还多两条3厘米的线段。
正确解答:(15 + 9)× 2 + 3 × 2 = 54(厘米)
例4、(已知两个量之间的分率关系与它们的和,求这两个量)
学校图书馆购进的科技书的册数是故事书的,购进的科技书和故事
书一共1500册。
购进科技书多少册?
分析与解:这类有关分数的实际问题可以用方程来解答。
需要注意的是根据“购进的科技书的册数是故事书的”故事书是单位“1”的量,
要设故事书有x册,而不能直接设科技书有x册。
解答:方法1:设故事书有x册,科技书有x册。
X + x = 1500
x = 1500
x = 1050 x = × 1050 = 450答:购进科技书450册。
很显然,上面解答过程比较复杂。
可以这样想:把总数看作单位“1”,根据“购进的科技书的册数是故事书的”,可以把故事
书看成7份,科技书有这样的3份,一共有10份,科技书占总数的
;可以看出科技书和故事书的比是3 :7,根据按比例分配问题的解
法,可以知道科技书占总数的。
方法2:3÷(3 + 7)= 1500 × = 450 (册)
答:购进科技书450册。
例5、(辨析)红花的朵数比蓝花多,蓝花的朵数就比红花少。
蓝花:
红花:
析与解:如图,根据“红花的朵数比蓝花多”,蓝花是单位“1”的量,平均分成7份,红花有这样的9份。
反过来,把红花看作单位“1”,
红花平均分成了9份,蓝花相当于这样的7份,蓝花的朵数比红花
少。
正确解答:红花的朵数比蓝花多,蓝花的朵数就比红花少。
例6、(综合题) 小明读一本书,已读的页数是未读页数的。
他再读30页,这时已读的页数是未读页数的。
这本书共多少页?
分析与解:本题中已读的页数和未读的页数均发生了变化,不变的量是一本书的总页数,即已
读的页数和未读页数的和没有变,把这本书的总页数看
作单位“1”。
“已读的页数是未读页数的”,可以转
化为“已读的页数是这本书总页数的”;再读30页
后“已读的页数是未读页数的”,可以转化为“已读的
页数是这本书总页数的”。
解答: 3 ÷ (3 + 2)=
7 ÷ (7 + 3)=
30 ÷ ( - )= 300(页)
答:这本书共300页。
例7、(综合题) 六(1)班原来女生占全班人数的,新学期转出了4名女生,这时女生占全班人数的。
六(1)班现在有女生多少人?
分析与解:本题中女生人数和全班人数均发生了变化,不变的量是男生的人数,因此把男生的人数看作单位“1”。
“女生占全班人数的”,
可以转化为“女生人数是男生人数的”;转出若干名女生后,“女
生占全班人数的”,可以转化为“女生人数是男生人数的”。
解答:4 ÷ (9 - 4)=
2 ÷ (5 - 2)=
4 ÷ ( - )= 30(人)┈┈ 男生人数
30 × = 20(人) ┈┈ 现有女生人数
答:现在有女生20人。
点评:分率的转化过程通常要借助于份数,可以先分析出单位“1”的份数,再根据关系分析出另外的量的份数,再结合具体的条件进行分
率的转化。
