材料力学第6章-弯曲应力分析与强度计算_4209846
合集下载
材料力学第6章-弯曲应力

实心与非薄壁截面梁
a与c 点处-单向应力
单辉祖,材料力学教程
b 点处-纯剪切
32
薄壁截面梁
d
a 点处-纯剪切
c 与d 点处-单向应力
b 点处- 与 联合作用
单辉祖,材料力学教程 33
梁的强度条件
梁的强度条件 弯曲正应力强度条件: 材料单向应力许用应力 max [ ] 弯曲切应力强度条件: 材料纯剪切许用应力 max [ ] 强度条件的应用 细长非薄壁梁 ( max max ) max [ ] 短而高梁、薄壁梁、 M 小 FS大的梁或梁段 max [ ] max [ ] 对一般薄壁梁,还应考虑 、 联合作用下的 强度问题(参见第 8 章中的强度理论) 单辉祖,材料力学教程
单辉祖,材料力学教程
28
例 3-2 已知梁段剪力FS,试分析铆钉的受力
单辉祖,材料力学教程
29
FS
F2 F1 2
单辉祖,材料力学教程
30
§4 梁的强度条件与合理强度设计
梁危险点处的应力状态 梁的强度条件
梁的合理强度设计
例题
单辉祖,材料力学教程
31
梁危险点处的应力状态
2 I z0 A y0 dA
A y0dA 0
Cy0z0-形心直角坐标系 Oyz -任意直角坐标系 二者平行
16
I z I z0 Aa2
同理得:
单辉祖,材料力学教程
I y I y0 Ab2
例 题
例 2-1 已知:F=15 kN, l=400 mm, b=120mm, d=20mm 试计算:截面 B-B 的最大拉应力t,max与压应力c,max
a与c 点处-单向应力
单辉祖,材料力学教程
b 点处-纯剪切
32
薄壁截面梁
d
a 点处-纯剪切
c 与d 点处-单向应力
b 点处- 与 联合作用
单辉祖,材料力学教程 33
梁的强度条件
梁的强度条件 弯曲正应力强度条件: 材料单向应力许用应力 max [ ] 弯曲切应力强度条件: 材料纯剪切许用应力 max [ ] 强度条件的应用 细长非薄壁梁 ( max max ) max [ ] 短而高梁、薄壁梁、 M 小 FS大的梁或梁段 max [ ] max [ ] 对一般薄壁梁,还应考虑 、 联合作用下的 强度问题(参见第 8 章中的强度理论) 单辉祖,材料力学教程
单辉祖,材料力学教程
28
例 3-2 已知梁段剪力FS,试分析铆钉的受力
单辉祖,材料力学教程
29
FS
F2 F1 2
单辉祖,材料力学教程
30
§4 梁的强度条件与合理强度设计
梁危险点处的应力状态 梁的强度条件
梁的合理强度设计
例题
单辉祖,材料力学教程
31
梁危险点处的应力状态
2 I z0 A y0 dA
A y0dA 0
Cy0z0-形心直角坐标系 Oyz -任意直角坐标系 二者平行
16
I z I z0 Aa2
同理得:
单辉祖,材料力学教程
I y I y0 Ab2
例 题
例 2-1 已知:F=15 kN, l=400 mm, b=120mm, d=20mm 试计算:截面 B-B 的最大拉应力t,max与压应力c,max
材料力学第6章-弯曲应力分析与强度计算_4209846

静矩、形心及其相互关系 (设x轴方向单位面积上的力为1个单位)
y
z
y
zC
dA
y
C
z
yC
O
O A
z
分力之矩之和
S y zdA
A
合力之矩
S y AzC
S z AyC
S z ydA
A
(联想中值定理)
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
静矩、形心及其相互关系
z
A dA
y
如果y、z轴通过图形形心C, 上述各式中的Sy=Sz=0
C
a O´
y1
z
b
I y1 I y b A 2 I z1 I z a A I y1z1 I yz abA
2
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
y z1
与应力分析相关的截面图形几何性质
例 题 10 y
dA
dr
已知:圆截面直径d 求:Iy, Iz, IP
解:取圆环微元面积
dA 2 π rdr
z
IP 1 I y I z r 2 dA 2 2 A 4 1 d π d 2 r 2 2 π r dr 0 2 64 πd 4 IP 2I y 32
A
iy
Iy A
——图形对 y 轴的惯性半径
iz
Iz A
——图形对 z 轴的惯性半径
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
惯性矩、极惯性矩、惯性积、惯性半径 y
z
I y z 2 dA
材料力学基本第六章 弯曲强度

(2)当梁的跨度与横截面高度的比值较大时(如l / h >5),纯 弯曲正应力公式对横力弯曲仍然适用。
6.3.3. 梁的弯曲正应力公式的应用于推广
在横力弯曲情况下: 横截面上既有正应力,又有切应力 横截面将发生翘曲,不再保持为平面
精确的分析表明:
当 l 5 时(细长梁) h
可按纯弯曲梁的正应力公式计算横力弯曲梁的正应力
组合图形——由几个简单图形(如矩形、圆形等) 组成的平面图形
如:
1.静矩
n
Sx
yd A
ydA
A n
A1 An n
i 1
Ai
yd A
S xi Ai yCi A yC
i 1
i 1
n
n
S y S yi Ai xCi A xC
i 1
i 1
y
xC C yC
x O
2.形心
n
Ai xCi
6.5.3 梁的弯曲强度计算机举例 例、图5-15a所示为起重设备简图。已知起重量(包含电
葫芦自重)F=30 kN,跨长l=5m。梁AB由No.20a工字钢
制成,许用应力 [σ]=170MPa,[τ]=100MPa。试校核梁
M Ey 2 dA E y2dA EI z
A
A
I z
y 2 dA
A
是梁横截面对中性轴的惯性矩。
1 M
EI z
EIz反映了梁抵抗弯曲变形的能力,称为梁的抗弯刚度。
1 M
EI z
代入
σ E y ρ
σ My Iz
梁在纯弯曲时横截面上任一点的正应力计算公式。
说明:
(1)纯弯曲正应力公式。
30
取参考坐标系 xy
6.3.3. 梁的弯曲正应力公式的应用于推广
在横力弯曲情况下: 横截面上既有正应力,又有切应力 横截面将发生翘曲,不再保持为平面
精确的分析表明:
当 l 5 时(细长梁) h
可按纯弯曲梁的正应力公式计算横力弯曲梁的正应力
组合图形——由几个简单图形(如矩形、圆形等) 组成的平面图形
如:
1.静矩
n
Sx
yd A
ydA
A n
A1 An n
i 1
Ai
yd A
S xi Ai yCi A yC
i 1
i 1
n
n
S y S yi Ai xCi A xC
i 1
i 1
y
xC C yC
x O
2.形心
n
Ai xCi
6.5.3 梁的弯曲强度计算机举例 例、图5-15a所示为起重设备简图。已知起重量(包含电
葫芦自重)F=30 kN,跨长l=5m。梁AB由No.20a工字钢
制成,许用应力 [σ]=170MPa,[τ]=100MPa。试校核梁
M Ey 2 dA E y2dA EI z
A
A
I z
y 2 dA
A
是梁横截面对中性轴的惯性矩。
1 M
EI z
EIz反映了梁抵抗弯曲变形的能力,称为梁的抗弯刚度。
1 M
EI z
代入
σ E y ρ
σ My Iz
梁在纯弯曲时横截面上任一点的正应力计算公式。
说明:
(1)纯弯曲正应力公式。
30
取参考坐标系 xy
材料力学06(第六章 弯曲应力)分析

F / 4 2 103 mm 134 mm
30 MPa 5493104 mm4
F 24.6 kN
因此梁的强度由截面B上的最大拉应力控制
[F] 19.2 kN
§6-3 梁横截面上的切应力•梁的切应力强度条件
Ⅰ、梁横截面上的切应力
分离体的平衡
横截面上切应力 分布规律的假设
横截面上弯曲切 应力的计算公式
二.工字形截面梁 1、腹板上的切应力
h
d
y
d
O
y b
O
' A*
y dA
FS
S
* z
Izd
S
* z
bd
2
h
d
d 2
h 2
d
2
y2
腹板与翼缘交界处
max
min
FS Izd
bd
h d
max O
中性轴处
max
FS
S
* z,m
ax
Izd
y
min
FS
bd
h
d
d
h
d
2
I z d 2
160 MPa 148 MPa
2
Ⅲ 梁的正应力强度条件
max 材料的许用弯曲正应力
中性轴为横截面对称轴的等直梁
M max
Wz
拉、压强度不相等的铸铁等脆性材料制成的梁
为充分发挥材料的强度,最合理的设计为
t,max
M max yt,max Iz
[
t]
c,max
M max yc,max Iz
Myc,max Iz
典型截面的惯性矩与抗弯截面系数 ( d D)
b
第六章 弯曲应力

近似公式:
Q
hb
47
腹板切应力的近似公式
因为: (1)腹板切应力近似为均匀分布;
(2)腹板负担了绝大部分剪力。
近似公式:
Q
hb
翼缘的切应力
特点
(1) 除了有平行于剪力Q的切应力 分量外,还有与剪力Q垂直的 切应力分量;
(2) 切应力数值与腹板的切应力相比较小。 48
箱形薄壁梁
假设 : t //
My
Iz
总结
假设 平面假设,单向受力假设
综合考虑三方面
( y) y
结论
( y) E ( y)
dA0 ydA M
A
A
中性轴位置:中性轴过截面形心
❖ 中性层曲率:1 M (Iz -惯性矩)
EI z (EIz -截面弯曲刚度)
正应力公式: ( y) My
Iz
max
M Wz
(Wz -抗弯截面系数)
y2)
8
24
则,距中性层 y处的切应力公式为:
Q
[
B
(H
2
h2 )
b
h2 (
y 2 )]
Izb 8
24
切应力分布如图。
45
距中性层 y处的切应力公式为:
Q [ B (H 2 h2) b (h2 y2)]
Izb 8
24
切应力分布如图。
最大切应力发生在中性轴处
max
Q[ Izb
BH 2 8
由切应力互等定理,得
QS
* z
Izb
计算Sz*
可用公式
S
* z
A1
y1
S
* z
b( h 2
y) [y
材料力学 第六章 弯曲应力

8
⒋ 变形物理关系
E E
y
其中y 为横截面上求应力那点相对中性轴的坐标, 为 中性层变形后的曲率半径。欲求横截面上一点应力必须知道 中性轴的位置和中性层的曲率半径。 ⒌ 静力关系 横截面正应力满足如下关系: z
N dA 0
A
M y z dA 0
A
y
x dA
第六章
§6–1 概述
弯曲应力
§6–2 弯曲正应力 § 6– 3 弯曲剪应力 §6–4 梁的强度计算
§6–5 提高梁强度的主要措施
2
§ 6–1
一、平面弯曲 P1
概述
P2
纵向对称面
3
二、弯曲 图示梁 AB 段横截面上 C 只有弯矩,而无剪力,该段 梁的弯曲称为纯弯曲。 Q
a A
P
P B
a D
C A与BD 段横截面上即
5.73106 mm4
18
P=50kN
A
P=20kN
C
30
B D 0.3m 0.3m 0.2m 4kN.m - ○
C
y1 38.2m m z y2 71.8m m
110
⊕
5.5kN.m
I z 5.73106 mm4
D 截面下边受拉,上边受压;B 截面上边受拉,下边
受压。比较可知最大压应力在D 截面的上边缘,而最大拉
A
157.5
Q图
RB=30kN RD=10kN 10kN ⊕
- ○ - ○
30
M图
20 72.5 20kN 10kN B 截面最大拉应力: Bl Iz 20kN.m 20 157.5 B 截面最大压应力: By - ○ Iz ⊕ 10 10kN.m C 截面最大拉应力: cl 157.5 Iz 10 C 截面最大压应力: Cy 72.5 Iz
⒋ 变形物理关系
E E
y
其中y 为横截面上求应力那点相对中性轴的坐标, 为 中性层变形后的曲率半径。欲求横截面上一点应力必须知道 中性轴的位置和中性层的曲率半径。 ⒌ 静力关系 横截面正应力满足如下关系: z
N dA 0
A
M y z dA 0
A
y
x dA
第六章
§6–1 概述
弯曲应力
§6–2 弯曲正应力 § 6– 3 弯曲剪应力 §6–4 梁的强度计算
§6–5 提高梁强度的主要措施
2
§ 6–1
一、平面弯曲 P1
概述
P2
纵向对称面
3
二、弯曲 图示梁 AB 段横截面上 C 只有弯矩,而无剪力,该段 梁的弯曲称为纯弯曲。 Q
a A
P
P B
a D
C A与BD 段横截面上即
5.73106 mm4
18
P=50kN
A
P=20kN
C
30
B D 0.3m 0.3m 0.2m 4kN.m - ○
C
y1 38.2m m z y2 71.8m m
110
⊕
5.5kN.m
I z 5.73106 mm4
D 截面下边受拉,上边受压;B 截面上边受拉,下边
受压。比较可知最大压应力在D 截面的上边缘,而最大拉
A
157.5
Q图
RB=30kN RD=10kN 10kN ⊕
- ○ - ○
30
M图
20 72.5 20kN 10kN B 截面最大拉应力: Bl Iz 20kN.m 20 157.5 B 截面最大压应力: By - ○ Iz ⊕ 10 10kN.m C 截面最大拉应力: cl 157.5 Iz 10 C 截面最大压应力: Cy 72.5 Iz
材料力学第6章-弯曲应力

Chapter Six
Stresses in Bending
第六章 弯曲应力
1
背景材料
本章基本要求 6.1 弯曲正应力 6.2 弯曲切应力 6.3 梁的强度及破坏
6.4 组合变形的应力 本章内容小结
2
背 景
材
料
F
横梁横截面上的应力如 何计算?行车移动时,这种 应力如何变化?
3
汽车在轮轴上的支 承为什么设计为叠板弹 簧的形式?这种结构有 什么优点?
3M max b 44.7 mm 2[ ] 故取 b = 45 mm
27
例6.2 欲把直径为 d 的圆木锯成承受竖直方向荷载的矩 形截面梁,若要使梁具有最大的强度,矩形的高 h 和宽 b
应成什么比例?
d b h
分析
强度最大
荷载相同时应力水平最低
max
M max W
W 为最大
建立 W 函数关系并求其极值
A
A
dA
z dx
A
1) 第一式:
FN dA
A
A
E
y dA
E
A
y dA
E
Sz 0
x
S z 0 重要结论:中性轴必定过形心
2) 第二式:
E
E
y
E M y z dA y zdA I yz A A
mn ( y ) d
z
dx dx x
mn mn ( y )d d mn d
y
m
d
y
n'
n
m'
Stresses in Bending
第六章 弯曲应力
1
背景材料
本章基本要求 6.1 弯曲正应力 6.2 弯曲切应力 6.3 梁的强度及破坏
6.4 组合变形的应力 本章内容小结
2
背 景
材
料
F
横梁横截面上的应力如 何计算?行车移动时,这种 应力如何变化?
3
汽车在轮轴上的支 承为什么设计为叠板弹 簧的形式?这种结构有 什么优点?
3M max b 44.7 mm 2[ ] 故取 b = 45 mm
27
例6.2 欲把直径为 d 的圆木锯成承受竖直方向荷载的矩 形截面梁,若要使梁具有最大的强度,矩形的高 h 和宽 b
应成什么比例?
d b h
分析
强度最大
荷载相同时应力水平最低
max
M max W
W 为最大
建立 W 函数关系并求其极值
A
A
dA
z dx
A
1) 第一式:
FN dA
A
A
E
y dA
E
A
y dA
E
Sz 0
x
S z 0 重要结论:中性轴必定过形心
2) 第二式:
E
E
y
E M y z dA y zdA I yz A A
mn ( y ) d
z
dx dx x
mn mn ( y )d d mn d
y
m
d
y
n'
n
m'
材料力学第6章弯曲应力

图6.5
页 退出
材料力学
出版社 理工分社
例6.1如图6.6所示,矩形截面悬臂梁受集中力和集中力偶作用。试求Ⅰ—Ⅰ 截面和固定端Ⅱ—Ⅱ截面上A,B,C,D 4点处的正应力。
图6.6
页 退出
材料力学
出版社 理工分社
解矩形截面对中性轴的惯性矩为 对于Ⅰ—Ⅰ截面,弯矩MⅠ=20 kN·m,根据式(6.2),各点正应力分别为
页 退出
材料力学
出版社 理工分社
(1)变形几何关系 弯曲变形前和变形后的梁段分别表示于图6.4(a)和(b)。以梁横截面的对称 轴为y轴且向下为正(见图6.4(c))。以中性轴为z轴,但中性轴的位置尚待确 定。在中性轴尚未确定之前,x轴只能暂时认为是通过原点的横截面的法 线。根据弯曲平面假设,变形前相距为dx的两个横截面,变形后各自绕中性 轴相对旋转了一个角度dθ ,且仍然保持为平面。这就使得距中性层为y的纵 向纤维bb的长度变为
式中积分
是横截面对y轴和z轴的惯性积。由于y轴是横截面的对
称轴,必然有Iyz=0(见附录)。所以式(g)是自然满足的。 将式(b)代入式(e),得
式中积分∫Ay2dA=Iz是横截面对z轴(中性轴)的惯性矩。于是式(h)改写为 式中 ——梁轴线变形后的曲率。
页 退出
材料力学
出版社 理工分社
式(6.1)表明,EIz越大,则曲率 越小,故EIz称为梁的抗弯刚度。从式 (6.1)和式(b)中消去 ,得
而对于变截面梁,虽然是等截面梁但中性轴不是横截面对称轴的梁,在计算 最大弯曲正应力时不能只注意弯矩数值最大的截面,应综合考虑My/Iz的值 (参看例6.5和例6.8)。
页 退出
材料力学
出版社 理工分社
引用记号
材料力学第六章弯曲应力
但相应的最大弯矩值变为
Fl ql2
M max
4
8
375 kN m 13 kN m 388 kN m
而危险截面上的最大正应力变为
max
388103 N m 2342106 m3
165.7106
Pa
165.7
MPa
显然,梁的自重引起的最大正应力仅为
165.7 160 MPa 5.7 MPa
<2>. 相邻横向线mm和nn,在梁弯曲后仍为直线,只是
相对旋转了一个角度,且与弧线aa和bb保持正交。
根据表面变形情况,并设想梁的侧面上的横向线mm和 nn是梁的横截面与侧表面的交线,可作出如下推论(假设):
平面假设 梁在纯弯曲时,其原来的横截面仍保持为平面, 只是绕垂直于弯曲平面(纵向平面)的某一轴转动,转动后 的横截面与梁弯曲后的轴线保持正交。
力的值max为
max
M ym a x Iz
M
Iz ymax
M Wz
式中,Wz为截面的几何性质,称为弯曲截面系数(对Z轴)
(section modulus in bending),其单位为m3。
b
h d
o
z
o
z
y
y
中性轴 z 不是横截面的对称轴时(参见图c),其横截面 上最大拉应力值和最大压应力值为
A
r
(b)
M z
y d A E
A
r
y2 d A EI z M
A
r
(c)
由于式(a),(b)中的
E
r
不可能等于零,因而该两式要求:
1. 横截面对于中性轴 z 的静矩等于零,A y d A 0 ;显
材力06弯曲应力详解

M y
(sdA)z
A
Eyz
E
dA
A
yzdA EI yz 0
A
(Iyz=0)
2020/9/29
材料力学 第六章 弯曲应力
10
M z
(sdA) y
A
Ey 2 dA E
A
y 2dA EI z M
A
1 Mz
EI z
… …(3)
由式(2)和(3)
s M y
x
Iz
...... (4)
2020/9/29
材料力学 第六章 弯曲应力
1
主要内容
§6–1 梁的纯弯曲 §6–2 纯弯曲时的正应力 §6–3 横力弯曲时的正应力 §6–4 弯曲切应力 §6–5 提高弯曲强度的措施
2020/9/29
材料力学 第六章 弯曲应力
2
§6–1 梁的纯弯曲
弯曲构件横截面上的(内力)应力
内力
剪力Q 弯矩M
剪应力t 正应力s
平面弯曲时横截面只有s
纯弯曲梁(横截面上只有M而无Q的情况)
平面弯曲时横截面既有s又有t
横力弯曲(横截面上既有Q又有M的情况)
例如:
P1
P2
纵向对称面
aP A
Q
Pa
纯弯曲(Pure Bending):
B 某段梁的内力只有弯矩
没有剪力时,该段梁的变 形称为纯弯曲。如AB段。 x
x M
F
B
D
1m
FBY=10.5KN
弯矩图 M
弯矩图
2.5KN· m
X
2020/9/29
4KN·m
材料力学 第六章 弯曲应力
15
B截面和C截面应力分布规律图
第六章扭转与弯曲的强度计算
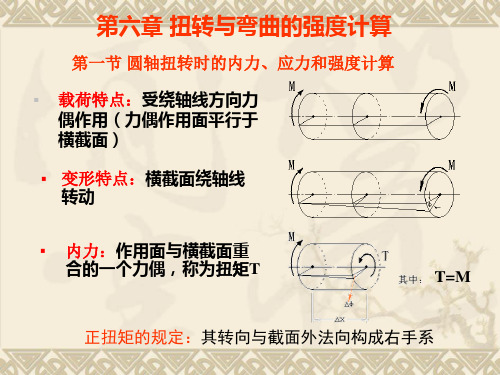
第六章 扭转与弯曲的强度计算
圆轴扭转时的内力、 第一节 圆轴扭转时的内力、应力和强度计算 载荷特点: 载荷特点:受绕轴线方向力 偶作用( 偶作用(力偶作用面平行于 横截面) 横截面) 变形特点:横截面绕轴线 变形特点: 转动 内力: 内力:作用面与横截面重 合的一个力偶,称为扭矩 扭矩T 合的一个力偶,称为扭矩
解:1)由外力偶矩的计算 1)由外力偶矩的计算 1) 公式求个轮的力偶矩:
M A = 9549 PA/n =9550x36/300 =1146 N.m M B =M C = 9549 PB/n = 350 N.m M D = 9549 PD/n = 446 N.m
2)分别求1 截面上的扭矩,即为BC,CA,AD 2)分别求1-1、2-2、3-3截面上的扭矩,即为BC,CA,AD 分别求 段轴的扭矩。 段轴的扭矩。
由
T1 + M B = 0 得:T1 = -M B =-350N.m 由 M B + M C + T2 =0
=-M B -M C =-700N.m 由 M D -T 3 = 0
得 :T 3
得 :T 2
= M D = 446N.m
T 446N.m x 350N.m 700N.m
3)画扭矩图: 3)画扭矩图: 画扭矩图
WP 0.2 D1
G实心轴 G空心轴
T 1.5 ×106 D1 = 3 =3 = 53.03mm 0.2τ max 0.2 × 50.3
A1 L D12 = = 2 A2 L D − d 2
53 2 = 2 = 3.21 2 90 − 85
第三节 弯曲内力
一、平面弯曲的概念 弯曲变形是指杆的轴线由 弯曲变形是指杆的轴线由 直线变成曲线。 直线变成曲线。 以弯曲变形为主的杆件称 为梁。 梁的受力特点是在轴线平面 梁的受力特点是在轴线平面 内受到力偶矩或垂直于轴线 方向的外力的作用。 方向的外力的作用。
圆轴扭转时的内力、 第一节 圆轴扭转时的内力、应力和强度计算 载荷特点: 载荷特点:受绕轴线方向力 偶作用( 偶作用(力偶作用面平行于 横截面) 横截面) 变形特点:横截面绕轴线 变形特点: 转动 内力: 内力:作用面与横截面重 合的一个力偶,称为扭矩 扭矩T 合的一个力偶,称为扭矩
解:1)由外力偶矩的计算 1)由外力偶矩的计算 1) 公式求个轮的力偶矩:
M A = 9549 PA/n =9550x36/300 =1146 N.m M B =M C = 9549 PB/n = 350 N.m M D = 9549 PD/n = 446 N.m
2)分别求1 截面上的扭矩,即为BC,CA,AD 2)分别求1-1、2-2、3-3截面上的扭矩,即为BC,CA,AD 分别求 段轴的扭矩。 段轴的扭矩。
由
T1 + M B = 0 得:T1 = -M B =-350N.m 由 M B + M C + T2 =0
=-M B -M C =-700N.m 由 M D -T 3 = 0
得 :T 3
得 :T 2
= M D = 446N.m
T 446N.m x 350N.m 700N.m
3)画扭矩图: 3)画扭矩图: 画扭矩图
WP 0.2 D1
G实心轴 G空心轴
T 1.5 ×106 D1 = 3 =3 = 53.03mm 0.2τ max 0.2 × 50.3
A1 L D12 = = 2 A2 L D − d 2
53 2 = 2 = 3.21 2 90 − 85
第三节 弯曲内力
一、平面弯曲的概念 弯曲变形是指杆的轴线由 弯曲变形是指杆的轴线由 直线变成曲线。 直线变成曲线。 以弯曲变形为主的杆件称 为梁。 梁的受力特点是在轴线平面 梁的受力特点是在轴线平面 内受到力偶矩或垂直于轴线 方向的外力的作用。 方向的外力的作用。
材料力学第六章弯曲应力1
d c
M
b
d
(1)弯曲平面假设:梁变形前原为平面的横截面变形后仍为平 面,且仍垂直于变形后的轴线,只是各横截面绕其上的某轴转 动了一个角度。
(2)纵向纤维假设:梁是由许多纵向纤维组成的,且各纵向纤维 之间无挤压。
凹入一侧纤维缩短 突出一侧纤维伸长
根据变形的连续性可知, 梁弯曲时从其凹入一侧的 纵向线缩短区到其凸出一 侧的纵向线伸长区,中间 必有一层纵向无长度改变 的过渡层--------称为中
q
y1 y2
y
z
b
解:1)画弯矩图
| M |max 0.5ql2 3 kNm
№10槽钢
2)查型钢表:
M
y1
y2
y
b 4.8cm, I z 25.6cm4 , y1 1.52cm y2 4.8 1.52 3.28cm
3)求应力:
M 3000 1.52 178 MPa t max y1 6 25 .6 10 Iz
中间层与横截面的交线 --中性轴
性层 。 梁的弯曲变形实际上是各截面绕各自的中性轴转 动了一个角度,等高度的一层纤维的变形完全相同。
4、线应变的变化规律:
A1 B1 AB AB
a
c
( y )d d d
A1 B1 OO1 OO1
y
y
...... (1)
Mycmax cmax Iz
几种简单截面的抗弯截面系数 b ⑴ 矩形截面
h
z
bh3 Iz 12 b3h Iy 12
⑵ 圆形截面
y d
Iz bh2 Wz h/2 6 Iy b2h Wy b/2 6
材料力学第六章弯曲应力

3l/8 H
CD
Bx
l/4 l/4
x
1 ql
8
1 ql2 32
x
D
知正应力、正应变最 大值发生在H截面。
应用下述关系求应力与内力
应力~变形 关系:
E y
max
E
ymax
内力~变形或内力~应力关系:
1 M
EI z
或
M maxW
Page 15
第六章 弯曲应力
2. 应力计算
max
E
ymax
D d 0.701m
22
ymax
d
2
1.0 103 m
Page 5
第六章 弯曲应力
二、 组合变形
杆件的一般变形通常可分解为拉压、 扭转与弯曲变形的两种或三种基本 变形的组合。
三、 梁横截面上的弯曲应力 弯曲正应力 M 弯曲切应力 FS
四、 对称弯曲 梁具有对称截面,且在 纵向对称面承受横向外 力(或外力的合力)时 的受力与变形形式。
对称截面
Page 7
第六章 弯曲应力
§6-2 弯曲正应力
一、实验观测与假设(动画) 1. 外部变形观测
•纵向线:成圆弧线,上方纵向线 缩短,下方伸长
•横向线:保持直线,与横线正交 •顶与底部纵、横线变形比:符合 单向受力泊松效应
2. 内部变形假设
•平面假设:变形后横截面保持平面,仍与纵线正交 •单向受力假设
A
S y
zdA
A
分别称为对坐标轴x和y的静矩 或一次矩。
静矩的量纲: L3
o
y
z
z
dA
CD
Bx
l/4 l/4
x
1 ql
8
1 ql2 32
x
D
知正应力、正应变最 大值发生在H截面。
应用下述关系求应力与内力
应力~变形 关系:
E y
max
E
ymax
内力~变形或内力~应力关系:
1 M
EI z
或
M maxW
Page 15
第六章 弯曲应力
2. 应力计算
max
E
ymax
D d 0.701m
22
ymax
d
2
1.0 103 m
Page 5
第六章 弯曲应力
二、 组合变形
杆件的一般变形通常可分解为拉压、 扭转与弯曲变形的两种或三种基本 变形的组合。
三、 梁横截面上的弯曲应力 弯曲正应力 M 弯曲切应力 FS
四、 对称弯曲 梁具有对称截面,且在 纵向对称面承受横向外 力(或外力的合力)时 的受力与变形形式。
对称截面
Page 7
第六章 弯曲应力
§6-2 弯曲正应力
一、实验观测与假设(动画) 1. 外部变形观测
•纵向线:成圆弧线,上方纵向线 缩短,下方伸长
•横向线:保持直线,与横线正交 •顶与底部纵、横线变形比:符合 单向受力泊松效应
2. 内部变形假设
•平面假设:变形后横截面保持平面,仍与纵线正交 •单向受力假设
A
S y
zdA
A
分别称为对坐标轴x和y的静矩 或一次矩。
静矩的量纲: L3
o
y
z
z
dA
材料力学课件第六章弯曲应力

第6章 弯曲应力
※ 梁的纯弯曲 ※ 纯弯曲时的正应力 ※ 横力弯曲时的正应力 ※ 弯曲切应力 ※ 提高弯曲强度的措施
第三章 扭 转
§6.1 梁的纯弯曲
横截面上同时存在弯矩和剪力
横力弯曲
横截面上只有弯矩并无剪力
纯弯曲
f1(M ) f2 (Q)
第三章 扭 转
aP P a
A
B
C
D
QP
x
P
a
2
h
2 4
2
b
a y
第三章 扭 转
附录 2. 惯性矩和惯性半径
一、惯性矩
z
定义:图形面积对某轴的二次矩
IzAy2dA , IyA z2dA
y
dA
z
工程中常把惯性矩表示为平面图形的
面积与某一长度平方的乘积, 即
O
y
Iz Az2i, IyAy2i
或
iy
Iy , A
iz
E E y
3. 静力学关系
M z
N A dA 0
(1 )
M yA zdA 0 (2 ) M zAy dA M (3 )
y z y
x
dA
E E y
第三章 扭 转
NxAdAAEρydA0
Sz 0
ydA 0
A
中性轴过形心
1、组合图形对某一轴的静矩等于组成它的各部分图形对同一 轴静矩的代数和,即:
n
n
Sz Aiyi , Sy Aizi
i1
i1
其中:Ai, yi, zi 分别代表第 i 个图形的面积和形心坐标, n为分割成的简单图形的个数。
※ 梁的纯弯曲 ※ 纯弯曲时的正应力 ※ 横力弯曲时的正应力 ※ 弯曲切应力 ※ 提高弯曲强度的措施
第三章 扭 转
§6.1 梁的纯弯曲
横截面上同时存在弯矩和剪力
横力弯曲
横截面上只有弯矩并无剪力
纯弯曲
f1(M ) f2 (Q)
第三章 扭 转
aP P a
A
B
C
D
QP
x
P
a
2
h
2 4
2
b
a y
第三章 扭 转
附录 2. 惯性矩和惯性半径
一、惯性矩
z
定义:图形面积对某轴的二次矩
IzAy2dA , IyA z2dA
y
dA
z
工程中常把惯性矩表示为平面图形的
面积与某一长度平方的乘积, 即
O
y
Iz Az2i, IyAy2i
或
iy
Iy , A
iz
E E y
3. 静力学关系
M z
N A dA 0
(1 )
M yA zdA 0 (2 ) M zAy dA M (3 )
y z y
x
dA
E E y
第三章 扭 转
NxAdAAEρydA0
Sz 0
ydA 0
A
中性轴过形心
1、组合图形对某一轴的静矩等于组成它的各部分图形对同一 轴静矩的代数和,即:
n
n
Sz Aiyi , Sy Aizi
i1
i1
其中:Ai, yi, zi 分别代表第 i 个图形的面积和形心坐标, n为分割成的简单图形的个数。
梁的弯曲应力和强度计算
20kN.m
M max
10kN.m
2、求最大正应力
s在smm正axax、负MWM弯Wmz矩amxza作x用10下200,6截2150面06 抗2 弯 1模9量.2相M同Pa
3、校核强度
smax 19.2MPa s 40MP 安全
弯曲正应力强度计算
六、综合计算题
6Q bh3线
t max
3Q 2bh
3Q 2A
Q
t
最大剪应力为平均剪应力的1.5倍
t tmax
2、工字型截面梁 (1)分工:
翼缘主要承担弯矩 腹板承担95%~97%的剪力
(2)公式: t QSZ*
bI Z
(3)规律: 剪应力沿腹板高度仍按抛物线变化。
h b
圆形:
z
D
空心圆截面:
外径为D,内径为d, d
D
WZ
IZ ymax
64
D4 d 4 D
D3 1 4
32
2
例题:图示一空心矩形截面悬臂梁受均布荷载作用。已知梁跨
l=1.2m,均布荷载集度q=20kN/m,横截面尺寸为H=12cm, B=6cm,h=8cm,b=3cm。试求此梁外壁和内壁最大正应力。
解:(1)作弯矩图,
求最大弯矩
M ql 2 201.22
max
2
2
14.4kN m
(2)计算截面的惯性矩
IZ
BH 3 12
bh3 12
736cm4
(3)计算应力
s 外max
M max IZ
H 2
14.4 106 736104
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M x IP
r max
r max
I P 2dA
A
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
研究杆件的应力与变形,研究失效问题以及强 度、刚度、稳定问题,都要涉及到与截面图形 的几何形状和尺寸有关的量。这些量统称为几 何量,包括形心、静矩、惯性矩、惯性半径、 极惯性矩、惯性积、主轴等。
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
惯性矩与惯性积的移轴定理
2 I z1 I z 2aS z a A I y1z1 I yz aS y bS z abA I y1 I y 2bS y b 2 A
y z1
A
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
y z1
z
惯性矩与惯性积的移轴定理
I y 1 z1 d A
2 A
dA O a O´ b
I y 1 z b dA
2 A 2 A
I z1 y1 dA
2 A
y
y1
z
I y1z1 y1 z1dA
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
y
z
I y z 2 dA
A
A
——图形对 y 轴的惯性矩
I z y 2 dA ——图形对 z轴的惯性矩
dA
I yz yzd A ——图形对 y z 轴的惯性积
A
A
O
r
y
z
I P r 2 dA ——图形对 O 点的极惯性矩
α O
I y1 I z1
z1
I y 1 z1 d A
2 A
α z
I z1 y1 dA
2 A
Iz I y 2 Iz I y 2
Iz I y 2 Iz I y 2
cos2 I yz sin2 cos2 I yz sin2
I y1z1 y1 z1dA
与应力分析相关的截面图形几何性质
惯性矩与惯性积的转轴公式
y 已知: Iy,Iz,Iyz ,α O α z 求: Iy1,Iz1,Iy1z1
α
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
y
y
y1 zsin ycos z1 zcos ysin
y1 z
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
I y1 I z1
Iz I y 2 Iz I y 2
Iz I y 2 Iz I y 2
cos2 I yz sin2 cos2 I yz sin2
I y0 z0 yzdA 0
A
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形 几何性质
返回总目录
返回
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
问题: 为什么要研究截面图形 的几何性质?
x const.
FN
dA F
A x
N
x dA FN
A
Mx
O
r
FN x A
y
I y0 z0 yzdA 0
A
α0 α0 O z
tan2 0
2 I yz Iy Iz
I y 0 I max I y I z 1 I z 0 I min 2 2
I
y
2 I z 4 I yz 2
可以证明,图形对于过一点不同坐标轴的惯性矩各不相同, 而对于主轴的惯性矩是这些惯性矩的极大值和极小值。
S y zdA
A
S y AzC
S z ydA
A
S z AyC
A
S yC z A
ydA A
zC
Sy A
zdA
A
A
已知静矩,可以确定图形的形心坐标 已知图形的形心坐标,可以确定静矩
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
y
zC
I y1z1
I y Iz 2
sin2 I yz cos2
tan2 0
2 I yz Iy Iz
I y 0 I max I y I z 1 I z 0 I min 2 2
I
y
2 I z 4 I yz 2
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
与应力分析相关的截面图形几何性质
静矩、形心及其相互关系
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
静矩、形心及其相互关系
y
z
S y zdA
A
——图形对于 y 轴的静矩
dA
y
O
z
S z ydA
A
——图形对于 z 轴的静矩
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
静矩、形心及其相互关系
对于组合图形
n
S z A1 y C1 A2 y C 2 An y Cn Ai y Ci i 1 n S y A1 z C1 A2 z C 2 An z Cn Ai z Ci i 1 n
A
I y1z1
I y Iz 2
sin2 I yz cos2
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
y
z
dA
y
O
I yz yzdA 0
A
z
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
z y
z y
dA
y z
y
O O
I yz yzdA 0
与应力分析相关的截面图形几何性质
例 题 10 y
dA
dr
已知:圆截面直径d 求:Iy, Iz, IP
解:取圆环微元面积
dA 2 π rdr
z
IP 1 I y I z r 2 dA 2 2 A 4 1 d π d 2 r 2 2 π r dr 0 2 64 πd 4 IP 2I y 32
z
A dA
y
如果y、z轴通过图形形心C, 上述各式中的Sy=Sz=0
C
a O´
y1
z
b
I y1 I y b A 2 I z1 I z a A I y1z1 I yz abA
2
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
y z1
A
I P r 2 dA
A
>0
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
惯性矩、极惯性矩、惯性积、惯性半径
y
z
I y z 2 dA
A
I z y 2 dA
A
dA
A
O
r
I P r 2 dA
A
y
z
IP I y I z
第6章 梁的应力分析与强度计算
A
y1=y+a z1=z+b
I z 1 y a dA
A
I y1z1 y a z b dA
2 I z1 I z 2aS z a A I y1z1 I yz aS y bS z abA I y1 I y 2bS y b 2 A
A
iy
Iy A
——图形对 y 轴的惯性半径
iz
Iz A
——图形对 z 轴的惯性半径
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
惯性矩、极惯性矩、惯性积、惯性半径 y
z
I y z 2 dA
A
>0
dA
y
I z y 2 dA > 0
A
O
z
I yz yzd A > 0 或 < 0
静矩、形心及其相互关系
Sz yC A
yC
A
ydA A
C
O z
zC
Sy A
zdA
A
A 如果轴通过图形形心,则图形对这一轴的静矩等于零。 如果图形对轴的静矩等于零,则这一轴通过图形形心。 图形形心与坐标系(观察者)无关。
A
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
第6章 梁的应力分析与强度计算
与应力分析相关的截面图形几何性质
静矩、形心及其相互关系 惯性矩、极惯性矩、惯性积、惯性半径 惯性矩与惯性积的移轴定理
惯性矩与惯性积的转轴的概念 主轴与形心主轴、主惯性矩与形心主惯性矩
组合图形的形心、形心主轴、形心主惯性矩 的计算方法
第6章 梁的应力分析与强度计算
z
惯性矩与惯性积的移轴定理
A dA
y
O
a O´
y1
I y1 I y b 2 A 2 I z1 I z a A z I y1z1 I yz abA
b 因为面积及包含a2、b2的项恒为正,故自形心 轴移至与之平行的任意轴,惯性矩总是增加的。
a、b为原坐标系原点在新坐标系中的坐标,要 注意二者的正负号;二者同号时abA为正,异号时 为负。所以,移轴后惯性积有可能增加也可能减少。
