角的比较与运算

合集下载

人教版数学七年级上册4.3.2角的比较与运算课件

则∠DEF ＜ ∠ABC
类比线段的比较方法，你认为该如何比较两个角的大小？
比较线段长短的方法
如图,∠AOB=∠COD=90,
＊角的大小比较方法：
∵OC 是∠AOB 的角平分线，
＊角的和差的表示
∠AOD=146°,则∠BOC=____.
2．如图，若∠AOB= 60°，
3．若∠AOB ＝60°，∠AOC ＝30°，则∠BOC ＝
度．
合作探究
类比线段的比较方法，你认为该如何比较两个角的大小？
D A
B
C
E
F
度量时注意：对中，重合，读数
叠合法比较∠ABC 和 ∠DEFD的大小
A
B（）
C（） A
B（）
C（）
A
B（）
C（）
ED落在∠ABC的外部，
则∠DEF ＞ ∠ABC。
E
F
ED落在∠ABC的D内部，
则∠DEF ＜ ∠ABC
借助一副三角尺，同学们能画出哪些度数的角？
2．如图，若∠AOB= 60°，则∠DEF ＜ ∠ABC
这节课，你掌握的方法思想 2．如图，若∠AOB= 60°，
∠BOC＝40°，则∠AOC＝度．类比线段的比较方法，你认为该如何比较两个角的大小？
3．若∠AOB ＝60°，∠AOC ＝30°，则∠BOC ＝

数学知识点总结之角的比较与运算

角的比较与运算

如果两个角的和等于90度(直角)，就说这两个叫互为余角(compiementary angle)，即其中每一个角是另一个角的余角。

如果两个角的和等于180度(平角)，就说这两个叫互为补角(supplementary angle)，即其中每一个角是另一个角的补角。

等角(同角)的补角相等。

等角(同角)的余角相等。

初中数学知识点大全之角的比较与运算，小编相信同学们都轻松掌握了吧，接下来还有更详细的初中数学知识点尽在哦，希望同学们关注了。

初中数学知识点总结：平面直角坐标系

下面是对平面直角坐标系的内容学习，希望同学们很好的掌握下面的内容。

平面直角坐标系

平面直角坐标系：在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系。

水平的数轴称为x轴或横轴，竖直的数轴称为y轴或纵轴，两坐标轴的交点为平面直角坐标系的原点。

平面直角坐标系的要素：①在同一平面②两条数轴③互相垂直④原点重合

三个规定：

①正方向的规定横轴取向右为正方向，纵轴取向上为正方向

②单位长度的规定；一般情况，横轴、纵轴单位长度相同；实际有时也可不同，但同一数轴上必须相同。

③象限的规定：右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。

相信上面对平面直角坐标系知识的讲解学习，同学们已经能很好

的掌握了吧，希望同学们都能考试成功。

初中数学知识点：平面直角坐标系的构成

对于平面直角坐标系的构成内容，下面我们一起来学习哦。

平面直角坐标系的构成

在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系，简称为直角坐标系。通常，两条数轴分别置于水平位置与铅直位置，取向右与向上的方向分别为两条数轴的正方向。水平的数轴叫做X轴或横轴，铅直的数轴叫做Y轴或纵轴，X轴或Y轴统称为坐标轴，它们的公共原点O称为直角坐标系的原点。

角的比较与运算

把∠DEF移动，使它的顶点E和∠ABC的顶点B重合，一边EF 和BC重合，另一边ED和BA落在BC的同旁。
A D
B（）
C（）
E
F
ED落在∠ABC的内部，则∠DEF ＜ ∠ABC
角的和差
C BB
顶
2
点
1
与
OO
A
一
边
重
合
B
B
2
C 1
Oபைடு நூலகம்
O
A
角的和差
顶点与一边重合
O
C B
2 1
O
A
（ AOC为 1 和 2 的和
定义：在角的内部，自顶点引一条射线把这个角分成
两个相等的角，那么，这条射线叫做角的平分线。
符号表达
练习：已知射线OC是∠AOB的角平分线，你能写出图中各角的关系吗？
Ａ
Ｃ
Ｏ
Ｂ
类似地：还有角的三等分线
D
C
B
32 ⌒
1
O
A
OB、OC是∠AOD的三等分线
如图
D
C B
O
A
D
C B
O
A
A E
B
D
C
把一个周角7等分，每一份是多少度的角？
（精确到分）（精确到秒）
解：360°÷7＝51°+3°÷7 ＝51°+180′÷7 ≈51°26′

4.3.2 角的比较与运算课件 (共25张PPT) 2023-2024学年初中数学人教版七年级上册

作业布置【知识技能类作业】
必做题：
2.如图，OC平分∠AOD，OD平分∠BOC，下列结论不成立的
是( B ) A.∠AOC＝∠BOD
B.∠COD＝
1 2
∠AOB
C.∠AOC＝
1 2
∠AOD
D.∠BOC＝2∠BOD
作业布置【知识技能类作业】
必做题： 3.如图，O是直线AB上一点, OC是∠AOB的平分线，∠COD=31º28′，
作业布置【综合实践类作业】
如图，已知∠DOE＝70º, OD平分∠AOB，OE平分∠BOC, 求∠AOC 的度数. 解：∵OD平分∠AOB， OE平分∠BOC， ∴∠AOB＝2∠DOB, ∠BOC＝2∠BOE， ∴ ∠AOC＝∠AOB＋∠BOC
＝2∠DOB+2∠BOE ＝2（∠DOB+∠BOE）＝2∠DOE ＝2 × 70º ＝140º.
∠AOB是 ∠AOC与∠BOC的差，记作：∠AOB＝∠AOC－∠BOC，
∠BOC是 ∠AOC与∠AOB的差，记作：∠BOC＝∠AOC－∠AOB.
新知讲解任务二：角的和、差借助三角尺，你能画出 15°，75° 的角吗？你还能画出哪些度数的角？
这些角有什么规律？
15°
105°
30°
120°
45°
135°
思考：我们通过角平分线可以把这个角分成两个相等的角，那

角的比较与计算

5
4.角平分线： (1)定义:从一个角的_顶__点__出发，把这个角分成两个_相__等__的角的射线. (2)表示:如图，OC平分∠AOB，①∠1＝_∠__2_；②_∠__1_＝_∠__2_＝ 1 ∠AOB；③∠AOB＝2_∠__1_＝2_∠__2_.
2
6
(打“√”或“×”) (1)角的大小与它们的度数大小是一致的.( √ ) (2)若∠A+∠B>∠C,那么∠A一定大于∠C.( × ) (3)用一副三角板可画出15°的角.( √ ) (4)平分一个角的射线叫做角的平分线.( × )
14
3.如图，已知直线AB，CD相交于点O，OE
平分∠COB,若∠EOB=55°，则∠BOD的度
数是( )
A.35°
B.55°
C.70°
D.110°
【解析】选C.由OE平分∠COB，∠EOB＝55°，得
∠COB=110°, 所以∠BOD= 180°-110°=70°.
15
4.如图，OC平分∠AOB，OD平分∠AOC，则图中相等的角有____.
(1)∠DEF_=_∠ABC.(2)∠DEF_＜__∠ABC. (3)∠DEF_＞__∠ABC.
4
3.角的和、差：
(1)如图①,∠2在wenku.baidu.com1内部，∠ABC是∠1与∠2的_差__，记作： ∠ABC＝_∠__1_－__∠__2_. (2)如图②,∠2在∠1外部，∠DEF是∠1与∠2的_和__，记作： ∠DEF＝_∠__1_＋__∠__2_.

角的比较和运算

方法二:测量法
小学我们学过用量角器测量一个角，角的大小也可以按其度数比较,度数大的角则大，度数小的则小．反之，角大度数大，角小度数小．注意：使用量角器应注意的问题．即三点：对中；重合；读数．
如: A 45, P 60 P A
.
.
.
.Leabharlann Baidu
.
.
.
；https://www.4080so.com 新视觉
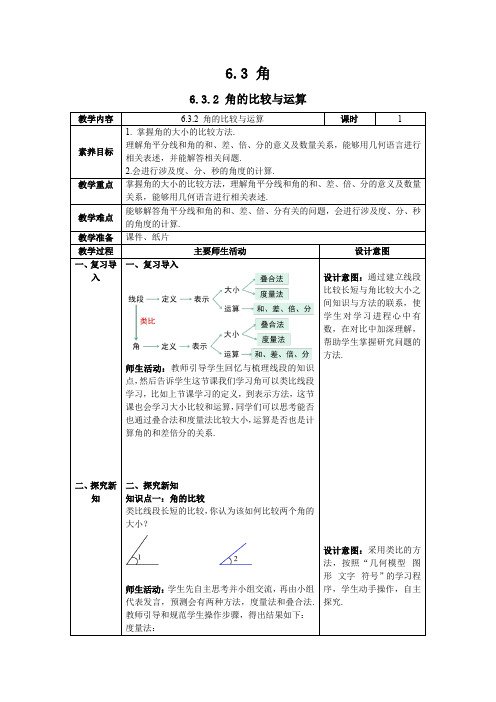
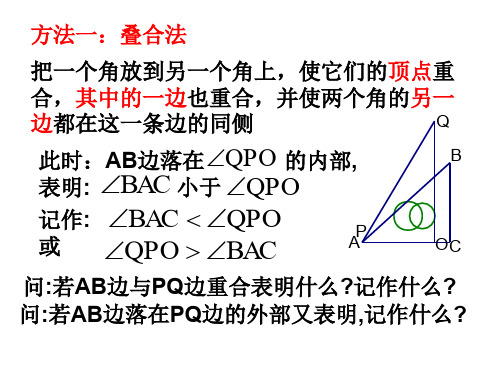
方法一：叠合法
把一个角放到另一个角上，使它们的顶点重
合，其中的一边也重合，并使两个角的另一
边都在这一条边的同侧
Q
此时：AB边落在QPO 的内部,
B
表明: BAC 小于 QPO
记作: BAC QPO 或 QPO BAC
AP
OC
问:若AB边与PQ边重合表明什么?记作什么? 问:若AB边落在PQ边的外部又表明,记作什么?
①EF与BC重合，∠DEF等于∠ABC，记作 ∠DEF=∠ABC． ②EF落在∠ABC的内部，∠DEF小于 ∠ABC，记作∠DEF＜∠ABC． ③EF落在∠ABC的外部，∠DEF大于 ∠ABC，记作∠DEF＞∠ABC
注意：角的大小只与开口大小有关，与边的长短无关，以及角的符号与小于号、大于号书写时的区别．

角及角的比较与运算

角

一. 角的概念和表示方法

引入：在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻（如图），当甲带球冲到A点时，乙已跟随冲到B点。从数学角度看，此时甲是自己射门好，还是将球传给乙，让乙射门好？

说明：事实上，在真正的比赛中，情况会很复杂。如果A、B两点到球门的距离相差不大，要确定较好的射门位置，关键看这两点各自对球门MN的张角大小，当张角小时，求容易被守门员拦截。

角在我们的生活中无处不在，例如三角尺的三个角，扇子打开后形成的角，时针与

分针形成角。

例1、角的定义

角的静态定义：有公共端点的两条射线所组成的图形叫做角。公共的端点叫做角的顶点，两条射线叫做角的角的两条边。

角的动态定义：把一条射线绕着它的端点旋转而成的图形叫做角。开始的边叫做角的始边，终止的边叫做角的终边。旋转经过的部分叫做角的内部，没有经过的部分叫做角的外部。通常用一个小的弧线来表示角的内部。

例2、角的分类

角的分类：（1）将一条射线OA绕着O旋转，当终止的位置OB与起始OA在一条线上

时，所形成的角是平角=180°（平角不是直线，因为平角有顶点，直线没有顶点）。（2）当射线OA绕着O旋转，当终止的位置OB与起始OA重合时，所形成的角是周角=360°（周角不是射线）

（3）等于=90°的角叫做直角，小于90°的角叫做锐角，大于90°且小于180°的角

叫做钝角。

练习：一个平角等于几个直角?

例3、表示方法

（1）用三个大写字母表示角，如图：∠AOB或∠BOA(∠的符号不要忘记，0为顶点一定要写在中间)

（2）用一个大写字母，∠0,（只适用于以该点为顶点的角只有一

角的比较重难点题型

角的比较--重难点题型

【知识点1 角的比较与运算】

【题型1 角的大小比较】

∠COD＝50°；小丽用叠合法比较，将两个角的顶点重合，边OB与OD重合，边OA 和OC置于重合边的同侧，则边OA．（填序号：①“在∠COD的内部”；②“在∠COD的外部”；③“与边OC重合”）

【变式1-1】（2021春•呼和浩特期末）如图，∠AOB＝∠COD，则∠AOC与∠DOB的大小关系是（）

A．∠AOC＞∠DOB

B．∠AOC＜∠DOB

C．∠AOC＝∠DOB

D．∠AOC与∠DOB无法比较大小

【变式1-2】（2021秋•开封期末）如图所示，其中最大的角是，∠DOC，∠DOB，∠DOA的大小关系是．

【变式1-3】（2021秋•门头沟区期末）如图所示的网格是正方形网格，点A，B，C，D，O 是网格线交点，那么∠AOB∠COD．（填“＞”，“＜”或“＝”）

【题型2 角的和差】

【例2】（2021秋•安庆期末）如图，已知∠BOC＝2∠AOC，OD平分∠AOB，且∠COD＝20°，求∠AOB的度数．

【变式2-1】（2021秋•五常市期末）用一副三角板不能画出的角是（）A．75°B．105°C．110°D．135°

【变式2-2】2021秋•北碚区期末）将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕．若∠ABE＝30°，则∠DBC为度．

【变式2-3】（2021秋•荔湾区期末）把一副三角尺ABC与BDE按如图所示那样拼在一起，其中A、D、B三点在同一直线上，BM为∠ABC的平分线，BN为∠CBE的平分线，则∠MBN的度数是（）

角的比较和运算

D A
B
DE边在∠ABC的外部, DE边在∠ABC的外部,则边在的外部
C
E
F
∠ABC<∠DEF
A
D
B
DE与AB边重合, DE与AB边重合,则边重合
C
E
F
∠ABC=∠DEF ∠
A D
B
C
E
F
DE边在∠ABC的内部, DE边在∠ABC的内部,则边在的内部
∠ABC>∠DEF
角的和差
1
2
3
分线，也可以说平分分线，也可以说OB平分
定义：在角的内部，定义：在角的内部，自顶点引一条射线把这个角分成两个相等的角，那么，这条射线叫做角的平分线两个相等的角，那么，这条射线叫做角的平分线。
练习：已知射线的角平分线，练习：已知射线OC是∠AOB的角平分线，是的角平分线你能写出图中各角的关系吗？你能写出图中各角的关系吗？
如图∠ 如图∠ AOB= ∠ COD=900， 0， ∠ BOC=_____. 340 ∠ AOD=146
练一
如图：是哪两个角的和? 如图： ∠AOC是哪两个角的和是哪两个角的和练两角的差? ∠BOD 是哪两角的差如果∠ 那么∠ 如果∠AOB=∠COD, 那么∠AOC和 ∠ 和相等吗? ∠BOD相等吗相等吗
（1） ∠AOC=∠AOB＋∠BOC ） ∠ ＋（2）∠BOD=∠AOD－∠AOB ） ∠ －（3）∠AOC=∠AOB＋∠BOC，） ∠ ＋， ∠BOD=∠BOC＋∠COD ∠ ＋因为∠ 因为∠AOB=∠COD ∠BOC=∠BOC ∠ ∠ 所以∠ 所以∠AOC=∠BOD ∠

角的比较和运算

角是物体运动和变形过程中最重要的空间量度，在数学中也被广泛地用于计算各种几何关系和建立数学模型。角的表示方式有很多种，其中度数角和弧度角是最常用的表示形式。同时，在角的比较和运算中，要根据表示形式的不同来进行正确的运算，并正确地转换表示形式。

一、角的表示形式

1、度数角

度数角是最常用的表示形式，它由圆心到圆周上任意一点的两条弧线的夹角组成，其定义为：在以圆心为原点的坐标系中，起点为原点，终点距离原点的长度为1的线段所与X轴正半轴之间的夹角的大小，单位为度（°）。

2、弧度角

弧度角是一种非常常用的表示形式，它由弧形与X轴正半轴之间的夹角组成，其定义为：在以圆心为原点的坐标系中，以圆心为原点，以圆周中某点为终点，且两点之间距离为圆周长度的一半时，这样的角被称为弧度角，其单位为弧度（rad）。

二、角的比较

在比较角的大小时，首先需要考虑到它们的表示形式。如果两个角的表示形式都是度数角，则可以按照一般的数理比较的方法进行比较。如果一个角的表示形式是度数角，另一个角的表示形式是弧度角，则需要先将弧度角转换为度数角，然后再进行比较。

三、角的运算

1、加法运算

加法运算也是角运算中比较重要的一个部分。在角的加法运算中，同样要根据表示形式的不同来进行正确的运算，如果两个角均为度数角，则将它们的角度相加即可；如果一个角表示形式是度数角，另一个角的表示形式是弧度角，则先将弧度角转换为度数角，然后再进行加法运算。

2、减法运算

减法运算也是角运算中比较重要的一个部分。在角的减法运算中，同样要根据表示形式的不同来进行正确的运算，如果两个角均为度数角，则将它们的角度相减即可；如果一个角表示形式是度数角，另一个角的表示形式是弧度角，则先将弧度角转换为度数角，然后再进行减法运算。

角的比较和计算

3.常用的度量角的工具是量角器
．
4.常用的度量角的单位是度、分、秒．
它们之间的关系是 1°=60′，1′=60″ ． 5.如果一个点把一条线段分成两条相等
的线段，那么这个点叫做线段的 6.比较两条线段大小的方法有观察法，度量法，叠合法中点．
．
如何比较两角的大小观察与思考：你认为∠ABC 与∠DEF 哪个角较大?你是怎样比较的?
∠AOB =2∠AOC= 2 ∠BOC ; ∠AOC =∠BOC=1／2∠AOB .
1、如图：填空 ∠ABC= ∠ABD+ ∠_____ DBC ；
BDC 。 ∠ADB= ∠ADC- ∠_____
B
A
D
C
2、如图：如果BD是∠ABC的平分线，那么： (1)∠ABD = ∠_____ CBD ； (2)∠ABC ___ =2∠ DBC。
例题1
如图，O是直线上一点， ∠AOC =53°17′，求 ∠BOC的度数。
解：因为∠AOB是平角，且 ∠AOB=∠AOC+∠BOC 所以∠BOC=∠AOB-∠AOC =180°-53°17′ =126°43′ A
C
O
B
1.计算: (1)48°35′+17°45′ =(48°+17°)+(35′+45′) =65°+80′=65°80′

角的比较与运算

注意：应用角平分线解题时常用到数形结合的思想，借助图形寻找角之间的和、差、倍、分关系是解题的关键，往往需要借助方程列出等量关系求解．
【迁移应用】角的和差运算中的分类讨论思想
已知∠AOB=40°，∠BOC=20°，求∠AOC的度数. 分析：本题需分情况讨论，一种情况是射线OC在 ∠AOB的内部，一种情况是射线OC在∠AOB的外部．
第四章几何图形初步 4.3 角
4.3.2 角的比较与运算
AD
BE
CF
图片导入
A
B
C
D
AB＞CD
A
B
AB=CD
C
D
AA
B
AB＜CD
C
D
类比线段大小的比较，你认为该如何比较两
个角的大小？
1.运用类比的方法，学会比较两个角的大小，会分析图中角的和差关系． 2.通过动手操作，学会借助三角板拼出不同度数的角，认识角的平分线. 3.会进行简单的角的运算.
你知道放大镜不能“放大”角的度数的原因吗？
类比探究
角的和差
（1）图中共有几个角？分别是什么？
解：共有3个角，分别是∠AOC、 ∠AOB 、 ∠BOC.
（2）这些角的角度有什么大小和等量关系？
解：∠BOC ＜ ∠AOB ＜ ∠AOC
∠AOC＝∠AOB＋∠BOC,
∠AOB＝∠AOC－∠BOC,

角的比较与运算

性质等角的余角相等。等角的补角相等。
作业：书本P139 5，10，11 精选P98 5——9
∠的补角是（180 °—∠ ）
5、如图，O是直线AB上一点，OC是∠AOB的平分线 ①∠AOD的补角是__∠__B__O_D_____ ②∠AOD的余角是__∠__C__O_D_____ ③∠DOB的补角是__∠__A__O_D_____
若∠1 + ∠2 =180 。,则 ∠1和∠2互补 .( 互补定义) 若∠1和∠2互补, 则 ∠1 + ∠2 =180 °.( 互补定义) 若∠3 + ∠4 =90 °,则 ∠3和∠4互余 .( 互余定义) 若∠3和∠4互余, 则 ∠3 + ∠4 =90 °.( 互余定义)
∠AEB和∠ CFB关系如何， F G 并说明理由。
A
D
如图∠AOB = 90 °
1
∠COD = 90 °
O2
B 则∠1与∠2是什么关系？
C
例：若一个角的补角等于它的余角的
4倍，求这个角的度数。
小结
互为余角互为补角
对应图形数量关系
1 2
21
∠1+ ∠2 = 90 ° ∠1+ ∠2 = 180 °
余角与补角
序言
本编为大家提供各种类型的PPT课件，如数学课件、语文课件、英语课件、地理课件、历史课件、政治课件、化学课件、物理课件等等，想了解不同课件格式和写法，敬请下载!

角及角的比较与运算

角

一. 角的概念和表示方法

角在我们的生活中无处不在，例如三角尺的三个角，扇子打开后形成的角，时针与

分针形成角。

例1、角的定义

角的静态定义：有公共端点的两条射线所组成的图形叫做角。公共的端点叫做角的顶点，两条射线叫做角的角的两条边。

例2、角的分类

角的分类：（1）将一条射线OA绕着O旋转，当终止的位置OB与起始OA在一条线上

（3）等于=90°的角叫做直角，小于90°的角叫做锐角，大于90°且小于180°的角

叫做钝角。

练习：一个平角等于几个直角?

例3、表示方法

（1）用三个大写字母表示角，如图：∠AOB或∠BOA(∠的符号不要忘记，0为顶点一定要写在中间)

（2）用一个大写字母，∠0,（只适用于以该点为顶点的角只有一

角的大小比较与运算

∠AOC =∠AOB + ∠ ＿BO＿C
∠BOD = ∠COD+ ∠ ＿B＿OC D
∠AOC= ∠AOD－∠ ＿CO＿D
∠BOD= ∠ ＿AO＿D－∠ ＿AO＿B
C O
B A
例1：如图O是直线AB上一点，∠AOC＝53°17′ 求∠BOC的度数
C
A
O
B
探究
借助一副三角尺，大家都能画出哪些度数的角？
∠AOB＝ 3 ∠AOM＝ 3 ∠MON＝ 3 ∠NOB.
变式练习
A B
C
1、填空
O
D
(1)∠AOD ＝_______＋________＋__________;
(2) ∠BOC ＝________－__________
＝__________－________;
(3) ∠AOB____∠AOC;（填>或<）
C D
A A
B D
B
C
4、如图：OC、OD分别是∠AOB 、∠BOE的平分线，
（1）如果∠AOB=70°，∠BOE=60°，求 ∠DOC的度数.
（2）如果∠1+ ∠2 =55°，求∠AOE的度数.
B
2 1
O
C A
通过这堂课的学习，你有什么收获？
1、比较两个角大小的方法 2、角的运算 3、角平分线

4.3.2 角的比较与运算(含答案)-

4.3.2 角的比较与运算

◆回顾归纳

1．角的比较有两种方法：（1）用量角器量出度数，然后比较它们的大小．（2）•也可以把它们________在一起比较大小，这种方法叫叠合法．

2．从一个角的顶点出发，把这个角分成_______的射线，叫做这个角的平分线．

3．如图1所示，∠AOC是∠AOB与∠BOC•的_______，•记作∠AOC=•∠AOB+•∠_____，∠AOB是∠AOC与∠BOC的______，记作∠AOB=∠AOC-_______．

图1 图2 图3

◆课堂测控

测试点1 角的比较与和、差

1．如图2所示，∠1与∠2的大小关系是_______．

2．如图3所示，∠ABC与∠DEF大小，移动∠DEF，使顶点E与B______，边EF•与边BC_______，此时DE落在______内部，则∠ABC_______∠DEF（填“>”、“<”、•“＝”）

3．如图4所示，∠AOD=∠AOB+_____=∠AOE-____=∠COD+______．

图4 图5 图6

4．用三角板画15°角，如图5所示，使30°角顶点与45°角顶点_____，30°的相邻直角边与45°相邻斜边重合，用铅笔沿AB，ED画线，移开三角板，延长DE与AB交于点

A，∠DAB=______．

5．已知∠AOB=120°，∠BOC=30°，求∠AOC的度数．测试点2 角的平分线

6．如图6所示，BD是∠ABC角平分线，则∠ABC=2_____，∠ABD=_____=1

____．

7．如图7所示，如果OC，OD是∠AOB三等分线，那么∠COD=______=_____，•∠BOD=1

角的比较与运算

人教版数学七年级上册4.3.2角的比较与运算课件

数学知识点总结之角的比较与运算

角的比较与运算

4.3.2 角的比较与运算 课件 (共25张PPT) 2023-2024学年初中数学人教版七年级上册

角的比较与计算

角的比较和运算

角及角的比较与运算

角的比较重难点题型

角的比较和运算

角的比较和运算

角的比较和计算

角的比较与运算

角的比较与运算

角及角的比较与运算

角的大小比较与运算

4.3.2 角的比较与运算(含答案)-

4.3.2 角的比较与运算课件 (共25张PPT) 2023-2024学年初中数学人教版七年级上册