全等三角形竞赛试题精选及答案

合集下载

全等三角形竞赛试题(含答案)

B
D、 E ，
C
D
A
A
E
7.
如图， AD 是△ ABC的角平分线， DE ⊥ AB ， DF⊥ AC，垂足分别是垂直吗？证明你的结论。
E、 F，连接 EF，交 AD于 G， AD 与 EF
E
G F
B
D
C
8.
如图所示，在△ ABC 中， AD 为∠ BAC 的角平分线， DE⊥ AB 于 E， DF⊥ AC 于 F，△ ABC 的面积是 2 A 28cm ,AB=20cm， AC=8cm ，求 DE 的长。
52°，得到△ A′ OB ′，边 A′ B′与边
B A' A O C
B'
3.
如图所示，在△ ABC中，∠ A=90°， D、 E 分别是 AC、 BC上的点，若△ ADB ≌△ EDB ≌△ EDC ，则∠ C 的 A 度数是多少？
D
B
E
A'
C
4.
如图所示，把△ ABC 绕点 C 顺时针旋转 35°，得到△ A′ B′ C， A′ B′交 AC 于点 D，若∠ A′ DC=90 °，则∠ A=
ADB=60 °， E 是 AD上一点，且
A
DE=DB ，
E D B C
19．如图所示，已知在△
AEC 中，∠ E=90 °， AD 平分∠ EAC ， DF⊥ AC ，垂足为 F， DB=DC ，求证： BE=CF

全等三角形竞赛试题(含答案)

全等三角形提高练习

如图，△ AOB 中，/ B=3 0°,将厶AOB 绕点 0顺时针旋转 0B 交于点C （A'不在0B 上）,则/ A CO 的度数为多少？

如图所示，在△ ABC 中，/ A=90°, D 、度数是多少？

1. 如图所示，△ AB3A ADE , BC 的延长线过点求

/ DEF 的度数。

E , / ACB= / AED=10 5°, / CAD=1 0 °, / B=50

如图所示，把厶ABC 绕点C 顺时针旋转则/ A= __________

35°,得到△ A B ' C , A 5. 已知，如图所示， AB=AC , AD 丄BC 于 D

如图，Rt △ ABC 中，/ BAC=90 , AB=AC 分别过点 B C 作过点A 的垂线BC CE,垂足分别为 D E , 若 BD=3 , CE=2，贝U DE=

7. 如图，AD 是厶ABC 的角平分线，DEI AB, DF 丄AC,垂足分别是 E 、F ,连接EF ,交AD 于Q AD 与EF

垂直吗？证明你的结

论。

如图所示，在△ ABC 中，AD 为/ BAC 的角平分线,

28cm ,AB=20cm, AC=8cm 求 DE 的长。

DE 丄AB 于E ,

° E 分别是AC BC 上的点，若△

15.

9. 已知，如图： AB=AE ，/ B=Z E ,Z BAC 2 EAD / CAF=/ DAF , A

10. 求证：AF 丄CD 如图, AD=BD , AD 丄BC 于 D, BE! AC 于E, AD 与BE 相交于点 H,贝U BH 与AC 相等吗？为什么?

全等三角形竞赛试题含答案

全等三角形提高练习

1. 如图所示，△AB C ≌△ADE ，BC 的延长线过点E ，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，

求∠DEF 的度数。

2. 如图，△AOB 中，∠B=30°，将△AOB 绕点O 顺时针旋转52°，得到△A ′OB ′，边A ′B ′与边

OB 交于点C （A ′不在OB 上），则∠A ′CO 的度数为多少？

3. 如图所示，在△ABC 中，∠A=90°，D 、E 分别是AC 、BC 上的点，若△ADB ≌△EDB ≌△EDC ，则∠C 的

度数是多少？

4. 如图所示，把△ABC 绕点C 顺时针旋转35°，得到△A ′B ′C ，A ′B ′交AC 于点D ，若∠A ′DC=90°，

则∠A=

5. 已知，如图所示，AB=AC ，A D ⊥BC 于D ，且AB+AC+BC=50cm,而AB+BD+AD=40cm ，则AD 是多少？

6. 如图，Rt △ABC 中，∠BAC=90°，AB=AC ，分别过点B 、C 作过点A 的垂线BC 、CE ，垂足分别为D 、E ，

若BD=3，CE=2，则DE= 7. 如图，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，连接EF ，交AD 于G ，AD 与EF

垂直吗？证明你的结论。

8. 如图所示，在△ABC 中，AD 为∠BAC 的角平分线，D E ⊥AB 于E ，DF ⊥AC 于F ，△ABC 的面积是

28cm 2

,AB=20cm ，AC=8cm ，求DE 的长。

全等三角形习题精选(含答案)

全等三角形提高练习

1. 如图所示，△ABC ≌△ADE ，BC 的延长线过点E ，∠ACB=∠AED=105°，∠CAD=10°，

∠B=50°，求∠DEF 的度数。

2. 如图，△AOB 中，∠B=30°，将△AOB 绕点O 顺时针旋转52°，得到△A ′OB ′，边A ′B ′

与边OB 交于点C （A ′不在OB 上），则∠A ′CO 的度数为多少？

3. 如图所示，在△ABC 中，∠A=90°，D 、E 分别是AC 、BC 上的点，若△ADB ≌△EDB ≌

△EDC ，则∠C 的度数是多少？

4. 如图所示，把△ABC 绕点C 顺时针旋转35°，得到△A ′B ′C ，A ′B ′交AC 于点D ，若∠A ′DC=90°，则∠A=

5. 已知，如图所示，AB=AC ，AD ⊥BC 于D ，且AB+AC+BC=50cm,而AB+BD+AD=40cm ，

则AD 是多少？

6. 如图，Rt △ABC 中，∠BAC=90°，AB=AC ，分别过点B 、C 作过点A 的垂线BC 、CE ，

垂足分别为D 、E ，若BD=3，CE=2，则DE= 7. 如图，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，连接EF ，交

AD 于G ，AD 与EF

8. 如图所示，在△ABC 中，AD 为∠BAC 的角平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，△ABC

的面积是28cm 2

,AB=20cm ，AC=8cm ，求DE 的长。

C A B

9. 已知，如图：AB=AE ，∠B=∠E ，∠BAC=∠EAD ，∠CAF=∠DAF ，求证：

全等三角形证明经典精彩试题50道

合用文档

全等三角形证明经典试题50 道

1.（已知：如图， E,F在 AC上， AD∥CB 且 AD=CB，∠ D＝∠ B.

求证： AE=CF.

【答案】∵ AD∥ CB

∴∠ A=∠C

又∵ AD=CB，∠ D=∠B

∴△ ADF≌△ CBE

∴AF=CE

∴AF+EF=CE+EF

即 AE=CF

2.已知：如图，∠ ABC=∠ DCB，BD、CA 分别是∠ ABC、∠ DCB的均分线．求证： AB=DC

证明：在△ ABC与△ DCB中

ABC DCB (已知）

ACB DBC（∵ AC均分∠ BCD，BD均分∠ ABC）

BC BC（公共边）

∴△ ABC≌△ DCB

∴AB=DC

3.如图，点 D， E 分别在 AC， AB 上．

(1) 已知， BD=CE，CD=BE，求证： AB=AC；

(2) 分别将“ BD=CE”记为①，“ CD=BE”记为②，“AB=AC”记为③．增加条件①、③，以②为结论构成命题1，增加条件②、③以①为结论构成命题2．命题 1 是命题 2 的命题，命题2是命题．（选择“真”或“假”填入空格）．

【答案】

∴ △ DBC≌△ ECB （SSS）

∴ ∠ DBC =∠ ECB

∴AB=AC

(2)逆，假；

4.如图，在□ABCD中，分别延长 BA，DC到点 E，使得 AE=AB，CH=CD，连接 EH，分别交 AD，BC于点 F,G。求证：△ AEF≌△ CHG.

【答案】证明：∵ □ABCD

∴AB=CD,∠ BAD=∠ BCD AB∥ CD

∴∠ EAF=∠ HCG ∠E=∠ H

∵AE=AB ，

CH=CD ∴ AE=CH

(完整)全等三角形提高练习精选27题及答案

全等三角形提高练习精选27题及答案

1•如图所示，△ ABC ^A ADE , BC 的延长线过点 E,/ ACB= / AED=105 / CAD=10 ° ,Z B=50。，求/DEF 的度数。

2•如图，△ AOB 中，/ B=30。，将A AOB 绕点O 顺时针旋转52。，得到厶A'OB ', 边A 'B '与边OB 交于点C （A '不在OB 上）,则/ A 'CO 的度数为多少？

3•如图所示，在△ ABC 中，/ A=90 ° ,D 、E 分别是 AC 、若厶ADB ◎△ EDB ^A EDC ，则/ C 的度数是多少？

4•如图所示，把△ ABC 绕点C 顺时针旋转35°，得到△ A'B'C , A '' 交 AC 于点 D ，若/ A 'DC=90 °,^U/A= ____________

6•如图，Rt A ABC 中，/ BAC=90 ° ,AB=AC ，分别过点 B C 作过点A 的垂线

BC 、CE,垂足分另【J 为 D 、E , 若 BD=3 , CE=2，贝U DE= ____________

7•如图，AD 是厶ABC 的角平分线，DE 丄AB , DF 丄AC ,垂足分别是 E 、F ,连接EF, 交AD 于G , AD 与EF 垂直吗？证明你的结论。

E G

5•已知，如图所示, 则AD 是多

AB=AC , AD 丄 BC 于 D ，且 AB+AC+BC=50cm,

14. 如图所示，已知△ ABC 和厶BDE 都是等边三角形，下列结论：① AE=CD ;②BF=BG ; ③BH 平分/ AHD ; ④/ AHC=60 ° ;⑤厶BFG 是等边三角形； ⑥FG// AD , E

全等三角形竞赛试题精选及答案

八年级数学《全等三角形》竞赛试题精选

注: 此卷试题有一定难度,可能每题都不会轻松做下来,你需要提高能力,而且要学会思考难题,这样你才能在考试中得心应手,一定要认真思考,并学会总结,把一类题型掌握透彻,望认真做. 一.选择题与填空题:

1. 如图，已知AB ∥CD,AD ∥BC ，AC 与BD 交于O ，AE ⊥BD 于E ，CF ⊥BD 于F ，那么图中全等的三角形有【】 A.5对 B.6对 C.7对 D.8对

2. 在△ABC 和A B C '''∆中, AB A B ''=,B B '∠=∠,补充件后仍不一定能保证ABC ∆≌A B C '''∆,则补充的条件是【】

A.BC B C ''=

B.A A '∠=∠

C.AC A C ''=

D.C C '∠=∠

3. 如图,在等边△ABC 中,AD ＝BE ＝CF,D 、E 、F 不是中点,连结AE 、BF 、CD,构成

一些三角形.如果三个全等的三角形组成一组,那么图中全等的三角形的组数是【】

A.3个

B.4个

C.5个

D.6个 4. 若在ABC ∆中,∠ABC 的平分线交AC 于D,BC ＝AB ＋AD,∠C ＝300

，则∠B 的度数

为【】

A.450

B.600

C.750

D.900

5. 如图，AD 是ΔABC 的中线，E 、F 分别在AB 、AC 上且DE ⊥DF ，则（） A ．BE+CF ＞EF B.BE+CF=EF

C ．BE+CF ＜EF D.EF 与BE+CF 大小关系无法确定

6. (黄冈市中考题)在△ABC 和A B C '''∆中, AB A B ''=,B B '∠=∠,补充条件后仍不一定能保证ABC

全等三角形竞赛试题精选及答案汇编

八年级数学《全等三角形》竞赛试题精选

1. 如图，已知AB ∥CD,AD ∥BC ，AC 与BD 交于O ，AE ⊥BD 于E ，CF ⊥BD 于F ，那

么图中全等的三角形有【】

A.5对

B.6对

C.7对

D.8对

2. 在△ABC 和A B C '''∆中, AB A B ''=,B B '∠=∠,补充件后仍不一定能保证

ABC ∆≌A B C '''∆,则补充的条件是【】 A.BC B C ''= B.A A '∠=∠ C.AC A C ''= D.C C '∠=∠

3. 如图,在等边△ABC 中,AD ＝BE ＝CF,D 、E 、F 不是中点,连结AE 、BF 、CD,构成

一些三角形.如果三个全等的三角形组成一组,那么图中全等的三角形的组数是【】

A.3个

B.4个

C.5个

D.6个 4. 若在ABC ∆中,∠ABC 的平分线交AC 于D,BC ＝AB ＋AD,∠C ＝300

，则∠B 的度数

为【】

A.45

B.60

C.75

D.900

5. 如图，AD 是ΔABC 的中线，E 、F 分别在AB 、AC 上且DE ⊥DF ，则（） A ．BE+CF ＞EF B.BE+CF=EF

C ．BE+CF ＜EF

D.EF 与BE+CF 大小关系无法确定

6. (黄冈市中考题)在△ABC 和A B C '''∆中, AB A B ''=,B B '∠=∠,补充条件后仍不一定能保证ABC

全等三角形经典题型50题(有答案)

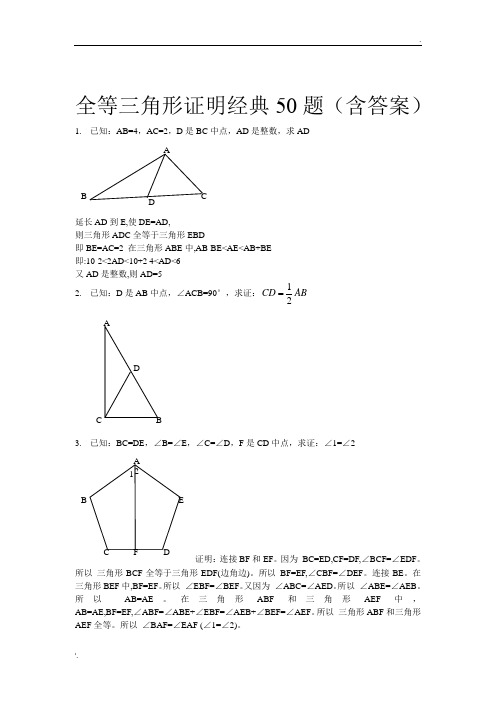
全等三角形证明经典50题（含答案）

1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD

延长AD 到E ，使DE=AD ，

则三角形ADC 全等于三角形EBD

即BE=AC=2 在三角形ABE 中，AB —BE<AE 〈AB+BE 即：10—2〈2AD<10+2 4<AD 〈6 又AD 是整数，则AD=5

2. 已知:D 是AB 中点,∠ACB=90°，求证:12

CD AB

3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2

证明：连接BF 和EF 。因为 BC=ED ，CF=DF,∠BCF=∠EDF 。

所以三角形BCF 全等于三角形EDF(边角边)。所以 BF=EF ，∠CBF=∠DEF 。连接BE 。在

三角形BEF 中，BF=EF.所以 ∠EBF=∠BEF.又因为 ∠ABC=∠AED 。所以 ∠ABE=∠AEB 。所以 AB=AE 。在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。所以三角形ABF 和三角形AEF 全等。所以 ∠BAF=∠EAF （∠1=∠2）.

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点,作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE(AAS)∴EG=AC ∵EF//AB ∴∠DF E=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC

全等三角形竞赛试题(含答案)

全等三角形提高练习

1. 如图所示，△AB C ≌△ADE ，BC 的延长线过点E ，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，

求∠DEF 的度数。

2. 如图，△AOB 中，∠B=30°，将△AOB 绕点O 顺时针旋转52°，得到△A ′OB ′，边A ′B ′与边

OB 交于点C （A ′不在OB 上），则∠A ′CO 的度数为多少？

3. 如图所示，在△ABC 中，∠A=90°，D 、E 分别是AC 、BC 上的点，若△ADB ≌△EDB ≌△EDC ，则∠C 的

度数是多少？

4. 如图所示，把△ABC 绕点C 顺时针旋转35°，得到△A ′B ′C ，A ′B ′交AC 于点D ，若∠A ′DC=90°，

则∠A=

5. 已知，如图所示，AB=AC ，A D ⊥BC 于D ，且AB+AC+BC=50cm,而AB+BD+AD=40cm ，则AD 是多少？

6. 如图，Rt △ABC 中，∠BAC=90°，AB=AC ，分别过点B 、C 作过点A 的垂线BC 、CE ，垂足分别为D 、E ，

若BD=3，CE=2，则DE= 7. 如图，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，连接EF ，交AD 于G ，AD 与EF

垂直吗？证明你的结论。

8. 如图所示，在△ABC 中，AD 为∠BAC 的角平分线，D E ⊥AB 于E ，DF ⊥AC 于F ，△ABC 的面积是

28cm 2

,AB=20cm ，AC=8cm ，求DE 的长。

全等三角形习题精选(含答案)

全等三角形提高练习

1. 如图所示，△ABC ≌△ADE ，BC 的延长线过点E ，∠ACB=∠AED=105°，∠CAD=10°，

∠B=50°，求∠DEF 的度数。

2. 如图，△AOB 中，∠B=30°，将△AOB 绕点O 顺时针旋转52°，得到△A ′OB ′，边A ′B ′

与边OB 交于点C （A ′不在OB 上），则∠A ′CO 的度数为多少？

3. 如图所示，在△ABC 中，∠A=90°，D 、E 分别是AC 、BC 上的点，若△ADB ≌△EDB ≌

△EDC ，则∠C 的度数是多少？

4. 如图所示，把△ABC 绕点C 顺时针旋转35°，得到△A ′B ′C ，A ′B ′交AC 于点D ，若∠A ′DC=90°，则∠A=

5. 已知，如图所示，AB=AC ，AD ⊥BC 于D ，且AB+AC+BC=50cm,而AB+BD+AD=40cm ，

则AD 是多少？

6. 如图，Rt △ABC 中，∠BAC=90°，AB=AC ，分别过点B 、C 作过点A 的垂线BC 、CE ，

垂足分别为D 、E ，若BD=3，CE=2，则DE= 7. 如图，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，连接EF ，交

AD 于G ，AD 与EF

8. 如图所示，在△ABC 中，AD 为∠BAC 的角平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，△ABC

的面积是28cm 2

,AB=20cm ，AC=8cm ，求DE 的长。

C A B

9. 已知，如图：AB=AE ，∠B=∠E ，∠BAC=∠EAD ，∠CAF=∠DAF ，求证：

全等三角形竞赛试题含答案

全等三角形提高练习

1. 如下列图，△ABC ≌△ADE ，BC 的延长线过点E ，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，

求∠DEF 的度数。 2. 如图，△AOB 中，∠B=30°，将△AOB 绕点O 顺时针旋转52°，得到△A ′OB ′，边A ′B ′与边

OB 交于点C 〔A ′不在OB 上〕，那么∠A ′CO 的度数为多少？

3. 如下列图，在△ABC 中，∠A=90°，D 、E 分别是AC 、BC 上的点，假设△ADB ≌△EDB ≌△EDC ，

那么∠C 的度数是多少？

4. 如下列图，把△ABC 绕点C 顺时针旋转35°，得到△A ′B ′C ，A ′B ′交AC 于点D ，假设∠A ′

DC=90°，那么∠A=

5. ，如下列图，AB=AC ，AD ⊥BC 于D ，且AB+AC+BC=50cm,而AB+BD+AD=40cm ，那么AD 是多少？

6. 如图，Rt △ABC 中，∠BAC=90°，AB=AC ，分别过点B 、C 作过点A 的垂线BC 、CE ，垂足分别为D 、E ，假设BD=3，CE=2，那么DE=

7. 如图，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，连接EF ，交AD 于G ，AD

与EF 垂直吗？证明你的结论。

8. 如下列图，在△ABC 中，AD 为∠BAC 的角平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，△ABC 的面积是

28cm 2,AB=20cm ，AC=8cm ，求DE 的长。

全等三角形习题精选(含答案)

全等三角形提高练习

1. 如图所示，△ABC ≌△ADE ，BC 的延长线过点E ，∠ACB=∠

B=50°，求∠DEF 的度数。

2. 如图，△AOB 中，∠B=30°，将△AOB

绕点O 顺时针旋转52边OB 交于点C

（A ′不在OB 上），则∠A ′CO 的度数为多少？

3. 如图所示，在△ABC 中，∠A=90°，D 、E 分别是AC 、BC EDC ，则∠

C 的度数是多少？

4. 如图所示，把△ABC 绕点C 顺时针旋转35°，得到△A ′B ′C ，A ′B DC=90°，则∠A=

5. 已知，如图所示，AB=AC ，AD ⊥BC 于D ，且AB+AC+BC=50cm,而则

AD 是多少？

6. 如图，Rt △ABC 中，∠BAC=90°，AB=AC ，分别过点B 、C

垂足分别为D 、E ，若BD=3，CE=2，则DE=

7. 如图，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC AD 于G ，AD 与EF 8. 如图所示，在△ABC 中，AD 为∠BAC 的面积是28cm 2,AB=20cm ，AC=8cm ，求DE 的长。

9. 已知，如图：AB=AE ，∠B=∠E ，∠BAC=∠EAD ，∠CAF=∠DAF ，求证：AF 10. 如图，AD=BD ，AD ⊥BC 于D ，BE ⊥AC 于E ，AD 与BE 相交于点H ，则等吗？为什么？

A B'

11. 如图所示，已知，AD 为△ABC 的高，E 为AC 上一点，BE 交

，

FD=CD ，求证：BE ⊥AC

12. △DAC 、△EBC 均是等边三角形，AF 、BD

全等三角形测试题含答案

《全等三角形》整章水平测试题

一、认认真真选，沉着应战！ 1．下列命题中正确的是（．下列命题中正确的是（） A ．全等三角形的高相等．全等三角形的高相等 B ．全等三角形的中线相等．全等三角形的中线相等 C ．全等三角形的角平分线相等．全等三角形的角平分线相等 D ．全等三角形对应角的平分线相等．全等三角形对应角的平分线相等 2．下列各条件中，不能作出惟一三角形的是（下列各条件中，不能作出惟一三角形的是（） A ．已知两边和夹角．已知两边和夹角 B ．已知两角和夹边．已知两角和夹边 C ．已知两边和其中一边的对角．已知两边和其中一边的对角 D ．已知三边．已知三边 4．下列各组条件中，能判定△ABC ≌△DEF 的是( )

A ．A

B =DE ，B

C =EF ，∠A =∠D

B ．∠A =∠D ，∠

C =∠F ，AC =EF

C ．AB =DE ，BC =EF ，△ABC 的周长= △DEF 的周长的周长

D ．∠A =∠D ，∠B =∠

E ，∠C =∠F

5．如图，在△ABC 中，∠A :∠B :∠C =3:5:10，又△MNC ≌△ABC ，则∠BCM ：∠BCN 等于（等于（）

A ．1:2

B ．1:3

C ．2:3

D ．1:4

6．如图，．如图， ∠AOB 和一条定长线段A ，在∠AOB 内找一点P ，使P 到OA 、OB 的距离都等于A ，做法如下：（1）作OB 的垂线NH ，使NH =A ，H 为垂足．（2）过N 作NM ∥OB ．（3）作∠AOB 的平的平分线OP ，与NM 交于P ．（4）点P 即为所求．其中（3）的依据是（）的依据是（） A ．平行线之间的距离处处相等平行线之间的距离处处相等

全等三角形测试题及答案

一、选择题

1. 在以下四组线段中，哪个组合的线段可以构成全等三角形？

A) AB = 6 cm, AC = 6 cm, BC = 5 cm

B) AB = 4 cm, AC = 3 cm, BC = 5 cm

C) AB = 5 cm, AC = 7 cm, BC = 5 cm

D) AB = 8 cm, AC = 6 cm, BC = 10 cm

答案：B) AB = 4 cm, AC = 3 cm, BC = 5 cm

2. 在△ABC中，AB = 5 cm, AC = 6 cm, BC = 7 cm。下列哪个陈述是正确的？

A) △ABC是全等三角形

B) △ABC是直角三角形

C) △ABC是等腰三角形

D) △ABC不存在

答案：A) △ABC是全等三角形

二、填空题

3. 完成下面的等式: △ABC ≌△___。

答案：ACD

4. 如果两个三角形的对应顶点对应着相等的角度，那么这两个三角

形是______的。

答案：全等

三、解答题

5. 已知图中的三个三角形，判断是否可以证明它们是全等三角形。

如果可以，请说明理由；如果不可以，请说明其中的不等条件。

（插入三个全等三角形的图示）

答案：根据提供的图示，可以确定△ABC和△DEF是全等三角形。理由是它们的对应边和对应角相等：AB = DE, AC = DF, BC = EF, ∠A

= ∠D, ∠B = ∠E, ∠C = ∠F。而△XYZ无法和△ABC或△DEF证明全等，其中的不等条件为对应的角度不相等。

6. 已知三角形ABC和DEF，如果AB = DE, AC = DF，并且∠A =

全等三角形竞赛试题(卷)(含答案解析)

全等三角形提高练习

1. 如图所示，△AB C ≌△ADE ，BC 的延长线过点E ，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，

求∠DEF 的度数。

2. 如图，△AOB 中，∠B=30°，将△AOB 绕点O 顺时针旋转52°，得到△A ′OB ′，边A ′B ′与边

OB 交于点C （A ′不在OB 上），则∠A ′CO 的度数为多少？

3. 如图所示，在△ABC 中，∠A=90°，D 、E 分别是AC 、BC 上的点，若△ADB ≌△EDB ≌△EDC ，则∠C 的

度数是多少？

4. 如图所示，把△ABC 绕点C 顺时针旋转35°，得到△A ′B ′C ，A ′B ′交AC 于点D ，若∠A ′DC=90°，

则∠A=

5. 已知，如图所示，AB=AC ，A D ⊥BC 于D ，且AB+AC+BC=50cm,而AB+BD+AD=40cm ，则AD 是多少？

6. 如图，Rt △ABC 中，∠BAC=90°，AB=AC ，分别过点B 、C 作过点A 的垂线BC 、CE ，垂足分别为D 、E ，

若BD=3，CE=2，则DE= 7. 如图，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，连接EF ，交AD 于G ，AD 与EF

垂直吗？证明你的结论。

8. 如图所示，在△ABC 中，AD 为∠BAC 的角平分线，D E ⊥AB 于E ，DF ⊥AC 于F ，△ABC 的面积是

28cm 2

,AB=20cm ，AC=8cm ，求DE 的长。