河海大学《几何与代数》3-3.ppt
合集下载
河海大学《几何与代数》几何与代数 第一章

定理3: 设1, 2 ,3不共面,则,必存在唯一的一组实数 1,2,3,使得 11 2 2 33 平行六面体
上页 下页
定义
设1 , 2 ,…, n 是一组向量,
1、若 k1,k2,… ,kn是一组实数,称向量
=k11 + k22+ …+ kn n
( x1 , y1 , z1 )
加法 数乘
i i j j k k 1
( x2 , y2 , z2 )
距离
2.内积
i j j i i k k i j k k j 0
?
cos( , ) ?
|| ||2 ?
上页 下页
例1:若,求 { [ ( ) ]} || ||4
例2:计算由向量 (3, 0, 1 ), (3, 3, 0), ( 1, 2, 3)
(30) 例3:已知Δ ABC的顶点A(1, 1,2),B(5, 6,2),
所张成的平行六面体的 体积。
z C O M B y
上页 下页
x
A
2.定义(方向余弦) 在空间直角坐标系中,向量与三个坐标向量 i, j ,k
的夹角 , , (0 , , ) 称为向量的方向角;
方向角的余弦 cos , cos , cos 称为向量 的方向余弦。 注1:||||=?(勾股定理) 注2:单位向量的表示法 例:已知=(-3,6,2),求的方向余弦和与平行的单位向量
( ) ?
?
上页
下页
3.外积
i i j j k k i j k jk i k i j
注意: i, j, k 的顺序
河海大学高等数学PPT
则
lim f [ ( k ) , ( k ) ]
0 k 1
n
n
注意 2 (t ) 2 (t ) 连续
lim f [ ( k ) , ( k ) ]
0 k 1
因此
说明:
(1) sk 0, t k 0, 因此积分限必须满足 !
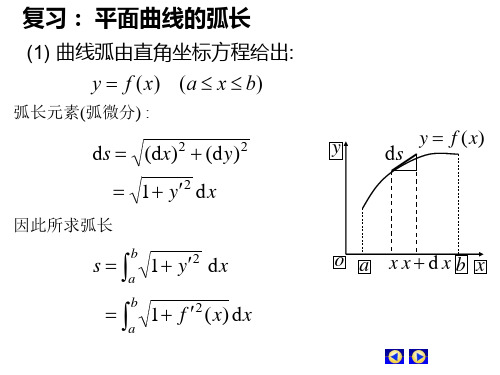
弧长元素(弧微分) :
ds (dx) 2 (d y ) 2
2 (t ) 2 (t ) d t
因此所求弧长
s
2 (t ) 2 (t ) d t
(3) 曲线弧由极坐标方程给出:
令 x r ( ) cos , y r ( ) sin , 则得
弧长元素(弧微分) :
ds [ x( )]2 [ y ( )]2 d
r 2 ( ) r 2 ( ) d
因此所求弧长
s
r 2 ( ) r 2 ( ) d
第十章 曲线积分与曲面积分
积分学 定积分 二重积分 三重积分 曲线积分 曲面积分
积分域
区间域
取极限 W lim [ P ( i , i ) xi Q( i , i ) yi ]. 0
i 1
n
精确值
2. 定义. 设 L 为xoy 平面内从 A 到B 的一条有向光滑
弧, 在L 上定义了一个向量函数
若对 L 的任意分割和在局部弧段上任意取点,
0
极限
L L
( 3) f ( x , y )ds f ( x , y )ds f ( x , y )ds.
L L1 L2
( L L1 L2 ).
( s 为曲线弧 L 的长度)
河海大学《几何与代数》课件

总结与展望
对《几何与代数》课件的总结
回顾了《几何与代数》课件的主要内容 总结了《几何与代数》课件中的重点和难点 分析了《几何与代数》课件的教学效果和影响 展望了《几何与代数》课件未来的发展方向和应用前景
对未来发展的展望
教学内容的更新与完善 教学方法的创新与改进 教学效果的评估与反馈 学科交叉与融合的发展趋势
结合实际,应用性强
结合实际案例:通过具体案例来解释几何与代数的概念和原理,帮助学生更好地理解和应用。
强调应用:注重几何与代数的实际应用,通过大量实例和练习题,培养学生的数学思维和应用 能力。
互动性强:课件中设置了许多互动环节,如问答、讨论等,鼓励学生积极参与,提高学习效果。
图文并茂:采用丰富的图表和图片来辅助讲解,使抽象的数学概念更加形象化、生动化。
掌握几何与代数的概念和基本原理
课件目标
培养学生的逻辑思维和数学素养
添加标题
添加标题
添加标题
添加标题
理解几何与代数在各个领域的应用
提高学生的解题能力和应试能力
适用对象
适用课程:《几 何与代数》
适用人群:河海 大学本科生、研 究生
适用学期:本科 一年级上学期
适用教学目标:掌 握几何与代数的基 本概念和原理
图文并茂,易于理解
图文并茂:通过丰富的图片和图表,帮助学生更好地理解抽象的概念和公式
易于理解:采用简洁明了的语言和生动的实例,降低学习难度,提高学生的学习兴趣
互动性强:设置互动环节,如问答、讨论等,鼓励学生积极参与,提高学习效果 内容丰富:涵盖了《几何与代数》的主要知识点,帮助学生系统地掌握学科知识
几何应用举例
微分几何在理论物理中的应用
添加标题
添加标题
几何与代数课件:lec1几何与代数绪论

三类方程组的根一定可以由原方程的系数,经过加、减、乘、 除及开平方这5种运算表示出来。
17
空间解析几何的基本思想 ——用代数方法研究几何问题
在三维空间中:
空间形式 — 点, 线, 面,二次曲面
数量关系 — 坐标,方程(组) 基本方法 — 坐标法; 向量法
几何与代数的关系: 三维→n维 18
“几何与代数”的基本思想方法 •解析几何的重要性
我想说
•课程的重要性 •大学与中学的区别 •“几何与代数”和“高等数学”的区别
•“几何与代数”的基本思想方法
•“几何与代数”的主要内容
•学什么?怎么学?
3
我想说
•课程的重要性
➢工科基础
电子工程与信息类专业有十多门课程要用矩阵建模和解题,比如电 路、数值计算方法、计算机图形学、信号与系统、数字信号处理、 系统动力学、自动控制原理、机械振动等。
❖问题式预习
❖引导式教学
❖自主性考试(期中占15%) ❖数学实验5%
❖学术性论文(考核占5%) ❖平时作业5%
❖演讲式展现
❖期末考试65%
8
武汉大学王林昌教授在谈到大一新生如何设计
自己的大学之路时说,上大学有四项任务,一
是要学会做人,二是要学会做事,三是要学会
学习,四是要学会处理人际关系。
9
我想说
几何与代数 绪论
课程中心:用户名:一卡通号 密码:问教务处初始密码
课程名称:几何与代数(B) 班级名称:关秀翠11-4-6
学生在获得选课码:MMVR-8261 之 后,只需在选课功能中直接输入选课 码即可成功的选上课程。
学ห้องสมุดไป่ตู้人数限制:270人
选课开始时间:2011-9-12
大学数学专业空间解析几何向量代数PPT课件

它 们 的 和 是 零 矢 量.
C
证 必 要 性 设 三 矢 量a,b,c可 以
构 成 三 角 形ABC, 即 有AB a, BC A
B
b,CA c, 那 么AB+BC+CA=AA 0,即a b c 0
充 分 性 设a b c 0, 作AB a, BC b, 那 么AC
a b, 所 以AC c 0, 从 而c是 AC的反矢 量,因此c=
叫 做 矢 量a1 , a2 ,, an的 线 性 组 合.
定理1.4.4 在n 2时,矢量a1, a2 ,, an线性相关的 充 要 条 件 是 其 中 有 一 个矢 量 是 其 余 矢 量 的 线 性组 合.
第34页/共137页
定理1.4.6 两矢量共线的充要条件是它们线性相关.
定 义1.4.2 对 于n(n 1)个 矢 量a1, a2 ,, an, 如 果 存
r xe1 ye2 ze3 ,
(1.4 3)
并 且 其 中 系 数x, y, z被e1 , e2 , e3 , r唯 一 确 定.
这时e1, e2 , e3叫做空间矢量的基底.
第38页/共137页
定 理1.4.3 如 果 矢 量e1 , e2 , e3不 共 面 , 那 么 空 间
任 意 矢 量r可 以 由 矢 量e1 , e2 , e3线 性 表 示 , 或 说 空 间 任 意 矢 量r可 以 分 解 成 矢 量e1 , e2 , e3的 线 性 组 合 , 即
A
Q M
B
P
CB
由条件可知: BC = 2BP, AC = 2AQ.
S
Q
T
P
C
设AS = AP, B2T = BQ,
2
3
河海大学《几何与代数》3-5

由阶梯形矩阵有三个非零行可知 R( A) 3.
求 A 的一个最高阶子式 .
R( A) 3, 知A的最高阶非零子式为3阶 .
A 的 3 阶子式共有 C43 • C53 40 个 . 考察A的行阶梯形矩阵,
记A (a1,a2 ,a3 ,a4 ,a5 ),则矩阵B (a1,a2 ,a4 )的行
阶梯形矩阵为 1
6
1
0 4 1
0 0 4 R(B) 3, 0 0 0
故 B 中必有 3 阶非零子式. 且共有 4 个. 计算B的前三行构成的子式
3 2 5 32 5 2 0 52 0 5 3 2 6 6 0 11
25
2
16 0.
6 11
则这个子式便是A 的一个最高阶非零子式.
2 0 1 2 0 5 0 1 5 2 1 5
0.
RA 2.
另解
对矩阵
A
1 0
3 2
2 1
2 3
做初等变换,
2 0 1 5
1 3 2 2 1 3 2 2 0 2 1 3 ~ 0 2 1 3,
2 0 1 5 0 0 0 0
显然,非零行的行数为2,
RA 2.
此方法简单!
3 2 0 5 0
A
3 2
2 0
3 1
6 1 5 3
1 6 4 1 4
r1 r4
1 0
6 4
4 3
1 1
4 1
r2 r4
2 3
0 2
1 0
5 3 5 0
3 2 0 5 0
A
3 2
2 0
3 1
6 1 5 3
1 6 4 1 4
r1 r4 r2 r4 r3 2r1 r4 3r1
代数与几何(PPT课件)

1870年海涅(德, 1821-1881)定义了一致连续
19世纪60年代魏尔斯特拉斯(德, 1815-1897)提出ε-δ语言 1875年达布(法, 1842-1917)提出了大和、小和
分析的严密化--实数理论
• 1817年波尔查诺(捷, 1781-1848)提出确界原理 • 1817年波尔查诺和19世纪60年代魏尔斯特拉斯 (德, 1815-1897)提出聚点定理 • 1821年柯西(法, 1789-1857)提出收敛准则 • 19世纪60年代魏尔斯特拉斯提出单调有界原理 • 1872年海涅(德, 1821-1881)和1895年波莱尔 (法, 1871-1956)提出有限覆盖定理
几何--射影几何
综合方法
1822年庞斯列(法, 1788-1867)的《论图 形的射影性质》
连 续 性 原 理
对 偶 原 理
几何--射影几何
代数方法
1827年麦比乌斯(德, 1790-1868)的 《重心计算》 1829年普吕克(德, 1801-1868)的三线坐标
麦比乌斯(德, 1790-1868)
第七讲: §2.6-2.8
分析、代数与几何
分析的严密化 代数学的新生 几何学的变革
分析的严密化
分析:关于函数的无穷小分析 问题:第二次数学危机 核心:函数、无穷小
贡献:柯西(法, 1789-1857 )
魏尔斯特拉斯(德, 1815-1897)
分析的严密化--函数
初等函数
1872年戴德金(德, 1831-1916)提出分割理论 1892年巴赫曼(德, 1837-1920)提出区间套原理
分析的严密化
波尔查诺 (捷克斯洛伐克,1981)
分析的严密化
高等代数与解析几何课件
•
b定义为一个
a • b | a || b | cos a,b .
量 讨论内积、向量的长度、两个向量的夹角的关系.
代
a
b
数
b0
第
命题6.3 向量a与b垂直的充分必要条件是 :ab 0.
一 章 a,
b,
定理6.4 向量的内积有下列性质:对任意的向量
c以及实数k , 有 (IP1)对称性质a
要条件是:
a
b
c
0.
章
C
向
A
B
量
例1.2用向量方法证明:对角 线互相平分的四边形
代 是平行四边形 . D
O
C
数
A
B
第
向量的标量乘法
一
定义1.3 实数k与向量a的标量乘积ka是一个向量, 它的长度是a的长度的| k | 倍,当k 0时它的方向与a
章 向
相同,当k 0时方向与a相反.
(对M任1)意k的(m向a量 ) a(,kbm以)a及; 实数 k有:
(3)推广到有限个点 线性流形.
量
(4)线性流形的基本特征.
(5)单纯形的概念.
代
例2.2 证明线性流形LM(A1,A2,,An )中任意
数 两点M1,M 2一定包含在这个线性流形内.
第
思考题:线性流形的基本特征.
(1)“直”、“平”,(2)是否包含零向量.
一
例2.3 设a和b是两个非零向量.试证由它们的线性
数
第
问题:(1)讨论两个非零向量共线的性质;
一
(2)讨论三个点共线的条件; (3)讨论三个向量共面的性质;
章 (4)讨论四个点共面的条件.
(5)将以上问题推广或一般化.
人教版高考总复习一轮数学精品课件 主题三 几何与代数 第八章 第2课时 求空间角与距离

(1)求证:平面 ⊥平面.
证明在等腰梯形中, = 4, = = 2,则∠ = 60∘ ,
则 = 2 3,所以2 + 2 = 2 , ⊥ .又 = 4, = 2,由
2 + 2 = 16 = 2 ,得到 ⊥ .
.设直线和所成的角为
6
6
6
3
3
2 6
,则cos = |cos⟨,⟩| =
1
2
3
3
×
2
2
=
2
.
3
规律方法
用向量法求异面直线所成角的一般步骤
(1)选择三条两两垂直的直线建立空间直角坐标系;
(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量;
(3)利用向量的夹角公式求出向量夹角的余弦值;
用公式 cos⟨,⟩ =
得结论
⋅
π
2
利用sin = |cos⟨,⟩|,直线和平面所成角的范围是[0, ],即可得出直线和平面所
成的角
[对点训练3]如图,在四棱锥 − 中,底面四边形
满足 = = 2, = = 5,∠ = 90∘ ,棱上的点
= − = −
1
,
2
=
1
(
2
+ ).
设向量与的夹角为,则直线和所成角的余弦值等于 cos .
⋅ =
1
2
1
−
8
+
1
2
1
1
−
4
8
1
2
1
2
1
4
1
2
1
4
+ ⋅ ( − ) = 2 − ⋅ + ⋅ − ⋅ =
证明在等腰梯形中, = 4, = = 2,则∠ = 60∘ ,
则 = 2 3,所以2 + 2 = 2 , ⊥ .又 = 4, = 2,由
2 + 2 = 16 = 2 ,得到 ⊥ .
.设直线和所成的角为
6
6
6
3
3
2 6
,则cos = |cos⟨,⟩| =
1
2
3
3
×
2
2
=
2
.
3
规律方法
用向量法求异面直线所成角的一般步骤
(1)选择三条两两垂直的直线建立空间直角坐标系;
(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量;
(3)利用向量的夹角公式求出向量夹角的余弦值;
用公式 cos⟨,⟩ =
得结论
⋅
π
2
利用sin = |cos⟨,⟩|,直线和平面所成角的范围是[0, ],即可得出直线和平面所
成的角
[对点训练3]如图,在四棱锥 − 中,底面四边形
满足 = = 2, = = 5,∠ = 90∘ ,棱上的点
= − = −
1
,
2
=
1
(
2
+ ).
设向量与的夹角为,则直线和所成角的余弦值等于 cos .
⋅ =
1
2
1
−
8
+
1
2
1
1
−
4
8
1
2
1
2
1
4
1
2
1
4
+ ⋅ ( − ) = 2 − ⋅ + ⋅ − ⋅ =
几何与线性代数(第三章 行列式与矩阵)

n
n 2时 ,D a11 A11 a12 A12 a1n A1n a1 j A1 j j1
其中A1 j (1)1 j M1 j
a21 a2, j1
M1 j
a31
a3, j1
an1 an, j1
a2, j1 a2n a3, j1 a3n
an, j1 ann
( j 1,2,..,n)
ai1 j1 ai2 j1
aik j1
ai1 j2 ai2 j2
aik j2
ai1 jk ai2 jk
aik jk
非零子式
定义(秩):非零矩阵A的非零子式的最高阶数称为A的秩, 记为r(A)或R(A)。规定:零矩阵的秩为0
注:最高阶数,即指A存在r阶非零子式,但所有r+1阶子式 (如果存在)都等于0,则最高阶数为r。 注:r(A)=r(AT)
例:
1 4 2
A 3 5 1
2 1 6
性质2:
a11
a12 a1n
a11 a12 a1n
kai1 kai2 kain k ai1 ai2 ann
推论:
** * * 0 0 0 0 ** * *
性质3:
***
*** ***
k (5) A1 1
A
规定:当A可逆时,A0 E, Ak ( A1 )k k N,则当r, s Z时,有
Ar As Ars , ( Ar )s Ars
伴随矩阵
a11
A
a21
an1
a12 a22
an2
a1n
A11
a2n ann
A*
A12
A1n
A21 A22
| A|
| A|
n 2时 ,D a11 A11 a12 A12 a1n A1n a1 j A1 j j1
其中A1 j (1)1 j M1 j
a21 a2, j1
M1 j
a31
a3, j1
an1 an, j1
a2, j1 a2n a3, j1 a3n
an, j1 ann
( j 1,2,..,n)
ai1 j1 ai2 j1
aik j1
ai1 j2 ai2 j2
aik j2
ai1 jk ai2 jk
aik jk
非零子式
定义(秩):非零矩阵A的非零子式的最高阶数称为A的秩, 记为r(A)或R(A)。规定:零矩阵的秩为0
注:最高阶数,即指A存在r阶非零子式,但所有r+1阶子式 (如果存在)都等于0,则最高阶数为r。 注:r(A)=r(AT)
例:
1 4 2
A 3 5 1
2 1 6
性质2:
a11
a12 a1n
a11 a12 a1n
kai1 kai2 kain k ai1 ai2 ann
推论:
** * * 0 0 0 0 ** * *
性质3:
***
*** ***
k (5) A1 1
A
规定:当A可逆时,A0 E, Ak ( A1 )k k N,则当r, s Z时,有
Ar As Ars , ( Ar )s Ars
伴随矩阵
a11
A
a21
an1
a12 a22
an2
a1n
A11
a2n ann
A*
A12
A1n
A21 A22
| A|
| A|
几何与代数习题课

D3 D
.
(二)向量及其运算 仿射坐标系与直角坐标系
向量旳 线性运算
向量概念
向量旳积
向量旳 表达法
数量积
混合积
向量积
1、向量旳概念
定义:既有大小又有方向旳量称为向量. 主要概念: 向量旳模、单位向量、 零向量、 自由向量、 相等向量、 负向量、 平行向量、 向径.
2、向量旳线性运算
(1) 加法:
a22
对于二元线性方程组
aa1211
x1 x1
a12 x2 a22 x2
b1 , b2 .
若记
D a11 a12 ,
系数行列式
a21 a22
aa1211
x1 x1
a12 x2 a22 x2
b1 , b2 .
D a11 a12 , a21 a22
aa1211
x1 x1
a12 x2 a22 x2
[2] 平面旳一般方程
Ax By Cz D 0
[3] 平面旳截距式方程 x yz 1 a bc
z
n
M0 M
o
y
x
M 0 ( x0 , y0 , z0 )
n { A, B, C}
z c
o xa
by
[4] 平面旳夹角 1 : A1 x B1 y C1z D1 0
n1
n2
2
2 : A2 x B2 y C2z D2 0
a11a23a32 a12a21a33 a13a22a31 .
(2)对角线法则 a11 a12 a13 a21 a22 a23 a31 a32 a33
a11a22a33 a12a23a31 a13a21a32 a13a22a31 a12a21a33 a11a23a32 .
河海大学《几何与代数》3-2

x2 xn
x
2 2
xn2
( xi x j ). (1)
ni j1
x1n1
x
n1 2
xnn1
四 方阵的行列式
定义 由 n 阶方阵 A 的元素所构成的行列式, 叫做方阵 A 的行列式,记作 A 或 det A.
例 A 2 6
3 8
则A2 6
3 2.
a11 a12 a1n
kai1 kai2 kain k ai1 ai2 ain
an1 an2 ann
an1 an2 ann
推论 行列式的某一行(列)中所有元素的公因 子可以提到行列式符号的外面.
性质4 行列式中如果有两行(列)元素成比 例,则此行列式为零.
D a21 a2i a2n a21 a2i a2n
an1 ani ann an1 an i ann
性质6 把行列式的某一列(行)的各元素乘以
同一数然后加到另一列(行)对应的元素上去,行 列式不变.
例如
a11 a1i a1 j a1n
例1 3 1 1 2 5 1 3 4
D 2 0 1 1 1 5 3 3
5 1 1 1
c1 2c3 11 1 3 1
c4 c3
0 010
5 5 3 0
5 11 (1)33 11 1 1
5 5 0
r2 r1
5 11 6 2 0 5 5 0
解 将第 2,3,,n 都加到第一列得
a n 1b b b b
a n 1b a b b
D a n 1b b a b
几何与代数线性方程组.ppt

故 x 1 2 也是Ax 0的解.
北京交通大学 几何与代数组
(2)若 x 1 为 Ax 0的解, k 为实数,则 x k1也是 Ax 0 的解.
证明 Ak1 kA1 k0 0.
证毕.
由以上两个性质可知,方程组的全体解向量 所组成的集合,对于加法和数乘运算是封闭的, 因此构成一个向量空间,称此向量空间为齐次线 性方程组 Ax 0 的解空间.
解
B
3 0
1 2
2 1
1 2
3 6
2 23
北京交通大学 几何与代数组
方程组
x1 b11 xr1 b1,nr xn
x
r
br1 xr1
br ,nr xn
所以与都是此方程组的解 ,
1
c 1
r
由
r 1
r2
c r
r1
r2
1 c1 ,,r cr .
n
n
北京交通大学 几何与代数组
取
北京交通大学 几何与代数组
x2 1及 0, 则 x1 1及 1, x4 0 1 x3 0 2
即得对应的齐次线性方程组的基础解系
1
1
1 0
,
0
1
2
0 2
,
1
北京交通大学 几何与代数组
于是所求通解为
x1 1 1 1 2
x2
ห้องสมุดไป่ตู้
x3 x4
c1
1 0 0
c2
证明 A A A 0 b b,
所以x 是方程 Ax b的解.
证毕.
北京交通大学 几何与代数组
2.非齐次线性方程组的通解 非齐次线性方程组Ax=b的通解为
x k11 knrnr . 其中 k11 knrnr 为对应齐次线性方程 组的通解, 为非齐次线性方程组的任意一个特
北京交通大学 几何与代数组
(2)若 x 1 为 Ax 0的解, k 为实数,则 x k1也是 Ax 0 的解.
证明 Ak1 kA1 k0 0.
证毕.
由以上两个性质可知,方程组的全体解向量 所组成的集合,对于加法和数乘运算是封闭的, 因此构成一个向量空间,称此向量空间为齐次线 性方程组 Ax 0 的解空间.
解
B
3 0
1 2
2 1
1 2
3 6
2 23
北京交通大学 几何与代数组
方程组
x1 b11 xr1 b1,nr xn
x
r
br1 xr1
br ,nr xn
所以与都是此方程组的解 ,
1
c 1
r
由
r 1
r2
c r
r1
r2
1 c1 ,,r cr .
n
n
北京交通大学 几何与代数组
取
北京交通大学 几何与代数组
x2 1及 0, 则 x1 1及 1, x4 0 1 x3 0 2
即得对应的齐次线性方程组的基础解系
1
1
1 0
,
0
1
2
0 2
,
1
北京交通大学 几何与代数组
于是所求通解为
x1 1 1 1 2
x2
ห้องสมุดไป่ตู้
x3 x4
c1
1 0 0
c2
证明 A A A 0 b b,
所以x 是方程 Ax b的解.
证毕.
北京交通大学 几何与代数组
2.非齐次线性方程组的通解 非齐次线性方程组Ax=b的通解为
x k11 knrnr . 其中 k11 knrnr 为对应齐次线性方程 组的通解, 为非齐次线性方程组的任意一个特
河海大学《几何与代数》3-3

说明 若 A 是可逆矩阵,则 A 的逆矩阵是唯一的.
若设 B 和 C 是 A 的可逆矩阵,则有
AB BA E, AC CA E,
可得 B EB CAB CAB CE C.
所以 A 的逆矩阵是唯一的,即 B C A1.
例 设 A 2 1, 求A的逆阵. 1 0
解
设利用B待定 a系数b 法 c d
A12 3
3, 3
同理可得 A13 2, A21 6, A22 6, A23 2, A31 4, A32 5, A33 2,
2 6 4
得
A
3
6
5 ,
2 2 2
故
A1
1 A
A
1 2
2 3 2
6 6 2
4 5
2
1 3 1
2
3 3 1
2 5 2. 1
例2
已
知A
a c
b d
求A1
.其
中ad
bc
0
1 0 0 例3 已 知A 0 2 0 求A1 .
0 0 3
解 因 A 3! 0, 故A1存在.
由伴随矩阵法得 A1 A A ,
1 3!
23 0 0
0 13 0
0 0 1 2
1
0
0 1
0
0 .
2
0
0
1 3
例4
பைடு நூலகம்
设
1 A 2
二、逆矩阵的概念和性质
定义 对于n 阶矩阵 A ,如果有一个n 阶矩阵B
,使得
AB BA E,
则说矩阵A是可逆的,并把矩阵 B 称为A 的逆矩阵. A的逆矩阵记作 A1. 例 设 A 1 1, B 1 2 1 2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A1E A1
证毕
逆矩阵的运算性质
1 若A可逆,则A1亦可逆,且 A1 1 A.
2 若A可逆,数 0,则A可逆,且 A1 1 A1.
3 若A, B为同阶方阵且均可逆,则AB亦可逆,且 AB 1 B1 A 1
证明 AB B1A1 A BB1 A1
AEA1 AA1 E,
AB1 B1 A1.
所以
A1 0 1. 1 2
定理1
矩阵 A 可逆的充要条件是 A 0 ,且 A1 1 A , A
其中A为矩阵A的伴随矩阵.
证明 若 A 可逆,即有A1使AA1 E .
故 A A1 E 1, 所以 A 0. 当 A 0时,
当 A 0时,
AA
a11 a12
a21 a22 a11 A11
一、概念的引入
在数的运算中,当数a 0 时, 有
aa1 a1a 1,
其中 a1 1 为 a 的倒数,(或称 a 的逆);
a
在矩阵的运算中,单位阵E相当于数的乘法运算中 的1, 那么,对于矩阵 A ,如果存在一个矩阵A1,
使得
AA1 A1 A E ,
则矩阵 A1称为 A 的可逆矩阵或逆阵.
A12 3
3, 3
同理可得 A13 2, A21 6, A22 6, A23 2, A31 4, A32 5, A33 2,
2 6 4
得
A
3
6
5 ,
2 2 2
故
A1
1 A
A
1 2
2 3 2
6 6 2
4 5
2
1 3 1
2
3 3 1
2 5 2. 1
4
且 A 2E 1 1 A 3E 3E A .
4
4
例6 设三阶矩阵A, B满足关系 :
o 1 2
A1BA 6A BA,且A
14
求B.
o
1 7
解 A1BA BA 6A
A1 E BA 6A A1 E B 6E
B
6
A1
二、逆矩阵的概念和性质
定义 对于n 阶矩阵 A ,如果有一个n 阶矩阵B
,使得
AB BA E,
则说矩阵A是可逆的,并把矩阵 B 称为A 的逆矩阵. A的逆矩阵记作 A1. 例 设 A 1 1, B 1 2 1 2,
1 1 1 2 1 2 AB BA E, B是A的一个逆矩阵.
a1n a2n
a12 A12
A11 A12
A21
A22 a1n A1n
An1 An2 A
aann11Ana1n2 an2 Aann2n A1n aAnn2nAnn AAnn
A
O
O
A
A
, A
AA
A A
AE
A A
A
A
E,
AA
按逆矩阵的定义得
A1 A . A
证毕
奇异矩阵与非奇异矩阵的定义
当 A 0时, A称为奇异矩阵,当 A 0时, A称为 非奇异矩阵. 由此可得A是可逆阵的充要条件是A为非奇异矩阵.
推论 若AB E或BA E ,则B A1.
证明 A B E 1, 故 A 0,
因而A1存在, 于是
B EB A1A B A1AB
是
A
的逆矩阵,
则 AB 2 1 a b 1 0 1 0 c d 0 1
2a c 2b d 1 0 a b 0 1
2a c 1,
2b
d a
0, 0,
b 1,
又因为 AB
a 0,
b 1,
c
1,
d 2.
BA
2 1 0 1 0 1 2 1 1 0, 1 01 2 1 2 1 0 0 1
3
2 2 4
3 1 3
,
B
2 5
1 , 3
C
1 2 3
3 0, 1
求矩阵X使满足 AXB C.
123
解
A 2
2
1 2 0,
2 B
1 1 0,
53
343
A1, B1都存在.
且
A1
1 3
2
1
3 3 1
2 5 2, 1
B1 3 5
1, 2
又由 AXB C A1 AXBB1 A1CB1
推广 A1 A2 Am 1 Am1 A21 A1.1
4 若A可逆,则AT亦可逆 ,且 AT 1 A1 T. 证明 AT A1 T A1A T ET E,
AT 1 A1 T .
另外, 当 A 0时,定义
A0 E, Ak A1 k .
k为正整数
当 A 0, , 为整数时,有
证明
由A2 A 2E 0,
A1
得AA E 2E A A E E
2 A A E 1 A 0, 故A可逆.
2
A1 1 A E .
2
又由A2 A 2E 0
A 2E A 3E 4E 0
A
2E
1 4
A
3E
E
A
2E
1
A 2E 1 A 3E 1,
故A 2E可逆.
说明 若 A 是可逆矩阵,则 A 的逆矩阵是唯一的.
若设 B 和 C 是 A 的可逆矩阵,则有
AB BA E, AC CA E,
可得 B EB CAB CAB CE C.
所以 A 的逆矩阵是唯一的,即 B C A1.
例 设 A 2 1, 求A的逆阵. 1 0
解
设利用B待定 a系数b 法 c d
例2
已
知A
a c
b d
求A1
.其
中ad
bc
0
1 0 0 例3 已 知A 0 2 0 求A1 .
0 0 3
解 因 A 3! 0, 故A1存在.
由伴随矩阵法得 A1 A A ,
1 3!
23 0 0
0 13 0
0 0 1 2
1
0
0 1
0
0 .
2
0
0
1 3
例4
设
1 A 2
E X A1CB1.
于是 X A1CB1
1 3 2
1
3 3 1
2 1 5 2 2 1 3
3 0 1
3 5
1 2
1 0
0
12 2
3 5
1 2
2 10 10
1 4. 4
例5 设方阵A满足方程A2 A 2E 0,证明: A, A 2E都可逆,并求它们的逆矩阵.
A A A ,
A A .
5 若A可逆,则有 A1 A 1 .
证明
AA1 E A A1 1
因此 A1 A 1 .
三、逆矩阵的求法
例1
求方阵
1 A 2
2 2
3 1
的逆矩阵.
3 4 3
123 解 A 2 2 1 2 0, A1存在.
343
21
A11 4
2, 3
21
