速算与巧算

合集下载

第一讲速算与巧算

一、知识要点

速算与巧算是计算中的一个重要组成部分，掌握一些速算与巧算的方法，有助于提高我们的计算能力和思维能力。我们学习加、减法的巧算方法，这些方法主要根据加、减法的运算定律和运算性质，通过对算式适当变形从而使计算简便。

在巧算方法里，蕴含着一种重要的解决问题的策略。转化问题法即把所给的算式，根据运算定律和运算性质，或改变它的运算顺序，或减整从而变成一个易于算出结果的算式。

二、精讲精练

【例题1】计算9+99+999+9999

【思路导航】这四个加数分别接近10、100、1000、10000。在计算这类题目时，常使用减整法，例如将99转化为100－1。这是小学数学计算中常用的一种技巧。

9+99+999+9999

=（10－1）+（100－1）+（1000－1）+（10000－1）

=10+100+1000+10000－4

=11106

练习1：

1计算1998+2997+4995+5994 2.计算19998+39996+49995+69996.

【例题2】计算489+487+483+485+484+486+488

【思路导航】认真观察每个加数，发现它们都和整数490接近，所以选490为基准数。

489+487+483+485+484+486+488

=490×7－1－3－7－5－6－4－2

=3430－28

=3402

想一想：如果选480为基准数，可以怎样计算？.

练习2：

1. 1032+1028+1033+1029+1031+1030

2.2451+2452+2446+245

速算与巧算

一、速算与巧算：

1、凑整与分拆

凑整：利用运算律将一些书凑成整一、整十或整百再计算。（分组凑整、加补凑整、基准数凑整）

例1：5

499999549999549995499549++++

分拆：为了计算方便，我们常常把一个数写成两个数或多个数的和差积的形式，这种方法叫分拆。

例2：29

1301573914017749150197?+?+?

2、提取公因数法

这个方法等同于课内所学的乘法分配律的逆运算。

例3：816.769.1184.214.345.1816.7?+?+?

例4：32.04868.61.36?+?

3、公式型计算

（1）基本公式

（2）平方类公式

（3）等差数列、等比数列公式

（4）特殊数列求和公式：①山顶和公式：1+2+3+4+……+n+……+3+2+1=2n

②奇数和公式：1+3+5+7+……+（2n-1）=2

③偶数和公式：2+4+6+……+2n=2n +n

④求和公式：1+2+3+……+n=2

)1(+?n n ⑤平方和公式：+++222321……+2n =6

)12)(1(++n n n ⑥立方和公式：+++333321……4)1(2

+=+n n n （5）几个特殊数的运算技巧：①1234321

111112*********

11222===

②ababab

ab abab ab =?=?10101101（这一类数我们称为“重码数”：循环重复的次数与1的个数相等，两个1之间所夹的0的个数比循环的位数少1.

③无“8”数：99

8112345679;3333333332712345679;2222222221812345679 ;111111111912345679=?=?=?=? 例5：670668666669668667??-??

速算与巧算方法

速算方法汇总

一、乘法

1. 几十乘十几：

口诀：头乘头，尾加尾，尾乘尾。

例：12×14=？12×14=168 （注：个位相乘，不够两位数要用0占位。）

2.头相同，尾互补(尾相加等于10)：

口诀：一个头加1后，头乘头，尾乘尾。

例：23×27=？23×27=621 （注：个位相乘，不够两位数要用0占位。）

3.第一个乘数互补，另一个乘数数字相同：

口诀：一个头加1后，头乘头，尾乘尾。

例：37×44=？

解：3+1=4

4×4=16

7×4=28

37×44=1628

注：个位相乘，不够两位数要用0占位。

4.几十一乘几十一：

口诀：头乘头，头加头，尾乘尾。

例：21×41=？

解：2×4=8

2+4=6

1×1=1

21×41=861

5.11乘任意数：

口诀：首尾不动下落，中间之和下拉。

例：11×23125=？

解：2+3=5

3+1=4

1+2=3

2+5=7

2和5分别在首尾

11×23125=254375

注：和满十要进一。

6.十几乘任意数：

口诀：第二乘数首位不动向下落，第一因数的个位乘以第二因数后面每一个数字，加下一位数，再向下落。

例：13×326=？

解：13个位是3

3×3+2=11

3×2+6=12

3×6=18

13×326=4238

注：和满十要进一。

2. 这种速算手法很奥妙，算起来也格外用意思，看待小学生来说，有助于建立一种全新研习思想，大概也会让不喜欢数学的孩子先导对数学爆发兴趣。还是那句老话，当作一种嗜好或者兴趣即可，不能以偏盖全。

3. 是速算专家周根项教授三十多年埋头商榷的效果。他用开创的“手指法”、“转换法”、“万能法”等轻易、易学、适用的兴趣运算方式，协助孩子完全研习没兴趣、做题速度慢、计算总出错、考试总丢分等研习题目。

速算和巧算

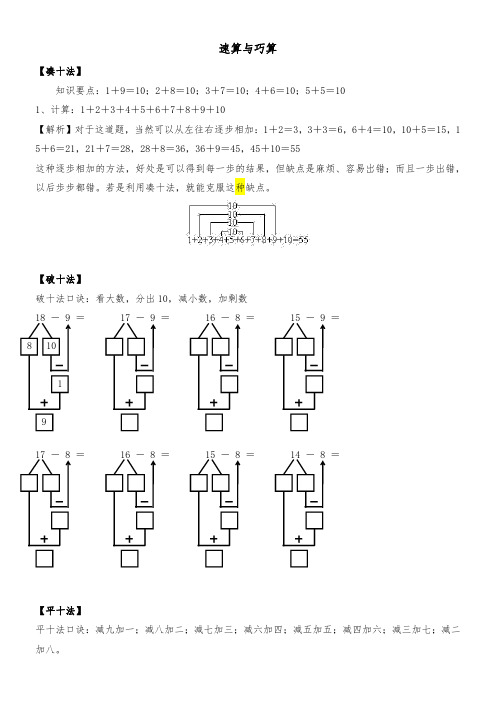
速算与巧算

【凑十法】

知识要点：1＋9＝10；2＋8＝10；3＋7＝10；4＋6＝10；5＋5＝10

1、计算：1＋2＋3＋4＋5＋6＋7＋8＋9＋10

【解析】对于这道题，当然可以从左往右逐步相加：1＋2＝3，3＋3＝6，6＋4＝10，10＋5＝15，1 5＋6＝21，21＋7＝28，28＋8＝36，36＋9＝45，45＋10＝55

这种逐歩相加的方法，好处是可以得到每一歩的结果，但缺点是麻烦、容易岀错；而且一歩出错，以后歩步都错。若是利用凑十法，就能克服这种缺点。

【破十法】

破十法口诀：看大数，分出10，减小数，加剩数

18－9＝17－9＝16－8＝15－9＝

810

17－8＝16－8＝15－8＝14－8＝

【平十法】

平十法口诀：减九加一；减八加二；减七加三；减六加四；减五加五；减四加六；减三加七；减二加八。

18－9＝17－9＝16－9＝15－9＝81

17－8＝16－8＝15－8＝14－8＝

【退十加补法】

18－9＝17－9＝16－9＝15－9＝101

17－8＝16－8＝15－8＝14－8＝【凑整法】

同学们还知道，有些数相加之和是整十、整百的数，如：

1＋19＝20；11＋19＝30；2＋18＝20；12＋28＝40；3＋17＝20；13＋37＝50

4＋16＝20；14＋46＝60；5＋15＝20；15＋55＝70；6＋14＝20；16＋64＝80

7＋13＝20；17＋73＝90；8＋12＝20；18＋82＝100；9＋11＝20

又如：

15＋85＝100；14＋86＝100；25＋75＝100；24＋76＝100

(完整版)常用的巧算和速算方法

小学数学速算与巧算方法例解【转】

速算与巧算

在小学数学中，关于整数、小数、分数的四则运算，怎么样才能算得既快又准确呢？这就需要我们熟练地掌握计算法则和运算顺序，根据题目本身的特点，综合应用各种运算定律和性质，或利用和、差、积、商变化规律及有关运算公式，选用合理、灵活的计算方法。速算和巧算不仅能简便运算过程，化繁为简，化难为易，同时又会算得又快又准确。

一、“凑整”先算

1.计算：（1）24+44+56

（2）53+36+47

解：（1）24+44+56=24+（44+56）

=24+100=124

这样想：因为44+56=100是个整百的数，所以先把它们的和算出来.

（2）53+36+47=53+47+36

=（53+47）+36=100+36=136

这样想：因为53+47=100是个整百的数，所以先把+47带着符号搬家，搬到+36前面；然后再把53+47的和算出来.

2.计算：（1）96+15

（2）52+69

解：（1）96+15=96+（4+11）

=（96+4）+11=100+11=111

这样想：把15分拆成15=4+11，这是因为96+4=100，可凑整先算.

（2）52+69=（21+31）+69

=21+（31+69）=21+100=121

这样想：因为69+31=100，所以把52分拆成21与31之和，再把31+69=100凑整先算.

3.计算：（1）63+18+19

（2）28+28+28

解：（1）63+18+19

=60+2+1+18+19

=60+（2+18）+（1+19）

=60+20+20=100

速算与巧算——精选推荐

速算与巧算

速算与巧算（⼀）

加减法中的巧算⽅法：1、运⽤运算律和运算性质；2、凑整；3、拆⼩补⼤；4、找准基数；5、数列求和等等。

练习：

1、147＋369＋353＋631 32＋81＋157＋19＋68

2、852－39－153－161 5613－（613+261）－239

3、656－289＋144－111 745＋(672－525)－572

4、537－（543－163）－57 756－576＋376＋244

5、659＋427－727－159 1256＋125＋875－256

6、9998＋3＋99＋998＋3＋9 9＋99＋999＋9999＋99999

7、75＋86＋83＋72＋78＋80＋81＋79＋87

8、1＋2＋3＋…＋9＋10＋9＋…＋3＋2＋1

速算与巧算⼆

乘除法的巧算主要靠乘法的运算律和除法的运算性质，并进⾏适当的扩展，使计算更灵活、合理；做到算得快、准。练习：

1、125×25×8×4 125×16×5

2、36×98 56×201

3、4400÷25÷4÷11 236＋1800÷（9×25）

4、720－198×25÷99×4 12000÷125＋325÷25

5、56×165÷7÷11 123×456÷789÷456×789÷123

7、9999×2222＋3333×3334 54＋99×99＋45

8、1÷（2÷3）÷（3÷4）÷（4÷5）÷（5÷6）

和差问题

1、和差问题基本模式：已知两个数的和与差，求两个数。

2、和差问题的基本关系式：

（和＋差）÷2=较⼤数（和－差）÷2=较⼩数

3、解题的关键要找准两个数的和与差。

小学生注意：10种最常见的速算与巧算方法！请收藏

数学速算法指利用数与数之间的特殊关系进行较快的加减乘除运算，这种运算方法称为速算法、心算法。

巧算或简算包括乘法，除法的分配律，结合律，交换律，加法交换、结合等，这需要在某个算式中找出，找到了可以应用的定律，及每个数的分解数，就可以巧妙地算出答案了。

让孩子学会速算和巧算，不仅可以提高孩子做题的准确度，更能让孩子的大脑反应明锐！今天，我特意整理了十种孩子们在学习过程中最常见的速算和巧算方法，希望各位家长抽空让孩子学习学习！

一、顺逆相加：用“顺逆相加”算式可求出若干个连续数的和。

二、凑整巧算：用“凑整方法”，常常能使计算变得比较简便、快速。

三、恒等变形：是一种重要的思想和方法，也是一种重要的解题技巧。

四、拆数加减：在分数加减法运算中，把一个分数拆成两个分数相减或相加，使隐含的数量关系明朗化，并抵消其中的一些分数，往

往可大大地简化运算。

（1）拆成两个分数相减。例如：

（2）拆成两个分数相加。例如：

五、先借后还：“先借后还”是一条重要的数学解题思想和解题技巧。

六、由小推大：一种数学思维方法，也是一种速算、巧算技巧。

七、巧妙试商：除数是两位数的除法，可以采用一些巧妙试商方法，提高计算速度。

八、同分子分数加减

九、个数折半：下面的几种情况下，可以运用“个数折半”的方

法，巧妙地计算出题目的得数

十、两分数相除：有些分数相除，可以采用以下的巧算方法。

速算与巧算大全

一、速算与巧算之凑整先算

【点拨】：加法、减法的简便计算中，基本思路是“凑整”，根据加法（乘法）的交换律、结合律以及减法的性质，其中若有能够凑整的，可以变更算式，使能凑整的数结成一对好朋友，进行凑整计算，能使计算简便。

例：298+304+196+502

【分析】：本题可以运用加法交换律和结合律，把能够凑成整十、整百、整千……的数先加起来，可以使计算简便。

【解答】：原式=（298+502）+（304+196）=800+500=1300

二、速算与巧算之带符号搬家

【点拨】：在加减混合，乘除混合同级运算中，可以根据运算的需要以及题目的特点，交换数字的位置，可以使计算变得简便。特别提醒的是：交换数字的位置，要注意运算符号也随之换位置。

例：464-545＋836-455

【分析】：观察例题我们会发现，如果按照惯例应该从左往右计算，464减545根本就不够减，在小学阶段，学生没办法做，所以要想做这道题，学生必须先观察数字特点，进行简便计算。

【解答】原式=464+836-545-455=1300-（545+455）=300

思考：4.75÷0.25-4.75能带符号搬家吗？什么情况下才能带符号搬家？带符号搬家需要注意什么？

三、速算与巧算之拆数凑整

【点拨】：根据运算定律和数字特点，常常灵活地把算式中的数拆分，重新组合，分别凑成整十、整百、整千。

例：998+1413+9989

【分析】：给998添上2能凑成1000，给9989添上11凑成10000，所以就把1413分成1400、2与11三个数的和。

【解答】原式==（998+2）+1400+（11+9989）=1000+1400+10000=12400 例：73.15×9.9

速算与巧算

第一讲速算与巧算（一）

【专题导引】

速算与巧算是计算中的一个重要组成部分，掌握一些速算与巧算的方法，有助于提高我们的计算能力和思维能力。这一周我们学习加、减法的巧算方法，这些方法主要根据加法、减法的运算定律和运算性质，通过对算式适当变形从而使计算简便。

在巧算方法里，蕴含着一种重要的解决问题的策略：转化问题法。即把所给的算式，根据运算定律和运算性质，或改变它的运算顺序，或凑整从而变成一个易于算出结果的算式。

【典型例题】

】计算：9+99+999

【C

【试一试】

1、计算：99+99+99

2、98+98+98

【C

】计算：49+18+39+78

【试一试】

1、计算：57+97+48

2、96+97+98

】计算：9+99+999+9999

【B

【试一试】

1、计算99999+9999+999+99+9 9+98+996+9997

2、计算19999+2998+396+497 198+297+396+495

【B

】计算：489+487+483+485+484+486+488

【试一试】

（1）50+52+53+54+51 （2）262+266+270+268+264 （3）89+94+92+95+93+94+88+96+87 （4）381+378+382+383+379 】计算下面各题。

【B

（1）632－136－232 （2）128+186+72－86

【试一试】

（1）1208－569－208 （2）283+69－183 】计算下面各题。

【A

（1）248 +（152－127）（2）324－（124－97）（3）283 +（358－183）

数学巧算速算方法

以下是一些常见的数学巧算速算方法：

1. 乘法速算：

- 相邻两位数相乘：如72 × 74 = 5376，先计算7 × 7 = 49，再计算2 × 4 = 8，最后将结果连接起来，得到5376。

- 一位数乘以11的倍数：如4 × 44 = 176，将原数首尾加起来得到第一位数（4 + 4 = 8），再将原数的个位数放在中间，得到结果176。

2. 除法速算：

- 除以10的倍数：如240 ÷ 30 = 8，将被除数末尾的0去掉，再将结果与被除数的个位数相乘，得到最终结果8。

- 除以2的倍数：如468 ÷ 12 = 39，将被除数每一位数相加得到和（4 + 6 + 8 = 18），再判断和是否能被12整除，如果可以，则商为和除以12，否则商加1。

3. 平方速算：

- 以5为基准的平方：如65² = 4225，将原数去掉个位数后乘以（原数加1），再在末尾加上25，得到结果4225。

- 以50为基准的平方：如57² = 3249，将原数去掉个位数后乘以（原数加1），再在末尾加上49，得到结果3249。

这些巧算速算方法可以帮助简化数学运算，提高计算速度。但需要注意的是，速算方法适用于简单的计算，对于复杂的计算仍然需要使用正常的计算方法。

小学四年级速算与巧算

第二讲速算与巧算(一)

一、考点、热点回顾

用简便方法计算：

（1）99999×88888÷11111 （2）1+2+3+…+99+100

知识要点：

1.若干个数排成一列称为数列。数列中的每一个数称为一项。其中第一项称为首项，最后一项称为末项，数列中项的个数称为项数。

2.从第二项开始，后项与其相邻的前项之差都相等的数列称为等差数列，后项与前项的差称为公差。

3.在这一章要用到两个非常重要的公式：“通项公式”和“项数公式”。

通项公式：第n项=首项+(项数-1)×公差

项数公式：项数=(末项-首项)÷公差+1

4.利用加法、减法的运算定律和运算性质使计算简便

5.根据乘、除法的运算定律和运算性质以及积、商的变化规律，通过对算式适当变形，将因数（或被除数、除数）转化成整百、整千的数，或者使算式中的一些数变得易于心算，从而简化计算。

6.用凑整和分解等方法进行乘、除法的速算。

教学重难点：

1.学生熟练加减乘除运算的基本性质，能随时想到变形，化复杂为简单。

2.要求学生了解运算的简单公式。用公式加快解题速度。

二、典型例题

例1用简便方法计算134859＋348591＋485913＋859134＋591348＋913485。(吉林省第九届小学数学邀请赛试题)

解：观察发现：各个数位上的数字都是“1、3、4、5、8、9”，所以

134859＋348591＋485913＋859134＋591348＋913485

＝111111×(1＋3＋4＋5＋8＋9)

＝111111×30＝3333330。

练习：245937+459372+593724+937245+372459+724593

速算与巧算

一、速算基础

在进行数学计算时，一般按“先乘除，后加减，括号优先”的顺序进行计算，但遇到一些计算题用常规运算比较麻烦时，就要考虑怎样更简便来计算。这就要求学生打破传统思维，运用发散思维，找出更好的解决办法，更快完成计算任务。

在计算时，利用数与数之间的特殊关系进行较快的加减乘除运算。这种运算方法称为速算法，也叫心算法。

1、速算要点

（1）找出最熟悉的速算数或接近数；如0、1、10、100、1000、10000.。。。。。。

（2）套用最基本的运算法则；

如：交换律、结合律、分配律、提取公因素、平方差、完全平方差等。

（3）牢记特殊数的计算方法。

如：111.。。。。111 X 111.。。。。。111=123.。。。。。321（位数小于等于9）

2、数学运算定律

（1）加法运算定律与性质

加法交换律：两个加数交换位置，和不变。

公式：a+b+c=(b+a)+c

加法结合律：先把前两个数相加或先把后两个数相加，再和另一个数相加，和不变。

公式：a+b+c=(a+b)+c=a+(b+c)

（2）乘法运算定律与性质

乘法交换律：两个因数交换位置，积不变。

公式：a x b=b x a

（3）乘法结合律：先把任意两个数相乘，再和另一个数相乘，积不变。

公式：a x b x c=(a x b) x c=a x (bxc)=(a x c)x b

（4）乘法分配律

两个数与一个数相乘，可以分别先把两个数分别与这一个数相乘，然后再要相加减。

公式：\(a+b) x c=a x c+b x c

(a-b) x c=a x c-b x c

2、减法运算定律与性质

最常用的巧算与速算方法

最常用的巧算和速算方法（1）

【顺逆相加】用“顺逆相加”算式可求出若干个连续数的和。例如著名的大数学家高斯（德国）小时候就做过的“百数求和”题，可以计算为：

1＋2＋3＋4＋……＋99＋100

＝（1+100）×100÷2

＝5050

1＋2＋3＋4+…….n ＝2

)1(n n ⨯+ 又如，计算“3+5+7+………＋97+99=？”，可以计算为：

3+5＋7＋……＋97+99=（99＋3）×49÷2= 2499

我们要注意它全是奇数，只是没有1，所以是49个数。

1+3+5＋7＋……＋97+99，同学们应该能算出来了吗？

【凑整巧算】用“凑整方法”巧算，常常能使计算变得比较简便、快速。例如：

1、加法“凑整”。利用加法交换律、结合律“凑整”，例如： 4673＋27689＋5327＋22311 99.9+11.1

=（4673＋5327）＋（27689＋22311）=（90＋10）+（9+1）＋（0.9+0.1） = 10000＋50000 =111

= 60000

9＋97＋998＋6

=（9+1）＋（97＋3）＋（998＋2）

=10＋100＋1000

=1110

2、减法“凑整”。利用减法性质“凑整”，例如：

3842－1562－438－842

= 3842－842－（1562+438）

= 3000－2000

= 1000

3、乘法“凑整”。利用乘法交换律、结合律、分配律“凑整”，

例如：

125×32×25

=125×4×8×25

=（125×4）×（25×8）

=500×200

=100000

125＋125＋125＋125＋120＋125＋125＋125

常用的巧算和速算方法

小学数学速算与巧算方法例解【转】

速算与巧算

一、“凑整”先算

1.计算：（1）24+44+56

（2）53+36+47

解：（1）24+44+56=24+（44+56）

=24+100=124

这样想：因为44+56=100是个整百的数，所以先把它们的和算出来.

（2）53+36+47=53+47+36

=（53+47）+36=100+36=136

这样想：因为53+47=100是个整百的数，所以先把+47带着符号搬家，搬到+36前面；然后再把53+47的和算出来.

2.计算：（1）96+15

（2）52+69

解：（1）96+15=96+（4+11）

=（96+4）+11=100+11=111

这样想：把15分拆成15=4+11，这是因为96+4=100，可凑整先算.

（2）52+69=（21+31）+69

=21+（31+69）=21+100=121

这样想：因为69+31=100，所以把52分拆成21与31之和，再把31+69=100凑整先算.

3.计算：（1）63+18+19

（2）28+28+28

解：（1）63+18+19

=60+2+1+18+19

=60+（2+18）+（1+19）

=60+20+20=100

常用的巧算和速算方法

小学数学速算与巧算方法例解【转】

速算与巧算

一、“凑整〞先算1.计算：〔1〕24+44+56

〔2〕53+36+47

解：〔1〕24+44+56=24+〔44+56〕=24+100=124

这样想：因为44+56=100是个整百的数，所以先把它们的和算出来.

〔2〕53+36+47=53+47+36

=〔53+47〕+36=100+36=136

这样想：因为53+47=100是个整百的数，所以先把+47带着符号搬家，搬到+36前面；然后再把53+47的和算出来.

2.计算：〔1〕96+15

〔2〕52+69

解：〔1〕96+15=96+〔4+11〕=〔96+4〕+11=100+11=111 这样想：把15分拆成15=4+11，这是因为96+4=100，可凑整先算.

〔2〕52+69=〔21+31〕+69

=21+〔31+69〕=21+100=121

这样想：因为69+31=100，所以把52分拆成21与31之和，再把31+69=100凑整先算.

3.计算：〔1〕63+18+19

〔2〕28+28+28

解：〔1〕63+18+19

=60+2+1+18+19

=60+〔2+18〕+〔1+19〕=60+20+20=100

常用的巧算和速算方法

小学数学速算与巧算方法例解【转】

速算与巧算

一、“凑整”先算

1.计算：（1）24+44+56

（2）53+36+47

解：（1）24+44+56=24+（44+56）

=24+100=124

这样想：因为44+56=100是个整百的数，所以先把它们的和算出来.

（2）53+36+47=53+47+36

=（53+47）+36=100+36=136

这样想：因为53+47=100是个整百的数，所以先把+47带着符号搬家，搬到+36前面；然后再把53+47的和算出来.

2.计算：（1）96+15

（2）52+69

解：（1）96+15=96+（4+11）

=（96+4）+11=100+11=111

这样想：把15分拆成15=4+11，这是因为96+4=100，可凑整先算.

（2）52+69=（21+31）+69

=21+（31+69）=21+100=121

这样想：因为69+31=100，所以把52分拆成21与31之和，再把31+69=100凑整先算.

3.计算：（1）63+18+19

（2）28+28+28

解：（1）63+18+19

=60+2+1+18+19

=60+（2+18）+（1+19）

=60+20+20=100