2018年中考数学专题复习卷《圆的有关知识》

合集下载

2018中考数学试题分类汇编考点28 圆的有关概念(含解析)

2018中考数学试题分类汇编：考点28圆的有关概念一．选择题（共26小题）1．（2018•安顺）已知⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB=8cm，则AC的长为（）A．2cm B．4cm C．2cm或4cm D．2cm或4cm【分析】先根据题意画出图形，由于点C的位置不能确定，故应分两种情况进行讨论．【解答】解：连接AC，AO，∵⊙O的直径CD=10cm，AB⊥CD，AB=8cm，∴AM=AB=×8=4cm，OD=OC=5cm，当C点位置如图1所示时，∵OA=5cm，AM=4cm，CD⊥AB，∴OM===3cm，∴CM=OC+OM=5+3=8cm，∴AC===4cm；当C点位置如图2所示时，同理可得OM=3cm，∵OC=5cm，∴MC=5﹣3=2cm，在Rt△AMC中，AC===2cm．故选：C．2．（2018•聊城）如图，⊙O中，弦BC与半径OA相交于点D，连接AB，O C．若∠A=60°，∠ADC=85°，则∠C的度数是（）A．25°B．27.5°C．30°D．35°【分析】直接利用三角形外角的性质以及邻补角的关系得出∠B以及∠ODC度数，再利用圆周角定理以及三角形内角和定理得出答案．【解答】解：∵∠A=60°，∠ADC=85°，∴∠B=85°﹣60°=25°，∠CDO=95°，∴∠AOC=2∠B=50°，∴∠C=180°﹣95°﹣50°=35°故选：D．3．（2018•张家界）如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=（）A．8cm B．5cm C．3cm D．2cm【分析】根据垂径定理可得出CE的长度，在Rt△OCE中，利用勾股定理可得出OE的长度，再利用AE=AO+OE即可得出AE的长度．【解答】解：∵弦CD⊥AB于点E，CD=8cm，∴CE=CD=4cm．在Rt△OCE中，OC=5cm，CE=4cm，∴OE==3cm，∴AE=AO+OE=5+3=8cm．故选：A．4．（2018•菏泽）如图，在⊙O中，OC⊥AB，∠ADC=32°，则∠OBA的度数是（）A．64°B．58°C．32°D．26°【分析】根据垂径定理，可得=，∠OEB=90°，根据圆周角定理，可得∠3，根据直角三角形的性质，可得答案．【解答】解：如图，由OC⊥AB，得=，∠OEB=90°．∴∠2=∠3．∵∠2=2∠1=2×32°=64°．∴∠3=64°，在Rt△OBE中，∠OEB=90°，∴∠B=90°﹣∠3=90°﹣64°=26°，故选：D．5．（2018•白银）如图，⊙A过点O（0，0），C（，0），D（0，1），点B是x轴下方⊙A上的一点，连接BO，BD，则∠OBD的度数是（）A．15°B．30°C．45°D．60°【分析】连接DC，利用三角函数得出∠DCO=30°，进而利用圆周角定理得出∠DBO=30°即可．【解答】解：连接DC，∵C（，0），D（0，1），∴∠DOC=90°，OD=1，OC=，∴∠DCO=30°，∴∠OBD=30°，故选：B．6．（2018•襄阳）如图，点A，B，C，D都在半径为2的⊙O上，若OA⊥BC，∠CDA=30°，则弦BC的长为（）A．4 B．2C．D．2【分析】根据垂径定理得到CH=BH，=，根据圆周角定理求出∠AOB，根据正弦的定义求出BH，计算即可．【解答】解：∵OA⊥BC，∴CH=BH，=，∴∠AOB=2∠CDA=60°，∴BH=OB•sin∠AOB=，∴BC=2BH=2，故选：D．7．（2018•济宁）如图，点B，C，D在⊙O上，若∠BCD=130°，则∠BOD的度数是（）A．50°B．60°C．80°D．100°【分析】首先圆上取一点A，连接AB，AD，根据圆的内接四边形的性质，即可得∠BAD+∠BCD=180°，即可求得∠BAD的度数，再根据圆周角的性质，即可求得答案．【解答】解：圆上取一点A，连接AB，AD，∵点A、B，C，D在⊙O上，∠BCD=130°，∴∠BAD=50°，∴∠BOD=100°，故选：D．8．（2018•通辽）已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是（）A．30°B．60°C．30°或150°D．60°或120°【分析】由图可知，OA=10，OD=5．根据特殊角的三角函数值求角度即可．【解答】解：由图可知，OA=10，OD=5，在Rt△OAD中，∵OA=10，OD=5，AD=，∴tan∠1=，∠1=60°，同理可得∠2=60°，∴∠AOB=∠1+∠2=60°+60°=120°，∴圆周角的度数是60°或120°．故选：D．9．（2018•南充）如图，BC是⊙O的直径，A是⊙O上的一点，∠OAC=32°，则∠B的度数是（）A．58°B．60°C．64°D．68°【分析】根据半径相等，得出OC=OA，进而得出∠C=32°，利用直径和圆周角定理解答即可．【解答】解：∵OA=OC，∴∠C=∠OAC=32°，∵BC是直径，∴∠B=90°﹣32°=58°，故选：A．10．（2018•铜仁市）如图，已知圆心角∠AOB=110°，则圆周角∠ACB=（）A．55°B．110°C．120°D．125°【分析】根据圆周角定理进行求解．一条弧所对的圆周角等于它所对的圆心角的一半．【解答】解：根据圆周角定理，得∠ACB=（360°﹣∠AOB）=×250°=125°．故选：D．11．（2018•临安区）如图，⊙O的半径OA=6，以A为圆心，OA为半径的弧交⊙O于B、C点，则BC=（）A．B．C．D．【分析】根据垂径定理先求BC一半的长，再求BC的长．【解答】解：设OA与BC相交于D点．∵AB=OA=OB=6∴△OAB是等边三角形．又根据垂径定理可得，OA平分BC，利用勾股定理可得BD==3所以BC=6．故选：A．12．（2018•贵港）如图，点A，B，C均在⊙O上，若∠A=66°，则∠OCB的度数是（）A．24°B．28°C．33°D．48°【分析】首先利用圆周角定理可得∠COB的度数，再根据等边对等角可得∠OCB=∠OBC，进而可得答案．【解答】解：∵∠A=66°，∴∠COB=132°，∵CO=BO，∴∠OCB=∠OBC=（180°﹣132°）=24°，故选：A．13．（2018•威海）如图，⊙O的半径为5，AB为弦，点C为的中点，若∠ABC=30°，则弦AB的长为（）A．B．5 C．D．5【分析】连接OC、OA，利用圆周角定理得出∠AOC=60°，再利用垂径定理得出AB即可．【解答】解：连接OC、OA，∵∠ABC=30°，∴∠AOC=60°，∵AB为弦，点C为的中点，∴OC⊥AB，在Rt△OAE中，AE=，∴AB=，故选：D．14．（2018•盐城）如图，AB为⊙O的直径，CD是⊙O的弦，∠ADC=35°，则∠CAB的度数为（）A．35°B．45°C．55°D．65°【分析】根据圆周角定理得到∠ABC=∠ADC=35°，∠ACB=90°，根据三角形内角和定理计算即可．【解答】解：由圆周角定理得，∠ABC=∠ADC=35°，∵AB为⊙O的直径，∴∠ACB=90°，∴∠CAB=90°﹣∠ABC=55°，故选：C．15．（2018•淮安）如图，点A、B、C都在⊙O上，若∠AOC=140°，则∠B的度数是（）A．70°B．80°C．110°D．140°【分析】作对的圆周角∠APC，如图，利用圆内接四边形的性质得到∠P=40°，然后根据圆周角定理求∠AOC的度数．【解答】解：作对的圆周角∠APC，如图，∵∠P=∠AOC=×140°=70°∵∠P+∠B=180°，∴∠B=180°﹣70°=110°，故选：C．16．（2018•咸宁）如图，已知⊙O的半径为5，弦AB，CD所对的圆心角分别是∠AOB，COD，若∠AOB与∠COD互补，弦CD=6，则弦AB的长为（）A．6 B．8 C．5D．5【分析】延长AO交⊙O于点E，连接BE，由∠AOB+∠BOE=∠AOB+∠COD知∠BOE=∠COD，据此可得BE=CD=6，在Rt△ABE中利用勾股定理求解可得．【解答】解：如图，延长AO交⊙O于点E，连接BE，则∠AOB+∠BOE=180°，又∵∠AOB+∠COD=180°，∴∠BOE=∠COD，∴BE=CD=6，∵AE为⊙O的直径，∴∠ABE=90°，∴AB===8，故选：B．17．（2018•衢州）如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（）A．75°B．70°C．65°D．35°【分析】直接根据圆周角定理求解．【解答】解：∵∠ACB=35°，∴∠AOB=2∠ACB=70°．故选：B．18．（2018•柳州）如图，A，B，C，D是⊙O上的四个点，∠A=60°，∠B=24°，则∠C的度数为（）A．84°B．60°C．36°D．24°【分析】直接利用圆周角定理即可得出答案．【解答】解：∵∠B与∠C所对的弧都是，∴∠C=∠B=24°，故选：D．19．（2018•邵阳）如图所示，四边形ABCD为⊙O的内接四边形，∠BCD=120°，则∠BOD 的大小是（）A．80°B．120°C．100°D．90°【分析】根据圆内接四边形的性质求出∠A，再根据圆周角定理解答．【解答】解：∵四边形ABCD为⊙O的内接四边形，∴∠A=180°﹣∠BCD=60°，由圆周角定理得，∠BOD=2∠A=120°，故选：B．20．（2018•苏州）如图，AB是半圆的直径，O为圆心，C是半圆上的点，D是上的点，若∠BOC=40°，则∠D的度数为（）A．100°B．110°C．120°D．130°【分析】根据互补得出∠AOC的度数，再利用圆周角定理解答即可．【解答】解：∵∠BOC=40°，∴∠AOC=180°﹣40°=140°，∴∠D=，故选：B．21．（2018•台湾）如图，坐标平面上，A、B两点分别为圆P与x轴、y轴的交点，有一直线L通过P点且与AB垂直，C点为L与y轴的交点．若A、B、C的坐标分别为（a，0），（0，4），（0，﹣5），其中a＜0，则a的值为何？（）A．﹣2B．﹣2C．﹣8 D．﹣7【分析】连接AC，根据线段垂直平分线的性质得到AC=BC，根据勾股定理求出OA，得到答案．【解答】解：连接AC，由题意得，BC=OB+OC=9，∵直线L通过P点且与AB垂直，∴直线L是线段AB的垂直平分线，∴AC=BC=9，在Rt△AOC中，AO==2，∵a＜0，∴a=﹣2，故选：A．22．（2018•衢州）如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC 于F，若BD=8cm，AE=2cm，则OF的长度是（）A．3cm B．cm C．2.5cm D．cm【分析】根据垂径定理得出OE的长，进而利用勾股定理得出BC的长，再利用相似三角形的判定和性质解答即可．【解答】解：连接OB，∵AC是⊙O的直径，弦BD⊥AO于E，BD=8cm，AE=2cm，在Rt△OEB中，OE2+BE2=OB2，即OE2+42=（OE+2）2解得：OE=3，∴OB=3+2=5，∴EC=5+3=8，在Rt△EBC中，BC=，∵OF⊥BC，∴∠OFC=∠CEB=90°，∵∠C=∠C，∴△OFC∽△BEC，∴，即，解得：OF=，故选：D．23．（2018•青岛）如图，点A、B、C、D在⊙O上，∠AOC=140°，点B是的中点，则∠D的度数是（）A．70°B．55°C．35.5°D．35°【分析】根据圆心角、弧、弦的关系定理得到∠AOB=∠AOC，再根据圆周角定理解答．【解答】解：连接OB，∵点B是的中点，∴∠AOB=∠AOC=70°，由圆周角定理得，∠D=∠AOB=35°，故选：D．24．（2018•广州）如图，AB是⊙O的弦，OC⊥AB，交⊙O于点C，连接OA，OB，BC，若∠ABC=20°，则∠AOB的度数是（）A．40°B．50°C．70°D．80°【分析】根据圆周角定理得出∠AOC=40°，进而利用垂径定理得出∠AOB=80°即可．【解答】解：∵∠ABC=20°，∴∠AOC=40°，∵AB是⊙O的弦，OC⊥AB，∴∠AOC=∠BOC=40°，∴∠AOB=80°，故选：D．25．（2018•遂宁）如图，在⊙O中，AE是直径，半径OC垂直于弦AB于D，连接BE，若AB=2，CD=1，则BE的长是（）A．5 B．6 C．7 D．8【分析】根据垂径定理求出AD，根据勾股定理列式求出OD，根据三角形中位线定理计算即可．【解答】解：∵半径OC垂直于弦AB，∴AD=DB=AB=，在Rt△AOD中，OA2=（OC﹣CD）2+AD2，即OA2=（OA﹣1）2+（）2，解得，OA=4∴OD=OC﹣CD=3，∵AO=OE，AD=DB，∴BE=2OD=6，故选：B．26．（2018•钦州三模）如图，BC是⊙O的弦，OA⊥BC，∠AOB=70°，则∠ADC的度数是（）A．70°B．35°C．45°D．60°【分析】欲求∠ADC，又已知一圆心角，可利用圆周角与圆心角的关系求解．【解答】解：∵A、B、C、D是⊙O上的四点，OA⊥BC，∴弧AC=弧AB（垂径定理），∴∠ADC=∠AOB（等弧所对的圆周角是圆心角的一半）；又∠AOB=70°，∴∠ADC=35°．故选：B．二．填空题（共13小题）27．（2018•孝感）已知⊙O的半径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB=16cm，CD=12cm，则弦AB和CD之间的距离是2或14cm．【分析】分两种情况进行讨论：①弦AB和CD在圆心同侧；②弦AB和CD在圆心异侧；作出半径和弦心距，利用勾股定理和垂径定理求解即可，小心别漏解．【解答】解：①当弦AB和CD在圆心同侧时，如图，∵AB=16cm，CD=12cm，∴AE=8cm，CF=6cm，∵OA=OC=10cm，∴EO=6cm，OF=8cm，∴EF=OF﹣OE=2cm；②当弦AB和CD在圆心异侧时，如图，∵AB=16cm，CD=12cm，∴AF=8cm，CE=6cm，∵OA=OC=10cm，∴OF=6cm，OE=8cm，∴EF=OF+OE=14cm．∴AB与CD之间的距离为14cm或2cm．故答案为：2或14．28．（2018•曲靖）如图：四边形ABCD内接于⊙O，E为BC延长线上一点，若∠A=n°，则∠DCE=n°．【分析】利用圆内接四边形的对角互补和邻补角的性质求解．【解答】解：∵四边形ABCD是⊙O的内接四边形，∴∠A+∠DCB=180°，又∵∠DCE+∠DCB=180°∴∠DCE=∠A=n°故答案为：n29．（2018•南通模拟）如图，AB是⊙O的直径，点C是⊙O上的一点，若BC=3，AB=5，OD⊥BC于点D，则OD的长为2．【分析】先利用圆周角定理得到∠ACB=90°，则可根据勾股定理计算出AC=4，再根据垂径定理得到BD=CD，则可判断OD为△ABC的中位线，然后根据三角形中位线性质求解．【解答】解：∵AB是⊙O的直径，∴∠ACB=90°，∴AC==4，∵OD⊥BC，∴BD=CD，而OB=OA，∴OD为△ABC的中位线，∴OD=AC=×4=2．故答案为2．30．（2018•北京）如图，点A，B，C，D在⊙O上，=，∠CAD=30°，∠ACD=50°，则∠ADB=70°．【分析】直接利用圆周角定理以及结合三角形内角和定理得出∠ACB=∠ADB=180°﹣∠CAB ﹣∠ABC，进而得出答案．【解答】解：∵=，∠CAD=30°，∴∠CAD=∠CAB=30°，∴∠DBC=∠DAC=30°，∵∠ACD=50°，∴∠ABD=50°，∴∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°．故答案为：70°．31．（2018•杭州）如图，AB是⊙O的直轻，点C是半径OA的中点，过点C作DE⊥AB，交⊙O于D，E两点，过点D作直径DF，连结AF，则∠DFA=30°．【分析】利用垂径定理和三角函数得出∠CDO=30°，进而得出∠DOA=60°，利用圆周角定理得出∠DFA=30°即可．【解答】解：∵点C是半径OA的中点，∴OC=OD，∵DE⊥AB，∴∠CDO=30°，∴∠DOA=60°，∴∠DFA=30°，故答案为：30°32．（2018•吉林）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC= 29度．【分析】根据∠BDC=∠BOC求解即可；【解答】解：连接O C．∵=，∴∠AOB=∠BOC=58°，∴∠BDC=∠BOC=29°，故答案为29．33．（2018•烟台）如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C在格点（两条网格线的交点叫格点）上，以点O为原点建立直角坐标系，则过A，B，C 三点的圆的圆心坐标为（﹣1，﹣2）．【分析】连接CB，作CB的垂直平分线，根据勾股定理和半径相等得出点O的坐标即可．【解答】解：连接CB，作CB的垂直平分线，如图所示：在CB的垂直平分线上找到一点D，CD═DB=DA=，所以D是过A，B，C三点的圆的圆心，即D的坐标为（﹣1，﹣2），故答案为：（﹣1，﹣2），34．（2018•无锡）如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA=AB，则∠ABC=15°．【分析】根据等边三角形的判定和性质，再利用圆周角定理解答即可．【解答】解：∵OA=OB，OA=AB，∴OA=OB=AB，即△OAB是等边三角形，∴∠AOB=60°，∵OC⊥OB，∴∠COB=90°，∴∠COA=90°﹣60°=30°，∴∠ABC=15°，故答案为：15°35．（2018•广东）同圆中，已知弧AB所对的圆心角是100°，则弧AB所对的圆周角是50°．【分析】直接利用圆周角定理求解．【解答】解：弧AB所对的圆心角是100°，则弧AB所对的圆周角为50°．故答案为50°．36．（2018•黑龙江）如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD=6，EB=1，则⊙O的半径为5．【分析】连接OC，由垂径定理知，点E是CD的中点，AE=CD，在直角△OCE中，利用勾股定理即可得到关于半径的方程，求得圆半径即可．【解答】解：连接OC，∵AB为⊙O的直径，AB⊥CD，∴CE=DE=CD=×6=3，设⊙O的半径为xcm，则OC=xcm，OE=OB﹣BE=x﹣1，在Rt△OCE中，OC2=OE2+CE2，∴x2=32+（x﹣1）2，解得：x=5，∴⊙O的半径为5，故答案为：5．37．（2018•绍兴）如图，公园内有一个半径为20米的圆形草坪，A，B是圆上的点，O为圆心，∠AOB=120°，从A到B只有路，一部分市民为走“捷径”，踩坏了花草，走出了一条小路A B．通过计算可知，这些市民其实仅仅少B走了15步（假设1步为0.5米，结果保留整数）．（参考数据：≈1.732，π取3.142）【分析】作OC⊥AB于C，如图，根据垂径定理得到AC=BC，再利用等腰三角形的性质和三角形内角和计算出∠A=30°，则OC=10，AC=10，所以AB≈69（步），然后利用弧长公式计算出的长，最后求它们的差即可．【解答】解：作OC⊥AB于C，如图，则AC=BC，∵OA=OB，∴∠A=∠B=（180°﹣∠AOB）=（180°﹣120°）=30°，在Rt△AOC中，OC=OA=10，AC=OC=10，∴AB=2AC=20≈69（步）；而的长=≈84（步），的长与AB的长多15步．所以这些市民其实仅仅少B走了15步．故答案为15．38．（2018•随州）如图，点A，B，C在⊙O上，∠A=40度，∠C=20度，则∠B=60度．【分析】连接OA，根据等腰三角形的性质得到∠OAC=∠C=20°，根据等腰三角形的性质解答即可．【解答】解：如图，连接OA，∵OA=OC，∴∠OAC=∠C=20°，∴∠OAB=60°，∵OA=OB，∴∠B=∠OAB=60°，故答案为：60．39．（2018•金华）如图1是小明制作的一副弓箭，点A，D分别是弓臂BAC与弓弦BC的中点，弓弦BC=60cm．沿AD方向拉动弓弦的过程中，假设弓臂BAC始终保持圆弧形，弓弦不伸长．如图2，当弓箭从自然状态的点D拉到点D1时，有AD1=30cm，∠B1D1C1=120°．（1）图2中，弓臂两端B1，C1的距离为30cm．（2）如图3，将弓箭继续拉到点D2，使弓臂B2AC2为半圆，则D1D2的长为10﹣10cm．【分析】（1）如图1中，连接B1C1交DD1于H．解直角三角形求出B1H，再根据垂径定理即可解决问题；（2）如图3中，连接B1C1交DD1于H，连接B2C2交DD2于G．利用弧长公式求出半圆半径即可解决问题；【解答】解：（1）如图2中，连接B1C1交DD1于H．∵D1A=D1B1=30∴D1是的圆心，∵AD1⊥B1C1，∴B1H=C1H=30×sin60°=15，∴B1C1=30∴弓臂两端B1，C1的距离为30（2）如图3中，连接B1C1交DD1于H，连接B2C2交DD2于G．设半圆的半径为r，则πr=，∴r=20，∴AG=GB2=20，GD1=30﹣20=10，在Rt△GB2D2中，GD2==10∴D1D2=10﹣10．故答案为30，10﹣10，三．解答题（共1小题）40．（2018•宜昌）如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，F C．（1）求证：四边形ABFC是菱形；（2）若AD=7，BE=2，求半圆和菱形ABFC的面积．【分析】（1）根据对角线相互平分的四边形是平行四边形，证明是平行四边形，再根据邻边相等的平行四边形是菱形即可证明；（2）设CD=x，连接B D．利用勾股定理构建方程即可解决问题；【解答】（1）证明：∵AB是直径，∴∠AEB=90°，∴AE⊥BC，∵AB=AC，∴BE=CE，∵AE=EF，∴四边形ABFC是平行四边形，∵AC=AB，∴四边形ABFC是菱形．（2）设CD=x．连接B D．∵AB是直径，∴∠ADB=∠BDC=90°，∴AB2﹣AD2=CB2﹣CD2，∴（7+x）2﹣72=42﹣x2，解得x=1或﹣8（舍弃）∴AC=8，BD==，∴S菱形ABFC=8．∴S半圆=•π•42=8π．。

河南2018中考数学总复习专题检测：圆(含答案)

圆(建议时间：90分钟总分：100分)一、选择题(本大题共7个小题，每小题4分，共28分)1．如图，△ABC内接于⊙O，若∠A＝α，则∠OBC等于(D) A．180°－2αB．2αC．90°＋αD．90°－α第1题图第2题图2．如图，AB是⊙O的直径，P A切⊙O于点A，PO交⊙O于点C.连接BC，若∠P＝40°，则∠B等于(B)A．20°B．25°C．30°D．40°3．如图，四边形ABCD内接于⊙O，AB经过圆心，∠B＝3∠BAC，则∠ADC等于(B)A．100°B．112.5°C．120°D．135°第3题图第5题图4．已知圆锥的底面面积为9π cm2，母线长为6 cm，则圆锥的侧面积是(A) A．18π cm2B．27π cm2C．18 cm2D．27 cm2 5．如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A＝15°，半径为2，则弦CD的长为(A)A．2 B．－1 C.2D．46．已知一个扇形的圆心角为60°，它所对的弧长为2π cm，则这个扇形的半径为(A)A ．6 cmB ．12cmC ．2 3 cm D. 6 cm7．如图，AB 是⊙O 的直径，C ，D 是⊙O 上的点，且OC ∥BD ，AD 分别与BC ，OC 相交于点E ，F ，则下列结论：①AD ⊥BD ；②∠AOC ＝∠AEC ；③BC 平分∠ABD ；④AF ＝DF ；⑤DB ＝2OF ； ⑥△CEF ≌△BED ，其中一定成立的是( D )A ．②④⑤⑥B ．①③⑤⑥C ．②③④⑥D ．①③④⑤二、填空题(本大题共6个小题，每小题4分，共24分)8．如图，AB 是⊙O 的直径，AC 与⊙O 相切，CO 交⊙O 于点D .若∠CAD ＝30°，则∠BOD ＝ 120 °.第8题图第9题图 9．如图，AB 为⊙O 的直径，C ，D 为⊙O 上的点，︵AD ＝︵CD .若∠CAB ＝40°，则∠CAD ＝ 25° .10．在半径为20的⊙O 中，弦AB ＝32，点P 在弦AB 上，且OP ＝15，则AP ＝7或25 .11．如图，小明自制一块乒乓球拍，正面是半径为8 cm 的⊙O ，︵AB ＝90°，弓形ACB (阴影部分)粘贴胶皮，则胶皮面积为 (48π＋32)cm 2 .第11题图第12题图12．如图，扇形OAB中，∠AOB＝60°，扇形半径为4，点C在︵AB上，CD⊥OA，垂足为点D，当△OCD的面积最大时，图中阴影部分的面积为2π－4. 13．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝1，E为BC边上的一点，以A为圆心，AE为半径的圆弧交AB于点D，交AC的延长线于点F，若图中两个阴影部分的面积相等，则AF的长为π(结果保留根号)．三、解答题(本大题共4个小题，共48分)14．(12分)如图，⊙O是△ABC的外接圆，BC为⊙O的直径，点E为△ABC的内心，连接AE并延长交⊙O于D点，连接BD并延长至F，使得BD＝DF，连接CF，BE.(1)求证：DB＝DE；(2)求证：直线CF为⊙O的切线．证明：(1)∵E是△ABC的内心，∴∠BAE＝∠CAE，∠EBA＝∠EBC.∵∠BED＝∠BAE＋∠EBA，∠DBE＝∠EBC＋∠DBC，∠DBC＝∠EAC，∴∠DBE＝∠DEB，∴DB＝DE；(2)连接CD ，如解图所示．∵E 是△ABC 的内心，∴∠DAB ＝∠DAC ，∴BD ＝CD .∵BD ＝DF ，∴CD ＝DB ＝DF ，∴∠BCF ＝90°，∴BC ⊥CF ，∴CF 是⊙O 的切线．15．(12分)如图，AB 为⊙O 的直径，C ，D 为⊙O 上两点，∠BAC ＝∠DAC ，过点C 作直线EF ⊥AD ，交AD 的延长线于点E ，连接BC .(1)求证：EF 是⊙O 的切线；(2)若DE ＝1，BC ＝2，求劣弧BC ︵)的长l .(1)证明：连接OC ，如解图所示．∵OA ＝OC ，∴∠OAC ＝∠OCA .又∵∠OAC ＝∠DAC ，∴∠DAC ＝∠OCA ，∴AD ∥OC .∵EF ⊥AD ，∴EF ⊥OC ，∴EF 是⊙O 的切线；。

2018中考数学中考数学复习模块4圆之典型中考题讲解有详细答案.docx

《中考数学复习模块4•圆》之典型中考题讲解1、（2017-金华）如图，已知：AB是的直径，点C在（DO上，CD是（DO的切线，AD丄CD于点D.E是AB延长线上一点，CE交（DO于点F,连结OC,AC.（1）求证:AC平分ZDA0.（2）若ZDAO=105°, ZE=30°.①求ZOCE的度数.②若的半径为2运，求线段EF的长.2、（2017浙江台州）.如图，已知等腰直角三角形ABC,点P是斜边BC 上一点（不与B, C重合），PE是△ ABP的外接圆（DO的直径.（1）求证：△ APE是等腰直角三角形；（2）若的直径为2,求PC2+PB2的值.3、（2017山东枣庄）.如图，在△ ABC中，ZC=90°, ZBAC的平分线交BC于点D,点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D,分别交AC, AB于点E, F.（1）试判断直线BC与。

0的位置关系，并说明理由；（2）若BD=2V3, BF=2,求阴影部分的面积（结果保留兀）. 4、（2017山东聊城）.如图，OO是△ ABC的外接圆，O点在BC边上，ZBAC的平分线交于点D,连接BD、CD,过点D 作BC的平行线，与AB的延长线相交于点P.（1）求证：PD是（DO的切线；（2）求证：APBDsADCA；D （3）当AB=6, AO8时，求线段PB的长.5、（2017山东东营）.如图，在△ ABC中，AB=AC,以AB为直径的（DO交BC于点D,过点D作的切线DE,交AC于点E, AC 的反向延长线交于点F.（1）求证：DE丄AG；（2）若DE+EA=8, OO的半径为10,求AF的长度.6、（2017山东潍坊）.如图，AB为半圆O的直径，AC是（DO 的一条弦，D为辰的中点，作DE丄AC,交AB的延长线于点F,连接DA.（1）求证：EF为半圆O的切线；（2）若DA=DF=6J5,求阴影区域的面积.（结果保留根号和兀）7、（2017江苏无锡）.如图，以原点O为圆心，3为半径的圆与x轴分别交于4, B两点（点B在点4的右边），P是半径OB上一点，过P且垂直于AB的直线与分别交于C, D两点（点C在点D的上方），直线AC, DB交于点E.若AC：CE=1： 2.（1）求点P的坐标；（2）求过点4和点E,且顶点在直线CD上的抛物线的函数表达式.8、（2017江苏盐城）.如图，在平面直角坐标系中，RtA ABC的斜边AB在y 轴9、(2017湖北襄阳).如图，AB为(DO的直径，C、D为©O ±的两点，ZBAOZDAC,过点C做直线EF丄AD,交AD的延长线于点E,连接BC.(1)求证：EF是(DO的切线；(2)若DE=1, BC=2,求劣弧晓的长1.10、(2017湖北恩施).如图，AB、CD是(DO的直径，BE是(DO 的弦，且BE〃CD,过点C的切线与EB的延长线交于点P,连接BC.(1)求证：BC平分ZABP；(2)求证：PC2=PB«PE；(3)若BE-BP=PC=4,求(DO 的半径.11、（2017 湖北随州）.如图，在RtA ABC 中，ZC=90°, AC=BC,点O在AB上，经过点A的（DO与BC相切于点D,交AB于点E.（1）求证：AD平分ZBAC；（2）若CD=1,求图中阴影部分的面积（结果保留兀）.12、（2017湖北宜昌）.已知，四边形ABCD中，E是对角线AC上一点，DE=EC, 以AE为直径的与边CD相切于点D. B点在（DO上，连接0B.（1）求证：DE=OE；/一:（2）若CD〃AB,求证：四边形ABCD是菱形. / 丿/答案：1、(1)解：•.•直线与(DO相切，AOC 丄CD；又VAD丄CD,.•.AD//OC,/.ZDAC=ZOCA;又VOC=OA,.*.ZOAC=ZOCA,.*.ZDAC=ZOAC;••.AC 平分ZDA.O.(2)解:①TAD//OC, ZDAO=105°,ZEOC=ZDAO=105°;T ZE=30°,ZOCE=45°.②作OG丄CE于点G,可得FG=CG,VOC=2\P,ZOCE=45°..\CG=OG=2,.*.FG=2;*.•在RTA OGE 中,ZE=30°,:.GE=2^, .\EF=GE-FG=2V3-2.2、(1)证明：VAB=AC, ZBAC=90°,/.ZC=ZABC=45°,A ZAEP=ZABP=45°,VPE是直径，/. ZPAB=90°,A ZAPE=ZAEP=45°,.*.AP=AE,•••△PAE是等腰直角三角形.(2)作PM丄AC于M, PN丄AB于N,则四边形PMAN是矩形, .*.PM=AN,「△PCM, △ PNB都是等腰直角三角形，.•.PCpPM, PBpPN,/.PC2+PB2=2 (PM2+PN2) =2 (AN2+PN2) =2PA2=PE2=22=4.3、解：(1) BC与(DO相切. 证明：连接OD.TAD是ZBAC的平分线，.*.ZBAD=ZCAD.又TODOA,.*.ZOAD=ZODA./.ZCAD=ZODA..•.OD〃AC..•.ZODB=ZC=90°,即0D±BC. 又TBC过半径OD的外端点D, ABC与(DO相切.(2)设0F=OD=x,则OB=OF+BF=x+2, 根据勾股定理得：OB2=C)D2+BD2,即(x+2) 2=X2+12,解得：x=2,即OD=OF=2,/. OB=2+2=4,VRtA ODB 中，OD=*3B,:.ZB=30°,/.ZDOB=60°,• u_60K X4_2H••S 號AOB-，则阴影部分的面积为S A ODB -S麻DOF=*X2X2*\/^-2? -故阴影部分的面积为2^3 -写.4、(1)证明：•.•圆心0在BC±,ABC是圆O的直径，.\ZBAC=90o, 连接OD,TAD 平分ZBAC,ZBAO2ZDAC,VZDOC=2ZDAC,.•.ZDOC=ZBAC=90°,即OD丄BC,VPD/7BC,AOD 丄PD,TOD为圆O的半径，.•.PD是圆O的切线；(2)证明：•.•PD〃BC,.*.ZP=ZABC,T ZABOZADC,.*.ZP=ZADC,T ZPBD+ZABD=180°, ZACD+ZABD=180°,A ZPBD=ZACD,.•.APBD^ADCA；(3)解：••'△ABC为直角三角形，BC2=AB2+AC2=62+82=100,.\BC=10,TOD垂直平分BC,.*.DB=DC,VBC为圆O的直径，.•.ZBDC=90°,在RtA DBC 中，DB2+DC2=BC2,即2DC2=BC2=100,.\DC=DB=5V2-V APBD^ADCA,.PB_BD''~DC~W川"9_DC・BD_Sx奶_25人AC 8 4 -5、(1)证明：VOB=OD,.*.ZABC=ZODB,VAB=AC,.•.ZABOZACB,.*.ZODB=ZACB,.•.OD〃AC.「DE是(DO的切线，OD是半径,.'.DE 丄OD,A DEX AC；(2)如图，过点0 作OH丄AF于点H,则ZODE= ZDEH= ZOHE=90°, •••四边形ODEH是矩形，.*.OD=EH, OH=DE.设AH=x.VDE+AE=8, OD=10,/. AE=10 - x, 0H=DE=8 - ( 10 - x) =x - 2.在RtA AOH中，由勾股定理知：AH2+OH2=OA2,即x2+ (x-2) 2=102,解得xi=8, x2= - 6 (不合题意，舍去)..\AH=8.TOHIAF,.*.AH=FH=—AF,2・：AF=2AH=2x8 二16.6、(1)证明：连接OD,VD为说的中点，/.ZCAD=ZBAD,VOA=OD,A ZBAD=ZADO,.•.ZCAD=ZADO,VDE 丄AC,ZE=90°,ZCAD+ZEDA=90°,即ZADO+ZEDA=90°,AOD 丄EF,・・.EF为半圆O的切线；(2)解：连接OC与CD,VDA=DF,A ZBAD=ZF,A ZBAD=ZF=ZCAD,又T ZBAD+ ZCAD+ ZF=90°,A ZF=30°, ZBAC=60°,VOC=OA,AAOC为等边三角形，ZAOC=60°, ZCOB=120°,TOD丄EF, ZF=30°,.•.ZDOF=60°,在RtA ODF 中,DF=6屈OD=DF *tan3 0°=6,在RtA AED 中，D26胰,ZCAD=30°, /. DE=DA*sin30 "晶,EA=DA*cos30°=9, T ZCOD=180° - ZAOC - ZDOF=60°, /. CD/7 AB,故S △ACD-S A COD，•'•S 阴萨S A AED -S扇旳COD=*<9X3后-~^Q nX^2=~^~ ~ ^71-7、解：(1)如图，作EF丄y轴于F, DC的延长线交EF于H.设H (m, “), 则P (m, 0), PA=m+3, PB=3 - m.EH//AP,△ACPs&CH,AC = PC = AP=j_CE_CH_'^7，CH=2n, EH=2m=6,CD 丄AB,PC=PD=n,PB//HE,ADPB s'DHE,PB」)P_ n _13-m _ 12nH-6 4'm=l,P (1, 0).(2)由(1)可知，PA=4, HE=8, EF=9, 连接OP,在R仏OCP中，PC=7OC^O P=2V2-:.CH=2PC=4皈 PH=6屈:.E (9, 6冋,•••抛物线的对称轴为CD,:.(-3, 0)和(5, 0)在抛物线上，设抛物线的解析式为尸a (x+3) (%-5), 把E (9, 6迈)代入得到a欝,•••抛物线的解析式为尸誓.&+3) &-5),即尸导2-孚-耳Z8、(1)证明：连接EF,TAE 平分ZBAC,/. ZFAE=ZCAE,VFA=FE,ZFAE=ZFEA, /. ZFEA=ZEAC,.・.FE〃AC,ZFEB=ZC=90°,即BC 是OF 的切线;(2)解：连接FD,设。

圆的基本性质(解析版)2018年数学全国中考真题-2

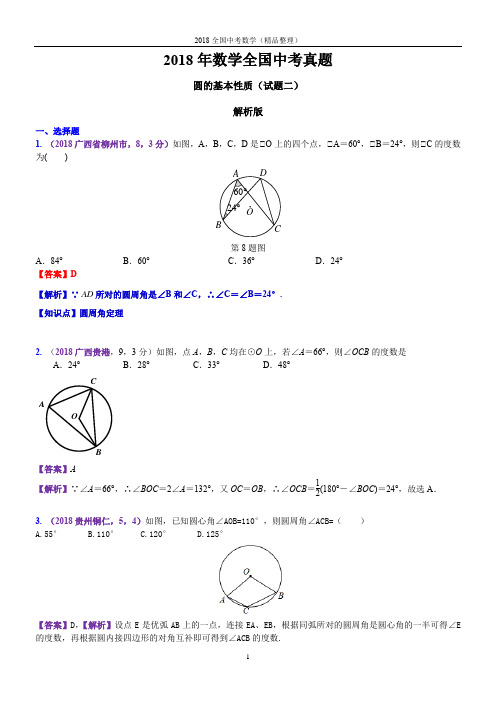
2018年数学全国中考真题圆的基本性质（试题二）解析版一、选择题1. （2018广西省柳州市，8，3分）如图，A ，B ，C ，D 是⊙O 上的四个点，⊙A ＝60°，⊙B ＝24°，则⊙C 的度数为( )第8题图 A ．84° B．60°C ．36°D ．24°【答案】D【解析】∵AD 所对的圆周角是∠B 和∠C ，∴∠C ＝∠B ＝24°.【知识点】圆周角定理2. （2018广西贵港，9，3分）如图，点A ，B ，C 均在⊙O 上，若∠A ＝66°，则∠OCB 的度数是 A ．24° B ．28° C ．33° D ．48°【答案】A【解析】∵∠A ＝66°，∴∠BOC ＝2∠A ＝132°，又OC ＝OB ，∴∠OCB ＝12(180°－∠BOC )＝24°，故选A ．3. （2018贵州铜仁，5，4）如图，已知圆心角∠AOB=110°，则圆周角∠ACB=（） A.55° B.110° C.120° D.125°【答案】D ，【解析】设点E 是优弧AB 上的一点，连接EA 、EB ，根据同弧所对的圆周角是圆心角的一半可得∠E 的度数，再根据圆内接四边形的对角互补即可得到∠ACB 的度数.【解答过程】设点E 是优弧AB 上的一点，连接EA 、EB ，如图， ∵∠AOB=110°，∴∠AEB=12∠AOB=55°，∴∠ACB=180°-∠E=125°.4. （2018江苏苏州，7，3分）如图，AB 是半圆的直径，O 为圆心，C 是半圆上的点，D 是AC 上的点．若∠BOC＝40°，则∠D 的度数为 A ．100° B ．110°C ．120°D ．130°【答案】B【解析】本题解答时要利用等腰三角形的性质和圆的内接四边形的对角互补的性质进行计算.∵OC =OB ，∠BOC =40゜，∴∠B =70゜，∴∠D =180゜-70゜=110゜，故选B .5. （2018内蒙古通辽，7，3分）已知⊙O 的半径为10，圆心O 到弦AB 的距离为5，则弦AB 所对圆周角的度数是 A ．30° B ．60° C ．30°或150° D ．60°或120° 【答案】D【解析】如答图，连接OA 、OB ，∵OC ⊥AB ，∴OC ＝5，OA ＝OB ＝10，又OC ＝12OA ，∴cos ∠AOC ＝12，∴∠AOC ＝60°∴∠AOB ＝120°，∴弦AB 所对的圆周角的度数是60°或120°．故选D ．6.（湖北省咸宁市，7，3）如图，已知⊙O 的半径为5，弦AB ，CD 所对的圆心角分别为∠AOB ，∠COD ，若∠AOB 与∠COD 互补，弦CD =6，则弦AB 的长为( )A ．6B ．8 C． D．【答案】【解析】解：作OF ⊥AB 于F ，作直径BE ，连接AE ，如图， ∵∠AOB+∠COD=180°，而∠AOE+∠AOB=180°， ∴∠AOE=∠COD ， ∴AE DC ，∴AE=DC=6，∵OF ⊥AB ， ∴BF=AF ，而OB=OE ，∴OF 为△ABE 的中位线，由勾股定理可得AF=4，∴AB=8，故选择B ．【知识点】圆周角定理；垂径定理；三角形中位线性质7. (2018湖北黄石，8，3分)如图，AB 是⊙O 的直径，点D 为⊙O 上一点，且∠ABD ＝30°，BO ＝4，则BD 的长为( )第8题图A ．23πB ．43πC ．2πD ．83π FE【答案】D 【解析】连接OD ，则∠AOD ＝2∠B ＝60°，∴∠BOD ＝120°.∴l BD ＝120180π×4＝83π.8. (2018湖南邵阳，6，3分)如图(二)所示，四边形ABCD 为⊙O 的内接四边形，∠BCD ＝120°，则∠BOD 的大小是( )A ．80°B ．120°C ．100°D ．90°图(二)【答案】B ，【解析】根据“圆内接四边形的对角互补”可得∠BCD ＋∠A ＝180°，因为∠BCD ＝120°所以∠A ＝60°．又根据“在同圆中，同弧所对的圆心角等于圆周角的2倍”，所以∠BOD ＝2∠A ＝120°．故选B ．9.（2018四川眉山，6，3分）如图所示，AB 是⊙O 的直径，P A 切⊙O 于点A ，线段PO 交⊙O 于点C ，连结BC ，若∠P ＝36°，则∠B 等于（）A ．27°B ．32°C ．36°D ．54°【答案】A ，【解析】由P A 是⊙O 的切线，可得⊙OAP ＝90°，∴∠AOP ＝54°，根据同弧所对的圆周角等于圆心角的一半，可得∠B ＝27°10. （2018辽宁锦州，7，3分）如图：在△ABC 中，∠ACB=90°，过B 、C 两点的⊙O 交AC 于点D ，交AB 于点E ，连接EO 并延长交⊙O 于点F ，连接BF 、CF ，若∠EDC=135°，CF=22，则AE 2+BE 2的值为A 、8B 、12C 、16D 、20D【答案】C，【解析】：如图，∠EDC=1350，∠ACB=90°，得△ACB是等腰直角三角形，ECF是等腰直角三角形，得△AEC与△BFC是全等三角形，AE=BF,△EBF是直角三角形，AE2+BE2=FE2=2FC2.二、填空题100，则弧AB所对的圆周角是°.1.（2018广东省，11，3）同圆中，已知弧AB所对的圆心角是【答案】50°【解析】同弧所对的圆周角是圆心角的一半，圆心角为100°，所以圆周角为50°.【知识点】圆周角、圆心角关系2. （2018海南省，18，4分）如图，在平面直角坐标系中，点A 的坐标是（20，0），点B 的坐标是（16，0），点C ， D 在以OA 为直径的半圆M 上，且四边形OCDB 是平行四边形，则点C 的坐标为________．【答案】（2，6）【思路分析】过点M 作MN ⊥CD ，垂足为点N ，连接CM ，过点C 作CE ⊥OA ，垂足为点E ，由题意可知OB 及圆的半径长，OB =CD ，由垂径定理可求得MN 的长，CN =EM ，从而求出OE 的长，进而得到点C 的坐标．【解题过程】过点M 作MN ⊥CD ，垂足为点N ，连接CM ，过点C 作CE ⊥OA ，垂足为点E ，点A 的坐标是（20，0），所以CM =OM =10，点B 的坐标是（16，0），所以CD =OB =16，由垂径定理可知，821==CD CN ，在Rt⊙CMN 中，CM =10，CN =8，由勾股定理可知MN =6，所以CE =MN =6，OE =OM ﹣EM =10﹣8=2，所以点C 的坐标为（2，6）．【知识点】垂径定理，勾股定理，平行四边形的性质3. （2018黑龙江省龙东地区，6，3分）如图，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，已知CD ＝6，EB ＝＝1，则⊙O 的半径为________．【答案】5【解析】连接OC ，∵AB 是⊙O 的直径，CD ⊥AB ，∴CE ＝12CD ，∵CD ＝6，∴CE ＝3．设⊙O 的半径为r ，则OC ＝r ，∵EB ＝1，∴OE ＝4，在Rt △OCE 中，由勾股定理得OE 2＋CE 2＝OC 2，∴（r －1）2＋32＝r 2，解得r ＝5，∴⊙O 的半径为5．D【知识点】垂径定理；勾股定理4.（2018黑龙江绥化，16，3分）如图，△ABC是半径为2的圆内接正三角形，则图中阴影部分的面积是．（结果用含π的式子表示）【答案】4π-.【解析】解：连接OA，OB，OC，过O点作OD⊥BC于点D.∵△ABC为等边三角形，∴∠OBD=30°.∵⊙O的半径为2，∴OB=2，∴OD=1，∴∴S△ABC=3S△OBC=3×12BC·OD=D∴S阴影=4π-故答案为：4π-【知识点】含30°角的直角三角形的性质，垂径定理，三角形面积计算，圆的面积计算5.（2018黑龙江绥化，20，3分）如图，一下水管道横截面为圆形，直径为100cm，下雨前水面宽为60cm，一场大雨过后，水面宽为80cm，则水位上升 cm【答案】10或70.【解析】解：作半径OD⊥AB于C，连接OB，由垂径定理得：BC=12AB=30，在Rt△OBC中，当水位上升到圆心以下时水面宽80 cm则OC′，水面上升的高度为：40-30=10cm；当水位上升到圆心以上时，水面上升的高度为：40+30=70cm，综上可得，水面上升的高度为10cm或70cm．故答案为10或70.【知识点】垂径定理，勾股定理6.7.（2018浙江嘉兴，14，4）如图，量角器的O度刻度线为AB．将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C，直尺另一边交量角器于点A、D，量得AD＝10cm，点D在量角器上的读数为60°．则该直尺的宽度为cm．【解析】根据题意，抽象出数学图形根据题意可知：AD ＝10，∠AOD ＝120°，由OA ＝OD ，∴∠DAO ＝30°，设OE ＝x ，则OA ＝2x ，∵OE ⊥AD ，∴AE ＝DE ＝5，在Rt △AOE 中，x 2+52＝（2x ）2，解得：xCE ＝OE8. （2018贵州省毕节市，19，3分）如图,AB 是⊙O 的直径，C 、D 为半圆的三等分点，CE ⊥AB 于点E ， ∠ACE 的度数为______.【答案】30°．【解题过程】∵AB 是⊙O 的直径,C 、D 为半圆的三等分点，∴∠A ＝∠BOD ＝13×180°＝60°，又∵CE ⊥AB ，∴∠ACE ＝90°－60°＝30°．【知识点】圆的性质；直角三角形的性质9.（2018吉林省，13, 2分）如图，A ，B ，C ，D 是⊙O 上的四个点，=⌒BC ，，若∠AOB=58°，则∠BDC=___ 度．BO【答案】29【解析】连接CO，根据同圆中，等弧所对圆心角相等，则∠COB=∠AOB=58°，∴∠BDC=29°【知识点】圆周角定理，圆心角、弧、弦之间的关系10.（2018江苏扬州，15，3）如图，已知⊙O的半径为2，△ABC内接于⊙O，∠ACB=135°，则AB= ．2【答案】2【思路分析】根据圆内接四边形对边互补和同弧所对的圆心角是圆周角的2倍，可以求得∠AOB的度数，然后根据勾股定理即可求得AB的长．【解题过程】连接AD、AE、OA、OB，∵⊙O的半径为2，△ABC内接于⊙O，∠ACB=135°，∴∠ADB=45°，∴∠AOB=90°，∵OA=OB=2，∴2，故答案为2．【知识点】三角形的外接圆和外心，圆内接四边形对边互补，圆周角的性质11.（2018青海，9，2分）如图5，A、B、C是⊙O上的三点，若∠AOC=110°,则∠ABC= . 【答案】125°．【解析】如图所示：优弧AC上任取一点D，连接AD、CD，∵∠AOC=110°，∴∠ADC=∠AOC=×110°=55°，∵四边形ABCD内接与⊙O，∴∠ABC=180°﹣∠ADC=180°﹣55°=125°．【知识点】圆内接四边形的性质，圆周角的性质12. （2018江苏镇江，9，2分）如图，AD 为△ABC 的外接圆⊙O 的直径，若∠BAD ＝50°，则∠ACD ＝________°．【答案】40°．【解析】如答图所示，连接B C ． ∵AB 是⊙O 的直径， ∴∠ACB ＝90°．∵∠BCD ＝∠BAD ＝50°，∴∠ACD ＝∠ACB －∠BCD ＝90°－50°＝40°．13. （2018内蒙古通辽，17，3分）如图，在平面直角坐标系中，反比例函数y ＝kx （k ＞0）的图象与半径为5的⊙O 相交于M 、N 两点，△MON 的面积为3.5，若动点P 在x 轴上，则PM ＋PN 的最小值是．【答案】52【解析】设M （a ，b ），则N （b ，a ），依题意，得：a 2＋b 2＝52……①（第9题答图）（第9题图）a 2－ab －12（a －b ）2＝3.5……②①、②联立解得a ＝572，b ＝432所以M 、N 的坐标分别为（572，432），（432，572）作M 关于x 轴的对称点M ′，则M ′的坐标为（572，－432），则M ′N 的距离即为PM ＋PN 的最小值．由于M ′N 2＝（572－432）2＋（－432－572）2＝50，所以M ′N ＝52，故应填：52．14. （2018山东莱芜，16，3分）如图，正方形ABCD 的边长为2a ，E 为BC 边的中点，⌒AE 、⌒DE 的圆心分别在边AB 、CD 上，这两段圆弧在正方形内交于点F ，则E 、F 间的距离为_______．【答案】32a【思路分析】先用勾股定理求出⌒DFE 的所在圆的半径，再由垂径定理求出EF 的长．【解题过程】解：如图，设⌒DFE 的圆心为G ，作GH ⊥EF 于H ，连接EG ．设⌒DFE 所在圆的半径为x ，在Rt △CEG 中，EG 2＝CG 2＋CE 2，则x 2＝(2a －x )2＋a 2，解得x ＝54a ；由垂径定理，得EF ＝2EH ＝2⎝ ⎛⎭⎪⎫54a 2－a 2＝32a ．故答案为32a ．【知识点】正方形的性质；勾股定理；垂径定理；15. （2018湖北随州12，3分）如图，点A ，B ，C 在⊙O 上，∠A ＝40度，∠C ＝20度，则∠B ＝______度．EEA D【答案】60．【解析】如图，连接OA ，根据“同圆的半径相等”可得OA ＝OC ＝OB ，所以∠C ＝∠OAC ，∠OAB ＝∠B ，故∠B ＝∠OAB ＝∠OAC ＋∠BAC ＝∠C ＋∠BAC ＝20°＋40°＝60°．16.（2018湖北随州16，3分）如图，在四边形ABCD 中，AB ＝AD ＝5，BC ＝CD 且BC ＞AB ，BD ＝8．给出下列判断：①AC 垂直平分BD ；②四边形ABCD 的面积S ＝AC ·BD ；③顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形；④当A 、B 、C 、D 四点在同一个圆上时，该圆的半径为256； ⑤将△ABD 沿直线BD 对折，点A 落在点E 处，连接BE 并延长交CD 于点F ，当BF ⊥CD 时，点F 到直线AB 的距离为678125．其中正确的是______________．（写出所有正确判断的序号）【答案】①③④．【解析】根据“到线段两个端点的距离相等的点在这条线段的垂直平分线上”可知，A ，C 两点都在线段BD 的垂直平分线上，又“两点确定一条直线”，所以AC 垂直平分BD ，故①正确；如图1，取AC ，BD 的交点为点O ，则由①知OB ⊥AC ，OD ⊥AC ，所以S 四边形ABCD ＝S △ABC ＋S △ADC ＝12AC ·OB ＋12AC ·OD ＝12AC ·(OB ＋OD )＝ 12AC ·BD ，故②错误；如图2，取AB ，BC ，CD ，AD 四边的中点分别为P ，Q ，M ，N ，则由三角形的中位线定理得PQ ∥AC ∥MN ，PQ ＝MN ＝12AC ，PN ∥BD ∥QM ，PN ＝QM ＝12BD ，于是知四边形PQMN 及阴影四边形都是平行四边形．又由①知AC ⊥BC ，所以可证∠AOB ＝∠QPN ＝90°，故四边形PQMN 为矩形．若AC ＝BD ，则有PQ ＝PN ，四边O ABCCBAO ABDC形PQMN 是正方形，所以顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形，故③正确；当A 、B 、C 、D 四点在同一个圆上时，四边形ABCD 是这个圆的内接四边形，则∠ABC ＋∠ADC ＝180°．根据“SSS ”可证△ABC ≌△ADC ，所以∠ABC ＝∠ADC ＝90°，则AC 是这个圆的直径．由①知BO ＝OD ＝12BD ＝4，在Rt △AOB 中，根据勾股定理，求得AO＝3．然后，证明△AOB ∽△ABC ，得到AB 2＝AO ·AC ，所以AC ＝253，该圆的半径为256，故④正确；如图1，过点F 作FG ⊥AB 于点G ，过点E 作EH ⊥AB 于点H ，由折叠知，AE ＝2AO ＝6，BE ＝BA ＝5．由于BF ⊥CD ，AE ⊥BD ，可证得△BOE ∽△BFD ，所以BO BF ＝BE BD ，即4BF ＝58，BF ＝325．因为S △ABE ＝12AB ·EH＝12AE ·BO ，所以EH ＝645⨯＝245．又可证△BEH ∽△BFG ，所以EH FG ＝BE BF ，即245FG ＝5325，FG ＝768125，故⑤错误．17. （2018云南曲靖，10，3分）如图，四边形ABCD 内接于⊙O ，E 为BC 延长线上一点，若∠A ＝n °，则∠DCE ＝_________【答案】n °【解析】圆内接四边形的对角互补，所以∠BCD ＝180°－∠A ，而三点BCD 在一条直线上，则∠DCE ＝180°－∠BCD ，所以∠DCE ＝∠A ＝n °.18. （2018年浙江省义乌市，13，5）如图，公园内有一个半径为20米的圆形草坪，A ，B 是圆上的点，O 为圆心，∠AOB =120°，从A 到B 只有路AB ，一部分市民为走“捷径”，踩坏了花草，走出了一条小路AB ．通过计算可知，这些市民其实仅仅少B 走了_________步（假设1步为0.5米，结果保留整数）．（参考数据：图1GFEH OABDC 图21.732，π取3.142）【答案】15【解析】作OC⊥AB于C，如图，则AC=BC，∵OA=OB，∴∠A=∠B=12（180°﹣∠AOB）=12（180°﹣120°）=30°，在Rt△AOC中，OC=12OA=10，，∴69（步）；而AB的长=12020180π⨯≈84（步），AB的长与AB的长多15步．所以这些市民其实仅仅少B走了15步．故答案为15．【知识点】垂径定理；勾股定理19.（2018浙江舟山，14，4）如图，量角器的O度刻度线为AB．将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C，直尺另一边交量角器于点A、D，量得AD＝10cm，点D在量角器上的读数为60°．则该直尺的宽度为cm．BC【解析】根据题意，抽象出数学图形根据题意可知：AD ＝10，∠AOD ＝120°，由OA ＝OD ，∴∠DAO ＝30°，设OE ＝x ，则OA ＝2x ，∵OE ⊥AD ，∴AE ＝DE ＝5，在Rt △AOE 中，x 2+52＝（2x ）2，解得：x ，∴CE ＝OE．三、解答题1. （2018年江苏省南京市，26，8分）如图，在正方形ABCD 中，E 是AB 上一点，连接DE .过点A 作AF DE ⊥，垂足为F .⊙O 经过点C 、D 、F ，与AD 相交于点G .（1）求证AFG DFC ∽△△；（2）若正方形ABCD 的边长为4，1AE =，求O 的半径.【思路分析】（1）欲证明△AFG ∽△DFC ，只要证明∠FAG=∠FDC ，∠AGF=∠FCD ；（2）首先证明CG 是直径，求出CG 即可解决问题；【解题过程】（1）证明：在正方形ABCD 中，90ADC ∠=. ∴90CDF ADF ∠+∠=. ∵AF DE ⊥. ∴90AFD ∠=.∴90DAF ADF ∠+∠=. ∴DAF CDF ∠=∠.∵四边形GFCD 是⊙O 的内接四边形， ∴180FCD DGF ∠+∠=. 又180FGA DGF ∠+∠=，O∴FGA FCD ∠=∠. ∴AFG DFC ∽△△. （2）解：如图，连接CG .∵90EAD AFD ∠=∠=，EDA ADF ∠=∠， ∴EDA ADF ∽△△. ∴EA DA AF DF =，即EA AFDA DF=. ∵AFG DFC ∽△△， ∴AG AFDC DF =. ∴AG EADC DA=. 在正方形ABCD 中，DA DC =，∴1AG EA ==，413DG DA AG =-=-=.∴5CG ===.∵90CDG ∠=， ∴CG 是⊙O 的直径. ∴⊙O 的半径为52.【知识点】相似三角形的判定和性质正方形的性质圆周角定理及推论2. （2018江苏徐州，28，10分）如图，将等腰直角三角形ABC 对折，折痕为CD ．展平后，再将点B 折叠再边AC 上，（不与A 、C 重合）折痕为EF ，点B 在AC 上的对应点为M ，设C D 与EM 交于点P ，连接PF ．已知BC ＝4．（1）若点M 为AC 的中点，求CF 的长；（2）随着点M 在边AC 上取不同的位置．①△PFM 的形状是否发生变化？请说明理由； ②求△PFM 的周长的取值范围.第28题图【解答过程】解：（1）根据题意，设BF ＝FM ＝x ，则CF ＝4－x ，∵M 为AC 中点，AC ＝BC ＝4，∴ CM ＝12AC ＝2，∵∠ACB ＝90°，∴CF 2+CM 2＝FM 2，∴(4－x )2+22＝x 2，解得x ＝52，∴CF ＝4－52＝32；（2）①△PFM 的形状不变，始终是以PM 、PF 为腰的等腰直角三角形，理由如下：∵等腰直角三角形ABC 中，CD ⊥AB ，∴AD ＝DB ，CD ＝12AB ＝DB ，∴∠B ＝∠DCB ＝45°，由折叠可得∠PMF ＝∠B ＝45°，∴∠PMF ＝∠DCB ，∴P 、M 、F 、C 四点共圆，∴∠FPM +∠FCM ＝180°，∴∠FPM ＝180°－∠FCM ＝90°，∠PFM ＝90°－∠PMF ＝45°＝∠PMF ，∴△PFM 的形状不变，始终是以PM 、PF 为腰的等腰直角三角形； ②当M 与C 重合时，F 为BC 中点，CF ＝12BC ＝2，PM ＝PF ＝cos 45CF=︒此时△PFM 的周长为2＋当M 与A 重合时，F 于C 重合，E 与D 重合，FM ＝AC ＝4，PM ＝PF ＝ACcos45°＝，此时△PFM 的周长为4＋B 不与A 、C 重合，所以△PFM 的周长的取值范围是大于2＋且小于4＋.3. (2018辽宁葫芦岛，25，12分)在△ABC 中，AB ＝BC ，点O 是AC 的中点，点P 是AC 上的一个动点(点P 不与点A ，O ，C 重合)．过点A ，点C 作直线BP 的垂线，垂足分别为点E 和点F ，连接OE ，OF ．（1）如图1，请直接写出线段OE 与OF 的数量关系；（2）如图2，当∠ABC ＝90°时，请判断线段OE 与OF 之间的数量关系和位置关系，并说明理由；（3）若｜CF －AE ｜＝2，EF ＝POF 为等腰三角形时，请直接写出线段OP 的长．【思路分析】（1）连接OB ，则OB ⊥AC ，进而得A 、E 、O 、B 四点共圆，B 、F 、O 、C 四点共圆．由同弧所对的圆周角相等得∠OEB ＝∠OAB ，∠OFC ＝∠OBC ．又因为∠OFE ＝90°－∠OFC ，∠ACB ＝90°－∠OBC ，所以∠OFE ＝∠OCB ，又因为∠OAB ＝∠OCB ，所以∠OE B ＝∠OFE ，所以OE ＝OF ；（2）类比（1）可得OE ＝OF ；由∠ABC ＝90°，AB ＝BC ，可得∠OAB ＝∠OCB ＝∠OEB ＝∠OFE ＝45°，所以OE ⊥OF ．（3）取EF的中点为M，则EM＝FMAM并延长交CF于D，连接OM．由△AME≌△DMF，｜CF－AE｜＝2，得OM＝1．进而得OF＝2．由sin∠OFM＝12，得∠OFM＝30°．因为点P在EF上，所以OP＜OE＝OF；因为AE⊥EF，∠APE、∠OPF均为锐角，故PF≠PO．当PF＝OF＝2时，PM＝2理得OP＝【解答过程】（1）OE＝OF；（2）OE＝OF，OE⊥OF．理由：连接OB，则OB⊥AC．∵∠AEB＝∠AOB＝90°，∴进而得A、E、O、B四点共圆，∴∠OEB＝∠OAB．∵∠BFC＝∠BOC＝90°，∴B、F、O、C四点共圆．∴∠OFC＝∠OBC．又∵∠OFE＝90°－∠OFC，∠ACB＝90°－∠OBC，∴∠OFE＝∠OCB，又∵∠ABC＝90°，AB＝BC，∴∠OAB＝∠OCB＝45°．∴∠OE B＝∠OFE＝45°．∴OE＝OF，OE⊥OF．（3）OP＝223．4.（2018上海，25，14分）已知圆O的直径AB=2，弦AC与弦BD，交于点E，且OD⊥AC，垂足为点F．(1)图11，如果AC=BD，求弦AC的长；(2)如图12，如果E为BD的中点，求∠ABD的余切值(3)联结BC、CD、DA，如果BC是圆O的内接正n边形的一边，CD是的内接正(n+4)边形的一边，求△ACD的面积．【思路分析】(1)连结CB．可以证明弧AD、弧DC、弧CB相等，从而得到∠ABC=60°．在△ABC中求出AC长．(2)运用中位线及全等转化求出CB长，再把直角三角形OBE中的两个直角边求出，即可∠ABD的余切值．(3)根据“BC是圆O的内接正n边形的一边，CD是的内接正(n+4)边形的一边”求出n值，从而求出∠AOD=45°，可得各线段长，再求△ACD的面积．【解答过程】（1）连结CB．∵AC=BD，∴弧AC=弧BD，∵OD⊥AC，∴弧AD=弧DC=12弧AC，∴弧AD=弧DC=弧CB，∴∠ABC=60°在Rt△ABC中, ∠ABC=60°，AB=2，∴AC=3（2）∵OD⊥AC，∴∠AFO=90°，AF=FC∵AO=OB，∴FO∥CB，FO=12 CB∵E为BD的中点，∴DE=EB∵FO∥CB，∴△DEF≌△BEC，∴DF=CB=2FO∴FO=13，CB=23在Rt △ABC 中，AB =2，CB =23，∴AC ，∴EC ∴EB ，∵E 为BD 的中点，OD =OB ，∴∠OEB =90°，∴EO cot ∠ABD =EB EO ．（3）∵BC 是圆O 的内接正n 边形的一边，∴∠COB =360n° ∵CD 是的内接正(n +4)边形的一边，∴∠COD =3604n +° ∵弧AD =弧DC ，∴∠AOD =3604n +° ∵∠COB +∠COD +∠AOD =180°，∴360n +3604n ++3604n +=180，解得n =4 ∴∠AOD =∠COD =3604n +°=45°∵OD =OA =OC =1，∴AC ，OF ，DF =1，∴S △ACD =12×AC ×DF =2－12．5. （2018黑龙江哈尔滨，26，10）已知:⊙O 是正方形ABCD 的外接圆，点E 在弧AB 上，连接BE 、DE ，点F 在弧AD 上，连接BF 、DF 、BF 与DE 、DA 分别交于点G 、点H ，且DA 平分∠EDF ．(1)如图1，求证:∠CBE ＝∠DHG ;(2)如图2，在线段AH 上取一点N (点N 不与点A 、点H 重合)，连接BN 交DE 于点L ，过点H 作HK //BN 交DE 于点K ，过点E 作EP ⊥BN ，垂足为点P ，当BP ＝HF 时，求证:BE ＝HK ;(3)如图3，在(2)的条件下，当3HF ＝2DF 时，延长EP 交⊙O 于点R ，连接BR ，若△BER 的面积与△DHK 的面积的差为47，求线段BR 的长．图1 图2 图3【思路分析】（1）问利用同弧和等弧所对圆周角等与三角形外角性质易证的结论．（2）过H 作HM ⊥KD ，易证得HM ＝BP ，加上直角条件，可导出第三个全等条件，得到△BEP ≌△HKM ，所以BE ＝HK ．（3）连接BD 后根据条件3HF ＝2DF 可得到tan ∠ABH ＝tan ∠ADE ＝ABAH ＝32，过点H 作HS ⊥BD 后再设边计算就能求出tan ∠BDE ＝tan ∠DBF ＝BSHS ＝51，在ER 上截取ET ＝DK ，连接BT 易证得△BET ≌△HKD ，这时21BP ·ER 21-HM ·DK ＝21BP (ER －DK )＝21BP (ER －ET )＝47，易求得BP ＝1，PR ＝5，BR ＝22RP BP +＝2251+＝26【解答过程】（1）证明:∵四边形ABCD 是正方形∴∠A ＝∠ABC ＝90°∵∠F ＝∠A ＝90°∴∠F ＝∠ABC∵DA 平分∠EDF ∴∠ADE ＝∠ADF ∵∠ABE ＝∠ADE ∴∠ABE ＝∠ADF又∵∠CBE ＝∠ABC ＋∠ABE ，∠DHG ＝∠F ＋∠ADF ∴∠CBE ＝∠DHG（2）证明:过H 作HM ⊥KD 垂足为点M ∵∠F ＝90°∴HF ⊥FD 又∵DA 平分∠EDF ∴HM ＝FH∵FH ＝BP ∴HM ＝BP ∵KH ∥BN ∴∠DKH ＝∠DLN ∵∠ELP ＝∠DLN ∴∠DKH ＝∠ELP∵∠BED ＝∠A ＝90°∴∠BEP ＋∠LEP ＝90°∵EP ⊥BN ∴∠BPE ＝∠EPL ＝90°∴∠LEP ＋∠ELP ＝90°∴∠BEP ＝∠ELP ＝∠DKH ∵HM ⊥KD ∴∠KMH ＝∠BPE ＝90°∴△BEP ≌△HKM ∴BE ＝HK(3)解:连接BD ∵3HF ＝2DF ，BP ＝FH ∴设HF ＝2a ，DF ＝3a ∴BP ＝FH ＝2a由(2)得HM ＝BP ，∠HMD ＝90°∵∠F ＝∠A ＝90°∴tan ∠HDM ＝tan ∠FDH ∴DM HM ＝DF FH ＝32 ∴DM ＝3a ∴四边形ABCD 是正方形∴AB ＝AD ∴∠ABD ＝∠ADB ＝45°∵∠ABF ＝∠ADF ＝∠ADE ，∠DBF ＝45°－∠ABF ，∠BDE ＝45°－∠ADE ∴∠DBF ＝∠BDE ∵∠BED ＝∠F ，BD ＝BD ∴△BED ≌△DFB ∴BE ＝FD ＝3a 过点H 作HS ⊥BD 垂足为点S ∵tan ∠ABH ＝tan ∠ADE ＝ABAH ＝32 ∴设AB ＝32m ，AH ＝22m ∴BD ＝2AB ＝6m DH ＝AD －AH ＝2m sin ∠ADB ＝DHHS ＝22 ∴HS ＝m ∴ DS ＝22HS DH -＝m ∴BS ＝BD －DS ＝5m ∴tan ∠BDE ＝tan ∠DBF ＝BS HS ＝51 ∵∠BDE ＝∠BRE ∵tan ∠BRE ＝PR BP ＝51∵BP ＝FH ＝2a ∴RP ＝10a 在ER 上截取ET ＝DK ，连接BT 由(2)得∠BEP ＝∠HKD ∴△BET ≌△HKD ∴∠BTE ＝∠KDH ∴tan ∠BTE ＝tan ∠KDH ∴PT BP ＝32 ∴PT ＝3a ∴TR ＝RP －PT ＝7a ∵S △BER －S △KDH ＝47∴21BP ·ER 21-HM ·DK ＝47 ∴21BP (ER －DK )＝21BP (ER －ET )＝47∴21×2a ×7a ＝47 ∴a 2＝41，a 1＝21，a 2＝21-(舍去)∴BP ＝1，PR ＝5 ∴BR ＝22RP BP +＝2251+＝26。

2018年全国中考数学试卷解析分类汇编专题30 圆的有关性质

【答案】C
考点：切线的性质、三角形外角的性质、圆的基本性质.
4．（2015•四川资阳,第8题3分）如图4，AD、BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动，设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是
考点：动点问题的函数图象．.
分析：根据图示，分三种情况：（1）当点P沿O→C运动时；（2）当点P沿C→D运动时；（3）当点P沿D→O运动时；分别判断出y的取值情况，进而判断出y与点P运动的时间x（单位：秒）的关系图是哪个即可．
S△ABC= •r•（AB+BC+AC）= =21r，
过点A作AD⊥BC交BC的延长线于点D，如图2，
设CD=x，
由勾股定理得：在Rt△ABD中，
AD2=AB2﹣BD2=400﹣（7+x）2，
在Rt△ACD中，AD2=AC2﹣x2=225﹣x2，
∴400﹣（7+x）2=225﹣x2，
解得：x=9，
∴AD=12，
解答：解：（1）当点P沿O→C运动时，
当点P在点O的位置时，y=90°，
当点P在点C的位置时，
∵OA=OC，
∴y=45°，
∴y由90°逐渐减小到45°；
（2）当点P沿C→D运动时，
根据圆周角定理，可得
y≡90°÷2=45°；
（3）当点P沿D→O运动时，
当点P在点D的位置时，y=45°，
当点P在点0的位置时，y=90°，
A. B. C. D. —1
【答案】B
【解析】
试题分析：如图，等腰直角三角形ABC中，⊙D为外接圆，可知D为AB的中点，因此AD=2，AB=2AD=4，根据勾股定理可求得AC= ，根据内切圆可知四边形EFCG是正方形，AF=AD,因此EF=FC=AC－AF= －2.

【中考专题】2018中考数学专项突破《圆的综合题》

2018年苏州中考数学专题辅导第六讲圆的综合专题选讲一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点；四、圆与圆的位置关系外离（图1）⇒无交点⇒d R r>+；外切（图2）⇒有一个交点⇒d R r=+；相交（图3）⇒有两个交点⇒R r d R r-<<+；内切（图4）⇒有一个交点⇒d R r=-；内含（图5）⇒无交点⇒d R r<-；图1A五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。

2018年中考数学总复习圆试题

2018年中考数学总复习圆试题单元检测六圆(时间90分钟满分120分)一、选择题(每小题3分,共30分)1.如图,在☉O中,∠ABC=50°,则∠AOC等于(D)A.50°B.80°C.90°D.100°2.如图所示,AB是☉O的直径,==,∠COD=34°,则∠AEO的度数是(A)A.51°B.56°C.68°D.78°(第2题图)(第3题图)3.如图,AB是☉O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立．．．的是(D)A.∠A=∠DB.=C.∠ACB=90°D.∠COB=3∠DA.2πB.πC.πD.π8.如图,AB是半圆O的直径,点P从点A出发,沿半圆弧AB顺时针方向匀速移动至点B,运动时间为t,△ABP 的面积为S,则下列图象能大致刻画S与t之间的关系的是(C)9.如图,AB为半圆所在☉O的直径,弦CD为定长且小于☉O的半径(C点与A点不重合),CF⊥CD交AB于点F,DE⊥CD交AB于点E,G为半圆弧上的中点.当点C 在上运动时,设的长为x,CF+DE=y.则下列图象中,能表示y与x的函数关系的图象大致是(B)10.如图,☉O是△ABC的内切圆,若∠ABC=60°,∠ACB=40°,则∠BOC=(A)A.130°B.135°C.120°D.150°二、填空题(每小题5分,共20分)11.如图,☉O的两条弦AB,CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则☉O的半径是.(第11题图)(第12题图)12.如图,AB是☉O的直径,OA=1,AC是☉O的弦,过点C的切线交AB的延长线于点 D.若BD=-1,则∠ACD=112.5°.13.如下图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是.14.如图,从☉O外的两点C和D分别引圆的两线DA,DC,CB,切点分别为点A、点E和点B,AB是☉O的直径,连接OC,连接OD交CB延长线于F,给出如下结论:①AD+BC=CD;②OD2=DE·CD;③OD=OC;④CD=CF.其中正确的是①②④.(把所有正确结论序号都填在横线上)三、解答题(共70分)15.(6分)如图,PA,PB是☉O的两条切线,A,B分别是切点,点C是上任意一点,连接OA,OB,CA,CB,∠P=70°,求∠ACB的度数.解∵PA,PB是☉O的切线,OA,OB是半径,∴∠PAO=∠PBO=90°.又∵∠PAO+∠PBO+∠AOB+∠P=360°,∠P=70°,∴∠AOB=110°.∵∠AOB是圆心角,∠ACB是圆周角,∴∠ACB=55°.16.(6分)已知在以点O为圆心的两个同心圆中,大圆的弦AB 交小圆于点C,D(如图所示).(1)求证:AC=BD;(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.(1)证明过点O作OE⊥AB于点E,则CE=DE,AE=BE.∴AE-CE=BE-DE,即AC=BD.(2)解由(1)可知,OE⊥AB且OE⊥CD,∴CE===2.AE===8.∴AC=AE-CE=8-2.〚导学号92034207〛17.(6分)已知A,B,C,D是☉O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求☉O的半径.图1图2(1)证明∵∠ADC=∠BCD=90°,∴AC,BD是☉O的直径,且交点为圆心O.∵AD=CD,AO=CO,∴AC⊥BD.(2)解如图,画直径CK,连接DK,BC,则∠KDC=90°,∴∠K+∠KCD=90°.∵AC⊥BD,∴∠ACB+∠EBC=90°.∵∠EBC=∠K,∴∠ACB=∠KCD,∴=,∴DK=AB=2.∵DC=4,∴KC==2,∴☉O的半径为.〚导学号92034208〛18.(6分)如图,O是△ABC的内心,BO的延长线和△ABC 的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC 为平行四边形.(1)求证:△BOC≌△CDA:(2)若AB=2,求阴影部分的面积.(1)证明∵O为△ABC的内心,∴∠2=∠3,∠5=∠6.∵∠1=∠2,∴∠1=∠3,由AD∥CO,AD=CO,∴∠4=∠5,∴∠4=∠6,∴△BOC≌△CDA.(2)解由(1)得BC=AC,∠3=∠4=∠6,∴∠ABC=∠ACB,∴AB=AC,△AB C为等边三角形,∴O为△ABC的内外心,∴OA=OB=OC.设E为BD与AC的交点,BE垂直平分AC.在Rt△OCE 中,CE=AB=1,∠OCE=30°,∴OA=OB=OC=,∵∠AOB=120°,∴S阴=S扇形AOB-S△AOB=-×2×=.19.(8分)如图,在边长为1的正方形网格中,△ABC 的顶点均在格点上,点A,B的坐标分别是A(4,3),B(4,1),把△ABC绕点C逆时针旋转90°后得到△A 1B1C.(1)画出△A1B1C,直接写出点A1,B1的坐标;(2)求在旋转过程中,△ABC所扫过的面积.解(1)所求作△A1B1C如图所示:由A(4,3),B(4,1)可建立如图所示坐标系,则点A1的坐标为(-1,4),点B1的坐标为(1,4);(2)∵AC===,∠ACA1=90°,∴在旋转过程中,△ABC所扫过的面积为+S△ABC=+×3×2=+3.20.(10分)已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB 于点E.(1)求证:AC·AD=AB·AE;(2)如果BD是☉O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.(1)证明连接DE.∵AE是直径,∴∠ADE=90°,∴∠ADE=∠ABC.在Rt△ADE和Rt△ABC中,∠A是公共角,故△ADE∽△ABC,则=,即AC·AD=AB·AE.(2)解连接OD.∵BD是圆O的切线,∴OD⊥BD.在Rt△OBD中,OE=BE=OD,∴OB=2OD,∴∠OBD=30°.同理∠BAC=30°.在Rt△ABC中,AC=2BC=2×2=4.〚导学号92034209〛21.(8分)如图,AB为☉O的直径,F为弦AC的中点,连接OF并延长交于点D,过点D作☉O的切线,交BA的延长线于点E.(1)求证:AC∥DE;(2)连接CD,若OA=AE=a,求四边形ACDE的面积.(1)证明∵ED与☉O相切于D,∴OD⊥DE.∵F为弦AC 中点,∴OD⊥AC,∴AC∥DE.(2)解作DM⊥OA于M,连接CD,CO,AD.∵AC∥DE,AE=AO,∴OF=DF.∵AF⊥DO,∴AD=AO,∴AD=AO=OD,∴△ADO是等边三角形,同理△CDO也是等边三角形,∴∠CDO=∠DOA=60°,AE=CD=AD=AO=CO=a,∴AO ∥CD,又AE=CD,∴四边形ACDE是平行四边形,易知DM=a,∴平行四边形ACDE面积为a2.22.(10分)已知:如图,☉O是△ABC的外接圆,=,点D 在边BC上,AE∥BC,AE=BD.(1)求证:AD=CE;(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.(1)证明在☉O 中,∵=,∴AB=AC,∴∠B=∠ACB.∵AE∥BC,∴∠EA C=∠ACB,∴∠B=∠EAC.在△ABD和△CAE 中,∵AB=CA,∠B=∠EA C,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE.(2)解连接AO并延长,交边BC于点H,∵=,OA为半径,∴AH⊥BC,∴BH=CH.∵AD=AG,∴DH=HG,∴BH-DH= CH-GH,即BD=CG.∵BD=AE,∴CG=AE.∵CG∥AE,∴四边形AGCE是平行四边形.23.(10分)如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.(1)求证:∠ACD=∠B.(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;①求tan∠CFE的值;②若AC=3,BC=4,求CE的长.图1图2(1)证明如图中,连接OC.∵OA=OC,∴∠1=∠2.∵CD是☉O切线,∴OC⊥CD,∴∠DCO=90°,∴∠3+∠2=90°.∵AB是直径,∴∠1+∠B=90°,∴∠3=∠B.∴∠ACD=∠B.(2)解①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∠CDE=∠FDB,∠ECD=∠B,∴∠CEF=∠CFE,∵∠ECF=90°,∴∠CEF=∠CFE=45°,∴tan∠CFE=tan 45°=1.②在Rt△ABC中,∵AC=3,BC=4,∴AB==5.∵∠CDA=∠BDC,∠DCA=∠B,∴△DCA∽△DBC,∴===.∵∠CDE=∠BDF,∠DCE=∠B,∴△DCE∽△DBF,∴=.设EC=CF=x,∴=,∴x=.∴CE=.。

【中考专题】2018年九年级数学中考圆专题复习(含答案)

2018年九年级数学中考圆专题复习一、选择题:1.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,∠AED=115°,则∠B的度数是（）A．50°B．75°C．80°D．100°2.如图,已知☉O是△ABD的外接圆,AB是☉O的直径,CD是☉O的弦,∠ABD=58°,则∠BCD等于( )A．16°B．32°C．58°D．64°3.已知圆内接正三角形的边心距为1，则这个三角形的面积为（）A．2B．3C．4D．64.如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C=( ) A．20°B．25°C．40°D．50°5.如图，PA．PB、AB都与⊙O相切，∠P=60°，则∠AOB等于（）A．50°B．60°C．70°D．70°6.如图，AB是⊙O的弦，CD与⊙O相切于点A，若∠BAD=66°，则∠B等于（）A．24°B．33°C．48°D．66°7.如图，圆弧形桥拱的跨度AB=12米，拱高CD=4米，则拱桥的半径为（）A．6.5米B．9米C．13米D．15米8.如图，△ABC是一张三角形纸片，⊙O是它的内切圆，点D、E是其中的两个切点，已知CD=6cm，小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形（△CMN），则剪下的△CMN的周长是（）A．9cm B．12cm C．15cm D．18cm9.如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切，交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是（）A．πB．2πC．D．10.如图，AB 为⊙O 的切线，切点为 B，连接 AO 与⊙O 交与点 C，BD 为⊙O 的直径，连接 CD，若∠A=30°，OA=2，则图中阴影部分的面积为（）二、填空题：11.若圆锥的母线长为3cm ，底面半径为2cm ，则圆锥的侧面展开图的面积 cm 2．12.如图，已知AB 是的直径，BD=CB,∠CAB=30°,请根据已知条件和所给图形，写出三个正确的结论：(除AO=OB=BD 外)①、；②、；③、13.如图，在△ABC 中，已知∠ACB=130°，∠BAC=20°，BC=2，以点C 为圆心，CB 为半径的圆交AB 于点D ，则BD 的长为．14.如图，AB 为半圆直径，O 为圆心，C 为半圆上一点，E 是弧AC 的中点，OE 交弦AC 于点D.若AC=8cm ，DE=2cm ，则OD 的长为 cm.15.如图5，PA ，PB 分别为⊙O 的切线，切点分别为A ．B ，∠P=80°，则∠C=16.如图，点C 在以AB 为直径的半圆上，AB=， AC=4，点D 在线段AB 上运动，点E 与点D 关于AC 对称，DF ⊥DE ，DF 交EC 的延长线于点F ，当点D 从点A 运动到点B 时，线段EF 扫过的面积是．图5 PC BAO三、解答题：17.如图，已知C是弧AB的中点，OC交弦AB于点D．∠AOB=120°，AD=8．求OA的长.18.如图，AB为⊙O的直径，C O⊥AB于O，D在⊙O上，连接BD，CD，延长CD与AB的延长线交于E，F在BE上，且FD=FE．（1）求证：FD是⊙O的切线；（2）若AF=8，tan∠BDF=0.25，求EF的长．19.如图，以AB为直径的⊙O交△ABC的边AC于D、BC于E，过D作⊙O的切线交BC于F，交BA延长线于G，且DF⊥BC．（1）求证：BA=BC；（2）若AG=2，cosB=0.6，求DE的长．20.如图，AB是⊙O的弦，D为OA半径的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．（1）求证：BC是⊙O的切线；（2）连接AF，BF，求∠ABF的度数；（3）如果CD=15，BE=10，sinA=，求⊙O的半径．21.如图，在图中求作⊙P，使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.（要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）22.如图,⊙O的半径r=25,四边形ABCD内接于圆⊙O，AC⊥BD于点H,P为CA延长线上的一点，且∠PDA=∠ABD．（1）试判断PD与⊙O的位置关系,并说明理由；（2）若tan∠ADB=，PA=AH,求BD的长；（3）在（2）的条件下,求四边形ABCD的面积．参考答案1.D2.B3.B4.D5.B6.A7.A8.B9.C10.A11.答案为：6πcm2．12.答案为：∠ACB=550；13.答案为：2．14.答案为：315.答案为：55°16.答案为：32；17.答案：.18. (1)证明:连接OD,∵CO⊥AB,∴∠E+∠C=90°,∵∠DFO为△EFD的外角,且FD=FE,∠ODC为△EOD的外角,且OD=OC,∴∠DFO=∠E+∠EDF=2∠E,∠DOF+∠E=∠ODC=∠C,得∠DOF+∠E+∠DFO=∠C+2∠E,即∠DOF+∠DFO=∠C+∠E=90°,∴FD是⊙O的切线. (2)解:连接AD,如图,∵AB为⊙O的直径,∴∠ADB=90°,∴∠A+∠ABD=90°,∵OB=OD,∴∠OBD=∠ODB,∴∠A+∠ODB=90°,∵∠BDF+∠ODB=90°,∴∠A=∠BDF,而∠DFB=∠AFD,∴△FBD∽△FDA,∴DF:AF=BD:AD,在Rt△ABD中,tan∠A=tan∠BDF=0.25,∴DF:8=0.25,∴DF=2,∴EF=2.19.（1）证明：连结OD，如图，∵DF为切线，∴OD⊥DF，∵DF⊥BC，∴OD∥BC，∴∠ODA=∠C，而OA=OD，∴∠ODA=∠OAD，∴∠OAD=∠C，∴BA=BC；（2）作DH⊥AB于H，如图，设⊙O的半径为r，∵OD∥BC，∴∠B=∠DOG，∴cos∠DOG=cosB=0.6，在Rt△ODG中，∵cos∠DOG=，即=，∴r=3，在Rt△ODH中，∵cos∠DOH==，∴OH=，∴AH=3﹣=，在Rt△ADH中，AD==，∵∠DEC=∠C，∴DE=DC，而OA=OB，OD∥BC，∴AD=CD，∴DE=AD=．20.（1）证明：连接OB∵OB=OA，CE=CB，∴∠A=∠OBA，∠CEB=∠ABC又∵CD⊥OA∴∠A+∠AED=∠A+∠CEB=90°∴∠OBA+∠ABC=90°∴OB⊥BC∴BC是⊙O的切线．（2）连接OF，AF，BF，∵DA=DO，CD⊥OA，∴△OAF是等边三角形，∴∠AOF=60°∴∠ABF=0.5∠AOF=30°（3）过点C作CG⊥BE于点G，由CE=CB，∴EG=0.5BE=5又Rt△ADE∽Rt△CGE∴sin∠ECG=sin∠A=，∴CE==13∴CG==12，又CD=15，CE=13，∴DE=2，由Rt△ADE∽Rt△CGE得=∴AD=•CG=4.8∴⊙O的半径为2AD=9.6．21.解：如图所示.圆P即为所作的圆.22.解：（1）PD与圆O相切．理由：如图，连接DO并延长交圆于点E，连接AE，∵DE是直径，∴∠DAE=90°，∴∠AED+∠ADE=90°，∵∠PDA=∠ABD=∠AED，∴∠PDA+∠ADE=90°，即PD⊥DO，∴PD与圆O相切于点D；（2）∵tan∠ADB=∴可设AH=3k，则DH=4k，∵PA=AH，∴PA=（4﹣3）k，∴PH=4k，∴在Rt△PDH中，tan∠P==，∴∠P=30°，∠PDH=60°，∵PD⊥DO，∴∠BDE=90°﹣∠PDH=30°，连接BE，则∠DBE=90°，DE=2r=50，∴BD=DE•cos30°=；（3）由（2）知，BH=﹣4k，∴HC=（﹣4k），又∵PD2=PA×PC，∴（8k）2=（4﹣3）k×[4k+（25﹣4k）]，解得：k=4﹣3，∴AC=3k+（25﹣4k）=24+7，∴S四边形ABCD=BD•AC=×25×（24+7）=900+．。

2018-2019学年中考数学专题复习：圆

2018-2019学年中考数学专题复习：圆一、选择题。

1. 如图，在⊙O中，直径CD垂直于弦AB，若∠C=25∘，则∠BOD的度数是( )A.25∘B.30∘C.40∘D.50∘2. 如图，四边形ABCD是⊙O的内接四边形，∠B=70∘，则∠D的度数是( )A.110∘B.90∘C.70∘D.50∘3. 如图，AB是⊙O的弦，AC是⊙O切线，A为切点，BC经过圆心．若∠B=20∘，则∠C的大小等于()A.20∘B.25∘C.40∘D.50∘4. 如图，AB是⊙O的直径，C,D是⊙O上的点，∠DCB=30∘，过点D作⊙O的切线交AB的延长线于点E，若AB=4，则DE的长为( )A.2B.4C.4√3D.2√35. 如图，正方形ABCD四个顶点都在⊙O上，点P是劣弧AB上的一点，则∠CPD的度数是( )A.35∘B.40∘C.45∘D.60∘6. 如图，在△ABC中，AB=AC，∠A=40∘，延长AC到点D，使CD=BC，点P是△ABD的内心，则∠BPC=( )A.105∘B.110∘C.130∘D.145∘7. 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30∘，CD=2√3，则阴影部分的面积为（）A.2πB.πC.π3D.2π38. 已知圆的半径是2√3，则该圆的内接正六边形的面积是（）A.3√3B.9√3C.18√3D.36√3二、填空题。

如图，AB是⊙O的直径，AC,BC是⊙O的弦，直径DE⊥BC于点M.若点E在优弧CAB 上,AC=8,BC=6,则EM=________.如图，⊙O是△ABC的外接圆，∠AOB=70∘，AB=AC则∠ABC________．如图，在⊙O中，CD⊥AB于点E，若∠BAD＝30∘，且BE＝2，则CD＝________．如图Rt△ABC中，∠C=90∘，以BC为直径的⊙O交AB于点E，OD⊥BC交⊙O于点D，DE交BC于点F，点P为CB延长线上的一点，延长PE交AC于点G，PE=PF．下列4个结论：①GE=GC；②AG=GE；③OG // BE；∠A=∠P．其中正确的结论是________.(填写所有正确结论的序号)如图，将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心，AB d的长为半径的扇形（忽略铁丝的粗细），则所得扇形FAB（阴影部分）的面积为________．如图，在圆心角为90∘的扇形OAB中，半径OA=4，C为AB^的中点，D，E分别为OA，OB的中点，则图中阴影部分的面积为________．三、解答题。

2018年中考数学真题分类汇编第一期专题30圆的有关性质试题含解析

圆的有关性质一、选择题1．（2018•山东枣庄•3分）如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（）A．B．2C．2D．8【分析】作OH⊥CD于H，连结OC，如图，根据垂径定理由OH⊥CD得到HC=HD，再利用AP=2，BP=6可计算出半径OA=4，则OP=OA﹣AP=2，接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH=OP=1，然后在Rt△OHC中利用勾股定理计算出CH=，所以CD=2CH=2．【解答】解：作OH⊥CD于H，连结OC，如图，∵OH⊥CD，∴HC=HD，∵AP=2，BP=6，∴AB=8，∴OA=4，∴OP=OA﹣AP=2，在Rt△OPH中，∵∠OPH=30°，∴∠POH=60°，∴OH=OP=1，在Rt△OHC中，∵OC=4，OH=1，∴CH==，∴CD=2CH=2．故选：C．【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理以及含30度的直角三角形的性质．2．（2018•四川凉州•3分）如图，⊙O是△ABC的外接圆，已知∠ABO=50°，则∠ACB的大小为（）A．40°B．30°C．45°D．50°【分析】首先根据等腰三角形的性质及三角形内角和定理求出∠AOB的度数，再利用圆周角与圆心角的关系求出∠ACB的度数．【解答】解：△AOB中，OA=OB，∠ABO=50°，∴∠AOB=180°﹣2∠ABO=80°，∴∠ACB=∠AOB=40°，故选：A．【点评】本题主要考查了圆周角定理的应用，涉及到的知识点还有：等腰三角形的性质以及三角形内角和定理．3. （2018•山东菏泽•3分）如图，在⊙O中，OC⊥AB，∠ADC=32°，则∠OBA 的度数是（）A．64°B．58°C．32°D．26°【考点】M5：圆周角定理；KD：全等三角形的判定与性质．【分析】根据垂径定理，可得=，∠OEB=90°，根据圆周角定理，可得∠3，根据直角三角形的性质，可得答案．【解答】解：如图，由OC⊥AB，得=，∠OEB=90°．∴∠2=∠3．∵∠2=2∠1=2×32°=64°．∴∠3=64°，在Rt△OBE中，∠OEB=90°，∴∠B=90°﹣∠3=90°﹣64°=26°，故选：D．【点评】本题考查了圆周角定理，利用垂径定理得出=，∠OEB=90°是解题关键，又利用了圆周角定理．4. （2018•江苏盐城•3分）如图，为的直径，是的弦，，则的度数为（）A.B.C. D.7.【答案】C【考点】圆周角定理【解析】【解答】解：∵，∠ADC与∠B所对的弧相同，∴∠B=∠ADC=35°，∵AB是⊙O的直径，∴∠ACB=90°，∴∠CAB=90°-∠B=55°，故答案为：C【分析】由同弧所对的圆周角相等可知∠B=∠ADC=35°；而由圆周角的推论不难得知∠ACB=90°，则由∠CAB=90°-∠B即可求得。

中考数学-2018年中考数学圆复习专题精品

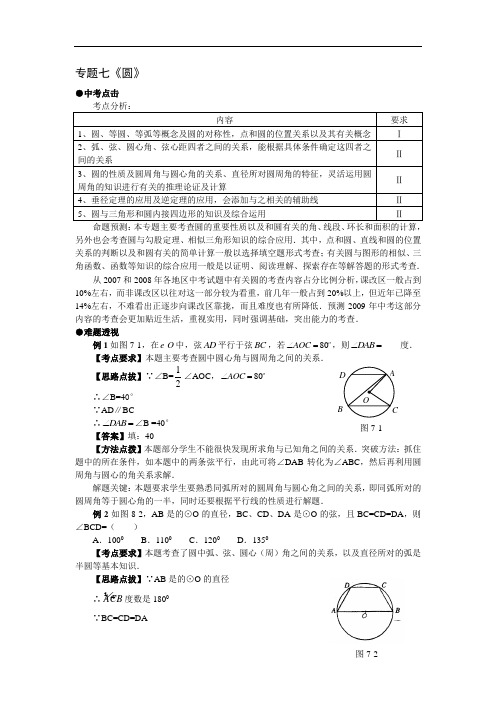
专题七《圆》●中考点击命题预测：本专题主要考查圆的重要性质以及和圆有关的角、线段、环长和面积的计算，另外也会考查圆与勾股定理、相似三角形知识的综合应用．其中，点和圆、直线和圆的位置关系的判断以及和圆有关的简单计算一般以选择填空题形式考查；有关圆与图形的相似、三角函数、函数等知识的综合应用一般是以证明、阅读理解、探索存在等解答题的形式考查．从2007和2008年各地区中考试题中有关圆的考查内容占分比例分析，课改区一般占到10%左右，而非课改区以往对这一部分较为看重，前几年一般占到20%以上，但近年已降至14%左右，不难看出正逐步向课改区靠拢，而且难度也有所降低．预测2009年中考这部分内容的考查会更加贴近生活，重视实用，同时强调基础，突出能力的考查．●难题透视例1如图7-1，在O 中，弦AD 平行于弦BC ，若80AOC ∠=，则DAB ∠=____度．【考点要求】本题主要考查圆中圆心角与圆周角之间的关系．【思路点拔】∵∠B=12∠AOC ，80AOC ∠= ∴∠B=40° ∵AD ∥BC∴DAB ∠=∠B =40° 【答案】填：40【方法点拨】本题部分学生不能很快发现所求角与已知角之间的关系．突破方法：抓住题中的所在条件，如本题中的两条弦平行，由此可将∠DAB 转化为∠ABC ，然后再利用圆周角与圆心的角关系求解．解题关键：本题要求学生要熟悉同弧所对的圆周角与圆心角之间的关系，即同弧所对的圆周角等于圆心角的一半，同时还要根据平行线的性质进行解题．例2如图8-2，AB 是的⊙O 的直径，BC 、CD 、DA 是⊙O 的弦，且BC=CD=DA ，则∠BCD=（）A ．1000B ．1100C ．1200D ．1350【考点要求】本题考查了圆中弧、弦、圆心（周）角之间的关系，以及直径所对的弧是半圆等基本知识．【思路点拔】∵AB 是的⊙O 的直径∴ACB 度数是1800∵BC=CD=DA图7-1∴BC =CD =DA∵∠BCD=001(18060)2=1200【答案】选填C【方法点拨】本题要求学生要能比较熟悉圆中的弧、弦和圆心角之间的有关系，即同圆中相等的弦所对的弧相等，所对的圆心角也相等，同时还要知道直径是圆的一条特殊的弦，其所对的圆心角等于180°，以及圆心角与圆周角之间的关系，综合运用这些知识，容易理解要求某个圆周角，只需求得其所对的弧的度数．例3已知：AB 和CD 为⊙O 的两条平行弦，⊙O 的半径为5cm ，AB=8cm ，CD=6cm ，求AB 、CD 间的距离是．【考点要求】本题考查圆中弦、弦心距等与弦有关的计算问题．【思路点拔】由于圆内的的两条弦均小于圆的直径，因此可确定出圆中的两条平行弦的位置关系有两种：一是位于圆心的同侧；二是位于圆心的异侧．如图8-3：过O 作EF ⊥AB ，分别交AB 、CD 于E 、F ，则AE=4㎝，CF=3㎝，由勾股定理可求出OE=3㎝，OF=4㎝．故当AB 、CD 在圆心异侧时，距离为7㎝，在圆心同侧时，距离为1㎝．【答案】填：7㎝或1㎝【方法点拨】本题难点有两个：一是有不少学生容易只考虑其中的一种情形，而忽视另一情形；二是辅助线的添加．突破方法：一般几何填空题中，如果不配图，在自己作图时，应全面考虑各种可能情况．圆中与弦有关的计算或证明问题，往往需要连结半径和弦心距，以构造直角三角形，从而应用勾股定理进行计算．例4用圆规、直尺作图，不写作法，但要保留作图痕迹．某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图7-5图是水平放置的破裂管道有水部分的截面．（1）请你补全这个输水管道的圆形截面；（2）若这个输水管道有水部分的水面宽AB ＝16cm ，水面最深地方的高度为4cm ，求这个圆形截面的半径．【考点要求】本题考查圆内心的确定，及与弦有关计算问题，同时考查学生动手操作图形的能力和利用基本知识解决简单问题的能力．【思路点拔】（1）正确作出图形，如图7-6并做答．（2）过O 作OC ⊥AB 于D ，交弧AB 于C ，∵OC ⊥AB ， ∴BD ＝21AB ＝21×16＝8cm ．由题意可知，CD ＝4cm ．设半径为x cm ，则OD ＝（x －4）cm ．在Rt △BOD 中，由勾股定理得：OD 2＋BD 2＝OB 2， ∴( x －4)2＋82＝x 2．∴x ＝10．【答案】这个圆形截面的半径为10cm ．【方法点拨】这是一道作图与解答相结合的中考题，部分学生不会补全整个圆面或者补图7-5B (B) 图7-3图7-6全之后不知如何进行计算．突破方法：补全圆面的关键在于确定圆心，然后再利用勾股定理进行计算．解题关键：确定圆心时，主要根据圆的定义，取弧上的两条弦，作出两条弦的垂直平分线，交点即为圆心，然后连结半径构造直角三角形．例5如图7-7，有一木制圆形脸谱工艺品，H 、T 两点为脸谱的耳朵，打算在工艺品反面两耳连线中点D 处打一小孔．现在只有一块无刻度单位的直角三角板（斜边大于工艺品的直径），请你用两种不同的方法确定点D 的位置（画出图形表示），并且分别说明理由．【考点要求】本题考查线段垂直平分线知识，通过对圆中弦的中点的确定，考查学生综合运用知识的能力．【思路点拔】方法一：画弦的垂直平分线常用的依据是根据垂径定理，如图7-8中，图①，画TH 的垂线L 交TH 于D ，则点D 就是TH 的中点．方法二：利用全等三角形，如图②，分别过点T 、H 画HC ⊥TO ，TE ⊥HO ，HC 与TE 相交于点F ，过点O 、F 画直线L 交HT 于点D ，由画图知，Rt △HOC ≌Rt △TOE ，易得HF=TF ，又OH=OT ，所以点O 、F 在HT 的中垂线上，所以HD=TD 了，则点D 就是HT 的中点．方法三：如图③，（原理同方法二）【答案】见图．【方法点拨】这一道题有一定的开放性，题目中只提供了一块无刻度单位的直角三角板（斜边大于工艺品的直径），工具的限至使用学生思维不易完全打开．突破方法：充分利用三角板直角，可画垂直线段，从而能够根据垂径定理或者构造全等的直角三角形来确定弦的中点．图7-7图7-8③②①例6如图7-9，AB 是⊙O 的直径，BD 是⊙O 的弦，延长BD 到点C ，使DC =BD ，连接AC 交⊙O 与点F ．（1）AB 与AC 的大小有什么关系?为什么?（2）按角的大小分类，请你判断△ABC 属于哪一类三角形，并说明理由．【考点要求】本题考查与圆有关的性质在三角中的应用．【思路点拔】（1）（方法1）连接DO ，∵OD 是△ABC 的中位线，∴DO ∥CA ，∵∠ODB ＝∠C ，∴OD ＝BO ，∴∠OBD＝∠ODB ，∴∠OBD ＝∠ACB ，∴AB ＝AC（方法2）连接AD ， ∵AB 是⊙O 的直径，∴AO ⊥BC ，∵BD ＝CD ，∴AB ＝AC（方法3）连接DO ∵OD 是△ABC 的中位线，∴OD=21AC ，OB=OD=21AB ，∴AB=AC （2）连接AD ，∵AB 是⊙O 的直径，∴∠ADB ＝90°∴∠B ＜∠ACB ＝90°．∠C ＜∠ACB ＝90°．∴∠B 、∠C 为锐角∵AC 和⊙O 交于点F ，连接BF ，∴∠A ＜∠BFC ＝90°．∴△ABC 为锐角三角形【答案】（1）AB ＝AC ；（2）△ABC 为锐角三角形【方法点拨】部分学生第（1）题会做出判断，但不知如何证明，而第（2）题又容易将问题结果简单、特殊化，易错误的判断为等边三角形．突破方法：判断或证明线段的大小关系时，一般结论是相等，在同一个三角形中可根据等角对等边证明，如果在两个三角形中，往往会根据三角形全等证明，同时还要看清题目要求，如本题就是要求按角的大小分类进行判断，而不是边的大小关系．解题关键：证明同一个三角形中的两边相等，一般根据等角对等边进行证明．例7如图7-13，已知AB 为⊙O 的直径，弦CD ⊥AB ，垂足为H ．（1）求证：AH ·AB =AC 2；（2）若过A 的直线与弦CD （不含端点）相交于点E ，与⊙O 相交于点F ，求证：AE ·AF =AC 2；（3）若过A 的直线与直线CD 相交于点P ，与⊙O 相交于点Q ，判断AP ·AQ =AC 2是否成立(不必证明)．【考点要求】本题考查与圆有关的三角形相似问题，是一道几何综合证明题．【思路点拔】（1）连结CB ，∵AB 是⊙O 的直径，∴∠ACB =90°．而∠CAH =∠BAC ，∴△CAH ∽△BAC ． ∴ACAH AB AC ，即AH ·AB =AC 2 ．（2）连结FB ，易证△AHE ∽△AFB ，∴ AE ·AF =AH ·AB ，∴ AE ·AF =AC 2 ．(也可连结CF ，证△AEC ∽△ACF )（3）结论AP ·AQ =AC 2成立．图7-9 OF DC B A 图7-13【答案】（3）结论AP ·AQ =AC 2成立．【规律总结】等积式的证明往往要转化为比例式进行，部分学生不知改写为何种比例式比较合适．突破方法：把等积式转化为比例式时，要结合图形书写，如证明AH ·AB =AC 2时，可将其先转化为ACAH AB AC ，然后从比例式中对应边的比容易看出证明的目标为△CAH ∽△BAC ，从而使得解题变得有的放矢．解题关键：证明圆中的等积式或比例式问题时，往往会利用三角形的相似，因为圆中容易证明角相等．●难点突破方法总结在求解有关圆的中考试题，尤其是难题时，应尽量注意巧妙而又快速地找到其突破口，把题目由繁化简，变难为易．归纳下来，有这样几个方面值得考生们注意：1.掌握解题的关键点．（1）有直径，常作其所对的圆周角；（2）有切线，常将切点与圆心连结起来；（3）有关弦的问题，常需作弦心距．联系垂径定理和直角三角形中的勾股定理；（4）研究两圆位置关系时，常作公切线和连心线；（5）有关切线的判定问题，根据题目条件，主要是两条思路，连半径证明垂直，或者是作垂直证明半径．2.重视基本定理与基本图形相结合，计算与推理相结合，灵活运用各种方法．3.重视数学思想方法的应用．运用分析法、演绎法、截补法，结合方程思想、分类讨论思想、数形结合思想解有关圆的应用题，探索开放性题和方案设计．●拓展演练一、选择题1．已知⊙O 的半径为5cm ，A 为线段OP 的中点，当OP=6cm ，点A 与⊙O 的位置关系时（）A ．点A 在⊙O 内B ．点A 在⊙O 上C ．点A 在⊙O 外D ．不能确定2．已知⊙O 1与⊙O 2的半径分别为3cm 和4cm ，圆心距=10cm ，那么⊙O 1与⊙O 2的位置关系是（）A ．内切B ．相交C ．外切D ．外离3．下列语句中正确的有（）①相等的圆心角所对的弧相等 ②平分弦的直径垂直于弦 ③长度相等的两条弧是等弧 ④ 经过圆心的每一条直线都是圆的对称轴．A ．1个B ．2个C ．3个D ．4个4．已知圆的半径为6．5cm ，如果一条直线和圆心的距离为9cm ，那么这条直线和这个圆的位置关系是（）A ．相交B ．相切C ．相离D ．相交或相离5．如图，点P 是⊙O 的直径BA 延长线上一点，PC 与⊙O 相切于点C ，CD ⊥AB ，垂足为D ，连结AC ．BC ．OC ，那么下列结论中：①PC 2=PA ·PB ；②PC ·OC =OP ·CD ；③OA 2=OD ·OP ．正确的有（）A ．0个B ．1个C ．2个D ．3个6．AB 是⊙O 的直径，点D ．E 是半圆的三等分点，AE ．BD 的延长线交于点C ，若CE=2，则图中阴影部分的面积是（）A ．43π B ．23πC ．23πD ．13π二、填空题7．直角三角形的两条边长分别为6和8，那么这个三角形的外接圆半径等于．8．如图，已知AB是⊙O的直径，CD是弦，且CD⊥AB，BC=6，AC=8，则sin∠ABD 的值是9．用48m长的竹篱笆在空地上，围成一个绿化场地，现有两种设计方案，一种是围成正方形场地；另一种是围成圆形场地．现请你选择，围成（圆形．正方形两者选一）场地的面积较大．10．某落地钟钟摆的摆长为0．5m，来回摆动的最大夹角为20°，已知在钟摆的摆动过程中，摆锤离地面的最低高度为am，最大高度为bm，则b a-=m（不取近似值）．11．如图，圆锥的底面半径为6cm，高为8cm，则将该圆锥沿母线剪开后所得扇形对应的圆心角为12．“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”此问题的实质就是解决下面的问题：“如图8，CD为⊙O的直径，弦AB⊥CD于点E，CE=1，AB=10，求CD的长”．根据题意可得CD的长为．三、解答题13．如图，在△ABC中，∠C=900，AC=8，AB=10，点P在AC上，AP=2，若⊙O 的圆心在线段BP上，且⊙O与AB．AC都相切，求⊙O的半径．14．已知: 如图，AB是⊙O的直径，⊙O过AC的中点D，DE切⊙O于点D，交BC 于点E．(1)求证: DE⊥BC; (2)如果CD=4，CE=3，求⊙O的半径．15．如图所示，外切于P点的⊙O1和⊙O2是半径为3cm的等圆，连心线交⊙O1于点A，交⊙O2于点B，AC与⊙O2相切于点C，连接PC，求PC的长．C16．如图，已知：C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B 点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G．（1）求证：点F是BD中点；（2）求证：CG是⊙O的切线；（3）若FB=FE=2，求⊙O的半径．17．已知：AB为⊙O的直径，P为AB弧的中点．（1）若⊙O′与⊙O外切于点P（见图甲），AP．BP的延长线分别交⊙O′于点C．D，连接CD，则△PCD是三角形；（2）若⊙O′与⊙O相交于点P．Q（见图乙），连接AQ．BQ并延长分别交⊙O′于点E．F，请选择下列两个问题中的一个．．作答：问题一：判断△PEF的形状，并证明你的结论；问题二：判断线段AE与BF的关系，并证明你的结论．我选择问题，结论：．●习题答案专题七《圆》1.【答案】A [点拨：根据圆的定义及点和圆的位置关系进行分析]2.【答案】D [点拨：根据圆与圆的位置关系进行判断]3.【答案】A [点拨：这是一道概念辨析题，正确理解等弧的概念是解此类题目的关键．等弧只能在同圆中，长度相等或度数相等的两条弧都不能判断是等弧，因此①③都是错误的，圆内任意两条直径都互相平分，但不一定垂直，故②不正确]4.【答案】C [点拨：根据已知条件圆心到直线的距离为9cm ，大于圆的半径6.5cm ，所以直线与圆相离]5.【答案】D [点拨：由题目已知条件，容易证明△PCA ∽△PBC ．△OCD ∽△OPC ，所以PC PB PA PC =，PC CD OP OC =，OC OP OD OC=，又由于OA=OC ，从而可推得三个结论全部正确] 6.【答案】A [点拨：∵AE ED DB ==，∴ ∠A=∠ABC=600，∴△ABC 是等边三角形，又 AB 是⊙O 的直径，∴∠AEB=900 ，即 BE ⊥AE ，∴AC=2CE=4=AB ， ∴S 阴=S 扇形OBE－S ▲ABE =43π7.【答案】5 [点拨：直角三角形外接圆的圆心在斜边的中点上，且半径等于斜边的一半]8.【答案】45 [由已知已知AB 是⊙O 的直径，得∠ACB=90O ，AB 垂直平分CD ，∴△BCD 为等腰三角形，∴∠ABD=∠ABC ，∴sin ∠ABD=sin ∠ABC=45AC AB =] 9.【答案】圆 [点拨：用同样长度的材料，圆形场地的面积较大]10.【答案】0.5(1cos10)-︒ [点拨：根据垂径定理计算]11.【答案】216o [10l ==（cm ），C=2πr=12π，∴n=00180216C L π=] 12.【答案】26 [点拨：由垂径定理可知，CD 平分弦AB ，所以152AE AB ==，设⊙O 的半径为R ，连结OA ，在Rt △AOE 中，222AO AE OE =+，所以2225(1)R R =+-，解之，得R=13，所以CD=2R=26]13.【答案】解：由题意，，过O 分别作OD ⊥AB ，OE ⊥OE ，则D ．E 分别是AB ．AC 与⊙O 相切的切点，则AD=AE ，OD=OE ，26AP CP AC AP BC =∴=-==，,OE CP BC CP ⊥⊥又，∴B C P △∽△OEP ，∴EP=OE ，设OE=x ，则BD =AB -AD =AB -AE =10-(2+x )=8-x ，OB =BP-OP =， ∴(8-x )2+x 2=2(6-x )2 ，∴x =1，∴⊙O 的半径为114.【答案】解：（1）连结OD ．∵DE 切⊙O 于点D ，∴DE ⊥OD ， ∴∠ODE =900 ，又∵AD =DC ，AO =OB ，∴OD //BC ，∴∠DEC =∠ODE =900，∴DE ⊥BC（2）连结BD ．∵AB 是⊙O 的直径， ∴∠ADB =900 ，∴BD ⊥AC ， ∴∠BDC =900 ，又∵DE ⊥BC ， △Rt CDB ∽△Rt CED ，∴CE DC DC BC =， ∴BC=3163422==CE DC 又∵OD=21BC ，∴OD =3831621=⨯，即⊙O 的半径为38．15.【答案】解：设PC =x cm ，BC =y cm ，连结BC ，则∠BCP =90o ，AC 2=AP ·AB ， ∴AC又∠ACP =∠CBP ，∴△ACP ∽△ABC ， PC BC AC AB ∴=，即①2AB PB +=2又PC ，即236x y +=2②，由①、②得，（舍去），∴PC 16.【答案】解：（1）∵CH ⊥AB ，DB ⊥AB ，∴△AEH ∽△AFB ，△ACE ∽△ADF ∴FDCE AF AE BF EH ==，∵HE ＝EC ，∴BF ＝FD （2）方法一：连接CB ．OC ，∵AB 是直径， ∴∠ACB ＝90°，∵F 是BD 中点，∴∠BCF =∠CBF =90°－∠CBA =∠CAB =∠ACO ，∴∠OCF =90°，∴CG 是⊙O 的切线方法二：可证明△OCF ≌△OBF（3）解：由FC =FB =FE 得：∠FCE=∠FEC ，可证得：FA ＝FG ，且AB ＝BG ，由切割线定理得：[2＋FG ]2＝BG ×AG =2BG 2 ①在Rt △BGF 中，由勾股定理得：BG 2＝FG 2－BF 2 ②由①、②得：FG 2－4FG －12=0，解之得：FG 1＝6，FG 2＝－2（舍去）∴AB ＝BG ＝24，∴⊙O 半径为22。

2018全国各地中考数学试题《圆》试题汇编(解答题)

2018全国各地中考数学试题《圆》试题汇编(解答题)2018全国各地中考数学试题《圆》解答题汇编1. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．求证：∠CBP=∠ADB．若OA=2，AB=1，求线段BP的长．2.如图，AB是⊙O的直径，AC切⊙O于点A，BC交⊙O 于点D．已知⊙O的半径为6，∠C=40°．求∠B的度数．求AD的长．3.如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E，点C是BF的中点．求证：AD⊥CD；若∠CAD=30°，⊙O的半径为3，一只蚂蚁从点B出发，沿着BE-EC-CB爬回至点B，求蚂蚁爬过的路程．第 1 页共 27 页4. 如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．求证：OP ⊥CD；连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．5. 如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O 于点F，AC平分∠BAD，连接BF．求证：AD⊥ED；若CD=4，AF=2，求⊙O的半径．6. 如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE 丄AB，交AB的延第 2 页共 27 页长线于点E．求证：CB平分∠ACE；若BE=3，CE=4，求⊙O的半径．7.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB 于点F．求证：BC是⊙O的切线；若⊙O的半径是2cm，E 是AD的中点，求阴影部分的面积8.已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，如图①，若D为AB的中点，求∠ABC和∠ABD的大小；如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，第 3 页共 27 页求∠OCD的大小．9. 如图，D是△ABC外接圆上的动点，且B，D位于AC 的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG ⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．求证：BG∥CD；设△ABC外接圆的圆心为O，若AB=3DH，∠OHD=80°，求∠BDE的大小．10. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．求证：AE与⊙O相切于点A；若AE∥BC，BC=27，AC=22，求AD的长．第 4 页共 27 页11.如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．12.如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．求证：DA=DE；若AB=6，CD=43，求图中阴影部分的面积．13.如图，△ABC中，AB=AC，以AB为直径的⊙O交BC 于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G．求证：DF是⊙O的切线；已知BD=25 第 5 页共27 页25. 如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D．过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F．求证：PC是⊙O的切线；若∠ABC=60°，AB=10，求线段CF的长．26. 如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．试判断直线DE与⊙O的位置关系，并说明理；若⊙O的半径为2，∠B=50°，AC=，求图中阴影部分的面积．第 11 页共 27 页27.如图，AB是⊙O的直径，点C为⊙O上一点，CN为⊙O的切线，OM⊥AB于点O，分别交AC、CN于D、M两点．求证：MD=MC；若⊙O的半径为5，AC=45，求MC的长．27. 如图，在⊙O中，AB为直径，AC为弦．过BC延长线上一点G，作GD⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF，CM．判断CM与⊙O的位置关系，并说明理；若∠ECF=2∠A，CM=6，CF=4，求MF的长．第 12 页共 27 页28.如图，在△ABC中，AB=AC，以AB为直径的圆交AC 于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC．求证：四边形ABFC是菱形；若AD=7，BE=2，求半圆和菱形ABFC的面积．29.如图，已知A、B、C、D、E是⊙O上五点，⊙O的直径BE=23，∠BCD=120°，A为BE的中点，延长BA到点P，使BA=AP，连接PE．求线段BD的长；求证：直线PE是⊙O的切线．第 13 页共 27 页30.如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB的延长线于点E、F．求证：EF是⊙O的切线；若AC=4，CE=2，求 BD的长度．31.已知：如图，AB是⊙O的直径，AB=4，点F，C是⊙O上两点，连接AC，AF，OC，弦AC平分∠FAB，∠BOC=60°，过点C作CD⊥AF交AF的延长线于点D，垂足为点D．求扇形OBC的面积；求证：CD是⊙O的切线．32.已知：如图，以等边△ABC的边BC为直径作⊙O，分别交AB，AC于点D，E，过点D作DF⊥AC交AC于点F．求证：DF是⊙O的切线；若等边△ABC的边长为8，求第 14 页共 27 页DE、DF、EF围成的阴影部分面积．33.如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．求证：AE=ED；若AB=10，∠CBD=36°，求AC的长．34.如图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D，OB与⊙O相交于点E．求证：AC是⊙O 的切线；若BD=3，BE=1．求阴影部分的面积．第 15 页共 27 页35.如图，已知⊙O是等边三角形ABC的外接圆，点D在圆上，在CD的延长线上有一点F，使DF=DA，AE∥BC交CF于E．求证：EA是⊙O的切线；求证：BD=CF．36. 如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C．若∠ADE=25°，求∠C的度数；若AB=AC，CE=2，求⊙O半径的长．37. 如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，点D是AM上一点，连接OD，过点B作BE∥OD交⊙O于点E，连接DE并延长交BN于点C．求证：DE是⊙O的切线；第 16 页共 27 页若AD=l，BC=4，求直径AB的长．38. 如图所示，PB是⊙O的切线，B为切点，圆心O在PC上，∠P=30°，D为弧BC的中点．求证：PB=BC；试判断四边形BOCD的形状，并说明理．39. 某居民小区的一处圆柱形的输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径．如图，若这个输水管道有水部分的水面宽AB=16cm，水最深的地方的高度为4cm，求这个圆形截面的半径．40. 如图，AB是⊙O的直径，弦CD⊥AB于点E，过点C 的切线交AB的延长线于点F，连接DF．求证：DF是⊙O的切线；连接BC，若∠BCF=30°，BF=2，求CD的长．第 17 页共 27 页41. 已知，如图AB是⊙O的直径，点P在BA的延长线上，弦BC平分∠PBD，且BD⊥PD于点D．求证：PD是⊙O 的切线．若AB=8cm，BD=6cm，求CD的长．42. 如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC 是平行四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．求证：CF是⊙O的切线；若∠F=30°，EB=8，求图中阴影部分的面积．43.如图，已知△ABC内接于⊙O，AB是直径，OD∥AC， AD=OC．求证：四边形OCAD是平行四边形；第 18 页共 27 页探究：①当∠B= °时，四边形OCAD是菱形；②当∠B满足什么条件时，AD与⊙O相切？请说明理．43. 如图，AB是⊙O的一条弦，OD⊥AB，垂足为点C，交⊙O于点D，点E在⊙O上．若∠AOD=52°，求∠DEB的度数；若OC=3，OA=5，求AB的长．44.如图，在⊙O中，弦AD、BC相交于点E，连接OE，已知AD=BC，AD⊥CB．求证：AB=CD；如果⊙O的半径为5，DE=1，求AE的长．第 19 页共 27 页45.如图，⊙O的直径AB=12，弦AC=6，∠ACB的平分线交⊙O于D，过点D作DE∥AB交CA的延长线于点E，连接AD，BD． AB，BD，AD围成的阴影部分的面积是；求线段DE的长．46.如图，在△ABC中，AB=AC，O为边AC上一点，以OC 为半径的圆分别交边BC，AC于点D，E，过点D作DF⊥AB于点F．求证：直线DF是⊙O的切线；若∠A=45°，OC=2，求劣弧DE的长．第 20 页共 27 页2018全国各地中考数学试题《圆》解答题汇编1. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．求证：∠CBP=∠ADB．若OA=2，AB=1，求线段BP的长．2.如图，AB是⊙O的直径，AC切⊙O于点A，BC交⊙O 于点D．已知⊙O的半径为6，∠C=40°．求∠B的度数．求AD的长．3.如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E，点C是BF的中点．求证：AD⊥CD；若∠CAD=30°，⊙O的半径为3，一只蚂蚁从点B出发，沿着BE-EC-CB爬回至点B，求蚂蚁爬过的路程．第 1 页共 27 页4. 如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．求证：OP ⊥CD；连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．5. 如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O 于点F，AC平分∠BAD，连接BF．求证：AD⊥ED；若CD=4，AF=2，求⊙O的半径．6. 如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE 丄AB，交AB的延第 2 页共 27 页长线于点E．求证：CB平分∠ACE；若BE=3，CE=4，求⊙O的半径．7.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB 于点F．求证：BC是⊙O的切线；若⊙O的半径是2cm，E是AD的中点，求阴影部分的面积8.已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，如图①，若D为AB的中点，求∠ABC和∠ABD的大小；如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，第 3 页共 27 页求∠OCD的大小．9. 如图，D是△ABC外接圆上的动点，且B，D位于AC 的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG ⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．求证：BG∥CD；设△ABC外接圆的圆心为O，若AB=3DH，∠OHD=80°，求∠BDE的大小．10. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．求证：AE与⊙O相切于点A；若AE∥BC，BC=27，AC=22，求AD的长．第 4 页共 27 页11.如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．12.如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．求证：DA=DE；若AB=6，CD=43，求图中阴影部分的面积．13.如图，△ABC中，AB=AC，以AB为直径的⊙O交BC 于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G．求证：DF是⊙O的切线；已知BD=25 第 5 页共27 页。

2018全国各地中考数学试题《圆》试题汇编（解答题）

2018全国各地中考数学试题《圆》试题汇编（解答题）2018全国各地中考数学试题《圆》解答题汇编1.（2018?黄冈）如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．（1）求证：∠CBP=∠ADB．（2）若OA=2，AB=1，求线段BP的长．2.（2018?长春）如图，AB是⊙O的直径，AC切⊙O于点A，BC交⊙O于点D．已知⊙O的半径为6，∠C=40°．（1）求∠B的度数．（2）求AD的长．（结果保留π）3.（2018?德州）如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E，点C是BF的中点．（1）求证：AD⊥CD；（2）若∠CAD=30°，⊙O的半径为3，⼀只蚂蚁从点B出发，沿着BE-EC-CB爬回⾄点B，求蚂蚁爬过的路程（π≈3.14，3≈1.73，结果保留⼀位⼩数）．4.（2018?北京）如图，AB是⊙O的直径，过⊙O外⼀点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．（1）求证：OP⊥CD；（2）连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．5.（2018?昆明）如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O于点F，AC平分∠BAD，连接BF．（1）求证：AD⊥ED；（2）若CD=4，AF=2，求⊙O的半径．6.（2018?兰陵县⼆模）如图，已知三⾓形ABC的边AB是⊙O的切线，切点为B．AC经过圆⼼O并与圆相交于点D、C，过C作直线CE丄AB，交AB的延长线于点E．（1）求证：CB平分∠ACE；（2）若BE=3，CE=4，求⊙O的半径．7.（2018?⾚峰）如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB于点F．（1）求证：BC是⊙O的切线；（2）若⊙O的半径是2cm，E是AD的中点，求阴影部分的⾯积（结果保留π和根号）8.（2018?天津）已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，（I）如图①，若D为AB的中点，求∠ABC和∠ABD的⼤⼩；（Ⅱ）如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD的⼤⼩．9.（2018?福建）如图，D是△ABC外接圆上的动点，且B，D位于AC的两侧，DE⊥AB，垂⾜为E，DE的延长线交此圆于点F．BG⊥AD，垂⾜为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．（1）求证：BG∥CD；⼩．10.（2018?潍坊）如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．（1）求证：AE与⊙O相切于点A；11.（2018?邵阳）如图所⽰，AB是⊙O的直径，点C为⊙O上⼀点，过点B作BD⊥CD，垂⾜为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．12.（2018?襄阳）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上⼀点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．（1）求证：DA=DE；13.（2018?孝感）如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作DF⊥AC于点F，交AB 的延长线于点G．（1）求证：DF是⊙O的切线；，CF=2，求AE和BG的长．14.（2018?抚顺）如图，Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上⼀点，且CD=CB，连接DO并延长交CB的延长线于点E．（1）判断直线CD与⊙O的位置关系，并说明理由；（2）若BE=4，DE=8，求AC的长．15.（2018?泰州）如图，AB为⊙O的直径，C为⊙O上⼀点，∠ABC的平分线交⊙O于点D，DE⊥BC于点E．（1）试判断DE与⊙O的位置关系，并说明理由；（2）过点D作DF⊥AB于点F，若BE=33，DF=3，求图中阴影部分的⾯积．15.（2018?攀枝花）如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作DF⊥AC于点F．（1）若⊙O的半径为3，∠CDF=15°，求阴影部分的⾯积；（2）求证：DF是⊙O的切线；（3）求证：∠EDF=∠DAC．16.（2018?扬州）如图，在△ABC中，AB=AC，AO⊥BC于点O，OE⊥AB于点E，以点O为圆⼼，OE为半径作半圆，交AO于点F．（1）求证：AC是⊙O的切线；（2）若点F是OA的中点，OE=3，求图中阴影部分的⾯积；（3）在（2）的条件下，点P是BC边上的动点，当PE+PF取最⼩值时，直接写出BP的长．17.（2018?云南）如图，已知AB是⊙O的直径，C是⊙O上的点，点D在AB 的延长线上，∠BCD=∠BAC．（1）求证：CD是⊙O的切线；（2）若∠D=30°，BD=2，求图中阴影部分的⾯积．18.（2018?聊城）如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆．（1）求证：AC是⊙O的切线；（2）已知⊙O的半径为2.5，BE=4，求BC，AD的长．19.（2018?长沙）如图，在△ABC中，AD是边BC上的中线，∠BAD=∠CAD，CE ∥AD，CE交BA的延长线于点E，BC=8，AD=3．（1）求CE的长；（2）求证：△ABC为等腰三⾓形．（3）求△ABC的外接圆圆⼼P与内切圆圆⼼Q之间的距离．20.（2018?河南）如图，AB是⊙O的直径，DO⊥AB于点O，连接DA交⊙O于点C，过点C作⊙O的切线交DO于点E，连接BC 交DO于点F．（1）求证：CE=EF；（2）连接AF并延长，交⊙O于点G．填空：21.（2018?咸宁）如图，以△ABC的边AC为直径的⊙O恰为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC 交BC的延长线于点E．（1）求证：DE是⊙O的切线；（2）若AB=25，BC=5，求DE的长．22.（2018?齐齐哈尔）如图，以△ABC的边AB为直径画⊙O，交AC于点D，半径OE∥BD，连接BE，DE，BD，设BE交AC于点F，若∠DEB=∠DBC．（1）求证：BC是⊙O的切线；（2）若BF=BC=2，求图中阴影部分的⾯积．23.（2018?郴州）已知BC是⊙O的直径，点D是BC延长线上⼀点，AB=AD，AE是⊙O的弦，∠AEC=30°．（1）求证：直线AD是⊙O的切线；（2）若AE⊥BC，垂⾜为M，⊙O的半径为4，求AE的长．24.（2018?陕西）如图，在Rt△ABC中，∠ACB=90°，以斜边AB上的中线CD为直径作⊙O，分别与AC、BC交于点M、N．（1）过点N作⊙O的切线NE与AB相交于点E，求证：NE⊥AB；（2）连接MD，求证：MD=NB．25.（2018?宿迁）如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D．过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F．（1）求证：PC是⊙O的切线；（2）若∠ABC=60°，AB=10，求线段CF的长．26.（2018?淮安）如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．（1）试判断直线DE与⊙O的位置关系，并说明理由；（2）若⊙O的半径为2，∠B=50°，AC=4.8，求图中阴影部分的⾯积．27.（2018?随州）如图，AB是⊙O的直径，点C为⊙O上⼀点，CN为⊙O的切线，OM⊥AB于点O，分别交AC、CN于D、M两点．（1）求证：MD=MC；（2）若⊙O的半径为5，AC=45，求MC的长．27.（2018?湖北）如图，在⊙O中，AB为直径，AC为弦．过BC延长线上⼀点G，作GD⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF，CM．（1）判断CM与⊙O的位置关系，并说明理由；（2）若∠ECF=2∠A，CM=6，CF=4，求MF的长．28.（2018?宜昌）如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE⾄点F，使EF=AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD=7，BE=2，求半圆和菱形ABFC的⾯积．29.（2018?黄⽯）如图，已知A、B、C、D、E是⊙O上五点，⊙O的直径BE=2 3，∠BCD=120°，A为BE的中点，延长BA到点P，使BA=AP，连接PE．（1）求线段BD的长；（2）求证：直线PE是⊙O的切线．30.（2018?衡阳）如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB 的延长线于点E、F．（1）求证：EF是⊙O的切线；（2）若AC=4，CE=2，求BD的长度．（结果保留π）31.（2018?怀化）已知：如图，AB是⊙O的直径，AB=4，点F，C是⊙O上两点，连接AC，AF，OC，弦AC平分∠FAB，∠BOC=60°，过点C作CD⊥AF交AF 的延长线于点D，垂⾜为点D．（1）求扇形OBC的⾯积（结果保留π）；（2）求证：CD是⊙O的切线．32.（2018?达州）已知：如图，以等边△ABC的边BC为直径作⊙O，分别交AB，AC于点D，E，过点D作DF⊥AC交AC于点F．（1）求证：DF是⊙O的切线；（2）若等边△ABC的边长为8，求由DE、DF、EF围成的阴影部分⾯积．33.（2018?湖州）如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．（1）求证：AE=ED；（2）若AB=10，∠CBD=36°，求AC的长．34.（2018?临沂）如图，△ABC为等腰三⾓形，O是底边BC的中点，腰AB与⊙O相切于点D，OB与⊙O相交于点E．（1）求证：AC是⊙O的切线；（2）若BD=3，BE=1．求阴影部分的⾯积．35.（2018?常德）如图，已知⊙O是等边三⾓形ABC的外接圆，点D在圆上，在CD的延长线上有⼀点F，使DF=DA，AE∥BC 交CF于E．（1）求证：EA是⊙O的切线；（2）求证：BD=CF．36.（2018?沈阳）如图，BE是O的直径，点A和点D是⊙O上的两点，过点A 作⊙O的切线交BE延长线于点C．（1）若∠ADE=25°，求∠C的度数；（2）若AB=AC，CE=2，求⊙O半径的长．37.（2018?官渡区⼆模）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，点D是AM上⼀点，连接OD，过点B作BE∥OD 交⊙O于点E，连接DE并延长交BN于点C．（1）求证：DE是⊙O的切线；（2）若AD=l，BC=4，求直径AB的长．38.（2018?⾦⽔区校级模拟）如图所⽰，PB是⊙O的切线，B为切点，圆⼼O在PC上，∠P=30°，D为弧BC的中点．（1）求证：PB=BC；（2）试判断四边形BOCD的形状，并说明理由．39.（2018?历城区⼀模）某居民⼩区的⼀处圆柱形的输⽔管道破裂，维修⼈员为更换管道，需要确定管道圆形截⾯的半径．如图，若这个输⽔管道有⽔部分的⽔⾯宽AB=16cm，⽔最深的地⽅的⾼度为4cm，求这个圆形截⾯的半径．40.（2018?昌平区⼆模）如图，AB是⊙O的直径，弦CD⊥AB于点E，过点C 的切线交AB的延长线于点F，连接DF．（1）求证：DF是⊙O的切线；（2）连接BC，若∠BCF=30°，BF=2，求CD的长．41.（2018?天⽔模拟）已知，如图AB是⊙O的直径，点P在BA的延长线上，弦BC平分∠PBD，且BD⊥PD于点D．（1）求证：PD是⊙O的切线．（2）若AB=8cm，BD=6cm，求CD的长．42.（2018?葫芦岛⼀模）如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC 是平⾏四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．（1）求证：CF是⊙O的切线；（2）若∠F=30°，EB=8，求图中阴影部分的⾯积．（结果保留根号和π）43.（2018?内乡县⼀模）如图，已知△ABC内接于⊙O，AB是直径，OD∥AC，AD=OC．（1）求证：四边形OCAD是平⾏四边形；（2）探究：②当∠B满⾜什么条件时，AD与⊙O相切？请说明理由．43.（2018?资中县⼀模）如图，AB是⊙O的⼀条弦，OD⊥AB，垂⾜为点C，交⊙O于点D，点E在⊙O上．（1）若∠AOD=52°，求∠DEB的度数；（2）若OC=3，OA=5，求AB的长．44.（2018?合肥模拟）如图，在⊙O中，弦AD、BC相交于点E，连接OE，已知AD=BC，AD⊥CB．（1）求证：AB=CD；（2）如果⊙O的半径为5，DE=1，求AE的长．。

2018年中考数学真题专题汇编------圆综合题

（ 1）求证： AC CE ；（ 2）求证： BC 2 AC 2 AB AC ；（ 3）已知 O 的半径为 3.
① 若 AB 5 ，求 BC 的长； AC 3
② 当 AB 为何值时， AB AC 的值最大？ AC
26.（2018 四川内江）如图，以 Rt ABC 的直角边 AB 为直径作 O 交斜边 AC 于
长线上一点，且 BC CD , CE AD 于点 E .
（ 1）求证：直线 EC 为 ⊙ O 的切线；（ 2）设 BE 与⊙ O 交于点 F ， AF 的延长线与 CE 交于点 P .已知 PCF ， PC 5 ， PF 4 ，求 sin PEF 的值 .
CBF
21. （2018 浙江金华）如图，在 Rt△ABC 中，点 O 在斜边 AB 上，以 O 为圆心，
OB 为半径作圆，分别与 BC,AB 相交于点 D,E，连结 AED.已知 ∠ 的切线 .
（ 2）若 BC=8， tanB= 1 ,求 ⊙O 的半径 .
A
2
O
C
D
B
22．（ 2018 浙江衢州）如图，已知 AB 为⊙ O 直径， AC 是⊙ O 的切线，连接 BC 交 ⊙O 于点 F，取的中点 D，连接 AD 交 BC 于点 E，过点 E 作 EH⊥AB 于 H．（ 1）求证： △HBE∽△ ABC ；（ 2）若 CF=4， BF=5，求 AC 和 EH 的长．
2018 年中考数学真题专题汇编 ------ 圆综合题
20.（2018 安徽）如图 ,⊙O 为锐角 △ABC 的外接圆 ,半径为 5. （ 1）用尺规作图作出 ∠BAC 的平分线，并标出它与劣弧 BC 的交点 E(保留作图痕迹 ,不写作法 )；（ 2）若（ 1）中的点 E 到弦 BC 的距离为 3,求弦 CE 的长 .

河北省2018年中考数学总复习-圆专题

圆1、如图1，AB 是⊙O 的弦,AC 切⊙O 于点A ,且∠BAC =45°，2=AB ，则⊙O 的面积为（结果可保留π）．2、如图2，O ⊙表示一个圆形工件，图中标注了有关尺寸,并且MB ∶MA ＝１∶４．求工件半径的长．3、某机械传动装置在静止状态时，如图3所示．连杆PB 与点B 运动所形成的⊙O 交于点A ，测量得PA ＝4cm ，AB ＝5cm, ⊙O 半径为4。

5cm ．求点P 到圆心O 的距离．4、如图4—1，在正方形铁皮上剪下一个圆形和扇形，使之恰好围成图4-2所示的一个圆锥模型．设圆的半径为r ，扇形半径为R ，则圆的半径与扇形半径之间的关系为A ．2R r =B ．94R r =C ．3R r =D ．4R r = 5、某工件形状如图5所示，圆弧BC 的度数为60°,AB =6cm ，点B 到点C 的距离等于AB ，∠BAC =30°,则工件的面积等于【】（A )π4 （B ）π6 （C )π8 (D ）π10 6、如图6-1，一个圆球放置在V 形架中．图6—2是它的平面示意图，CA 和CB 都是⊙O 的切线，切点分别是A ，B ．如果⊙O 的半径为23cm ，且AB =6cm ，求∠ACB ．7、如图7，已知圆锥的母线长OA =8,底面圆的半径r =2．若一只小虫从A 点出发,绕圆锥的侧面爬行一周后又回到A 点，则小虫爬行的最短路线的长是 (结果保留根式）．8、（2005）工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图8—1所示的工件槽，其中工件槽的两个底角均为90º,尺寸如图（单位:cm ）．将形状规则的铁球放入槽内时,若同时具有图8—1所示的A ,B ,E 三个接触点，该球的大小就符合要求．图8—2是过球心O 及A ，B ，E 三点的截面示意图．已知⊙O 的直径就是铁球的直径，AB 是⊙O 的弦,CD 切⊙O 于点E ,AC ⊥CD ，BD ⊥CD ．请你结合图8-1中的数据，计算这种铁球的直径．9、图9中，EB 为半圆O 的直径,点A 在EB 的延长线上，AD 切半圆O 于点D ，BC ⊥AD 于点C ，AB=2，半圆O 的半径为2,则BC 的长为( )A ．2 B ．1 C ．1.5 D ．0。

中考数学专题复习卷圆的有关知识(无答案)(2021年整理)

2018年中考数学专题复习卷圆的有关知识（无答案）编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年中考数学专题复习卷圆的有关知识（无答案））的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年中考数学专题复习卷圆的有关知识（无答案）的全部内容。

圆的有关知识一、选择题1。

如图,线段是⊙的直径，弦，垂足为,点是上任意一点，，则的值为（）A.B.C。

D.2.如图，⊙是的外接圆，则点是的（）A. 三条高线的交点B. 三条边的垂直平分线的交点C. 三条中线的交点D。

三角形三内角角平分线的交点3.如图，点A,B，C都在⊙O上，若∠AOC＝140°，则∠B的度数是( ）。

A.70°B.80° C。

110° D。

140°4。

如图，PA，PB分别与相切于点A，B，连结OP．则下列判断错误的是( ）A. ∠PA0=∠PB0=90B. OP平分∠APB C. PA=PBD.5。

如图，△ABC是⊙O的内接三角形，AB＝AC，∠BCA＝65°,作CD∥AB，并与○O相交于点D，连接BD,则∠DBC的大小为（）A。

15°B。

35°C。

25°D. 45°6。

如图，⊙O是△ABC的外接圆，已知∠ABO＝40°,则∠ACB的大小为（）A.30° B。

40° C.50° D。

60°7.如图，⊙O的直径AB=6，若∠BAC=50°,则劣弧AC的长为（）A. 2πB。

C.D。

8。

如图，与相切于点，若,则的度数为（）A。