偏摩尔量-课件(PPT·精·选)

偏摩尔量.ppt

dT
X p
T ,nj
dp
K i 1
X
i
dni
X i def
X ni
T , p,nji
Vi
V ni
T , p,nji
Ui
U ni
T , p,nji
Hi
H ni
T , p,nji
Si
S ni
T , p,nji
Ai
A ni
T , p,nji
Gi
G ni
T , p,nji
nB A mA
量纲为一 mol kg1
组成表示法：
(5)物质B的浓度（物质的量浓度）
cB
B
def
nB V
mol m3
换算关系（二元系A—B)：
xB
M A wB MBwA MAwB
VA* B VB* A VA*B
M AbB
M AcB
M AbB 1 M AcB MBcB
3.2 偏摩尔量
Xi 是在系统恒定T，p 和其它物质的量时，改变 1mol i 物质引起的系统广延性质X的变化.
X i def
X ni
T , p,nji
只有广延量才有偏摩尔量，强度量是不存在偏摩尔量的。
X ni
T , p,nji
U ni
S ,V ,n ji
H ni
S , p,nji
Xi 是状态函数，强度性质
表 3–1 101325Pa，20℃
xB
Vmid
Vm
cm3 mol1 cm3 mol1
与 C2H5OH(B) H2O(A) 混合时的体积变化
Vm
nB / mol
V id / cm3 V / cm3

2 偏摩尔量大学物理

偏摩尔量的定义
2. 只有广度性质才有偏摩尔量，而偏摩尔量是强度性质。 3. 纯物质的偏摩尔量就是它的摩尔量。 4. 任何偏摩尔量都是T，p和组成的函数。
加和公式
按偏摩尔量定义,
k
∑ 则= dZ Z1dn1 + Z2dn2 + ⋅ ⋅ ⋅ + Zk dnk = ZBdnB
B=1
在保持偏摩尔量不变的情况下，对上式积分
物理化学
偏摩尔量
偏摩尔量
偏摩尔量的定义加和公式与Duhem公式
偏摩尔量的定义
多组分系统与单组分系统的差别：
单组分系统的广度性质具有加和性
若1 mol单组分B物质的体积为
V* m,B
则2 mol单组分B物质的体积为
2×
V* m,B
偏摩尔量的定义
而1 mol单组分B物质和1 mol单组分C物质混合,
系统中任一容量性质Z（代表V，U，H，S，A，G等）除了与温度、压力有关外，还与各组分的数量有关，即
Z = Z (T , p, n1, n2 ,… , nk )
偏摩尔量的定义
如果温度、压力和组成有微小的变化，则系统中任一容量性质Z的变化为：
dZ
=
∂Z ∂T
p,n1 ,n2 ,n3 ,,nk
ZB 代表偏摩尔量
GB def
∂G ∂n B T , p,nC(C≠B)
Z* m, B
代表纯物的摩尔量
偏摩尔量的定义
1.偏摩尔量的含义是：在等温、等压条件下，在大量的定组成系统中，加入单位物质的量的B物质所引起广度性质Z的变化值。
或在等温、等压、保持B物质以外的所有组分的物质的量不变的有限系统中，改变 dnB 所引起广度性质Z 的变化值。

偏摩尔量与化学势ppt课件

S B,m
S nB
T ,P,nC (C B)
注意
• 对偏摩尔量的定义都是指等温等压条件下，若非此条件，如
H nB
T ,V ,nC (C B)
H B,m
• 这个偏微商就不是偏摩尔量，当然也就不
能用
H nB
T ,V ,nC (C B)
来求算H。
二、化学势
• 1.定义
• 当某均相体系含有不止一种物质时，它的任何热力学性质都应是P、V、T等热力学函数中任取两个独立变量再加上各物质物质的量的函数，如吉布斯自由能：
Z Z (T , P, n1, n2 , n3...... nk )
• 等温等压下，有
•令
dZ
B
Z nB
dnB
T ,P,nC (C B)
Z nB
T ,P,nC (C B)
Z B,m
•则
k
dZ Z B,m dnB B 1
• ZB,m即为物质B的某种容量性质Z的偏摩尔量（Partial molar quantity）。
• 正如温度T决定相间是否存在热平衡、压力P决定
相间是否存在力学平衡一样，状态函数化学势 B
决定相间是否存在物质平衡。
b.化学势在反应平衡中的应用
• 化学反应中的平衡条件：
B B 0
B
• 应用于达到反应平衡，只做P-V功的封闭体系。
• 式中 B 是反应中各物种B的化学势， B 是各物质的化学计量系数，对生成物取正值，对反应物取负值。
二、亨利定律
• 针对挥发性溶质在溶液中的溶解度，亨利定律规定：
在一定温度和平衡状态下，气体在溶液中的
溶解度（物质的量分数）与该气体的平衡分压成

2.14偏摩尔量

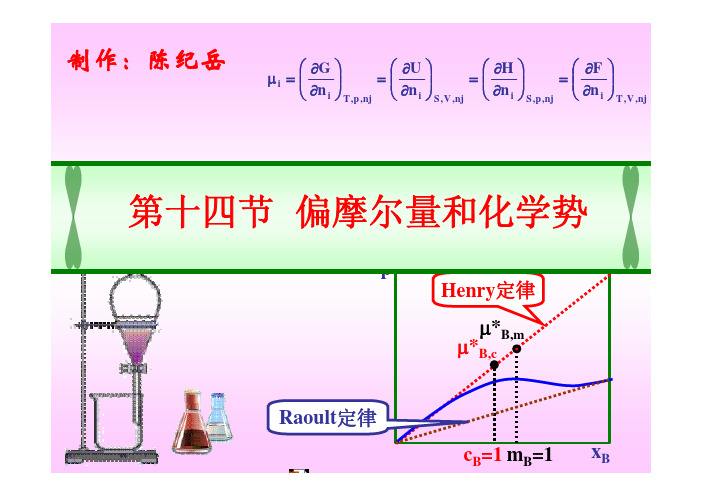
pnj,V,Tinj,p,Sinj,V,Sinj,p,Tii nFnHnUnG⎟⎟⎠⎞⎜⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂=μ制作：陈纪岳第十四节偏摩尔量和化学势返回=？mL 由于分子间的作用力，总体积减少。

减少的量与两者的比例有关。

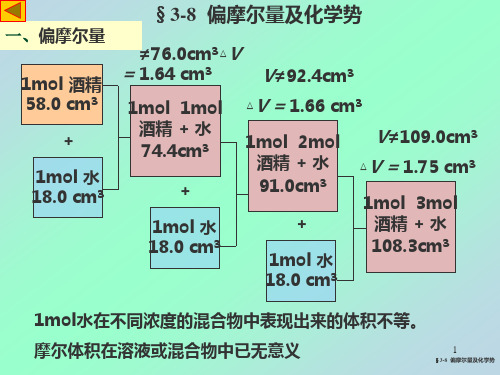
100105110115120125130020406080100乙醇浓度％总体积（mL）50 mL 水＋50 mL 乙醇≠100 mL混合前总体积混合后总体积20601008040因此V = f ( T, p , n 水, n 乙醇)混合返回""""23n ,1n ,p ,T 213n ,2n ,p ,T 1dn n V dn n V dV ⎟⎟⎠⎞⎜⎜⎝⎛∂∂+⎟⎟⎠⎞⎜⎜⎝⎛∂∂== V 1, m dn 1+ V 2, m dn 2+ ……= ΣV i, m dn i式中"3n ,2n ,p ,T 1m,1n V V ⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质1 的偏摩尔体积"3n ,1n ,p ,T 2m,2n V V ⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质2 的偏摩尔体积若在恒温恒压下，多种物质混合，V = f ( n 1, n 2, ……)1. 偏摩尔量体积返回式中"3n ,2n ,p ,T 1m,1n V V ⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质1 的偏摩尔体积"3n ,1n ,p ,T 2m ,2n V V ⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质2 的偏摩尔体积通式()i j nj ,p ,T i m ,i n V V ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质i 的偏摩尔体积其意义为恒温恒压和其它物质不变时，i 物质的改变引起的总体积的改变率。

返回偏摩尔内能，()i j nj ,p ,T i m,i n U U ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔焓，()i j nj ,p ,T i m ,i n H H ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔熵，()i j nj ,p ,T i m ,i n S S ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔亥姆霍滋能，()i j nj ,p ,T im,i n F F ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔吉布斯能，()i j nj ,p ,T i m ,i n G G ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔量特点：（1）只有容量性质的热力学函数才有偏摩尔量（2）T ，p 恒定，n j 不变2．偏摩尔量恒温恒压和其它物质不变时，某物质的改变引起的热力学函数的改变率返回3. 偏摩尔量集合公式如果两种物质混合，总体积不变（分子间作用力相同）V = n 1V 1+ n 2V 2( V 1，V 2为摩尔体积)如总体积改变，V = n 1V 1,m + n 2V 2,m ( V 1,m ，V 2,m 为偏摩尔体积)一般地，容量性质X = Σn i X i,m称为偏摩尔量集合公式返回4. 吉布斯－杜亥姆公式二组分体系dX=X 1,m dn 1+ X 2,m dn 2按集合公式X = n 1X 1,m + n 2X 2,m全微分dX = X 1,m dn 1 + n 1 dX 1,m +X 2,m dn 2+ n 2dX 2,m 吉-杜公式n 1 dX 1,m + n 2dX 2,m = 0 多组分通式Σn i dX i,m =0意义：等温等压时，由浓度变化引起偏摩尔量变化时受到制约的条件返回对于多组分体系，应考虑组分对热力学函数的影响，如G = f ( T ，p ，n 1，n 2…)∑⎟⎟⎠⎞⎜⎜⎝⎛∂∂+⎟⎟⎠⎞⎜⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂=i nj,p ,T i ni ,T ni ,p dn n G dp p G dT T G dG ∑⎟⎟⎠⎞⎜⎜⎝⎛∂∂++−=i nj,p ,T i dn n G Vdp SdT 同理，还有∑⎟⎟⎠⎞⎜⎜⎝⎛∂∂+−=i nj,V ,S i dn n U pdV TdS dU 1. 化学势定义返回⎞⎛∂G 以上四式中加和号内的偏导式是相等的。

偏摩尔量

由于偏摩尔量只决定于组成，与总量无关；当我们按比例加入n1, n2,...nB…时, XB偏 (简写为 XB) 不变
由dXT,p=X1dn1+ X2dn2+...+ XBdnB+... dXT,p= X1dn1+ X2dn2+...+ XBdnB+... XT,p = X1n1 + X2n2+...+ XBnB+...
确定系统状态的独立变量数多于三个
V f (T, p, n1, n2,)
2019/11/20
物理化学II
5
溶液体系热力学
偏摩尔量
（一）偏摩尔量的定义
对一个处于热平衡和力平衡的均相系统，其任一广度性质除取决于温度和压力外，还取决于组成该系统的某组分的量（nB）
以体积为例:
V f (T , p, n1, n2,)
dV (V T ) p,n1,n2 ,dT (V p)T ,n1,n2 ,dp (V n1)T , p,n2 ,dn1 (V n2 )T , p,n1,dn2
2019/11/20
物理化学II
6
溶液体系热力学
偏摩尔量
定义 VB (V n )B T , p,nc,
偏摩尔体积
同理:
偏摩尔内能偏摩尔焓偏摩尔熵
U B (U nB )T , p,nc , H B (H nB )T , p,nc ,
SB (S nB )T , p,nc ,
偏摩尔量并不等于 B 组分本身的性质，还取决于体系内其他组分的存在。
2019/11/20
物理化学II
(G/p)T, x= V
(Gm/p)T, x= Vm (GB/p)T, x = VB

《物理化学第4版》第四章4-2 偏摩尔量ppt课件

def
V nB
T
,
p,n
CB
VB 的物理意义可理解为:在等温、等压以及除B 物质的量 nB 之外其它组分物质的量保持不变条件下，V 随 nB的变化率.
4
也可以理解为：在T、p条件下，向一个包含物质的量无比巨大的系统中加入 1mol 物质B 引起的系统体积 V 的变化。
例如: 25℃和p, 向一大池某浓度的乙醇水溶液中加入1mol的水(18.0cm3), 而整池溶液的体积增大了17.3cm3 ,则此时水的偏摩尔体积为17.3 cm3mol-1。
V2/cm3mol-1=(V/n2)T,p,n1 =234.69[(b/b) -0.07]
b2=0.05 molkg-1时， V2/cm3mol-1= -1.39
20
V=n1V1+n2V2 V1/cm3mol-1= (V-n2V2) /n1 1000g水中, n2=b21kg=0.05mol; n1=1000g/18.02 gmol-1=55.49mol，
例如乙醇水溶液的体积为： V=n乙醇V乙醇+n水V水
12
单组分系统中，体积对物质的摩尔体积具有加和性，
多组分系统的体积对物质的摩尔体积
不具有加和性，V混合 nB V*m,B, 对偏摩
尔体积具有加和性。
13
集合公式同样适用于任一广延性质。如： U = nB UB ； H = nB HB ； S = nB SB ； A= nB AB ； G = nB GB ；
偏摩尔量在少数情况下可能为负值。例如当质量摩尔浓度小于0.07 molkg-1 时，向MgSO4稀溶液中继续加入 MgSO4，系统的体积不增大却减小，对应MgSO4的偏摩尔体积小于零。

《偏摩尔量》PPT课件

y
1 x z
y
z z w x y w y x y
x
z y
x
y
y
z x
y
x
2021/4/25
13
1.22 混合物及溶液
1. 概念
含一个以上组分的系统称多组分系统多组分均相系统又可以区分为混合物或溶液
溶液中的各组分区分为溶剂及溶质，并选用不同的标准态加以研究
H2O，18.07cm3 + C2H5OH，5.74cm3
定温、定压混合
混合物， 23.30cm3
298K,101.325kPa
23.30cm3≠23.81cm3
2021/4/25
17
说明什么?
18.07cm3 (T，p) 水单独存在或在大量水中体积贡献都是
18.07 cm3；但同样量的水对乙醇水混合物的体积贡献不是 18.07cm3
滴加2
• 定温、定压、n1不变条件下，滴加2
• 测定n2和V
n2
……
V
……
组分 1，2
• 利用实验数据绘制 V—n2 曲线
2021/4/25
20
• 利用实验数据绘制 V—n2 曲线
如何从V—n2图得到浓度是
V V'
x2'=n2 ' /（n1+n2 ' ）的V2=？
.. ..
n2 ' n2
V n2
T，p，n1
公式
2021/4/25
33
2. 再谈热力学基本方程
已学过组成一定，量一定的均相系统的热力学基本方程
利用化学势，热力学基本方程可扩展到多组分组成可变的均相系统多组分组成可变的多相系统

§4.3 偏摩尔量

, nk
Z dT p T ,n1 ,n2 ,n3 , dn2
, nk
Z dp n 1 T , p ,n2 ,n3 , dnk
, nk-1
dn1
, nk
Z n 2 T , p ,n1 ,n3 ,
, nk
Z n k T , p ,n1 ,n2 ,n3 ,
Gibbs-Duhem公式
n1dZ1 n2dZ2 nk dZk 0
即
n dZ
B B=1
k
B
0
Байду номын сангаас
这就称为Gibbs-Duhem公式，说明偏摩尔量之间是具有一定联系的。某一偏摩尔量的变化可从其它偏摩尔量的变化中求得。
例4例5
这个公式在多组分系统中很有用
12
Z BdnB
B=1 k
5
常见的偏摩尔量定义式有：
VB
def
V nB T , p ,nC(C B) H nB T , p ,nC(C B) A nB T , p ,nC(C B)
UB
def
U nB T , p ,nC(C B) S nB T , p ,nC(C B) G nB T , p ,nC(C B)
§4.3 偏摩尔量
偏摩尔量的定义
偏摩尔量的加和公式
Gibbs-Duhem公式—— 系统中偏摩尔量之间的关系
1
多组分系统与单组分系统的差别单组分系统的广度性质具有加和性若1 mol单组分B物质的体积为则2 mol单组分B物质的体积为
* Vm,B * 2 Vm,B

3-8偏摩尔量

12
3、相平衡条件
5、化学势与T、p的关系
G p
T
V
G S T p
一般
B
p
T
VB
>0
一般
B
T
p
SB
<0
dG = -SdT + Vdp 对于组成恒定的系统：
恒温时 p μB
恒压时 T μB
注意：化学势不是某种形式的能量！
例题：
化学势是一个状态函数，没有确切的物理意义。化学势是一个表示变化方向的指标。
V GB p T ,nC
Bp
G nB
T
,
p
,nAB
T
,nA
nB
G p
T
,nA
V
nB
T , p ,nAB
T , p ,nAB
VB
10
4. 偏摩尔量之间的函数关系
二、化学势
1、化学势的定义
B
def
GB
G nB
T ,P ,n(C,CB)
G＝f (T，p，nA，nB……)
对多组分系统 X＝ f (T, p, nB, nC, …)
全微分为
dX
X T
dT
p,nB;nC
X p
dp
T ,nB;nC
X nB
T ,
dnB
p,nC;nD
X nC
T
,
dnC
p,nB ;nD
定义
X
B
def
X nB
T
,
p,nC
XB 偏摩尔量
该式表示在恒温恒压和除B 组分以外其它组分的含量都不变的条件下, 任一广延性质X 随B组分物质的量的变化率, 相当于每单位量引起的X 的增量( 折合值, 对应于一定状态)4.

偏摩尔量的理解

偏摩尔量的理解好的，那咱们就来说说偏摩尔量这个事儿。

偏摩尔量啊，就像是在一个大杂烩里，每种成分都有自己独特的“小脾气”。

你看啊，比如说咱们煮一锅汤，这锅汤里有肉、有菜、有调料啥的。

这整个汤的总体积啊、能量啊之类的性质，可不能简单地就把肉、菜、调料各自单独时的那些性质直接加起来。

这就有点像偏摩尔量的概念呢。

咱们具体点说，假设有一杯混合溶液，里面有两种溶质A和B。

这溶液的总体积可不是A溶质单独在这个量的溶剂里的体积加上B溶质单独在这个量的溶剂里的体积。

每个溶质都好像在这个混合体系里有了新的身份，它对总体积的贡献就有了一个特殊的量，这个量就是偏摩尔体积。

就好比一群人一起合作做一件事，每个人发挥的作用可不能简单按照他自己单独干的时候来算，在这个集体里，他的贡献有了新的衡量方式。

再往深里想，偏摩尔量这东西就像是一个神秘的小魔法。

你想啊，在化学体系里，物质们相互混合、相互作用，就像一群小伙伴在一个大院子里玩耍。

每个小伙伴的行为、对这个院子整体氛围的影响都不一样。

偏摩尔量就是在准确地抓住每个小伙伴在这个特定混合体系里独特的影响力。

那这个偏摩尔量有啥用呢？哎呀，用处可大了去了。

你要是在化工生产里，想要调配出最合适的溶液比例，那你就得知道每种物质的偏摩尔量。

这就好比你要组织一场完美的聚会，你得清楚每个朋友的喜好和特长，这样才能让这个聚会既和谐又有趣。

如果不知道偏摩尔量，那就像是你随便乱请人来聚会，可能最后就乱成一锅粥了。

从更微观的角度看，偏摩尔量也反映了分子间的相互作用。

你看那些分子，就像一个个小生灵，在溶液里游来游去。

它们之间有吸引力、有排斥力。

当不同分子混在一起的时候，这种相互作用就改变了每个分子对整体性质的贡献。

这偏摩尔量就像是在记录这种微观世界里微妙的变化。

这就好比在一个小社区里，每个家庭之间的关系不同，有的家庭喜欢热闹，会经常组织活动，对社区的活力贡献就大；有的家庭比较安静，但他们把自家周围打扫得干干净净，对社区的整洁贡献大。

第1节偏摩尔量

稀释后，含乙醇56%的乙醇溶液的质量为
m乙 n乙 M 乙 m x% x%
1.679 10
5
mol 46 103 kg mol1 56%

1.379 104 kg
mH 2O m m乙 6.607 103 kg
1.379 104 kg - 1.679 105 mol 46 103 kg mol1
96% 56%
14.61 17.11
58.01 56.58
解：(1) 首先求算10.0 m3的含乙醇96%的酒中水和
乙醇的物质的量。
n乙 M 乙 0.96 n乙 M 乙 n水 M 水
n乙 4610 kg mol n水 1810 kg mol

n乙 46103 kg mol1
在等温等压保持b物质以外的所有组分的物质的量不变的条件下改变物质以外的所有组分的物质的量不变的条件下改变dnb所引起广度性质x的变化值或在等温等压条件下在大量的定组成体系中加入单位物质的量的的变化值或在等温等压条件下在大量的定组成体系中加入单位物质的量的b物质所引起广度性质x的变化值
第三章化学势
§3.1 偏摩尔量 §3.2 化学势
3 1

3 1

0.96
偏摩尔量的集合公式：
V = n乙V乙 + n水V水
10.0m 3 n乙 58.01 10 6 m 3 mol 1 n水 14.61 10 6 m 3 mol 1

上面两个方程式联立，得：
n乙 1.679 10 5 mol n水 1.788 10 4 mol
三、偏摩尔量的集合公式

4-1 偏摩尔量

6．偏摩尔量之间的关系．组成固定系统热力学函数之间的关系，组成固定系统热力学函数之间的关系，对于偏摩尔量同样成立。同样成立。如 HB＝UB＋pVB 例求证 AB＝UB－TSB GB=HB－TSB
∂GB 。VB = ∂p T . n B ∂GB GB = 证明：证明：根据定义 ∂n B T . p , n
103.03 108.29 113.55 118.81 124.07
101.84 104.84 109.43 115.25 122.25
1.19 3.45 4.12 3.56 1.82
混合物中1mol物质对系统的贡献不同于纯态；混合物中物质对系统的贡献不同于纯态；物质对系统的贡献不同于纯态该贡献值与混合物的组成有关；该贡献值与混合物的组成有关；确定组成可变的多组分均相系统的状态，需指明T、和组成和组成；确定组成可变的多组分均相系统的状态，需指明、p和组成；
非电解质溶液 √ 电解质溶液( (第七章) )
研究方法：研究方法：理想 → 实际
§4.0 组成表示法
摩尔分数——混合物，溶液混合物， ⒈ 摩尔分数混合物
nB xB = ∑ nB
B
nB yB = ∑ nB
B
∑x
B
B
=1
⒉ 质量分数质量分数——混合物，溶液混合物，混合物
mB wB = ∑ mB
乙醇浓度 wB%
混合前乙醇体积 V1/cm3
混合前水体积 V2/cm3
混合前总体积计算值 (V1+V2)/cm3
混合后实测总体积 V/cm3
偏差 ∆V=(V1+V2)–V/cm3
10 30 50 70 90

2010-4-1偏摩尔量

第四章多组分系统热力学
1
引
言
实际系统绝大多数为多组分系统或变组成系统, 必须掌握处理多组分系统的热力学方法. 混合物气态混合物液态混合物 l1 + l2 + … 固态混合物(相平衡章) 液态溶液 l + (l , s, g) 理想液态混合物
多各组分组等同对待分均相溶液系统区分溶剂
和溶质
真实液态混合物
理想稀溶液真实溶液
固态溶液(相平衡章)
电解质溶液在电化学章讨论.
2
补充：
(1) ① ② ③
混合物的组成标度和溶液中溶质B的组成标度
混合物常用的组成标度
B的分子浓度 CB B的质量浓度 B的质量分数
def
def def
N B /V
mB / V mB / mA
A
(1) (2) (3)
偏摩尔内能偏摩尔焓
V VB n B
U UB n B
T , p,nC nB
T , p,nC nB
H HB n B T , p,nC nB S SB n B T , p,nC nB
17
§4.2 化学势
化学势的定义式
B
def G GB n B T , p ,nC nB
1. 多组分单相系统的热力学公式对多组分组成可变的单相系统 G＝f (T, p, nB, nC , ……) G G G dG dT dp dnB p n T p,nC T ,n B T , p ,n n B
C2H5OH *(l)