第五章梁弯曲时的位移解析
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-梁弯曲时的位移(圣才出品)

圣才电子书
ql3/6,D=-ql4/24。
十万种考研考证电子书、题库视频学习平台
故挠曲线方程和转角方程分别为:
w(x)=qx2(x2+6l2-4lx)/(24EI),θ(x)=q(x3-3lx2+3l2x)/(6EI)
则最大挠度 wmax=w(x)|x=l=ql4/(8EI);梁端转角 θB=θ(x)| x=l=ql3/(6EI)。
表 5-1-4 叠加原理计算梁的挠度和转角
四、梁的刚度校核·提高梁的刚度的措施(见表 5-1-5)
表 5-1-5 梁的刚度校核及提高措施
3 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
五、梁内的弯曲应变能 定义:由于梁弯曲变形而存储的能量称为梁内的弯曲应变能。梁在弹性变形过程中,其 弯曲应变能与作用在梁上的外力所作的功相等,常见梁内的弯曲应变能见表 5-1-6。
则最大挠度 wmax=w(x)|x=l=Fl3/3EI;梁端转角 θB=θ(x)| x=l=Fl2/2EI。
图 5-2-1(a)(b) (2)建立如图 5-2-1(b)所示坐标系。 首先列弯矩方程:M(x)=-q(l-x)2/2,由此可得挠曲线近似方程: EIw″=-M(x)=q(l-x)2/2 积分得: EIw′=-q(l-x)3/6+C① EIw=q(l-x)4/24+Cx+D② 该梁的边界条件:x=0,w=0,x=0,w'=0。代入式①、②可确定积分常数:C=
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 5 章 梁弯曲时的位移
5.1 复习笔记
梁在承受荷载时发生相应的变形,变形后轴线相对原位置将会发生位移、梁的截面将出 现转角,梁内会因变形存储能量。本章首先介绍梁的位移概念,并基于坐标系统建立挠曲线 方程;接着介绍求解梁的位移的方法,根据挠曲线近似微分方程积分和按叠加原理计算;再 介绍梁刚度校核以及提高梁刚度的方法;最后介绍梁弯曲应变能的概念及计算方法。
工学梁弯曲时的位移

A
B l
ql 2 / 2
M-
EIw M (x)dx C1 EIw M (x)dxdx C1x C2
如果梁的弯矩方程是分段描述的,如M1(x) , M2(x) ,则挠曲线近似微分方程也应分段建立。 如下例:
F
1
2
A
C
B
l
M
+
Fab/ l梁的位移—挠度,转角的概念 2 梁的挠曲线近似微分方程及其积分 (重点)
3 叠加法计算梁的挠度和转角 4 梁的刚度条件 5 提高梁刚度的措施
1 梁的位移—挠度、转角的概念
弯曲变形:梁在垂直于其轴线的荷载 作用下,使原为直线的轴线变为曲线的变 形。
F
q
(5-2a)
式(5-2a)称为挠曲线近似微分方程。显然, 挠曲线近似微分方程仅适用于小挠度、线 弹性范围内的平面弯曲问题。
若为等截面直梁, EIz为常量,式(5-2a)为:
EIw M(x) (5-2b)
(2)积分法求梁的挠度和转角 (熟练掌握)
EIw M(x) (5-2b)
将式(5-2b)分别对 x 积分一次和二次:
(1)梁的挠曲线近似微分方程
梁在荷载作用下轴线形状的变化称 为变形,一般用各段梁曲率的变化表示。
(1)梁的挠曲线近似微分方程
1/ρ=θ / l
纯弯变形
θ
ρ
M
M
中性层
l
梁纯弯曲时平面弯曲的曲率公式为:
1 M
EIz
(4-4)
式(4-4)表明梁轴线上任一点的曲率与该 点处横截面上的弯矩成正比,而与该截面
1
w
M(x)
( x)
交通第五章梁弯曲时的位移解析

max
B
Pl 2 2EI
Pl 3 wmax wB 3EI
P
θBB x
例4: 已知梁的抗弯刚度为EI。试求图示简支梁在集 中力P作用下的转角方程、挠曲线方程,并确定θmax 和 wmax。
A
y l 2
P
C l 2
B
x
解:AC段:M(x) P x
2
EIw P x 2
x
A
EIw P x2 C 4
w=0
w=0
w=0
=0
自由端:无位移约束条件。
➢位移连续条件和光滑条件
F
M
挠曲线在B、C点连续且光滑 A
B
C
D
连续:wB左= wB右
光滑:B左 = B右
F
弯曲变形的对称点上 C=0
A
C
B
例1:写出梁的挠曲线方程的约束条件和连续条件
F
A
B
C
D
E
思考: 该梁可分几段积分?各段边界点有多少 位移约束与连续条件? 分4段
F
w
x
挠曲线
挠曲线方程
y
EIw x M (x) dx C
w f (x)
转角方程
tan w f (x)
EIw x M (x) dxdx Cx D
式中积分常数C、D由边界条件确定
位移约束条件 位移连续条件
EIwx M xdx Cx D
• 位移约束条件与连续条件
➢位移约束条件
P
C l
2
2
最大转角和最大挠度分别为:
max
A
B
Pl 2 16 EI
wm a x
w
x l 2
Pl3 48EI
梁弯曲时的位移

qmax q A qB
ql3
24 EI
最大挠度在跨中,其值为
wmax
w
|xl
2
ql 2
24 EI
l 3
2l
l 2
2
l 2
3
5ql 4 384 EI
18
第五章 梁弯曲时的位移
例题5-3 试求图示等直梁的挠曲线方程和转角方程,并确定其最大挠度 wmax和最大转角qmax。
wC
Fl 3 48 EI
29
第五章 梁弯曲时的位移
思考: 试绘出图示两根简支梁的弯矩图,并描出它们的挠曲线。并指出:(1) 跨中挠度是否最大?(2)跨中挠度的值是否接近最大挠度值?
l/2
l/4
30
第五章 梁弯曲时的位移
§5-3 按叠加原理计算梁的挠度和转角
当梁的变形微小,且梁的材料在线弹性范围内工作时,梁的挠度和转角均 与梁上的荷载成线性关系。在此情况下,当梁上有若干荷载或若干种荷载作用 时,梁的某个截面处的挠度和转角就等于每个荷载或每种荷载单独作用下该截 面的挠度和转角的代数和。这就是计算梁的位移时的叠加原理(principle of superposition)。
19
第五章 梁弯曲时的位移
解:约束力为
FA
F
b, l
a FB F l
两段梁的弯矩方程分别为
M1x
FA x
F
b l
x
0 x a
M
2
x
FA
x
F
x
a
F
b l
x
F
x
a
材料力学第五章梁弯曲时的位移

实例3 :均布载荷
分析受均布载荷作用下梁的位移。
材料力学第五章梁弯曲时 的位移
在材料力学的第五章中,我们将学习有关梁在弯曲时的位移。掌握梁的基本 知识、位移方程和位移计算方法,以及梁的挠度与转角关系。
梁的基本知识
1 定义
梁是一种长条形结构,承受着沿其长度方向的外部力。
2 类型
常见的梁包括简支梁、悬臂梁和受力梁。
3 材料
梁可以由不同类型的材料制成,例如钢、木材或混凝土。
梁的位移方程
1 弯曲位移
2 挠度
3 转角
梁在弯曲时,沿梁的长度方 向发生位移。
挠度是梁的中点相对于其自 由状态的偏移量。
转角是指梁在弯曲时端部角 度的变化。
简支梁的位移计算方法
1
载荷和反力
计算简支梁上的载荷和反力分布。
2
弯矩方程
使用弯矩方程推导出简支梁的位移方程。
3
边界条件
应用适当的边界条件来解决位移方程中的未知量。
悬臂梁的位移计算方法
加载和支座反力
确定悬臂梁上的加载和支座反力。
弯曲力矩方程
通过推导弯曲力矩方程来解决悬臂 梁的位移问题。
解决边界条件
应用边界条件来计算悬臂梁的位移。
受力梁的位移计算方法
1
截面转动方程
2
推导出受力梁的截面转动方程。
3
确定力的分布
分析受力梁上的力分布,包括集中力和均布 力。
边界条件和位移方程
应用边界条件,求解受力梁的位移方程。ຫໍສະໝຸດ 梁的挠度与转角关系挠度
挠度是梁在弯曲时沿其长度方向上的位移。
转角
转角是梁在弯曲时端部偏离初始位置的角度。
关系公式
挠度和转角之间存在一定的关系,可以通过公式计算。
材料力学上册第五章梁弯曲时的位移

Mechanics of Materials
wmax 在AC段
wmax
=
Fb( l 2 − b2 )3 2 9 3EIl
Mechanics of Materials
例题:已知梁的刚度EI,用奇异函数法求梁的位移
θA、θD、wB、wD。
qa
q
A
B
C Dx
FA a
y
aa
FC
解:建立图示坐标系
1、求约束反力
( ) M(x) = − EI
w′′ 1+ w′2
32
Mechanics of Materials
若挠曲线是较平坦的光滑连续曲线, w′ << 1,
可忽略不计。
则
M (x) = −w′′
EI
即
EIw′′ = − M (x)
——挠曲线近似微分方程
适用条件: 线弹性小变形; 对称弯曲的细长梁。
2、积分法确定梁的位移
一、挠曲线近似微分方程
材力 数学
1 = M(x)
ρ EI
( ) 1 = w′′
ρ 1 + w′2 3 2
x y M > 0 w′′ < 0
( ) M(x) = ± EI
w′′ 1+ w′2
32
x
( ) M(x) = − EI
w′′ 1+ w′2
32
y M < 0 w′′ > 0
☻挠曲线微分方程的正负号与选取的坐标系有关
2
Mechanics of Materials
弯矩的通用方程
∑ ∑ ∑ ∑ ( ) M x =
i
Mi < x −ai >0 +
材料力学第五章梁弯曲时的位移课件

4E 8I
w(0)0 q (0) q0l3
48EI
固定铰支座 活动铰支座
w(l)0 q(l) 0
固定端 活动铰支座
材料力学第五章梁弯曲时的位移
22
M (x)Ew Iq0(3lx 4x2) 抛物线 8
FS(x)ddM xq 80(3l8x)
直线
q(x)dFS dx
材料力学第五章梁弯曲时的位移
12
x
FA
x
FA
Fb l
FB
FB
Fa l
AD段( 0≤ x ≤ a ):
M1(x)
Fbx l
DB段( a ≤ x ≤ l ):
M2(x)F l b xF(xa)
材料力学第五章梁弯曲时的位移
13
x a AD段( 0≤ ≤ ):
M1(x)
Fbx l
EIw1
Fbx l
Ew I1 EqI1F l bx22C1
q0
M(0)0
FS(0)
3 8
q0l
M(l) 81q0l2
FS(l) 85q0l
材料力学第五章梁弯曲时的位移
23
q0
1 8
q0l
材料力学第五章梁弯曲时的位移
7
挠曲线上某些点的已知位移(挠度和 转角)条件 —— 边界条件
wA = 0 wB = 0
wA = 0 qA = 0
边界条件 —— 支座处的约束条件
材料力学第五章梁弯曲时的位移
8
挠曲线的任意点上,有唯一确定的挠 度和转角 —— 连续条件
错!
错!
当弯矩方程需要分段建立时,在相邻梁 段的交接处,应具有相同的挠度和转角。
梁的位移
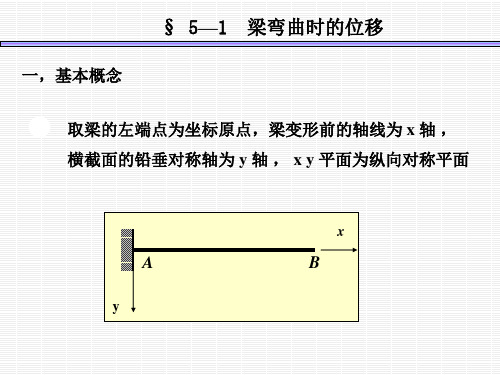
A
C
B
x
w挠度
C'
B'
衡量梁弯曲变形程度的曲线是曲率,我们为什么用挠度和转
角?
2、转角 (slope)
横截面对其原来位置的角位移,称为该截面的转角. 用 表示
横截面的转角也就是曲线在该点处的切线与X轴之间的夹角
A
C
B
x
C'
w挠度(
B 转角
3、挠曲线 (Deflection curve) 梁变形后的轴线称为挠曲线 . 也称弹性曲线
EIz2
Fb 6L
x3
1 6
Fx
a3
Fb
L2 b2 6L
x
EIz1
Fb 2L
x2
Fb
L2 6L
b2
EIz1
Fb 6L
x3
Fb
L2 6L
b2
x
例题 5.3 求图示简支梁在集中荷载F的作用下(F力在右半跨)的最大挠度。
a A
Fb L
6EIz 2EIz 3EIz
例题 5.2
求图所示悬臂梁B端的挠度与转角。
A
x
l
y
边界条件
x0 0 x0 0
xL
B
qL3 6EI z
M x 1 qL x2
B
2
x
EI z
M
x
1 2
q
L
x
2
EI z
EI z
材料力学:梁弯曲时的位移

C1=0 C2=0
(3)
(4)
梁的转角方程和挠曲线方程分别为
Flx Fx 2 w' EI 2 EI
Flx 2 Fx3 w 2 EI 6 EI
24
F
A B x
w
max
l
θ max
y
max 及 wmax都发生在自由端截面处
M ( x) EI
12
(1 w' )
2
3
2
M
M
在规定的坐标系中,x 轴水平向右 为正,y 轴竖直向下为正。 曲线向下凸 时 : w’’< 0 , M > 0 曲线向上凸 时 : w’’ > 0 , M < 0
y
M>0
w" 0
o
M
x
M
M<0
因此, M 与 w’’ 的正负号相反 y
w" 0
挠曲线方程为
w w( x)
式中 ,x 为梁变形前轴线上任一点的横坐标 ,w 为该点的挠度。
A
C
B
x
w挠度
挠曲线
y
C'
转角
5
三、挠度与转角的关系:
A
C
B
x
w挠度
挠曲线
y
C'
转角
tg w' w' ( x)
6
四、挠度和转角符号的规定
挠度:向下为正,向上为负。
转角:自 x 转至 切线方向,顺时针转为正,逆时针转为负。
A
C
B
x
w 挠度
材料力学第五章 梁弯曲时的位移 PPT

M(x) E Iz
高等数学:
1
r (x)
=±(1+ww2)3/2
± w w (1+ 2)3/2
=
M(x) E Iz
M < 0,w > 0
M > 0,w < 0
取负号!
- w w (1+ 2)3/2
=
M(x) E Iz
w w (1+ 2)3/2
=-
M(x) E Iz
挠曲线微分方程
小 变 形
w
=-
DB段(a≤x≤l): M2(x)F l b xF(xa) Ew I2 Fl b xF(xa)
q E w 2 IE2I F l b x 2 2 F (x 2 a )2 C 2
E2 I w F l b x 6 3F(x 6 a )3 C 2xD 2
确定积分常数 连续条件
x = a 时:
w1 w2 w1 w2
边界条件
x = 0 时: w1 0 x = l 时: w2 0
D1D20 C1C2F 6lb(l2b2)
AD段( 0≤ x ≤ a ):
w 1 q1F(6 b lE 2b I2)l2F Eb Ix2l
w1F(6 b lE 2b I2l)x6F EbIx3 l
DB段( a ≤ x ≤ l ):
q w 2 2 F ( 6 lE 2 b b 2 I ) l2 F Ex b 2 I l 2 F E (x I a )2
对于受任意荷载的简支梁,若挠曲线上无拐点, 则可用梁中点的挠度代替最大挠度。
例3:悬臂梁如图,已知F、a,M=0.5 Fa,
梁的弯曲刚度 EI 为常数,试画出挠曲线的大致形 状。
FM
A
B
C
D
a
a
材料力学第五章梁弯曲时的位移分析

a)2
C2 x2 D2
C2
B B x
FBy
目录
5.2 积分法求梁的挠度和转角
4)由边界条件确定积分常数
位移边界条件
x1 0, w1(0) 0 x2 l, w2 (l) 0
光滑连续条件
x1 x2 a, 1(a) 2 (a)
x1 x2 a, w1(a) y2 (a) 代入求解,得
x1 ,0
x1
a
y
CB 段:
M x2
FAy
x2
F ( x2
a)
Fb l
x2
F ( x2
a),
a x2 l
目录
5.2 积分法求梁的挠度和转角
3)列挠曲线近似微分方程并积分
F
AC 段: 0 x1 a
EI
d 2w1 dx12
M (x1)
Fb l
x1
EI
dw1 dx1
EI (x1)
Fb 2l
x2 1
EI dw EI 1 F (l x)2 C
dx
2
EIw 1 F (l x)3 Cx D 6
代入求解
C 1 Fl2, D 1 Fl3
2
6
5)确定转角方程和挠度方程
EI 1 F (l x)2 1 Fl2
2
2
Ax
y
yB
l
F Bx
B
EIw 1 F (l x)3 1 Fl2x 1 Fl3
目录
5.2 积分法求梁的挠度和转角
例2 求梁的转角方程和挠度方程,并求最大转角和最大挠度,
梁的EI已知,l=a+b,a>b。
F
解 1)由梁整体平衡分析得:
材料力学笔记(第五章)

材料力学(土)笔记第五章 梁弯曲时的位移1.梁的位移——挠度及转角为研究等直梁在对称弯曲时的位移取梁在变形前的轴线为x 轴,梁横截面的铅垂对称轴为y 轴而xy 平面即为梁上荷载作用的纵向对称平面梁发生对称弯曲变形后,其轴线将变成在xy 平面内的曲线1AC B度量梁变形后横截面位移的两个基本量是挠度:横截面形心(即轴线上的点)在垂直于x 轴方向的线位移ω转角:横截面对其原来位置的角位移θ 梁变形后的轴线是一条光滑的连续曲线,且横截面仍与该曲线保持垂直因此横截面的转角θ也就是曲线在该点处的切线与x 轴之间的夹角度量等直梁弯曲变形程度的是曲线的曲率梁的变形还受到支座约束的影响通常就用这两个位移量来反映梁的变形情况梁轴线弯曲成曲线后,在x 轴方向也将发生线位移 但在小变形情况下,梁的挠度远小于跨长,梁变形后的轴线是一条平坦的曲线横截面形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不记因此在选定坐标后,梁变形后的轴线可表达为()f x ω=式中,x 为梁在变形前轴线上任一点的横坐标;ω为该点的挠度梁变形后的轴线称为挠曲线,在线弹性范围内,也称为弹性曲线上述表达式则称为挠曲线(或弹性曲线)方程由于挠曲线为一平坦曲线,故转角θ可表达为''tan ()f x θθω≈== 称为转角方程即挠曲线上任一点处的切线斜率'ω可足够精确地代表该点处横截面的转角θ 由此可见,求得挠曲线方程后,就能确定梁任一横截面挠度的大小,指向及转角的数值 正值的挠度向下,负值的挠度向上正值的转角为逆时针转向,负值的转角为顺时针方向2.梁的挠曲线近似微分方程及其积分为求得梁的挠曲线方程,利用曲率κ与弯矩M 间的物理关系,即 1M EIκρ== 式中曲率κ为度量挠曲线弯曲程度的量,是非负的这是梁在线弹性范围内纯弯曲情况下的曲率表达式在横力弯曲时,梁横截面上除弯矩M 外尚有剪力S F 但工程用梁,其跨长l 一般均大于横截面高度的10倍剪力S F 对于梁位移的影响很小,可略去不计,故该式子依然适用式中的M 和ρ均为x 的函数,即1()()()M x x x EIκρ== 在数学中,平面曲线的曲率与曲线方程导数间的关系有'''23/21()(1)x ωρω=±+ 取x 轴向右为正,y 轴向下为正时曲线凸向上时''ω为正,凸向下时为负而按弯矩的正、负号规定,梁弯曲后凸向下时为正,凸向上为负,符号相反于是得到 '''23/2()(1)M x EIωω=-+ 由于梁的挠曲线为一平坦曲线,因此,'2ω与1相比十分微小可以略去不计故上式可近似的写为 ''()M x EIω=-上式略去了剪力S F 的影响,并略去了'2ω项 故称为梁的挠曲线近似微分方程若为等截面直梁,其弯曲刚度EI 为一常量,上式可改写为''()EI M x ω=-对于等直梁,上式进行积分,并通过由梁的变形相容条件给出的边界条件确定积分常数 即可求得梁的挠曲线方程当全梁各横截面上的弯矩可用单一的弯矩方程表示时,梁的挠曲线近似微分方程仅有一个 将上式的两端各乘以dx ,经积分一次,得'1()EI M x dx C ω=-+⎰再积分一次,即得12[()]EI M x dx dx C x C ω=-++⎰两式子中积分常数1C 、2C 可通过挠曲线的边界条件确定例如在简支梁中,左右铰支座处的挠度均等于零在悬臂梁中,固定端处的挠度和转角均等于零确定积分常数1C 、2C 后,就分别得到梁的转角方程和挠曲线方程从而可以确定任一横截面的转角和挠度1C 和2C 的几何意义 由于以x 为自变量,在坐标原点即0x =处的定积分恒等于零因此,积分常数'100x C EI EI ωθ===,20C EI ω=式中,0θ和0ω分别表示坐标原点处截面的转角和挠度若梁上的荷载不连续即分布荷载在跨度中间的某点处开始或结束,以及集中荷载或集中力偶作用处梁的弯矩需分段写出,各段梁的挠曲线近似微分方程也随之不同在对各段梁的近似微分方程积分时,均将出现两个积分常数为确定这些积分常数,除需利用支座处的约束条件外还需利用相邻两段梁在交界处位移的连续条件例如左、右两段梁在交界处的截面应具有相等的挠度和转角不论是约束条件和连续条件,均发生在各段挠曲线的边界处故均成为边界条件,即弯曲位移中的变形相容条件遵循两个原则①对各段梁,都是从同一坐标原点到截面之间的梁段上的外力列出弯矩方程所以后一段梁的弯矩方程包括前一段的弯矩方程的新增的()x a -项②对()x a -项的积分,以()x a -作为自变量于是由x a =处的连续条件,就能得到两段梁上相应的积分常数分别相等的结果 对于弯矩方程需分为任意几段的情况,只要遵循上述规则同样可以得到各梁段上相应的积分常数分别相等的结果从而简化确定积分常数的运算3.按叠加原理计算梁的挠度和转角梁在微小变形条件下,其弯矩与荷载成线性关系 在线弹性范围内,挠曲线的曲率与弯矩成正比当挠度很小时,曲率与挠度间呈线性关系梁的挠度和转角均与作用在梁上的荷载成线性关系在这种情况下梁在几项荷载(如集中力、集中力偶或分布力)同时作用下某一横截面的挠度或转角 就分别等于每项荷载单独作用下该截面的挠度或转角的叠加,即为叠加原理 已知梁在每项荷载单独作用下的挠度和转角表则按叠加原理来计算梁的最大挠度和最大转角将较为方便4.奇异函数·梁挠曲线的初参数方程5.梁的刚度校核·提高梁的刚度的措施5.1 梁的刚度校核对于梁的挠度,其许可值通常用许可挠度与跨长之比值[]l ω作为标准 梁的刚度条件可表达为 max[]ll ωω≤ max []θθ≤ 一般土建工程中的构件,强度要求是主要的刚度要求一般处于从属地位但当对构件的位移限制很严,或按强度条件所选用的构件截面过于单薄时刚度条件也可能起控制作用5.2 提高梁的刚度的措施由梁的位移表可见梁的位移(挠度和转角)除了与梁的支承和荷载情况有关还与其弯曲刚度EI 成反比,与跨长l 的n 次幂成正比减小梁的位移,可采取下列措施①增大梁的弯曲刚度EI②调整跨长和改变结构5.梁内的弯曲应变能当梁弯曲时,梁内将积蓄应变能梁在线弹性变形过程中弯曲应变能V ε在数值上等于作用在梁上的外力所作的功W梁在纯弯曲时各横截面上的弯矩M 为常数,并等于外力偶矩e M当梁处于线弹性范围内e EI EI θρ=== θ与e M 呈线性关系直线下的三角形面积就代表外力偶所作的功W ,即12e W M θ=从而得纯弯曲时梁的弯曲应变能 12e V M εθ=即得2222e M l M l V EI EIε== 横力弯曲时,梁内应变能包含两个部分:与弯曲变形相应的弯曲应变能和与切应变形相应的剪切应变能对于弯曲应变能,取长为dx 的梁段,其相邻两横截面的弯矩应分别为()M x 和()()M x dM x +在计算微段的应变能时,弯矩的增量为一阶无穷小,可略去不计 计算器弯曲应变能为2()2M x dV dx EIε= 全梁的弯曲应变能则可通过积分求得为2()2l M x V dx EIε=⎰ 式中,()M x 为梁任一横截面上的弯矩表达式 当各段梁的弯矩表达式不同时,积分需分段进行梁的剪切应变能远小于弯曲应变能,可略去不计。
第五章 弯曲位移讲解
q8E244a8I1ZqE4aIZ3
2EqIaZ4L
1 500
B
I
ZB
41 250qa
2 24C E
3
qa34 050cm4
8EIZ
查Iz表B33:40选0Cc2am24,a号6qE工aWI3Z字z a钢309c6qmEa3I4Z
2,提高刚度的途径
FL22L1 EI z1
例题 5.10 多跨静定梁如图示,试求力作用点E处的挠度ωE.
A
D
3L B L E LC L
A
1F 2
B
1F 2
C
E
1 2
B
C E1
D
3L
L
B
F
2 3L3
3EI z
9FL3 2EI z
C
F 2L3
3EI z
FL3 6 EI z
B处 的 总 转 角 为: B BP1 BP2
13.54 105 2.53 105 11.01105 rad
(2)校核刚度 主轴的许用挠度和许用转角为:
y 0.0001l 0.0001 40 40104cm 0.001 103rad
F
B
C
BM
FL2 L12 2 EI z1
BM
FL2 L1 EI z1
F
C2 BF BM
A
M FL2
B
C3 BF BM L2
C
C3
C1 C2 C3
FL22 3EI z 2
FL13 3EI z1
FL2 FL12L12L2FL12L2 2EIz1EI z1 2EI z1
第五章梁弯曲时的位移

式中 ,x 为梁变形前轴线上任一点的横坐标 ,w 为该点的挠度。
A
挠曲线
y
CB
x
w挠度
C'
转角
5
三、挠度与转角的关系:
A
挠曲线
y
CB
x
w挠度
C'
转角
tg w' w'(x)
6
四、挠度和转角符号的规定 挠度:向下为正,向上为负。 转角:自 x 转至 切线方向,顺时针转为正,逆时针转为负。
b
l
FB
两段梁的弯矩方程分别为
b M1 FA x F l x
(0 x a)
b M2 F l x F(x a) (a x l)
36
两段梁的挠曲线方程分别为
挠曲线方程
1 ( 0 x a)
EIw1"
M1
F
b l
x
转角方程 挠度方程
EIw1'
F
b l
x2 2
C1
EIw1
F
b l
x3 6
l
EIw Fl
46
l
F x
b(x)
b1
bmax h
EIw Fl
EIw Flx C
EIw Fl x2 Cx D 2
47
l
F x
b(x)
b1
bmax h
EIw Flx C
EIw Fl x2 Cx D 2
边界条件: x l , w 0
xl , w0
48
l
F x
b(x)
b1
w2 与 1 相比十分微小而可以忽略不计, 故上式可近似为
材料力学第五章梁弯曲时的位移

57.4 MPa [ ]
切应力强度条件满足
④ 校核刚度 wmaxwCi 41Fibi(4 3l2E 84Ibi2)
C
b3 0.9 m b4 0.6 m
bi为Fi离支座最 近的距离
b1 0.4 m b2 0.8 m
wmax4.94mm
[w][w]l6mm l
wmax[w]
刚度条件满足
§5-3 按叠加原理计算梁的挠度和转角
积分法
挠度和转角的普遍方程
梁上荷载复杂时,须分段建立弯矩方程,积分常数 成倍增长,确定积分常数十分烦琐。
叠加法、奇异函数法〔初参数法〕、能量法等
叠加原理
当某一参数〔如内力、应力、位移等〕与荷 载成线性关系时, 多个荷载作用下引起的参数等 于各个荷载单独作用下所引起的参数的叠加。
M2(x)F l x bF(xa)
AD段〔 0≤ x ≤ a 〕:
M1(x)
Fbx l
EIw1
Fbx l
Ew I1 EqI1F l bx22C1
EI1w Fl b x63C1xD1
DB段〔 a ≤ x ≤ l 〕: M2(x)F l b xF(xa) EwI2 Fl xbF(xa)
q E w 2 IE2 IF l b x 2 2 F (x 2 a )2 C 2
吊车梁: [w] 1 ~ 1
l 500 600
屋梁和楼板梁: [w] 1 ~ 1
l 200 400
钢闸门主梁: [w] 1 ~ 1
l 500 750
普通机床主轴: [w] 1 ~ 1
l 5000 10000
[q]0.00r1 a~ d0.00r5ad
例:简支梁横截面由两个槽钢组成,受力如图。 F1 =120 kN、F2 =30 kN、F3 =40 kN、F4 =12 kN;钢 [s ]=170 MPa,[t ]=100 MPa;E =2.1×105 MPa;梁 [w / l]= 1 / 400。试选择槽钢的型号。
第5章-梁弯位移1
背板的厚度t起着四次方的作用,手机本身的厚度b的幂次也是3
结构:又长又薄总要出事故
q (转角)
A
B x C1 y w(挠度)
挠度:横截面的形心(即轴线上的点)在y方 向的线位移w。在图示坐标系中,w向下为正。
转角:横截面对其原来位置的角位移q。 也等 于平面曲线AC1B在C1点的切线和x轴的夹角。在图 示坐标系中, 顺时针转向的q为正。
边界条件:
A
B wB=0 B
简支梁 悬臂梁
wA=0 A
连续性条件: 在挠曲线的任一点上 , 有唯一的 挠度和转角。如:
wA=0
A
qA=0
c
B
wC wC q C q C
不可能
A
B
不可能
例:弯曲刚度为EI的悬臂梁如图,求梁的挠曲线方 程及其最大挠度wmax。 解: x截面处弯矩方程为: q
b) x 2l 处, 则: 2lC2 D2 0 (2)连续条件: x l
w2 0
处, w1 w2
则: C1l D1 C2l D2 故:
最后可得:
1 3 C2 ql 8 1 4 D2 ql 4
wB w1 x l
C1l D1 ql3 (向下) EI 8EI
2
而此时梁中点C截面处的挠度为:
wC
2 2 Fb Fbl Fbl (3l 2 - 4b 2) 0. 0625 48EI 16EI EI
两者相差也不超过中点挠度的3%。
因此,在简支梁中,只要挠曲线无拐点,即可有 中点挠度来代替最大挠度。 当载荷作用在梁的中点,即a=b=l/2时,其最大转 角和挠度为:
q max
Fl 16EI
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题
指出以下各梁共几个积分常数并写出全部定解条件。
(1)
F
q
a w w1(x)
a w2(x)
解: 此梁应分为3段积分, 共6个常数。
定解条件:
a w3(x)
x 0, x a,
x 2a,
x
w1 0
w1
w2 ,
dw1 dx
dw2 dx
w2
w3
0, dw2 dx
dw3 11dx
例题
一、度量梁变形的两个基本位移量
1.挠度:横截面形心沿垂直于轴线方向的线位移,用w表示。
与 y同向为正,反之为负。
P
C
x 2.转角:横截面绕其中性轴转
w
动的角度。用 表示,顺时
y
C1
针转动为正,反之为负。
二、挠曲线:变形后,轴线变为光滑曲线,该曲线称为挠曲线。
其方程为:
w =f (x)
三、小变形时转角与挠曲线的关系:
1 2
Pa2
C1
0
a
P
L
x
y
(a ) (a ) C1 D1
w(a ) w(a )
C1a C2 D1a D2
C1
D1
1 2
Pa2
; C2
D2
1 6
Pa3
17
写出弹性曲线方程并画出曲线
w(x)
P
6 EI
P
6 EI
(a x)3 3a2x 3a2 x a3
a3
(0 x a) (a x L)
(1)、固定支座处:挠度等于零、转角等于零。 (2)、固定铰支座处;可动铰支座处:挠度等于零。 8
(3)、常见的分段点连续条件: 一般情况下稍左稍右的两个截面挠度相等、转角相等。
连续挠曲线上任意一点只有一个挠度、一个转角。
第i个分段点处:
Mi(x) Mi+1(x) i x
xi
wi(x) wi+1(x)
M
(x)
P(x 0
a)
(0 x a) (a x L)
a
P
L
x
y 写出微分方程并积分
EI
P(a 0
x)
(0 x a) (a x L)
EI
1 2
P(a
x)2
C1
D1
EIw
1 6
P(a
x)3
C1x
C2
D1x D2
16
应用位移边界条件求积分常数
EIw(0)
1 6
Pa3
C2
0
EI
(0)
挠度连续 转角连续
w w i xxi
i1 xxi
i xxi
i1 xxi
(4) 中间铰处
仅挠度连续,转角不连续
w1(x) A
w2(x) C B点挠度连续
lB l
w1 xl w2 xl 9
4、确定挠曲线方程和转角方程 。 5、计算任意截面的挠度、转角;挠度的最大值、转角的最大值。
讨论: ①适用于小变形情况下、线弹性材料、细长构件的平面弯曲。 ②可应用于求解承受各种载荷的等截面或变截面梁的位移。 ③积分常数由挠曲线变形的几何相容条件(边界条件、连续条 件)确定。 ④优点:使用范围广,直接求出较精确; 缺点:计算较繁。
M (x) P(x L)
y
写出微分方程并积分
应用位移边界条件求积分常数
EIw'' M (x) P(L x)
EIw
1 2
P(L
x)2
C1
EIw
1 6
P(L
x)3
C1x
C2
EIw(0)
1 6
PL3
C2
0
EI
(0)
EIw '(0)
1 2
PL2
C1
0
C1
1 2
PL2
;
C2
1 6
PL3
13
P L
x
(2)
q
弹簧系数为k
a
l
x
w w1(x)
w2(x)
解: 此梁应分为2段积分,共4个常数。
定解条件: q
x 0, w1 0,1 0
x a, w1 w2
ql/2
ql/2
x a l,
w2
ql 2k
12
例1 求下列各等截面直梁的弹性曲线、最大挠度及最大转角。
解:
P L
建立坐标系并写出弯矩方程
x
L
1
第五章 梁弯曲时的位移
§5–1 概述 §5–2 梁的挠曲线近似微分方程及其积分 §5–3 按叠加原理求梁的挠度与转角 §5–4 梁的刚度校核、提高梁的刚度的措施 §5–5 梁内的弯曲应变能
2
§5—1 概述
研究范围:等直梁在平面弯曲时位移的计算。 研究目的:①对梁作刚度校核;
②解超静定梁(变形几何条件提供补充方程)3。
w =w(x)上任一点处—— tg dw w(x) w
dx
tg w
4
§5—2 梁的挠曲线近似微分方程及其积分
一、曲率与弯矩的关系:
1 M 1 M(x)
r EI
r(x) EI
……(1)
二、曲率与挠曲线的关系:
1
r ( x)
ห้องสมุดไป่ตู้
w 1 (w)2
3 2
→→
1 w
r(x)
……(2)
三、挠曲线与弯矩的关系: 联立(1)、(2)两式得
f
写出弹性曲线方程并画出曲线
w(x)
P 6EI
(L
x)3
3L2 x
L3
最大挠度及最大转角
m ax
(L)
PL2 2EI
wmax
w(L)
PL3 3EI
14
解二:建立坐标系并写出弯矩方程
M (x) F(L x)
写出微分方程并积分
EIw M (x) FL Fx
w
EIw
FLx
1 2
Fx2
C1
EIw
FLx2 2
Fx3 6
C1x
C2
应用位移边界条件求积分常数
x=0, w=0 ; θ =0
C1 0 ; C2 0
x
L
F
x
确定挠曲线、转角方程
w(x)
F 6EI
3Lx2
x3
w
F 2EI
2Lx
x2
最大挠度及转角
wmax
w(L)
FL3 3EI
max
(L)
FL2 15
2EI
解:建立坐标系并写出弯矩方程
最大挠度及最大转角
m ax
(a)
Pa 2 2EI
wmax
w(L)
Pa2 6EI
3L a
a
P
L
x
f
18
例2 解:建立坐标系并写出弯矩方程
M (x) 1 qlx 1 qx2
q
22
写出微分方程的积分并积分 A
B
EIw" M (x) 1 qlx 1 qx2
22
x
EIw' EI 1 qlx2 1 qlx3 C
EIw(x) M (x)
EIw(x) M (x)dx C1
EIw(x) ( M (x)dx)dx C1x C2
7
3.位移边界条件
P
A
C
B
D
P
支点位移条件:
wA 0 wB 0
连续条件: wC wC
光滑条件: C C
wD 0 wD 0
或写成w C
左
wC右
或写成 C 左 C 右
M(x) w EI
EIw M(x)
5
x M>0
w(x) 0 y
x
M<0
y
w(x) 0
结论:挠曲线近似微分方程—— EIw M(x)
挠曲线近似微分方程的近似性——忽略了“Fs(”w、)2 对变形的影响。 使用条件:弹性范围内工作的细长梁。
6
二、积分法计算梁的变形
步骤:(EI为常量) 1、根据荷载分段列出弯矩方程 M(x)。 2、根据弯矩方程列出挠曲线的近似微分方程并进行积分
