材料力学-第五章 梁弯曲时的位移
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-梁弯曲时的位移(圣才出品)

圣才电子书
ql3/6,D=-ql4/24。
十万种考研考证电子书、题库视频学习平台
故挠曲线方程和转角方程分别为:
w(x)=qx2(x2+6l2-4lx)/(24EI),θ(x)=q(x3-3lx2+3l2x)/(6EI)
则最大挠度 wmax=w(x)|x=l=ql4/(8EI);梁端转角 θB=θ(x)| x=l=ql3/(6EI)。
表 5-1-4 叠加原理计算梁的挠度和转角
四、梁的刚度校核·提高梁的刚度的措施(见表 5-1-5)
表 5-1-5 梁的刚度校核及提高措施
3 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
五、梁内的弯曲应变能 定义:由于梁弯曲变形而存储的能量称为梁内的弯曲应变能。梁在弹性变形过程中,其 弯曲应变能与作用在梁上的外力所作的功相等,常见梁内的弯曲应变能见表 5-1-6。
则最大挠度 wmax=w(x)|x=l=Fl3/3EI;梁端转角 θB=θ(x)| x=l=Fl2/2EI。
图 5-2-1(a)(b) (2)建立如图 5-2-1(b)所示坐标系。 首先列弯矩方程:M(x)=-q(l-x)2/2,由此可得挠曲线近似方程: EIw″=-M(x)=q(l-x)2/2 积分得: EIw′=-q(l-x)3/6+C① EIw=q(l-x)4/24+Cx+D② 该梁的边界条件:x=0,w=0,x=0,w'=0。代入式①、②可确定积分常数:C=
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 5 章 梁弯曲时的位移
5.1 复习笔记
梁在承受荷载时发生相应的变形,变形后轴线相对原位置将会发生位移、梁的截面将出 现转角,梁内会因变形存储能量。本章首先介绍梁的位移概念,并基于坐标系统建立挠曲线 方程;接着介绍求解梁的位移的方法,根据挠曲线近似微分方程积分和按叠加原理计算;再 介绍梁刚度校核以及提高梁刚度的方法;最后介绍梁弯曲应变能的概念及计算方法。
《材料力学》 第五章 弯曲内力与弯曲应力

第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁,火车的轮轴,楼房的横梁,阳台的挑梁等。
二、弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线。
变形特点——杆轴线由直线变为一条平面的曲线。
三、梁的概念:主要产生弯曲变形的杆。
四、平面弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在梁的纵向对称平面内(通过或平行形心主轴且过弯曲中心)。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。
五、弯曲的分类:1、按杆的形状分——直杆的弯曲;曲杆的弯曲。
2、按杆的长短分——细长杆的弯曲;短粗杆的弯曲。
3、按杆的横截面有无对称轴分——有对称轴的弯曲;无对称轴的弯曲。
4、按杆的变形分——平面弯曲;斜弯曲;弹性弯曲;塑性弯曲。
5、按杆的横截面上的应力分——纯弯曲;横力弯曲。
六、梁、荷载及支座的简化(一)、简化的原则:便于计算,且符合实际要求。
(二)、梁的简化:以梁的轴线代替梁本身。
(三)、荷载的简化:1、集中力——荷载作用的范围与整个杆的长度相比非常小时。
2、分布力——荷载作用的范围与整个杆的长度相比不很小时。
3、集中力偶(分布力偶)——作用于杆的纵向对称面内的力偶。
(四)、支座的简化:1、固定端——有三个约束反力。
2、固定铰支座——有二个约束反力。
3、可动铰支座——有一个约束反力。
(五)、梁的三种基本形式:1、悬臂梁:2、简支梁:3、外伸梁:(L 称为梁的跨长) (六)、静定梁与超静定梁静定梁:由静力学方程可求出支反力,如上述三种基本形式的静定梁。
超静定梁:由静力学方程不可求出支反力或不能求出全部支反力。
§5—2 弯曲内力与内力图一、内力的确定(截面法):[举例]已知:如图,F ,a ,l 。
求:距A 端x 处截面上内力。
解:①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力:剪力和弯矩1. 弯矩:M ;构件受弯时,横截面上存在垂直于截面的内力偶矩。
材料力学第五章梁弯曲时的位移

实例3 :均布载荷
分析受均布载荷作用下梁的位移。
材料力学第五章梁弯曲时 的位移
在材料力学的第五章中,我们将学习有关梁在弯曲时的位移。掌握梁的基本 知识、位移方程和位移计算方法,以及梁的挠度与转角关系。
梁的基本知识
1 定义
梁是一种长条形结构,承受着沿其长度方向的外部力。
2 类型
常见的梁包括简支梁、悬臂梁和受力梁。
3 材料
梁可以由不同类型的材料制成,例如钢、木材或混凝土。
梁的位移方程
1 弯曲位移
2 挠度
3 转角
梁在弯曲时,沿梁的长度方 向发生位移。
挠度是梁的中点相对于其自 由状态的偏移量。
转角是指梁在弯曲时端部角 度的变化。
简支梁的位移计算方法
1
载荷和反力
计算简支梁上的载荷和反力分布。
2
弯矩方程
使用弯矩方程推导出简支梁的位移方程。
3
边界条件
应用适当的边界条件来解决位移方程中的未知量。
悬臂梁的位移计算方法
加载和支座反力
确定悬臂梁上的加载和支座反力。
弯曲力矩方程
通过推导弯曲力矩方程来解决悬臂 梁的位移问题。
解决边界条件
应用边界条件来计算悬臂梁的位移。
受力梁的位移计算方法
1
截面转动方程
2
推导出受力梁的截面转动方程。
3
确定力的分布
分析受力梁上的力分布,包括集中力和均布 力。
边界条件和位移方程
应用边界条件,求解受力梁的位移方程。ຫໍສະໝຸດ 梁的挠度与转角关系挠度
挠度是梁在弯曲时沿其长度方向上的位移。
转角
转角是梁在弯曲时端部偏离初始位置的角度。
关系公式
挠度和转角之间存在一定的关系,可以通过公式计算。
材料力学第五章梁弯曲时的位移

工程实例
7-1
工程实例
工程实例
5-1 梁的位移——挠度及转角
建立坐标系,oxy为梁对称面,外力作用在对 称面内。所以,挠曲线为o xy面内的平面曲线。
挠度
y 向下为正。
y
x
y
转角
x
挠曲线
挠曲线方程:
7-2
w= f (x)
挠度
略去剪力的影响,则平面假设成立,发
y
5.2 积分法求梁的挠度和转角
例1 求梁的转角方程和挠度方程,并求最大转角和最大挠度, 梁的EI已知。
解 1)由梁的整体平衡分析可得:
2)写出x截面的弯矩方程
FAx 0, FAy F (), M A Fl (
)
A
x
l
yB
F B
B
x
M ( x ) F (l x ) F ( x l )
A
FAx 0, FAy
Fb Fa , FBy l l
2)弯矩方程
FAy x1
ymax
x2
FBy
AC 段:
M x1 FAy x1 Fb x1 ,0 x1 a l
y
a
b
CB 段:
Fb M x2 FAy x2 F ( x2 a ) x2 F ( x2 a ), l
目录
a x2 l
5.2 积分法求梁的挠度和转角
A d 2 w1 Fb EI M ( x1 ) x1 2 dx1 l FAy x1 dw1 Fb 2 EI EI ( x1 ) x1 C1 x2 dx1 2l Fb 3 a EIw1 x C1 x1 D1 6l a x2 l CB 段: y d 2 w2 Fb EI M ( x2 ) x2 F ( x2 a) 2 dx2 l dw Fb 2 F EI 2 EI ( x2 ) x 2 ( x2 a ) 2 C 2 dx2 2l 2 Fb 3 F EIw2 x 2 ( x2 a)3 C2 x2 D2 6l 6
第五章 梁弯曲时的位移

李田军材料力学课件 10 第五章 梁弯曲时的位移
积分法求解梁位移的思路: 积分法求解梁位移的思路: 建立合适的坐标系; ① 建立合适的坐标系; 求弯矩方程M(x) ; ② 求弯矩方程 ③ 建立近似微分方程: EIw′′ = M ( x ) 建立近似微分方程: 根据本书的规定坐标系,取负号进行分析. 根据本书的规定坐标系,取负号进行分析. ④ 积分求
李田军材料力学课件 9 第五章 梁弯曲时的位移
积分法求梁的变形 对于等刚度梁, 对于等刚度梁,梁挠曲线的二阶微分方程可写为
Ely'' = M(x)
对此方程连续积分两次,可得 对此方程连续积分两次,
Ely' (x) = ∫ M(x)dx + c1 Ely(x) = ∫ M(x)dxdx + c1x + c2
最大转角,显然在支座处
Pab θA =θ (0) = (L + b) 6EIz Pab θB =θ (L) = (L + a) 6EI 6EIz
P a L y
C
b B x
a >b a <b
θmax =θB θmax =θA
A
从A→B, θ + → 中间必经过0
李田军材料力学课件
19
第五章
梁弯曲时的位移
第五章 梁弯曲时的位移
梁的位移——挠度及转角 §5.1 梁的位移 挠度及转角 §5.2 梁的挠曲线近似微分方程及其积分 §5.3 按叠加原理计算梁的挠度和转角 *§5.4 梁挠曲线的初参数方程 § §5.5 梁的刚度校核.提高梁的刚度的措施 §5.6 梁内的弯曲应变能
材料力学(土木类)第五章 梁弯曲时的位移(2)

3 3 3
利用叠加原理求图示弯曲刚度为EI的悬臂梁 例5-6 利用叠加原理求图示弯曲刚度为 的悬臂梁 自由端B截面的挠度和转角 截面的挠度和转角。 自由端 截面的挠度和转角。
F A l C EI l F D l B
原荷载可看成为图a和 两种荷载的叠加 两种荷载的叠加, 解:原荷载可看成为图 和 b两种荷载的叠加,对应 的变形和相关量如图所示。 的变形和相关量如图所示。
Fl θ C1 = 2 EI
2
3
由位移关系可得此时B截面的挠度和转角为: 由位移关系可得此时 截面的挠度和转角为: 截面的挠度和转角为
Fl 3 Fl 2 4 Fl 3 wB1 = wC1 + θ C1 ⋅ BC = + × 2l = 向下) (向下) 3EI 2 EI 3EI Fl θ B1 = θ C1 = 2 EI
q ( x) x 2 dθ B = dθ ( x) = dx 2 EI
范围对q(x)dx的作用进行叠加,相当于 的作用进行叠加, 在x=0, l范围对 范围对 的作用进行叠加 对上两式在前述范围内积分, 对上两式在前述范围内积分,即:
wB = ∫ d wB = ∫
0
l
l
0
11q 0 l q ( x ) x (3l − x ) dx = 6 EI 120 EI
上次课回顾: 上次课回顾:
1、度量梁变形的两个基本位移量:挠度和转角 度量梁变形的两个基本位移量: 2、挠曲线近似微分方程
EIw′′ = − M ( x )
3、挠曲线近似微分方程的积分 、
EIw ' ( x ) = ∫ ( − M ( x )) dx + C1
EIw ( x ) =
材料力学——5梁的变形与刚度计算

d
dx
M (x) EI Z
dx
C1
M (x) EI Z
dx
•
dx
C1 x
C2
可写成:
EIZ M xdx C1
EIz M xdx • dx C1x C2
积分常数C1、C2由边界条件确定
X
x0 xL
0 0
X
y
x0
0
0
y
例题 5.1
求图所示悬臂梁A端的挠度与转角。
Fb 6L
x3
1 6
Fx
a3
Fb
L2 b2 6L
x
EIz1
Fb 2L
x2
Fb
L2 6L
b2
EI z1
Fb 6L
x3
Fb
L2 6L
b2
x
例题 5.3 求图示简支梁在集中荷载F的作用下(F力在右半跨)的最
大挠度。 F
a
b
A
C
Fb
l
L
x
B
x
EI z1
Fb 2L
x2
Fb
L2 6L
b2
Fa
各梁的挠曲线近似微分方程应分几段;将分别出
现几个积分常数,并写出其确定积分常数的边界
条件。
挠曲线方程应分两段AB,BC.
q
EI z
L
Cx
共有四个积分常数
边界条件
xa
xaL
连续条件
yB 0 yC 0
xa
yB1 yB2
B1 B2
例题 5.6
用积分法求图示各梁挠曲线方程时,试问下列
各梁的挠曲线近似微分方程应分几段;将分别
材料力学-- 梁的位移计算.

D
Fa
q
qa
A
Ⅰ
B
Ⅱ
C
Ⅲ
D
x
y
Fc
方法一:积分法
解:(1)挠曲线方程 有平衡方程可得梁的两个支反力(如图)为
qa FA 4 9qa Fc 4
Fa
q Ⅰ B Ⅱ
qa
A
C Fc
Ⅲ
D
x
AB段
弯 矩 方 程 转 角 方 程 挠 度 方 程
BC段
qa 1 2 M x x q x a 4 2
4
积分法和奇异函数法的比较
• 积分法:
积分常数由变形相容的几何条件(边界条件、光 滑连续条件)确定 • 优点:可以求出挠曲线方程和转角方程,因此可 以求任意截面的转角和挠度,使用范围广,直接 求出较精确。 • 缺点:当轴上载荷较复杂时,计算比较麻烦。
• 奇异函数法:
使用奇异函数法求解时必须把坐标原点置 于梁的一端;
边界条件
x0 w0; xl w0
A y
a l
C
F
b
B
x
光滑连续条件
x a w1 w2 x a 1 2
例题1:如图所示简支梁,在C截面承受集中力偶M作用,已知
梁的刚度为 EI,试求梁的挠曲线方程,并确定位移 A 和 max 。
、 B
M
A
C
B
a
b
解:建立坐标系如图所示 1、求约束反力 ᵞ↑
M1
M x ab
M2
Mx M ab
M x2 EI1 ' C1 ab 2
EI1 M x C1 x C2 ab 6
3
材料力学第五章 梁的变形

连续条件
xa
wB1 wB2
例题 画出挠曲线大致形状。图中C为中间铰。
解: 边界条件
A
C
F
B
wA 0 qA 0
wB 0
两根梁由中间铰连接,挠
曲线在中间铰处,挠度连
续,但转角不连续。
wC左 wC右
qC左 qC右
A
挠曲线的凸向由弯矩的正
负号决定,正弯矩向下凸,
负弯矩向上凸。
例 图示等截面梁,弯曲刚度EI。设梁下有一曲面 y Ax3 ,欲
)
6l
bF l
F
b
C
Bx
x l
aF FRB l
AC段 (0 x a)
EIw1
bF l
x
EIw1
bF 2l
x2
C1
EIw1
bF 6l
x3
C1 x
D1
CB段 (a x l)
EIw2
bF l
x
F(x a)
EIw2
bF 2l
x2
F ( x a)2 2
C2
EIw2
bF 6l
x3
F ( x a)3 6
转角方程,挠度方程
EIw M ( x)
q w m 6lx 3x2 2l 2 6EIl A
m
l
C
w mx 3lx x2 2l 2 6EIl
2 m
y FRA l
l
x B
m FRB l
求 wmax w q 0
3 x0 1 3 l 0.423l
wmax
w
x0
F2 60kN
C
A
F1 200kN
F2
D
材料力学:梁弯曲时的位移

C1=0 C2=0
(3)
(4)
梁的转角方程和挠曲线方程分别为
Flx Fx 2 w' EI 2 EI
Flx 2 Fx3 w 2 EI 6 EI
24
F
A B x
w
max
l
θ max
y
max 及 wmax都发生在自由端截面处
M ( x) EI
12
(1 w' )
2
3
2
M
M
在规定的坐标系中,x 轴水平向右 为正,y 轴竖直向下为正。 曲线向下凸 时 : w’’< 0 , M > 0 曲线向上凸 时 : w’’ > 0 , M < 0
y
M>0
w" 0
o
M
x
M
M<0
因此, M 与 w’’ 的正负号相反 y
w" 0
挠曲线方程为
w w( x)
式中 ,x 为梁变形前轴线上任一点的横坐标 ,w 为该点的挠度。
A
C
B
x
w挠度
挠曲线
y
C'
转角
5
三、挠度与转角的关系:
A
C
B
x
w挠度
挠曲线
y
C'
转角
tg w' w' ( x)
6
四、挠度和转角符号的规定
挠度:向下为正,向上为负。
转角:自 x 转至 切线方向,顺时针转为正,逆时针转为负。
A
C
B
x
w 挠度
材料力学第五章 梁弯曲时的位移 PPT

M(x) E Iz
高等数学:
1
r (x)
=±(1+ww2)3/2
± w w (1+ 2)3/2
=
M(x) E Iz
M < 0,w > 0
M > 0,w < 0
取负号!
- w w (1+ 2)3/2
=
M(x) E Iz
w w (1+ 2)3/2
=-
M(x) E Iz
挠曲线微分方程
小 变 形
w
=-
DB段(a≤x≤l): M2(x)F l b xF(xa) Ew I2 Fl b xF(xa)
q E w 2 IE2I F l b x 2 2 F (x 2 a )2 C 2
E2 I w F l b x 6 3F(x 6 a )3 C 2xD 2
确定积分常数 连续条件
x = a 时:
w1 w2 w1 w2
边界条件
x = 0 时: w1 0 x = l 时: w2 0
D1D20 C1C2F 6lb(l2b2)
AD段( 0≤ x ≤ a ):
w 1 q1F(6 b lE 2b I2)l2F Eb Ix2l
w1F(6 b lE 2b I2l)x6F EbIx3 l
DB段( a ≤ x ≤ l ):
q w 2 2 F ( 6 lE 2 b b 2 I ) l2 F Ex b 2 I l 2 F E (x I a )2
对于受任意荷载的简支梁,若挠曲线上无拐点, 则可用梁中点的挠度代替最大挠度。
例3:悬臂梁如图,已知F、a,M=0.5 Fa,
梁的弯曲刚度 EI 为常数,试画出挠曲线的大致形 状。
FM
A
B
C
D
a
a
材料力学笔记(第五章)

材料力学(土)笔记第五章 梁弯曲时的位移1.梁的位移——挠度及转角为研究等直梁在对称弯曲时的位移取梁在变形前的轴线为x 轴,梁横截面的铅垂对称轴为y 轴而xy 平面即为梁上荷载作用的纵向对称平面梁发生对称弯曲变形后,其轴线将变成在xy 平面内的曲线1AC B度量梁变形后横截面位移的两个基本量是挠度:横截面形心(即轴线上的点)在垂直于x 轴方向的线位移ω转角:横截面对其原来位置的角位移θ 梁变形后的轴线是一条光滑的连续曲线,且横截面仍与该曲线保持垂直因此横截面的转角θ也就是曲线在该点处的切线与x 轴之间的夹角度量等直梁弯曲变形程度的是曲线的曲率梁的变形还受到支座约束的影响通常就用这两个位移量来反映梁的变形情况梁轴线弯曲成曲线后,在x 轴方向也将发生线位移 但在小变形情况下,梁的挠度远小于跨长,梁变形后的轴线是一条平坦的曲线横截面形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不记因此在选定坐标后,梁变形后的轴线可表达为()f x ω=式中,x 为梁在变形前轴线上任一点的横坐标;ω为该点的挠度梁变形后的轴线称为挠曲线,在线弹性范围内,也称为弹性曲线上述表达式则称为挠曲线(或弹性曲线)方程由于挠曲线为一平坦曲线,故转角θ可表达为''tan ()f x θθω≈== 称为转角方程即挠曲线上任一点处的切线斜率'ω可足够精确地代表该点处横截面的转角θ 由此可见,求得挠曲线方程后,就能确定梁任一横截面挠度的大小,指向及转角的数值 正值的挠度向下,负值的挠度向上正值的转角为逆时针转向,负值的转角为顺时针方向2.梁的挠曲线近似微分方程及其积分为求得梁的挠曲线方程,利用曲率κ与弯矩M 间的物理关系,即 1M EIκρ== 式中曲率κ为度量挠曲线弯曲程度的量,是非负的这是梁在线弹性范围内纯弯曲情况下的曲率表达式在横力弯曲时,梁横截面上除弯矩M 外尚有剪力S F 但工程用梁,其跨长l 一般均大于横截面高度的10倍剪力S F 对于梁位移的影响很小,可略去不计,故该式子依然适用式中的M 和ρ均为x 的函数,即1()()()M x x x EIκρ== 在数学中,平面曲线的曲率与曲线方程导数间的关系有'''23/21()(1)x ωρω=±+ 取x 轴向右为正,y 轴向下为正时曲线凸向上时''ω为正,凸向下时为负而按弯矩的正、负号规定,梁弯曲后凸向下时为正,凸向上为负,符号相反于是得到 '''23/2()(1)M x EIωω=-+ 由于梁的挠曲线为一平坦曲线,因此,'2ω与1相比十分微小可以略去不计故上式可近似的写为 ''()M x EIω=-上式略去了剪力S F 的影响,并略去了'2ω项 故称为梁的挠曲线近似微分方程若为等截面直梁,其弯曲刚度EI 为一常量,上式可改写为''()EI M x ω=-对于等直梁,上式进行积分,并通过由梁的变形相容条件给出的边界条件确定积分常数 即可求得梁的挠曲线方程当全梁各横截面上的弯矩可用单一的弯矩方程表示时,梁的挠曲线近似微分方程仅有一个 将上式的两端各乘以dx ,经积分一次,得'1()EI M x dx C ω=-+⎰再积分一次,即得12[()]EI M x dx dx C x C ω=-++⎰两式子中积分常数1C 、2C 可通过挠曲线的边界条件确定例如在简支梁中,左右铰支座处的挠度均等于零在悬臂梁中,固定端处的挠度和转角均等于零确定积分常数1C 、2C 后,就分别得到梁的转角方程和挠曲线方程从而可以确定任一横截面的转角和挠度1C 和2C 的几何意义 由于以x 为自变量,在坐标原点即0x =处的定积分恒等于零因此,积分常数'100x C EI EI ωθ===,20C EI ω=式中,0θ和0ω分别表示坐标原点处截面的转角和挠度若梁上的荷载不连续即分布荷载在跨度中间的某点处开始或结束,以及集中荷载或集中力偶作用处梁的弯矩需分段写出,各段梁的挠曲线近似微分方程也随之不同在对各段梁的近似微分方程积分时,均将出现两个积分常数为确定这些积分常数,除需利用支座处的约束条件外还需利用相邻两段梁在交界处位移的连续条件例如左、右两段梁在交界处的截面应具有相等的挠度和转角不论是约束条件和连续条件,均发生在各段挠曲线的边界处故均成为边界条件,即弯曲位移中的变形相容条件遵循两个原则①对各段梁,都是从同一坐标原点到截面之间的梁段上的外力列出弯矩方程所以后一段梁的弯矩方程包括前一段的弯矩方程的新增的()x a -项②对()x a -项的积分,以()x a -作为自变量于是由x a =处的连续条件,就能得到两段梁上相应的积分常数分别相等的结果 对于弯矩方程需分为任意几段的情况,只要遵循上述规则同样可以得到各梁段上相应的积分常数分别相等的结果从而简化确定积分常数的运算3.按叠加原理计算梁的挠度和转角梁在微小变形条件下,其弯矩与荷载成线性关系 在线弹性范围内,挠曲线的曲率与弯矩成正比当挠度很小时,曲率与挠度间呈线性关系梁的挠度和转角均与作用在梁上的荷载成线性关系在这种情况下梁在几项荷载(如集中力、集中力偶或分布力)同时作用下某一横截面的挠度或转角 就分别等于每项荷载单独作用下该截面的挠度或转角的叠加,即为叠加原理 已知梁在每项荷载单独作用下的挠度和转角表则按叠加原理来计算梁的最大挠度和最大转角将较为方便4.奇异函数·梁挠曲线的初参数方程5.梁的刚度校核·提高梁的刚度的措施5.1 梁的刚度校核对于梁的挠度,其许可值通常用许可挠度与跨长之比值[]l ω作为标准 梁的刚度条件可表达为 max[]ll ωω≤ max []θθ≤ 一般土建工程中的构件,强度要求是主要的刚度要求一般处于从属地位但当对构件的位移限制很严,或按强度条件所选用的构件截面过于单薄时刚度条件也可能起控制作用5.2 提高梁的刚度的措施由梁的位移表可见梁的位移(挠度和转角)除了与梁的支承和荷载情况有关还与其弯曲刚度EI 成反比,与跨长l 的n 次幂成正比减小梁的位移,可采取下列措施①增大梁的弯曲刚度EI②调整跨长和改变结构5.梁内的弯曲应变能当梁弯曲时,梁内将积蓄应变能梁在线弹性变形过程中弯曲应变能V ε在数值上等于作用在梁上的外力所作的功W梁在纯弯曲时各横截面上的弯矩M 为常数,并等于外力偶矩e M当梁处于线弹性范围内e EI EI θρ=== θ与e M 呈线性关系直线下的三角形面积就代表外力偶所作的功W ,即12e W M θ=从而得纯弯曲时梁的弯曲应变能 12e V M εθ=即得2222e M l M l V EI EIε== 横力弯曲时,梁内应变能包含两个部分:与弯曲变形相应的弯曲应变能和与切应变形相应的剪切应变能对于弯曲应变能,取长为dx 的梁段,其相邻两横截面的弯矩应分别为()M x 和()()M x dM x +在计算微段的应变能时,弯矩的增量为一阶无穷小,可略去不计 计算器弯曲应变能为2()2M x dV dx EIε= 全梁的弯曲应变能则可通过积分求得为2()2l M x V dx EIε=⎰ 式中,()M x 为梁任一横截面上的弯矩表达式 当各段梁的弯矩表达式不同时,积分需分段进行梁的剪切应变能远小于弯曲应变能,可略去不计。
材料力学第五版课后习题答案修订版

材料力学第五版课后习题答案Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】二、轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
2-2 试求图示等直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:2-3试求图示阶梯状直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11.5 cm2(拉)(拉)2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向。
解:2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)2-7(2-9)一根直径、长的圆截面杆,承受轴向拉力,其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解:2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E,,试求C与D两点间的距离改变量。
解:横截面上的线应变相同因此2-9(2-12) 图示结构中,AB为水平放置的刚性杆,杆1,2,3材料相同,其弹性模量E=210GPa,已知,,,。
第5章(梁的挠度和转角及挠曲线近似微分方程)

第五章 梁弯曲时的位移
知识点:梁的挠度和转角及挠曲线近似微分方程
一、梁的位移——挠度和转角 二、梁的挠曲线的概念
三、梁的挠曲线近似微分方程
1
材 料 力 学 Ⅰ 电 子 教 案
一、梁的位移——挠度和转角
直梁在对称平面xy内弯曲时其原来的轴线AB将弯曲成 平面曲线AC1B。梁的横截面形心(即轴线AB上的点)在垂直
ห้องสมุดไป่ตู้
生影响。但工程上常用的梁其跨长l 往往大于横截面高度h
的10倍,此时剪力FS对梁的变形的影响可略去不计,而有
1 M x x x EI
注意:对于有些l/h>10的梁,例如工字形截面等直梁,如同
在核电站中会遇到的那样,梁的翼缘由不锈钢制作,而主 要承受剪力的腹板则由价廉但切变模量较小的复合材料制 作,此时剪切变形对梁的变形的影响是不可忽略的。
8
材 料 力 学 Ⅰ 电 子 教 案
从几何方面来看,平面曲线的曲率可写作
1 w x 1 w2
3/ 2
式中,等号右边有正负号是因为曲率1/为度量平面曲线 (挠曲线)弯曲变形程度的非负值的量,而w"是q = w' 沿x方 向的变化率,是有正负的。
9
材 料 力 学 Ⅰ 电 子 教 案
原来位置的角位移,即挠度和转角。梁的变形体现在梁轴
线的变化:梁的各截面发生位移,导致梁变形;梁的各截 面形心的线位移所描述的曲线即为变形后的轴线。
4
材 料 力 学 Ⅰ 电 子 教 案
二、梁的挠曲线的概念
弯曲后梁的轴线——挠曲线为一平坦而光滑的曲线, 它可以表达为w=f(x),此式称为挠曲线方程。由于梁变形 后的横截面仍与挠曲线保持垂直,故横截面的转角q 也就
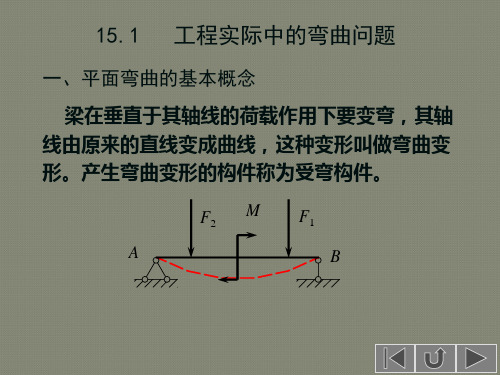
材料力学梁的弯曲问题
F2 M
F1
A
B
●工程实例
建筑工程中的各类梁、火车轴、水压作用下的水 槽壁等。
火车轴
厂房吊车梁
●对称(平面)弯曲 (Planar bending)
对称平面 F2
F1
(b)
F2
F1
(a)
A
B
(c)
平面弯曲:梁的轴线在变形后仍保持在同一平面( 荷载作用面)内,即梁的轴线成为一条平面曲线。
梁的荷载和支座反力
1.5m
FRB
3m
15.3 内力图──剪力图和弯矩图
为了形象地看到内力的变化规律,通常将剪力、弯 矩沿梁长的变化情况用图形表示出来,这种表示剪力 和弯矩变化规律的图形分别称为剪力图和弯矩图。
具体作法是:
剪力方程: FQFQx 函数图形 弯矩方程: MMx
例4 求作图示受均布荷载作用的简支梁的剪力图和
FQ2FRAF1F2
FQ2 FRB
M O
0
M 2 F R A 2 F 1 1 . 5 F 2 0 . 5 0 M 2 7 k N m
M 2 F R A 2 F 1 1 .5 F 2 0 .5
FQ2FRAF1F2
FQ
F1
M 2 F R A 2 F 1 1 .5 F 2 0 .5
当变形为微小时,可采用变
形前尺寸进行计算。
MB
1、叠加原理:当梁在各项
A
荷载作用下某一横截面上
的弯矩等于各荷载单独作
用下同一横截面上的弯矩
的代数和。
2、区段叠加法作弯矩图:
设简支梁同时承受跨间荷
MB
载q与端部力矩MA、MB的作用 。其弯矩图可由简支梁受端部
力矩作用下的直线弯矩图与跨
材料力学第五章 梁弯曲时的位移

分
F
F
B
M
+
B a wC (F )
C qB×a wC (F )
qB = qB ( q ) + qB ( M )
§5-5 梁的刚度校核 提高梁的刚度的措施
一、梁的刚度校核
wmax w [ ] l l
qmax [q ]
刚度条件
吊车梁:
w 1 1 [ ] ~ l 500 600
屋梁和楼板梁: 钢闸门主梁: 普通机床主轴:
wA = 0 wB = 0
wA = 0
qA = 0
边界条件 —— 支座处的约束条件
挠曲线的任意点上,有唯一确定的挠 度和转角 —— 连续条件
错!
错!
当弯矩方程需要分段建立时,在相邻梁 段的交接处,应具有相同的挠度和转角。
约束条件 本教材中 连续条件 边界条件
例1:悬臂梁在自由端受集中力F作用, 试求梁的转角方程和挠度方程,并求最大转 角和最大挠度。设梁的弯曲刚度为 EI。
F
A a B a
M
C a D
F
A H B a
M
C a D x
y
0.5Fa
-
a
+
M图
0.5Fa
M<0,挠曲线上凸; M>0,挠曲线下凸; H 为挠曲线的拐点; M=0,挠曲线为直线。
例4:已知一直梁的挠曲线方程为
试求:
q0 x 3 2 3 w (l 3lx 2 x ) 48EI
① 端点( x =0 及 x =l )的约束情况; ② 画弯矩图、剪力图; ③ 荷载情况,并画出梁的简图。
1
高等数学:
w = ± 3/2 r (x) (1+ w2)
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
A l
Bx
精选课件
23
解:M (x)P (lx) y
Ew I PxPl
A
x
Ew IPx2PlxC
l
2
EIw Px3Plx2C xD 62
由边界条件:x 0 时 w , 0 ,w 0
得: CD 0
精选课件
P
Bx
24
梁的转角方程和挠曲线方程分别为:
Px (x2l)y源自2EIAw Px2 ( x3l ) 6EI
Ew Iqlxqx2 22
A
B x
Ew Iqlx2qx3C
x
l
46
EIw qx l3qx4C xD 12 24
由边界条件:x 0时,w0
x l时,w0
得:
ql3 C , D0
24精选课件
21
q (6lx24x3l3)
24EI
y
w qx(2lx2x3l3)
q
2E 4 I
A
最大转角和最大挠度:
x θA
θB
B x
maxAB2q4lE 3I (
l
)
wmax wxl 2
5ql4 384EI
(↓)
★转角为正时,表示其转向和由x轴转向y轴的时针相
同;挠度为正时,表示其方向和y轴正向相同。
精选课件
22
例2.已知梁的抗弯刚度为EI。试求图示悬臂梁 在集中力P作用下的转角方程、挠曲线方程, 并确定θmax和wmax。
y
F
A
B
C
x
l
l
2
2
精选课件
28
解:AC 段:M(x)Fx
2 EIw F x
y
2
A
EIw Fx2 C
x
4
l
F
C l
B x
EIw Fx3CxD 12
2
2
思考:c 0 ?
由边界条件: x0时 , w0 由对称条件: xl 时, w0
2 精选课件
得: D0 得: C Fl 2
16 29
AC段梁的转角方程和挠曲线方程分别为:
4
●桥式起重机的横梁变形过大,则会使小车行 走困难,出现爬坡现象。
●传动轴的支座处转角过大,轴承发生磨损。
精选课件
5
★变形的有利方面(工程实例) ●车辆上的板弹簧,要求有足够大的变形,以 缓解车辆受到的冲击和振动作用。
P
P
2
2
P
●求解超静定问题。
精选课件
6
二.梁的位移─挠度及转角 梁对称弯曲时用什么参数表示轴线的变形?
y
F (4x2l2)
16EI
A
F
C
w Fx (4x23l2) 48EI
x l
l
2
2
最大转角和最大挠度分别为:
B x
max AB1P 6lE2I
wmaxwxl 2
Pl3
48EI精选课件
30
例4.已知梁的抗弯刚度为EI。试求图示简支 梁的转角方程、挠曲线方程,并确定θmax和 wmax。(请同学课后思考)
D Pl 3 3EI
精选课件
y
P
x
B
26
梁的转角方程和挠曲线方程分别为:
Px2 Pl2
2EI 2EI
xA
Px3 Pl2x Pl3
x
w
6EI 2EI 3EI
最大转角和最大挠度分别为:
maxB
Pl2 2EI
wmaxwB
Pl3 3EI
精选课件
y
P
B
θB
27
例3已知梁的抗弯刚度为EI。试求图示简支梁 在集中力F作用下的转角方程、挠曲线方程, 并确定θmax和 wmax。
(1w2)3/2
梁纯弯曲时曲率由几何关系得
1 M(x)
(x) EIz
精选课件
12
考虑小变形条件:
(1x)(1w w 2)3/2w
1 M(x)
(x) EIz
Ezw IM (x)
问题的关键:考虑上式中的取正还是取负?
精选课件
13
问题的关键:考虑上式中的取正还是取负?
y M0 Mw0 M
y M0 M w0M
x l
最大转角和最大挠度分别为:
maxB
Pl2 2EI
B
Pl 2 2EI
wmaxwB
Pl3 3EI
wB
Pl 3 3EI
精选课件
P
θBB x
25
另解: M(x)Px Ew IM(x)
Ew IPx
xA
EIwPx2 C 2
EIw Px3CxD 6
边界条件:xl时 , w 0 ,w 0
C Pl 2 2 EI
x
x
Ew IM
精选课件
14
思考:与小挠度微分方程 Ezw I相M 对(x应) 的坐标系 为? ( )
xx
y
x
y
y
(a)
(b)
(c)
教材中采用(a)图坐标系
精选课件
15
2. 积分法求弯曲变形
●弯矩方程不分段时 Ew IM(x)
Ew IM (x)dxC
E Iw M (x )d x d x C D x
9
★工程中测量挠度的方法、仪器
精密水准仪、全站仪、GPS、机电百分表、
光电方法等
精选课件
10
三.挠曲线近似微分方程
1.挠曲线方程(deflection equation)
w
x
挠曲线
y
挠曲线方程:wf(x)
转角方程: ta n w f(x )
精选课件
11
曲线 w = f (x) 的曲率为
w
1
(x)
M(x) EIz
?
w
挠度w:横截面形心处的铅垂位移。
转角:横截面绕中性轴转过的角度。
精选课件
7
挠度w:横截面形心处的铅垂位移。
转角:横截面绕中性轴转过的角度。
w
x
挠曲线
y
挠曲线(deflection curve):变形后的轴线。
精选课件
8
★工程实例
控制截面的挠度、控精制选课桥件 墩的水平位移
连续光滑曲线(A、B处转角、挠度唯一)
精选课件
18
边界条件
固定端约束对位移的影响:B处转角、挠 度?
连续光滑曲线
精选课件
19
例1.已知梁的抗弯刚度为EI。试求图示简 支梁在均布载荷q作用下的转角方程、挠 曲线方程,并确定θmax和wmax。
y
q
l
精选课件
x
20
解:M(x)qlxqx2 y
22
q
式中积分常数C、D由边界条件确定 ●弯矩方程分n段时,积分常数个数为 2n
由边界条件确定的方程需要2n个
方法的局限性:外力复杂或多跨静定梁时计算量过大
精选课件
16
边界条件
光滑连续条件:
F
√
wc wc c c
C
×
×
约束条件:两端铰处精挠选课度件 为零。
17
边界条件
铰支座对位移的限制(A、B处挠度为零)
在工程中,对某些受弯构件,要求变形不能 过大,即要求构件有足够的刚度,以保证正常 工作。
在另外一些情况下,却要求构件具有较大的 弹性变形,以满足特定的工作需要。
★变形过大的不利影响(工程实例)
精选课件
3
●摇臂钻床的摇臂等变形过大,就会影响 零件的加工精度,甚至会出现废品。
摇臂钻床
(自重、钻头等约精束选课件力影响)
第五章 梁弯曲时的位移
(Displacements of Bending Beam)
廖东斌 编制 13451911061
精选课件
1
第五章 梁弯曲时的位移
一.概 述
二.梁的位移─挠度及转角
三.挠曲线近似微分方程 四.叠加法计算梁的位移
能量法I-静定结构变形计算
五.梁的刚度计算
精选课件
2
一.概 述 1.工程实践中的弯曲变形问题
