第五章 弯曲位移习题_3
第五章习题答案

5-1 把直径1d mm =的钢丝绕在直径为2m 的卷筒上,试计算该钢丝中产生的最大应力。
设200E GPa =解:钢丝绕在直径为D 的卷筒上后产生弯曲变形,其中性层的曲率半径为22D d Dρ+=≈(因D d >>) 该钢丝中产生的最大应力为39maxmax/211020010100/22y d d E E E Pa MPa D D σρ-⨯====⨯⨯=5.4 矩形截面悬臂梁如图所示。
已知4l m =,23b h =,10/q kN m =,[]10MPa σ=,试确定此梁横截面的尺寸。
解:作梁的弯矩图如图所示。
梁的最大弯矩发生在固定端截面上。
22max 111048022M ql kN m ==⨯⨯=⋅ 由强度条件,有max maxmax 26[]z M M W bhσσ==≤ 将23b h =代入上式,得0.416416h m mm ≥=== 22773b h mm =≥ 5.5 20a 工字钢梁的支承和受力情况如图所示。
若[]160MPa σ=,试求许可载荷F 。
解:(1)求支座反力。
选整个梁为研究对象,受力分析如图所示。
列平衡方程,有0yF =∑,0A B F F F F ++-=()0AM=∑F ,6240B F F F ⨯-⨯+⨯=解得:13A F F =,13B F F =-M O212qlM O(2)作梁的弯矩图如图所示。
由图可知该梁的最大弯矩为max 23C M M F ==查表得No.20a 工字钢的抗弯截面系数为3237z W cm =,由强度条件,有max max 2/3[]z zM F W W σσ==≤ 解得663[]3237101601056.922z W F kN σ-⨯⨯⨯⨯≤==所以许可载荷56.9F kN =。
5.8 压板的尺寸和载荷情况如图所示。
材料为45钢,380s MPa σ=,取安全因数1.5n =。
试校核压板的强度。
解:由受力分析可知最大弯矩发生在m m -截面处,且其值为3max 10.0215.4100.02308M P N m =⨯=⨯⨯=⋅m m -截面的抗弯截面系数z W 为333max11302030121212156810zz I W mm y ⨯⨯-⨯⨯=== 压板的最大应力为max max 9308197156810z M MPa W σ-===⨯ 而许用应力为380[]2531.5sMPa nσσ===截面m-m因最大应力小于许用应力,所以压板的强度足够。
弯曲位移 习题与试题集

弯曲位移习题与试题集一选择题1 dx dx C x++1.用积分法求图示梁的挠曲线方程时,确定积分常数的四个条件,除 0A ω=,0A θ= 外,另外两个条件是 。
A .C C C C ωωθθ==左右左右,; B. 0B C C ωωω==左右,; C . 00C B ωω==,; D . D. 00B C ωθ==,;答案:B2.图示圆截面梁,若直径d 增大一倍(其他条件不变),则梁的最大正应力、最大挠度分别降至原来的 。
A .12 14B .14 18C .18 18D .18 116答案:D3.梁变形前的轴线为x 轴,若取图(a )图(b )两个坐标系,则其挠曲线近似微分方程分别为 。
A . ''''a b EI M EI M ωω==-和B . ''''a bEI M EI M ωω==和 C . ''''a b EI M EI M ωω=-=-和D . ''''a bEI M EI M ωω=-=和 答案:D4.设图示悬臂梁的挠曲线方程为()EI M x dxdx Cx D ω=++⎰⎰,则积分常A .C=0 D ≠0 B.C=0 D=0 C .C ≠0 D ≠0 D.C ≠0 D=0答案:B5.对于图示(a )(b )(c )(d )4种坐标系,挠曲线近似微分方程()EI M x ω''=-适用的坐标系是 。
A.(a ) (c )B.(b ) (c )C.(a ) (d )D.(b ) (d )()a ()b答案:D6.梁的受力如图,挠曲线正确的是。
答案:B7.图示两根梁的材料相同,截面惯性矩分别为I1 和I2 ,梁长分别为i1=l2,若I1=2I2,l1=2l2,两根梁在中点处接触,在无处载时两梁刚好接触,在F作用下,上下梁分别承担的荷载之比为A.14B. 4C.18D. 8 答案:A二判断题1、小挠度微分方程的使用条件是线弹性范围内的直梁。
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-梁弯曲时的位移(圣才出品)

圣才电子书
ql3/6,D=-ql4/24。
十万种考研考证电子书、题库视频学习平台
故挠曲线方程和转角方程分别为:
w(x)=qx2(x2+6l2-4lx)/(24EI),θ(x)=q(x3-3lx2+3l2x)/(6EI)
则最大挠度 wmax=w(x)|x=l=ql4/(8EI);梁端转角 θB=θ(x)| x=l=ql3/(6EI)。
表 5-1-4 叠加原理计算梁的挠度和转角
四、梁的刚度校核·提高梁的刚度的措施(见表 5-1-5)
表 5-1-5 梁的刚度校核及提高措施
3 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
五、梁内的弯曲应变能 定义:由于梁弯曲变形而存储的能量称为梁内的弯曲应变能。梁在弹性变形过程中,其 弯曲应变能与作用在梁上的外力所作的功相等,常见梁内的弯曲应变能见表 5-1-6。
则最大挠度 wmax=w(x)|x=l=Fl3/3EI;梁端转角 θB=θ(x)| x=l=Fl2/2EI。
图 5-2-1(a)(b) (2)建立如图 5-2-1(b)所示坐标系。 首先列弯矩方程:M(x)=-q(l-x)2/2,由此可得挠曲线近似方程: EIw″=-M(x)=q(l-x)2/2 积分得: EIw′=-q(l-x)3/6+C① EIw=q(l-x)4/24+Cx+D② 该梁的边界条件:x=0,w=0,x=0,w'=0。代入式①、②可确定积分常数:C=
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 5 章 梁弯曲时的位移
5.1 复习笔记
梁在承受荷载时发生相应的变形,变形后轴线相对原位置将会发生位移、梁的截面将出 现转角,梁内会因变形存储能量。本章首先介绍梁的位移概念,并基于坐标系统建立挠曲线 方程;接着介绍求解梁的位移的方法,根据挠曲线近似微分方程积分和按叠加原理计算;再 介绍梁刚度校核以及提高梁刚度的方法;最后介绍梁弯曲应变能的概念及计算方法。
材料力学-求弯曲位移)

④ 积分求 EIw 和 EIw; ⑤ 用约束条件或连续条件,确定积分常数; ⑥ 求指定截面的挠度和转角
5.2 积分法求梁的挠度和转角 讨论
??? 积分法求变形有什么优缺点?
优点:易理解;可得到挠度方程w(x)和转角方程
(x) , 因而可求出任意截面的挠度和转角。
缺点:适用范围有限。
目录
例 如图所示简支梁,在C截面承受集中力
偶M作用,已知梁的刚度为EI,试求梁的挠曲
线方程, 并确定位移 A 、 B 和 wmax 。
M
A
C
B
a
b
积分法求梁的弯曲位移
1.由平衡条件求A.B端的约束反力
M
FA
M ab
()
FB
M ab
()
A
C a
b
B
2.建立弯矩方程
AC段:
M1
M ab
x
Mx
CB段:
M2
ab
M
(0 x a)
(a x a b)
3.建立挠度方程和转角方程
AC段:
EIw1 '
M ab
x2 2
C1
M x3 EIw1 a b 6 C1x D1
CB段:
EIw2
'
M ab
x2 2
Mx C2
EIw2
M ab
x3 6
M 2
x2
C2 x D2
4.由边界条件确定积分常数
x 0处,w1 0
x a处,1=2 x a处,w1 w2 x a b处,w2 0
D1 0
C1
M 3
(b 2a)
Ma 2 2(a b)
家电公司研发部资料材料力学习题答案(五)

+-++(a)(b)(c)(d)M M M MeMeMeFa图图图M 图挠曲线挠曲线挠曲线挠曲线第五章梁弯曲时的位移5-1试画出图示梁挠曲线的大致形状。
根据梁的弯矩图确定梁挠曲线的大致形状,M >0,挠曲线向下凸;M <0,挠曲线向上凸。
5-2图示各梁EI=常数。
试写出各梁的位移边界条件,并画出梁挠曲线的大致形状。
F(c)题 5 - 1 图(a)(b)(d)++-M 图M 图FL/2m/32m/3FL挠曲线挠曲线(a)(b)设梁的最左端断点为坐标原点,x 轴正方向向右。
则各梁边界条件、弯矩图及梁的挠曲线大致形状如下: (a)(0)0ω=(b)(0)()0L ωω== (c)(0)()0L ωω== (d)(0)(2)0a ωω==(e)()(3)0a a ωω==(f)(0)0ω=(a)(b)qL/4F(d)(c)L(f)(e)题 5 - 2 图+--M 图M 图+qL2/64qL2/8FaFa挠曲线挠曲线(c)(d)+-M 图M 图-2mmFL挠曲线挠曲线(e)(f)5-3试画出图示梁挠曲线的大致形状。
2(a)(b)(c)题 5 - 3 图(3)++--qa2qa/423qa/42qa2/2qa2/2(a)(b)+-m(c)5-4如要使图示结构B端的挠度为零,则长度x应为多少?试画出此时AB梁的挠曲线大致形状。
答:Lx32=解:固定端约束反力如图所示。
则AB梁上距离A端l处的横截面上的弯矩为M(l)=Fl-F(L-x)由挠曲线微分方程得:EIω”=-M(l)=F(L-x)-Fl积分得:EIω’=F(L-x)l-2Fl2+C1;再积分得:EIω=2F(L-x)l2-6Fl3+C1l+C2;由边界条件l=0 ,ω’=0得C1=0;由ω=0得C2=0L题 5 - 4 图题 5 - 5 图刚性杆qBB∴EI ω=2F (L -x )l 2-6F l 3;由题意知l =L 时,ω=0得x =32L AB 梁挠曲线大致形状:M (l )=Fl -3F L ;0<l <3L 时,M (l )<0;3L<l <L 时,M (l )>05-5图示刚架在端点C 处受集中力F 作用,试求当B 点的铅垂位移为零时La的比值。
《材料力学》第5章-梁弯曲时的位移-习题解

第五章 梁弯曲时的位移 习题解[习题5-1] 试用积分法验算附录IV 中第1至第8项各梁的挠曲线方程及最大挠度、梁端转角的表达式。
解:序号1(1)写弯矩方程(2)写挠曲线近似微分方程,并积分 把边界条件:当0=x 时,0'=w,0=w 代入以上方程得:01=C,02=C。
故:转角方程为:x M EI EIw e ==θ',EIxM e =θ 挠曲线方程:221x M EIw e =, EI x M w e 22=(3)求梁端的转角和挠度 解:序号2(1)写弯矩方程(2)写挠曲线近似微分方程,并积分 把边界条件:当0=x 时,0'=w,0=w 代入以上方程得:01=C,02=C。
故:转角方程为:2'21Fx Flx EI EIw -==θ,)2(22x lx EIF-=θ 挠曲线方程:326121Fx Flx EIw -=,)3(62x l EIFx w -=(3)求梁端的转角和挠度解:序号3(1)写弯矩方程当a x ≤≤0时, Fx Fa x a F x M +-=--=)()( 当l x a ≤≤时, 0)(=x M(2)写挠曲线近似微分方程,并积分当a x ≤≤0时,把边界条件:当0=x 时,0'=w,0=w 代入以上方程得:01=C,02=C。
故:转角方程为:2'21Fx Fax EI EIw -==θ,)2(22x ax EIF-=θ 挠曲线方程:326121Fx Fax EIw -=,)3(62x a EIFx w -=(3)求梁端的转角和挠度设集中力的作用点为C ,则:EI Fa a a a EI F a C 2)2(2)(22=-⋅==θθ EIFa a a EI Fa a w w C 3)3(6)(32=-== 由于CB 段没有外力作用,故该段没有变形,所以:EIFa B 22=θ)233(62)(3tan )(223a a x EIFa EI Fa a x EI Fa a x w w C C B +-=-+≈-+=θ )3(62a x EIFa w B -= 解:序号4(1)写弯矩方程 2)(21)(x l q x M --= (2)写挠曲线近似微分方程,并积分)("x M EIw -= 2")(21x l q EIw -=1322'6)()()(2)(2C x l q x l d x l q dx x l q EIw +--=---=-=⎰⎰ 当0=x 时,0'=w ,即:136)0(0C l q +--=,631ql C =66)(33'ql x l q EIw +--= 23433624)(6)()(6C x ql x l q x ql x l d x l q EIw ++-=+--=⎰ 当0=x 时,0=w 代入以上方程得:24240C ql +=,2442ql C -=24624)(434ql x ql x l q EIw -+-=故:转角方程为:66)(33'ql x l q EIw +--= 挠曲线方程:24624)(434ql x ql x l q EIw -+-=]4)[(24434l x l x l qEIw -+-=)4464(2443432234l x l x lx x l x l l q -++-+-= )46(244322x lx x l q +-= )46(24222x lx l qx +-= (3)求梁端的转角和挠度66)()(33'ql l l q EI l EIw B +--=θEIql B 63=θEIql l l l l ql EIw l EIw B 8)46(24)(4222=+⋅-==解:序号5(1)写弯矩方程l xl q x q -=0)(,lx l q x q )()(0-= lx l q x l l x l q x l x M 6)(3])()(21[)(300--=-⋅-⋅-⋅-=(2)写挠曲线近似微分方程,并积分)("x M EIw -= 30")(6x l lq EIw -=1403030'24)()()(6)(6C lx l q x l d x l l q dx x l l q EIw +--=---=-=⎰⎰ 当0=x 时,0'=w ,即:14024)0(0C l l q +--=,24301l q C =2424)(3040'l q l x l q EIw +--=23050304024120)(24)()(24C x l q l x l q x l q x l d x l l q EIw ++-=+--=⎰ 当0=x 时,0=w 代入以上方程得:250120)0(0C l l q +-=,120402l q C -=12024120)(403050l q x l q l x l q EIw -+-=故:转角方程为:2424)(3040'l q l x l q EIw +--=挠曲线方程:12024120)(403050l q x l q l x l q EIw -+-=)51010(120322320x lx x l l lx q EIw -+-=(3)求梁端的转角和挠度24)(30'l q EI l EIw B ==θ,EIl q B 2430=θ12024120)()(403050l q l l q l l l q EIw l EIw B -⋅+--==, EIl q w B 3040=解:序号6(1)写弯矩方程 l M R A B =(↑),lM R AA = (↓) x lM M x R M x M AA A A -=-=)( (2)写挠曲线近似微分方程,并积分)("x M EIw -= A AM x lM EIw -=" 12'2C x M x lM EIw A A +-=2123216C x C x M x l M EIw A A ++-=把边界条件:当0=x 时,0=w 代入以上方程得:02=C 。
材料力学课后习题答案5章

保留有限量,略去一阶和二阶微量后,得
足标 C 系指梁微段右端面的形心,对题图(b)亦同。 根据题图 b,由
∑F
略去微量 qdx 后,得
y
=0 ,FS左 + qdx − FS右 = 0
FS右 = FS左
仍据题图 b,由
(c)
∑M
C
=0 ,M 右 − M e − qdx(
dx ) − FS左 dx − M 左 = 0 2
11l 处有 FS2 = 0 , M 2 有极大值,其值为 24 121 2 M 2 max = M max = ql 1152
(d)解:1.建立剪力、弯矩方程
8
图 5-9d 坐标如图 5-9d(1)所示,由截面法易得剪力、弯矩方程分别为
q( x1 ) ⋅ x1 qx 2 =− 1 2 l ql FS2 = − + qx2 4 qx 3 M1 = − 1 3l q 2 ql l M 2 = x2 − ⋅ ( + x2 ) 2 4 6 FS1 = −
2 q0l q 0 x2 FS = − + 4 l q x3 ql M = 0 x2 − 0 2 4 3l
l (0 ≤ x2 ≤ ) 2 l (0 ≤ x2 ≤ ) 2
(e) (f)
3.画剪力、弯矩图 依据式(c)和(e)可绘剪力图,如图 5-9b(2)所示;依据式(d)和(f)可绘弯矩图,如图 5-9b(3) 所示。 (c)解:1.求支反力
=0 ,FS左 + F + qdx − FS右 = 0
保留有限量,略去微量 qdx 后,得
FS右 − FS左 = F
为了更一般地反映 F 作用处剪力的突变情况(把向下的 F 也包括在内) ,可将上式改写为
材料力学第五章梁弯曲时的位移

实例3 :均布载荷
分析受均布载荷作用下梁的位移。
材料力学第五章梁弯曲时 的位移
在材料力学的第五章中,我们将学习有关梁在弯曲时的位移。掌握梁的基本 知识、位移方程和位移计算方法,以及梁的挠度与转角关系。
梁的基本知识
1 定义
梁是一种长条形结构,承受着沿其长度方向的外部力。
2 类型
常见的梁包括简支梁、悬臂梁和受力梁。
3 材料
梁可以由不同类型的材料制成,例如钢、木材或混凝土。
梁的位移方程
1 弯曲位移
2 挠度
3 转角
梁在弯曲时,沿梁的长度方 向发生位移。
挠度是梁的中点相对于其自 由状态的偏移量。
转角是指梁在弯曲时端部角 度的变化。
简支梁的位移计算方法
1
载荷和反力
计算简支梁上的载荷和反力分布。
2
弯矩方程
使用弯矩方程推导出简支梁的位移方程。
3
边界条件
应用适当的边界条件来解决位移方程中的未知量。
悬臂梁的位移计算方法
加载和支座反力
确定悬臂梁上的加载和支座反力。
弯曲力矩方程
通过推导弯曲力矩方程来解决悬臂 梁的位移问题。
解决边界条件
应用边界条件来计算悬臂梁的位移。
受力梁的位移计算方法
1
截面转动方程
2
推导出受力梁的截面转动方程。
3
确定力的分布
分析受力梁上的力分布,包括集中力和均布 力。
边界条件和位移方程
应用边界条件,求解受力梁的位移方程。ຫໍສະໝຸດ 梁的挠度与转角关系挠度
挠度是梁在弯曲时沿其长度方向上的位移。
转角
转角是梁在弯曲时端部偏离初始位置的角度。
关系公式
挠度和转角之间存在一定的关系,可以通过公式计算。
材料力学第五章梁弯曲时的位移

工程实例
7-1
工程实例
工程实例
5-1 梁的位移——挠度及转角
建立坐标系,oxy为梁对称面,外力作用在对 称面内。所以,挠曲线为o xy面内的平面曲线。
挠度
y 向下为正。
y
x
y
转角
x
挠曲线
挠曲线方程:
7-2
w= f (x)
挠度
略去剪力的影响,则平面假设成立,发
y
5.2 积分法求梁的挠度和转角
例1 求梁的转角方程和挠度方程,并求最大转角和最大挠度, 梁的EI已知。
解 1)由梁的整体平衡分析可得:
2)写出x截面的弯矩方程
FAx 0, FAy F (), M A Fl (
)
A
x
l
yB
F B
B
x
M ( x ) F (l x ) F ( x l )
A
FAx 0, FAy
Fb Fa , FBy l l
2)弯矩方程
FAy x1
ymax
x2
FBy
AC 段:
M x1 FAy x1 Fb x1 ,0 x1 a l
y
a
b
CB 段:
Fb M x2 FAy x2 F ( x2 a ) x2 F ( x2 a ), l
目录
a x2 l
5.2 积分法求梁的挠度和转角
A d 2 w1 Fb EI M ( x1 ) x1 2 dx1 l FAy x1 dw1 Fb 2 EI EI ( x1 ) x1 C1 x2 dx1 2l Fb 3 a EIw1 x C1 x1 D1 6l a x2 l CB 段: y d 2 w2 Fb EI M ( x2 ) x2 F ( x2 a) 2 dx2 l dw Fb 2 F EI 2 EI ( x2 ) x 2 ( x2 a ) 2 C 2 dx2 2l 2 Fb 3 F EIw2 x 2 ( x2 a)3 C2 x2 D2 6l 6
T05弯曲应力

材料力学习题 第五章 弯曲应力 P166,5-3已知:如图。
AB 段直径D =0.06m ,BE 段外径D =0.06m ,内径d =0.045m 求:σmax 。
解:1. 内力:危险截面C 、B2. 应力:截面C MP a38.63m 10121.232m,.kN 344.1353==⨯===-W M D W M CC σπ截面B MP a09.62m 10450.1)1(32m,.kN 9.03543==⨯=-==-W M D W M BB σαπP168,5-11已知:内力及截面如图。
材料4[σt ]= [σc ]。
求:合理的b 。
解:1. 根据强度条件:最佳的截面设计可以使122121t 4,][][][],[y y y y y I My I Mt t c zc t z ======即σσσσσσ2. 根据截面高可得:32080,4002121===+y y y y ,3. 按照z 轴为形心轴的要求:)(5100506010203016032030021mm b b S S ==⨯+⨯⨯+-⨯⨯=+)(P168,5-12已知:受力及截面如图。
材料 [σt ] =40MPa ,[σc ] =160MPa 。
I z =1.018×10-4m 4,h 1=0.0964m ,h 2=0.1536m 。
求:[F ]。
解:1. 内力:危险截面A 、C ,M A =0.8F ,M B =0.6F2. 应力:截面A 2221116.1328.0][],[80.528.0][],[F kN h I F h I M F kN h I F h I M c z c z A c t z t z A t ==≤≤===≤≤=σσσσσσ截面C 4113226.2816.0][],[18.446.0][],[F kN h I F h I M F kN h I F h I M c z c z C c t z t z C t ==≤≤===≤≤=σσσσσσ3. 结论:34321},,,m in{][F F F F F F ==P168,5-13已知:内力及截面如图。
弯曲应力习题
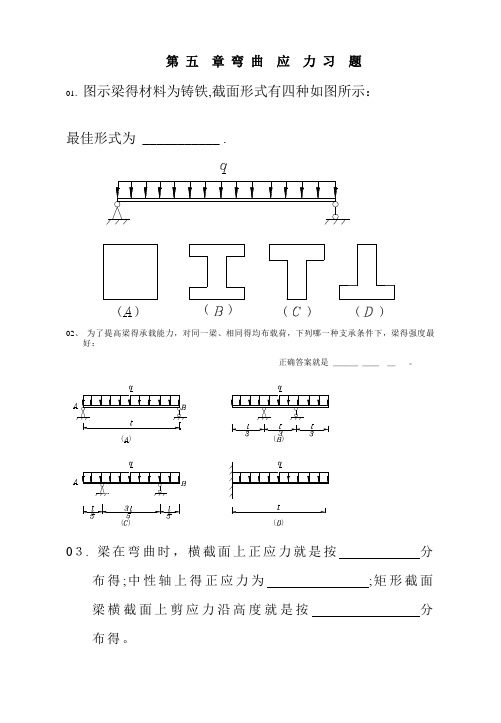
31.槽形截面悬臂梁受力如图所示,已知,,,[σ]=160MPa,指出危险点得位置并校核梁得强度.(A点为弯心)
32、梁AB与杆CB均为圆形截面,而且材料相同。,,杆CB直径。在图示载荷作用下测得CB杆轴向伸长为。求载荷得值及梁AB得安全直径.
12.图示结构中,FB为圆杆,直径,AE梁为T字形截面,尺寸如图所示,C为形心,。材料得许用拉应力,许用压应力.试校核结构得强度。
13。集中力P直接作用简支梁AB得中点时,梁内最大应力超过许用值,为了消除此过载现象,配置了辅助梁CD如图所示,试求CD梁得跨度。
14。图示梁为两个工字钢组成,一个工字钢得,,,,试校核梁得强度并计算。
15.图示梁由三块等厚木板胶合而成,已知,试校核胶缝得剪切强度.
16.某T字形截面外伸梁ABC,在端面C处用一铰与圆截面杆相连,在及作用下,测得拉杆伸长,试求梁中最大拉应力及最大压应力。已知拉杆横截面积,。
17.图示矩形截面梁,受均布载荷作用。若沿中性层取水平截面,截出梁得下半部,问在水平截面上得剪应力得分布规律如何?该截面上总得水平剪力有多大?它由什么来平衡.
18.图示简支梁,由四块尺寸相同得木板胶合而成,试校核其强度。已知,,,,木板得许用应力,胶缝得许用剪应力。
19.梁得横截面积一定,若分别采用圆形、正方形、矩形,放置如图所示,载荷沿y方向,则截面梁得刚度最好;截面梁得刚度最差。
20。( 5 )一梁拟用图示两种方式搁置,则两种情况下得最大应力之比为:
(1)截面为矩形,h= 2b;
( 2 )截面为圆形.
23.图示结构中, FB为圆杆,直径d =30mm,AE梁为T字形截面,尺寸如图所示,C为形心,.材料得许用拉应力[σt]= 40MPa,许用压应力[σc]=60 MPa。试校核结构得强度。
弯曲应力

第5章 弯 曲 应 力 习题(1) 如图5.18所示吊车梁,吊车的每个轮子对梁的作用力都是F ,试问: ① 吊车在什么位置时,梁内的弯矩最大?最大弯矩等于多少?② 吊车在什么位置时,梁的支座反力最大?最大支反力和最大剪力各等于多少?(2) 如图5.19所示一由16号工字钢制成的简支梁承受集中荷载F ,在梁的截面C —C 处下边缘上,用标距s =20mm 的应变仪量得纵向伸长s ∆=0.008mm 。
已知梁的跨长l =1.5m ,a =1m ,弹性模量E =210GPa 。
试求F 力的大小。
图5.18 习题(1)图图5.19 习题(2)图(3) 由两根28a 号槽钢组成的简支梁受三个集中力作用,如图5.20所示。
已知该梁材料为Q235钢,其许用弯曲正应力[]σ=170MPa 。
试求梁的许可荷载[F ]。
图5.20 习题(3)图(4) 简支梁的荷载情况及尺寸如图5.21所示,试求梁的下边缘的总伸长。
图5.21 习题(4)图(5) 一简支木梁受力如图5.22所示,荷载F =5kN ,距离a =0.7m ,材料的许用弯曲正应力[]σ=10MPa ,横截面为bh =3的矩形。
试按正应力强度条件确定梁横截面的尺寸。
图5.22 习题(5)图(6) 如图5.23所示,一矩形截面简支梁由圆柱形木料锯成。
已知F =5kN , 1.5a =m ,[]σ=10MPa 。
试确定弯曲截面系数为最大时矩形截面的高宽比bh ,以及梁所需木料的最小直径d 。
图5.23 习题(6)图(7) 一正方形截面悬臂木梁的尺寸及所受荷载如图5.24所示。
木料的许用弯曲正应力[]σ=10MPa 。
现需在梁的截面C 上中性轴处钻一直径为d 的圆孔,试问在保证梁强度的条件下,圆孔的最大直径d (不考虑圆孔处应力集中的影响)可达多大?图5.24 习题(7)图(8) 当荷载F 直接作用在跨长为l =6m 的简支梁AB 之中点时,梁内最大正应力超过许可值30%。
材料力学 第五章 梁弯曲时的位移 A

材料力学
第五章梁弯曲时的位移
主讲:韩玉林教授
东南大学工程力学系
§5-1 梁的位移
一.工程实例
在工程实践中,对某些受弯构件,除要求具有足够的强度外,还要求变形不能过大,即要求构件有足够的刚度,以保证结构或机器正常工作,如摇臂钻床。
约束对位移的影响
没有约束无法确定位移
连续光滑曲线;铰支座对位移的限制。
边界条件:
A B w w ==约束对位移的影响
连续光滑曲线;固定端对位移的限制。
边界条件:
0,0
B B w θ==约束对位移的影响
注意:
1.分段连续弯矩方程必须从原点沿x 的正向依次写出;
2.对含(x-a)项可不展开,把它视为新变量积分,更为方便;
试绘制图示梁挠曲轴的大致形状
绘制原则
•挠曲轴是一条连续而光滑的曲线(中间铰链除外
,该处只连续而不光滑),为此必须满足连续光滑
条件。
•挠曲轴必须符合梁的边界条件
•弯矩为正的梁段是一条凹曲线;弯矩为负的梁段是一条凸曲线;弯矩为零的梁段不变形,为一条直线
•弯矩图由正变负或由负变正处,弯矩为零处,
挠曲轴出现拐点
下列图示梁的Q、M图和挠曲轴大致形状先用虚线标出,请读者自行检查是否正确,如有错,请在原图上改正
图示梁有一中间铰链,试勾画出挠曲轴大致形状,并求C处的挠度。
图示梁,左右端各作用一力偶矩m 1和m 2,要使挠曲轴的拐点位于距左端为L/3处,问m 1和m 2应保持何种比例?
作业
•5-8,5-11,5-13,5-17,5-25
谢谢大家!。
材料力学 梁 弯曲位移 课件 (3)

解:根据对称关系,梁左段和右段内的弯曲应变能相同 根据对称关系, (取左段研究) 取左段研究) 左段 ( AC段 ) 弯矩方程 段
F M x) = x ( 2
F A C l/2 l B
F M x) = x ( 2
左段 ( AC段 ) 弯曲应变能 段
F x l2 2 F2l3 ⋅d = U =∫ x 1 0 2I E 12 I 9E
θ 与 Me 成线性关系
Me
l
外力偶所做的功
θ
θ
1 W= Mθ e 2
Ml θ= = e I ρ E
纯弯曲时梁的应变能
l
1 W= Mθ e 2
2 2 Ml Ml 1 U=W= Mθ = e = e 2 2I 2 I E E
二、横力弯曲时梁的应变能 横力弯曲时梁的应变能包含两部分: 剪切应变能。 横力弯曲时梁的应变能包含两部分:弯曲应变能 和 剪切应变能。 在工程中常用的梁(跨度比高度大得多),剪切应变能比弯曲 在工程中常用的梁(跨度比高度大得多),剪切应变能比弯曲 ), 应变能小的多,因而剪切应变能不计。 应变能小的多,因而剪切应变能不计。 剪切应变能不计
U=∫
l
2 2 Ml Ml 1 U=W= Mθ = e = e 2 2 I 2I E E
式中: 为梁任一横截面上的弯矩表达式。 式中: M(x) 为梁任一横截面上的弯矩表达式。
例题:求图示等截面简支梁内的弯曲应变能, 例题:求图示等截面简支梁内的弯曲应变能,并求跨中 C 截面的 挠度。 挠度。
F A C l/2 l B
2
整个梁的弯曲应变能
F2l3 U=2 1 = U 9E 6I
F A C l/2 l B
w C
所求挠度 wC,就是荷载 F 的作用点 C 沿荷载作用方向的位移 因此在加载过程中荷载所作的功为
第五章 弯曲位移

yCP2
则C处 的 总 挠 度 为 yC yCP1 yCP2 : 40.6 10 4 5.06 10 4 35.5 10 4 cm B处 的 总 转 角 为 B BP1 BP2 : 13.54 10 5 2.53 10 5 11.01 10 5 rad
1 2
1 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
挠曲线方程应分两段AB,BC.
F A
a
q
B
L
共有四个积分常数
EI z
C
x
边界条件
xa
x aL
连续条件
B 0
C 0
FA FB FC 2qL 0
叠加法求挠度
FC qL
5q2 L 48EI Z 384 EI z
4
C Cq C k
k FC
FCy 2 L
3
qL4 24 EI Z
FC C k
C
24 EI Z L3
例题 5.12
悬臂梁受力如图示.关于梁的挠曲线,由四种答案,请分析判断,哪一 个是正确的?
L1
q
C EA
边界条件
x
A
x0 xL
A 0
B
EIZ
L
y
qLL1 B LBC 2 EA
§3
按叠加原理计算梁的挠度和转角
叠加法计算位移的条件:
1、梁在荷载作用下产生的变形是微小的;
2、材料在线弹性范围内工作,梁的位移与荷载呈线
性关系;
材料力学-第五章 梁弯曲时的位移

V W
H
46
★ 杆件应变能计算
1、轴向拉伸和压缩
V
W
1 2
P
l
P2l FN2l 2EA 2EA
一般地
V
l
FN 2dx 2 EA
H
P P
l
l
47
2、扭转
V W
1 m
2
1m ml 2 G Ip
应用卡氏第二定理
M(x) M(x)
Δi
l
.
dx
EI H Fi
59
对于梁,有莫尔积分
Δi
l
M(x)Mi (x) dx EI
Mi ( x) 对应于去掉原结构中外力,只在i
处加相应单位力后的弯矩方程 ●计算梁截面转角时,加单位力偶矩1 ●计算梁截面挠度时,加单位集中力1
M ( x) 对应于原结构的弯矩方程。
maxB
Pl2 2EI
wmaxwB
Pl3 3EI
H
y
P
B
θB
27
例3已知梁的抗弯刚度为EI。试求图示简支梁 在集中力F作用下的转角方程、挠曲线方程, 并确定θmax和 wmax。
y
F
A
B
C
x
l
l
2
2
H
28
解:AC 段:M(x)Fx
2 EIw F x
y
2
A
EIw Fx2 C
x
4
l
F
C l
B
x
EIw Fx3CxD 12
得: CD 0
H
P
材料力学第五章弯曲例题
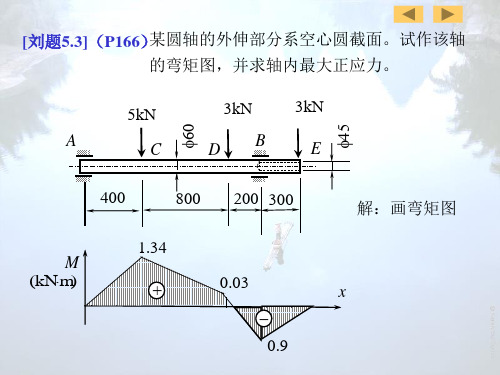
sb [ FS ]
其中: [ FS ] 21.1( kN)
[ FS ] 21.1103 s 117mm b 0.377225
[刘题5.32](P174) 在№18工字梁上作用着活动载荷F。为提 高梁的承载能力,试确定a和b的合理数值及相应的许可载 荷。[]=160MPa。
C截面:
[ c]
(可以不计算)
[刘题5.17](P169) 试计算图示矩形截面简支梁的1-1截 面上a点和b点的正应力和切应力。
F=8kN 1 1m 1.2m 1 1m
b
40
a
150 10
解: FS 1 3.64kN
M 1 3.64kNm
75
3 bh Iz 2110 104 mm 4 12 M (7540) 6.04( MP a) (1)a点 1 Iz
F A B
50
250
1400
0.8F
C
2F
600
ZC
h2 h1
150
50
M
+
-
0.6F
0.8Fh M h 1 A 1 解: A截面: tmax ≤ [ t ] I zC I zC
4 [ t ]I zc 4010180 10 52.8( kN) F 0.8h1 0.8106 96.4
M A h2 0.8 Fh2 c max ≤ I zC I zC
[ c ]
4 [ c ]I zc 160 10180 10 132.6( kN) F 0.8h2 0.8106 153.6
M C h2 0.6 Fh2 C截面: tmax ≤ [ t ] I zC I zC
30 q=10kN/m B A
弯曲应力习题
中性轴上的正应力为;矩形截面梁横截面上剪应力沿高度是按分布的。
04. 矩形截面梁若m ax
Q 、m ax M 和截面宽度b 不变,而将高度增加一倍,则最大弯曲正应力为原来的 倍,最大弯曲剪应力为原来的 倍。
05.图示正方形截面简支梁,若载荷不变,而将边长增加一
变应
][τ,,
力
截
T字4。
材。
试
应力助梁
3mm,
3
的强
圆截
.,
mm
15
横截
取水
力的分布规律如何?该截面上总的水平剪力有多大?它由什
么来平衡。
试校核
mm,木
MPa
5。
矩形,
面梁的
正确答案是
点
字形
[P。
] CD,
,F2 = 1.6
( 1 ) 截面为矩形,h = 2 b;
( 2 ) 截面为圆形。
28.图示结构,拉杆EB的直径mm
D100
=,
=,梁AF的直径mm
d8
两者材料相同,[σ] = 160 MPa ,l = 6 m。
求:
a
=
?
1、2与梁的许用应力均为[σ],杆1和杆2的横截面面积分别为A和2A,梁的抗弯截面模量为W = l A /3,试确定该结构的许可载荷[ P ]。
向伸长为mm
∆。
求载荷q的值与梁AB的安全直径。
CB5.0
=
11 /
11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空
1.1 平面弯曲梁上弯矩等于零的截面处,挠曲线的曲率________,转角________。
(必为零、必不为零、不一定为零)
1.2 几何形状完全相同的一根铝材梁和一根钢材梁,若它们受力相同,则它们弯曲变形后的弯曲应力________,轴线曲率________。
(相同、不相同、不一定相同)
1.3 用积分法求图示悬臂梁的挠曲线方程时,求解积分常数所用到的边界条件是_______、______,连续条件是_______、______、______、______。
二、使用积分法求解图示悬臂梁D 端的绕度D w 和转角D .
D
三、使用叠加原理并利用附录IV 求解习题二
四、使用叠加原理并利用附录IV 求外伸梁的B w 、D w 、D θ。
a
五:悬臂梁AB 受力如图,已知均布荷载q=15KN/m ,长度a=1m ,钢材弹性模量E=200GP ,许用弯曲正应力[]160MPa σ=,许用切应力[]100MPa τ=,许可绕度[]/500w l =(l=3a ),试选取工字钢的型号。
B。
