高中化学计算技巧
高中化学常见化学计算方法

常见化学计算方法主要有:差量法、十字交叉法、平均法、守恒法、极值法、关系式法、方程式叠加法、等量代换法、摩尔电子质量法、讨论法、图象法(略)、对称法(略)。
一、差量法在一定量溶剂的饱和溶液中,由于温度改变(升高或降低),使溶质的溶解度发生变化,从而造成溶质(或饱和溶液)质量的差量;每个物质均有固定的化学组成,任意两个物质的物理量之间均存在差量;同样,在一个封闭体系中进行的化学反应,尽管反应前后质量守恒,但物质的量、固液气各态物质质量、气体体积等会发生变化,形成差量。
差量法就是根据这些差量值,列出比例式来求解的一种化学计算方法。
该方法运用的数学知识为等比定律及其衍生式:a c a c或c a。
差量法是简化化学计算的一种主要手段,在中学阶段运用相当普遍。
常见的b d b d d b类型有:溶解度差、组成差、质量差、体积差、物质的量差等。
在运用时要注意物质的状态相相同,差量物质的物理量单位要一致。
1. 将碳酸钠和碳酸氢钠的混合物21.0g ,加热至质量不再变化时,称得固体质量为12.5g 。
求混合物中碳酸钠的质量分数。
2.实验室用冷却结晶法提纯KNO 3,先在100℃时将KNO 3配成饱和溶液,再冷却到30℃,析出KNO 3。
现欲制备 500g 较纯的 KNO 3,问在 100℃时应将多少克 KNO 3溶解于多少克水中。
( KNO 3的溶解度 100℃时为 246g,30℃时为 46g)3.某金属元素R 的氧化物相对分子质量为m,相同价态氯化物的相对分子质量为n,则金属元素R 的化合价为多少?4.将镁、铝、铁分别投入质量相等、足量的稀硫酸中,反应结束后所得各溶液的质量相等,则投入的镁、铝、铁三种金属的质量大小关系为()( A ) Al > Mg >Fe(B)Fe>Mg>Al(C)Mg>Al>Fe(D)Mg=Fe=Al5.取 Na2CO3和 NaHCO 3混和物 9.5g,先加水配成稀溶液,然后向该溶液中加9.6g 碱石灰(成分是 CaO 和 NaOH ),充分反应后,使Ca2+、 HCO 3-、 CO32-都转化为CaCO3沉淀。
高中化学计算题解题技巧

In places deeper than night, there must be darker eyes than night.简单易用轻享办公(页眉可删)高中化学计算题解题技巧高中化学计算题解题技巧就在下面,欢迎大家一起学习高中化学解题技巧、高中化学题解题技巧、高中化学解题方法哦!高中化学计算题解题技巧一.守恒法:化学上,常用的守恒方法有以下几种:电荷守恒、电子守恒、原子守恒、质量守恒1、某露置的苛性钠经分析含水:9%(质量分数,下同)、Na2CO3:53%、NaOH :38%。
取此样品 10.00 g放入 100.00 mL 2.00 molL-1 的 HCl(aq) 中,过量的 HCl 可用 1.00mol/L NaOH(aq)中和至中性,蒸发中和后的溶液可得固体_______克。
2、Fe、Cu合金42g与足量的稀HNO3反应,生成标准状况下的无色气体为13.44L,将此溶液中加过量的NaOH充分沉淀,过滤,洗涤,灼烧,最后得混和氧化物,求氧化物的总重量。
二.估算法:1、甲、乙两种化合物都只含X、Y 两种元素,甲、乙中 X 元素的百分含量分别为 30.4% 和 25.9%。
若已知甲的分子式是XY2,则乙的分子式只可能是( )A.XYB.X2YC.X2Y3D.X2Y52、有一种不纯的铁,已知它含有铜、铝、钙或镁中的一种或几种,将5.6克样品跟足量稀H 2SO4完全反应生成0.2克氢气,则此样品中一定含有(A)Cu(B)Al(C)Ca (D)Mg三.差量法:遇到反应前后固体或液体的质量、物质的量、体积发生变化时,可尝试用“差量法”解题:总压强为 3.0107 Pa 时,N2、H2 混合气体(体积之比为 1∶3)通入合成塔中,反应达平衡时,压强降为2.5107 Pa,则平衡时混合气体中 NH3 的体积分数为( )A.35%B.30%C.D.四.和量法:与差量法相反,为解决问题方便,有时需要将多个反应物(或生成物)合在一起进行计算。
高中化学常见化学计算方法

高中化学常见化学计算方法高中化学中,常见的化学计算方法主要涉及元素定量关系、物质的质量与物质的量关系、物质的质量和体积关系以及溶液稀释等方面。
下面将逐一介绍这些常见的化学计算方法。
1.元素定量关系元素定量关系是指在反应中各元素的质量之间的定量关系。
在元素定量关系的计算中,首先需要根据化学方程式确定反应中的元素的原子数目比例,然后根据其中一元素的质量或物质的质量,计算其他元素的质量或物质的质量。
例如,在氧化铁的合成反应中,反应方程式为:4Fe+3O2→2Fe2O3、如果已知Fe的质量,想要计算Fe2O3的质量,可首先根据方程式计算出Fe2O3中Fe的原子数目,然后根据Fe的质量计算出Fe2O3的质量。
2.物质的质量与物质的量关系物质的质量与物质的量之间的关系即摩尔质量的概念。
在化学计算中,物质的质量与物质的量可以通过摩尔质量进行转化。
摩尔质量是指一个物质中1摩尔(6.022 × 10^23个实体)的质量,单位是g/mol。
物质的质量与物质的量之间的关系可以通过以下公式表示:物质的量=物质的质量/摩尔质量。
例如,已知NaCl的物质的质量为5g,想要计算其中的物质的量时,可以根据NaCl的摩尔质量(即Na的原子量+Cl的原子量)计算出物质的量。
3.物质的质量和体积关系物质的质量和体积之间的关系可以通过物质的密度来计算。
密度是指物质的单位体积质量,其计算公式为密度=物质的质量/物质的体积。
由于1mol气体占据相等的体积,因此,在气体状态下,物质的质量和物质的量之间的关系可以通过气体的摩尔质量和气体的密度来计算。
例如,已知气体的摩尔质量为28.96 g/mol,密度为2.77 g/L,想要计算其质量时,可以根据摩尔质量和密度计算出其质量。
4.溶液稀释溶液稀释是指通过添加溶剂来稀释溶液,从而改变溶液的浓度。
在溶液稀释中,可以通过溶液的体积和浓度来计算沉淀的物质的质量。
根据溶液的浓度可以计算出溶液中的溶质的物质的质量,然后根据稀释前后溶液的质量和浓度的关系计算出沉淀的物质的质量。
高中化学常见化学计算方法归纳

高中化学常见化学计算方法归纳高中化学常见化学计算方法归纳:在学习化学的过程中,化学计算是非常重要的一部分。
通过化学计算,我们可以推导出物质的量、质量、体积等实验数据,帮助我们解决化学实验和理论问题。
下面将对高中化学中常见的化学计算方法进行归纳总结。
一、摩尔计算1. 摩尔的定义:一个摩尔的物质包含6.02×10^23个基本粒子,通常用符号mol表示。
2. 摩尔质量计算:物质的摩尔质量等于其相对分子质量或相对原子质量的数值单位为克/mol。
计算公式为:摩尔质量 = 质量/物质的量。
3. 摩尔浓度计算:摩尔浓度是指单位体积溶液中所含物质的摩尔数。
计算公式为:摩尔浓度 = 物质的量/溶液的体积。
4. 摩尔配比计算:通过化学方程式中的摩尔数关系,可以推导出反应物质的摩尔比,从而实现实验中物质的定量使用。
二、质量计算1. 反应质量计算:通过化学方程式中的物质的相对分子质量可以推导出反应物质的质量关系。
根据化学平衡的原理,可以计算出反应物的输入质量以及生成物的产量。
2. 溶液配制计算:通过溶质的摩尔质量和溶液的摩尔浓度,可以计算出溶液中所需溶质的质量。
3. 蒸汽压计算:通过物质的分子量和温度,可以计算出其在一定温度下的蒸汽压大小。
4. 气体摩尔体积计算:根据熟悉的气体状态方程式,可以计算出气体在一定条件下的摩尔体积。
三、体积计算1. 溶液体积计算:通过摩尔浓度和溶质的摩尔质量,可以计算出所需配制溶液的体积。
2. 气体气体体积计算:通过气体的温度、压强以及摩尔体积,可以计算出气体在不同条件下的体积变化规律。
3. 气体密度计算:通过气体的分子量和标况下的气体密度,可以计算出气体在一定条件下的密度。
以上就是高中化学中常见的化学计算方法的归纳总结。
熟练掌握这些计算方法,可以帮助我们更好地理解化学知识,提高实验操作和理论分析的运用能力。
希望同学们在学习化学的过程中能够认真掌握这些计算方法,将理论知识与实际操作相结合,为未来的学习和发展打下良好的基础。
化学高中化学化学计算解题技巧提高答题速度

化学高中化学化学计算解题技巧提高答题速度化学作为一门基础科学学科,是中学阶段学生必修的科目之一。
在化学学习中,学生们经常需要进行化学计算。
掌握一些化学计算解题技巧,可以有效提高答题速度。
本文将分享一些实用的化学计算解题技巧,帮助学生们在考试中取得更好的成绩。
一、摩尔计算摩尔是化学计量的基本单位,通过摩尔计算可以进行化学方程式的配平、物质的摩尔质量计算等。
在进行摩尔计算时,有以下几个核心公式需要掌握:1. 摩尔物质质量 = 物质的质量 / 物质的相对分子质量这个公式可以帮助我们求解物质的摩尔质量。
例如,如果一个物质的质量为10克,其相对分子质量为40g/mol,那么该物质的摩尔质量就是10克 / 40g/mol = 0.25mol。
2. 摩尔物质的质量 = 摩尔数 ×物质的相对分子质量通过这个公式,我们可以根据物质的摩尔数和相对分子质量来计算摩尔物质的质量。
例如,如果某个物质的摩尔数为0.5mol,其相对分子质量为30g/mol,那么摩尔物质的质量就是0.5mol ×30g/mol = 15克。
3. 摩尔物质的质量 = 摩尔浓度 ×溶液的体积这个公式常用于溶液的摩尔浓度计算。
例如,如果某个溶液的摩尔浓度为0.1mol/L,溶液体积为500mL,那么摩尔物质的质量就是0.1mol/L × 500mL = 50克。
二、溶解度计算溶解度是指单位温度和压力下,溶质在溶剂中能够溶解的最大量。
在溶解度计算中,可以运用以下几个关键公式:1. 溶解度 = 溶质的质量 / 溶剂的质量这个公式可用于求解溶解度。
例如,如果某个化合物在100克水中溶解了20克,那么其溶解度就是20克 / 100克 = 0.2。
2. 溶解度 = 溶质的物质的量 / 溶剂的体积这个公式适用于溶解度的摩尔计算。
例如,如果某个化合物的溶质物质的量为0.2mol,溶剂的体积为500mL,那么其溶解度就是0.2mol /0.5L = 0.4mol/L。
高一化学计算题解题技巧

高一化学计算题解题技巧高一化学计算题解题技巧1.守恒法:包括原子个数守恒、得失电子守恒、电荷守恒法、质量守恒法等。
2.极值法:从问题的极端去考虑、去推理、判断,使问题得到解决。
3.讨论法:当题中含有不确定的因素时,对每一种可能情况进展的讨论。
4.量量关系法:利用量物质与未知量物质之间的关系来解题。
5.数形结合法:将复杂或抽象的数量关系与直观形象的图形互为浸透、互相补充。
6.差量法:运用前后量的差,根据方程式中的计量数的关系直接求解。
7.定量问题定性化;8.近似估算;9.运用整体思维,化繁为简;10.利用图象解题等等。
11.注意解题标准格式,这方面主要是指要带单位运算和利用化学方程式计算时的标准格式。
12.注意分步作答。
每年国家考试中心的评分标准都是分步计分,往往分步计分之和不等于总分。
13.注意有效数字的取用近年来有效数字的取用越来越重视,在平时的练习中就要引起注意。
14.价配平法当化学方程式中某些元素的化合价较难确定时,通常采用0价配平法,所选配平标准可以是反响物,也可以是生成物。
15.万能配平法万能配平法所配平的化学方程式只是原子个数守恒,化合价的升降总值不一定相等,因此不一定正确,虽然中学阶段很少遇到这样的化学方程式,但在最后进展化合价升降总值是否相等的验证,还是必要的。
16.合并配平法关键是找出发生氧化复原反响的两种物质间的某种数量关系,常用方法有〔1〕通过某种物质的分子中原子间的数量关系,确定其他两种〔或多种〕物质的数量关系。
〔2〕通过电荷守恒等方法确定其他两种〔或多种〕物质的数量关系。
17.拆分配平法合适氧化剂和复原剂是同一种物质,且氧化产物和复原产物也是同一种物质的化学方程式的配平,其配平技巧是将氧化复原剂〔或氧化复原产物〕根据需要进展合理拆分。
拓展阅读:高考化学选择题有什么解题技巧 1、列举特例、速排选项高考选择题往往考察一般规律中的特殊情况,这就要求考生熟悉特例,对于一些概念判断、命题式判断正误类题目,假如从正面不能直接作出判断,可以列举反例、特例,迅速判断选项正误。
高中化学14种基本计算题解法

高中化学14种基本计算题解法作为一门重要的理科科目,化学在高中教育中占有重要的地位。
在化学学习过程中,计算题是学生们最常接触到的题型之一。
为了帮助学生更好地应对化学计算题,本文将介绍高中化学14种基本计算题解法。
1. 摩尔质量计算法任何一个元素或化合物的摩尔质量只与它的分子量或原子量有关,因此,可以用元素或化合物摩尔质量计算分子、离子、原子等问题。
计算公式:n(物质的摩尔数)=物质的质量(g)÷物质的摩尔质量(g/mol)2. 摩尔占比计算法摩尔占比是指一个分子中某个元素的摩尔数与该分子中所有元素摩尔数总和之比。
求解这种计算题时,必须先求出化学式中各元素的数量,然后再计算摩尔占比。
计算公式:某元素的摩尔占比=该元素的摩尔数÷分子中所有元素的摩尔数总和×100%3. 摩尔浓度计算法摩尔浓度是指一个体系中溶质的摩尔数与溶液体积之比。
在该计算中,需先求出摩尔数,然后再算出溶液体积。
计算公式:C(溶液的摩尔浓度)=溶质摩尔数÷溶液体积(L)4. 用比化学式求出分子式的计算法比化学式是指化合物中各元素原子数的比,求出比化学式即可推断出化合物的分子式。
计算公式:分子式= n(最简整数倍的原子数)×比化学式5. 化学计量法化学计量法是指通过实验探究,确定元素化合的准确数量关系的方程式。
其中,摩尔比等于化学计量数。
计算公式:化学计量数=元素的摩尔比÷最小的摩尔数6. 工业制备量计算法工业制备量是指在某一生产过程中,制备特定化学物质的最终产品量。
在该计算中,需考虑到有机合成过程中的需要损耗、产率等因素。
计算公式:制备量=原料摩尔数×反应摩尔比×产率7. 反应的质量计算法化学反应中,反应物质的质量与终产物质量之间存在一定的关系,可通过反应方程式来进行计算。
计算公式:质量计算式=质量与化学计量数的乘积÷化学计量数8. 等效质量计算法等效质量是指化学物质与特定反应物质之间的质量之比。
高中化学常见化学计算方法总结

高中化学常见化学计算方法总结在高中化学学习中,化学计算是一个至关重要的部分。
通过化学计算,我们可以根据实验数据或化学反应方程式来推导出一些未知的化学量,进而解决化学实验和理论问题。
下面将总结高中化学中常见的化学计算方法。
一、摩尔计算在化学计算中,常用的一个基本单位是摩尔(mol)。
摩尔计算是指根据物质的摩尔之间的关系来进行计算。
摩尔计算最常见的应用是计算物质的质量、体积、浓度等。
例如,根据化学方程式计算反应物质的摩尔比,从而确定生成物的摩尔量;或者根据物质的摩尔量和摩尔质量计算质量之间的关系等。
二、质量计算质量计算是高中化学中常见的一种计算方法。
根据物质的质量和化学式来计算摩尔数或质量之间的关系。
例如,通过质量和化学方程式计算出反应物质的摩尔量,从而确定生成物的质量;或者通过已知的摩尔量计算出物质的质量等。
三、体积计算在溶液稀释、气体体积比计算等化学实验中,体积计算是一种常见的计算方法。
通过体积计算可以了解不同溶液浓度之间的关系,或者根据气体体积的变化来推导出化学反应的结果。
例如,根据浓度计算出一定体积溶液所含的溶质的质量;或者通过气体体积比计算出气体在不同条件下的压力等。
四、浓度计算浓度计算是高中化学中常见的一种计算方法。
浓度是指溶液中溶质的质量或摩尔数与溶剂的体积之比。
通过浓度计算可以推导出溶液中溶质的质量、溶质的摩尔数等重要信息。
例如,通过浓度计算出一定体积溶液所含溶质的摩尔量,从而进一步计算出质量等。
通过以上四种常见的化学计算方法,我们可以更好地理解化学实验和理论问题,提高化学学习的效率。
希望以上内容对您的化学学习有所帮助。
化学计算的常见方法

化学计算的常见方法1.守恒法守恒法是一种中学化学典型的解题方法,它利用物质变化过程中某一特定的量固定不变来列式求解,可以免去一些复杂的数学计算,大大简化解题过程,提高解题速度和正确率。
它的优点是用宏观的统揽全局的方式列式,不去探求某些细枝末节,直接抓住其中的特有守恒关系,快速建立计算式,巧妙地解答题目。
物质在参加反应时,化合价升降的总数,反应物和生成物的总质量,各物质中所含的每一种原子的总数,各种微粒所带的正负电荷总和等等,都必须守恒。
所以守恒是解计算题时建立等量关系的依据,守恒法往往穿插在其它方法中同时使用,是各种解题方法的基础。
例1.将几种铁的氧化物的混合物加入100ml、7molol―1的盐酸中。
氧化物恰好完全溶解,在所得的溶液中通入0.56l(标况)氯气时,恰好使溶液中的fe2+完全转化为fe3+,则该混合物中铁元素的质量分数为()a. 72.4%b. 71.4%c. 79.0%d. 63.6%解析:铁的氧化物中含fe和o两种元素,由题意,反应后,hcl 中的h全在水中,o元素全部转化为水中的o,由关系式:2hc——h2o——o,得:n(o)=,m(o)=0.35mol×16g·mol―1=5.6 g;而铁最终全部转化为fecl3,n(cl)=0.56l ÷22.4l/mol×2+0.7mol=0.75mol,n(fe)=,m(fe)=0.25mol×56g·mol―1=14 g,则,选b。
2.差量法差量法是根据物质变化前后某种量发生变化的化学方程式或关系式,找出所谓”理论差量”,这个差量可以是质量差、气态物质的体积差、压强差,也可以是物质的量之差、反应过程中的热量差等。
解题时将”差量”看作化学方程式右端的一项,将已知差量(实际差量)与化学方程式中的对应差量(理论差量)列成比例,其他解题步骤与按化学方程式列比例或解题完全一样。
该法适用于解答混合物间的反应,且反应前后存在上述差量的反应体系。
高中化学常见化学计算方法复习

高中化学常见化学计算方法复习化学计算是高中化学学习中的重要内容,通过化学计算可以帮助我们解决各种化学实验和计算题的问题。
了解常见的化学计算方法对于学习化学和备考考试都具有重要意义。
本文将对高中化学中常见的化学计算方法进行复习。
一、摩尔计算摩尔是用来表示物质的数量的单位,化学计算中常用摩尔来进行计算。
在化学方程式中,摩尔的概念非常重要,它指的是反应物和生成物之间的摩尔比关系。
例如,在化学反应中,如果已知反应物的摩尔数,可以根据化学方程式计算生成物的摩尔数,进而计算反应物之间的摩尔比。
摩尔计算是化学计算中的基础,大家要熟练掌握。
二、质量计算在化学实验中,我们常常需要根据化学方程式计算反应物和生成物的质量。
质量计算是化学计算中的重要内容。
通过摩尔计算和相对原子质量的概念,可以轻松地进行质量计算,计算反应物和生成物之间的质量比。
在质量计算中,还需要注意化学反应的化学方程式,以及反应物的质量和生成物的质量之间的关系。
三、体积计算在一些化学实验中,我们需要根据反应物的体积来计算反应物和生成物之间的摩尔比。
体积计算也是化学计算的常见方法之一。
在体积计算中,我们需要根据气体的摩尔体积与摩尔之间的关系来进行计算。
同时,体积计算还需要考虑到气体在不同条件下的压力和温度,这对于体积计算也有一定的影响。
四、溶液浓度计算溶液浓度是溶质溶于溶剂中的比例。
在化学计算中,我们需要根据溶质和溶剂的质量或摩尔数来计算溶液的浓度。
溶液浓度计算常用的单位有摩尔/升、质量百分比、体积百分比等。
在溶液浓度计算中,还需要注意到浓度和浓度之间的关系,以及在不同条件下浓度的变化。
五、热量计算在一些化学反应中,会伴随着吸热或放热的现象。
热量计算是化学计算中的一个重要内容。
在热量计算中,我们需要根据反应物和生成物的热化学方程式来计算反应的热量变化。
热量计算也是化学实验中常用的方法之一,需要注意到放热和吸热的情况,以及热量与其他物质性质之间的关系。
以上就是高中化学常见的化学计算方法的复习内容。
化学计算常用的方法与规律
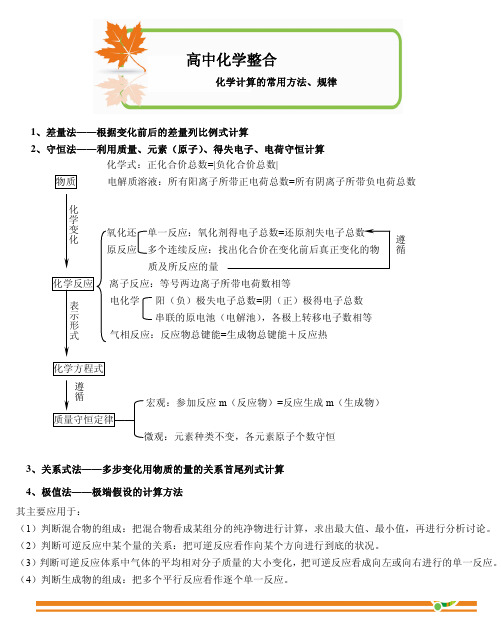
遵 循
原反应 多个连续反应:找出化合价在变化前后真正变化的物
质及所反应的量
化学反应
表 示 形 式
离子反应:等号两边离子所带电荷数相等 电化学 阳(负)极失电子总数=阴(正)极得电子总数
串联的原电池(电解池),各极上转移电子数相等 气相反应:反应物总键能=生成物总键能+反应热
化学方程式 遵 循 宏观:参加反应 m(反应物)=反应生成 m(生成物)
(1)强酸的 pH
(2)稀释强酸溶液
(3)稀释弱酸溶液
(4)混合酸溶液的 pH
【小结】求酸溶液的 pH 须先求
,再求
。求算中注意混合溶液的体积变化。
[H+]= 浓酸中H +的物质的量+稀酸中H +的物质的量 V总
(二)碱性体系
(1)强碱溶液的 pH 计算
(2)稀释碱溶液
【小结】求碱性溶液 pH 的方法:先求
求该酯的分子式
。
8、水的离子积 水是极弱的电解质,存在着电离平衡。水的离子积常数 KW=[H+]·[OH-]。
25℃时,Kw=10-14,Kw 只随温度的升高而增大,无论是中性、酸性、碱性的稀溶液中都有[H+]·[OH-]=KW。
高中化学整合
化学计算的常用方法、规律
9、有关 PH 的计算
(一)酸性体系:
6、十字交叉法
运用“十字交叉法”的要领是:
(1)首先判断哪种计算题可用本法:二元混合物(a>c>b),且有平均值 C 的计算题;
(2)两物质所取的基准量 m、n 可相加;
(3)要有两物质的平均值,且平均值的单位要与两物质所表示的单位相同;
(4)m/n 是所取的基准量之比。
求解元素、同位素、原子、电子等微粒间量的变化的试题。
高中化学常见化学计算方法大全

高中化学常见化学计算方法大全化学计算在学习化学过程中扮演着至关重要的角色,它可以帮助我们理解和应用化学知识,解决实际问题。
在高中化学学习中,有许多常见的化学计算方法,本文将为大家总结归纳,希望能够帮助大家更好地掌握这些技巧。
一、摩尔计算摩尔计算是化学中最基本也是最常见的计算方法之一。
在进行化学计算时,常常需要将物质的质量、摩尔数和粒子数之间进行转换。
通过摩尔计算,我们可以根据已知条件计算出所需的结果,为化学实验和实际应用提供便利。
二、质量分数计算质量分数是指溶液中溶质的质量占溶液总质量的比例。
在化学实验和生产中,常常需要计算溶液的质量分数,以确定溶液的浓度、配比等信息。
通过质量分数计算,可以准确把握溶液中各组分的含量,为实验操作提供依据。
三、物质平衡计算物质平衡计算是化学反应中常见的计算方法之一。
在化学反应过程中,原料和产物之间存在着一定的化学平衡关系,通过物质平衡计算,我们可以确定反应过程中各组分的相对含量,帮助我们理解反应机理和优化反应条件。
四、体积计算体积计算是化学实验中常见的计算方法之一。
在进行实验操作时,常常需要计算反应容器的体积、气体的体积等信息,通过体积计算,可以精确控制反应条件,保障实验结果的准确性和可靠性。
五、溶液配制计算溶液配制计算是化学实验和生产中常见的计算方法之一。
在实验操作中,我们需要根据给定的浓度和体积要求,配制出符合要求的溶液。
通过溶液配制计算,可以快速准确地计算出所需的溶质质量或溶液体积,为实验操作提供便利。
六、氧化还原反应计算氧化还原反应是化学中重要的反应类型之一。
在进行氧化还原反应计算时,我们常常需要确定氧化数、电子转移数等信息,通过氧化还原反应计算,可以帮助我们理解反应机理,预测反应结果,并指导实验操作。
七、热化学计算热化学计算是在热力学领域中常见的计算方法之一。
通过热化学计算,我们可以确定各种热化学参数,如反应焓、反应熵、反应自由能等信息,帮助我们评价反应的热力学性质,优化反应条件。
高中化学计算中常用的几种方法

高中化学计算中常用的几种方法一.差量法(1)不考虑变化过程,利用最终态(生成物)与最初态(反应物)的量的变化来求解的方法叫差量法。
无须考虑变化的过程。
只有当差值与始态量或终态量存在比例关系时,且化学计算的差值必须是同一物理量,才能用差量法。
其关键是分析出引起差量的原因。
(2)差量法是把化学变化过程中引起的一些物理量的增量或减量放在化学方程式的右端,作为已知量或未知量,利用各对应量成正比求解。
(3)找出“理论差量”。
这种差量可以是质量、物质的量、气态物质的体积和压强、反应过程中的热量等。
用差量法解题是先把化学方程式中的对应差量(理论差量)跟实际差量列成比例,然后求解。
如:-12C(s)+O2(g)===2CO(g) ΔH=-221 kJ·mol Δm(固),Δn(气),ΔV(气)2 mol 1 mol 2 mol 221 kJ 24 g 1 mol 22.4 L(标况)1例1.将质量为100克的铁棒插入硫酸铜溶液中,过一会儿取出,烘干,称量,棒的质量变为100.8克。
求有多少克铁参加了反应。
(答:有5.6克铁参加了反应。
)解:设参加反应的铁的质量为x。
Fe+CuSO4===FeSO4+Cu 棒的质量增加(差量)56 6464-56=8x 100.8克-100克=0.8克56:8=x:0.8克答:有5.6克铁参加了反应。
2.例2.将a L NH3通过灼热的装有铁触媒的硬质玻璃管后,气体体积变为b L(气体体积均在同温同压下测定),该b L气体中NH3的体积分数是(C ) 2a-bb-a2a-bb-aA. C. abba设参加反应的氨气为x ,则2NH3N2+3H2 ΔV2 2x b-ax=(b-a) L所以气体中NH3的体积分数建立关系式一般途径是:(1)利用微粒守恒建立关系式;(2)利用化学方程式之间物质的量的关系建立关系式;(3)利用方程式的加和建立关(1)化合物中元素正负化合价总数守恒。
(8种)高中化学计算题解题方法

(8种)高中化学计算题解题方法一、关系式法关系式法是根据化学方程式计算的巧用,其解题的核心思想是化学反应中质量守恒,各反应物与生成物之间存在着最基本的比例(数量)关系。
例题:某种H2和CO的混合气体,其密度为相同条件下再通入过量O2,最后容器中固体质量增加了()A.3.2gB.4.4gC.5.6gD.6.4g[解析]固体增加的质量即为H2的质量。
固体增加的质量即为CO的质量。
所以,最后容器中固体质量增加了3.2g,应选A。
二、方程或方程组法根据质量守恒和比例关系,依据题设条件设立未知数,列方程或方程组求解,是化学计算中最常用的方法,其解题技能也是最重要的计算技能。
例题:有某碱金属M及其相应氧化物的混合物共10g,跟足量水充分反应后,小心地将溶液蒸干,得到14g无水晶体。
该碱金属M可能是()(锂、钠、钾、铷的原子量分别为:6.94、23、39、85.47)A.锂B.钠C.钾D.铷[解析]设M的原子量为x,解得42.5>x>14.5,分析所给锂、钠、钾、铷的原子量,推断符合题意的正确答案是B、C。
三、守恒法化学方程式既然能够表示出反应物与生成物之间物质的量、质量、气体体积之间的数量关系,那么就必然能反映出化学反应前后原子个数、电荷数、得失电子数、总质量等都是守恒的。
巧用守恒规律,常能简化解题步骤、准确快速将题解出,收到事半功倍的效果。
例题:将5.21g纯铁粉溶于适量稀H2SO4中,加热条件下,用2.53gKNO3氧化Fe2+,充分反应后还需0.009molCl2才能完全氧化Fe2+,则KNO3的还原产物氮元素的化合价为___。
[解析]0.093=0.025x+0.018,x=3,5-3=2。
应填:+2。
(得失电子守恒)四、差量法找出化学反应前后某种差量和造成这种差量的实质及其关系,列出比例式求解的方法,即为差量法。
其差量可以是质量差、气体体积差、压强差等。
差量法的实质是根据化学方程式计算的巧用。
它最大的优点是:只要找出差量,就可求出各反应物消耗的量或各生成物生成的量。
高中化学计算

高中化学计算方法和技巧最基本的方法:列方程组求解:(关键是找出2个方程式联立形成方程组) 这是我认为最基本的解题方法,例如:例1. 标准状况下,CO 2和CO 的混合气体15g ,体积为10.08L ,则此混合气体中的CO 2和CO 的物质的量各是多少?例2. 标况下SO 2和SO 3混合气体在不考虑化学变化时,其中含O 的质量分数是60%,求SO 2的质量分数。
常用技巧:技巧一:守恒法以化学反应中存在的某些守恒关系作为依据,如:质量守恒、原子守恒、元素守恒、电荷守恒、电子得失守恒等。
来解答一些较复杂的题型,以达到简化计算过程,避免繁琐计算,从而迅速求解的目的。
1. 原子守恒例4. 有0.4g 铁的氧化物, 用足量的CO 在高温下将其还原,把生成的全部CO 2通入到足量的澄清的石灰水中得到0.75g 固体沉淀物,这种铁的氧化物的化学式为( )A. FeOB. Fe 2O 3C. Fe 3O 4D. Fe 4O 5 解析:由题意得知,铁的氧化物中的氧原子最后转移到沉淀物CaCO 3中。
且n(O) = n(CaCO 3) = 0.0075mol , m(O)=0.0075 mol × 16 g / mol = 0.12 g 。
m(Fe) = 0.4 g - 0.12 g = 0.28 g ,n(Fe) = 0.005 mol 。
n(Fe)∶n(O) = 2:3,选B2. 元素守恒例5. 将几种铁的氧化物的混合物加入100mL 、7mol •L ―1的盐酸中。
氧化物恰好完全溶解,在所得的溶液中通入0.56L (标况)氯气时,恰好使溶液中的Fe 2+完全转化为Fe 3+,则该混合物中铁元素的质量分数为( )A. 72.4%B. 71.4%C. 79.0%D. 63.6% 解析:铁的氧化物中含Fe 和O 两种元素,由题意,反应后,HCl 中的H 全在水中,O 元素全部转化为水中的O ,由关系式:2HCl~H 2O~O ,得:n (O )= mol mol HCl n 35.07.021)(21=⨯=⨯,m (O )= 0.35 mol ×16 g • mol ―1= 5.6 g ;而铁最终全部转化为FeCl 3,n (Cl )= 0.56 L ÷22.4 L / mol ×2 + 0.7 mol = 0.75 mol ,n (Fe )= mol mol Cl n 25.075.031)(31=⨯=⨯,m(Fe) = 0.25 mol ×56 g • mol―1 = 14 g ,则%4.71%1006.51414)(=⨯+=gg g Fe ω,选B 。
高中化学化学计算知识点归纳总结

高中化学化学计算知识点归纳总结化学计算是高中化学学习中的重要部分,它涉及到化学方程式、物质的量、摩尔质量、溶液的浓度等概念,是分析和解决实际问题的基础。
本文将对高中化学中的常见计算知识点进行归纳总结,包括质量计算、物质的量计算、摩尔质量计算和溶液的浓度计算。
一、质量计算1. 质量百分比计算质量百分比是指某种元素在化合物或混合物中所占的质量比例,计算方法为:质量百分比 = (某种元素的质量 / 化合物或混合物的总质量) × 100%2. 化合物的化学式根据化合物的质量百分比,可以推导出其化学式。
具体步骤包括以下几个方面:- 计算各元素的质量,例如质量百分比为50%的元素质量为50g;- 计算元素的物质的量,通过元素的质量除以摩尔质量,例如50g 的元素的物质的量为50g/摩尔质量;- 确定元素的摩尔比例,以最小的物质的量除以最小物质的量为1,得出其他元素的物质的量比例;- 根据元素的摩尔比例推导出化学式。
二、物质的量计算1. 物质的量与质量的关系物质的量与质量的关系可以通过以下公式计算:物质的量 = 质量 / 物质的摩尔质量2. 物质的量与体积的关系在液体和气体的计算中,物质的量与体积的关系可以通过以下公式计算:物质的量 = 体积 / 摩尔体积三、摩尔质量计算1. 摩尔质量的概念摩尔质量是指物质的摩尔质量与物质的质量之间的关系,计量单位为g/mol。
2. 计算方法要计算摩尔质量,可以按照以下步骤进行:- 确定化学物质的化学式;- 查找元素的原子质量表,获取各个元素的相对原子质量;- 计算各元素相对原子质量的总和,即为化学物质的摩尔质量。
四、溶液的浓度计算1. 溶液的浓度溶液的浓度是指单位体积溶液中所含溶质的质量或物质的量,常用的浓度单位有质量百分比、摩尔浓度等。
2. 计算方法根据不同的浓度单位,计算方法也会有所不同,例如:- 质量百分比浓度 = (溶质质量 / 溶液总质量) × 100%- 摩尔浓度 = 物质的量 / 溶液的体积以上是高中化学化学计算的一些知识点的归纳总结。
高中化学化学式计算的技巧与题目解析

高中化学化学式计算的技巧与题目解析在高中化学学习中,化学式计算是一个重要的知识点,也是考试中常见的题型。
掌握化学式计算的技巧对于学生来说非常关键,下面将介绍一些常见的计算方法和解题技巧,并通过具体的题目进行解析,帮助学生更好地理解和掌握这一知识点。
一、化学式计算的基本原理化学式计算是通过已知物质的质量、摩尔数或体积等信息,推算其他物质的质量、摩尔数或体积。
在进行化学式计算时,需要根据化学方程式中的摩尔比例关系和物质的化学式来确定计算方法。
二、质量计算1. 已知质量求摩尔数当已知物质的质量时,可以通过质量与摩尔质量的关系计算摩尔数。
例如,已知氧化铁的质量为10克,求其摩尔数。
解析:首先,查找氧化铁的化学式为Fe2O3,摩尔质量为159.69 g/mol。
然后,利用质量与摩尔质量的关系进行计算:10 g / 159.69 g/mol ≈ 0.0627 mol。
2. 已知质量求摩尔质量当已知物质的质量和摩尔数时,可以通过质量与摩尔数的比值计算摩尔质量。
例如,已知质量为5克的物质含有0.05摩尔,求其摩尔质量。
解析:首先,利用质量与摩尔数的比值计算摩尔质量:5 g / 0.05 mol = 100g/mol。
3. 已知质量求其他物质的质量当已知物质的质量和化学式时,可以通过化学式中的摩尔比例关系计算其他物质的质量。
例如,已知硫酸铜的质量为10克,求其中的铜的质量。
解析:首先,查找硫酸铜的化学式为CuSO4,摩尔质量为159.61 g/mol。
然后,利用化学式中的摩尔比例关系进行计算:10 g × (1 mol / 159.61 g/mol) × (63.55g/mol / 1 mol) ≈ 3.98 g。
三、摩尔数计算1. 已知摩尔数求质量当已知物质的摩尔数和摩尔质量时,可以通过摩尔数与摩尔质量的乘积计算质量。
例如,已知氧气的摩尔数为2 mol,求其质量。
解析:首先,查找氧气的摩尔质量为32 g/mol。
高中化学化学计算题解题技巧

高中化学化学计算题解题技巧在高中化学学习过程中,化学计算题是必不可少的一部分。
对于很多学生来说,这些计算题可能是比较困难和复杂的。
然而,只要我们掌握了一些解题技巧,就能轻松应对这些题目。
本文将介绍一些高中化学计算题的解题技巧,帮助学生们更好地应对这一部分的考试内容。
一、摩尔计算题摩尔计算题是高中化学中常见的一种计算题型。
在这类题目中,我们需要根据化学反应方程式和物质的摩尔比例来计算物质的质量、体积或摩尔数等。
解决这类题目的关键是正确理解反应方程式和摩尔比例。
例如,题目如下:已知反应方程式:2H2 + O2 → 2H2O问:当氢气和氧气的摩尔比为2:1时,生成的水的摩尔数是多少?解答:根据题目中给出的摩尔比,我们可以知道氢气和氧气的摩尔数分别为2x和x。
而根据反应方程式,氢气和氧气的摩尔比为2:1,所以氢气的摩尔数是氧气的两倍。
因此,我们可以得出以下计算式:2x + x = 2解这个方程可得x=1,代入原式可知氢气的摩尔数为2,因此生成的水的摩尔数为2。
二、溶液浓度计算题溶液浓度计算题也是高中化学中常见的一种计算题型。
在这类题目中,我们需要根据溶质的质量和溶液的体积来计算溶液的浓度,常用的浓度单位有质量百分比、摩尔浓度和体积百分比等。
例如,题目如下:已知某溶液中含有NaCl 20g,溶液的体积为100mL,求该溶液的质量百分比浓度。
解答:质量百分比浓度的计算公式为:质量百分比浓度 = (溶质的质量 / 溶液的质量) × 100%首先,我们需要计算溶液的质量。
溶液的质量 = 溶质的质量 + 溶剂的质量。
由于题目中没有给出溶剂的质量,但给出了溶液的体积,我们可以根据溶液的密度来计算溶剂的质量。
假设溶液的密度为1g/mL,那么溶液的质量 = 100mL × 1g/mL = 100g。
根据计算公式,质量百分比浓度 = (20g / 100g) × 100% = 20%。
因此,该溶液的质量百分比浓度为20%。
高中化学14种基本计算题解法

高中化学14种基本计算题解法化学计算题是中同学在化学学习中比较头痛的一类题目,也是同学们在测验和考试中最难得分的一类题,能选用最合适的(方法)精确而快速地解决计算题,对于提高学习成果,增加学习效率,有着重要意义。
那么,解题方法有哪些呢?今日给同学(总结)了以下14种!1.商余法这种方法主要是应用于解答有机物(尤其是烃类)知道分子量后求出其分子式的一类题目。
对于烃类,由于烷烃通式为CnH2n+2,分子量为14n+2,对应的烷烃基通式为CnH2n+1,分子量为14n+1,烯烃及环烷烃通式为CnH2n,分子量为14n,对应的烃基通式为CnH2n-1,分子量为14n-1,炔烃及二烯烃通式为CnH2n-2,分子量为14n-2,对应的烃基通式为CnH2n-3,分子量为14n-3,所以可以将已知有机物的分子量减去含氧官能团的式量后,差值除以14(烃类直接除14),则最大的商为含碳的原子数(即n值),余数代入上述分子量通式,符合的就是其所属的类别。
[例1]某直链一元醇14克能与金属钠完全反应,生成0.2克氢气,则此醇的同分异构体数目为()A、6个B、7个C、8个D、9个由于一元醇只含一个-OH,每mol醇只能转换出molH2,由生成0.2克H2推断出14克醇应有0.2mol,所以其摩尔质量为72克/摩,分子量为72,扣除羟基式量17后,剩余55,除以14,最大商为3,余为13,不合理,应取商为4,余为-1,代入分子量通式,应为4个碳的烯烃基或环烷基,结合“直链”,从而推断其同分异构体数目为6个.、2.平均值法这种方法最适合定性地求解混合物的组成,即只求出混合物的可能成分,不用考虑各组分的含量。
依据混合物中各个物理量(例如密度,体积,摩尔质量,物质的量浓度,质量分数等)的定义式或结合题目所给条件,可以求出混合物某个物理量的平均值,而这个平均值必需介于组成混合物的各成分的同一物理量数值之间,换言之,混合物的两个成分中的这个物理量确定一个比平均值大,一个比平均值小,才能符合要求,从而可推断出混合物的可能组成。
高中化学计算的常用方法

高中化学计算的常用方法一、守恒法一切物质的组成与转化均遵循“守恒”定律,如化合物中元素正化合价与负化合价的绝对值守恒;电解质溶液中阳离子所带正电荷总数与阴离子所带负电荷总数守恒;化学反应前后同种元素的原子个数守恒;氧化还原反应中得失电子数目守恒;溶液稀释、浓缩、混合前后溶质的量守恒。
由于上述守恒关系不随微粒的组合方式或转化过程的改变而改变,因此可不追究中间过程,直接利用守恒关系列式计算即可。
二、差量法利用反应终态和始态的某些量的变化,以差量和物质间反应的化学计量数列出对应比例式解题的一种方法。
包括质量差、气体体积差、物质的量差等。
三、关系式法关系式是表示两种或多种物质之间物质的量关系的一种简化式子,在多步反应的计算中,通过叠加化学方程式或利用原子守恒关系,找出关系式,将多步计算一步完成。
四、十字交叉法若a、b分别表示某二元混合物中两种组分A、B的量,c 为a、b的平均值,为体系中A和B的组成比,则有。
十字交叉法是巧解二元混合物问题的一种常规有效方法。
五、平均值法平均值法就是根据两组分物质的某种平均值来推断两物质范围的解题方法。
其原理是:X1(平均)2,只要知道X(平均)便可判断X1和X2的取值范围,适合于缺少数据而不能直接求解的混合物判断题。
六、极值法在解决复杂问题或化学过程中,根据解题的需要,采取极植法,将问题或过程推向极限,使复杂的问题极端化、简单化。
极值法的特点是抓两端,定中间,其思路是将混合物各成分的含量以两种极端情况考虑,由此推算出反应的结果,从而缩小范围,简化计算过程。
七、讨论法有些化学计算中不确定因素较多,答案也有多种可能,因此要分不同情况进行讨论,讨论时不仅要依靠数学方法,还要在化学概念的范围内加以推断,将不确定的因素转化为确定因素,从而求算出结果。
八、整体思维法整体思维法是将化学问题作为整体看待,抓住构成问题的各个因素与整体间的关系,从整体变化中寻找变量和恒量,并对有关信息进行复形、替代、转化等技术处理,拓展思维空间,简化解题过程,以便迅速解题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中化学计算技巧一、守恒法化学反应的实质是原子间重新组合,依据质量守恒定律在化学反应中存在一系列守恒现象,如:质量守恒、元素守恒、电荷守恒、电子得失守恒等,利用这些守恒关系解题的方法叫做守恒法。
(一)质量守恒法质量守恒就是化学反应前后各物质的质量总和不变,在配制或稀释溶液的过程中,溶质的质量不变。
【例题】1500C时,碳酸铵完全分解产生气态混合物,其密度是相同条件下氢气密度的(A)96倍(B)48倍(C)12倍(D)32倍【分析】(NH4)2CO3=2NH3↑+H2O↑+CO2↑ 根据质量守恒定律可知混和气体的质量等于碳酸铵的质量,从而可确定混和气体的平均分子量为=24 ,混和气体密度与相同条件下氢气密度的比为=12 ,所以答案为C(二)元素守恒法元素守恒即反应前后各元素种类不变,各元素原子个数不变,其物质的量、质量也不变。
【例题】有一在空气中放置了一段时间的KOH固体,经分析测知其含水2.8%、含K2CO337.3% 取1克该样品投入25毫升2摩/升的盐酸中后,多余的盐酸用1.0摩/升KOH溶液30.8毫升恰好完全中和,蒸发中和后的溶液可得到固体(A)1克(B)3.725克(C)0.797克(D)2.836克【分析】KOH、K2CO3跟盐酸反应的主要产物都是KCl,最后得到的固体物质是KCl,根据元素守恒,盐酸中含氯的量和氯化钾中含氯的量相等,所以答案为B(三)电荷守恒法电荷守恒即对任一电中性的体系,如化合物、混和物、溶液等,电荷的代数和为零,即正电荷总数和负电荷总数相等。
【例题】在Na2SO4和K2SO4的混和溶液中,如果[Na+]=0.2摩/升,[SO42-]=x摩/升,[K+]=y摩/升,则x和y的关系是(A)x=0.5y (B)x=0.1+0.5y (C)y=2(x-0.1) (D)y=2x-0.1【分析】可假设溶液体积为1升,那么Na+物质的量为0.2摩,SO42-物质的量为x摩,K+物质的量为y摩,根据电荷守恒可得[Na+]+[K+]=2[SO42-],所以答案为BC(四)电子得失守恒法电子得失守恒是指在发生氧化—还原反应时,氧化剂得到的电子数一定等于还原剂失去的电子数,无论是自发进行的氧化—还原反应还是原电池或电解池中均如此。
【例题】将纯铁丝5.21克溶于过量稀盐酸中,在加热条件下,用2.53克KNO3去氧化溶液中亚铁离子,待反应后剩余的Fe2+离子尚需12毫升0.3摩/升KMnO4溶液才能完全氧化,写出硝酸钾和氯化亚铁完全反应的方程式。
【分析】铁跟盐酸完全反应生成Fe2+,根据题意可知Fe2+分别跟KMnO4溶液和KNO3溶液发生氧化还原反应,KMnO4被还原为Mn2+,那么KNO3被还原的产物是什么呢?根据电子得失守恒进行计算可得KNO3被还原的产物是NO,所以硝酸钾和氯化亚铁完全反应的化学方程式为:KNO3+3FeCl2+4HCl=3FeCl3+KCl+NO+2H2O二、差量法差量法是依据化学反应前后的某些“差量”(固体质量差、溶液质量差、气体体积差、气体物质的量之差等)与反应或生成物的变化量成正比而建立的一种解题方法。
此法将“差量”看作化学方程式右端的一项,将已知差量(实际差量)与化学方程式中的对应差量(理论差量)列成比例,其他解题步骤与按化学方程式列比例或解题完全一样。
(一)质量差法【例题】在1升2摩/升的稀硝酸溶液中加入一定量的铜粉,充分反应后溶液的质量增加了13.2克,问:(1)加入的铜粉是多少克?(2)理论上可产生NO气体多少升?(标准状况)【分析】硝酸是过量的,不能用硝酸的量来求解。
铜跟硝酸反应后溶液增重,原因是生成了硝酸铜,所以可利用这个变化进行求解。
3Cu + 8HNO3 = 3Cu(NO3)2 + 2N O↑+ 4H2O 增重192 44.8 636-504=132X克Y升13.2 可得X=19.2克,Y=4.48升(二)体积差法【例题】10毫升某气态烃在80毫升氧气中完全燃烧后,恢复到原来状况(1.01×105Pa , 270C)时,测得气体体积为70毫升,求此烃的分子式。
【分析】原混和气体总体积为90毫升,反应后为70毫升,体积减少了20毫升。
剩余气体应该是生成的二氧化碳和过量的氧气,下面可以利用烃的燃烧通式进行有关计算。
CxHy + (x+ )O2 → xCO2 + H2O 体积减少1 1+10 20计算可得y=4 ,烃的分子式为C3H4或C2H4或CH4(三)物质的量差法【例题】白色固体PCl5受热即挥发并发生分解:PCl5(气)= PCl3(气)+ Cl2 现将5.84克PCl5装入2.05升真空密闭容器中,在2770C达到平衡时,容器内的压强为1.01×105Pa ,经计算可知平衡时容器内混和气体物质的量为0.05摩,求平衡时PCl5的分解百分率。
【分析】原PCl5的物质的量为0.028摩,反应达到平衡时物质的量增加了0.022摩,根据化学方程式进行计算。
PCl5(气)= PCl3(气)+ Cl2 物质的量增加1 1X 0.022计算可得有0.022摩PCl5分解,所以结果为78.6%三、十字交叉法十字交叉法是进行二组分混和物平均量与组分量计算的一种简便方法。
凡可按M1n1 + M2n2 = (n1 + n2)计算的问题,均可用十字交叉法计算的问题,均可按十字交叉法计算,算式为:M1 n1=(M2- )M2 n2=(-M1)式中,表示混和物的某平均量,1、M2则表示两组分对应的量。
如表示平均分子量,1、M2则表示两组分各自的分子量,1、n2表示两组分在混和物中所占的份额,n1:n2在大多数情况下表示两组分物质的量之比,有时也可以是两组分的质量比,如在进行有关溶液质量百分比浓度的计算。
十字交叉法常用于求算:混和气体平均分子量及组成、混和烃平均分子式及组成、同位素原子百分含量、溶液的配制、混和物的反应等。
(一)混和气体计算中的十字交叉法【例题】在常温下,将1体积乙烯和一定量的某气态未知烃混和,测得混和气体对氢气的相对密度为12,求这种烃所占的体积。
【分析】根据相对密度计算可得混和气体的平均式量为24,乙烯的式量是28,那么未知烃的式量肯定小于24,式量小于24的烃只有甲烷,利用十字交叉法可求得甲烷是0.5体积(二)同位素原子百分含量计算的十字叉法【例题】溴有两种同位素,在自然界中这两种同位素大约各占一半,已知溴的原子序数是35,原子量是80,则溴的两种同位素的中子数分别等于。
(A)79 、81 (B)45 、46 (C)44 、45 (D)44 、46【分析】两种同位素大约各占一半,根据十字交叉法可知,两种同位素原子量与溴原子量的差值相等,那么它们的中子数应相差2,所以答案为D(三)溶液配制计算中的十字交叉法【例题】某同学欲配制40%的NaOH溶液100克,实验室中现有10%的NaOH溶液和NaOH固体,问此同学应各取上述物质多少克?【分析】10%NaOH溶液溶质为10,NaOH固体溶质为100,40%NaOH溶液溶质为40,利用十字交叉法得:需10%NaOH溶液为×100=66.7克,需NaOH固体为×100=33.3克(四)混和物反应计算中的十字交叉法【例题】现有100克碳酸锂和碳酸钡的混和物,它们和一定浓度的盐酸反应时所消耗盐酸跟100克碳酸钙和该浓度盐酸反应时消耗盐酸量相同。
计算混和物中碳酸锂和碳酸钡的物质的量之比。
【分析】可将碳酸钙的式量理解为碳酸锂和碳酸钡的混和物的平均式量,利用十字交叉法计算可得碳酸锂和碳酸钡的物质的量之比97:26四、关系式法实际化工生产中以及化学工作者进行科学研究时,往往涉及到多步反应:从原料到产品可能要经过若干步反应;测定某一物质的含量可能要经过若干步中间过程。
对于多步反应体系,依据若干化学反应方程式,找出起始物质与最终物质的量的关系,并据此列比例式进行计算求解方法,称为“关系式”法。
利用关系式法可以节省不必要的中间运算步骤,避免计算错误,并能迅速准确地获得结果。
(一)物质制备中的关系式法【例题】含有SiO2的黄铁矿试样1克,在O2中充分灼烧后残余固体为0.76克,用这种黄铁矿100吨可制得98%的浓硫酸多少吨?(设反应过程有2%的硫损失)【分析】根据差量法计算黄铁矿中含FeS2的量为72% ,而反应过程损失2%的硫即损失2%的FeS2 ,根据有关化学方程式找出关系式:FeS2 — 2H2SO4 利用关系式计算可得结果为:制得98%的浓硫酸117.6吨。
(二)物质分析中的关系式法测定漂白粉中氯元素的含量,测定钢中的含硫量,测定硬水中的硬度或测定某物质组成等物质分析过程,也通常由几步反应来实现,有关计算也需要用关系式法。
【例题】让足量浓硫酸与10克氯化钠和氯化镁的混合物加强热反应,把生成的氯化氢溶于适量的水中,加入二氧化锰使盐酸完全氧化,将反应生成的氯气通入KI溶液中,得到11.6克碘,试计算混和物中NaCl的百分含量。
【分析】根据有关化学方程式可得:4HCl — I2 ,利用关系式计算可得生成氯化氢的质量是6.7克,再利用已知条件计算得出混和物中NaCl的百分含量为65% 。
五、估算法(一)估算法适用于带一定计算因素的选择题,是通过对数据进行粗略的、近似的估算确定正确答案的一种解题方法,用估算法可以明显提高解题速度。
【例题】有一种不纯的铁,已知它含有铜、铝、钙或镁中的一种或几种,将5.6克样品跟足量稀H2SO4完全反应生成0.2克氢气,则此样品中一定含有(A)Cu (B)Al (C)Ca (D)Mg【分析】计算可知,28克金属反应失去1摩电子就能符合题目的要求。
能跟稀H2SO4反应,失1摩电子的金属和用量分别为:28克Fe、9克Al、20克Ca、12克Mg,所以答案为A(二)用估算法确定答案是否合理,也是我们检查所做题目时的常用方法,用此法往往可以发现因疏忽而造成的计算错误。
【例题】24毫升H2S在30毫升O2中燃烧,在同温同压下得到SO2的体积为(A)24毫升(B)30毫升(C)20毫升(D)18毫升【分析】2H2S + 3O2 = 2SO2 + 2H2O 根据方程式系数的比例关系估算可得答案为D六、类比法类比法是将问题类比于旧问题,从而运用旧知识解决新问题的方法。
类比法的实质是能力的迁移,即将熟悉问题的能力迁移到新情景或生疏问题上来,实现这种迁移的关键就是找准类比对象,发现生疏问题与熟悉问题本质上的类同性。
运用类比法的题又可分为:自找类比对象和给出类比对象两种。
前者一般比较简单,后者则可以很复杂,包括信息给予题中的大部分题目。
【例题】已知PH3在溶液中呈弱碱性,下列关于PH4Cl的叙述不正确的是(A)PH4Cl水解呈酸性(B)PH4Cl含有配位键(C)PH4Cl是分子晶体(D)PH4Cl与NaOH溶液共热可产生PH3【分析】NH3和H4Cl的性质我们已经学过,N和P是同一主族元素性质相似,所以答案为C七、始终态法始终态法是以体系的开始状态与最终状态为解题依据的一种解题方法。
