时间序列分析基于R——习题答案
时间序列分析基于R——习题答案

第一章习题答案略第二章习题答案2。
1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0。
079—0。
258—0。
376(3)典型的具有单调趋势的时间序列样本自相关图2。
2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0。
2023 0。
013 0。
042 —0。
043 -0。
179-0.251 -0.094 0.0248 —0.068 -0。
072 0.0140.109 0.217 0.3160。
0070-0。
025 0。
075 -0.141 -0。
204 -0。
245 0。
066 0。
0062 -0.139 -0.0340。
206 -0.010 0.080 0。
118(2)平稳序列(3)白噪声序列2。
4,序LB=4.83,LB统计量对应的分位点为0.9634,P值为0。
0363.显著性水平=0.05列不能视为纯随机序列。
2。
5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机2。
6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3。
1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ=3.2 1715φ=,2115φ=3。
3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3。
4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
8章时间序列分析练习题参考答案

8章时间序列分析练习题参考答案第⼋章时间数列分析⼀、单项选择题1.时间序列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值⼤⼩排列的C 前者是根据时间顺序排列的,后者是根据变量值⼤⼩排列的D 前者是根据变量值⼤⼩排列的,后者是根据时间顺序排列的 C2.时间序列中,数值⼤⼩与时间长短有直接关系的是( )A 平均数时间序列B 时期序列C 时点序列D 相对数时间序列 B3.发展速度属于( )A ⽐例相对数B ⽐较相对数C 动态相对数D 强度相对数 C4.计算发展速度的分母是( )A 报告期⽔平B 基期⽔平C 实际⽔平D 计划⽔平 B5.某车间⽉初⼯⼈⼈数资料如下:则该车间上半年的平均⼈数约为( )A 296⼈B 292⼈C 295 ⼈D 300⼈ C6.某地区某年9⽉末的⼈⼝数为150万⼈,10⽉末的⼈⼝数为150.2万⼈,该地区10⽉的⼈⼝平均数为( )A 150万⼈B 150.2万⼈C 150.1万⼈D ⽆法确定 C7.由⼀个9项的时间序列可以计算的环⽐发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 A8.采⽤⼏何平均法计算平均发展速度的依据是( )A 各年环⽐发展速度之积等于总速度B 各年环⽐发展速度之和等于总速度C 各年环⽐增长速度之积等于总速度D 各年环⽐增长速度之和等于总速度 A9.某企业的科技投⼊,2010年⽐2005年增长了58.6%,则该企业2006—2010年间科技投⼊的平均发展速度为( ) A5%6.58 B 5%6.158 C6%6.58 D 6%6.158B10.根据牧区每个⽉初的牲畜存栏数计算全牧区半年的牲畜平均存栏数,采⽤的公式是( ) A 简单平均法 B ⼏何平均法 C 加权序时平均法 D ⾸末折半法 D11.在测定长期趋势的⽅法中,可以形成数学模型的是( )A 时距扩⼤法B 移动平均法C 最⼩平⽅法D 季节指数法12.动态数列中,每个指标数值相加有意义的是()。
时间序列分析作业及答案-精共16页PPT

36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
谢谢!
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
时间序列分析——基于R(王燕)第四章

第四章:非平稳序列的确定性分析题目一:()()()()()()()12312123121231ˆ14111ˆˆ2144451.1616T T T T T T T T T T T T T T T T T T T T T xx x x x xx x x x x x x x x x x x x x x -------------=+++⎡⎤=+++=++++++⎢⎥⎣⎦=+++ 题目二:因为采用指数平滑法,所以1,t t x x +满足式子()11t t t x x x αα-=+-,下面式子()()11111t t t t t tx x x x x x αααα-++=+-⎧⎪⎨=+-⎪⎩ 成立,由上式可以推导出()()11111t t t t x x x x αααα++-=+-+-⎡⎤⎣⎦,代入数据得:2=5α. 题目三:()()()21221922212020192001ˆ1210101113=11.251ˆ 1010111311.2=11.04.5ˆˆˆ10.40.6.i i i xxxx x x x x αα-==++++=++++===+-=⋅∑(1)(2)根据程序计算可得:22ˆ11.79277.x= ()222019181716161ˆ2525xx x x x x =++++(3)可以推导出16,0.425a b ==,则425b a -=-. 题目四:因为,1,2,3,t x t t ==,根据指数平滑的关系式,我们可以得到以下公式:()()()()()()()()()()()()()()()221221 11121111 1111311. 2t t t t t tt x t t t x t t αααααααααααααααααααα----=+-------=-+---+--+++2+, ++2+用(1)式减去(2)式得:()()()()()221=11111.t t tt x t αααααααααααα-------------所以我们可以得到下面的等式:()()()()()()122111=11111=.t t t tt x t t αααααααα+-----------------()111lim lim 1.ttt ttxt tααα+→∞→∞----==题目五:1. 运行程序:最下方。
时间序列分析基于r

时间序列分析基于r时间序列分析是一种用于分析时间序列数据的统计方法,它可以帮助我们了解数据的趋势、季节性、周期性和随机性等特征。
R是一种流行的编程语言和环境,提供了丰富的时间序列分析工具和函数。
以下是一个基于R进行时间序列分析的详细步骤:1. 导入数据:首先,你需要将时间序列数据导入R环境中。
可以使用read.csv()或read.table()函数来读取CSV或文本文件,或使用其他适当的函数来读取其他类型的数据。
2. 转换为时间序列对象:将数据转换为R中的时间序列对象。
可以使用ts()函数来创建一个时间序列对象,指定数据和频率。
例如,如果数据是按月收集的,可以使用ts(data, start = c(year, month), frequency = 12)来创建一个月度频率的时间序列对象。
3. 可视化数据:使用plot()函数来绘制时间序列数据的图形。
这可以帮助你观察数据的趋势、季节性和周期性等特征。
4. 检查数据的平稳性:时间序列分析通常假设数据是平稳的,即数据的均值和方差在时间上保持不变。
可以使用adf.test()函数或kpss.test()函数来检验数据的平稳性。
5. 去除趋势和季节性:如果数据不是平稳的,你需要对其进行差分或转换来消除趋势和季节性。
可以使用diff()函数来进行一阶差分,或使用decompose()函数来分解数据为趋势、季节性和随机成分。
6. 拟合时间序列模型:根据数据的特征选择适当的时间序列模型。
常见的模型包括自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)和季节性自回归积分移动平均模型(SARIMA)。
可以使用arima()函数来拟合ARIMA模型。
7. 模型诊断:拟合模型后,需要对模型进行诊断,以评估其拟合优度和残差的性质。
可以使用tsdiag()函数来绘制模型的诊断图形,或使用Box.test()函数来进行残差的白噪声检验。
8. 预测未来值:根据拟合的时间序列模型,可以使用forecast()函数来预测未来的时间序列值。
《时间序列分析——基于R》王燕,读书笔记

《时间序列分析——基于R》王燕,读书笔记笔记:⼀、检验:1、平稳性检验:图检验⽅法:时序图检验:该序列有明显的趋势性或周期性,则不是平稳序列⾃相关图检验:(acf函数)平稳序列具有短期相关性,即随着延迟期数k的增加,平稳序列的⾃相关系数ρ会很快地衰减向0(指数级指数级衰减),反之⾮平稳序列衰减速度会⽐较慢衰减构造检验统计量进⾏假设检验:单位根检验adfTest()——fUnitRoots包2、纯随机性检验、⽩噪声检验(Box.test(data,type,lag=n)——lag表⽰输出滞后n阶的⽩噪声检验统计量,默认为滞后1阶的检验统计量结果)1、Q统计量:type=“Box-Pierce”2、LB统计量:type=“Ljung-Box”⼆、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf(),pacf(),auto.arima()⾃动定阶1.3建模arima()1.4模型显著性检验:残差的⽩噪声检验Box.test();参数显著性检验t分布2、⾮平稳确定性分析2.1趋势拟合:直线、曲线(⼀般是多项式,还有其它函数)2.2平滑法移动平均法:SMA()——TTR包指数平滑法:HoltWinters()3、⾮平稳随机性分析3.1ARIMA1平稳性检验,差分运算2拟合ARMA3⽩噪声检验3.2疏系数模型arima(p,d,f)3.3季节模型可以叠加的模型4、残差⾃回归模型:4.1建⽴线性模型4.2对滞后的因变量间拟合线性模型,对模型做残差⾃相关DW检验。
dwtest()——lmtest包,增加选项order.by指定延迟因变量4.3对残差建⽴ARIMA模型5、条件异⽅差模型:异⽅差检验:LM检验ArchTest()——FinTS包,⽤ARCH、GARCH模型建模第⼀章简介统计时序分析⽅法:1、频域分析⽅法2、时域分析⽅法步骤:1、观察序列特征2、根据序列特征选择模型3、确定模型的⼝径4、检验模型,优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展⽅向:1、AR,MA,ARMA,ARIMA(Box-Jenkins模型)2、异⽅差场合:ARCH,GARCH等(计量经济学)3、多变量场合:“变量是平稳”不再是必需条件,协整理论3、⾮线性场合:门限⾃回归模型,马尔科夫转移模型第⼆章时间序列的预处理预处理内容:对它的平稳性和纯随机性进⾏检验,最好是平稳⾮⽩噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述⼀个随机变量的统计特征,同样⼀个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。
时间序列分析课后习题答案1

时间序列分析课后习题答案(上机第二章 2、328330332334336338340342(1时序图如上:序列具有明显的趋势和周期性,该序列非平稳。
(2样本自相关系数:(3该样本自相关图上,自相关系数衰减为 0的速度缓慢,且有正弦波状,显示序列具有趋势和周期,非平稳。
3、 (1样本自相关系数:(2序列平稳。
(3因 Q 统计量对应的概率均大于 0.05,故接受该序列为白噪声的假设,即序列为村随机序列。
5、 (1时序图和样本自相关图:50100150200250300350(2序列具有明显的周期性,非平稳。
(3序列的 Q 统计量对应的概率均小于 0.05,该序列是非白噪声的。
6、 (1根据样本相关图可知:该序列是非平稳,非白噪声的。
(2对该序列进行差分运算:1--=t t t x x y {t y }的样本相关图:该序列平稳,非白噪声。
第三章:17、 (1结论:序列平稳,非白噪声。
(2 拟合 MA(2 model:VariableCoefficient Std. Error t-Statistic Prob. C 80.40568 4.630308 17.36508 0.0000 MA(1 0.336783 0.114610 2.938519 0.0047 R-squared0.171979 Mean dependent var 80.29524 Adjusted R-squared 0.144379 S.D. dependent var 23.71981 S.E. of regression 21.94078 Akaike info criterion 9.061019 Sum squared resid 28883.87 Schwarz criterion 9.163073 Log likelihood -282.4221 F-statistic 6.230976 Durbin-Watson stat 2.072640 Prob(F-statistic 0.003477Residual tests(3拟合 AR(2model:C 79.71956 5.442613 14.64729 0.0000 AR(10.2586240.1288102.0077940.0493R-squared0.154672 Mean dependent var 79.50492 Adjusted R-squared 0.125522 S.D. dependent var 23.35053 S.E. of regression 21.83590 Akaike info criterion 9.052918 Sum squared resid 27654.79 Schwarz criterion 9.156731 Log likelihood -273.1140 F-statistic 5.306195 Durbin-Watson stat 1.939572 Prob(F-statistic 0.007651Inverted AR Roots.62-.36Residual tests:(4 拟合 ARMA (2, 1 model :Variable Coefficient Std. Error t-Statistic Prob. C 79.17503 4.082908 19.39183 0.0000 AR(1 -0.586834 0.118000 -4.973170 0.0000 AR(2 0.376120 0.082091 4.581756 0.0000 MA(11.1139990.09712211.470120.0000R-squared0.338419 Mean dependent var 79.50492 Adjusted R-squared 0.303599 S.D. dependent var 23.35053 S.E. of regression 19.48617 Akaike info criterion 8.840611 Sum squared resid 21643.51 Schwarz criterion 8.979029 Log likelihood-265.6386 F-statistic9.719104Inverted AR Roots .39-.97 Inverted MA Roots-1.11Estimated MA process is noninvertible残差检验:(5拟合 ARMA (1, (2 model:Variable Coefficient Std. Error t-Statistic Prob. C 79.52100 4.621910 17.205230.0000 AR(1 0.270506 0.125606 2.153603 0.0354 R-squared0.157273 Mean dependent var 79.55161 Adjusted R-squared 0.128706 S.D. dependent var 23.16126 S.E. of regression 21.61946 Akaike info criterion 9.032242 Sum squared resid 27576.65 Schwarz criterion 9.135167 Log likelihood -276.9995 F-statistic 5.505386 Durbin-Watson stat 1.981887 Prob(F-statistic 0.006423Inverted AR Roots.27残差检验:(6优化根据 SC 准则,最优模型为 ARMA(2,1模型。
(完整word版)时间序列分析基于R__习题答案及解析
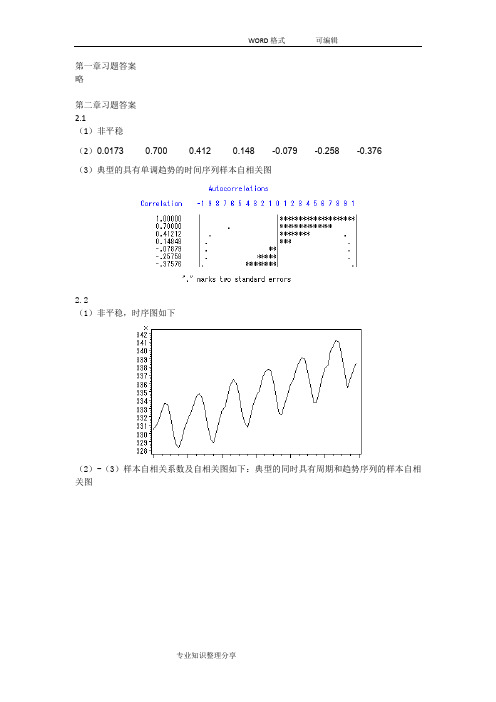
第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
课后习题答案-时间序列分析及应用(R语言原书第2版)

stationary.
(b) Find the autocovariance function for {Yt}. Cov(Yt,Yt − k) = Cov(X,X) = σ2 for all t and k, free of t (and k). (c) Sketch a “typical” time plot of Yt. The plot will be a horizontal “line” (really a discrete-time horizontal line)
relation functions are the same for θ = 3 and θ = 1/3. For simplicity, suppose that the process mean is known
to be zero and the variance of Yt is known to be 1. You observe the series {Yt} for t = 1, 2,..., n and suppose that you can produce good estimates of the autocorrelations ρk. Do you think that you could determine which value of θ is correct (3 or 1/3) based on the estimate of ρk? Why or why not?
人大版时间序列分析基于R(第2版)习题答案
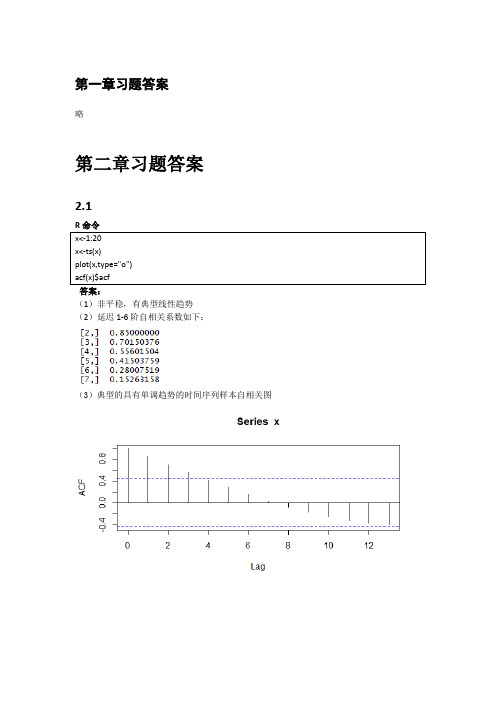
第一章习题答案略第二章习题答案2.1答案:(1)非平稳,有典型线性趋势(2)延迟1-6阶自相关系数如下:(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)1-24阶自相关系数如下(3)自相关图呈现典型的长期趋势与周期并存的特征2.3R命令答案(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列Box-Pierce testdata: rainX-squared = 0.2709, df = 3, p-value = 0.9654X-squared = 7.7505, df = 6, p-value = 0.257X-squared = 8.4681, df = 9, p-value = 0.4877X-squared = 19.914, df = 12, p-value = 0.06873X-squared = 21.803, df = 15, p-value = 0.1131X-squared = 29.445, df = 18, p-value = 0.04322.4答案:我们自定义函数,计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列Box-Pierce testdata: xX-squared = 36.592, df = 3, p-value = 5.612e-08X-squared = 84.84, df = 6, p-value = 3.331e-162.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列Box-Pierce testdata: xX-squared = 47.99, df = 3, p-value = 2.14e-10X-squared = 60.084, df = 6, p-value = 4.327e-11(2)差分序列平稳,非白噪声序列Box-Pierce testdata: yX-squared = 22.412, df = 3, p-value = 5.355e-05X-squared = 27.755, df = 6, p-value = 0.00010452.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
时间序列分析基于-R——习题与答案
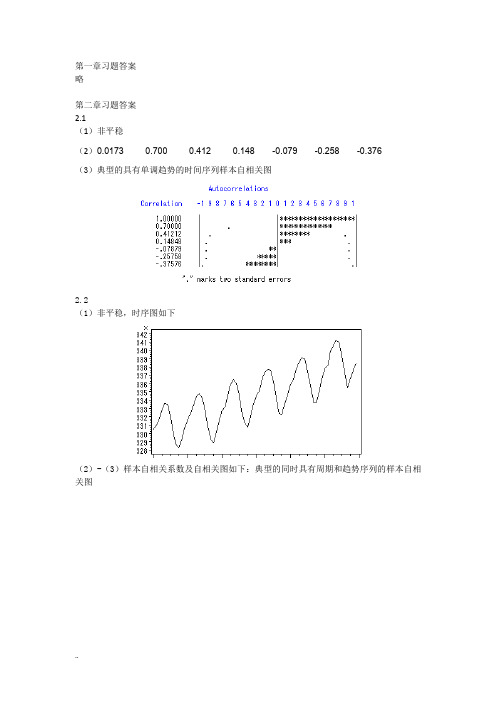
第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
时间序列分析参考答案

时间序列分析参考答案时间序列分析参考答案时间序列分析是一种研究随时间变化的数据模式和趋势的统计方法。
它可以帮助我们理解数据的变化规律,预测未来的趋势,以及制定相应的决策。
在本文中,我们将探讨时间序列分析的基本概念、方法和应用。
一、时间序列分析的基本概念时间序列是按照时间顺序排列的一系列数据观测值。
它可以是连续的,比如每天的股票价格,也可以是离散的,比如每月的销售额。
时间序列分析的目标是找出数据中的模式和趋势,以便进行预测和决策。
时间序列分析的基本概念包括趋势、季节性和周期性。
趋势是指数据在长期内的整体变化方向,可以是上升、下降或平稳。
季节性是指数据在一年中周期性重复出现的变化模式,比如节假日销售额的增长。
周期性是指数据在较长时间内出现的波动,通常周期长度大于一年。
二、时间序列分析的方法时间序列分析的方法包括描述性分析、平稳性检验、模型建立和预测等。
描述性分析是对时间序列数据进行可视化和统计分析,以了解数据的基本特征。
常用的描述性分析方法包括绘制折线图、直方图和自相关图等。
折线图可以显示数据的整体趋势和季节性变化,直方图可以展示数据的分布情况,自相关图可以帮助我们发现数据的相关性。
平稳性检验是判断时间序列数据是否具有平稳性的方法。
平稳性是指数据的均值和方差在时间上保持不变。
常用的平稳性检验方法包括单位根检验和ADF检验等。
模型建立是根据时间序列数据的特征,选择合适的模型来描述数据的变化规律。
常用的模型包括AR模型、MA模型和ARMA模型等。
AR模型是自回归模型,表示当前观测值与过去观测值之间的线性关系;MA模型是移动平均模型,表示当前观测值与过去观测值的误差之间的线性关系;ARMA模型是自回归移动平均模型,综合考虑了自回归和移动平均的效果。
预测是利用已知的时间序列数据,通过建立模型来预测未来的观测值。
常用的预测方法包括滚动预测、指数平滑法和ARIMA模型等。
滚动预测是指根据当前观测值和过去观测值的模型,逐步预测未来的观测值;指数平滑法是基于历史数据的加权平均值,对未来的观测值进行预测;ARIMA模型是自回归移动平均差分整合模型,可以处理非平稳的时间序列数据。
时间序列分析基于r第2版

时间序列分析基于r第2版《时间序列分析基于R第2版》(Time Series Analysis and Its Applications: With R Examples, 2nd Edition)是由Shumway和Stoffer合著的一本经典时间序列分析教材。
该书详细介绍了时间序列分析的理论和实践应用,并使用R语言进行实例演示和编程实现。
以下是《时间序列分析基于R第2版》的主要内容概述:第1章:时间序列分析简介介绍时间序列分析的基本概念和应用领域,并概述本书的内容和使用R语言进行时间序列分析的优势。
第2章:时间序列的基本特性介绍时间序列的基本特性,包括平稳性、自相关性和白噪声等概念,并通过实例演示如何使用R进行时间序列数据的可视化和描述性统计分析。
第3章:时间序列的线性模型介绍时间序列的线性模型,包括自回归模型(AR)、滑动平均模型(MA)和自回归滑动平均模型(ARMA)等,并通过R语言实现模型的参数估计和预测。
第4章:时间序列的谱分析介绍时间序列的谱分析方法,包括周期图和功率谱密度估计等,并通过R语言实现谱分析方法的应用和结果可视化。
第5章:时间序列的非线性模型介绍时间序列的非线性模型,包括ARCH、GARCH和非线性AR模型等,并通过R语言实现模型的参数估计和预测。
第6章:时间序列的状态空间模型介绍时间序列的状态空间模型,包括线性状态空间模型和非线性状态空间模型,并通过R语言实现模型的参数估计和预测。
第7章:多变量时间序列分析介绍多变量时间序列分析的方法,包括向量自回归模型(VAR)、向量误差修正模型(VEC)和协整模型等,并通过R语言实现模型的参数估计和预测。
第8章:季节性和周期性时间序列介绍季节性和周期性时间序列的分析方法,包括季节性自回归移动平均模型(SARMA)和周期性自回归移动平均模型(PARMA)等,并通过R语言实现模型的参数估计和预测。
第9章:时间序列的预测介绍时间序列的预测方法,包括简单指数平滑、Holt线性趋势模型和ARIMA模型等,并通过R语言实现模型的参数估计和预测。
时间序列分析——基于R答案

时间序列分析——基于R 王燕答案第一章时间序列分析简介略第二章时间序列的预处理#========================================## 2.5习题-1##========================================library(tseries)par(mfrow=c(1,2))x=rep(1:20)temp=ts(x)plot(temp)#不是平稳序列as.vector(acf(temp)$acf[1:6])#序列的自相关系数递减到零的速度相当缓慢,#在很长的延迟时期里,自相关系数一直为正,#而后又一直为负,在自相关图上显示出明显的#三角对称性,这是具有单调趋势的非平稳序列#的一种典型的自相关图形式。
这和该序列时序#图显示的显著的单调递增性是一致的。
#======================================== ## 2.5习题-2##======================================== library(tseries)par(mfrow=c(1,2))volcano.co2=read.table('习题2.2数据.txt',sep='\t',header=F) data=ts(as.vector(t(as.matrix(volcano.co2))),start=c(1975,1)) plot(data)#不是平稳序列as.vector(acf(data,lag.max=23)$acf)#序列自相关系数长期位于零轴的一边。
这是#具有单调趋势序列的典型特征,同时自相关#图呈现出明显的正弦波动规律,这是具有周#期变化规律的非平稳序列的典型特征。
自相#关图显示出来的这两个性质和该序列时序图#显示出的带长期递增趋势的周期性质是非常#吻合的。
#========================================## 2.5习题-3##======================================== library(tseries)par(mfrow=c(1,2))rain=read.table('习题2.3数据.txt',sep='\t',header=F) data=ts(as.vector(t(as.matrix(rain))),start=c(1945,1)) plot(data)#该序列为平稳序列as.vector(acf(data,lag.max = 23)$acf)#该序列的自相关系数一直都比较小,#基本控制在2倍的标准差范闹以内,#可以认为该序列自始至终都在零轴附#近波动,这是随机性非常强的平稳时#间序列通常具有的自相关图特征。
时间序列分析——基于R(王燕)第二章
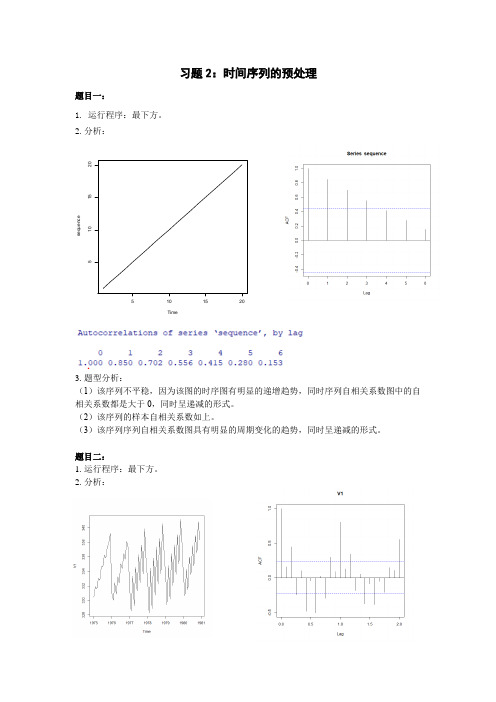
习题2:时间序列的预处理题目一:1. 运行程序:最下方。
2. 分析:3. 题型分析:(1)该序列不平稳,因为该图的时序图有明显的递增趋势,同时序列自相关系数图中的自相关系数都是大于0,同时呈递减的形式。
(2)该序列的样本自相关系数如上。
(3)该序列序列自相关系数图具有明显的周期变化的趋势,同时呈递减的形式。
题目二:1. 运行程序:最下方。
2. 分析:Times e q u e n c e51015205101523.题型分析:(1)通过该数据的时序图,我们可以看出时序图呈周期变化的趋势,所以该序列是非平稳序列。
(2)通过计算结果可以计算出该序列的样本自相关系数。
(3)从该样本自相关图呈周期变化趋势,同时该自相关系数偶尔超过二倍标准差范围以外,因此也可以看出该序列是不平稳序列。
题目三:1.运行程序:见下方。
2.分析:3.题目分析:(1)通过计算结果可以计算出该序列的样本自相关系数。
(2)通过时序图可以看出该序列无周期性,同时无明显的单调变化趋势,通过自相关系数图可以发现很多自相关系数很多落于两倍标准差里面,则该序列是平稳序列。
(3)通过白噪声分析,我们可以看出p值大于0.05,则该序列接受原假设,我们可以以很大的把握断定降雨量数据是白噪声序列。
题目四:1. 运行程序:见下方。
2. 分析:3. 题目分析:通过程序计算,算出Q 统计量为4.57,通过卡方分位数表可以查到()20.9512=5.226X ,由于Q 统计量小于5.226,所以以95%的把握接受原假设,认为该序列是白噪声序列,即认为该序列是纯随机序列。
题目五:1. 运行程序:见下方。
2. 分析:3. 题目分析:(1)该序列时序图和样本自相关图如上。
(2)该序列的时序图呈现周期变化的趋势,同时该模型的样本自相关图也呈周期变化的趋势,也超过2倍标准差,则该序列是非平稳序列。
(3)观察到序列的p 值是小于0.05,所以拒绝原假设,所以该序列是非白噪声序列,该序列不含有纯随机波动。
R语言时间序列作业

2016年第二学期时间序列分析及应用R 语言课后作业 第三章 趋势3.4(a) data(hours);plot(hours,ylab='Monthly Hours',type='o') 画出时间序列图(b) data(hours);plot(hours,ylab='Monthly Hours',type='l')type='o' 表示每个数据点都叠加在曲线上;type='b' 表示在曲线上叠加数据点,但是该数据点附近是断开的;type='l' 表示只显示各数据点之间的连接线段;type='p' 只想显示数据点。
points(y=hours,x=time(hours),pch=as.vector(season(hours)))TimeM o n t h l y H o u r s1983198419851986198739.039.540.040.541.041.5TimeM o n t h l y H o u r s1983198419851986198739.039.540.040.541.041.53.10(a)data(hours);hours.lm=lm(hours~time(hours)+I(time(hours)^2));summary(hours.lm) 用最小二乘法拟合二次趋势,结果显示如下: Call:lm(formula = hours ~ time(hours) + I(time(hours)^2))Residuals:Min 1Q Median 3Q Max -1.00603 -0.25431 -0.02267 0.22884 0.98358Coefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) -5.122e+05 1.155e+05 -4.433 4.28e-05 *** time(hours) 5.159e+02 1.164e+02 4.431 4.31e-05 *** I(time(hours)^2) -1.299e-01 2.933e-02 -4.428 4.35e-05 *** ---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1TimeM o n t h l y H o u r s1983198419851986198739.039.540.040.541.041.5J A SO N D J FM A M J J AS O N DJ F M AM J J A S O N DJ F MA M JJA S ON DJ FM AMJ JA S ONDJ F M AM JResidual standard error: 0.423 on 57 degrees of freedom Multiple R-squared: 0.5921, Adjusted R-squared: 0.5778 F-statistic: 41.37 on 2 and 57 DF, p-value: 7.97e-12 (b)plot(y=rstudent(hours.lm),x=as.vector(time(hours)),type='l',ylab='StandardizedResiduals')points(y=rstudent(hours.lm),x=as.vector(time(hours)),pch=as.vector(season(hours))) 标准残差的时间序列,应用月度绘图标志。
时间序列分析R语言分析
2、(1)时序图
自相关图
偏自相关图
Box-Ljung test data: M X-squared = 21.8815, df = 16, p-value = 0.1471 由时序图、自相关图和偏自相关图可知,该序列的都有类似余弦函数的衰减趋势,故该序列 不是平稳随机序列;由 LB 检验量的 P 值知,P 大于 0.05,故接收原假设,即改序列是纯随 机序列。 代码: q<-read.table("2.txt") M=ts(q$V1,frequency=1,start=126.4) plot.ts(M) acf(M,col="red",lag.max=25) pacf(M,col="red",lag.max=25) Box.test(M,lag=16,type="Ljung-Box") (2)由于该序列非平稳,故对该序列进行差分,得差分后的 自相关图 偏自相关图
故预测其今后五年的降雪量: 160.2985,
3、(1)时序图如下:
(2)对其进行季节性和趋势性分解
பைடு நூலகம்
上图从上到下依次为:时序图、趋势分解图、季节性分解图、随机项图 a.趋势分解: Qtr1 2010 2011 2012 2013 2014 2015 NA 33.375 36.000 38.625 40.250 41.625 NA Qtr2 30.625 Qtr3 Qtr4
-0.5062 -0.0555 -1.0000 s.e. 0.1317 0.1316 0.0572
sigma^2 estimated as 567.8: log likelihood = -282.62, aic = 573.24 由以上用 ARMA(2,1)模型进行估计后的其模型表达式为:
时间序列分析习题及答案
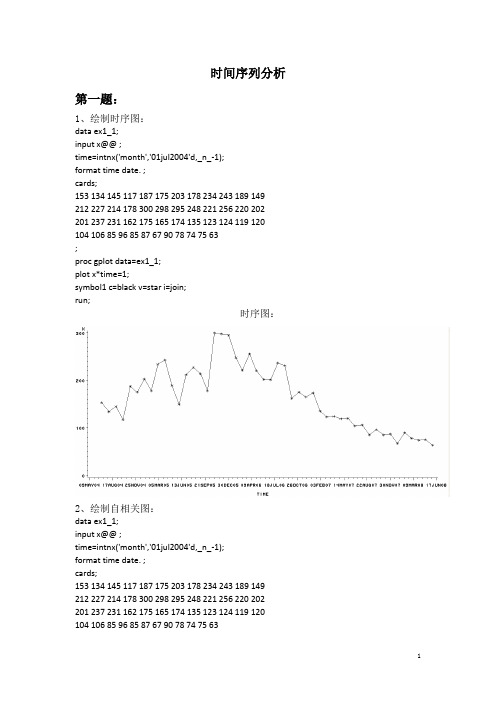
时间序列分析第一题:1、绘制时序图:data ex1_1;input x@@ ;time=intnx('month','01jul2004'd,_n_-1);format time date. ;cards;153 134 145 117 187 175 203 178 234 243 189 149 212 227 214 178 300 298 295 248 221 256 220 202 201 237 231 162 175 165 174 135 123 124 119 120 104 106 85 96 85 87 67 90 78 74 75 63;proc gplot data=ex1_1;plot x*time=1;symbol1 c=black v=star i=join;run;时序图:2、绘制自相关图:data ex1_1;input x@@ ;time=intnx('month','01jul2004'd,_n_-1);format time date. ;cards;153 134 145 117 187 175 203 178 234 243 189 149 212 227 214 178 300 298 295 248 221 256 220 202 201 237 231 162 175 165 174 135 123 124 119 120 104 106 85 96 85 87 67 90 78 74 75 63;proc arima data=ex1_1;identify var=x;run;样本自相关图:白噪声检验输出结果:因为P值小于α,所以该序列为非白噪声序列,根据时序图看出数据并不在一个常数值附近随机波动,后期有递减的趋势,所以不是平稳序列。
第二题:1、选择拟合模型方法一:首先绘制该序列的时序图,直观检验序列平稳性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
略第二章习题答案(1)非平稳(2)(3)典型的具有单调趋势的时间序列样本自相关图(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图(1)自相关系数为:(2)平稳序列(3)白噪声序列,序列不能视为纯随机序列。
LB=,LB统计量对应的分位点为,P值为。
显著性水平=0.05(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 1715φ=,2115φ=()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=10c -<<, 1121,1,2k k k cc k ρρρρ--⎧=⎪-⎨⎪=+≥⎩证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
证毕。
(1)错 (2)错 (3)对 (4)错 (5)该模型有两种可能的表达式:112t t t x εε-=-和12t t t x εε-=-。
将123100.50.8t t t t t x x C εεε---=++-+等价表达为()2323223310.82010.510.8(10.50.50.5)t ttB CB x B B CB B B B εε-+-=-=-+++++L 展开等号右边的多项式,整理为22334423243410.50.50.50.50.80.80.50.80.50.5B B B B B B B CB CB +++++--⨯-⨯-+++L L L合并同类项,原模型等价表达为233020[10.50.550.5(0.50.4)]k k t t k x B B C B ε∞+=-=+-+-+∑当30.50.40C -+=时,该模型为(2)MA 模型,解出0.275C =。
()0t E x =,22()10.70.4 1.65t Var x =++=10.70.70.40.591.65ρ--⨯==-,20.40.241.65ρ==,0,3k k ρ=≥(1)证明:因为22()lim(1)t k Var x kC εσ→∞=+=∞,所以该序列为非平稳序列。
(2)11(1)t t t t t y x x C εε--=-=+-,该序列均值、方差为常数,()0t E y =,22()1(1)t Var y C εσ⎡⎤=+-⎣⎦自相关系数只与时间间隔长度有关,与起始时间无关121,0,21(1)k C k C ρρ-==≥+-所以该差分序列为平稳序列。
(1)非平稳,(2)平稳,(3)可逆,(4)不可逆,(5)平稳可逆,(6)不平稳不可逆01G =,11010.60.30.3G G φθ=-=-=,1111110.30.6,2k k k k G G G k φφ---===⨯≥所以该模型可以等价表示为:100.30.6kt t t k k x εε∞--==+⨯∑0123121110.25φμφφ===---+证明:已知112φ=,114θ=,根据(1,1)ARMA 模型Green 函数的递推公式得:01G =,2110110.50.25G G φθφ=-=-=,1111111,2k k k k G G G k φφφ-+-===≥01ρ=52232111112245011111142422(1)11112011170.27126111j jj j j j jj j G GGφφφφφφφφρφφφφφ∞∞++==∞∞+==++--+======-+++-∑∑∑∑()11111122200,2jj kjj k jj k j j j k k jjjj j j G G G GG Gk GGGφρφφρ∞∞∞++-+-===-∞∞∞=======≥∑∑∑∑∑∑(1)成立 (2)成立 (3)成立 (4)不成立(1)95%置信区间为(,)(2)更新数据后95%置信区间为(,)(1)平稳非白噪声序列(2)AR(1)(3) 5年预测结果如下:(1)平稳非白噪声序列 (2)AR(1)(3) 5年预测结果如下:(1)平稳非白噪声序列 (2)MA(1)(3) 下一年95%的置信区间为(,)(1)平稳非白噪声序列 (2)ARMA(1,3)序列(3)拟合及5年期预测图如下:第四章习题答案 3T x -的系数为116, 1T x -的系数为516解下面的方程组,得到0.4α=5.255(1)5.26 5.5(1)t t χααααχ=+-⎧⎨=+-⎩%% (1) (2) (3)0.40.240.16b a -=-=根据指数平滑的定义有(1)式成立,(1)式等号两边同乘(1)α-有(2)式成立2323(1)(1)(2)(1)(2)(1)(1)(1)(1)(1)(1)(2)(1)(2)t t x t t t t x t t t αααααααααααααα=+--+--+--+-=-+--+--+%L %L(1)-(2)得22(1)(1)(1)(1)1t t x t x t t αααααααααα=-----=------=-%L %L则1lim lim 1t t t t x t t αα→∞→∞-⎛⎫- ⎪==⎪⎪⎝⎭%。
该序列为显著的线性递增序列,利用本章的知识点,可以使用线性方程或者holt 两参数指数平滑法进行趋势拟合和预测,答案不唯一,具体结果略。
该序列为显著的非线性递增序列,可以拟合二次型曲线、指数型曲线或其他曲线,也能使用holt 两参数指数平滑法进行趋势拟合和预测,答案不唯一,具体结果略。
本例在混合模型结构,季节指数求法,趋势拟合方法等处均有多种可选方案,如下做法仅是可选方法之一,结果仅供参考(1)该序列有显著趋势和周期效应,时序图如下(2)该序列周期振幅几乎不随着趋势递增而变化,所以尝试使用加法模型拟合该序列:t t t t x T S I =++。
(注:如果用乘法模型也可以)首先求季节指数(没有消除趋势,并不是最精确的季节指数)消除季节影响,得序列t t t y x S x =-,使用线性模型拟合该序列趋势影响(方法不唯一):97.70 1.79268t T t =-+,1,2,3,t =L(注:该趋势模型截距无意义,主要是斜率有意义,反映了长期递增速率) 得到残差序列t t t t t I x S x y T =-=-,残差序列基本无显著趋势和周期残留。
预测1971年奶牛的月度产量序列为()mod 12ˆ,109,110,,120t t t x T S x t =+=))L得到(3)该序列使用x11方法得到的趋势拟合为趋势拟合图为这是一个有着曲线趋势,但是有没有固定周期效应的序列,所以可以在快速预测程序中用曲线拟合(stepar )或曲线指数平滑(expo )进行预测(trend=3)。
具体预测值略。
第五章习题拟合差分平稳序列,即随机游走模型 -1=+t t t x x ε,估计下一天的收盘价为289 拟合模型不唯一,答案仅供参考。
拟合ARIMA(1,1,0)模型,五年预测值为:12(1,1,0)(1,1,0)ARIMA ⨯(1)AR(1), (2)有异方差性。
最终拟合的模型为-12-1=7.472+=-0.5595+=11.9719+0.4127t ttt t tt tt x vv h v εεε⎧⎪⎪⎨⎪⎪⎩ (1)非平稳(2) 取对数消除方差非齐,对数序列一节差分后,拟合疏系数模型AR(1,3)所以拟合模型为ln ~((1,3),1,0)x ARIMA(3)预测结果如下:原序列方差非齐,差分序列方差非齐,对数变换后,差分序列方差齐性。
第六章习题单位根检验原理略。
例 原序列不平稳,一阶差分后平稳 例 原序列不平稳,一阶与12步差分后平稳 例 原序列带漂移项平稳 例 原序列不带漂移项平稳例 原序列带漂移项平稳(=0.06)α,或者显著的趋势平稳。
(1)两序列均为带漂移项平稳(2)谷物产量为带常数均值的纯随机序列,降雨量可以拟合AR (2)疏系数模型。
(3)两者之间具有协整关系(4)23.55210.775549t t =+谷物产量降雨量(1)掠食者和被掠食者数量都呈现出显著的周期特征,两个序列均为非平稳序列。
但是掠食者和被掠食者延迟2阶序列具有协整关系。
即-2{-}t t y x β为平稳序列。
(2)被掠食者拟合乘积模型:5(0,1,0)(1,1,0)ARIMA ⨯,模型口径为:551=1+0.92874t t x B ε∇∇拟合掠食者的序列为: -2-1=2.9619+0.283994+-0.47988t t t t y x εε 未来一周的被掠食者预测序列为:Forecasts for variable xObs Forecast Std Error 95% Confidence Limits49 50 51 52 53545556575859606162掠食者预测值为:Forecasts for variable yObs Forecast Std Error 95% Confidence Limits4950515253545556575859606162(1)进出口总额序列均不平稳,但对数变换后的一阶差分后序列平稳。
所以对这两个序列取对数后进行单个序列拟合和协整检验。
(2)出口序列拟合的模型为ln ~(1,1,0)t x ARIMA ,具体口径为:1ln =0.14689+1-0.38845t t x Bε∇进口序列拟合的模型为ln ~(1,1,0)t y ARIMA ,具体口径为:1ln =0.14672+1-0.36364t t y Bε∇(3)ln t y 和ln t x 具有协整关系(4)协整模型为:-1ln =0.99179ln +-0.69938t t t t y x εε (5)误差修正模型为:-1ln =0.97861ln -0.22395ECM t t t y x ∇∇。
