厦门大学1998数学分析真题
1998考研数学三真题和详解

1998年全国硕士研究生入学统一考试数学三试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1) 设曲线()nf x x =在点(1,1)处的切线与x 轴的交点为(,0)n ξ,则lim ()n n f ξ→∞= .(2)2ln 1x dx x -=⎰ .(3) 差分方程121050t t y y t ++-=的通解为 .(4) 设矩阵,A B 满足*28A BA BA E =-,其中100020001A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,E 为单位矩阵,*A 为A 的伴随矩阵,则B = .(5) 设1234,,,X X X X 是来自正态总体()20,2N 的简单随机样本,()2122X a X X =-+()23434b X X -.则当a = ,b = 时,统计量X 服从2χ分布,其自由度为 .二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1) 设周期函数()f x 在(),-∞+∞内可导,周期为 4.又()()011lim1,2x f f x x→--=-则曲线()y f x =在点()()5,5f 处的切线的斜率为 ( ) (A)12(B) 0 (C) 1- (D) 2- (2) 设函数()21lim ,1nn xf x x →∞+=+讨论函数()f x 的间断点,其结论为 ( )(A) 不存在间断点 (B) 存在间断点1x = (C) 存在间断点0x = (D) 存在间断点1x =-(3) 齐次线性方程组21231231230,0,0x x x x x x x x x λλλλ⎧++=⎪++=⎨⎪++=⎩的系数矩阵记为A .若存在三阶矩阵0B ≠使得0AB =,则 ( )(A) 2λ=-且||0B = (B) 2λ=-且||0B ≠(C) 1λ=且||0B = (D) 1λ=且||0B ≠ (4) 设()3n n ≥阶矩阵1111a a a a a a A aa a aaa⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 若矩阵A 的秩为1n -,则a 必为 ( ) (A) 1 (B)11n - (C) 1- (D) 11n - (5) 设1()F x 与2()F x 分别为随机变量1X 与2X 的分布函数.为使()12()()F x aF x bF x =-是某一变量的分布函数,在下列给定的各组数值中应取 ( )(A) 32,55a b ==- (B) 22,33a b == (C) 13,22a b =-= (D) 13,22a b ==-三、(本题满分5分)设arctan22()y xz x y e-=+,求dz 与2zx y∂∂∂.四、(本题满分5分)设(){}22,D x y xy x =+≤,求D.五、(本题满分6分)设某酒厂有一批新酿的好酒,如果现在(假定0t =)就售出,总收入为0()R 元.如果窖藏起来待来日按陈酒价格出售,t年末总收入为0R R =假定银行的年利率为r ,并以连续复利计息,试求窖藏多少年售出可使总收入的现值最大.并求0.06r =时的t 值.六、(本题满分6分)设函数()f x 在[],a b 上连续,在(,)a b 内可导,且()0.f x '≠试证存在,(,),a b ξη∈使得().()b a f e e e f b aηξη-'-=⋅'-七、(本题满分6分)设有两条抛物线21y nx n =+和21(1)1y n x n =+++,记它们交点的横坐标的绝对值为.n a(1) 求这两条抛物线所围成的平面图形的面积n S ; (2) 求级数1nn nS a ∞=∑的和.八、(本题满分7分)设函数()f x 在[1,)+∞上连续.若由曲线(),y f x =直线1,(1)x x t t ==>与x 轴所围成的平面图形绕x 轴旋转一周所形成的旋转体体积为2()()(1).3V t t f t f π⎡⎤=-⎣⎦ 试求()y f x =所满足的微分方程,并求该微分方程满足条件229x y ==的解.九、(本题满分9分)设向量1212(,,,),(,,,)T T n n a a a b b b αβ==都是非零向量,且满足条件0.T αβ=记n 矩阵.T A αβ=求:(1) 2A ;(2) 矩阵A 的特征值和特征向量.十、(本题满分7分)设矩阵101020,101A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦矩阵2(),B kE A =+其中k 为实数,E 为单位矩阵.求对角矩阵Λ,使B 与Λ相似,并求k 为何值时,B 为正定矩阵.十一、(本题满分10分)一商店经销某种商品,每周进货的数量X 与顾客对该种商品的需求量Y 是相互独立的随机变量,且都服从区间[10,20]上的均匀分布.商店每售出一单位商品可得利润1000元;若需求量超过了进货量,商店可从其他商店调剂供应,这时每单位商品获利润为500元.试计算此商店经销该种商品每周所得利润的期望值.十二、(本题满分9分)设有来自三个地区的各10名、15名和25名考生的报名表,其中女生的报名表分别为3份、7份和5份.随机地取一个地区的报名表,从中先后抽出两份.(1) 求先抽到的一份是女生表的概率p ;(2) 已知后抽到的一份是男生表,求先抽到的一份是女生表的概率q .1998年全国硕士研究生入学统一考试数学三试题解析一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1)【答案】1e【解析】曲线ny x =在点(1,1)处的切线斜率1x y ='()1nx x='=11n x n x n -===,根据点斜式,切线方程为:1(1).y n x -=-令0y =,代入1(1)y n x -=-,则11x n =-,即在x 轴上的截距为11n n ξ=-, lim ()n n f ξ→∞lim n n n ξ→∞=1lim(1)n n n →∞=-()()11lim(1)x x x --→∞=-1e=.(2)【答案】ln xC x-+【解析】由分部积分公式,2ln 1x dx x -⎰()1ln 1x dx x '⎛⎫=-- ⎪⎝⎭⎰()1ln 1x d x ⎛⎫=-- ⎪⎝⎭⎰ ln 11(ln 1)x d x x x - -+-⎰分部2ln 11x dx x x-=-+⎰ ln 11x dx x x '-⎛⎫=-- ⎪⎝⎭⎰ln 11x C x x -=--+ln x C x =-+. 【相关知识点】分部积分公式:假定()u u x =与()v v x =均具有连续的导函数,则,uv dx uv u vdx ''=-⎰⎰或者.udv uv vdu =-⎰⎰(3)【答案】51(5)()126tt y C t =-+- 【解析】首先把差分方程改写成标准形式1552t t y y t ++=,其齐次方程对应的特征方程及特征根分别为50,5,r r +==-故齐次方程的通解为(5),tt Y C C =-为常数.将方程右边的52t 改写成512t t ⋅,此处“1”不是特征根,故令非齐次方程的一个特解为,t y At B *=+从而1(1),t y A t B *+=++代入原方程,得5(1)5(),2A tB At B t ++++=56,60,2A A B =+=故 55,1272A B ==-.于是通解为 51(5)().126tt t t y Y y C t *=+=-+-(4)【答案】200040002⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦【解析】由题设 *28A BA BA E =-,由于20A =-≠,所以A 可逆.上式两边左乘A ,右乘1A -,得*11128AA BAA ABAA AA ---=-28A B AB E =-(利用公式:*1,AA A E AA E -==) 28A B AB E -=-(移项)()28A E A B E -=-(矩阵乘法的运算法则)将2A =-代入上式,整理得()14E A B E +=. 由矩阵可逆的定义,知E A +,B 均可逆,且()114B E A --=+1102002401040100021002-⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦200040002⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦.(5)【答案】11,,220100【解析】由于1234,,,X X X X 相互独立,均服从2(0,2)N ,所以由数学期望和方差的性质,得2221212(2)0,(2)122220E X X D X X -=-=⨯+⨯=,所以12(2)(0,20)X X N -,同理34(34)(0,100)X X N -.又因为12(2)X X -与34(34)X X -相互独立,且122)(0,1)X X N -344)(0,1)X X N -,由2χ分布的定义,当11,20100a b ==时, 222123411(2)(34)(2)20100X X X X X χ=-+-.即当11,20100a b ==时,X 服从2χ分布,其自由度为2. 严格地说,当10,100a b ==时,2(1)X χ;当1,020a b ==时,2(1)X χ也是正确的.【相关知识点】1、对于随机变量X 与Y 均服从正态分布,则X 与Y 的线性组合亦服从正态分布.若X 与Y 相互独立,由数学期望和方差的性质,有()()()E aX bY c aE X bE Y c ++=++, 22()()()D aX bY c a D X b D Y ++=+,其中,,a b c 为常数. 2、定理:若2(,)XN μσ,则(0,1)X N μσ-.3、2χ分布的定义:若1,,n Z Z 相互独立,且都服从标准正态分布(0,1)N ,则221~()nii Zn χ=∑.二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1)【答案】(D)【解析】根据导数定义:()0()()limx f x x f x f x x∆→+∆-'=∆0(1)(1)lim 2x f f x x →--01(1)(1)lim 2x f x f x →--=-1(1)2f '=1=- 所以 0(1)(1)(1)lim2.x f x f f x→--'==-- 因为()f x 周期为4,()f x '的周期亦是4,即()(4)f x f x ''=+, 所以(5)f '(14)f '=+(1)2f '==-.所以曲线()y f x =在点()5,(5)f 处的切线的斜率为(5)f '(1)2f '==-.选(D). (2)【答案】(B)【分析】讨论由极限表示的函数的性质,应分两步走.先求出该()f x 的(分段)表达式,然后再讨论()f x 的性质.不能隔着极限号去讨论. 【解析】现求()f x 的(分段)表达式: 当1x >时,21()lim 1n n xf x x →∞+=+2122lim 1n n n n x x x ---→∞+=+()()2122lim 01lim 1n n n n n x x x --→∞-→∞+==+0=; 当1x =时,21()lim1n n x f x x →∞+=+211lim 11n n →∞+=+22=1=;当1x =-时,21()lim1n n x f x x →∞+=+()211lim 11n n →∞-=+-02=0=; 当1x <时,21()lim 1n n x f x x →∞+=+()()2lim 1lim 1n n n x x →∞→∞+=+2011n x x →+ 1x =+. 由此, 0,1,0,1,()1,1,1,1,0,1.x x f x x x x x <-⎧⎪=-⎪⎪=+<⎨⎪=⎪>⎪⎩当当当当当 即0,11,()1,1,1, 1.x x f x x x x ≤->⎧⎪=+ <⎨⎪ =⎩当或当当 再讨论函数()f x 的性质:在1x =-处,()1lim x f x +→-()1lim 1x x +→-=+11=-0=,()()1lim 10x f x f -→-=-=,所以,()()11lim lim 0x x f x f x +-→-→-==,函数()f x 在1x =-处连续,不是间断点.在1x =处,()1lim x f x +→1lim 0x +→=0=;()1lim x f x -→()1lim 1x x -→=+2=; 所以()1lim x f x +→()1lim x f x -→≠,函数()f x 在1x =处不连续,是第一类间断点.故选(B). (3)【答案】(C)【解析】方法1:由0AB =知()()3r A r B +≤,又0,0A B ≠≠,于是1()3,r A ≤<1()3r B ≤<,故0,0A B ==,即2210101011011(1)0111111A λλλλλλλλλλλλ--==--==-=--,得 1.λ=应选(C).方法2:由0AB =知()()3r A r B +≤,又0,0A B ≠≠,于是1()3,r A ≤<1()3r B ≤<,故0B =.显然,1λ=时111111111A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,有1()3,r A ≤<故应选(C). 作为选择题,只需在2λ=-与1λ=中选择一个,因而可以用特殊值代入法.评注:对于条件0AB =应当有两个思路:一是B 的列向量是齐次方程组0Ax =的解;二是秩的信息,即()()r A r B n +≤,要有这两种思考问题的意识. (4)【答案】(B) 【解析】1111100(1)110101101a a a aa aa a a a a A aa a a a aaaa a ⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦1(1)0100(2)00100001n aa a a a a a +-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦其中(1)变换:将1行乘以(-1)再分别加到其余各行;(2)变换:将其余各列分别加到第1列.由阶梯形矩阵知,当1(1)0n a +-=,即11a n=-时,有()1r A n =-,故应选(B). (5)【答案】(A)【解析】根据分布函数的性质lim ()1x F x →+∞=,即121lim ()()()()x F x F aF bF a b →+∞==+∞=+∞-+∞=-.在所给的四个选项中只有(A)满足1a b -=,故应选(A). 【相关知识点】分布函数()F x 的性质:(1) ()F x 单调不减;(2) lim ()()0,lim ()()1;x x F x F F x F →-∞→+∞=-∞==+∞=(3) ()F x 是右连续的.三、(本题满分5分) 【解析】 arctanarctan2222()()()y y xxdz ed x y x y d e--=+++[]arctan22arctan222arctan22arctan22()(arctan )122()()1(22(2)(2)y xyxy xy xy exdx ydy x y d x y exdx ydy x y d y x x xdy ydx e xdx ydy x x ex y dx y x dy ----⎡⎤=+++-⎢⎥⎣⎦⎡⎤⎢⎥=+-+⎢⎥⎢⎥+⎣⎦-⎡⎤=+-⋅⎢⎥⎣⎦=++- 由全微分与偏微分的关系可知,其中dx 的系数就是z x∂∂,即arctan (2)yxz x y ex -∂=+∂.再对y 求偏导数,得222arctanarctanarctan 222211(2).1yyyxxxzy xy x e x y ee y x yx x y x ---⎛⎫⎪∂--=-+= ⎪∂∂+ ⎪+⎪⎝⎭四、(本题满分5分)【解析】22{(,)}D x y x y x =+≤表示圆心为1,02⎛⎫ ⎪⎝⎭,半径为12的圆及其内部,画出区域D ,如右图. 方法1:{(,)|01,D x y x y =≤≤≤所以, 1102D===⎰⎰⎰,t =,则21x t =-,2dx tdt =-,:10t →所以上式1350122210082(1)(2)4(1)43515t t t t t dt t t dt ⎛⎫=-⋅-=-=-= ⎪⎝⎭⎰⎰.方法2:引入极坐标系cos ,sin x r y r θθ= =,于是(,)|,0cos 22D r r ππθθθ⎧⎫=-≤≤≤≤⎨⎬⎩⎭,3cos cos 2222232048cos .515Dd r drd ππθθπππθθθθ--====⎰⎰⎰⎰⎰其中倒数第二步用了华里士公式:21342cos 1253n n n d n n πθθ--=⋅⋅⋅⋅⋅-⎰,其中n 为大于1的正奇数.五、(本题满分6分)【分析】根据连续复利公式,在年利率为r 的情况下,现时的A (元)在t 时的总收入为()e rt R t A =,反之,t 时总收入为()R t 的现值为()()ertA t R t -=,将0R R =入的现值与窖藏时间t 之间的关系式,从而可用微分法求其最大值.【解析】由连续复利公式知,这批酒在窖藏t 年末售出总收入R 的现值为()e rt A t R -=,而由题设,t年末的总收入0R R =,据此可列出()A t :0()ert rtA t R R -==,令 dAdt0rtd R dt ⎛⎫= ⎪⎝⎭00rtR r ⎫=-=⎪⎭, 得惟一驻点 02125t t r ==. 22dA dtd dA dt dt ⎛⎫= ⎪⎝⎭0rtd R r dt ⎛⎫⎫=⎪⎪⎭⎝⎭00rtrtd d R r R r dt dt ⎛⎫⎫⎫=⋅-+- ⎪⎪⎪⎭⎭⎝⎭200rt rtR r R⎛⎫⎫=-+⎪⎭⎝ 20rt R r ⎡⎤⎫=-⎢⎪⎭⎢⎣1232502(12.5)0r t td AR e r dt ==-<.根据极值的第二充分条件,知:0t t =是()A t 的极大值点,又因驻点惟一,所以也是最大值点.故窖藏2125t r=年出售,总收入的现值最大.当0.06r =时, ()21250.06t =⋅100119=≈(年). 【相关知识点】极值的第二充分条件:设函数()f x 在0x 处具有二阶导数且0()0f x '=,0()0f x ''≠,当0()0f x ''<时,函数()f x 在0x 处取得极大值;当0()0f x ''>时,函数()f x 在0x 处取得极小值.六、(本题满分6分)【分析】本题要证的结论中出现两个中值点ξ和η,这种问题一般应将含有ξ和η的项分别移到等式两边后再用微分中值定理,为此本题只要证()()()()b a f b a e e f e ηξη-''-=-.【解析】方法1: 函数()f x 在[],a b 上连续,在(,)a b 内可导,满足拉格朗日中值定理的条件,对函数()f x 在[],a b 上用拉格朗日中值定理,有()()()(),.f b f a f b a a b ξξ'-=-<<又函数()f x 与xe 满足柯西中值定理的条件,将函数()f x 与xe 在[],a b 上用柯西中值定理,有()()(),b a f b f a f a b e e e ηηη'-=<<-,即()()()b a f f b f a e e eηη'-=-(). 从而有()()()baf f b a e e eηηξ''-=-(),即(),,(,)()b a f e e e a b f b a ηξξηη-'-=⋅∈'-. 方法2:题中没有限制ξη≠,因此取ξη=,即成为要去证存在(,)a b η∈使.b ae e e b aη-=- 在[],a b 上对函数xe 用拉格朗日中值定理,存在(,)a b η∈使, 1.b a b a e e e e e e b a b aηη---=⋅=--即 再取ξη=,则()1()b a f e e e f b aηξη-'-==⋅'-,原题得证.【相关知识点】1.拉格朗日中值定理:如果函数()f x 满足在闭区间[,]a b 上连续,在开区间(),a b 内可导,那么在(),a b 内至少有一点()a b ξξ<<,使等式()()()()f b f a f b a ξ'-=-成立. 2. 柯西中值定理:如果函数()f x 及()F x 满足(1) 在闭区间[,]a b 上连续; (2) 在开区间(,)a b 内可导; (3) 对任一(,)x a b ∈,()0F x '≠, 那么在(,)a b 内至少有一点ξ,使等式()()()()()()f b f a f F b F a F ξξ'-='-成立.七、(本题满分6分) 【解析】(1)由21y nx n =+与21(1)1y n x n =+++得n a =因图形关于y 轴对称,所以,所求图形的面积为220320112(1)121422(1)(1)33nn a n a n n S nx n x dx n n a a x dx n n n n ⎡⎤=+-+-⎢⎥+⎣⎦⎡⎤=-+=-=⎢⎥++⎣⎦⎰⎰ (2)由(1)的结果知41411()3(1)31n n S a n n n n ==-++, 根据级数和的定义,111411414lim lim lim 1.31313n nn k n n n n k k n k S S a a k k n ∞→∞→∞→∞===⎛⎫⎡⎤==-=-= ⎪⎢⎥++⎝⎭⎣⎦∑∑∑八、(本题满分7分)【分析】本题是微分方程的几何应用问题.在题目中给出了由曲线()y f x =等围成的平面图形绕x 轴旋转一周所形成的旋转体体积()V t 与包含函数f 的一个恒等式,这正是列方程的依据.【解析】由绕x 轴旋转的旋转体体积公式得21()()tV t f x dx π=⎰,于是,依题意得221()()(1)3t f x dx t f t f ππ⎡⎤=-⎣⎦⎰,即2213()()(1)tf x dx t f t f =-⎰. 两边对t 求导,化成微分方程223()2()()f t tf t t f t '=+,其中()f t 为未知函数.按通常以x 表示自变量,y 表示未知函数()f t ,于是上述方程可写为2232,x y y xy '=-即23()2().dy y ydx x x=- 这是一阶齐次微分方程.令y ux =,有dy duu x dx dx=+⋅,则上式化为 2()32,duu x u u dx+=- 即 3(1).duxu u dx=- (*) 若0u =,则0,y ux ==不满足初始条件229x y ==,舍弃;若1u =,则,y ux x ==也不满足初始条件229x y ==,舍弃;所以,0u ≠,且1u ≠.由(*)式分离变量得3,(1)du dx u u x =-两边积分得31u Cx u-=.从而方程(*)的通解为3,y x Cx y C -=为任意常数.再代入初值,由229x y==,得1C =-,从而所求的解为 33,,(1).1xy x x y y x x-=-=≥+或 【相关知识点】1. 对积分上限的函数的求导公式:若()()()()t t F t f x dx βα=⎰,()t α,()t β均一阶可导,则 [][]()()()()()F t t f t t f t ββαα'''=⋅-⋅.九、(本题满分9分)【解析】(1)对等式0Tαβ=两边取转置,有()0TTT αββα==,即0T βα=.利用0Tβα=及矩阵乘法的运算法则,有()22TT T A αβαβαβ==()00T T T T αβαβαβαβ===0=,即2A 是n 阶零矩阵.(2)设λ是A 的任一特征值,(0)ξξ≠是A 属于特征值λ的特征向量,即A ξλξ=.对上式两边左乘A 得2A ξ()()A A λξλξλλξ===2λξ=,由(1)的结果20A =,得220A λξξ==,因0ξ≠,故0λ=(n 重根),即矩阵的全部特征值为零.下面求A 的特征向量:先将A 写成矩阵形式[]1111212212221212,,,n n Tn n n n n n a a b a b a b a a b a b a b A b b b a a b a b a b αβ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦.不妨设110,0a b ≠≠,则有111211221222212221121212(0)1()01(2,,)n n n n n n n n n n n n n i a b a b a b b b b a ba b a b a b a b a b E A a a b a b a b a b a b a b b b b a i i n ---⎡⎤⎡⎤⎢⎥⎢⎥------⎢⎥⎢⎥-=÷-⎢⎥⎢⎥⎢⎥⎢⎥------⎣⎦⎣⎦⨯=行行加到行00000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦于是得方程组(0)0E A x -=同解方程组11220n n b x b x b x +++=,这样基础解系所含向量个数为(0)1n r E A n --=-.选2,,n x x 为自由未知量,将它们的组值111(,0,,0),(0,,,0),(0,0,,)b b b 代入,可解得基础解系为12123111(,,0,,0),(,0,,,0),,(,0,0,,)n n b b b b b b ξξξ-=-=-=-则A 的属于0λ=的全部特征向量为112211n n k k k ξξξ--+++,其中121,,,n k k k -为不全为零的任意常数.十、(本题满分7分)【分析】由于B 是实对称矩阵,B 必可相似对角化,而对角矩阵Λ即B 的特征值,只要求出B 的特征值即知Λ,又因正定的充分必要条件是特征值全大于零,k 的取值亦可求出. 【解析】方法1:由211112(2)(2)1111E A λλλλλλλλλ-----=-=-=-----,可得A 的特征值是1232,0.λλλ===那么,kE A +的特征值是2,2,k k k ++,而2()B kE A =+的特征值是222(2),(2),.k k k ++又由题设知A 是实对称矩阵,则,TA A =故222()()()TTTB kE A kE A kE A B ⎡⎤⎡⎤=+=+=+=⎣⎦⎣⎦, 即B 也是实对称矩阵,故B 必可相似对角化,且222(2)000(2)000k Bk k ⎡⎤+⎢⎥Λ=+⎢⎥⎢⎥⎣⎦. 当20k k ≠-≠且时,B 的全部特征值大于零,这时B 为正定矩阵.方法2:由2101112(2)(2)1111E A λλλλλλλλλ-----=-=-=-----,可得A 的特征值是1232,0.λλλ===因为A 是实对称矩阵,故存在可逆矩阵P 使1220P AP -⎡⎤⎢⎥=Λ=⎢⎥⎢⎥⎣⎦,即1A P P -=Λ.那么 221121()()()B kE A kPP P P P kE P ---⎡⎤=+=+Λ=+Λ⎣⎦1121()()().P kE P P kE P P kE P ---=+Λ+Λ=+Λ即12()P BP kE -=+Λ.故222(2)000(2)000k Bk k ⎡⎤+⎢⎥+⎢⎥⎢⎥⎣⎦. 当20k k ≠-≠且时,B 的全部特征值大于零,这时B 为正定矩阵.【相关知识点】1.特征值的性质:若A 有特征值λ,则A 的特征多项式()f A 有特征值()f λ.2.矩阵正定的充要条件是特征值全大于零.十一、(本题满分10分)【解析】设Z 表示商店每周所得的利润, 当Y X ≤时,卖得利润为1000Z Y =(元); 当Y X >时,调剂了Y X -,总共得到利润1000500()500()Z X Y X X Y =+-=+(元).所以,1000, ,500(), .Y Y X Z X Y Y X ≤⎧=⎨+>⎩由题设X 与Y 都服从区间[10,20]上的均匀分布,联合概率密度为1, 1020,1020,(,)1000, x y f x y ⎧≤≤≤≤⎪=⎨⎪⎩其他.由二维连续型随机变量的数学期望定义得1212202020101010202021010()1000(,)500()(,)111000500()100100105()310(20)5(1050)2200005150014166.67().3D D D D yyE Z y f x y dxdy x y f x y dxdyy dxdy x y dxdy dy ydx dy x y dxy y dy y y dy=⋅++⋅=⋅++⋅=++=-+--=+⨯≈⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰元十二、(本题满分9分)【解析】记事件j B =“第j 次抽到的报名表是女生表”(1,2)j =,i A =“报名表是第i 个地区的”(1,2,3)i =.易见,123,,A A A 构成一个完备事件组,且1112131{}(1,2,3),3375{},{},{}.101525i P A i P B A P B A P B A =====(1) 应用全概率公式,知3111137529{}{}{}()310152590i i i p P B P A P B A ===⋅=++=∑.(2) 12{}q P B B =.需先计算概率12{}P B B 与2{}P B .对事件12B B 再次用全概率公式:3121211377852020{}{}{}()31091514252490i i i P B B P A P B B A ==⋅=⋅+⋅+⋅=∑,由“抽签原理”可知2161()()90P B P B ==, 12122()209020{}906161()P B B q P B B P B ===⋅=. 【相关知识点】1.全概率公式:如果事件1,,n A A 构成一个完备事件组,即它们是两两互不相容,其和为Ω(总体的样本空间);并且()0,1,2,,i P A i n >=,则对任一事件B 有()1()(|)ni i i P B P A P B A ==∑.。
1998考研数一真题答案及详细解析

A ,
( 0) .
由 A 0 ,知 0 (如果0是 A 的特征值 A 0 ),将上式两端左乘 A ,得
A A A A A ,
从而有
A*
A
,
(即
A
的特征值为
A
).
将此式两端左乘 A ,得
A*
2
A
A*
A
2 .
又 E ,所以
A*
2 E
A
2
1
的条件下与求导次序无关,先求 z 或 z 均可,但不同的选择可能影响计算的繁简. x y
z
方法1:先求 .
x
z x
1 x x
f (xy)
y(x
y)
1 x2
f (xy)
y x
f
(xy)
y (x
y)
,
2z xy
y
1 x2
f (xy)
y x
f (xy)
y(x
y )
1 x2
f (xy)x 1 x
(2)【答案】(B) 【解析】当函数中出现绝对值号时,就有可能出现不可导的“尖点”,因为这时的函数是
分段函数. f (x) (x2 x 2) x x2 1 ,当 x 0, 1 时 f (x) 可导,因而只需在 x 0, 1 处
考察 f (x) 是否可导.在这些点我们分别考察其左、右导数.
由
o2
x2
,
从而
原式
lim
1
1 2
x
1 8
x
2
o1
x0
x2
1
1 2
x
1 8
x2
o2
x2
1998年全国硕士研究生入学统一考试数学(一)真题及解析

1998年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)0x →(2)设1()(),,z f xy y x y f x ϕϕ=++具有二阶连续导数,则2z x y∂∂∂=_____________.(3)设l 为椭圆221,43x y +=其周长记为,a 则22(234)Lxy x y ds ++⎰=_____________. (4)设A 为n 阶矩阵*,0,≠A A 为A 的伴随矩阵,E 为n 阶单位矩阵.若A 有特征值,λ则*2()+A E 必有特征值_____________.(5)设平面区域D 由曲线1y x=及直线20,1,e y x x ===所围成,二维随机变量(,)X Y 在区域D 上服从均匀分布,则(,)X Y 关于X 的边缘概率密度在2x =处的值为_____________. 二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设()f x 连续,则220()xd tf x t dt dx -⎰= (A)2()xf x (B)2()xf x - (C)22()xf x(D)22()xf x -(2)函数23()(2)f x x x x x =---不可导点的个数是 (A)3 (B)2 (C)1(D)0(3)已知函数()y y x =在任意点x 处的增量2,1y xy xα∆∆=++且当0x ∆→时,α是x ∆的高阶无穷小,(0)y π=,则(1)y 等于(A)2π (B)π(C)4e π(D)4e ππ(4)设矩阵111222333a b c a b c a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦是满秩的,则直线333121212x a y b z c a a b b c c ---==---与直线111232323x a y b z c a a b b c c ---==---(A)相交于一点 (B)重合 (C)平行但不重合(D)异面(5)设,A B 是两个随机事件,且0()1,()0,(|)(|),P A P B P B A P B A <<>=则必有 (A)(|)(|)P A B P A B = (B)(|)(|)P A B P A B ≠ (C)()()()P AB P A P B =(D)()()()P AB P A P B ≠三、(本题满分5分)求直线11:111x y z l --==-在平面:210x y z π-+-=上的投影直线0l 的方程,并求0l 绕y 轴旋转一周所成曲面的方程.四、(本题满分6分)确定常数,λ使在右半平面0x >上的向量42242(,)2()()x y xy x y x x y λλ=+-+A i j为某二元函数(,)u x y 的梯度,并求(,).u x y 五、(本题满分6分)从船上向海中沉放某种探测仪器,按探测要求,需确定仪器的下沉深度(y 从海平面算起)与下沉速度v 之间的函数关系.设仪器在重力作用下,从海平面由静止开始铅直下沉,在下沉过程中还受到阻力和浮力的作用.设仪器的质量为,m 体积为,B 海水密度为,ρ仪器所受的阻力与下沉速度成正比,比例系数为(0).k k >试建立y 与v 所满足的微分方程,并求出函数关系式().y y v =六、(本题满分7分)计算222212(),()axdydz z a dxdy x y z ∑++++⎰⎰其中∑为下半平面z =,a 为大于零的常数.七、(本题满分6分)求2sin sin sin lim .1112x n n n n n n πππ→∞⎡⎤⎢⎥+++⎢⎥+⎢⎥++⎣⎦设正向数列{}n a 单调减少,且1(1)nn n a ∞=-∑发散,试问级数11()1nn n a ∞=+∑是否收敛?并说明理由.九、(本题满分6分)设()y f x =是区间[0,1]上的任一非负连续函数.(1)试证存在0(0,1),x ∈使得在区间0[0,]x 上以0()f x 为高的矩形面积,等于在区间0[,1]x 上以()y f x =为曲边的曲边梯形面积.(2)又设()f x 在区间(0,1)内可导,且2()(),f x f x x'>-证明(1)中的0x 是唯一的. 十、(本题满分6分)已知二次曲面方程2222224x ay z bxy xz yz +++++=可以经过正交变换x y z ξηζ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦P 化为椭圆柱面方程2244,ηξ+=求,a b 的值和正交矩阵.P 十一、(本题满分4分)设A 是n 阶矩阵,若存在正整数,k 使线性方程组k x =A 0有解向量,α且1.k -≠A α0 证明:向量组1,,,k -αA αA α是线性无关的.十二、(本题满分5分)已知方程组(Ⅰ)1111221,222112222,221122,22000n n n n n n n n n a x a x a x a x a x a x a x a x a x +++=+++=+++=的一个基础解析为11121,221222,212,2(,,,),(,,,),,(,,,).T T T n n n n n n b b b b b b b b b 试写出线性方程组(Ⅱ)1111221,222112222,221122,22000n n n n n n n n n b y b y b y b y b y b y b y b y b y +++=+++=+++=的通解,并说明理由.设两个随机变量,X Y 相互独立,且都服从均值为0、方差为12的正态分布,求随机变量X Y -的方差.十四、(本题满分4分)从正态总体2(3.4,6)N 中抽取容量为n 的样本,如果要求其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n 至少应取多大? 附:标准正态分布表22()t zx dt -Φ=⎰十五、(本题满分4分)设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生地成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70 分?并给出检验过程.附:t 分布表 {()()}p P t n t n p ≤=1998年全国硕士研究生入学统一考试数学一试题解析一、填空题(本题共5小题,每小题3分,满分15分.) (1)【答案】14-【解析】方法1:用四则运算将分子化简,再用等价无穷小替换,原式22x →=24x →-=)221lim4x x →=2220112112lim 24x x xx →-- =-.方法2:采用洛必达法则.原式)()022limxx →''洛0x→= 0x →=0x →=0x → 洛 14==-.方法3:将分子按佩亚诺余项泰勒公式展开至2x 项,()22111128x x o x =+-+()22211128x x o x =--+, 从而 原式()()2222122011111122828lim x x x o x x x o x x →+-++--+-= ()()222122014lim x x o x o x x →-++=14=-. (2)【答案】()()()yf xy x y y x y ϕϕ'''''++++ 【分析】因为1()(),,z f xy y x y f xϕϕ=++具有二阶连续导数,利用混合偏导数在连续的条件下与求导次序无关,先求z x ∂∂或z y∂∂均可,但不同的选择可能影响计算的繁简. 方法1:先求z x∂∂. 211()()()()()z y f xy y x y f xy f xy y x y x x x x x ϕϕ∂∂⎡⎤''=++=-+++⎢⎥∂∂⎣⎦,2221()()()11()()()()()11()()()()()()()().z y f xy f xy y x y x y y x x yf xy x f xy f xy x x y y x y x x xf xy f xy yf xy x y y x y x xyf xy x y y x y ϕϕϕϕϕϕϕ∂∂⎛⎫''=-+++ ⎪∂∂∂⎝⎭'''''''=-++++++'''''''=-++++++'''''=++++ 方法2:先求z y∂∂. 11()()()()()()()(),z f xy y x y f xy x x y y x y y y x xf xy x y y x y ϕϕϕϕϕ∂∂⎡⎤''=++=++++⎢⎥∂∂⎣⎦''=++++ []22()()()()()().z z f xy x y y x y x y y x xyf xy x y y x y ϕϕϕϕ∂∂∂''==++++∂∂∂∂∂'''''=++++ 方法3:对两项分别采取不同的顺序更简单些:()[][][]21()()1()()()()()()().z f xy y x y x y x y x y x f xy x y x y x x y f xy y x y x yyf xy x y y x y ϕϕϕϕϕ⎡⎤∂∂∂∂∂⎛⎫⎡⎤=++ ⎪⎢⎥⎢⎥∂∂∂∂∂∂⎝⎭⎣⎦⎣⎦∂∂⎡⎤''=++⎢⎥∂∂⎣⎦∂∂''=++∂∂'''''=++++ 评注:本题中,,f ϕ中的中间变量均为一元,因此本题实质上是一元复合函数的求导,只要注意到对x 求导时,y 视为常数;对y 求导时,x 视为常数就可以了. (3)【答案】12a【解析】L 关于x 轴(y 轴)对称,2xy 关于y (关于x )为奇函数20Lxyds ⇒=⎰.又在L 上,22222213412(34)1212.43L L x y x y x y ds ds a +=⇒+=⇒+==⎰⎰因此, 原式222(34)12LLxyds x y ds a =++=⎰⎰.【相关知识点】对称性:平面第一型曲线积分(),lf x y ds ⎰,设(),f x y 在l 上连续,如果l 关于y 轴对称,1l 为l 上0x ≥的部分,则有结论:()()()()12,,,,0,l lf x y ds f x y x f x y ds f x y x ⎧ ⎪=⎨ ⎪⎩⎰⎰关于为偶函数,,关于为奇函数. 类似地,如果l 关于x 轴对称,2l 为l 上0y ≥的部分,则有结论:()()()()22,,,,0,l lf x y ds f x y y f x y ds f x y y ⎧ ⎪=⎨ ⎪⎩⎰⎰关于为偶函数,,关于为奇函数. (4)【答案】 21A λ⎛⎫+ ⎪⎝⎭【解析】方法1:设A 的对应于特征值λ的特征向量为ξ,由特征向量的定义有,(0)A ξλξξ=≠.由0A ≠,知0λ≠(如果0是A 的特征值0A ⇔=),将上式两端左乘A *,得A A A A A ξξλξλξ***===,从而有 *,AA ξξλ=(即A *的特征值为Aλ).将此式两端左乘A *,得()22**AA A A ξξξλλ⎛⎫== ⎪⎝⎭.又E ξξ=,所以()()22*1A A E ξξλ⎛⎫⎛⎫ ⎪+=+ ⎪ ⎪⎝⎭⎝⎭,故*2()A E +的特征值为21A λ⎛⎫+ ⎪⎝⎭.方法2:由0A ≠,A 的特征值0λ≠(如果0是A 的特征值0A ⇔=),则1A -有特征值1λ,A *的特征值为A λ;*2()A E +的特征值为21A λ⎛⎫+ ⎪⎝⎭.【相关知识点】1.矩阵特征值与特征向量的定义:设A 是n 阶矩阵,若存在数λ及非零的n 维列向量X 使得AX X λ=成立,则称λ是矩阵A 的特征值,称非零向量X 是矩阵A 的特征向量.由λ为A 的特征值可知,存在非零向量α使A αλα=,两端左乘1A -,得1A αλα-=.因为0α≠,故0λ≠,于是有11Aααλ-=.按特征值定义知1λ是1A -的特征值.若AX X λ=,则()()A kE X AX kX k X λ+=+=+.即若λ是A 的特征值,则A kE +的特征值是k λ+.2.矩阵A 可逆的充要条件是0A ≠,且11AA A-*=. (5)【答案】14【解析】首先求(,)X Y 的联合概率密度(,)f x y .21(,)|1,0D x y x e y x ⎧⎫=≤≤≤≤⎨⎬⎩⎭, 区域D 的面积为22111ln 2.e e D S dx x x===⎰1,(,),(,)20, x y D f x y ⎧∈⎪=⎨⎪⎩其他.其次求关于X 的边缘概率密度.当1x <或2x e >时,()0X f x =;当21x e ≤≤时,1011()(,)22x X f x f x y dy dy x+∞-∞===⎰⎰. 故1(2).4X f =二、选择题(本题共5小题,每小题3分,共15分.) (1)【答案】(A)【解析】为变限所定义的函数求导数,作积分变量代换22,u x t =-2:0:0t x u x →⇒→,()222du d x t tdt =-=-12dt du t⇒=-, 222022220001()()211()(),22xx xx tf x t dt u x t tf u dt t f u du f u du ⎛⎫-=-- ⎪⎝⎭=-=⎰⎰⎰⎰()2220022221()()211()()2(),22x x d d tf x t dt f u du dx dx f x x f x x xf x -='=⋅=⋅=⎰⎰选(A).【相关知识点】对积分上限的函数的求导公式:若()()()()t t F t f x dx βα=⎰,()t α,()t β均一阶可导,则[][]()()()()()F t t ft t f t ββαα'''=⋅-⋅.(2)【答案】(B)【解析】当函数中出现绝对值号时,就有可能出现不可导的“尖点”,因为这时的函数是分段函数.22()(2)1f x x x x x =---,当0,1x ≠±时()f x 可导,因而只需在0,1x =±处考察()f x 是否可导.在这些点我们分别考察其左、右导数.由 22222222(2)(1),1,(2)(1),10,()(2)(1),01,(2)(1),1,x x x x x x x x x x f x x x x x x x x x x x ⎧---<-⎪----≤<⎪=⎨---≤<⎪⎪---≤⎩⇒ ()()22111(2)(1)0(1)lim lim 011x x f x f x x x x f x x ---→-→-------'-===++, ()()22111(2)(1)0(1)lim lim 011x x f x f x x x x f x x +++→-→-------'-===++,即()f x 在1x =-处可导.又()()22000(2)(1)0(0)lim lim 2x x f x f x x x x f x x ---→→-----'===, ()()22000(2)(1)0(0)lim lim 2x x f x f x x x x f x x+++→→-----'===-,所以()f x 在0x =处不可导.类似,函数()f x 在1x =处亦不可导.因此()f x 只有2个不可导点,故应选(B). 评注:本题也可利用下列结论进行判断:设函数()()f x x a x ϕ=-,其中()x ϕ在x a =处连续,则()f x 在x a =处可导的充要条件是()0a ϕ=. (3)【答案】(D) 【解析】由2,1y x y x α∆∆=++有2.1y y x x xα∆=+∆+∆ 令0,x ∆→得α是x ∆的高阶无穷小,则0lim0x xα∆→=∆,0limx y x ∆→∆∆20lim 1x yx x α∆→⎛⎫=+ ⎪+∆⎝⎭200lim lim 1x x y x x α∆→∆→=++∆21y x =+ 即21dy y dx x=+. 分离变量,得2,1dy dx y x=+ 两边积分,得 ln arctan y x C =+,即arctan 1.xy C e=代入初始条件(0),y π=得()arctan0110.y C e C π===所以,arctan xy eπ=.故 arctan 1(1)xx y eπ==arctan1eπ=4.e ππ=【相关知识点】无穷小的比较:设在同一个极限过程中,(),()x x αβ为无穷小且存在极限 ()lim ()x l x αβ=, (1) 若0,l ≠称(),()x x αβ在该极限过程中为同阶无穷小; (2) 若1,l =称(),()x x αβ在该极限过程中为等价无穷小,记为()()x x αβ;(3) 若0,l =称在该极限过程中()x α是()x β的高阶无穷小,记为()()()x o x αβ=. 若()lim()x x αβ不存在(不为∞),称(),()x x αβ不可比较. (4)【答案】(A) 【解析】设3331121212:x a y b z c L a a b b c c ---==---,1112232323:x a y b z c L a a b b c c ---==---,题设矩阵111222333a b c a b c a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦是满秩的,则由行列式的性质,可知 11112121222223232333333312230a b c a a b b c c a b c a a b b c c a b c a b c ------≠行减行,行减行, 故向量组121212(,,)a a b b c c ---与232323(,,)a a b b c c ---线性无关,否则由线性相关的定义知,一定存在12,k k ,使得11212122232323(,,)(,,)0k a a b b c c k a a b b c c ---+---=,这样上面行列式经过初等行变换值应为零,产生矛盾.121212(,,)a a b b c c ---与232323(,,)a a b b c c ---分别为12,L L 的方向向量,由方向向量线性相关,两直线平行,可知12,L L 不平行.又由333121212x a y b z c a a b b c c ---==---得333121212111x a y b z c a a b b c c ----=-=----,即()()()312312312121212x a a a y b b b z c c c a a b b c c ---------==---. 同样由111232323x a y b z c a a b b c c ---==---,得111232323111x a y b z c a a b b c c ---+=+=+---,即 ()()()123323323232323x a a a y b b b z c c c a a b b c c -+--+--+-==---, 可见12,L L 均过点()213213213,,a a a b b b c c c ------,故两直线相交于一点,选(A). (5)【答案】C【分析】由题设条件(|)(|)P B A P B A =,知A 发生与A 不发生条件下B 发生的条件概率相等,即A 发生不发生不影响B 的发生概率,故,A B 相互独立.而本题选项(A)和(B)是考虑(|)P A B 与(|)P A B 是否相等,选项(C)和(D)才是事件A 与B 是否独立. 【解析】由条件概率公式及条件(|)(|),P B A P B A =知{}{}{}{}{}{}{}1P AB P AB P B P AB P A P A P A-==-, 于是有 {}{}{}{}{}1P AB P A P A P B P AB -=⋅-⎡⎤⎡⎤⎣⎦⎣⎦, 可见 {}{}{}P AB P A P B =. 应选(C).【相关知识点】条件概率公式:{}{}{}|P AB P B A P A =.三、(本题满分5分)【解析】方法1:求直线L 在平面∏上的投影0L :方法1:先求L 与∏的交点1N .以1,:,1x t L y t z t =+⎧⎪=⎨⎪=-⎩代入平面∏的方程,得(1)2(1)101t t t t +-+--=⇒=.从而交点为1(2,1,0)N ;再过直线L 上点0(1,0,1)M 作平面∏的垂线11:112x y z L --'==-,即1,,12.x t y t z t =+⎧⎪=-⎨⎪=+⎩并求L '与平面∏的交点2N :1(1)()2(12)103t t t t +--++-=⇒=-,交点为2211(,,)333N .1N 与2N 的连接线即为所求021:421x y zL --==-. 方法2:求L 在平面∏上的投影线的最简方法是过L 作垂直于平面∏的平面0∏,所求投影线就是平面∏与0∏的交线.平面0∏过直线L 上的点(1,0,1)与不共线的向量(1,1,1)l =- (直线L 的方向向量)及(1,1,2)n =-(平面∏的法向量)平行,于是0∏的方程是111110112x y z ---=-,即3210x y z --+=. 投影线为 0210,:3210.x y z L x y z -+-=⎧⎨--+=⎩下面求0L 绕y 轴旋转一周所成的旋转曲面S 的方程.为此,将0L 写成参数y 的方程:2,1(1).2x y z y =⎧⎪⎨=--⎪⎩ 按参数式表示的旋转面方程得S 的参数方程为,,.xy yzθθ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩消去θ得S的方程为()222212(1)2x z y y⎡⎤+=+--⎢⎥⎣⎦,即2224174210.x y z y-++-=四、(本题满分6分)【解析】令42(,)2(),P x y xy x yλ=+242(,)(),Q x y x x yλ=-+则(,)((,),(,))A x y P x y Q x y=在单联通区域右半平面0x>上为某二元函数(,)u x y的梯度Pdx Qdy⇔+在0x>上∃原函数(,)u x y⇔,0.Q Pxx y∂∂=>∂∂其中, 42242132()()4Qx x y x x y xxλλλ-∂=-+-+⋅∂,424212()2()2Px x y xy x y yyλλλ-∂=+++⋅∂.由Q Px y∂∂=∂∂,即满足4224213424212()()42()2()2x x y x x y x x x y xy x y yλλλλλλ---+-+⋅=+++⋅,424()(1)01x x yλλλ⇔++=⇔=-.可见,当1λ=-时,所给向量场为某二元函数的梯度场.为求(,)u x y,采用折线法,在0x>半平面内任取一点,比如点(1,0)作为积分路径的起点,则根据积分与路径无关,有2(,)42(1,0)2(,)x yxydx x dyu x y Cx y-=++⎰24421020x yx xdx dy Cx x y⋅-=++++⎰⎰(折线法)242y x dy Cx y-=++⎰2242(1)yx dy C y x x -=+⎛⎫+ ⎪⎝⎭⎰(第一类换元法)222222004221(1)(1)yy x x y y d C d C x x y y x x x ⋅⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎰⎰ 2arctan yC x=-+(基本积分公式) 其中C 为任意常数.【相关知识点】1.二元可微函数(,)u x y 的梯度公式:u u gradu i +j x y∂∂=∂∂. 2.定理:设D 为平面上的单连通区域,函数()P x,y 与(,)Q x y 在D 内连续且有连续的一阶偏导数,则下列六个命题等价:(1),(,)Q Px y D x y∂∂≡∈∂∂; (2) 0,LPdx Qdy L +=⎰为D 内任意一条逐项光滑的封闭曲线;(3)LABPdx Qdy +⎰仅与点,A B 有关,与连接,A B 什么样的分段光滑曲线无关;(4) 存在二元单值可微函数(,)u x y ,使du Pdx Qdy =+(即Pdx Qdy +为某二元单值可微函数(,)u x y 的全微分; (5) 微分方程0Pdx Qdy +=为全微分方程;(6) 向量场P +Q i j 为某二元函数(,)u x y 的梯度u P +Q =grad i j .换言之,其中任一组条件成立时,其它五组条件皆成立.当条件成立时,可用试图法或折线法求函数(,)u x y .五、(本题满分6分)【解析】先建立坐标系,取沉放点为原点O ,铅直向下作为Oy 轴正向,探测器在下沉过程中受重力、浮力和阻力的作用,其中重力大小:mg ,浮力的大小:F B ρ=-浮;阻力:kv -,则由牛顿第二定律得202,0,0.t t d ym mg B g kv y vdtρ===--== (*)由22,dy d y dv dv dy dv dy v v v dv dt dt dt dy dt dy===⋅==,代入(*)得y 与v 之间的微分方程10,0y dy mv mg B kv v dv ρ-=⎛⎫=--= ⎪⎝⎭.分离变量得 mvdy dv mg B kv ρ=--,两边积分得 mvdy dv mg B kv ρ=--⎰⎰,2222()()()Bm m g Bm m g mv k k k k y dv mg B kv m Bm m g mg B kv k k k dv mg B kv m g Bm m k dvk mg B kv m m mg B dv dvk k mg B kv ρρρρρρρρρρ+--+=------+=--⎛⎫- ⎪=-+ ⎪-- ⎪ ⎪⎝⎭-=-+--⎰⎰⎰⎰⎰1()()()()m mg B m k v d mg B kv k k mg B kv ρρρ-⋅-=-+----⎰ (第一类换元法) 2()ln()m m mg B v mg B kv C k kρρ-=----+.再根据初始条件0|0,y v ==即22()()ln()0ln()m mg B m mg B mg B C C mg B k k ρρρρ----+=⇒=-.故所求y 与v 函数关系为()2ln .m mg B m mg B kv y v k k mg B ρρρ-⎛⎫--=-- ⎪-⎝⎭六、(本题满分7分)【解析】方法1:本题属于求第二类区面积分,且不属于封闭区面,则考虑添加一平面使被积区域封闭后用高斯公式进行计算,但由于被积函数分母中包含12222()x y z ++,因此不能立即加、减辅助面2221:0x y a z ⎧+≤∑⎨=⎩,宜先将曲面方程代入被积表达式先化简:2212222()1().()axdydz z a dxdy I axdydz z a dxdy a x y z ∑∑++==++++⎰⎰⎰⎰ 添加辅助面2221:0x y a z ⎧+≤∑⎨=⎩,其侧向下(由于∑为下半球面z =侧,而高斯公式要求是整个边界区面的外侧,这里我们取辅助面的下侧,和∑的上侧组成整个边界区面的内侧,前面取负号即可),由高斯公式,有11222211()()()1()().D I axdydz z a dxdy axdydz z a dxdy a a z a ax dV a dxdy a x z ∑+∑∑Ω=++-++⎛⎫⎡⎤∂+⎛⎫∂⎣⎦ ⎪=-+-- ⎪ ⎪∂∂⎝⎭⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰第一个积分前面加负号是由于我们取边界区面的内侧,第二个积分前面加负号是由于1∑的方向向下;另外由曲面片1∑在yoz 平面投影面积为零,则10axdydz ∑=⎰⎰,而1∑上0z =,则()22z a a +=.21(2())D I a z a dV a dxdy a Ω⎛⎫=-+++ ⎪⎝⎭⎰⎰⎰⎰⎰,其中Ω为∑与1∑所围成的有界闭区域,D 为1∑在xoy 面上的投影222{(,)|}D x y x y a =+≤. 从而,220322001321232.3D a I a dv zdv a dxdy a a a d rdr a a a ππθπΩΩ⎛⎫=--+ ⎪⎝⎭⎛⎫=-⋅-+⋅ ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰第一个积分用球体体积公式;第二个用柱面坐标求三重积分;第三个用圆的面积公式.()2042400242200242300224224440411222112()21()1122242412a a a aI a d r z dr a a a d r a r dr a a d a r r draa r r a a a a a a a a a a ππππθππθπθππππππ⎛⎫⎛=--+ ⎪⎝⎝⎭⎛⎫⎛⎫=---- ⎪ ⎪⎝⎭⎝⎭=-+-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪=-+⋅-=-+⋅- ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=-+⋅⎰⎰⎰⎰⎰⎰4342a π⎛⎫=- ⎪⎝⎭ 方法2:逐项计算:2212222212()1()()1().axdydz z a dxdyI axdydz z a dxdy a x y z xdydz z a dxdy I I a ∑∑∑∑++==++++=++=+⎰⎰⎰⎰⎰⎰⎰⎰其中,12,Dyz DyzDyzI xdydz ∑==-+=-⎰⎰⎰⎰⎰⎰⎰⎰第一个负号是由于在x 轴的正半空间区域∑的上侧方向与x 轴反向;第二个负号是由于被积函数在x 取负数.yz D 为∑在yoz 平面上的投影域222{(,)|,0}yz D y z y z a z =+≤≤,用极坐标,得2102203223320212()2222()(0),333aI d a r a r a a ππθππππ=-=-⋅--=-=-=-⎰⎰⎰(222222002302300042230044411()1(22)2(22)2222123422(3Dxya a a a a a a I z a dxdy a dxdya a d a r rdra a r r dr a a rdr a r dr a r a r a a a a a a aπθππππ∑=+=-=-=-⎡⎤=--⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫⎢⎥=-⋅- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=--⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰3),46a π=其中yz D 为∑在yoz 平面上的投影域222{(,)|}yz D y z y z a =+≤.故312.2I I I a π=+=-【相关知识点】高斯公式:设空间闭区域Ω是由分片光滑的闭曲面∑所围成,函数(,,)P x y z 、(,,)Q x y z 、(,,)R x y z 在Ω上具有一阶连续偏导数,则有,P Q R dv Pdydz Qdzdx Rdxdy x y z Ω∑⎛⎫∂∂∂++=++ ⎪∂∂∂⎝⎭⎰⎰⎰⎰⎰ 或()cos cos cos ,P Q R dv P Q R dS x y z αβγΩ∑⎛⎫∂∂∂++=++ ⎪∂∂∂⎝⎭⎰⎰⎰⎰⎰这里∑是Ω的整个边界曲面的外侧,cos α、cos β、cos γ是∑在点(,,)x y z 处的法向量的方向余弦.上述两个公式叫做高斯公式.七、(本题满分6分)【分析】这是n 项和式的极限,和式极限通常的方法就两种:一、把和式放缩,利用夹逼准则求极限;二、把和式转换成定积分的定义形式,利用定积分求极限.这道题,把两种方法结合到一起来求极限.当各项分母均相同是n 时,n 项和式2sin sinsin n n n n n x nnnπππ=+++是函数sin x π在[0,1]区间上的一个积分和.于是可由定积分1sin xdx π⎰求得极限lim nn x→∞.【解析】由于sinsin sin ,1,2,,11i i i n n n i n n n n iπππ≤≤=⋅⋅⋅++,于是,111sinsin sin 11nn ni i i i i i n n n n nn iπππ===≤≤++∑∑∑.由于 1011sin12limlim sin sin nnn n i i i i n xdx n n n ππππ→∞→∞=====∑∑⎰,10111sin112lim lim sin lim sin sin 11nn nn n n i i i i n i i n xdx n n n n n n πππππ→∞→∞→∞===⎡⎤=⋅===⎢⎥++⎣⎦∑∑∑⎰根据夹逼定理知,1sin2lim1nn i i n n iππ→∞==+∑. 【相关知识点】夹逼准则:若存在N ,当n N >时,n n n y x z ≤≤,且有lim lim n n n n y z a →+∞→+∞==,则lim n n x a →+∞=.八、(本题满分5分)【解析】方法1:因正项数列{}n a 单调减少有下界0,知极限lim n n a →∞存在,记为a ,则n a a ≥且0a ≥.又1(1)nn n a ∞=-∑发散,根据莱布尼茨判别法知,必有 0a >(否则级数1(1)n n n a ∞=-∑收敛).又正项级数{}n a 单调减少,有11,11nnn a a ⎛⎫⎛⎫≤ ⎪ ⎪++⎝⎭⎝⎭而1011a <<+,级数11()1n n a ∞=+∑收敛.根据正项级数的比较判别法,知级数11()1nn n a ∞=+∑也收敛. 方法2:同方法1,可证明lim 0n n a a →∞=>.令1,1nn n b a ⎛⎫= ⎪+⎝⎭则11lim1,11n n na a →∞==<++根据根值判别法,知级数11()1nn n a ∞=+∑也收敛. 【相关知识点】1.交错级数的莱布尼茨判别法:设交错级数11(1)n n n u ∞-=-∑满足:(1)1,1,2,;n n u u n +≥= (2)lim 0.n n u →∞=则11(1)n n n u ∞-=-∑收敛,且其和满足1110(1),n n n u u ∞-=<-<∑余项1.n n r u +<反之,若交错级数11(1)n n n u ∞-=-∑发散,只是满足条件(1),则可以反证说明此级数一定不满足条件(2)lim 0n n u →∞=,所以有lim 0.n n u →∞>(否则级数11(1)n n n u ∞-=-∑收敛)2.正项级数的比较判别法:设1n n u ∞=∑和1n n v ∞=∑都是正项级数,且lim,nn nv A u →∞=则(1)当0A <<+∞时,1nn u∞=∑和1nn v∞=∑同时收敛或同时发散;(2)当0A =时,若1nn u∞=∑收敛,则1nn v∞=∑收敛;若1nn v∞=∑发散,则1nn u∞=∑发散;(3)当A =+∞时,若1nn v∞=∑收敛,则1nn u∞=∑收敛;若1nn u∞=∑发散,则1nn v∞=∑发散.3.根值判别法:设0n u >,则当111, 1, lim 0,1, .n n n n n n n u u u ρ∞=∞→∞=⎧<⎪⎪⎪=>≠⎨⎪⎪=⎪⎩∑∑时收敛,时发散,且时此判别法无效九、(本题满分6分)【解析】(1)要证0(0,1)x ∃∈,使0100()()x x f x f x dx =⎰;令1()()()x x xf x f t dt ϕ=-⎰,要证0(0,1)x ∃∈,使0()0x ϕ=.可以对()x ϕ的原函数0()()x x t dt ϕΦ=⎰使用罗尔定理:(0)0Φ=,11111111000(1)()()(())()()()0,xx x x x dx xf x dx f t dt dxxf x dx x f t dt xf x dx ϕ==Φ==-⎡⎤=-+=⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰⎰分部又由()f x 在[0,1]连续()x ϕ⇒在[0,1]连续,()x Φ在[0,1]连续,在(0,1)可导.根据罗尔定理,0(0,1)x ∃∈,使00()()0x x ϕ'Φ==.(2) 由()()()()()2()0x xf x f x f x xf x f x ϕ'''=++=+>,知()x ϕ在(0,1)内单调增,故(1)中的0x 是唯一的.评注:若直接对()x ϕ使用零点定理,会遇到麻烦:1(0)()0,(1)(1)0f t dt f ϕϕ=-≤=≥⎰.当()0f x ≡时,对任何的0(0,1)x ∈结论都成立;当()f x ≡0时,(0)0,ϕ<但(1)0ϕ≥,若(1)0ϕ=,则难以说明在(0,1)内存在0x .当直接对()x ϕ用零点定理遇到麻烦时,不妨对()x ϕ的原函数使用罗尔定理. 【相关知识点】1.罗尔定理:如果函数()f x 满足 (1) 在闭区间[,]a b 上连续; (2) 在开区间(,)a b 内可导;(3) 在区间端点处的函数值相等,即()()f a f b =, 那么在(,)a b 内至少有一点ξ(a b ξ<<),使得()0f ξ'=.十、(本题满分6分)【解析】经正交变换化二次型为标准形,二次型矩阵与标准形矩阵既合同又相似.由题设知,二次曲面方程左端二次型对应矩阵为111111b A b a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则存在正交矩阵P ,使得 1000010004P AP -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦B 记,即A B 与相似.由相似矩阵有相同的特征值,知矩阵A 有特征值0,1,4.从而,211014,3, 1.(1)0.a a b A b B ++=++⎧⎪⇒==⎨=--==⎪⎩从而,111131.111A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦当10λ=时,()1110131111E A ---⎡⎤⎢⎥-=---⎢⎥⎢⎥---⎣⎦1(1)23⨯-行分别加到,行111020000---⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦于是得方程组(0)0E A x -=的同解方程组为12320,20.x x x x ---=⎧⎨-=⎩(0)2r E A -=,可知基础解系的个数为(0)321n r E A --=-=,故有1个自由未知量,选1x 为自由未知量,取11x =,解得基础解系为1(1,0,1).Tα=-当21λ=时,()011121110E A --⎡⎤⎢⎥-=---⎢⎥⎢⎥--⎣⎦3(1)2⨯-加到行011011110--⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦1(1)2⨯-行加到行011000110--⎡⎤⎢⎥⎢⎥⎢⎥--⎣⎦23,行互换011110000--⎡⎤⎢⎥--⎢⎥⎢⎥⎣⎦, 于是得方程组()0E A x -=的同解方程组为23120,0.x x x x --=⎧⎨--=⎩()2r E A -=,可知基础解系的个数为()321n r E A --=-=,故有1个自由未知量,选1x 为自由未知量,取11x =,解得基础解系为2(1,1,1).Tα=-当34λ=时,()3114111113E A --⎡⎤⎢⎥-=--⎢⎥⎢⎥--⎣⎦12,行互换111311113--⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦1行的3,(-1)倍分别加到2,3行111024024--⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦23行加到行111024000--⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦,于是得方程组(4)0E A x -=的同解方程组为123230,240.x x x x x -+-=⎧⎨-=⎩(4)2r E A -=,可知基础解系的个数为(4)321n r E A --=-=,故有1个自由未知量,选2x 为自由未知量,取22x =,解得基础解系为3(1,2,1).Tα=由实对称矩阵不同特征值对应的特征向量相互正交,可知123,,ααα相互正交. 将123,,ααα单位化,得111222333,,.TTTαηααηααηα======因此所求正交矩阵为0P ⎡⎢⎢⎢=⎢⎢⎢⎢⎣. 评注:利用相似的必要条件求参数时,iiiia b=∑∑是比较好用的一个关系式.亦可用E A E B λλ-=-比较λ同次方的系数来求参数.【相关知识点】1.特征值的性质:11nni iii i aλ===∑∑2.相似矩阵的性质:若矩阵A B 与相似,则A B =.十一、(本题满分4分)【解析】用线性无关的定义证明.设有常数011,,,,k λλλ-⋅⋅⋅使得10110.()k k A A λαλαλα--++⋅⋅⋅+=*两边左乘1k A -,则有()110110k k k A A A λαλαλα---++⋅⋅⋅+=,即 12(1)0110k k k k A A Aλαλαλα---++⋅⋅⋅+=. 上式中因0kA α=,可知()2110k k A A αα-+===,代入上式可得100.k A λα-=由题设10k Aα-≠,所以00.λ=将00λ=代入()*,有1110k k A A λαλα--+⋅⋅⋅+=.两边左乘2k A -,则有 ()21110k k k A A A λαλα---+⋅⋅⋅+=,即123110k k k A A λαλα---+⋅⋅⋅+=.同样,由0kA α=,()2110k k A A αα-+==,可得110.k A λα-=由题设10k Aα-≠,所以10.λ=类似地可证明210,k λλ-=⋅⋅⋅==因此向量组1,,,k A A ααα-⋅⋅⋅是线性无关的. 【相关知识点】向量组线性相关和线性无关的定义:存在一组不全为零的数12m k ,k ,,k 使11220m m k k k ααα+++=,则称12m ,,,ααα线性相关;否则,称12m ,,,ααα线性无关.十二、(本题满分5分) 【解析】()II 的通解为1122n n k k k ξξξ++⋅⋅⋅+,其中,111121,2(,,,),Tn a a a ξ=⋅⋅⋅221222,2(,,,),,T n a a a ξ=⋅⋅⋅12,2(,,,)T n n n n n a a a ξ=⋅⋅⋅,12,,,n k k k ⋅⋅⋅为任意常数.理由:可记方程组22()0,()0,n n n n I A X II B Y ⨯⨯==()I ,()II 的系数矩阵分别记为,A B ,由于B 的每一行都是20n n A X ⨯=的解,故0T AB =.TB 的列是()I 的基础解系,故由基础解系的定义知,T B 的列向量是线性无关的,因此()r B n =.故基础解系所含向量的个数2()n n r A =-,得()2r A n n n =-=.因此,A 的行向量线性无关.对0TAB =两边取转置,有()0TT T ABBA ==,则有T A 的列向量,即A 的行向量是0BY =的线性无关的解.又()r B n =,故0BY =基础解系所含向量的个数应为2()2n r B n n n -=-=,恰好等于A 的行向量个数.故A 的行向量组是0BY =的基础解系,其通解为1122n n k k k ξξξ++⋅⋅⋅+,其中,111121,2(,,,),Tn a a a ξ=⋅⋅⋅221222,2(,,,),,T n a a a ξ=⋅⋅⋅12,2(,,,)T n n n n n a a a ξ=⋅⋅⋅,12,,,n k k k ⋅⋅⋅为任意常数.十三、(本题满分6分)【分析】把X Y -看成一个随机变量,根据独立正态随机变量的线性组合必然为正态分布的性质,可以知道N(0,1)X Y-,这样可以简化整题的计算.【解析】令Z X Y =-,由于,X Y 相互独立,且都服从正态分布,因此Z 也服从正态分布,且()()()0E Z E X E Y =-=,11()()()122D Z D X D Y =+=+=. 于是,(0,1)Z X Y N =-~.()()()()()()()22222()1.D X Y D ZE ZE Z D Z E Z E ZE Z-==-=+-=-而2222z z E Z z dz ze dz +∞+∞---∞==⎰2222202z z z ed e+∞+∞--⎡⎤⎛⎫==-=⎥ ⎪⎝⎭⎥⎦ 故21.D X Y π-=-【相关知识点】1.对于随机变量X 与Y 均服从正态分布,则X 与Y 的线性组合亦服从正态分布.若X 与Y 相互独立,由数学期望和方差的性质,有()()()E aX bY c aE X bE Y c ++=++,22()()()D aX bY c a D X b D Y ++=+,其中,,a b c 为常数.2.方差的定义:22()DX EX EX =-.3.随机变量函数期望的定义:若()Y g X =,则()()EY g x f x dx +∞-∞=⎰.十四、(本题满分4分) 【解析】由题知:212,,,~(3.4,6)n X X X N ,11nn i i X X n ==∑,各样本相互独立,根据独立正态随机变量的性质,211~(,)n n i i X X N n μσ==∑.其中11n n i i EX E X n μ=⎛⎫== ⎪⎝⎭∑,211n n i i DX D X n σ=⎛⎫== ⎪⎝⎭∑.根据期望和方差的性质,1122222211111 3.4 3.4,11166.n nn i i i i n n nn i i i i i i n EX E X EX n n n n DX D X D X DX n n n n n μσ=====⎛⎫===== ⎪⎝⎭⎛⎫⎛⎫====== ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∑所以,2116~(3.4,)n n i i X X N n n ==∑.把n X 标准化,~(0,1)X U N =. 从而,{}{}{}{}1.4X 5.4 1.4 3.4X 3.4 5.4 3.42X 3.42X 3.42210.95,P P P P P <<=-<-<-=-<-<=-<=<=Φ-≥⎝⎭⎪⎩⎭故0.975,Φ≥⎝⎭查表得到 1.96,3≥即()21.96334.57,n ≥⨯≈所以n 至少应取35. 【相关知识点】1.对于随机变量X 与Y 均服从正态分布,则X 与Y 的线性组合亦服从正态分布.若X 与Y 相互独立,由数学期望和方差的性质,有()()()E aX bY c aE X bE Y c ++=++,22()()()D aX bY c a D X b D Y ++=+,其中,,a b c 为常数. 2.若2~(,)Z N u σ,则~(0,1)Z uN σ-十五、(本题满分4分)【解析】设该次考试的考生成绩为X ,则2~(,)X N μσ,设X 为从总体X 抽取的样本容量为n 的样本均值,S 为样本标准差,则在显著性水平0.05α=下建立检验假设:001:70,:70,H H μμμ==≠由于2σ未知,故用t 检验.选取检验统计量,X T ==在070μμ==时,2~(70,),~(35).X N T t σ 选择拒绝域为{}R T λ=≥,其中λ满足:{}0.05P T λ≥=,即{}0.9750.975,(35) 2.0301.P T t λλ≤===由0 36,66.5,70,15,n x s μ====可算得统计量T 的值:1.42.0301t ==<.所以接受假设0:70H μ=,即在显著性水平0.05下,可以认为这次考试全体考生的平均成绩为70分.。
1998年全国高考文科数学试题及其解析
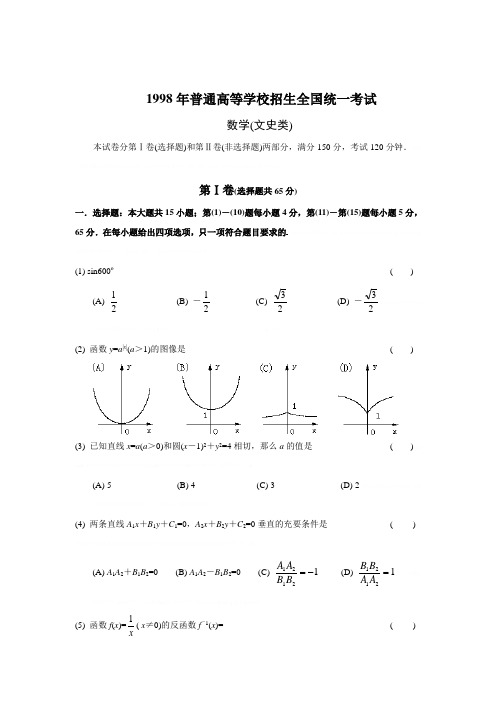
1998年普通高等学校招生全国统一考试数学(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试120分钟.第Ⅰ卷(选择题共65分)一.选择题:本大题共15小题;第(1)-(10)题每小题4分,第(11)-第(15)题每小题5分,65分.在每小题给出四项选项,只一项符合题目要求的学教案并加给事中化学教案后又迁为吏部尚书试卷试题八年化学教(1) sin600º( )(A)21 (B) -21(C) 23 (D) -232(2) 函数y =a |x |(a >1)的图像是 ( )(3) 已知直线x =a (a >0)和圆(x -1)2+y 2=4相切,那么a 的值是( )(A) 5 (B) 4 (C) 3 (D) 2(4) 两条直线A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0垂直的充要条件是( )(A) A 1A 2+B 1B 2=0 (B) A 1A 2-B 1B 2=0 (C)12121-=B B A A (D) 12121=A A BB (5) 函数f (x )=x1( x ≠0)的反函数f -1(x )= ( )(A) x (x ≠0) (B)x 1(x ≠0) (C) -x (x ≠0) (D) -x1(x ≠0)(6) 已知点P(sin α-cos α,tg α)在第一象限,则[ 0,2π]内α的取值范围是( )(A) (432ππ,)∪(45ππ,) (B) (24ππ,)∪(45ππ,)(C) (432ππ,)∪(2325ππ,) (D) (24ππ,)∪(ππ,43)(7) 已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面积展开图扇形的圆心角为( )(A) 120º (B) 150º (C) 180º (D) 240º(8) 复数-i 的一个立方根是i ,它的另外两个立方根是( )(A)2123±I (B) -2123±I (C) ±2123+I (D) ±2123-i (9) 如果棱台的两底面积是S ,S ′,中截面的面积是S 0,那么( )(A) 2S S S '+=0 (B) S 0=S S '(C) 2S 0=S +S ′ (D) S S S '=220(10) 2名医生和4名护士被分配到2所学校为学生体检,每校分配1名医生和2名护士.不同的分配方法共( )(A) 6种 (B) 12种 (C) 18种 (D) 24种(11) 向高为H 的水瓶中注水,注满为止,如果注水量V 与水深h 的函数关系的图像如右图所示,那么水瓶的形状是( )(12) 椭圆31222y x +=1的焦点为F 1,点P 在椭圆上,如果线段PF 1的中点M 在y 轴上,那么点M 的纵坐标是( )(A) ±43 (B) ±23 (C) ±22 (D) ±43显化学教案见景仁化学(13) 球面上有3个点,其中任意两点的球面距离都等于大圆周长为61,经过这3个点的小圆的周长为4π,那么这个球的半径为( )(A) 43 (B)23 (C) 2 (D)3孩子的一个暑假》里提(14) 一个直角三角形三内角的正弦值成等比数列,其最小内角的正弦值为( )(A)251- (B) 2252- (C) 215- (D) 2252+D (15) 等比数列{a n }的公比为-21,前n 项的和S n 满足∞→n lim S n =11a ,那么11a 的值为 ( )(A)3± (B)±23 (C) 2±(D) 26±的影响化学教案乙二.填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.(16) 设圆过双曲线116922=-y x 的一个顶点和一个焦点,圆心在双曲线上,则圆心到双曲线中心距离是__________不为退试卷试题”只愿(用这话)时时提醒自己试卷试题我近来要好好研读各种经书(17) (x +2)10(x 2-1)的展开的x 10系数为____________(用数字作答)震撼化学教案(18) 如图,在直四棱柱A 1B 1C 1D 1-ABCD 中,当底面四边形ABCD 满足条件____________时,有A 1C ⊥B 1D 1.(注:填上你认为正确的一种条件即可,不必考试所有可能的情形)(19) 关于函数f (x )=4sin(2x +3π)(x ∈R ),有下列命题①y =f (x )的表达式可改写为y =4cos(2x -6π);②y =f (x )是以2π为最小正周期的周期函数;③y =f (x )的图像关于点⎪⎭⎫⎝⎛-06,π对称; ④y =f (x )的图像关于直线x =-6π对称.其中正确的命题的序号是______ (注:把你认为正确的命题的序号都.填上.)三.解答题:本大题共6小题;共69分.解答应写出文字说明、证明过程或演算步骤.(20) (本小题满分10分)设a ≠b ,解关于x 的不等式a 2x +b 2(1-x )≥[ax +b (1-x )]2.21) (本小题满分11分)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,设a +c =2b ,A -C=3π,求sin B 的值.以下公式供解题时参考:2cos2sin2sin sin ϕθϕθϕθ-+=+, 2sin2cos2sin sin ϕθϕθϕθ-+=-,2cos 2cos 2cos cos ϕθϕθϕθ-+=+, 2sin2sin 2cos cos ϕθϕθϕθ-+-=-.(22) (本小题满分12分)如图,直线l 1和l 2相交于点M ,l 1 ⊥l 2,点N ∈l 1.以A 、B 为端点的曲线段C 上的任一点到l 2的距离与到点N 的距离相等.若△AMN 为锐角三角形,|AM |=17,|AN |=3,且|BN |=6.建立适当的坐标系,求曲线C 的方程.(23) (本小题满分12分)已知斜三棱柱ABC -A 1 B 1 C 1的侧面A 1 ACC 1与底面ABC 垂直,∠ABC =90º,BC =2,AC=23,且AA 1 ⊥A 1C ,AA 1= A 1 C 1.(Ⅰ)求侧棱A 1A 与底面ABC 所成角的大小;(Ⅱ)求侧面A 1 ABB 1 与底面ABC 所成二面角的大小; (Ⅲ)求侧棱B 1B 和侧面A 1 ACC 1的距离.(24) (本小题满分12分)如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱.污水从A 孔流入,经沉淀后从B 孔流出.设箱体的长度为a 米,高度为b 米.已知流出的水中该杂质的质量分数与a ,b 的乘积ab 成反比.现有制箱材料60平方米.问当a ,b 各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A 、B 孔的面积忽略不计).(25) (本小题满分12分)已知数列{b n }是等差数列,b 1=1,b 1+b 2+…+b 10=100.(Ⅰ)求数列{b n }的能项b n ; (Ⅱ)设数列{a n }的通项a n =lg(1+nb 1),记S n 是数列{a n }的前n 项的和.试比较S n 与21lg b n +1的大小,并证明你的结论.1998年普通高等学校招生全国统一考试数学试题(文史类)参考解答及评分标准一.选择题:本题考查基本知识和基本运算.第(1)-(10)题每小题4分,第(11)-(15)题每小题5分.满分65分.(1) D (2) B (3) C (4) A (5) B (6) B (7) C (8) D (9) A (10) B (11) B (12) A (13) B (14) C (15) D 二.填空题:本题考查基本知识和基本运算.每小题4分,满分16分.(16)316(17) -5120 (18) AC ⊥BD ,或任何能推导出这个条件的其他条件.例如ABCD 是正方形,菱形等(19)①,③注:第(19)题多填、漏填的错填均给0分. 三.解答题:(20)本小题主要考查不等式基本知识,不等式的解法.满分10分.解:将原不等式化为(a 2-b 2)x +b 2≥(a -b )2x 2+2(a -b )bx +b 2, 移项,整理后得 (a -b )2(x 2-x ) ≤0, ∵ a ≠b 即 (a -b )2>0, ∴ x 2-x ≤0, 即 x (x -1) ≤0.解此不等式,得解集 {x |0≤x ≤1}.(21) 本小题考查正弦定理,同角三角函数基本公式,诱导公式等基础知识,考查利用三角公式进行恒等变形的技能及运算能力.满分11分.解:由正弦定理和已知条件a +c =2b 得sin A +sin C =2sin B .由和差化积公式得B CA C A sin 22cos 2sin 2=-+. 由A +B +C =π,得 2)sin(C A +=2cos B,又A -C =3π,得23cos 2B=sin B ,∴23cos 2B =2sin 2B cos 2B. ∵ 0<2B <2π, 2cos B≠0, ∴sin2B =43, 从而cos2B =2sin 12B -=413 ∴ sin B =⨯23413=839(22) 本小题主要考查根据所给条件选择适当的坐标系,求曲线方程的解析几何的基本思想.考查抛物线的概念和性质,曲线与方程的关系以及综合运用知识的能力.满分12分.解法一:如图建立坐标系,以l 1为x 轴,MN 的垂直平分线为y 轴,点O 为坐标原点.依题意知:曲线段C 是以点N 为焦点,以l 2为准线的抛线段的一段,其中A 、B 分别为C 的端点.设曲线段C 的方程为y 2=2px (p >0),(x A ≤x ≤x B ,y >0),其中x A ,x B 分别为A ,B 的横坐标,P =|MN |.所以 M (-2P ,0),N (2P,0). 由 |AM |=17,|AN |=3得(x A +2P )2+2Px A =17, ① (x A -2P)2+2Px A =9. ②由①、②两式联立解得x A =P4,再将其代入①式并由p >0解得⎩⎨⎧==14A x p 或⎩⎨⎧==22Ax p . 因为△AMN 是锐角三角形,所以2P>x A ,故舍去⎩⎨⎧==22A x p . ∴ P =4,x A =1.由点B 在曲线段C 上,得x B =|BN |-2P=4. 综上得曲线段C 的方程为y 2=8x (1≤x ≤4,y >0).解法二:如图建立坐标系,分别以l 1、l 2为x 、y 轴,M 为坐标原点.作AE ⊥l 1,AD ⊥l 2,BF ⊥l 2,垂足分别为E 、D 、F .设 A (x A ,y A )、B (x B ,y B )、N (x N ,0).依题意有x A =|ME|=|DA|=|AN|=3, y A =|DM |=22DA AM-=22,由于△AMN 为锐角三角形,故有x N =|AE |+|EN |=4. =|ME |+22AE AN -=4X B =|BF |=|BN |=6.设点P (x ,y )是曲线段C 上任一点,则由题意知P 属于集合{(x ,y )|(x -x N )2+y 2=x 2,x A ≤x ≤x B ,y >0}. 故曲线段C 的方程y 2=8(x -2)(3≤x ≤6,y >0).(23) 本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,棱柱的性质,空间的角和距离的概念,逻辑思维能力、空间想象能力及运算能力.满分12分.注:题中赋分为得到该结论时所得分值,不给中间分. 解:(Ⅰ)作A 1D ⊥AC ,垂足为D ,由面A 1ACC 1⊥面ABC ,得A 1D ⊥面ABC ,∴ ∠A 1AD 为A 1A 与面ABC 所成的角. ∵ AA 1⊥A 1C ,AA 1=A 1C ,∴ ∠A 1AD=45º为所求.(Ⅱ)作DE ⊥AB ,垂足为E ,连A 1E ,则由A 1D ⊥面ABC ,得A 1E ⊥AB .∴∠A 1ED 是面A 1ABB 1与面ABC 所成二面角的平面角.由已知,AB ⊥BC ,得ED ∥BC .又D 是AC 的中点,BC =2,AC =23,∴ DE =1,AD =A 1D =3,tg A 1ED=DEDA 1=3. 故∠A 1ED=60º为所求.(Ⅲ) 作BF ⊥AC ,F 为垂足,由面A 1ACC 1⊥面ABC ,知BF ⊥面A 1ACC 1.∵ B 1B ∥面A 1ACC 1,∴ BF 的长是B 1B 和面A 1ACC 1的距离. 在Rt △ABC 中,2222=-=BC AC AB ,∴ 362=⋅=AC BC AB BF 为所求. (24) 本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力,考查建立函数关系、不等式性质、最大值、最小值等基础知识.满分12分.解法一:设y 为流出的水中杂质的质量分数,则y =abk,其中k >0为比例系数,依题意,即所求的a ,b 值使y 值最小.根据题设,有4b +2ab +2a =60(a >0,b >0), 得 aab +-=230 (0<a <30=, ① 于是 aa a k ab k y +-==230226432+-+-=a a k⎪⎭⎫ ⎝⎛+++-=264234a a k()2642234+⋅+-≥a a k18k =当a +2=264+a 时取等号,y 达最小值.这时a =6,a =-10(舍去).将a =6代入①式得b =3.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小.解法二:依题意,即所求的a ,b 的值使ab 最大.由题设知 4a +2ab +2a =60 (a >0,b >0)即 a +2b +ab =30 (a >0,b >0).∵ a +2b ≥2ab ,∴ 22ab +ab ≤30,当且仅当a =2b 时,上式取等号.由a >0,b >0,解得0<ab ≤18.即当a =2b 时,ab 取得最大值,其最大值18.∴ 2b 2=18.解得b =3,a =6.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小.(25) 本小题主要考查等差数列基本概念及其通项求法,考查对数函数性质,考查归纳,推理能力以及用数学归纳法进行论证的能力.满分12分.解:(Ⅰ)设数列工{b n }的公差为d ,由题意得 b 1=1,10b 1+d2)110(10-=100. 解得 b 1=1,d =2. ∴ b n =2n -1.(Ⅱ)由b n =2n -1,知S n =lg(1+1)+lg(1+31)+…+lg(1+121-n ) =lg[(1+1)(1+31)· … ·(1+121-n )], 21lg b n +1=lg 12+n .因此要比较S n 与21lg b n +1的大小,可先比较(1+1)(1+31)· … ·(1+121-n )与12+n 的大小.取n =1有(1+1)>112+⋅,取n =2有(1+1)(1+31)>112+⋅ 由此推测(1+1)(1+31)· … ·(1+121-n )>12+n . ① 若①式成立,则由对数函数性质可判定:S n >21lgb n +1. 下面用数学归纳法证明①式.(i)当n =1时已验证①式成立.(ii)假设当n =k (k ≥1)时,①式成立,即(1+1)(1+31)· … ·(1+121-k )>12+k , 那么,当n =k +1时,(1+1)(1+31)· … ·(1+121-k )(1+1)1(21-+k ) >12+k (1+121+k ) =1212++k k (2k +2). ∵ [1212++k k (2k +2)]2-[32+k ]2 =123848422+++++k k k k k =121+k >0, ∴1212++k k (2k +2) >32+k =()112++k . 因而 (1+1)(1+31)· … ·(1+121-k )(1+121+k )>1)1(2++k . 这就是说①式当n =k +1时也成立.1由(i),(ii)知①式对任何正整数n都成立.由此证得:S n>lg b n+1.2。
厦门大学(已有10试题)

厦门大学中文系文学理论与文学评论写作2008--2009语言文学基础2008—-2009文学2007文学基础2003——2006中西文艺理论基础2000—-2002,2004--2005文艺评论写作2000——2002中国现当代文学2000-—2006文艺理论2000—-2003,2006——2007中国文学史2001—-2002中国古代文学理论2001——2005中国文学批评史2006语言理论2004中外文学2000—-2002欧美文学与比较文学2004——2006戏剧基础知识2003—-2006文艺基础知识2003——2005美学与文艺理论2000-—2002美学与艺术概论2005语言学2008——2009历史系世界近代史2002世界现代史2002中国近现代史2003——2004世界近现代史2003——2004专门史2002经济专门史2001经济史1999—-2000中国古代史2000中国通史1999—-2002通史1999中国考古学1999-—2005考古学通论1999考古学概论2000——2002中国古代史1999——2005哲学系哲学基础理论2008—-2009中西哲学史2008——2009新闻传播系新闻与传播实务2007——2010(注:2007、2010年试卷为回忆版)新闻学与传播学基础2006——2009(注:2006——2007年试卷为回忆版)新闻业务1999——2006广告学原理1996—-1997,2001-—2002公共关系原理与实务2002中国传播史1999——2005传播学理论2001——2004传播实务2004,2006广告与公关2003(回忆版)2003年传播学复试题目人类学与民族学系人类学理论方法2003人类学概论1999—-2001,2003人类学通论2008——2009文化人类学1999--2001人类学史1999--2001民族学通论2008——2009经济系宏、微观经济学2005-—2009(2005有答案)西方经济学2002,2005经济学2003—-2004,2006,2009—2010世界经济综合2000世界经济A 2000政治经济学2000综合考试(含政治经济学、宏观经济学)2002计划统计系宏、微观经济学2006,2009-2010西方经济学2002,2005经济学2003-—2004,2006,2009-2010世界经济综合2000世界经济A 2000政治经济学2000综合考试(含政治经济学、宏观经济学)2002财政系宏、微观经济学2006,2009-2010西方经济学2002,2005经济学2003—-2004,2006,2009-2010世界经济综合2000世界经济A 2000政治经济学2000综合考试(含政治经济学、宏观经济学)2002财政学1996——1998财政学综合考试1996——1998金融系金融学基础(联考)2002-—2010(2002-—2010有答案) 货币银行学综合考试1998—-2000货币银行学1998——2000货币银行学(复试)2000国际经济与贸易系宏、微观经济学2006,2009-2010西方经济学2002,2005经济学2003--2004,2006,2009-2010世界经济综合2000世界经济A 2000政治经济学2000综合考试(含政治经济学、宏观经济学)2002国际贸易1998——2002经济研究所宏、微观经济学2006,2009—2010西方经济学2002,2005经济学2003——2004,2006,2009—2010世界经济综合2000世界经济A 2000政治经济学2000综合考试(含政治经济学、宏观经济学)2002王亚南经济研究院经济学2003——2004,2006,2009-2010西方经济学2002,2005世界经济综合2000世界经济A 2000政治经济学2000综合考试(含政治经济学、宏观经济学)2002会计系会计学2000--2005会计学综合考试2000-—2002管理学与管理经济学2003——2009(注:2005—-2007年为回忆版)企业管理专业综合考试(含人力资源管理、市场营销学)1998——2002 企业管理(含管理学、财务管理)1998—-2002企业管理系管理学与管理经济学2003—-2007(注:2005--2007年为回忆版)企业管理专业综合考试(含人力资源管理、市场营销学)1998——2002 企业管理(含管理学、财务管理)1998——2002管理科学系运筹学(管理科学系)2002——2009旅游系(无此试卷)法学院法理学与民法学2000--2006法理学1995——2002,2005-—2006法理学与民事诉讼法学2003——2006法理学与宪法学2002,2005——2010(2010为回忆版)民法学1990,1998——2002民法学与商法学2003——2006民法学与宪法学2005-—2006民法学与刑法学2007,2009—-2010(2010为回忆版)综合国际法学2003-—2005国际公法与国际私法1997—-2002国际经济法1997—-2002(国际法学专业)综合考试1997——1999(民商法学、经济法学专业)综合考试2002民事诉讼法2000—-2002商法学2003经济法学1998-—2003民事诉讼法与刑事诉讼法2003宪法学与行政法学2003刑法学与刑事诉讼法学2003,2005——2006行政法与行政诉讼法学2005-—2006政治学系政治学与公共管理学2007—-2009政治学与行政学2003——2006政治学原理2002行政学2002现代政治思想(中、西)2008-—2009公共管理系政策科学与经济学2007--2009政治学与公共管理学2007——2009政治学与行政学2003—-2006(word版本)政治学原理2002行政学2002综合考试(行政管理)2002——2006(注:无管理学部分)(word版本) 社会保障专业试题2004社会学系社会学原理2005,2008—-2009社会调查研究方法2005,2008-—2009人口研究所宏、微观经济学2006,2009—2010西方经济学2002,2005经济学2003——2004,2006,2009-2010政治经济学2000综合考试(含政治经济学、宏观经济学)2002思想政治教育系政治学与公共管理学2007——2009政治学与行政学2003——2006政治学原理2002行政学2002政治学2008——2009中共党史与思想政治教育学2008——2009英文系二外法语2001,2003—-2005(注:2001年的试卷共14页,缺第4页)二外日语2003二外德语2006——2009英语基础知识2003—-2005(2005有答案)英语语言文学基础知识2002阅读及英美文学、语言学基础2003-—2009(2006-—2009有答案)(注:2006—-2009年的答案只有语言学基础部分的答案)阅读理解与英美文学基础知识1998——2000阅读理解及语言学、英美文学基础知识2001阅读与写作2002翻译与写作2003——2004写作与英汉互译2003—-2006,2009英语写作2000英汉、汉英翻译1998——2002欧洲语言文学系二外英语2003——2006,2009(2009有答案)公共外语教学部二外法语2001,2003-—2005(注:2001年的试卷共14页,缺第4页)二外日语2003二外德语2006—-2009英语基础知识2003--2005(2005有答案)英语语言文学基础知识2002阅读及英美文学、语言学基础2003——2009(2006——2009有答案)(注:2006—-2009年的答案只有语言学基础部分的答案)阅读理解与英美文学基础知识1998--2000阅读理解及语言学、英美文学基础知识2001阅读与写作2002翻译与写作2003——2004写作与英汉互译2003--2006,2009英语写作2000英汉、汉英翻译1998-—2002日本语言文学系二外英语2003—-2006,2009(2009有答案)基础日语2005-—2006综合日语2003——2006日本文学2004日本文学史2003日语语言文化2004音乐系音乐学基础2008—-2009中外音乐史2008——2009美术系设计史2007——2009设计史论2004——2006艺术概论2007——2009中外美术史2008—-2009物理系高等数学(无线电物理专业)1998,2001-—2005电子线路2001——2002,2008——2009[其中2001年试题名称为:综合考试] 普通物理学2002——2004,2006——2009(2006-—2007有答案)电动力学2002量子力学2002量子力学与电动力学2003——2004机电工程系自动控制原理2000-—2002,2004——2006,2008——2009模拟电路与数字逻辑2000-—2002微机原理2003-—2005微机原理及应用2000——2002电子线路2001--2002,2008——2009[其中2001年试题名称为:综合考试]普通物理学2002——2004,2006——2009(2006——2007有答案)电动力学2002量子力学2002量子力学与电动力学2003——2004数学科学学院综合基础Ⅱ(数学各专业)(含高等代数、抽象代数)2007,2010基础综合Ⅰ(含数学分析、实变函数、常微分方程)2005—-2006数学分析2003——2004高等代数2003化学系物理化学1990—-1991,2000—-2002,2004,2007——2009(2008有答案)高分子化学1999高分子化学与物理2008-—2010分析化学2008——2010无机化学2008—-2009化学工程与生物工程系高分子化学1999高分子化学与物理2008——2010传递过程与单元操作2008-—2009材料科学与工程系高分子化学1999高分子化学与物理2008-—2010材料科学基础2008-—2009基础化学2008——2010生命科学学院生物化学1999-—2001,2003--2010细胞生物学1994——2009微生物学2002——2010生物学2005普通生物学1994—-2000,2002——2003,2005生物学概论1999,2001,2004生态学2007——2010普通生态学2001——2010植物生态学1996——2003,2005普通生物学基础2004——2005海洋生态学1987——2002,2004——2005动物生理与海洋生态学2003普通动物学1998-—2003植物生理学1998——2002植物生理生化2003植物生物学2005——2009动物生物学2003,2005,2007-—2010动物学1993——2005海洋系生物化学1999——2001,2003-—2010细胞生物学1994-—2009微生物学2002—-2010生物学2005普通生物学1994——2000,2002—-2003,2005,2008--2009 生物学概论1999,2001,2004生态学2007——2010普通生态学2001——2010植物生态学1996-—2003,2005普通生物学基础2004——2005海洋生态学1987—-2002,2004——2005动物生理与海洋生态学2003普通动物学1998—-2003植物生理学1998——2002植物生理生化2003植物生物学2005——2009动物生物学2003,2005,2007——2010动物学1993—-2005海洋地质学2008——2009海洋管理概论2005——2009海洋科学导论2008——2009声学基础与数字电路2003——2009数学物理基础2008--2009无机化学2008——2009物理化学2008——2009环境科学中心环境评价规划与管理2001—-2009(其中2001、2002年分为规划管理与评价学两份试题)环境学导论2002—-2009环境工程学2007-2010有机化学(环境科学、环境管理专业)2002—-2006分析化学(环境科学、环境管理专业)2002——2006,2008——2009生物化学1999-—2001,2003-—2010细胞生物学1994——2009微生物学2002--2010生物学2005普通生物学1994——2000,2002——2003,2005生物学概论1999,2001,2004生态学2007——2010普通生态学2001—-2010植物生态学1996——2003,2005普通生物学基础2004——2005海洋生态学1987——2002,2004-—2005动物生理与海洋生态学2003普通动物学1998——2003植物生理学1998——2002植物生理生化2003植物生物学2005—-2009动物生物学2003,2005,2007--2010动物学1993——2005普通物理学2008——2009计算机科学系数据结构与计算机组成原理2003——2007数据结构与高级程序设计1997—-2002(2001有答案,答案只有数据结构部分)数据结构与C语言2004操作系统与编译原理1997-—2001组成原理与汇编语言2002电子工程系高等数学(无线电物理专业)1998,2001—-2005模拟电路与数字逻辑2000——2002信号与系统2007——2008(2007有答案)电路、信号与线性系统2003—-2006,2009(2006有答案)(注:2006年试卷缺电路的题,只有信号与线性系统的题,共4页,缺第3、4页)自动控制原理2000-—2002,2004——2006,2008-—2009电子线路2001——2002,2008——2009[其中2001年试题名称为:综合考试]普通物理学2002—-2004,2006-—2009(2006——2007有答案)电动力学2002量子力学2002量子力学与电动力学2003—-2004光电子技术2008——2009自动化系模拟电路与数字逻辑2000——2002自动控制原理2000——2002,2004——2006,2008-—2009电子线路2001——2002,2008——2009[其中2001年试题名称为:综合考试] 普通物理学2002——2004,2006——2009(2006-—2007有答案)电动力学2002量子力学2002量子力学与电动力学2003--2004数据结构2008—-2009通信工程系信号与系统2007-—2008(2007有答案)电路、信号与线性系统2003——2006,2009(2006有答案)(注:2006年试卷缺电路的题,只有信号与线性系统的题,共4页,缺第3、4页)电子线路2001—-2002,2008--2009[其中2001年试题名称为:综合考试]医学院生物医学研究院药物化学2008-—2009有机化学(医)2008-—2009生物化学2007——2009物理化学(医学院)2010生理学2010建筑系建筑设计2001——2002中外建筑历史2001——2002,2008——2009概念性快速建筑设计2008——2009建筑技术概论2008—-2009土木系材料力学2008——2009结构力学2008-—2009南洋研究院国际政治2003-—2009国际关系史2003——2009宏、微观经济学2006,2009—2010经济学2003——2004,2006,2009-2010西方经济学2002,2005世界经济综合2000世界经济A 2000政治经济学2000综合考试(含政治经济学、宏观经济学)2002台湾研究院宏、微观经济学2006,2009—2010经济学2003-—2004,2006,2009—2010西方经济学2002,2005世界经济综合2000世界经济A 2000政治经济学2000综合考试(含政治经济学、宏观经济学)2002 政治学与行政学2004——2005(缺案例分析)中西文艺理论基础2000-—2002,2004—-2005 文艺评论写作2000-—2002中国现当代文学2000--2005文学基础2003——2004中外文学2000—-2002世界近代史2002世界现代史2002中国古代史2000通史1999中国近现代史2002——2004世界近现代史2003——2004现代政治思想(中、西)2008--2009教育研究院普通心理学1986-—1988,2000-—2005普通教育学2000——2005教育学1985,1987——1988高等教育学专业综合考试1985——1987心理学1985,1987发展心理学与教育心理学1987—-1988 中外教育史、比较教育学1999—-2001。
1998考研数三真题及解析

1998年全国硕士研究生入学统一考试数学三试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1) 设曲线()nf x x =在点(1,1)处的切线与x 轴的交点为(,0)n ξ,则lim ()n n f ξ→∞= .(2)2ln 1x dx x -=⎰ .(3) 差分方程121050t t y y t ++-=的通解为 .(4) 设矩阵,A B 满足*28A BA BA E =-,其中100020001A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,E 为单位矩阵,*A 为A 的伴随矩阵,则B = .(5) 设1234,,,X X X X 是来自正态总体()20,2N 的简单随机样本,()2122X a X X =-+()23434b X X -.则当a = ,b = 时,统计量X 服从2χ分布,其自由度为 .二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1) 设周期函数()f x 在(),-∞+∞内可导,周期为 4.又()()11lim1,2x f f x x→--=-则曲线()y f x =在点()()5,5f 处的切线的斜率为 ( ) (A)12(B) 0 (C) 1- (D) 2- (2) 设函数()21lim ,1nn xf x x →∞+=+讨论函数()f x 的间断点,其结论为 ( )(A) 不存在间断点 (B) 存在间断点1x = (C) 存在间断点0x = (D) 存在间断点1x =-(3) 齐次线性方程组21231231230,0,0x x x x x x x x x λλλλ⎧++=⎪++=⎨⎪++=⎩的系数矩阵记为A .若存在三阶矩阵0B ≠使得0AB =,则 ( )(A) 2λ=-且||0B = (B) 2λ=-且||0B ≠(C) 1λ=且||0B = (D) 1λ=且||0B ≠ (4) 设()3n n ≥阶矩阵1111aa a a a a A a a a a a a ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦L L L M M M M L ,若矩阵A 的秩为1n -,则a 必为 ( )(A) 1 (B) 11n - (C) 1- (D) 11n -(5) 设1()F x 与2()F x 分别为随机变量1X 与2X 的分布函数.为使()12()()F x aF x bF x =-是某一变量的分布函数,在下列给定的各组数值中应取 ( )(A) 32,55a b ==- (B) 22,33a b == (C) 13,22a b =-= (D) 13,22a b ==-三、(本题满分5分)设arctan22()y xz x y e-=+,求dz 与2zx y∂∂∂.四、(本题满分5分)设(){}22,D x y xy x =+≤,求Dxdxdy .五、(本题满分6分)设某酒厂有一批新酿的好酒,如果现在(假定0t =)就售出,总收入为0()R 元.如果窖藏起来待来日按陈酒价格出售,t 年末总收入为250t R R =假定银行的年利率为r ,并以连续复利计息,试求窖藏多少年售出可使总收入的现值最大.并求0.06r =时的t 值.六、(本题满分6分)设函数()f x 在[],a b 上连续,在(,)a b 内可导,且()0.f x '≠试证存在,(,),a b ξη∈使得().()b a f e e e f b aηξη-'-=⋅'-七、(本题满分6分)设有两条抛物线21y nx n =+和21(1)1y n x n =+++,记它们交点的横坐标的绝对值为.n a(1) 求这两条抛物线所围成的平面图形的面积n S ; (2) 求级数1nn nS a ∞=∑的和.八、(本题满分7分)设函数()f x 在[1,)+∞上连续.若由曲线(),y f x =直线1,(1)x x t t ==>与x 轴所围成的平面图形绕x 轴旋转一周所形成的旋转体体积为2()()(1).3V t t f t f π⎡⎤=-⎣⎦ 试求()y f x =所满足的微分方程,并求该微分方程满足条件229x y ==的解.九、(本题满分9分)设向量1212(,,,),(,,,)T T n n a a a b b b αβ==L L 都是非零向量,且满足条件0.Tαβ=记n 矩阵.T A αβ=求:(1) 2A ;(2) 矩阵A 的特征值和特征向量.十、(本题满分7分)设矩阵101020,101A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦矩阵2(),B kE A =+其中k 为实数,E 为单位矩阵.求对角矩阵Λ,使B 与Λ相似,并求k 为何值时,B 为正定矩阵.十一、(本题满分10分)一商店经销某种商品,每周进货的数量X 与顾客对该种商品的需求量Y 是相互独立的随机变量,且都服从区间[10,20]上的均匀分布.商店每售出一单位商品可得利润1000元;若需求量超过了进货量,商店可从其他商店调剂供应,这时每单位商品获利润为500元.试计算此商店经销该种商品每周所得利润的期望值.十二、(本题满分9分)设有来自三个地区的各10名、15名和25名考生的报名表,其中女生的报名表分别为3份、7份和5份.随机地取一个地区的报名表,从中先后抽出两份.(1) 求先抽到的一份是女生表的概率p ;(2) 已知后抽到的一份是男生表,求先抽到的一份是女生表的概率q .1998年全国硕士研究生入学统一考试数学三试题解析一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1)【答案】1e【解析】曲线ny x =在点(1,1)处的切线斜率1x y ='()1nx x='=11n x n x n -===,根据点斜式,切线方程为:1(1).y n x -=-令0y =,代入1(1)y n x -=-,则11x n =-,即在x 轴上的截距为11n n ξ=-, lim ()n n f ξ→∞lim n n n ξ→∞=1lim(1)n n n →∞=-()()11lim(1)x x x --→∞=-1e=.(2)【答案】ln xC x-+【解析】由分部积分公式,2ln 1x dx x -⎰()1ln 1x dx x '⎛⎫=-- ⎪⎝⎭⎰()1ln 1x d x ⎛⎫=-- ⎪⎝⎭⎰ ln 11(ln 1)x d x x x - -+-⎰分部2ln 11x dx x x-=-+⎰ ln 11x dx x x '-⎛⎫=-- ⎪⎝⎭⎰ln 11x C x x -=--+ln x C x =-+. 【相关知识点】分部积分公式:假定()u u x =与()v v x =均具有连续的导函数,则,uv dx uv u vdx ''=-⎰⎰或者.udv uv vdu =-⎰⎰(3)【答案】51(5)()126tt y C t =-+- 【解析】首先把差分方程改写成标准形式1552t t y y t ++=,其齐次方程对应的特征方程及特征根分别为50,5,r r +==-故齐次方程的通解为(5),tt Y C C =-为常数.将方程右边的52t 改写成512t t ⋅,此处“1”不是特征根,故令非齐次方程的一个特解为,t y At B *=+从而1(1),t y A t B *+=++代入原方程,得5(1)5(),2A tB At B t ++++=56,60,2A A B =+=故 55,1272A B ==-.于是通解为 51(5)().126tt t t y Y y C t *=+=-+-(4)【答案】200040002⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦【解析】由题设 *28A BA BA E =-,由于20A =-≠,所以A 可逆.上式两边左乘A ,右乘1A -,得*11128AA BAA ABAA AA ---=-28A B AB E =-(利用公式:*1,AA A E AA E -==) 28A B AB E -=-(移项)()28A E A B E -=-(矩阵乘法的运算法则)将2A =-代入上式,整理得()14E A B E +=. 由矩阵可逆的定义,知E A +,B 均可逆,且()114B E A --=+1102002401040100021002-⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦200040002⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦.(5)【答案】11,,220100【解析】由于1234,,,X X X X 相互独立,均服从2(0,2)N ,所以由数学期望和方差的性质,得2221212(2)0,(2)122220E X X D X X -=-=⨯+⨯=,所以12(2)(0,20)X X N -:,同理34(34)(0,100)X X N -:.又因为12(2)X X -与34(34)X X -相互独立,且122)(0,1)20X X N -:344)(0,1)100X X N -:, 由2χ分布的定义,当11,20100a b ==时, 222123411(2)(34)(2)20100X X X X X χ=-+-:.即当11,20100a b ==时,X 服从2χ分布,其自由度为2. 严格地说,当10,100a b ==时,2(1)X χ:;当1,020a b ==时,2(1)X χ:也是正确的.【相关知识点】1、对于随机变量X 与Y 均服从正态分布,则X 与Y 的线性组合亦服从正态分布.若X 与Y 相互独立,由数学期望和方差的性质,有()()()E aX bY c aE X bE Y c ++=++, 22()()()D aX bY c a D X b D Y ++=+,其中,,a b c 为常数.2、定理:若2(,)X N μσ:,则(0,1)X N μσ-:.3、2χ分布的定义:若1,,n Z Z L 相互独立,且都服从标准正态分布(0,1)N ,则221~()nii Zn χ=∑.二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1)【答案】(D)【解析】根据导数定义:()0()()limx f x x f x f x x∆→+∆-'=∆0(1)(1)lim 2x f f x x →--01(1)(1)lim 2x f x f x →--=-1(1)2f '=1=- 所以 0(1)(1)(1)lim2.x f x f f x→--'==-- 因为()f x 周期为4,()f x '的周期亦是4,即()(4)f x f x ''=+,所以(5)f '(14)f '=+(1)2f '==-.所以曲线()y f x =在点()5,(5)f 处的切线的斜率为(5)f '(1)2f '==-.选(D). (2)【答案】(B)【分析】讨论由极限表示的函数的性质,应分两步走.先求出该()f x 的(分段)表达式,然后再讨论()f x 的性质.不能隔着极限号去讨论. 【解析】现求()f x 的(分段)表达式: 当1x >时,21()lim 1n n x f x x →∞+=+2122lim 1n n n n x x x ---→∞+=+()()2122lim 01lim 1n n n n n x x x --→∞-→∞+==+0=; 当1x =时,21()lim1n n x f x x →∞+=+211lim 11n n →∞+=+22=1=;当1x =-时,21()lim1n n x f x x →∞+=+()211lim 11n n →∞-=+-02=0=; 当1x <时,21()lim 1n n x f x x →∞+=+()()2lim 1lim 1n n n x x →∞→∞+=+2011n x x →+ 1x =+. 由此, 0,1,0,1,()1,1,1,1,0,1.x x f x x x x x <-⎧⎪=-⎪⎪=+<⎨⎪=⎪>⎪⎩当当当当当 即0,11,()1,1,1, 1.x x f x x x x ≤->⎧⎪=+ <⎨⎪ =⎩当或当当 再讨论函数()f x 的性质:在1x =-处,()1lim x f x +→-()1lim 1x x +→-=+11=-0=,()()1lim 10x f x f -→-=-=,所以,()()11lim lim 0x x f x f x +-→-→-==,函数()f x 在1x =-处连续,不是间断点.在1x =处,()1lim x f x +→1lim 0x +→=0=;()1lim x f x -→()1lim 1x x -→=+2=; 所以()1lim x f x +→()1lim x f x -→≠,函数()f x 在1x =处不连续,是第一类间断点.故选(B).(3)【答案】(C)【解析】方法1:由0AB =知()()3r A r B +≤,又0,0A B ≠≠,于是1()3,r A ≤<1()3r B ≤<,故0,0A B ==,即2210101011011(1)0111111A λλλλλλλλλλλλ--==--==-=--,得 1.λ=应选(C).方法2:由0AB =知()()3r A r B +≤,又0,0A B ≠≠,于是1()3,r A ≤<1()3r B ≤<,故0B =.显然,1λ=时111111111A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,有1()3,r A ≤<故应选(C). 作为选择题,只需在2λ=-与1λ=中选择一个,因而可以用特殊值代入法.评注:对于条件0AB =应当有两个思路:一是B 的列向量是齐次方程组0Ax =的解;二是秩的信息,即()()r A r B n +≤,要有这两种思考问题的意识. (4)【答案】(B) 【解析】1111100(1)1101011001a a a aa aa a a a a A aa a a a aaa a a ⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦L L L LL L u u r M M M M M M M M LL1(1)0100(2)00100001n aa a a a a a +-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦L L L u u r M M M M L 其中(1)变换:将1行乘以(-1)再分别加到其余各行;(2)变换:将其余各列分别加到第1列.由阶梯形矩阵知,当1(1)0n a +-=,即11a n=-时,有()1r A n =-,故应选(B). (5)【答案】(A)【解析】根据分布函数的性质lim ()1x F x →+∞=,即yxO 121lim ()()()()x F x F aF bF a b →+∞==+∞=+∞-+∞=-.在所给的四个选项中只有(A)满足1a b -=,故应选(A). 【相关知识点】分布函数()F x 的性质: (1) ()F x 单调不减;(2) lim ()()0,lim ()()1;x x F x F F x F →-∞→+∞=-∞==+∞=(3) ()F x 是右连续的.三、(本题满分5分) 【解析】 arctanarctan2222()()()y y xxdz ed x y x y d e--=+++[]arctan22arctan222arctan22arctan22()(arctan )122()()1(22(2)(2)y xyxy xy xy exdx ydy x y d x y exdx ydy x y d y x x xdy ydx e xdx ydy x x ex y dx y x dy ----⎡⎤=+++-⎢⎥⎣⎦⎡⎤⎢⎥=+-+⎢⎥⎢⎥+⎣⎦-⎡⎤=+-⋅⎢⎥⎣⎦=++- 由全微分与偏微分的关系可知,其中dx 的系数就是z x∂∂,即arctan (2)yxz x y ex -∂=+∂.再对y 求偏导数,得222arctanarctanarctan 222211(2).1yyyxxxzy xy x e x y ee y x yx x y x ---⎛⎫⎪∂--=-+= ⎪∂∂+ ⎪+⎪⎝⎭四、(本题满分5分)【解析】22{(,)}D x y x y x =+≤表示圆心为1,02⎛⎫ ⎪⎝⎭,半径为12的圆及其内部,画出区域D ,如右图. 方法1: {}22(,)|01,D x y x x x y x x=≤≤-≤≤-所以, 22112221x x x x Dxdxdy xdx x x x dx x xdx ---==-=-⎰⎰⎰,1x t -=,则21x t =-,2dx tdt =-,:10t →所以上式1350122210082(1)(2)4(1)43515t t t t t dt t t dt ⎛⎫=-⋅-=-=-= ⎪⎝⎭⎰⎰.方法2:引入极坐标系cos ,sin x r y r θθ= =,于是(,)|,0cos 22D r r ππθθθ⎧⎫=-≤≤≤≤⎨⎬⎩⎭,3cos cos 22222320cos cos 48cos .515Dxdxdy d r rdr d r drd ππθθπππθθθθθθ--====⎰⎰⎰⎰⎰其中倒数第二步用了华里士公式:21342cos 1253n n n d n n πθθ--=⋅⋅⋅⋅⋅-⎰L ,其中n 为大于1的正奇数.五、(本题满分6分)【分析】根据连续复利公式,在年利率为r 的情况下,现时的A (元)在t 时的总收入为()e rt R t A =,反之,t 时总收入为()R t 的现值为()()ertA t R t -=,将250t R R e=入的现值与窖藏时间t 之间的关系式,从而可用微分法求其最大值.【解析】由连续复利公式知,这批酒在窖藏t 年末售出总收入R 的现值为()e rt A t R -=,而由题设,t 年末的总收入250t R R e=,据此可列出()A t :250()eet rt rtA t R R -==,令 dA dt 250et rtd R dt -⎛⎫= ⎪⎝⎭250e 05t rtR r t -⎫==⎪⎭, 得惟一驻点 02125t t r==. 22d A dtd dA dt dt ⎛⎫= ⎪⎝⎭250e 5t rtd R r dt t ⎛⎫⎫= ⎪⎪⎭⎝⎭225500e e 55t rtt rtd d R r R r dt dt t t -⎛⎫⎫⎫=⋅-+- ⎪⎪⎪⎭⎭⎝⎭ 22255003510t rt t rtR er R e t t⎛⎫⎫=-+ ⎪⎭⎝22503510t rt R er t t ⎡⎤⎫=-⎢⎪⎭⎢⎣1232502(12.5)0r t td AR e r dt ==-<. 根据极值的第二充分条件,知:0t t =是()A t 的极大值点,又因驻点惟一,所以也是最大值点.故窖藏2125t r =年出售,总收入的现值最大.当0.06r =时, ()21250.06t =⋅100119=≈(年). 【相关知识点】极值的第二充分条件:设函数()f x 在0x 处具有二阶导数且0()0f x '=,0()0f x ''≠,当0()0f x ''<时,函数()f x 在0x 处取得极大值;当0()0f x ''>时,函数()f x 在0x 处取得极小值.六、(本题满分6分)【分析】本题要证的结论中出现两个中值点ξ和η,这种问题一般应将含有ξ和η的项分别移到等式两边后再用微分中值定理,为此本题只要证()()()()b a f b a e e f e ηξη-''-=-.【解析】方法1: 函数()f x 在[],a b 上连续,在(,)a b 内可导,满足拉格朗日中值定理的条件,对函数()f x 在[],a b 上用拉格朗日中值定理,有()()()(),.f b f a f b a a b ξξ'-=-<<又函数()f x 与xe 满足柯西中值定理的条件,将函数()f x 与xe 在[],a b 上用柯西中值定理,有()()(),b a f b f a f a b e e e ηηη'-=<<-,即()()()b a f f b f a e e eηη'-=-(). 从而有()()()baf f b a e e eηηξ''-=-(),即(),,(,)()b a f e e e a b f b a ηξξηη-'-=⋅∈'-. 方法2:题中没有限制ξη≠,因此取ξη=,即成为要去证存在(,)a b η∈使.b ae e e b aη-=-在[],a b 上对函数xe 用拉格朗日中值定理,存在(,)a b η∈使, 1.b a b a e e e e e e b a b aηη---=⋅=--即 再取ξη=,则()1()b a f e e e f b aηξη-'-==⋅'-,原题得证. 【相关知识点】1.拉格朗日中值定理:如果函数()f x 满足在闭区间[,]a b 上连续,在开区间(),a b 内可导,那么在(),a b 内至少有一点()a b ξξ<<,使等式()()()()f b f a f b a ξ'-=-成立. 2. 柯西中值定理:如果函数()f x 及()F x 满足(1) 在闭区间[,]a b 上连续; (2) 在开区间(,)a b 内可导; (3) 对任一(,)x a b ∈,()0F x '≠, 那么在(,)a b 内至少有一点ξ,使等式()()()()()()f b f a f F b F a F ξξ'-='-成立.七、(本题满分6分) 【解析】(1)由21y nx n =+与21(1)1y n x n =+++得(1)n a n n =+ 因图形关于y 轴对称,所以,所求图形的面积为220320112(1)121422(1)(1)33(1)(1)n n a n a n n S nx n x dx n n a a x dx n n n n n n n n ⎡⎤=+-+-⎢⎥+⎣⎦⎡⎤=-+=-=⎢⎥++++⎣⎦⎰⎰ (2)由(1)的结果知41411()3(1)31n n S a n n n n ==-++, 根据级数和的定义,111411414lim lim lim 1.31313n nn k n n n n k k n k S S a a k k n ∞→∞→∞→∞===⎛⎫⎡⎤==-=-= ⎪⎢⎥++⎝⎭⎣⎦∑∑∑八、(本题满分7分)【分析】本题是微分方程的几何应用问题.在题目中给出了由曲线()y f x =等围成的平面图形绕x 轴旋转一周所形成的旋转体体积()V t 与包含函数f 的一个恒等式,这正是列方程的依据.【解析】由绕x 轴旋转的旋转体体积公式得21()()tV t f x dx π=⎰,于是,依题意得221()()(1)3tf x dx t f t f ππ⎡⎤=-⎣⎦⎰,即2213()()(1)tf x dx t f t f =-⎰. 两边对t 求导,化成微分方程223()2()()f t tf t t f t '=+,其中()f t 为未知函数.按通常以x 表示自变量,y 表示未知函数()f t ,于是上述方程可写为2232,x y y xy '=-即23()2().dy y ydx x x=- 这是一阶齐次微分方程.令y ux =,有dy duu x dx dx=+⋅,则上式化为 2()32,duu x u u dx+=- 即 3(1).duxu u dx=- (*) 若0u =,则0,y ux ==不满足初始条件229x y ==,舍弃;若1u =,则,y ux x ==也不满足初始条件229x y ==,舍弃;所以,0u ≠,且1u ≠.由(*)式分离变量得3,(1)du dx u u x =-两边积分得31u Cx u-=.从而方程(*)的通解为3,y x Cx y C -=为任意常数.再代入初值,由229x y==,得1C =-,从而所求的解为 33,,(1).1xy x x y y x x -=-=≥+或【相关知识点】1. 对积分上限的函数的求导公式:若()()()()t t F t f x dx βα=⎰,()t α,()t β均一阶可导,则 [][]()()()()()F t t f t t f t ββαα'''=⋅-⋅.九、(本题满分9分)【解析】(1)对等式0Tαβ=两边取转置,有()0TTT αββα==,即0T βα=.利用0Tβα=及矩阵乘法的运算法则,有()22TT T A αβαβαβ==()00T T T T αβαβαβαβ===0=,即2A 是n 阶零矩阵.(2)设λ是A 的任一特征值,(0)ξξ≠是A 属于特征值λ的特征向量,即A ξλξ=.对上式两边左乘A 得2A ξ()()A A λξλξλλξ===2λξ=,由(1)的结果20A =,得220A λξξ==,因0ξ≠,故0λ=(n 重根),即矩阵的全部特征值为零.下面求A 的特征向量:先将A 写成矩阵形式[]1111212212221212,,,n n T n n n n n n a a b a b a b a a b a b a b A b b b a a b a b a b αβ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦L L L M L L L L. 不妨设110,0a b ≠≠,则有111211221222212221121212(0)1()01(2,,)n n n n n n n n n n n n n i a b a b a b b b b a ba b a b a b a b a b E A a a b a b a b a b a b a b b b b a i i n ---⎡⎤⎡⎤⎢⎥⎢⎥------⎢⎥⎢⎥-=÷-⎢⎥⎢⎥⎢⎥⎢⎥------⎣⎦⎣⎦⨯=LL L L u u u u u u u u u u u r L L L L LL L LL L u u u u u u u u u u u u u u u u u u u u u u u u u u u u u r 行行加到行00000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦L L L L L于是得方程组(0)0E A x -=同解方程组11220n n b x b x b x +++=L ,这样基础解系所含向量个数为(0)1n r E A n --=-.选2,,n x x L 为自由未知量,将它们的组值111(,0,,0),(0,,,0),(0,0,,)b b b L L L L 代入,可解得基础解系为12123111(,,0,,0),(,0,,,0),,(,0,0,,)n n b b b b b b ξξξ-=-=-=-L L L L则A 的属于0λ=的全部特征向量为112211n n k k k ξξξ--+++L ,其中121,,,n k k k -L 为不全为零的任意常数.十、(本题满分7分)【分析】由于B 是实对称矩阵,B 必可相似对角化,而对角矩阵Λ即B 的特征值,只要求出B 的特征值即知Λ,又因正定的充分必要条件是特征值全大于零,k 的取值亦可求出. 【解析】方法1:由2101112(2)(2)1111E A λλλλλλλλλ-----=-=-=-----, 可得A 的特征值是1232,0.λλλ===那么,kE A +的特征值是2,2,k k k ++,而2()B kE A =+的特征值是222(2),(2),.k k k ++ 又由题设知A 是实对称矩阵,则,TA A =故222()()()TTT B kE A kE A kE A B ⎡⎤⎡⎤=+=+=+=⎣⎦⎣⎦, 即B 也是实对称矩阵,故B 必可相似对角化,且222(2)000(2)000k B k k ⎡⎤+⎢⎥Λ=+⎢⎥⎢⎥⎣⎦:. 当20k k ≠-≠且时,B 的全部特征值大于零,这时B 为正定矩阵.方法2:由2101112(2)(2)1111E A λλλλλλλλλ-----=-=-=-----, 可得A 的特征值是1232,0.λλλ===因为A 是实对称矩阵,故存在可逆矩阵P 使1220P AP -⎡⎤⎢⎥=Λ=⎢⎥⎢⎥⎣⎦,即1A P P -=Λ.那么 221121()()()B kE A kPP P P P kE P ---⎡⎤=+=+Λ=+Λ⎣⎦1121()()().P kE P P kE P P kE P ---=+Λ+Λ=+Λ即12()P BP kE -=+Λ.故222(2)000(2)000k B k k ⎡⎤+⎢⎥+⎢⎥⎢⎥⎣⎦:. 当20k k ≠-≠且时,B 的全部特征值大于零,这时B 为正定矩阵.O 10 20 xy 2D 1D1020 【相关知识点】1.特征值的性质:若A 有特征值λ,则A 的特征多项式()f A 有特征值()f λ.2.矩阵正定的充要条件是特征值全大于零.十一、(本题满分10分)【解析】设Z 表示商店每周所得的利润, 当Y X ≤时,卖得利润为1000Z Y =(元); 当Y X >时,调剂了Y X -,总共得到利润1000500()500()Z X Y X X Y =+-=+(元).所以,1000, ,500(), .Y Y X Z X Y Y X ≤⎧=⎨+>⎩由题设X 与Y 都服从区间[10,20]上的均匀分布,联合概率密度为1, 1020,1020,(,)1000, x y f x y ⎧≤≤≤≤⎪=⎨⎪⎩其他.由二维连续型随机变量的数学期望定义得1212202020101010202021010()1000(,)500()(,)111000500()100100105()310(20)5(1050)2200005150014166.67().3D D D D yyE Z y f x y dxdy x y f x y dxdyy dxdy x y dxdy dy ydx dy x y dx y y dy y y dy=⋅++⋅=⋅++⋅=++=-+--=+⨯≈⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰元十二、(本题满分9分)【解析】记事件j B =“第j 次抽到的报名表是女生表”(1,2)j =,i A =“报名表是第i 个地区的”(1,2,3)i =.易见,123,,A A A 构成一个完备事件组,且1112131{}(1,2,3),3375{},{},{}.101525i P A i P B A P B A P B A =====(1) 应用全概率公式,知3111137529{}{}{}()310152590i i i p P B P A P B A ===⋅=++=∑.(2) 12{}q P B B =.需先计算概率12{}P B B 与2{}P B .对事件12B B 再次用全概率公式:3121211377852020{}{}{}()31091514252490i i i P B B P A P B B A ==⋅=⋅+⋅+⋅=∑,由“抽签原理”可知2161()()90P B P B ==, 12122()209020{}906161()P B B q P B B P B ===⋅=. 【相关知识点】1.全概率公式:如果事件1,,n A A L 构成一个完备事件组,即它们是两两互不相容,其和为Ω(总体的样本空间);并且()0,1,2,,i P A i n >=L ,则对任一事件B 有()1()(|)ni i i P B P A P B A ==∑.P。
1998数三真题标准答案及解析

⎡1 a a⎤ ⎡1− a 0 a⎤ ⎡1− a 0
a福昕⎤ 软件(C)2005-2009,版权所有,
A = ⎢⎢a
1
a⎥⎥
→
⎢ ⎢
0
1− a
a⎥⎥
→
⎢ ⎢
0
1− a
a仅供⎥⎥ 试用。
⎢⎣a a 1⎥⎦ ⎢⎣a −1 a −1 1⎥⎦ ⎢⎣ 0 0 1+ 2a⎥⎦
因而 r ( A) = 2, 所以1+ 2a = 0.
e x,
⎡
⎤
( ) ( ) ∂z
=
− arctan y
2 ye x
−
∂y
x2 + y2
− arctan yex Nhomakorabea⎢1
⎢ ⎢⎢⎣1 +
y2 x2
⎥ ⎥ ⎥ ⎥⎦
1 x
=
2y− x
− arctan y
e x.
所以
dz
=
− arctan
e
y x
⎡⎣( 2 x
+
y)
dx
+
(2y
−
x) dy⎤⎦ ,
⎡
⎤
( ) ∂2z
D (3X3 − 4X 4 ) = 9E ( X3 ) +16E ( X 4 ) = 100,
于是 X1 − 2X 2 ~ N (0,1), 3X3 − 4X 4 ~ N (0,1),
20
10
且相互独立,由 χ 2 分布的构成知:
X = ( X1 − 2X2 )2 + (3X3 − 4X4 )2 ~ χ 2 (2),
1998 年全国硕士研究生入学统一考试 经济数学三试题详解及评析
1998年考研数学三真题及全面解析

1998年全国硕士研究生入学统一考试数学三试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1) 设曲线()n f x x =在点(1,1)处的切线与x 轴的交点为(,0)n ξ,则lim ()n n f ξ→∞= .(2)2ln 1x dx x -=⎰ .(3) 差分方程121050t t y y t ++-=的通解为 .(4) 设矩阵,A B 满足*28A BA BA E =-,其中100020001A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,E 为单位矩阵,*A 为A 的伴随矩阵,则B = .(5) 设1234,,,X X X X 是来自正态总体()20,2N 的简单随机样本,()2122X a X X =-+()23434b X X -.则当a = ,b = 时,统计量X 服从2χ分布,其自由度为 .二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1) 设周期函数()f x 在(),-∞+∞内可导,周期为 4.又()()11lim1,2x f f x x→--=-则曲线()y f x =在点()()5,5f 处的切线的斜率为 ( )(A)12(B) 0 (C) 1- (D) 2- (2) 设函数()21lim,1nn xf x x →∞+=+讨论函数()f x 的间断点,其结论为 ( ) (A) 不存在间断点 (B) 存在间断点1x = (C) 存在间断点0x = (D) 存在间断点1x =-(3) 齐次线性方程组21231231230,0,0x x x x x x x x x λλλλ⎧++=⎪++=⎨⎪++=⎩的系数矩阵记为A .若存在三阶矩阵0B ≠使得0AB =,则 ( )(A) 2λ=-且||0B = (B) 2λ=-且||0B ≠(C) 1λ=且||0B = (D) 1λ=且||0B ≠ (4) 设()3n n ≥阶矩阵1111a a a a a a A aa a aaa⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 若矩阵A 的秩为1n -,则a 必为 ( ) (A) 1 (B)11n - (C) 1- (D) 11n - (5) 设1()F x 与2()F x 分别为随机变量1X 与2X 的分布函数.为使()12()()F x aF x bF x =-是某一变量的分布函数,在下列给定的各组数值中应取 ( )(A) 32,55a b ==- (B) 22,33a b == (C) 13,22a b =-= (D) 13,22a b ==-三、(本题满分5分)设arctan22()y xz x y e-=+,求dz 与2zx y∂∂∂.四、(本题满分5分)设(){}22,D x y xy x =+≤,求D.五、(本题满分6分)设某酒厂有一批新酿的好酒,如果现在(假定0t =)就售出,总收入为0()R 元.如果窖藏起来待来日按陈酒价格出售,t年末总收入为0R R =假定银行的年利率为r ,并以连续复利计息,试求窖藏多少年售出可使总收入的现值最大.并求0.06r =时的t 值.六、(本题满分6分)设函数()f x 在[],a b 上连续,在(,)a b 内可导,且()0.f x '≠试证存在,(,),a b ξη∈使得().()b a f e e e f b aηξη-'-=⋅'- 七、(本题满分6分)设有两条抛物线21y nx n =+和21(1)1y n x n =+++,记它们交点的横坐标的绝对值为.n a(1) 求这两条抛物线所围成的平面图形的面积n S ; (2) 求级数1nn nS a ∞=∑的和.八、(本题满分7分)设函数()f x 在[1,)+∞上连续.若由曲线(),y f x =直线1,(1)x x t t ==>与x 轴所围成的平面图形绕x 轴旋转一周所形成的旋转体体积为2()()(1).3V t t f t f π⎡⎤=-⎣⎦ 试求()y f x =所满足的微分方程,并求该微分方程满足条件229x y ==的解.九、(本题满分9分)设向量1212(,,,),(,,,)T T n n a a a b b b αβ== 都是非零向量,且满足条件0.Tαβ=记n 矩阵.T A αβ=求:(1) 2A ;(2) 矩阵A 的特征值和特征向量.十、(本题满分7分)设矩阵101020,101A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦矩阵2(),B kE A =+其中k 为实数,E 为单位矩阵.求对角矩阵Λ,使B 与Λ相似,并求k 为何值时,B 为正定矩阵.十一、(本题满分10分)一商店经销某种商品,每周进货的数量X 与顾客对该种商品的需求量Y 是相互独立的随机变量,且都服从区间[10,20]上的均匀分布.商店每售出一单位商品可得利润1000元;若需求量超过了进货量,商店可从其他商店调剂供应,这时每单位商品获利润为500元.试计算此商店经销该种商品每周所得利润的期望值.十二、(本题满分9分)设有来自三个地区的各10名、15名和25名考生的报名表,其中女生的报名表分别为3份、7份和5份.随机地取一个地区的报名表,从中先后抽出两份.(1) 求先抽到的一份是女生表的概率p ;(2) 已知后抽到的一份是男生表,求先抽到的一份是女生表的概率q .1998年全国硕士研究生入学统一考试数学三试题解析一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1)【答案】1e【解析】曲线n y x =在点(1,1)处的切线斜率1x y ='()1nx x ='=11n x n x n -===,根据点斜式,切线方程为:1(1).y n x -=-令0y =,代入1(1)y n x -=-,则11x n =-,即在x 轴上的截距为11n n ξ=-, lim ()n n f ξ→∞lim n n n ξ→∞=1lim(1)n n n →∞=-()()11lim(1)x x x --→∞=-1e =. (2)【答案】ln xC x-+ 【解析】由分部积分公式,2ln 1x dx x -⎰()1ln 1x dx x '⎛⎫=-- ⎪⎝⎭⎰()1ln 1x d x ⎛⎫=-- ⎪⎝⎭⎰ ln 11(ln 1)x d x x x - -+-⎰分部2ln 11x dx x x-=-+⎰ ln 11x dx x x '-⎛⎫=-- ⎪⎝⎭⎰ln 11x C x x -=--+ln xC x =-+.【相关知识点】分部积分公式:假定()u u x =与()v v x =均具有连续的导函数,则,uv dx uv u vdx ''=-⎰⎰或者.udv uv vdu =-⎰⎰(3)【答案】51(5)()126tt y C t =-+- 【解析】首先把差分方程改写成标准形式1552t t y y t ++=,其齐次方程对应的特征方程及特征根分别为50,5,r r +==-故齐次方程的通解为(5),t t Y C C =-为常数.将方程右边的52t 改写成512t t ⋅,此处“1”不是特征根,故令非齐次方程的一个特解为,t y At B *=+从而1(1),t y A t B *+=++代入原方程,得5(1)5(),2A tB At B t ++++=56,60,2A A B =+=故 55,1272A B ==-. 于是通解为 51(5)().126tt t t y Y y C t *=+=-+- (4)【答案】200040002⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦【解析】由题设 *28A BA BA E =-,由于20A =-≠,所以A 可逆.上式两边左乘A ,右乘1A -,得*11128AA BAA ABAA AA ---=-28A B AB E =-(利用公式:*1,AA A E AA E -==) 28A B AB E -=-(移项)()28A E A B E -=-(矩阵乘法的运算法则)将2A =-代入上式,整理得()14E A B E +=. 由矩阵可逆的定义,知E A +,B 均可逆,且()114B E A --=+11002002401040100021002-⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦200040002⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦.(5)【答案】11,,220100【解析】由于1234,,,X X X X 相互独立,均服从2(0,2)N ,所以由数学期望和方差的性质,得2221212(2)0,(2)122220E X X D X X -=-=⨯+⨯=,所以12(2)(0,20)X X N - ,同理34(34)(0,100)X X N - .又因为12(2)X X -与34(34)X X -相互独立,且122)(0,1)X X N - 344)(0,1)X X N - , 由2χ分布的定义,当11,20100a b ==时, 222123411(2)(34)(2)20100X X X X X χ=-+- .即当11,20100a b ==时,X 服从2χ分布,其自由度为2. 严格地说,当10,100a b ==时,2(1)X χ ;当1,020a b ==时,2(1)X χ 也是正确的. 【相关知识点】1、对于随机变量X 与Y 均服从正态分布,则X 与Y 的线性组合亦服从正态分布.若X 与Y 相互独立,由数学期望和方差的性质,有()()()E aX bY c aE X bE Y c ++=++,22()()()D aX bY c a D X b D Y ++=+,其中,,a b c 为常数.2、定理:若2(,)X N μσ ,则(0,1)X N μσ- .3、2χ分布的定义:若1,,n Z Z 相互独立,且都服从标准正态分布(0,1)N ,则221~()nii Zn χ=∑.二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1)【答案】(D)【解析】根据导数定义:()0()()limx f x x f x f x x∆→+∆-'=∆0(1)(1)lim 2x f f x x →--01(1)(1)lim 2x f x f x →--=-1(1)2f '=1=- 所以 0(1)(1)(1)lim2.x f x f f x→--'==-- 因为()f x 周期为4,()f x '的周期亦是4,即()(4)f x f x ''=+, 所以(5)f '(14)f '=+(1)2f '==-.所以曲线()y f x =在点()5,(5)f 处的切线的斜率为(5)f '(1)2f '==-.选(D). (2)【答案】(B)【分析】讨论由极限表示的函数的性质,应分两步走.先求出该()f x 的(分段)表达式,然后再讨论()f x 的性质.不能隔着极限号去讨论. 【解析】现求()f x 的(分段)表达式: 当1x >时,21()lim 1n n x f x x →∞+=+2122lim 1n n n n x x x ---→∞+=+()()2122lim 01lim 1n nn n n x x x --→∞-→∞+==+0=; 当1x =时,21()lim1n n x f x x →∞+=+211lim 11n n →∞+=+22=1=; 当1x =-时,21()lim1n n x f x x →∞+=+()211lim 11n n →∞-=+-02=0=; 当1x <时,21()lim 1n n x f x x →∞+=+()()2lim 1lim 1n n n x x→∞→∞+=+2011nx x →+ 1x =+. 由此, 0,1,0,1,()1,1,1,1,0,1.x x f x x x x x <-⎧⎪=-⎪⎪=+<⎨⎪=⎪>⎪⎩当当当当当 即0,11,()1,1,1, 1.x x f x x x x ≤->⎧⎪=+ <⎨⎪ =⎩当或当当再讨论函数()f x 的性质:在1x =-处,()1lim x f x +→-()1lim 1x x +→-=+11=-0=,()()1lim 10x f x f -→-=-=,所以,()()11lim lim 0x x f x f x +-→-→-==,函数()f x 在1x =-处连续,不是间断点.在1x =处,()1lim x f x +→1lim 0x +→=0=;()1lim x f x -→()1lim 1x x -→=+2=; 所以()1lim x f x +→()1lim x f x -→≠,函数()f x 在1x =处不连续,是第一类间断点.故选(B). (3)【答案】(C)【解析】方法1:由0AB =知()()3r A r B +≤,又0,0A B ≠≠,于是1()3,r A ≤<1()3r B ≤<,故0,0A B ==,即2210101011011(1)0111111A λλλλλλλλλλλλ--==--==-=--,得 1.λ=应选(C).方法2:由0AB =知()()3r A r B +≤,又0,0A B ≠≠,于是1()3,r A ≤<1()3r B ≤<,故0B =.显然,1λ=时111111111A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,有1()3,r A ≤<故应选(C). 作为选择题,只需在2λ=-与1λ=中选择一个,因而可以用特殊值代入法.评注:对于条件0AB =应当有两个思路:一是B 的列向量是齐次方程组0Ax =的解;二是秩的信息,即()()r A r B n +≤,要有这两种思考问题的意识. (4)【答案】(B) 【解析】1111100(1)110101101a a a aa aa a a a a A aa a a a aaaa a ⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦1(1)0100(2)00100001n aa a a a a a +-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦其中(1)变换:将1行乘以(-1)再分别加到其余各行;(2)变换:将其余各列分别加到第1列.由阶梯形矩阵知,当1(1)0n a +-=,即11a n=-时,有()1r A n =-,故应选(B). (5)【答案】(A)【解析】根据分布函数的性质lim ()1x F x →+∞=,即121lim ()()()()x F x F aF bF a b →+∞==+∞=+∞-+∞=-.在所给的四个选项中只有(A)满足1a b -=,故应选(A). 【相关知识点】分布函数()F x 的性质:(1) ()F x 单调不减;(2) lim ()()0,lim ()()1;x x F x F F x F →-∞→+∞=-∞==+∞=(3) ()F x 是右连续的.三、(本题满分5分) 【解析】 arctanarctan2222()()()y y xxdz ed x y x y d e--=+++[]arctan22arctan222arctan22arctan22()(arctan )122()()1(22(2)(2)y xy xyxy xy exdx ydy x y d x y exdx ydy x y d y x x xdy ydx e xdx ydy x x ex y dx y x dy ----⎡⎤=+++-⎢⎥⎣⎦⎡⎤⎢⎥=+-+⎢⎥⎢⎥+⎣⎦-⎡⎤=+-⋅⎢⎥⎣⎦=++- 由全微分与偏微分的关系可知,其中dx 的系数就是z x∂∂,即arctan (2)yxz x y e x -∂=+∂.再对y 求偏导数,得222arctanarctanarctan 222211(2).1yyyxxxzy xy x e x y ee y x yx x y x ---⎛⎫⎪∂--=-+= ⎪∂∂+ ⎪+⎪⎝⎭四、(本题满分5分)【解析】22{(,)}D x y x y x =+≤表示圆心为1,02⎛⎫⎪⎝⎭,半径为 12的圆及其内部,画出区域D ,如右图. 方法1:{(,)|01,D x y x y =≤≤≤≤所以, 1102D===⎰⎰⎰,t ,则21x t =-,2dx tdt =-,:10t →所以上式1350122210082(1)(2)4(1)43515t t t t t dt t t dt ⎛⎫=-⋅-=-=-= ⎪⎝⎭⎰⎰.方法2:引入极坐标系cos ,sin x r y r θθ= =,于是(,)|,0cos 22D r r ππθθθ⎧⎫=-≤≤≤≤⎨⎬⎩⎭,3cos cos 2222232048cos .515Dd r drd ππθθπππθθθθ--====⎰⎰⎰⎰⎰其中倒数第二步用了华里士公式:21342cos 1253n n n d n n πθθ--=⋅⋅⋅⋅⋅-⎰,其中n 为大于1的正奇数.五、(本题满分6分)【分析】根据连续复利公式,在年利率为r 的情况下,现时的A (元)在t 时的总收入为()e rt R t A =,反之,t 时总收入为()R t 的现值为()()ertA t R t -=,将0R R =入的现值与窖藏时间t 之间的关系式,从而可用微分法求其最大值.【解析】由连续复利公式知,这批酒在窖藏t 年末售出总收入R 的现值为()e rt A t R -=,而由题设,t年末的总收入0R R =,据此可列出()A t :0()ert rtA t R R -==,令 dAdt 0rtd R dt ⎛⎫= ⎪⎝⎭00rtR r ⎫=-=⎪⎭, 得惟一驻点 02125t t r ==. 22d A dt d dA dt dt ⎛⎫= ⎪⎝⎭0rtd R r dt ⎛⎫⎫=- ⎪⎪⎭⎝⎭00rtrtd d R r R r dt dt ⎛⎫⎫⎫=⋅-+- ⎪⎪⎪⎭⎭⎝⎭200rt rtR r R ⎛⎫⎫=-+ ⎪⎭⎝20rt R r ⎡⎤⎫=-⎢⎪⎭⎢⎣ 01232502(12.5)0rt td A Re r dt ==-<.根据极值的第二充分条件,知:0t t =是()A t 的极大值点,又因驻点惟一,所以也是最大值点.故窖藏2125t r=年出售,总收入的现值最大.当0.06r =时, ()21250.06t =⋅100119=≈(年). 【相关知识点】极值的第二充分条件:设函数()f x 在0x 处具有二阶导数且0()0f x '=, 0()0f x ''≠,当0()0f x ''<时,函数()f x 在0x 处取得极大值;当0()0f x ''>时,函数()f x 在0x 处取得极小值.六、(本题满分6分)【分析】本题要证的结论中出现两个中值点ξ和η,这种问题一般应将含有ξ和η的项分别移到等式两边后再用微分中值定理,为此本题只要证()()()()b a f b a e e f e ηξη-''-=-.【解析】方法1: 函数()f x 在[],a b 上连续,在(,)a b 内可导,满足拉格朗日中值定理的条件,对函数()f x 在[],a b 上用拉格朗日中值定理,有()()()(),.f b f a f b a a b ξξ'-=-<<又函数()f x 与xe 满足柯西中值定理的条件,将函数()f x 与xe 在[],a b 上用柯西中值定理,有()()(),b a f b f a f a b e e e ηηη'-=<<-,即()()()b a f f b f a e e eηη'-=-(). 从而有()()()baf f b a e e e ηηξ''-=-(),即(),,(,)()b a f e e e a b f b aηξξηη-'-=⋅∈'-.方法2:题中没有限制ξη≠,因此取ξη=,即成为要去证存在(,)a b η∈使.b ae e e b aη-=- 在[],a b 上对函数xe 用拉格朗日中值定理,存在(,)a b η∈使, 1.b a b a e e e e e e b a b aηη---=⋅=--即 再取ξη=,则()1()b a f e e e f b aηξη-'-==⋅'-,原题得证.如果函数()f x 满足在闭区间[,]a b 上连续,在开区间(),a b 内可导,那么在(),a b 内至少有一点()a b ξξ<<,使等式()()()()f b f a f b a ξ'-=-成立. 2. 柯西中值定理:如果函数()f x 及()F x 满足(1) 在闭区间[,]a b 上连续; (2) 在开区间(,)a b 内可导; (3) 对任一(,)x a b ∈,()0F x '≠, 那么在(,)a b 内至少有一点ξ,使等式()()()()()()f b f a f F b F a F ξξ'-='-成立.七、(本题满分6分) 【解析】(1)由21y nx n =+与21(1)1y n x n =+++得n a = 因图形关于y 轴对称,所以,所求图形的面积为220320112(1)121422(1)(1)33nna n a n n S nx n x dx n n a a x dx n n n n ⎡⎤=+-+-⎢⎥+⎣⎦⎡⎤=-+=-=⎢⎥++⎣⎦⎰⎰(2)由(1)的结果知41411()3(1)31n n S a n n n n ==-++, 根据级数和的定义,111411414lim lim lim 1.31313n nn k n n n n k k n k S S a a k k n ∞→∞→∞→∞===⎛⎫⎡⎤==-=-= ⎪⎢⎥++⎝⎭⎣⎦∑∑∑八、(本题满分7分)【分析】本题是微分方程的几何应用问题.在题目中给出了由曲线()y f x =等围成的平面图形绕x 轴旋转一周所形成的旋转体体积()V t 与包含函数f 的一个恒等式,这正是列方程的依据.【解析】由绕x 轴旋转的旋转体体积公式得21()()tV t f x dx π=⎰,于是,依题意得221()()(1)3tf x dx t f t f ππ⎡⎤=-⎣⎦⎰,即2213()()(1)tf x dx t f t f =-⎰. 两边对t 求导,化成微分方程223()2()()f t tf t t f t '=+,其中()f t 为未知函数.按通常以x 表示自变量,y 表示未知函数()f t ,于是上述方程可写为2232,x y y xy '=-即23()2().dy y y dx x x=- 这是一阶齐次微分方程.令y ux =,有dy duu x dx dx=+⋅,则上式化为 2()32,duu x u u dx+=- 即 3(1).duxu u dx=- (*) 若0u =,则0,y ux ==不满足初始条件229x y ==,舍弃;若1u =,则,y ux x ==也不满足初始条件229x y ==,舍弃;所以,0u ≠,且1u ≠.由(*)式分离变量得3,(1)du dxu u x=-两边积分得31u Cx u -=.从而方程(*)的通解为 3,y x Cx y C -=为任意常数.再代入初值,由229x y==,得1C =-,从而所求的解为 33,,(1).1xy x x y y x x-=-=≥+或 【相关知识点】1. 对积分上限的函数的求导公式:若()()()()t t F t f x dx βα=⎰,()t α,()t β均一阶可导,则 [][]()()()()()F t t f t t f t ββαα'''=⋅-⋅.九、(本题满分9分) 【解析】(1)对等式0Tαβ=两边取转置,有()0TT T αββα==,即0T βα=.利用0Tβα=及矩阵乘法的运算法则,有()22TT T A αβαβαβ==()00T T T T αβαβαβαβ===0=,即2A 是n 阶零矩阵.(2)设λ是A 的任一特征值,(0)ξξ≠是A 属于特征值λ的特征向量,即A ξλξ=.对上式两边左乘A 得2A ξ()()A A λξλξλλξ===2λξ=,由(1)的结果20A =,得220A λξξ==,因0ξ≠,故0λ=(n 重根),即矩阵的全部特征值为零.下面求A 的特征向量:先将A 写成矩阵形式[]1111212212221212,,,n n Tn n n n n n a a b a b a b a a b a b a b A b b b a a b a b a b αβ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦.不妨设110,0a b ≠≠,则有111211221222212221121212(0)1()01(2,,)n n n n n n n n n n n n n i a b a b a b b b b a b a b a b a b a b a b E A a a b a b a b a b a b a b b b b a i i n ---⎡⎤⎡⎤⎢⎥⎢⎥------⎢⎥⎢⎥-=÷-⎢⎥⎢⎥⎢⎥⎢⎥------⎣⎦⎣⎦⨯= 行行加到行00000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦于是得方程组(0)0E A x -=同解方程组11220n n b x b x b x +++= ,这样基础解系所含向量个数为(0)1n r E A n --=-.选2,,n x x 为自由未知量,将它们的组值111(,0,,0),(0,,,0),(0,0,,)b b b 代入,可解得基础解系为12123111(,,0,,0),(,0,,,0),,(,0,0,,)n n b b b b b b ξξξ-=-=-=-则A 的属于0λ=的全部特征向量为112211n n k k k ξξξ--+++ ,其中121,,,n k k k - 为不全为零的任意常数.十、(本题满分7分)【分析】由于B 是实对称矩阵,B 必可相似对角化,而对角矩阵Λ即B 的特征值,只要求出B 的特征值即知Λ,又因正定的充分必要条件是特征值全大于零,k 的取值亦可求出. 【解析】方法1:由2101112(2)(2)1111E A λλλλλλλλλ-----=-=-=-----,可得A 的特征值是1232,0.λλλ===那么,kE A +的特征值是2,2,k k k ++,而2()B kE A =+的特征值是222(2),(2),.k k k ++ 又由题设知A 是实对称矩阵,则,T A A =故222()()()TTTB kE A kE A kE A B ⎡⎤⎡⎤=+=+=+=⎣⎦⎣⎦, 即B 也是实对称矩阵,故B 必可相似对角化,且222(2)000(2)000k B k k ⎡⎤+⎢⎥Λ=+⎢⎥⎢⎥⎣⎦. 当20k k ≠-≠且时,B 的全部特征值大于零,这时B 为正定矩阵.方法2:由2101112(2)(2)1111E A λλλλλλλλλ-----=-=-=-----,可得A 的特征值是1232,0.λλλ===因为A 是实对称矩阵,故存在可逆矩阵P 使1220P AP -⎡⎤⎢⎥=Λ=⎢⎥⎢⎥⎣⎦,即1A P P -=Λ.那么 221121()()()B kE A kPP P P P kE P ---⎡⎤=+=+Λ=+Λ⎣⎦1121()()().P kE P P kE P P kE P ---=+Λ+Λ=+Λ即12()P BP kE -=+Λ.故222(2)000(2)000k B k k ⎡⎤+⎢⎥+⎢⎥⎢⎥⎣⎦. 当20k k ≠-≠且时,B 的全部特征值大于零,这时B 为正定矩阵.【相关知识点】1.特征值的性质:若A 有特征值λ,则A 的特征多项式()f A 有特征值()f λ.2.矩阵正定的充要条件是特征值全大于零.十一、(本题满分10分)【解析】设Z 表示商店每周所得的利润, 当Y X ≤时,卖得利润为1000Z Y =(元); 当Y X >时,调剂了Y X -,总共得到利润1000500()500()Z X Y X X Y =+-=+(元).所以,1000, ,500(), .Y Y X Z X Y Y X ≤⎧=⎨+>⎩由题设X 与Y 都服从区间[10,20]上的均匀分布,联合概率密度为1, 1020,1020,(,)1000, x y f x y ⎧≤≤≤≤⎪=⎨⎪⎩其他.由二维连续型随机变量的数学期望定义得1212202020101010202021010()1000(,)500()(,)111000500()100100105()310(20)5(1050)2200005150014166.67().3D D D D yyE Z y f x y dxdy x y f x y dxdyy dxdy x y dxdy dy ydx dy x y dxy y dy y y dy=⋅++⋅=⋅++⋅=++=-+--=+⨯≈⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰元十二、(本题满分9分)【解析】记事件j B =“第j 次抽到的报名表是女生表”(1,2)j =,i A =“报名表是第i 个地区的”(1,2,3)i =.易见,123,,A A A 构成一个完备事件组,且1112131{}(1,2,3),3375{},{},{}.101525i P A i P B A P B A P B A =====(1) 应用全概率公式,知3111137529{}{}{}()310152590i i i p P B P A P B A ===⋅=++=∑. (2) 12{}q P B B =.需先计算概率12{}P B B 与2{}P B .对事件12B B 再次用全概率公式:3121211377852020{}{}{}()31091514252490i i i P B B P A P B B A ==⋅=⋅+⋅+⋅=∑, 由“抽签原理”可知2161()()90P B P B ==, 12122()209020{}906161()P B B q P B B P B ===⋅=. 【相关知识点】1.全概率公式:如果事件1,,n A A 构成一个完备事件组,即它们是两两互不相容,其和为Ω(总体的样本空间);并且()0,1,2,,i P A i n >= ,则对任一事件B 有()1()(|)ni i i P B P A P B A ==∑.。
考研数学历年真题(1998-2007)年数学一参考答案

分离变量,得
dy y
dx 1 x2
,
两边积分,得 ln y arctan x C ,即 y C1earctan x.
代入初始条件 y(0) , 得 y
0
C earctan 0 1
C1
.
所以,
y
earctan x
.
故
y(1) earctan x earctan1 e 4 .
(3) 若 l 0, 称在该极限过程中 (x) 是 (x) 的高阶无穷小,记为 (x) o (x) .
若
lim
( (
x) x)
不存在(不为
),称
(
x),
(
x)
不可比较.
(4)【答案】(A)
【解析】设
L1
:
x a1
a3 a2
y b3 b1 b2
z c3 c1 c2
, L2
:
x a1 a2 a3
当 x 1或 x e2 时, fX (x) 0 ;
(2, 1) 2
O
12
e2 x
当1 x e2 时, fX (x)
f (x, y)dy
1 x
1dy
1
.
0 2 2x
故
fX
(2)
1. 4
二、选择题(本题共5小题,每小题3分,共15分.) (1)【答案】(A)
【解析】为变限所定义的函数求导数,作积分变量代换 u x2 t 2 ,
(x2 x 2)x(1 x2 ),
f
(x)
( x 2
(
x
2
x x
2)x(x2 1), 2)x(1 x2 ),
(x2 x 2)x(x2 1),
1998考研数学一真题及答案解析

关系式 y = y v .
六、(本题满分7分)
计算
axdydz (z (x2 y2
a)2 z2)
dxdy
12
,
其中
为下半球面
z
a2 x2 y2 的上侧, a 为大
化为椭圆柱面方程 2 4 2 4 ,求 a, b 的值和正交矩阵 P .
十一、(本题满分4分)
设 A 是 n 阶矩阵,若存在正整数 k ,使线性方程组 Ak x 0 有解向量 ,且 Ak1 0 , 证明:向量组 , A ,, Ak1 是线性无关的.
十二、(本题满分5分)
区域 D 上服从均匀分布,则 ( X ,Y ) 关于 X 的边缘概率密度在 x 2 处的值为 _ .
二、选择题(本题共5小题,每小题3分,共15分.)
(1) 设 f (x) 连续,则 d x tf (x2 t2 )dt
dx 0
(A) xf (x2 )
(B) xf (x2 )
(C) 2xf (x2 )
y
y ( x
y)
f (xy) y(x y)
x
y
yf (xy) (x y) y(x y).
评注:本题中, f , 中的中间变量均为一元,因此本题实质上是一元复合函数的求导,只要注
意到对 x 求导时, y 视为常数;对 y 求导时, x 视为常数就可以了. (3)【答案】12a
(A) 相交于一点
(B) 重合
()
资料搜集 QQ1836989006 微信 1836989006
98年全国高校招生数学统考试题-数学试题

98年全国高校招生数学统考试题-数学试题一、选择题:本大题共15小题;第(1)-(10)题每小题4分,第(11)-(15)题每小题5分,共65分。
在每小题给出的四项选项中,只有一项是符合题目要求的。
(1)sin600°的值是(A)1/2 (B)-1/2(C)/2(D)-/2(2)函数y=a|x|(a>1)的图象是(3)曲线的极坐标方程ρ=4sinθ化成直角坐标方程式为(A)x2+(y+2)2=4(B)x2+(y-2)2=4(C)(x-2)2+y2=4(D)(x+2)2+y2=4(4)两条直线A1x+B1y+C1=0,A2x+B2y+C2=0垂直的充要条件是(A)A1A2+B1B2=0(B)A1A2-B1B2=0(C)A1A2/B1B2=-1(D)B1B2/A1A2=1(5)函数f(x)=1/x(x≠0)的反函数f-1(x)=(A)x(x≠0)(B)1/x(x≠0)(C)-x(x≠0)(D)-1/x(x≠0)(6)已知点P(sinα-cosα,tgα)在第一象限,则[0,2π)内α的取值范围是(A)(π/2,3π/4)∪(π,5π/4) (B)(π/4,π/2)∪(π,5π/4)(C)(π/2,3π/4)∪(5π/2,3π/2) (D)(π/4,π/2)∪(3π/4,π)(7)已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面积展开图扇形的圆心角为(A)120° (B)150° (C)180° (D)240°(8)复数-i的一个立方根是i,它的另外两个立方根是(A)/2±(1/2)i(B)-/2±(1/2)i(C)±/2+(1/2)i(D)±/2-(1/2)i(9)如果棱台的两底面积分别是S,S‘,中截面的面积是S0,那么(A)2=+(B)S0=(C)2SO=S+S’(D)S02=2S‘。
1998年高考数学试题及其解析

1998年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试120分钟.第Ⅰ卷(选择题共65分)一.选择题:本大题共15小题;第1—10题每小题4分,第11— 15题每小题5分,共65分.在每小题给出的四个选项中,只有一项是符合题目要求的(1) sin600º( )(A)21 (B) -21(C) 23 (D) -23(2) 函数y =a |x |(a >1)的图像是( )(3) 曲线的极坐标方程ρ=4sin θ化成直角坐标方程为( )(A) x 2+(y +2)2=4 (B) x 2+(y -2)2=4 (C) (x -2)2+y 2=4 (D) (x +2)2+y 2=4 (4) 两条直线A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0垂直的充要条件是( )(A) A 1A 2+B 1B 2=0 (B) A 1A 2-B 1B 2=0 (C)12121-=B B A A (D) 12121=A A BB (5) 函数f (x )=x1( x ≠0)的反函数f -1(x )= ( ) (A) x (x ≠0) (B) x 1(x ≠0) (C) -x (x ≠0) (D) -x1(x ≠0)(6) 已知点P (sin α-cos α,tg α)在第一象限,则在)20[π,内α的取值是 ( )(A) (432ππ,)∪(45ππ,) (B) (24ππ,)∪(45ππ,) (C) (432ππ,)∪(2345ππ,) (D) (24ππ,)∪(ππ,43) (7) 已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为 ( )(A) 120º (B) 150º (C) 180º (D) 240º (8) 复数-i 的一个立方根是i ,它的另外两个立方根是( )(A)2123± i (B) -2123± i (C) ±2123+ i (D) ±2123-i (9) 如果棱台的两底面积分别是S ,S ′,中截面的面积是S 0,那么( )(A) 2S S S '+=0 (B) S 0=S S '(C) 2 S 0=S +S ′ (D) S S S '=22(10) 向高为H 的水瓶中注水,注满为止,如果注水量V 与水深h 的函数关系的图像如下图所示,那么水瓶的形状是( )(11) 3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士.不同的分配方法共有( )(A) 90种 (B) 180种 (C) 270种 (D) 540种(12) 椭圆31222y x +=1的焦点为F 1和F 2,点P 在椭圆上,如果线段PF 1的中点在y 轴上,那么|P F 1|是|P F 2|的( )(A) 7倍 (B) 5倍 (C) 4倍 (D) 3倍 (13) 球面上有3个点,其中任意两点的球面距离都等于大圆周长的61,经过这3个点的小圆的周长为4π,那么这个球的半径为( )(A) 43 (B)23 (C) 2 (D) 3(14) 一个直角三角形三内角的正弦值成等比数列,其最小内角为( )(A) arccos215- (B) arcsin215- (C) arccos251- (D) arcsin 251-(15) 在等比数列{a n }中,a 1>1,且前n 项和S n 满足∞→n lim S n =11a ,那么a 1的取值范围是( ) (A)(1,+∞) (B)(1,4) (C) (1,2) (D)(1,2)第Ⅱ卷(非选择题共85分)二、填空题:本大题共4小题;每小题4分,共16分.把答案填在题中横线上.16.设圆过双曲线116922=-y x 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是_________17.(x +2)10(x 2-1)的展开式中x 10的系数为____________(用数字作答)18.如图,在直四棱柱A 1B 1C 1 D 1-ABCD 中,当底面四边形ABCD 满足条件____________时,有A 1 C ⊥B 1 D 1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)19.关于函数f (x )=4sin(2x +3π)(x ∈R ),有下列命题: ①由f (x 1)= f (x 2)=0可得x 1-x 2必是π的整数倍; ②y =f (x )的表达式可改写为y =4cos(2x -6π); ③y =f (x )的图像关于点(-6π,0)对称; ④y =f (x )的图像关于直线x =-6π对称.其中正确的命题的序号是_______ (注:把你认为正确的命题的序号都.填上.) 三、解答题:本大题共6小题;共69分.解答应写出文字说明,证明过程或演算步骤. (20)(本小题满分10分)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,设a +c =2b ,A -C=3π.求sin B 的值. 以下公式供解题时参考: sin θ+sin ϕ =2sin2ϕθ+cos2ϕθ-, sin θ-sin ϕ=2cos2ϕθ+sin2ϕθ-,cos θ+cos ϕ=2cos 2ϕθ+cos 2ϕθ-, cos θ-cos ϕ=-2sin 2ϕθ+sin 2ϕθ-.(21)(本小题满分11分)如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A,B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=17,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.(22)(本小题满分12分)如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米.问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计).(23)(本小题满分12分)已知斜三棱柱ABC -A 1 B 1 C 1的侧面A 1 ACC 1与底面ABC 垂直,∠ABC =90º,BC =2,AC=23,且AA 1 ⊥A 1C ,AA 1= A 1 C .Ⅰ.求侧棱A 1A 与底面ABC 所成角的大小;Ⅱ.求侧面A 1 ABB 1 与底面ABC 所成二面角的大小; Ⅲ.求顶点C 到侧面A 1 ABB 1的距离.(24)(本小题满分12分)设曲线C 的方程是y =x 3-x ,将C 沿x 轴、y 轴正向分别平行移动t 、s 单位长度后得曲线C 1.Ⅰ.写出曲线C 1的方程; Ⅱ.证明曲线C 与C 1关于点A (3t ,2s)对称; Ⅲ.如果曲线C 与C 1有且仅有一个公共点,证明s =43t -t 且t ≠0.(25)(本小题满分12分)已知数列{b n }是等差数列,b 1=1,b 1+b 2+…+b 10=145. Ⅰ.求数列{b n }的通项b n ; Ⅱ.设数列{a n }的通项a n =log a (1+nb 1)(其中a >0,且a ≠1),记S n 是数列{a n }的前n 项和.试比较S n 与31log a b n +1的大小,并证明你的结论.1998年普通高等学校招生全国统一考试数学试题(理工农医类)参考答案一、选择题(本题考查基本知识和基本运算.)1.D 2.B 3.B 4.A 5.B 6.B 7.C 8.D 9.A 10.B 11.D 12.A 13.B 14.B 15.D 二、填空题(本题考查基本知识和基本运算.)16.31617.179 18.AC ⊥BD ,或任何能推导出这个条件的其他条件.例如ABCD 是正方形,菱形等 19.②,③ 三、解答题20.本小题考查正弦定理,同角三角函数基本公式,诱导公式等基础知识,考查利用三角公式进行恒等变形的技能及运算能力.解:由正弦定理和已知条件a +c =2b 得 sin A +sin C =2sin B .由和差化积公式得2sin 2C A +cos 2CA -=2sinB . 由A +B +C =π 得 sin 2C A +=cos 2B,又A -C =3π 得 23cos 2B=sin B ,所以23cos 2B =2sin 2B cos 2B. 因为0<2B <2π,cos 2B≠0, 所以sin2B =43, 从而cos2B =4132sin 12=-B所以sinB=83941323=⨯.21.本小题主要考查根据所给条件选择适当的坐标系,求曲线方程的解析几何的基本思想.考查抛物线的概念和性质,曲线与方程的关系以及综合运用知识的能力.解法一:如图建立坐标系,以l 1为x 轴,MN 的垂直平分线为y 轴,点O 为坐标原点.依题意知:曲线段C 是以点N 为焦点,以l 2为准线的抛物线的一段,其中A ,B 分别为C 的端点.设曲线段C 的方程为y 2=2px (p >0),(x A ≤x ≤x B ,y >0),其中x A ,x B 分别为A ,B 的横坐标,p =|MN |. 所以 M (2p -,0),N (2p,0). 由|AM |= 17 ,|AN |=3 得(x A +2p )2+2px A =17, ① (x A -2p)2+2px A =9. ②由①,②两式联立解得x A =p4.再将其代入①式并由p >0解得 ⎩⎨⎧==⎩⎨⎧==.2,2;1,4AA x p x p 或 因为ΔAMN 是锐角三角形,所以2p> x A ,故舍去⎩⎨⎧==22Ax p所以p =4,x A =1.由点B 在曲线段C 上,得x B =|BN |-2p=4. 综上得曲线段C 的方程为y 2=8x (1≤x ≤4,y >0).解法二:如图建立坐标系,分别以l 1、l 2为x 、y 轴,M 为坐标原点. 作AE ⊥ l 1,AD ⊥ l 2,BF ⊥ l 2,垂足分别为E 、D 、F . 设A (x A ,y A )、B (x B ,y B )、N (x N ,0).依题意有x A =|ME |=|DA |=|AN |=3, y A =|DM |=2222=-DAAM,由于ΔAMN 为锐角三角形,故有 x N =|ME |+|EN | =|ME |+22AE AN -=4x B =|BF |=|BN |=6.设点P (x ,y )是曲线段C 上任一点,则由题意知P 属于集合{(x ,y )|(x -x N )2+y 2=x 2,x A ≤x ≤x B ,y >0}.故曲线段C 的方程为y 2=8(x -2)(3≤x ≤6,y >0).22.本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力,考查建立函数关系、不等式性质、最大值、最小值等基础知识.解法一:设y 为流出的水中杂质的质量分数,则y =abk,其中k >0为比例系数.依题意,即所求的a ,b 值使y 值最小.根据题设,有4b +2ab +2a =60(a >0,b >0), 得 b =aa+-230(0<a <30). ① 于是 y =ab k=aaa k +-230226432+-+-=a a k ⎪⎭⎫ ⎝⎛+++-=264234a a k≥()2642234+⋅+-a a k18k =, 当a +2=264+a 时取等号,y 达到最小值. 这时a =6,a =-10(舍去). 将a =6代入①式得b =3.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小. 解法二:依题意,即所求的a ,b 的值使ab 最大. 由题设知 4b +2ab +2a =60(a >0,b >0),即 a +2b +ab =30(a >0,b >0). 因为 a +2b ≥2ab 2, 所以 ab 22+ab ≤30, 当且仅当a =2b 时,上式取等号. 由a >0,b >0,解得0<ab ≤18.即当a =2b 时,ab 取得最大值,其最大值为18. 所以2b 2=18.解得b =3,a =6.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小.23.本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,棱柱的性质,空间的角和距离的概念,逻辑思维能力、空间想象能力及运算能力.Ⅰ.解:作A 1D ⊥AC ,垂足为D ,由面A 1ACC 1⊥面ABC ,得A 1D ⊥面ABC ,所以∠A 1AD 为A 1A 与面ABC 所成的角. 因为AA 1⊥A 1C ,AA 1=A 1C , 所以∠A 1AD =45º为所求.Ⅱ.解:作DE ⊥AB ,垂足为E ,连A 1E ,则由A 1D ⊥面ABC ,得A 1E ⊥AB . 所以∠A 1ED 是面A 1ABB 1与面ABC 所成二面角的平面角. 由已知,AB ⊥BC ,得ED ∥BC . 又D 是AC 的中点,BC =2,AC =23, 所以DE =1,AD =A 1D =3, tg ∠A 1ED =DEDA 1=3. 故∠A 1ED =60º为所求.Ⅲ.解法一:由点C 作平面A 1ABB 1的垂线,垂足为H ,则CH 的长是C 到平面A 1ABB 1的距离.连结HB ,由于AB ⊥BC ,得AB ⊥HB . 又A 1E ⊥AB ,知HB ∥A 1E ,且BC ∥ED , 所以∠HBC =∠A 1ED =60º 所以CH =BC sin60º=3为所求. 解法二:连结A 1B .根据定义,点C 到面A 1ABB 1的距离,即为三棱锥C -A 1AB 的高h . 由ABC A AB A C V V --=11锥锥得D A S h S ABC B AA 131311∆∆=, 即 322312231⨯⨯=⨯h 所以3=h 为所求.24.本小题主要考查函数图像、方程与曲线,曲线的平移、对称和相交等基础知识,考查运动、变换等数学思想方法以及综合运用数学知识解决问题的能力.Ⅰ.解:曲线C 1的方程为y =(x -t )3-(x -t )+s .Ⅱ.证明:在曲线C 上任取一点B 1(x 1,y 1).设B 2(x 2,y 2)是B 1关于点A 的对称点,则有2221t x x =+, 2221sy y =+. 所以 x 1=t -x 2, y 1=s -y 2.代入曲线C 的方程,得x 2和y 2满足方程:s -y 2=(t -x 2)3-(t -x 2),即 y 2=(x 2-t )3-(x 2-t )+ s , 可知点B 2(x 2,y 2)在曲线C 1上.反过来,同样可以证明,在曲线C 1上的点关于点A 的对称点在曲线C 上. 因此,曲线C 与C 1关于点A 对称.Ⅲ.证明:因为曲线C 与C 1有且仅有一个公共点,所以,方程组⎪⎩⎪⎨⎧+---=-=st x t x y xx y )()(33有且仅有一组解.消去y ,整理得3tx 2-3t 2x +(t 3-t -s )=0, 这个关于x 的一元二次方程有且仅有一个根. 所以t ≠0并且其根的判别式Δ=9t 4-12t (t 3-t -s )=0.即 ⎩⎨⎧=--≠.0)44(,03s t t t t所以 t t s -=43且 t ≠0. 25.本小题主要考查等差数列基本概念及其通项求法,考查对数函数性质,考查归纳、推理能力以及用数学归纳法进行论证的能力.解:Ⅰ.设数列{b n }的公差为d ,由题意得⎪⎩⎪⎨⎧=-+=.1452)110(1010,111d b b 解得⎩⎨⎧==.3,11d b 所以 b n =3n -2.Ⅱ.由b n =3n -2,知S n =log a (1+1)+ log a (1+41)+…+ log a (1+231-n ) = log a [(1+1)(1+41)……(1+231-n )], 31log a b n +1= log a 313+n . 因此要比较S n 与31log a b n +1的大小,可先比较(1+1)(1+41)……(1+231-n )与313+n 的大小.取n =1有(1+1)>3113+⋅,取n =2有(1+1)(1+41)>3123+⋅, ……由此推测(1+1)(1+41)……(1+231-n )>313+n . ① 若①式成立,则由对数函数性质可断定:当a >1时,S n >31log a b n +1. 当0<a <1时,S n <31log a b n +1.下面用数学归纳法证明①式.(ⅰ)当n =1时已验证①式成立.(ⅱ)假设当n =k (k ≥1)时,①式成立,即(1+1)(1+41)……(1+231-k )>313+k . 那么,当n =k +1时,(1+1)(1+41)……(1+231-k )(1+()2131-+k )>313+k (1+131+k ) =13133++k k (3k +2). 因为()[]333343231313+-⎥⎦⎤⎢⎣⎡+++k k k k ()()()()22313134323+++-+=k k k k()013492>++=k k , 所以13133++k k (3k +2)>().1134333++=+k k 因而(1+1)(1+41)……(1+231-k )(1+131+k )>().1133++k 这就是说①式当n=k +1时也成立.由(ⅰ),(ⅱ)知①式对任何正整数n 都成立.由此证得:当a >1时,S n >31log a b n +1. 当0<a <1时,S n <31log a b n +1.。
1998考研数学真题+答案

1998年全国硕士研究生入学统一考试数学试题参考解答及评分标准数 学(试卷一)一、填空题:(本题共5小题,每小题3分,满分15分)(1) 41211lim20-=--++→xx x x . (2) 设1()()z f xy y x y xϕ=++,其中ϕ,f 具有二阶连续导数,则)('')(')(''2y x y y x xy yf yx z ++++=∂∂∂ϕϕ.(3) 设L 为椭圆13422=+y x ,其周长记为a ,则a ds y x xy L 12)432(22=++⎰.(4) 设A 为n 阶矩阵,*0,A A ≠为A 的伴随矩阵,E 为n 阶单位矩阵,若A 有特征值λ,则E A +2*)(必有特征值2()1Aλ+.(5) 设平面区域D 由曲线y =1x及直线20,1,y x x e ===所围成,二维随机变量(X,Y)在区域D 上服从均匀分布,则(X,Y)关于X 的边缘概率密度在2x =处的值为14.二、选择题:(本题共5小题,每小题3分,满分15分) (1) 设)(x f 连续,则=-⎰dt t x f t dxd x )(220 (A) (A) 2()x f x (B) 2()x f x - (C) 22()x f x (D) 2()x f x -(2) 函数23()(2)f x x x x x =---的不可导点的个数是 (B)(A) 3 (B) 2 (C) 1 (D) 0 (3) 已知函数()y f x =在任意点x 处的增量α,0,12时且当→∆++∆=∆x a xxy y 是x ∆的高阶无穷小量,(0)y π=,则(1)y 等于 (D)(A) 2π (B)π (C) 4e π(D) 4e ππ(4) 设矩阵 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333222111c b a c b a c b a 是满秩的,则直线 213a a a x -- = 213b b b y --= 213c c c z --与直线321a a a x -- = 321b b b y --= 321c c c z -- (A)(A) 相交于一点 (B) 重合 (D) 平行但不重合 (D) 异面(5) 设A 、B 是随机事件,且0<P (A )<1,P (B )>0,)()(A B P A B P =,则必有 (C)(A) ()()P A B P A B = (B) ()()P A B P A B ≠ (C) ()()()P AB P A P B = (D) ()()()P AB P A P B ≠ 三、(本题满分5分) 求直线 11111:--==-z y x l 在平面012:=-+-z y x π上的投影直线0l 的方程,并0l 求绕y 轴旋转一周所成的方程.解一:设经过l 且垂直于平面π的平面方程为1:(1)(1)0A x By C z π-++-=, 则由条件可知20,0A B C A B C -+=+-=,由此解得::1:3:2A B C =-. 于是1π的方程为3210x y z --+=.……2分 从而0l 的方程为0l 210:3210x y z x y z -+-=⎧⎨--+=⎩,……3分即02:1(1)2x y l z y =⎧⎪⎨=--⎪⎩. 于是0l 绕y 轴旋转一周所成曲面的方程为222214(1)4x z y y +=+-,即2224174210x y z y -++-=.……5分解二:由于直线l 的方程可写为1010x y y z --=⎧⎨+-=⎩,所以过l 的平面方程可设为1(1)0x y y z λ--++-=,即(1)(1)0x y z λλλ+-+-+=.由它与平面π垂直,得1(1)20λλ--+=,解得2λ=-. 于是经过l 且垂直与π的平面方程为3210x y z --+=. ……2分 从而0l 的方程为0l 210:3210x y z x y z -+-=⎧⎨--+=⎩.……3分(下同解法一)四、(本题满分6分)确定常数λ,使在右半平面0x >上的向量42242(,)2()()A x y xy x y i x x y jλλ=+-+ 为某二元函数(,)u x y 的梯度,并求(,)u x y .解:令422422(),()P xy x y Q x x y λλ=+=-+. 则(,)A x y在右半平面0x >上为某二元函数(,)u x y 的梯度的充要条件是Q Px y∂∂≡∂∂. ……1分 此即444()(1)0x x y λλ++=,解之得1λ=-. ……3分于是,在右半平面内任取一点,例如(1,0)作为积分路径的起点,则得(,)242(1,0)2(,)x y xydx x dy u x y C x y -=++⎛⎜⎠ ……4分242421020yxx dx x dyC x y x y⋅=-+++⎛⎛⎜⎜⎠⎠2arctan y C x =-+. ……6分(注:不加C 不扣分.)五、(本题满分6分)从船上向海中沉放某种探测仪器,按探测要求,需确定仪器的下沉深度y (从海平面算起)与下沉速度v 之间的函数关系.设仪器在重力作用下,从海平面由静止开始铅直下沉,在下沉过程中还受到阻力和浮力的作用.设仪器的质量为m ,体积为B ,海水比重为ρ,仪器所受的阻力与下沉速度成正比,比例系数为k(k>0).试建立y 与v 所满足的微分方程,并求出函数关系式y=y(v),解:取沉放在原点O ,OY 轴正向铅直向下,则由牛顿第二定律得22d ym mg B kv dt ρ=--,……1分 将22d y dy v dt dt =代入以消去t ,得v y 与之间的微分方程dy mv mg B kv dtρ=--, ……2分 即mv dy dv mg B kv ρ=--,积分得2()ln()m m mg B y v mg B kv C k kρρ-=----+. ……4分 由初始条件0|0y v ==定出2()ln()m mg B C mg B kρρ-=-,故所求的函数关系式为2()lnm m mg B mg B kvy v k k mg B ρρρ---=---. ……6分 六、(本题满分7分) 计算⎰⎰∑++++212222)()(z y x dxdy a z axdydz ,其中∑为下半球面222y x a z ---=的上侧,a 为大于零的常数.解一:212222()()axdydz z a dxdy x y z ∑++++⎛⎛⎜⎜⎠⎠21()axdydz z a dxdy a ∑=++⎰⎰. ……1分补一块有向曲面2220:,x y a z S -+≤=⎧⎨⎩,其法向量与z 轴正向相反,从而得到221[()()]S S I axdydz z a dxdy axdydz z a dxdy a --∑+=++-++⎰⎰⎰⎰ ……2分 21(32)D a z dv a dxdy a Ω⎡⎤=-++⎢⎥⎣⎦⎰⎰⎰⎰⎰ ……4分其中Ω为S -∑+围成的空间区域,D 为0z =上的平面区域222x y a +≤. 于是22204440011222a a r I a zdv a a d rdr a a ππππθ-Ω⎡⎤⎡⎤=--+=--⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰⎰⎰⎰32a π=-. ……7分 解二:21()I axdydz z a dxdy a ∑=++⎰⎰. ……1分记222112()yzD I axdydz a y z dydz a ∑==--+⎰⎰,其中yz D 为YOZ 平面上的半圆222,0y z a z +≤≤. 利用极坐标计算,得222310223I d a r rdr a ππθπ=--=-⎰⎰,……4分22222211()[()]xyD I z a dxdy a a x y dxdy a a ∑=+=-+⎰⎰⎰⎰222223001(22)6a d a a a r r rdr a a ππθ=--=⎰⎰,其中xy D 为XOY 平面上的圆域222x y a +≤. 因此3122I I I a π=+=-.……7分七、(本题满分6分)求2sin sin sin lim 1112n n n n n n n πππ→∞⎡⎤⎢⎥+++⎢⎥+⎢⎥++⎣⎦ . 解:2sinsinsin12sin sin sin 1112n n n n n n n n n n n n nππππππ⎛⎫+++<+++ ⎪+⎝⎭++11sinni i n nπ==∑ ……2分而10112lim sin sin n n i i xdx n n πππ→∞===∑⎰.……3分又2sinsinsin 12sin sin sin 11112n n n n n n n n n ππππππ⎛⎫+++>+++ ⎪++⎝⎭++11sin1ni n i n n nπ==⋅+∑ ……5分 而10112lim sin sin 1n n i n i xdx n n n πππ→∞=⋅==+∑⎰.故由夹逼定理知2sin sin sin 2lim 1112n n n n n n n ππππ→∞⎛⎫ ⎪+++= ⎪+ ⎪++⎝⎭ . ……6分八、(本题满分5分)设正项数列}{n a 单减,且级数∑∞=-1)1(n n na 发散,试问级数nn n a ∑∞=+1)11(是否收敛?并说明理由.解: 级数111nn n a ∞=⎛⎫⎪+⎝⎭∑收敛.……1分理由:由于正项数列{}n a 单调减少有下界,故lim n n a →∞存在,记这个极限值为a ,则0a ≥. ……2分若0a =,则由莱布尼兹定理知1(1)nn n a ∞=-∑收敛,与题设矛盾,故0a >.……3分于是11111n a a <<++,从而1111nnn a a ⎛⎫⎛⎫< ⎪ ⎪++⎝⎭⎝⎭.而111nn n a ∞=⎛⎫ ⎪+⎝⎭∑是公比为111a <+的几 何级数,故收敛.因此由比较判别法知原级数收敛.……5分(注:(1) 若未说明0a >,本题至多给2分,(2) 本题也可用根植判别法)九、(本题满分6分)设()y f x =是区间[0,1]上的任一非负连续函数(1) 试证:存在0(0,1)x ∈,使得在区间0[0,]x 上以0()f x 为高的矩形面积,等于在区间0[,1]x 上以()y f x =为曲边的曲边梯形面积;(2) 又设)(x f 在区间(0,1)内可导,且2()()f x f x x '>-,证明(1)中的0x 是唯一的.证一:(1) 设1()()xF x xf t dt =⎰,……2分则(0)(1)0F F ==,且1()()()x F x f td t x f x '=-⎰. 对()F x 在区间[0,1]上应用罗尔定理知,存在一点0(0,1)x ∈使0()0F x '=,因而0100()()0x f t dt x f x -=⎰. 即矩形面积00()x f x 等于曲边梯形面积1()x f x dx ⎰.……4分 (2) 设1()()()xx f t dt xf x ϕ=-⎰,……5分则当(0,1)x ∈时,有()()()()0x f x f x xf x ϕ''=---<.所以()x ϕ在区间(0,1)内单调减 少,故此时(1)中的0x 是唯一的.……6分(注:在证明(1)时,若对所设辅助函数利用闭区间上连续函数的介值定理仅得出0[0,1]x ∈,但未排除端点,或者排除端点的理由不充分,则只给1分.)十、(本题满分6分) 已知二次曲面方程2222224x ay zbxy xz yz +++++=可以经过正交变换⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛ζηξP z y x 化为椭圆柱面方程4422=+ζη,求,a b 的值和正交矩阵P .解:由111111b b a ⎛⎫ ⎪ ⎪ ⎪⎝⎭与014⎛⎫ ⎪ ⎪⎪⎝⎭相似得11111114b b a λλλλλλ------=-----……1分 解之得到3,1a b ==.……2分对应于特征值10λ=的单位特征向量为122Tx =;对应于特征值21λ=的单位特征向量为2333Tx =;对应于特征值34λ=的单位特征向量为3666T x =; ……5分因此P =236036236⎛⎝. ……6分十一、(本题满分4分)设A 是n 阶矩阵,若存在正整数k ,使线性方程组0k A x =有解向量α,且10k A α-≠, 证明:向量组1,,,k A A ααα- 是线性无关的.解:设有常数12,,,k λλλ ,使得1120k k AA λαλαλα-+++= ,则有1112()0k k k A AA λαλαλα--+++= , ……2分 从而有110k A λα-=.由于10k A α-≠,所以10λ=. 类似可证得230k λλλ==== ,因此向量组1,,,k A A ααα- 线性无关.……4分十二、(本题满分5分)已知线性方程组()I 1111221,222112222,221122,2200n n n n n n n n n a x a x a x a x a x a x a x a x a x +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ 的一个基础解系为 11121,2(,,,)T n b b b ,21222,2(,,,)T n b b b ,…,12,2(,,,)T n n n n b b b试写出线性方程组 1111221,222112222,221122,2200()0n n n n n n n n n b y b y b y b y b y b y b y b y b y +++=⎧⎪+++=⎪II ⎨⎪⎪+++=⎩的通解,并说明理由.解:(II )的通解为11112122212222122(,,,,(,,,,(,,,,T T Tn n n n n n n y c a a a c a a a c a a a =+++)))其中12,,,n c c c 为任意常数.……2分理由:方程组(I )、(II )的系数矩阵分别记为,A B ,则由(I )的已知基础解系可知0T AB =,于是()0T T T BA AB ==,因此可知A 的n 个行向量的转置向量为(II )的n 个解向量.……3分由于B 的秩为n ,故(II )的解空间维数为2n n n -=.又A 的秩为2n 与(I )的解空间 维数之差,即为n ,故A 的n 个行向量线性无关,从而它们的转置向量构成(II )的一个基 础解系,于是得到(II)的上述通解.……5分十三、(本题满分6分)设两个随机变量X ,Y 相互独立,且都服从均值为0、方差为21的正态分布,求随机变量Y X -的方差.解:令Z X Y =-.由于22(0,(),(0,(),22X N Y N ~~且X Y 和相互独立,故(0,1)Z N ~.……2分 因为2222(||)()(||)[(||)]()[(||)]D X Y D Z E Z E Z E Z E Z -==-=-, ……3分而22()()()101E Z D Z EZ =+=+=,22222(||)||22z z E Z z dz zedz πππ+∞+∞---∞===⎛⎜⎠,所以2(||)1D X Y π-=-.……6分十四、(本题满分4分)从正态总体)6,4.3(2N 中抽取容量为n 的样本,如果要求其样本均值位于区间(1.4,5.4 ) 内的概率不小于0.95,问样本容量n 至少应取多大?附表:标准正态分布表 dt e z t z2221)(-∞-⎰=Φπ解:以X 3.4(0,1)6X n N -~, ……1分从而有{1.4 5.4}{2 3.42}{| 3.4|2}P X P X P X <<=-<-<=-<| 3.4|2{}6X n P n -=<2(10.95n=Φ-≥.……2分故(0.975n Φ≥ 1.96n ≥,即2(1.963)34.57n ≥⨯≈,所以n 至少应取35.……4分十五、(本题满分4分)设某次考试的考生成绩服从正态分布,从中随机抽取36位考生的成绩,算得平均成绩为66.5分,标准差为15分,问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?并给出检验过程.附表:t 分布表 p n t n t P p =≤})()({z1.28 1.645 1.962.33 )(z Φ0.9000.9500.9750.990解:设该次考试的考生成绩为X ,则2(,)X N μσ~. 把从X 中抽取的容量为n 的样本 均值记为X ,样本标准差记为S .本题是在显著性水平0.05α=下检验假设01:70;:70H H μμ=≠,……1分 拒绝域为12||70||-1)x t n t n s α--=≥(. 由0.97536,66.5,15,(361) 2.0301n x s t ===-=,算得|66.570|36|| 1.4 2.030115t -==<,……3分 所以接受假设0:70H μ=,即在显著性水平0.05下,可以认为这次考试全体考生的平均成绩为70分. ……4分数 学(试卷二)一、填空题:(本题共5小题,每小题3分,满分15分) (1) 【 同数学一 第一、(1)题 】(2) 曲线322y x x x =-++与x 轴所围成的图形的面积A=3712(3)2lnsin cot lnsin cot sin xdx x x x x C x =---+⎰.(4) 设)(x f 连续,则=-⎰dt t x f t dxd x )(2202()x f x . (5) 曲线)1ln(xe x y +=(0)x >的渐近线方程为1y x e -=+.二、选择题:(本题共5小题,每小题3分,满分15分)(1) 设数列n x 与n y 满足0lim =∞→n n n y x ,则下类断言正确的是 (A )(A) 若n x 发散,则n y 必发散 (B) 若n x 无界,则n y 必有界 (C) 若n x 有界,则n y 必为无穷小(D) 若nx 1为无穷小,则n y 必为无穷小 (2) 【 同数学一 第二、(2)题 】 (选项的排列顺序不同) (3) 【 同数学一 第二、(3)题 】 (选项的排列顺序不同)(4) 设函数()f x 在x a =的某个领域内连续,且()f a 为极大值,则存在0δ>,当(,)x a a δδ∈-+时,必有 (A )(A) 0)]()()[(≥--a f x f a x . (B) 0)]()()[(≤--a f x f a x .(C) )(0)()()(lim 2a x x t x f t f a t ≠≥--→. (D) )(0)()()(lim 2a x x t x f t f a t ≠≤--→. (5) 设A 是任一)3(≥n n 阶方阵,A *是其伴随矩阵,又k 为常数,且1,0±≠k ,则必有(kA)*= (B) (A) kA * (B) k n-1A * (C) k n A * (D) k -1A 三、(本题满分5分)求函数)4tan()1()(π-+=x xx x f 在区间)2,0(π内的间断点,并判断其类型.解:()f x 在(0,2)π内的间断点为357,,,4444x ππππ=. ……1分在4x π=处,(0)4f π+=+∞,在54x π=处,5(0)4f π+=+∞, 故5,44x ππ=为第二类(或无穷)间断点; ……3分在34x π=处,34lim ()1x f x π→=,在74x π=处,74lim ()1x f x π→=,故37,44x ππ=为第一类(或可去)间断点; ……5分四、(本题满分5分)确定常数c b a ,,的值,使)0()1ln(sin lim20≠=+-⎰→c c dt tt xax x b x . 解:由于0x →时,sin 0ax x -→,且极限c 不为0,所以当0x →时,3ln(1)0xbt dt t +→⎛⎜⎠,故必有0b =.……1分又因为3330000sin cos (cos )lim lim lim ln(1)ln(1)ln(1)x x x x ax x a x x a x x x t dtx t →→→---==+++⎛⎜⎠ 3200(cos )cos lim lim (0)x x x a x a x c c x x →→--===≠. ……3分 故必有1a =,从而12c =.……5分五、(本题满分6分) 利用代换x e x y x y x y xuy =+-''=cos 3sin '2cos cos 将方程化简,并求出原方程的通解.解一:由cos u y x =两端对x 求导,得cos sin u y x y x ''=-,cos 2sin cos u y x y x y x '''''=--.……2分 于是原方程化为4xu u e ''+=,……3分其通解为12cos 2sin 25xe u C x C x =++,从而原方程的通解为12cos 22sin cos 5cos xx e y C C x x x=++. ……5分解二:sec y u x =,sec sec tan y u x u x x ''=+,23sec 2sec tan sec tan sec y u x u x x u x x u x '''''=+++,……2分代入原方程得4xu u e ''+=. ……3分以下同解法一.六、(本题满分6分) 计算积分⎰-232121dx x x .解:注意到被积函数内有绝对值且1x =是其无穷间断点,故31222112x x x x=--⎛⎜⎜⎠⎠原式 ……1分而1121212211()42x xx =---⎛⎛⎜⎜⎜⎠⎠112arcsin(21)arcsin12x π=-==, ……3分3322221111()24x xx =---⎛⎛⎜⎜⎜⎠⎠3221111ln ()()ln(23)224x x ⎡⎤=-+--=+⎢⎥⎣⎦.……5分因此3221ln(23)2x xπ=++-⎛⎜⎠. ……6分七、(本题满分6分)【 同数学一 第五题 】 八、(本题满分6分)【 同数学一 第九题 】 九、(本题满分8分) 设有曲线1-=x y ,过原点作其切线,求由此曲线、切线及x 轴围成的平面图形绕x轴旋转一周所得到的旋转体的表面积.解:设切点为00(1)x x -,则过原点的切线方程为021y x x =-. 再以点00(1)x x -代入,解得0002,11x y x ==-=,则切线方程为12y x =. ……3分 由曲线1(12)y x x =-≤≤绕x 轴一周所得到的旋转面的面积221112143(551)6S y dx x dx πππ'=+=-=⎰⎰;……6分由直线段1(12)2y x x =≤≤绕x 轴一周所得到的旋转面的面积 22015252S ππ=⋅=⎰.因此,所求旋转体的表面积为12(1151)6S S S π=+=.……8分十、(本题满分8分)设y=y(x)是一向上凸的连续曲线,其上任意一点(x,y)处的曲率为211y '+,且此曲线上的点(0,1)处的切线方程为y=x+1,求该曲线的方程,并求函数y=y(x)的极值.解:因曲线向上凸,故0y ''<()32211y y ''='+'+, ……2分即211y y ''=-'+. 令,p y p y ''''==则,从而上述方程化为211p p '=-+,分离变量得21dpdx p =-+,解之得1arctan p C x =-.……4分因为()y y x =在点(0,1)处切线方程为1y x =+,所以00||1x x p y =='==,代入上式得14C π=,故tan()4y x π'=-.积分得2ln |cos()|4y x C π=-+.……6分因为曲线过点(0,1),所以0|1x y ==,代入上式得211ln 22C =+,故所求曲线的方程为13ln |cos()|1ln 2,(,)4244y x x πππ=-++∈-.……7分因为cos()14x π-≤且当4x π=时,cos()14x π-=,所以当4x π=时函数取得极大值11ln 22y =+.……8分十一、(本题满分8分) 设(0,1)x ∈,证明:(1) 22)1(ln )1(x x x <++; (2)211)1ln(112ln 1<-+<-x x . 证:(1) 令22()(1)ln (1)x x x x ϕ=++-,则有(0)0ϕ=,……1分22()ln (1)2ln(1)2,(0)0x x x x ϕϕ''=+++-=.因为当(0,1)x ∈时,2()[ln(1)]01x x x xϕ''=+-<+, 所以()0x ϕ'<,从而()0x ϕ<,即22(1)ln (1)x x x ++<.……3分 (2) 令11(),(0,1]ln(1)f x x x x=-∈+,则有2222(1)ln (1)()(1)ln (1)x x x f x x x x ++-'=++. ……4分由(1)知,()0f x '<(当(0,1)x ∈).于是在(0,1)内()f x 单调减少.又()f x 在区间(0,1]上连续,且1(1)1ln 2f =-, 故当(0,1)x ∈时,111()1ln(1)ln 2f x x x =->-+.……6分又20000ln(1)ln(1)1lim ()lim lim lim ln(1)2(1)2x x x x x x x x x f x x x x x x ++++→→→→-+-+====++, 故当(0,1)x ∈时,111()ln(1)2f x x x =-<+.……8分十二、(本题满分5分)设11(2)T E C B A C ---=,其中E 是4阶单位矩阵,TA 是4阶矩阵A 的转置矩阵,B =1232012300120001--⎛⎫⎪- ⎪ ⎪⎪⎝⎭,C =1201012000120001⎛⎫⎪⎪⎪⎪⎝⎭,求A .解: 由题设得1(2)T C E C B A E --=,即(2)T C B A E -=.……1分由于12340123001200012C B ⎛⎫⎪⎪= ⎪⎪⎝⎭-,|2|10C B -=≠,故2C B -可逆. 于是11[(2)][(2)]T T A C B C B --=-=-……3分110001000210021003210121043210121-⎛⎫⎛⎫⎪⎪- ⎪⎪= ⎪ ⎪- ⎪⎪-⎝⎭⎝⎭=. ……5分十三、(本题满分8分)[],]4,,10,3[,],1,1,0[,]3,1,7,2[,2,0,4,1321T T T T b a a a a =-===β问:(1) b a ,取何值时, β不能由321,,ααα 线性表示?(2) b a ,取何值时, β可由321,,ααα线性表示? 并写出此表示式.解: 因120312031203471100112011201101100102340120002b b a a a b ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪----⎪ ⎪ ⎪→→⎪ ⎪ ⎪--- ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭, ……2分故 (1) 当2b ≠时,线性方程组123(,,)x αααβ=无解,此时β不能由123,,ααα线性表出;……4分(2) 当2,1b a =≠时,线性方程组123(,,)x αααβ=有唯一解:123(,,)(1,2,0)T T x x x x ==-,于是β可唯一表示为122βαα=-+;……6分当2,1b a ==时,线性方程组123(,,)x αααβ=有无穷多个解:123(,,)(2,1,1)(1,2,0)T T T x x x x k ==-+-,其中k 为任意常数,这时β可由123,,ααα线性表示为123(21)(2)k k k βααα=-++++. ……8分数 学(试卷三)一、填空题:(本题共5小题,每小题3分,满分15分)(1) 设曲线()nf x x =在点(1,1)处的切线与x 轴的交点为,0n ξ(),则1lim ()n n f e ξ-→∞=.(2)⎰=-dx x x 21ln 1ln x c x-+.(3) 差分方程121050t t y y t ++-=的通解为51(5)()126t t y C t =-+-.(4) 设矩阵,A B 满足*28A BA BA E =-,其中A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-100020001,E 为单位矩阵,*A 为A 的伴随矩阵,A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-10020001,则B =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-20040002. (5) 设4321,,,X X X X 是来自正态总体2(0,2)N 的简单随机样本,243221)43()2(X X b X X a X -+-=,则当11,20100a b ==时,统计量X 服从2χ分布,其自由度为 2二、选择题:(本题共5小题,每小题3分,满分15分) (1) 设()f x 为可导函数,且满足条件12)1()1(lim-=--→xx f f x ,则曲线()y f x =在点(1,(1))f 处的切线斜率为 (D) (A)21 (B) 0(C) 1-(D) 2-(2) 设函数nn x xx f 211lim)(++=∞→,讨论函数f (x) 的间断点,其结论为 (B)(A) 不存在间断点. (B) 存在间断点x = 1 (C) 存在间断点x = 0 (D) 存在间断点x = -1(3) 齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0003213213221x x x x x x x x x λλλλ 的系数矩阵记为A ,若存在三阶矩阵B ≠0,使得AB = 0,则 (C) (A) 02=-=B 且λ (B) 02≠-=B 且λ (C) 01==B 且λ (D) 01≠=B 且λ (4) 设(3)n n ≥阶矩阵A=1111aaa a a a a a a a a a ⎛⎫⎪⎪⎪⎪⎪ ⎪⎝⎭ ,若矩阵A 的秩为1n -,则a 必为 (B)(A) 1 (B)n-11(C) 1- (D) 11-n(5) 设1()F x 与2()F x 分别为随机变量1X 与2X 的分布函数,为使)()(21x bF x aF x F -=)( 是某一随机变量的分布函数,在下列给定的各组数值中应取 (A ) (A )52,53-==b a ;(B )32,32==b a ;(C )23,21=-=b a ;(D ) 23,21-==b a三、(本题满分5分)设arctan22yxz x y e -=+(),dz 与2.zx y ∂∂∂解:arctan arctan arctan 2222212()()()(2)1y y yx x xz y xe x y e x y e y x x x---∂=-+-=+∂+,……1分arctan arctan arctan 2222112()()()(2)1y y yx x xz ye x y e y x e y y x x---∂=-+=-∂+. ……2分所以arctan[(2)(2)]y xdz ex y dx y x dy -=++-.……3分 222arctan arctan arctan 222211(2)()()1y y y x x x z y xy x e x y e e y x y x x y x---∂-+=-+=∂∂++. ……5分四、(本题满分5分)设22{(,)}D x y x y x =+≤,求.Dxdxdy解一:22{(,)|01,}D x y x x x y x x =≤≤-≤-,所以220x x x x Dxdxdy xdx --=⎰……2分 121x xdx =-⎰……3分1351220081(1)43515t t x t t t dt ⎛⎫-=-=-= ⎪⎝⎭⎰.……5分解二:cos 202cos Dxdxdy d r rdr πθπθθ-=⎰⎰……2分 13cos 2222cos d r dr πθπθθ-=⎰⎰……3分 3204cos 5d πθθ=⎰ ……4分 815=. ……5分五、(本题满分6分)设某酒厂有一批新酿的好酒,如果现在(假定0t =)就售出,总收入为0R (元),如果窖藏起来,待来日按陈酒价格出售,t 年末总收入为250t R R e=.假定银行的年利率为r ,并以连续复利计息,试求窖藏多少年售出可使总收入的现值最大,并求0.06r =时的t 值..解:根据连续复利公式,这批酒在窖藏t 年未售出总收入R 的现值为()Re rt A t -=, 而250t R R e=,所以250()t rt A t R e=. ……2分令25005t rtdA R e r dtt ⎫=-=⎪⎭,得唯一驻点02125t r =. ……3分 又2225023510t rt d A R r dt t t -⎡⎤⎫=-⎢⎪⎭⎢⎣,则有0123250212.50r t t d A R e r dt =⎡⎤=-<⎣⎦. 于是,02125t r =是极大值点即最大值点, 故窖藏2125t r =(年)售出,总收入的现值最大. ……5分当0.06r =时,100119t =≈(年).……6分 六、(本题满分6分)设函数)(x f 在[b a ,]上连续,在(b a ,)内可导, 且0)('≠x f ,试证: 存在,(,),a b ξη∈使得'()'()b a f e e e f b aηξη--=-.证:令()x g x e =,则()()g x f x 与在[,]a b 上满足柯西中值定理条件,故由柯西中值定理, 存在(,)a b η∈,使得()()()b af b f a f e e eηη'-=-, ……2分 即()()()()b a f b f a e e e f b a b aηη---'=⋅--.……3分 又()f x 在[,]a b 上满足拉格朗日中值定理条件,故由拉格朗日中值定理,存在(,)a b ξ∈,使得()()()f b f a f b aξ-'=-.……5分 由题设()0f x '≠知()0f η'≠,从而()()()b a f e e e f b aηξη-'-=⋅'-.……6分七、(本题满分6分)设有两条抛物线11)1(122+++=+=n x n y n nx y 和, 记它们交点的横坐标的绝对值为n a . (1)求这两条抛物线所围成的平面图形的面积n S ;(2)求级数∑∞=1n nn a S 的和.解:由2211(1)1y nx y n x n n =+=+++与得(1)n a n n =+. ……2分因图形关于y 轴对称,所以220112[(1)]1n a n S nx n x dx n n =+-+-+⎰2012[](1)3(1)(1)n a x dx n n n n n n =-=+++⎰.……4分 因此414113(1)31n n S a n n n n ⎛⎫==- ⎪++⎝⎭,……5分 从而11414lim lim 1313nn k n n n k n k S S a a n ∞→∞→∞==⎡⎤⎛⎫==-= ⎪⎢⎥+⎝⎭⎣⎦∑∑. ……6分八、(本题满分7分)设函数)(x f 在 [)+∞,1上连续,若由曲线)(x f y =),直线)1(,1>==t t x x 与x 轴所围成的平面图形绕x 轴旋转一周所成的旋转体体积为)]1()([3)(2f t f t t v -=π,试求)(x f y =所满足的微分方程,并求该微分方程满足条件 922==x y 的解.解:依题意得221()()[()(1)]3tV t f x dx t f t f ππ==-⎰,即2213()()(1)tf x dx t f t f =-⎰.……2分 两边对t 求导,得223()2()()f t tf t t f t '=+.……3分将上式改写为2232x y y xy '=-,即232dy y y dx x x ⎛⎫=-⋅ ⎪⎝⎭(*)令y u x =,则有3(1)du x u u dx=-, ……4分 当0u ≠时,1u ≠时,由3(1)du dx u u x =-两边积分得31u cx u-=.……5分 从而(*)式的通解为3()y x cx y C -=为任意常数.……6分 由已知条件,求得1c =-,从而所求的解为33()1x y x x yy x-=-=+或. ……7分九、(本题满分9分)设向量1212(,,,),(,,,)T T n n a a a b b b αβ== 都是非零向量,且满足条件0=βT a ,记n 阶矩阵T a A β=,求:(1) 2A ; (2) 矩阵A 的特征值和特征向量. 解:(1) 由T a A β=和0=βT a ,有2()()()()T T T T T T A AA αβαβαβαββααβ====……1分 即2A 为n 阶零矩阵.……3分(2) 设λ为A 的任一特征值,A 的属于特征值λ的特征向量为(0)x x ≠,则λ=Ax x ,于是22λλ==A x Ax x .……4分 因为2=A x O ,所以2λ=x O .而≠x O ,故0λ=,即矩阵A 的特征值全为零.……5分不妨设向量,αβ中分量110,0a b ≠≠,对齐次线性方程组(0)-=E A O 的系数矩阵施以初等行变换:11121122122212000000n n n n n n n a b a b a b b b b a b a b a b a b a b a b ---⎛⎫⎛⎫⎪⎪--- ⎪⎪-=→ ⎪ ⎪⎪⎪---⎝⎭⎝⎭A……6分由此可得该方程组的基础解系为:32121111,1,0,,0,,0,1,,0,,,0,0,,1T T Tn n b b b b b b ααα-⎛⎫⎛⎫⎛⎫=-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ , ……8分于是,A 的属于特征值0λ=的全部特征向量为112211n n c c c ααα--+++ ,(121,,,n cc c - 是不全为0的任意常数.)……9分十、(本题满分7分)设矩阵A =101020101⎛⎫⎪ ⎪ ⎪⎝⎭,矩阵2)(A kE B +=,其中k 为实数,E 为单位阵,求对角矩Λ,使B 与Λ相似,并求k 为何值时,B 为正定矩阵.解:由2||(2)E A λλλ-=-,可得A 的特征值为1232,0λλλ===. ……2分记对角矩阵200020000D ⎛⎫ ⎪= ⎪ ⎪⎝⎭. 因为A 是实对称矩阵,故存在正交矩阵P ,使得TP AP D =. ……4分所以11()T T A P DP PDP --==.于是22()()[()][()]T T T T B kE A kPP PDP P kE D P P kE D P =+=+=++2()T P kE D P =+222(2)(2)Tk P k P k ⎛⎫+⎪=+⎪ ⎪⎝⎭, ……5分可见222(2)(2)k k k ⎛⎫+ ⎪Λ=+ ⎪ ⎪⎝⎭, ……6分因此,当2k ≠-,且0k ≠时B 的全部特征值均为正数,这时B 为正定矩阵.……7分注:考生也可直接由A 的特征值得到矩阵kE A +的特征值为2k +(二重)和k (4分). 进而得到B 的特征值为2(2)k +(二重)和2k (5分),并得到实对称矩阵B ~Λ(6分).十一、(本题满分10分)一商店经销某种商品,每周进货的数量X 与顾客对该种商品的需求量Y 是相互独立的随机变量,且都服从区间[10,20]上的均匀分布.商店每售出一单位商品可得利润1000元;若需求量超过了进货量,商店可从其他商店调剂供应,这时每单位商品获利润为500元.试计算此商店经销该种商品每周所得利润的期望值.解:设Z 表示商品每周所得的利润,则1000,,1000500()500(),Y Y X Z X Y X X Y Y X≤⎧=⎨+-=+>⎩ ……3分 由于X 与Y 的联合概率密度为:1,1020,1020,(,)1000,x y x y ϕ⎧≤≤≤≤⎪=⎨⎪⎩其它.……5分所以12111000500()100100D D EZ y dxdy x y dxdy =⨯++⨯⎰⎰⎰⎰ ……7分 202020101010105()yydy ydx dy x y dx =++⎰⎰⎰⎰……8分 202021010310(20)5(1050)2y y dy y y dy =-+--⎰⎰……9分 200005150014166.673=+⨯≈(元).……10分十二、(本题满分9分)设有来自三个地区的各10名、15名和25名考生的报名表,其中女生的报名表分别为3份、7份和5份.随机地取一个地区的报名表,从中先后抽出两份.(1) 求先抽到的一份是女生表的概率p ;(2) 已知后抽到的一份是男生表,求先抽到的一份是女生表的概率q . 解:设i H ={报名表是第i 区考生的}(1,2,3,i =)j A ={第j 次抽到的报名表是男生的}(1,2j =), 则1231()()()3P H P H P H ===;1112137820(|),(|),(|)101525P A H P A H P A H ===; ……1分(1) 3111137529()()(|)()310152590i i i P P A P H P A H ====++=∑.……3分 (2) 由全概率公式得2122237820(|),(|),(|)101525P A H P A H P A H ===. ……4分 121122123785(|),(|),(|)303030P A A H P A A H P A A H ===.……5分32211782061()()(|)()310152590i i i P A P H P A H ===++=∑. ……6分 31212117852()()(|)()33030309i i i P A A P H P A A H ===++=∑.……7分 因此,12122()20(|)()61P A A q P A A P A ===.……9分数 学(试卷四)一、填空题:(本题共5小题,每小题3分,满分15分) (1) 【 同数学三 第一、(1)题 】 (2) 【 同数学三 第一、(2)题 】 (3) 【 同数学三 第一、(4)题 】(4) 设A ,B 均为n 阶矩阵,21*122,3,23n A B A B--==-=-则.(5) 设一次试验成功的概率为p ,进行100次独立重复试验,当p =12时,成功次数的标准差的值最大;其最大值为 5 .二、选择题:(本题共5小题,每小题3分,满分15分) (1) 【 同数学三 第二、(1)题 】 (2) 【 同数学三 第二、(2)题 】(3) 若向量组 γβα,,线性无关;δβα,,线性相关,则 (C)(A)α 必可由δγβ,,线性表示 (B) β 必不可由δγα,,线性表示(C) δ 必可由γβα,,线性表示 (D) δ 必不可由γβα,,线性表示(4) 设A ,B ,C 是三个相互独立的随机事件,且0 < P (C )<1,则在下列给定的四对事件 中不相互独立的是 (B) (A) C B A 与+ (B) C AC 与 (C) C B A 与- (D) C AB 与. (5) 【 同数学三 第二、(5)题 】三、(本题满分6分) 求21lim(tan )n n n n→∞(n 为自然数).解:因为32tan 1tan 00tan tan lim lim 1x xxx x xx x x x x x x x ++--→→⎡⎤-⎛⎫⎛⎫⎢⎥=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, ……2分其中23200tan sec 11lim lim 33x x x x x x x ++→→--==,……4分故21130tan lim x x x e x +→⎛⎫= ⎪⎝⎭. ……5分取1x n=,则原式13e =.……6分(注:对数列极限直接用洛必达法则,扣2分.)四、(本题满分6分)【 同数学三 第三题 分值不同】 五、(本题满分5分)【 同数学三 第四题 】 六、(本题满分6分)【 同数学三 第五题 】 七、(本题满分6分)设函数()f x 在[,]a b 上连续,在(b a ,)内可导,且()()1f a f b ==,试证存在,(,)a b ξη∈,使得[]1)()(='+-ηηξηf f e .证:令()()x F x e f x =,则()F x 在[,]a b 上满足拉格朗日中值定理条件,故存在(,)a b η∈,使得()()[()()]b a e f b e f a e f f b aηηη-'=+-.……3分 由条件()()1f a f b ==,得[()()]b ae e ef f b aηηη-'=+-. (1)……4分 再令()xx e ϕ=,则()x ϕ在[,]a b 上满足拉格朗日中值定理条件,故存在(,)a b ξ∈,使得b ae e e b a ξ-=-. (2) ……5分 综合(1)、(2)两式,有[()()]1ef f ηξηη-'+=.……6分八、(本题满分9分)设直线y ax =与抛物线2y x =所围成图形的面积为1S ,它们与直线1X =所围成的图形面积为2S ,并且1a <.(1) 试确定a 的值,使12S S +达到最小,并求出最小值;(2) 求该最小值所对应的平面图形绕x 轴旋转一周所得旋转体的体积. 解:(1) 当01a <<时,(如图一)122120()()a aS S S ax x dx x ax dx =+=-+-⎰⎰123323012332323aa ax x x ax a a ⎛⎫⎛⎫=-+-=-+ ⎪ ⎪⎝⎭⎝⎭. ……2分令2102S a '=-=,得2a =.又(202S ''=>,则(2S 是极小值,即最小值.其值为122(326222S -=+=. ……4分当0a ≤时,(如图二)122120()()aS S S ax x dx x ax dx =+=-+-⎰⎰31623a a =--+.因2211(1)0222a S a '=--=-+<,S 单调减少,故0a =时,S 取得最小值,此时13S =.综上所述,当2a =,(2S 为所求最小值,最小值为226-. ……6分(2) 1244220211())22x V x x dx x x dx ππ=-+-⎰11552331021121655630x x x x πππ⎛⎛=-+-=⎝⎝. ……9分九、(本题满分9分)【 同数学三 第九题 】 十、(本题满分9分)已知下列非齐次线性方程组 )(I 和)(II124123412326():4133x x x x x x x x x x +-=-⎧⎪I ---=⎨⎪--=⎩ , 1234234345():21121x mx x x nx x x x x t +--=-⎧⎪II --=-⎨⎪-=-+⎩(1) 求解方程组()I ,用其导出组的基础解系表示通解.(2) 当方程组()II 中的参数,,m n t 为何值时,方程组()I 与()II 同解.解:(1) 设方程组()I 的系数矩阵为1A ,增广矩阵为1A ,对1A 作初等行变换,得1110261001241111010143110300125A ⎛--⎫⎛--⎫⎪ ⎪=---→-- ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭.由于秩(1A )=秩(1A )34=<,所以方程组有无穷多解,其通解为21415201X k -⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭(k 为任意常数). ……3分(2) 将通解X 代入()II 的第一个方程,得(2)(4)(52)5k m k k k -++-+--+-=-,解得2m =.将通解X 代入()II 的第二个方程,得(4)(52)211n k k k -+--+-=-,解得4n =. 将通解X 代入()II 的第三个方程,得(52)21k k t -+-=-+,解得6t =. 因此,方程组()II 的参数为2m =,4n =,6t =.……5分即当2m =,4n =,6t =时,方程组()I 的全部解都是方程组()II 的解.这时,方程组()II 化为()II 12342343425,4211,25,x x x x x x x x x +--=-⎧⎪--=-⎨⎪-=-⎩.又设方程组()II 的系数矩阵为2A ,增广矩阵为2A ,对2A 施以初等行变换,得21211510012041211010140012500125A ⎛---⎫⎛--⎫⎪ ⎪=---→-- ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭……6分于是方程组()II 的通解为21415201X k -⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭(k 为任意常数).显然,方程组()I 与()II 的解完全相同. 即方程组()I 与()II 同解.……7分十一、(本题满分7分)求某种商品每周的需求量X 是服从区间[10,30]上均匀分布的随机变量,而经销商进货数量为区间[10,30]中的某一整数,商店每销售一单位商品可获利500元;若供大于求则削价处理,每处理1单位商品亏损100元;若供不应求,则可从外部调剂供应,此时每1单位商品仅获利300元,为使商品所获利润期望值不小于9280元,试确定最少进货量.解:设进货数量为α,则利润为500()300,30,500()100,10X a a X M X a X X a αα+-<≤⎧=⎨--≤≤⎩300200,30,600100,10X a a X X a X a +<≤⎧=⎨-≤≤⎩……3分期望利润30301010111(600100)(300200)202020a aEM M dx x a dx x a dx αα=⋅=-++⎰⎰⎰ 3022210116001003002007.53505250202202aax x ax ax a a ⎛⎫⎛⎫=⋅-+⋅+=-++ ⎪ ⎪⎝⎭⎝⎭,……6分 依题意,有27.535052509280a a -++≥,……7分 即27.535040300a a -+≤,解得220263a ≤≤. ……8分 故期望利润不少于9280元的最少进货量为21单位.……9分十二、(本题满分7分)某箱装有100件产品,其中一、二、三等品分别为80件、10件和10件,现在从中随机抽取一件,记)3,2,1(01=⎩⎨⎧=i i X i 他其等品若抽到,试求:(1) 随机变量X 1与X 2的联合分布; (2) 随机变量X 1与X 2的相关系数ρ.解:(1) 设事件i A =“抽到i 等品”123i (=,,). 由题意知123,,A A A 两两互不相容.123()0.8,()()0.1P A P A P A ===.……1分易见123{0,0}()0.1P X X P A ====,122{0,1}()0.1P X X P A ====;121{1,0}()0.8P X X P A ====,12{1,1}()0P X X P φ====.……3分故随机变量X 1与X 2的联合分布为2X1X0 1 0 0.1 0.8 10.1(2) 120.8,0.1EX EX ==.120.80.20.16,0.10.90.09DX DX =⨯==⨯=. ……4分 12000.1010.1100.81100EX X =⨯⨯+⨯⨯+⨯⨯+⨯⨯=. ……5分 121212(,)00.80.10.08Cov X X EX X EX EX =-⋅=-⨯=-.……6分 1212230.160.09DX DX ρ===-⋅⨯.……7分。
1998考研数学三真题及答案解析

1998年全国硕士研究生入学统一考试数学三试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)设曲线()nf x x 在点(1,1)处的切线与x 轴的交点为(,0)n,则lim ()nnf .(2)2ln 1x dx x.(3)差分方程121050tt y y t 的通解为.(4)设矩阵,A B 满足*28A BABA E ,其中10002001A,E 为单位矩阵,*A 为A的伴随矩阵,则B .(5)设1234,,,X X X X 是来自正态总体20,2N 的简单随机样本,2122X a X X 23434b X X .则当a,b 时,统计量X 服从2分布,其自由度为.二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)设周期函数f x 在,内可导,周期为 4.又011lim1,2xf f x x则曲线yf x在点5,5f 处的切线的斜率为()(A)12(B)(C)1(D)2(2)设函数21lim ,1nnx f xx讨论函数f x 的间断点,其结论为()(A)不存在间断点(B)存在间断点1x (C)存在间断点x (D)存在间断点1x(3)齐次线性方程组21231231230,0,0x x x x x x x x x 的系数矩阵记为A .若存在三阶矩阵0B 使得0AB,则()(A)2且||0B (B)2且||0B (C)1且||0B (D)1且||0B (4)设3n n阶矩阵1111a a a a a a Aa a a aaa,若矩阵A 的秩为1n ,则a 必为()(A)1(B)11n(C)1(D)11n (5)设1()F x 与2()F x 分别为随机变量1X 与2X 的分布函数.为使12()()F x aF x bF x 是某一变量的分布函数,在下列给定的各组数值中应取()(A)32,55a b (B)22,33a b (C)13,22ab(D)13,22ab三、(本题满分5分)设arctan 22()yxz xy e,求dz 与2z x y.四、(本题满分5分)设22,Dx y xyx ,求Dxdxdy .五、(本题满分6分)设某酒厂有一批新酿的好酒,如果现在(假定0t)就售出,总收入为0()R 元.如果窖藏起来待来日按陈酒价格出售,t 年末总收入为250.tR R e假定银行的年利率为r ,并以连续复利计息,试求窖藏多少年售出可使总收入的现值最大.并求0.06r 时的t 值.六、(本题满分6分)设函数()f x 在,a b 上连续,在(,)a b 内可导,且()0.f x 试证存在,(,),a b 使得().()baf eee f b a七、(本题满分6分)设有两条抛物线21y nxn和21(1)1yn xn ,记它们交点的横坐标的绝对值为.n a (1)求这两条抛物线所围成的平面图形的面积n S ;(2)求级数1n n nS a 的和.八、(本题满分7分)设函数()f x 在[1,)上连续.若由曲线(),y f x 直线1,(1)x x t t与x 轴所围成的平面图形绕x 轴旋转一周所形成的旋转体体积为2()()(1).3V t t f t f 试求()yf x 所满足的微分方程,并求该微分方程满足条件229x y的解.九、(本题满分9分)设向量1212(,,,),(,,,)TT n n a a a b b b 都是非零向量,且满足条件0.T记n 矩阵.TA求:(1)2A;(2)矩阵A的特征值和特征向量.十、(本题满分7分)设矩阵101020,101A矩阵2(),B kE A其中k为实数,E为单位矩阵.求对角矩阵,使B与相似,并求k为何值时,B为正定矩阵.十一、(本题满分10分)一商店经销某种商品,每周进货的数量X与顾客对该种商品的需求量Y是相互独立的随机变量,且都服从区间[10,20]上的均匀分布.商店每售出一单位商品可得利润1000元;若需求量超过了进货量,商店可从其他商店调剂供应,这时每单位商品获利润为500元.试计算此商店经销该种商品每周所得利润的期望值.十二、(本题满分9分)设有来自三个地区的各10名、15名和25名考生的报名表,其中女生的报名表分别为3份、7份和5份.随机地取一个地区的报名表,从中先后抽出两份.(1)求先抽到的一份是女生表的概率p;(2)已知后抽到的一份是男生表,求先抽到的一份是女生表的概率q.1998年全国硕士研究生入学统一考试数学三试题解析一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)【答案】1e【解析】曲线ny x 在点(1,1)处的切线斜率1x y1nx x11n x n xn ,根据点斜式,切线方程为:1(1).y n x 令0y,代入1(1)y n x ,则11x n ,即在x 轴上的截距为11nn,lim ()nnf lim nnn1lim(1)nn n 11lim(1)xxx1e.(2)【答案】ln x Cx【解析】由分部积分公式,2ln 1x dx x1ln 1x dx x1ln 1x dxln 11(ln 1)x d x xx分部2ln 11x dxx x ln 11x dxxx ln 11x Cxxln x C x.【相关知识点】分部积分公式:假定()uu x 与()v v x 均具有连续的导函数,则,uv dxuvu vdx 或者.udvuvvdu (3)【答案】51(5)()126tty C t【解析】首先把差分方程改写成标准形式1552tty y t ,其齐次方程对应的特征方程及特征根分别为50,5,r r 故齐次方程的通解为(5),ttY C C 为常数.将方程右边的52t 改写成512tt ,此处“1”不是特征根,故令非齐次方程的一个特解为,ty AtB 从而1(1),ty A t B 代入原方程,得5(1)5(),2A tB AtB t 56,60,2AA B 故55,1272A B .于是通解为51(5)().126tttty Y y C t(4)【答案】20004002【解析】由题设*28A BABA E ,由于20A,所以A 可逆.上式两边左乘A ,右乘1A ,得*11128AA BAA ABAAAA28A B AB E (利用公式:*1,AA A E AAE )28A B AB E (移项)28A EA BE (矩阵乘法的运算法则)将2A 代入上式,整理得14EA BE .由矩阵可逆的定义,知EA ,B 均可逆,且114BE A11002002401040100210220004002.(5)【答案】11,,220100【解析】由于1234,,,X X X X 相互独立,均服从2(0,2)N ,所以由数学期望和方差的性质,得2221212(2)0,(2)122220E X X D X X ,所以12(2)(0,20)X X N ,同理34(34)(0,100)X X N .又因为12(2)X X 与34(34)X X 相互独立,且121(2)(0,1)20X X N ;341(34)(0,1)100X X N ,由2分布的定义,当11,20100ab时,222123411(2)(34)(2)20100XX X X X .即当11,20100ab 时,X 服从2分布,其自由度为2.严格地说,当10,100ab时,2(1)X ;当1,020ab 时,2(1)X也是正确的.【相关知识点】1、对于随机变量X 与Y 均服从正态分布,则X 与Y 的线性组合亦服从正态分布.若X 与Y 相互独立,由数学期望和方差的性质,有()()()E aX bY c aE X bE Y c ,22()()()D aXbYc a D X b D Y ,其中,,a b c 为常数.2、定理:若2(,)X N ,则(0,1)XN .3、2分布的定义:若1,,n Z Z 相互独立,且都服从标准正态分布(0,1)N ,则221~()nii Z n .二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)【答案】(D)【解析】根据导数定义:0()()lim x f x x f x f x x(1)(1)lim 2x f f x x 01(1)(1)lim 2x f x f x 1(1)2f 1所以(1)(1)(1)lim 2.x f x f f x因为()f x 周期为4,()f x 的周期亦是4,即()(4)f x f x,所以(5)f (14)f (1)2f .所以曲线()yf x 在点5,(5)f 处的切线的斜率为(5)f (1)2f .选(D).(2)【答案】(B)【分析】讨论由极限表示的函数的性质,应分两步走.先求出该()f x 的(分段)表达式,然后再讨论()f x 的性质.不能隔着极限号去讨论.【解析】现求()f x 的(分段)表达式:当1x时,21()lim1nnx f x x2122lim1nnnnxxx 2122lim 01lim 1n nnnnx xx0;当1x 时,21()lim 1nnx f x x211lim 11nn221;当1x 时,21()lim1nnx f x x211lim11nn020;当1x 时,21()lim 1nnx f x x2lim 1lim 1n nnx x2011nxx1x .由此,0,1,0,1,()1,1,1,1,0,1.x xf x x xx x当当当当当即0,11,()1,1,1,1.x x f x x xx当或当当再讨论函数()f x 的性质:在1x处,1lim xf x1lim 1xx110,1lim 10xf xf ,所以,11lim lim 0xxfxf x,函数()f x 在1x 处连续,不是间断点.在1x 处,1lim x f x1lim 0x 0;1lim xf x1lim 1xx 2;所以1lim xfx1lim x f x ,函数()f x 在1x处不连续,是第一类间断点.故选(B).(3)【答案】(C)【解析】方法1:由0AB知()()3r A r B ,又0,0A B ,于是1()3,r A 1()3r B ,故0,0A B ,即221010111011(1)0111111A,得1.应选(C).方法2:由0AB知()()3r A r B ,又0,0AB,于是1()3,r A 1()3r B ,故0B .显然,1时111111111A,有1()3,r A 故应选(C).作为选择题,只需在2与1中选择一个,因而可以用特殊值代入法.评注:对于条件0AB 应当有两个思路:一是B 的列向量是齐次方程组0Ax的解;二是秩的信息,即()()r A r B n ,要有这两种思考问题的意识.(4)【答案】(B)【解析】1111100(1)110101101a a a a a a a a aa aAa a a a aaaaa a1(1)0100(2)001001n aaa a a a a其中(1)变换:将1行乘以(-1)再分别加到其余各行;(2)变换:将其余各列分别加到第1列.由阶梯形矩阵知,当1(1)0n a ,即11an时,有()1r A n ,故应选(B).(5)【答案】(A)【解析】根据分布函数的性质lim ()1xF x ,即121lim ()()()()xF x F aF bF ab .在所给的四个选项中只有(A)满足1a b ,故应选(A).【相关知识点】分布函数F x 的性质:(1)F x 单调不减;(2)lim ()()0,lim ()()1;xxF x F F x F (3)F x 是右连续的.三、(本题满分5分)【解析】arctanarctan2222()()()y y xxdz e d x y x y d eyxO arctan22arctan222arctan22arctan22()(arctan )122()()1()22(2)(2)y xy xy xy xye xdx ydy xy d x ye xdx ydy xy d y x xxdyydxe xdx ydy x x exy dxyx dy由全微分与偏微分的关系可知,其中dx 的系数就是z x ,即arctan(2)y xz x y ex.再对y 求偏导数,得222arctanarctanarctan222211(2).1y y y xxxzyxy x e x y ee y x yx xyx四、(本题满分5分)【解析】22{(,)}D x y xyx 表示圆心为1,02,半径为12的圆及其内部,画出区域D ,如右图.方法1:22(,)|01,D x y x x xy xx所以,2211120221x xx xDxdxdyxdxdyx x x dxx xdx ,令1x t ,则21xt ,2dxtdt ,:10t 所以上式1351222182(1)(2)4(1)43515ttt t t dtt t dt.方法2:引入极坐标系cos ,sin x r y r ,于是(,)|,0cos22D r r ,3cos cos 222022320cos cos 48cos.515Dxdxdydr rdr dr drd其中倒数第二步用了华里士公式:201342cos1253nn n dn n,其中n 为大于1的正奇数.五、(本题满分6分)【分析】根据连续复利公式,在年利率为r 的情况下,现时的A (元)在t 时的总收入为()e rtR t A ,反之,t 时总收入为()R t 的现值为()()ertA t R t ,将250tRR e代入即得到总收入的现值与窖藏时间t 之间的关系式,从而可用微分法求其最大值.【解析】由连续复利公式知,这批酒在窖藏t 年末售出总收入R 的现值为()ertA t R ,而由题设,t 年末的总收入250tR R e,据此可列出()A t :250()e et rtrtA t R R ,令dA dt 250e t rtd R dt2501e05t rtR rt,得惟一驻点02125tt r.22d A dt d dA dt dt 2501e 5t rtdR rdtt22550011e e55trtt rtdd R rR rdtdt tt 2225500311510t rt t rtR erR ett2250311510t rtR ertt1232502(12.5)0rt t d A R er dt.根据极值的第二充分条件,知:0t t 是()A t 的极大值点,又因驻点惟一,所以也是最大值点.故窖藏2125tr年出售,总收入的现值最大.当0.06r 时,21250.06t100119(年).【相关知识点】极值的第二充分条件:设函数()f x 在0x 处具有二阶导数且0()0f x ,0()0f x ,当0()0f x 时,函数()f x 在0x 处取得极大值;当0()0f x 时,函数()f x 在0x 处取得极小值.六、(本题满分6分)【分析】本题要证的结论中出现两个中值点和,这种问题一般应将含有和的项分别移到等式两边后再用微分中值定理,为此本题只要证()()()()baf b a e e f e.【解析】方法1:函数()f x 在,a b 上连续,在(,)a b 内可导,满足拉格朗日中值定理的条件,对函数()f x 在,a b 上用拉格朗日中值定理,有()()()(),.f b f a f b a a b 又函数()f x 与xe 满足柯西中值定理的条件,将函数()f x 与xe 在,a b 上用柯西中值定理,有()()(),baf b f a f ab eee,即()()()baf f b f a ee e().从而有()()()baf f b a ee e(),即(),,(,)()baf eee a bf b a.方法2:题中没有限制,因此取,即成为要去证存在(,)a b 使.bae ee b a在,a b 上对函数xe 用拉格朗日中值定理,存在(,)a b 使, 1.babaee ee e ebab a即再取,则()1()baf ee ef ba,原题得证.【相关知识点】 1.拉格朗日中值定理:如果函数()f x 满足在闭区间[,]a b 上连续,在开区间,a b 内可导,那么在,a b 内至少有一点()a b ,使等式()()()()f b f a f ba 成立.2.柯西中值定理:如果函数()f x 及()F x 满足(1)在闭区间[,]a b 上连续;(2)在开区间(,)a b 内可导;(3)对任一(,)xa b ,()0F x ,那么在(,)a b 内至少有一点,使等式()()()()()()f b f a f F b F a F 成立.七、(本题满分6分)【解析】(1)由21y nxn与21(1)1y n xn 得1.(1)na n n 因图形关于y 轴对称,所以,所求图形的面积为22032112(1)1214122.(1)(1)33(1)(1)n n a n a nnS nxn x dxnna axdxn n n n n n n n (2)由(1)的结果知41411()3(1)31n nS a n n nn ,根据级数和的定义,111411414lim lim lim 1.31313nnnk nnnn k k nkS S a a kkn八、(本题满分7分)【分析】本题是微分方程的几何应用问题.在题目中给出了由曲线()y f x 等围成的平面图形绕x 轴旋转一周所形成的旋转体体积()V t 与包含函数f 的一个恒等式,这正是列方程的依据.【解析】由绕x 轴旋转的旋转体体积公式得21()()tV t f x dx ,于是,依题意得221()()(1)3t f x dxt f t f ,即2213()()(1)t f x dxt f t f .两边对t 求导,化成微分方程223()2()()f t tf t t f t ,其中()f t 为未知函数.按通常以x 表示自变量,y 表示未知函数()f t ,于是上述方程可写为2232,x yy xy 即23()2().dy yydxx x 这是一阶齐次微分方程.令yux ,有dy du u xdxdx,则上式化为2()32,du ux u u dx即3(1).du xu u dx(*)若0u ,则0,y ux 不满足初始条件229x y,舍弃;若1u ,则,y ux x 也不满足初始条件229x y,舍弃;所以,0u,且1u.由(*)式分离变量得3,(1)du dx u u x两边积分得31u Cx u.从而方程(*)的通解为3,y x Cx y C 为任意常数.再代入初值,由229x y,得1C,从而所求的解为33,,(1).1x y xx y yx x或【相关知识点】 1.对积分上限的函数的求导公式:若()()()()t t F t f x dx ,()t ,()t 均一阶可导,则()()()()()F t t f t t f t .九、(本题满分9分)【解析】(1)对等式0T两边取转置,有0TTT,即0T.利用0T及矩阵乘法的运算法则,有22TTTAT TTT0,即2A 是n 阶零矩阵.(2)设是A 的任一特征值,(0)是A 属于特征值的特征向量,即A.对上式两边左乘A 得2A()()AA 2,由(1)的结果20A,得220A,因0,故0(n 重根),即矩阵的全部特征值为零.下面求A 的特征向量:先将A 写成矩阵形式1111212212221212,,,n n Tnnn n n na ab a b a b a a b a b a b Ab b b a a b a b a b .不妨设110,0a b ,则有111211221222212221121212(0)1()01(2,,)n n n n n n n n n n n nn i a b a b a b b b b a b a b a b a b a b a b E A a a b a b a b a b a b a b b b b a i in 行行加到行000于是得方程组(0)0E A x 同解方程组11220n n b x b x b x ,这样基础解系所含向量个数为(0)1nr E A n .选2,,n x x 为自由未知量,将它们的组值111(,0,,0),(0,,,0),(0,0,,)b b b 代入,可解得基础解系为12123111(,,0,,0),(,0,,,0),,(,0,0,,)n n b b b b b b 则A 的属于0的全部特征向量为112211nn k k k ,其中121,,,n k k k 为不全为零的任意常数.十、(本题满分7分)【分析】由于B 是实对称矩阵,B 必可相似对角化,而对角矩阵即B 的特征值,只要求出B 的特征值即知,又因正定的充分必要条件是特征值全大于零,k 的取值亦可求出.【解析】方法1:由210111020(2)(2)1111EA,可得A 的特征值是1232,0.那么,kEA 的特征值是2,2,k kk ,而2()BkE A 的特征值是222(2),(2),.kkk 又由题设知A 是实对称矩阵,则,TAA 故222()()()TTTBkE A kEA kE AB ,即B 也是实对称矩阵,故B 必可相似对角化,且222(2)000(2)000kBk k.当20kk 且时,B 的全部特征值大于零,这时B 为正定矩阵.方法2:由O 1020xy 2D 1D 1020210111020(2)(2)1111EA,可得A 的特征值是1232,0.因为A 是实对称矩阵,故存在可逆矩阵P 使122P AP,即1AP P.那么221121()()()B kE A kPPP P P kE P 1121()()().P kEP P kEPP kEP 即12()P BPkE.故222(2)000(2)000kBk k.当20k k 且时,B 的全部特征值大于零,这时B 为正定矩阵.【相关知识点】1.特征值的性质:若A 有特征值,则A 的特征多项式()f A 有特征值()f .2.矩阵正定的充要条件是特征值全大于零.十一、(本题满分10分)【解析】设Z 表示商店每周所得的利润,当Y X 时,卖得利润为1000Z Y (元);当YX 时,调剂了Y X ,总共得到利润1000500()500()ZXY X X Y (元).所以,1000,,500(),.Y Y X ZXY YX 由题设X 与Y 都服从区间[10,20]上的均匀分布,联合概率密度为1, 1020,1020,(,)1000,xyf x y 其他.由二维连续型随机变量的数学期望定义得1212202020101010202021010()1000(,)500()(,)111000500()100100105()310(20)5(1050)2200005150014166.67().3D D D D yyE Z y f x y dxdyx y f x y dxdy ydxdyxy dxdydyydx dyx y dx y y dyyy dy元十二、(本题满分9分)【解析】记事件j B “第j 次抽到的报名表是女生表”(1,2)j ,iA “报名表是第i 个地区的”(1,2,3)i.易见,123,,A A A 构成一个完备事件组,且1112131{}(1,2,3),3375{},{},{}.101525i P A i P B A P B A P B A (1)应用全概率公式,知3111137529{}{}{}()310152590i i i pP B P A P B A .(2)12{}q P B B .需先计算概率12{}P B B 与2{}P B .对事件12B B 再次用全概率公式:3121211377852020{}{}{}()31091514252490i i i P B B P A P B B A ,由“抽签原理”可知2161()()90P B P B ,12122()209020{}906161()P B B qP B B P B .【相关知识点】 1.全概率公式:如果事件1,,nA A构成一个完备事件组,即它们是两两互不相容,其和为(总体的样本空间);并且0,1,2,,iP A i n,则对任一事件B有1()(|)ni iiP B P A P B A.。
1998考研数学三真题及超详细答案解析

1998年全国硕士研究生入学统一考试数学三试题解析一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1)【答案】1e【解析】曲线ny x =在点(1,1)处的切线斜率1x y ='()1nx x='=11n x n x n -===,根据点斜式,切线方程为:1(1).y n x -=-令0y =,代入1(1)y n x -=-,则11x n =-,即在x 轴上的截距为11n n ξ=-, lim ()n n f ξ→∞lim n n n ξ→∞=1lim(1)n n n →∞=-()()11lim(1)x x x --→∞=-1e=.(2)【答案】ln xC x-+【解析】由分部积分公式,2ln 1x dx x -⎰()1ln 1x dx x '⎛⎫=-- ⎪⎝⎭⎰()1ln 1x d x ⎛⎫=-- ⎪⎝⎭⎰ ln 11(ln 1)x d x x x - -+-⎰分部2ln 11x dx x x-=-+⎰ ln 11x dx x x '-⎛⎫=-- ⎪⎝⎭⎰ln 11x C x x -=--+ln x C x =-+. 【相关知识点】分部积分公式:假定()u u x =与()v v x =均具有连续的导函数,则,uv dx uv u vdx ''=-⎰⎰或者.udv uv vdu =-⎰⎰(3)【答案】51(5)()126tt y C t =-+- 【解析】首先把差分方程改写成标准形式1552t t y y t ++=,其齐次方程对应的特征方程及特征根分别为50,5,r r +==-故齐次方程的通解为(5),tt Y C C =-为常数.将方程右边的52t 改写成512t t ⋅,此处“1”不是特征根,故令非齐次方程的一个特解为,t y At B *=+从而1(1),t y A t B *+=++代入原方程,得5(1)5(),2A tB At B t ++++=56,60,2A A B =+=故 55,1272A B ==-.于是通解为 51(5)().126tt t t y Y y C t *=+=-+-(4)【答案】200040002⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦【解析】由题设 *28A BA BA E =-,由于20A =-≠,所以A 可逆.上式两边左乘A ,右乘1A -,得*11128AA BAA ABAA AA ---=-28A B AB E =-(利用公式:*1,AA A E AA E -==) 28A B AB E -=-(移项)()28A E A B E -=-(矩阵乘法的运算法则)将2A =-代入上式,整理得()14E A B E +=. 由矩阵可逆的定义,知E A +,B 均可逆,且()114B E A --=+1102002401040100021002-⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦200040002⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦.(5)【答案】11,,220100【解析】由于1234,,,X X X X 相互独立,均服从2(0,2)N ,所以由数学期望和方差的性质,得2221212(2)0,(2)122220E X X D X X -=-=⨯+⨯=,所以12(2)(0,20)X X N -,同理34(34)(0,100)X X N -.又因为12(2)X X -与34(34)X X -相互独立,且122)(0,1)X X N -344)(0,1)X X N -,由2χ分布的定义,当11,20100a b ==时, 222123411(2)(34)(2)20100X X X X X χ=-+-.即当11,20100a b ==时,X 服从2χ分布,其自由度为2. 严格地说,当10,100a b ==时,2(1)X χ;当1,020a b ==时,2(1)X χ也是正确的.【相关知识点】1、对于随机变量X 与Y 均服从正态分布,则X 与Y 的线性组合亦服从正态分布.若X 与Y 相互独立,由数学期望和方差的性质,有()()()E aX bY c aE X bE Y c ++=++, 22()()()D aX bY c a D X b D Y ++=+,其中,,a b c 为常数. 2、定理:若2(,)XN μσ,则(0,1)X N μσ-.3、2χ分布的定义:若1,,n Z Z 相互独立,且都服从标准正态分布(0,1)N ,则221~()nii Zn χ=∑.二、选择题(本题共5小题,每小题3分,共15分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1)【答案】(D)【解析】根据导数定义:()0()()limx f x x f x f x x∆→+∆-'=∆0(1)(1)lim 2x f f x x →--01(1)(1)lim 2x f x f x →--=-1(1)2f '=1=- 所以 0(1)(1)(1)lim2.x f x f f x→--'==-- 因为()f x 周期为4,()f x '的周期亦是4,即()(4)f x f x ''=+, 所以(5)f '(14)f '=+(1)2f '==-.所以曲线()y f x =在点()5,(5)f 处的切线的斜率为(5)f '(1)2f '==-.选(D).(2)【答案】(B)【分析】讨论由极限表示的函数的性质,应分两步走.先求出该()f x 的(分段)表达式,然后再讨论()f x 的性质.不能隔着极限号去讨论. 【解析】现求()f x 的(分段)表达式: 当1x >时,21()lim 1n n x f x x →∞+=+2122lim 1n n n n x x x ---→∞+=+()()2122lim 01lim 1n n n n n x x x --→∞-→∞+==+0=; 当1x =时,21()lim1n n x f x x →∞+=+211lim 11n n →∞+=+22=1=;当1x =-时,21()lim1n n x f x x →∞+=+()211lim 11n n →∞-=+-02=0=; 当1x <时,21()lim 1n n x f x x →∞+=+()()2lim 1lim 1n n n x x →∞→∞+=+2011n x x →+ 1x =+. 由此, 0,1,0,1,()1,1,1,1,0,1.x x f x x x x x <-⎧⎪=-⎪⎪=+<⎨⎪=⎪>⎪⎩当当当当当 即0,11,()1,1,1, 1.x x f x x x x ≤->⎧⎪=+ <⎨⎪ =⎩当或当当 再讨论函数()f x 的性质:在1x =-处,()1lim x f x +→-()1lim 1x x +→-=+11=-0=,()()1lim 10x f x f -→-=-=,所以,()()11lim lim 0x x f x f x +-→-→-==,函数()f x 在1x =-处连续,不是间断点.在1x =处,()1lim x f x +→1lim 0x +→=0=;()1lim x f x -→()1lim 1x x -→=+2=; 所以()1lim x f x +→()1lim x f x -→≠,函数()f x 在1x =处不连续,是第一类间断点.故选(B). (3)【答案】(C)【解析】方法1:由0AB =知()()3r A r B +≤,又0,0A B ≠≠,于是1()3,r A ≤<1()3r B ≤<,故0,0A B ==,即2210101011011(1)0111111A λλλλλλλλλλλλ--==--==-=--,得 1.λ=应选(C).方法2:由0AB =知()()3r A r B +≤,又0,0A B ≠≠,于是1()3,r A ≤<1()3r B ≤<,故0B =.显然,1λ=时111111111A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,有1()3,r A ≤<故应选(C). 作为选择题,只需在2λ=-与1λ=中选择一个,因而可以用特殊值代入法.评注:对于条件0AB =应当有两个思路:一是B 的列向量是齐次方程组0Ax =的解;二是秩的信息,即()()r A r B n +≤,要有这两种思考问题的意识. (4)【答案】(B) 【解析】1111100(1)110101101a a a aa aa a a a a A aa a a a aaaa a ⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦1(1)0100(2)00100001n aa a a a a a +-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦其中(1)变换:将1行乘以(-1)再分别加到其余各行;(2)变换:将其余各列分别加到第1列.由阶梯形矩阵知,当1(1)0n a +-=,即11a n=-时,有()1r A n =-,故应选(B). (5)【答案】(A)【解析】根据分布函数的性质lim ()1x F x →+∞=,即121lim ()()()()x F x F aF bF a b →+∞==+∞=+∞-+∞=-.在所给的四个选项中只有(A)满足1a b -=,故应选(A). 【相关知识点】分布函数()F x 的性质:yxO (1) ()F x 单调不减;(2) lim ()()0,lim ()()1;x x F x F F x F →-∞→+∞=-∞==+∞=(3) ()F x 是右连续的.三、(本题满分5分) 【解析】 arctanarctan2222()()()y y xxdz ed x y x y d e--=+++[]arctan22arctan222arctan22arctan22()(arctan )122()()1()22(2)(2)y xyxy xy xy exdx ydy x y d x y exdx ydy x y d y x x xdy ydx e xdx ydy x x ex y dx y x dy ----⎡⎤=+++-⎢⎥⎣⎦⎡⎤⎢⎥=+-+⎢⎥⎢⎥+⎣⎦-⎡⎤=+-⋅⎢⎥⎣⎦=++- 由全微分与偏微分的关系可知,其中dx 的系数就是z x∂∂,即arctan (2)yxz x y ex -∂=+∂.再对y 求偏导数,得222arctanarctanarctan 222211(2).1yyyxxxzy xy x e x y ee y x yx x y x ---⎛⎫⎪∂--=-+= ⎪∂∂+ ⎪+⎪⎝⎭四、(本题满分5分)【解析】22{(,)}D x y x y x =+≤表示圆心为1,02⎛⎫ ⎪⎝⎭,半径为12的圆及其内部,画出区域D ,如右图. 方法1: {}22(,)|01,D x y x x x y x x=≤≤-≤≤-所以, 221120221x x x xDxdxdy xdx x x x dx x xdx ---==-=-⎰⎰⎰, 1x t -=,则21x t =-,2dx tdt =-,:10t →所以上式1350122210082(1)(2)4(1)43515t t t t t dt t t dt ⎛⎫=-⋅-=-=-= ⎪⎝⎭⎰⎰.方法2:引入极坐标系cos ,sin x r y r θθ= =,于是(,)|,0cos 22D r r ππθθθ⎧⎫=-≤≤≤≤⎨⎬⎩⎭,3cos cos 2222232048cos .515Dd r drd ππθθπππθθθθ--====⎰⎰⎰⎰⎰其中倒数第二步用了华里士公式:21342cos 1253n n n d n n πθθ--=⋅⋅⋅⋅⋅-⎰,其中n 为大于1的正奇数.五、(本题满分6分)【分析】根据连续复利公式,在年利率为r 的情况下,现时的A (元)在t 时的总收入为()e rt R t A =,反之,t 时总收入为()R t 的现值为()()ertA t R t -=,将0R R =代入即得到总收入的现值与窖藏时间t 之间的关系式,从而可用微分法求其最大值.【解析】由连续复利公式知,这批酒在窖藏t 年末售出总收入R 的现值为()e rt A t R -=,而由题设,t年末的总收入0R R =据此可列出()A t :()ert rtA t R R -==,令 dAdt0rtd R dt ⎛⎫= ⎪⎝⎭00rtR r ⎫==⎪⎭, 得惟一驻点 02125t t r ==. 22d Adtd dA dt dt ⎛⎫= ⎪⎝⎭0rtdR r dt⎛⎫⎫=⎪⎪⎭⎝⎭00rtrtd d R r R r dt dt ⎛⎫⎫⎫=⋅-+- ⎪⎪⎪⎭⎭⎝⎭200rt rtR r R⎛⎫⎫=-+⎪⎭⎝ 20rt R r ⎡⎤⎫=-⎢⎪⎭⎢⎣1232502(12.5)0r t td AR e r dt ==-<.根据极值的第二充分条件,知:0t t =是()A t 的极大值点,又因驻点惟一,所以也是最大值点.故窖藏2125t r=年出售,总收入的现值最大.当0.06r =时, ()21250.06t =⋅100119=≈(年). 【相关知识点】极值的第二充分条件:设函数()f x 在0x 处具有二阶导数且0()0f x '=,0()0f x ''≠,当0()0f x ''<时,函数()f x 在0x 处取得极大值;当0()0f x ''>时,函数()f x 在0x 处取得极小值.六、(本题满分6分)【分析】本题要证的结论中出现两个中值点ξ和η,这种问题一般应将含有ξ和η的项分别移到等式两边后再用微分中值定理,为此本题只要证()()()()b a f b a e e f e ηξη-''-=-.【解析】方法1: 函数()f x 在[],a b 上连续,在(,)a b 内可导,满足拉格朗日中值定理的条件,对函数()f x 在[],a b 上用拉格朗日中值定理,有()()()(),.f b f a f b a a b ξξ'-=-<<又函数()f x 与xe 满足柯西中值定理的条件,将函数()f x 与xe 在[],a b 上用柯西中值定理,有()()(),b a f b f a f a b e e e ηηη'-=<<-,即()()()b a f f b f a e e eηη'-=-(). 从而有()()()baf f b a e e eηηξ''-=-(),即(),,(,)()b a f e e e a b f b a ηξξηη-'-=⋅∈'-. 方法2:题中没有限制ξη≠,因此取ξη=,即成为要去证存在(,)a b η∈使.b ae e e b aη-=- 在[],a b 上对函数xe 用拉格朗日中值定理,存在(,)a b η∈使, 1.b a b a e e e e e e b a b aηη---=⋅=--即 再取ξη=,则()1()b a f e e e f b aηξη-'-==⋅'-,原题得证.【相关知识点】1.拉格朗日中值定理:如果函数()f x 满足在闭区间[,]a b 上连续,在开区间(),a b 内可导,那么在(),a b 内至少有一点()a b ξξ<<,使等式()()()()f b f a f b a ξ'-=-成立. 2. 柯西中值定理:如果函数()f x 及()F x 满足(1) 在闭区间[,]a b 上连续; (2) 在开区间(,)a b 内可导; (3) 对任一(,)x a b ∈,()0F x '≠, 那么在(,)a b 内至少有一点ξ,使等式()()()()()()f b f a f F b F a F ξξ'-='-成立.七、(本题满分6分) 【解析】(1)由21y nx n =+与21(1)1y n x n =+++得n a =因图形关于y 轴对称,所以,所求图形的面积为220320112(1)121422(1)(1)33nn a n a n n S nx n x dx n n a a x dx n n n n ⎡⎤=+-+-⎢⎥+⎣⎦⎡⎤=-+=-=⎢⎥++⎣⎦⎰⎰ (2)由(1)的结果知41411()3(1)31n n S a n n n n ==-++, 根据级数和的定义,111411414lim lim lim 1.31313n nn k n n n n k k n k S S a a k k n ∞→∞→∞→∞===⎛⎫⎡⎤==-=-= ⎪⎢⎥++⎝⎭⎣⎦∑∑∑八、(本题满分7分)【分析】本题是微分方程的几何应用问题.在题目中给出了由曲线()y f x =等围成的平面图形绕x 轴旋转一周所形成的旋转体体积()V t 与包含函数f 的一个恒等式,这正是列方程的依据.【解析】由绕x 轴旋转的旋转体体积公式得21()()tV t f x dx π=⎰,于是,依题意得221()()(1)3t f x dx t f t f ππ⎡⎤=-⎣⎦⎰,即2213()()(1)tf x dx t f t f =-⎰. 两边对t 求导,化成微分方程223()2()()f t tf t t f t '=+,其中()f t 为未知函数.按通常以x 表示自变量,y 表示未知函数()f t ,于是上述方程可写为2232,x y y xy '=-即23()2().dy y ydx x x=- 这是一阶齐次微分方程.令y ux =,有dy duu x dx dx=+⋅,则上式化为 2()32,duu x u u dx+=- 即 3(1).duxu u dx=- (*) 若0u =,则0,y ux ==不满足初始条件229x y ==,舍弃;若1u =,则,y ux x ==也不满足初始条件229x y ==,舍弃;所以,0u ≠,且1u ≠.由(*)式分离变量得3,(1)du dx u u x =-两边积分得31u Cx u-=.从而方程(*)的通解为3,y x Cx y C -=为任意常数.再代入初值,由229x y==,得1C =-,从而所求的解为 33,,(1).1xy x x y y x x-=-=≥+或 【相关知识点】1. 对积分上限的函数的求导公式:若()()()()t t F t f x dx βα=⎰,()t α,()t β均一阶可导,则 [][]()()()()()F t t f t t f t ββαα'''=⋅-⋅.九、(本题满分9分)【解析】(1)对等式0Tαβ=两边取转置,有()0TTT αββα==,即0T βα=.利用0Tβα=及矩阵乘法的运算法则,有()22TT T A αβαβαβ==()00T T T T αβαβαβαβ===0=,即2A 是n 阶零矩阵.(2)设λ是A 的任一特征值,(0)ξξ≠是A 属于特征值λ的特征向量,即A ξλξ=.对上式两边左乘A 得2A ξ()()A A λξλξλλξ===2λξ=,由(1)的结果20A =,得220A λξξ==,因0ξ≠,故0λ=(n 重根),即矩阵的全部特征值为零.下面求A 的特征向量:先将A 写成矩阵形式[]1111212212221212,,,n n Tn n n n n n a a b a b a b a a b a b a b A b b b a a b a b a b αβ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦.不妨设110,0a b ≠≠,则有111211221222212221121212(0)1()01(2,,)n n n n n n n n n n n n n i a b a b a b b b b a ba b a b a b a b a b E A a a b a b a b a b a b a b b b b a i i n ---⎡⎤⎡⎤⎢⎥⎢⎥------⎢⎥⎢⎥-=÷-⎢⎥⎢⎥⎢⎥⎢⎥------⎣⎦⎣⎦⨯=行行加到行00000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦于是得方程组(0)0E A x -=同解方程组11220n n b x b x b x +++=,这样基础解系所含向量个数为(0)1n r E A n --=-.选2,,n x x 为自由未知量,将它们的组值111(,0,,0),(0,,,0),(0,0,,)b b b 代入,可解得基础解系为12123111(,,0,,0),(,0,,,0),,(,0,0,,)n n b b b b b b ξξξ-=-=-=-则A 的属于0λ=的全部特征向量为112211n n k k k ξξξ--+++,其中121,,,n k k k -为不全为零的任意常数.十、(本题满分7分)【分析】由于B 是实对称矩阵,B 必可相似对角化,而对角矩阵Λ即B 的特征值,只要求出B 的特征值即知Λ,又因正定的充分必要条件是特征值全大于零,k 的取值亦可求出. 【解析】方法1:由y 20211112(2)(2)1111E A λλλλλλλλλ-----=-=-=-----, 可得A 的特征值是1232,0.λλλ===那么,kE A +的特征值是2,2,k k k ++,而2()B kE A =+的特征值是222(2),(2),.k k k ++又由题设知A 是实对称矩阵,则,TA A =故222()()()TTTB kE A kE A kE A B ⎡⎤⎡⎤=+=+=+=⎣⎦⎣⎦, 即B 也是实对称矩阵,故B 必可相似对角化,且222(2)000(2)000k Bk k ⎡⎤+⎢⎥Λ=+⎢⎥⎢⎥⎣⎦. 当20k k ≠-≠且时,B 的全部特征值大于零,这时B 为正定矩阵.方法2:由2101112(2)(2)1111E A λλλλλλλλλ-----=-=-=-----, 可得A 的特征值是1232,0.λλλ===因为A 是实对称矩阵,故存在可逆矩阵P 使1220P AP -⎡⎤⎢⎥=Λ=⎢⎥⎢⎥⎣⎦,即1A P P -=Λ.那么 221121()()()B kE A kPP P P P kE P ---⎡⎤=+=+Λ=+Λ⎣⎦1121()()().P kE P P kE P P kE P ---=+Λ+Λ=+Λ即12()P BP kE -=+Λ.故222(2)000(2)000k Bk k ⎡⎤+⎢⎥+⎢⎥⎢⎥⎣⎦. 当20k k ≠-≠且时,B 的全部特征值大于零,这时B 为正定矩阵.【相关知识点】1.特征值的性质:若A 有特征值λ,则A 的特征多项式()f A 有特征值()f λ. 2.矩阵正定的充要条件是特征值全大于零.十一、(本题满分10分)【解析】设Z 表示商店每周所得的利润,当Y X ≤时,卖得利润为1000Z Y =(元); 当Y X >时,调剂了Y X -,总共得到利润1000500()500()Z X Y X X Y =+-=+(元).所以,1000, ,500(), .Y Y X Z X Y Y X ≤⎧=⎨+>⎩由题设X 与Y 都服从区间[10,20]上的均匀分布,联合概率密度为1, 1020,1020,(,)1000, x y f x y ⎧≤≤≤≤⎪=⎨⎪⎩其他.由二维连续型随机变量的数学期望定义得1212202020101010202021010()1000(,)500()(,)111000500()100100105()310(20)5(1050)2200005150014166.67().3D D D D yyE Z y f x y dxdy x y f x y dxdyy dxdy x y dxdy dy ydx dy x y dxy y dy y y dy=⋅++⋅=⋅++⋅=++=-+--=+⨯≈⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰元十二、(本题满分9分)【解析】记事件j B =“第j 次抽到的报名表是女生表”(1,2)j =,i A =“报名表是第i 个地区的”(1,2,3)i =.易见,123,,A A A 构成一个完备事件组,且1112131{}(1,2,3),3375{},{},{}.101525i P A i P B A P B A P B A =====(1) 应用全概率公式,知3111137529{}{}{}()310152590i i i p P B P A P B A ===⋅=++=∑.(2) 12{}q P B B =.需先计算概率12{}P B B 与2{}P B .对事件12B B 再次用全概率公式:3121211377852020{}{}{}()31091514252490i i i P B B P A P B B A ==⋅=⋅+⋅+⋅=∑,由“抽签原理”可知2161()()90P B P B ==, 12122()209020{}906161()P B B q P B B P B ===⋅=. 【相关知识点】1.全概率公式:如果事件1,,n A A 构成一个完备事件组,即它们是两两互不相容,其和为Ω(总体的样本空间);并且()0,1,2,,i P A i n >=,则对任一事件B 有()1()(|)ni i i P B P A P B A ==∑.。
1998年全国高考文科数学试题及其解析

1998年普通高等学校招生全国统一考试数学(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试120分钟.第Ⅰ卷(选择题共65分)一.选择题:本大题共15小题;第(1)-(10)题每小题4分,第(11)-第(15)题每小题5分,65分.在每小题给出四项选项,只一项符合题目要求的(1) sin600º( )(A)21 (B) -21 (C) 23 (D) -23 (2) 函数y =a |x |(a >1)的图像是( )(3) 已知直线x =a (a >0)和圆(x -1)2+y 2=4相切,那么a 的值是( )(A) 5 (B) 4 (C) 3 (D) 2 (4) 两条直线A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0垂直的充要条件是( )(A) A 1A 2+B 1B 2=0 (B) A 1A 2-B 1B 2=0 (C)12121-=B B A A (D) 12121=A A BB (5) 函数f (x )=x1( x ≠0)的反函数f -1(x )= ( ) (A) x (x ≠0) (B) x 1(x ≠0) (C) -x (x ≠0) (D) -x1(x ≠0)(6) 已知点P(sin α-cos α,tg α)在第一象限,则[ 0,2π]内α的取值范围是( )(A) (432ππ,)∪(45ππ,) (B) (24ππ,)∪(45ππ,) (C) (432ππ,)∪(2325ππ,) (D) (24ππ,)∪(ππ,43) (7) 已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面积展开图扇形的圆心角为( )(A) 120º (B) 150º (C) 180º (D) 240º (8) 复数-i 的一个立方根是i ,它的另外两个立方根是( )(A)2123±I (B) -2123±I (C) ±2123+I (D) ±2123-i (9) 如果棱台的两底面积是S ,S ′,中截面的面积是S 0,那么( )(A) 2S S S '+=0 (B) S 0=S S '(C) 2S 0=S +S ′ (D) S S S '=22(10) 2名医生和4名护士被分配到2所学校为学生体检,每校分配1名医生和2名护士.不同的分配方法共( )(A) 6种 (B) 12种 (C) 18种 (D) 24种(11) 向高为H 的水瓶中注水,注满为止,如果注水量V 与水深h 的函数关系的图像如右图所示,那么水瓶的形状是( )(12) 椭圆31222y x +=1的焦点为F 1,点P 在椭圆上,如果线段PF 1的中点M 在y 轴上,那么点M 的纵坐标是( )(A) ±43 (B) ±23 (C) ±22(D) ±43(13) 球面上有3个点,其中任意两点的球面距离都等于大圆周长为61,经过这3个点的小圆的周长为4π,那么这个球的半径为( )(A) 43 (B)23 (C) 2 (D) 3(14) 一个直角三角形三内角的正弦值成等比数列,其最小内角的正弦值为( )(A)251- (B) 2252- (C) 215- (D) 2252+(15) 等比数列{a n }的公比为-21,前n 项的和S n 满足∞→n lim S n =11a ,那么11a 的值为 ( )(A)3± (B)±23(C) 2± (D) 26±二.填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.(16) 设圆过双曲线116922=-y x 的一个顶点和一个焦点,圆心在双曲线上,则圆心到双曲线中心距离是__________(17) (x +2)10(x 2-1)的展开的x 10系数为____________(用数字作答)(18) 如图,在直四棱柱A 1B 1C 1D 1-ABCD 中,当底面四边形ABCD 满足条件____________时,有A 1C ⊥B 1D 1.(注:填上你认为正确的一种条件即可,不必考试所有可能的情形)(19) 关于函数f (x )=4sin(2x +3π)(x ∈R ),有下列命题 ①y =f (x )的表达式可改写为y =4cos(2x -6π);②y =f (x )是以2π为最小正周期的周期函数;③y =f (x )的图像关于点⎪⎭⎫⎝⎛-06,π对称; ④y =f (x )的图像关于直线x =-6π对称.其中正确的命题的序号是______ (注:把你认为正确的命题的序号都.填上.) 三.解答题:本大题共6小题;共69分.解答应写出文字说明、证明过程或演算步骤. (20) (本小题满分10分)设a ≠b ,解关于x 的不等式a 2x +b 2(1-x )≥[ax +b (1-x )]2.21) (本小题满分11分)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,设a +c =2b ,A -C=3π,求sin B 的值.以下公式供解题时参考:2cos2sin2sin sin ϕθϕθϕθ-+=+, 2s i n2c o s 2s i n s i nϕθϕθϕθ-+=-,2cos 2cos 2cos cos ϕθϕθϕθ-+=+, 2sin 2sin 2cos cos ϕθϕθϕθ-+-=-.(22) (本小题满分12分)如图,直线l 1和l 2相交于点M ,l 1 ⊥l 2,点N ∈l 1.以A 、B 为端点的曲线段C 上的任一点到l 2的距离与到点N 的距离相等.若△AMN 为锐角三角形,|AM |=17,|AN |=3,且|BN |=6.建立适当的坐标系,求曲线C 的方程.(23) (本小题满分12分)已知斜三棱柱ABC -A 1 B 1 C 1的侧面A 1 ACC 1与底面ABC 垂直,∠ABC =90º,BC =2,AC=23,且AA 1 ⊥A 1C ,AA 1= A 1 C 1.(Ⅰ)求侧棱A 1A 与底面ABC 所成角的大小;(Ⅱ)求侧面A 1 ABB 1 与底面ABC 所成二面角的大小; (Ⅲ)求侧棱B 1B 和侧面A 1 ACC 1的距离.(24) (本小题满分12分)如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱.污水从A 孔流入,经沉淀后从B 孔流出.设箱体的长度为a 米,高度为b 米.已知流出的水中该杂质的质量分数与a ,b 的乘积ab 成反比.现有制箱材料60平方米.问当a ,b 各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A 、B 孔的面积忽略不计).(25) (本小题满分12分)已知数列{b n }是等差数列,b 1=1,b 1+b 2+…+b 10=100. (Ⅰ)求数列{b n }的能项b n ; (Ⅱ)设数列{a n }的通项a n =lg(1+nb 1),记S n 是数列{a n }的前n 项的和.试比较S n 与21lg b n +1的大小,并证明你的结论.1998年普通高等学校招生全国统一考试数学试题(文史类)参考解答及评分标准一.选择题:本题考查基本知识和基本运算.第(1)-(10)题每小题4分,第(11)-(15)题每小题5分.满分65分.(1) D (2) B (3) C (4) A (5) B (6) B (7) C (8) D (9) A (10) B (11) B (12) A (13) B (14) C (15) D二.填空题:本题考查基本知识和基本运算.每小题4分,满分16分.(16)316(17) -5120 (18) AC ⊥BD ,或任何能推导出这个条件的其他条件.例如ABCD 是正方形,菱形等 (19)①,③注:第(19)题多填、漏填的错填均给0分. 三.解答题:(20)本小题主要考查不等式基本知识,不等式的解法.满分10分. 解:将原不等式化为(a 2-b 2)x +b 2≥(a -b )2x 2+2(a -b )bx +b 2, 移项,整理后得 (a -b )2(x 2-x ) ≤0, ∵ a ≠b 即 (a -b )2>0, ∴ x 2-x ≤0, 即 x (x -1) ≤0.解此不等式,得解集 {x |0≤x ≤1}.(21) 本小题考查正弦定理,同角三角函数基本公式,诱导公式等基础知识,考查利用三角公式进行恒等变形的技能及运算能力.满分11分.解:由正弦定理和已知条件a +c =2b 得sin A +sin C =2sin B .由和差化积公式得B CA C A sin 22cos 2sin 2=-+. 由A +B +C =π,得 2)sin(C A +=2cos B,又A -C =3π,得23cos 2B =sin B ,∴23cos 2B =2sin 2B cos 2B .∵ 0<2B <2π, 2cos B ≠0,∴sin2B =43, 从而cos2B =2sin 12B -=413 ∴ sin B =⨯23413=839 (22) 本小题主要考查根据所给条件选择适当的坐标系,求曲线方程的解析几何的基本思想.考查抛物线的概念和性质,曲线与方程的关系以及综合运用知识的能力.满分12分.解法一:如图建立坐标系,以l 1为x 轴,MN 的垂直平分线为y 轴,点O 为坐标原点.依题意知:曲线段C 是以点N 为焦点,以l 2为准线的抛线段的一段,其中A 、B 分别为C 的端点.设曲线段C 的方程为y 2=2px (p >0),(x A ≤x ≤x B ,y >0),其中x A ,x B 分别为A ,B 的横坐标,P =|MN |.所以 M (-2P ,0),N (2P,0). 由 |AM |=17,|AN |=3得(x A +2P )2+2Px A =17, ① (x A -2P)2+2Px A =9. ②由①、②两式联立解得x A =P4,再将其代入①式并由p >0解得⎩⎨⎧==14A x p 或⎩⎨⎧==22Ax p . 因为△AMN 是锐角三角形,所以2P>x A ,故舍去⎩⎨⎧==22A x p . ∴ P =4,x A =1.由点B 在曲线段C 上,得x B =|BN |-2P=4. 综上得曲线段C 的方程为y 2=8x (1≤x ≤4,y >0).解法二:如图建立坐标系,分别以l 1、l 2为x 、y 轴,M 为坐标原点.作AE ⊥l 1,AD ⊥l 2,BF ⊥l 2,垂足分别为E 、D 、F . 设 A (x A ,y A )、B (x B ,y B )、N (x N ,0). 依题意有x A =|ME|=|DA|=|AN|=3, y A =|DM |=22DA AM -=22,由于△AMN 为锐角三角形,故有x N =|AE |+|EN |=4. =|ME |+22AE AN -=4X B =|BF |=|BN |=6.设点P (x ,y )是曲线段C 上任一点,则由题意知P 属于集合 {(x ,y )|(x -x N )2+y 2=x 2,x A ≤x ≤x B ,y >0}. 故曲线段C 的方程y 2=8(x -2)(3≤x ≤6,y >0).(23) 本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,棱柱的性质,空间的角和距离的概念,逻辑思维能力、空间想象能力及运算能力.满分12分.注:题中赋分为得到该结论时所得分值,不给中间分. 解:(Ⅰ)作A 1D ⊥AC ,垂足为D ,由面A 1ACC 1⊥面ABC ,得A 1D ⊥面ABC ,∴ ∠A 1AD 为A 1A 与面ABC 所成的角. ∵ AA 1⊥A 1C ,AA 1=A 1C ,∴ ∠A 1AD=45º为所求.(Ⅱ)作DE ⊥AB ,垂足为E ,连A 1E ,则由A 1D ⊥面ABC ,得A 1E ⊥AB . ∴∠A 1ED 是面A 1ABB 1与面ABC 所成二面角的平面角.由已知,AB ⊥BC ,得ED ∥BC .又D 是AC 的中点,BC =2,AC =23,∴ DE =1,AD =A 1D =3,tg A 1ED=DEDA 1=3. 故∠A 1ED=60º为所求.(Ⅲ) 作BF ⊥AC ,F 为垂足,由面A 1ACC 1⊥面ABC ,知BF ⊥面A 1ACC 1. ∵ B 1B ∥面A 1ACC 1,∴ BF 的长是B 1B 和面A 1ACC 1的距离. 在Rt △ABC 中,2222=-=BC AC AB ,∴ 362=⋅=AC BC AB BF 为所求. (24) 本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力,考查建立函数关系、不等式性质、最大值、最小值等基础知识.满分12分.解法一:设y 为流出的水中杂质的质量分数,则y =abk,其中k >0为比例系数,依题意,即所求的a ,b 值使y 值最小.根据题设,有4b +2ab +2a =60(a >0,b >0), 得 aab +-=230 (0<a <30=, ① 于是 aa a k ab k y +-==230226432+-+-=a a k⎪⎭⎫ ⎝⎛+++-=264234a a k()2642234+⋅+-≥a a k18k =当a +2=264+a 时取等号,y 达最小值.这时a =6,a =-10(舍去). 将a =6代入①式得b =3.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小. 解法二:依题意,即所求的a ,b 的值使ab 最大. 由题设知 4a +2ab +2a =60 (a >0,b >0) 即 a +2b +ab =30 (a >0,b >0). ∵ a +2b ≥2ab , ∴ 22ab +ab ≤30,当且仅当a =2b 时,上式取等号. 由a >0,b >0,解得0<ab ≤18.即当a =2b 时,ab 取得最大值,其最大值18. ∴ 2b 2=18.解得b =3,a =6.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小.(25) 本小题主要考查等差数列基本概念及其通项求法,考查对数函数性质,考查归纳,推理能力以及用数学归纳法进行论证的能力.满分12分.解:(Ⅰ)设数列工{b n }的公差为d ,由题意得 b 1=1, 10b 1+d2)110(10-=100.解得 b 1=1,d =2. ∴ b n =2n -1. (Ⅱ)由b n =2n -1,知S n =lg(1+1)+lg(1+31)+…+lg(1+121-n ) =lg[(1+1)(1+31)· … ·(1+121-n )],21lg b n +1=lg 12+n . 因此要比较S n 与21lg b n +1的大小,可先比较(1+1)(1+31)· … ·(1+121-n )与12+n 的大小.取n =1有(1+1)>112+⋅,取n =2有(1+1)(1+31)>112+⋅ 由此推测(1+1)(1+31)· … ·(1+121-n )>12+n . ①若①式成立,则由对数函数性质可判定: S n >21lgb n +1. 下面用数学归纳法证明①式. (i)当n =1时已验证①式成立. (ii)假设当n =k (k ≥1)时,①式成立,即 (1+1)(1+31)· … ·(1+121-k )>12+k ,那么,当n =k +1时, (1+1)(1+31)· … ·(1+121-k )(1+1)1(21-+k )>12+k (1+121+k ) =1212++k k (2k +2).∵ [1212++k k (2k +2)]2-[32+k ]2=123848422+++++k k k k k=121+k >0, ∴1212++k k (2k +2) >32+k =()112++k .因而 (1+1)(1+31)· … ·(1+121-k )(1+121+k )>1)1(2++k . 这就是说①式当n =k +1时也成立.由(i),(ii )知①式对任何正整数n 都成立.由此证得:S n >21lg b n +1.。
