简支栓焊桁架桥主杆件内力计算_secret
2桁架杆件内力的求解方法

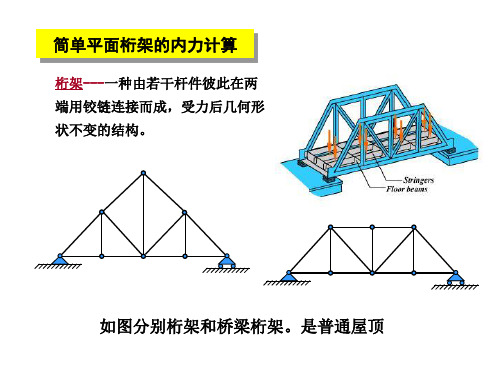
求解桁架内力的方法
将每个节点视为平面汇交力系平衡对象,逐个节点求解。
例1:平面桁架如图示,已知:F=2kN,
试求:各杆的内力与支座约束力。
F
y
A
B
C
解: F
FAB
A
4m
x
D
E
333 3
FAD
[A]
Fiy = 0 : − F − FAD
4 =0 32 + 42
FAD
=
−
25 4
=
−2.5kN
Fix
= 0:
FAB
+ FAD
3 5
=0
FAB = 1.5kN
FDA D
FDB
[D]
Fiy
= 0:
FDA
4 5
+
FDB
4 5
=0
FDE
Fix
= 0:
FDB
3 5
−
FDA
3 5
+
FDE
=0
FDB = 2.5kN
FDE = −3kN
F
[B]
FBA B
FBC
A
B
C
FBD
FBE
4m
D
E
Fiy = 0 : Fix = 0
FC
a
a
n B
F [节点H]
FEH
=
4 3
F
D
F =0 ix
a FEH + FGH a2 + b2 − FHK = 0
F FCF C
n
A
Fy = 0,
F
− FGH
b a2 + b2
桁架内力计算

21
一、节点法 (1)一般先研究整体,求支座约束力; (2)逐个取各节点为研究对象; (3)求杆件内力; (4)所选节点的未知力数目不大于2,由此 开始计算。
练习1
判断结构中的零杆
F F
F
FP
2015-3-5
15
结点法
基本概念 结点法 截面法 联合法 小结
۞
练习2
计算桁架各杆件内力
2F a
4×a
第一步:求支座反力 第二步:判断零杆和单杆,简化问题 第三步:逐次去结点,列平衡方程 第四步:自我检查
16
2015-3-5
结点法
基本概念 结点法 截面法 联合法 小结
目 ≤ 独立方程数(即2个);
小结
基本思路:尽可能简化问题,一般先求支座反力,
然后逐次列结点平衡方程。
2015-3-5 10
结点法
۞
例题1
如图所示为一施工托架计算简图,求图示 荷载作用下各杆轴力(单位:kN)。
基本概念 结点法 截面法 联合法 小结
8 A
1.5m
8
C 6 E8 G F
8
B
截面法
基本概念
۞ 例题2
求图示桁架25、34、35三杆内力(单位:kN)。 10 20
I 4
7 2m 8
结点法
10
3
a
截面法 联合法 小结
1
2
5 I8 m
6
解: 1)求支座反力。2)截面法,取分离体受力 分析,求内力。
简直栓焊桁架桥的设计计算

简直栓焊桁架桥的设计计算A1A2A3A4A3'A2'A1'E0E1E2E3E4E3'E2'E1'E0'l=64 m 11m主桁结构图弦杆影响线简直栓焊桁架桥的设计计算⼀单线铁路简直栓焊桁架桥,l=64 m 设计荷载为中荷载,主桁尺⼨如下图所⽰,钢材为Q345qE ,主桁中⼼矩B=6.4m⼀、计算主⼒作⽤下个主横杆件内⼒1、横载计算主桁:19.2kN/m 。
桥⾯系;7.8kN/m 。
⾼强螺栓:1.0kN/m 。
桥⾯及⼈⾏道为双侧设钢筋混凝⼟⼈⾏道板:10kN/m 。
连接系:4.1kN/m 。
故每⽚主桁重19.27.8 1.010 4.1p 21.05/2kN m ++++==2、影响线⾯积计算2l 12l l y lH=1l Lα=L1L1'L2'L2yy'斜杆影响线3、内⼒计算由恒载和活载产⽣的各杆件的内⼒见下表列车横向摇摆⼒:以下弦杆E2E4举例说明,如下图所⽰该杆件受到的列车摇摆⼒引起的弦杆内⼒计算图,其它结果见下表。
4、列表将计算结果列⼊下表1sin θ1sin θl =80m下弦杆受到列车摇摆⼒的计算图⽰2410015.75284.386.4E E M N kNB ?==±=±⼆、附加⼒作⽤下主桁杆件的内⼒(⼀)横向风⼒标准设计中,桥上有车时的风荷载采⽤1250Pa[][]=0.50.411+3+1.51-0.41250=6.125k /=0.50.411+3+1.51-0.41250=3.25k /N m N m ωω下上()()()()0.21. 上平纵联由横向风⼒引起上弦杆内⼒的计算图⽰见下图A1A3:1123648 3.425248115.596.4M N kN B==±=± A3A3’1282048 3.425248149.846.4==±=±2. 下平纵联由横向风⼒引起下弦杆内⼒的计算图⽰见上图E0E2:1125264 6.125264597.196.4M N kN B==±=±E2E4:1283664 6.125264964.696.4M N kN B==±=±l =64m下平纵联横向风⼒计算图⽰上平纵联横向风⼒计算图⽰l =48mω下ω上(⼆)桥门架效应桥门架效应引起的主桁杆件内⼒计算,其计算图⽰如下图所⽰。
桁架结构内力计算方法

桁架结构内力计算方法
在计算桁架结构内力时,可以采用以下步骤:
1.给定载荷:首先确定桁架结构所受到的外部载荷,包括竖向荷载、
水平荷载和斜向荷载等。
这些载荷可以通过静力学分析或者实际测量得到。
2.确定支座反力:根据结构平衡条件,计算出桁架结构支座的反力。
支座反力是由桁架结构与支座之间的约束关系决定的。
3.确定节点平衡条件:桁架结构中的每个节点都应满足平衡条件,即
节点受力平衡。
根据节点的受力平衡条件,可以得到每个节点处的力平衡
方程。
4.建立杆件的受力方程:根据构件材料的力学性质和几何形状,建立
每根杆件的受力方程。
通常使用杆件受力平衡和伸缩力平衡方程。
5.解方程求解内力:将节点平衡条件和杆件受力方程组合起来,得到
一个线性方程组。
通过求解这个方程组,可以求解出各个构件的内力大小
和方向。
在具体计算过程中,可以采用不同的计算方法来求解桁架结构的内力。
以下是几种常用的计算方法:
1.切线法:切线法是一种基于几何形状的方法,通过假设桁架结构各
个构件处于弧形变形状态,利用切线关系计算出内力。
该方法适用于相对
简单的桁架结构。
2.牛顿-拉夫逊法:牛顿-拉夫逊法是一种基于力的平衡条件的方法,
通过迭代计算桁架结构内力。
该方法适用于复杂的桁架结构。
3.力法:力法是一种基于力平衡方程和几何条件的方法,通过逐个构件计算内力。
该方法适用于任意形状的桁架结构。
以上是桁架结构内力计算的基本方法和一些常用的计算方法。
在实际应用中,还可以根据具体情况选择适合的方法进行计算。
桁架的内力计算

�
平面内 计算长度: 桁架 桁架平面内 平面内计算长度:
l0 x = 0.5l
�
无论另一杆为拉杆或压杆,两杆互为支承点。 平面外 计算长度: 桁架 桁架平面外 平面外计算长度: 拉杆可作为压杆的平面外支承点, 压杆除非受力较小且不断开,否则不起侧向支点 的作用。 GB50017 规范中交叉腹杆中压杆的平面外 GB50017规范中交叉腹杆中压杆的平面外 计算长度计算公式:
4)相交另一杆受拉,此拉杆在交叉点中断但以 节点板搭接。 3N 0 loy = l 1 − ≥ 0.5l 4N
当此拉杆连续而压杆在交叉点中断但以节点板搭接。 若
N0 ≥ N
或拉杆在桁架平面外的抗弯刚度
3 N 0l 2 N EI y ≥ ( − 1) 2 4π N0
时,
l0 y = 0.5l
式中, l 为节点之间的距离, N 为所计算杆内力,N0 为相交另一杆内力,取绝对值。
2.3.2 桁架杆件的计算长度 2.3.2桁架杆件的计算长度 2.3.2 桁架杆件的计算长度 2.3.2桁架杆件的计算长度
计算长度概念:将端部有约束的压杆化作等 效的两端铰接的理想轴心压杆。 (a) (b)
Pcr1 =
Pcr 2 = Pcr 3 =
π 2 EI L2 π 2 EI
( 0.5 L ) 2
l0 y = l1 (0.75 + 0.25 N 2 N1
)
l1 = 2 d
考虑受力较小的杆件对受力大的杆件的 “援助”作用。
交叉腹杆中压杆的计算长度 2.3.2.3 2.3.2.3交叉腹杆中压杆的计算长度 2.3.2.3 交叉腹杆中压杆的计算长度 2.3.2.3交叉腹杆中压杆的计算长度
�
交叉腹杆中交叉点处构造: 1)两杆不断开。 2)一杆不断开,另一杆断开 用节点板拼接。
简单平面桁架的内力计算
思考题
C
D
用截面法求杆1,2,3的内力。 用截面m,并取上半部分。 m
a
1
E 2 F
3
m
a B
F
a
x
0, 求出杆2的内力F2。
C
A
a
a
F
M
0, 求出杆3的内力F3。
M
D
0, 求出杆1的内力F1。
3. 计算桁架杆件内力的方法
节点法—— 应用共点力系平衡条件,逐一研究桁架上每个
节点的平衡。
截面法—— 用应用平面任意力系的平衡条件,研究桁架由 截面切出的某些部分的平衡。
例3-10 如图平面桁架,求各杆内力。已知铅垂力FC=4 kN, 水平力FE=2 kN。
F E a A a C a a B
FE
a
C
FAx
解得
FC
FCE 2 2 kN ,
FCD 2 kN
FDE
D
8.取节点D,受力分析如图。 列平衡方程
FDB
FDC
F
x
0,
FDB FDC 0
F E a D
FAy
A a
FE
a
F
FB
B
y
0,
FDE 0
解得
a
C
FAx
FC
FDB 3 kN ,
FDE 0
9.取节点B,受力分析如图。
D
FC
解: 节点法
1.取整体为研究 对象,受力分析如图。
FAy
A a C F
E
a
FE
a
FB
B
a
FAx
D
FC
3.列平衡方程。
桁架的内力计算

图1 屋架节点荷载的计算桁架的内力计算当桁架只受节点荷载时,其杆件内力一般按节点荷载作用下的铰接桁架计算。
这样,所有杆件都是轴心受压或轴心受拉杆件,不承受弯矩。
具体计算可用数解法(节点法或截面法)、图解法(主要是节点法)、图解法(主要是节点法)、计算机法(常用有限元位移法)等。
实际桁架节点为焊缝、铆钉或螺栓连接,具有很大的刚性,接近于刚接。
按刚接节点分析桁架时,各杆件将既受力又受弯矩。
但是,通常钢桁架中各杆件截面的高度都较小,仅为其长度的1/15(腹杆)和1/10(弦杆)以下,抗弯刚度较小;因而按刚接桁架算得的杆件弯矩M 常较小,且杆件轴心力N 也与桁架计算结果相差很小。
故一般情况都按铰接桁架计算。
对少数荷载较大的重型桁架,例如铁路桥梁等,当杆件截面高度超过其长度的1/10时,次应力份额逐渐增大,可达10~30%或以上,必要时应作计算。
目前用计算机计算刚接桁架已无困难。
据上所述,檩条或大型屋面板等集中荷载只作用在屋架节点处时,可按铰接桁架承受节点荷载计算杆件内力,例如图1。
这时节点荷载值即为檩条或边肋处的集中荷载值,按式上一小节公式,即:100011122F qA qbd d F qA qb d d d F qA qb == ==++== 来计算。
该图中檐口檩条集中荷载F 0在桁架计算时可归并入F 1内(或端节间按伸臂梁而将F 0(1+d 1/ d )并入F 1,-F 0 d 1/d 并入第二节点F );另外在计算上弦杆的支座截面时,除考虑轴心压力外还考虑偏心弯矩M e =F 0 d 1。
当檩条或屋面板等布置未与屋架节点相配合,屋面板没有边肋而是全宽度支图2 承受节间荷载的屋架 承于屋架上弦(上弦均布荷载)、或其它特殊情况时,桁架将受节间荷载,例如图1。
这时桁架内力计算可按下列近似方法:(1)把所有节间内荷载按该段节间为简支的支座反力关系分配到相邻两个节点上作为节点荷载,据此按铰接桁架计算杆件的轴心力。
结构力学 静定桁架的内力计算

F Ay= 2 F P
(b)
参照图(b)计算如下:
见图(b),未知杆力在隔离体上的一 般表示。
MD 0
F NG 1 h C(F P bF 2 P2 b2 F P2 b )
由几何关系得:h 2 b 代入上式,
5
FNGC 5FP
MG 0
FNE Db 2(2FPF 2P)b3FP
图(d):
在反对称荷载下,桁架应具有反对称 的内力分布,即在桁架的对称轴两侧 的对称位置上的杆件,应有大小相等、 性质相反的轴力。
考查结点E:见图(f) EJ为零杆,继而JA、 JB为零杆。
(f )
§6.3 桁架内力计算的截面法
➢截面法:用一个假想的截面,将桁架 截成两部分,取其任一部分为隔离体 ,建立该隔离体的平衡方程,求解杆 轴力的方法。
利用该结点的对称性,且由水平方 向的投影方程得:
FNa
2 2 FP
(a)
§6.4 组合结构的内力分析
❖既有梁式杆又有桁架杆的结构称作 组合结构。见图6-4-1所示。
图6-4-1
组合结构内力计算的一般途径是: 先计算桁架杆,再计算梁式杆。
例6-4-1
计算图(a)所示组合结构,求出二力 杆中的轴力,并作梁式杆的弯矩图。
D
F NDC
F NGE
G
A
K
F NKH
FP FP
(c)
由图(c)所示截面左侧隔离体求出截面
截断的三根杆的轴力后,即可依次按
结点法求出所有杆的轴力。
❖ 方法1:
见图(d) ,由结点H的结点单杆 EH上的轴力,再由结点E(当 杆EH轴力已知时,杆a既是结 点E上的结点单杆)可求出杆a 的轴力。
工程力学-桁架内力的计算

34
摩擦的存在既有利也有弊: 利——用于传动机械、启动或制动。 弊——消耗能量,磨损零件,降低精度和机械效率。
摩擦的分类:
滑动摩擦 滚动摩擦
静摩擦 ——仅有相对运动趋势时产生的 动摩擦 ——已有相对运动时产生的
干摩擦 ——接触表面凸凹不平引起的 湿摩擦 ——物体接触面之间有液体成膜的
35
2.静摩擦力(静滑动摩擦力)
未知力的节点。
(4)将未知数(各杆内力)统一设为拉力
(即节点处各杆的内力矢量方向从节点指向外)。
取节点C为分离体:
P
C
D
F
P
C
F1
F1
12
例题
例题6
§7 力系的平衡
C
E
GP
A
B
D
桁架结构受力如图,杆
AE=EC=CG=GB=AD=
ED=DG=DB=a ,求各
杆的内力。
13
例题
例题6
§7 力系的平衡
0杆 等轴力杆
无主动力的三杆节点,其中二杆共线
0杆
0杆 无主动力的不共线二杆节点
0杆
不共线的二杆节点,主动力沿其中一杆 F
无主动力,共线的二杆节点
等轴力杆
或两两共线的四杆节点 两对等轴力杆
6
还可利用对称性:
等轴力杆 F
注意:桁架中的零杆,不承担载荷,只起到维持结 构几何稳定性的作用。故虽列力系平衡方程时零杆 不起作用,但结构本身不可将零杆去掉。 求桁架的内力通常有两种方法:
FAD
P
P 2
1 2
3 4
P
FAxA
FAE
FAy FAD
0
E \\
FAx
简单桁架内力的计算方法

25您的位置:在线学习—>在线教程—>教学内容上一页返回目录下一页3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如南京长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于铰的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的铰结点。
(2)各杆的轴线都是直线并通过铰的中心。
(3)荷载和支座反力都作用在铰结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3 桁架的分类(1)简单桁架:由基础或一个基本铰接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的铰接体系。
(图3-14b)(3)复杂桁架:不属于前两类的桁架。
(图3-14c)3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法――适用于计算简单桁架。
截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法――在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
简单桁架内力计算

3.4静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法一一结点法、截面法、联合法3.4.1桁架的特点和组成3.4.1.1静定平面桁架桁架结构是指若干直杆在两端较接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如南京长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于较的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的较结点。
(2)各杆的轴线都是直线并通过钱的中心。
(3)荷载和支座反力都作用在较结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3桁架的分类(1)简单桁架:由基础或一个基本较接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的较接体系。
(图3-14b)(3)复杂桁架:不属于前两类的桁架。
(图3-14c)图3-图3-14c3.4.2桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法一一适用于计算简单桁架。
截面法一一适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法一一在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
解题的关键是从几何构造分析着手,利用结点单杆、截面单杆的特点,使问题可解。
桁架支撑计算

施工平台支撑验算支架搭设高度为7.4米,搭设尺寸为:立杆的纵距b=1.20m,立杆的横距l=1.20m,立杆的步距顶托下部h=1.50m, 采用2根50*100的方通。
方通下方为桁架。
1. 立杆计算:(1)荷载计算:取1 个计算单元:(1.2m*1.2m)立杆自重:7.4m*3.5kg/m=0.26kN;施工荷载取1 00kg/m 2;堆放荷载取1 00kg/m 2;水平杆作用在单根立杆上的重量为(5 道双向):2.4*5*3.5kg/m=0.42kN ;单根立杆荷载总和为:N=2*1.44+0.26+0.42=3.6kN;(2)立杆稳定性验算:2A=4.24cm2, i=1.6cm计算长度l0=uh=1.75*1.5=2.6m入=l o/i=26O/1.6=162.5, © =0.29422f=N/ ① A=3.6/(424*0.294)=28.9N/mm2v[f]=215N/mm2满足要求。
2. 方通验算:按三跨连续梁计算:用SAP 200(进行计算,结果如下:最大挠度位于1.6m处,(双方通)挠度为14mm/2=7mm<3600mm/250=14.4mm满足要求。
(2)刚度验算:弯矩图如下(kN.m):M max=3.54kN.m, W=15.52cm3;2 2f=M/W=3.54/ (2*15.52) =114N/mm2v[f]=215N/mm 2 满足要求。
(3) 支座反力:支座反力如下:3. 桁架验算:计算模型:a. Y-Z平面:内力计算结果为: 上部横杆计算结果为:F部横杆计算结果为:今.沪乜严1¥ ,OK J J |DEAO .-J aA^Jji : ns 0iL (n>Q0m( Jffijjlc 7 OCCOfMOn (SieffiDOrrj)IPb. X-Y 平面:平行于X 轴杆件计算结果为:重住応抽甲笛JI 换 r 工住 |KKl,hi.C _2_Cut I EUM I |?dir|QdfiKhftn dlZ'JjLft) m 獲察當力Shear ¥2HgiOKFldt?^KDQmMimwrMl3^JSXEOmDnirfliM^Mm i(2 dir)OQOOQ^m& 幅iCDCOmFtf-iive : i i -2 di =Ji_"c. X-Z 平面:内力计算结果为:d. Y-Z 平面内中间跨:内力计算结果为::毗.虫喚SZiZiija.IT IX |DUD*J 谄1 Jjt 価|材勺芦阳2堀』H3] ▼ |邙ngh j 凶Z * | ----- ormnoom[0 EDOODni} Jffi : Lit IM ----- octnirom pi eocra^ * XTftt;-冃日和口幣味中p '?f +N, :Mwri 亦;讥 冷:"蚀"|莖住社訪事直_ I 新 ] 卫位|KKtn C杆件计算:横梁内力计算结果为:M=7.94kN.m刚度验算:F=M/W=7.94kN.m/477cm3=16.6N/mm2<215N/mm2型钢立柱验算:支座反力为:N=102.74kN2A=64.28cm , i=8.61cm, l=1.5m入=l/i=150/8.61=17, © =0.9862 2f=N/ ① A=102.74/(0.986*642.8)=16.2N/mm2v[f]=215N/mm满足要求。
简单桁架内力的计算方法

25您的位置:在线学习—>在线教程—>教学内容上一页返回目录下一页3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如南京长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于铰的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的铰结点。
(2)各杆的轴线都是直线并通过铰的中心。
(3)荷载和支座反力都作用在铰结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3 桁架的分类(1)简单桁架:由基础或一个基本铰接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的铰接体系。
(图3-14b))3-14c复杂桁架:不属于前两类的桁架。
(图)3(.3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法――适用于计算简单桁架。
截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法――在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
桁架的内力计算

好运动者健,好思考者智,好助人
11
者乐,好读书者博,好旅游者悦,
2.3.2.2 变内力压杆的计算长度
平面内计算长度:
l0x d
平面外计算长度:
l0y l1(0.75 0.25 N2 N1)
l1 2d
考虑受力较小的杆件对受力大的杆件的“援助”作用。
好运动者健,好思考者智,好助人
12
者乐,好读书者博,好旅游者悦,
简化计算:
M0为将上弦节间视为简支梁所得跨中弯矩。
好运动者健,好思考者智,好助人
6
者乐,好读书者博,好旅游者悦,
2.3.2桁架杆件的计算长度
计算长度概念:将端部有约束的压杆化作等 效的两端铰接的理想轴心压杆。
P 2EI cr1
(a)
L2
P 2EI
(b) cr2
( 0.5 L ) 2
(c)
P 2EI cr3 ( L ) 2
刚度要求:
[]
容许长细比,查规范(GB50017)。
好运动者健,好思考者智,好助人
18
者乐,好读书者博,好旅游者悦,
2.3.3杆件截面型式
杆件截面选取的原则:
承载能力高,抗弯强度大, 便于连接,用料经济通常 选用角钢和T型钢
截面伸展 壁厚较薄 外表平整
等强设计: 压杆对截面主轴具有相等或接近的稳定性。
3)与所分析杆直接刚性相连的杆件作用大, 较远的杆件作用小。
好运动者健,好思考者智,好助人
8
者乐,好读书者博,好旅游者悦,
➢ 2. 杆件计算长度:
桁架平面内计算长度 l0x
弦杆
支座斜杆 支座竖杆
l0x l (节件长度)
中间腹杆 l0x 0.8l
平面简单桁架的内力计算

非共线杆
F2
F1
F3=0
F1 F
F2=0
(b)无载三根杆, (c)有载二根非
二根共线杆
共线杆
两杆形成的节点,如果没有外力或约束力作用于该节点,则两 杆为零力杆;三杆形成的节点,其中有两杆共线如,果没有 外力或约束力作用 于该节点,则第三杆为零力杆。
节点法与截面法的联合应用
节点法:因为桁架中各杆都是二力杆,所以每个节点都受 到平面汇交力系的作用,为计算各杆内力,可以逐个地取 各节点为研究对象,根据平面汇交力系的平衡条件,计算 桁架内各个杆件内力的方法。
)所有杆件的内力先设为拉力,计算结果为负,说明该杆为
压力;(3)用节点法时,节点上的未知力一般不能多于两个
,用截面法时,节点上的总未知力一般不能多于三个,否则
不能全部解出。(4)若只要求桁架中某几个杆件的内力时,
可以采用截面法或节点法结合截面法,可较快地求得某些杆
的内力。
41
本章小结
一、力线平移定理是力系简化的理论基础 力 力+力偶
Q q
2l
l
3
3
3、梯形荷载
可以看作一个三角形荷载和一 个均布荷载的叠加
q1
q2
l
49
50
51
组合梁AC和CE用铰链C相连,A端为固定端,E端为活动 铰链支座。受力如图所示。已知: l =8 m,F=5 kN,均布载 荷集度q=2.5 kN/m,力偶矩的大小M= 5 kN•m,试求固端A, 铰链C和支座E的约束力。
1.对称性
结构对称,载荷对称,则内力必对称; 结构对称,载荷反对称,则内力必反对称;
求内力时,可利用下列情况简化计算:
2.零杆的判别
桁架内力计算方法

桁架内力计算方法
桁架内力计算方法是结构力学中的重要内容,用于确定桁架各个构件的内力大小和性质。
桁架是由多个杆件和节点组成的刚性结构,节点是杆件的连接点,杆件则是连接节点的直线构件。
在计算桁架内力时,常用的方法有以下几种:
1. 静力平衡法:静力平衡法是最常用的计算桁架内力的方法。
根据静力平衡的原理,可以根据桁架的外部受力和支座反力,利用平衡条件推导出各个构件的内力。
通过将桁架分解为多个杆件,然后应用平衡方程和静力学原理,可以很容易地求解出各杆件的内力。
2. 方法之力法:方法之力法是一种辅助计算桁架内力的方法。
通过在桁架图上引入一些虚拟杆件,形成一个平衡闭合图,然后根据静力平衡法计算出这些虚拟杆件的内力,再通过力的平衡推算出桁架实际构件的内力。
这种方法可以简化计算过程,尤其适用于复杂桁架的内力计算。
3. 图解法:图解法是一种直观的计算桁架内力的方法,通过在桁架图上绘制受力图和内力图,可以直接读取出各个构件的内力大小和方向。
图解法适用于简单桁架的内力计算,但对于复杂桁架的计算可能较为繁琐。
4. 位移法:位移法是一种基于结构变形原理的计算桁架内力的方法。
根据桁架的刚度矩阵和位移向量的关系,可以建立起位移方程,通过求解位移方程组来求解桁架的内力。
位移法适用于计算复杂桁架的内力,但需要较高的数学和计算机软件的支持。
综上所述,桁架内力的计算方法多种多样,可以根据具体情况选择合适的方法进行计算。
在实际工程中,通常会结合多种方法进行计算,以确保计算结果的准确性和可靠性。
单线铁路下承式栓焊简支钢桁梁桥计算书

第一节 第二节 第三节 第四节 第五节 第六节 第四章
拼接板和节点板的计算…………………………………… …… ……35 弦杆拼接计算…………………………………………………… 35 节点板计算……………………………………………………… 38 39
第一节 第二节 第五章
挠度计算及预拱度设计………………………………………………
杆件内力计算…………………………………………………………
第一节 第二节 第三节
主力作用下主桁杆件内力计算…………… ………… …… …5 横向风力作用下的主桁杆件附加内力计算………………… …9 制动力作用下的主桁杆件附加内力计算……………………… 12
单线铁路下承式栓焊简支钢桁梁
单线铁路下承式栓焊简支钢桁梁桥课程设计
1
单线铁路下承式栓焊简支钢桁梁桥
目 录
第一章 设计资料…………………………………………………………………3 第一节基本资料…………………………………………………………… 3 第二节 第三节 第二章 设计内容………………………………………………………… 4 设计要求………………………………………………………… 4 5
22.38 52.22 26 1.526 74.6 10.26
其余弦杆计算方法同上,计算结果列于下表中。 (2) 斜杆
1 1 l '2 1 1 l2 ' ,y , 1 1.236 , y sin l sin sin l tan 2
1 1 (l1 l 2 ) y, ' (l1 l 2 ) y ' 2 2
E 4 E5:N k 52.79 (12.81) 676.23KN , N ' k 54.80 8.20 449.36 KN A5 E5:N k 61.21 7.46 456.63KN
杆件的内力计算

线重合的内力称为轴力,用FN表示。
1.2.3 轴力图
用平行于杆件轴线的x轴 表示横截面的位置,垂直于x
求约束力 分段 求各段轴力 逐段画出轴力图
轴的FN表示横截面上轴力的大小,在x—FN坐标系中按选定的比例画出轴 力沿轴线方向变化的图形,称为轴力图。
杆件的内力计算
1.3 梁的内力与内力图
返回
3.1.1 弯曲的概念
杆件的内力计算
1.2 轴向拉压杆的内力与内力图
返回
1.2.1 轴向拉压杆件的受力与变形特征
杆件是直杆,作用于杆件上的外力合力作用线与杆件轴线重合,杆件
变形是沿轴线方向的伸长或缩短。这种变形形式称为轴向拉伸或轴向压缩,
这类杆件称为拉杆或压杆。
1.2.2 拉压杆横截面上的内力——轴力
杆件轴向拉伸或压缩时,横截面上的内力与轴线重合,这种与杆件轴
式中,Me为外力偶矩(N·m);P为功率(kW);n为转速(r/min)。
杆件的内力计算
1.4 受扭圆轴的内力与内力图
1.4.3 扭矩与扭矩图
受扭圆轴横截面上的内力偶矩称为轴的扭矩,用T表示。通常用右手 螺旋法则确定扭矩的正负号:用右手四指沿扭矩的转向握着轴,大拇指的 指向(扭矩的矢量方向)背离截面时,扭矩为正;反之,扭矩为负,如下 图所示。
(1)对于无分布载荷作用的梁段,剪力等于常数,剪力图是一条水平直 线;弯矩图是一条斜直线,其斜率等于剪力。
(2)对于均布载荷作用的梁段,剪力图是一条斜直线,其斜率等于载荷 集度,弯矩图为二次抛物线。
(3)在剪力等于0的截面上,弯矩取极值。 (4)在集中力作用的截面上,剪力发生突变,突变值等于集中力的大小, 自左向右突变的方向与集中力的指向相同,弯矩图出现尖点。 (5)在集中力偶作用的截面上,剪力图无变化,弯矩图发生突变,突变 值等于集中力偶矩的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A1A2A3A4A3'A2'A1'E0E1E2E3E4E3'E2'E1'E0'
l=64 m
11m
主桁结构图
弦杆影响线
简支栓焊桁架桥的设计计算
一单线铁路简支栓焊桁架桥,l=64 m 设计荷载为中荷载,主桁尺寸如下图所示,钢材为Q345qE ,主桁中心矩B=6.4m
一、 计算主力作用下个主横杆件内力
1、 横载计算 主桁:19.2kN/m 。
桥面系;7.8kN/m 。
高强螺栓:1.0kN/m 。
桥面及人行道为双侧设钢筋混凝土人行道板:10kN/m 。
连接系:4.1kN/m 。
故每片主桁重19.27.8 1.010 4.1
p 21.05/2
kN m ++++=
=
2、 影响线面积计算
2
l 12l l y lH
=
1l L
α=
L1
L1'L2'
L2
y
y'
斜杆影响线
3、 内力计算
由恒载和活载产生的各杆件的内力见下表
列车横向摇摆力:以下弦杆E2E4举例说明,如下图所示该杆件受到的列车摇摆力引起的弦杆内力计算图,其它结果见下表。
4、 列表
将计算结果列入下表
116m 吊杆影线线
1sin θ
1sin θ
l=80m
下弦杆受到列车摇摆力的计算图示
2410015.75284.386.4
E E M N kN B ⨯=
=±=±
0.125
0.125
0.125
二、 附加力作用下主桁杆件的内力 (一) 横向风力
标准设计中,桥上有车时的风荷载采用1250Pa
[][]=0.50.411+3+1.51-0.41250=6.125k /=0.50.411+3+1.51-0.41250=3.25k /N m N m
ωω⨯⨯⨯⨯⨯⨯⨯⨯⨯下上()()()()0.2
1. 上平纵联
由横向风力引起上弦杆内力的计算图示见下图
A1A3: 11236
48 3.425
248115.596.4
M N kN B ⨯⨯⨯⨯==±=± A3A3’ 1282048 3.425
248149.846.4
M N kN B ⨯⨯⨯⨯==±=± 2. 下平纵联
由横向风力引起下弦杆内力的计算图示见上图
E0E2:11252
64 6.125
264597.196.4
M N kN B ⨯⨯⨯⨯==±=± E2E4: 1283664 6.125
264964.696.4
M N kN B ⨯⨯⨯⨯==±=±
l=64m
下平纵联横向风力计算图示
ω上
(二)桥门架效应
桥门架效应引起的主桁杆件内力计算,其计算图示如下图所示。
桥门架所受总风力l' 3.42548
82.222
w w H kN ⨯⨯=
==上 腿杆反弯点位置029.69.6213.6
5.38522229.613.6c c L l m c L ++⨯=
⨯=⨯=+⨯+ 腿杆竖向反力0()109.6(13.6 5.385)
140.76.4
w
H L L N kN B ⨯-⨯-=±=±=± 下弦杆E0E2所受的纵向水平力''
8cos 140.782.813.6
w N N kN θ=∙=±⨯=± 端斜杆所受附加弯矩0109.6
()(9.6 5.385)23122w F H M c L kN =-=
⨯-= 0109.6
5.38529522
w B H M L kN ==
⨯= (三)制动力
按相应于下弦杆在主力共用下时的静活载计算。
E 0E 1:将活载作如图素所示的布置,根据结构力学方法,若能满足以下关系则为产生最大杆力的活载位置:
Mf
D
C 4.0
敲门架结构尺寸图
1
1
a b
a b R P R a b
R R P a b
+>+<
3220+220
22092
302380
110
868
56
3220220292302380
82.590856
⨯+⨯+⨯=>=⨯⨯+⨯+⨯=<=
于是制动力 00(522030922380)7399T kN =⨯+⨯+⨯⨯= 杆件E0E2所产生的内力为199.52
T
N kN =±
=±
a b
R R a b
= 于是得22059292(30)80(10)
2440
⨯+X ⨯-X +⨯+X =
解之得:4X =m
于是制动力00(522030921480)7348.6T kN =⨯+⨯+⨯⨯=
杆件E2E4所产生的内力为174.32
T
N kN =±
=±
下弦杆E0E2活载布置图
下弦杆E2E4活载布置图
三、确定杆件计算内力
端斜杆E0A1:
1w
2
'2
2
N=-2863.21kN,N-140.7 +N=-2863.21-140.7=3003.91
25032863(
1.2
kN
kN
N
N kN kN
=
==<
主力附加力:
主附
主控)
上弦杆A1A3
1w
2
'2
2
N=-2835.19kN,N-115.19 +N=-2835.19-115.19=2950.38
24582835(
1.2
kN
kN
N
N kN kN
=
==<
主力附加力:
主附
主控)
上弦杆A3A3’
1w
2
'2
2
N=-3707kN,N-149 +N=-3707-149=3586
32133707(
1.2
kN
kN
N
N kN kN
=
==<
主力附加力:
主附
主控)
下弦杆E0E2
1w
2
'2
2
3
'3
3
N=1836kN,N59782.8679.8
199.5
+N=1836+679=3109
25901836(
1.2
N1836199.52035.5
1628.41836(
1.25
T
kN N kN
kN
N
N kN kN
kN
N
N kN kN
=+= =
==>
=+=
==<
主力附加力:
主附
主+附控)
主控)
下弦杆E2E4
1w
2
'2
2
3
'3
3
N=3752kN,N964,174.3 +N=3752+964=4716
39303752(
1.2
N3752174.33926
31413752(
1.25
T
kN N kN
kN
N
N kN kN
kN
N
N kN kN
== ==>
=+=
==<
主力附加力:
主附
主+附控)
主控)。
