第5章桁架内力计算(第11周)(截面法)
合集下载
第五章静定平面桁架(李廉锟_结构力学)全解
除一杆外，其余均汇交于一点(力矩法)或均平行(投影法)，则该杆
内力仍可首先求得。
返回
退出
02:31
§5-3 截面法
结构力学
示例1：试求图示桁架中杆EF、ED，CD，DG的内力。
截面如何选择？
退出
返回
02:31
§5-3 截面法
解: (1) 求出支座反力FA和FB。
结构力学
(2) 求下弦杆CD内力，利用I-I截面 ，力矩法 取EF和ED杆的交点E为矩心， CD杆内力臂为竖杆 高h，由力矩平衡方程∑ME=0，可求CD杆内力。
结构力学
退出
返回
02:31
§5-1 平面桁架的计算简图
二、按外型分类
1. 平行弦桁架
结构力学
2. 三角形桁架
3. 抛物线桁架
退出
返回
02:31
§5-1 平面桁架的计算简图
三、按几何组成分类
1. 简单桁架 （simple truss）
结构力学
2. 联合桁架 （combined truss）
3. 复杂桁架 （complicated truss）
1 F A
2 F
退出
返回
02:31
§5-2 结点法
结点法计算简化的途径：
结构力学
2.对称结构受对称荷载作用, 内力和反力均为对称:
受反对称荷载作用, 内力和反力均为反对称。
E 点无荷载,红色杆不受力 垂直对称轴的杆不受力 对称轴处的杆不受力
FAy FAy
FBy FBy
退出
返回
02:31
§5-3 截面法
退出
返回
02:31
§5-2 结点法
10 kN 5 kN 2m
平面简单桁架内力计算
截面法
假想用一截面截取出桁架的某一部分作为研究对象求解方法
1. 被截开杆件的内力成为该研究对象外力，可应用平面一
求
解
般力系的平衡条件求出这些被截开杆件的内力。
要 2. 由于平面一般力系只有三个独立平衡方程，所以一般说 点
来，被截杆件应不超出三个。
适用于求桁架中某些指定杆件的内力
平面简单桁架内力计算
平面简单桁架内力计算
1.桁架：一种由杆件彼此在两端用铰链连接而成的结构。
按 平面桁架：所有杆件的轴
空间桁架：杆件轴线不
空 间
线都在同一平面内的桁架；
在同一平面内的桁架。
形
式
分
类
所有杆件、结点、荷载和反力都共面。
平面简单桁架内力计算
按内力计算分类 静定桁架:杆件的内力可用静力平衡方程全部求得的桁架。 超静定桁架:杆件的内力不能用静力平衡方程全部求得的桁架。
即表示该杆受压。
节点法适用于求解全部杆件内力的情况
平面简单桁架内力计算
1.节点法：逐一取桁架节点 为研究对象，利用平面汇交 力系的平衡条件求解桁架杆 件内力的方法。
F1
3
5
R1X 1
4
6
ห้องสมุดไป่ตู้
R1y
F2
7
2 8
R2y
N13 R1X
N14
R1y
F1
3
N35
N31
N36
N34
N43
N41
N46
4
平面简单桁架内力计算桁架的内力计算
2.截面法
3 F1 N355
F2 7
R1X 1
4 R1y
N36 N46 6
应用平面一般力系平衡条件
结构力学第五章平面桁架详解
1‘ 2‘ 3‘ 4‘ e
a
cd
b
4d d3
A 1 2 3 4 5
B
P PP 6d
VA 1.5P
(1) Na Nb
1‘ 2‘
4
Na
d 3
1 2 Nb
1.5P
P
Y 0 M 2 0
VB 1.5P
Na P VA 0.5P
Nb
4 3
d
1.5P 2d
0
Nb 2.25 P
1‘ 2‘ 3‘ 4‘ e
a
cd
b
A 1 2 3 4 5
P PP 6d
4d d3
B
(2) N c
VA 1.5P
Yc 1.5P P 0.5P
Nc
5 4
Yc
0.625P
VB 1.5P
4‘ e
d
Nc
B
45
P 1.5P
A VA 1.5P
1‘
2‘
3‘
4‘
e
a
cd
b
12345 P P P 6d
4d d3
B
VB 1.5P
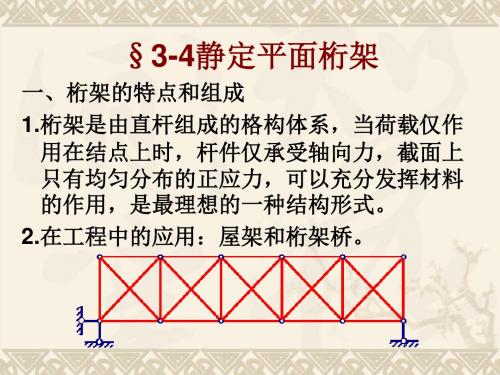
5-1 桁架的特点和组成分类
桁架是由链杆组成的格构体系，当荷载仅作用在结点上时，
杆件仅承受轴向力，截面上只有均匀分布的正应力，是最理想
的一种结构形式。
上弦杆
理想桁架：
腹杆
下弦杆
（1）桁架的结点都是光滑无摩擦的铰结点； （2）各杆的轴线都是直线，并通过铰的中心； （3）荷载和支座反力都作用在结点上
主应力、次应力
桁架的分类（按几何构造） 1、简单桁架
2、联合桁架
3、复杂桁架
§5-2 结点法
分析时的注意事项：
05静定平面桁架内力计算
上弦杆 竖杆 斜杆 桁高 节间长度 跨度 弦杆：上弦杆，下弦杆 腹杆：斜杆，竖杆
2
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2018/11/7
下弦杆
基本概念 ۞桁架的特性 直杆铰接、结点受荷 杆件只有轴力，没有弯矩和剪力
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2018/11/7 3
结点法
基本概念
结点法 截面法 联合法
۞结点法
B D
A
4m
60 E 20 40 15 30 3m 15 25 -50 C -20 F -20 G 15 kN 15 kN 15 kN 4m 4m
解：(3)取E结点为隔离体分析 E 20 YNGE 30 kN FNED 15 4 拱式桁架 X NGF YNGE XNEC F NEC 3 15 25 扩展内容 YNEC 40 kN FNEC=-50
2L
L
L
2L
对称结构在反对称荷载作用下，内力和反 力都反对称
结点法
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2018/11/7 26
۞简化问题 对称性的利用
反对称荷载：荷载的大小、作用点关 于一个轴对称，对应位置的荷载方向相反
FP
FP
2L
L
L
2L
结点法
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2018/11/7 20
解：(4)取D结点为隔离体分析 (5)取C结点为隔离体分析 (6)取B、A结点为隔离体分析 (7)取整体作为隔离体，求支反力，核实 结果。
结点法
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2018/11/7
下弦杆
基本概念 ۞桁架的特性 直杆铰接、结点受荷 杆件只有轴力，没有弯矩和剪力
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2018/11/7 3
结点法
基本概念
结点法 截面法 联合法
۞结点法
B D
A
4m
60 E 20 40 15 30 3m 15 25 -50 C -20 F -20 G 15 kN 15 kN 15 kN 4m 4m
解：(3)取E结点为隔离体分析 E 20 YNGE 30 kN FNED 15 4 拱式桁架 X NGF YNGE XNEC F NEC 3 15 25 扩展内容 YNEC 40 kN FNEC=-50
2L
L
L
2L
对称结构在反对称荷载作用下，内力和反 力都反对称
结点法
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2018/11/7 26
۞简化问题 对称性的利用
反对称荷载：荷载的大小、作用点关 于一个轴对称，对应位置的荷载方向相反
FP
FP
2L
L
L
2L
结点法
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
2018/11/7 20
解：(4)取D结点为隔离体分析 (5)取C结点为隔离体分析 (6)取B、A结点为隔离体分析 (7)取整体作为隔离体，求支反力，核实 结果。
结点法
基本概念
结点法 截面法 联合法 拱式桁架 扩展内容
结构力学 第五章 作业参考答案
结构力学 第五章习题 参考答案2005级 TANG Gui-he （整理）5－1 试用结点法计算图示桁架各杆的内力。
5－2 试用结点法计算图示桁架各杆的内力。
解:由整体平衡条件可解得支座反力 F A =1.5F F B =1.5F 取结点A 为隔离体,如图,用数解法可解得 F A C =-2.12F F A B =1.5F 同理,依次取结点B 、C 、 D 、E 为隔离体,并由对称性可得各杆的内力如图。
4 * 8m60k N60k N6M 2MA B C D E FG H 解：由 M H =0 可得支座F a y=75kN.由 F Y=0 得 F h y=45kN 取 A 结点为隔离体，利用数解法可得 F N AB=-100kN. F NAC=125kN. 再取 C 点为隔离体，利用投影法和力平衡 可得 F N BC=-50,F NCE=103.1kN.同理依次取 B ， D ， E ， G ， F 可得各杆内力（如图所标）AC-60k N -90k N -100k N 45k N75k N125k N 75k N 42.4k N61.8k N 103.1k N -60k N -50k N -30k N55－4试判断图示桁架中的零杆。
解：图中红色的杆件为零杆在杆中标有 为零杆其中用到K 型和T 型结构判断原理5－5试用截面法计算图示桁架中指定杆件的内力。
2解:（1）求出支座竖向反力为2.5F (↑),（2）作截面I -I ，由∑M A=0得: 2.5F ×15-10F -5F +6F N 1=0 → F N 1=-3.75F （3）由∑M B=0得: 2.5F ×10-F ×5-F N 2×6=0 → F N 2=3.33F （4）利用勾股定理求出A B 杆长7.8F N 4x =5F N 4/3.84 由∑M C=0得: 2.5F ×10-5F +F N 1×6+6×5F N 4/7.8=0 → F N 4=0.65F （5）取结点B 为分析对象,由∑F Y=0得: F N 4×6/7.8+F N 3=0 → F N 3=-0.5F5－6试用截面法计算图示桁架中指定杆件的内力。
理论力学 第五章 桁架和摩擦
理想桁架 工程实际中计算桁架受力情况时，常 作如下简化： (1) 构成桁架的杆件都是直杆； (2) 杆件两端都用光滑铰链连接； (3) 所有外力（主动力及支座反力） 都作用在节点上； (4) 杆件自重略去不计。
这种桁架称为理想桁架。
平面桁架各杆内力
1.节点法 2.截面法
汇交力系 平面一般力系
已知平面桁架尺寸、载荷。求：各杆内力。
3 因 0 Fs Fmax ，问题的解有时在一个范围内．
考虑摩擦的平衡问题
(1)判断物体是否平衡，并求滑动摩擦力。
先假设物体处于平衡，根据平衡方程求出物体平衡时需 要的摩擦力以及相应接触面间的正压力。再根据摩擦定 律求出相应于正压力的最大静摩擦力并与之比较。若满
足F≤Fmax这一关系，说明物体接触面能提供足够的摩擦
当仅有滑动趋势时，产生的摩擦力，称为静滑动摩擦力
静滑动摩擦力性质
1)静滑动摩擦力FS 的方向与滑动趋势相反，大小由平衡
条件确定；
0≤FS ≤Fmax （物体平衡范围）
2)只有当物体处于将动未动的平衡临界状态时,静滑动摩
擦力FS 达到最大值，即 FS =Fmax=f FN
f — 静滑动摩擦系数；
FN— 法向反力（一般也由平衡条件决定）。
摩擦角和自锁现象
1 摩擦角
FRA ---全约束力
物体处于临界平衡状态时，全约束 力和法线间的夹角---摩擦角
tan f
Fmax FN
fs FN FN
fs
全约束力和法线间的夹角的正切等于静 滑动摩擦系数．
摩擦锥
0 f
2 自锁现象
摩擦自锁的实例
1.粗糙斜面。当 a<m时,
不论W多大，物块A均保持 平衡－－摩擦自锁。
第五章 静定桁架
解：1.求支座反力
4m
a
D
A
60kN
b
M
A
0, VB 6 60 9 0
VB 90kN ()
c
B
3m 3m VB
HA
3m 3m VA
Y 0, X 0,
VA VB 60 0
VA 30kN ()
HA 0
第五章 静定桁架
[例5-3]用截面法求图示桁 架a、b、c三杆的内力。 4m
1)判别零杆 2)由结点法求内力
D
P
图5-10
B
第五章 静定桁架
思考/讨论：试判断下图所示桁架结构中的零杆 p p
第五章 静定桁架
思考/讨论：试判断下图所示桁架结构中的零杆
P P P
第五章 静定桁架
思考/讨论：试判断下图所示桁架结构中的零杆
P
第五章 静定桁架
思考/讨论：试判断下图所示桁架结构中的零杆
F 2
30
o
NAD NAC
RA 2F
N AD 3F N AC 2.598 F
(压力） (拉力）
x
第五章 静定桁架
练习：试求图示桁架的各杆内力
(2)求各杆内力
取D结点为脱离体，列结 点平衡方程： Y 0,
- F cos 30 N DC 0
2F
y
2F
x
N DC 0.866 F
第五章 静定桁架
3、按桁架受竖向荷载作用有否水平反力分为
a、梁式桁架
b、拱式桁架
第五章 静定桁架
§5-2 静定平面桁架的计算
一、结点法： 以结点作为研究对象来计算结构内力的方法 结点法的计算要点：
4m
a
D
A
60kN
b
M
A
0, VB 6 60 9 0
VB 90kN ()
c
B
3m 3m VB
HA
3m 3m VA
Y 0, X 0,
VA VB 60 0
VA 30kN ()
HA 0
第五章 静定桁架
[例5-3]用截面法求图示桁 架a、b、c三杆的内力。 4m
1)判别零杆 2)由结点法求内力
D
P
图5-10
B
第五章 静定桁架
思考/讨论：试判断下图所示桁架结构中的零杆 p p
第五章 静定桁架
思考/讨论：试判断下图所示桁架结构中的零杆
P P P
第五章 静定桁架
思考/讨论：试判断下图所示桁架结构中的零杆
P
第五章 静定桁架
思考/讨论：试判断下图所示桁架结构中的零杆
F 2
30
o
NAD NAC
RA 2F
N AD 3F N AC 2.598 F
(压力） (拉力）
x
第五章 静定桁架
练习：试求图示桁架的各杆内力
(2)求各杆内力
取D结点为脱离体，列结 点平衡方程： Y 0,
- F cos 30 N DC 0
2F
y
2F
x
N DC 0.866 F
第五章 静定桁架
3、按桁架受竖向荷载作用有否水平反力分为
a、梁式桁架
b、拱式桁架
第五章 静定桁架
§5-2 静定平面桁架的计算
一、结点法： 以结点作为研究对象来计算结构内力的方法 结点法的计算要点：
《输电线路基础》第5章-杆塔强度校核-第五节-铁塔构件内力的计算.
图5-5-2 单斜材平面桁架内力计算图
由于桁架主材坡度
所以
0 用Ⅰ-Ⅰ线截开U1、U2、s5三个构件，按照上述方法，取 M A ，即
Hale Waihona Puke 求得U1 PH 5 5 8.5034kN (受压) b6 cos 3.0 0.98
同理，取占 M 0 0
可得
U2
5 4 7.8493 kN (受拉 ) 2.6 0.98
所以，采用截面法时，一次截取未知内力的构件数不得超过三个。 求任意一个构件的内力时，取另外两个构件的交点为力矩中心。 如果截取的构件多于三个，但是除拟求内力的构件外，其余各构 件都交汇在一点，那么就取这一交点为力矩中心。
这样，在 M 0 的方程式里只有一个未知数，能够很快地求出拟 求的构件内力。 截面法的优点是，一次能求出桁架内任意构件的内力，而不必计 算其它各构件的内力，因此在铁塔的计算中广泛采用截面法。 利用截面法求构件内力的步骤： (1)将桁架截为两部分，截断桁架时，要在截断面内包括拟求内力的 构件，同时将未知内力的构件交汇于一点。 (2)将桁架另一部分舍去并用构件的内力代替舍去部分对留下部分的 作用。同时假定所有构件受拉，就是说，其内力的方向是离开节点 的。 (3)在求某一构件内力时，取其余各构件的汇交点作为力矩中心，并 写出作用在留下部分桁架上诸力的力矩平衡方程式。 (4)从列出的方程式中，如果算出的各构件内力是正值(+)的，那么 表示该构件受拉，如果是负值(-)，则表明构件受压。
上式中的r1为自O点至斜材s3的垂直距离，用作图法求得。 交点0的距离a可按下式计算。 (5-5-4)
例题5-5-1 如图5-5-2所示的单斜材平面桁架，水平作用力P=5kN， 试求主材U1～U5和斜材s1～s5的内力。 【解】 由式(8-6)可得水平力P的作用点到主材 交点0的距离a为
第5章桁架内力计算(第11周)(截面法)
3×8－SDE×2=0 SED=12kN(拉） 再考虑结点D、E的平 衡可求出各链杆的内力。
-6
19 返回
3. 分析受弯杆件
取AC杆为隔离体， 考虑其平衡可求得：
A
12kN
F
8kN C 6kN V=3kN C
HC =12kN
HC=12kN←
5kN
6kN
VC=3kN↑
B
6kN 12 3kN
8kN
A
1kN 6kN 4 0 6
18 返回
例 5－2 分析此组合结构的内力。 解：
HA=0
6
-6
Ⅰ
13· 4
51
+12 2
12
VA=5kN
Ⅰ
RB=3kN
1. 由整体平衡 条件求出支反力。 2. 求各链杆的内 力：作Ⅰ－Ⅰ截面
HC SDE
VC +12
12
4 13· 6 12
拆开C铰和截断DE 杆，取右部为隔离体。 由∑MC=0 有
2 .截面法据所选方程类型的不同 又分为力矩法、投影法。
返7回
（1）力矩法 以例说明
Ⅰ
设支反力已求出。 求EF、ED、CD三杆的 内力。作截面Ⅰ-Ⅰ，取左 部分为隔离体。
由∑ME=0 有 RAd－P1d－P2×0－SCDh=0 R d − P1d − P2 × 0 SCD = A （拉） h RA×2d－P1×2d－P2d+XEFH=0
YEF SEF
∽
XEF
பைடு நூலகம்
∽
SED
SCD a RA d d YED
XED
9
（2）投影法
Ⅱ
求DG杆内力 作Ⅱ—Ⅱ截面， 取左部分为隔离体。 由∑Y=0 有
桁架求解的几种方法
故知反力计算无误。 2.计算a杆内力。 (1) 作Ⅰ-Ⅰ截面，取左部分为
FA=40kN
a A G III 20kN II H III 20kN I 20kN
6x3m =18m F B= 20kN
C
隔离体，由ΣMF=0，得： F ×4-20×3-40×3 = 0，
图5-12
4m
B
(2) 取结点H为隔离体，由ΣFx = 0， 得：FNGH =FNHC = 45 kN (3) 作截面Ⅱ-Ⅱ，仍取左部分为隔离体，由ΣMF = 0，得 FNa×3/ 13 ×4+45×4-40×3 = 0， FNa = -513 = -18.0 kN 在该题中，若取截面Ⅲ-Ⅲ所截取的一部分为隔离体(图 5-12)，由于ED杆为零，FNED = 0。 由平衡方程ΣMC = 0，可得 FNa×2/ 13 ×3+FNa×3/ ×2+20×3 = 0， 13 FNa = -513 = -18.0 kN 可见，按后一种方法计算更简单。
E
G
(a)
2m
A
D
2kN
C
4kN
F
2kN
B
解：该桁架为简单桁架， 由
于桁架及荷载都对称，故可计 算其中的一半杆件的内力，最 后由结点C的平衡条件进行校 核。 1.计算支座反力。 ΣFx = 0, FAx = 0
(d) (b)
4X 2m =8 m
F A Y = 4kN F B Y = 4kN
FNDE F NAE
60×3-10×3-FNa×3 = 0， FNa = 50 kN
(2) 求上弦杆c的内力时，以a、b两杆的交点D为矩心， 此时要计算FNc的力臂不太方便，为此将FNc分解为水平和
竖直方向的两个分力。则各分力的力臂均为已知。 10 10
FA=40kN
a A G III 20kN II H III 20kN I 20kN
6x3m =18m F B= 20kN
C
隔离体，由ΣMF=0，得： F ×4-20×3-40×3 = 0，
图5-12
4m
B
(2) 取结点H为隔离体，由ΣFx = 0， 得：FNGH =FNHC = 45 kN (3) 作截面Ⅱ-Ⅱ，仍取左部分为隔离体，由ΣMF = 0，得 FNa×3/ 13 ×4+45×4-40×3 = 0， FNa = -513 = -18.0 kN 在该题中，若取截面Ⅲ-Ⅲ所截取的一部分为隔离体(图 5-12)，由于ED杆为零，FNED = 0。 由平衡方程ΣMC = 0，可得 FNa×2/ 13 ×3+FNa×3/ ×2+20×3 = 0， 13 FNa = -513 = -18.0 kN 可见，按后一种方法计算更简单。
E
G
(a)
2m
A
D
2kN
C
4kN
F
2kN
B
解：该桁架为简单桁架， 由
于桁架及荷载都对称，故可计 算其中的一半杆件的内力，最 后由结点C的平衡条件进行校 核。 1.计算支座反力。 ΣFx = 0, FAx = 0
(d) (b)
4X 2m =8 m
F A Y = 4kN F B Y = 4kN
FNDE F NAE
60×3-10×3-FNa×3 = 0， FNa = 50 kN
(2) 求上弦杆c的内力时，以a、b两杆的交点D为矩心， 此时要计算FNc的力臂不太方便，为此将FNc分解为水平和
竖直方向的两个分力。则各分力的力臂均为已知。 10 10
静定桁架的内力计算
aaa
a
B RB =2kN
NCD
D
N2
N3
F
B
2kN RB
将桁架从Ⅰ－ Ⅰ部位截开，取右侧。
ΣY=0；
2 N 2 2 RB 2 0;
N2=0
ΣmD=0； N3·a－RB·a=0 ；
N3 =2kN
【例5－3】求图示桁架指定杆件的轴力，α=60°。
C
Ⅰ
NCF
E2
F 2kN
N2
F
2kN
N2 N3
【例5－2】求图示桁架指定杆件的轴力。
2kN C
D
2 A1
XA YA
E3 F 2kN
aaa
解：1杆为零杆； N1=0
a
B RB =2kN
取整体，ΣmA=0； RB·3a－2×a－2×2a=0 RB=2kN
【例5－2】求图示桁架指定杆件的轴力。
2kN C Ⅰ D
2 A1
XA YA
E 3Ⅰ F 2kN
(2) 不共线二杆结点有外力(包括支座反力) ，且外力与其中
一杆共线，则另一杆为零杆；
y P
Ｎ１= 0 Ｎ２ x
ΣY=0； Ｎ1= 0
(3) 三杆结点无外力(包括支座反力) ，且其中两杆共线，则 第三杆为零杆。
y
Ｎ3 = 0
Ｎ1
Ｎ2
x
解题时，零杆可以去掉。
ΣY=0； Ｎ3= 0
【例5－1】试判断图示桁架中的零杆。
第五章 静定平面桁架的内力计算
1．零杆的判断 桁架的外力都是作用在结点上，因此，桁架中的杆皆为二力 杆，内力只有轴力。轴力为零的杆称为零杆，零杆可由结点平衡 条件直接判断。
(1) 不共线二杆结点无外力(包括支座反力) ，此二杆为零杆；
a
B RB =2kN
NCD
D
N2
N3
F
B
2kN RB
将桁架从Ⅰ－ Ⅰ部位截开，取右侧。
ΣY=0；
2 N 2 2 RB 2 0;
N2=0
ΣmD=0； N3·a－RB·a=0 ；
N3 =2kN
【例5－3】求图示桁架指定杆件的轴力，α=60°。
C
Ⅰ
NCF
E2
F 2kN
N2
F
2kN
N2 N3
【例5－2】求图示桁架指定杆件的轴力。
2kN C
D
2 A1
XA YA
E3 F 2kN
aaa
解：1杆为零杆； N1=0
a
B RB =2kN
取整体，ΣmA=0； RB·3a－2×a－2×2a=0 RB=2kN
【例5－2】求图示桁架指定杆件的轴力。
2kN C Ⅰ D
2 A1
XA YA
E 3Ⅰ F 2kN
(2) 不共线二杆结点有外力(包括支座反力) ，且外力与其中
一杆共线，则另一杆为零杆；
y P
Ｎ１= 0 Ｎ２ x
ΣY=0； Ｎ1= 0
(3) 三杆结点无外力(包括支座反力) ，且其中两杆共线，则 第三杆为零杆。
y
Ｎ3 = 0
Ｎ1
Ｎ2
x
解题时，零杆可以去掉。
ΣY=0； Ｎ3= 0
【例5－1】试判断图示桁架中的零杆。
第五章 静定平面桁架的内力计算
1．零杆的判断 桁架的外力都是作用在结点上，因此，桁架中的杆皆为二力 杆，内力只有轴力。轴力为零的杆称为零杆，零杆可由结点平衡 条件直接判断。
(1) 不共线二杆结点无外力(包括支座反力) ，此二杆为零杆；
(仅供参考)桁架内力计算的截面法
C
S
∑MC = 0
S
S
∑Y = 0
S=0
例3 试求图示桁架杆a、b的内力。21
3l
VA=P
3l
VB=P
联合桁架
求1杆的内力
Ⅰ
1
22
建立竖直投影方程 ∑Fy=0，可求出 y1 = 0
N1 = 0
VA=P
Ⅰ
VB=P
求a杆内力
23
作Ⅱ-Ⅱ截面，截开
b杆，取出隔离体.
0
0
Na
Xa
O
Ya
ⅡⅡ
对0点取矩，有∑M0=
截面法
1
截面法可以快速求出某一内力，通常取结构
的一部分为隔离体，其上力系为平面一般力
系。每个隔离体上有3个独立平衡方程。一般
表示为：
∑FX = 0 ∑FY = 0 ∑M = 0
投影法 力矩法
计算要点： 尽量使一个方程解一个未知数，避免求解
联立方程。
一. 力矩法
2
例：求图示桁架1、2、3杆的轴力。
Xa=－ P
由比例关系得到 Na 。
投影法要点：
15
欲求某指定杆内力，则作一截面，截开待求 杆； 当隔离体上除待求未知力外，其余未知力均相 互平行。
建立投影方程，求出待求未知力。
例2. 试求图示桁架a、b杆的内力 16
Ⅰ
Ⅰ
2l
3l
作Ⅰ-Ⅰ截面，截开a 杆，取截面以上为隔 离体。其上共有三个未知力。
求3杆内力
31
5
7P
2
ⅡⅡ
7P 2
作Ⅱ-Ⅱ截面，截开3杆，取出隔离体。
求3杆内力
32
N3
X3
工程力学第5节 平面静定桁架的内力计算
F1 sin 30 G 0
n
Fiy 0
i1
F1 cos 30 F2 0
得 F1 40 kN（拉） F2 34.6 kN（压）
节点 B：
n
Fix 0
i1 n
Fiy 0
i1
F2 F6 0
得
F3 G 0
F6 34.6 kN（压） F3 20 kN（拉）
i1 n
Fiy 0
i1
FS1 sin 60 FS4 sin 60 0 FS1 cos 60 FS4 cos 60 FS3 0
解得
FS4 FS1 2F（压） 校核计算结果
将各杆内力计算结果列表如下
杆号
1
2
3
内 力 2F 1.73F 2F
半部分为研究对象进行受力分析，列平衡方程：
n
M E (Fi ) 0
FS1 1sin 60 FAy 1 0
i1
n
M D (Fi ) 0
i1 n
Fiy 0
i1
F1
1 2
FS3
1
sin
60
FAy
2 3
0
FAy FS2 sin 60 F1 0
• 因为只有三个独立平衡方程，因此作假想截面时， 一般每次最多只能截断三根杆件。
注意
• 由于平面汇交力系只能列出两个独立平衡方程，所 以应用节点法必须从只含两个未知力大小的节点开 始计算。
例2-15 平面桁架的受力及尺寸如图所示， 试求桁 架各杆的内力。
解 1）先求支座反力：以整体桁架为研究对象进行
第5章 静定平面桁架
2. T形结点：三杆结点上无 荷载作用时如果其中有两杆 在一直线上，则另一杆必为 零杆。此结点成为T形结点
3. X形结点：四杆结点且 两两共线，并且结点上无 荷载时，则共线两杆内力 大小相等方向相同
4. K形结点：四杆结点，其中两杆 共线，而另外两杆在此直线同侧且 交角相等，并且结点上无荷载，则 非共线两杆内力大小相等方向相反
§5.4
静定结构特性
静定结构有静定梁、静定刚架、三铰拱、静定桁架等类型。 虽然这些结构形式各有不同，但它们有如下的共同特性：
1. 在几何组成方面，静定结构是没有多余联系的几何不变体 系。在静力平衡方面，静定结构的全部反力可以有静力平衡方 程求得，其解答是唯一的确定值。
2. 由于静定结构的反力和内力仅用静力平衡条件就可以确定， 不需要考虑结构的变形条件，所以静定结构的反力和内力只与 荷载、结构的几何形状和尺寸有关，而与构件所用的材料、截 面的形状和尺寸无关。
§5.2
桁架内力的计算方法
5. 对称性：首先结构对称，结构的杆件以及支座对一个轴 对称，则称该结构为对称结构。其次荷载对称，荷载的大 小、作用点、方向都关于一个轴对称。并且结构与荷载同 一个对称轴，其内力和反力也基于该对称轴对称。
§5.2
桁架内力的计算方法
上述结论都不难由结点平衡条件得到证实。在分析桁架时， 可先利用上述原则找出特殊结点，然后进行下一步的计算，使 计算变得1、平行弦桁架 图b所示桁架，上下弦受力两头小中间大，这与图5.21a所示
简支梁的上下层纤维受力相似，即与梁的弯矩分布相似。腹杆 内力与简支梁的剪力分布规律一致，两头大中间小。因此静定 平行弦桁架的受力相当于一个空腹梁。
为使得设计上的受力合理，应按杆轴力的大小选取截面大小。 所以平行弦桁架杆件的截面积变化较大，给施工带来不便。在 实际工程中，常采用标准节间，逐段改变截面的大小，把材料
第五章静定平面桁架
（2）求FNEF：Σ mD=0， FNEF沿作用线平移到F点分解
1 F [ F 2 dF dFd ] x E F A 1 2 2 H
M H
0 D
（压力）
结论：可证简支桁架，竖直向下荷载作用 下弦杆受拉力，上弦杆受压力 —— 对应梁，受竖直向下荷载的下、上边缘
（3）斜杆FNED EF、CD交点O，Σm0=0，FNED平移到D分解
桁架各部分名称
弦杆：上、下弦杆 腹杆：斜杆、竖杆 节间：弦杆上， 相邻结点区间 跨度、桁髙
桁架类型
（外形） a）平行弦 b）折弦 c）三角形 （是否有推力） a,b,c）无推力 d）有推力（拱式）
（几何组成方式）——与求解方法有关 （1）简单桁架（a，b，c）——二元体 （2）联合桁架（d，e）——三、二刚片规则 （3）复杂桁架（f）——非基本组成规则方式
1 F [ F aF ( ad ) ] Y E D A 1aF 2 a 2 d
（可能＋、－）
2．投影（方程）法 （上、下弦杆平行） （1）求斜杆DG Ⅱ—Ⅱ截面（左） ∑Y=0 FYDG＝-（FA－F1－F2－F3） ＝－F0SDG ——剪力法
F0SDG
截面法： ①所截杆件一般不超过三根 ——三个独立平衡方程可解 ②截面多于三个未知力， 如其中除一根外，其余均交于一点、或平行 ——可解此杆——截面单杆 ③几何组成相反次序求解
§5－6 组 合 结 构 计 算
组合结构——链杆与梁式杆，组合而成结构 （轴力杆：FN）（受弯杆件：M、FS、FN） 计算顺序：反力—链杆—梁式杆 【例5－3】 ①几何组成 ②求解次序 ③反力 FAV=5kN， FBV=3kN ④链杆 FNDE： ⑤梁式杆：受荷载、 链杆的作用力FN ⑥校核结点A/B，F/G
1 F [ F 2 dF dFd ] x E F A 1 2 2 H
M H
0 D
（压力）
结论：可证简支桁架，竖直向下荷载作用 下弦杆受拉力，上弦杆受压力 —— 对应梁，受竖直向下荷载的下、上边缘
（3）斜杆FNED EF、CD交点O，Σm0=0，FNED平移到D分解
桁架各部分名称
弦杆：上、下弦杆 腹杆：斜杆、竖杆 节间：弦杆上， 相邻结点区间 跨度、桁髙
桁架类型
（外形） a）平行弦 b）折弦 c）三角形 （是否有推力） a,b,c）无推力 d）有推力（拱式）
（几何组成方式）——与求解方法有关 （1）简单桁架（a，b，c）——二元体 （2）联合桁架（d，e）——三、二刚片规则 （3）复杂桁架（f）——非基本组成规则方式
1 F [ F aF ( ad ) ] Y E D A 1aF 2 a 2 d
（可能＋、－）
2．投影（方程）法 （上、下弦杆平行） （1）求斜杆DG Ⅱ—Ⅱ截面（左） ∑Y=0 FYDG＝-（FA－F1－F2－F3） ＝－F0SDG ——剪力法
F0SDG
截面法： ①所截杆件一般不超过三根 ——三个独立平衡方程可解 ②截面多于三个未知力， 如其中除一根外，其余均交于一点、或平行 ——可解此杆——截面单杆 ③几何组成相反次序求解
§5－6 组 合 结 构 计 算
组合结构——链杆与梁式杆，组合而成结构 （轴力杆：FN）（受弯杆件：M、FS、FN） 计算顺序：反力—链杆—梁式杆 【例5－3】 ①几何组成 ②求解次序 ③反力 FAV=5kN， FBV=3kN ④链杆 FNDE： ⑤梁式杆：受荷载、 链杆的作用力FN ⑥校核结点A/B，F/G
结构力学第05章桁架结构和组合结构
结点荷载
15-3-25
力力 学 教 研 室
7
第五章 桁架结构和组合结构
桁架结构（truss structure）
力力 学 教 研 室
第五章 桁架结构和组合结构
力力 学 教 研 室
第五章 桁架结构和组合结构
力力 学 教 研 室
第五章 桁架结构和组合结构 3、桁架简图
上承荷载
斜杆 下弦杆 节间
竖杆
Ø 力力矩法： （适用用于另外两个力力相交） 力力矩方方程 结论： 弦杆的水水平分力力等于X=±Mo/h 三个杆件不能相交于一一点。 限制： Ø 投影法： （适用用于另外两个力力平行行） 投影方方程 结论： 腹杆竖向分力力等于YDG=±V0 限制： 三个杆不能完全互相平行行。 示示例
15-3-25
Ø 复杂桁架： 不属于以上两类桁架之外的其它桁架。
l静 力力特性 Ø 静定桁架： 无无多余约束的几几何不变体 Ø 超静定桁架： 有多余约束的几几何不变体
15-3-25
力力 学 教 研 室
14
第五章 桁架结构和组合结构 三、桁架分析方方法
l 支支座反力力： 与梁或者拱一一致 P3 P2 G F P E
4m
D
0
+60 40 30
E
15
3m
!
20 Ê -20
15kN 4m
+15
C
-20
15kN 4m
F
G
15kN
力力 学 教 研 室
第五章 桁架结构和组合结构
练习
力力 学 教 研 室
第五章 桁架结构和组合结构
以节点为平衡对象，画出受力力图：
FC y F BC FB A FA B FA D FD B FD A FD y FBD FD C FC B FC FC
第5章静定平面桁架.
截面单杆: 用截面切开后，通过一个方程可求出内力的杆.
截面上被切断的未知轴力的 杆件只有三个,三杆均为单杆.
截面上被切断的未知轴力的 杆件除一个外交于一点,该杆 为单杆.
截面上被切断的未知轴力的 杆件除一个均平行, 该杆为单 杆.
相
交
情
FP FP FP FP FP
况
FP
a 为 截 面 单 杆
FP FP
平行情况
b为截面单杆
0 -33
-33
34.8 -8
19
19
0 -33
-33
34.8
-8 -5.4
19
37.5
19
-8 kN
YDE CD 0.75 X DE CE 0.5
0 -33
-33
34.8 19
-8 -5.4 37.5
-33
-33
-8 -5.4
34.8
19
标后求
,
在 杆 件 旁 。
应 把 轴 力
出 所 有 轴 力
④梯形桁架
ｂ.按几何组成分类： 简单桁架—在基础或一个铰结三角形上依次
加二元体构成的 联合桁架—由简单桁架按基本组成规则构成 复杂桁架—非上述两种方式组成的静定桁架
简单桁架
简单桁架
联合桁架 复杂桁架
二、桁架的内力分析 1.结点法（主要用于求解简单桁架的内力）
选取隔离体时,每个隔离体只包含一个结点 的方法。
结点法是考虑的桁架中结点的平衡，此时隔 离体上的力是平面汇交力系,只有两个独立的 平衡方程可以利用,故一般应先截取只包含两 个未知轴力杆件的结点。
分析时的注意事项： 1、尽量建立独立方程：
2、避免使用三角函数
第5章 静定平面桁架
- 23/85页 -
FP
FP 1
D
FP
C
3FP
E
1.5FP -
2
1m B 1m
A
3FP F
G
H
2m 2m 2m 2m
1.5FP
1.5FP
FP C
3FP A
F
即
FNAC
1.5FP
可由比例关系求得
Fy1
FN1
D Fx1
G
Fx2
Fy2
FN2
24
《 第5章 静定平面桁架 》
- 24/85页 -
【例】 用结点法求AC、AB杆轴力。
F6=120kN
6
4
3
F7H=120kN 7
F7V=45kN
4m
5 15kN 4m
2 15kN 4m
3m
1 15kN
按结点1，2，…，6依次计算各结点相关杆件轴力 。
结点7用于校核。
17
《 第5章 静定平面桁架 》
- 17/85页 -
2. 零杆和等力杆
(1) 关于零杆的判断 在给定荷载作用下，桁架中轴力为零的杆件， 称为零杆。 1) L形结点：成L形汇交的两杆结点无荷载作 用，则这两杆皆为零杆。
FyAC
FyAB
4m
2m
1 2
3 2
27
《 第5章 静定平面桁架 》
- 27/85页 -
【例】用结点法求各杆轴力。 解： 1）支座反力
FAy=FBy=30kN(↑)
FAx=0
2）判断零杆
3）求各杆轴力 取结点隔离体顺序为：A、E、D、C。 结构对称，荷载对称，只需计算半边结构。
28
《 第5章 静定平面桁架 》
第五章 静定平面桁架
第五章静定平面桁架§5-1 概述梁刚架：受载后主要弯矩，应力不均匀（变截面；截面形式工形拱式结构：M小N大，应力分布比较均匀；施工复杂，需要坚固的结构支承桁架：M小，应力分布均匀，适用于较大空间，用料省自重轻大跨屋架、托架、吊车梁、南京长江大桥主体结构一、桁架定义：桁架：由若干直杆在其两端全用铰连接而成的结构，当荷载只作用在结点上时，各杆只有N，截面上的应力分布均匀，可以充分发挥材料的作用。
桁架可分为{ 平面桁架：空间桁架：（网架、井架）实际桁架（较复杂、结合例子）1）}结点：焊接、铆接、近乎刚结、介于铰于刚结之间。
2）}轴线：不能绝对平、直。
3）}杆的结合区：各杆也不一定完全相交于一点。
有个结合区域、应力十分复杂。
4）}自重：非结点荷载，荷载、支反力：不全是作用在结点上。
但经过实验和工程实践证明：以上因素对于桁架属次要因素，对桁架受力影响较小。
取桁架的计算简图时，引入如下假定：（计算时）理想桁架：（计算简图）满足这些假定的桁架1）桁架结点：所有结点为理想铰，光滑、无摩擦。
2）杆件的轴线：绝对平直、一平面内、通过铰的中心（理想轴）。
3）荷载、支反力：所有外力作用于结点上并且位于桁架平面内。
（结点荷载）4）线弹性材料，小变形。
主应力（基本应力）：按理想平面桁架计算得到的应力。
按理想桁架计算，可以反映桁架的主要受力性能次应力（附加应力）：实际桁架与理想桁架之间的差异引起杆件弯曲，产生附加的弯曲内力由此产生的应力理想桁架，各杆只产生轴力(二力杆、轴力杆)二、桁架的组成名称（坡屋顶、房子屋架）弦杆(上弦杆、下弦杆)、腹杆(竖杆、斜杆)、端斜杆(端柱)d:节间距离，l:跨度，H:桁高三、桁架的分类（结合图例）按外形特点分：平行弦桁架三角形桁架抛物线桁架折弦桁架按支座反力的性质分：梁式桁架(无推力桁架)拱式桁架(有推力桁架)按静力特性：静定桁架（有无多余约束、计算方法）拱式桁架超静定桁架按几何组成方式分：简单桁架：由基础或一个基本的铰结三角形开始，每次用不在同一直线上的两链杆联结一新结点联合桁架：由简单桁架组成；按两刚片规则组成的联合桁架、按三刚片规则组成的联合桁架复杂桁架：凡不属于前两类的均为此类。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
结点法与截面法各有所长，据具体情况选用。有些情况下，截面法和结点 法联合使用，更为方便。举例说明。
例5-1 试求图a所示K式桁架中a、b杆的内力。
解：算法一 作截面I-I，取其左侧为隔离体。 由结点K
FNa = − FNc Fya = − Fyc
5F F ∑ Fy = 0 Fya = − 4 → FNa = − 12
由∑MC=0可求得FNb。
算法二：作截面II-II，取其左侧为隔离体。
∑ M D = 0 FNb = −
8F 3
14
§5-5 各式桁架比较
平跨中递增。构 造上各类杆长度相同，结点处各杆交角相同， 便于 标准化。因制作施工较为方便，铁路桥常采用。
15
抛物线形桁架
特点：内力分布均匀，在材料使用上经济。但构造上 复杂。大跨度桥梁(100—150m)及大跨度屋架(18-30m) 中常采用。
16
三角形桁架
特点：内力分布不均匀，弦杆内力两端大，两端结点 夹角甚小，构造复杂。因两斜面符合屋 顶要求，在屋 架中常采用。
17
§5－6 组合结构计算
1. 组合结构的概念： 由链杆（受轴向力）和梁式杆（受弯杆件 ）混合组成的结构。 2. 组合结构的计算步骤： （1）求支座反力； （2）计算各链杆的轴力； （3）分析受弯杆件的内力。
X EF = R A × 2d - P1 × 2d - P2 d （压） H
RA
Ⅰ
RB
YEF
SEF
由∑MD=0 得
∽ ∽
XEF
SED
XED
SCD
由∑MO=0 －RAa+P1a+P2(a+d)+YED(a+2d)=0
YED = R Aa − P1a − P2 (a + d8) a + 2d
a
RA
d
d
YED
（3）X形结点
当结点上无荷载时: S1=S2 , S3=S4
（4）K形结点
当结点上无荷载时 S1≠S2 , S3=－S4
返5回
S1 S2
图a L形结点
S1
S2
S3
图b T形结点
S1
S3
S1
α
S3
S4
图c X形结点
S2
S2
α
S4
返6回
图d K形结点
§5－3 截 面 法
1. 截面法的概念：
截面法是作一截面将桁架分成两部 分，任取一部分为隔离体（含两个以上 的结点），用平衡方程计算所截杆件的 内力（一般内力不超过三个）。
可首先求出S1 P
P
Y1 S1 ∽ r S2
A
A x
a
C
②
d
C
(2)改用力矩式平衡方程 将力S1在B点分解为X1、Y1
由∑MC=0 一次求出
Pd X1 = h
返4回
6 .几种特殊结点及零杆
（1）L形结点
当结点上无荷载时: S1=0, 内力为零的杆称为零杆。 S2=0
（2）T形结点
当结点上无荷载时: S3=0
1
第五章
§5-1 §5-2 §5-3 §5-4 §5-5
静定平面桁架
平面桁架的计算简图 结点法 截面法 截面法和结点法的联合运用 组合结构的计算
2
§5－2 结点法 1. 求桁架内力的基本方法： 结点法和截面法。 2. 结点法： 所取隔离体只包含一个结点，称为结点法。 3. 预备知识：在计算中，经常需要把斜杆的内力S分 Y。
Y α
S
解为水平分力X和竖向分力 则由比例关系可知
S X Y = = L Lx Ly
⌒
X
L
α
Lx
Ly
S
在S、 X、Y三者中，任知其一 便可求出其余两个，无需使用 3 三角函数。
⌒
5. 计算中的技巧
当遇到一个结点上未知力均为斜向时，为简化计算：
(1)改变投影轴的方向
B
① b h
由∑X=0
∽ X1 B
YEF SEF
∽
XEF
∽
SED
SCD a RA d d YED
XED
9
（2）投影法
Ⅱ
求DG杆内力 作Ⅱ—Ⅱ截面， 取左部分为隔离体。 由∑Y=0 有
Ⅱ
RA－P1－P2－P3+YDG=0
YDG
YDG=SDGsinα=－(RA－P1－P2－P3)
RA
XDG
10
3 . 几点结论
杆件一次不能多于三个(特殊情况例外)。 时， 应用结点法；若只求个别杆件内力， 用截面法。 合杆件的内力求出，然后再对各简单桁架 进行分析(见图)。
3×8－SDE×2=0 SED=12kN(拉） 再考虑结点D、E的平 衡可求出各链杆的内力。
-6
19 返回
3. 分析受弯杆件
取AC杆为隔离体， 考虑其平衡可求得：
A
12kN
F
8kN C 6kN V=3kN C
HC =12kN
HC=12kN←
5kN
6kN
VC=3kN↑
B
6kN 12 3kN
8kN
A
1kN 6kN 4 0 6
2 .截面法据所选方程类型的不同 又分为力矩法、投影法。
返7回
（1）力矩法 以例说明
Ⅰ
设支反力已求出。 求EF、ED、CD三杆的 内力。作截面Ⅰ-Ⅰ，取左 部分为隔离体。
由∑ME=0 有 RAd－P1d－P2×0－SCDh=0 R d − P1d − P2 × 0 SCD = A （拉） h RA×2d－P1×2d－P2d+XEFH=0
11
(1) 用截面法求内力时，一般截断的
(2) 对于简单桁架，求全部杆件内力
(3) 对于联合桁架，先用截面法将联
ⅠC
A D
Ⅰ E
B
12 返回
特殊情况
取I-I截面左侧部分为隔离体由
∑M
K
= 0 可求得FNa
取I-I截面上侧部分为隔离体由
∑F
x
=0
可求得FNb
13
§5－4 截面法和结点法的联合应用
18 返回
例 5－2 分析此组合结构的内力。 解：
HA=0
6
-6
Ⅰ
13· 4
51
+12 2
12
VA=5kN
Ⅰ
RB=3kN
1. 由整体平衡 条件求出支反力。 2. 求各链杆的内 力：作Ⅰ－Ⅰ截面
HC SDE
VC +12
12
4 13· 6 12
拆开C铰和截断DE 杆，取右部为隔离体。 由∑MC=0 有
C
并可作出弯矩图。
0
0 M图 （kN·m)
20
例5-1 试求图a所示K式桁架中a、b杆的内力。
解：算法一 作截面I-I，取其左侧为隔离体。 由结点K
FNa = − FNc Fya = − Fyc
5F F ∑ Fy = 0 Fya = − 4 → FNa = − 12
由∑MC=0可求得FNb。
算法二：作截面II-II，取其左侧为隔离体。
∑ M D = 0 FNb = −
8F 3
14
§5-5 各式桁架比较
平跨中递增。构 造上各类杆长度相同，结点处各杆交角相同， 便于 标准化。因制作施工较为方便，铁路桥常采用。
15
抛物线形桁架
特点：内力分布均匀，在材料使用上经济。但构造上 复杂。大跨度桥梁(100—150m)及大跨度屋架(18-30m) 中常采用。
16
三角形桁架
特点：内力分布不均匀，弦杆内力两端大，两端结点 夹角甚小，构造复杂。因两斜面符合屋 顶要求，在屋 架中常采用。
17
§5－6 组合结构计算
1. 组合结构的概念： 由链杆（受轴向力）和梁式杆（受弯杆件 ）混合组成的结构。 2. 组合结构的计算步骤： （1）求支座反力； （2）计算各链杆的轴力； （3）分析受弯杆件的内力。
X EF = R A × 2d - P1 × 2d - P2 d （压） H
RA
Ⅰ
RB
YEF
SEF
由∑MD=0 得
∽ ∽
XEF
SED
XED
SCD
由∑MO=0 －RAa+P1a+P2(a+d)+YED(a+2d)=0
YED = R Aa − P1a − P2 (a + d8) a + 2d
a
RA
d
d
YED
（3）X形结点
当结点上无荷载时: S1=S2 , S3=S4
（4）K形结点
当结点上无荷载时 S1≠S2 , S3=－S4
返5回
S1 S2
图a L形结点
S1
S2
S3
图b T形结点
S1
S3
S1
α
S3
S4
图c X形结点
S2
S2
α
S4
返6回
图d K形结点
§5－3 截 面 法
1. 截面法的概念：
截面法是作一截面将桁架分成两部 分，任取一部分为隔离体（含两个以上 的结点），用平衡方程计算所截杆件的 内力（一般内力不超过三个）。
可首先求出S1 P
P
Y1 S1 ∽ r S2
A
A x
a
C
②
d
C
(2)改用力矩式平衡方程 将力S1在B点分解为X1、Y1
由∑MC=0 一次求出
Pd X1 = h
返4回
6 .几种特殊结点及零杆
（1）L形结点
当结点上无荷载时: S1=0, 内力为零的杆称为零杆。 S2=0
（2）T形结点
当结点上无荷载时: S3=0
1
第五章
§5-1 §5-2 §5-3 §5-4 §5-5
静定平面桁架
平面桁架的计算简图 结点法 截面法 截面法和结点法的联合运用 组合结构的计算
2
§5－2 结点法 1. 求桁架内力的基本方法： 结点法和截面法。 2. 结点法： 所取隔离体只包含一个结点，称为结点法。 3. 预备知识：在计算中，经常需要把斜杆的内力S分 Y。
Y α
S
解为水平分力X和竖向分力 则由比例关系可知
S X Y = = L Lx Ly
⌒
X
L
α
Lx
Ly
S
在S、 X、Y三者中，任知其一 便可求出其余两个，无需使用 3 三角函数。
⌒
5. 计算中的技巧
当遇到一个结点上未知力均为斜向时，为简化计算：
(1)改变投影轴的方向
B
① b h
由∑X=0
∽ X1 B
YEF SEF
∽
XEF
∽
SED
SCD a RA d d YED
XED
9
（2）投影法
Ⅱ
求DG杆内力 作Ⅱ—Ⅱ截面， 取左部分为隔离体。 由∑Y=0 有
Ⅱ
RA－P1－P2－P3+YDG=0
YDG
YDG=SDGsinα=－(RA－P1－P2－P3)
RA
XDG
10
3 . 几点结论
杆件一次不能多于三个(特殊情况例外)。 时， 应用结点法；若只求个别杆件内力， 用截面法。 合杆件的内力求出，然后再对各简单桁架 进行分析(见图)。
3×8－SDE×2=0 SED=12kN(拉） 再考虑结点D、E的平 衡可求出各链杆的内力。
-6
19 返回
3. 分析受弯杆件
取AC杆为隔离体， 考虑其平衡可求得：
A
12kN
F
8kN C 6kN V=3kN C
HC =12kN
HC=12kN←
5kN
6kN
VC=3kN↑
B
6kN 12 3kN
8kN
A
1kN 6kN 4 0 6
2 .截面法据所选方程类型的不同 又分为力矩法、投影法。
返7回
（1）力矩法 以例说明
Ⅰ
设支反力已求出。 求EF、ED、CD三杆的 内力。作截面Ⅰ-Ⅰ，取左 部分为隔离体。
由∑ME=0 有 RAd－P1d－P2×0－SCDh=0 R d − P1d − P2 × 0 SCD = A （拉） h RA×2d－P1×2d－P2d+XEFH=0
11
(1) 用截面法求内力时，一般截断的
(2) 对于简单桁架，求全部杆件内力
(3) 对于联合桁架，先用截面法将联
ⅠC
A D
Ⅰ E
B
12 返回
特殊情况
取I-I截面左侧部分为隔离体由
∑M
K
= 0 可求得FNa
取I-I截面上侧部分为隔离体由
∑F
x
=0
可求得FNb
13
§5－4 截面法和结点法的联合应用
18 返回
例 5－2 分析此组合结构的内力。 解：
HA=0
6
-6
Ⅰ
13· 4
51
+12 2
12
VA=5kN
Ⅰ
RB=3kN
1. 由整体平衡 条件求出支反力。 2. 求各链杆的内 力：作Ⅰ－Ⅰ截面
HC SDE
VC +12
12
4 13· 6 12
拆开C铰和截断DE 杆，取右部为隔离体。 由∑MC=0 有
C
并可作出弯矩图。
0
0 M图 （kN·m)
20