合肥工业大学-单服务员单队列系统仿真
Witness单服务台排队系统实验详细步骤

第8章 单服务台排队系统仿真排队系统是离散事件系统中的典型的问题。
制造系统、生产系统、服务系统、修理和维护设备、交通运输和物资材料管理系统都是典型的有形或无形的排队系统。
由于排队系统的应用已越来越广泛,排队特征、排队规则、服务机构也变得越来越复杂,用解析方法已无法求解,计算机模拟是求解排队系统和分析排队系统性能的非常有效的方法。
8.1 单服务台排队系统系统描述与仿真目的1)了解排队系统的设计。
2)熟悉系统元素Part 、Machine 、Buffer 、Variable 、Timeseries 的用法。
3)深入研究系统元素Part 的用法。
4)研究不同的顾客服务时间和顾客的到达特性对仿真结果的影响。
8.2 单服务台排队系统工作流程8.2.1 顾客到达特性在该系统中,顾客的到达规模(成批到达还是单个到达)是单个到达,顾客到达率Ai 服从均值为 的指数分布,即8.2.2 顾客服务时间顾客服务时间为Si ,服从指数分布,均值为 ,即 8.3 仿真模型的设计8.3.1 元素定义(Define )本系统的元素定义如表8-1所示。
表8-1 实体元素定义min 5=A βAs Ae Af ββ/)(-=)0(≥A min 4=s βSA Se Sf ββ/)(-=)0(≥S8.3.2 元素可视化(Display)设置各个实体元素的显示特征定义设置如图8-1所示。
图8-1 各个实体元素的显示特征1.Part元素可视化设置在元素选择窗口选择Guke元素,鼠标右键点击Display,跳出Display对话框(图8-2),设置它的Text(图8-3)、Icon(图8-4)。
图8-2 Display对话框图8-3 Display Text对话框图8-4 Display Icon对话框2.Buffer元素可视化设置在元素选择窗口选择Paidui元素,鼠标右键点击Display,跳出Display对话框(图8-2),设置它的Text、Icon、Rectangle(图8-5)。
第六章 排队系统仿真

6.2 排队系统的组成部分
– 6.2.1 输入过程 – 6.2.2 排队规则 – 6.2.3 服务机构
6.3 排队系统的特性 6.4 排队系统的类型
– 6.4.1 最简单的排队系统 – 6.4.2 M/M/n成批到达队列 – 6.4.3 M/M/1串联服务系统 – 6.4.4 M/M/n系统
Page 2
Page 8
第六章 排队系统仿真
6.2 排队系统的组成部分 排队系统又称服务系统。服务系统由服务机构和服务对象(顾客)构 成。服务对象到来的时刻和对他服务的时间(即占用服务系统的时间)都 是随机的。排队系统包括三个组成部分:输入过程、排队规则和服务机构 。
Page 9
第六章 排队系统仿真
6.2 排队系统的组成部分 输入过程 输入过程描述了顾客来源和顾客按怎样的规律到达排队系统。 顾客的来源可能是有限的,也可能是无限的;顾客是单个到达还是成 批到达;相继到达的顾客的时间服从什么样的概率分布,分布的参数是什 么,到达的间隔时间之间是否独立。 输入过程考察的是顾客到达服务系统的规律。它可以用一定时间内顾 客到达数或前后两个顾客相继到达的间隔时间来描述,一般分为确定型和 随机型两种。
∑µ
i =1 k
i
P 该顾 客在 k 个顾 客中 排在第 i个 位置 =
∞
∑µ
i =1
k
i 1 k +1 = k 2µ
平均逗留时间为 W = ∑ µ + 2µ P = µ = 2µ L = λ k (W ) ,带入上式,解出 W = k + 1 , µ > λ k 。
第六章 排队系统仿真
排队系统是由顾客和为顾客提供服务的服务台组成的系统。 排队系统是由顾客和为顾客提供服务的服务台组成的系统。顾客先进 入等待队列排队,然后接受服务台提供的服务。排队系统在服务业、物流 业及生产制造等行业有广泛的应用。例如,顾客到银行办理业务时先排队 ,然后在柜台(服务台)接受服务;物流系统中车辆(顾客)在装卸点排 队,然后接受装卸机械(服务台)的装卸服务;生产系统中产品(顾客) 在加工机器前排队,然后接受机器(服务台)的加工服务等。 排队系统由两方构成,一方要求得到服务,另一方设法给予服务。 排队系统由两方构成,一方要求得到服务,另一方设法给予服务。把 要求得到服务的人或物(设备)统称为顾客,给予服务的服务人员或服务机 构统称为服务员或服务台(有时服务员专指人,而服务台是指给予服务的设 备)。顾客与服务台就构成一个排队系统,或称为随机服务系统。显然,缺 少顾客和服务台任何一方都不会形成排队系统。
单服务台排队系统仿真

单服务台排队系统仿真单服务台排队系统是指在一个服务台只有一个服务员的情况下,客户需要按顺序等待服务的系统。
本文将介绍一个针对单服务台排队系统的仿真模型。
在设计仿真模型之前,我们需要确定一些重要的参数。
首先是服务时间,即每个客户接受服务所需要的时间。
服务时间可以通过实际观察数据或者估算得出。
其次是到达间隔时间,即每个客户到达的时间间隔。
到达间隔时间可以通过实际观察数据或者使用随机数生成器进行模拟。
首先,我们需要创建一个事件队列来模拟客户的到达和离开。
事件队列是一个按照发生时间顺序排序的队列,每个事件都包含两个属性:时间和类型。
接下来,我们创建一个时钟来记录仿真进行的时间。
初始时,时钟指向第一个到达事件的时间。
然后,我们从事件队列中取出第一个事件,并更新时钟指向该事件的时间。
如果当前事件类型是到达事件,我们需要进行如下操作:首先,模拟下一个客户到达的时间,并将该事件添加到事件队列中。
然后,判断当前是否有客户正在接受服务。
如果没有,我们将当前事件类型设置为离开事件,并模拟该客户的服务时间和离开时间,并将该离开事件添加到事件队列中。
如果有客户正在接受服务,我们将当前事件类型设置为到达事件。
如果当前事件类型是离开事件,我们需要进行如下操作:首先,更新服务台的空闲状态。
然后,判断是否还有等待服务的客户。
如果有,我们将当前事件类型设置为离开事件,并模拟下一个客户的服务时间和离开时间,并将该离开事件添加到事件队列中。
如果没有等待服务的客户,我们将当前事件类型设置为到达事件。
重复上述步骤,直到事件队列中没有事件为止。
最后,我们可以根据仿真的结果,比如客户的等待时间、服务时间和系统繁忙率等指标,来评估和优化该排队系统的性能。
通过以上的模型,我们可以对单服务台排队系统进行仿真,并评估其性能。
我们可以通过改变服务时间、到达间隔时间等参数,来探究不同情况下系统的表现和优化方案。
同时,我们还可以根据仿真结果,对系统进行调整和改进,以提高客户的满意度和服务效率。
单服务员排队模型在青藏电务管理系统中的应用

摘 要: 工 申请信 息的提 交和反馈是 青藏电务管理 系统的重要 功能 。青 藏电务段 管理 系统 实行 电务 施
段、 车间、 区三级管理 , 工 当很 多工 区向车间和电务段提 交施 工 申请 时, 将涉及到信 息的排 队 问题。 由于 有大量的信 息需要 传递 , 且在 服务 器和客 户端使 用不同的操作 系统 , 还有不兼容 问题 。 因此 需要 消息 中
收 稿 日期 :0 6—0 —3 20 3 0
基 金 项 目 : 家 自然 基 金 资 助 项 目(0 7 0 5 国 6 52 3 )
基金项 目: 通信与信息系统北京市重点实验室资助项 目(D 0 0 0 1 ) J 1 0 4 5 3
维普资讯
第1 4卷
青藏铁路 即将于今年全线通车 , 高效性和可靠性 已成为 电务信息管理 系统 的主要 目标 。由于在青藏 电务管理 系统 中采 用服务器/ 客户端 的模式 , 客户端需要 向服务 器端提交 大量 的申请 信息 , 服务器 端不可能 在同一时 间处理完所有 的 申请信 息 , 以存 在信息的排队论 问题。而且服务器端和客户端 的操作系统分 别是 Ln x和 Wi o s 还存 在其他方面 的不兼 容 , 所 iu n w, d
第六章-排队系统建模与仿真(New)
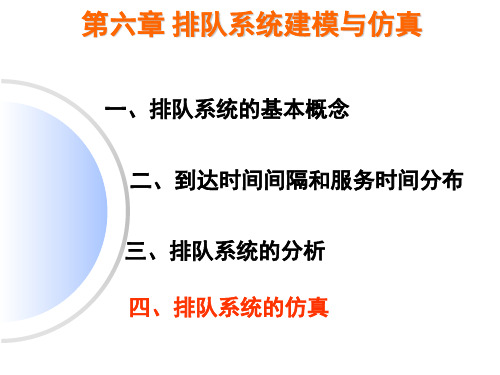
出现的次数ft 38 25 17 9 6 5 0 100
三、排队系统的分析
解:(1)计算 平均到达速度:
nfn 2.1人 / 小时
100
平均手术时间: 平均服务速度:
Ts
tft 100
0.37小时 / 人
1 1 2.5人 / 小时
Ts 0.4
(2)取λ=2.1,μ=2.5,通过统计检验方法的检验,可以认 为病人到达数服从参数为2.1的泊松分布,手术时间服从参数 为2.5的负指数分布。
服务员空闲否?
Y
开始服务
经过Si
服务完毕
N
排队等待
顾客离去
四、排队系统的仿真
仿真方法:手工仿真 仿真初始条件:系统中没有顾客,即:排队的队列中没有顾客等待,服务台 无服务对象。 仿真开始:以第一个顾客到达时刻为仿真的起始点。
四、排队系统的仿真
? 事件何时出现?
在仿真中,通过随机数来产生!
四、排队系统的仿真
• M——负指数分布 • M/M/1表示相继到达时间为负指数分布,服务时 间为负指数分布,单服务设备的模型。
三、排队系统的分析
1 单服务台M/M/1模型(M/M/1/∞/ ∞/FCFS)
(1)到达模式。动态实体源是无限的,动态实体单个 到达,相互独立,一定时间的到达数服从泊松分布。
(2)排队规则。单对,且队列长度没有限制,先到先 服务。
混合制
队列的度量
队列的度量
(1)服务强度
1
T0
n
1 Ts
ns
(2)实际业务强度u‘
u' ' 1
(3)服务设备利用率
n
三、排队系统的分析
随机排队系统的运行指标: 在系统中动态实体数量的期望值Ls, 在系统队列中等待的动态实体数量(队列长度)的 期望值Lq。 在系统中动态实体逗留时间的期望值Ws, 在队列中动态实体等待时间(排队时间)的 期望值Wq。
MMN排队系统建模与仿真

.《系统仿真与matlab》综合试题....................... 错误!未定义书签。
M/M/N 排队系统的模拟仿真 (1)摘要 (1)1. 问题分析 (3)2. 模型假设 (4)3. 符号说明 (5)4. 模型准备 (5)4.1 排队系统的组成和特征 (5)4.1.1输入过程 (6)4.1.2排队规则 (6)4.1.3服务过程 (7)4.1.4排队系统的主要指标 (7)4.2输入过程与服务时间的分布 (8)4.2.1负指数分布 (8)4.2.2泊松分布 (8)4.3生灭过程 (9)5. 标准M/M/N模型 (11)5.1多服务台模型准备 (11)5.2多服务台模型建立 (12)5.2.1服务利用率 (12)5.2.2平均排队长 (13)5.2.3平均队长 (13)5.2.4平均等待时间 (14)6. 程序设计 (14)6.1动画流程图 (14)6.2 M/M/N流程图 (15)7. 程序运行实例介绍 (16)7.1动画实例讲解 (16)7.2M/M/N排队系统实例讲解 (18)8. 程序实现难点和模型评价 (21)8.1程序实现难点 (21)8.2模型评价 (21)9. 参考文献 (21)10. 附录 (22)10.1动画实现的核心程序 (22)10.2 M/M/N模型计算主要程序 (32)M/M/N 排队系统的模拟仿真摘要排队是在日常生活中经常遇到的事,由于顾客到达和服务时间的随机性,使得排队不可避免。
因此,本文建立标准的M/M/N模型,并运用Matlab软件,对M/M/N排队系统就行了仿真,从而更好地深入研究排队问题。
问题一,基于顾客到达时间服从泊松分布和服务时间服从负指数分布,建立了标准的M/M/N模型。
运用Matlab软件编程,通过输入服务台数量、泊松分布参数以及负指数分布参数,求解出平均队长、服务利用率、平均等待时间以及平均排队长等重要指标。
然后,分析了输入参数与输出结果之间的关系。
lecture 3- simulation by__ hand系统建模与仿真

第3步:构造仿真表。(手算仿真的本质是仿 真表格)
顾客
1
到达 间隔
0
到达 时间
服务 时间
4
等待 时间
服务 结束 时间
逗留 服务员 时间 空闲时间
第4步:对每个顾客进行仿真。
顾客
到达 间隔
到达 时刻
服务时间
等待 服务结 时间 束时间
逗留 时间
服务员空闲 时间
1 2 3 4 5 6
1 1 6 3 7
订购量=上限订货水平-盘点库存量+短缺量;订货将 首先满足短缺;
(M,N)库存模型的研究目的: 对不同的M,N组合,哪个成本最小?
系统模型
状态:
库存水平
事件:
“ 顾客需求”事件(出库) “库存检查”事件(清库) “订单到达”事件 (入库)
(M,N)库存系统仿真(冰箱) Example 2.4
2.确定仿真的每个输入数据(主要指概率分 布). 3.构造仿真表 4.对仿真表的每一行,进行仿真。计算统计数 据. 5. 仿真完毕,累加数据,计算性能指标。
教材例题:单队列排队系统
顾客以1-8min分钟等概率分布到达 Checkout Counter(见Table2.6)。 服务员的服务时间为1-6min(概率见 Table2.7) 要求:仿真6个顾客,以分析系统的性能。
仿真目的: 预测系统的期末平均库存、平均缺货数量等。
日需求量的随机数字分配表-表2.19
需求 概率 累计需求 随机数字 分配区间
0 1 2
3
0.1 0.25 0.35
0.21
0.1 0.35 0.7
0.91
01-11 11-35 36-70
合肥工业大学大学生创新性计划项目成果汇总表

计算机与信息学院2012年度校级大学生创新性实验计划项目成果汇
总表
项目名称
车门安全开关避险系统的研究与开发基于物联网的物流在线监管追溯系统基于单片机的无线定位装置自习室信息数字化管理系统
新型无线无声鼠标
基于物联网的公共交通客运车辆监管基于单片机的无线温控及其应用运用单片机设计出电子秤
高效率音频放大器设计与制作红外线火
灾预警系统
基于传感器的家居环境温度检测便携装
置
室内分布式系统3G基站程序仿真
可测量人体心率的多功能手表
无线电子黑板
基于大气偏振模式特征感知的导航系统
设计
智能阳台控制系统的研发检验漏水及控制水量校正电路
项目负
责人
所在年级专业
09级电子信息
项目成果
功能实现,较完整
通过李仕川物联碉0级功能实现,较完整良好09级电子信
功能实现,较完整良好
息
徐礼超
工程
功能实现,较完整良好09级电子信
庞洪岗息功能没有实现不通过工程
傅江彪功能基本实现通过09级龟子科
刘晓星功能基本实现通过与授术
陈贵良
09绷汞科
功能实现,较完整良好
学
李屹坤
09驾戯|信
功能没有实现不通过
息
蒋明哲工程功能没有实现不通过09级电子信
汤婿女青息功能基本实现通过
工程
刘让WWW终止通信JMS10-1功能基本实现
朱宏声通过
険
通信工程10」功能实现,有创新点
张雪麒
班
优秀
陈鹏通信工程10'1功能实现,较完整良好
班
、帘/亠工口功能实现,有创新点
朱召鹏通宿工程优秀
班
杨智为计算机10」班功能没有实现不通过。
数学建模:排队系统仿真

4、外部信号分路形式:需添加外部信号产生器和 分路器进行连接,根据外部信号产生器产生结果, 决策出口。
2、带概率分路形式:等概率的随机 选择分路模块的各出口。
Exopential:指数分布。(Mean:数
学期望值,即顾客达到平均间隔时间)
Uniform:均匀分布。(Mean:均匀
分布的数学期望值)
Constant:常数值。(Mean:对应常
数值,每隔常数值时间发出一个顾客)
打开“Time-Based Entity Generator”对话框
双击“Time-Based Entity Generator”模块(基 于时间的实体生成器)
双击“Discrete Event Signal to Workspace” 模块打开对话框
把排队离开顾客数记录信息赋值给变量 paiduilikaigukeshujilu 存储格式为数组(Array)
在Matlab窗口下敲入变量名称”paiduilikaigukeshujilu”打回车,即显示模拟时间 内的顾客累计离开数。
服务台模块(共 3 种)
打开“Single Server”对话框
双击“Single Server”模块
服务时间,所有顾客服务时间均一样
Service time from(服务时间形式):选择”signal port t”时,需要为其指定服务时间分布。
随机数产生器
将随机数产生器 (Events-Based random number)拖 动到模型编辑器中, 并同服务器(Single Server)的 t 端口建立 输入连接。
排队系统的建模仿真研究

( ) 件 表 : 件 表 列 举 了 系 统 运 行 过 程 所 发 生 的各 种 7事 事
1 排 队 系 统
1 1 基 本 概 念 . .
也就 是仿真要 解决 的问题 , 是系统调 研和建模 的依据 。 这
2 2 系统 调 研 . ’
排 队 是 生 活 中 经 常 出 现 的 现 象 。如 到 银 行 办 理 业 务 ,
系 统 结 构 调 研 的 目 的 是 为 了 深 入 了 解 系 统 的 总 体 流
13 排 队 系统 常 用 的 输 出 参 数 .
n
① 平 均 等 待 时 间 d i ∑ L —l m J i
n —一
() 1
() 2
() 3
真 的 专 业 性 特 点 , 真 模 型 和 运 行 模 型 的 工 作 一 般 由 专 业 仿 的 仿 真 人 员 来 做 。 但 是 对 系 统 的 分 析 常 常 需 要 仿 真 需 求 方 的 密 切 配 合 。为 了 使 仿 真 需 求 方 了 解 仿 真 的 一 般 过 程 , 以 配 合 仿 真 前 期 的 调 研 工 作 , 以 将 上 述 调 研 所 需 获 取 的 数 可 据 和参数 整理并列 表 , 仿真需 求 方进 行针 对性 的 填写 , 由 以 保 证资料 的完整性 和准确性 。 系 统 模 型 的形 式 可 以是 多 样 的 , 文 字 叙 述 型 、 程 图 有 流 建 立 系 统 的 流 程 图 模 型 。 流 程 图 模 型 中 应 包 含 有 : 时 实 临
单服务排队系统仿真实验

模型3D图见下图所示:
六、结果分析
教材中仿真结果可知,其30次的仿真情况可知,该系统在 每天8h的工作时间内,平均队长不超过2,最大队长只有8, 每个顾客的平均被服务时间小于4min,而顾客的平均排队 纯等待时间大多数抽样都小于2min,只有个别抽样接近 5min。可见,该系统的服务状况良好,顾客基本得到及时 的服务。从业务员的工作量看,一个业务员每天大约要处 理100多(输出结果的抽样小于115)位顾客的银行业务, 其利用率,也就是其处理业务时间与总工作时间的比在 63.1%-82.5%之间。
根据表格调查的数据计算出该排队系统的M/M/ 1 模型(见上 个模块的解说),并用仿真软件Flexsim6.0版运行30次得统 计数据如下: 举例其中一次的仿真的统计数据的图形: (1)排队等待的相关统 计数据表图
2)服务处理的相关统计数据表图
LOGO
本报告研究对象为中国银行重庆大学处分行某一服务窗口, 数据取自银行内唯一非现金业务柜台。研究对象的选取虽然 不是最典型的,但是综合考虑了研究地域范围和小组成员作 业时间有限,另有其他方案由于各种原因无法进行,故选择 离学习型较近的有代表性的中国银行中的服务窗口作为最史最为悠久的银行之
本排队系统用: 顾客的数目 到达模式 服务模式 系统容量 排队规则
为探求此排队系统的规律, 首先需确定顾客流在一定 时间内到达的概率分布函数。抵达本银行服务窗口的顾客 流量大体上服从Poisson 分布, 顾客流抵达银行便按先后 顺序排队, 进入单服务窗口,即排队论中的M/M/1系统。 所谓M/M/1排队系统是指这样的一种排队模型: 顾客的到 达为Poisson 流, 银行对每位顾客的服务时间独立同负指 数分布,顾客按先到先服务( FCFS) 规则排队, 当顾客到 达时, 若服务台正在忙碌, 则顾客排成一个队列等待服务。 在实际工作中,客户存取款、转账汇款、缴费、理财、开 销户等业务是随机发生的,客户办理业务的种类不同,服 务时间必然有所差别。
第8章+单服务台排队系统仿真

Fuwuyuan的PartQueue属性设置
选择Fuwuyuan的PartQueue属性
Direction设置为:Diagona Display Size为:10
4.Variable元素Jifen0的可视化设置
Jifen0 的display对话框
Jifen0的text属性设置 Jifen0的Value属性设置 Width:9 Decimal:2
Type:Active Input to Model.Inter Arrival:1.0 Lot Size:1
点击Input to Model.To…,输入:PUSH to SHIP,点击“OK”按钮
点击Actions on Create,输入:Jifen0 = Jifen0 + NPARTS (Paidui),点击 “OK”按钮
• 用同样的方法完成其它元素的定义
添加Guke元素,点击“Create” 按钮
元素添加完成时的元素选择窗口
2.元素可视化的设置
• 1.part元素可视化的设置
(1)Guke 的可视化设置
Guke的display 对话框
选择Guke 元素的text属性项, 点击 进入text属性设置
Guke 元素的Icon属性
Paidui的PartQueue属性设置
选择Paidui的PartQueue属性
设置Direction为Diagona Display Sizห้องสมุดไป่ตู้:10
3.Machine元素Fuwuyuan的可视化设置
Fuwuyuan的display对话框
Fuwuyuan的text属性设置
Fuwuyuan的icon属性设置
1.定义元素
• 在系统布局窗口右键添加元素
单服务台排队系统离散事件系统仿真实验

单服务台排队系统离散事件系统仿真实验在单服务台排队系统中,存在一个服务台和一些顾客。
顾客根据一定的到达规律到达系统,并进行排队等候服务。
每个顾客需要一定的时间来接受服务,然后离开系统。
在整个过程中,需要记录每个顾客的到达时间、完成时间、等候时间等信息,以评估系统的性能。
以下是进行单服务台排队系统离散事件系统仿真实验的步骤:1.制定实验目标和假设:明确实验的目标和假设,例如评估平均等候时间、系统的利用率等。
2.定义实验参数:设置模拟的时间段、顾客到达的规律、服务时间分布等。
可以根据实际情况选择不同的参数值。
3.创建顾客队列:使用队列数据结构来表示顾客队列,顾客到达时将其加入队列中。
4.初始化系统状态:初始化服务台为空闲状态,设置初始时钟为0。
5.模拟顾客到达:根据到达规律随机生成顾客到达的时间,并将其加入队列。
6.模拟服务过程:当服务台空闲时,从队列中取出下一个顾客进行服务。
根据服务时间分布生成一个随机的服务时间,将服务结束时间设置为当前时钟加上服务时间。
7.记录统计信息:记录每个顾客的到达时间、服务开始时间、完成时间、等候时间等信息。
同时记录系统的状态信息,如系统空闲时间、顾客总数等。
8.更新系统状态:更新服务台的状态,如果队列为空,则服务台为空闲状态,否则继续进行下一个顾客的服务。
9.终止条件判断:判断是否继续模拟,可以根据实验目标设定条件,如模拟时间达到一定阈值或顾客数量达到一定数量。
10.实验结果分析:根据记录的统计信息,计算实验结果,如平均等候时间、系统的利用率等。
通过对比不同参数设置下的实验结果,评估系统的性能情况,并对系统设计进行优化。
在实验过程中,需要注意选择合适的离散事件系统仿真工具,如MATLAB、Python等,进行系统的建模和实验的实施。
同时,应合理选择实验参数和统计指标,以保证实验结果的可靠性和可解释性。
通过进行单服务台排队系统离散事件系统仿真实验,可以评估系统的性能,并对系统设计进行优化,提高系统的效率和顾客的满意度。
合肥工业大学操作系统精品课程试题资料

合肥工业大学操作系统精品课程试题资料合肥工业大学操作系统精品课程习题资料习题一1、多道程序设计是指( )A.在实时系统中并发运行多个程序B.在分布系统中同一时刻运行多个程序C.在一台处理机上同一时刻运行多个程序D.在一台处理机上并发运行多个程序2、LINUX的基本特点是()A.多用户,单任务,实时 B.多用户,多任务,交互式C.单用户,单任务,分时D.多用户,多任务,分时3、从用户的观点看,操作系统是 _______ 。
A.用户与计算机之间的接口 B.控制和管理计算机资源的软件C.合理的组织计算机工作流程的软件 D.由若干层次的程序按一定的结构组成的有机体4.操作系统中采用多道程序设计技术提高了CPU 和外部设备的 ______ 。
A.利用率 B.可靠性 C.稳定性D.兼容性5.允许多个用户以交互方式使用计算机的操作图C.屏蔽所有中断 D.改变磁盘空间分配位图9、如何理解虚拟机的概念?10、处理为什么要区分核心态和用户态两种方式?在什么情况下进行转换?11、试比较操作系统的原语和事务两个概念的异同点。
习题二1、设某类资源有5个,由3个进程共享,每个进程最多可申请()个资源而使系统不会死锁。
A. 1 B. 2 C. 3D. 42.在分时系统中,假设就绪队列中有10个进程,系统将时间片设为200ms,CPU进行进程切换要花费10ms。
则系统开销所占的比率约为()A.1% B.5% C.10% D.20%3.进程从等待状态进入就绪状态可能是由于()A.现运行进程运行结束 B.现运行进程执行了P操作C.现运行进程执行了V操作D.现运行进程时间片用完4、通过破坏产生死锁的四个必要条件之一,可以保证不让死锁发生。
其中采用资源按顺序申请法,是破坏()A.互斥条件B.不可剥夺条件C.部分分配条件D.循环等待条件5.操作系统中,对信号量S的P原语操作定义中,使进程进入相应等待队列等待的条件是()A.S>0 B.S=0C.S<0D .S!=06.计算机操作系统中,若P、V操作的信号量S 初值为2,当前值为-1,则表示有()等待进程A.0个B.1个C.2个D.3个7.LINUX的基本特点是()A.多用户,单任务,实时B.多用户,多任务,交互式C.单用户,单任务,分时D.多用户,多任务,分时8.一个进程被唤醒,意味着()A.该进程重新占有了CPU B.进程状态变为就绪C.它的优先权变为最大D.其PCB移到就绪队列的队首9、设有三个作业J1、J2、J3,它们的到达时间分别为8:00、8:45、9:30,计算时间分别为2小时、1小时、0.25小时如下表,它们在一台处理机上按单道运行,若采用响应比高者优先的调度算法,这三个作业的执行次序是()A. J1、J2、J3 B. J2、J1、J3 C. J2、J3、J1 D. J3、J2、J110、将以下有关死锁的问题及其解决方式用直线连起来预防死锁避免死锁检测死锁解除死锁银行家算法最小生成树法资源分配图资源分配序列11、下面有关进程概念的描述正确的是()A.进程是程序的一次执行过程;B.进程是一段简单程序,是指令的静态集合;C.进程是可并发执行的程序,是在一个数据集合上的一次执行过程;D.进程是可以和其它计算并发执行的一个计算;12、在多进程并发的环境中,可以通过分时的方法在单个物理CPU上运行多个进程,在一段时间内,宏观上每个进程都在执行,好像每个进程都拥有一个CPU一样,此即操作系统中广泛使用的所谓()技术。
MM1排队系统仿真matlab试验报告

M/M/1排队系统实验报告一、实验目的本次实验要求实现M/M/1单窗口无限排队系统的系统仿真,利用事件调度法实现离散事件系统仿真,并统计平均队列长度以及平均等待时间等值,以与理论分析结果进行对比。
二、实验原理根据排队论的知识我们知道,排队系统的分类是根据该系统中的顾客到达模式、服务模式、服务员数量以及服务规则等因素决定的。
1、顾客到达模式设到达过程是一个参数为入的Poisson过程,则长度为t的时间内到达k个呼p (t)=(入“ e 4叫的概率服从Poisson分布,即k k!,k = 01,2, .. ,其中入>0为一常数,表示了平均到达率或Poisson呼叫流的强度。
2、服务模式设每个呼叫的持续时间为二,服从参数为N的负指数分布,即其分布函数为P{ X < t } = 1 - e-k t > 03、服务规则先进先服务的规则(FIFO)4、理论分析结果入P = Q = -2—在该M/M/1系统中,设口,则稳态时的平均等待队长为Q 1-P,顾客上乙T T T T =的平均等待时间为N-九。
三、实验内容M/M/1排队系统:实现了当顾客到达分布服从负指数分布,系统服务时间也服从负指数分布,单服务台系统,单队排队,按FIFO (先入先出队列)方式服务。
四、采用的语言MatLab语言源代码:clear;clc;%M/M/1排队系统仿真SimTotal=input('请输入仿真顾客总数SimTotal='); %仿真顾客总数;Lambda=0.4; % 到达率 Lambda;Mu=0.9; % 服务率 Mu;t_Arrive=zeros(1,SimTotal);t_Leave=zeros(1,SimTotal);ArriveNum=zeros(1,SimTotal);LeaveNum=zeros(1,SimTotal);Interval_Arrive=-log(rand(1,SimTotal))/Lambda;% 到达时间间隔Interval_Serve=-log(rand(1,SimTotal))/Mu;% 服务时间 t_Arrive(1)=Interval_Arrive(1);% 顾客到达时间ArriveNum(1)=1;for i=2:SimTotalt_Arrive(i)=t_Arrive(i-1)+Interval_Arrive(i);ArriveNum(i)=i;endt_Leave(1)=t_Arrive(1)+Interval_Serve(1);% 顾客离开时间 LeaveNum(1)=1;for i=2:SimTotalif t_Leave(i-1)<t_Arrive(i)t_Leave(i)=t_Arrive(i)+Interval_Serve(i);elset_Leave(i)=t_Leave(i-1)+Interval_Serve(i);endLeaveNum(i)=i;endt_Wait=t_Leave-t_Arrive; %各顾客在系统中的等待时间 t_Wait_avg=mean(t_Wait);t_Queue=t_Wait-Interval_Serve;%各顾客在系统中的排队时间 t_Queue_avg=mean(t_Queue);Timepoint=[t_Arrive,t_Leave];%系统中顾客数随时间的变化Timepoint=sort(Timepoint);ArriveFlag=zeros(size(Timepoint));% 至 U达时间标志CusNum=zeros(size(Timepoint));temp=2;CusNum(1)=1;for i=2:length(Timepoint)if (temp<=length(t_Arrive))&&(Timepoint(i)==t_Arrive(temp)) CusNum(i)=CusNum(i-1)+1;temp=temp+1;ArriveFlag(i)=1;elseCusNum(i)=CusNum(i-1)-1;endend%系统中平均顾客数计算Time_interval=zeros(size(Timepoint));Time_interval(1)=t_Arrive(1);for i=2:length(Timepoint)Time_interval(i)=Timepoint(i)-Timepoint(i-1);endCusNum_fromStart=[0 CusNum];CusNum_avg=sum(CusNum_fromStart.*[Time_interval 0] )/Timepoint(end);QueLength=zeros(size(CusNum));for i=1:length(CusNum)if CusNum(i)>=2QueLength(i)=CusNum(i)-1;elseQueLength(i)=0;endendQueLength_avg=sum([0 QueLength].*[Time_interval 0] )/Timepoint(end);% 系统平均等待队长%仿真图figure(1);set(1,'position',[0,0,1000,700]);subplot(2,2,1);title('各顾客到达时间和离去时间’);stairs([0 ArriveNum],[0 t_Arrive],'b');hold on;stairs([0 LeaveNum],[0 t_Leave],'y');legend('到达时间‘,‘离去时间’); hold off;subplot(2,2,2);stairs(Timepoint,CusNum,'b')title('系统等待队长分布');xlabel('时间');ylabel('队长’); subplot(2,2,3);title('各顾客在系统中的排队时间和等待时间’);stairs([0 ArriveNum],[0 t_Queue],'b');hold on;stairs([0 LeaveNum],[0 t_Wait],'y');hold off;legend('排队时间‘,‘等待时间’);%仿真值与理论值比较disp(['理论平均等待时间t_Wait_avg=',num2str(1/(Mu-Lambda))]);disp(['理论平均排队时间t_Wait_avg=',num2str(Lambda/(Mu*(Mu-Lambda)))]);disp(['理论系统中平均顾客数=',num2str(Lambda/(Mu-Lambda))]);disp(['理论系统中平均等待队长=',num2str(Lambda*Lambda/(Mu*(Mu-Lambda)))]);disp(['仿真平均等待时间t_Wait_avg=',num2str(t_Wait_avg)])disp(['仿真平均排队时间t_Queue_avg=',num2str(t_Queue_avg)])disp(['仿真系统中平均顾客数=',num2str(CusNum_avg)]);disp(['仿真系统中平均等待队长=',num2str(QueLength_avg)]);五、数据结构1.仿真设计算法(主要函数)利用负指数分布与泊松过程的关系,产生符合泊松过程的顾客流,产生符合负指数分布的随机变量作为每个顾客的服务时间:Interval_Arrive=-log(rand(1,SimTotal))/Lambda;% 至U 达时间间隔,结果与调用exprnd(1/Lambda, m)函数产生的结果相同Interval_Serve=-log(rand(1,SimTotal))/Mu;% 服务时间间隔七_A「后8(1)=加七8~31_八「用8(1);%顾客到达时间时间计算t_Wait=t_Leave-t_Arrive; %各顾客在系统中的等待时间t_Queue=t_Wait-Interval_Serve; %各顾客在系统中的排队时间由事件来触发仿真时钟的不断推进。
单服务员排队模型及其蒙特卡洛模拟

单服务员排队模型及其蒙特卡洛模拟
张建航;李宗成;宋晓峰
【期刊名称】《现代电子技术》
【年(卷),期】2006(29)24
【摘要】单服务员的排队模型(M/M/1模型)是排队论中重要的排队系统.介绍排队论的基本概念,讨论和研究单服务员排队模型的过程和基本原理,通过数学计算得出单服务员排队模型中重要的运行指标.针对典型实例,借助于计算机软件包Matlab 6.5进行了蒙特卡洛模拟.
【总页数】3页(P44-45,48)
【作者】张建航;李宗成;宋晓峰
【作者单位】西安通信学院,陕西,西安,710106;西安通信学院,陕西,西安,710106;西安通信学院,陕西,西安,710106
【正文语种】中文
【中图分类】O226;TP311.12
【相关文献】
1.单服务员排队模型在青藏电务管理系统中的应用 [J], 周旭;张振江
2.单服务员排队模型某些指标的优化研究 [J], 尹向飞;陈焕然
3.多服务台等待制排队模型M/G/c/∞的蒙特卡洛模拟 [J], 王培勋;王志芳
4.服务员强制休假的M/M/1排队模型主算子的点谱 [J], 阿里米热·阿布拉
5.具有备用服务员和不耐烦顾客的排队模型及其仿真 [J], 潘恒毅
因版权原因,仅展示原文概要,查看原文内容请购买。
单服务排队系统MATLAB仿真程序

单服务台系统MATLA仿真一、引言排队是日常生活中经常遇到的现象。
通常, 当人、物体或是信息的到达速率大于完成服务的速率时, 即出现排队现象。
排队越长, 意味着浪费的时间越多, 系统的效率也越低。
在日常生活中, 经常遇到排队现象, 如开车上班、在超市等待结账、工厂中等待加工的工件以及待修的机器等。
总之, 排队现象是随处可见的。
排队理论是运作管理中最重要的领域之一, 它是计划、工作设计、存货控制及其他一些问题的基础。
Matlab 是MathWorks 公司开发的科学计算软件, 它以其强大的计算和绘图功能、大量稳定可靠的算法库、简洁高效的编程语言以及庞大的用户群成为数学计算工具方面的标准, 几乎所有的工程计算领域,Matlab 都有相应的软件工具箱。
选用Matlab 软件正是基于Matlab 的诸多优点。
二、排队模型三.仿真算法原理(1)顾客信息初始化根据到达率入和服务率卩来确定每个顾客的到达时间间隔和服务时间间隔。
服务间隔时间可以用负指数分布函数exprnd() 来生成。
由于泊松过程的时间间隔也服从负指数分布, 故亦可由此函数生成顾客到达时间间隔。
需要注意的是exprnd()的输入参数不是到达率入和服务率卩而是平均到达时间间隔1/入和平均服务时间1/卩。
根据到达时间间隔,确定每个顾客的到达时刻.学习过C语言的人习惯于使用FOR循环来实现数值的累加,但FOR循环会引起运算复杂度的增加而在MATLAB仿真环境中,提供了一个方便的函数cumsum() 来实现累加功能读者可以直接引用对当前顾客进行初始化。
第 1 个到达系统的顾客不需要等待就可以直接接受服务其离开时刻等于到达时刻与服务时间之和。
(2)进队出队仿真在当前顾客到达时刻,根据系统内已有的顾客数来确定是否接纳该顾客。
若接纳则根据前一顾客的离开时刻来确定当前顾客的等待时间、离开时间和标志位;若拒绝,则标志位置为0.流程图如下:四、程序实现单服务台服务,服务参数M/M/1,入=卩=,排队规则为FIFO,以分为单位,仿真时间240 分钟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机仿真单服务员单队列系统仿真实验班级:机设13-4班学号: ***********名:***授课教师:**日期: 2016年4月13日实验二单服务员单队列系统仿真实验一、实验目的通过实验了解离散事件系统仿真一般过程,了解离散事件系统中典型的单服务员单队列系统的仿真一般过程,了解不同分布随机数的计算机实现过程,了解事件扫描法在离散事件系统中的应用。
二、实验要求通过实验了解离散事件系统仿真一般过程,了解离散事件系统中典型的单服务员单队列系统的仿真一般过程,了解不同分布随机数的计算机实现过程,了解事件扫描法在离散事件系统中的应用。
同学能在参考源程序的基础上,独立编写C源程序,或其他高级语言程序,能正确计算仿真结果,并对结果进行分析。
三、参考C语言程序#include "stdio.h"#include "math.h"FILE * fp;float seed;int sstop,ip;float miat,msvt,svt;float tval,tlq,tmen;float sigma,time,lqt,lst,tle;float wkst[100];float b,mq,s,f,nd,ts,is,ta,ia,clock,fel[3];int imevt,numevs;void rptgen() //报告生成子程序{ float rho,w,pc,amts,amta,lq,l,wq;rho=b/clock;w=s/nd;pc=f/nd;amts=ts/is;amta=ta/ia;lq=tlq/clock;l=tmen/clock;wq=tlq/nd;if((fp=fopen("fz22","wb"))==NULL){printf("cannot open file\n");}printf("time=%f\n",time);fprintf(fp,"miat=%f,msvt=%f,sigma=%f,time=%f\n",miat,msvt,sigma,time) ;fprintf(fp,"rho=%f,mq=%f,pc=%f,clock=%f\n",rho,mq,pc,clock);fprintf(fp,"nd=%f,amts=%f,amta=%f\n",nd,amts,amta);fprintf(fp,"lq=%f,l=%f,wq=%f,w=%f\n",lq,l,wq,w);}float rand() //随机数生成子程序{float a,c,m;float rand1;a=25173.0;c=13849.0;m=65535.0;seed=(seed*a+c)-m*(int)((seed*a+c)/m);if(seed==0.0) seed=1.0;rand1=seed/m;return rand1;}float normal(float ex,float stdx) //正态分布随机数生成子程序//float ex,stdx;{float sum,x;int i;float r;sum=0.0;for(i=1;i<=12;i++){r=rand();sum=sum+r;}x=stdx*(sum-6.0)+ex;printf=(“normal=%\n”,x);return x;}float expent(float ex) //指数分布随机数生成子程序{float r,x;r=rand();x=-ex*log(r);return x;}void initlz() //系统初始化子程序{float aat;clock=0.0; //置仿真时钟为.0imevt=0; //假定系统在时间为空闲lqt=0.0; //置以下各统计量初值为lst=0.0;tle=0.0;b=0.0;mq=0.0;s=0.0;f=0.0;nd=0.0;ts=0.0;is=0.0;ta=0.0;ia=0.0;tlq=0.0;tmen=0.0;aat=expent(miat);fel[1]=clock+aat; //产生第一次到达,并安排在FEL()fel[2]=1.0e+30; //置FEL()为无穷大,表示系统空闲时,不会发生离开事件}void timadv() //时间推进子程序{ float fmin;int i;fmin=1.0e+29;imevt=0;for (i=1;i<=numevs;i++) //搜索FEL以找出下一事件{if(fel[i]>=fmin) continue;fmin=fel[i];imevt=i;}if(imevt>0) //判断有无将来事件{clock=fel[imevt]; //设定仿真时钟为下一事件时间,事件将在时间FEL (IMEVT)发生tval=clock-tle;tlq=tlq+lqt*tval;tmen=tmen+(lqt+lst)*tval;}else{rptgen(); //若将来事件为空,调用报告子程序sstop=1;}}void arrvl() //到达事件子程序{float aat,svt;if(lst==1.0) goto loop2; //检查服务员是否被占lst=1.0; //若服务员空闲,修改系统状态并记录新的顾客的到达时间wkst[ip]=clock;svt=normal(msvt,sigma); //为新到达顾客产生服务时间并安排离开事件fel[2]=clock+svt;ts=ts+svt;is=is+1.0; //修改累积统计量tle=clock;if(lqt>mq)mq=lqt;goto loop3;loop2: lqt=lqt+1.0; //若服务员被占,修改系统状态,记录新的顾客到达时间及系统中顾客数ip=lqt+lst;if(ip>100) goto loop4; //现设系统容量为人,若超过即给出报告wkst[ip]=clock;b=b+(clock-tle); //修改累积统计量tle=clock;if(lqt>mq) mq=lqt;loop3: aat=expent(miat); //产生一个到达时间间隔并安排下一到达事件ta=ta+aat;ia=ia+1.0;fel[1]=clock+aat;goto loop31;loop4: printf("overflow in array wkst");rptgen();sstop=1;loop31:return;}void dpart() //离开事件子程序{ int i,i1;float rt,svt;b=b+(clock-tle); //修改累积统计量tle=clock;rt=clock-wkst[ip];s=s+rt;nd=nd+1.0;if(rt>=4.0)f=f+1.0; //记录(累计)停留时间大于等于的顾客数if(lqt>1.0) //检查队列空否{for(i=1;i<=lqt;i++){i1=i+1; //此时至少有一个顾客在队列中,使每个顾客向前移动一个位置wkst[i]=wkst[i1];}lqt=lqt-1.0; //队列中的顾客数减svt=normal(msvt,sigma); //对将被服务的顾客产生一个新的服务,时间且安排下一个//离开事件fel[2]=clock+svt;}else{ //队列空,服务员空闲,下一离开事件置在无穷大时间lst=0.0;fel[2]=1.0e+30;}}void main() //主程序{ip=0;seed=2.0; //输入随机数种子miat=10.0; //msvt=3.0;sigma=1.0;time=500.0;numevs=2; //确定事件总数为initlz(); //调用初始化子程序sstop=0; //程序终止变量,sstop=0,程序循环,sstop=1,程序终止loop: timadv(); //调用时间推进子程序if(sstop==1) goto loopp; //判断sstop=1,程序终止if (imevt==1) //IMEVT=1为到达,IMEVT=2为离开{arrvl(); //调用到达事件子程序if(sstop==1) goto loopp; //判断sstop=1,程序终止goto loop; //程序循环执行}if (imevt==2) dpart(); //调用离开事件子程序if (clock<time) goto loop; //判断仿真是否结束,若未结束继续循环执行rptgen(); //当仿真结束时生成报告输出loopp:return;}四、实验报告1.给出RAND()子程序输出的10个数据,以及对应的符合正态分布和指数分布的随机数。
2.分别输入下列三组数据,给出相应的计算结果(包括服务员忙度、平均服务时间、平均到达间隔时间、顾客在系统中平均时间、系统中平均顾客数、队列中平均顾客数、停留4个小时单位以上的顾客比例等),并加以文字说明。
(1)输入数据为:MIAT=10,MSVT=5,SIGMA=2,TIME=100计算结果为:平均到达间隔时间miat=10.000000平均服务时间msvt=5.000000服务时间标准差sigma=2.000000仿真停止时间time=100.000000服务员忙度rho=0.482677到当前时间为止等待队列的最大长度mq=2.000000停留4个小时单位以上的顾客比例pc=0.454545仿真时钟当前时间clock=114.048820到当前时间为止离开的顾客数nd=11.000000平均服务时间amts=4.362051平均到达间隔时间amta=9.973741队列中平均顾客数lq=1.026730系统中平均顾客数l=1.509407顾客在队列中平均时间wq=10.645217顾客在系统中平均时间w=3.600372(2)输入数据为:MIAT=10,MSVT=3,SIGMA=1,TIME=100计算结果为:平均到达间隔时间miat=10.000000平均服务时间msvt=3.000000服务时间标准差sigma=1.000000仿真停止时间time=100.000000服务员忙度rho=0.242204到当前时间为止等待队列的最大长度mq=1.000000停留4个小时单位以上的顾客比例pc=0.111111仿真时钟当前时间clock=108.105759到当前时间为止离开的顾客数nd=9.000000平均服务时间amts=2.909301平均到达间隔时间amta=11.269994队列中平均顾客数lq=0.682092系统中平均顾客数l=0.924297顾客在队列中平均时间wq=8.193123顾客在系统中平均时间w=2.863684(3)输入数据为:MIAT=10,MSVT=30,SIGMA=2,TIME=100计算结果为:平均到达间隔时间miat=10.000000平均服务时间msvt=30.000000服务时间标准差sigma=2.000000仿真停止时间time=100.000000服务员忙度rho=0.998272到当前时间为止等待队列的最大长度mq=8.000000 停留4个小时单位以上的顾客比例pc=1.000000 仿真时钟当前时间clock=119.530281到当前时间为止离开的顾客数nd=4.000000平均服务时间amts=29.953489平均到达间隔时间amta=9.972269队列中平均顾客数lq=5.037513系统中平均顾客数l=6.035784顾客在队列中平均时间wq=150.533829顾客在系统中平均时间w=15.594049。
